Integrity Analysis of the Sheath Considering Temperature Effect under Deep and Large-Scale Multi-Section Hydraulic Fracturing
Abstract
:1. Introduction
2. Basic Mechanical Model and Hypothesis
- 1.
- The components of sheath are mixed evenly. Therefore, the sheath is isotropic.
- 2.
- The cement can be regarded as an ideal elastic-plastic material under the high temperature and pressure environment.
- 3.
- Before the formation–sheath–casing system bears the load, it is intact. The cementing quality is good, and both formation–sheath and sheath–casing interfaces maintain deformation coordination before yielding of the sheath occurs.
- 4.
- The yielding of the sheath follows the Mohr–Coulomb yielding criterion.
- 5.
- The temperature of the outer wall of the sheath is always the same as the conditions of the formation in which it is located, and the temperature change of the inner wall varies periodically with the fracturing process.
3. Analytical Method
4. Theoretical Analysis of Cement Sheath Integrity
4.1. Temperature Requirement of the Sheath Considering Only Temperature Effect
4.2. Simultaneous Action of Temperature and Internal Pressure
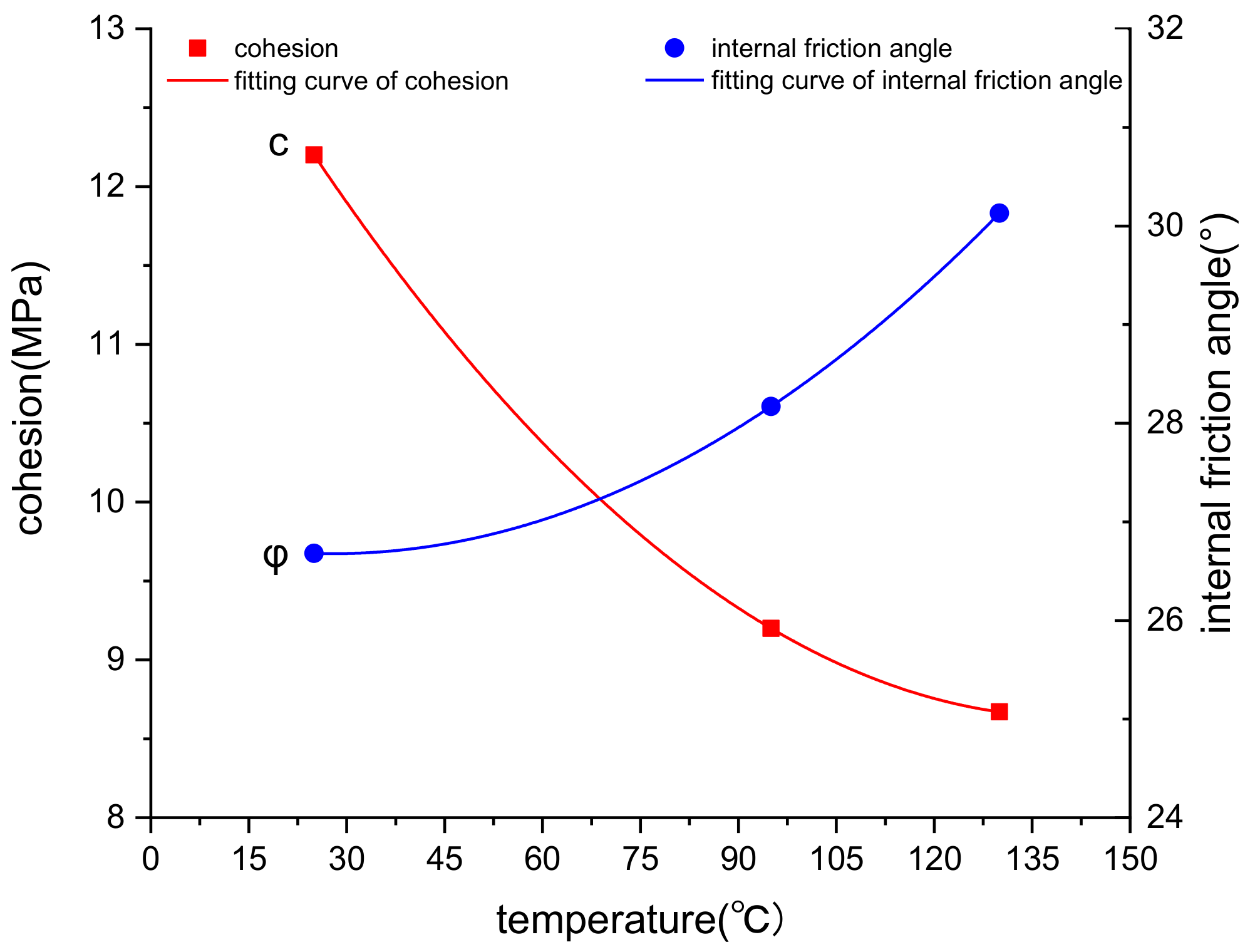
5. The Influence of Temperature on Cohesion and Internal Friction Angle of Cement
5.1. Samples Preparation
5.2. Tests Results and Analysis
6. Analysis Based on Multiple Factors
- When temperature alone acts:
- When fracturing and temperature cycling act simultaneously:
- (1)
- The case of temperature as stress
- (2)
- The influence of temperature on the properties of cement materials:
- (3)
- The result of the combined effect of temperature:
7. An Engineering Example
8. Conclusions
- 1.
- When only the temperature inside the sheath varies cyclically, the range of cyclical changes in temperature brought about by the operation process has a negligible effect on the sheath.
- 2.
- When the fracturing pressure and temperature act together on the sheath, the effect of temperature on it is reflected in two aspects. The temperature stress due to the existence of the difference between the internal and external surface causes the maximum cyclic load declining; however, the change in temperature causes the material parameters of the cement to change.
- 3.
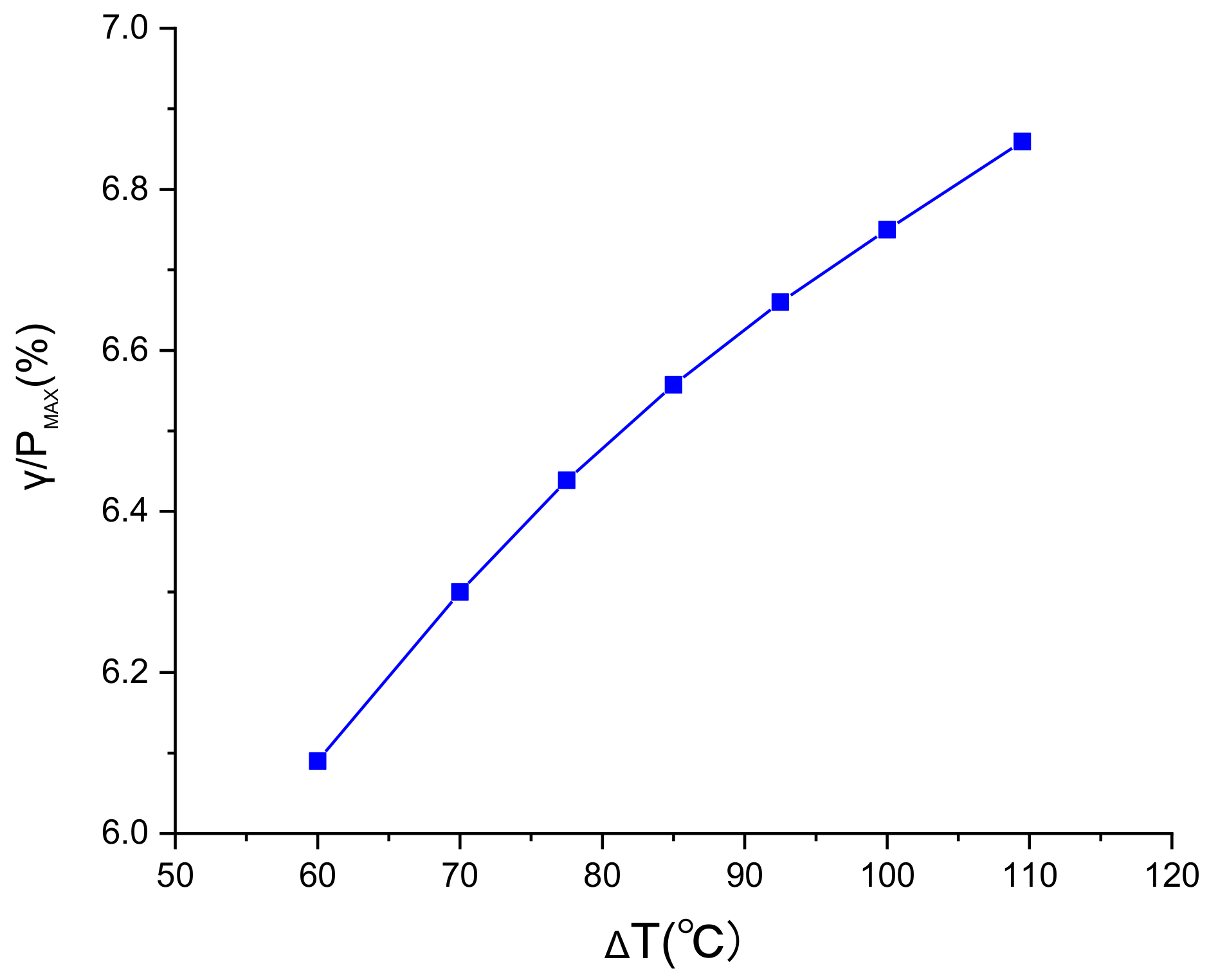
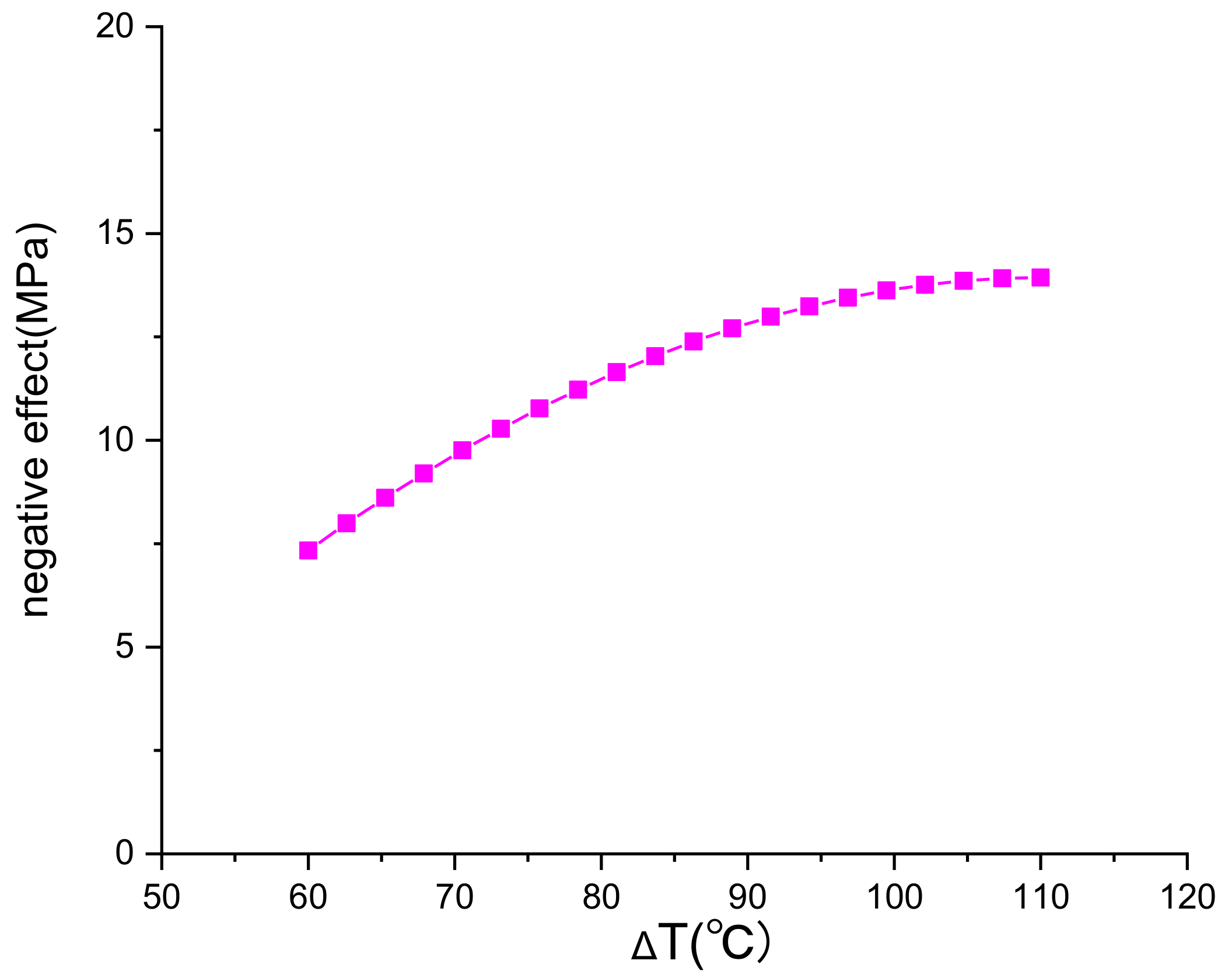
- The effect of temperature stress on sheath is proportional to the ∆T. The larger the temperature difference is, the greater the γ is. When the ∆T ranges from 70 to 110 °C, the negative effect of temperature stress on the total stress accounts for about 6–7%.
- 4.
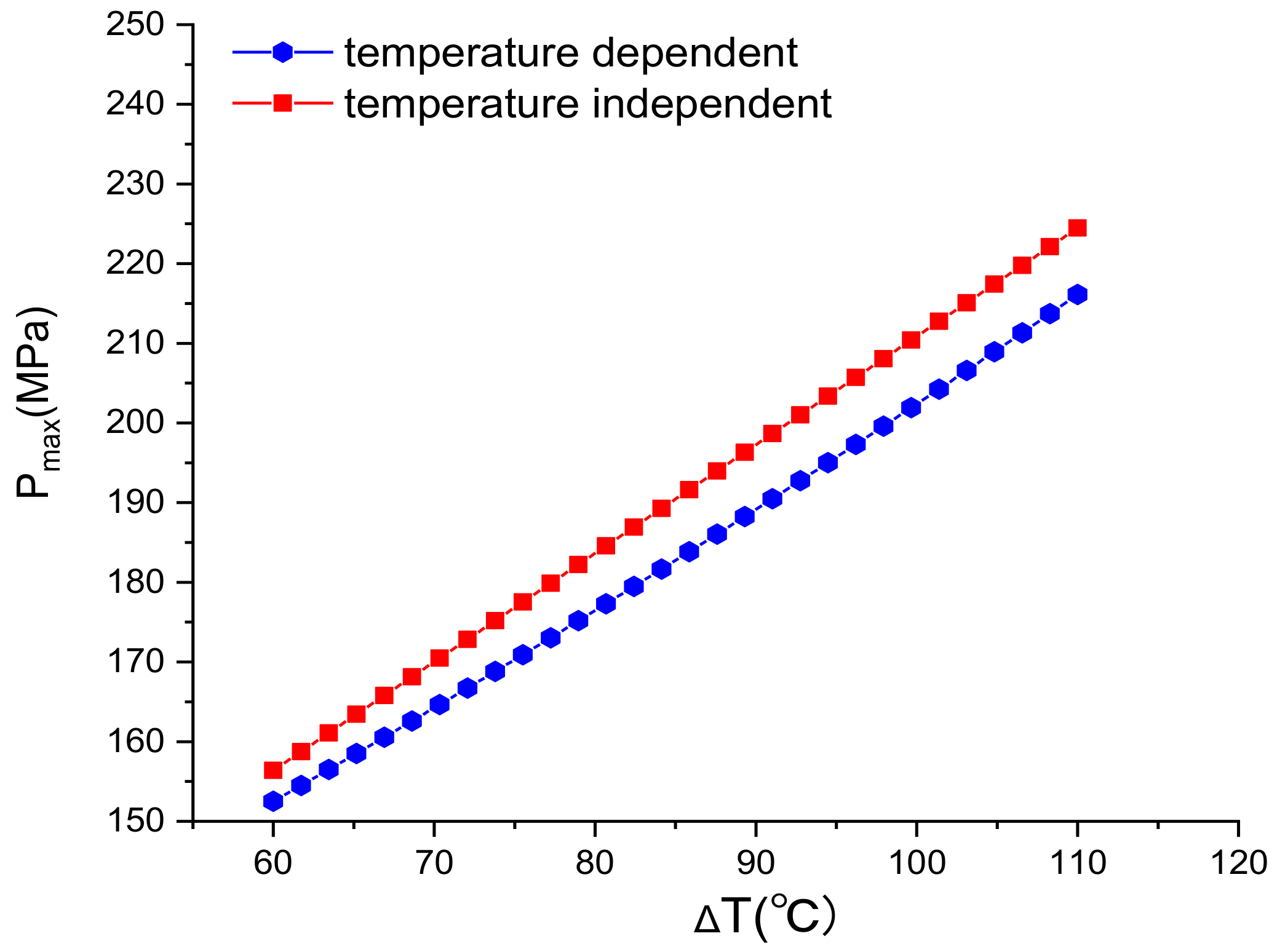
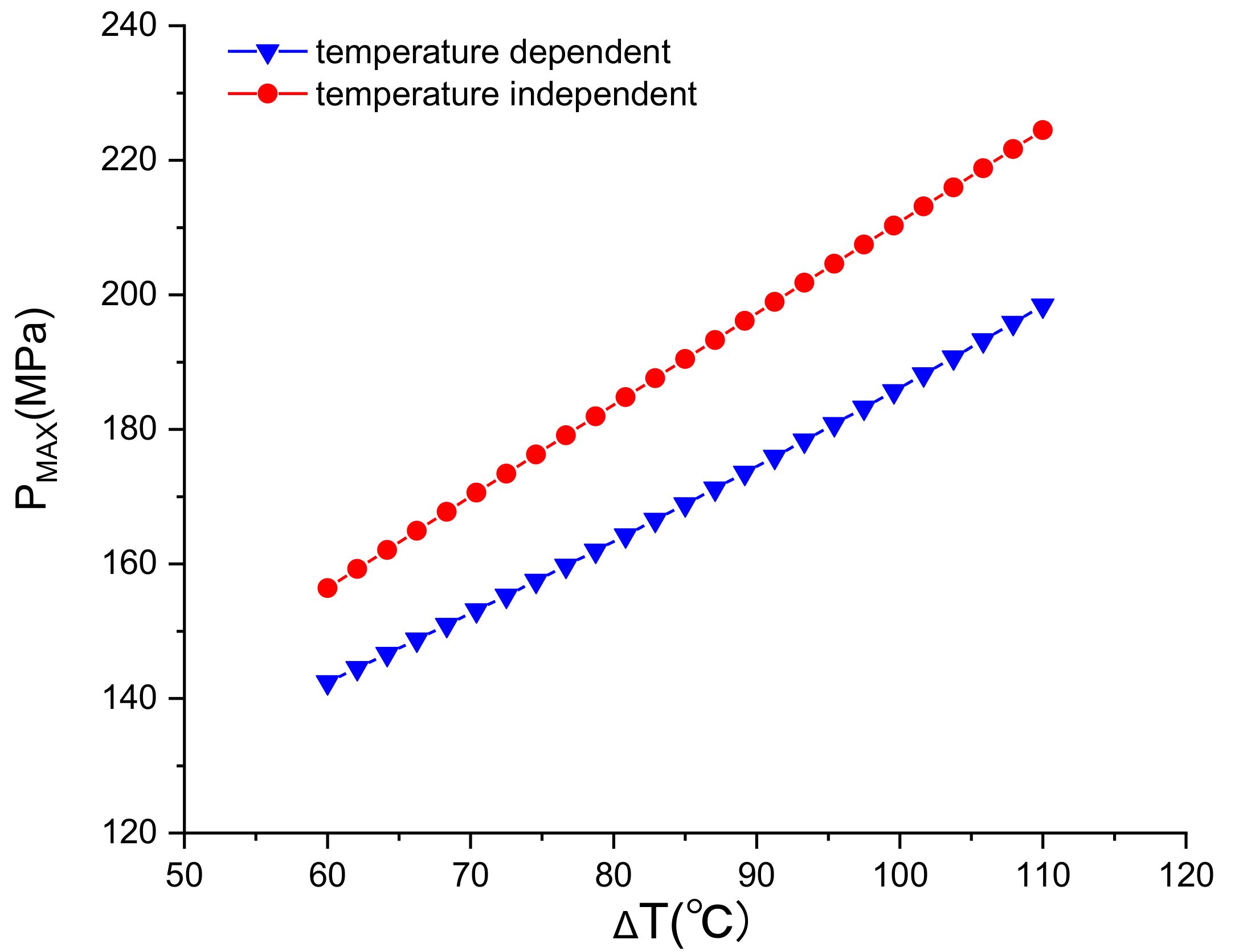
- The influence of temperature on the material properties of cement is as follows: with the rising of temperature, the cohesion of cement declines, and the internal friction angle increases. The plastic characteristics of the cement can be enhanced. With the change of ∆T, the negative effect of the Pmax ascends slowly.
- 5.
- Comprehensive consideration of the role of temperature on the sheath, their total bad impact grows with the increase of the temperature difference. In the range of 60 to 110 °C, the temperature-induced reduction of the bearing capacity accounted for 10% to 12% of the total bearing capacity of the sheath. Therefore, during fracturing design, the engineer should reasonably design the fracture scheme according to the formation temperature and the characteristics of the cement.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shadravan, A.; Schubert, J.; Amani, M.; Teodoriu, C. HPHT cement sheath integrity evaluation method for unconventional wells. In Proceedings of the SPE International Conference on Health, Safety, and Environment, Long Beach, CA, USA, 17–19 March 2014. [Google Scholar]
- Wang, W.; Taleghani, A.D. Cement sheath integrity during hydraulic fracturing: An integrated modeling approach. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 4–6 February 2014. [Google Scholar]
- Vrålstad, T.; Skorpa, R.; Opedal, N.; Andrade, J.D. Effect of thermal cycling on cement sheath integrity: Realistic experimental tests and simulation of resulting leakages. In Proceedings of the SPE Thermal Well Integrity and Design Symposium, Banff, AB, Canada, 23–25 November 2015. [Google Scholar]
- Xu, H.; Peng, N.; Ma, T.; Yang, B. Investigation of thermal stress of cement sheath for geothermal wells during fracturing. Energies 2018, 11, 2581. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Zeng, Y.J.; Zhang, Q.Q. Experimental study on mechanical properties of oil well cement under high temperature. J. China Univ. Pet. 2018, 42, 88–95. [Google Scholar]
- Lian, W.; Li, J.; Tao, Q.; Du, J.; Wang, L.; Xi, Y. Formation mechanism of continuous gas leakage paths in cement sheath during hydraulic fracturing. Energy Sci. Eng. 2020, 8, 2527–2547. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.I.U.; Zhengqing, A.I.; Zaoyuan, L.I.; Xiaoyang, G. Discussion on the Influence Factors of Cementing Circulating Temperature. J. Southwest Pet. Univ. (Sci. Technol. Ed.) 2012, 34, 154–158. [Google Scholar]
- Kuanhai, D.; Xie, P.; Yue, Y.; Dezhi, Z.; Qiong, L.; Yuanhua, L. Study on the effect of interface failure between casing and cement sheath on casing stress under non-uniform in-situ stress. Appl. Math. Model. 2021, 91, 632–652. [Google Scholar] [CrossRef]
- Zhao, H.; Wen, D. Study on influencing factors of temperature field distribution in deep water cementing. Shipbuild. China 2019, 60, 135–145. [Google Scholar]
- Kruszewski, M.; Montegrossi, G.; Ramírez Montes, M.; Wittig, V.; Gomez Garcia, A.; Sánchez Luviano, M.; Bracke, R. A wellbore cement sheath damage prediction model with the integration of acoustic wellbore measurements. Geothermics 2019, 80, 195–207. [Google Scholar] [CrossRef]
- Wang, C.; Liu, S.; Zhai, Y.; Qu, Y.; Wen, M. Discussion on circulating temperature during cementing. Nat. Gas Explor. Dev. 2015, 38, 70–76. [Google Scholar]
- Yu, Y.; Ding, Z.; Zhang, C.; Zhang, H.; Guo, J. A cement slurry used at ultra-high circulation temperature of 210 °C. Drill. Fluid Completion Fluid 2019, 36, 349–354. [Google Scholar]
- Ye, Z.; Zhu, Z.; Wu, P.; Liu, W.; Xu, Z. The influence of temperature, pressure and pH value on cement curing. China Cem. 2010, 11, 58–62. [Google Scholar]
- Li, Q.H.; Yao, Y.; Sun, B.; Li, Z.J. Investigation on behavior of thermal expansion of hydraulic cement paste. J. Build. Mater. 2007, 6, 631–635. [Google Scholar]
- Deng, K.; Liu, W.; Liu, B.; Lin, Y.; Singh, A. Repairing force for deformed casing shaping with spinning casing swage and damage behaviour of cement sheath. Appl. Math. Model. 2019, 70, 425–438. [Google Scholar] [CrossRef]
- Walske, M.L.; McWilliam, H.; Doherty, J.; Fourie, A. Influence of curing temperature and stress conditions on mechanical properties of cementing paste backfill. Can. Geotech. J. 2015, 53, 88–95. [Google Scholar] [CrossRef]
- Gao, B. The mechanism of radial separation of cement sheath and casing during temperature cycling. Pet. Sci. 2006, 3, 45–50. [Google Scholar]
- Al-Yami, A.S.; Wagle, V.B.; Abdurrahman, R.; Taoutaou, S. Engineered fit-for-purpose cement system to withstand life-of-the-well pressure and temperature cycling. J. China Univ. Pet. 2018, 42, 88–95. [Google Scholar]
- Sabins, F. Ultra-Lightweight Cement; Office of Scientific & Technical Information Technical Reports; Department of Energy (DOE) Office: Texas, TX, USA, 2002. [Google Scholar]
- Wang, C.; Chen, X.; Zhou, W.; Wang, Y.; Xue, Y.; Luo, F. Working mechanism of nano-SiO2 sol to alleviate the strength declineof oil well cement under high temperature. Nat. Gas Ind. 2019, 6, 517–523. [Google Scholar] [CrossRef]
- Wu, Y.; Patel, H.; Salehi, S. Parametric study of mechanical stresses within cement sheath in geothermal wells. Geothermics 2021, 90, 102000. [Google Scholar] [CrossRef]
- Kuanhai, D.; Wanying, L.; Tianguo, X.; Dezhi, Z.; Ming, L.; Yuanhua, L. Experimental study the collapse failure mechanism of cemented casing under non-uniform load. Eng. Fail. Anal. 2017, 73, 1–10. [Google Scholar] [CrossRef]
- Zheng, Y.; Xu, B.; Pu, J.; Li, M.; Wang, B. Mechanical behavior of cementing system under different conditions. Nat. Gas Ind. 2017, 37, 119–123. [Google Scholar]
- Park, M.; Min, S.; Lim, J.; Choi, J.M.; Choi, H. Applicability of cement-based grout for ground heat exchanger considering heating-cooling cycles. Sci. China Technol. Sci. 2018, 7, 1661–1667. [Google Scholar] [CrossRef]
- Hager, I. Behaviour of cement concrete at high temperature. Bull. Pol. Acad. Sci. Tech. Sci. 2013, 61, 145–154. [Google Scholar] [CrossRef]
- Patel, H.; Salehi, S. Structural integrity of liner cement in oil & gas wells: Parametric study, sensitivity analysis, and risk assessment. Eng. Fail. Anal. 2021, 122, 105203. [Google Scholar] [CrossRef]
- De Andrade, J.; Sangesland, S. Cement sheath failure mechanisms: Numerical estimates to design for long-term well integrity. J. Pet. Sci. Eng. 2016, 147, 682–698. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, R.; Zeng, H.; Zeng, Y.; Zhang, L.; Zhang, J.; Li, X. Mechanical characteristics of well cement under cyclic loading and its influence on the integrity of shale gas wellbores. Fuel 2019, 250, 132–143. [Google Scholar] [CrossRef]
- Arjomand, E.; Bennett, T.; Nguyen, G.D. Evaluation of cement sheath integrity subject to enhanced pressure. J. Pet. Sci. Eng. 2018, 170, 1–13. [Google Scholar] [CrossRef]
- Bois, A.-P.; Garnier, A.; Galdiolo, G.; Laudet, J.-B.; Total, S.A. Use of a mechanistic model to forecast cement-sheath integrity. SPE Drill. Complet. 2012, 27, 303–314. [Google Scholar] [CrossRef]
- Yan, X.; Jun, L.; Gonghui, L.; Qian, T.; Wei, L. A new numerical investigation of cement sheath integrity during multistage hydraulic fracturing shale gas wells. J. Nat. Gas Sci. Eng. 2018, 49, 331–341. [Google Scholar] [CrossRef]
- Koiter, W.T. General theorems for elastic-plastic solids. Prog. Solid Mech. 1960, 6, 167–221. [Google Scholar]
- Melan, E. Theorie statisch unbestimmter systeme aus idealplasticschen baustoff. Sitz. Akad. Wiss. 1938, 195, 145–195. [Google Scholar]
- Neal, B.G. The Plastic Methods of Structural Analysis; Chapman and Hall Ltd.: London, UK, 1956. [Google Scholar]
- Zarka, J.; Casier, J. Cyclic loading on elastic-plastic structures. Mech. Today 1979, 6, 93–198. [Google Scholar]
- El Bitouri, Y.; Jamin, F.; Pélissou, C.; El Youssoufi, M.S. Tensile and shear bond strength between cement paste and aggregate subjected to high temperature. Mater. Struct. 2017, 50, 234. [Google Scholar] [CrossRef] [Green Version]





| Cement Slurry System | Formula |
|---|---|
| High temperature and high-pressure resistant formula | G-grade oil well cement 35%SiO2 (silica powder) 6% SFP-1 4%DZJ-Y (fluid loss reducer) 0.2% SFP-2 42% H2O |
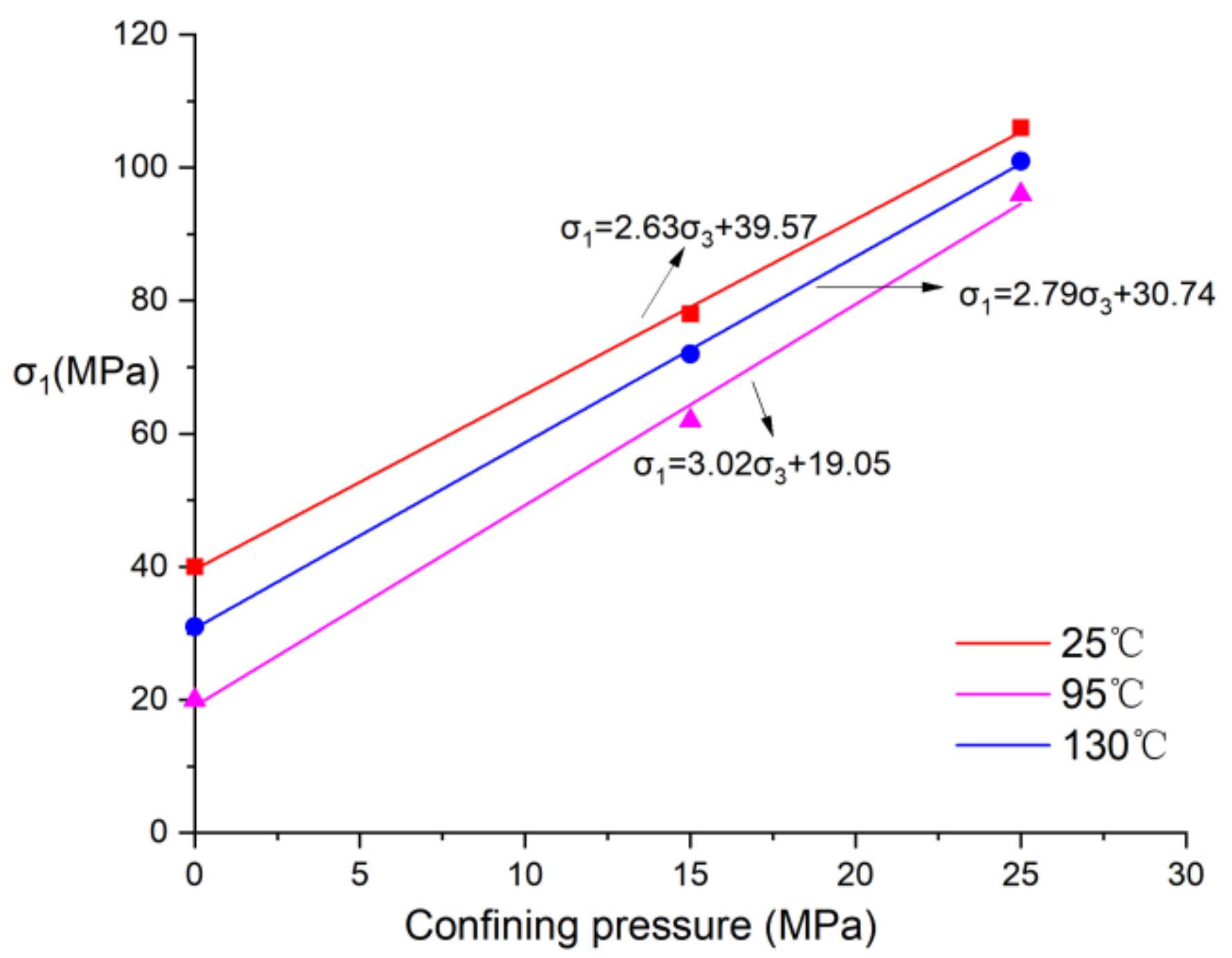
| Sample Number | Diameter (mm) | Height (mm) | Confining Pressure σ3(MPa) | σ1–σ3 (MPa) | μ | E (GPa) | Temperature (°C) |
|---|---|---|---|---|---|---|---|
| C-1-2 | 49.89 | 99.91 | 0 | 39.80 | 0.152 | 4.85 | 25 |
| C-1-7 | 50.01 | 100.07 | 15 | 63.23 | 0.133 | 6.86 | 25 |
| C-1-8 | 50.06 | 99.85 | 25 | 81.50 | 0.121 | 9.90 | 25 |
| C-1-3 | 49.92 | 99.85 | 0 | 30.96 | 0.124 | 4.32 | 95 |
| C-1-10 | 49.89 | 100.02 | 15 | 56.89 | 0.111 | 5.96 | 95 |
| C-1-18 | 49.96 | 100.02 | 25 | 76.02 | 0.103 | 8.14 | 95 |
| C-1-5 | 50.07 | 99.94 | 0 | 19.98 | 0.097 | 3.01 | 130 |
| C-1-6 | 50.01 | 100.00 | 15 | 47.11 | 0.075 | 3.96 | 130 |
| C-1-4 | 49.89 | 99.93 | 25 | 70.94 | 0.062 | 5.81 | 130 |
| Temperature (°C) | k | σc (MPa) | C (MPa) | ϕ (°) |
|---|---|---|---|---|
| 25 | 2.63 | 39.57 | 12.20 | 26.68 |
| 95 | 2.79 | 30.74 | 9.20 | 28.17 |
| 130 | 3.02 | 19.05 | 8.67 | 30.13 |
| Casing Parameters | Environmental Parameters | Structure Parameters |
|---|---|---|
| E1 = 210 GPa | Depth; 3533–5530 m | ai = 127.36 mm |
| bi = 139.7 mm | ||
| μ1 = 0.2 | P0 = 74–116 MPa | a = 139.7 mm |
| b = 233.45 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wang, L.; Yang, C.; Chang, X.; Guo, Y.; Bi, Z.; Yang, H. Integrity Analysis of the Sheath Considering Temperature Effect under Deep and Large-Scale Multi-Section Hydraulic Fracturing. Energies 2021, 14, 7162. https://doi.org/10.3390/en14217162
Zhang X, Wang L, Yang C, Chang X, Guo Y, Bi Z, Yang H. Integrity Analysis of the Sheath Considering Temperature Effect under Deep and Large-Scale Multi-Section Hydraulic Fracturing. Energies. 2021; 14(21):7162. https://doi.org/10.3390/en14217162
Chicago/Turabian StyleZhang, Xiaoyu, Lei Wang, Chunhe Yang, Xin Chang, Yintong Guo, Zhenhui Bi, and Hanzhi Yang. 2021. "Integrity Analysis of the Sheath Considering Temperature Effect under Deep and Large-Scale Multi-Section Hydraulic Fracturing" Energies 14, no. 21: 7162. https://doi.org/10.3390/en14217162
APA StyleZhang, X., Wang, L., Yang, C., Chang, X., Guo, Y., Bi, Z., & Yang, H. (2021). Integrity Analysis of the Sheath Considering Temperature Effect under Deep and Large-Scale Multi-Section Hydraulic Fracturing. Energies, 14(21), 7162. https://doi.org/10.3390/en14217162







