Egalitarian Kinetic Models: Concepts and Results
Abstract
:1. Introduction
1.1. Hierarchical Kinetic Models (HKM)
1.2. Egalitarian Kinetic Models (EKM)
1.2.1. EKM for Polymerization Reactions
1.2.2. EKM for Heterogeneous Catalytic Reactions
2. Goal of the Paper
- The structure of the mechanism: is the mechanism cyclic or acyclic?
- Reversibility of reactions: are the reactions reversible or irreversible?
- The type of reactor in which the reactions occur: i.e., a batch reactor (BR), or a steady-state CSTR.
3. Results
3.1. Irreversible Reactions
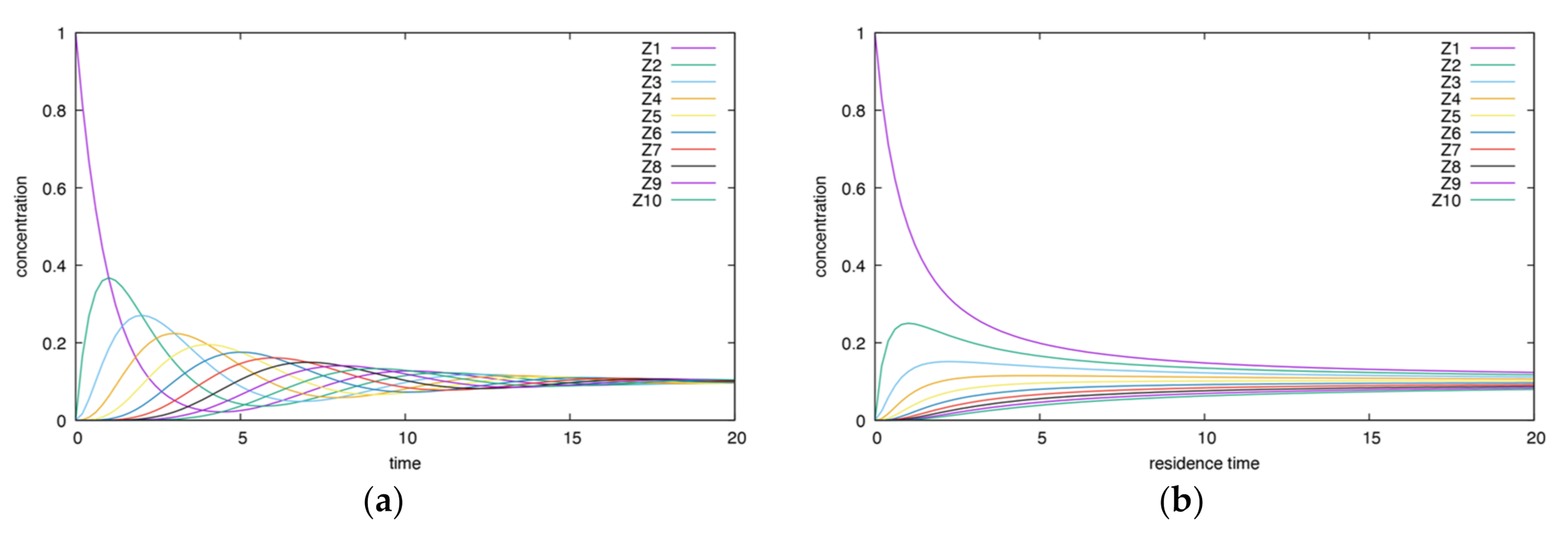
3.1.1. Acyclic Mechanism
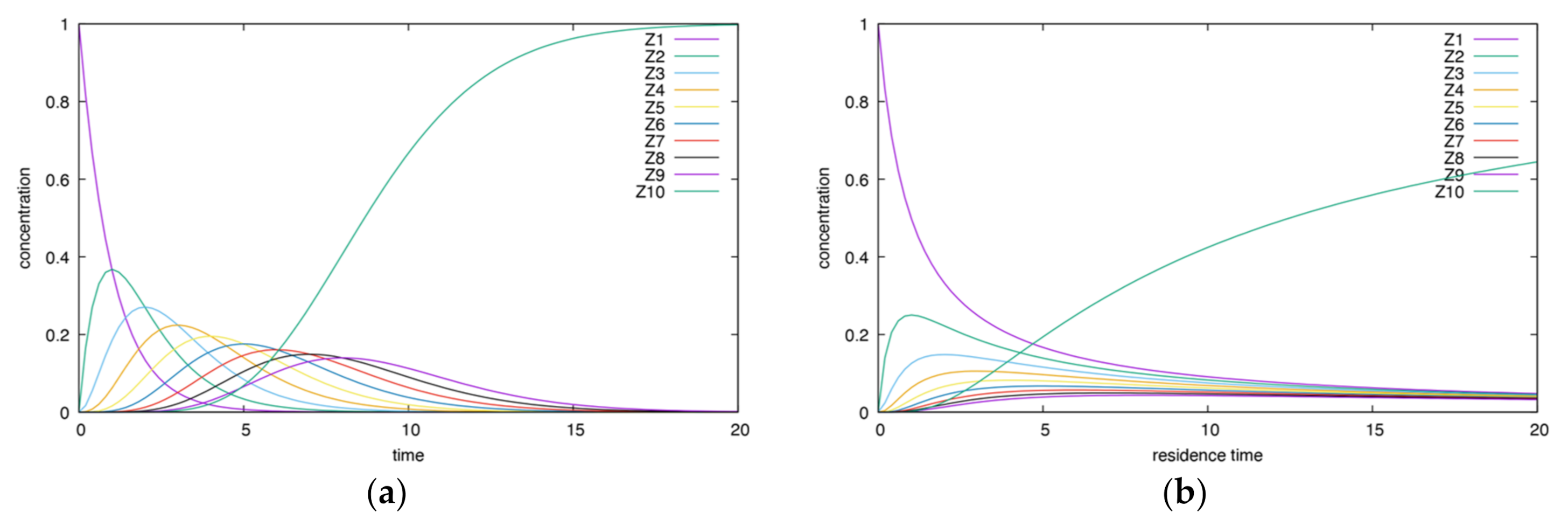
- The height and time of maxima for CSTR dependencies are smaller than for BR ones.
- In the CSTR, all dependencies enclose each other, except for the final product curve, which increases.
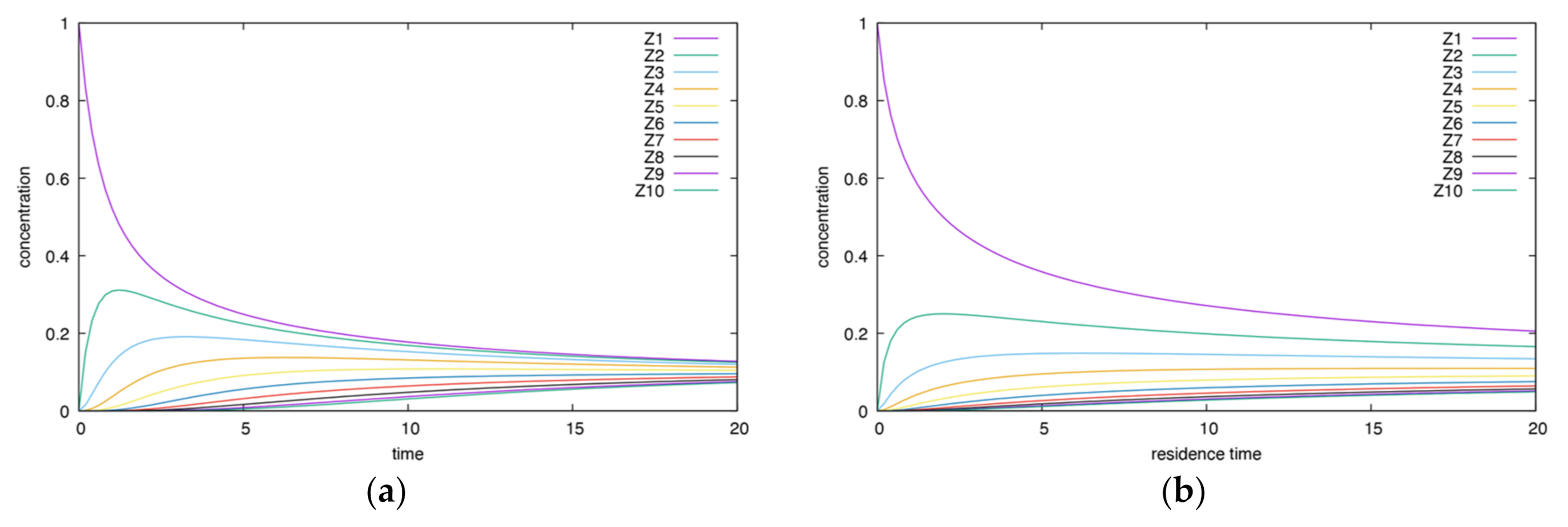
3.1.2. Cyclic Mechanism
- Different from the acyclic case, both the BR and CSTR dependencies are characterized by the final value.
- BR dependencies exhibit the undershoot but CSTR dependencies do not.
- BR curves exhibit damped oscillations caused by imaginary characteristic roots. The CSTR dependencies approach the final value in a monotonic way.
- The property of the intersections of BR dependencies is similar to the previous acyclic case. The CSTR curves do not exhibit these intersections, similarly to the previous case as well.
- In the BR, both upper and lower envelopes are present. In the CSTR, such envelopes are absent.
3.2. Reversible Reactions
3.2.1. Single Reversible Reaction (Racemization)
3.2.2. Multiple Reversible Reactions with Equal Equilibrium Constants
- Kinetic models of isotope exchange in the vicinity of chemical equilibrium.
- 2.
- Kinetic models of complex racemization reactions.
4. Discussion and Conclusions
- Within the Flory’s paradigm, the equilibrium constants are considered equal for some series of reversible chemical reactions.
- The kinetic parameters of forward reactions are considered equal for all irreversible steps of some chemical sequences, e.g., the kinetic parameters of radical polymerization, homopolymerization, etc.
- Is it possible to formulate and apply an additional principle in accordance with which all kinetic parameters for reverse reactions will be equal as well? In this case, the modified Bronsted-Evans-Polanyi relationship can be used.
- Is it possible, in some cases, to use a strong simplification of all equal kinetic parameters, both forward and reverse?
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
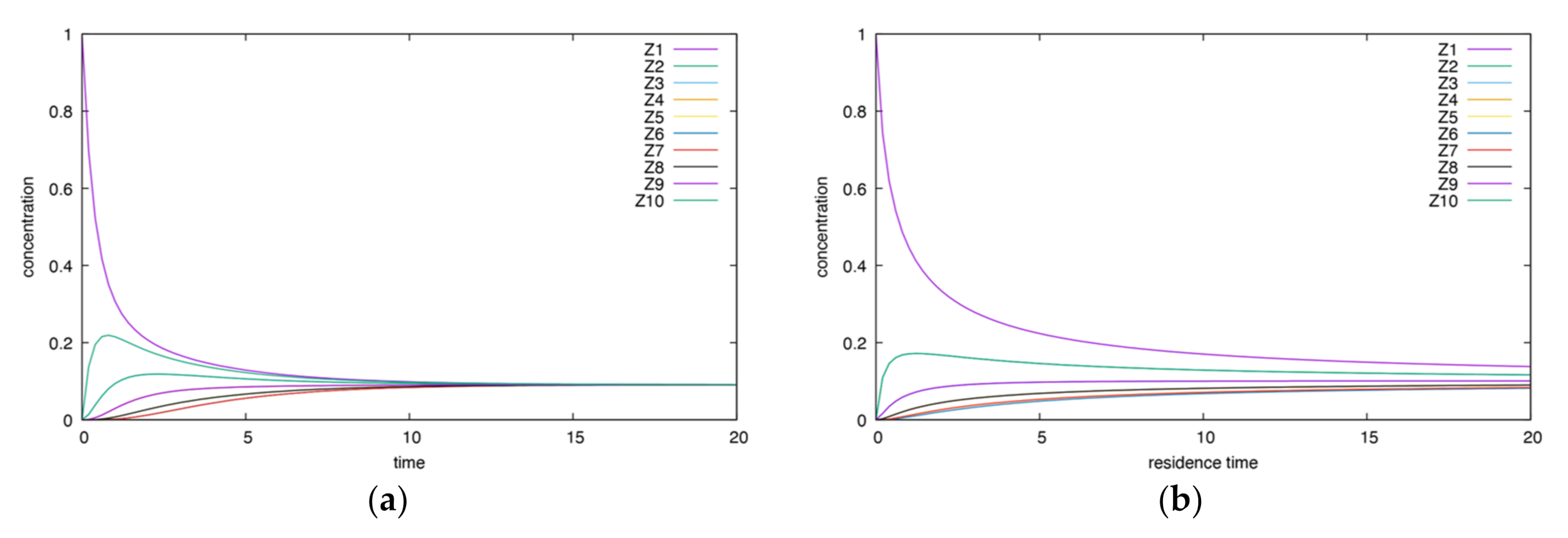
Appendix A.1. Acyclic Mechanism
- The height and time of maxima for CSTR are smaller than for BR.
- Unlike the corresponding irreversible case, the final state is not zero. For both the BR and CSTR, the final state is the same.
- Both intersections and oscillations are absent.
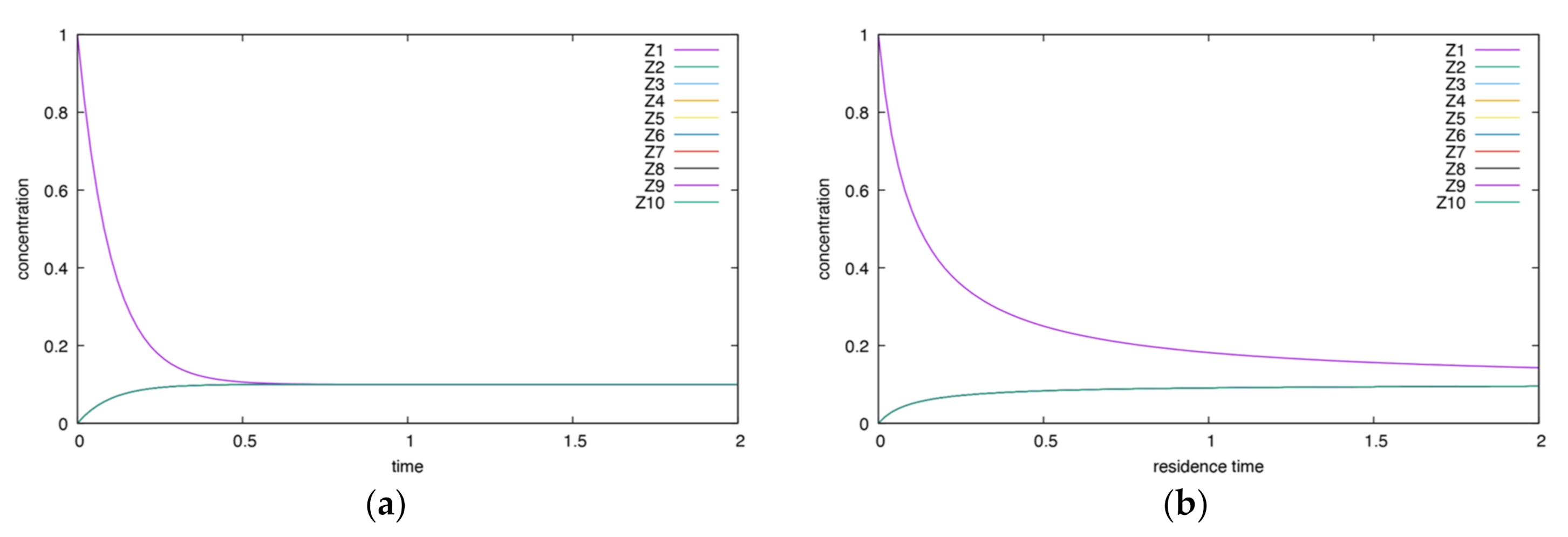
Appendix A.2. Cyclic Mechanism
- The height and time of maxima for the CSTR are smaller than for the BR.
- The behavior is less complex than for the corresponding irreversible case.
Appendix A.3. Full Graph
References
- Marin, G.; Yablonsky, G.; Constales, D. Kinetics of Chemical Reactions: Decoding Complexity, 2nd ed.; John Wiley–VCH: Weinheim, Germany, 2019; 464p. [Google Scholar]
- Bodenstein, M. Eine Theorie der photochemischen Reaktionsgeschwindigkeiten. Z. Phys. Chem. 1913, 85, 329–397. [Google Scholar] [CrossRef] [Green Version]
- Chapman, D.L.; Underhill, L.K. LV—The interaction of chlorine and hydrogen. The influence of mass. J. Chem. Soc. Trans. 1913, 103, 496–508. [Google Scholar] [CrossRef] [Green Version]
- Christiansen, J.A. The elucidation of reaction mechanisms by the method of intermediates in quasi-stationary concentrations. In Advances in Catalysis; Frankenburg, W.G., Komarewsky, V.I., Rideal, E.K., Eds.; Academic Press: Cambridge, MA, USA, 1953; Volume 5, pp. 311–353. [Google Scholar]
- Michaelis, L.; Menten, M. Die Kinetik der Invertinwirkung. Biochem. Z. 1913, 49, 333–369. [Google Scholar]
- Gorban, A.N.; Shahzad, M. The Michaelis-Menten-Stueckelberg Theorem. Entropy 2011, 13, 966–1019. [Google Scholar] [CrossRef] [Green Version]
- Briggs, G.E.; Haldane, J.B.S. A Note on the Kinetics of Enzyme Action. Biochem. J. 1925, 19, 338–339. [Google Scholar] [CrossRef] [Green Version]
- Tikhonov, A.N. Systems of differential equations containing small parameters in the derivatives. Matematicheskii Sbornik 1952, 31, 575–586. [Google Scholar]
- Sayasov, Y.A.; Vasil’eva, A.B. Semenov-Bodenstein’s method of quasi-steady-state concentrations: Justification and applicability to the gas chain reaction. Zh. Fiz. Khim. 1955, 29, 802–810. [Google Scholar]
- Vasilieva, A.B. Asymptotic Expansion for Solutions of Singularly Perturbed Equations; Nauka: Moscow, Russia, 1973. [Google Scholar]
- Tikhonov, A.N.; Sossinskij, A.B.; Vasil’eva, A.B.; Sveshnikov, A.G. Differential Equations; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Bowen, J.; Acrivos, A.; Oppenheim, A. Singular perturbation refinement to quasi-steady state approximation in chemical kinetics. Chem. Eng. Sci. 1963, 18, 177–188. [Google Scholar] [CrossRef]
- Heineken, F.; Tsuchiya, H.; Aris, R. On the mathematical status of the pseudo-steady state hypothesis of biochemical kinetics. Math. Biosci. 1967, 1, 95–113. [Google Scholar] [CrossRef]
- Yablonskii, G.S.; Bykov, V.I.; Gorban, A.N.; Elokhin, V.I. Kinetic models of catalytic reactions. In Comprehensive Chemical Kinetics; Compton, R.G., Ed.; Elsevier: Amsterdam, The Netherlands, 1991; Volume 32, 396p. [Google Scholar]
- Yablonskii, G.S.; Bykov, V.I.; Gorban, A.N. Kinetic Models of Catalytic Reactions; Nauka: Novosibirsk, Russia, 1983; 254p. (In Russian) [Google Scholar]
- Gorban, A.; Radulescu, O.; Zinovyev, A. Asymptotology of chemical reaction networks. Chem. Eng. Sci. 2010, 65, 2310–2324. [Google Scholar] [CrossRef] [Green Version]
- Gorban, A.; Karlin, I.V. Method of invariant manifold for chemical kinetics. Chem. Eng. Sci. 2003, 58, 4751–4768. [Google Scholar] [CrossRef] [Green Version]
- Gorban, A. Model reduction in chemical dynamics: Slow invariant manifolds, singular perturbations, thermodynamic estimates, and analysis of reaction graph. Curr. Opin. Chem. Eng. 2018, 21, 48–59. [Google Scholar] [CrossRef] [Green Version]
- Flory, P.J. Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953; 688p. [Google Scholar]
- Hermans, P.H.; Heikens, D.; Van Velden, P.F. A direct analytical test of the Flory-Schulz distribution in nylon 6 type equilibrium polymers. Preliminary communication. J. Polym. Sci. 1955, 16, 451–457. [Google Scholar] [CrossRef]
- O’Driscoll, K.F.; Mahabadi, H.K. Spatially intermittent polymerization. J. Polym. Sci. Polym. Chem. Ed. 1976, 14, 869–881. [Google Scholar] [CrossRef]
- Yamada, B.; Kageoka, M.; Otsu, T. ESR study on radical polymerization of styrene. Polym. Bull. 1992, 28, 75–80. [Google Scholar] [CrossRef]
- Moad, G.; Solomon, D.H. The Chemistry of Free Radical Polymerization; Elsevier Science: Amsterdam, The Netherlands, 1995; pp. 220–222. [Google Scholar]
- Boudart, M. Kinetics of Chemical Processes; Elsevier BV: Amsterdam, The Netherlands, 1991; p. 262. [Google Scholar]
- Temkin, M.I. Rate relaxation in a two-step catalytic reaction. Kinet. Katal. 1976, 17, 1095–1099. [Google Scholar]
- Cheresiz, V.M.; Yablonskii, G.S. Estimation of Relaxation Times for Chemical Kinetic Equations. React. Kinet. Catal. Lett. 1982, 19, 69–73. [Google Scholar]
- Cheresiz, V.M.; Yablonskii, G.S. Four Types of Relaxation in Chemical Kinetics (Linear Case). React. Kinet. Catal. Lett. 1984, 24, 49–50. [Google Scholar]
- Gorban, A.N.; Jarman, N.; Steur, E.; Van Leeuwen, C.; Tyukin, I.Y. Leaders Do Not Look Back, or Do They? Math. Model. Nat. Phenom. 2015, 10, 212–231. [Google Scholar] [CrossRef] [Green Version]
- Heuts, J.P.A.; Russell, G.T.; Smith, G.B.; van Herk, A.M. The importance of chain-length dependent kinetics in free-radical polymerization: A preliminary guide. Macromol. Symp. 2007, 248, 12–22. [Google Scholar] [CrossRef] [Green Version]
- Johan, P.A.H.; Gregory, T.R. The nature of the chain-length dependence of the propagation rate coefficient and its effect on the kinetics of free-radical polymerization. Small-molecule studies. Eur. Polym. J. 2006, 42, 3–20. [Google Scholar]
- Ehlers, F.; Barth, J.; Vana, P. Fundamentals of Controlled/Living Radical Polymerization; The Royal Society of Chemistry: London, UK, 2013; 364p. [Google Scholar]
- Yablonsky, G.; Constales, D.; Marin, G. Coincidences in chemical kinetics: Surprising news about simple reactions. Chem. Eng. Sci. 2010, 65, 6065–6076. [Google Scholar] [CrossRef] [Green Version]
- Breveglieri, B.; Mazzotti, M. Role of Racemization Kinetics in the Deracemization Process via Temperature Cycles. Cryst. Growth Des. 2019, 19, 3551–3558. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Constales, D.; Yablonsky, G.; Xi, Y.; Marin, G. Egalitarian Kinetic Models: Concepts and Results. Energies 2021, 14, 7230. https://doi.org/10.3390/en14217230
Constales D, Yablonsky G, Xi Y, Marin G. Egalitarian Kinetic Models: Concepts and Results. Energies. 2021; 14(21):7230. https://doi.org/10.3390/en14217230
Chicago/Turabian StyleConstales, Denis, Gregory Yablonsky, Yiming Xi, and Guy Marin. 2021. "Egalitarian Kinetic Models: Concepts and Results" Energies 14, no. 21: 7230. https://doi.org/10.3390/en14217230






