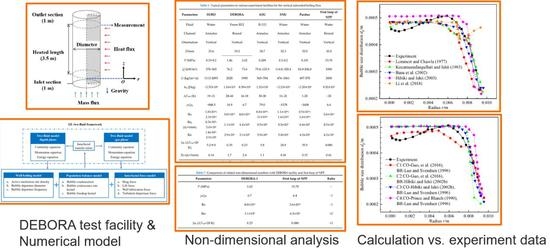
Evaluation on Coupling of Wall Boiling and Population Balance Models for Vertical Gas-Liquid Subcooled Boiling Flow of First Loop of Nuclear Power Plant
Abstract
:1. Introduction
1.1. Gas-Liquid Subcooled Boiling Flow
1.2. PBM for the Subcooled Boiling Flow
1.3. Coupling of Wall Boiling and PBM Model
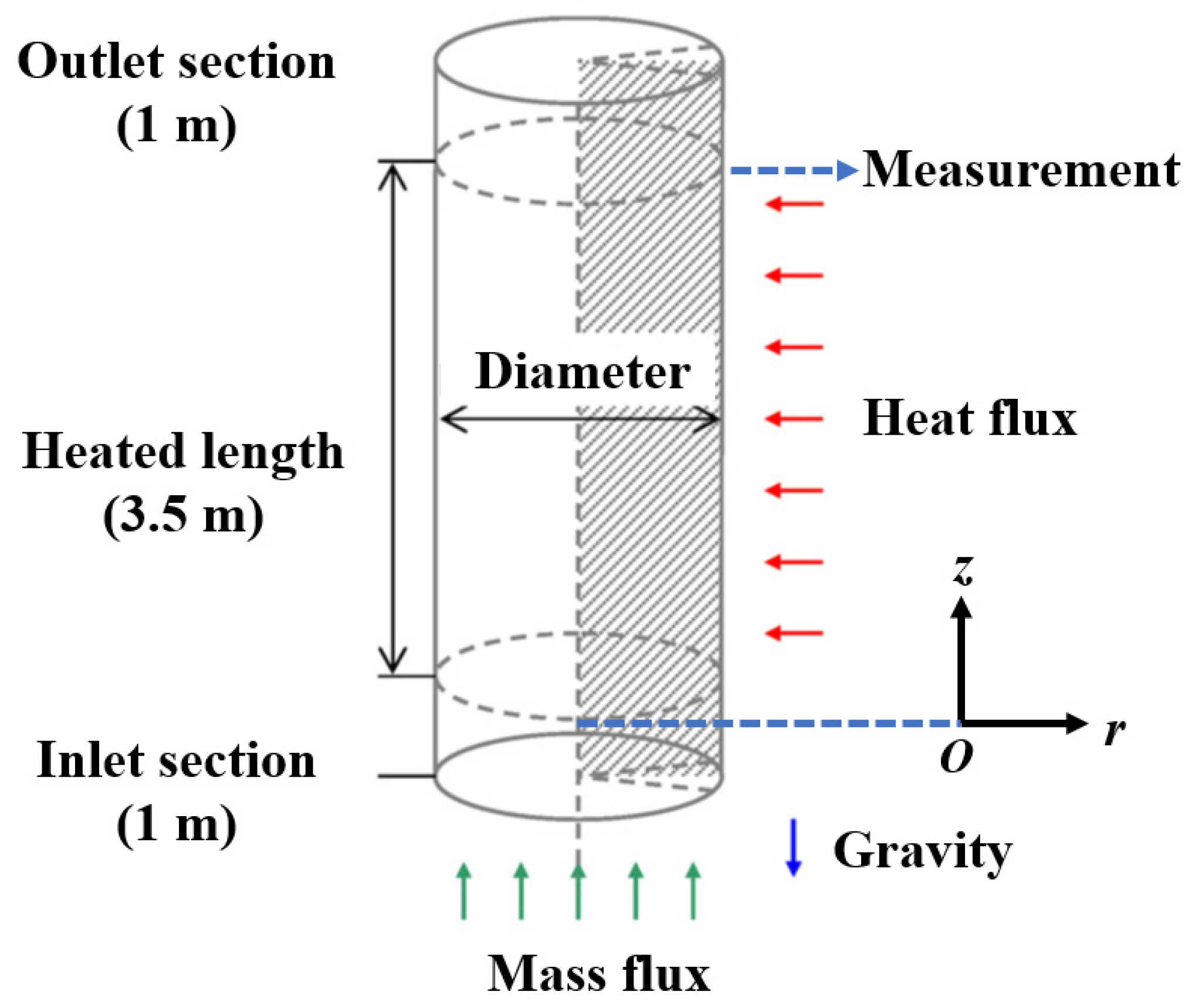
1.4. Experiment Setup and First Loop of NPP
1.5. Scope of this Paper
2. Models and Setup
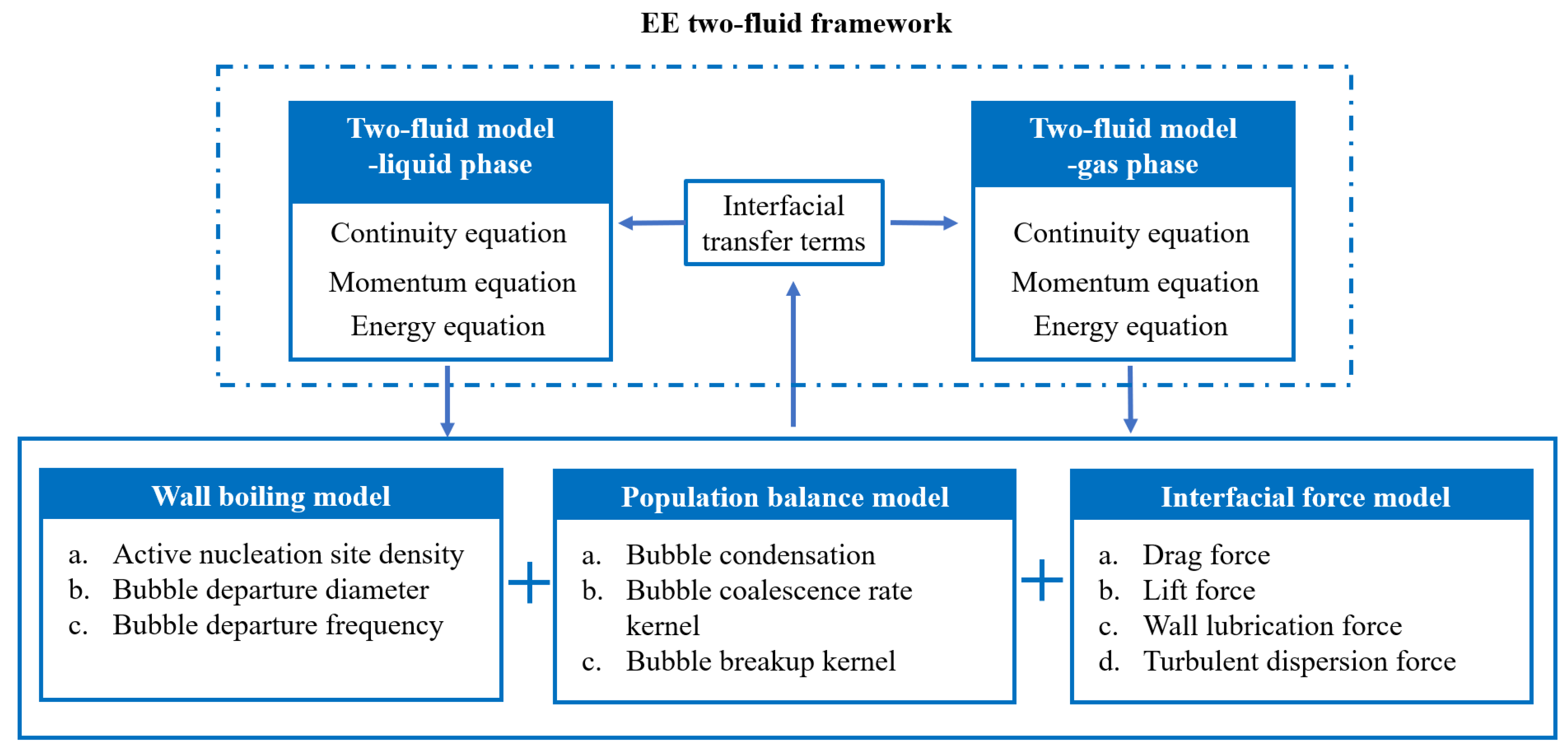
2.1. EE Two-Fluid Framework
2.2. Two-Fluid Model
2.3. Wall Boiling Model
2.3.1. Typical Models of Active Nucleation Site Density Nn
| Author/Year | Active Nucleation Site Density Nn (1/m2) | Conditions |
|---|---|---|
| Lemmert and Chawla, 1977 [35] | Nn= (185ΔTsup)1.805 | P = 0.1 − 0.2 MPa; ΔTsup = Tw − Tsat |
| Kocamustafaogullari and Ishii, 1983 [36] | P = 0.1 − 19.8 MPa; For subcooled flow boiling | |
| Basu et al., 2002 [40] | , ΔTONB < ΔTsup < 15 K; 15 K | P = 0.1 − 13.75 MPa; = 0° − 85°; ΔTsub = 1.7 − 80 °C (liquid subcooling temperature); For subcooled flow boiling |
| Hibiki and Ishii, 2003 [21] | P = 0.1 − 19.8 MPa; 1010 m−2; = 5°–90°; 10−6 m; For pool boiling and subcooled flow boiling | |
| Li et al., 2018 [5] | P = 0.1 − 19.8 MPa; A = −0.0002P2 + 0.0108P + 0.0119; B = 0.122P + 1.988; For vertical subcooled flow boiling |
2.3.2. Typical Models of Bubble Departure Diameter
| Author/Year | Bubble Departure Diameter Dd | Conditions |
|---|---|---|
| Tolubinsky and Kostanchuk, 1970 [41] | P = 0.1 MPa; For subcooled flow boing | |
| Kocamustafaogullari and Ishii, 1983 [36] | P = 0.1 − 19.8 MPa; For pooling boiling | |
| Situ et al., 2005 [4] | P = 0.1 MPa; ; ; b = 1.73; For subcooled flow boing | |
| Krepper et al., 2013 [8] | High pressure; For subcooled flow boing |
2.3.3. Typical Models of Bubble Departure Frequency f
| Author/Year | Bubble Departure Frequency f | Conditions |
|---|---|---|
| Hatton and Hall, 1966 [42] | ~ | |
| Ivey, 1967 [43] | Dd > 5 mm at medium and high heat fluxes; 1 mm < Dd < 5 mm at high heat fluxes | |
| Stephan, 1992 [44] | P = 0.1 MPa | |
| Kocamustafaogullari and Ishii, 1995 [45] | Derived from the interfacial area transport equation | |
| Brooks and Hibiki, 2015 [46] | 3.85 mm < D < 39.2 mm; 5.56 < f < 39.2 |
2.4. Population Balance Model
2.4.1. Bubble Condensation Model
2.4.2. Typical Kernels of Bubble Coalescence
2.4.3. Typical Kernels of Bubble Breakup
2.4.4. Numerical Solutions of PBM
2.5. Interfacial Force Model
2.5.1. Drag Force
2.5.2. Lift Force
2.5.3. Wall Lubrication Force
2.5.4. Turbulent Dispersion Force
3. Results and Discussion
3.1. Experiment Test Case for First Loop of NPP
3.1.1. Nondimensional Number Approximation Analysis
3.1.2. Experimental Test Case
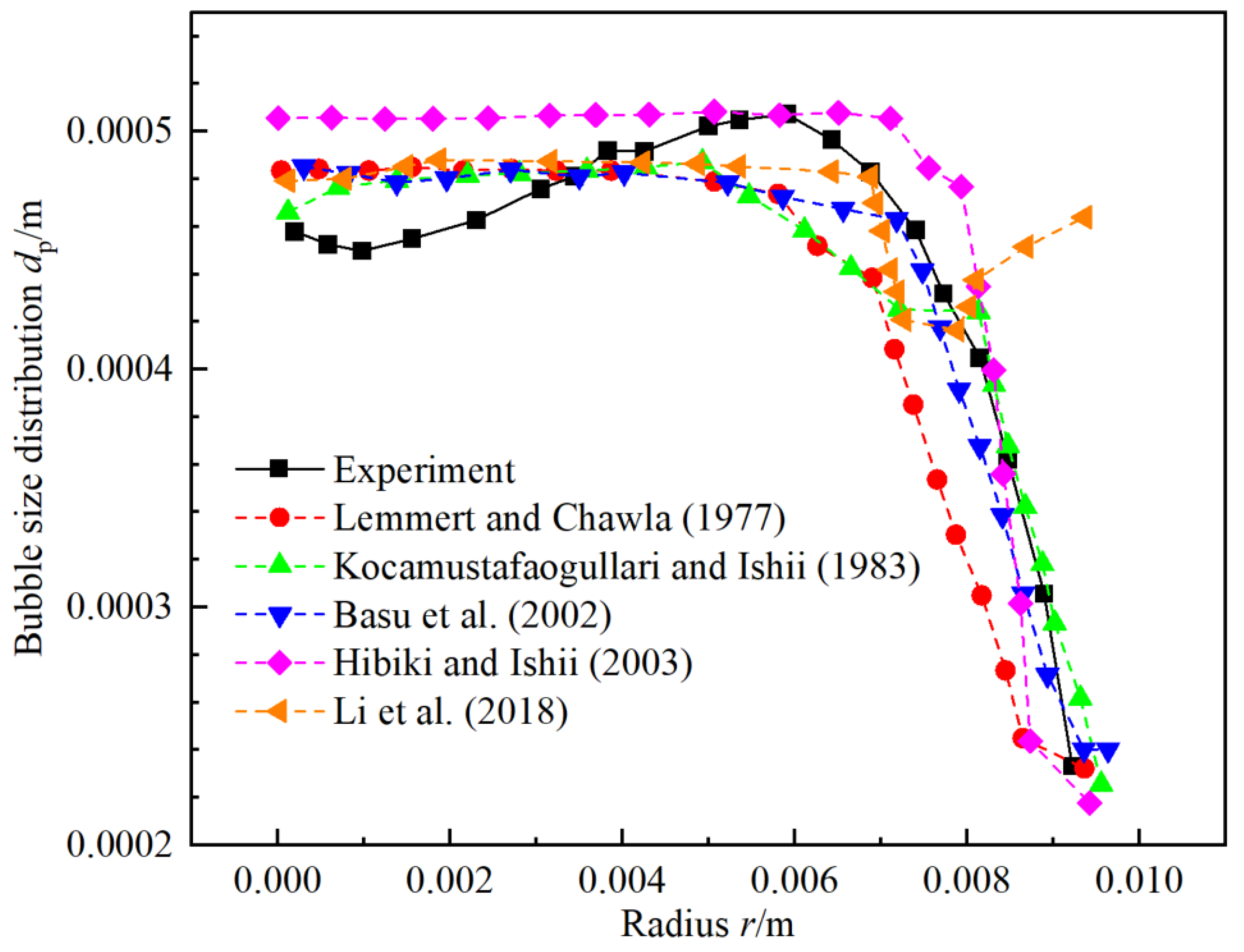
3.2. Analysis of Bubble Size Distribution dp
3.2.1. Influence of Wall Boiling Model with DEBORA-1 for First Loop of NPP
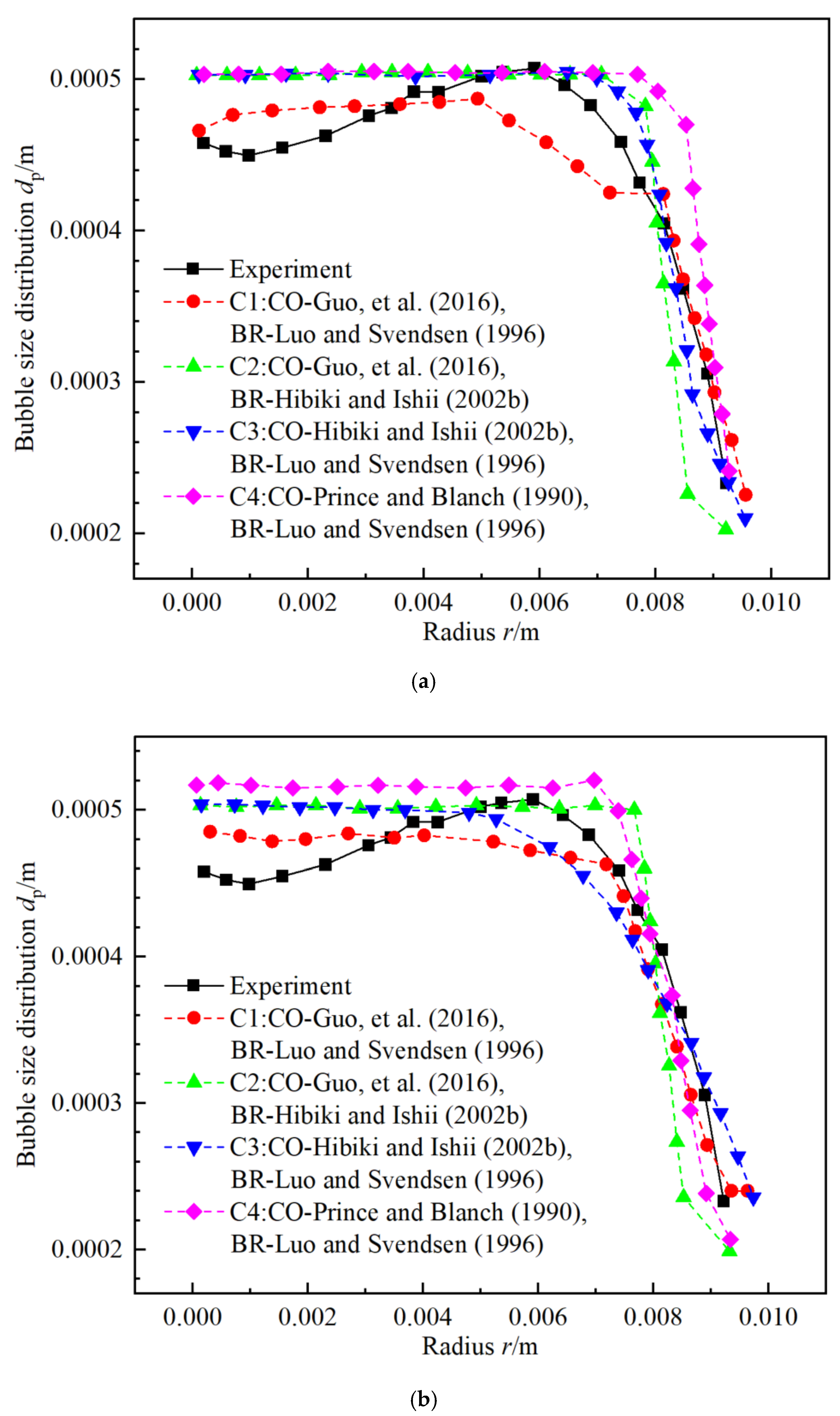
3.2.2. Combinations of Coalescence and Breakup Kernel with DEBORA-1 for First Loop of NPP
3.2.3. Error Analysis on Bubble Size Distribution
3.3. Calculation of Void Fraction α
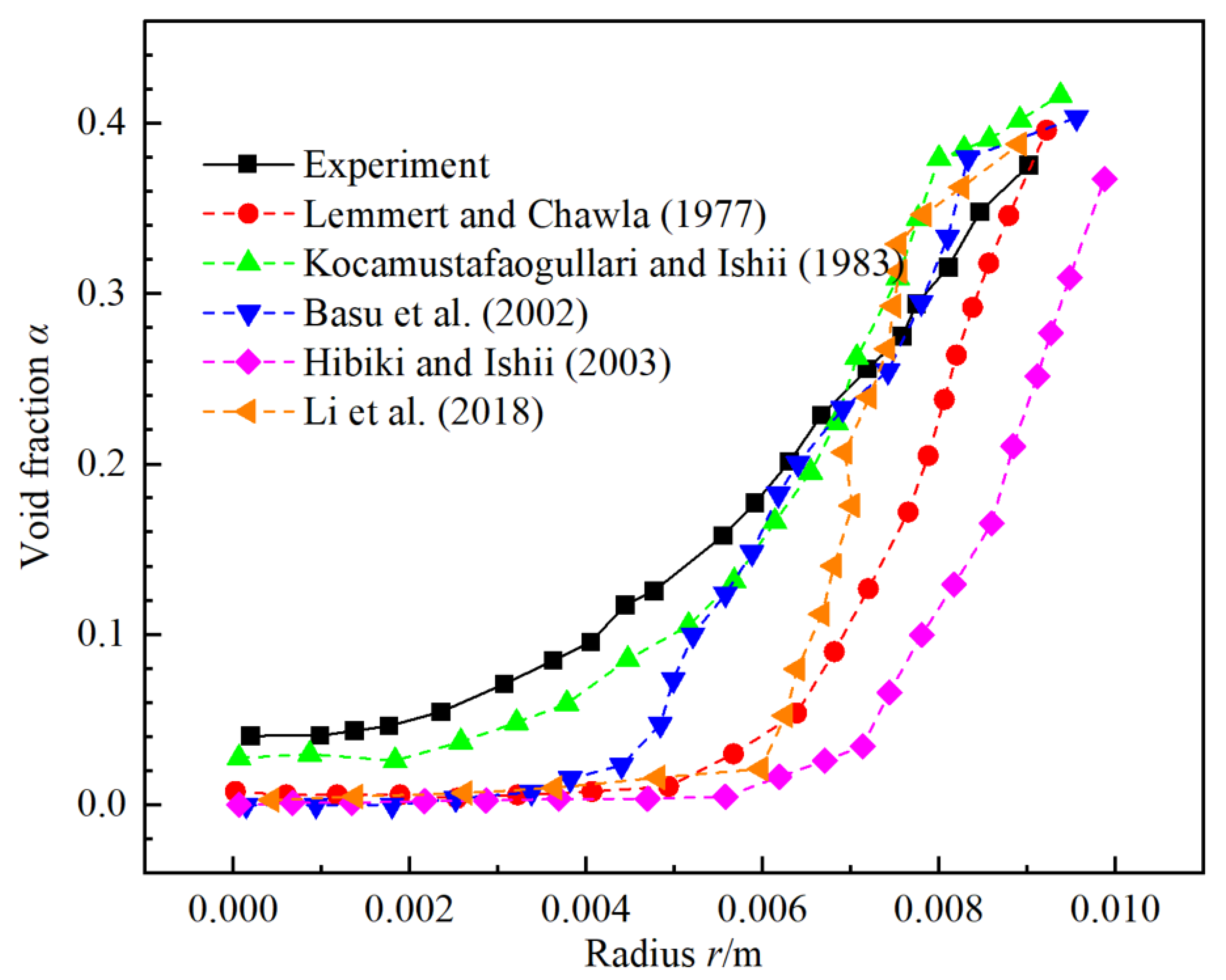
3.3.1. Influence of Wall Boiling Model with DEBORA-1 for First Loop of NPP
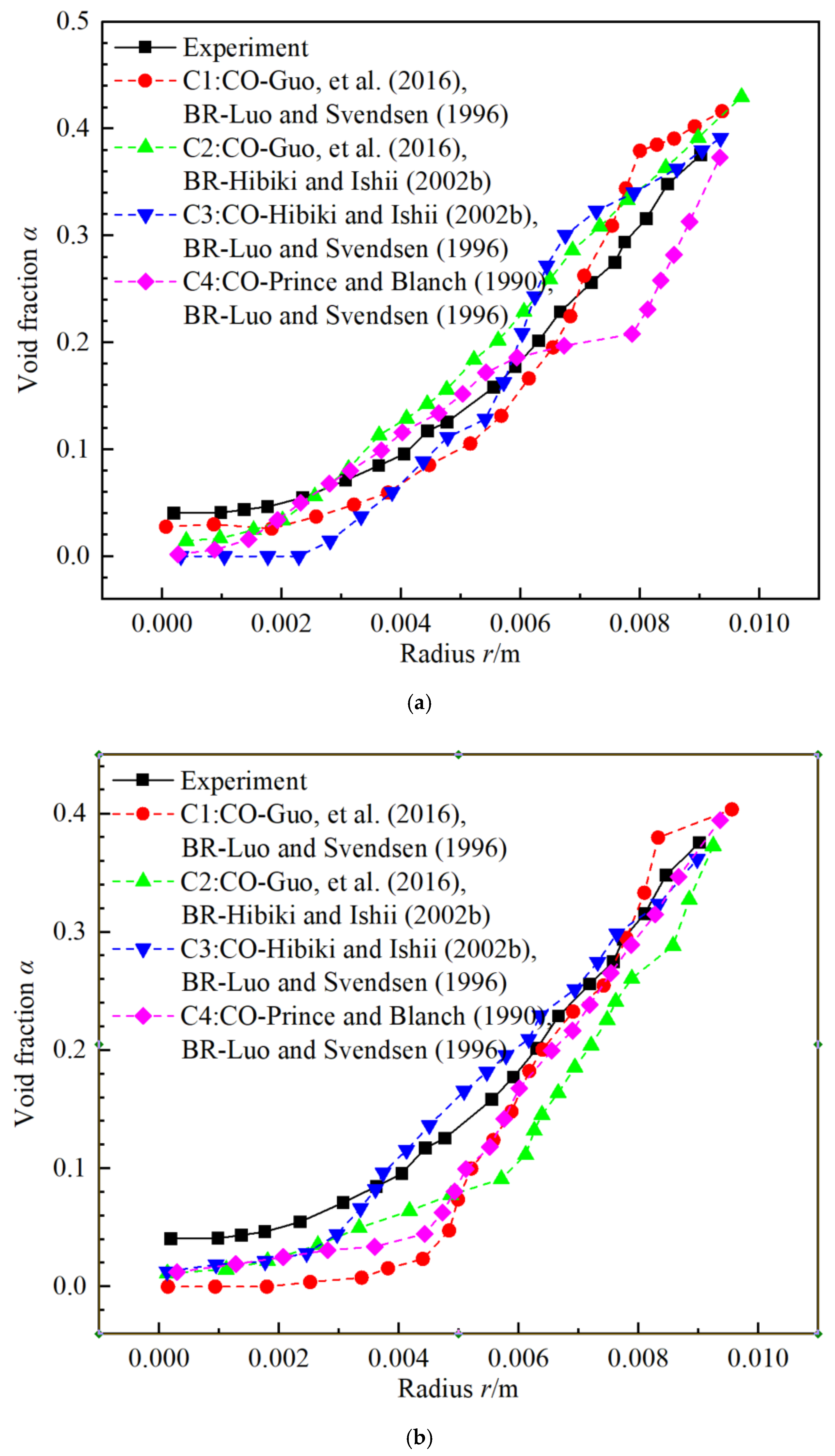
3.3.2. Combinations of Coalescence and Breakup Kernel with DEBORA-1 for First Loop of NPP
3.3.3. Error Analysis on Void Fraction α
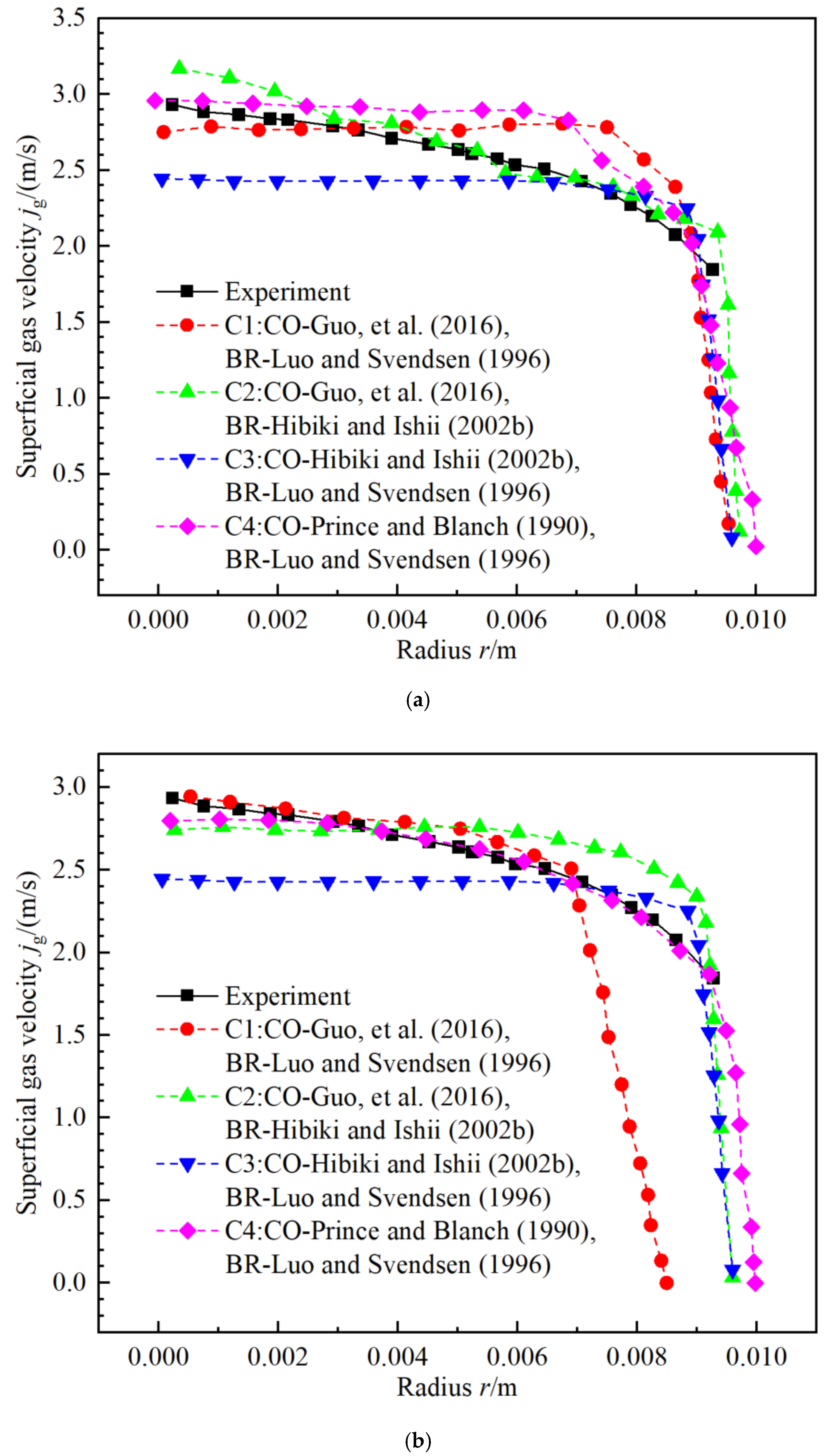
3.4. Comparison of Gas Superficial Velocity jg
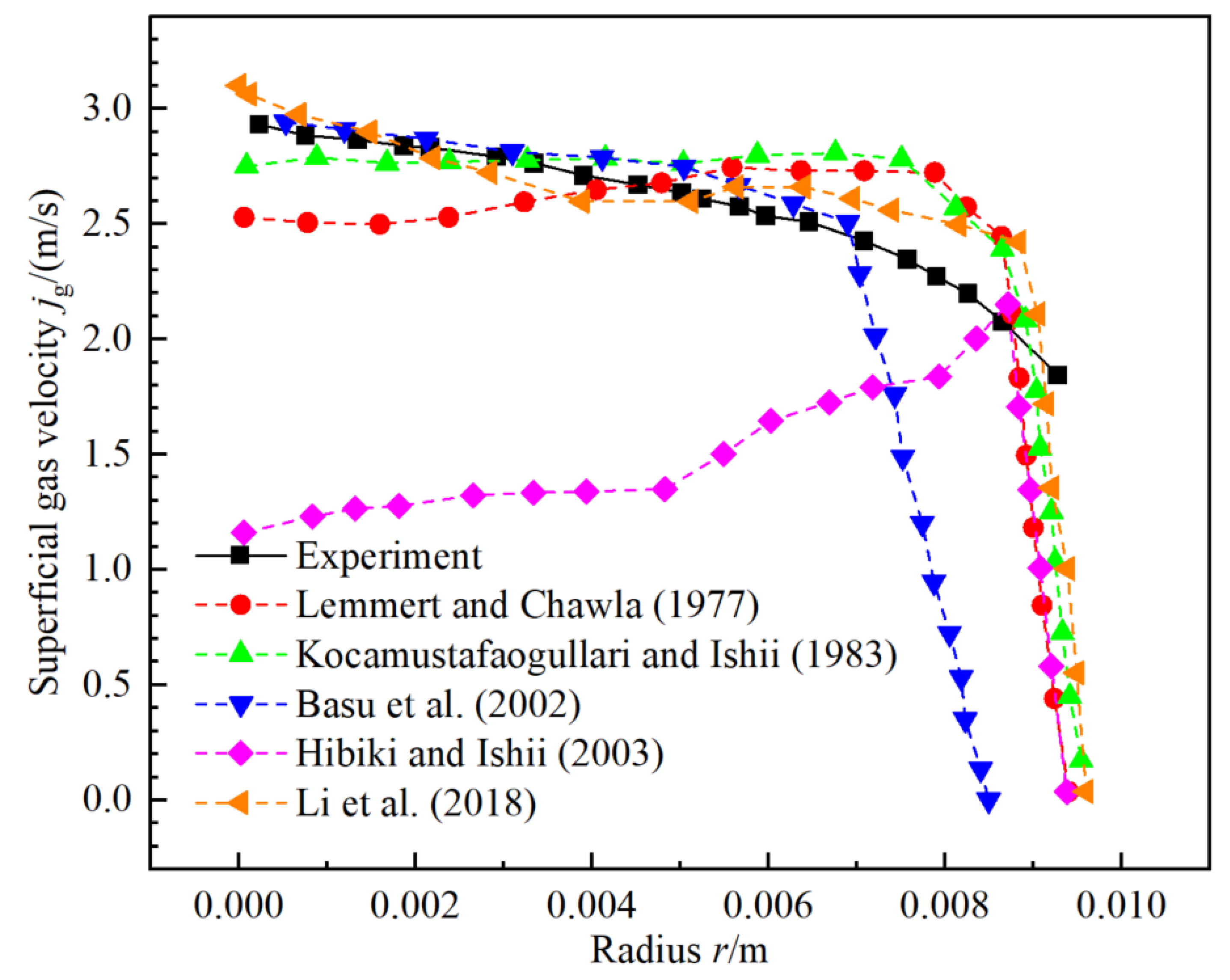
3.4.1. Influence of Wall Boiling Model with DEBORA-1 for First Loop of NPP
3.4.2. Combinations of Coalescence and Breakup Kernel with DEBORA-1 for First Loop of NPP
3.4.3. Error Analysis on Gas Superficial Velocity jg
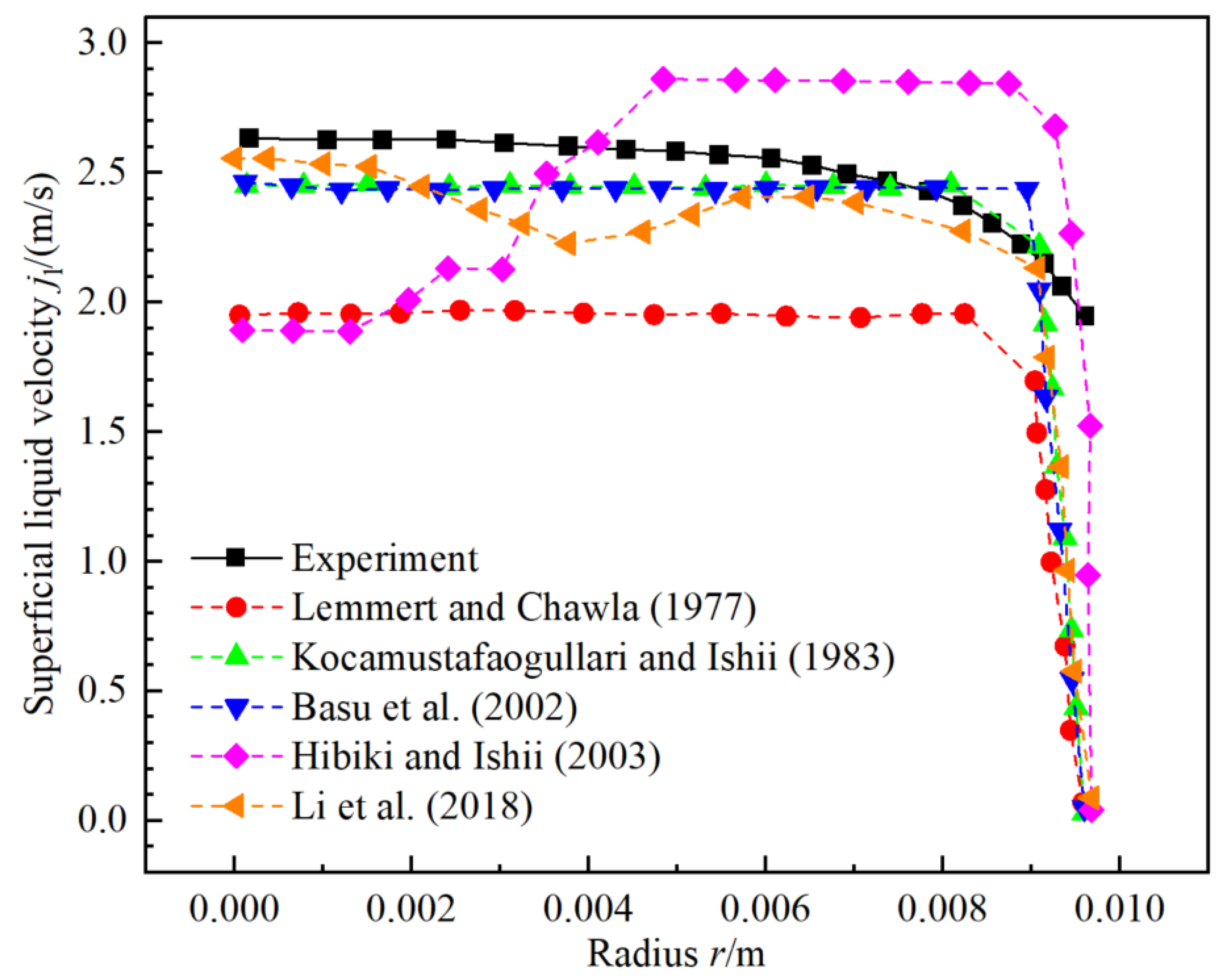
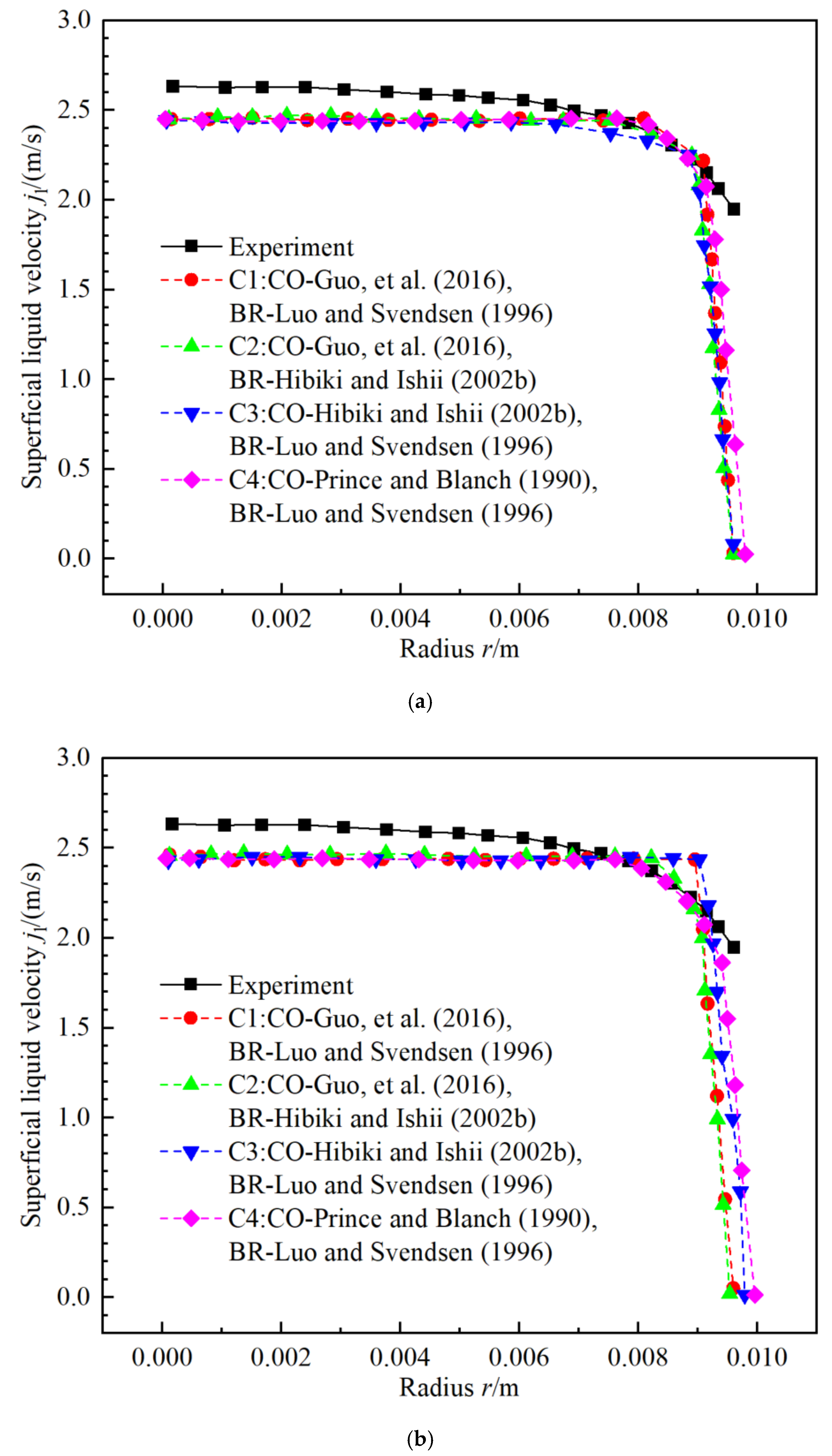
3.5. Tendency of Liquid Superficial Velocity jl
3.5.1. Influence of Wall Boiling Model with DEBORA-1 for First Loop of NPP
3.5.2. Combinations of Coalescence and Breakup Kernel with DEBORA-1 for First Loop of NPP
3.5.3. Error Analysis on Liquid Superficial Velocity jl
4. Conclusions
- Afterwards, for the bubble size distribution SMD dp, the Nn model of Kocamustafaogullari and Ishii [36] with C1 (maximum relative error 9.63%) has relatively better behaviors for the first loop of the NPP.
- Then, for the void fraction α, the Nn model of Kocamustafaogullari and Ishii [36] with C1 (maximum relative error 29.64%) performs best than others for the first loop of the NPP.
- Furthermore, for the gas superficial velocity jg, the model of Basu [40] coupled with C4 (maximum relative error 4.67%) has nice behaviors for the first loop of the NPP.
- In addition, the Nn model of Kocamustafaogullari and Ishii [36] relates with the nondimensional cavity radius , wall superheat ΔTsup and density ratio . On the other hand, the Nn model of Basu [40] relies on the wall superheat ΔTsup and contact angle . These two models have more insights into the wall boiling mechanisms for the subcooled boiling flow in the first loop of the NPP.
- Especially, the combination C4 is more suitable than C1 for the calculation of the gas superficial velocity jg for the first loop of the NPP. The gas superficial velocity jg could mainly dependent on the turbulence-induced collision which the C4 is mainly related with.
- At last, the CO kernel of Guo [57] contains four collision frequency mechanisms and more complete than others. At the same time, the BR kernel of Luo and Svendsen [54] which is based on the BR kernel of Lee [59] are more sophisticated. Therefore, the combinations of C1 are applicable for the calculation of the bubble size distribution dp, void fraction α, and liquid superficial velocity jl.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| ABND | The average bubble number density transportation method |
| ASU | The experiment facility in Arizona State University |
| Bo | The Boiling number |
| BR | The breakup kernel in the PBM |
| CFD | The computational fluid dynamics |
| CHF | The critical heat flux |
| CO | The coalescence rate kernel in the PBM |
| C1 | The combination of the coalescence rate kernel of Guo et al. (2016) and breakup kernel of Luo and Svendsen (1996) |
| C2 | The combination of the coalescence rate kernel of Guo et al. (2016) and breakup kernel of Hibiki and Ishii (2002b) |
| C3 | The combination of the coalescence rate kernel of Hibiki and Ishii (2002b) and breakup kernel of Luo and Svendsen (1996) |
| C4 | The combination of the coalescence rate kernel of Prince and Blanch (1990) and breakup kernel of Luo and Svendsen (1996) |
| DEBORA | The Development of Borehole Seals for High-Level Radioactive Waste facility |
| DNB | The departure from nucleate boiling |
| DQMOM | The direct quadrature method of moments |
| EE | The Eulerian–Eulerian approach |
| EL | The Eulerian–Lagrangian approach |
| Eo | The Eötvös number |
| Ja | The Jakob number |
| Jae | The effective Jakob number |
| MOM | The method of moments |
| MUSIG | The multiple size group method |
| NPP | The nuclear power plant |
| Nu | The Nusselt number |
| Pr | The Prandtl number |
| Prl | The Prandtl number of the liquid phase |
| PBE | The population balance equation |
| PBM | The population balance model |
| QMOM | The quadrature method of moments method |
| Re | The Reynolds number |
| Reg | The Reynolds number of the gas phase (bubbles) |
| RPI | The Rensselaer Polytechnic Institute model |
| Rel | The Reynolds number of the liquid phase |
| SG | The steam generator |
| SMD | The Sauter mean diameter, dp |
| SNU | The experiment facility in Seoul National University |
| SUBO | The Subcooled boiling facility |
| UDF | The User-Defined Functions |
| We | The Weber number |
| Weij | The equivalent Weber number of two colliding bubbles in the coalescence rate model |
| a(di, dj) | The coalescence rate, m3/s |
| ai | The interface area concentration, 1/m |
| Ab | The |
| AC | The cross-sectional area of the boiling channel, m2 |
| BC, DC | The source term and sink term related to the coalescence of bubbles |
| BB, DB | The source term and sink term related to the breakup of bubbles |
| c1~c6 | The coefficients in the coalescence rate models |
| ~ | The coefficients in the breakup models |
| CD, CD,i, CD,j | The drag coefficient |
| Cf | The coefficient of the surface area |
| CL | The lift coefficient |
| CPl | The specific heat capacity of the liquid phase at a certain pressure, J/(kg·K) |
| CR | The circulation ratio of the steam generator |
| CTD | The turbulent diffusion coefficient, CTD = 1 |
| Cw1,Cw2 | The wall lubrication coefficients |
| di, dj | The diameter of two colliding bubbles in the coalescence rate model, m |
| dij | The equivalent diameter of two colliding bubbles with the unequal size in the coalescence model, m |
| dp | The bulk bubble diameter or the parent bubble diameter or Sauter mean diameter, m |
| dsm | The Sauter mean diameter, m |
| dtube | The outer diameter of the U-shaped tube, m |
| D | The Equivalent hydraulic diameter, mm or m |
| Dd | The bubble departure diameter, m |
| The nondimensional bubble departure diameter | |
| DdF | The bubble departure diameter with the Fritz equation, m |
| Dsteam | The steam mass flow rate in the steam generator, kg/s |
| Dtotal | The total mass flow rate in the ascending channel of the steam generator, kg/s |
| Dwi | The inner diameter of the down cylinder of the steam generator, m |
| f | The bubble departure frequency, 1/s |
| fbv | The bubble breakup volume fraction, Vd/Vp |
| fbv,min | The minimum bubble breakup volume fraction, Vdmin/Vp |
| Ftube | The heat transfer area of the tubes of the steam generator, m2 |
| FD | The drag force, N |
| FL | The lift force, N |
| FTD | The turbulent dissipative force, N |
| Fu | The area of the ascending channel area of the secondary side in the steam generator, m2 |
| FW | The wall lubrication force, N |
| g | The gravity acceleration, g = 9.80 m/s2 |
| G | The mass flux, kg/(m2·s) |
| hi, hf | The initial and critical film thickness of bubbles in the coalescence model, m |
| H | The height of the unaerated liquid, m |
| h | The inter-phase heat transfer coefficient, W/(m2·K) |
| hlg | The latent heat, J/(kg) |
| hs | The single-phase heat transfer coefficient, W/(m2·K) |
| h(di, dj) | The collision frequency, m3/s |
| h(di, dj)T | The collision frequency due to turbulent fluctuation, m3/s |
| h(di, dj)B | The collision frequency due to buoyancy driven, m3/s |
| h(di, dj)W | The collision frequency due to wake entrainment, m3/s |
| h(di, dj)V | The collision efficiency due to viscous shear, m3/s |
| hfe | The feed water enthalpy, J/kg |
| hgs | The saturated gas enthalpy, J/kg |
| hls | The saturated liquid enthalpy, J/kg |
| jg | The superficial gas velocity, m/s |
| jgo | The outlet superficial gas velocity, m/s |
| jl | The superficial liquid velocity, m/s |
| jlo | The outlet superficial liquid velocity, m/s |
| jr | The relative velocity between the two phases, m/s |
| js | The nondimensional fluid velocity gradient |
| kl | The liquid thermal conductivity, W/(m·K) |
| ktube | The heat transfer coefficient of the heat transfer tube of the steam generator, W/(m2·K) |
| K | The empirical constant in the term of Ab |
| KTD | The empirical constant in the turbulent dispersion force model, KTD = 90 |
| The mass of bubbles, kg | |
| The time change rate of the bubble property (mass or volume) state | |
| m | The number of daughter bubbles in the breakup model |
| Nn | The active nucleation site density, m−2 |
| Nnc | The active nucleation site density in the forced convective boiling, m−2 |
| The nondimensional active nucleation site density in the forced convective boiling | |
| ni | The number density of bubbles in the discrete bubble class i, m−3 |
| n1 | The number of U-shaped tubes in the steam generator |
| n2 | The number of support bars in the steam generator |
| nw | The unit outward normal vector on the wall surface |
| P | The pressure, MPa |
| q | The interphase heat flux, W/m2 |
| qc | The liquid-phase convection heat flux, W/m2 |
| qe | The evaporation heat flux, W/m2 |
| The quenching heat flux, W/m2 | |
| Q | The wall heat flux, W/m2 |
| Qtotal | The total heat exchange, W or kW |
| r | The radius of the pipe, m |
| R | The ideal gas constant, R = 8.3144 J/(K·mol) |
| Rc | The critical cavity radius based on the wall superheat, m |
| The = (Rc/(Dd/2)) | |
| S | The suppression factor in the forced convective boiling, 0 < S < 1 |
| t | The time, s |
| tij | The time required for coalescence of bubbles in the coalescence model, s |
| T | The temperature, °C or K |
| T0 | The room temperature, °C or K |
| Tc | The critical temperature at which contact angle becomes 0, °C or K |
| Tg | The temperature of the gas phase, °C or K |
| Tl | The temperature of the liquid phase, °C or K |
| Tw | The temperature of the heated wall, °C or K |
| Tsat | The saturation temperature, °C or K |
| ucrit | The critical velocity for coalescence, m/s |
| ubi, ubj | The rising velocity of bubbles of size di and dj, m/s |
| ug | The average velocity of gas phase, m/s |
| ul | The average velocity of liquid phase, m/s |
| uwi, uwj | The wake entrainment velocity of bubbles of size di and dj, m/s |
| u’ | The turbulent fluctuating velocity, m/s |
| ulcir | The circulation velocity in the steam generator, m/s |
| Vp | The volume of parent bubbles in the breakup model, m3 |
| Vd | The volume of the daughter bubble in the breakup model, m3 |
| Vdmin | The minimum volume of the daughter bubble in the breakup model, m3 |
| The spatial vector | |
| The time change rate of bubble physical position | |
| x, y, z | The spatial coordinates, m |
| yw | The distance between the bubble and wall, m |
| α | The void fraction |
| αmax | The maximum void fraction |
| α1 | The constant for damping effect in the breakup model |
| α2 | The ratio of the minimum energy required for bubble breakup to the bubble surface energy |
| βg | The gas volume fraction |
| βl | The liquid volume fraction |
| β(Vd, Vp) | The daughter size distribution |
| β(fbv, 1) | The dimensionless form of the daughter size distribution |
| Γ | The gamma function |
| Γij | The ratio of the distance between bubbles and bubble turbulent path length |
| σ | The surface tension, N/m |
| ρg | The density of the gas phase, kg/m3 |
| ρl | The density of the liquid phase, kg/m3 |
| The ratio between the density difference and gas density, = Δρ/ | |
| The model parameter, = | |
| Δtln | The logarithmic average temperature difference between the primary side of the steam generator, Δtln = (Δtmax − Δtmin)/ln(Δtmax/Δtmin), °C or K |
| ΔTln | The logarithmic average temperature difference of the liquid subcooling temperature, ΔTln = (ΔTmax − ΔTmin)/ln(ΔTmax/ΔTmin), °C or K |
| ΔTe | The effective wall superheat in the forced convective boiling, ΔTe = SΔTsup = S(Tw − Tsat), °C or K |
| ΔTsub | The inlet liquid subcooling temperature, ΔTsub = Tsat − Tl, °C or K |
| ΔTsup | The wall superheat above saturation, ΔTsup = Tw − Tsat, °C or K |
| ΔTONB | The wall superheat above saturation at the onset of nucleate boiling, °C or K |
| λ(di, dj) | The coalescence efficiency |
| τij | The contact time for two bubbles in the coalescence model, s |
| τcritical | The critical stress force, kg/m3 |
| Ω(Vp) | The breakup frequency, s−1 |
| vg | The kinetic viscosity of the gas phase, m2/s |
| vl | The kinetic viscosity of the liquid phase, m2/s |
| vsg | The specific volume of the gas phase, m3/kg |
| vsl | The specific volume of the liquid phase, m3/kg |
| μg | The dynamic viscosity of the gas phase, Pa·s |
| μl | The dynamic viscosity of the liquid phase, Pa·s |
| The ratio of the diameter of eddy size and the diameter of the parent bubble | |
| The minimum value of | |
| The heated perimeter of the boiling channel, m | |
| The ratio of the diameter of bubble i and j | |
| γ | The coefficient of virtual mass, γ = 0.5 |
| ε | The turbulent dissipation rate, m2/s3 |
| ηl | The liquid thermal diffusivity, m2/s |
| φ | The gas volume fraction |
| θ | The contact angle, ° or rad |
| θ0 | The contact angle at the room temperature |
| φ | The gas volume fraction |
| The bubble nucleation rate, 1/(m·s) |
References
- Situ, R.; Ishii, M.; Hibiki, T.; Tu, J.Y.; Yeoh, G.H.; Mori, M. Bubble departure frequency in forced convective subcooled boiling flow. Int. J. Heat Mass Transf. 2008, 51, 6268–6282. [Google Scholar] [CrossRef]
- Chuang, T.-J.; Hibiki, T. Vertical upward two-phase flow CFD using interfacial area transport equation. Prog. Nucl. Energy 2015, 85, 415–427. [Google Scholar] [CrossRef]
- Zhang, R.; Cong, T.; Tian, W.; Qiu, S.; Su, G. Effects of turbulence models on forced convection subcooled boiling in vertical pipe. Ann. Nucl. Energy 2015, 80, 293–302. [Google Scholar] [CrossRef]
- Situ, R.; Hibiki, T.; Ishii, M.; Mori, M. Bubble lift-off size in forced convective subcooled boiling flow. Int. J. Heat Mass Transf. 2005, 48, 5536–5548. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Jiao, Y.; Avramova, M.; Chen, P.; Yu, J.; Chen, J.; Hou, J. Development, verification and application of a new model for active nucleation site density in boiling systems. Nucl. Eng. Des. 2018, 328, 1–9. [Google Scholar] [CrossRef]
- Krepper, E.; Končar, B.; Egorov, Y. CFD modelling of subcooled boiling—Concept, validation and application to fuel assembly design. Nucl. Eng. Des. 2007, 237, 716–731. [Google Scholar] [CrossRef]
- Yeoh, G.; Tu, J. Numerical modelling of bubbly flows with and without heat and mass transfer. Appl. Math. Model. 2006, 30, 1067–1095. [Google Scholar] [CrossRef]
- Krepper, E.; Rzehak, R.; Lifante, C.; Frank, T. CFD for subcooled flow boiling: Coupling wall boiling and population balance models. Nucl. Eng. Des. 2013, 255, 330–346. [Google Scholar] [CrossRef]
- Liao, Y.; Lucas, D. Possibilities and limitations of CFD simulation for flashing flow scenarios in nuclear applications. Energies 2017, 10, 139. [Google Scholar] [CrossRef]
- Deju, L.; Cheung, S.C.P.; Yeoh, G.H.; Qi, F.; Tu, J. Comparative Analysis of Coalescence and Breakage Kernels in Vertical Gas-Liquid Flow. Can. J. Chem. Eng. 2015, 93, 1295–1310. [Google Scholar] [CrossRef]
- Hu, G.; Ma, Y.; Zhang, H.; Liu, Q. Investigation on Sub-models of Population Balance Model for Subcooled Boiling in Vertical Gas-liquid Flow by Comprehensive Evaluation. Int. J. Heat Mass Transf. 2021, 167, 120816. [Google Scholar] [CrossRef]
- Bridgeman, J.; Jefferson, B.; Parsons, S.A. Computational fluid dynamics modelling of flocculation in water treatment: A review. Eng. Appl. Comput. Fluid Mech. 2009, 3, 220–241. [Google Scholar] [CrossRef] [Green Version]
- Cheung, S.C.P.; Deju, L.; Yeoh, G.H.; Tu, J.Y. Modeling of bubble size distribution in isothermal gas-liquid flows: Numerical assessment of population balance approaches. Nucl. Eng. Des. 2013, 265, 120–136. [Google Scholar] [CrossRef]
- Liao, Y.; Krepper, E.; Lucas, D. A baseline closure concept for simulating bubbly flow with phase change: A mechanistic model for interphase heat transfer coefficient. Nucl. Eng. Des. 2019, 348, 1–13. [Google Scholar] [CrossRef]
- Halfi, E.; Arad, A.; Brenner, A.; Katoshevski, D. Development of an oscillation-based technology for the removal of colloidal particles from water: CFD modeling and experiments. Eng. Appl. Comput. Fluid Mech. 2020, 14, 622–641. [Google Scholar] [CrossRef] [Green Version]
- Liao, Y. Update to the MUSIG model in ANSYS CFX for reliable modelling of bubble coalescence and breakup. Appl. Math. Model. 2020, 81, 506–521. [Google Scholar] [CrossRef]
- Warrier, G.R.; Dhir, V.K. Heat transfer and wall heat flux partitioning during subcooled flow nucleate boiling-a review. J. Heat Transf. 2006, 128, 1243–1256. [Google Scholar] [CrossRef]
- Kurul, N.; Podowski, M.Z. Multidimensional effects in forced convection subcooled boiling. In Proceedings of the 9th International Heat Transfer Conference, Jerusalem, Israel, 19–24 August 1990. [Google Scholar]
- Yao, W.; Morel, C. Volumetric interfacial area prediction in upward bubbly two-phase flow. Int. J. Heat Mass Transf. 2004, 47, 307–328. [Google Scholar] [CrossRef]
- Colombo, M.; Fairweather, M. Accuracy of Eulerian–Eulerian, two-fluid CFD boiling models of subcooled boiling flows. Int. J. Heat Mass Transf. 2016, 103, 28–44. [Google Scholar] [CrossRef]
- Hibiki, T.; Ishii, M. Active nucleation site density in boiling systems. Int. J. Heat Mass Transf. 2003, 46, 2587–2601. [Google Scholar] [CrossRef]
- Chen, P.; Sanyal, J.; Duduković, M.P. Numerical simulation of bubble columns flows: Effect of different breakup and coalescence closures. Chem. Eng. Sci. 2005, 60, 1085–1101. [Google Scholar] [CrossRef]
- Liao, Y.; Lucas, D. A literature review of theoretical models for drop and bubble breakup in turbulent dispersions. Chem. Eng. Sci. 2009, 64, 3389–3406. [Google Scholar] [CrossRef]
- Liao, Y.; Lucas, D. A literature review on mechanisms and models for the coalescence process of fluid particles. Chem. Eng. Sci. 2010, 65, 2851–2864. [Google Scholar] [CrossRef]
- Yun, B.; Bae, B.; Euh, D.; Park, G.; Song, C.-H. Characteristics of the local bubble parameters of a subcooled boiling flow in an annulus. Nucl. Eng. Des. 2010, 240, 2295–2303. [Google Scholar] [CrossRef] [Green Version]
- Chu, I.C.; Lee, S.J.; Youn, Y.J.; Park, J.K.; Choi, H.S.; Euh, D.J.; Song, C.H. Experimental evaluation of local bubble parameters of subcooled boiling flow in a pressurized vertical annulus channel. Nucl. Eng. Des. 2017, 312, 172–183. [Google Scholar] [CrossRef]
- Yao, W.; Morel, C. Prediction of parameters distribution of upward boiling two-phase flow with two-fluid models. In Proceedings of the International Conference on Nuclear Engineering, Arlington, VA, USA, 14–18 April 2002; pp. 801–808. [Google Scholar]
- Krepper, E.; Rzehak, R. CFD for subcooled flow boiling: Simulation of DEBORA experiments. Nucl. Eng. Des. 2011, 241, 3851–3866. [Google Scholar] [CrossRef]
- Roy, R.P.; Kang, S.; Zarate, J.A.; LaPorta, A. Turbulent Subcooled Boiling Flow—Experiments and Simulations. J. Heat Transf. 2001, 124, 73–93. [Google Scholar] [CrossRef]
- Lee, T.H.; Park, G.C.; Lee, D.J. Local flow characteristics of subcooled boiling flow of water in a vertical concentric annulus. Int. J. Multiph. Flow 2002, 28, 1351–1368. [Google Scholar] [CrossRef]
- Yeoh, G.; Tu, J. A unified model considering force balances for departing vapour bubbles and population balance in subcooled boiling flow. Nucl. Eng. Des. 2005, 235, 1251–1265. [Google Scholar] [CrossRef]
- Situ, R.; Hibiki, T.; Sun, X.; Mi, Y.; Ishii, M. Flow structure of subcooled boiling flow in an internally heated annulus. Int. J. Heat Mass Transf. 2004, 47, 5351–5364. [Google Scholar] [CrossRef] [Green Version]
- Hu, G.; Ma, Y.; Zhang, H.; Liu, Q. A mini-review on population balance model for gas-liquid subcooled boiling flow in nuclear industry. Ann. Nucl. Energy 2021, 157, 108174. [Google Scholar] [CrossRef]
- Yeoh, G.; Tu, J. Two-fluid and population balance models for subcooled boiling flow. Appl. Math. Model. 2006, 30, 1370–1391. [Google Scholar] [CrossRef] [Green Version]
- Lemmert, M.; Chawla, J.M. Influence of flow velocity on surface boiling heat transfer coefficient. In Heat Transfer in Boiling; Hahne, E., Grigull, U., Eds.; Academic Press and Hemisphere: New York, NY, USA, 1977; pp. 237–247. [Google Scholar]
- Kocamustafaogullari, G.; Ishii, M. Interfacial area and nucleation site density in boiling systems. Int. J. Heat Mass Transf. 1983, 26, 1377–1387. [Google Scholar] [CrossRef]
- Bae, B.-U.; Yun, B.-J.; Yoon, H.-Y.; Song, C.-H.; Park, G.-C. Analysis of subcooled boiling flow with one-group interfacial area transport equation and bubble lift-off model. Nucl. Eng. Des. 2010, 240, 2281–2294. [Google Scholar] [CrossRef]
- Gu, J.; Wang, Q.; Wu, Y.; Lyu, J.; Li, S.; Yao, W. Modeling of subcooled boiling by extending the RPI wall boiling model to ultra-high pressure conditions. Appl. Therm. Eng. 2017, 124, 571–584. [Google Scholar] [CrossRef]
- Khoshnevis, A.; Sarchami, A.; Ashgriz, N. Effect of nucleation bubble departure diameter and frequency on modeling subcooled flow boiling in an annular flow. Appl. Therm. Eng. 2018, 135, 280–288. [Google Scholar] [CrossRef]
- Basu, N.; Warrier, G.R.; Dhir, V.K. Onset of nucleate boiling and active nucleation site density during subcooled flow boiling. J. Heat Transf. 2002, 124, 717–728. [Google Scholar] [CrossRef] [Green Version]
- Tolubinsky, V.I.; Kostanchuk, D.M. Vapour bubbles growth rate and heat transfer intensity at subcooled water boiling. In Proceedings of the 4th International Heat Transfer Conference, Paris, France, 31 August–5 September 1970. [Google Scholar]
- Hatton, A.P.; Hall, I.S. Photographic study of boiling on prepared surfaces. In Proceedings of the Third International Heat Transfer Conference, Chicago, IL, USA, 7–12 August 1966. [Google Scholar]
- Ivey, H. Relationships between bubble frequency, departure diameter and rise velocity in nucleate boiling. Int. J. Heat Mass Transf. 1967, 10, 1023–1040. [Google Scholar] [CrossRef]
- Stephan, K. Heat Transfer in Condensation and Boiling; Springer: New York, NY, USA, 1992. [Google Scholar]
- Kocamustafaogullari, G.; Ishii, M. Foundation of the interfacial area transport equation and its closure relations. Int. J. Heat Mass Transf. 1995, 38, 481–493. [Google Scholar] [CrossRef]
- Brooks, C.S.; Hibiki, T. Wall nucleation modeling in subcooled boiling flow. Int. J. Heat Mass Transf. 2015, 86, 183–196. [Google Scholar] [CrossRef]
- Kocamustafaogullari, G.; Huang, W.; Razi, J. Measurement and modeling of average void fraction, bubble size and interfacial area. Nucl. Eng. Des. 1994, 148, 437–453. [Google Scholar] [CrossRef]
- Hibiki, T.; Ishii, M. Interfacial area concentration of bubbly flow systems. Chem. Eng. Sci. 2002, 57, 3967–3977. [Google Scholar] [CrossRef]
- Hibiki, T.; Lee, T.H.; Lee, J.Y.; Ishii, M. Interfacial area concentration in boiling bubbly flow systems. Chem. Eng. Sci. 2006, 61, 7979–7990. [Google Scholar] [CrossRef]
- Labuntzov, D.A.; Lolchugin, B.A.; Golovin, V.S.; Zakharova, E.A.; Vladimirova, L.N. High speed camera investigation of bubble growth for saturated water boiling in a wide range of pressure variations. Thermophys. High Temp. 1964, 2, 446–453. [Google Scholar]
- Chen, Y.M.; Mayinger, F. Measurement of heat transfer at the phase interface of condensing bubbles. Int. J. Multiph. Flow 1992, 18, 877–990. [Google Scholar] [CrossRef]
- Tomiyama, A. Progress in computational bubble dynamics. In Proceedings of the 7th Workshop on Multiphase Flow, Dresden, Germany, 26 May 2009. [Google Scholar]
- Prince, M.J.; Blanch, H.W. Bubble coalescence and break-up in air-sparged bubble columns. AIChE J. 1990, 36, 1485–1499. [Google Scholar] [CrossRef]
- Luo, H. Coalescence, Breakup and Liquid Circulation in Bubble Column Reactors. Ph.D. Thesis, Norwegian Institute of Technology, Trondheim, Norway, 1993. [Google Scholar]
- Hibiki, T.; Ishii, M. Development of one-group interfacial area transport equation in bubbly flow systems. Int. J. Heat Mass Transf. 2002, 45, 2351–2372. [Google Scholar] [CrossRef]
- Wang, T.; Wang, J.; Jin, Y. Population balance model for gas-liquid flows: Influence of bubble coalescence and breakup models. Ind. Eng. Chem. Res. 2005, 44, 7540–7549. [Google Scholar] [CrossRef]
- Guo, X.; Zhou, Q.; Li, J.; Chen, C. Implementation of an improved bubble breakup model for TFM-PBM simulations of gas–liquid flows in bubble columns. Chem. Eng. Sci. 2016, 152, 255–266. [Google Scholar] [CrossRef] [Green Version]
- Coulaloglou, C.; Tavlarides, L. Description of interaction processes in agitated liquid-liquid dispersions. Chem. Eng. Sci. 1977, 32, 1289–1297. [Google Scholar] [CrossRef]
- Lee, C.H.; Erickson, L.E.; Glasgow, L.A. Bubble breakup and coalescence in turbulent gas-liquid dispersions. Chem. Eng. Communications. 1987, 59, 65–84. [Google Scholar] [CrossRef]
- Luo, H.; Svendsen, H.F. Theoretical model for drop and bubble breakup in turbulent dispersions. AIChE J. 1996, 42, 1225–1233. [Google Scholar] [CrossRef]
- Patil, D.P.; Andrews, J.R. An analytical solution to continuous population balance model describing floc coalescence and breakage-a special case. Chem. Eng. Sci. 1998, 53, 599–601. [Google Scholar] [CrossRef]
- Ho, M.; Yeoh, G.; Tu, J. Population balance models for subcooled boiling flows. Int. J. Numer. Methods Heat Fluid Flow 2008, 18, 160–172. [Google Scholar] [CrossRef]
- Petitti, M.; Nasuti, A.; Marchisio, D.L.; Vanni, M.; Baldi, G.; Mancini, N.; Podenzani, F. Bubble size distribution modeling in stirred gas-liquid reactors with QMOM augmented by a new correction algorithm. AIChE J. 2010, 56, 36–53. [Google Scholar] [CrossRef]
- Dutta, A.; Constales, D.; Heynderickx, G.J. Applying the direct quadrature method of moments to improve multiphase FCC riser reactor simulation. Chem. Eng. Sci. 2012, 83, 93–109. [Google Scholar] [CrossRef]
- Frank, T.; Zwart, P.J.; Shi, J.; Krepper, E.; Lucas, D.; Rohde, U. Inhomogeneous MUSIG model-A population balance approach for polydispersed bubbly flows. In Proceedings of the International Conference for Nuclear Energy for New Europe, Bled, Slovenia, 5–8 September 2005. [Google Scholar]
- Krepper, E.; Lucas, D.; Frank, T.; Prasser, H.-M.; Zwart, P.J. The inhomogeneous MUSIG model for the simulation of polydispersed flows. Nucl. Eng. Des. 2008, 238, 1690–1702. [Google Scholar] [CrossRef]
- Mali, C.R.; Vinod, V.; Patwardhan, A.W. Comparison of phase interaction models for high pressure subcooled boiling flow in long vertical tubes. Nucl. Eng. Des. 2017, 324, 337–359. [Google Scholar] [CrossRef]
- Ishii, M.; Zuber, N. Drag coefficient and relative velocity in bubbly, droplet or particulate flows. AIChE J. 1979, 25, 843–855. [Google Scholar] [CrossRef]
- Tomiyama, A. Struggle with computational bubble dynamics. Multiph. Sci. Technol. 1998, 10, 369–405. [Google Scholar]
- Antal, S.P.; Lahey, R.T., Jr.; Flaherty, J.E. Analysis of phase distribution in fully developed laminar bubbly two-phase flow. Int. J. Multiph. Flow. 1991, 17, 635–652. [Google Scholar] [CrossRef]
- Burns, A.D.; Frank, T.; Hamill, I.; Shi, J.M. The Favre averaged drag model for turbulent dispersion in Eulerian multi-phase flows. In Proceedings of the 5th International Conference on Multiphase Flow, ICMF, Yokohama, Japan, 30 May–4 June 2004; pp. 1–17. [Google Scholar]
| Parameters | SUBO | DEBORA | ASU | SNU | Purdue | First Loop of NPP | |
|---|---|---|---|---|---|---|---|
| Fluid | Water | Freon R12 | R-113 | Water | Water | Water | |
| Channel | Annulus | Round | Annulus | Annulus | Annulus | Round | |
| Orientation | Vertical | Vertical | Vertical | Vertical | Vertical | Vertical | |
| D/mm | 33.6 | 19.2 | 34.7 | 32.3 | 33.0 | 10.0 | |
| P (MPa) | 0.15–0.2 | 1.46 | 2.62 | 0.269 | 0.1–0.2 | 0.101 | 15.70 |
| Q (kW/m2) | 370–565 | 76.2 | 73.6 | 79.4–125.9 | 114.8–320.4 | 54.0–206.0 | 1000 |
| G (kg/(m2·s)) | 1113–2093 | 2028 | 1990 | 565–784 | 476–1061 | 497–570 | 3000 |
| hlg (J/kg) | 106 | 105 | 104 | 105 | 106 | 106 | 105 |
| ΔTsub (K) | 19–31 | 28–44 | 16–18 | 30–38 | 11–21 | 1–20 | ~20 |
| ρl/ρg | ~848.5 | 14.9 | 6.7 | 79.0 | ~1178 | ~1608 | 6.4 |
| Bo | 10−4 | 10−4 | 10−4 | 10−4 | 10−4 | 10−4 | 10−4 |
| Reg (dp = 1 mm) | 103 | 103 | 103 | 103 | 103 | 103 | 103 |
| Rel | 105 | 105 | 104 | 104 | 104 | 105 | |
| Jae (ΔTsup = 20 K) | 5.2–9.0 | 0.35 | 0.23 | 5.8 | 24.9 | 35.5 | 0.080 |
| Eo (dp = 1 mm) | 0.16 | 1.7 | 2.4 | 1.1 | 0.16 | 0.15 | 0.61 |
| Author/Year | Collision Frequency h(di, dj) | Coalescence Efficiency λ(di, dj) |
|---|---|---|
| Prince and Blanch, 1990 [53] | ] | |
| Luo, 1993 [54] | λ(di, dj) = | |
| Hibiki and Ishii, 2002 [55] | ||
| Wang et al., 2005 [56] | λ(di, dj) = | |
| Guo et al., 2016 [57] | h(di, dj) = h(di, dj)T + h(di, dj)B + h(di, dj)W + h(di, dj)V |
| Author/Year | Breakup Frequency Ω(Vp) | Daughter Size Distribution β(fbv, 1) |
|---|---|---|
| Coulaloglou and Tavlarides, 1977 [58] | ||
| Lee et al., 1987 [59] | ||
| Luo and Svendsen, 1996 [60] | ||
| Hibiki and Ishii, 2002 [55] | ], Binary breakup | |
| Guo et al., 2016 [57] | Binary breakup | |
| Parameters | DEBORA-1 | First Loop of NPP | Ratio |
|---|---|---|---|
| P (MPa) | 2.62 | 15.70 | ~ |
| ρl/ρg | 6.7 | 6.4 | ~1 |
| Bo | 10−4 | 10−4 | ~1 |
| Rel | 105 | 105 | <2 |
| Jae (ΔTsup = 20 K) | 0.23 | 0.080 | <3 |
| Wall Boiling Model with C1 | Maximum Relative Error | Combinations with Kocamustafaogullari and Ishii, 1983 | Maximum Relative Error | Combinations with Basu et al., 2002 | Maximum Relative Error |
|---|---|---|---|---|---|
| Lemmert and Chawla, 1977 [35] | 24.45% | C1 | 9.63% | C1 | 11.18% |
| Kocamustafaogullari and Ishii, 1983 [36] | 9.63% | C2 | 37.54% | C2 | 34.86% |
| Basu et al., 2002 [40] | 11.18% | C3 | 12.97% | C3 | 25.72% |
| Hibiki and Ishii, 2003 [21] | 20.23% | C4 | 29.88% | C4 | 21.99% |
| Li et al., 2018 [5] | 47.74% | ~ | ~ | ~ | ~ |
| Wall Boiling Model with C1 | Maximum Relative Error | Combinations with Kocamustafaogullari and Ishii, 1983 | Maximum Relative Error | Combinations with Basu et al., 2002 | Maximum Relative Error |
|---|---|---|---|---|---|
| Lemmert and Chawla, 1977 [35] | 96.41% | C1 | 29.64% | C1 | 100.00% |
| Kocamustafaogullari and Ishii, 1983 [36] | 29.64% | C2 | 64.06% | C2 | 72.16% |
| Basu et al., 2002 [40] | 80.07% | C3 | 100.00% | C3 | 68.57% |
| Hibiki and Ishii, 2003 [21] | 90.65% | C4 | 95.07% | C4 | 69.82% |
| Li et al., 2018 [5] | 88.03% | ~ | ~ | ~ | ~ |
| Wall Boiling Model with C1 | Maximum Relative Error | Combinations with Kocamustafaogullari and Ishii, 1983 | Maximum Relative Error | Combinations with Basu et al., 2002 | Maximum Relative Error |
|---|---|---|---|---|---|
| Lemmert and Chawla, 1977 [35] | 19.84% | C1 | 18.56% | C1 | 100.00% |
| Kocamustafaogullari and Ishii, 1983 [36] | 18.56% | C2 | 8.06% | C2 | 14.74% |
| Basu et al., 2002 [40] | 93.50% | C3 | 16.65% | C3 | 16.65% |
| Hibiki and Ishii, 2003 [21] | 60.42% | C4 | 12.77% | C4 | 4.67% |
| Li et al., 2018 [5] | 13.65% | ~ | ~ | ~ | ~ |
| Wall Boiling Model with C1 | Maximum Relative Error | Combinations with Kocamustafaogullari and Ishii, 1983 | Maximum Relative Error | Combinations with Basu et al., 2002 | Maximum Relative Error |
|---|---|---|---|---|---|
| Lemmert and Chawla, 1977 [35] | 25.95% | C1 | 6.97% | C1 | 6.50% |
| Kocamustafaogullari and Ishii, 1983 [36] | 6.97% | C2 | 6.97% | C2 | 6.63% |
| Basu et al., 2002 [40] | 6.50% | C3 | 7.19% | C3 | 7.68% |
| Hibiki and Ishii, 2003 [21] | 28.12% | C4 | 6.97% | C4 | 7.21% |
| Li et al., 2018 [5] | 14.43% | ~ | ~ | ~ | ~ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, G.; Ma, Y.; Liu, Q. Evaluation on Coupling of Wall Boiling and Population Balance Models for Vertical Gas-Liquid Subcooled Boiling Flow of First Loop of Nuclear Power Plant. Energies 2021, 14, 7357. https://doi.org/10.3390/en14217357
Hu G, Ma Y, Liu Q. Evaluation on Coupling of Wall Boiling and Population Balance Models for Vertical Gas-Liquid Subcooled Boiling Flow of First Loop of Nuclear Power Plant. Energies. 2021; 14(21):7357. https://doi.org/10.3390/en14217357
Chicago/Turabian StyleHu, Guang, Yue Ma, and Qianfeng Liu. 2021. "Evaluation on Coupling of Wall Boiling and Population Balance Models for Vertical Gas-Liquid Subcooled Boiling Flow of First Loop of Nuclear Power Plant" Energies 14, no. 21: 7357. https://doi.org/10.3390/en14217357
APA StyleHu, G., Ma, Y., & Liu, Q. (2021). Evaluation on Coupling of Wall Boiling and Population Balance Models for Vertical Gas-Liquid Subcooled Boiling Flow of First Loop of Nuclear Power Plant. Energies, 14(21), 7357. https://doi.org/10.3390/en14217357