Study on Optimum IUPAC Adsorption Isotherm Models Employing Sensitivity of Parameters for Rigorous Adsorption System Performance Evaluation
Abstract
:1. Introduction
- (i)
- Examining the isotherm models and statistical methodologies.
- (ii)
- The model parameters have been optimized employing the generalized reduced gradient (GRG) non-linear optimization technique.
- (iii)
- The optimized parameters are varied deliberately within a small range of a large number (N = 10,000) of times to generate the empirical distributions of the RMSD.
- (iv)
- Box-and-whisker plots have been constructed of all candidate models for all types of IUPAC isotherms.
- (v)
- The parametric method ANOVA and Tukey HSD tests, as well as non-parametric method Kruskal–Wallis and Wilcoxon rank-sum tests, have been applied to find the significantly optimum models by minimizing RMSD.
- (vi)
- The robustness has been confirmed by determining the specific cooling effect (SCE) of Maxsorb III/ethanol and silica gel/water pairs.
2. Adsorption Isotherm Models
3. Error Evaluation Function
4. Simulation Approach
- (a)
- Randomly select a vector from from a multivariate normal distribution with mean vector and variance–covariance matrix . We assume that the variances are small (0.01, 0.001, etc.), i.e., the variability in the choice of estimates from the GRG graph is not substantial.
- (b)
- Obtain the predicted values of the experimental outcomes by using the selected estimates and compute the corresponding RMSD’s.
- (c)
- Repeat (a) and (b) a large number (10,000) of times and compare the prediction performance of the models based on the empirical distributions of the RSMD’s.
5. Statistical Tools
5.1. The Box-and-Whisker Plot
5.2. Analysis of Variance (ANOVA)
5.3. Pairwise Test (Tukey’s HSD Test)
5.4. Non-Parametric Method
5.5. Kruskal–Wallis Rank-Sum Test
5.6. Wilcoxon Rank-Sum Test with Continuity Correction
6. Specific Cooling Effect
7. Results and Discussion
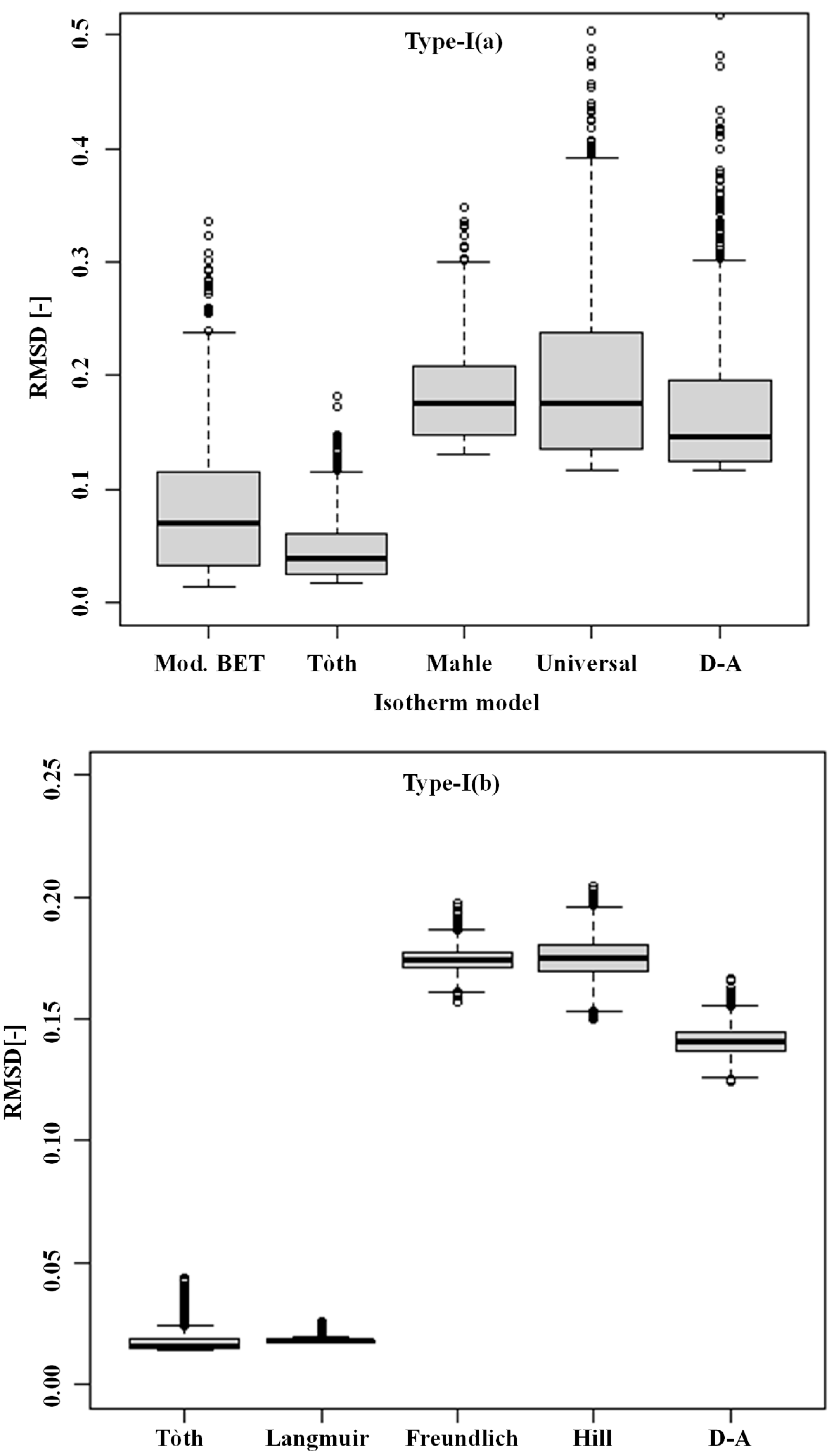
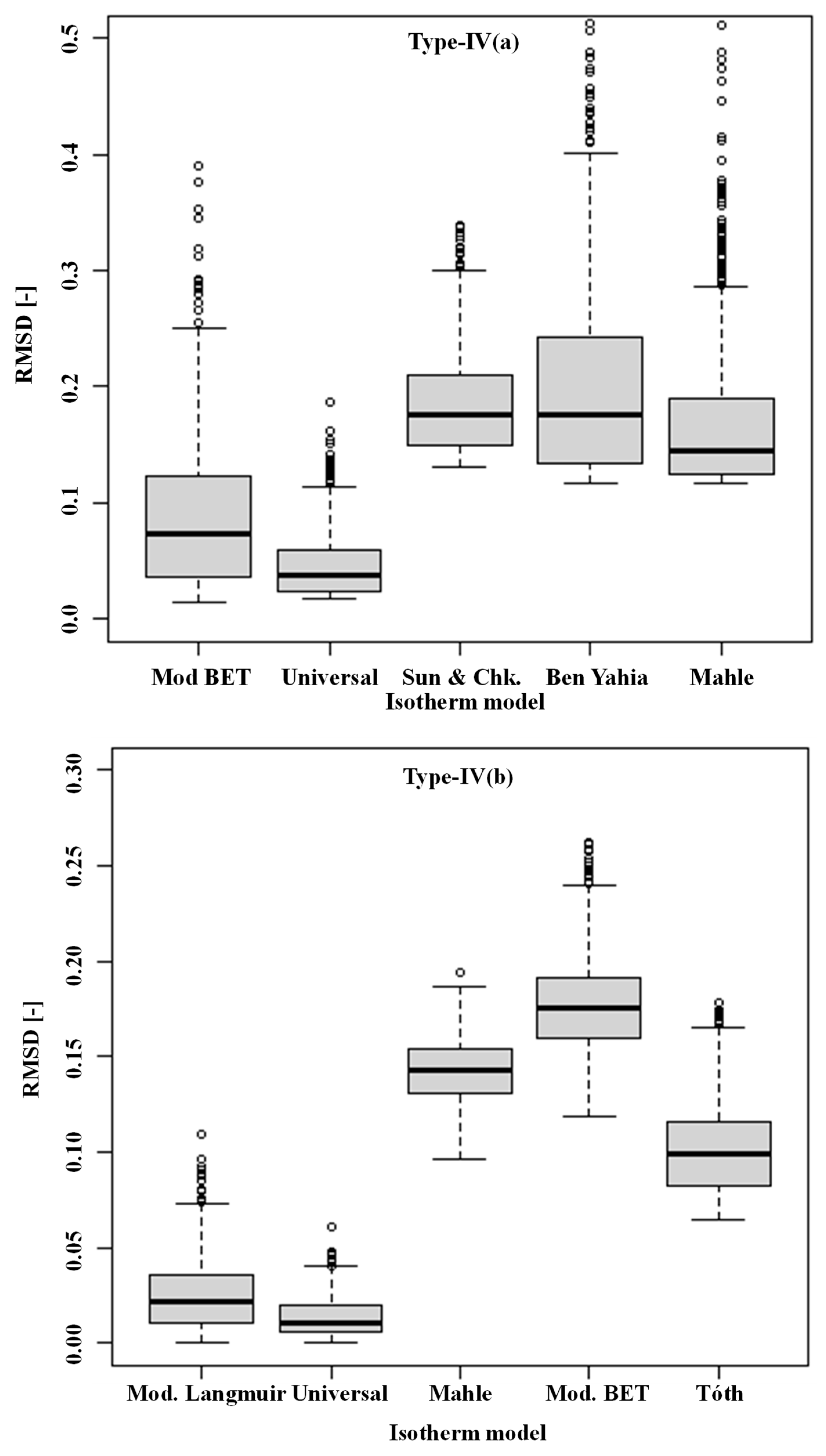
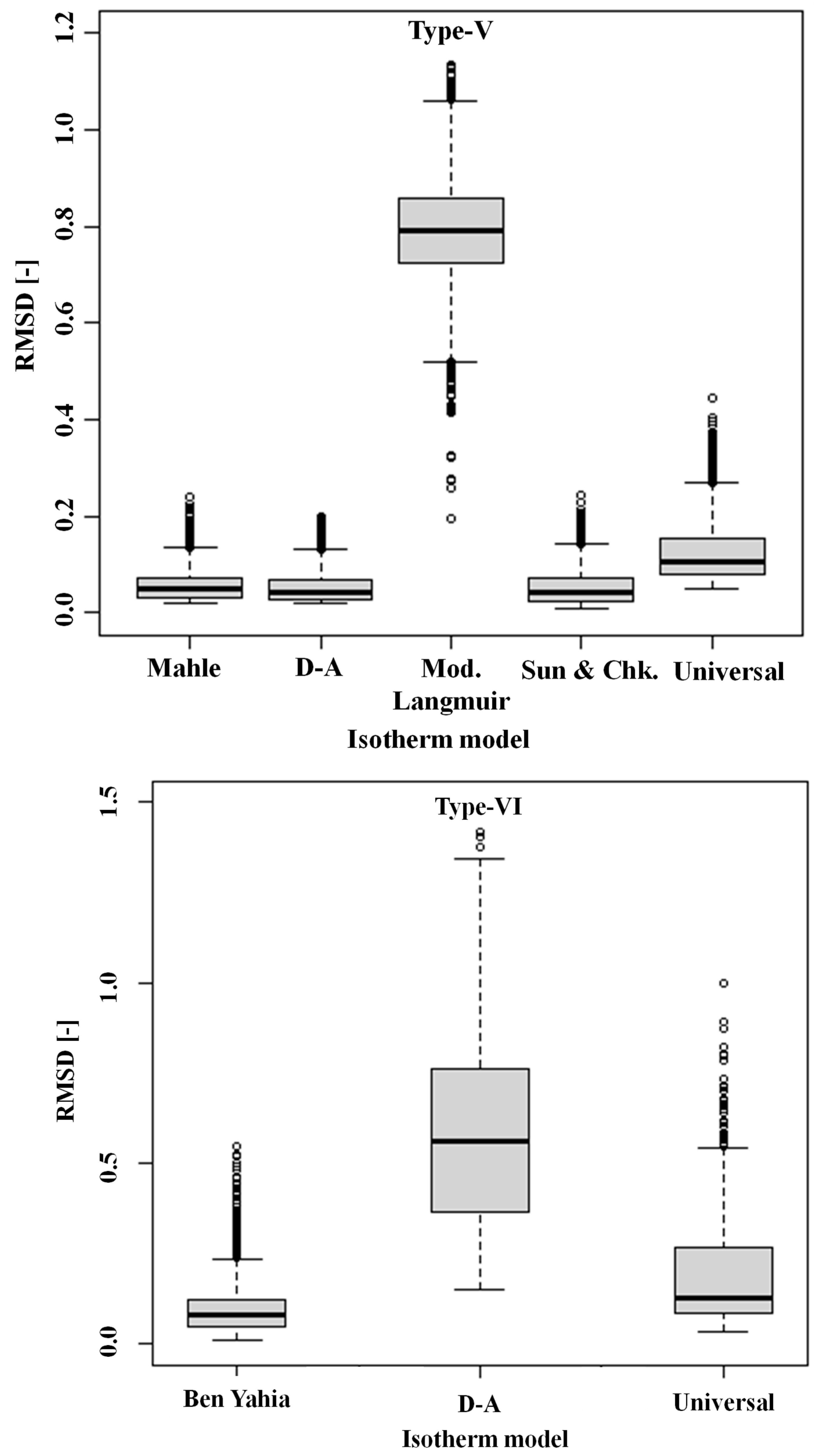
7.1. Box-and-Whisker Plot
7.2. Non-Parametric Test: Kruskal–Wallis Rank-Sum Test
7.3. Physical Description with Merit and Demerits of the IUPAC Isotherm Model
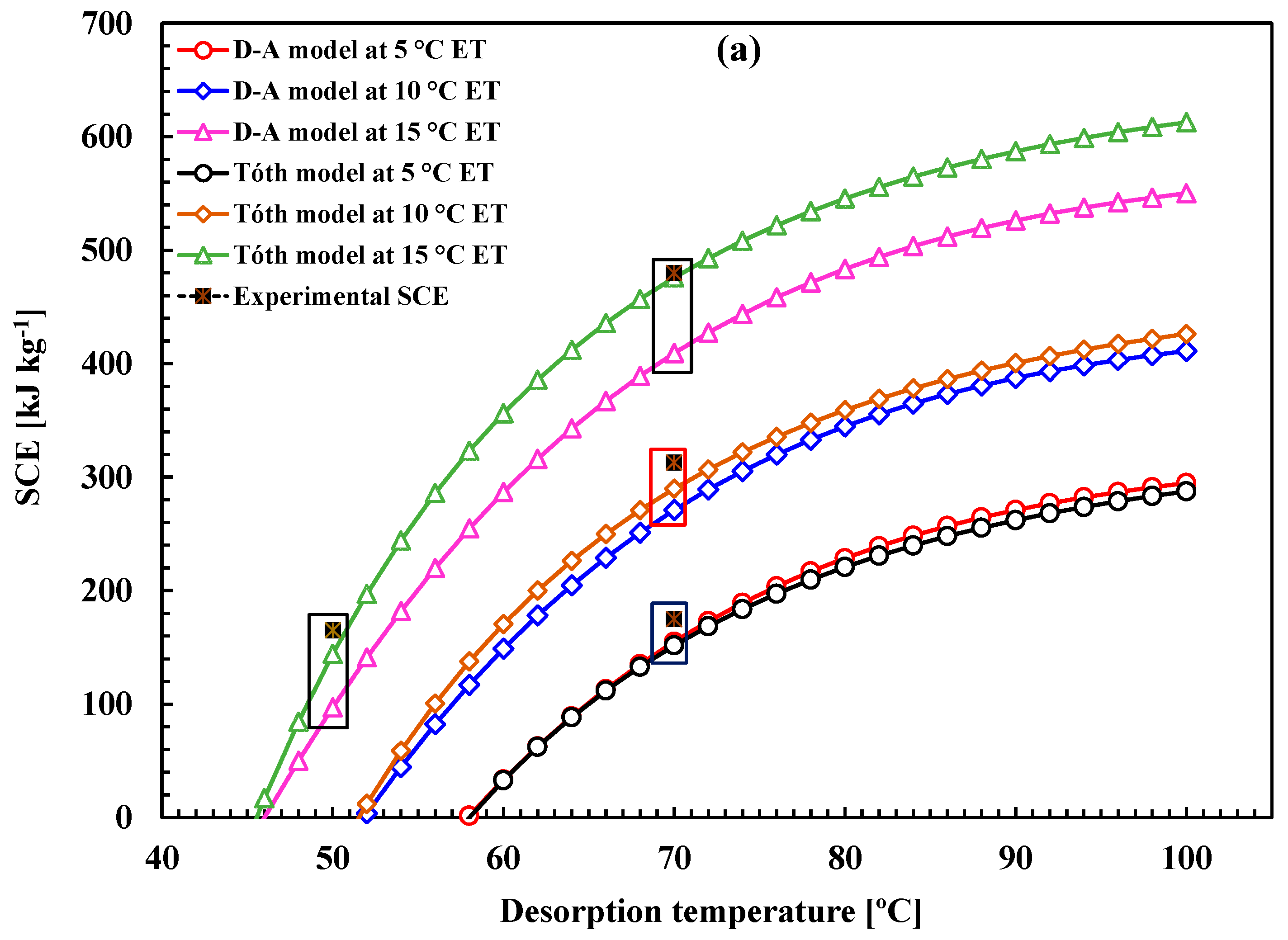
7.4. Specific Cooling Effect (SCE)
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Saha, B.B.; Koyama, S.; Kashiwagi, T.; Akisawa, A.; Ng, K.C.; Chua, H.T. Waste heat driven dual-mode, multi-stage, multi-bed regenerative adsorption system. Int. J. Refrig. 2003, 26, 749–757. [Google Scholar] [CrossRef]
- Palomba, V.; Aprile, M.; Motta, M.; Vasta, S. Study of sorption systems for application on low-emission fishing vessels. Energy 2017, 134, 554–565. [Google Scholar] [CrossRef]
- Ng, K.C.; Thu, K.; Saha, B.B.; Chakraborty, A. Study on a waste heat-driven adsorption cooling cum desalination cycle. Int. J. Refrig. 2012, 35, 685–693. [Google Scholar] [CrossRef]
- Balaras, C.A.; Grossman, G.; Henning, H.-M.; Ferreira, C.A.I.; Podesser, E.; Wang, L.; Wiemken, E. Solar air conditioning in Europe—An overview. Renew. Sustain. Energy Rev. 2007, 11, 299–314. [Google Scholar] [CrossRef]
- Saha, B.B.; El-Sharkawy, I.I.; Shahzad, M.W.; Thu, K.; Ang, L.; Ng, K.C. Fundamental and application aspects of adsorption cooling and desalination. Appl. Therm. Eng. 2016, 97, 68–76. [Google Scholar] [CrossRef] [Green Version]
- Jaiswal, A.K.; Mitra, S.; Dutta, P.; Srinivasan, K.; Srinivasa Murthy, S. Influence of cycle time and collector area on solar driven adsorption chillers. Sol. Energy 2016, 136, 450–459. [Google Scholar] [CrossRef]
- Islam, M.A.; Saha, B.B. TEWI Assessment of Conventional and Solar Powered Cooling Systems. In Solar Energy; Tyagi, H., Ed.; Springer Nature: Singapore, 2020; pp. 147–177. ISBN 9789811506758. [Google Scholar]
- Muttakin, M.; Islam, M.A.; Malik, K.S.; Pahwa, D.; Saha, B.B. Study on optimized adsorption chiller employing various heat and mass recovery schemes. Int. J. Refrig. 2020, 126, 222–237. [Google Scholar] [CrossRef]
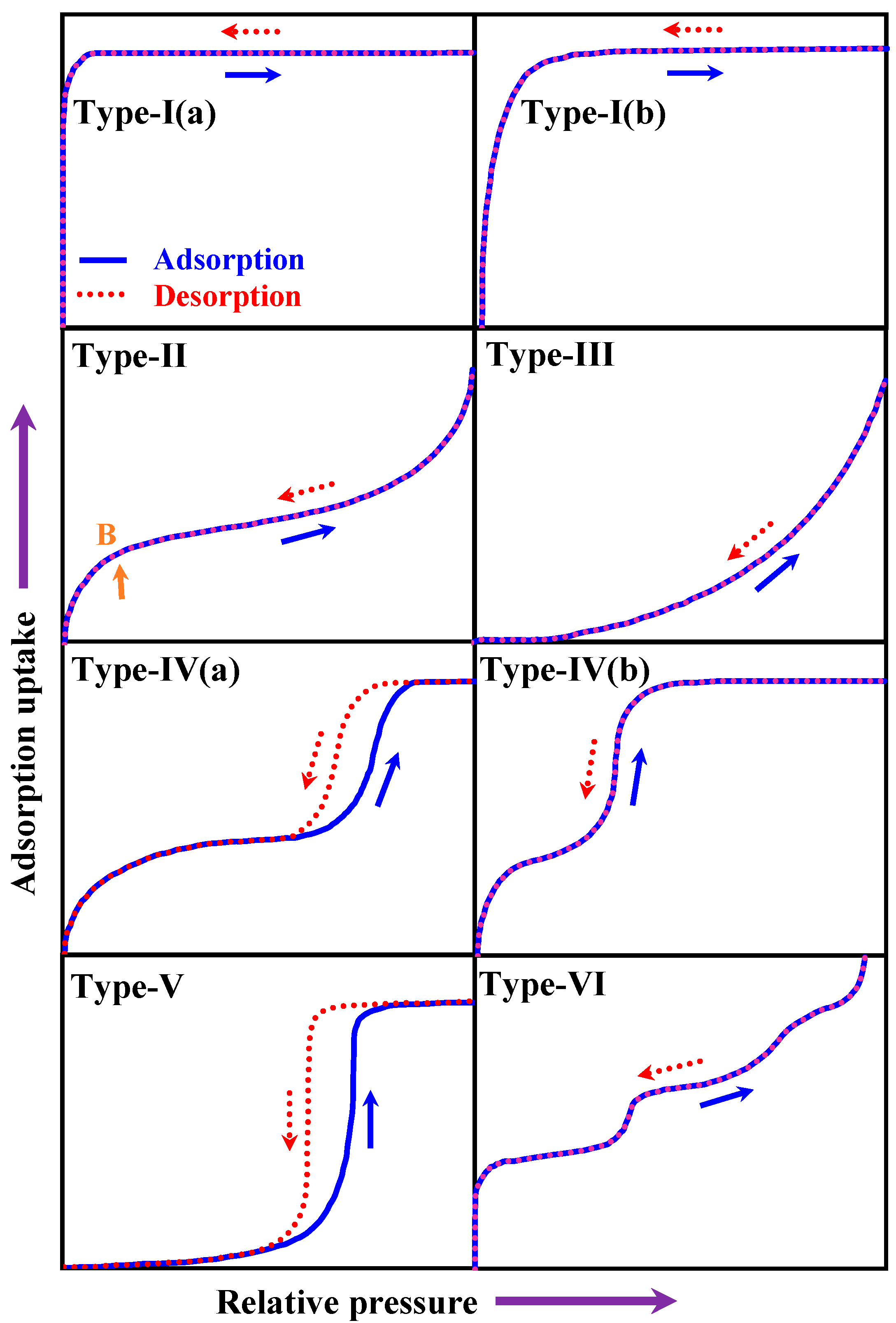
- Thommes, M.; Kaneko, K.; Neimark, A.V.; Olivier, J.P.; Rodriguez-Reinoso, F.; Rouquerol, J.; Sing, K.S.W. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef] [Green Version]
- Rocky, K.A.; Pal, A.; Rupam, T.H.; Nasruddin; Saha, B.B. Zeolite-graphene composite adsorbents for next generation adsorption heat pumps. Microporous Mesoporous Mater. 2021, 313, 110839. [Google Scholar] [CrossRef]
- Jahan, I.; Rupam, T.H.; Palash, M.L.; Rocky, K.A.; Saha, B.B. Energy efficient green synthesized MOF-801 for adsorption cooling applications. J. Mol. Liq. 2021, 117760. [Google Scholar] [CrossRef]
- Rahman, M.M.; Muttakin, M.; Pal, A.; Shafiullah, A.Z.; Saha, B.B. A Statistical Approach to Determine Optimal Models for IUPAC-Classified Adsorption Isotherms. Energies 2019, 12, 4565. [Google Scholar] [CrossRef] [Green Version]
- Muttakin, M.; Mitra, S.; Thu, K.; Ito, K.; Saha, B.B. Theoretical framework to evaluate minimum desorption temperature for IUPAC classified adsorption isotherms. Int. J. Heat Mass Transf. 2018, 122, 795–805. [Google Scholar] [CrossRef]
- Pal, A.; Thu, K.; Mitra, S.; El-Sharkawy, I.I.; Saha, B.B.; Kil, H.S.; Yoon, S.H.; Miyawaki, J. Study on biomass derived activated carbons for adsorptive heat pump application. Int. J. Heat Mass Transf. 2017, 110, 7–19. [Google Scholar] [CrossRef]
- Nebaghe, K.C.; El Boundati, Y.; Ziat, K.; Naji, A.; Rghioui, L.; Saidi, M. Comparison of linear and non-linear method for determination of optimum equilibrium isotherm for adsorption of copper(II) onto treated Martil sand. Fluid Phase Equilib. 2016, 430, 188–194. [Google Scholar] [CrossRef]
- Ringot, D.; Lerzy, B.; Chaplain, K.; Bonhoure, J.P.; Auclair, E.; Larondelle, Y. In vitro biosorption of ochratoxin A on the yeast industry by-products: Comparison of isotherm models. Bioresour. Technol. 2007, 98, 1812–1821. [Google Scholar] [CrossRef]
- Do, D.D. Adsorption Analysis: Equilibria and Kinetics: (With CD Containing Computer Matlab Programs); Imperial College Press: London, UK, 1998; Volume 2, ISBN 978-1-78326-224-3. [Google Scholar]
- Sun, B.; Chakraborty, A. Thermodynamic frameworks of adsorption kinetics modeling: Dynamic water uptakes on silica gel for adsorption cooling applications. Energy 2015, 84, 296–302. [Google Scholar] [CrossRef]
- Kumar, K.V.; Porkodi, K. Relation between some two- and three-parameter isotherm models for the sorption of methylene blue onto lemon peel. J. Hazard. Mater. 2006, 138, 633–635. [Google Scholar] [CrossRef]
- Karmaker, S.C.; Eljamal, O.; Saha, B.B. Response surface methodology for strontium removal process optimization from contaminated water using zeolite nanocomposites. Environ. Sci. Pollut. Res. 2021. [Google Scholar] [CrossRef]
- Rahman, M.M.; Pal, A.; Uddin, K.; Thu, K.; Saha, B.B. Statistical Analysis of Optimized Isotherm Model for Maxsorb III/Ethanol and Silica Gel/Water Pairs. Evergreen 2018, 5, 1–12. [Google Scholar] [CrossRef]
- Askalany, A.A.; Saha, B.B.; Uddin, K.; Miyzaki, T.; Koyama, S.; Srinivasan, K.; Ismail, I.M. Adsorption isotherms and heat of adsorption of difluoromethane on activated carbons. J. Chem. Eng. Data 2013, 58, 2828–2834. [Google Scholar] [CrossRef]
- Amankwah, K.A.G.; Schwarz, J.A. A modified approach for estimating pseudo-vapor pressures in the application of the Dubinin-Astakhov equation. Carbon N. Y. 1995, 33, 1313–1319. [Google Scholar] [CrossRef]
- Pal, A.; Uddin, K.; Rocky, K.A.; Thu, K.; Saha, B.B. CO2 adsorption onto activated carbon–graphene composite for cooling applications. Int. J. Refrig. 2019, 106, 558–569. [Google Scholar] [CrossRef]
- Rocky, K.A.; Pal, A.; Moniruzzaman, M.; Saha, B.B. Adsorption characteristics and thermodynamic property fields of polymerized ionic liquid and polyvinyl alcohol based composite/CO2 pairs. J. Mol. Liq. 2019, 294, 111555. [Google Scholar] [CrossRef]
- Allen, S.J.; Gan, Q.; Matthews, R.; Johnson, P.A. Comparison of optimised isotherm models for basic dye adsorption by kudzu. Bioresour. Technol. 2003, 88, 143–152. [Google Scholar] [CrossRef]
- Berdenova, B.; Pal, A.; Saha, B.B.; Kaltayev, A. Non-isothermal pore change model predicting CO2 adsorption onto consolidated activated carbon. Int. J. Heat Mass Transf. 2021, 177, 121480. [Google Scholar] [CrossRef]
- Foo, K.Y.; Hameed, B.H. Insights into the modeling of adsorption isotherm systems. Chem. Eng. J. 2010, 156, 2–10. [Google Scholar] [CrossRef]
- Rahman, M.M.; Karmaker, S.C.; Pal, A.; Eljamal, O.; Saha, B.B. Statistical techniques for the optimization of cesium removal from aqueous solutions onto iron-based nanoparticle-zeolite composites. Environ. Sci. Pollut. Res. 2020, 28, 12918–12931. [Google Scholar] [CrossRef]
- Mahle, J.J. An adsorption equilibrium model for Type 5 isotherms. Carbon N. Y. 2002, 40, 2753–2759. [Google Scholar] [CrossRef]
- Peleg, M. Assessment of a semi-empirical four parameter general model for sigmoid moisture sorption isotherm. J. Food Process Eng. 1993, 16, 21–37. [Google Scholar] [CrossRef]
- Maroulis, Z.B.; Tsami, E.; Marinos-Kouris, D.; Saravacos, G.D. Application of the GAB model to the moisture sorption isotherms for dried fruits. J. Food Eng. 1988, 7, 63–78. [Google Scholar] [CrossRef]
- McMinn, W.A.M.; Magee, T.R.A. Thermodynamic properties of moisture sorption of potato. J. Food Eng. 2003, 60, 157–165. [Google Scholar] [CrossRef]
- Kayal, S.; Baichuan, S.; Saha, B.B. Adsorption characteristics of AQSOA zeolites and water for adsorption chillers. Int. J. Heat Mass Transf. 2016, 92, 1120–1127. [Google Scholar] [CrossRef]
- Zou, J.; Rezaee, R. A prediction model for methane adsorption capacity in shale gas reservoirs. Energies 2019, 12, 280. [Google Scholar] [CrossRef] [Green Version]
- Sun, B.; Chakraborty, A. Thermodynamic formalism of water uptakes on solid porous adsorbents for adsorption cooling applications. Appl. Phys. Lett. 2014, 104, 201901. [Google Scholar] [CrossRef]
- Yahia, M.B.; Khalfaoui, M.; Hachicha, M.A.; Lamine, A.B.; Torkia, Y.B.; Knani, S. Models for Type VI Adsorption Isotherms from a Statistical Mechanical Formulation. Adsorpt. Sci. Technol. 2013, 31, 341–357. [Google Scholar] [CrossRef]
- Aouaini, F.; Knani, S.; Ben Yahia, M.; Ben Lamine, A. Statistical physics studies of multilayer adsorption isotherm in food materials and pore size distribution. Phys. A Stat. Mech. Its Appl. 2015, 432, 373–390. [Google Scholar] [CrossRef]
- Ng, K.C.; Burhan, M.; Shahzad, M.W.; Ismail, A. Bin A Universal Isotherm Model to Capture Adsorption Uptake and Energy Distribution of Porous Heterogeneous Surface. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Saha, B.B.; Jribi, S.; Koyama, S.; El-Sharkawy, I.I. Carbon dioxide adsorption isotherms on activated carbons. J. Chem. Eng. Data 2011, 56, 1974–1981. [Google Scholar] [CrossRef]
- Vardeman, S.B.; Walpole, R.E.; Myers, R.H.; Miller, I.; Freund, J.E. Probability and Statistics for Engineers and Scientists. Probability and Statistics for Engineers; Pearson Education Inc.: Upper Saddle River, NJ, USA, 1986; Volume 81, ISBN 0132047675. [Google Scholar]
- Hogg, R.V.; Tanis, E.A.; Zimmerman, D.L. Probability and Statistical Interference; Pearson Education Inc.: Upper Saddle River, NJ, USA, 2003; ISBN 9780133936544. [Google Scholar]
- Saville, D.J. Multiple comparison procedures: The practical solution. Am. Stat. 1990, 44, 174–180. [Google Scholar] [CrossRef]
- Altman, D.G.; Bland, J.M. Practical statistics for medical research. BMJ 1995, 310, 170. [Google Scholar] [CrossRef] [Green Version]
- Siegel, S. Nonparametric Statistics. Am. Stat. 1957, 11, 13–19. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, W. A SAS macro for testing differences among three or more independent groups using Kruskal-Wallis and Nemenyi tests. J. Huazhong Univ. Sci. Technol.-Med. Sci. 2012, 32, 130–134. [Google Scholar] [CrossRef] [PubMed]
- Bergmann, R.; Ludbrook, J. Different outcomes of the wilcoxon—mann—whitney test from different statistics packages. Am. Stat. 2000, 54, 72–77. [Google Scholar] [CrossRef]
- Uddin, K.; El-Sharkawy, I.I.; Miyazaki, T.; Baran Saha, B.; Koyama, S. Thermodynamic analysis of adsorption cooling cycle using ethanol-surface treated maxsorb III Pairs. Evergreen 2014, 1, 25–31. [Google Scholar] [CrossRef]





| Isotherm | Nonlinear Form | Parameters | Reference |
|---|---|---|---|
| Freundlich | W0, n | [14,15,16] | |
| Langmuir | W0, Q, b0 | [17,18,19,20] | |
| D-A | W0, E, n | [21,22] | |
| Mod. (D-A) | where, and | W0, E, n, K | [23,24] |
| Tόth | W0, b0, Q, t | [25,26,27] | |
| Hill | W0, nH, KD | [16,28,29] | |
| Mahle | ; where, and | Ws, A0, A1, B | [30] |
| BET | ; and | Vm, C | [17,31] |
| Modified BET | Vm, C, K | [12,17] | |
| GAB | ; where, ; ; and | Vm, C0, K0, ΔH1 and ΔH2 | [32,33] |
| Mod. Langmuir | ; Where, | W0, z, β, α, n1, ϕm, m | [34,35] |
| Sun and Chakraborty | ; Where, | W0, Qst *, m, α | [11,34,36] |
| Ben Yahia | ; and | n1, n2, n3, n4, NM1, NM2, NM3, NM4, P1, P2, P3, P4 | [37,38] |
| Universal | ; Where, | q*, αi, εoi, mi | [13,39] |
| Type-I(a) (Carbon K4-700/N2 pair at 77 K) | |
| Model | Parameters |
| Mahle | W0 = 0.62, A0 = 0.045, A1 = −720, B = 0.01 |
| Universal | W0 = 0.709, ε01 = 4120, ε02 = 0.0345, m1 = 320, m2 = 1000, α1 = 0.71, α2 = 0.29 |
| D-A | W0 = 0.607, E = 320, n = 3.31 |
| Tóth | W0 = 0.61, b0 = 9.79 × 10−5, Q = 6013.84, t = 1.3 |
| Mod BET | Vm = 0.594, C = 5334.78, k = 0.0446 |
| Type-I(b) (Maxsorb III/ethanol) | |
| Freundlich | W0 = 1.482082, n = 2.214175 |
| Langmuir | W0 = 1.38, b0 = 3.10 × 10−9, Q = 48,600 |
| D-A | W0 = 1.17, E = 143.00, n = 1.9 |
| Tóth | W0 = 1.2, b0 = 3.10 × 10−9, Q = 47,635, t = 1.69 |
| Hill | W0 = 1.266, nh = 1.321, KD = 0.080297 |
| Type-II (Alumina/water) | |
| Mod BET | Vm = 0.21, C = 25.5, k = 0.8186 |
| Universal | W0 = 1.22, ε01 = 217.88, ε02 = 0.1762.69, m1 = 262.59, m2 = 3231.58, α1 = 0.42, α2 = 0.57 |
| D-A | W0 = 1.068, E = 73.72, n = 0.504 |
| Tóth | W0 = 1.23, b0 = 2.32 × 10−3, Q = 16,932.30, t = 0.4165 |
| Langmuir | W0 = 0.891, b0 = 3.69 × 10−5, Q = 24,041.91 |
| Type-III (Dried raisins/moisture) | |
| GAB | Vm = 10.517, C0 = 0.0011, K0 = 1.767, ΔH1 = 18.25, ΔH2 = −1.47 |
| Mod BET | Vm = 10.421, C = 1.47, k = 0.980 |
| Universal | W0 = 120, ε01 = 547.67, ε02 = 120.12, m1 = 199.95, m2 = 1846.68, α1 = 0.65, α2 = 0.35 |
| Mod Langmuir | W0 = 90.24, z = 0.1416, β = 0.0859, α = 0.958, n1 = 0.95, ϕm = 3.22, m = 0.7632 |
| Sun and Chakrabarty | W0 = 93.3581, Qst* = 3166.83, m = 2.449, α = 1.81 × 10−6 |
| Type-IV(a) (PVDC/water) | |
| Universal | W0 = 0.36, ε01 = 2096.47, ε02 = 5613.18, m1 = 478.42, m2 = 4025.91, α1 = 0.67, α2 = 0.33 |
| Ben Yahia | n1 = 1.30, n2 = 0.13, n3 = 0.032, n4 = 1.3, NM1 = 0.123, NM2 = 0.150, NM3 = 0.495, NM4 = 0.399 |
| Mod BET | Vm = 1.0533, C = 453.92, k = 0.00112 |
| Sun and Chakrabarty | W0 = 0.341, Qst* = 3497.21, m = 2.099, α = 9.00 × 10−7 |
| Mahle | W0 = 0.35, A0 = 0.89, A1 = −575, B = 0.2 |
| Type-IV(b) (IRMOF-74-V-hex/nitrogen) | |
| Universal | W0 = 2.85, ε01 = 852.32, ε02 = 2364.60, m1 = 138.23, m2 = 608.42, α1 = 0.54, α2 = 0.46 |
| Mod BET | Vm = 0.21, C = 28, k = 0.8186 |
| Mahle | W0 = 0.21, A0 = 0.6, A1 = −650, B = 0.075 |
| Mod Langmuir | W0 = 80, z = 0.119, β = 0.03622, α = 0.9941, n1 = 0.98, ϕm = 3.22, m = 0.478 |
| Tóth | W0 = 2.9, b0 = 0.0001041, Q = 4302.19, t = 1.3183 |
| Type-V (FAM-Z01/water) | |
| Sun and Chakrabarty | W0 = 0.2042, Qst* = 3027.841, m = 4.893, α = 9 × 10−7 |
| Mod Langmuir | W0 = 0.210, z = 2.955, β = 0.60086, α = 0, n1 = −1.5, ϕm = 510.79, m = 1.82 |
| Mahle | W0 = 0.21, A0 = 0.60, A1 = −650, B = 0.075 |
| DA | W0 = 0.212, E = 3985.785, n = 3.7075 |
| Universal | W0 = 0.25, ε01 = 3841.16, ε02 = 0.01, m1 = 530.08, m2 = 2583.121, α1 = 0.67, α2 = 0.33 |
| Type-VI (MgO/methane) | |
| Universal | W0 = 12, ε01 = 3450, ε02 = 1015.22, ε03 = 235, ε04 = 45, m1 = 342, m2 = 24.96, m3 = 135.21, m4 = 93.44, α1 = 0.062, α2 = 0.05, α3 = 0.55, α4 = 0.40 |
| Ben Yahia | n1 = 2.95, n2 = 19.52, n3 = 77.27, n4 = 23.26, NM1 = 0.252, NM2 = 0.036, NM3 = 0.007, NM4 = 0.071, P1 = 0.70, P2 = 20.82, P3 = 36.06, P4 = 47.10 |
| Mod. Langmuir | W0 = 4, z = 4.38, β = 0.044, α = 0.033, n1 = −1.5, ϕm = 44.77, m = 0.683 |
| Mahle | W0 = 4.457, A0 = 2.013 × 10−5, A1 = 62.92, B = 0.0927 |
| D-A | W0 = 4.012, E = 1219.71, n = 0.9 |
| DF | SS | Mean SS | F-Value | p-Value | |
|---|---|---|---|---|---|
| Type-I(a) | 4 | 261.72 | 65.43 | 2,532,683 | <2 × 10−16 *** |
| Type-I(b) | 4 | 25.23 | 6.308 | 8452 | <2 × 10−16 *** |
| aType-II | 3 | 82.69 | 27.56 | 306,633 | <2 × 10−16 *** |
| Type-III | 4 | 24.35 | 6.0875 | 2534 | <2 × 10−16 *** |
| Type-IV(a) | 4 | 4896 | 1224 | 52,346 | <2 × 10−16 *** |
| Type-IV(b) | 4 | 112.95 | 28.23 | 49,863 | <2 × 10−16 *** |
| Type-V | 4 | 4184 | 1046 | 318,711 | <2 × 10−16 *** |
| Type-VI | 4 | 3524.18 | 881.04 | 214,241 | <2 × 10−16 *** |
| Type | df | Chi-Square (χ2) | p-Value |
|---|---|---|---|
| Type-I(a) | 4 | 25,356 | 2.16 × 10−13 |
| Type-I(b) | 4 | 43,636 | 2.21 × 10−14 |
| Type-II | 3 | 28,296 | 2.22 × 10−16 |
| Type-III | 4 | 54,263 | 1.48 × 10−11 |
| Type-IV(a) | 4 | 35,421 | 2.25 × 10−13 |
| Type-IV(b) | 4 | 29,653 | 3.25 × 10−15 |
| Type-V | 4 | 24,806 | 2.20 × 10−16 |
| Type-VI | 4 | 35,412 | 2.22 × 10−16 |
| Type-I(a) | ||||
| Model | Tóth | D-A | Mod BET | Universal |
| D-A | 1.7 × 10−7 (2.61 × 10−8) | - | - | - |
| Mod BET | 1.6 × 10−9 (1.96 × 10−16) | 1.8 × 10−15 (2.21 × 10−16) | - | - |
| Universal | 1.8 × 10−7 (1.35 × 10−16) | 0.00360 (2.31 × 10−16) | 2.2 × 10−11 (2.36 × 10−16) | |
| Mahle | 3.1 × 10−4 (2.34 × 10−16) | 2.1 × 10−12 (1.74 × 10−16) | 1.2 × 10−5 (2.23 × 10−16) | 2.9 × 10−7 (5.3 × 10−16) |
| Type-I(b) | ||||
| Tóth | Langmuir | Freundlich | Hill | |
| Langmuir | 1.3 × 10−11 (2 × 10−16) | - | - | - |
| Freundlich | 2.3 × 10−13 (2 × 10−16) | 2.5 × 10−8 (2 × 10−16) | - | - |
| Hill | 0.00021 (2 × 10−16) | 4.2 × 10−5 (2 × 10−16) | 1.8 × 10−16 (2 × 10−16) | |
| D-A | 0.00032 (2 × 10−16) | 2.3 × 10−6 (2 × 10−16) | 3.2 × 10−16 (2 × 10−16) | 2.6 × 10−8 (2 × 10−16) |
| Type-II | ||||
| Mod BET | Universal | D-A | ||
| Universal | 2.1 × 10−15 (2 × 10−16) | - | - | |
| D-A | 0.00898 (2 × 10−16) | 1.6 × 10−14 (2 × 10−16) | - | |
| Tóth | 3.5 × 10−12 (2 × 10−16) | 3.5 × 10−15 (2 × 10−16) | 2.6 × 10−11 (2 × 10−16) | |
| Type-III | ||||
| GAB | Mod BET | Universal | D-A | |
| Mod BET | 1.9 × 10−16 (2.10 × 10−16) | - | - | - |
| Universal | 2.3 × 10−14 (1.96 × 10−16) | 6.5 × 10−14 (2.21 × 10−16) | - | - |
| D-A | 5.9 × 10−14 (1.35 × 10−16) | 2.3 × 10−13 (2.31 × 10−16) | 3.1 × 10−12 (2.36 × 10−16) | |
| Sun and Chk | 2.6 × 10−15 (2.34 × 10−16) | 3.5 × 10−14 (1.74 × 10−16) | 2.8 × 10−15 (2.23 × 10−16) | 2.4 × 10−14 (5.3 × 10−16) |
| Type-IV(a) | ||||
| Mod BET | Universal | Sun and Chk | Ben Yahia | |
| Universal | 2.3 × 10−8 (2.10 × 10−16) | - | - | - |
| Sun and Chk | 1.8 × 10−9 (1.96 × 10−16) | 3.4 × 10−10 (2.21 × 10−16) | - | - |
| Ben Yahia | 3.6 × 10−11 (1.35 × 10−16) | 2.4 × 10−13 (2.31 × 10−16) | 2.7 × 10−15 (2.36 × 10−16) | |
| Mahle | 2.8 × 10−8 (2.34 × 10−16) | 3.1 × 10−10 (1.74 × 10−16) | 2.5 × 10−10 (2.23 × 10−16) | 3.2 × 10−16 (5.3 × 10−16) |
| Type-IV(b) | ||||
| Mod Langmuir | Universal | Mahle | Mod BET | |
| Universal | 2.4 × 10−15 (2.10 × 10−16) | - | - | - |
| Mahle | 2.3 × 10−14 (1.96 × 10−16) | 1.4 × 10−15 (2.21 × 10−16) | - | - |
| Mod BET | 2.1 × 10−12 (1.35 × 10−16) | 1.9 × 10−13 (2.31 × 10−16) | 2.2 × 10−12 (2.36 × 10−16) | |
| Tóth | 2.5 × 10−14 (2.34 × 10−16) | 3.4 × 10−11 (1.74 × 10−16) | 3.4 × 10−16 (2.23 × 10−16) | 2.4 × 10−16 (5.3 × 10−16) |
| Type-V | ||||
| Mahle | D-A | Universal | Sun and Chk | |
| D-A | 2.1 × 10−10 (7.98 × 10−4) | - | - | - |
| Universal | 3.1 × 10−12 (1.96 × 10−16) | 1.8 × 10−9 (2.21 × 10−16) | - | - |
| Sun and Chk | 2.7 × 10−5 (1.13 × 10−4) | 0.7158 (0.35142) | 2.3 × 10−8 (2.36 × 10−16) | |
| Mod Langmuir | 2.7 × 10−14 (2.34 × 10−16) | 1.6 × 10−12 (1.74 × 10−16) | 3.4 × 10−15 (2.23 × 10−16) | 2.9 × 10−13 (5.3 × 10−16) |
| Type-VI | ||||
| Ben Yahia | Universal | D-A | Mod. Langmuir | |
| Universal | 2.2 × 10−2 (2.10 × 10−3) | - | - | - |
| D-A | 3.1 × 10−12 (2.56 × 10−12) | 1.3 × 10−12 (3.21 × 10−12) | - | - |
| Mod. Langmuir | 3.6 × 10−10 (2.51 × 10−13) | 3.9 × 10−10 (5.23 × 10−8) | 3.5 × 10−10 (7.65 × 10−8) | |
| Mahle | 2.8 × 10−9 (3.51 × 10−11) | 4.3 × 10−7 (1.74 × 10−12) | 3.2 × 10−12 (4.23 × 10−11) | 3.6 × 10−14 (3.3 × 10−13) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, M.M.; Shafiullah, A.Z.; Pal, A.; Islam, M.A.; Jahan, I.; Saha, B.B. Study on Optimum IUPAC Adsorption Isotherm Models Employing Sensitivity of Parameters for Rigorous Adsorption System Performance Evaluation. Energies 2021, 14, 7478. https://doi.org/10.3390/en14227478
Rahman MM, Shafiullah AZ, Pal A, Islam MA, Jahan I, Saha BB. Study on Optimum IUPAC Adsorption Isotherm Models Employing Sensitivity of Parameters for Rigorous Adsorption System Performance Evaluation. Energies. 2021; 14(22):7478. https://doi.org/10.3390/en14227478
Chicago/Turabian StyleRahman, Md. Matiar, Abu Zar Shafiullah, Animesh Pal, Md. Amirul Islam, Israt Jahan, and Bidyut Baran Saha. 2021. "Study on Optimum IUPAC Adsorption Isotherm Models Employing Sensitivity of Parameters for Rigorous Adsorption System Performance Evaluation" Energies 14, no. 22: 7478. https://doi.org/10.3390/en14227478
APA StyleRahman, M. M., Shafiullah, A. Z., Pal, A., Islam, M. A., Jahan, I., & Saha, B. B. (2021). Study on Optimum IUPAC Adsorption Isotherm Models Employing Sensitivity of Parameters for Rigorous Adsorption System Performance Evaluation. Energies, 14(22), 7478. https://doi.org/10.3390/en14227478