Control Strategies of DC Microgrids Cluster: A Comprehensive Review
Abstract
:1. Introduction
- A complete review of various control schemes covering centralized, decentralized, distributed, and hierarchical methods in DC multiple MGs is presented.
- This paper provides a detailed comparative discussion on challenges faced with the control strategies of DC MGCs presented in the existing literature.
- Possible areas of research and future trends of DC MGCs are proposed.
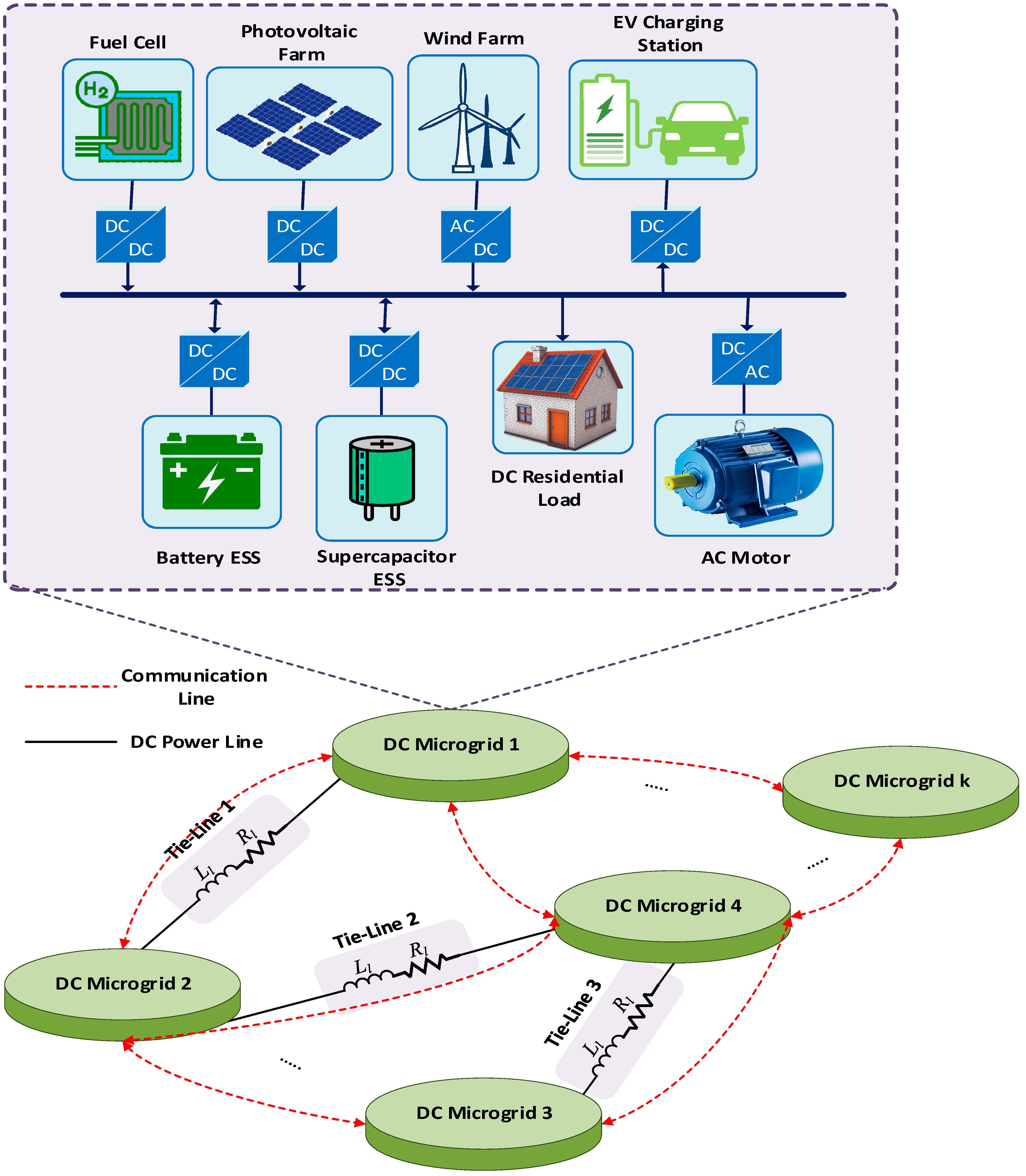
2. Multiple DC Microgrids: Architecture
3. Control Strategies
3.1. Centralized Control Methods
3.2. Decentralized Control Methods
3.3. Distributed Control Methods
3.4. Hierarchical Control Methods
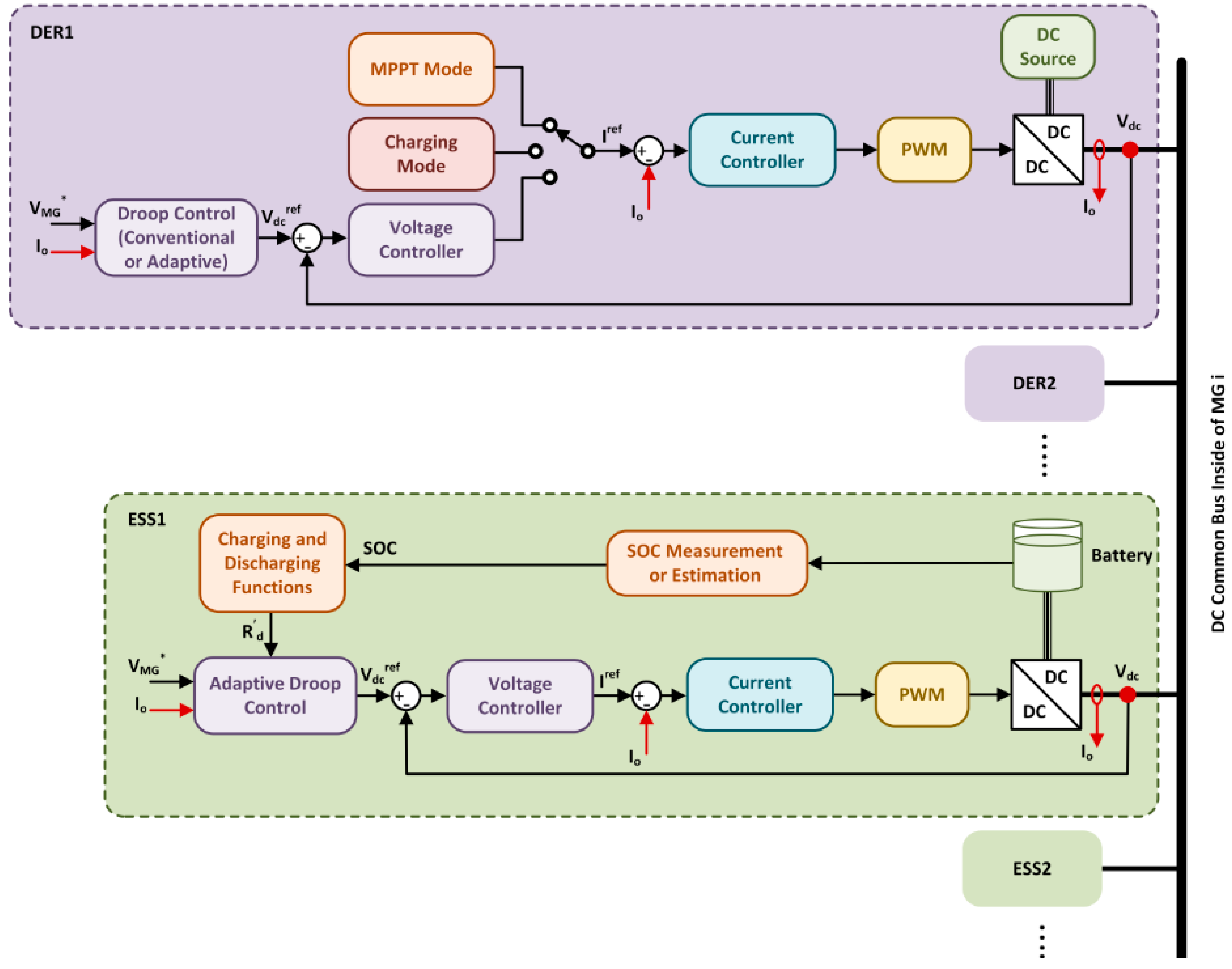
3.4.1. Primary Control Layer
A. DC–DC Power Converters
Droop Control Strategies
B. Traditional Droop Control
C. Adaptive Droop Control
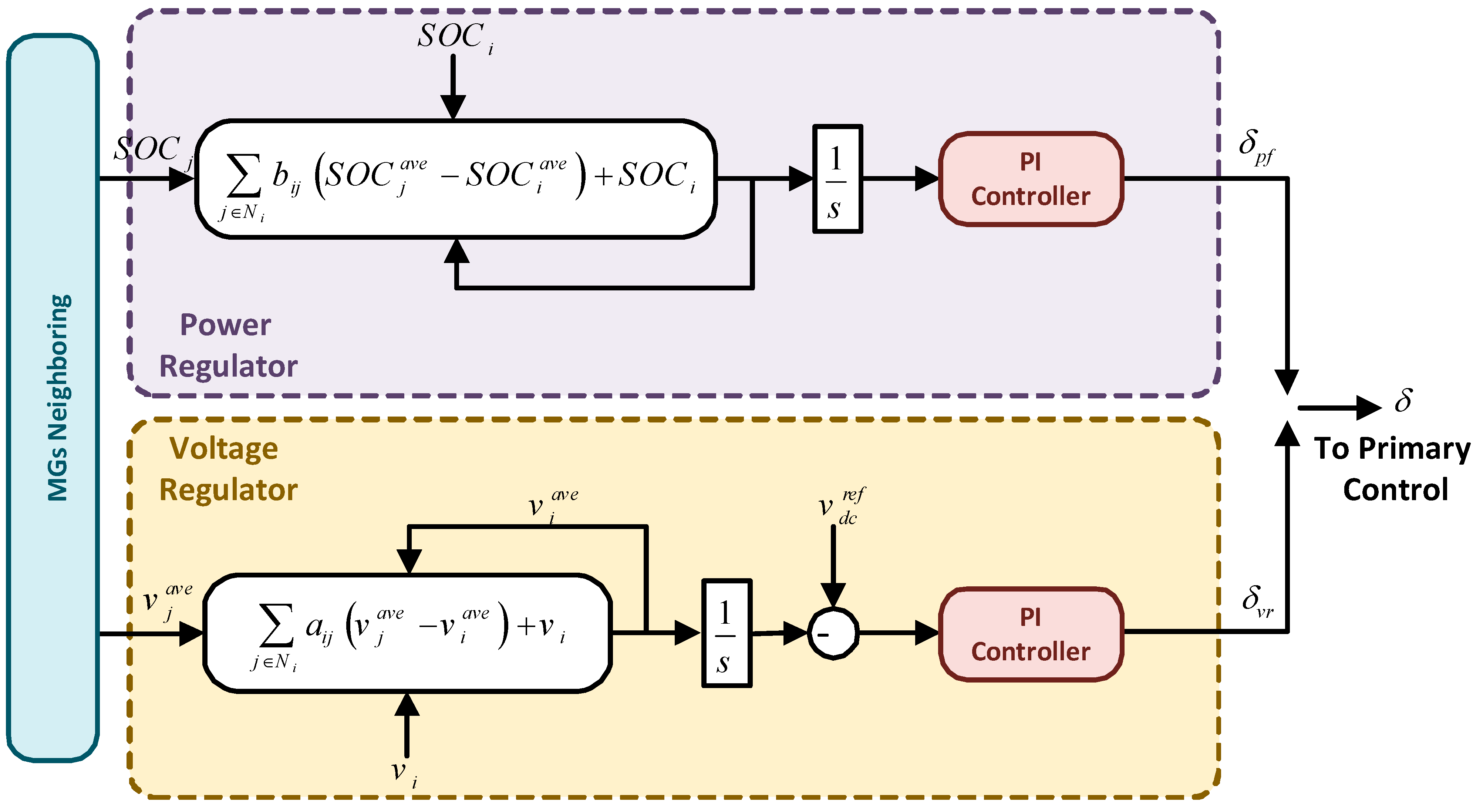
3.4.2. Secondary Control Layer
3.4.3. Tertiary Control Layer
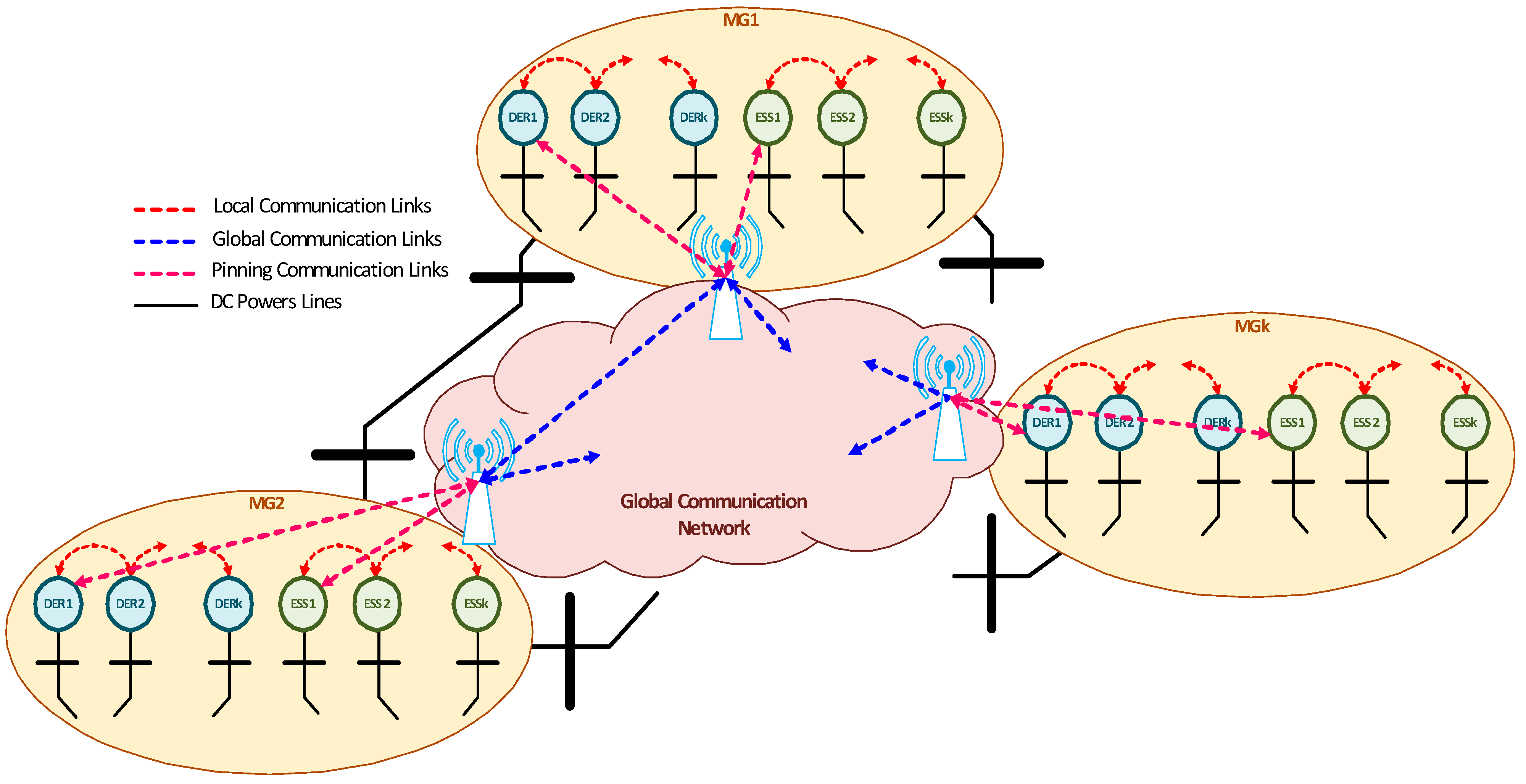
4. Consensus Protocols of the Global Control Layer
4.1. Non-Pinning Consensus Protocol
4.2. Pinning Consensus Protocol
5. Findings and Discussions
- (i)
- The centralized control strategy is the least considered technique in recent years.
- (ii)
- Real-time data of both load demand and RES have not been considered to validate the proposed control methods.
- (iii)
- There is no emphasis on load forecasting, which is vital to be considered, although load demand is varied over time.
- (iv)
- Classical PI controllers are dominant in all control levels, which may not always be able to face uncertainties or unpredictable conditions.
- (v)
- Communication networks are required to transfer data, whether to the central controller or among neighboring MGs. Hence, the effect of the communication delays on the cluster’s performance is noticeable in some articles.
- (vi)
- Linear consensus protocol-based point is usually used in coordinating MG in a cluster, so it may not be able to experience the abrupt fluctuations in load demand and generated power; however, the fixed-time and finite time consensus approaches have been considered in recent years to overcome the defects of the infinite time consensus method.
- (vii)
- Although the importunacy of the pinning approach in simplifying communication networks and accordingly cost reduction, it has not been adopted on a large scale in microgrid clusters.
- (viii)
- It can be easily noticed that a fixed-time consensus distributed hierarchy control strategy based on a pinning-based approach can be chosen as the best option to be adopted in coordinating DC MGs in a cluster.
- Forecasting renewable energy sources and load is considered an essential factor that needs to be included in future research because of its importunacy in improving system reliability. From the literature, it is noticed that there is no holistic model that can forecast the amount of solar radiation, temperature, wind speed, load demand, and SOCs of the batteries simultaneously; however, only one article presents a model that includes MGs mentioned parameters by using hybrid machine learning algorithms [101]; therefore, a new model that includes parameters in [101] and SOCs of the batteries can be forecasted by means of hybrid machine learning algorithms that need to be considered in future research.
- Machine learning can be used as a decision-maker instead of a consensus. By adopting this new technique, the system can be able to predict any disturbance that may occur because of uncertainty in the load and renewable energy sources and other disturbances.
- PSO, GA, and consensus algorithms are the main algorithms that have been used in the literature to coordinate the global control layer in microgrids. Hybridization among them would be a better choice to be adopted in future research.
- Classical PI controllers are dominant in the literature as the main controller for both local and global control layers. These controllers can be replaced by new controllers such as non-linear, predictive, super-twisting sliding mode controllers (STMC); thereby, the system will be able to resist any abnormal operating conditions that may occur because of uncontrollable loads and the intermittency of renewable energy sources.
- A classical tuning method is usually used in the literature to determine controllers’ parameters; however, meta-heuristic algorithms are preferable options to be used to optimize the parameters of classical and advanced controllers.
- Repetitive, predictive controllers, STMC, and artificial neural networks can be used in the local control layer (LCL) to enhance the performance of droop and adaptive control techniques. Moreover, metaheuristics algorithms can play a vital role in improving the LCL performance.
- PnP operation is a highly significant feature that needs to be focused on to realize the stable operation of the MGs cluster by isolating faulty parts in case of any abnormal conditions may occur. Still, it is found that there is not much focus on the topic in the DC MG clusters.
- Communication delays are one of the issues that negatively impact the performance of the MGs cluster. Some communication protocols, including UWB and WIFI, have been proposed in [15] that can be used to overcome this issue.
- A bypass coupler can be used in the DC MGs cluster to boost its reliability in case of any fault in the main feeder that provides power to a specific MG in a cluster.
- Based on item I in the main findings, a holistic model can be designed by adopting the best control technique in item I, including items A, D, and E from recommendations points.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumaravel, S.; Ashok, S. Adapted multilayer feedforward ANN based power management control of solar photovoltaic and wind integrated power system. In Proceedings of the ISGT2011-India, Kollam, India, 1–3 December 2011. [Google Scholar] [CrossRef]
- Iqbal, S.; Khan, H.A.; Nasir, M.; Guerrero, J.M. Efficient Resource Sizing and Placement for Clustered Solar DC Microgrids. In Proceedings of the IEEE Power Engineering Society Transmission and Distribution Conference, Chicago, IL, USA, 12–15 October 2020. [Google Scholar] [CrossRef]
- Kollimalla, S.K.; Mishra, M.K.; Narasamma, N.L. Design and analysis of novel control strategy for battery and supercapacitor storage system. IEEE Trans. Sustain. Energy 2014, 5, 1137–1144. [Google Scholar] [CrossRef]
- Han, Y.; Ning, X.; Yang, P.; Xu, L. Review of Power Sharing, Voltage Restoration and Stabilization Techniques in Hierarchical Controlled DC Microgrids. IEEE Access 2019, 7, 149202–149223. [Google Scholar] [CrossRef]
- Wahid, A.; Iqbal, J.; Qamar, A.; Ahmed, S.; Basit, A.; Ali, H.; Aldossary, O.M. A novel power scheduling mechanism for islanded DC microgrid cluster. Sustainability 2020, 12, 6918. [Google Scholar] [CrossRef]
- Gao, F.; Kang, R.; Cao, J.; Yang, T. Primary and secondary control in DC microgrids: A review. J. Mod. Power Syst. Clean Energy 2019, 7, 227–242. [Google Scholar] [CrossRef] [Green Version]
- Tah, A.; Das, D. An Enhanced Droop Control Method for Accurate Load Sharing and Voltage Improvement of Isolated and Interconnected DC Microgrids. IEEE Trans. Sustain. Energy 2016, 7, 1194–1204. [Google Scholar] [CrossRef]
- Mudaliyar, S.; Duggal, B.; Mishra, S. Distributed Tie-Line Power Flow Control of Autonomous DC Microgrid Clusters. IEEE Trans. Power Electron. 2020, 35, 11250–11266. [Google Scholar] [CrossRef]
- Sathishkumar, R.; Kollimalla, S.K.; Mishra, M.K. Dynamic energy management of micro grids using battery super capacitor combined storage. In Proceedings of the 2012 Annual IEEE India Conference (INDICON), Kochi, India, 7–9 December 2012. [Google Scholar] [CrossRef]
- Xu, Q.; Xu, Y.; Xu, Z.; Xie, L.; Blaabjerg, F. A Hierarchically Coordinated Operation and Control Scheme for DC Microgrid Clusters under Uncertainty. IEEE Trans. Sustain. Energy 2021, 12, 273–283. [Google Scholar] [CrossRef]
- Lasseter, R.H. MicroGrids. In Proceedings of the 2002 IEEE Power Engineering Society Winter Meeting. Conference Proceedings (Cat. No.02CH37309), New York, NY, USA, 27–31 January 2002; Volume 1, pp. 305–308. [Google Scholar] [CrossRef]
- Yang, J.; Jin, X.; Wu, X.; Acuna, P.; Aguilera, R.P.; Morstyn, T.; Agelidis, V.G. Decentralised control method for DC microgrids with improved current sharing accuracy. IET Gener. Transm. Distrib. 2017, 11, 696–706. [Google Scholar] [CrossRef]
- Adhikari, S.; Xu, Q.; Tang, Y.; Wang, P. Decentralized control of DC microgrid clusters. In Proceedings of the 2017 IEEE 3rd International Future Energy Electronics Conference and ECCE Asia, Kaohsiung, Taiwan, 3–7 June 2017. [Google Scholar] [CrossRef]
- Ghorbal, M.J.B.; Moussa, S.; Ziani, J.A.; Slama-Belkhodja, I. A comparison study of two DC microgrid controls for a fast and stable DC bus voltage. Math. Comput. Simul. 2021, 184, 210–224. [Google Scholar] [CrossRef]
- Moayedi, S.; Davoudi, A. Distributed Tertiary Control of DC Microgrid Clusters. IEEE Trans. Power Electron. 2016, 31, 1717–1733. [Google Scholar] [CrossRef]
- Al-Ismail, F.S. DC Microgrid Planning, Operation, and Control: A Comprehensive Review. IEEE Access 2021, 9, 36154–36172. [Google Scholar] [CrossRef]
- Peyghami, S.; Mokhtari, H.; Blaabjerg, F. Hierarchical Power Sharing Control in DC Microgrids. In Microgrid: Advanced Control Methods and Renewable Energy System Integration; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar] [CrossRef]
- Elhassaneen, H.A.E.; Tsuji, T. Cooperative Decentralized Tertiary Based Control of DC Microgrid with Renewable Distributed Generation. In Proceedings of the 2019 IEEE Third International Conference on DC Microgrids (ICDCM), Matsue, Japan, 20–23 May 2019. [Google Scholar] [CrossRef]
- Aboelsoud, H.; Tsuji, T. Cooperative decentralized hierarchical based voltage control of DC microgrids. In Proceedings of the 2019 29th Australasian Universities Power Engineering Conference (AUPEC), Nadi, Fiji, 26–29 November 2019. [Google Scholar] [CrossRef]
- Saleh, M.S.; Althaibani, A.; Esa, Y.; Mhandi, Y.; Mohamed, A.A. Impact of clustering microgrids on their stability and resilience during blackouts. In Proceedings of the 2015 International Conference on Smart Grid and Clean Energy Technologies (ICSGCE), Offenburg, Germany, 20–23 October 2015. [Google Scholar] [CrossRef] [Green Version]
- Shafiee, Q.; Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M. Hierarchical control for multiple DC-microgrids clusters. In Proceedings of the 2014 IEEE 11th International Multi-Conference on Systems, Signals & Devices (SSD14), Barcelona, Spain, 11–14 February 2014; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Uhlemeyer, B.; Jakob, J.; Zdrallek, M.; Baumann, C.; Wellßow, W.; Dickert, J.; Rasti, S.J.; Blumberg, G.; Schinke-Nendza, A. Cellular Approach as a Principle in Integrated Energy System Planning and Operation. In Proceedings of the CIRED Workshop, Online Conference, 22–23 September 2020. [Google Scholar] [CrossRef]
- Hoth, K.; Steffen, T.; Wiegel, B.; Youssfi, A.; Babazadeh, D.; Venzke, M.; Becker, C.; Fischer, K.; Turau, V. Holistic Simulation Approach for Optimal Operation of Smart Integrated Energy Systems under Consideration of Resilience, Economics and Sustainability. Infrastructures 2021, 6, 150. [Google Scholar] [CrossRef]
- Thier, P.; Giese, B.; Brand, U.; Schnuelle, C.; Petschow, U.; Heinbach, K.; Goessling-Reisemann, S.; von Gleich, A. Investigating the opportunities to implement a ‘cellular approach’ in two regional energy systems in Germany from a socio-technical point of view. In Proceedings of the International ETG Congress, Bonn, Germany, 28–29 November 2017. [Google Scholar]
- Han, Y.; Pu, Y.; Li, Q.; Fu, W.; Chen, W.; You, Z.; Liu, H. Coordinated power control with virtual inertia for fuel cell-based DC microgrids cluster. Int. J. Hydrogen. Energy 2019, 44, 25207–25220. [Google Scholar] [CrossRef]
- Guo, L.; Li, P.; Li, X.; Huang, D.; Zhu, J. Flexible control of DC interlinked multiple MGs cluster. IET Gener. Transm. Distrib. 2019, 13, 2088–2101. [Google Scholar] [CrossRef]
- Fan, Z.; Fan, B.; Peng, J.; Liu, W. Distributed Hierarchical Control for Optimal Power Dispatch in Multiple DC Microgrids. IEEE Syst. J. 2020, 14, 1–11. [Google Scholar] [CrossRef]
- Ciornei, I.; Albu, M.; Sănduleac, M.; Rodriguez-Diaz, E.; Teodorescu, R.; Guerrero, J. Adaptive Distributed EMS for Small Clusters of Resilient LVDC Microgrids. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Palermo, Italy, 12–15 June 2018. [Google Scholar] [CrossRef]
- Lai, J.; Lu, X.; Yu, X.; Yao, W.; Wen, J.; Cheng, S. Distributed multi-DER cooperative control for master-slave-organized microgrid networks with limited communication bandwidth. IEEE Trans. Ind. Inform. 2019, 15, 3443–3456. [Google Scholar] [CrossRef]
- Tsikalakis, A.G.; Hatziargyriou, N.D. Centralized control for optimizing microgrids operation. In Proceedings of the IEEE Transactions on Energy Conversion, Detroit, MI, USA, 24–28 July 2011; Volume 23. [Google Scholar] [CrossRef]
- Babazadeh-Dizaji, R.; Hamzeh, M.; Hekmati, A. Power Sharing in Multiple DC Microgrids Based on Concentrated Control. In Proceedings of the Electrical Engineering (ICEE), Iranian Conference, Mashhad, Iran, 8–10 May 2018. [Google Scholar] [CrossRef]
- Kumar, M.; Srivastava, S.C.; Singh, S.N.; Ramamoorty, M. Development of a control strategy for interconnection of islanded direct current microgrids. IET Renew. Power Gener. 2015, 9, 284–296. [Google Scholar] [CrossRef]
- Meng, L.; Shafiee, Q.; Trecate, G.F.; Karimi, H.; Fulwani, D.; Lu, X.; Guerrero, J.M. Review on Control of DC Microgrids and Multiple Microgrid Clusters. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 928–948. [Google Scholar] [CrossRef] [Green Version]
- Abhishek, A.; Devassy, S.; Akbar, S.A.; Singh, B. Consensus Algorithm based Two-Level Control Design for a DC Microgrid. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy (PESGRE2020), Cochin, India, 2–4 January 2020. [Google Scholar] [CrossRef]
- Abhishek, A.; Ranjan, A.; Devassy, S.; Verma, B.K.; Ram, S.K.; Dhakar, A.K. Review of hierarchical control strategies for DC microgrid. IET Renew. Power Gener. 2020, 14, 1631–1640. [Google Scholar] [CrossRef]
- Shuai, Z.; Fang, J.; Ning, F.; Shen, Z.J. Hierarchical structure and bus voltage control of DC microgrid. Renew. Sustain. Energy Rev. 2018, 82, 3670–3682. [Google Scholar] [CrossRef]
- Dam, D.H.; Lee, H.H. An adaptive power distributed control method to ensure proportional load power sharing in DC microgrid considering equivalent line impedances. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016. [Google Scholar] [CrossRef]
- Papadimitriou, C.N.; Zountouridou, E.I.; Hatziargyriou, N.D. Review of hierarchical control in DC microgrids. Electr. Power Syst. Res. 2015, 122, 159–167. [Google Scholar] [CrossRef]
- Jena, S.; Padhy, N.P.; Guerrero, J.M. Decentralized Primary and Distributed Secondary Control for Current Sharing and Voltage Regulation in DC Microgrid Clusters with HESS. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 16–19 December 2020. [Google Scholar] [CrossRef]
- Eisapour-Moarref, A.; Kalantar, M.; Esmaili, M. Power sharing in hybrid microgrids with multiple DC subgrids. Int. J. Electr. Power Energy Syst. 2021, 128, 106716. [Google Scholar] [CrossRef]
- Lagudu, J.; Sathya Narayana, S.; Vulasala, G. Power sharing scheme in interconnected DC microgrids–A new approach. Int. J. Ambient. Energy 2020, 1–12. [Google Scholar] [CrossRef]
- Wu, C.; Hou, X.; Wang, Y.; Chen, X.; Liao, C. SOC-featured Distributed Tertiary Control for Energy Management in DC Microgrid Clusters. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019. [Google Scholar] [CrossRef]
- Bharath, K.R.; Krishnan, M.M.; Kanakasabapathy, P. A review on DC microgrid control techniques, applications and trends. Int. J. Renew. Energy Res. 2019, 9, 1328–1338. [Google Scholar]
- Dragičević, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC Microgrids-Part I: A Review of Control Strategies and Stabilization Techniques. IEEE Trans. Power Electron. 2016, 31, 4876–4891. [Google Scholar] [CrossRef] [Green Version]
- Dragičević, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC Microgrids-Part II: A Review of Power Architectures, Applications, and Standardization Issues. IEEE Trans. Power Electron. 2016, 31, 3528–3549. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, S.K.; Sinha, A.K.; Kishore, N.K. Control Techniques in AC, DC, and Hybrid AC-DC Microgrid: A Review. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 738–759. [Google Scholar] [CrossRef]
- Bandeiras, F.; Pinheiro, E.; Gomes, M.; Coelho, P.; Fernandes, J. Review of the cooperation and operation of microgrid clusters. Renew. Sustain. Energy Rev. 2020, 133, 110311. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, K.; Li, H.; Coelho, E.A.A.; Guerrero, J.M. MAS-Based Distributed Coordinated Control and Optimization in Microgrid and Microgrid Clusters: A Comprehensive Overview. IEEE Trans. Power Electron. 2018, 33, 6488–6508. [Google Scholar] [CrossRef] [Green Version]
- Alam, M.N.; Chakrabarti, S.; Ghosh, A. Networked Microgrids: State-of-the-Art and Future Perspectives. IEEE Trans. Ind. Inform. 2019, 15, 1238–1250. [Google Scholar] [CrossRef]
- Shafiee, Q.; Dragičević, T.; Vasquez, J.C.; Guerrero, J.M. Hierarchical control for multiple DC-microgrids clusters. IEEE Trans. Energy Convers. 2014, 29, 922–933. [Google Scholar] [CrossRef] [Green Version]
- Samende, C.; Gao, F.; Bhagavathy, S.M.; McCulloch, M. Decentralized Voltage Control for Efficient Power Exchange in Interconnected DC Clusters. IEEE Trans. Sustain. Energy 2021, 12, 103–115. [Google Scholar] [CrossRef]
- Konar, S.; Ghosh, A. Interconnection of islanded DC microgrids. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference, APPEEC, Brisbane, Australia, 15–18 November 2015. [Google Scholar] [CrossRef]
- Li, X.; Guo, L.; Li, Y.; Hong, C.; Zhang, Y.; Guo, Z.; Huang, D.; Wang, C. Flexible Interlinking and Coordinated Power Control of Multiple DC Microgrids Clusters. IEEE Trans. Sustain. Energy 2018, 9, 904–915. [Google Scholar] [CrossRef]
- Ma, J.; Zhu, M.; Cai, X.; Li, Y.W. Configuration and operation of DC microgrid cluster linked through DC-DC converter. In Proceedings of the 2016 IEEE 11th Conference on Industrial Electronics and Applications (ICIEA), Hefei, China, 5–7 June 2016. [Google Scholar] [CrossRef]
- Lee, M.; Choi, W.; Kim, H.; Cho, B.H. Operation schemes of interconnected DC microgrids through an isolated bi-directional DC-DC converter. In Proceedings of the 2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015. [Google Scholar] [CrossRef]
- Singh, P.; Lather, J.S. Accurate power-sharing, voltage regulation, and SOC regulation for LVDC microgrid with hybrid energy storage system using artificial neural network. Int. J. Green Energy 2020, 17, 756–769. [Google Scholar] [CrossRef]
- Kumar, G.V.; Kaliannan, P.; Padmanaban, S.; Holm-Nielsen, J.B.; Blaabjerg, F. Effective management system for solar PV using real-time data with hybrid energy storage system. Appl. Sci. 2020, 10, 1108. [Google Scholar] [CrossRef] [Green Version]
- Saraswathi, K.T.; Swaminathan, G.V.; Periasamy, S. Hybrid power management for DC microgrid cluster. Electr. Power Syst. Res. 2021, 199, 107454. [Google Scholar] [CrossRef]
- Shahraeini, M.; Javidi, M.H.; Ghazizadeh, M.S. Comparison between communication infrastructures of centralized and decentralized wide area measurement systems. IEEE Trans. Smart Grid 2011, 2, 206–211. [Google Scholar] [CrossRef]
- Zaery, M.; Wang, P.; Lu, X.; Wang, W.; Xu, D. Fully Distributed Controller for Economic Load Sharing of DC Microgrid Clusters. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020. [Google Scholar] [CrossRef]
- Li, Y.; Dong, P.; Liu, M.; Yang, G. A distributed coordination control based on finite-time consensus algorithm for a cluster of dc microgrids. IEEE Trans. Power Syst. 2019, 34, 2205–2215. [Google Scholar] [CrossRef]
- Park, G.C.; Lee, W.P.; Won, D.J. Power Sharing Algorithm for Voltage Regulation in Islanded DC Multi-Microgrid System. In Proceedings of the 2018 53rd International Universities Power Engineering Conference (UPEC), Glasgow, UK, 4–7 September 2018. [Google Scholar] [CrossRef]
- Reddy, G.S.; Mini, V.P.; Mayadevi, N.; Kumar, R.H. Optimal Energy Sharing in Smart DC Microgrid Cluster. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy (PESGRE2020), Cochin, India, 2–4 January 2020. [Google Scholar] [CrossRef]
- Keshta, H.E.; Saied, E.M.; Malik, O.P.; Bendary, F.M.; Ali, A.A. Fuzzy PI controller-based model reference adaptive control for voltage control of two connected microgrids. IET Gener. Transm. Distrib. 2021, 15, 602–618. [Google Scholar] [CrossRef]
- Chinea-Herranz, J.A.; Rodriguez, M. Control of integrated unit operations. Comput. Aided Chem. Eng. 2012, 31, 325–329. [Google Scholar] [CrossRef] [Green Version]
- Ren, L. Coordinated control stategy for DC microgrid clusters considering intelligent power allocation. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration, EI2 2017, Beijing, China, 26–28 November 2017. [Google Scholar] [CrossRef]
- Adhikari, S.; Xu, Q.; Tang, Y.; Wang, P.; Li, X. Decentralized control of two DC microgrids interconnected with tie-line. J. Mod. Power Syst. Clean Energy 2017, 5, 599–608. [Google Scholar] [CrossRef] [Green Version]
- Luo, Z.; Geng, H.; Zhu, G. Hierarchical Cooperative Control for Islanded DC Microgrid Cluster ∗note: Sub-titles are not captured in Xplore and should not be used. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018. [Google Scholar] [CrossRef]
- Sanjeev, P.; Padhy, N.P.; Agarwal, P. Autonomous Power Control and Management between Standalone DC Microgrids. IEEE Trans. Ind. Inform. 2018, 14, 2941–2950. [Google Scholar] [CrossRef]
- Kirtane, P.S.; Shendge, A.D. Control and Management of Autonomous Power between Standalone DC Microgrids. In Proceedings of the 2019 International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 17–19 July 2019. [Google Scholar] [CrossRef]
- Nasir, M.; Jin, Z.; Khan, H.A.; Zaffar, N.A.; Vasquez, J.C.; Guerrero, J.M. A Decentralized Control Architecture Applied to DC Nanogrid Clusters for Rural Electrification in Developing Regions. IEEE Trans. Power Electron. 2019, 34, 1773–1785. [Google Scholar] [CrossRef] [Green Version]
- Han, R.; Tucci, M.; Martinelli, A.; Guerrero, J.M.; Ferrari-Trecate, G. Plug-and-Play Voltage/Current Stabilization DC Microgrid Clusters with Grid-Forming/Feeding Converters. In Proceedings of the American Control Conference, Milwaukee, WI, USA, 27–29 June 2018. [Google Scholar] [CrossRef] [Green Version]
- Shafiee, Q.; Dragicevic, T.; Andrade, F.; Vasquez, J.C.; Guerrero, J.M. Distributed consensus-based control of multiple DC-microgrids clusters. In Proceedings of the IECON 2014-40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014. [Google Scholar] [CrossRef] [Green Version]
- Shahbazi, M.; Kazemtabrizi, B.; Dent, C. Coordinated control of DC voltage magnitudes and state of charges in a cluster of DC microgrids. In Proceedings of the 2016 IEEE PES innovative smart grid technologies conference Europe (ISGT-Europe), Ljubljana, Slovenia, 9–12 October 2016. [Google Scholar] [CrossRef]
- Moayedi, S.; Davoudi, A. Cooperative power management in DC microgrid clusters. In Proceedings of the 2015 IEEE First International Conference on DC Microgrids (ICDCM), Atlanta, GA, USA, 7–10 June 2015. [Google Scholar] [CrossRef]
- Amini, M.H.; Boroojeni, K.G.; Dragičević, T.; Nejadpak, A.; Iyengar, S.S.; Blaabjerg, F. A comprehensive cloud-based real-time simulation framework for oblivious power routing in clusters of DC microgrids. In Proceedings of the 2017 IEEE Second International Conference on DC Microgrids (ICDCM), Nuremburg, Germany, 27–29 June 2017. [Google Scholar] [CrossRef]
- Lu, X.; Lai, J. Distributed Cluster Cooperation for Multiple DC MGs over Two-Layer Switching Topologies. IEEE Trans. Smart Grid 2020, 11, 4676–4687. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, X.; Xu, W.; Wen, G. Modeling and Control of Islanded DC Microgrid Clusters with Hierarchical Event-Triggered Consensus Algorithm. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 376–386. [Google Scholar] [CrossRef]
- Liu, R.; Liu, S.; Zheng, J.; Fang, W.; Liu, X. Function Controller Design in Tertiary Level for DC Microgrid Clusters. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November–2 December 2020. [Google Scholar] [CrossRef]
- Zaery, M.; Wang, P.; Wang, W.; Xu, D. Distributed Finite-Time Controller for Economic Operation of DC Multi-Microgrids. In Proceedings of the IECON Proceedings (Industrial Electronics Conference), Lisbon, Portugal, 14–17 October 2019. [Google Scholar] [CrossRef]
- Zaery, M.; Wang, P.; Wang, W.; Xu, D. A novel fully distributed fixed-time optimal dispatch of DC multi-microgrids. Int. J. Electr. Power Energy Syst. 2021, 129, 106792. [Google Scholar] [CrossRef]
- Jena, S.; Padhy, N.P.; Guerrero, J.M. Cyber-Resilient Cooperative Control of DC Microgrid Clusters. IEEE Syst. J. 2021, 1–12. [Google Scholar] [CrossRef]
- Meng, L.; Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M.; Perez, J.R. Modeling and sensitivity analysis of consensus algorithm based distributed hierarchical control for DC microgrids. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition-APEC, Charlotte, NC, USA, 15–19 March 2015. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Ertugrul, N. An overview of hierarchical control strategies for microgrids. In Proceedings of the 2019 29th Australasian Universities Power Engineering Conference (AUPEC), Nadi, Fiji, 26–29 November 2019. [Google Scholar] [CrossRef]
- Han, R.; Tucci, M.; Martinelli, A.; Guerrero, J.M.; Ferrari-Trecate, G. Stability Analysis of Primary Plug-and-Play and Secondary Leader-Based Controllers for DC Microgrid Clusters. IEEE Trans. Power Syst. 2019, 34, 1780–1800. [Google Scholar] [CrossRef] [Green Version]
- Mingsheng, Z.; Peilei, F.; Hesong, W.; Wenkui, W.; Pengcheng, C. Hierarchical Control Strategy for Microgrid. In Proceedings of the 2018 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 25–27 May 2018. [Google Scholar] [CrossRef]
- Zaery, M.; Wang, P.; Wang, W.; Xu, D. Distributed Global Economical Load Sharing for a Cluster of DC Microgrids. IEEE Trans. Power Syst. 2020, 35, 3410–3420. [Google Scholar] [CrossRef]
- Lu, X.; Li, Q. Two-Layer Discrete-Time Iterative Cooperation for Interconnected DC Microgrids. In Proceedings of the IECON Proceedings (Industrial Electronics Conference), Singapore, Singapore, 18–21 October 2020. [Google Scholar] [CrossRef]
- Yilin, L.I.; Ping, D.O.N.G. A distributed control based on finite-time consensus algorithm for the cluster of DC microgrids. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–8 November 2018. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, Z.; Mi, Y.; Li, Z.; Li, F. Droop Control for DC Multi-Microgrids Based on Local Adaptive Fuzzy Approach and Global Power Allocation Correction. IEEE Trans. Smart Grid 2018, 10, 5468–5478. [Google Scholar] [CrossRef]
- Wu, P.; Huang, W.; Tai, N.; Ma, Z.; Zheng, X.; Zhang, Y. A multi-layer coordinated control scheme to improve the operation friendliness of grid-connected multiple microgrids. Energies 2019, 12, 255. [Google Scholar] [CrossRef] [Green Version]
- Shafiee, Q.; Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M. Modeling, stability analysis and active stabilization of multiple DC-microgrid clusters. In Proceedings of the 2014 IEEE international energy conference (ENERGYCON), Cavtat, Croatia, 13–16 May 2014. [Google Scholar] [CrossRef] [Green Version]
- Dragičević, T.; Guerrero, J.M.; Vasquez, J.C.; Škrlec, D. Supervisory control of an adaptive-droop regulated DC microgrid with battery management capability. IEEE Trans. Power Electron. 2014, 29, 695–706. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Sun, K.; Guerrero, J.M.; Vasquez, J.C.; Huang, L. State-of-charge balance using adaptive droop control for distributed energy storage systems in DC microgrid applications. IEEE Trans. Ind. Electron. 2014, 61, 2804–2815. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, S.; Mishra, S.; Fazeli, S.M.; Li, F.; Dragičević, T. A Distributed fixed-Time secondary controller for dc microgrid clusters. IEEE Trans. Energy Convers. 2019, 34, 1997–2007. [Google Scholar] [CrossRef]
- Tu, C.; Xiao, F.; Lan, Z.; Guo, Q.; Shuai, Z. Analysis and Control of a Novel Modular-Based Energy Router for DC Microgrid Cluster. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 331–342. [Google Scholar] [CrossRef]
- Li, Z.; Duan, Z. Cooperative Control of Multi-Agent Systems: A Consensus Region Approach; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Zhou, Q.; Shahidehpour, M.; Paaso, A.; Bahramirad, S.; Alabdulwahab, A.; Abusorrah, A. Distributed Control and Communication Strategies in Networked Microgrids. IEEE Commun. Surv. Tutor. 2020, 22, 2586–2633. [Google Scholar] [CrossRef]
- Guo, F.; Wen, C.; Mao, J.; Song, Y.D. Distributed Economic Dispatch for Smart Grids with Random Wind Power. IEEE Trans. Smart Grid 2016, 7, 1572–1583. [Google Scholar] [CrossRef]
- Lu, X.; Lai, J.; Yu, X.; Wang, Y.; Guerrero, J.M. Distributed coordination of islanded microgrid clusters using a two-layer intermittent communication network. IEEE Trans. Ind. Inform. 2018, 14, 3956–3969. [Google Scholar] [CrossRef]
- Faraji, J.; Ketabi, A.; Hashemi-Dezaki, H.; Shafie-Khah, M.; Catalao, J.P. Optimal day-ahead self-scheduling and operation of prosumer microgrids using hybrid machine learning-based weather and load forecasting. IEEE Access 2020, 8, 83561–83582. [Google Scholar] [CrossRef]





| Ref. | Objectives | Problems | Proposed Methods | Method’s Issues/Gaps |
|---|---|---|---|---|
| [50] | Voltage regulation and power flow control | SOCs/Load–generation mismatch | Distributed hierarchical approach |
|
| [5] | Power exchange management and no circulating current | Load–generation mismatch (circulating currents) | Novel Power Scheduling Mechanism |
|
| [63] | Energy sharing management | Power mismatch because of the stochastic nature of RES | A novel cloud-based hierarchical control strategy |
|
| [10] | Optimal coordination of both real-time and operation control, power balance among MGs, and power losses minimization | Uncertainty in renewable energy and load variations | The hierarchically coordinated control scheme |
|
| [76] | Congestion management and losses minimization | Power routing mismatching between generation and load among MGs | A novel cloud-basedapproach |
|
| [7] | Voltage regulation, power flow control, and stability analysis | Loading mismatch and constant power load line impedance (CPL) | A distributed local control scheme |
|
| [68] | Control of the tie-line current and maintaining bus voltage | High penetration in renewable energy resourcesMismatching between the DGs and ESS | A hierarchical cooperative control scheme |
|
| [13] | Control the flow of power and DC-link voltage | Mismatching between generation and load for each MG. | A decentralized control approach |
|
| [95] | Proper power-sharing, appropriate voltage regulation, loading mismatch mitigation, and losses minimization | Line impedance and load changes | A fully distributed fixed-time based dual-layer hierarchy control |
|
| [75] | Power exchange and voltage regulation | Loading mismatch and line impedance | Distributed tertiary control method |
|
| [79] | Control of power flow and voltage regulation | Load–generation mismatch | PFC-hierarchical control method |
|
| [28] | Power flow control | RES/load variations | The adaptive distributed control scheme |
|
| [61] | Proper load distribution, voltage stabilization, and the minimization of total generation | Load and generation fluctuations | Fully distributed finite-time hierarchical control |
|
| [42] | SOC equalization and power balancing in system | Mismatching between load and supply | SOC-featured distributed tertiary control |
|
| [15] | Power exchange and voltage regulation | Loading mismatch among neighboring MGs | Distributed tertiary hierarchical control strategy |
|
| [74] | SOCs equalization and voltage regulation | The mismatch between generation and load | Distributed control framework |
|
| [53] | Power flow control, global voltage regulation, seamless transition | MGs coupling issues (fault, terminal bus failure) | A novel coordinated power control scheme |
|
| [96] | Multidirectional power flow control and fault isolation | Power fluctuations/load changes | A novel modular-based energy router |
|
| [25] | Power flow control, voltage regulation, and coordination of fuel cell/battery power | Uncertainty in RES/LoadThe low inertia of MGsTie-line power losses | MAS- coordinated power control scheme |
|
| [64] | Optimal power flow and voltage regulation | RES/load variations and faults | The optimized hierarchical control scheme |
|
| Ref | Method | Objectives | Merits | Demerits |
|---|---|---|---|---|
| [78] | A distributed hierarchical control strategy | Current sharing and voltage regulation | 1. Less computational burdens. | 1. Natures of DGs have not been considered. |
| 2. Both current sharing alongside DC voltage regulation is partially realized. | 2. Uncertainties in Load and RES are ignored. | |||
| 3. PnP operation is obtained. | 3. Minimization of internal power losses is disregarded. | |||
| 4. Because of PI-controller settings, there is still a conflict between voltage adjustment and current distribution. | ||||
| [27] | A fully distributed consensus-based control scheme | Optimal power-sharing, voltage regulation, and generation costs | 1. The optimum power dispatch is obtained. | 1. It is more susceptible to communication reliability problems, including packet loss and communication delays. |
| 2. DC bus voltage. regulation is improved. | 2. Infinite-time convergence is adopted, so it may not be able to face the fast and sudden disturbances caused by RES and load variations. | |||
| 3. It is resilient to the failure of a single link. | 3. Uncertainties in Load and RES are ignored. | |||
| 4. It is featured by robustness against physical failures. | 4. Classical PI controllers are used. | |||
| 5. Natures of DGs have not been considered. | ||||
| 6. Extra costs are added because of using interlinking converters. | ||||
| 7. Minimization of power losses is not included. | ||||
| [95] | A fully distributed fixed-time based dual-layer hierarchy control | Power-exchange and voltage adjustment | 1. Power exchange and voltage adjustment are achieved. | 1. Uncertainties in Load and RES are ignored. |
| loading mismatch mitigation and losses minimization. | 2. Loading mismatch and power losses are decreased. | 2. The issues of communication delays exist. | ||
| 3. Real data of RESs are not used, such as historical/prediction data of solar irradiance or wind speed. | ||||
| 4. Load and RES forecasting are not included. | ||||
| 5. It is sensitive to slight inaccuracy in the system. | ||||
| [80] | A fully distributed finite-time based dual layer hierarchy control | Economic power sharing and voltage regulation | 1. Optimal power exchange alongside DC bus voltage adjustment are controlled within a limited-time domain. | 1. It is susceptible to communication delays. |
| 2. It is featured by resiliency against failures on the virtual communication network. | 2. Incremental costs and TGC is increased during PnP operation. | |||
| 3. It has a more robust functioning with a faster convergence time and better dynamism, making it more suited to multi-MGs with rapid intermittent DRGs. | 3. Load and RES uncertainties are ignored. | |||
| 4. PnP capability is supported. | 4. Natures of DGs have not been considered. | |||
| [87] | A distributed two-layer control approach | Economic power sharing and voltage adjustment | 1. DGs’ generation cost is reduced. | 1. It is sensitive to communication delays. |
| 2. The global power balance is achieved. | 2. Incremental costs and TGC is increased during the PnP process. | |||
| 3. It has PnP capability. | 3. Uncertainties in load and RES are ignored. | |||
| 4. It is featured by robustness against cyber communication failures and latency. | 4. Natures of DGs have not been considered. | |||
| 5. Pinning-based control approach is adopted to reduce communication links and lessen control costs. | 5. Linear consensus protocol is employed. | |||
| [60] | A distributed two-layer control approach | DC bus voltage adjustment and optimum load sharing | 1. A simpler communication network is required. | 1. It may be vulnerable to communication delays. |
| 2. It is featured by the resiliency against both physical and losses. | 2. Computational burdens still exist. | |||
| 3. Total generation costs are reduced. | 3. The convergence rate may not be ensured. | |||
| 4. Voltage regulation and optimal load sharing are achieved. | 4. Uncertainties in load and RES are ignored. | |||
| 5. Natures of DGs have not been considered. | ||||
| [88] | A two-layer discrete-time iterative cooperative (TDIC) scheme | Voltage regulation and current sharing | 1. Communication pressure reduction and faster convergence speed are realized. | 1. Uncertainties in RES and load demand are ignored. |
| 2. Accurate current sharing and regulated voltage are achieved. | 2. Natures of DGs have not been considered. | |||
| 3. Classical PI controllers are adopted. | ||||
| 4. Power losses reduction has not been considered. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Tameemi, Z.H.A.; Lie, T.T.; Foo, G.; Blaabjerg, F. Control Strategies of DC Microgrids Cluster: A Comprehensive Review. Energies 2021, 14, 7569. https://doi.org/10.3390/en14227569
Al-Tameemi ZHA, Lie TT, Foo G, Blaabjerg F. Control Strategies of DC Microgrids Cluster: A Comprehensive Review. Energies. 2021; 14(22):7569. https://doi.org/10.3390/en14227569
Chicago/Turabian StyleAl-Tameemi, Zaid Hamid Abdulabbas, Tek Tjing Lie, Gilbert Foo, and Frede Blaabjerg. 2021. "Control Strategies of DC Microgrids Cluster: A Comprehensive Review" Energies 14, no. 22: 7569. https://doi.org/10.3390/en14227569






