Resilience Assessment: A Performance-Based Importance Measure
Abstract
:1. Introduction
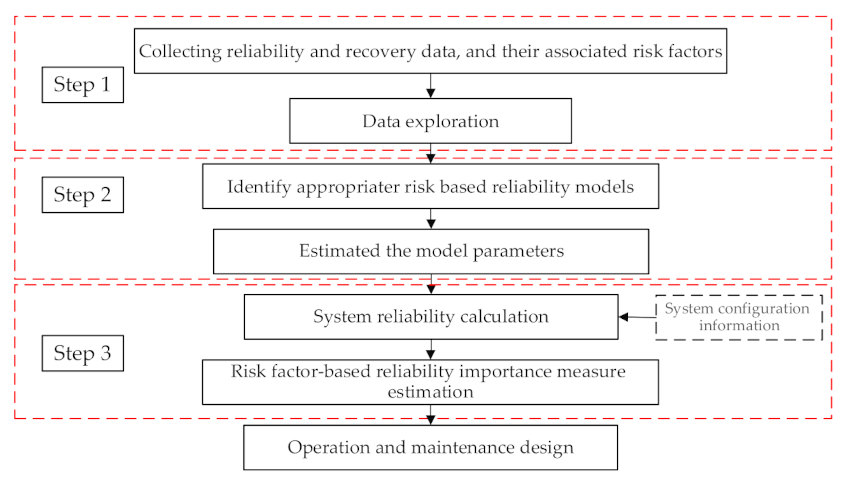
2. Methodology and Framework: Risk Factor-Based Reliability Importance Measure (RF-RIM)
3. Case Study
3.1. Data Collection and Classification
3.2. Risk Factor Test
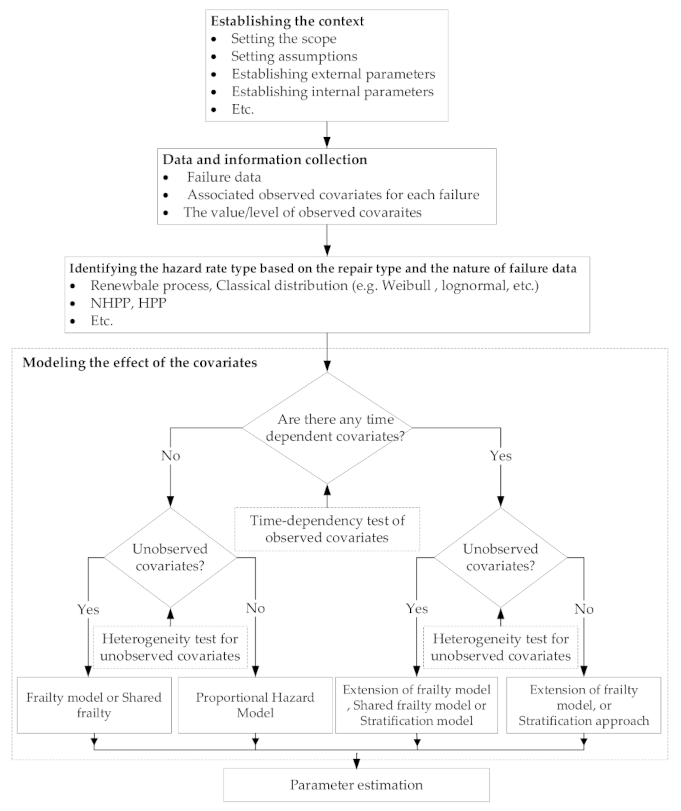
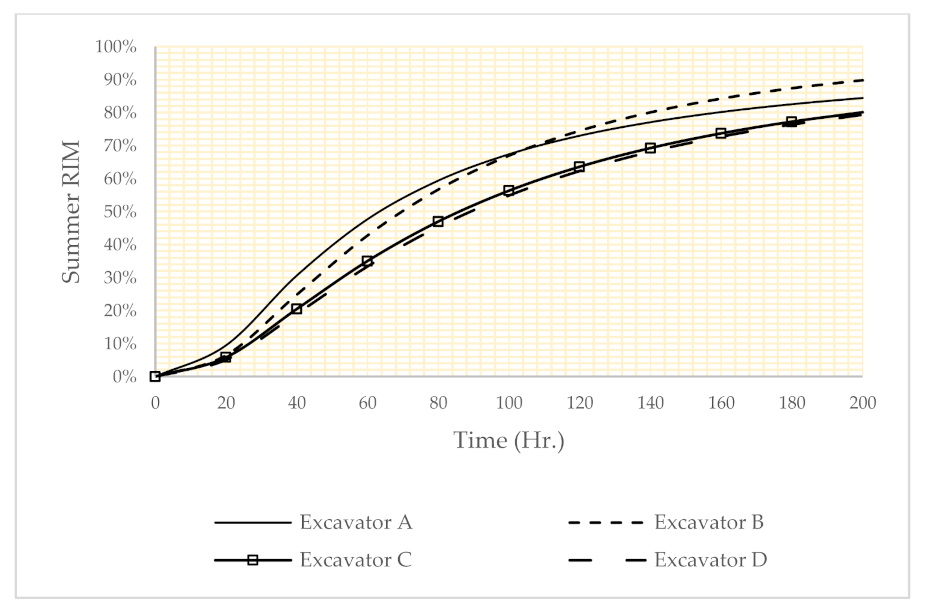
3.3. RF-RIM Molding
- Weibull proportional hazard model (Weibull-PHM);
- Exponential proportional hazard model (Exponential-PHM);
- Weibull Mix-proportional hazard model (Weibull-MPHM);
- Exponential Mix-proportional hazard model (Exponential-MPHM).
3.4. System RF-RIM
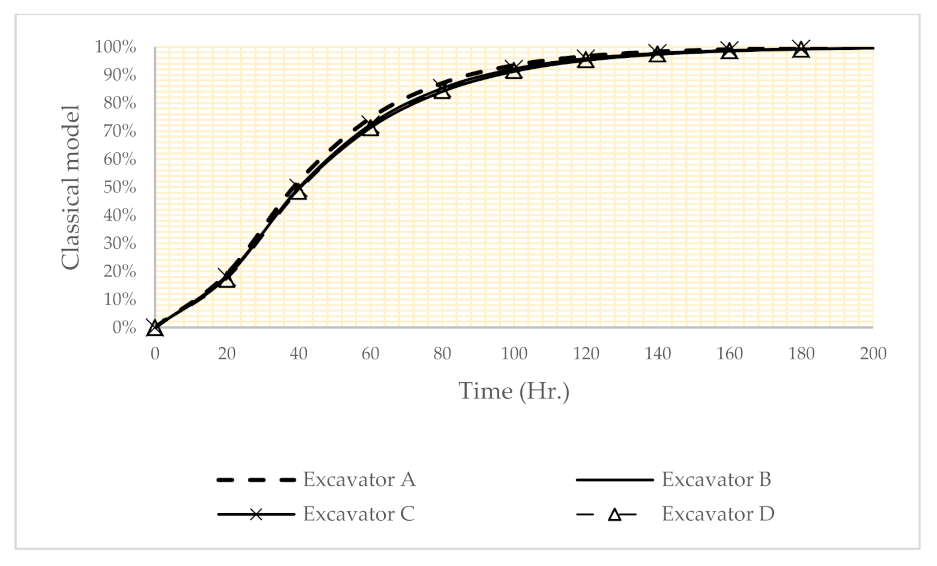
- Classical model: only time data be analyzed.
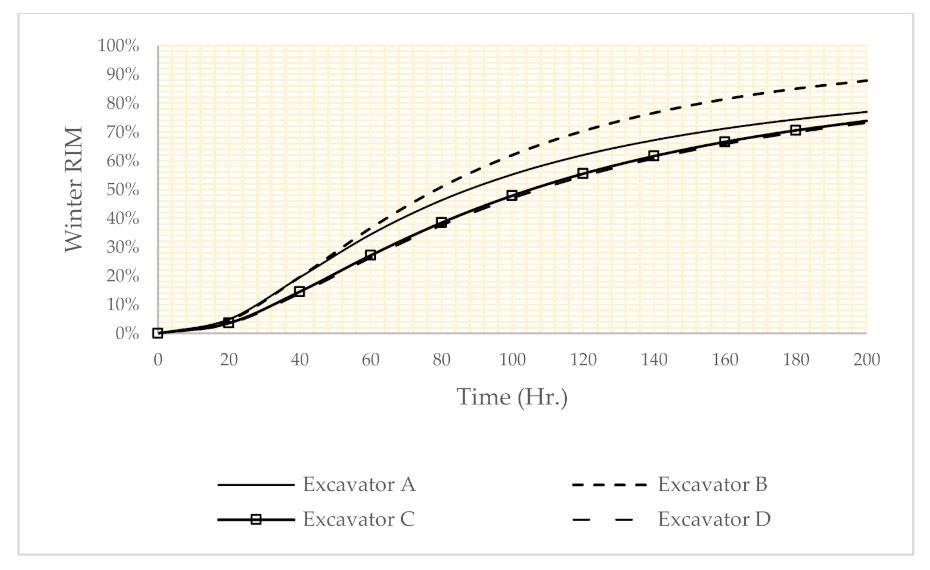
- Winter: temperature = 10, night shift, west, and operation team C
- Summer: temperature = 20, afternoon shift, ore and operation team B
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Haimes, Y.Y. On the Definition of Resilience in Systems. Risk Anal. Int. J. 2009, 29, 498–501. [Google Scholar] [CrossRef]
- Barabadi, A.; Ghiasi, M.H.; Nouri Qarahasanlou, A.; Mottahedi, A. A Holistic View on Medical Infrastructures Resilience Before and After COVID-19. Arch. Bone Jt. Surg. 2020, 8, 262–269. [Google Scholar] [CrossRef]
- Ali, N.G.; Reza, K.; Mohammad, A.; Ashkan, M. Power Law Model for Reliability Analysis of Crusher System in Khoy Cement Factory. In Proceedings of the CIVILICA, 2015, Istanbul, Turkey, 21 July 2015. [Google Scholar]
- Nouri Qarahasanlou, A.; Barabadi, A.; Ataei, M.; Einian, V. Spare Part Requirement Prediction under Different Maintenance Strategies. Int. J. Min. Reclam. Environ. 2019, 33, 169–182. [Google Scholar] [CrossRef]
- Lange, D.; Honfi, D.; Theocharidou, M.; Giannopoulos, G.; Reitan, N.K.; Storesund, K. Incorporation of Resilience Assessment in Critical Infrastructure Risk Assessment Frameworks; CRC Press/Balkema: Boca Raton, FL, USA, 2017; pp. 1031–1038. [Google Scholar]
- Hoseinie, S.H.; Heydari, S.; Ghodrati, B.; Kumar, U. Resilience Measurement of Longwall Machinery. Rud.-Geološko-Naft. Zb. 2020, 35, 39–44. [Google Scholar]
- Hariri-Ardebili, M.A. Risk, Reliability, Resilience (R3) and beyond in Dam Engineering: A State-of-the-Art Review. Int. J. Disaster Risk Reduct. 2018, 31, 806–831. [Google Scholar] [CrossRef]
- Gu, Y.; Fu, X.; Liu, Z.; Xu, X.; Chen, A. Performance of Transportation Network under Perturbations: Reliability, Vulnerability, and Resilience. Transp. Res. Part E Logist. Transp. Rev. 2020, 133, 101809. [Google Scholar] [CrossRef]
- Salomon, J.; Broggi, M.; Kruse, S.; Weber, S.; Beer, M. Resilience Decision-Making for Complex Systems. ASCE-ASME J. Risk Uncert. Engrg. Sys. Part. B Mech. Engrg. 2020, 6, 1–11. [Google Scholar] [CrossRef]
- Yarveisy, R.; Gao, C.; Khan, F. A Simple yet Robust Resilience Assessment Metrics. Reliab. Eng. Syst. Saf. 2020, 197, 106810. [Google Scholar] [CrossRef]
- Mottahedi, A.; Sereshki, F.; Ataei, M.; Nouri Qarahasanlou, A.; Barabadi, A. The Resilience of Critical Infrastructure Systems: A Systematic Literature Review. Energies 2021, 14, 1571. [Google Scholar] [CrossRef]
- Qarahasanlou, A.N.; Khalokakaie, R.; Ataei, M.; Ghodrati, B. Operating Environment-Based Availability Importance Measures for Mining Equipment (Case Study: Sungun Copper Mine). J. Fail. Anal. Prev. 2017, 17, 56–67. [Google Scholar] [CrossRef]
- Birnbaum, Z.W. On the Importance of Different Components in a Multicomponent System; DTIC Document; Washington Univ Seattle Lab of Statistical Research: Seattle, WA, USA, 1968. [Google Scholar]
- Chang, H.-W.; Chen, R.-J.; Hwang, F.K. The Structural Birnbaum Importance of Consecutive-k Systems. J. Comb. Optim. 2002, 6, 183–197. [Google Scholar] [CrossRef]
- Amrutkar, K.P.; Kamalja, K.K. An Overview of Various Importance Measures of Reliability System. Int. J. Math. Eng. Manag. Sci. 2017, 2, 150–171. [Google Scholar] [CrossRef]
- Almoghathawi, Y.; Barker, K. Component Importance Measures for Interdependent Infrastructure Network Resilience. Comput. Ind. Eng. 2019, 133, 153–164. [Google Scholar] [CrossRef]
- Chacko, V.M. New Joint Importance Measures for Multistate Systems. Int. J. Stat. Reliab. Eng. 2020, 7, 140–148. [Google Scholar]
- Xu, A.; Zhang, Z.; Zhang, H.; Wang, H.; Zhang, M.; Chen, S.; Ma, Y.; Dong, X. Research on Time-Dependent Component Importance Measures Considering State Duration and Common Cause Failure. Front. Energy Res. 2020, 8, 259. [Google Scholar] [CrossRef]
- Kamra, R.; Pahuja, G. Reliability Importance Measures-Based Analysis of Substation Communication Network. In Computational Methodologies for Electrical and Electronics Engineers; IGI Global: Hershey, PA, USA, 2021; pp. 48–66. [Google Scholar]
- Niu, M.; Xu, N.Z.; Kong, X.; Ngin, H.T.; Ge, Y.Y.; Liu, J.S.; Liu, Y.T. Reliability Importance of Renewable Energy Sources to Overall Generating Systems. IEEE Access 2021, 9, 20450–20459. [Google Scholar] [CrossRef]
- Zaki, R.; Barabadi, A.; Qarahasanlou, A.N.; Garmabaki, A. A Mixture Frailty Model for Maintainability Analysis of Mechanical Components: A Case Study. Int. J. Syst. Assur. Eng. Manag. 2019, 10, 1646–1653. [Google Scholar] [CrossRef] [Green Version]
- Rod, B.; Barabadi, A.; Naseri, M. Recoverability Modeling of Power Distribution Systems Using Accelerated Life Models: Case of Power Cut Due to Extreme Weather Events in Norway. J. Manag. Eng. 2020, 36, 05020012. [Google Scholar] [CrossRef]
- Ghomghale, A.; Ataei, M.; Khalokakaie, R.; Barabadi, A.; Nouri Qarahasanlou, A. The Application of Frailty Model in Remaining Useful Life Estimation (Case Study: Sungun Copper Mine’s Loading System). J. Modeling Eng. 2020, 18, 129–142. [Google Scholar] [CrossRef]
- Barabadi, R.; Ataei, M.; Khalokakaie, R.; Nouri Qarahasanlou, A. Spare-Part Management in a Heterogeneous Environment. PLoS ONE 2021, 16, e0247650. [Google Scholar] [CrossRef]
- Barabadi, A.; Barabady, J.; Markeset, T. Maintainability Analysis Considering Time-Dependent and Time-Independent Covariates. Reliab. Eng. Syst. Saf. 2011, 96, 210–217. [Google Scholar] [CrossRef]
- Barabadi, R.; Ataei, M.; Khalokakaie, R.; Nouri Qarahasanlou, A. Observed and Un-Observed Covariate Effects on Baseline Hazard Rate-Case Study: Jajarm Bauxite Mine. J. Modeling Eng. 2019, 0. [Google Scholar] [CrossRef]
- Allahkarami, Z.; Sayadi, A.R.; Ghodrati, B. Identifying the Mixed Effects of Unobserved and Observed Risk Factors on the Reliability of Mining Hauling System. Int. J. Syst. Assur. Eng. Manag. 2021, 12, 281–289. [Google Scholar] [CrossRef]
- Barabady, J.; Kumar, U. Availability Allocation through Importance Measures. Int. J. Qual. Reliab. Manag. 2007, 24, 643–657. [Google Scholar] [CrossRef] [Green Version]
- Signoret, J.-P.; Leroy, A. Critical States and Importance Factors. In Springer Series in Reliability Engineering; Springer: Berlin/Heidelberg, Germany, 2021; pp. 333–371. [Google Scholar]
- Dui, H.; Zheng, X.; Guo, J.; Xiao, H. Importance Measure-Based Resilience Analysis of a Wind Power Generation System. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2021, 1–11. [Google Scholar] [CrossRef]
- Zaki, R.; Barabadi, A.; Barabadi, J.; Qarahasanlou, A.N. Observed and Unobserved Heterogeneity in Failure Data Analysis. J. Risk Reliab. 2021, 1–14. [Google Scholar] [CrossRef]
- Youn, B.D.; Hu, C.; Wang, P. Resilience-Driven System Design of Complex Engineered Systems. J. Mech. Des. 2011, 133, 101011. [Google Scholar] [CrossRef]
- Hu, Z.; Mahadevan, S. Resilience Assessment Based on Time-Dependent System Reliability Analysis. J. Mech. Des. 2016, 138, 111404. [Google Scholar] [CrossRef]
- Asha, G.; Raja, A.V.; Ravishanker, N. Reliability Modelling Incorporating Load Share and Frailty. Appl. Stoch. Models Bus. Ind. 2018, 34, 206–223. [Google Scholar] [CrossRef]
- Xu, M.; Li, X. Negative Dependence in Frailty Models. J. Stat. Plan. Inference 2008, 138, 1433–1441. [Google Scholar] [CrossRef]
- Misra, N.; Gupta, N.; Gupta, R.D. Stochastic Comparisons of Multivariate Frailty Models. J. Stat. Plan. Inference 2009, 139, 2084–2090. [Google Scholar] [CrossRef]
- Giorgio, M.; Guida, M.; Pulcini, G. Repairable System Analysis in Presence of Covariates and Random Effects. Reliab. Eng. Syst. Saf. 2014, 131, 271–281. [Google Scholar] [CrossRef]
- Barker, K.; Baroud, H. Proportional Hazards Models of Infrastructure System Recovery. Reliab. Eng. Syst. Saf. 2014, 124, 201–206. [Google Scholar] [CrossRef]
- Mottahedi, A.; Sereshki, F.; Ataei, M.; Qarahasanlou, A.N.; Barabadi, A. Resilience Analysis: A Formulation to Model Risk Factors on Complex System Resilience. Int. J. Syst. Assur. Eng. Manag. 2021, 12, 871–883. [Google Scholar] [CrossRef]
- Rød, B.; Barabadi, A.; Gudmestad, O.T. Characteristics of Arctic Infrastructure Resilience: Application of Expert Judgement. In Proceedings of The 26th International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–1 July 2016. [Google Scholar]
- Gutierrez, R.G. Parametric Frailty and Shared Frailty Survival Models. Stata J. 2002, 2, 22–44. [Google Scholar] [CrossRef] [Green Version]
- Kumar, D.; Klefsjö, B. Proportional Hazards Model: A Review. Reliab. Eng. Syst. Saf. 1994, 44, 177–188. [Google Scholar] [CrossRef]
- Schoenfeld, D. Chi-Squared Goodness-of-Fit Tests for the Proportional Hazards Regression Model. Biometrika 1980, 67, 145–153. [Google Scholar] [CrossRef]
- Park, S.; Hendry, D.J. Reassessing Schoenfeld Residual Tests of Proportional Hazards in Political Science Event History Analyses. Am. J. Political Sci. 2015, 59, 1072–1087. [Google Scholar] [CrossRef] [Green Version]
- Brewer, M.J.; Butler, A.; Cooksley, S.L. The Relative Performance of AIC, AICC and BIC in the Presence of Unobserved Heterogeneity. Methods Ecol. Evol. 2016, 7, 679–692. [Google Scholar] [CrossRef]
- Kuha, J. AIC and BIC: Comparisons of Assumptions and Performance. Sociol. Methods Res. 2004, 33, 188–229. [Google Scholar] [CrossRef]
- Garmabaki, A.H.S.; Ahmadi, A.; Mahmood, Y.A.; Barabadi, A. Reliability Modelling of Multiple Repairable Units. Qual. Reliab. Eng. Int. 2016, 32, 2329–2343. [Google Scholar] [CrossRef]



| Risk Factors (z) | Classification | Quantification |
|---|---|---|
| Shift () | Morning | 1 |
| Afternoon | 2 | |
| Night | 3 | |
| Rock kind () | Waste | 1 |
| Ore | 2 | |
| Operation team () | A | 1 |
| B | 2 | |
| C | 3 | |
| D | 4 | |
| Precipitation () | Continues | |
| ) | Continues | |
| ) | Continues | |
| Correlation | ||||||
| Pearson value. | 1 | −0.04 | . | 0.11 | −0.01 | |
| p-value | 0.45 | . | 0.04 | 0.83 | ||
| Pearson value | −0.04 | 1 | . | −0.11 | 0.02 | |
| p-value | 0.45 | . | 0.04 | 0.68 | ||
| Pearson value | . | . | . | . | . | |
| p-value | . | . | . | . | . | |
| Pearson value | 0.11 | −0.11 | . | 1 | −0.08 | |
| p-value | 0.04 | 0.04 | . | 0.15 | ||
| Pearson value | −0.01 | 0.023 | . | −0.08 | 1 | |
| p-value | 0.83 | 0.68 | . | 0.15 | ||
| Risk Factors | Regression Coefficient | Chi-Square | Degree of Free | p-Value |
|---|---|---|---|---|
| shift | . | . | . | . |
| −0.02 | 0.11 | 1.00 | 0.75 | |
| 0.01 | 0.02 | 1.00 | 0.89 | |
| Rock kind | . | . | 1.00 | . |
| −0.01 | 0.08 | 1.00 | 0.78 | |
| Operation team | . | . | . | . |
| −0.10 | 3.56 | 1.00 | 0.06 | |
| −0.02 | 0.17 | 1.00 | 0.68 | |
| 0.00 | 0.00 | 1.00 | 0.98 | |
| −0.01 | 0.04 | 1.00 | 0.84 | |
| 0.02 | 0.16 | 1.00 | 0.69 | |
| . | . | . | . |
| Subsystem | Model | Observations | Goodness of Fit Test | LR Test | ||
|---|---|---|---|---|---|---|
| AIC | BIC | Statistic | p-Value | |||
| A | Weibull-PHM | 323 | 1086.709 | 1124.485 | 2.6 | 0.053 |
| Weibull-MPHM | 323 | 1086.105 | 1127.659 | |||
| Exponential-PHM | 323 | 1090.162 | 1124.161 | 8.04 | 0.002 | |
| Exponential-MPHM | 323 | 1084.120 | 1121.896 | |||
| B | Weibull-PHM | 325 | 1025.301 | 1066.924 | 0 | 1 |
| Weibull-MPHM | 325 | 1027.301 | 1072.707 | |||
| Exponential-PHM | 325 | 1023.951 | 1061.789 | 0 | 1 | |
| Exponential-MPHM | 325 | 1025.951 | 1067.573 | |||
| C | Weibull-PHM | 387 | 1236.524 | 1279.808 | 23.59 | 0 |
| Weibull-MPHM | 387 | 1214.935 | 1262.153 | |||
| Exponential-PHM | 387 | 1239.260 | 1278.609 | 18.81 | 0 | |
| Exponential-MPHM | 387 | 1222.446 | 1265.730 | |||
| D | Weibull-PHM | 319 | 1051.128 | 1092.545 | 11.29 | 0 |
| Weibull-MPHM | 319 | 1041.839 | 1083.022 | |||
| Exponential-PHM | 319 | 1052.404 | 1090.056 | 11.04 | 0 | |
| Exponential-MPHM | 319 | 1043.364 | 1084.781 | |||
| Risk Factors | Coefficient | Standard Error | Z | p-Value | (95% Conf. Interval) | |
|---|---|---|---|---|---|---|
| shift | ||||||
| 0.00 | 0.18 | −0.01 | 0.99 | −0.36 | 0.36 | |
| 0.22 | 0.19 | 1.12 | 0.26 | −0.16 | 0.59 | |
| 0.61 | 0.17 | 3.61 | 0.00 | 0.28 | 0.94 | |
| Operation team | ||||||
| −0.26 | 0.19 | −1.36 | 0.18 | −0.63 | 0.12 | |
| −0.12 | 0.21 | −0.60 | 0.55 | −0.53 | 0.28 | |
| −0.16 | 0.33 | −0.47 | 0.64 | −0.80 | 0.49 | |
| −0.03 | 0.01 | −2.57 | 0.01 | −0.05 | −0.01 | |
| −0.01 | 0.01 | −0.97 | 0.33 | −0.02 | 0.01 | |
| 0.01 | 0.06 | 0.22 | 0.83 | −0.10 | 0.12 | |
| Constant value | −2.89 | 0.34 | −8.52 | 0.00 | −3.55 | −2.22 |
| Subsystem | θ | Reliability | |||
|---|---|---|---|---|---|
| Best fit | Parameters | ||||
| A | Ex.--MPHM | β = 1, η = 25.98 | 0.173 | - | |
| B | Ex.--PHM | β = 1, η = 19.88 | - | ||
| C | We.-MPHM | β = 1.27, η = 11.93 | 0.544 | ||
| D | We.-MPHM | β = 1.17, η = 11.83 | 0.404 | ||
| Subsystem | Model | Observations | AIC | BIC |
|---|---|---|---|---|
| A | Weibull | 323 | 1085.048 | 1092.603 |
| Exponential | 323 | 1092.531 | 1096.309 | |
| B | Weibull | 325 | 1028.085 | 1035.652 |
| Exponential | 325 | 1026.086 | 1029.870 | |
| C | Weibull | 387 | 1246.804 | 1254.674 |
| Exponential | 387 | 1254.551 | 1258.486 | |
| D | Weibull | 319 | 1061.103 | 1068.634 |
| Exponential | 319 | 1067.325 | 1071.091 |
| Subsystem | Classical Model | Parameters | Reliability | |
|---|---|---|---|---|
| β | η | |||
| A | Weibull | 0.882 | 26.725 | |
| B | Exponential | 1.000 | 24.603 | |
| C | Weibull | 0.891 | 23.800 | |
| D | Weibull | 0.890 | 22.220 | |
| Priority | Condition | Time | |||||
|---|---|---|---|---|---|---|---|
| 0–20 | 20–40 | 40–60 | 60–80 | 80–100 | 100–200 | ||
| First | Classical Model | D | D | D | D | D | D |
| Winter | D | B | B | B | B | B | |
| Summer | D | D | D | D | D | B | |
| Second | Classical Model | B | C | C | C | C | C |
| Winter | B | A | A | A | A | A | |
| Summer | B | B | B | B | B | A | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nouri Qarahasanlou, A.; Zamani, A.; Barabadi, A.; Mokhberdoran, M. Resilience Assessment: A Performance-Based Importance Measure. Energies 2021, 14, 7575. https://doi.org/10.3390/en14227575
Nouri Qarahasanlou A, Zamani A, Barabadi A, Mokhberdoran M. Resilience Assessment: A Performance-Based Importance Measure. Energies. 2021; 14(22):7575. https://doi.org/10.3390/en14227575
Chicago/Turabian StyleNouri Qarahasanlou, Ali, Ali Zamani, Abbas Barabadi, and Mahdi Mokhberdoran. 2021. "Resilience Assessment: A Performance-Based Importance Measure" Energies 14, no. 22: 7575. https://doi.org/10.3390/en14227575
APA StyleNouri Qarahasanlou, A., Zamani, A., Barabadi, A., & Mokhberdoran, M. (2021). Resilience Assessment: A Performance-Based Importance Measure. Energies, 14(22), 7575. https://doi.org/10.3390/en14227575







