Intelligent Algorithm for Variable Scale Adaptive Feature Separation of Mechanical Composite Fault Signals
Abstract
:1. Introduction
2. Sensing Systems and Signal Models
3. Proposed Method
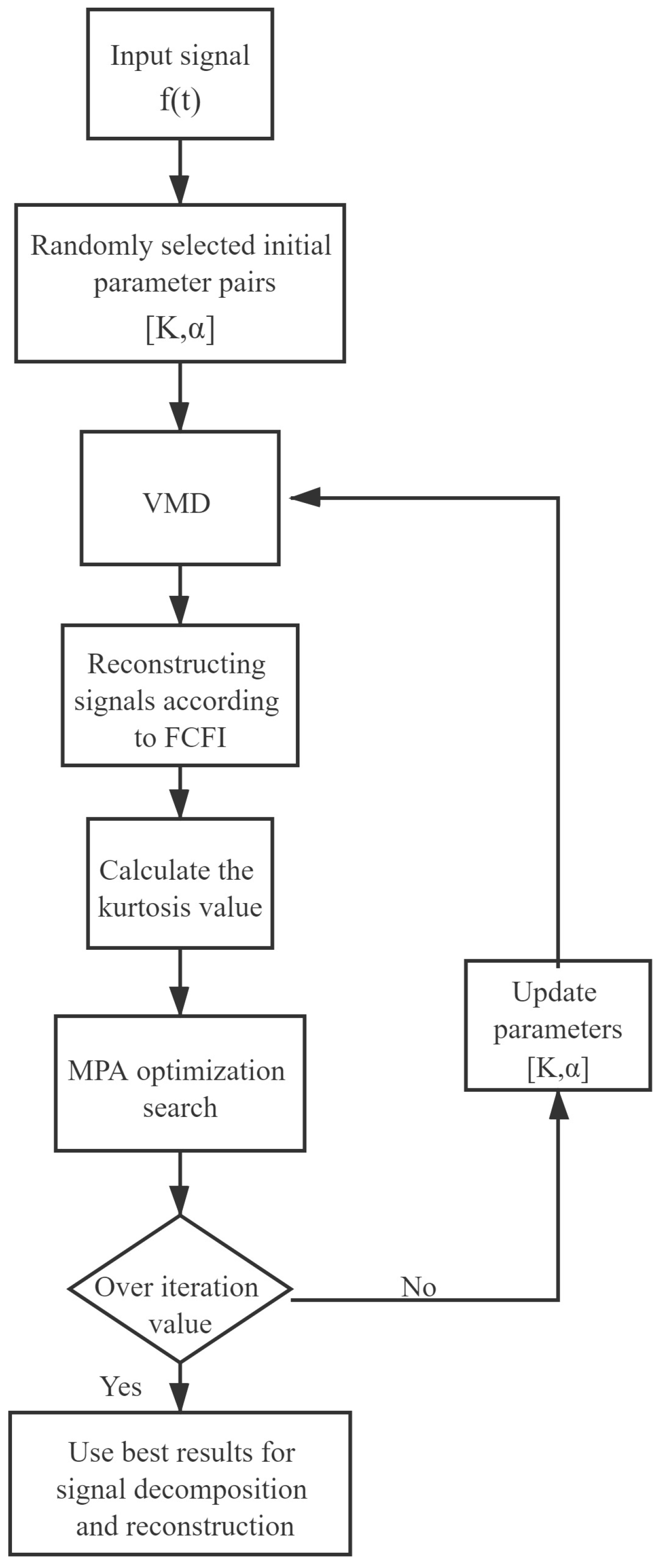
3.1. Algorithm Framework
3.2. VMD Decomposition and Reconfiguration
3.2.1. Decomposition
3.2.2. Reconfiguration
3.3. MPA Algorithm
4. Experiments and Results Analysis
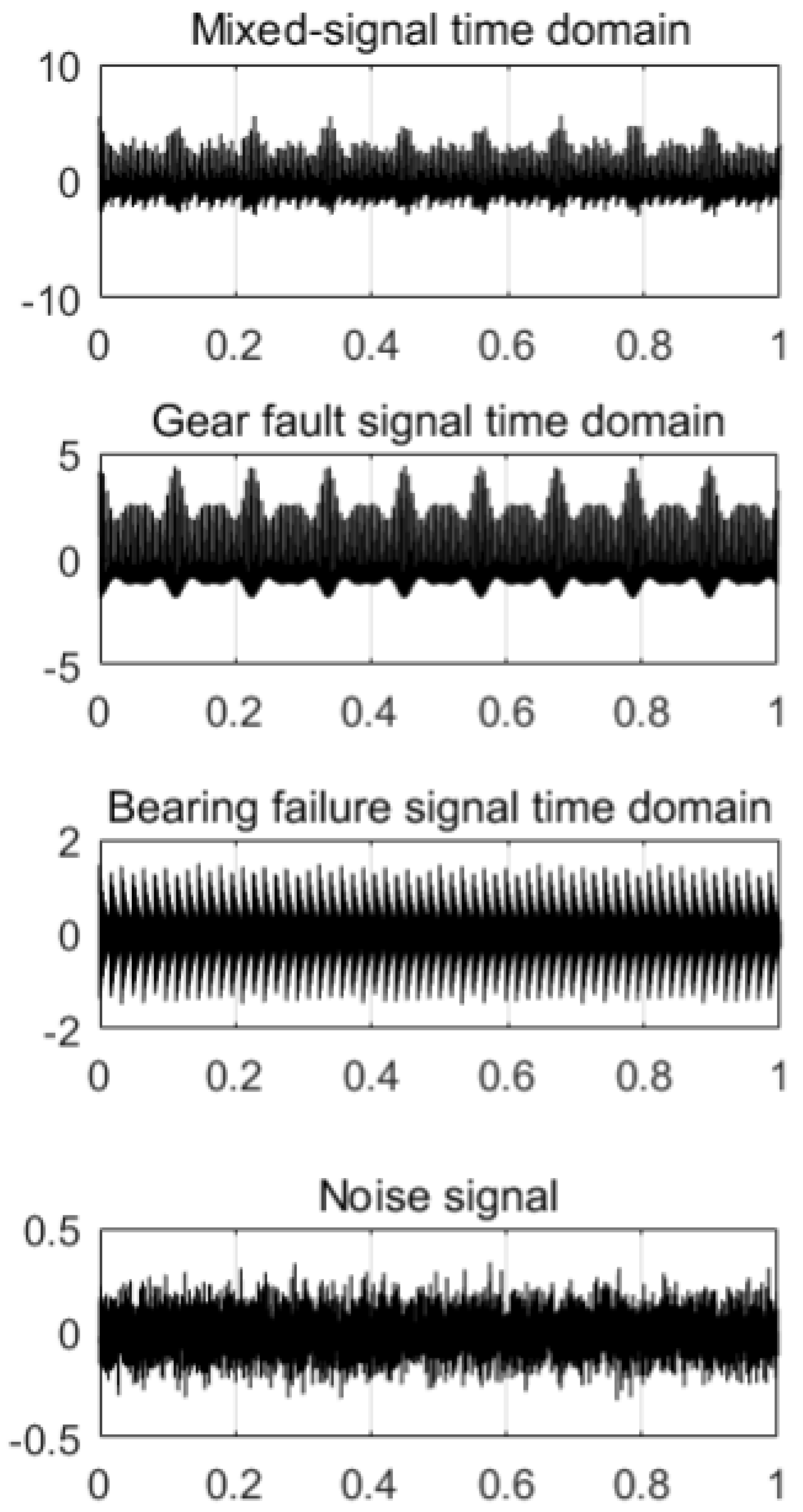
4.1. Experiment Settings
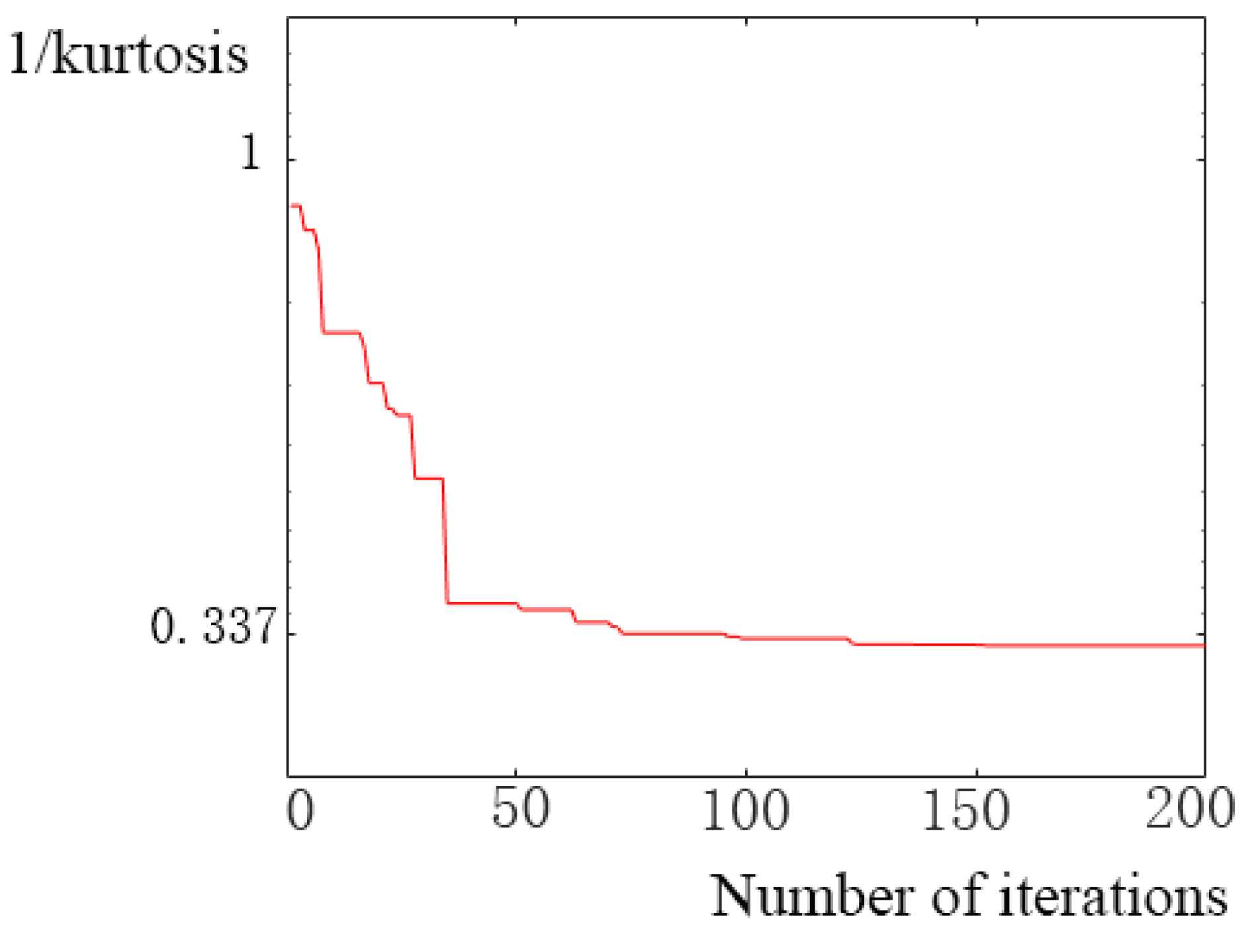
4.2. Parameter Optimization
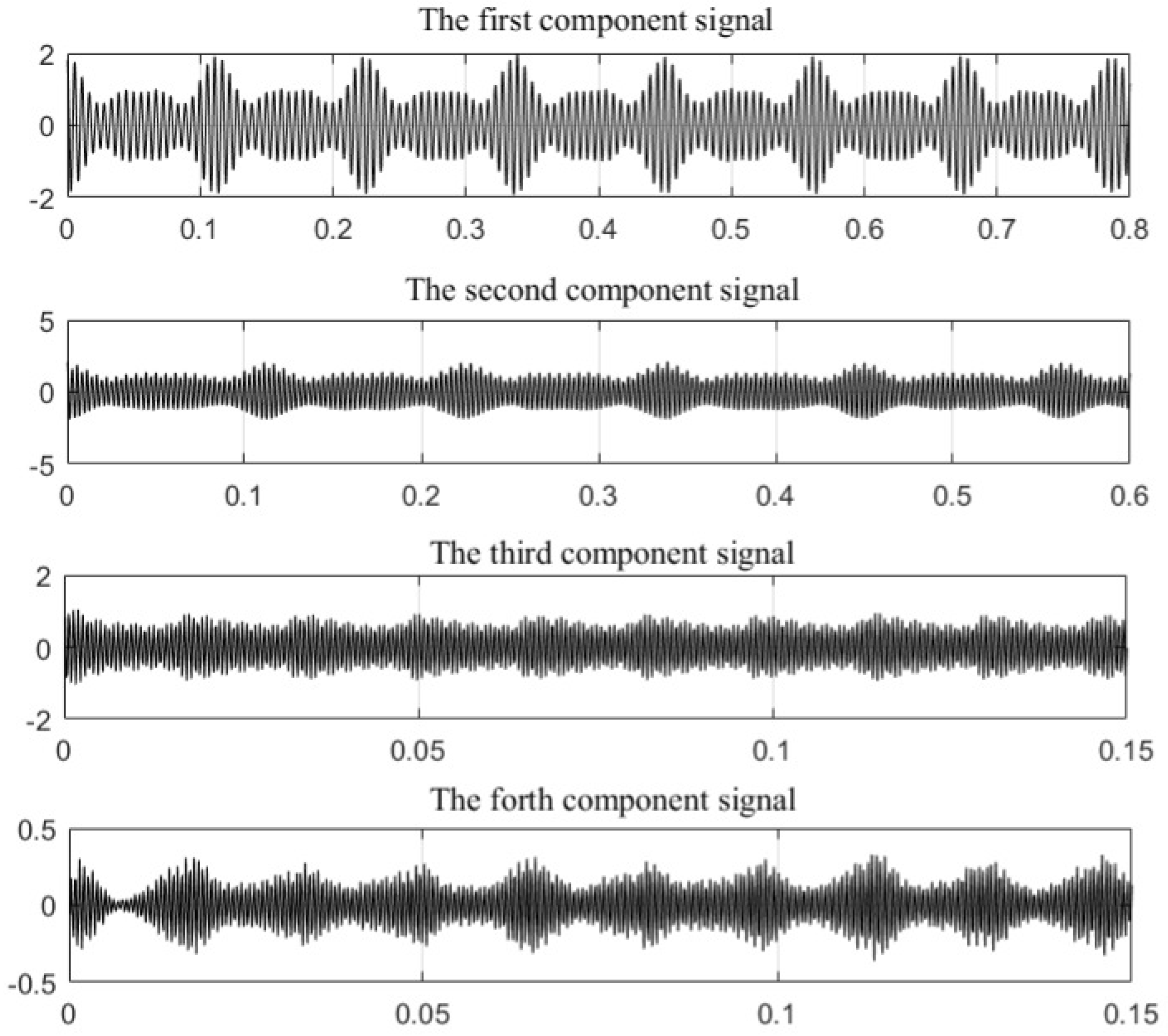
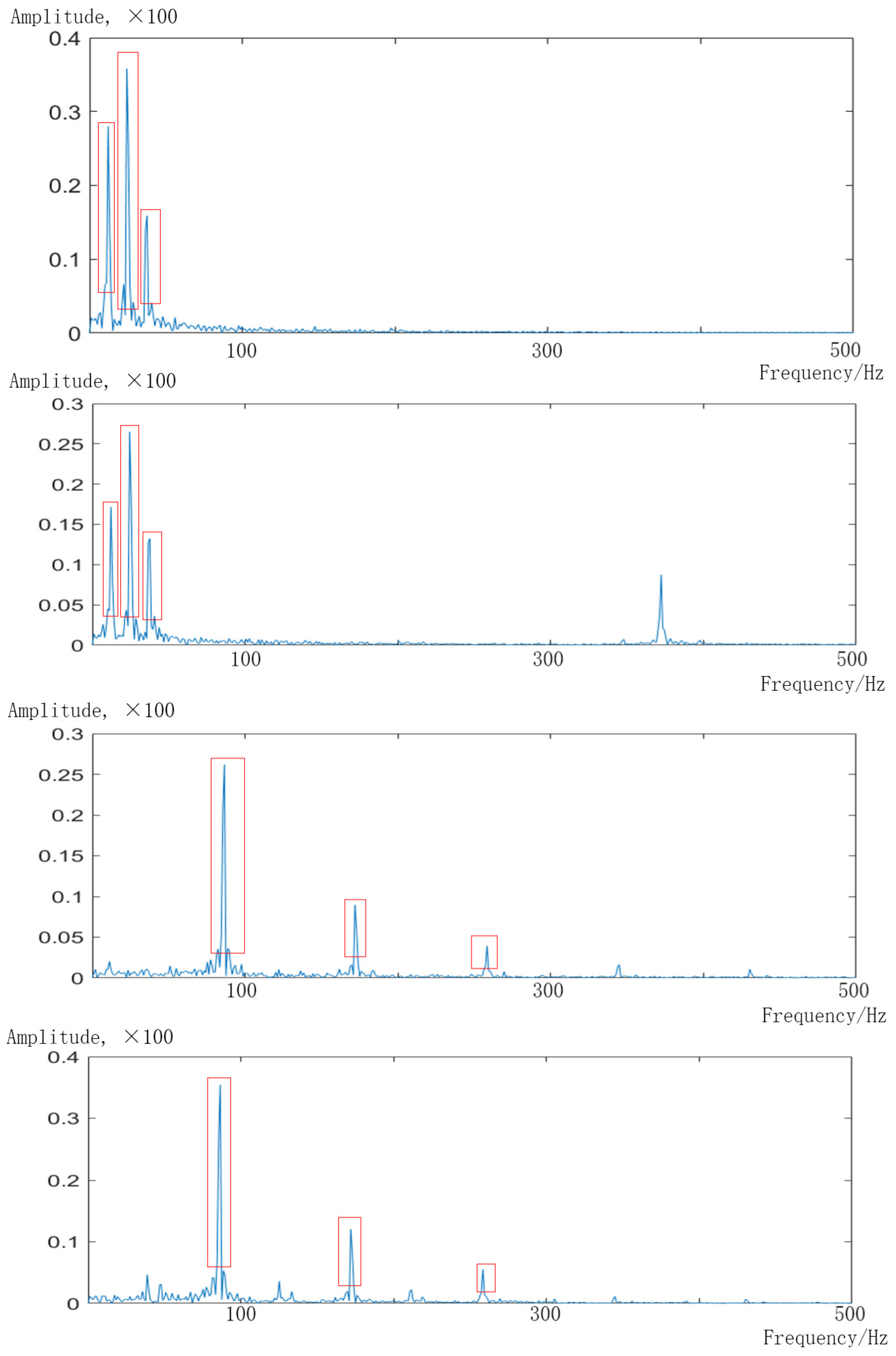
4.3. Decomposition and Reconstruction of Signals
4.4. Quantitative Analysis and Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Da Lpiaz, G.; Rivola, A.; Rubini, R. Effectiveness and Sensitivity of Vibration Processing Techniques. Mech. Syst. Signal Process. 2008, 10, 387–412. [Google Scholar]
- Liu, J.; Tang, C.; Pan, G. Dynamic modeling and simulation of a flexible-rotor ball bearing system. J. VIib. Control 2021. [Google Scholar] [CrossRef]
- Xia, C.; Wang, Z. Drivers analysis and empirical mode decomposition based forecasting of energy consumption structure—ScienceDirect. J. Clean. Prod. 2020, 254, 120107. [Google Scholar] [CrossRef]
- Ghelardoni, L.; Ghio, A.; Anguita, D. Energy Load Forecasting Using Empirical Mode Decomposition and Support Vector Regression. IEEE Trans. Smart Grid 2013, 4, 549–556. [Google Scholar] [CrossRef]
- Corizzo, R.; Ceci, M.; Fanaee-T, H. Multi-aspect Renewable Energy Forecasting. Inf. Sci. 2020, 546, 701–722. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, J.; Pan, G. A multi-stage predicting methodology based on data decomposition and error correction for ultra-short-term wind energy prediction. J. Clean. Prod. 2021, 292, 125981. [Google Scholar] [CrossRef]
- Ceci, M.; Corizzo, R.; Japkowicz, N. ECHAD: Embedding-Based Change Detection from Multivariate Time Series in Smart Grids. IEEE Access 2020, 99, 156053–156066. [Google Scholar] [CrossRef]
- Aubras, F.; Damour, C.; Benne, M. A Non-Intrusive Signal-Based Fault Diagnosis Method for Proton Exchange Membrane Water Electrolyzer Using Empirical Mode Decomposition. Energies 2021, 14, 4458. [Google Scholar] [CrossRef]
- Soualhi, A.; El Yousfi, B.; Razik, H.; Wang, T. A Novel Feature Extraction Method for the Condition Monitoring of Bearings. Energies 2021, 14, 2322. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Daubechies, I.; Lu, J.; Wu, H. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 2010, 30, 243–261. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.; Sun, H.; Wang, S. SSWT and VMD Linked Mode Identification and Time-of-Flight Extraction of Denoised SH Guided Waves. IEEE Sens. J. 2021, 21, 14709–14717. [Google Scholar] [CrossRef]
- Zhong, J.; Gou, X.; Shu, Q. A FOD Detection Approach on Millimeter-Wave Radar Sensors Based on Optimal VMD and SVDD. Sensors 2021, 21, 997. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, D. Bearing Fault Diagnosis Based on BFA Optimized VMD Parameters. Modul. Mach. Tool Autom. Manuf. Tech. 2020, 555, 50–56. [Google Scholar]
- Shanshan, W.; Guobing, H.; Bing, G. Variational Mode Decomposition(VMD) Based Method of Leakage Locating in Water Delivery Lines. Sensor Lett. 2016, 14, 846–851. [Google Scholar] [CrossRef]
- Soman, K.P.; Poornach, P.; Athira, S. Recursive Variational Mode Decomposition Algorithm for Real Time Power Signal Decomposition. Procedia Technol. 2015, 21, 540–546. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Z.; Zhou, T.; Liu, J. Fault Diagnosis Approach for Rotating Machinery Based on Feature Importance Ranking and Selection. Shock Vib. 2021, 2021, 8899188. [Google Scholar] [CrossRef]
- Sahani, M.; Dash, P.K. Variational mode decomposition and weighted online sequential extreme learning machine for power quality event patterns recognition. Neurocomputing 2018, 310, 10–17. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 14, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S. Marine Predators Algorithm: A Nature-inspired Metaheuristic. Expert Syst. Appl. 2020, 152, 77–104. [Google Scholar] [CrossRef]
- Viswanathan, G.M.; Buld, S.V. Optimizing the success of random searches. Nature 1999, 401, 911–914. [Google Scholar] [CrossRef] [PubMed]
- Bartumeus, F.; Catalan, J.; Fulco, U.L. Optimizing the Encounter Rate in Biological Interactions: Lévy versus Brownian Strategies. Phys. Rev. Lett. 2002, 88, 16–19. [Google Scholar] [CrossRef] [PubMed]
- Amarnath, M.; Krishna, I.R.P. Empirical mode decomposition of acoustic signals for diagnosis of faults in gears and rolling element bearings. IET Sci. Meas. Technol. 2012, 6, 279–287. [Google Scholar] [CrossRef]
- Nahler, G. Pearson Correlation Coefficient; Springer: Vienna, Austria, 2009; Volume 1025, p. 132. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
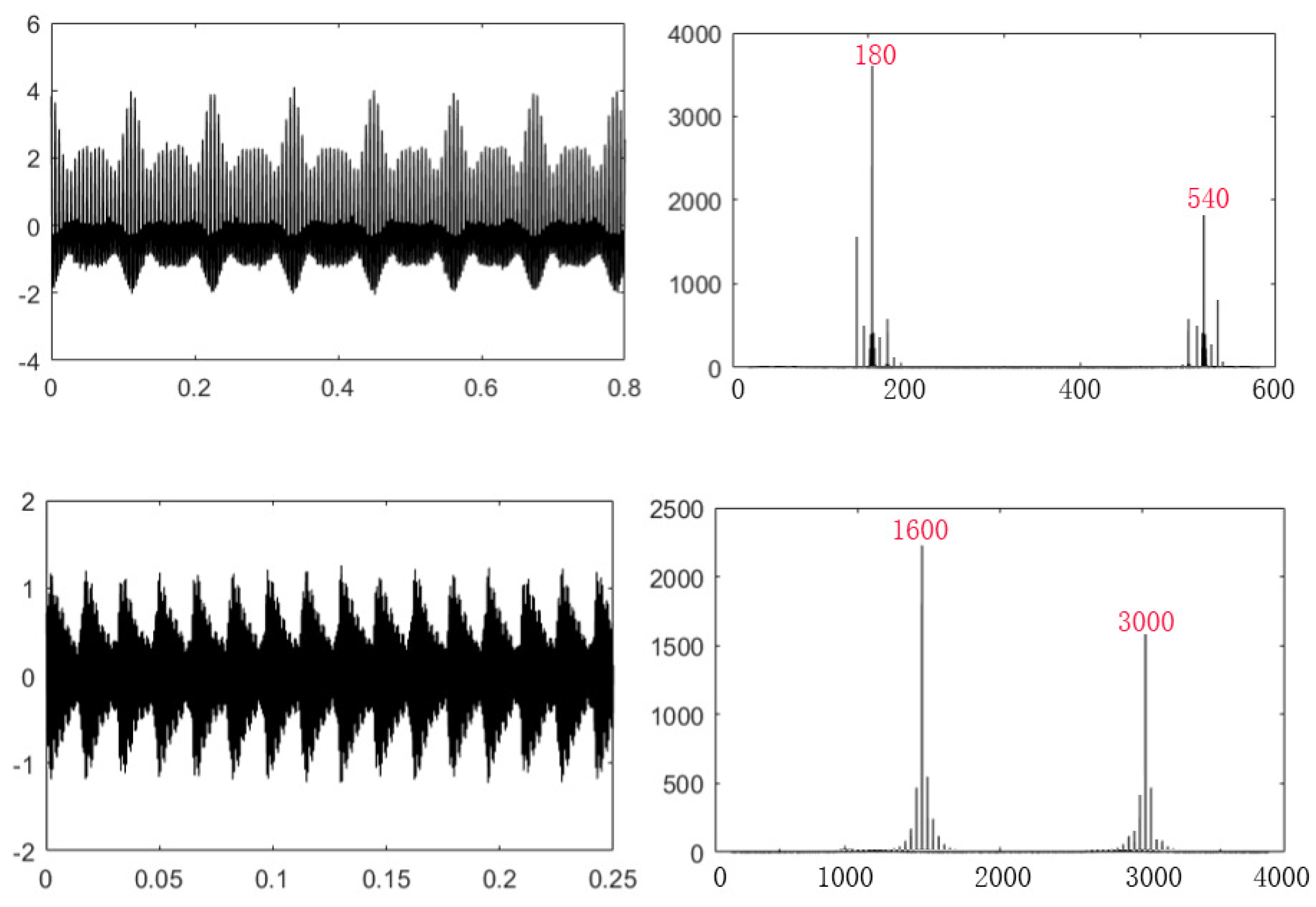

| Bearing Simulation Signal Parameters | |
| Parameter Name | Numerical value |
| Resonant Frequency Order (I) | 2 |
| Resonant Frequency () | [1600, 3000] |
| Gear Simulation Signal Parameters | |
| Parameter Name | Numerical value |
| Engagement Frequency Order (P) | 3 |
| Magnitude Modulation Order (Q) | 3 |
| Engagement Frequency () | 180 |
| Engagement Frequency Amplitude () | [1, 1.2, 0.5] |
| Fault Frequency () | 8.9 |
| [0.3, 0.15, 0.1] | |
| Amplitude Modulation Factor () | [0.4, 0.25, 0.15] |
| [0.2, 0.15, 0.05] | |
| Outer Ring Fault Frequency () | 62 |
| Resonance Frequency Amplitude () | [1.5, 2] |
| Attenuation Coefficient (b) | 100 |
| EMD | VMD Parameter as [3, 2000] | Our Method | |
|---|---|---|---|
| Average Correlation Coefficient () | 0.5232 | 0.4778 | 0.5914 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, S.; Liu, X.; Yang, Y.; Cao, H.; Zhong, Y.; Luo, C. Intelligent Algorithm for Variable Scale Adaptive Feature Separation of Mechanical Composite Fault Signals. Energies 2021, 14, 7702. https://doi.org/10.3390/en14227702
Han S, Liu X, Yang Y, Cao H, Zhong Y, Luo C. Intelligent Algorithm for Variable Scale Adaptive Feature Separation of Mechanical Composite Fault Signals. Energies. 2021; 14(22):7702. https://doi.org/10.3390/en14227702
Chicago/Turabian StyleHan, Shu, Xiaoming Liu, Yan Yang, Hailin Cao, Yuanhong Zhong, and Chuanlian Luo. 2021. "Intelligent Algorithm for Variable Scale Adaptive Feature Separation of Mechanical Composite Fault Signals" Energies 14, no. 22: 7702. https://doi.org/10.3390/en14227702
APA StyleHan, S., Liu, X., Yang, Y., Cao, H., Zhong, Y., & Luo, C. (2021). Intelligent Algorithm for Variable Scale Adaptive Feature Separation of Mechanical Composite Fault Signals. Energies, 14(22), 7702. https://doi.org/10.3390/en14227702






