Reinforcement Learning Path Planning Method with Error Estimation
Abstract
:1. Introduction
2. Background
3. Planning Strategy
3.1. Principle of Q-Learning
3.2. Proposed Strategy
| Algorithm 1: Path planning algorithm considering cumulative error statistics |
| Require: Original map data, reward and punishment function rules, algorithm termination conditions |
| 1: initial according to map size; |
| 2: repeat (for each episode): |
| 3: Initialize s |
| 4: repeat (for each step of episode): |
| 5: Choose a from s using from Q; |
| 6: if a and is not consistent then |
| 7: Give extra punishment; |
| 8: else |
| 9: Normal rewards and punishments; |
| 10: end if |
| 11: Take action a, observe r, ; |
| 12: until s is terminal |
| 13: until the path expectation and variance meet the set value or |
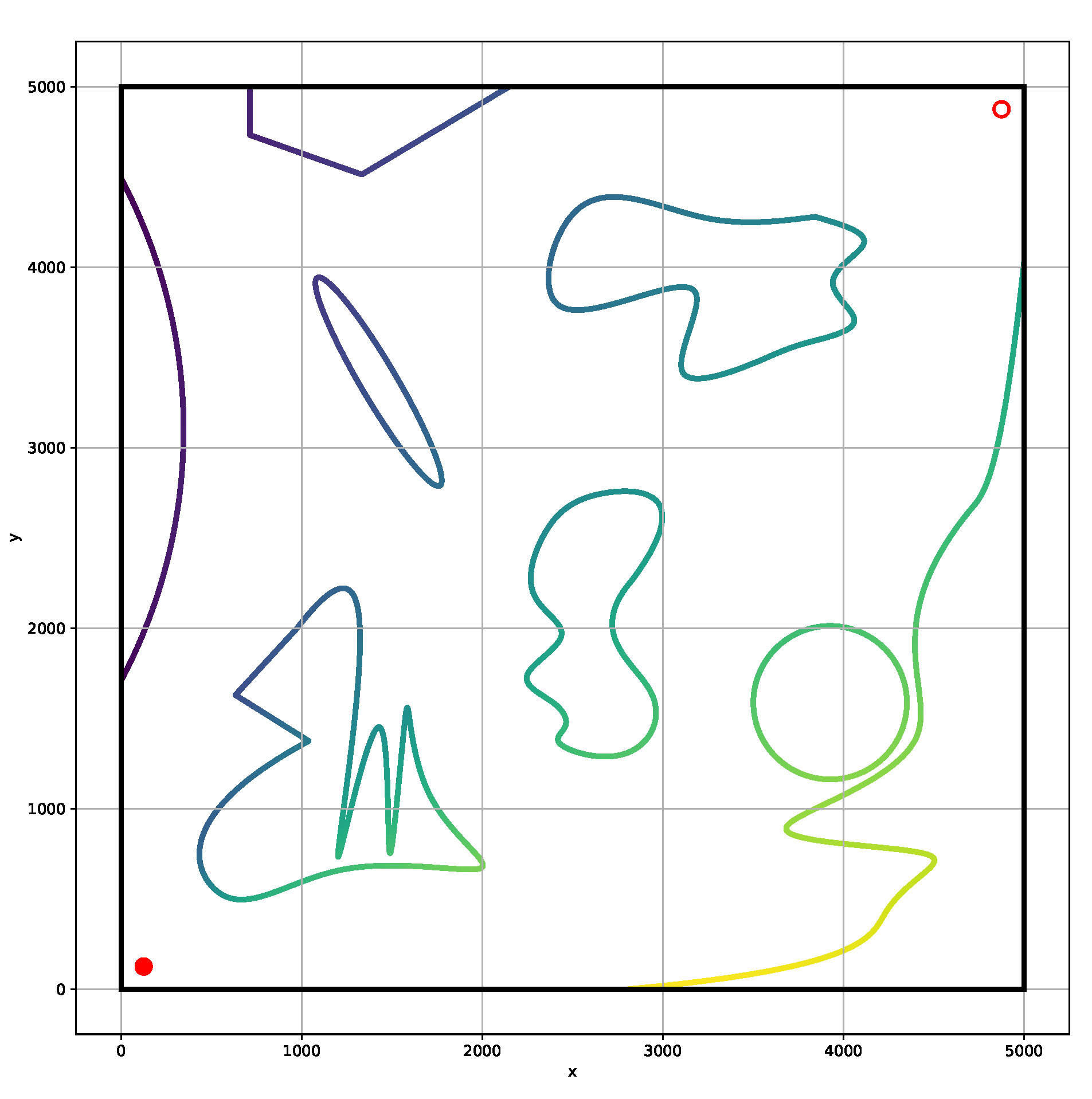
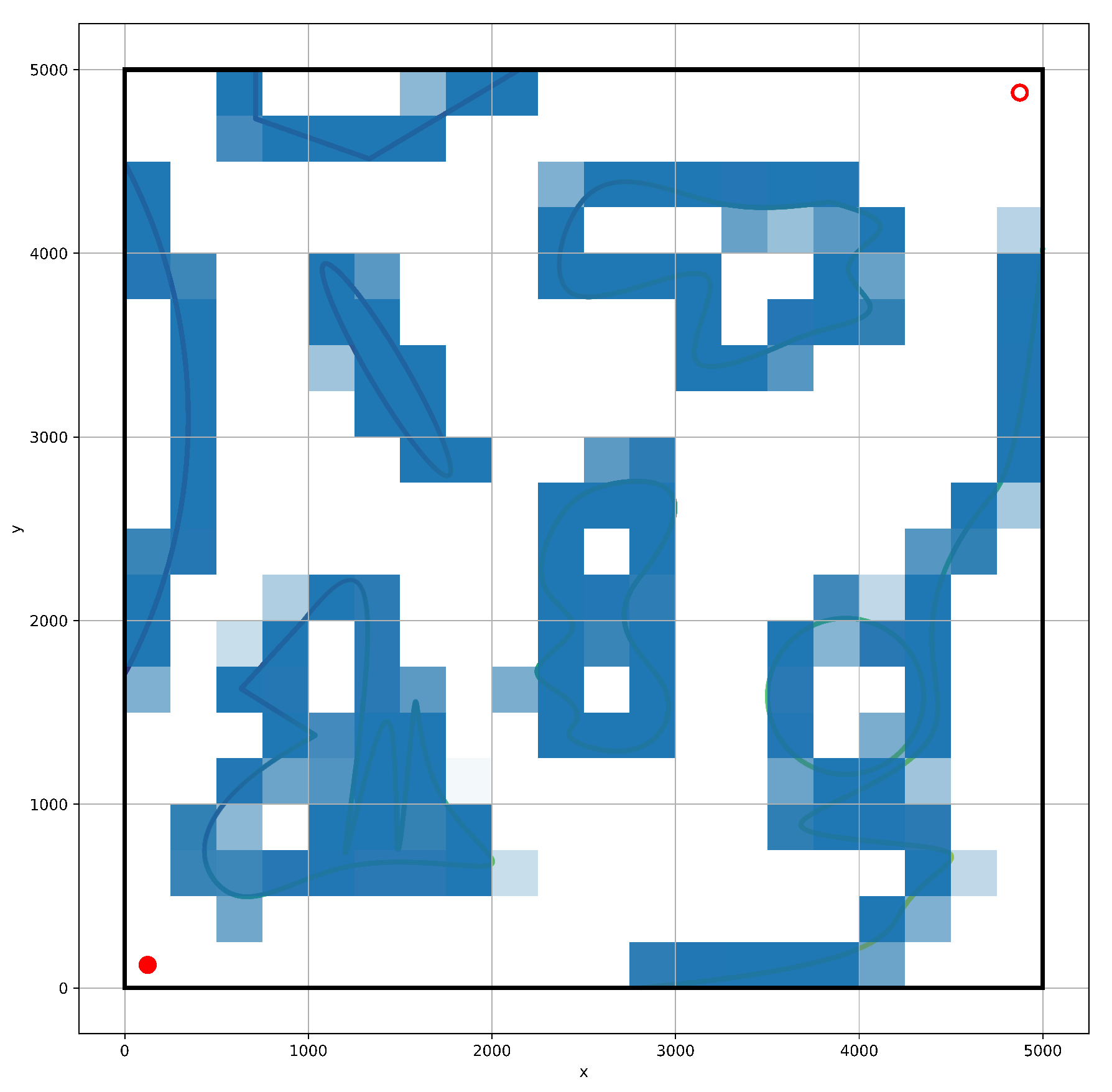
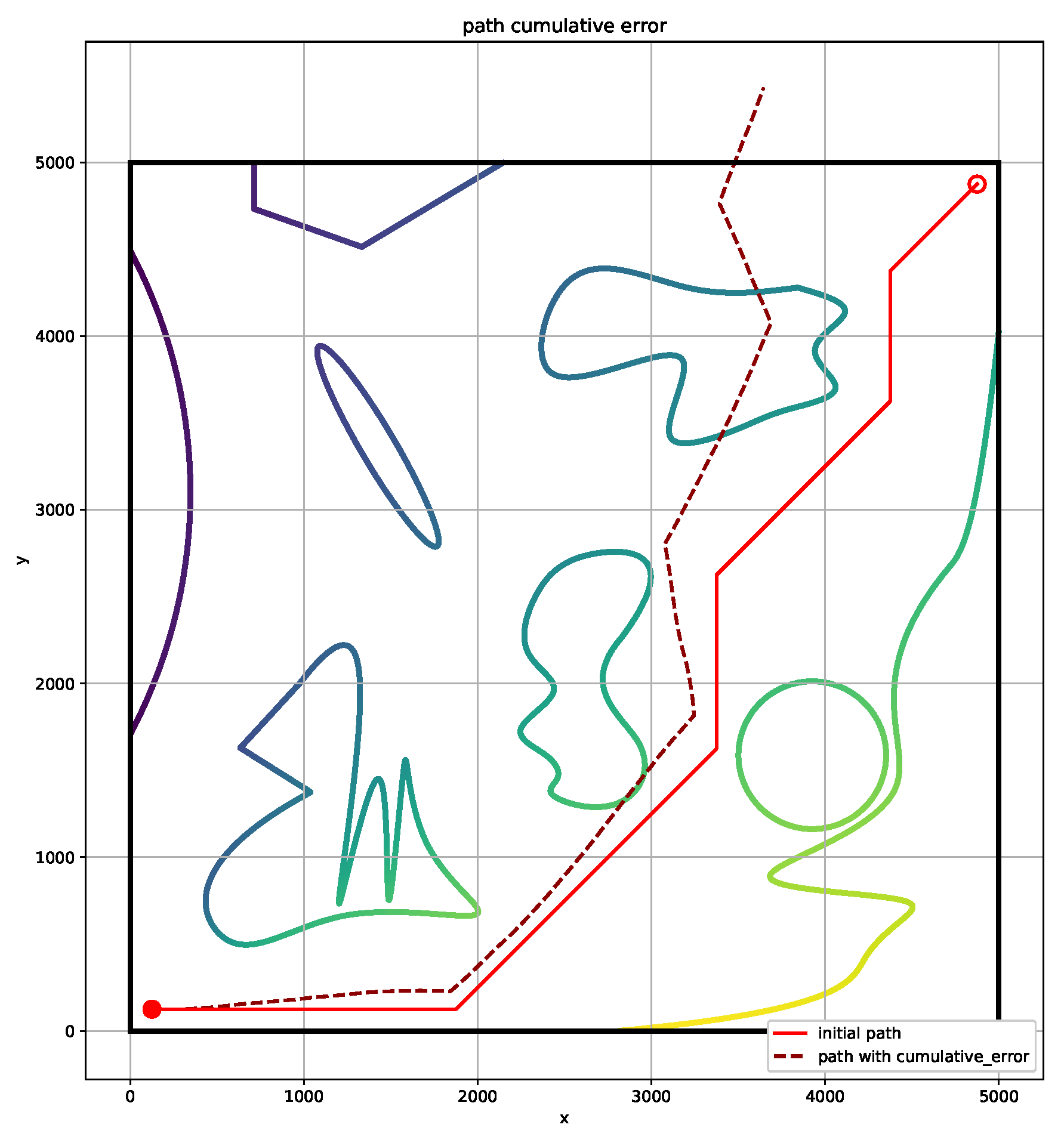
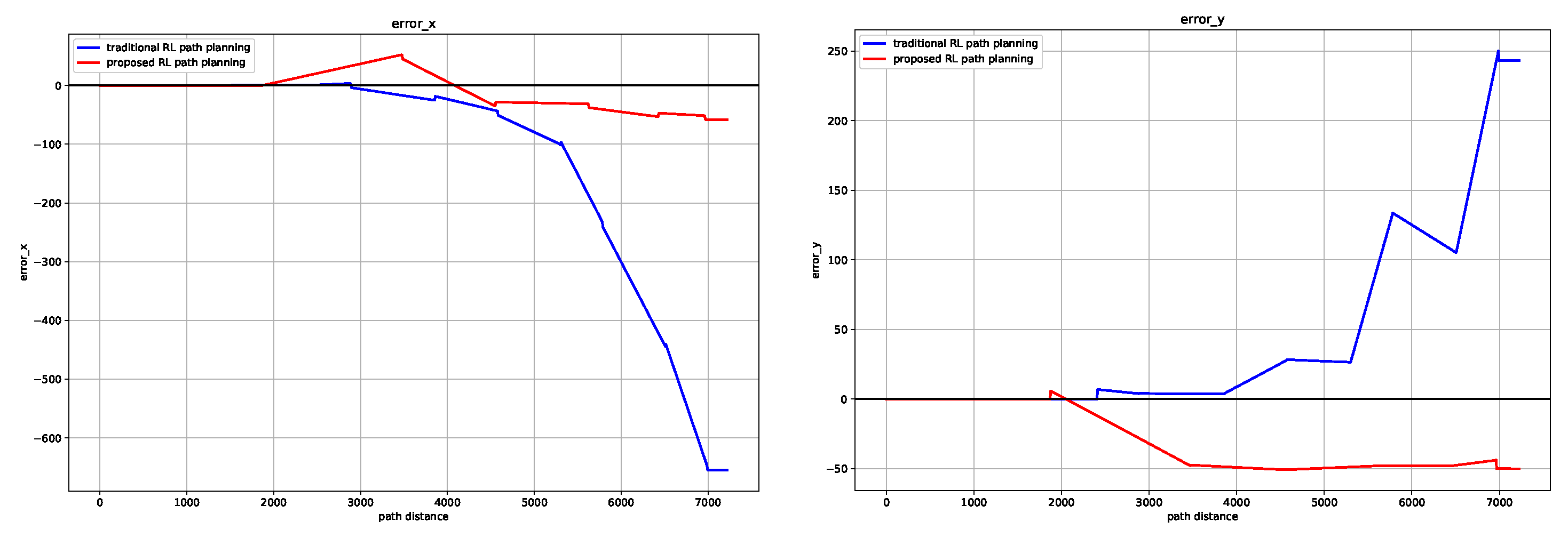
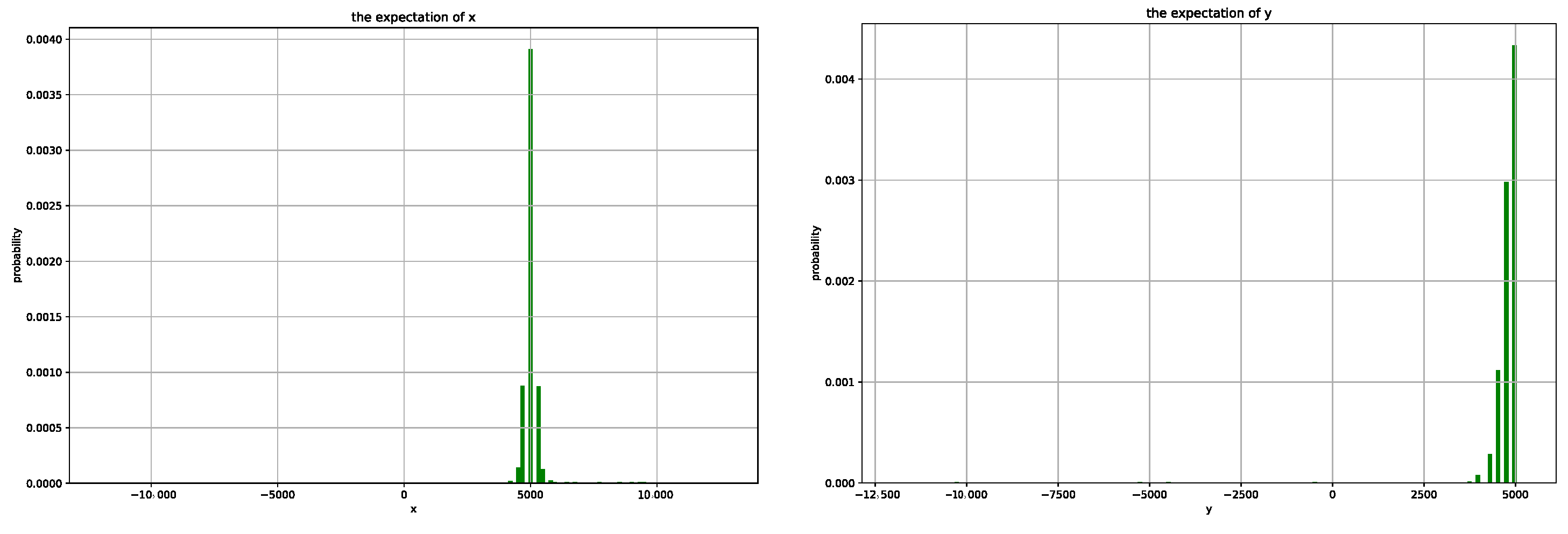
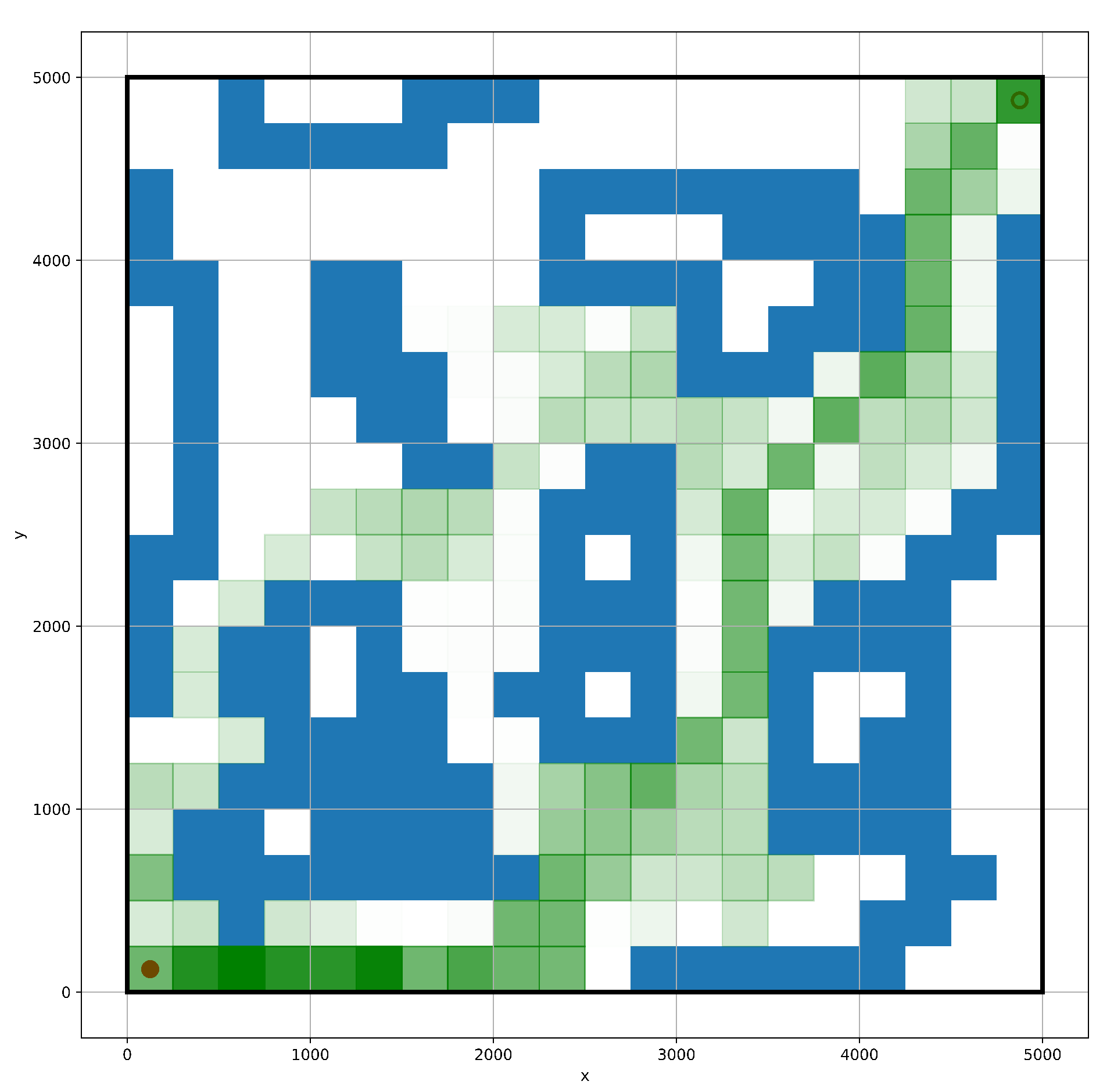
4. Simulation and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GPS | Global Positioning System |
| IID | Independent Identically Distribution |
| R.L | Reinforcement Learning |
References
- Bidot, J.; Karlsson, L.; Lagriffoul, F.; Saffiotti, A. Geometric backtracking for combined task and motion planning in robotic systems. Artif. Intell. 2013, 247, 229–265. [Google Scholar] [CrossRef]
- Peng, Y.; Green, P.N. Environment mapping, map constructing, and path planning for underwater navigation of a low-cost μAUV in a cluttered nuclear storage pond. IAES Int. J. Robot. Autom. 2019, 8, 277–292. [Google Scholar] [CrossRef]
- Choset, H.; Lynch, K.; Hutchinson, S.; Kantor, G.; Burgard, W.; Kavraki, L.; Thrun, S. Principles of Robot Motion: Theory, Algorithms, and Implementation. 2005. Available online: https://ieeexplore.ieee.org/servlet/opac?bknumber=6267238 (accessed on 9 November 2021).
- Ibraheem, I.K.; Hassan, F. Path Planning of an Autonomous Mobile Robot in a Dynamic Environment using Modified Bat Swarm Optimization. arXiv 2018, arXiv:1807.05352. [Google Scholar]
- Zeng, J.; Qin, L.; Hu, Y.; Yin, Q.; Hu, C. Integrating a Path Planner and an Adaptive Motion Controller for Navigation in Dynamic Environments. Appl. Sci. 2019, 9, 1384. [Google Scholar] [CrossRef] [Green Version]
- Yilmaz, N.K.; Evangelinos, C.; Lermusiaux, P.; Patrikalakis, N.M. Path Planning of Autonomous Underwater Vehicles for Adaptive Sampling Using Mixed Integer Linear Programming. IEEE J. Ocean. Eng. 2008, 33, 522–537. [Google Scholar] [CrossRef] [Green Version]
- Konar, A.; Chakraborty, I.; Singh, S.; Jain, L.; Nagar, A. A Deterministic Improved Q-Learning for Path Planning of a Mobile Robot. Syst. Man Cybern. Syst. IEEE Trans. 2013, 43, 1141–1153. [Google Scholar] [CrossRef] [Green Version]
- Kaiqiang, T.; Fu, H.; Jiangt, H.; Liu, C.; Wang, L. Reinforcement Learning for Robots Path Planning with Rule-based Shallow-trial. In Proceedings of the 2019 IEEE 16th International Conference on Networking, Sensing and Control (ICNSC), Banff, AB, Canada, 9–11 May 2019; pp. 340–345. [Google Scholar] [CrossRef]
- Johnson, J.J.; Li, L.; Liu, F.; Qureshi, A.H.; Yip, M.C. Dynamically Constrained Motion Planning Networks for Non-Holonomic Robots. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October–24 January 2021. [Google Scholar] [CrossRef]
- He, C.; Wan, Y.; Gu, Y.; Lewis, F. Integral reinforcement learning-based approximate minimum time-energy path planning in an unknown environment. Int. J. Robust Nonlinear Control 2020, 31, 1905–1922. [Google Scholar] [CrossRef]
- Luo, M.; Wan, Z.; Sun, Y.; Skorina, E.H.; Tao, W.; Chen, F.; Gopalka, L.; Yang, H.; Onal, C.D. Motion Planning and Iterative Learning Control of a Modular Soft Robotic Snake. Front. Robot. AI 2020, 7, 191. [Google Scholar] [CrossRef] [PubMed]
- Kulvicius, T.; Herzog, S.; Lüddecke, T.; Tamosiunaite, M.; Wörgötter, F. One-Shot Multi-Path Planning Using Fully Convolutional Networks in a Comparison to Other Algorithms. Front. Neurorobotics 2021, 14, 600984. [Google Scholar] [CrossRef] [PubMed]
- Rolland, L. Path Planning Kinematics Simulation of CNC Machine Tools Based on Parallel Manipulators. Mech. Mach. Sci. 2015, 29, 147–192. [Google Scholar] [CrossRef] [Green Version]
- Pérez Higueras, N.; Caballero, F.; Merino, L. Learning Human-Aware Path Planning with Fully Convolutional Networks. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 5897–5902. [Google Scholar] [CrossRef] [Green Version]
- Lv, L.; Zhang, S.; Ding, D.; Wang, Y. Path Planning via an Improved DQN-based Learning Policy. IEEE Access 2019, 7, 67319–67330. [Google Scholar] [CrossRef]
- Sainte Catherine, M.; Lucet, E. A modified Hybrid Reciprocal Velocity Obstacles approach for multirobot motion planning without communication. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October–24 January 2021; pp. 5708–5714. [Google Scholar] [CrossRef]
- Zhang, F.; Simon, C.; Chen, G.; Buckl, C.; Knoll, A. Cumulative error estimation from noisy relative measurements. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013), The Hague, Netherlands, 6–9 October 2013; pp. 1422–1429. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Knoll, A. Systematic Error Modeling and Bias Estimation. Sensors 2016, 16, 729. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cjc, H.W. Learning with Delayed Rewards. Ph.D. Thesis, University of Cambridge, Cambridge, MA, USA, 1989; pp. 233–235. [Google Scholar] [CrossRef]
- Chen, C.; Chen, X.Q.; Ma, F.; Zeng, X.J.; Wang, J. A knowledge-free path planning approach for smart ships based on reinforcement learning. Ocean Eng. 2019, 189, 106299. [Google Scholar] [CrossRef]
- Haghzad Klidbary, S.; Bagheri Shouraki, S.; Sheikhpour, S. Path planning of modular robots on various terrains using Q-learning versus optimization algorithms. Intell. Serv. Robot. 2017, 10, 121–136. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Peng, J.; Liu, W. A Cooperative Q-Learning Path Planning Algorithm for Origin-Destination Pairs in Urban Road Networks. Math. Probl. Eng. 2015, 2015, 146070. [Google Scholar] [CrossRef] [Green Version]
- Su, M.C.; Huang, D.Y.; Chou, C.H.; Hsieh, C.C. A reinforcement-learning approach to robot navigation. In Proceedings of the IEEE International Conference on Networking, Sensing and Control, Taipei, Taiwan, 21–23 March 2004; Volume 1, pp. 665–669. [Google Scholar] [CrossRef]
- Sutton, R.; Barto, A. Reinforcement Learning: An Introduction. IEEE Trans. Neural Networks 1998, 9, 1054. [Google Scholar] [CrossRef]
- Petres, C.; Pailhas, Y.; Patron, P.; Petillot, Y.; Evans, J.; Lane, D. Path Planning for Autonomous Underwater Vehicles. Robot. IEEE Trans. 2007, 23, 331–341. [Google Scholar] [CrossRef]
- Poddar, S.; Kumar, V.; Kumar, A. A Comprehensive Overview of Inertial Sensor Calibration Techniques. J. Dyn. Syst. Meas. Control 2017, 139, 011006. [Google Scholar] [CrossRef]
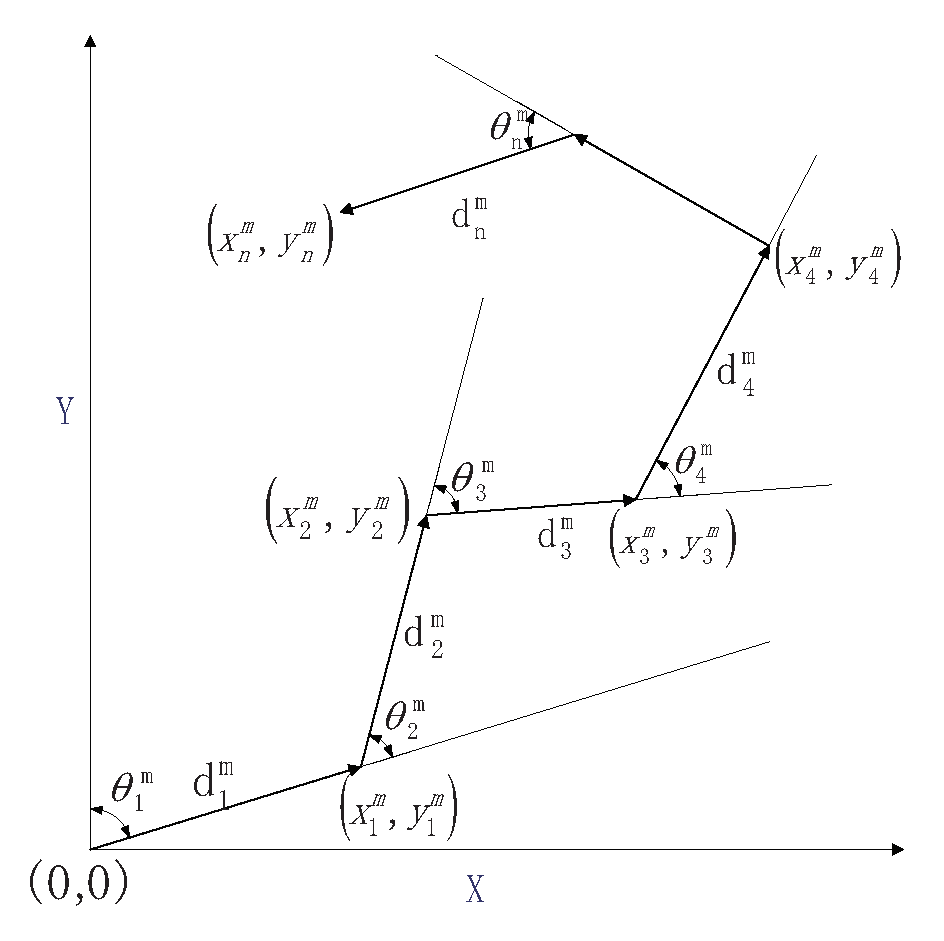

| States | Reward/Penalty | Value |
|---|---|---|
| Reach the boundary or obstacle | penalty | −1 |
| Reach the end point | reward | 100 |
| Drive straight | penalty | −0.0001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Wang, C.; Cheng, C.; Yang, D.; Pan, G. Reinforcement Learning Path Planning Method with Error Estimation. Energies 2022, 15, 247. https://doi.org/10.3390/en15010247
Zhang F, Wang C, Cheng C, Yang D, Pan G. Reinforcement Learning Path Planning Method with Error Estimation. Energies. 2022; 15(1):247. https://doi.org/10.3390/en15010247
Chicago/Turabian StyleZhang, Feihu, Can Wang, Chensheng Cheng, Dianyu Yang, and Guang Pan. 2022. "Reinforcement Learning Path Planning Method with Error Estimation" Energies 15, no. 1: 247. https://doi.org/10.3390/en15010247
APA StyleZhang, F., Wang, C., Cheng, C., Yang, D., & Pan, G. (2022). Reinforcement Learning Path Planning Method with Error Estimation. Energies, 15(1), 247. https://doi.org/10.3390/en15010247







