Effects of Front Plate Geometry on Brush Seal in Highly Swirling Environments of Gas Turbine
Abstract
:1. Introduction
2. CFD Modeling
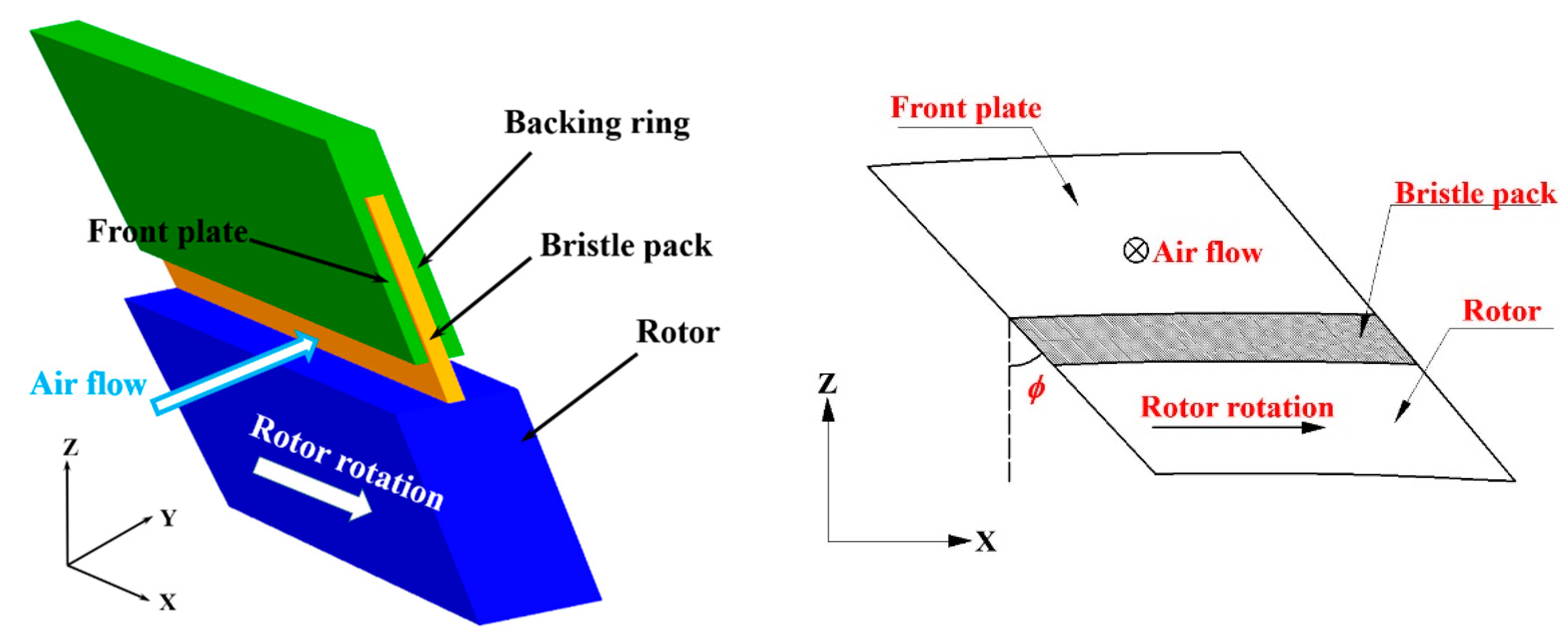
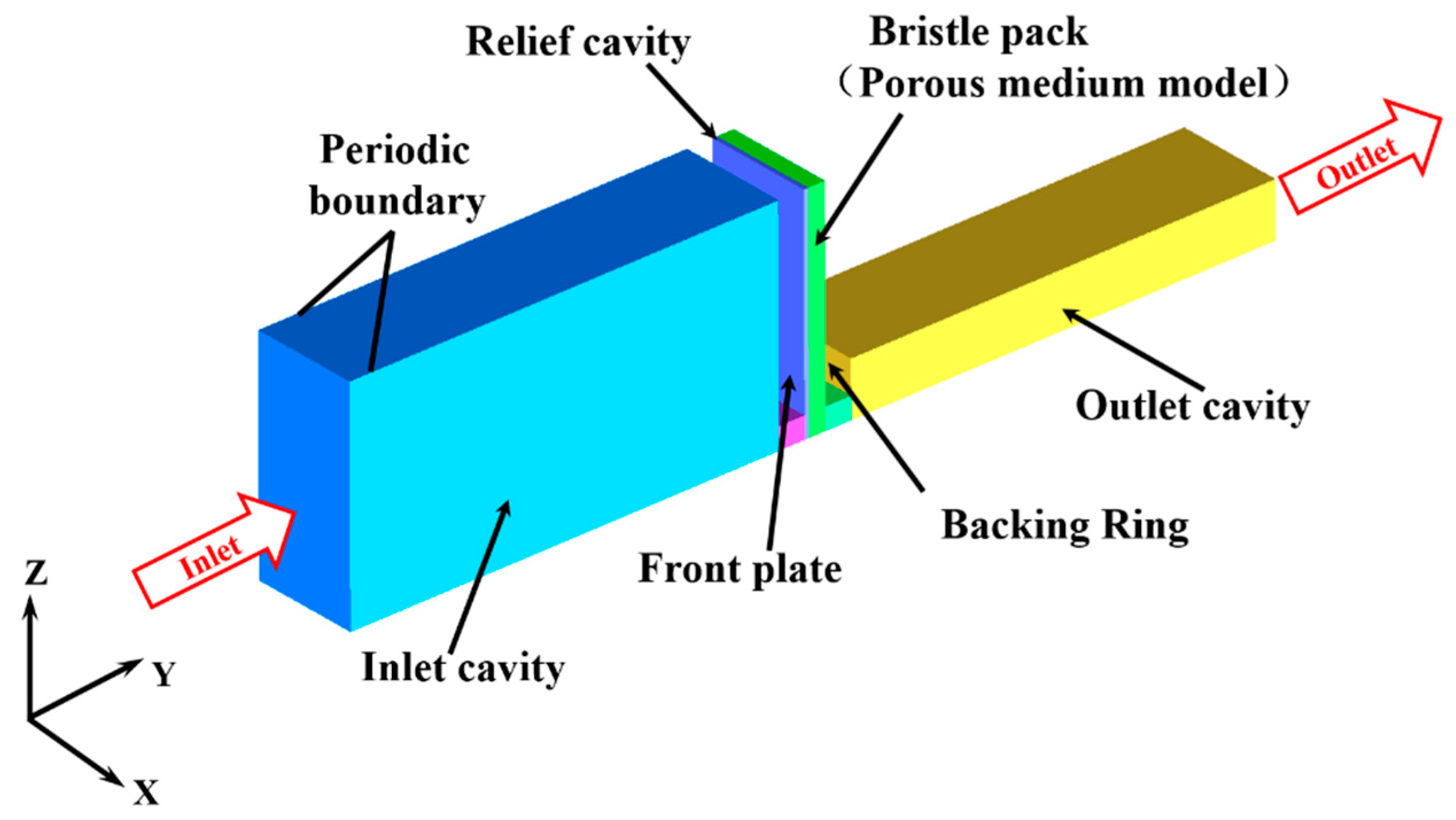
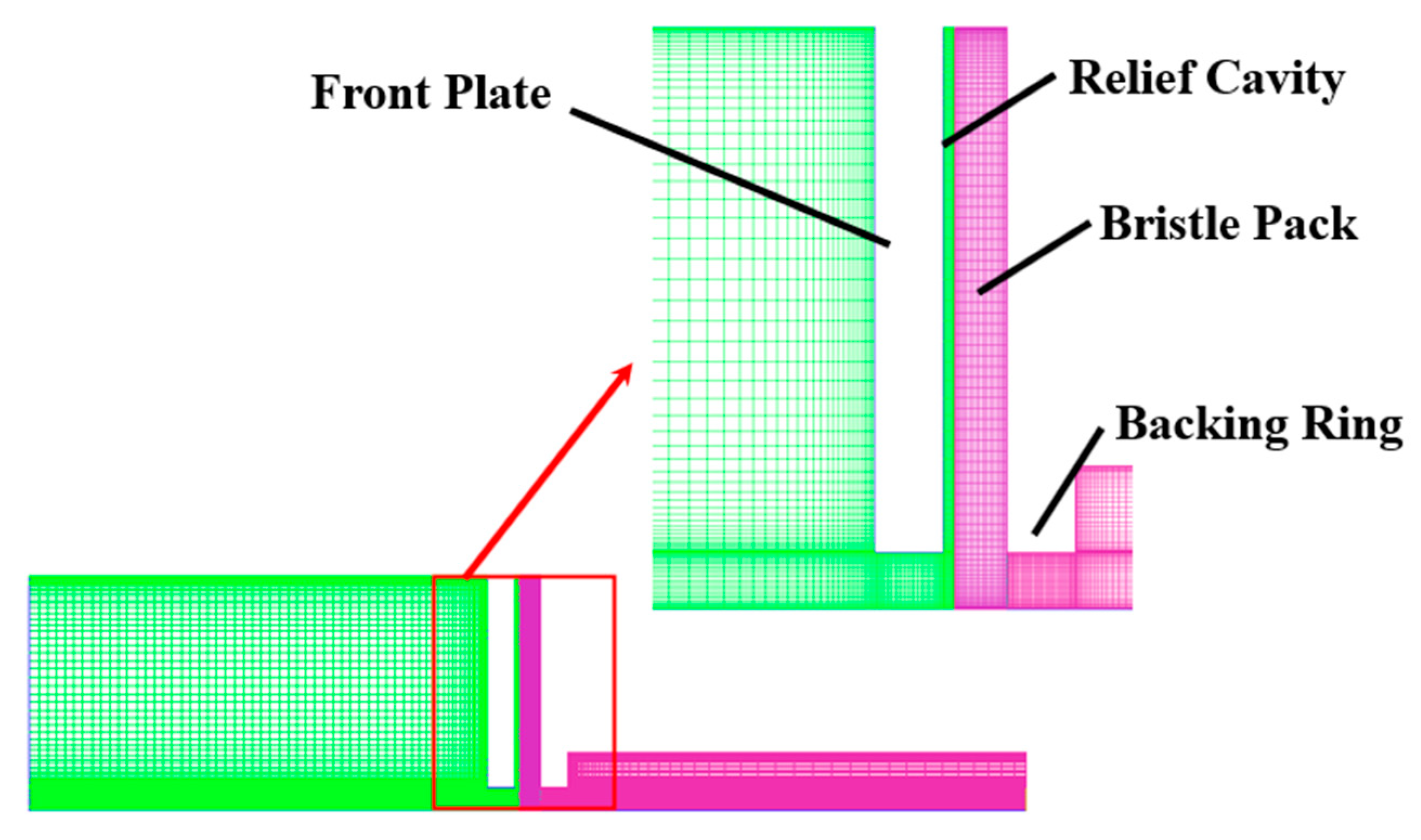
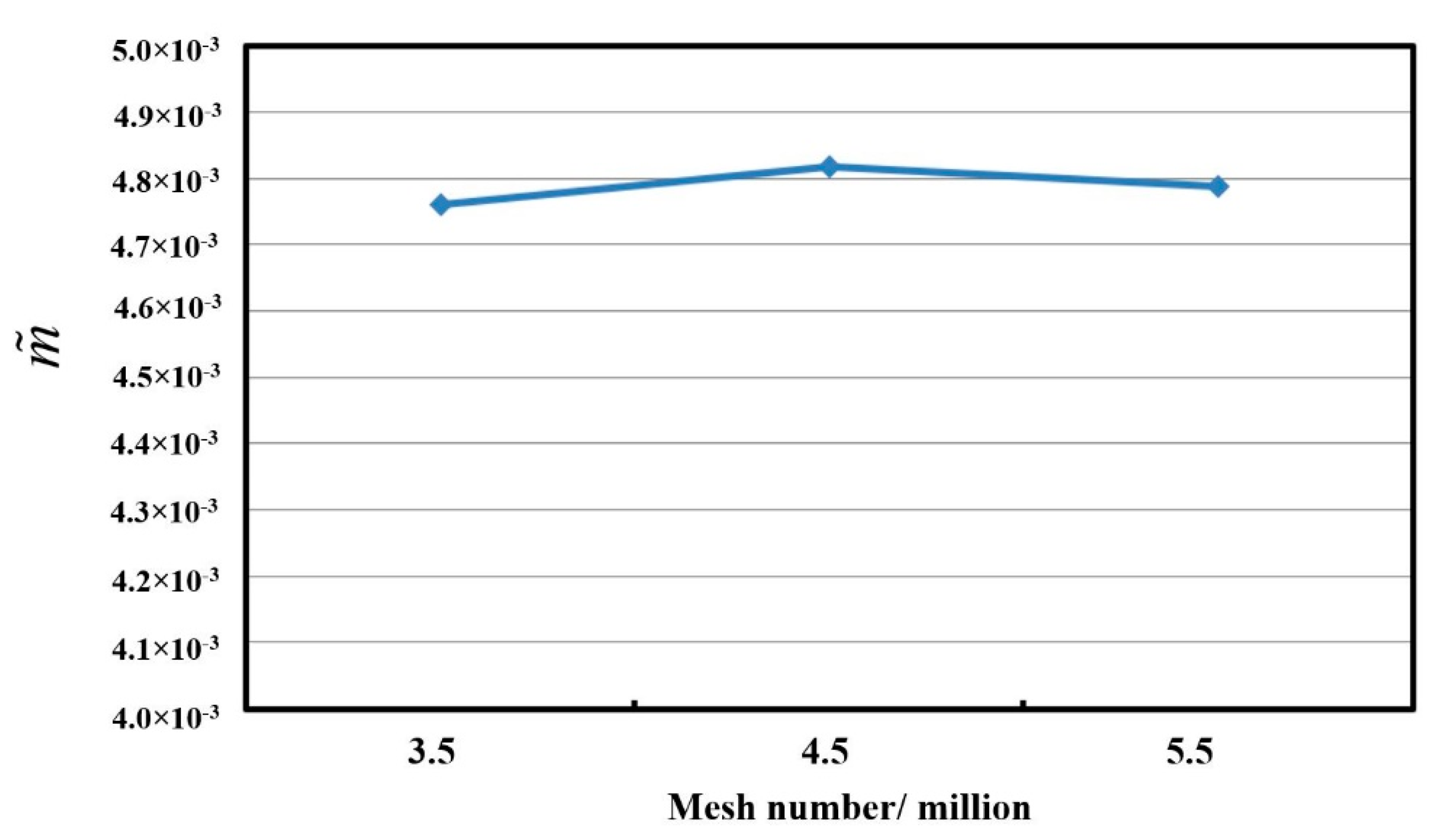
2.1. Geometry and CFD Mesh Generation
2.2. Numerical Method
2.3. Porous Medium Model
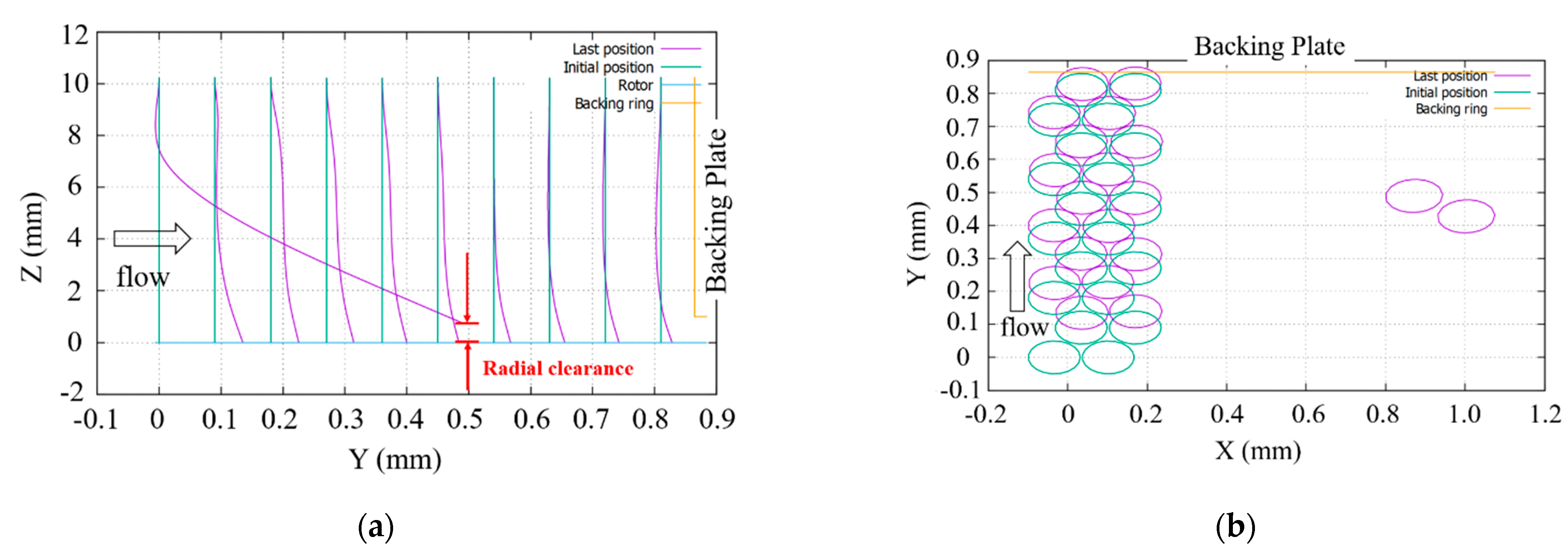
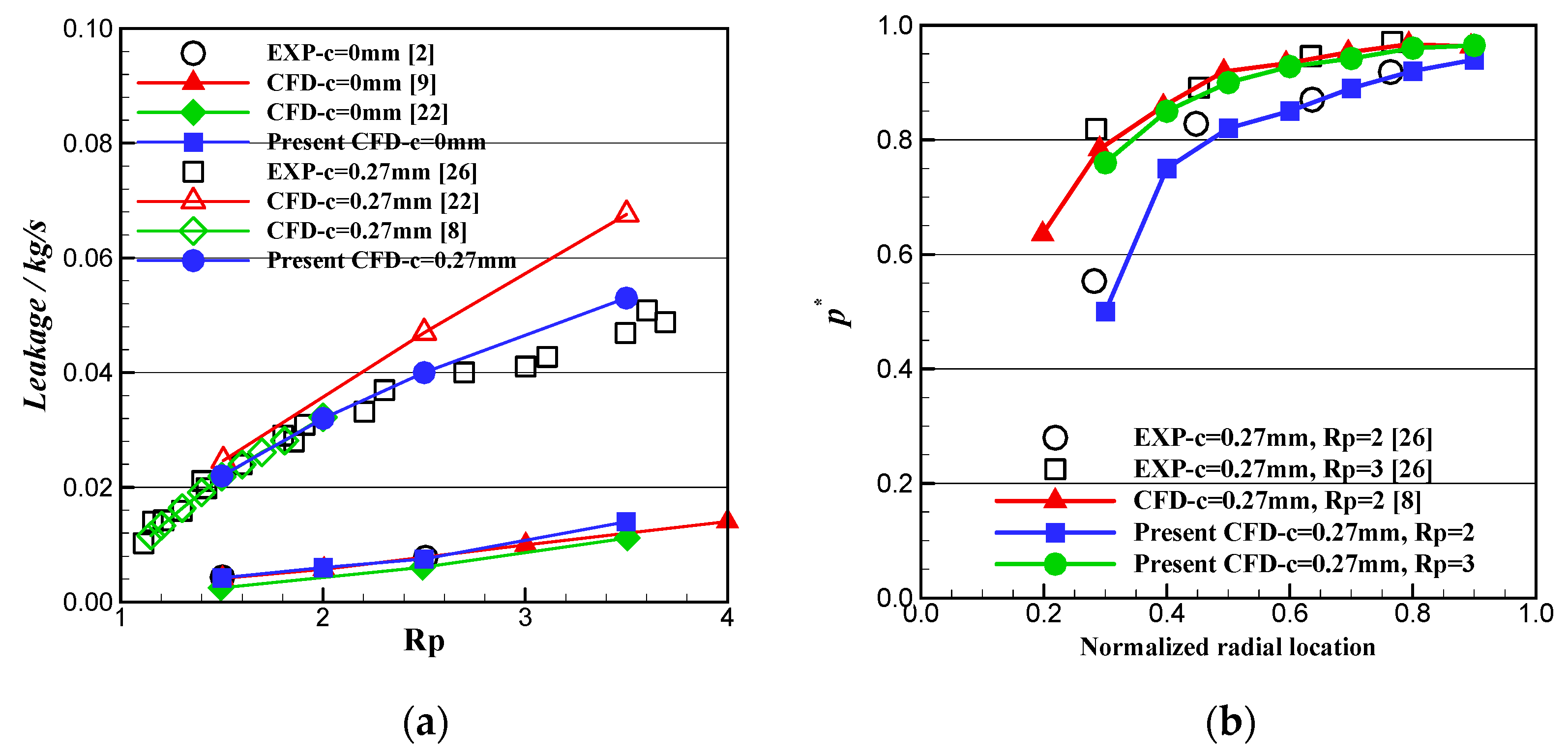
2.4. Numerical Method Validation
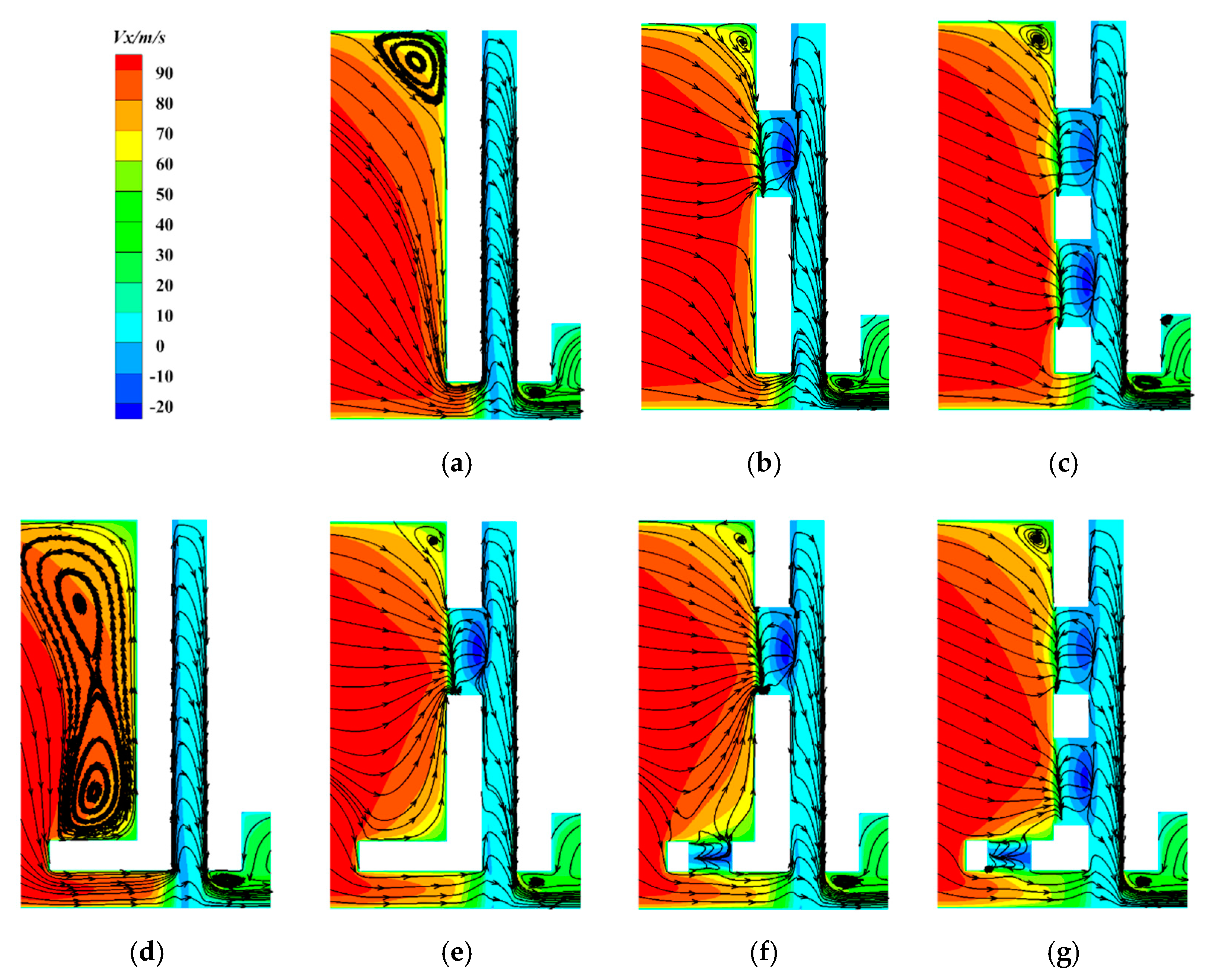
3. Analysis and Discussion
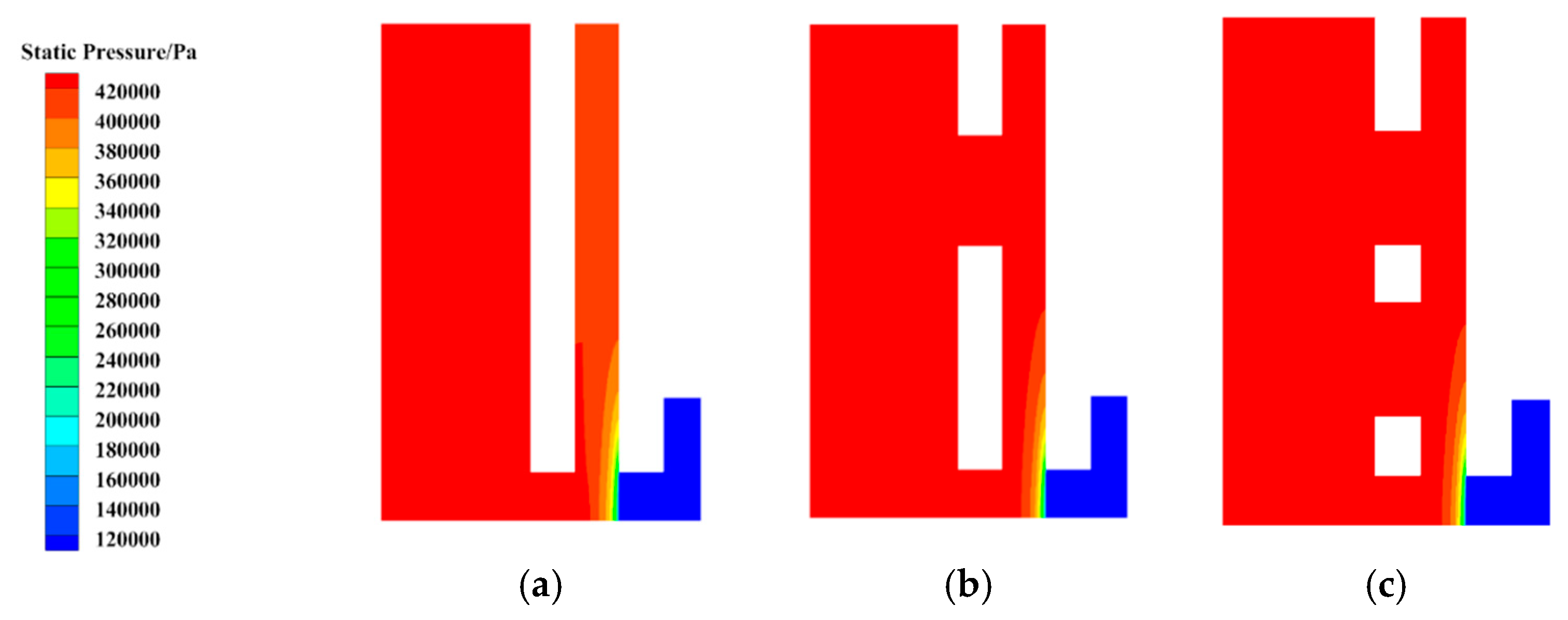
3.1. Static Pressure
3.2. Swirl Velocity
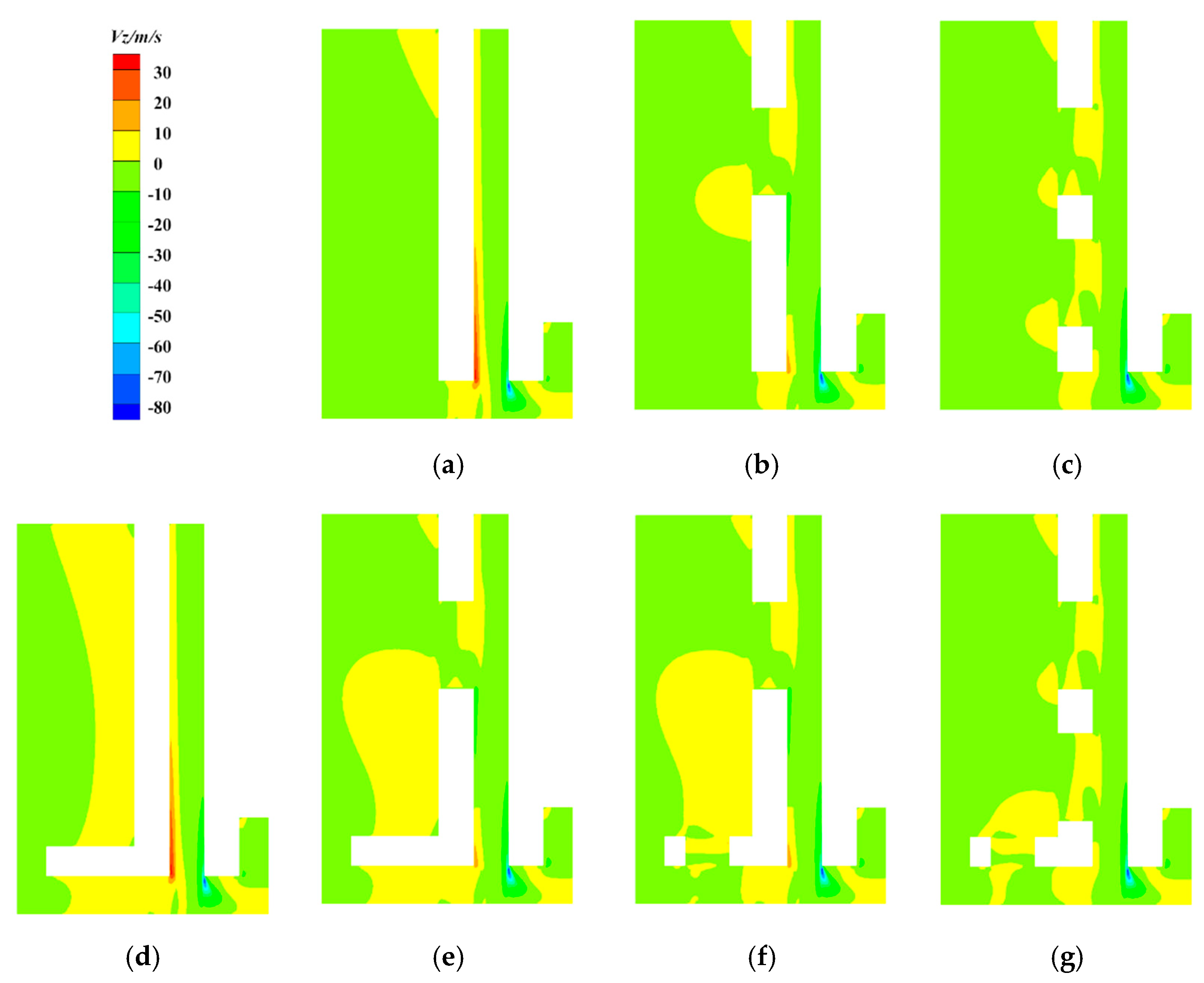
3.3. Radial Velocity
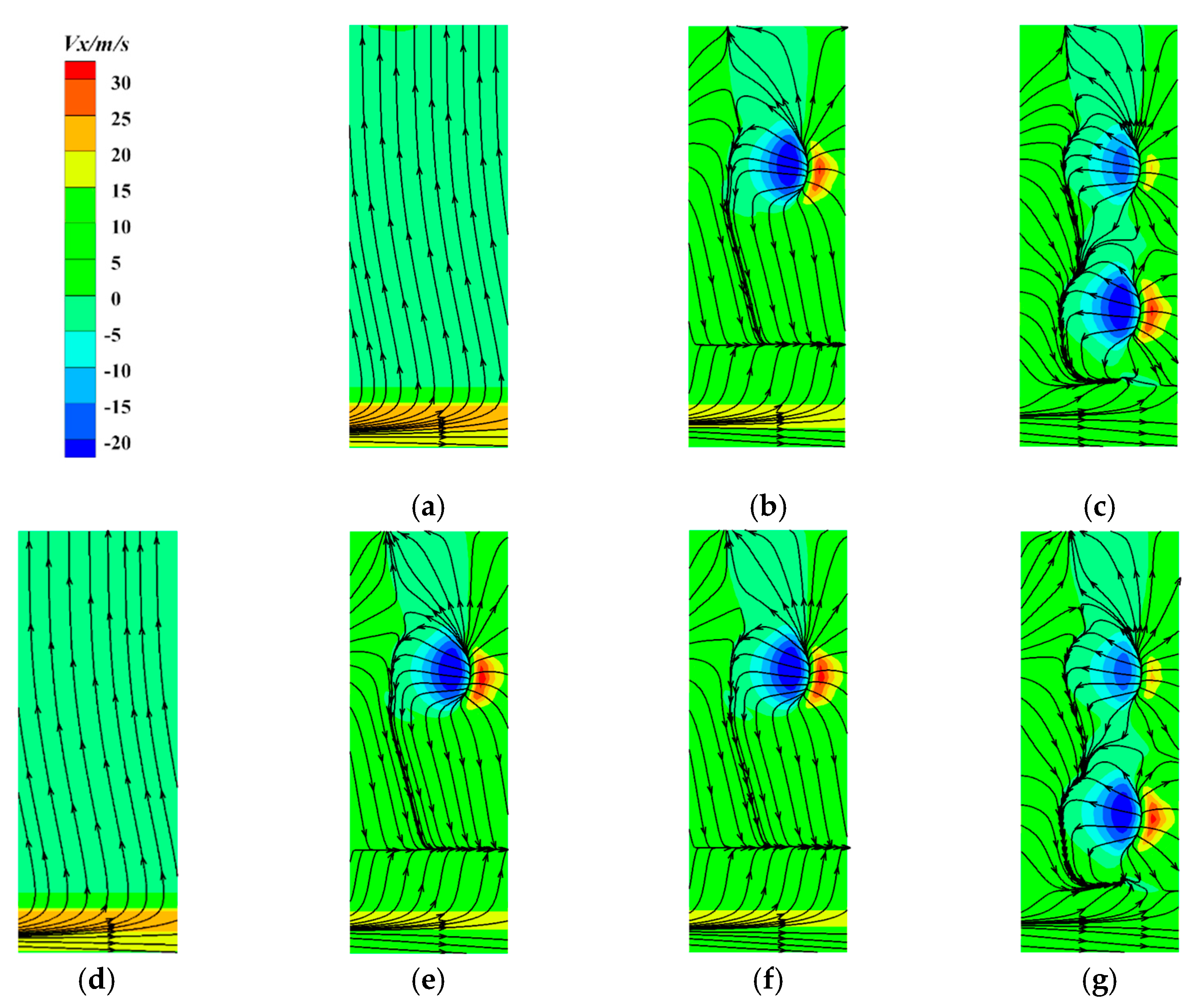
3.4. Flow Fields Analysis in Relief Cavity
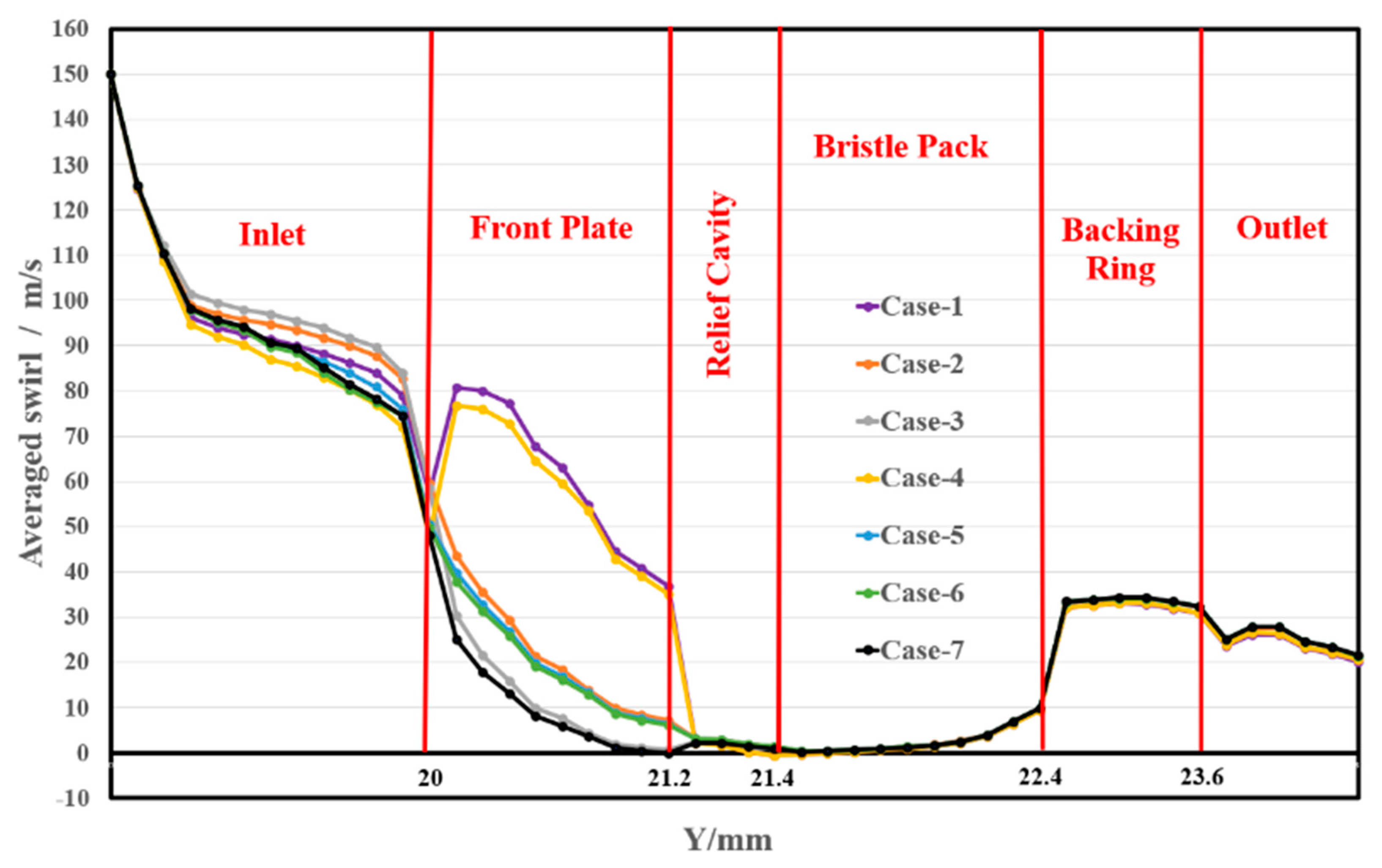
3.5. Swirl Velocity Variation along Axial Direction
3.6. Leakage Characteristics
4. Conclusions
- The flow through the front plate axial holes generate an inward radial flow in the relief cavity to suppress the upward tendance of the flow in the cavity. This can promote the blow-down effect of bristles and result in a significant reduction in swirl upstream of the bristle tips. This will reduce the circumferential forces impacting the bristle pack, thereby enhancing the stability of bristle.
- The anti-“L”-type front plate leads to large vortices near the windward surface of the front plate and relatively long channel before the bristle tips, both help to decrease the swirl velocity slightly. However, the radial holes on the reverse axial length appear to have little effect upon the swirl reduction.
- Compared to the plane front plate model, one axial hole designed structure decreases the swirl around 28%, and the application of two axial holes further reduce the value by 42%. Case-7, which has two axial holes and one radial hole on the anti-“L”-type front plate, shows the best performance in reducing swirl. The swirl velocity upstream the bristle pack is declined 50%, reaching 18.4 m/s, which can result in the circumferential aerodynamic force being reduced by a factor of 4.
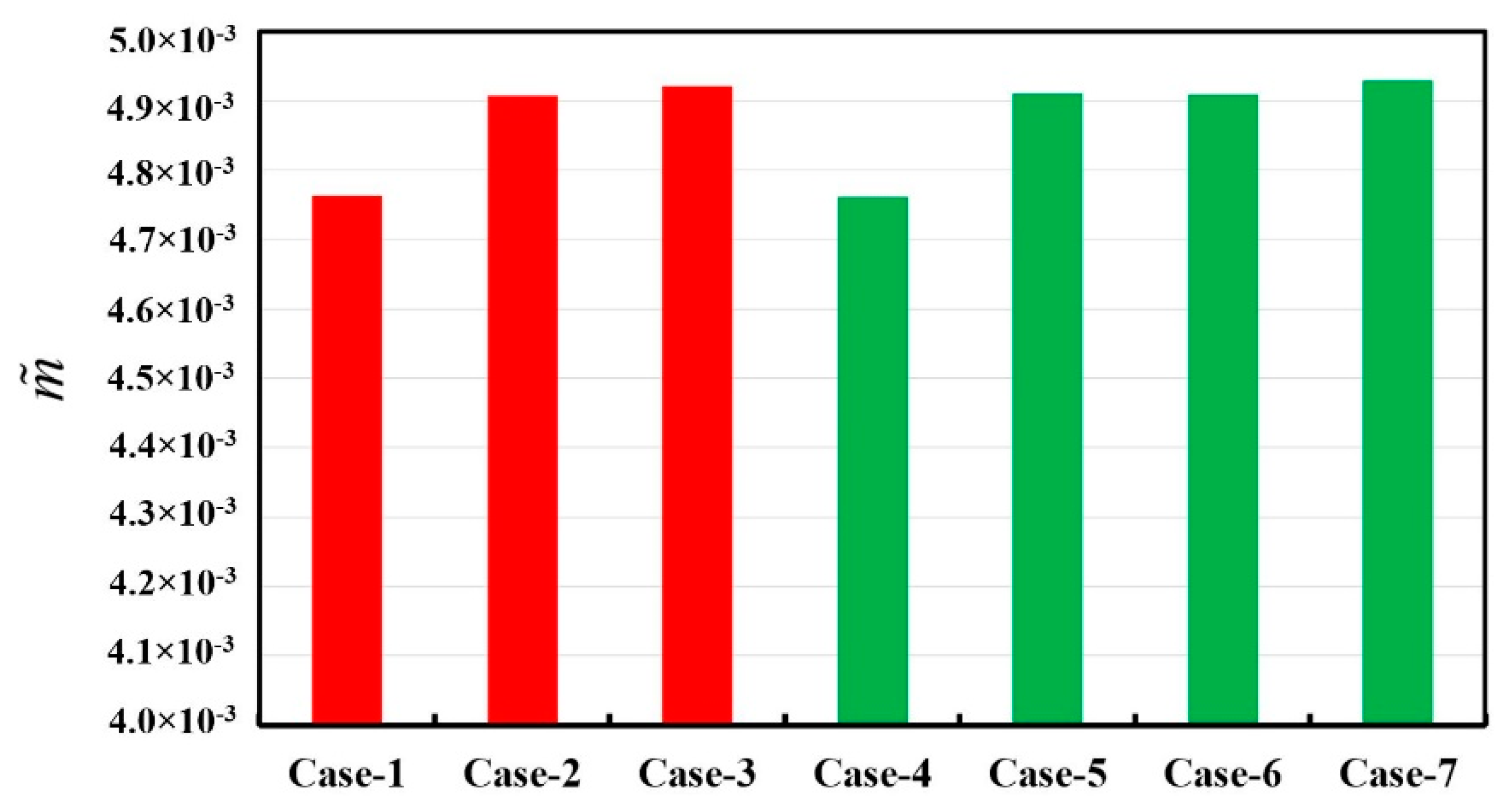
- Front plate configuration will not affect the leakage dramatically, while the axially designed hole on the front plate increases the leakage slightly by around 3.5%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Area, m2 |
| a | Viscous resistance coefficient |
| b | Inertial resistance coefficient |
| D | Bristle diameter, m |
| H | Height of bristle overhang, m |
| Lb | Bristle length, m |
| dimensionless mass flow rate | |
| N | Number of the bristles per unit circumferential length, bristles/mm |
| p* | Non-dimensional pressure = (p − pout)/(pin − pout) |
| R | Radial location, m |
| Rp | Pressure ratio |
| r | Radius of axial/radial hole, m |
| X, Y, Z | Circumferential, axial, radial direction respectively |
| wb | Thickness of the bristle pack, m |
| Zrotor | Radial Clearance between Bristles and Rotor, m |
| δ | Minimum clearance between bristles, m |
| ε | Porosity of the bristle pack |
| ρ | Density of the flow, kg/m3 |
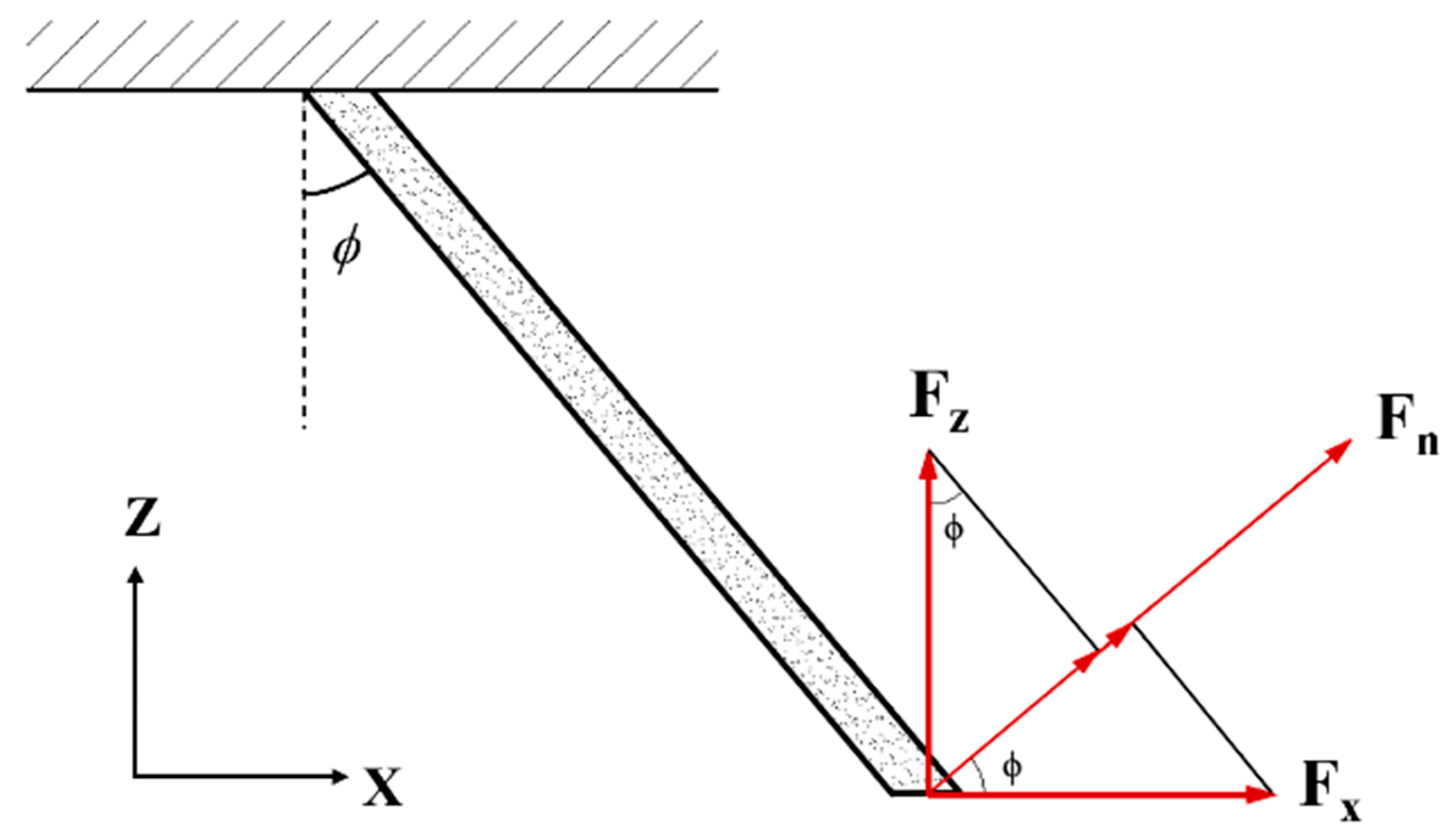
| ϕ | Incline angle of bristle pack |
| Subscripts | |
| in | At system inlet |
| m | Parallel to the bristles |
| n | Perpendicular to the bristles |
| z | Parallel to the rotating shaft |
References
- Chupp, R.E.; Ghasripoor, F.; Turnpuist, N.A.; Demiroglu, M.; Aksit, M.F. Advanced seals for industrial turbine applications: Dynamics seal development. J. Propuls. Power 2002, 18, 1260–1266. [Google Scholar] [CrossRef]
- Bayley, F.J.; Long, C.A. A combined experimental and theoretical study of flow and pressure distributions in a brush seal. J. Eng. Gas Turbines Power 1993, 115, 404–410. [Google Scholar] [CrossRef]
- Hur, M.S.; Moon, S.W.; Kim, T.S. A Study on the Leakage Characteristics of a Stepped Labyrinth Seal with a Ribbed Casing. Energies 2021, 14, 3719. [Google Scholar] [CrossRef]
- Basu, P.; Datta, A.; Loewenthal, R.; Short, J.; Johnson, R. Hysteresis and bristle stiffening effects in brush seals. J. Propuls. Power 1994, 10, 569–575. [Google Scholar] [CrossRef]
- Stango, R.J.; Zhao, H.; Shia, C.Y. Analysis of contact mechanics for rotor-bristle interference of brush seal. J. Tribol. 2003, 125, 414–420. [Google Scholar] [CrossRef]
- Zhao, H.; Stango, R.J. Effect of flow-induced radial load on brush/rotor contact mechanics. J. Tribol. 2004, 126, 208–214. [Google Scholar] [CrossRef]
- Zhao, H.; Stango, R.J. Analytical approach for investigating bristle/backplate hysteresis phenomenon in brush seals. J. Propuls. Power 2007, 23, 273–282. [Google Scholar] [CrossRef]
- Sun, D.; Liu, N.; Fei, C.; Hu, G.Y.; Ai, Y.T.; Choy, Y.S. Theoretical and Numerical Investigation on the Leakage Characteristics of Brush Seals Based on Fluid-Structure Interaction. Aerosp. Sci. Technol. 2016, 58, 207–216. [Google Scholar] [CrossRef]
- Chew, J.W.; Lapworth, B.L.; Millener, P.J. Mathematical modeling of brush seals. Int. J. Heat Fluid Flow 1995, 16, 493–500. [Google Scholar] [CrossRef] [Green Version]
- Chew, J.W. Porosity modeling of brush seals. J. Tribol. 1997, 19, 769–775. [Google Scholar] [CrossRef]
- Li, J.; Yan, X.; Feng, Z.; Shengke, J.; Xianglin, K.; Qi, S.; Jianlu, W. Study on the Leakage Flow Characteristics of Brush Seal Based on Porous Medium Model. J. Xi’an Jiaotong Univ. 2007, 41, 768–779. [Google Scholar]
- Sharatchandra, C.; Rhode, L. Computed Effects of Rotor-Induced Swirl on Brush Seal Performance-Part 2: Bristle Force Analysis. J. Tribol. 1996, 118, 920–926. [Google Scholar] [CrossRef]
- Helm, P.; Pugachev, A.; Neef, M. Breaking the Swirl with Brush Seals: Numerical Modeling and Experimental Evidence. In Proceedings of the ASME Turbo Expo 2008: Power for Land, Sea and Air, Berlin, Germany, 9–13 June 2008; p. GT2008-50257. [Google Scholar]
- Choi, S.M.; Choi, S.; Cho, H.H. Effect of Various Coolant Mass Flow Rates on Sealing Effectiveness of Turbine Blade Rim Seal at First Stage Gas Turbine Experimental Facility. Energies 2020, 13, 4105. [Google Scholar] [CrossRef]
- Outirba, B.; Hendrick, P. Influence of Geometrical Parameters on the Performance of Brush Seals for Aero-Engines Bearing Chambers. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015; p. GT2015-43519. [Google Scholar]
- Aksit, M.; Dogu, Y.; Tichy, J.; Gursoy, M. Hydrodynamic Lift of Brush Seals in Oil Sealing Applications. In Proceedings of the 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Fort Lauderdale, FL, USA, 11–14 July 2004; p. AIAA 2004-3721. [Google Scholar]
- Liu, Y.; Chew, J.W.; Pekris, M.J.; Kong, X. The Effect of Inlet Swirl on Brush Seal Bristle Deflections and Stability. J. Eng. Gas Turbines Power 2020, 142, 071002. [Google Scholar] [CrossRef]
- Kong, X.; Huang, T.; Liu, Y.; Chen, H.; Lu, H. Fluid-Structure Interaction Study on the Effect of Inlet Swirl on the Brush Seal Bristle Deflections. J. Eng. Thermophys. 2021, 42, 1224–1232. [Google Scholar]
- Chi, J.; Wang, Z. Analysis of front plate’s effect on low hysteresis brush seal. J. Aerosp. Power 2012, 27, 1902–1906. [Google Scholar]
- Dogu, Y.; Aksit, M.F. Effects of geometry on brush seal pressure and flow fields-I: Front plate configurations. J. Turbomach. 2006, 128, 367–378. [Google Scholar] [CrossRef]
- Dogu, Y.; Akist, M.F.; Demiroglu, M. Evaluation of flow behavior for clearance brush seals. J. Eng. Gas Turbines Power 2008, 130, 012507-1–012507-9. [Google Scholar] [CrossRef]
- Dogu, Y.; Bahar, A.S.; Sertcakan, M.C.; Pişkin, A.; Arıcan, E.; Kocagül, M. Computational fluid dynamics investigation of brush seal leakage performance depending on geometric dimensions and operating conditions. J. Eng. Gas Turbines Power 2016, 138, 032506-1–052506-13. [Google Scholar] [CrossRef]
- Kong, X.; Liu, Y.; Lu, H.; Tian, Z.; Xin, J. Performance Analysis of Inter-Stage Leakage Flows at Rotating Conditions in an Axial Compressor. J. Therm. Sci. 2020, 29, 1558–1568. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, J.; Li, J. Investigations on Leakage Flow Characteristics of Brush Seal with Consideration of Blow down Effect. Lubr. Eng. 2017, 42, 36–42. [Google Scholar]
- Hildebrandt, M.; Schwitzke, C.; Bauer, H.J. Analysis of Heat Flux Distribution during Brush Seal Rubbing Using CFD with Porous Media Approach. Energies 2021, 14, 1888. [Google Scholar] [CrossRef]
- Turner, M.T.; Chew, J.W.; Long, C.A. Experimental Investigation and Mathematical Modelling of Clearance Brush Seals. J. Eng. Gas Turbines Power 1998, 120, 573–579. [Google Scholar] [CrossRef]


| Lay Angle to Radial Direction | ϕ | 40° |
| Bristle Diameter | D | 0.10 mm |
| Bristle Length | l | 13.35 mm |
| Height of Bristle Overhang | H | 1.00 mm |
| Number of Axial Rows | 10 | |
| Minimum Clearance between Bristles | δ | 0.004 mm |
| Radial Clearance between Bristles and Rotor | Zrotor | 0 mm |
| Axial length of Front Plate | LFP | 1.2 mm |
| Axial length of Backing Ring | LBR | 1.2 mm |
| Axial length of Relief cavity | LRC | 0.2 mm |
| Model | Averaged Swirl Velocity |
|---|---|
| Case-1 | 36.7 m/s |
| Case-2 | 26.5 m/s |
| Case-3 | 21.4 m/s |
| Case-4 | 35.1 m/s |
| Case-5 | 24.8 m/s |
| Case-6 | 24.1 m/s |
| Case-7 | 18.4 m/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Yue, B.; Kong, X.; Chen, H.; Lu, H. Effects of Front Plate Geometry on Brush Seal in Highly Swirling Environments of Gas Turbine. Energies 2021, 14, 7768. https://doi.org/10.3390/en14227768
Liu Y, Yue B, Kong X, Chen H, Lu H. Effects of Front Plate Geometry on Brush Seal in Highly Swirling Environments of Gas Turbine. Energies. 2021; 14(22):7768. https://doi.org/10.3390/en14227768
Chicago/Turabian StyleLiu, Yuxin, Benzhuang Yue, Xiaozhi Kong, Hua Chen, and Huawei Lu. 2021. "Effects of Front Plate Geometry on Brush Seal in Highly Swirling Environments of Gas Turbine" Energies 14, no. 22: 7768. https://doi.org/10.3390/en14227768
APA StyleLiu, Y., Yue, B., Kong, X., Chen, H., & Lu, H. (2021). Effects of Front Plate Geometry on Brush Seal in Highly Swirling Environments of Gas Turbine. Energies, 14(22), 7768. https://doi.org/10.3390/en14227768





