Advanced Modeling of Enclosed Airspaces to Determine Thermal Resistance for Building Applications
Abstract
:1. Introduction
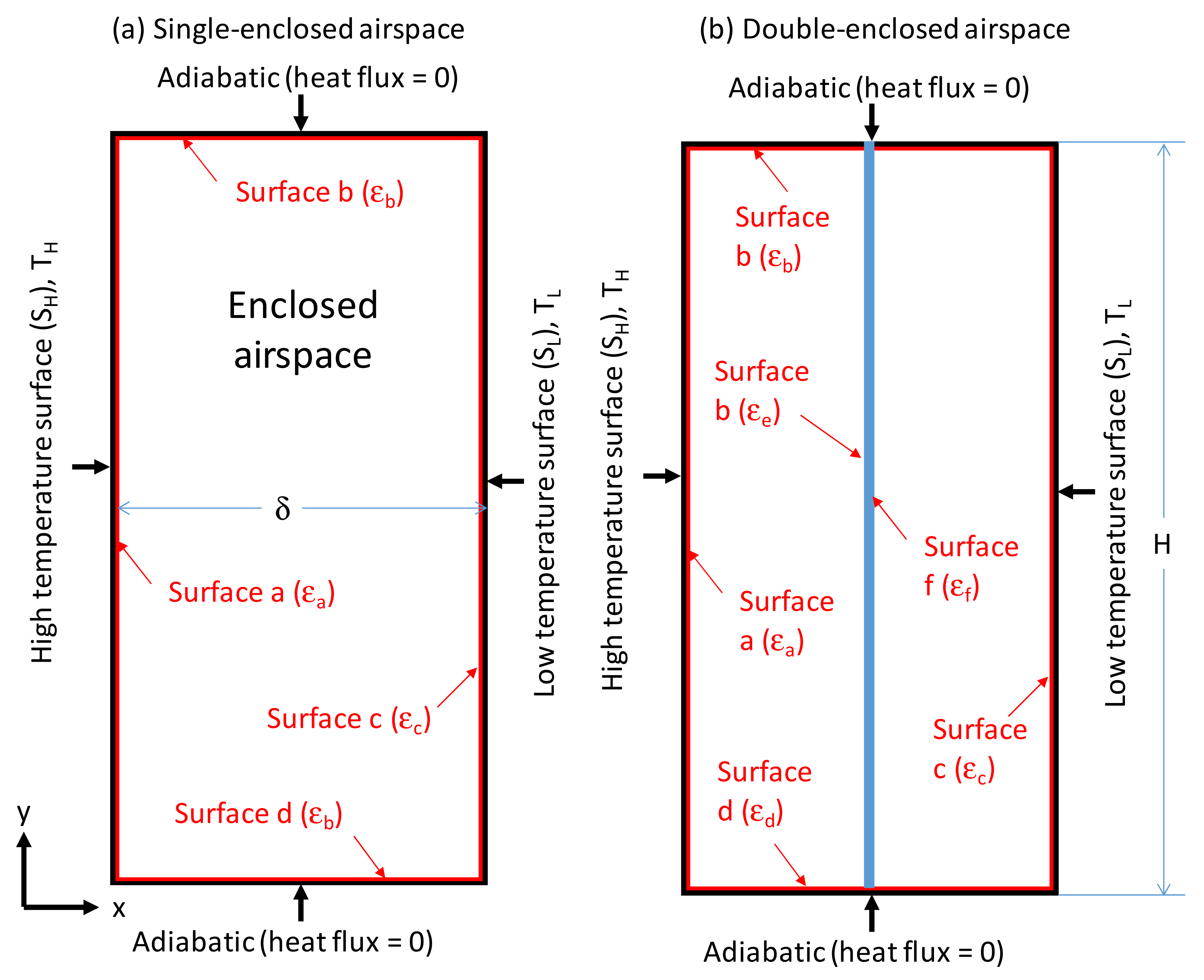
2. Description and Validation of the Numerical Model
3. Objectives
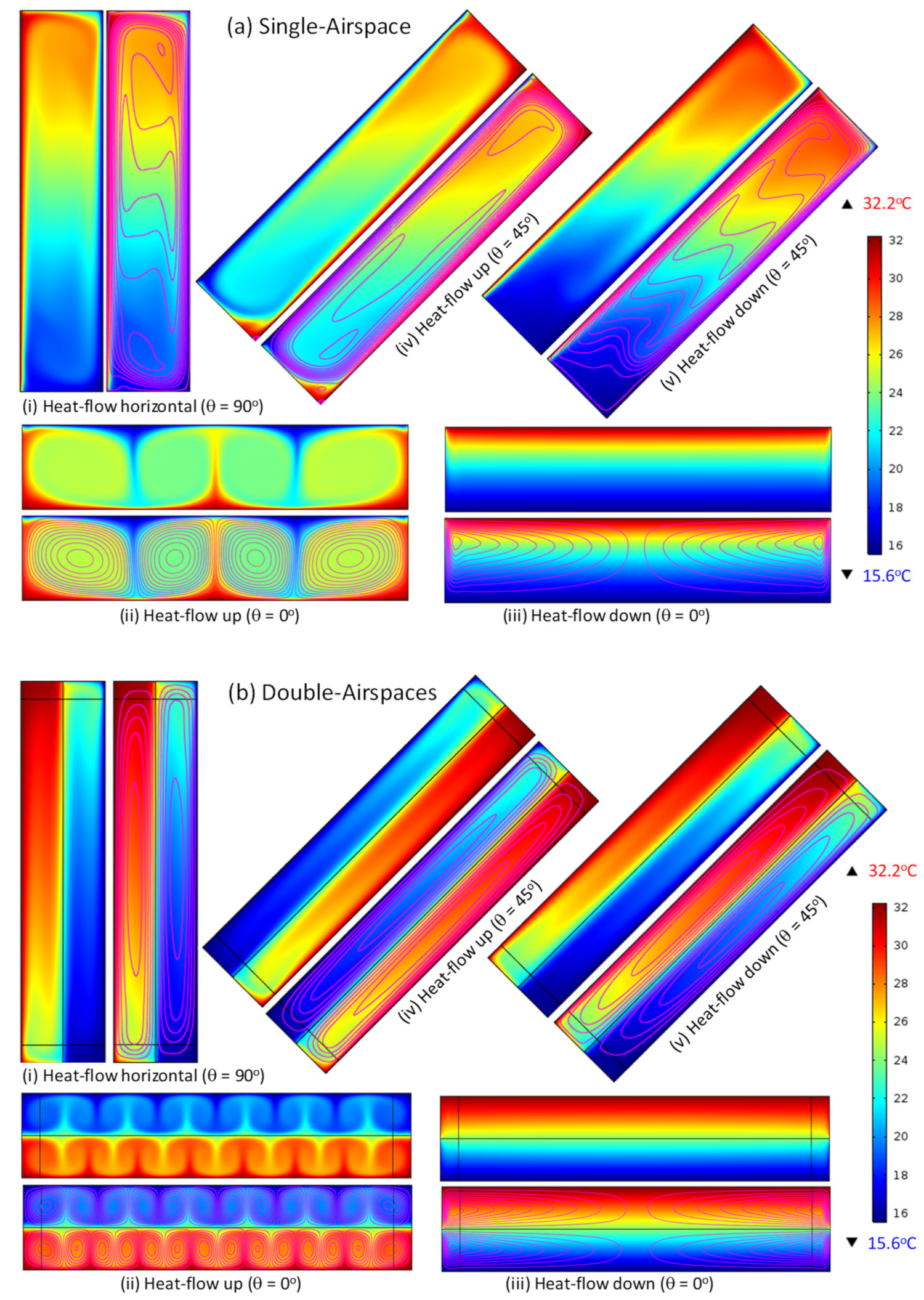
4. Results and Discussions
- (a)
- Vertical airspaces (θ = 90°) with horizontal heat flow to represent walls, windows and curtain walls with reflective insulation (RI).
- (b)
- Horizontal airspaces (θ = 0°) with upward heat flow to represent building components such as flat roofs or skylights with RI during the cold season.
- (c)
- Horizontal airspaces (θ = 0°) with downward heat flow to represent building components such as flat roofs or flat skylights with RI during the hot season.
- (d)
- Sloped airspaces (θ = 45°) with upward heat flow to represent building components such as sloped roofs or skylights with RI during the cold season.
- (e)
- Sloped airspaces (θ = 45°) with downward heat flow to represent building components such as sloped roofs or flat skylights with RI during the hot season.
- (i)
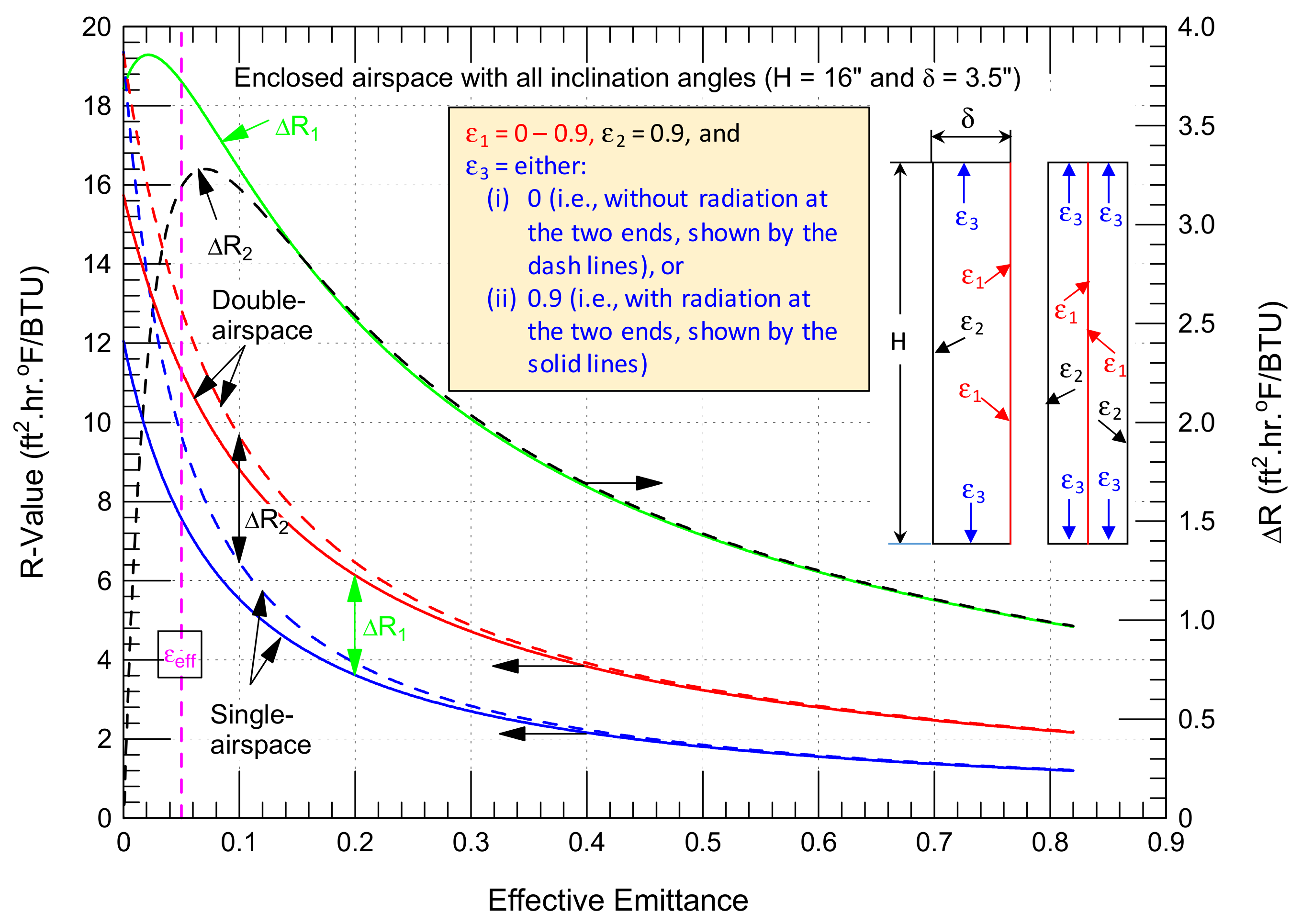
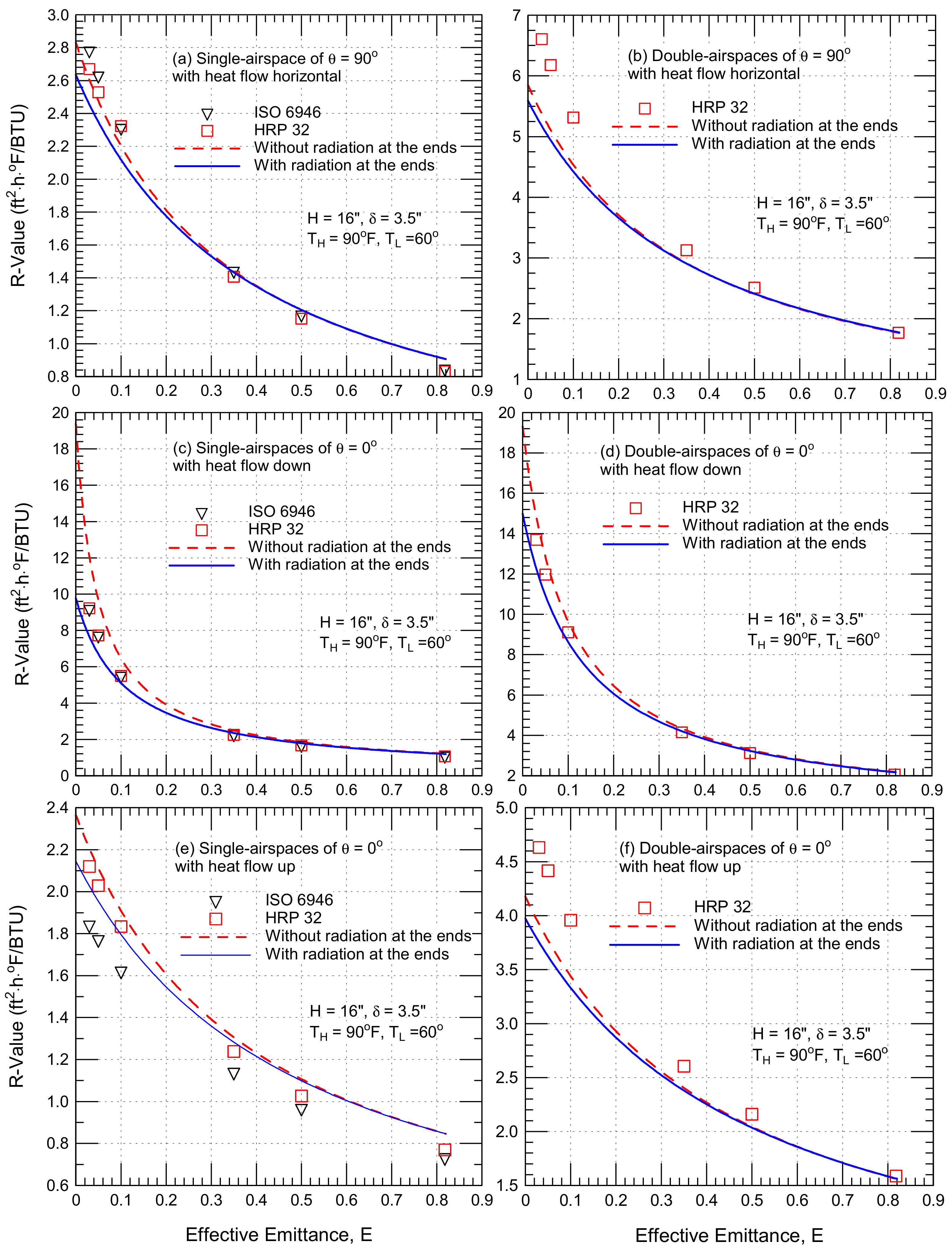
- No radiation takes place at the two ends of airspace surfaces (i.e., ε3 = 0.0, see the insert in Figure 3). This case is called “without end effect”, which represents the case of net radiative transport between two large/infinite parallel surfaces that are currently being used in the ISO 6946 [9] and ASHRAE [5,6] methods. The surfaces of the two ends of the airspace are usually the surfaces of the framing (e.g., furring or spacers) that bind the airspace. Note that the case of without end effect would represent the situation in which low-e material is present on the surfaces of the framing/spacers facing the airspace. It is important to point out that the main reason to address this case in this study is to explore, for reflective insulation manufactures, building authorities and designers, the impact on R value due to installing low-e foil or coating on the surfaces of the framing/spacers that face the airspace and parallel to the heat-flow direction (see the green lines in Figure 1a,b).
- (ii)
4.1. R Values in Absence of Convection
4.2. Impact of Convection on R Values
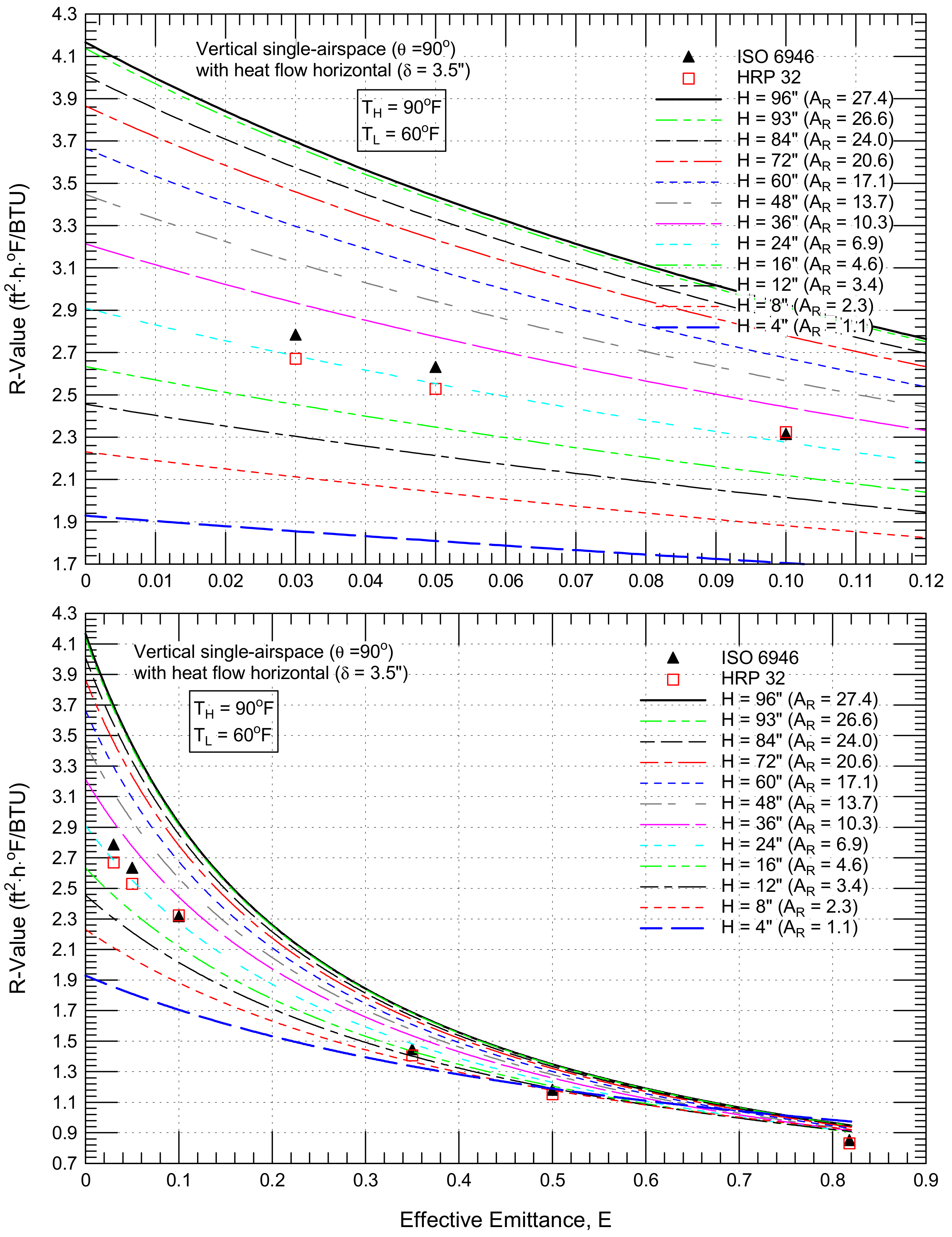
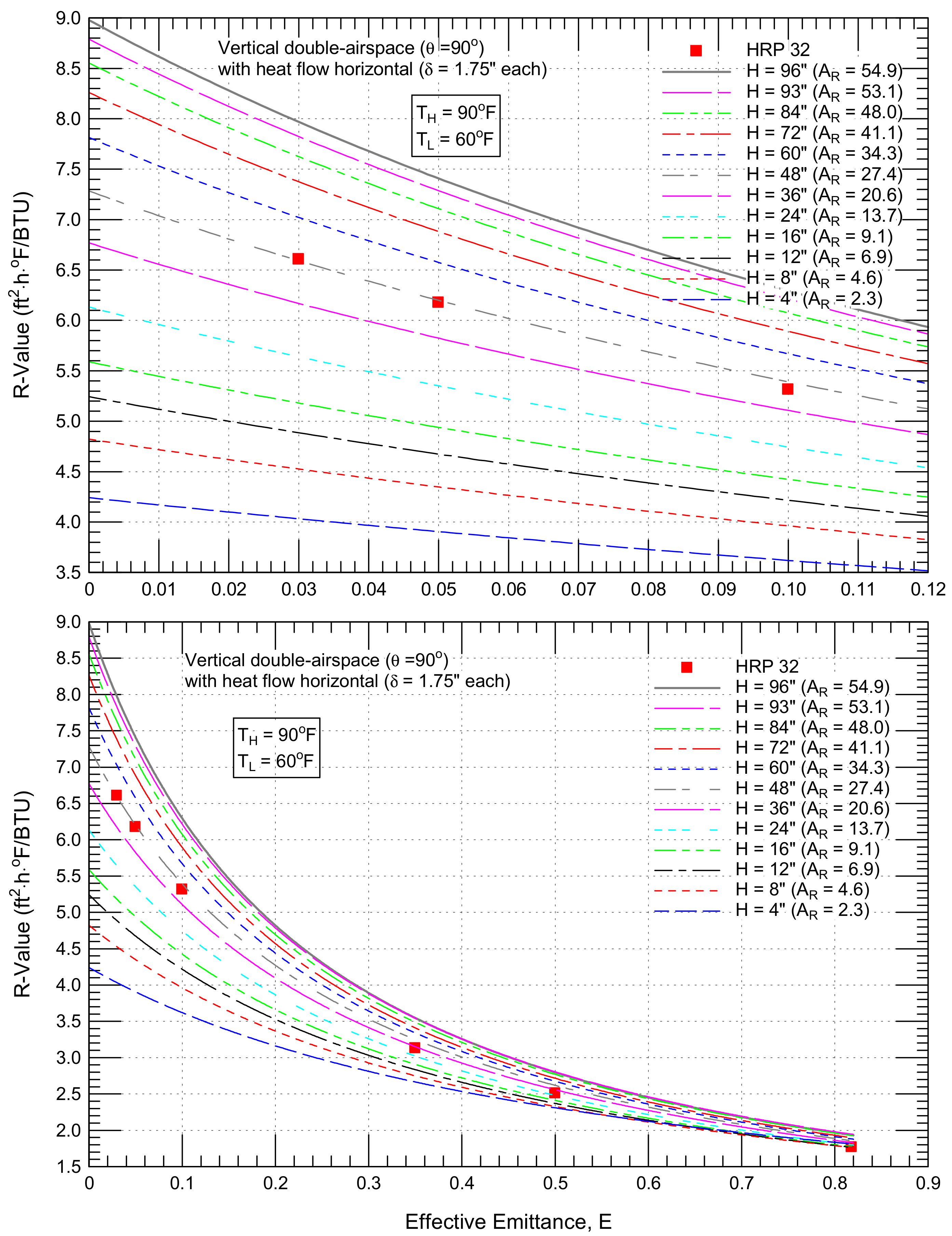
4.2.1. Vertical Airspaces (θ = 90°) with Horizontal Heat Flow
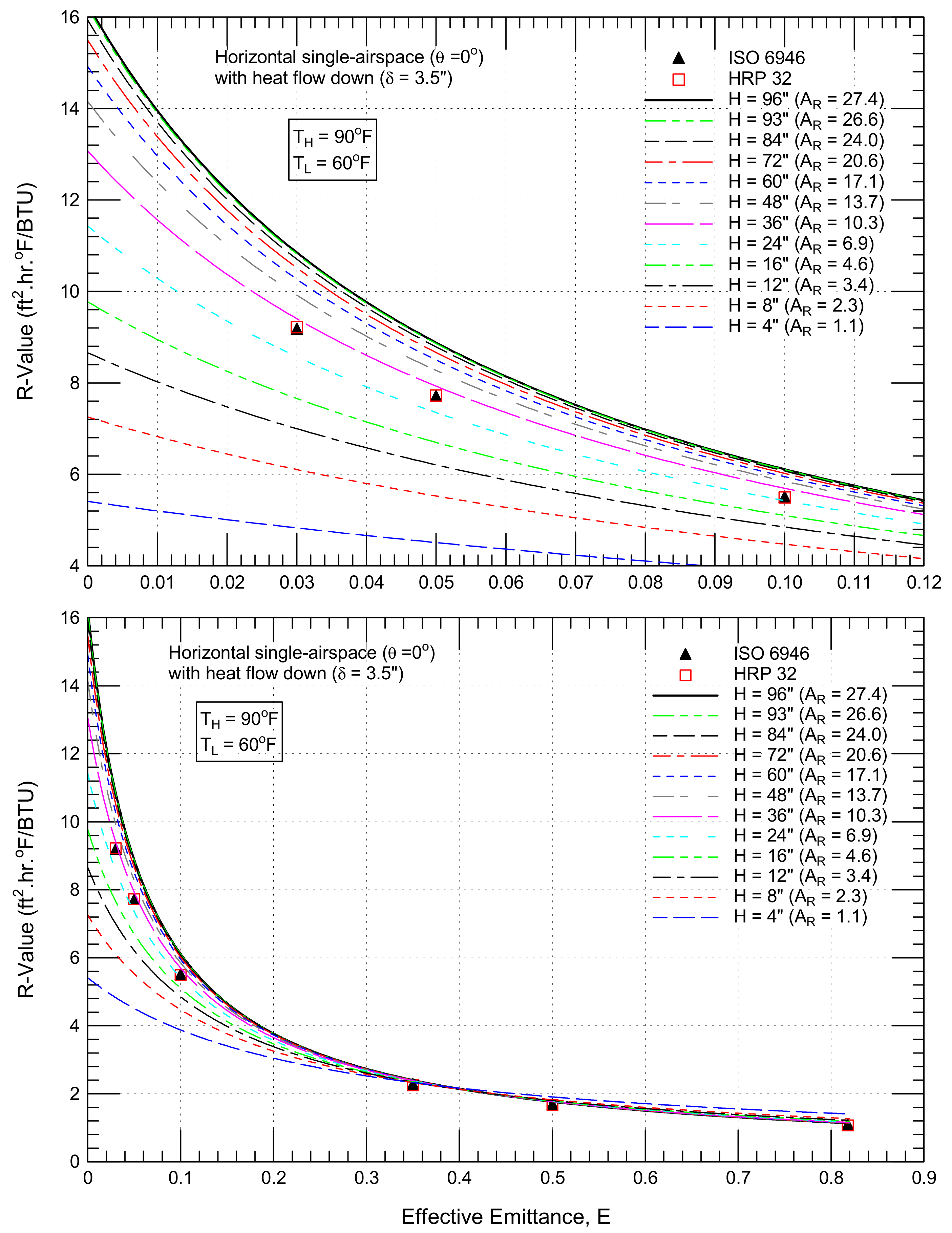
4.2.2. Horizontal Airspaces (θ = 0°) with Downward Heat Flow
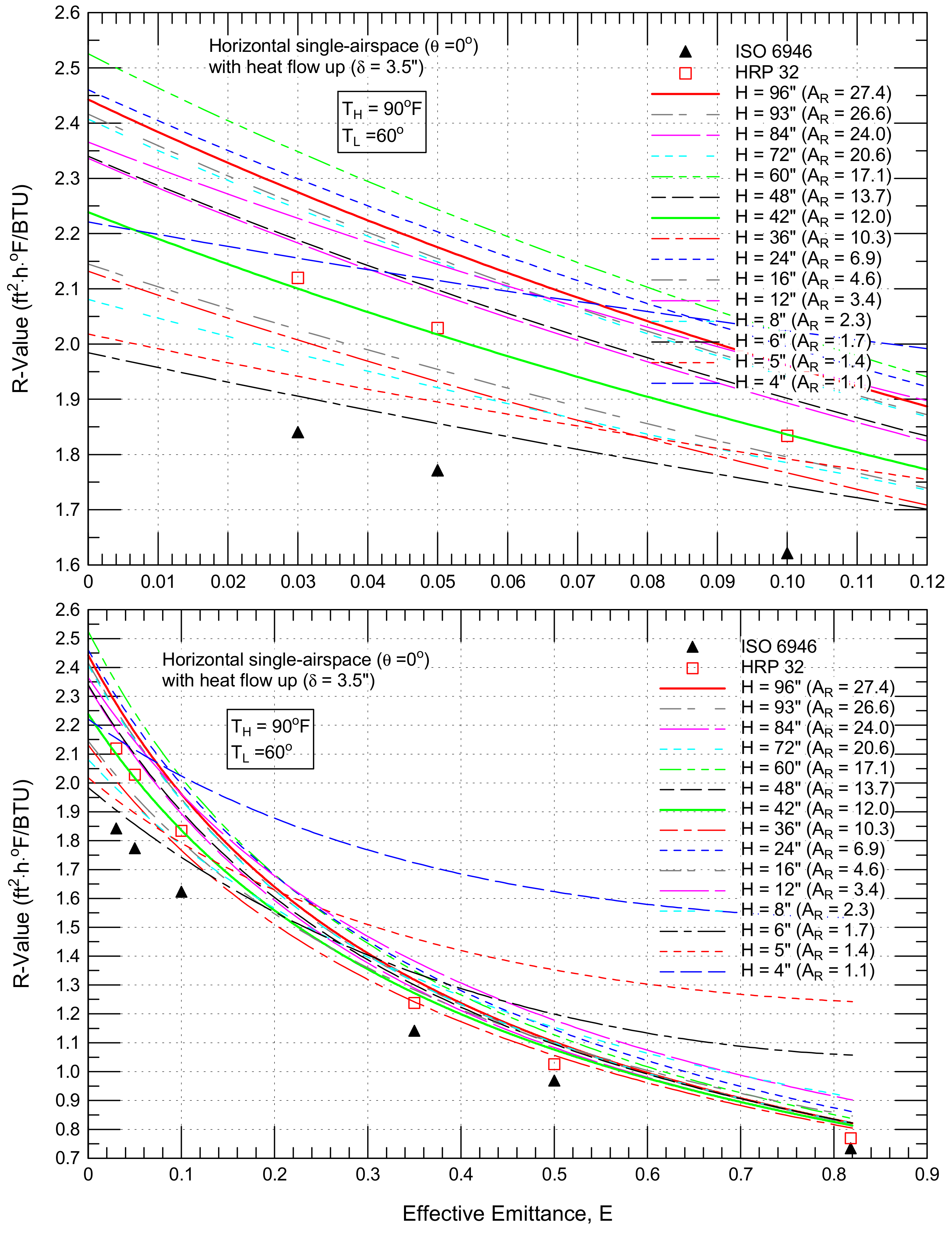
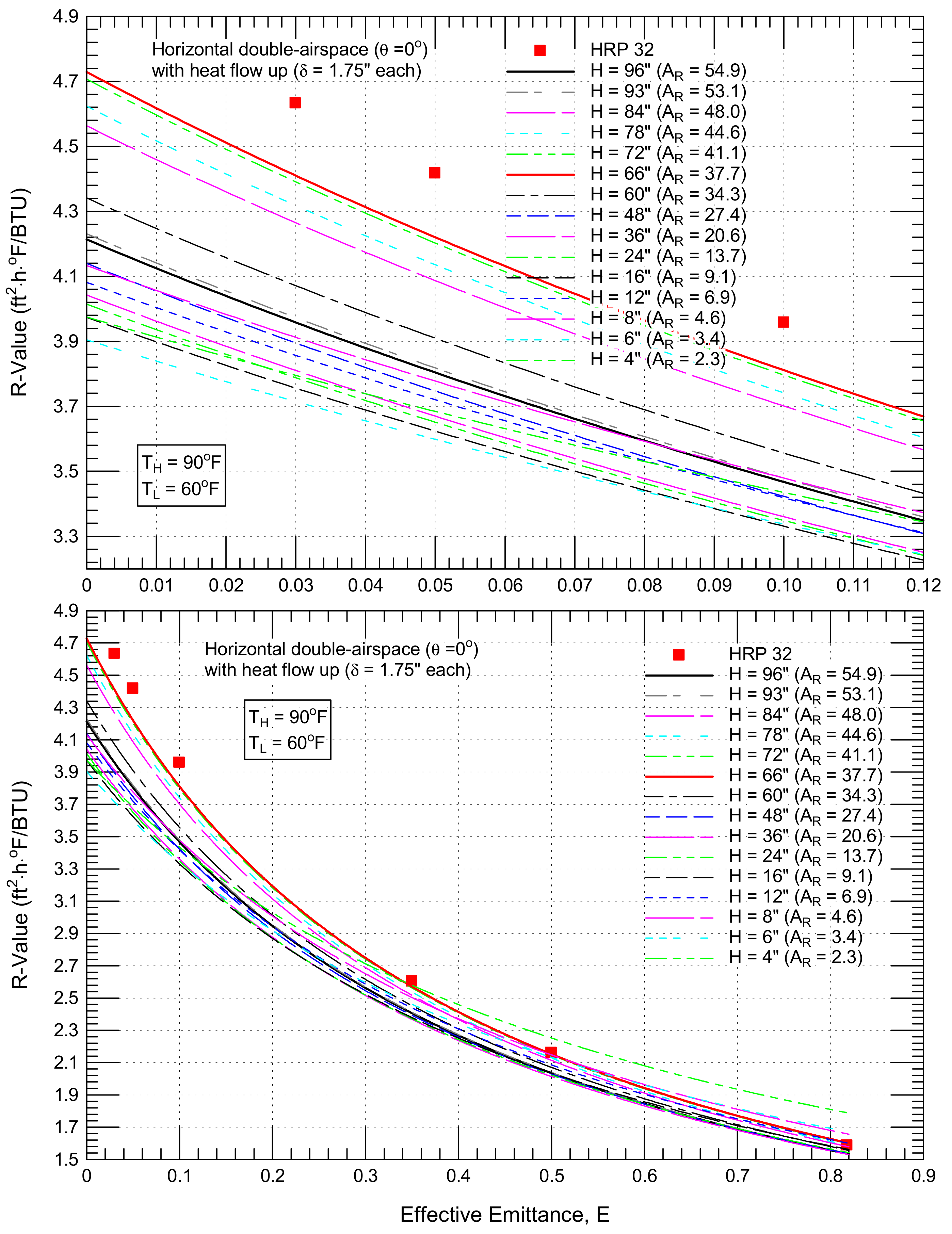
4.2.3. Horizontal Airspaces (θ = 0°) with Upward Heat Flow
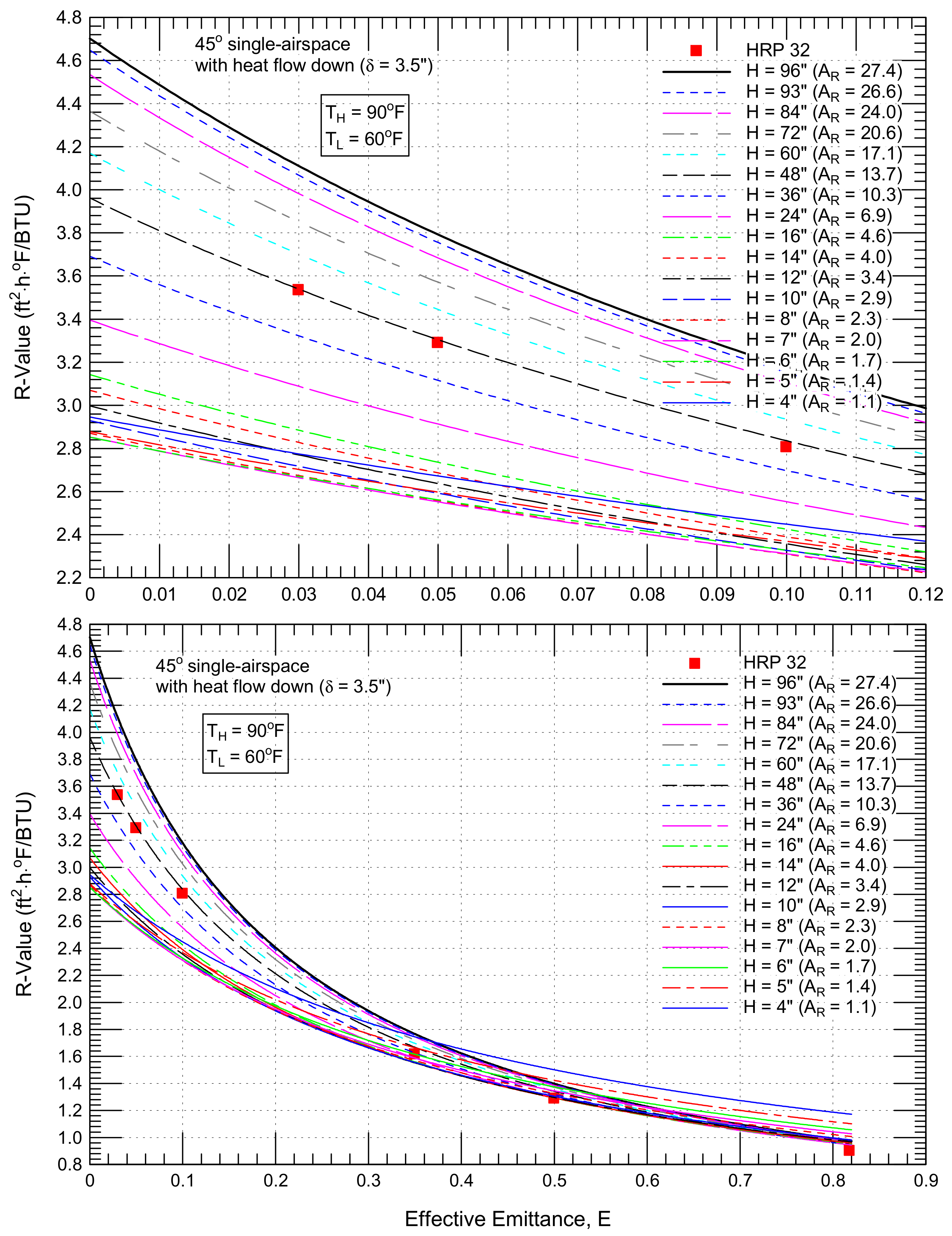
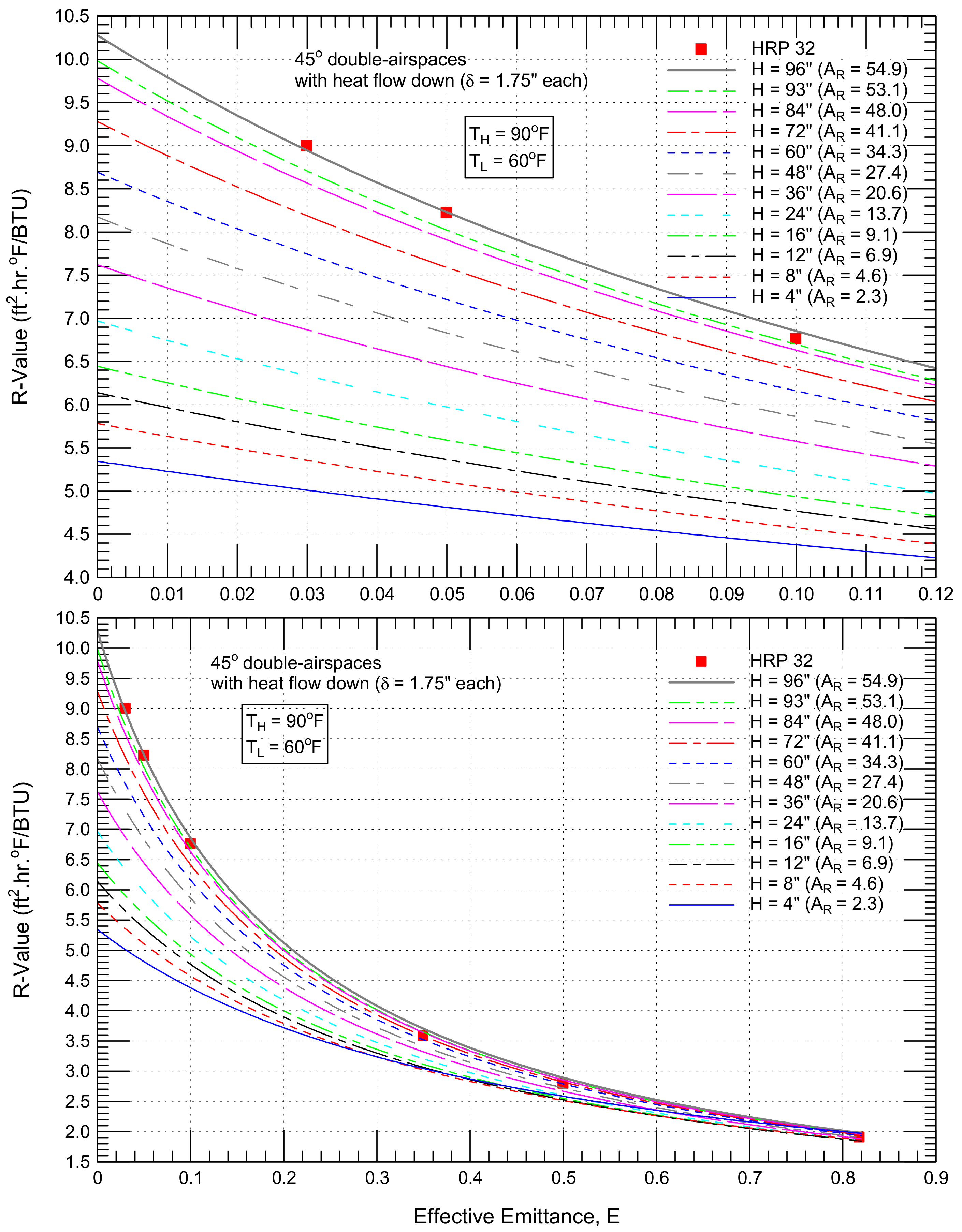
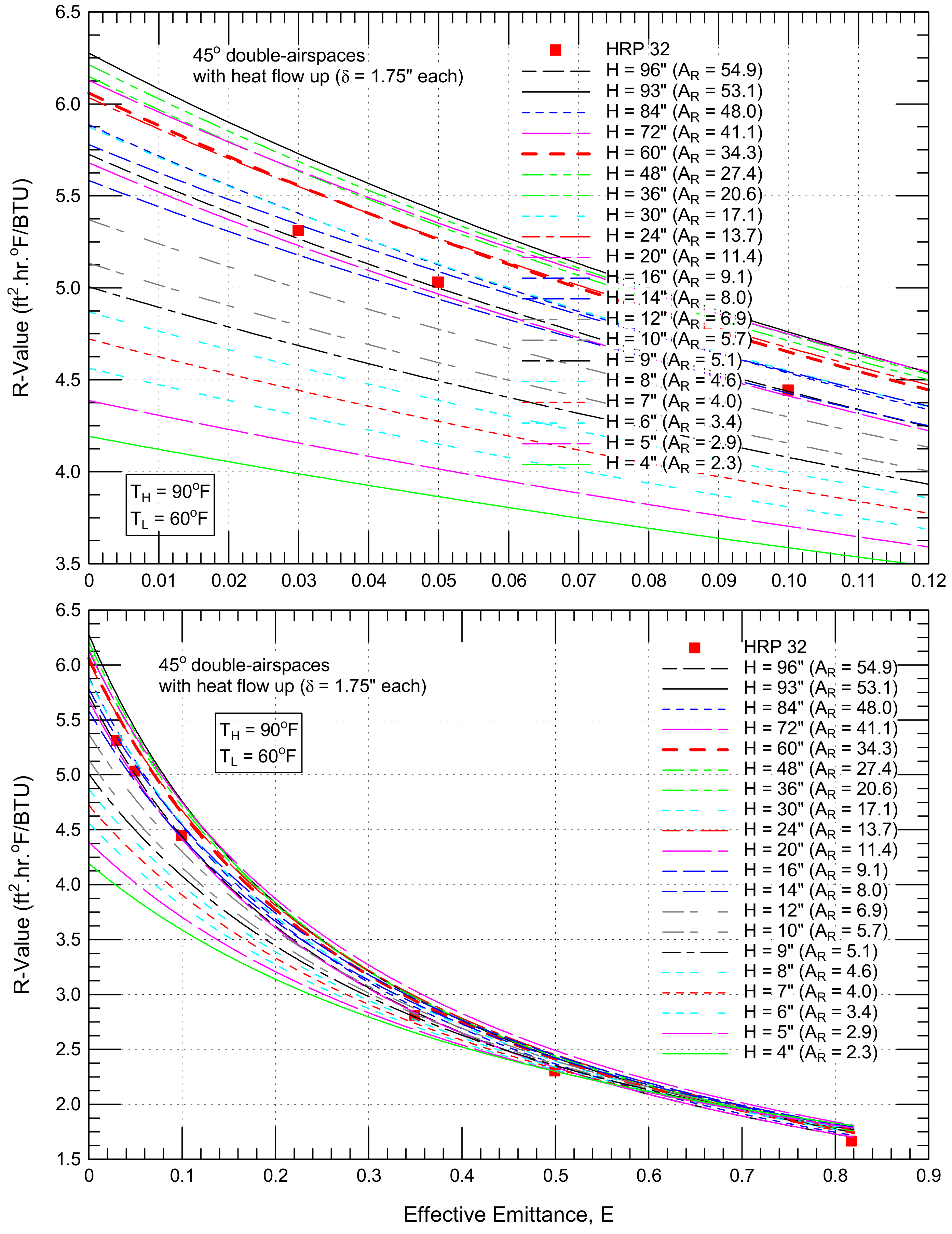
4.2.4. Sloped Airspaces (θ = 45°) with Downward Heat Flow
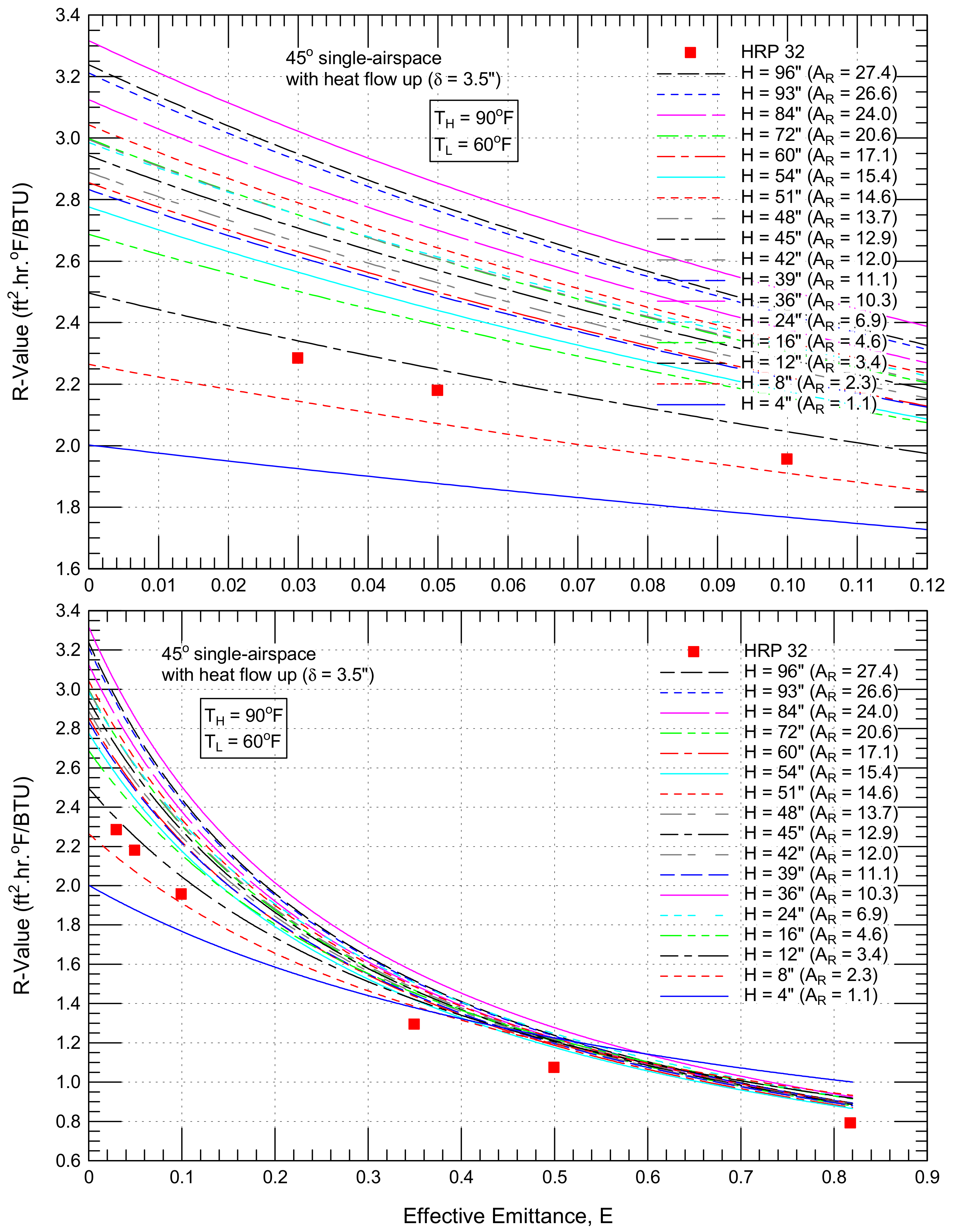
4.2.5. Sloped Airspaces (θ = 45°) with Upward Heat Flow
4.3. Effect of Aspect Ratio on the R Values
4.3.1. Vertical Airspaces (θ = 90°) with Horizontal Heat Flow
4.3.2. Horizontal Airspaces (θ = 0°) with Downward Heat Flow
4.3.3. Horizontal Airspaces (θ = 0°) with Upward Heat Flow
4.3.4. Sloped Airspaces (θ = 45°) with Downward Heat Flow
4.3.5. Sloped Airspaces (θ = 45°) with Upward Heat Flow
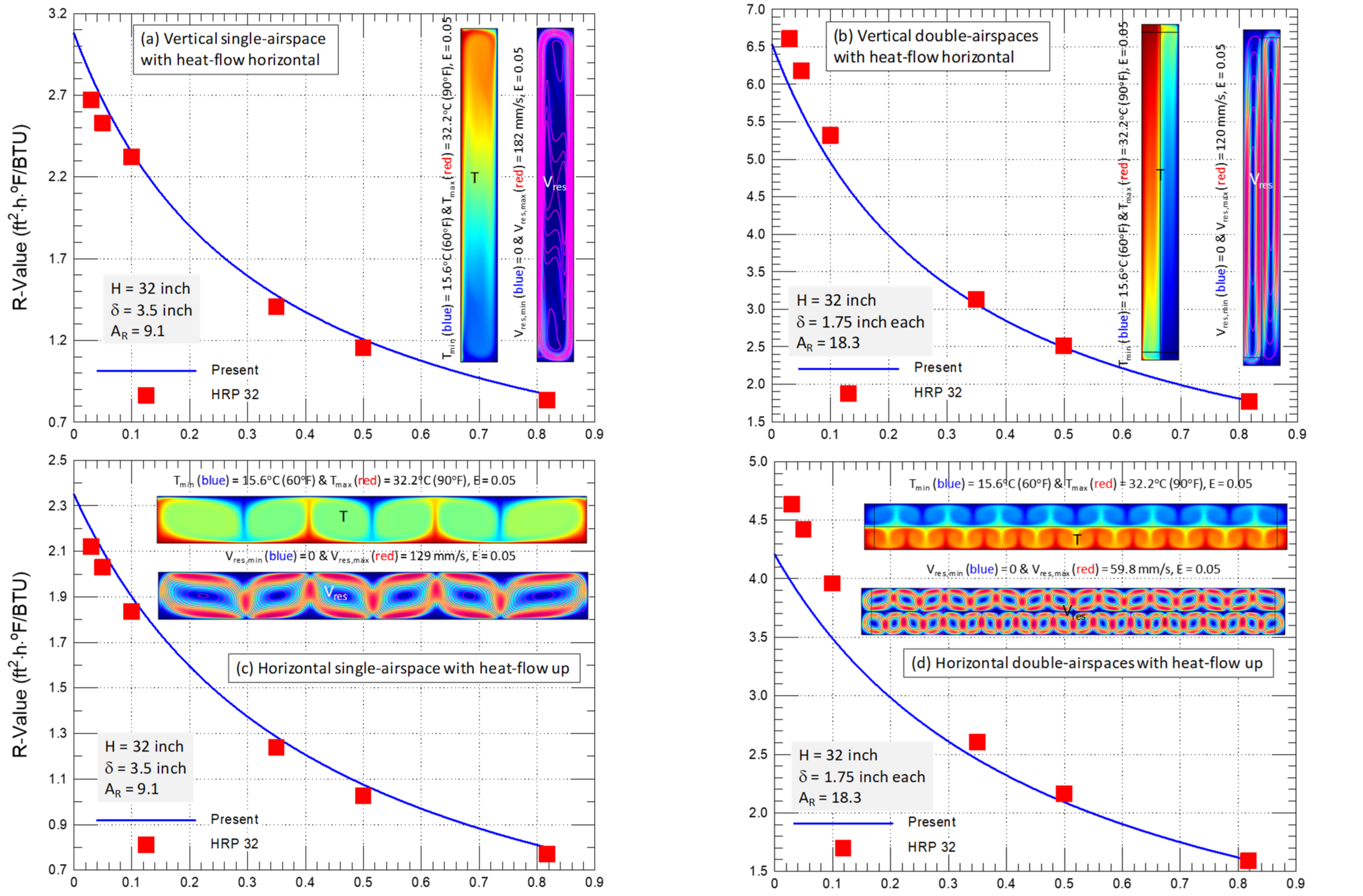
- 99% (from 1.86 to 3.70 ft2·h·°F/BTU for a vertical single airspace with a horizontal heat flow, Figure 10),
- 98% (from 4.03 to 7.97 ft2·h·°F/BTU for vertical double airspaces with a horizontal heat flow, Figure 11),
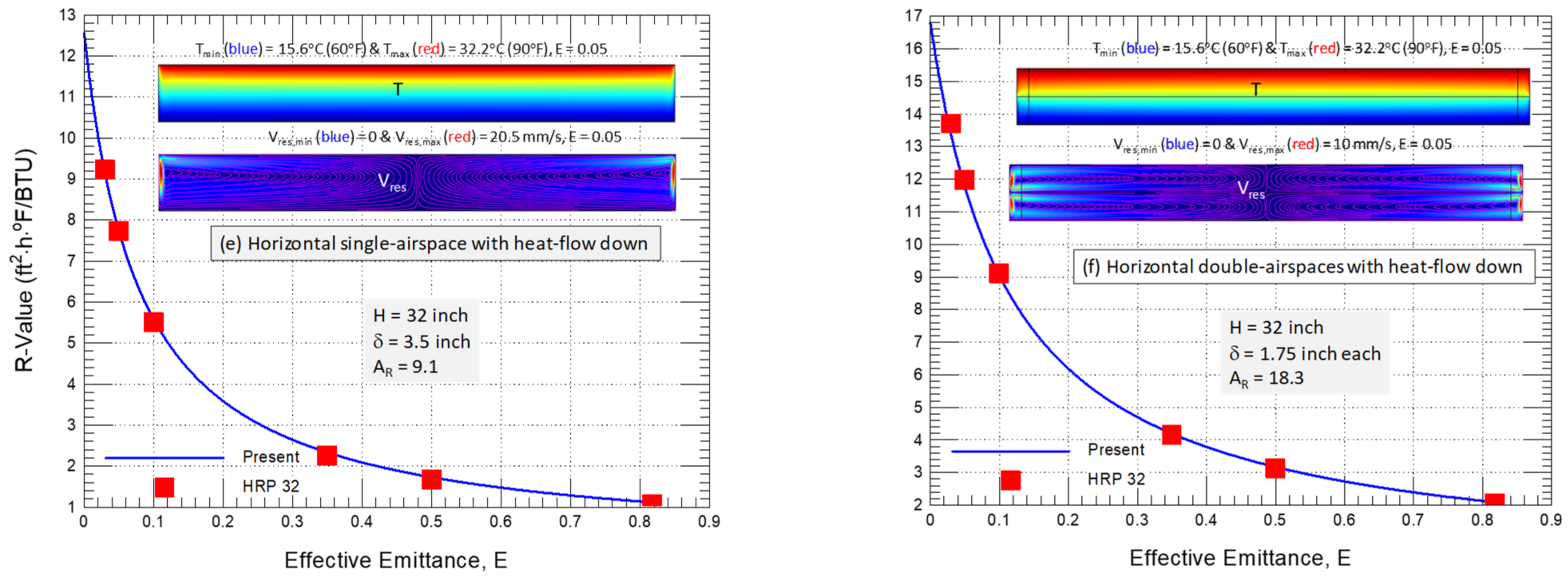
- 125% (from 4.84 to 10.87 ft2·h·°F/BTU for a horizontal single airspace with a downward heat flow, Figure 12),
- 65% (from 8.66 to 14.31 ft2·h·°F/BTU for horizontal double airspaces with a downward heat flow, Figure 13),
- 23% (from 1.91 to 2.35 ft2·h·°F/BTU for a horizontal single airspace with an upward heat flow, Figure 14),
- 19% (from 3.72 to 4.41 ft2·h·°F/BTU for horizontal double airspaces with an upward heat flow, Figure 15),
- 54% (from 2.66 to 4.11 ft2·h·°F/BTU for a 45° single airspace with a downward heat flow, Figure 16),
- 78% (from 5.02 to 8.95 ft2·h·°F/BTU for 45° double airspaces with a downward heat flow, Figure 17),
- 57% (from 1.93 to 3.02 ft2·h·°F/BTU for a 45° single airspace with an upward heat flow, Figure 18) and
- 44% (from 3.99 to 5.73 ft2·h·°F/BTU for 45° double airspaces with an upward heat flow, Figure 19).
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Governing Equations
Appendix A.2. Boundary Conditions and Simulation Parameters
References
- Goss, W.P.; Miller, R.G. Literature Review of Measurements and Predictions of Reflective Building Insulation Systems Performance: 1900–1986. ASHRAE Trans. 1989, 95, 651–664. [Google Scholar]
- Stephan, K.; Laesecke, A. The Thermal Conductivity of Fluid Air. J. Phys. Chem. Ref. Data 1985, 14, 227–234. [Google Scholar] [CrossRef] [Green Version]
- Pratt, A.W. Heat Transmission in Buildings; John Wiley and Sons: New York, NY, USA, 1981; pp. 31–40. [Google Scholar]
- Robinson, H.E.; Powell, F.J. The Thermal Insulation Value of Air Spaces, Housing Research Paper 32; National Bureau of Standards (now N.I.S.T), Project ME-12; U.S. Department of Commerce, U.S. Government Printing Office: Washington, DC, USA, 1956.
- American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE). Design Heat Transmission Coefficients. In ASHRAE Handbook of Fundamentals; ASHRAE: Peachtree Corners, GA, USA, 1972; Chapter 20. [Google Scholar]
- American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE). Heat, Air, and Moisture Control in Building Assemblies-Material Properties. In ASHRAE Handbook of Fundamentals; Table 3; ASHRAE: Peachtree Corners, GA, USA, 2017; Chapter 26. [Google Scholar]
- Desjarlais, A.O.; Tye, R.P. Research and Development Data to Define the Thermal performance of Reflective Materials Used to Conserve Energy in Building Applications. In Oak Ridge National Laboratory Report ORNL/Sub/88-SA825/1; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1990. [Google Scholar]
- Desjarlais, A.O.; Yarbrough, D.W. Prediction of the Thermal Performance of Simple and Multi-Airspaces Reflective insulation Materials. In Insulation Materials: Testing and Applications; Graves, R.S., Wysoci, D.C., Eds.; ASTM STP 1116; ASTM International: West Conshohocken, PA, USA, 1991; Volume 2, pp. 24–43. [Google Scholar]
- ISO 6946:2017. Building Components and Building Elements-Thermal Resistance and Thermal Transmittance-Calculation Methods-Annex D-Thermal Resistance of Airspaces; European Committee for Standardization, CEN-CENELEC Management Centre: Avenue Marnix, Belgium, 2017. [Google Scholar]
- Seigel, R.; Howell, J.R. Thermal Radiation Heat Transfer; McGraw-Hill Book Company: New York, NY, USA, 1972; pp. 240–241. [Google Scholar]
- Yam, K.W.; Teh, K.S.; Loi, P.; Yarbrough, D.W. Reflective insulation assemblies for above-ceiling applications. J. Build. Phys. 2020, 44, 272–283. [Google Scholar] [CrossRef]
- Saber, H.H.; Maref, W.; Elmahdy, A.H.; Swinton, M.C.; Glazer, R. 3D thermal model for predicting the thermal resistances of spray polyurethane foam wall assemblies. In Proceedings of the Building XI Conference, Clearwater, FL, USA, 5–9 December 2010. [Google Scholar]
- Saber, H.H.; Maref, W.; Lacasse, M.A.; Swinton, M.C.; Kumaran, M.K. Benchmarking of hygrothermal model against measurements of drying of full-scale wall assemblies. In Proceedings of the 2010 International Conference on Building Envelope Systems and Technologies, ICBEST 2010, Vancouver, BC, Canada, 27–30 June 2010; pp. 369–377. [Google Scholar]
- Saber, H.H.; Maref, W.; Elmahdy, H.; Swinton, M.C.; Glazer, R. 3D heat and air transport model for predicting the thermal resistances of insulated wall assemblies. J. Build. Perform. Simul. 2012, 5, 75–91. [Google Scholar] [CrossRef]
- Saber, H.H.; Maref, W.; Swinton, M.C.; St-Onge, C. Thermal analysis of above-grade wall assembly with low emissivity materials and furred airspace. Build. Environ. 2011, 46, 1403–1414. [Google Scholar] [CrossRef] [Green Version]
- Saber, H.H. Investigation of thermal performance of reflective insulations for different applications. Build. Environ. 2011, 52, 32–44. [Google Scholar] [CrossRef] [Green Version]
- Saber, H.H.; Maref, W.; Hajiah, A.E. Effective R-value of enclosed reflective air spaces for different building applications. J. Build. Phys. 2020, 43, 398–427. [Google Scholar] [CrossRef]
- Saber, H.H.; Maref, W.; Hajiah, A.E. Hygrothermal Performance of Cool Roofs Subjected to Saudi Climates. Front. Energy Res. 2019, 7. [Google Scholar] [CrossRef]
- Saber, H.H. Practical correlations for the thermal resistance of vertical enclosed airspaces for building applications. Build. Environ. 2013, 59, 379–396. [Google Scholar] [CrossRef] [Green Version]
- Saber, H.H. Practical correlations for thermal resistance of horizontal enclosed airspaces with upward heat flow for building applications. Build. Environ. 2013, 61, 169–187. [Google Scholar] [CrossRef] [Green Version]
- Saber, H.H. Practical correlation for thermal resistance of horizontal enclosed airspaces with downward heat flow for building applications. J. Build. Phys. 2013, 37, 403–435. [Google Scholar] [CrossRef] [Green Version]
- Saber, H.H. Practical correlation for thermal resistance of 45° sloped-enclosed airspaces with upward heat flow for building applications. J. Build. Phys. 2021. [Google Scholar] [CrossRef]
- Saber, H.H. Practical correlation for thermal resistance of 45o sloped enclosed airspaces with downward heat flow for building applications. Build. Environ. 2013, 65, 154–169. [Google Scholar] [CrossRef]
- Saber, H.H. Practical correlation for thermal resistance of low-sloped enclosed airspaces with downward heat flow for building applications. HVAC&R Res. 2014, 20, 92–112. [Google Scholar] [CrossRef] [Green Version]
- Saber, H.H.; Yarbrough, D.W. Advancements in the Evaluation of Reflective Insulation Assemblies. Constr. Specif. 2021, in press. [Google Scholar]
- RIMA International. Be Our Zoom Guest November 5th for Dr. Hamed Saber. September 2020. Available online: https://rimainternational.org/news/press-room/09-20-be-our-zoom-guest-for-dr-hamed-saber-november-5th/ (accessed on 13 May 2021).
- ASTM C1363. Standard Test Method for the Thermal Performance of Building Assemblies by Means of a Hot Box Apparatus; ASTM: Philadelphia, PA, USA, 2006; pp. 717–759. [Google Scholar]
- ASTM C518. Standard Test Method for Steady-State Heat Flux Measurements and Thermal Transmission Properties by Means of the Heat Flow Meter Apparatus; ASTM: Philadelphia, PA, USA, 2003; pp. 153–164. [Google Scholar]
- Saber, H.H.; Maref, W.; Sherrer, G.; Swinton, M.C. Numerical modeling and experimental investigations of thermal performance of reflective insulations. J. Build. Phys. 2012, 36, 163–177. [Google Scholar] [CrossRef] [Green Version]
- Saber, H.H.; Maref, W.; Swinton, M.C. Thermal response of basement wall systems with low-emissivity material and furred airspace. J. Build. Phys. 2011, 35, 353–371. [Google Scholar] [CrossRef] [Green Version]
- Saber, H.H. Thermal performance of wall assemblies with low emissivity. J. Build. Phys. 2012, 36, 308–329. [Google Scholar] [CrossRef] [Green Version]
- Cook, J.C.; Yarbrough, D.W.; Wilkes, K.E. Contamination of reflective foils in horizontal applications and the effect on thermal performance. ASHRAE Trans. 1989, 95, 677–681. [Google Scholar]
- Lee, S.W.; Lim, C.H.; Bin Salleh, E.I. Reflective thermal insulation systems in building: A review on radiant barrier and reflective insulation. Renew. Sustain. Energy Rev. 2016, 65, 643–661. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1960. [Google Scholar]

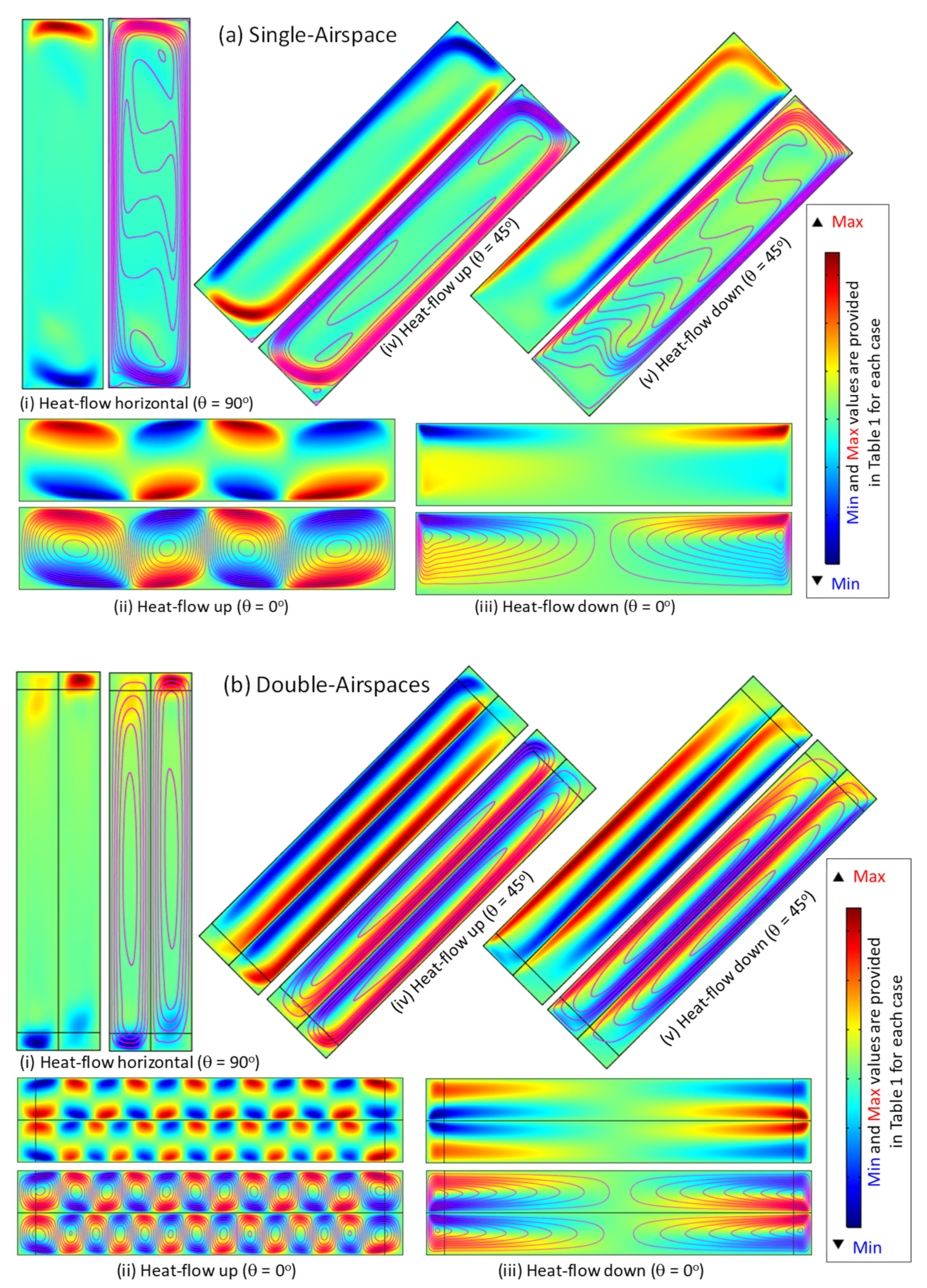
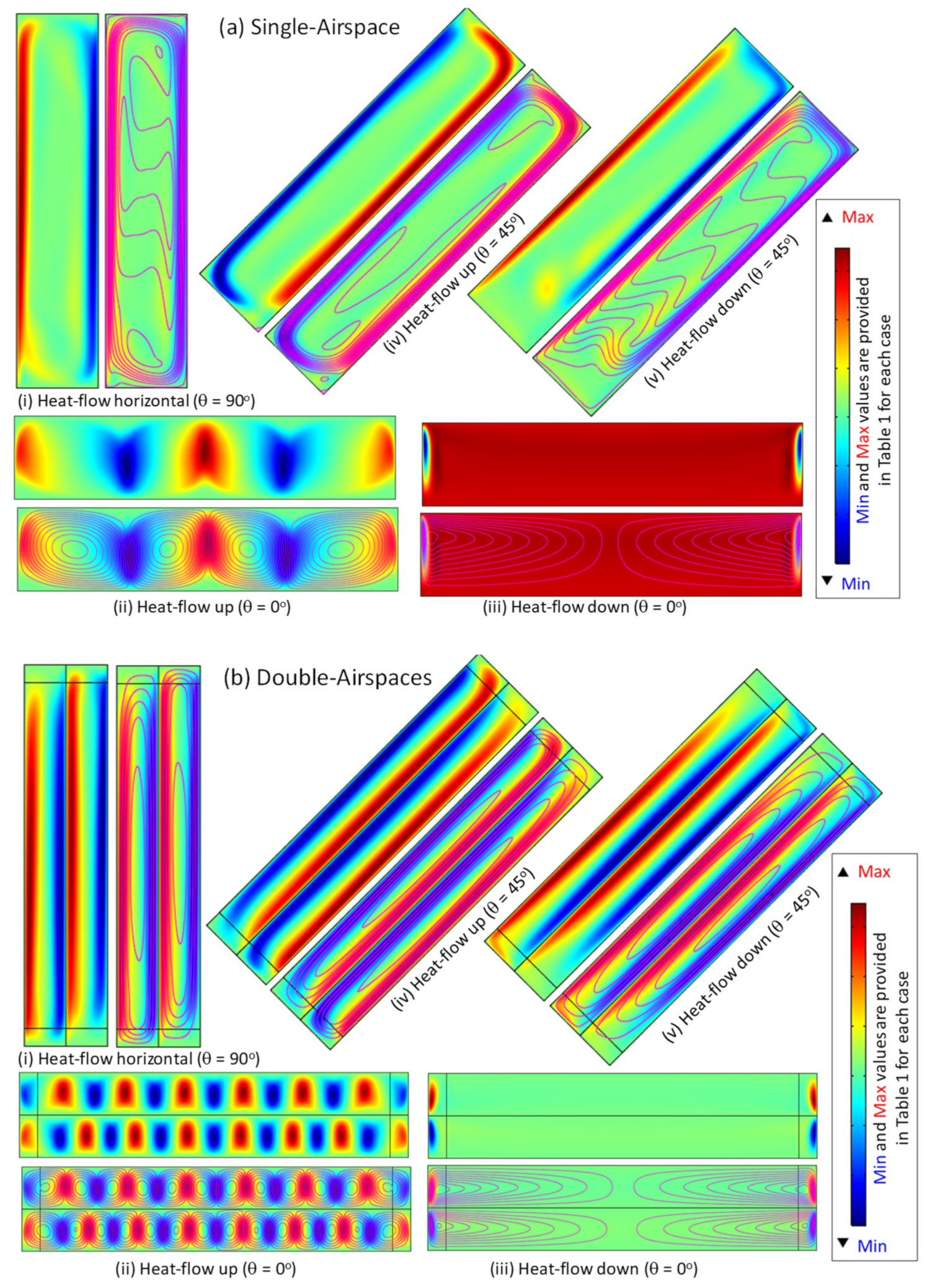



| Angle, θ | Heat-Flow Direction | Vx(mm/s) | Vy(mm/s) | Vres(mm/s) |  | |||
| Min | Max | Min | Max | Min | Max | |||
| Single airspace Having H = 16 inches, ™ = 3.5 inches, TH = 90 °F, TL = 60 °F, E = 0.05 | ||||||||
| 0° | Up | −125 | 125 | −126 | 133 | 0 | 133 | |
| Down | −7.53 | 7.53 | −17.4 | 1.4 | 0 | 17.4 | ||
| 45° | Up | −86.5 | 101 | −86.9 | 86.9 | 0 | 123 | |
| Down | −68.2 | 69 | −67.7 | 68.4 | 0 | 97.1 | ||
| 90° | Horizontal | −71.6 | 92.1 | −128 | 128 | 0 | 128 | |
| Double airspaces having H = 16 inches, ™ = 1.75 inches each, TH = 90 °F, TL = 60 °F, E = 0.05 | ||||||||
| 0° | Up | −51.3 | 51.3 | −63.3 | 63.3 | 0 | 63.3 | |
| Down | −5.33 | 5.33 | −9.52 | 9.77 | 0 | 9.78 | ||
| 45° | Up | −55.2 | 54.9 | −55.5 | 55.4 | 0 | 78.3 | |
| Down | −46.1 | 45.9 | −45.7 | 45.5 | 0 | 64.9 | ||
| 90° | Horizontal | −44.2 | 44.4 | −82.8 | 82.5 | 0 | 82.8 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saber, H.H.; Yarbrough, D.W. Advanced Modeling of Enclosed Airspaces to Determine Thermal Resistance for Building Applications. Energies 2021, 14, 7772. https://doi.org/10.3390/en14227772
Saber HH, Yarbrough DW. Advanced Modeling of Enclosed Airspaces to Determine Thermal Resistance for Building Applications. Energies. 2021; 14(22):7772. https://doi.org/10.3390/en14227772
Chicago/Turabian StyleSaber, Hamed H., and David W. Yarbrough. 2021. "Advanced Modeling of Enclosed Airspaces to Determine Thermal Resistance for Building Applications" Energies 14, no. 22: 7772. https://doi.org/10.3390/en14227772
APA StyleSaber, H. H., & Yarbrough, D. W. (2021). Advanced Modeling of Enclosed Airspaces to Determine Thermal Resistance for Building Applications. Energies, 14(22), 7772. https://doi.org/10.3390/en14227772







