Probabilistic Load Flow–Based Optimal Placement and Sizing of Distributed Generators

Abstract

Distributed generation (DG) is gaining importance as electrical energy demand increases. DG is used to decrease power losses, operating costs, and improve voltage stability. Most DG resources have less environmental impact. In a particular region, the sizing and location of DG resources significantly affect the planned DG integrated distribution network (DN). The voltage profiles of the DN will change or even become excessively increased. An enormous DG active power, inserted into an improper node of the distribution network, may bring a larger current greater than the conductor’s maximum value, resulting in an overcurrent distribution network. Therefore, DG sizing and DG location optimization is required for a systematic DG operation to fully exploit distributed energy and achieve mutual energy harmony across existing distribution networks, which creates an economically viable, secure, stable, and dependable power distribution system. DG needs to access the location and capacity for rational planning. The objective function of this paper is to minimize the sum of investment cost, operation cost, and line loss cost utilizing DG access. The probabilistic power flow calculation technique based on the two-point estimation method is chosen for this paper’s load flow computation. The location and size of the DG distribution network are determined using a genetic algorithm in a MATLAB environment. For the optimum solution, the actual power load is estimated using historical data. The proposed system is based on the China distribution system, and the currency is used in Yuan. After DG access, active and reactive power losses are reduced by 53% and 26%, respectively. The line operating cost and the total annual cost are decreased by 53.7% and 12%, respectively.

1. Introduction

Distributed generation (DG) is a small-scale (usually 1 kW–50 MW) distributed power production unit, located near the load, meant to fulfil the load requirement of specialized customers or supplement the grid for economic efficiency. DG entails installing and operating a portfolio of tiny, compact, and environmentally-friendly mechanisms [1]. DG may be used to produce a whole customer’s electrical supply to reduce peak demand, backup emergency production, or improve dependability of the grid. DG technology is less expensive since it removes the need for costly distribution and transmission line installation. Based on the DG demand, the power system’s technical, economic, and environmental effects are being studied. The study examines voltage profile, power loss, power quality, reliability, and availability [2,3].

Newton Raphson and rapid decoupled power flow algorithms are common solutions. However, the conventional load flow algorithms are avoided since the R/X ratio of radial distribution systems is high [4]. The approach utilized most often for radial distribution networks is the backward forward sweep (BFS) that effectively analyzes the load flow [5,6]. E. Bompard et al. analyze the convergence of the BFS technique with various load models [7]. The influence of load models on DG planning is examined to determine its technical implications and practicality. The load model may influence the placement and size of DGs. D. Singh et al. examine the various load models, including residential, industrial, and commercial loads [8]. The optimum placement and DG sizing within a distribution network are difficult [9]. The authors in [10] present a dynamic programming technique for locating and sizing DGs to improve voltage stability while reducing network losses. The susceptible buses, from a voltage stability standpoint, are identified and evaluated for DG installation in this section using bifurcation analysis. The number of DGs is selected so that the system voltage falls within the specified voltage security limitations. A novel index, based on steady node voltages, determines the most sensitive bus for DG placement [11]. An analytical method is utilized to determine the optimal size and placement of the DG to reduce power loss. In [12], a mixed-integer linear programming method is used to solve the steady state functioning of a radial distribution system with varying load levels. The impact of load models on DG planning is studied and found to be substantial [13]. In [14], a new technique is suggested for determining the position of DG using a loss sensitivity factor and a simulated annealing method.

Numerous academics have suggested numerous methods for determining the location and magnitude of DGs. One of the popular meta-heuristic methods is particle swarm optimization (PSO). PSO involves two steps: computing the particle velocity and updating the particle’s location based on the population that speeds up the processing time, consuming less memory. However, PSO is prone to incomplete optimization [15,16]. Another population-based method, shuffled frog jumping (SFJ), can handle a wide variety of problems. However, SFJ delays convergence and sometimes results in impulsive convergence [17,18]. A genetic algorithm (GA) is a straightforward technique. However, real-time GA applications are constrained by random solutions and a slower convergence rate [19]. The optimum placement and size of DG are determined using a combination of GA and PSO algorithms [20]. The bacterial foraging optimization algorithm (BFOA) is used to solve various optimization problems in power systems; therefore, we need to find a simple way to accelerate the convergence [21]. S. Abdi et al. use an improved particle swarm optimization (IPSO) and Monte Carlo hybrid algorithms for DG sizing. The Monte Carlo technique is versatile and practically limitless in the investigation. However, the answers are not precise [22]. It varies according to the number of frequent runs. The modified teaching-learning method is a novel optimization technique for addressing uninterrupted nonlinear challenges. However, it is restricted to situations with fewer dimensions [23]. The ecological invasive weed optimization (IWO) algorithm simulates weed invasion, suggested in [24] for electromagnetic applications [25]. Luis A. Gallego offers a probabilistic optimum power flow (POPF). The POPF is a fast-specialized point estimate approach implemented in electrical distribution systems with renewable DG units [26]. South Asian countries have a significant transmission and distribution loss of 16.13%, because of the poor transmission system and distribution network [27]. It is a significant challenge to reduce the transmission and distribution losses.

The probability of trend, Probabilistic Load Flow (PLF), is calculated using mathematical probability statistical methods. It can reflect the impact of various uncertainties and random changes, in the grid system of electricity, to run the system [28]. It can also be the network topology of the grid system. The assembly parameters, node load power, and generator power uncertainty variables change together and are then calculated. The calculated results and the power system voltage of each branch node start load probability statistical properties of the trend. The random trend and probabilistic load flow methods are the most mainstream methods to solve the flow problems. The random method, in which the trend is an uncertain factor of the system as a random variable at a certain point in time, to study these random variables affects the calculation of the uncertainty of the results brought about at each time point to the traditional trend. The probability of the trend method is the study of uncertain variables’ impact on the grid over some time. The nonlinear flow equations to solve the error caused by the linear model is shown in reference [29]. Monte Carlo simulation is randomly selected from the random variable data, subject to the probability distribution characteristic variable. Then, the data is associated with the selected simulation solution as an input variable, so the node voltage is determined to be accurate and branch flows.

The cumulate bind Gram–Charlier series expansion is shown in [30]. The series expansion uses a relatively simple calculation rather than complex mathematical convolution calculation. The method reduces the memory footprint, the linear model of the trend, to improve the calculation speed and accuracy. However, the Convolution Method and cumulative probability trend assume that the random variables are unrelated, and there is a relationship between the random variables’ practical problems. The point estimate method (PEM) is a probability-to-certainty problem solving technique that considers the correlation between input variables [30,31]. It can be used, in conjunction with the existing probabilistic load flow algorithm, to obtain an accurate distribution for quantity. The PEM is then used to fit the more probabilistic trend solution. The point estimation method is the most widely used two-point and three-point estimation method, wherein the two methods [32], including the Two Point Estimate Method (2PEM), are the most common.

The main contributions of this paper are as follows:

• This paper collects and analyzes a series of research works on probabilistic power flow, DG location, and capacity problems based on the point estimation method.
• Genetic algorithm is used to optimize DG location and capacity. The forward and backward substitution method is used to calculate probabilistic power flow.
• The economic model of distribution network planning with DG is established. The objective function is to minimize DG cost, line loss cost, and power purchase cost. The three inequality constraints are node voltage constraints, conductor current constraints, and DG operation constraints. The penalty factor is introduced to establish a new comprehensive, objective function.
• Historical load data of the actual power grid is used for the simulation, the genetic algorithm is used to optimize the calculation. The optimization results are compared with those of the DG distribution network without access.
• A graphical interface software for DG location is developed by MATLAB programming.

2. Proposed Approach

There are several types of power flow calculation methods in the power system. In this paper, probabilistic load flow is based on a two-point estimate method chosen for power flow calculation. For the DG sizing and location, the genetic algorithm is used.

2.1. Probabilistic Power Flow Algorithm Based on Two-Point Estimation Method

Suppose there are n nodes in a grid structure, branch b, PQ node l, then its flow equations system, Cartesian coordinates can be expressed as [21]:

$$Y=g\left(V\right)$$

(1)

$$Z=h(V)$$

(2)

where: $Y$ random column vector, representing.

$Y={\left[P_1,Q_1,V_1^2,\dots ,P_l,Q_l,P_{l+1},V_{l+1}^2,\dots ,P_{n-1},Q_{n-1},V_{n-1}^2\right]}^T$ where $P$ is the reactive power, $Q_i$ It means no power, $V$ it represents a node voltage; $Z$ represents active and reactive power; $g$ represents node power, $h$ is representing the branch power.

The two-point estimation method is a method based on the point estimation method. It is called the two-point estimation method because only two values are needed in the calculation. These two values are distributed on both sides of the mean value of each random variable. Then, the two values are used to replace the mean of corresponding random variables. The probabilistic power flow in Equations (1) and (2) are used to calculate deterministic power flow. The other random variables are still taken at the mean. If there are $m$ random variables in a power system, then deterministic power flow calculation needs to be calculated $2m$ times. The probabilistic power flow of the two-point estimation method depends on the results of deterministic and probabilistic power flow calculations. It can be applied with only minor changes in the deterministic power flow calculation program, improving efficiency and ensuring accuracy. This is one of the reasons why the two-point estimation method is chosen.

2.2. Power Flow Calculation of Distribution Network with DG

Through the power flow calculation of the distribution network, we can intuitively understand and evaluate the operation status of the target grid. For the power flow calculation of a distribution network with DG, because DG itself is a power generation equipment, it can provide power, it is necessary to consider the influence of different installation locations and capacity of DG on power transmission. DG is usually used as an additional alternative power supply. The installation site is usually directly located at or around the load. This paper assumes that all DG installation sites are now installed on load nodes.

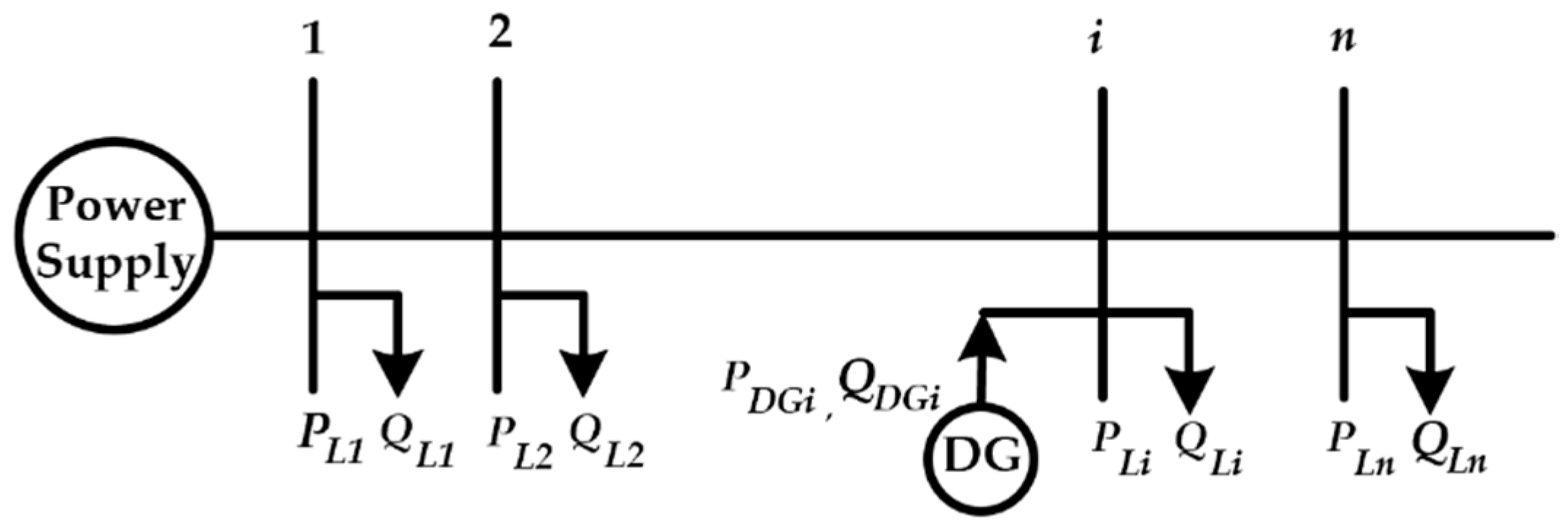
Figure 1 is a single radial line topology. There are $n$ nodes on this line. Assuming that the DG accessed is on the $i$ node, according to the active $P_{DGi}$, size of active $P_{Li}$ and DG, and the loads on the node, the active flow of the node will encounter some situations.

• When, $P_{DGi}>P_{Li}$ the load node is equivalent to an active power supply node, which provides $P_{DGi}-P_{Li}$ active power to the distribution network, and the reverse power flow will occur.
• When, $P_{DGi}=P_{Li}$ there is no active power flow between the distribution network and the load node, excluding other factors.
• When $P_{DGi}<P_{Li}$ the substation will continue to transmit power to the load node, and the active power transferred will be reduced to $P_{DGi}-P_{Li}$ compared with the case without DG.

From the above analysis, it can be seen that, when DG is only connected to node $i$ on the distribution line and the active power $P_{DGi}$ of load node, $i$ is larger than the total active load time of feeder node $i$ to $n$, i.e., $P_{DGi}>P_{Li}+P_{Li+1}+P_{Li+2}+\dots +P_{Ln}$ The direction of power flow will be reversed, and DG will conversely transmit power to the power side of the distribution network, which is also a potentially adverse effect on the stable operation of the distribution system after DG is connected. When multiple load nodes are connected to DG on this line, the flow direction of other branches can also be obtained by similar analysis. It is not difficult to see that, when many DGs are connected to the distribution network, the power flow direction of the line may change. Most scholars believe that the capacity of DG access should be limited to ensure that the direction of power flow will not change after DG access to the distribution network. According to the characteristics of distribution network structure, there are many methods to calculate power flow in literature. At present, the more mature algorithms include the forward and backward substitution method, fast decoupling method, and $Z_{bus}$ method [33]. Due to the rapid stability of the forward and backward substitution method in power flow calculation of the distribution network, this paper uses forward and backward substitution methods to solve power flow calculation of a distribution network with DG, which connects DG as a “negative” load to the load point. The following Equations can describe the power flow equations in radiation lines:

$$P_i=P_{i-1}-\frac{R_{i-1}\left(P_{i-1}^2+Q_{i-1}^2\right)}{U_{i-1}^2}-P_{Li}+P_{DGi}$$

(3)

$$Q_i=Q_{i-1}-\frac{X_{i-1}\left(P_{i-1}^2+Q_{i-1}^2\right)}{U_{i-1}^2}-Q_{Li}+Q_{DGi}$$

(4)

$$U_i^2=U_{i-1}^2-2\left(P_{i-1}{R}_{i-1}+Q_{i-1}{X}_{i-1}\right)+\left(R_{i-1}^2+X_{i-1}^2\right)\left(P_{i-1}^2+Q_{i-1}^2\right)/U_{i-1}^2$$

(5)

where: $i=1,2,\dots \dots , n$, the active load power $P_L$, load reactive power $P_L$, DG active power $P_o$.

All the above variables are random variables with mean and probability distribution density. In power flow calculation, the rotation is combined with the two-point estimation method. Figure 2 shows the probabilistic power flow calculation flowchart based on the two-point estimate method.

2.3. Network Loss Calculating Model of Distribution Network

Generally, the calculation of network loss is divided into two parts: one is the line loss of the distribution network, the other is the power loss of the transformer. The sum of all branch line losses in the feeder is the distribution network line. Transformer losses are divided into no-load and load losses. The operating voltage and capacity of the transformer determine the size of no-load losses, and the size of load determines the size of load losses. Much of the literature about line loss is very clear. The calculation method of transformer loss is mainly introduced below. There are two ways to measure transformers: high-supply meter and low-supply meter. For high-supply meter users, copper loss and iron loss of transformers have been counted as inactive meter and reactive meter without additional calculation. Voltage transformer capacity below 160 kVA is measured by high supply and low meter. Transformer loss is related to parameters and load curve. The previous calculation process was rather complicated. This paper uses the following formulas [34] to calculate transformer loss:

Transformer power loss calculation:

$$P_L=\left[P_o+{\left(KB\right)}^2\times P_e\right]\times T$$

(6)

$$B=\frac{A}{\left(T\times \cos \alpha \times S_e\right)}$$

(7)

where, $P_L$ is representing power loss of transformer; $P_o$ is the no-load active power loss of transformer; $K$ is equivalent coefficient RMS of daily load; $B$ is load factor; $P_e$ is active load loss for transformer rated load; Operation hour is $T$ which is 720 h; $A$ is for daily consumption; $\cos \propto$ is for the secondary side force ratio of the transformer, take 0.85 here; $S_e$ is transformer rated capacity.

The reactive power loss of the transformer is calculated by the following equations [34]:

$$Q_L=[{\theta }_o+\left(KB{)}^2\times {\theta }_e\right]\times T$$

(8)

$${\theta }_o=I_o\times S_e$$

(9)

$${\theta }_e=V_e\times S_e$$

(10)

where reactive power loss of the transformer is $Q_L$; reactive power loss for no-load transformer is ${\theta }_o$; $K$ is equivalent coefficient RMS of daily load; $B$ is the load factor; ${\theta }_e$ is the reactive power loss of the transformer rated load; Operation hour is $T$ which is 720 h; $L_o$ is no-load current of the transformer as a percentage of rated current (%); $S_e$ is the transformer rated capacity; $V_e$ is the impedance voltage percentage.

For aspect calculation, the values of $K$ and $B$ can be divided into four cases, according to the nature of electricity consumption, as shown in

Table 1. K and B value.

Electrical Properties	K	B
No longer daily electricity consumption	0.15	2
Small load	0.3	1.5
All-day long power time	0.5	1.2
Heavy load	0.7	1.14

below:

3. Problem Definition and Mathematical Model

This paper establishes an economic model of distribution network planning with DG for the time of 10 years. When the number, location, and capacity of DG are uncertain, the objective function is to minimize the sum of investment and operation cost, line loss cost, and all purchase costs after DG access. The penalty factor is introduced to restrict the operation of node voltage, conductor current, and distributed generation. Inequality constraints are converted into equality constraints and added to the calculation of objective functions.

Objective Function:

$$min Z_{\mathrm{cost}}=C_{DG}+C_L+C_{en}$$

(11)

Goal 1. Minimal DG’s investment and operating costs

$$C_{DG}={\displaystyle \sum }_{i=1}^{n_{DG}}({\partial }_i{C}_{DGi}+C_{pu}\Delta E_{DGi}+W_{DGi})$$

(12)

Goal 2. Minimum operating costs for distribution network systems

$$C_L={\displaystyle \sum }_{i=1}^{n_l}{C}_{pu}{\tau }_{max}\Delta P_{Li}$$

(13)

Goal 3. The minimum cost of purchasing electricity

$$C_{en}=T_{max}\left(P_{\sum Newload}-P_{\sum DG}\right)C_{pu}$$

(14)

among them, $P_{\sum DG}\sum _{i=1}^{n_{DG}}{\lambda }_i{S}_{DGi}$.

Equation (12) is minimizing the DG investment and operation cost. Where $C_{DG}$ is converted to the annual investment and operating expenses of DG, $n_{DG}$ indicates the number of DGs connected to the distribution network; ${\partial }_i$ represents the average annual cost coefficient of fixed investment for the $i\prime th$ DG;$C_{DGi}$ fixed investment cost of the $i\prime th$ DG (10,000 yuan);$C_{pu}$ is the unit prize (RMB/kWh);$\Delta E_{DGi}$ is the total annual energy loss of $i\prime th$ DG; $W_{DGi}$ is inspection and maintenance costs of the $i\prime th$ DG.

Equation (13), where $C_L$ is converted to annual line operating costs; $n_l$ is the total number of branches; $C_{pu}$ is unit prize (RMB/kWh); ${\tau }_{max}$ is annual maximum load loss hours of the $i\prime th$ branch; $\Delta P_{Li}$ is active power loss on branch $i$. Equation (14) represents the minimum cost of purchasing electricity, where $C_{en}$ is the electricity purchasing cost;$T_{max}$ is the maximum load annual utilization hours (h); $P_{\sum Newload}$ is total additional load; $P_{\sum DG}$ is DG’s total active output;$C_{pu}$ is the total unit prize;$n_{DG}$ is represents the number of DGs connected to the distribution network;${\lambda }_i$ is the power factor of $i\prime th$ DG;$S_{DGi}$ is capacity of $i\prime th$ DG.

3.1. Constraints

Constraints include two types: equality and inequality constraints. Among them, the power flow calculation Equations (3)–(5) are equality constraints. Inequality constraints include node voltage constraints, conductor current inequality constraints and DG access capacity constraints. The node voltage control is set to 7% of the reference voltage within a safe range, and the upper limit of the branch current is set to 420 A. As mentioned above, the relay protection devices of radial lines only allow one-way power flow to pass. To control the DG access capacity not to exceed the node’s load, the DG access capacity does not exceed 10% of the total maximum load of the power grid.

(1)

Node voltage constraints

$$K_u\left(U_i\right)=\{\begin{array}{cccccc}{K}_u {\left(U_{i min}-U_i\right)}^2\hfill & & & U_i& <& U_{i min}\\ K_u {\left(U_i-U_{i max}\right)}^2\hfill & & & U_i& >& U_{i max}\\ 0\hfill & U_{i min}& \le & U_i& \le & U_{i max}\end{array}$$

(15)

where, $U_i$ represents the voltage of the $i\prime th$ node (kv); $U_{imax}-U_i$ is the upper limit (kv); $U_{imin}-U$ is the lower limit; $K_u$ is the penalty factor of node voltage, $K_u$ generally takes a larger value, when meeting the requirements, it takes a value of 0.

(2)

Conductor current inequality constraints

$$K_I\left(I_j\right)=\{\begin{array}{cc}{K}_I {\left(I_j-I_{j max}\right)}^2\hfill & I_j\ge I_{j max}\\ 0\hfill & I_j<I_{i max}\end{array}$$

(16)

where, $I_j$ is represents the current of branch $j$; $I_{jmax}$ is the upper limit of the current allowed by the $j\prime th$ branch; $K_I$ is conductor current penalty factor, the principle of value is the same as $K_U$.

(3)

Distributed power operating constraints

$$K_{\sum DG}\left(S_{\sum DG}\right)=\{\begin{array}{cc}{K}_{\sum DG}{\left(S_{\sum DG}-S_L\right)}^2\hfill & S_{{\sum }^{ }DG}>S_L\\ 0\hfill & S_{\sum DG}\le S_L\end{array}$$

(17)

where, $S_{\sum DG}$ is the total capacity for DG access to the grid; $S_L$ is the 10% of total grid load; $K_{\sum DG}$ is the DG injection amount penalty factor, the principle of value is the same as $K_U$.

The above inequality constraint, in the form of a penalty factor, is introduced into the objective function. The new objective function is obtained:

$$min{Z}_{\cos t}=C_{DG}+C_L+C_{en}+{\displaystyle \sum }_{i=1}^n{K}_U\left(U_i\right)+{\displaystyle \sum }_{j=1}^L{K}_I\left(I_j\right)+K_{\sum DG}\left(S_{\sum DG}\right)$$

(18)

In this paper, the genetic algorithm (GA) is used to solve the minimum value problem of DG location and the capacity objective function problem, also known as a multi-objective optimization problem.

3.2. DG Location and Sizing

The single value of all groups is the average installed capacity of DG at the location. Apparently, DG, based on natural climate effects, exhibits volatility, interstitially, and randomness. Figure 3 shows the DG location and sizing algorithm flowchart. In the power flow calculation with DG, DG is described as a probability variable, but in the decision-making, the following decision variables (one chromosome in the genetic algorithm) are determined: DG = (DG1, DG2,…DGn) the value is the expected value with a probability distribution, so it is a certain value in each decision. Therefore, when the genetic algorithm is introduced, each time the chromosome group to be selected is given, it will be used as the power generation capacity of the $i\prime th$ DG. The two-point estimation is also entered into the power flow calculation to obtain the objective function. In solving the DG location and size problem, an initial population is generated by random generation, which contains the location and size information of DG. This paper assumes that each DG is installed on a load node, and one load node can only install one DG. For a radial distribution topology that allows $n$ nodes to install DG, the location and size information of DG access can be represented by a set of variables $C=\left(c_1,c_2,\dots , c_n\right)$. The value of $c_i$ is converted to binary coding by real coding in the genetic algorithm, and the output is converted to real number output. The size of $c_i$ represents the location and capacity information of DG access to the corresponding load node $i$, and if $c_i=0$, the load node does not access DG. If multiplying the capacity base value is the DG access capacity of the node. To reduce the error, the capacity base value $a_i$ of each node is equal to the maximum load value $P_{maxi}$ of the node divided by the maximum of the actual decision variables. The range of actual decision variables is [0, 15], so $c_6=5$ node 6 is the maximum load value,

$$P_{max6}=100 \mathrm{kW}, a_6=\frac{P_{max6}}{15}=\frac{100}{15}$$

The access node capacity 6 is

$$C_6=c_6{a}_6=5\times \frac{100}{15}=\frac{100}{3} \mathrm{kW}$$

The range of actual decision variables in this paper is taken [0, 31]. Choosing an appropriate fitness function has a significant impact on the results of optimization calculation. The objective function is regarded as the fitness function, and the constraint condition is transformed into an unconstrained form in the form of a penalty factor. Finally, the final planning scheme is determined according to the individual fitness. In this paper, the roulette method is used to select and then execute related transfer operations. We have tested different parameters. Therefore, the most satisfactory results come from these values. Thus, we set crossover rate $P_{c1}=0.9, P_{c2}=0.6$, mutation rate $P_{m1}=0.1, P_{m2}=0.001$. In this paper, the maximum number of cycles $T=100$, and the minimum number of optimal individuals $T_p=30$. The linear scaling algorithm is used to individually loop calculations. If the number of loops is 100, the program exits the loop and proceeds with the following calculation. If the number of cycles does not reach 100, but the optimal solution of the objective function has been found, then the cycle also exits in advance.

4. Results and Case Studies

This article takes the modified IEEE 62 nodes as an example. A configuration diagram of the power distribution network is shown in Figure 4. The radial distribution network [35] structure consists of 62 nodes and 61 branches. Among them, node 24 and node 31 are connected by small hydropower stations as power points, so load data is calculated as a negative number, while the other nodes are load points.

The load nodes in the network can run and install DG, which is directly installed on the load nodes. Load data, herein provided by the examples, and basic parameters are as follows in

Table 2. The list of basic parameters.

Price (Yuan/kWh)	0.4816
DG unit price (yuan/kW)	2400
The annual average cost of fixed investment coefficient	0.35
The maximum number of access DG (a)	62
Reference voltage (kV)	10
The maximum loss of load hours (h)	3000
Using the maximum load in hours (h)	3000
DG Power Factor	0.9
Node voltage, current leads, DG injection amount penalty factor	100

. Assuming that each node load is independent of each other, the input and output have the same probability distribution, and the load parameters of the nodes obey the normal distribution.

In addition, the unit resistance value of the line is R = 0.46 Ω/km, and the unit reactance value is X = 0.368 Ω/km. The probabilistic load flow is calculated using the forward and backward probabilistic load flow algorithm. Hence, it is necessary to know the connection relationship of each node and other parameters needed for power flow calculation. This paper assumes that only load and DG random fluctuations are considered, and other variables are not considered for the time being. For a given distribution network structure shown in Figure 4, when the number, location and capacity of DG access are uncertain, the objective function is minimized. The improved genetic algorithm is used to obtain the DG location and capacity selection results in

Table 3. DG locating and sizing information.

Node No.	Access Capacity (kW)	Node No.	Access Capacity (kW)	Node No.	Access Capacity (kW)
1	0	22	29.13	43	31.1432
2	0	23	43.02	44	41.113
3	0	24	10.2	45	41.113
4	0	25	23.025	46	0
5	0	26	14.25	47	0
6	0	27	1.375	48	8.1
7	0	28	0	49	35.75
8	0	29	0	50	49.162
9	0	30	0	51	47.3134
10	0	31	41.0625	52	0
11	0	32	37.225	53	0
12	0	33	49.475	54	29.0625
13	0	34	49.475	55	9.8721
14	0	35	21	56	23.9259
15	0	36	0	57	19.8187
16	22.625	37	0	58	29.7561
17	4	38	0	59	33.5712
18	16.0625	39	26	60	17.3217
19	0	40	0	61	27.1425
20	0	41	0	62	18.875
21	0	42	0

. Wherein the compensation capacity of the node 0 indicates that the node does not access DG, locating and sizing of the actual program can be simplified, as shown in

Table 4. DG actual locating and sizing scheme.

Node No.	Access Capacity (kW)	Node No.	Access Capacity (kW)	Node No.	Access Capacity (kW)
16	22.625	33	49.475	54	29.0625
17	4	34	49.475	55	9.8721
18	16.0625	35	21	56	23.9259
22	29.13	39	26	57	19.8187
23	43.02	43	31.1432	58	29.7561
24	10.2	44	41.113	59	33.5712
25	23.025	45	41.113	60	17.3217
26	14.25	48	8.1	61	27.1425
27	1.375	49	35.75	62	18.875
31	41.0625	50	49.162	0	0
32	37.225	51	47.3134

.

Comparative analysis of before and after DG access is shown in

Table 5. Comparative analysis of before and after DG access.

Comparison Items	Before DG Access	After DG Access
Total load (kW)	3267.97	3267.97
The total power loss (kW)	76.0013	36.8039
The total reactive power loss (kvar)	121.645	90.2868
Access DG total (kW)	0	851.25
The total amount of power required (kW)	3267.97	2430.4
The total annual cost (million RMB)	501.683	442.3748
Purchase annual cost (million RMB)	490.1953	361.4664
Line operating cost (million RMB)	11.4878	5.3174
DG operation in investment costs (million RMB)	0	75.5910

. This program’s objective function value corresponds to the average annual total cost of 490.1953 million before DG access, which, converted into the purchase of electricity per year, is 361.4664 million yuan. The annual operating costs for the line are 5.3174 yuan. The annual investment and operation of DG cost are 75.5910 million yuan. The annual DG operation constraint penalty fee is 0 Yuan. At the same time, the annual node current penalty fee is also 0 Yuan. The annual node voltage penalty fee is 0 Yuan. All penalties are zero, indicating that each constraint is met after access to the DG, and no crossover occurs.

Figure 5 shows that each node voltage (red line), after the access DG, is significantly higher than the previous access (blue) for each node voltage. Still, the voltage does not exceed the upper limit, indicating that access DG improves the voltage’s quality. Before DG multiple access, the closer and distal branches’ node voltage dropped due to losses caused by the system. The DG ratio is greater in the peripheral access node and the voltage boost; therefore, the phase node voltage near the tip is reduced more than the head-end node voltage. This is because the access DG can effectively reduce the power flow on the line, thereby reducing the line loss, but it does not eliminate the loss of the node voltage compared to tip or head-end node voltage reduction. Such as peripheral node 15, the compensation voltage before 9.4916 kV, compensation voltage 9.7443 kV, increases by 2.67%, while the front 17 of the node voltage compensation distal 9.8956 kV, compensation voltage 9.9600 kV, increases by 0.5134%.

It can be seen from Figure 6 that each branch current (red line) after DG access is smaller than each branch current (blue line) before DG access, and the line current corresponds to the corresponding line network. The loss will be reduced. Figure 7 shows the change in active loss before and after the DG is connected. The trends in Figure 5, Figure 6 and Figure 7 are generally consistent. The node voltage, node current, and branch loss closely relate to a given distribution network structure. It is necessary to configure the location and capacity of the DG properly. To demonstrate the changes produced by the distribution network to the access DG, the figure below compares the parameters before and after DG access.

5. Conclusions

Based on the summarized relevant results, a comparative analysis of probabilistic power flow calculation is presented in this paper. Here, a probabilistic power flow calculation, based on the two-point estimation method, is proposed. It applies this method to the DG customized capacity problem of a given distribution network grid structure. The objective function is to minimize the sum of investment and operation cost, line loss cost, and purchase cost of DG every year. DG access results show that the proposed method can reduce active power losses by 53% as well reactive power losses. The proposed method can reduce active power losses by 53% and reactive power losses by 26%. The line operating cost is decreased by 53.7%, and the total annual cost reduced by 12%. The penalty factor is introduced to transform the three inequality constraints of node voltage, conductor current, and operation of distributed generation into equality constraints, which are also added to the objective function calculation. In the future, the mathematical model for DG-based distribution network design will be further researched and enhanced to account for the effect of other important variables on the distribution network.