1. Introduction
In recent years, the global offshore wind energy sector has been in a continuous and comprehensive stage of development, arising from the eminent desire to reach international climate goals [
1,
2,
3,
4]. Considering Europe only, ∼450 GW of offshore wind has been deemed necessary to meet the increasing energy demand as well as addressing climate change [
1]. As a consequence, recent years have seen an increasing focus on floating offshore wind turbines (FOWTs), which allow for utilization of sites with water depths larger than ∼60 m in which traditional bottom-fixed turbines are generally deemed economically infeasible [
5,
6,
7].
Several FOWT projects are under development worldwide, putting even more stress on the need for reducing the levelized cost of energy (LCOE) to secure competitiveness and future deployments. WindEurope predicts that at least 350 MW of FOWTs will be online by 2022, and an LCOE of 50-65 EUR/MWh will be reached by 2030. This decrease in cost is expected to be resulting from technological development, government policies, and mass production [
7].
The TetraSpar FOWT foundation, cf.
Figure 1, is a Danish concept developed during recent years [
8]. The design relies purely on highly industrialized components with an existing supply chain [
9]. In summer 2021, a 3.6 MW demonstrator completed manufacturing in Denmark and was installed off the Norwegian coast [
8].
During the design phase of the concept, several experimental test campaigns and studies were conducted [
10,
11,
12], while the final design highly relied on numerical modeling [
13,
14,
15]. Naturally, this resembles the procedure applied by most other FOWT developers and designers of offshore structures and is recommended by most design standards such as DNVGL-OS-E301 [
16], DNVGL-RP-C205 [
17], IEC TS 61400-3-2:2019 [
18], and DNVGL-ST-0119 [
19].
Most numerical models of floating structures rely on either a Morison approach [
20] or a boundary element method (BEM) [
21,
22,
23,
24]. In most cases, the global six degrees-of-freedom (DoF) loads and motions of the FOWT are solved considering the structure as a rigid body. However, for a final design of an FOWT, the local load distribution is needed to conduct structural design and secure sufficient structural strength of all components. In addition, the flexibility of each component might affect the global response of the structure as seen in [
25].
The present paper presents modeling approaches for an FOWT concept considering the structure as fully flexible. The study uses the commercial software package OrcaFlex [
26,
27], the open-source software OpenFAST (formerly known as FAST) [
28,
29,
30,
31,
32], and the TetraSpar demonstrator as a case study. More detail on the structure can be seen in [
9].
The paper is structured with this introduction followed by a section describing the modeling approaches.
Section 3 presents normalized load and motion results and compares the difference between a fully rigid and flexible structure, and between OrcaFlex and OpenFAST. Finally,
Section 4 discusses the results and concludes the paper.
2. Methodology
As seen from
Figure 1, the TetraSpar FOWT platform is composed of 10 cylinders, with 3 additional cylinders at the keel. The components are connected to form a tetrahedral shape and are moored to the seabed through three catenary lines connected to the end of the radial elements. The design is equipped with a 3.6 MW turbine. A simplified description of the floating platform can be found in [
9], while the present study uses an accurate description of the TetraSpar 3.6 MW demonstrator.
In this paper, the time-domain response of the structure is modeled in the software packages OrcaFlex [
26,
27] and OpenFAST [
28]. Both packages are capable of solving the equations of motion (EoM) using the Morison equation [
20] for estimation of hydro loads on the structure.
In the present study, the inertia coefficient is defined as , where is the added mass coefficient. The drag coefficient is defined as . Axial hydrodynamic loads are not included in the calculations. The aerodynamic loads are not solved within the numerical models, but applied as a prescribed loads time series. The hydrodynamic loads are computed based on the relative form of the Morison equation, while the hydrostatics are computed according to the actual position and orientation of the substructure at every simulation time step.
2.1. The OrcaFlex Model
When modeling the structure in OrcaFlex, other studies such as [
33] have used the “
6D Buoy” objects of the “
Spar Buoy” type to model each component of the TetraSpar platform. These rigid objects allow for estimation of the environmental loads on each component and solve the bodies’ six DoF motion response. The tower has similarly been modeled as a rigid “
6D Buoy” and with a lumped mass and inertia at the tower top resembling the rotor nacelle assembly (RNA).
The above methodology does not allow for inclusion of any flexibility of the components. Due to the simplicity of the TetraSpar, being composed of only cylindrical shapes with tapered ends, the present study uses the “Line” elements in OrcaFlex to model the structure. This means that the components can be modeled with flexibility and are treated in the same way as, e.g., the mooring lines. In order to build the structure, the following approach is applied:
End nodes are defined for all components. In OrcaFlex, “
6D Buoys” are used as nodes. The buoys are defined as “
Lumped Buoys” with negligible properties. The position of the nodes is based on information on the structure as defined in [
9]. The connectivity of each node is then defined. As an example, one end node of each radial is connected to the bottom node of the center column (cf.
Figure 1).
“Line” elements are connected to the nodes, thereby forming each of the components of the foundation.
The end connection stiffness for each line element is defined in order to model the desired connection type. For the TetraSpar, all connections are pinned, meaning that the “x-bending” should be defined as infinite, while not applying any “y-bending”. For simplicity, the present study considers fixed connections, hence infinite stiffness around both the x- and y-axis.
The “
Line Type” is defined for each type of component to resemble the structure. The lines are considered “
Homogeneous pipes”. Parameters are defined including inner and outer diameters, material density, Young’s Modulus and hydrodynamic coefficient (
,
, and
). The parameters are similar to those of the rigid body model and defined in [
9]. Bending stiffness is calculated by OrcaFlex from cross-sectional parameters and material properties.
Structural damping is applied using stiffness proportional Rayleigh damping with 0.5% critical damping for the first tower bending mode.
The tower is modeled in a similar way to the rest of the foundation, namely as a flexible “Line” with a lumped mass and inertia at the tower top (RNA). The tower is fixed to the center column at the bottom and free in all DoFs at the top.
2.2. The OpenFAST Model
OpenFAST has been recently upgraded to account for floating substructure (platform) flexibility and member-level loads [
29,
30]. The tower is modeled in ElastoDyn, and the substructure is modeled in SubDyn. The structural damping considered in ElastoDyn is 0.5% critical damping for the first tower bending mode and 1% critical damping for the second tower bending mode. For the substructure, the tetrahedron and keel are modeled by means of Timoshenko beams that account for axial, shear, bending, and torsion DoFs. The six keel lines (see
Figure 1) are included by means of pretensioned cable elements. To improve the computational efficiency, a modal reduction by means of a Craig–Bampton fixed-interface method together with a static-improvement method is performed for the substructure. SubDyn now accounts for a floating frame of reference formulation. The Guyan modes capture the rigid-body motion, and the Craig–Bampton and static modes capture the structural elasticity. In this case, 15 internal Craig–Bampton modes are retained (with the higher modes treated statically). The HydroDyn module is used to compute the hydro loads. HydroDyn accounts for the distributed viscous-drag, added-mass, fluid-inertia, and hydrostatic buoyancy loads along members. The hydrostatic loads are based on the instantaneous position, orientation, and deflection of the members. The MoorDyn module is used to model the three mooring lines by means of a lumped-mass theory that captures the dynamic behavior.
2.3. Test Cases
This study seeks to present the possibility of modeling a structure such as the TetraSpar as a fully flexible structure and compare it to a fully rigid structure. The tests used for the comparison are presented in
Table 1. Regular waves are modeled as linear Airy waves, while the irregular sea states are modeled with a JONSWAP spectrum. Wind loads are calculated in an external software tool using a similar turbine and afterwards applied as a prescribed load time series at the tower top. The loads at the tower top location are obtained by means of simulations that consider the structural components of the wind turbine (i.e., supporting structure, drivetrain, and blades) as rigid and do not account for the gravity acceleration. In this way, the inertial and gravity loads are disregarded, and the loads can be considered as externally applied loads. The simulations in OpenFAST and OrcaFlex can then be run accounting for the gravity and inertia loading with these time series of loads prescribed as non-follower loads applied at the tower top location.
3. Results
For comparison between the rigid and flexible models, primarily motions and loads are considered. Sensors at the RNA and the interface between the tower and platform are used for extraction of data. The sensors and the OrcaFlex and OpenFAST models can be seen in
Figure 2. The rigid model used for comparison is modeled in OrcaFlex.
In the following sections, the results and comparisons are presented. Due to confidentiality, only normalized data are presented. However, this still clearly illustrates differences between the models and identifies capabilities of them, hence fulfilling the objectives of the present study.
3.1. Static Tests
Results from the static test, where only gravity is present, are shown in
Figure 3. The test is useful for assessing if dimensions, masses, and buoyancy are modeled similarly in the models. As seen from the figure, some differences are obtained. No significant displacement is expected for the sway, heave, roll, and yaw DoF, which is why the values are near zero and not relevant for comparison. The overhang of the RNA (cf.
Figure 2) causes the structure to pitch in the static position. Due to the flexibility of the tower, the pitch is up to 10% larger in the flexible model compared to the rigid one. This also affects the overall surge position with a difference up to 20% between the rigid and flexible models. The flexibility of the tower also results in variation of the resulting force
and moment
. The
and
at the interface are approximately 5–10% larger, while mooring loads and
show no significant difference.
Clearly, the rigid and flexible approaches provide results of the same order of magnitude and can be used for further modeling. It is further noticed that OrcaFlex and OpenFAST are in relatively good agreement.
3.2. Free Decay Tests and Natural Periods
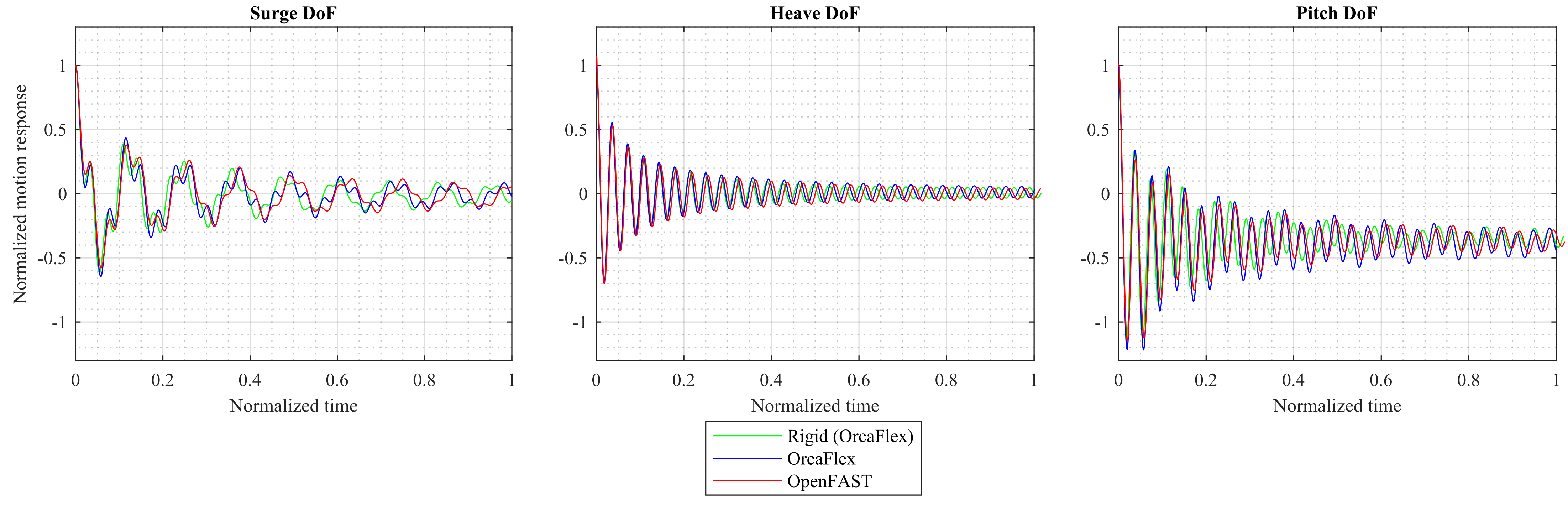
In the free decay tests, the structure is displaced in each of the three DoFs: surge, heave, and pitch. The resulting response is seen from
Figure 4.
Both the flexible and rigid model result in similar tendencies in the decay response but with some variations in the natural periods.
Figure 5 compares the natural periods for the two flexible modeling approaches compared to the rigid model. As expected, the flexibility in the flexible model creates a larger natural period, which can also be seen in
Figure 4. The surge, heave, and pitch natural periods are respectively 3–5%, 3%, and 4–5% larger when modeling the structure as flexible. Good agreement is observed between OpenFAST and OrcaFlex for the different free-decay tests performed.
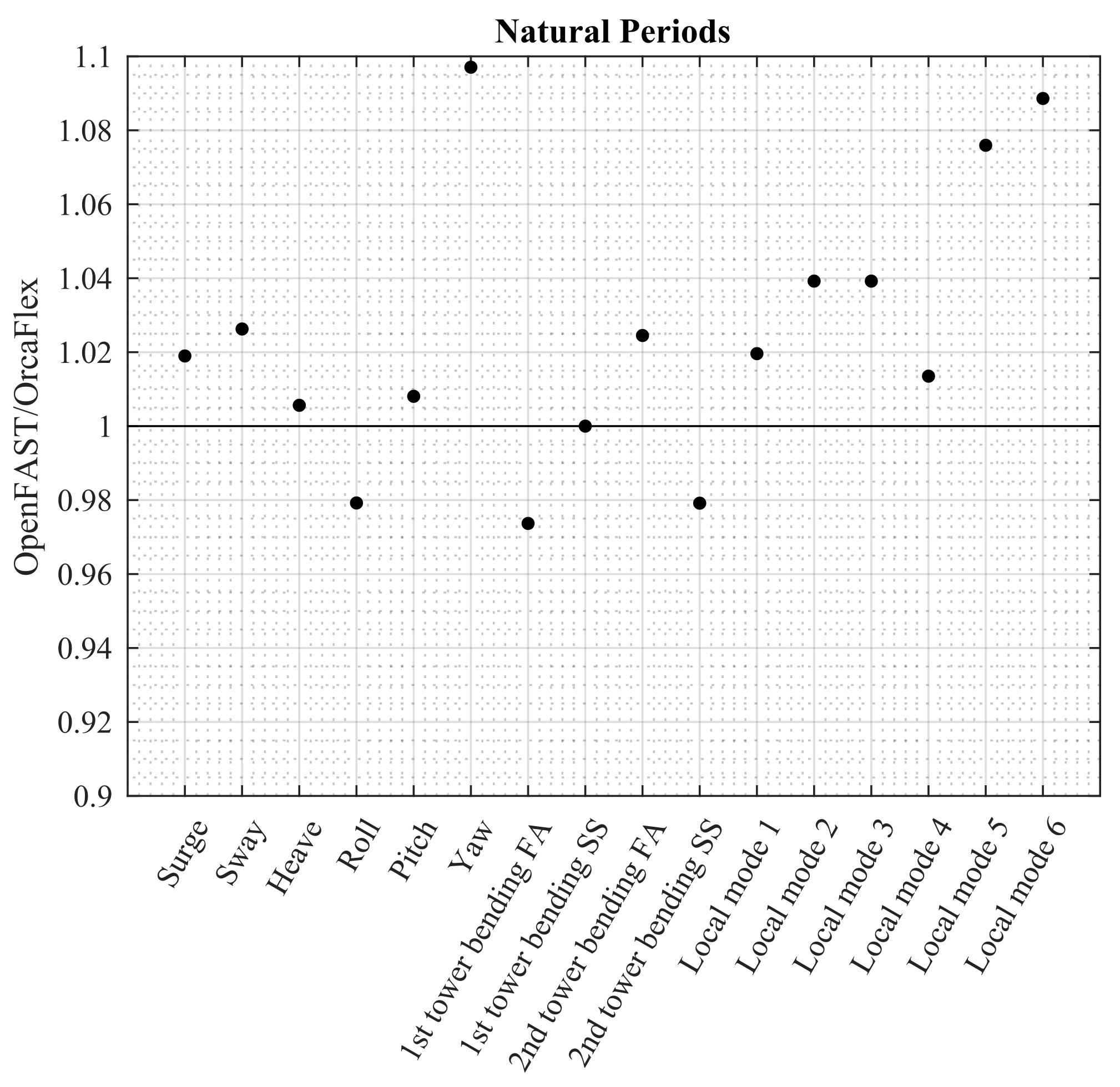
Figure 6 shows the comparison in terms of natural period between the flexible models in OpenFAST and OrcaFlex. This information is obtained from the system linearization capability available in OpenFAST and OrcaFlex. The comparison includes the motion in the six DoFs (surge, sway, heave, roll, pitch, yaw), the first two tower bending modes in the fore/aft (FA) and side/side (SS) directions, and the first six local flexural modes of the substructure. The largest difference observed is smaller than 10% and corresponds to the yaw mode. It is interesting to note that when the OpenFAST and OrcaFlex rigid models are compared, this difference in yaw is already observed. This denotes that the difference is not due to including the flexibility in the system. This small disagreement could be explained by some differences in the moment of inertia around the z-axis (which also accounts for the added mass from the water) and/or the yaw stiffness provided by the mooring lines. One additional static test allowing the platform to only rotate around the z-axis was performed in OrcaFlex and OpenFAST rigid models. In this test, it is observed that the yaw stiffness in OrcaFlex is 11.4% higher than in OpenFAST. This explains, in part, the differences observed in
Figure 6. For reference, the mooring lines used in the TetraSpar design combine synthetic materials, chains, and clump weights, which makes the numerical models challenging.
3.3. Regular Sea State
For comparison of dynamic behavior, a case with regular waves and steady wind is considered; cf.
Table 1. The motion response of the sensor at the interface between the tower and substructure is presented in
Figure 7.
As seen from the figure, the motion response varies between the models. The most prominent difference is observed for the pitch DoF. While the motion amplitude is similar, the mean value of the flexible model is larger, which is most likely caused by the bending of the structure.
When considering the moment
at the interface (cf.
Figure 8), it is further observed that the flexible model provides a slightly larger mean value. However, the rigid structure results in the largest amplitude.
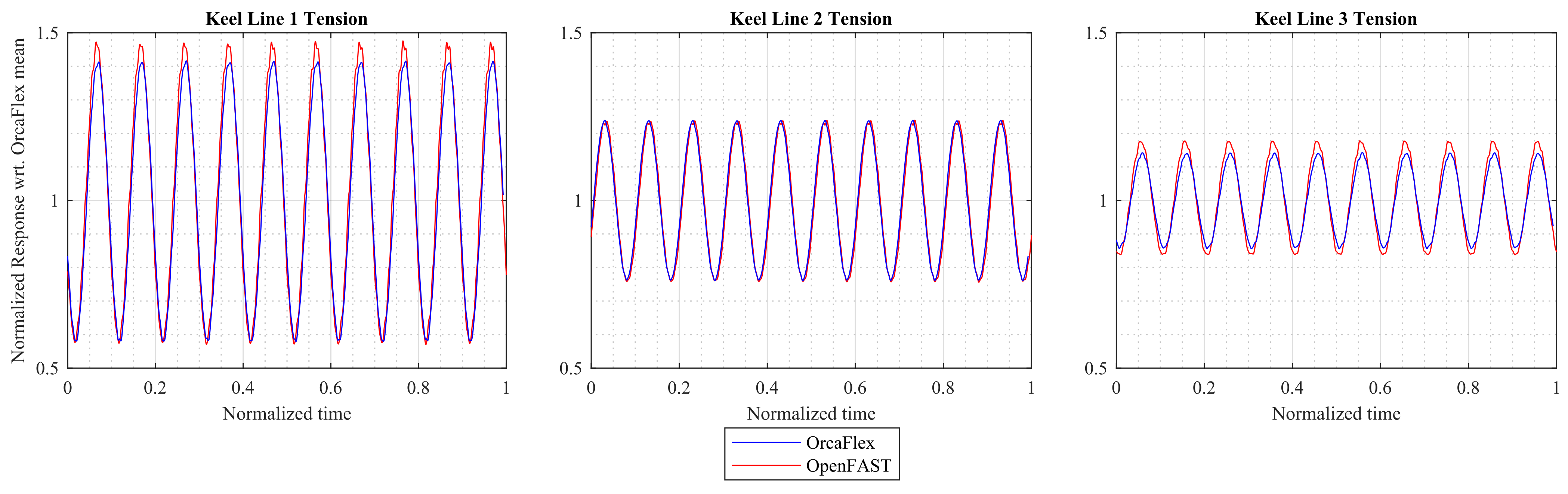
Figure 9 presents the time series of keel line tension in the flexible OrcaFlex and OpenFAST models. Only lines 1–3 are presented because lines 4–6 are similar to 1–3 due to the symmetry of the system with regard to the XZ plane and the specific loading considered (the regular waves propagate along the X direction). Generally good agreement is observed, with OpenFAST showing a tendency of slightly larger tension. For keel lines 1 and 3, a difference of 3–4% between maximum tension is obtained, while there is no difference in the response of keel line 2.
Evidently, some differences are seen between the rigid and flexible modeling approaches in both motions and loads. As mentioned, the objective of this paper is to investigate whether it is possible to extract internal structural loads in a flexible model in OrcaFlex and OpenFAST. As seen in
Figure 10, the normalized resultant bending moment in the middle of each component of the structure can be plotted as time series (here only one of each type is presented). These data are not available for a rigid structure. Internal bending moments in the radial brace and central column show good agreement between OrcaFlex and OpenFAST. However, the agreement for the diagonal brace and lateral brace locations is not as good.
Since no data are extractable for the rigid model and no experimental data are available, it is not possible to compare or validate these results in this study.
3.4. Irregular Sea State
For irregular sea states, similar internal loads from the substructure can be extracted for the flexible model. The results are not included in this paper because
Figure 10 already presented the capability. For the irregular sea states, a time series is simulated using a JONSWAP wave spectrum, while a time-varying wind load is applied at the tower top (
,
,
,
,
, and
in the global coordinate system). The wind loads are simulated in an external software with a similar turbine and correspond to relevant wind conditions for the sea state.
Figure 11 presents the most probable maximum (MPM) values for the loads at the sensors. The MPM-value is calculated from the following equation and is defined in, e.g., DNVGL-OS-E301 as a design value for design verification [
16]:
where
is the mean of the response,
is the standard deviation, and
is the number of up-crossings in the time series.
T corresponds to the duration of the time series, while
is the mean up-crossing period.
As seen from
Figure 11, in general, the flexible model results in larger motion and load responses compared to the rigid body model. The most critical difference is seen in pitch, where the MPM is ∼15% larger in the flexible model than in the rigid. This pitch rotation is especially important in the design of FOWTs. On one hand, the mean pitch value is mainly determined by the aerodynamic thrust force and the hub height. On the other hand, the pitch motion variations are due to the stochastic nature of the aero and hydro loads. The loads are up to 60% larger for the
at the interface, and all the investigated forces and moments are larger in the flexible model. The largest difference between OrcaFlex and OpenFAST models is observed for the
load. It is also interesting to note that the natural periods in
Figure 6 also showed the largest difference for this same direction (yaw). This denotes that the two numerical models behave differently in this direction. The mooring lines also show slightly larger loads for the flexible models compared to the rigid one. The largest difference is observed for the mooring line 1 (located upwind, see
Figure 1), where the flexible model results in ∼8% larger line tension, most likely caused by the larger pitch motion.
Figure 12 shows the comparison between OpenFAST and OrcaFlex for the MPM in the six keel lines of the substructure. As can be observed, the agreement is very good with differences smaller than 6%. This good agreement is also aligned with the results obtained for the regular case (see
Figure 9 for reference).
The power spectral density (PSD) of the loads at the interface for the irregular case can be observed in
Figure 13. Three spectra are shown for the main directions of interest:
(surge),
(heave), and
(pitch). The wave excitation can be seen in the lower frequency range of the spectrum. The first tower bending mode can also be observed specially in the surge and pitch directions, as expected. The response of the tower occurs at almost the same frequency for both numerical models (as anticipated in
Figure 6). However, the tower response in OrcaFlex is larger than in OpenFAST. This would denote some differences in the structural damping. The 3P excitation corresponding to the blade-passing frequency can also be observed in the surge direction. This excitation and the corresponding harmonics are included in the wind loads prescribed at the tower top.
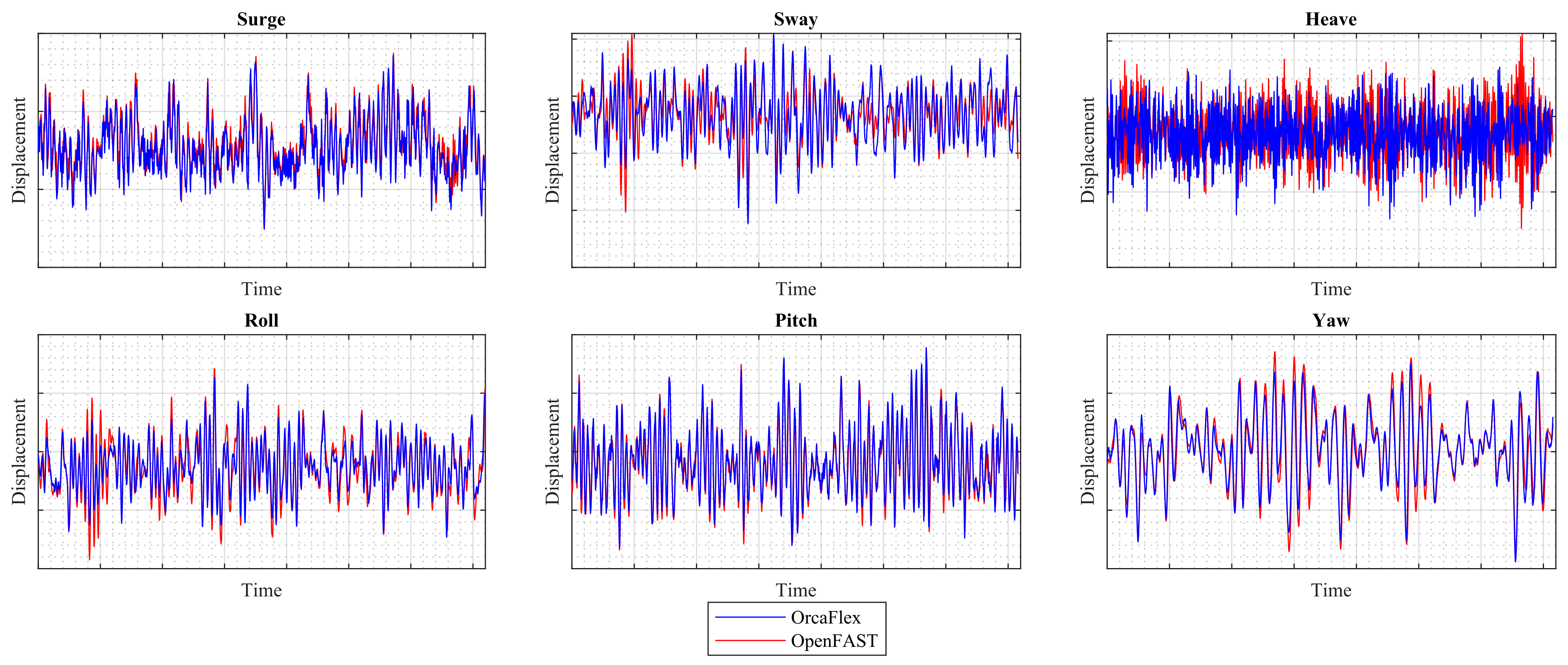
Figure 14 shows the three mooring lines tension for the irregular case. In general, both models agree well with each other. However, OpenFAST experiences some slack events for the mooring line 1 (mooring line tension drops to 0 N). These events are not observed in OrcaFlex. The reason is not known yet, although slack events are seen in OrcaFlex under more severe conditions. It is interesting to note that the motion experienced by both models at the interface is very similar (see
Figure 15 for reference). This could denote that the slack events observed in OpenFAST are not due to different motions of the substructure but rather differences in the modeling of the mooring lines.
4. Discussion and Concluding Remarks
The present paper has presented results from two modeling approaches (rigid and flexible) in both OrcaFlex and OpenFAST for an FOWT concept: the TetraSpar. The two approaches include a traditional rigid six DoF model and a fully flexible model where all components in the structure are modeled using “Lines” in OrcaFlex and a Craig–Bampton reduction with static improvement method in OpenFAST.
The paper proves that a flexible model is possible, and it provides results comparable to the rigid model. Some differences were observed, primarily the pitch response and natural frequencies, mostly resulting from the flexibility of the tower. This corresponds well to what was expected. Consequently, the dynamic response of the structure becomes different between the two models when exposed to wind and wave loads. In most cases, the loads and moments in the structure increase when using the flexible model.
The comparison between OpenFAST and OrcaFlex shows good agreement both in terms of global motion, loads, and resulting bending moments in the structure. Overall, motions are modeled similarly with very close natural periods, static displacement, and dynamic behavior. The largest difference was observed in the yaw DoF. Tensions in the keel lines showed good agreement, while some difference was observed in the mooring line tension. In the OpenFAST model, several slack events were observed in the lines, which was not observed in the OrcaFlex model. This difference cannot yet be explained, but despite the difference, the global motion is similar, indicating that the difference is related to the mooring line model. Finally, the PSD of the loads at the interface highlighted some difference in the structural damping between the two models.
Since no experimental data are available in the present study, it is not possible to validate the accuracy of the results. A rigid body model has been validated in other studies, giving some confidence in the results. Considering the comparison between the flexible and the rigid models, the results from the flexible models are considered representative and are expected to provide a better description of the response due to the inclusion of more effects (flexibility).
Modeling substructure flexibility is important for calculating loads within the members of the structure. The effect of modeling the substructure flexibility on the loads on the tower, RNA, and mooring system is low in this study, but this likely depends on the substructure (the more structurally flexible it is, the more effect it will have). Also, flexible substructures can be coupled with the wind turbine structural modes changing the overall system dynamics. For example, a relatively soft substructure could be coupled with the first tower bending mode and that would change significantly the dynamic system behavior.
The greatest benefit of using flexible models is the possibility to extract information on local internal loads, e.g., the bending moments, which can be used further in structural design. This paper has illustrated this capability and the agreement between OrcaFlex and OpenFAST, thereby forming the basis for future studies, which can further validate the results.
Author Contributions
Conceptualization, R.B., J.J., A.R., N.M. and J.B.T.; methodology, R.B., J.J., A.R., N.M. and J.B.T.; software, J.B.T., R.B. and J.J.; formal analysis, J.B.T. and R.B.; investigation, J.B.T. and R.B.; resources, C.B., C.G. and H.S.; visualization, J.B.T.; writing—original draft preparation, J.B.T.; writing—review and editing, R.B., J.J., A.R., N.M., J.B.T., C.B., C.G. and H.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partly funded by the Energy Technology Development and Demonstration Program (EUDP) through the project ”TetraSpar” (Grant number 64017-05171). The work was authored in part by the National Renewable Energy Laboratory, operated by the Alliance for Sustainable Energy, LLC, for the U.S. Department of Energy (DOE) under Contract No. DE-AC36-08GO28308. Funding was provided by the U.S. Department of Energy Office of Energy Efficiency and Renewable Energy under a 2018 Technology Commercialization Fund project titled “Demonstration of NREL Modeling Capability to Design the Next Generation of Floating Offshore Wind Turbines”. The views expressed in the article do not necessarily represent the views of the DOE or the U.S. Government. The publisher, by accepting the article for publication, acknowledges that the U.S. Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wind Europe. Our Energy, Our Future; Wind Europe: Brussels, Belgium, 2019. [Google Scholar]
- IRENA. Future of Wind—Deployment, Investment, Technology, Grid Integration and Socio-Economic Aspects; A Global Energy Transformation Paper; International Renewable Energy Agency (IRENA): Abu Dhabi, United Arab Emirates, 2019. [Google Scholar]
- BloombergNEF. New Energy Outlook 2020—Executive Summary; BloombergNEF: London, UK, 2020. [Google Scholar]
- IRENA. World Energy Transistion Outlook—1.5 °C Pathway; International Renewable Energy Agency (IRENA): Abu Dhabi, United Arab Emirates, 2021. [Google Scholar]
- Wind Europe. Floating Offshore Wind Vision Statement; Wind Europe: Brussels, Belgium, 2017. [Google Scholar]
- Wind Europe. Offshore Wind in Europe—Key Trends and Statistics 2018; Wind Europe: Brussels, Belgium, 2019. [Google Scholar]
- Wind Europe. Floating Offshore Wind; Wind Europe: Brussels, Belgium, 2020. [Google Scholar]
- Stiesdal. The TetraSpar Full-Scale Demonstration Project. 2021. Available online: https://www.stiesdal.com/offshore-technologies/the-tetraspar-full-scale-demonstration-project/ (accessed on 5 May 2021).
- Borg, M.; Jensen, M.W.; Urquhart, S.; Andersen, M.T.; Thomsen, J.B.; Stiesdal, H. Technical Definition of the TetraSpar Demonstrator Floating Wind Turbine Foundation. Energies 2020, 13, 4911. [Google Scholar] [CrossRef]
- Borg, M.; Viselli, A.; Allen, C.K.; Fowler, M.; Sigshøj, C.; Grech La Rosa, A.; Andersen, M.T.; Stiesdal, H. Physical Model Testing of the TetraSpar Demo Floating Wind Turbine Prototype. In Proceedings of the ASME 2019 2nd International Offshore Wind Technical Conference (IOWTC), St George’s Bay, St. Julian’s, Malta, 3–6 November 2019; American Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 51975, p. V001T01A024. [Google Scholar]
- Bredmose, H.; Borg, M.; Pegalajar-Jurado, A.; Nielsen, T.R.; Madsen, F.J.; Lomholt, A.K.; Mikkelsen, R.; Mirzaei, M. TetraSpar Floating Wind Turbine Scale Model Testing Summary Report; Technical Report; DTU: Roskilde, Denmark, 2017; Volume 1. [Google Scholar]
- Thomsen, J.B.; Têtu, A.; Andersen, M.T. Experimental Testing of the TetraSpar in Towing and Installation Configuration; Departent of the Built Environment, Aalborg University: Aalborg, Denmark, 2020. [Google Scholar]
- Pereyra, B.T.; Jiang, Z.; Gao, Z.; Andersen, M.T.; Stiesdal, H. Parametric study of a counter weight suspension system for the tetraspar floating wind turbine. In Proceedings of the International Offshore Wind Technical Conference (IOWTC), San Francisco, CA, USA, 4–8 November 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 51975, p. V001T01A003. [Google Scholar]
- Pegalajar-Jurado, A.; Madsen, F.J.; Bredmose, H. Damping Identification of the TetraSpar Floater in Two Configurations with Operational Modal Analysis. In Proceedings of the International Offshore Wind Technical Conference (IOWTC), St George’s Bay, St. Julian’s, Malta, 3–6 November 2019; American Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 51975, p. V001T01A024. [Google Scholar]
- Bach-Gansmo, M.T.; Garvik, S.K.; Thomsen, J.B.; Andersen, M.T. Parametric Study of a Taut Compliant Mooring System for a FOWT Compared to a Catenary Mooring. J. Mar. Sci. Eng. 2020, 8, 431. [Google Scholar] [CrossRef]
- DNV-GL. Position Mooring; DNV-GL Offshore Standard DNVGL-OS-E301; DNV-GL: Høvik, Norway, 2018. [Google Scholar]
- DNV-GL. Environmental Conditions and Environmental Loads; DNV-GL Recommended Practice DNVGL-RP-C205; DNV-GL: Høvik, Norway, 2010. [Google Scholar]
- IEC. Wind Energy Generation Systems—Part 3-2: Design Requirements for Floating Offshore Wind Turbines; International Electrotechnical Commission: Geneva, Switzerland, 2019. [Google Scholar]
- DNV-GL. Floating Wind Turbine Structures; DNV-GL Offshore Standard DNVGL-ST-0119; DNV-GL: Høvik, Norway, 2018. [Google Scholar]
- Morison, J.; Johnson, J.; Schaaf, S.; others. The force exerted by surface waves on piles. J. Pet. Technol. 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Newman, J.N. Marine Hydrodynamics; MIT Press: Cambridge, MA, USA, 1977. [Google Scholar]
- Faltinsen, O. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1993; Volume 1. [Google Scholar]
- Falnes, J. Ocean Waves and Oscillating Systems: Linear Interactions Including Wave-Energy Extraction; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Lee, C.H.; Newman, J.N. WAMIT User Manual; WAMIT, Inc.: Chestnut Hill, MA, USA, 2006. [Google Scholar]
- Wehmeyer, C.; Ferri, F.; Andersen, M.; Refstrup Pedersen, R. Hybrid Model Representation of a TLP Including Flexible Topsides in Non-Linear Regular Waves. Energies 2014, 7, 5047–5064. [Google Scholar] [CrossRef] [Green Version]
- Orcina Ltd. OrcaFlex User Manual; Orcina Ltd.: Ulverston, UK, 2021. [Google Scholar]
- Orcina Ltd. Orcina. 2021. Available online: https://https://www.orcina.com/ (accessed on 5 May 2021).
- National Renewable Energy Laboratory (NREL). OpenFAST. 2021. Available online: https://github.com/OpenFAST/openfast (accessed on 27 August 2021).
- Jonkman, J.M.; Damiani, R.R.; Branlard, E.S.; Hall, M.; Robertson, A.N.; Hayman, G.J. Substructure Flexibility and Member-Level Load Capabilities for Floating Offshore Wind Turbines in OpenFAST. In Proceedings of the International Offshore Wind Technical Conference (IOWTC), St George’s Bay, St. Julian’s, Malta, 3–6 November 2019; American Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 51975, p. V001T01A024
. [Google Scholar]
- Branlard, E.; Hall, M.; Platt, A.; Robertson, A.; Hayman, G.; Jonkman, J. Implementation of Substructure Flexibility and Member-Level Load Capabilities for Floating Offshore Wind Turbines in OpenFAST; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2020. [Google Scholar]
- Jonkman, J. Demonstration of NREL Modeling Capability to Design the Next Generation of Floating Offshore Wind Turbines with Stiesdal and Magellan Wind—Cooperative Research and Development Final Report; Technical Report; National Renewable Energy Laboratory: Golden, CO, USA, 2021. [Google Scholar]
- Jonkman, J.M.; Bergua, R.; Medoza, N.; Robertson, A.; Thomsen, J.B.; Borg, M.; Brown, C.; Galinos, C. Verification of Substructure Flexibility and Member-Level Load Capabilities in OpenFAST Against OrcaFlex for the TetraSpar Floating Offshore Wind Turbine Prototype. In Proceedings of the Wind Energy Science Conference (WESC), Hannover, Germany, 25–28 May 2021. [Google Scholar]
- Thomsen, J.; Têtu, A.; Stiesdal, H. A Comparative Investigation of Prevalent Hydrodynamic Modelling Approaches for Floating OffshoreWind Turbine Foundations: A TetraSpar Case Study. J. Mar. Sci. Eng. 2021, 9, 683. [Google Scholar] [CrossRef]
Figure 1.
Illustration of the TetraSpar FOWT foundation with definition of components and coordinate system. Left: perspective view. Right: top view.
Figure 1.
Illustration of the TetraSpar FOWT foundation with definition of components and coordinate system. Left: perspective view. Right: top view.
Figure 2.
OrcaFlex (left) and OpenFAST (right) models of the TetraSpar FOWT foundation with definition of data sensor locations.
Figure 2.
OrcaFlex (left) and OpenFAST (right) models of the TetraSpar FOWT foundation with definition of data sensor locations.
Figure 3.
Comparison for the static loading condition. The rigid model is modeled in OrcaFlex. (Left) Comparison of displacements. (Right) Comparison of loads at interface and in mooring lines. ML1-3 indicate mooring line tension in line 1-3, while F and M denote force and moment, respectively.
Figure 3.
Comparison for the static loading condition. The rigid model is modeled in OrcaFlex. (Left) Comparison of displacements. (Right) Comparison of loads at interface and in mooring lines. ML1-3 indicate mooring line tension in line 1-3, while F and M denote force and moment, respectively.
Figure 4.
Comparison of free decay tests. (Left) Surge, (Middle) Heave, (Right) Pitch.
Figure 4.
Comparison of free decay tests. (Left) Surge, (Middle) Heave, (Right) Pitch.
Figure 5.
Comparison of natural periods in surge, heave, and pitch. The rigid model is modeled in OrcaFlex.
Figure 5.
Comparison of natural periods in surge, heave, and pitch. The rigid model is modeled in OrcaFlex.
Figure 6.
Comparison of natural periods between OrcaFlex and OpenFAST. FA and SS indicate fore/aft and side/side, respectively.
Figure 6.
Comparison of natural periods between OrcaFlex and OpenFAST. FA and SS indicate fore/aft and side/side, respectively.
Figure 7.
Comparison of motion response of the interface in a regular sea state and with a steady wind load.
Figure 7.
Comparison of motion response of the interface in a regular sea state and with a steady wind load.
Figure 8.
Comparison of the interface moment in a regular sea state and with a steady wind load.
Figure 8.
Comparison of the interface moment in a regular sea state and with a steady wind load.
Figure 9.
Comparison of the keel line tension in a regular sea state and with a steady wind load. Only keel line 1–3 is presented because line 4–6 is identical to 1–3.
Figure 9.
Comparison of the keel line tension in a regular sea state and with a steady wind load. Only keel line 1–3 is presented because line 4–6 is identical to 1–3.
Figure 10.
Internal bending moment in the middle of the different components of the structure. The test is for a regular sea state and with a steady wind load. Data are normalized according to the mean bending moment in the center column in OrcaFlex. Only one of each component type is presented.
Figure 10.
Internal bending moment in the middle of the different components of the structure. The test is for a regular sea state and with a steady wind load. Data are normalized according to the mean bending moment in the center column in OrcaFlex. Only one of each component type is presented.
Figure 11.
Comparison of MPM-values for motion and loads at the RNA and interface. (Left) Motion response. (Right) Load response.
Figure 11.
Comparison of MPM-values for motion and loads at the RNA and interface. (Left) Motion response. (Right) Load response.
Figure 12.
Comparison of MPM-values for keel line tension in an irregular sea state.
Figure 12.
Comparison of MPM-values for keel line tension in an irregular sea state.
Figure 13.
Power spectral density (PSD) of loads at the interface.
Figure 13.
Power spectral density (PSD) of loads at the interface.
Figure 14.
Comparison of mooring line tension. Note that the irregular sea states are different realizations of the same wave spectrum.
Figure 14.
Comparison of mooring line tension. Note that the irregular sea states are different realizations of the same wave spectrum.
Figure 15.
Comparison of six DoF motion of the interface. Note that the irregular sea states are different realizations of the same wave spectrum.
Figure 15.
Comparison of six DoF motion of the interface. Note that the irregular sea states are different realizations of the same wave spectrum.
Table 1.
Cases used for investigation of modeling approaches and comparison between them.
Table 1.
Cases used for investigation of modeling approaches and comparison between them.
| Case | Initial
Conditions | Wind
Conditions | Marine
Conditions | Comparison
Type |
|---|
| Static | - | - | Still water | Static response |
| Surge decay | Surge displacement | - | Still water | Natural frequency |
| Heave decay | Heave displacement | - | Still water | Natural frequency |
| Pitch decay | Pitch displacement | - | Still water | Natural frequency |
| Regular case | - | Steady | Regular waves | Time series, loads, motions |
| Irregular case | - | Time-varying | Irregular waves | Time series, loads, motions |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).