Floating Offshore Vertical Axis Wind Turbines: Opportunities, Challenges and Way Forward
Abstract
:1. Introduction
2. Novelty of the Review
3. Background of VAWT Technology
4. Power Capture
4.1. Power Coefficient
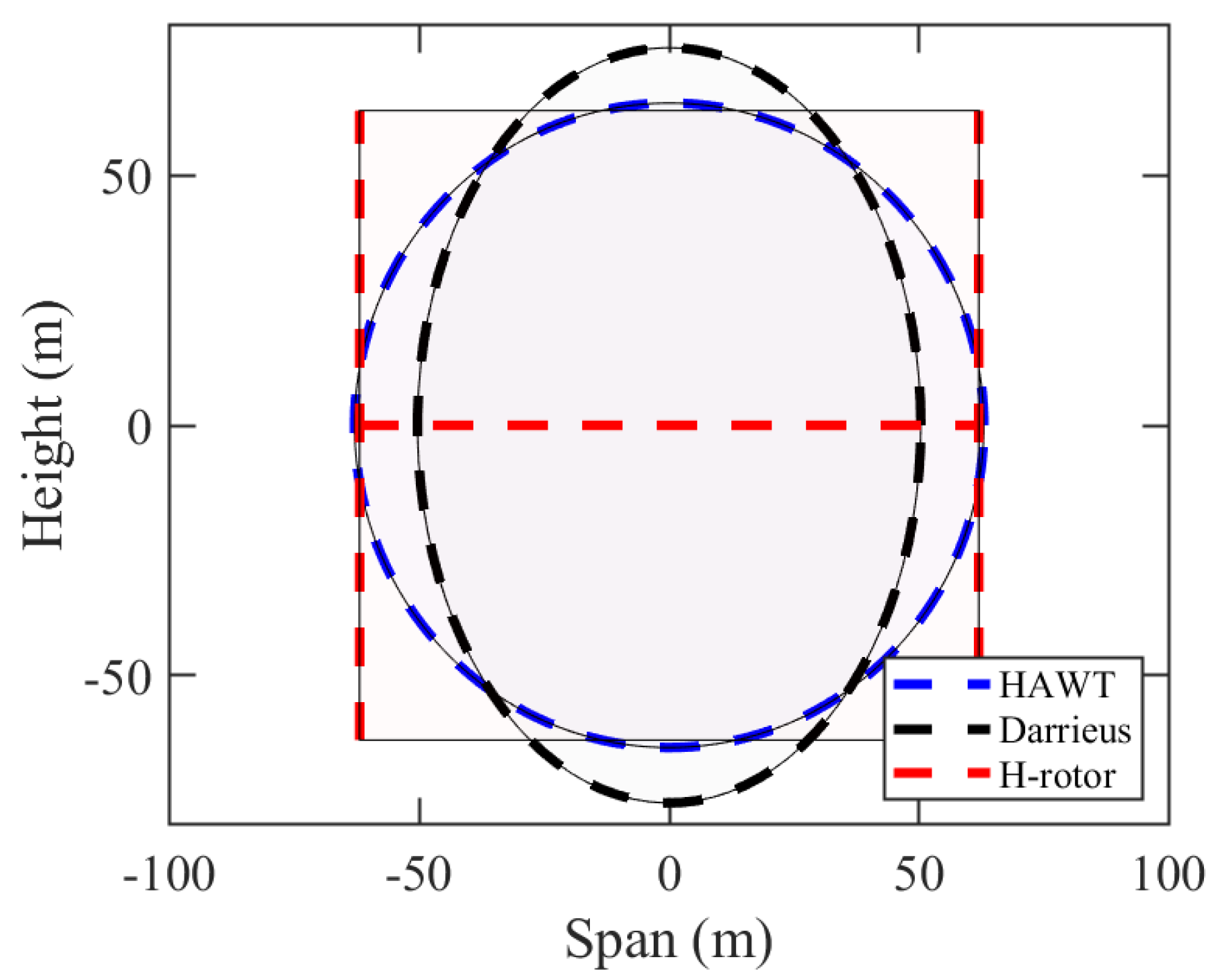
4.2. Swept Area
4.3. Wind Shear Profile
4.4. Orientation of Turbine towards Wind
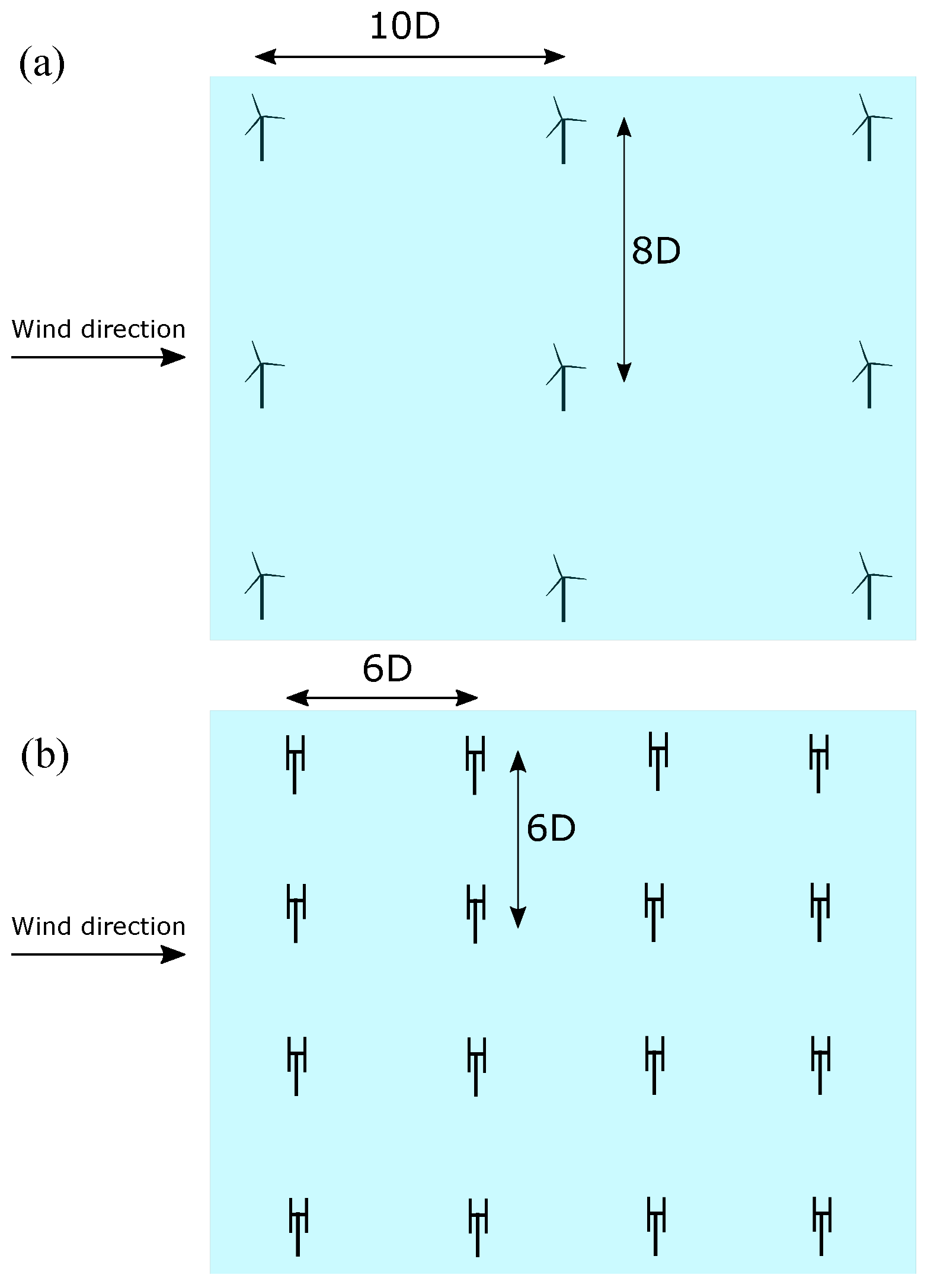
4.5. Wind Farm Power Density
5. Loading Characteristics
6. Floating Structures
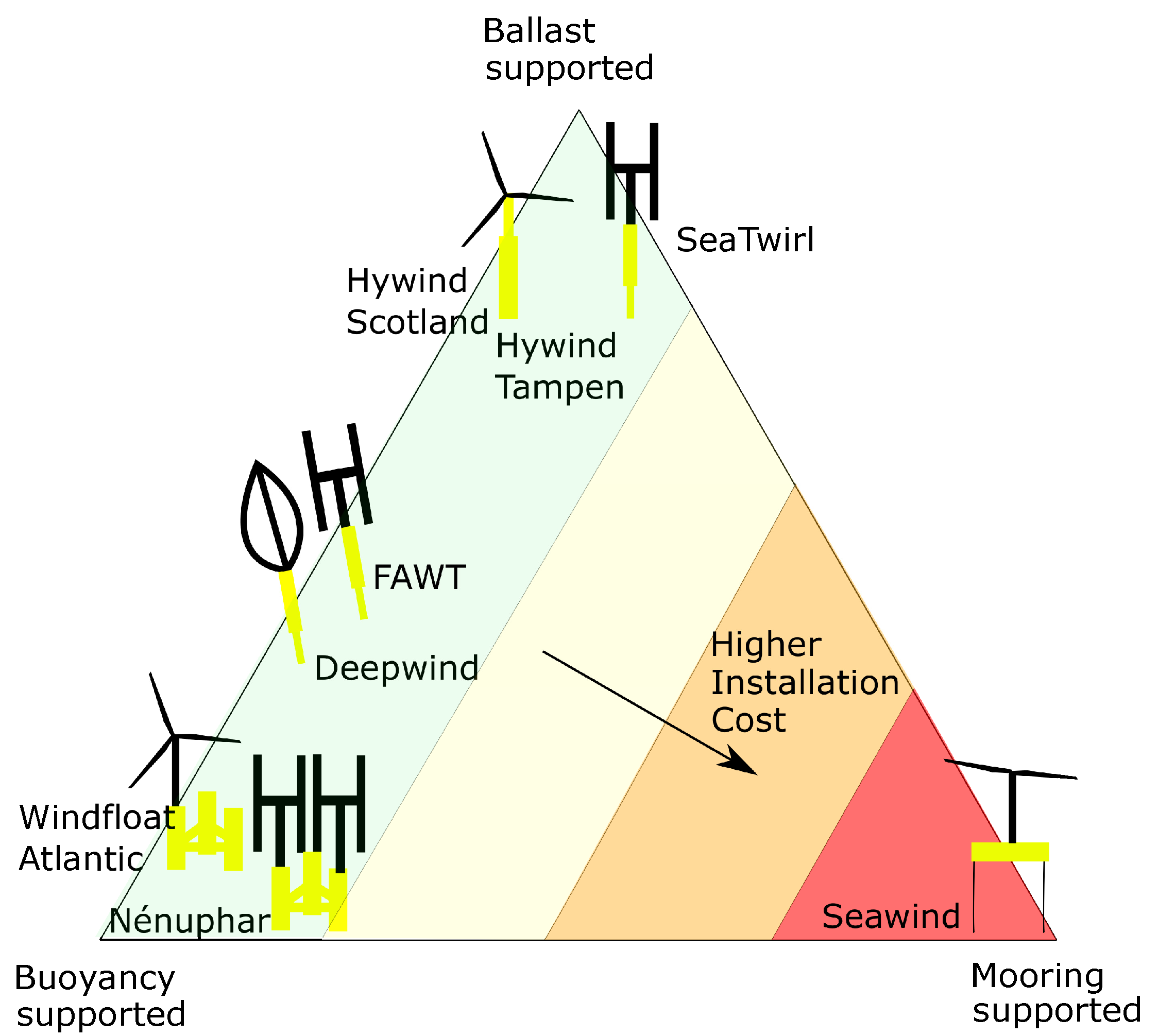
6.1. Types of Floating Structures
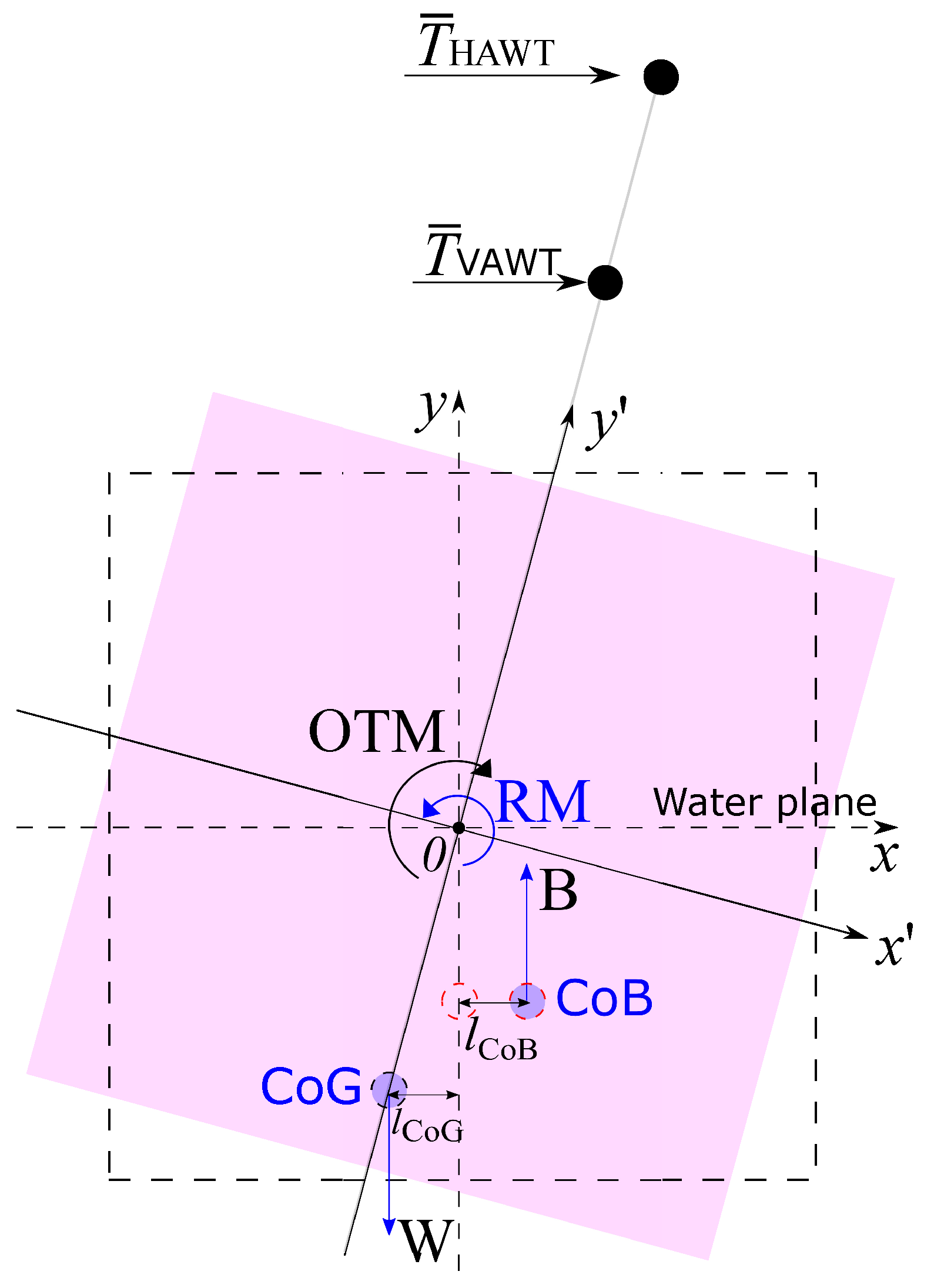
6.2. Stability
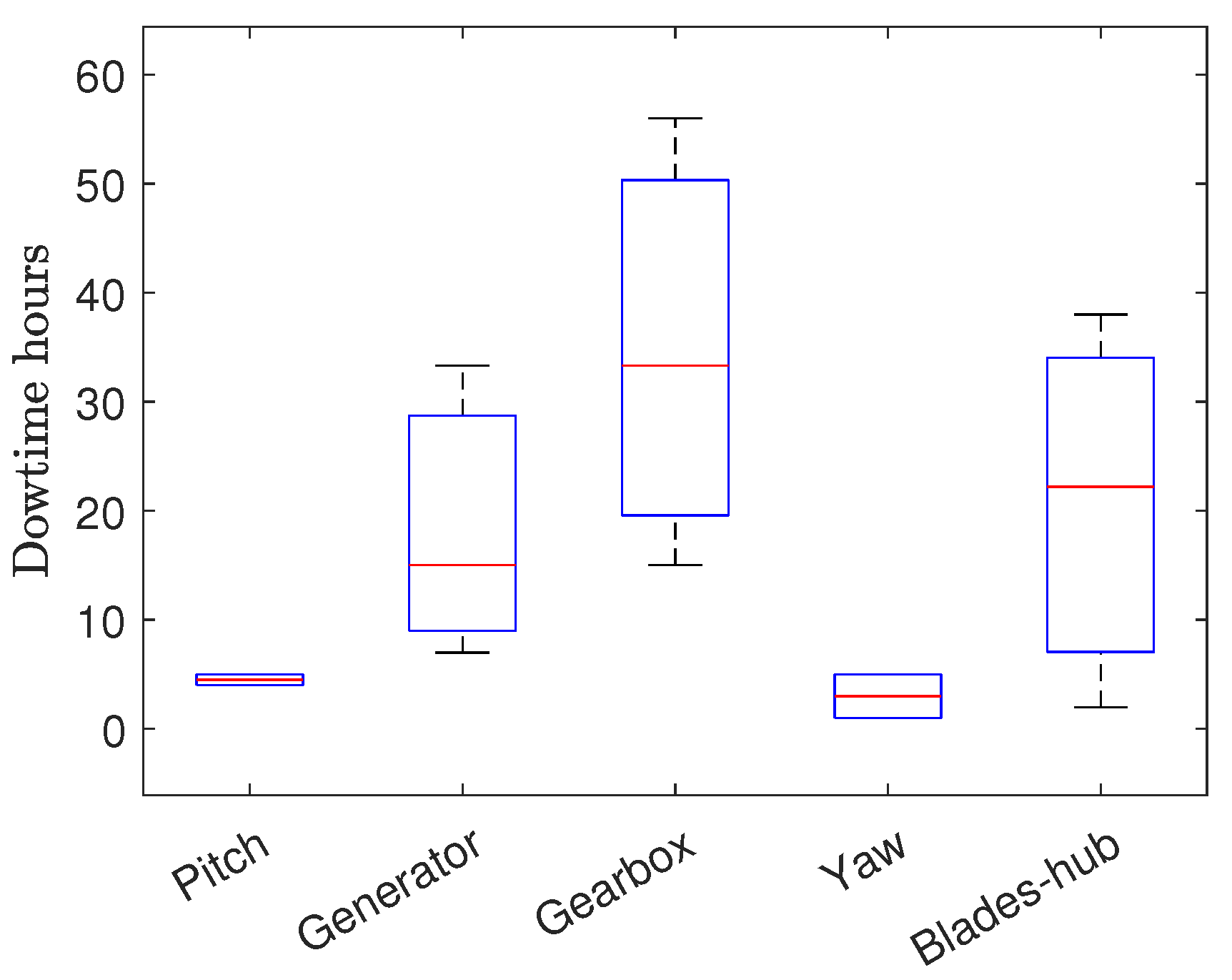
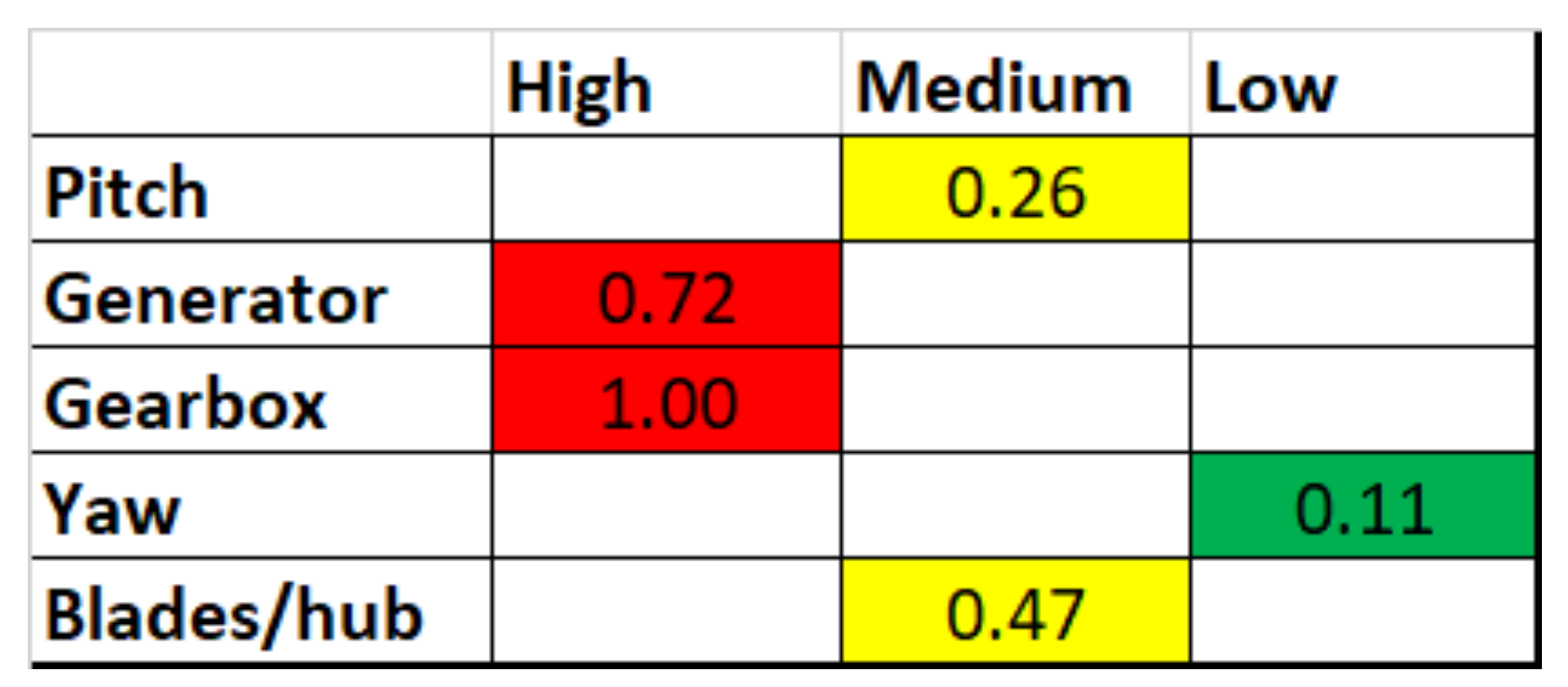
7. Offshore Reliability
8. Environmental Impact and Sustainable Manufacturing
8.1. Environment
8.2. Sustainable Manufacturing
9. Technology Readiness Level (TRL)
10. Way Forward to Increase TRL
11. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| HAWT Parameter | 5 MW | 10 MW | 15 MW |
|---|---|---|---|
| Hub height (m) | 90 | 113 | 125 |
| Diameter (m) | 126 | 169 | 195 |
| Height (m) | 153 | 198 | 223 |
| Blade length (m) | 61.5 | 83 | 95 |
| Swept Area () | 12,469 | 22,444 | 29,926 |
| Rated wind speed (m/s) | 11.4 | 11.7 | 12.0 |
| Thrust (N) | 5.7 | 11 | 15 |
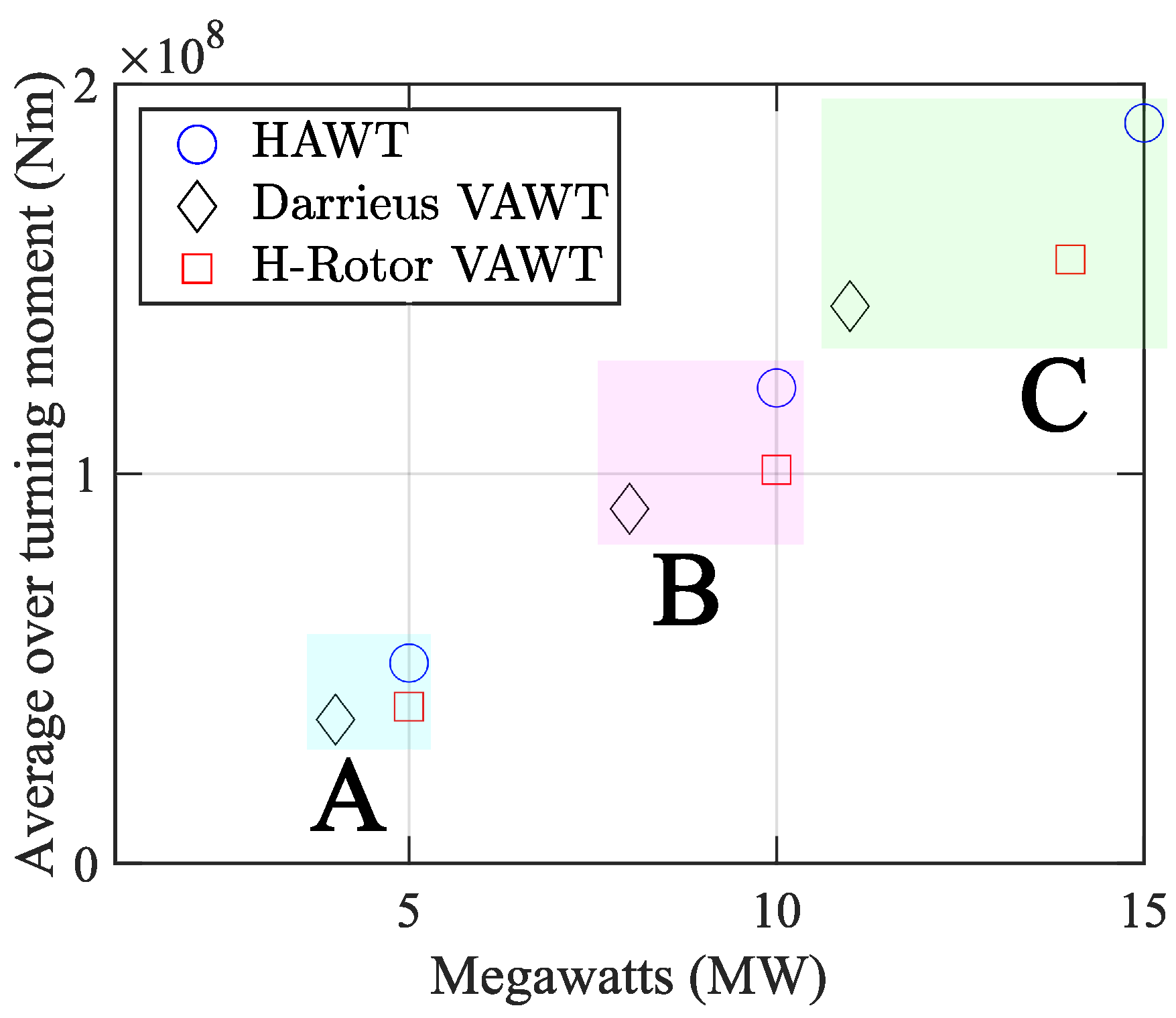
| OTM (Nm) | 5.1 | 12 | 19 |
| HAWT Parameter | 3 MW | 8 MW | 11 MW |
|---|---|---|---|
| Diameter (m) | 101 | 135 | 156 |
| Height (m) | 161 | 213 | 244 |
| Blade length (m) | 200 | 268 | 309 |
| Swept Area () | 11,970 | 21,534 | 28,670 |
| Rated wind speed (m/s) | 11.3 | 11.6 | 11.8 |
| Thrust (N) | 4.3 | 8.2 | 11 |
| OTM (Nm) | 3.7 | 9.1 | 14 |
| HAWT Parameter | 5 MW | 10 MW | 15 MW |
|---|---|---|---|
| Diameter (m) | 126 | 169 | 195 |
| Height (m) | 136 | 179 | 205 |
| Blade length (m) | 126 | 169 | 195 |
| Swept Area () | 15,589 | 28,561 | 38,025 |
| Rated wind speed (m/s) | 11.2 | 11.5 | 11.6 |
| Thrust (N) | 5.5 | 1 | 14 |
| OTM (Nm) | 4.07 | 10 | 16 |
References
- Rodrigues, S.; Restrepo, C.; Kontos, E.; Teixeira Pinto, R.; Bauer, P. Trends of offshore wind projects. Renew. Sustain. Energy Rev. 2015, 49, 1114–1135. [Google Scholar] [CrossRef]
- Higgins, P.; Foley, A. The evolution of offshore wind power in the United Kingdom. Renew. Sustain. Energy Rev. 2014, 37, 599–612. [Google Scholar] [CrossRef]
- Policy Paper. Offshore Wind: Sector Deal. Available online: https://www.gov.uk/government/publications/offshore-wind-sector-deal (accessed on 19 August 2021).
- Press Release. New Plans to Make UK World Leader in Green Energy. Available online: https://www.gov.uk/government/news/new-plans-to-make-uk-world-leader-in-green-energy (accessed on 19 August 2021).
- Danish Energy Agency. Energy Island in the North Sea. Available online: https://ens.dk/en/our-responsibilities/wind-power/energy-islands/energy-island-north-sea (accessed on 14 July 2021).
- China’s First Floating Wind Turbine Heads Offshore. Available online: https://www.offshorewind.biz/2021/07/13/chinas-first-floating-wind-turbine-heads-offshore/ (accessed on 14 July 2021).
- V236-15.0 MW at a Glance. Available online: https://www.vestas.com/en/products/offshore-platforms/ (accessed on 14 July 2021).
- Li, L.; Liu, Y.; Yuan, Z.; Gao, Y. Wind field effect on the power generation and aerodynamic performance of offshore floating wind turbines. Energy 2018, 157, 379–390. [Google Scholar] [CrossRef] [Green Version]
- Griffith, D.T.; Barone, M.F.; Paquette, J.; Owens, B.C.; Bull, D.L.; Simao-Ferriera, C.; Goupee, A.; Fowler, M. Design Studies for Deep-Water Floating Offshore Vertical Axis Wind Turbines; Sandia Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2018. [Google Scholar] [CrossRef] [Green Version]
- Tjiu, W.; Marnoto, T.; Mat, S.; Ruslan, M.H.; Sopian, K. Darrieus vertical axis wind turbine for power generation II: Challenges in HAWT and the opportunity of multi-megawatt Darrieus VAWT development. Renew. Energy 2015, 75, 560–571. [Google Scholar] [CrossRef]
- Eriksson, S.; Bernhoff, H.; Leijon, M. Evaluation of different turbine concepts for wind power. Renew. Sustain. Energy Rev. 2008, 12, 1419–1434. [Google Scholar] [CrossRef]
- Mohan Kumar, P.; Sivalingam, K.; Lim, T.C.; Ramakrishna, S.; Wei, H. Review on the Evolution of Darrieus Vertical Axis Wind Turbine: Large Wind Turbines. Clean Technol. 2019, 1, 205–223. [Google Scholar] [CrossRef] [Green Version]
- Islam, M.; Ting, D.S.K.; Fartaj, A. Aerodynamic models for Darrieus-type straight-bladed vertical axis wind turbines. Renew. Sustain. Energy Rev. 2008, 12, 1087–1109. [Google Scholar] [CrossRef]
- Möllerström, E.; Gipe, P.; Beurskens, J.; Ottermo, F. A historical review of vertical axis wind turbines rated 100 kW and above. Renew. Sustain. Energy Rev. 2019, 105, 1–13. [Google Scholar] [CrossRef]
- 4navitas. Available online: https://www.4navitas.com/ (accessed on 12 June 2021).
- Swift TG Energy. Available online: http://www.swifttgenergy.com/ (accessed on 13 June 2021).
- Shires, A. Design optimisation of an offshore vertical axis wind turbine. Proc. Inst. Civ. Eng.-Energy 2013, 166, 7–18. [Google Scholar] [CrossRef] [Green Version]
- Collu, M.; Brennan, F.; Patel, M. Conceptual design of a floating support structure for an offshore vertical axis wind turbine: The lessons learnt. Ships Offshore Struct. 2014, 9, 3–21. [Google Scholar] [CrossRef]
- Paulsen, U.S.; Madsen, H.A.; Kragh, K.A.; Nielsen, P.H.; Baran, I.; Hattel, J.; Ritchie, E.; Leban, K.; Svendsen, H.; Berthelsen, P.A. DeepWind-from Idea to 5 MW Concept. Energy Procedia 2014, 53, 23–33. [Google Scholar] [CrossRef] [Green Version]
- Floating Wind & Current Hybrid Power Generation [Skwíd]. Available online: https://www.cleanenergy-project.de/wp-content/uploads/2013/06/www.modec.com_fps_skwid_pdf_skwid.pdf (accessed on 18 November 2021).
- Ademe. Vertiwind. Available online: https://www.ademe.fr/sites/default/files/assets/documents/en_vertiwind.pdf (accessed on 12 June 2021).
- SEATWIRL. The Future of Offshore Wind. Available online: https://seatwirl.com/ (accessed on 13 June 2021).
- Akimoto, H.; Tanaka, K.; Uzawa, K. Floating axis wind turbines for offshore power generation—A conceptual study. Environ. Res. Lett. 2011, 6, 044017. [Google Scholar] [CrossRef] [Green Version]
- Akimoto, H.; Iijima, K.; Takata, Y. Feasibility Study of the Floating Axis Wind Turbine: Preliminary Model Experiments. In Proceedings of the 36th International Conference on Offshore Mechanics and Arctic Engineering, Trondheim, Norway, 25–30 June 2017. [Google Scholar] [CrossRef]
- Hand, B.; Kelly, G.; Cashman, A. Aerodynamic design and performance parameters of a lift-type vertical axis wind turbine: A comprehensive review. Renew. Sustain. Energy Rev. 2021, 139, 110699. [Google Scholar] [CrossRef]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Hand Book, 2nd ed.; John Wiley & Sons Ltd.: Chichester, UK, 2011. [Google Scholar]
- Jonkman, J.; Matha, D. Quantitative Comparison of the Responses of Three Floating Platforms; National Renewable Energy Laboratory: Golden, CO, USA, 2010. [Google Scholar]
- Marten, D.; Wendler, J.; Pechlivanoglou, G.; Nayeri, C.; Paschereit, C. QBlade: An open source tool for desing and siulation of a horizontal and vertical axis wind turbines. Int. J. Emerg. Technol. Adv. Eng. 2013, 3, 264–269. [Google Scholar]
- Zanon, A.; De Gennaro, M.; Kühnelt, H. Wind energy harnessing of the NREL 5 MW reference wind turbine in icing conditions under different operational strategies. Renew. Energy 2018, 115, 760–772. [Google Scholar] [CrossRef]
- Ashwill, T.D. Measured Data for the Sandia 34-meter Vertical Axis Wind Turbine; Td Sandia Natl. Lab.: Albuquerque, NM, USA, 1992. [Google Scholar]
- Sutherland, H.J.; Berg, D.E.; Ashwill, T.D. A Retrospective of VAWT Technology; Td Sandia Natl. Lab.: Albuquerque, NM, USA; Livermore, CA, USA, 2012. [Google Scholar]
- Morgan, C.A.; Gardner, P.; Mays, I.D.; Anderson, M.B. The demonstration of a stall regulated 100 kW vertical axis wind turbine. In Proceedings of the European Wind Energy Conference, Glasgow, Scotland, 10–13 July 1989. [Google Scholar]
- Brusca, S.; Lanzafame, R.; Messina, M. Design of a vertical-axis wind turbine: How the aspect ratio affects the turbine’s performance. Int. J. Energy Environ. Eng. 2014, 5, 333–340. [Google Scholar] [CrossRef] [Green Version]
- Rezaeiha, A.; Montazeri, H.; Blocken, B. Characterization of aerodynamic performance of vertical axis wind turbines: Impact of operational parameters. Energy Convers. Manag. 2018, 169, 45–77. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Laboratory: Golden, CO, USA, 2009. [Google Scholar] [CrossRef] [Green Version]
- Schwartz, M.; Heimiller, D.; Haymes, S.; Musial, W. Assessment of Offshore Wind Energy Resources for the United States; National Renewable Energy Laboratory: Golden, CO, USA, 2010. [Google Scholar] [CrossRef] [Green Version]
- Vorpahl, F.; Schwarze, H.; Fischer, T.; Seidel, M.; Jonkman, J. Offshore wind turbine environment, loads, simulation, and design. Wires Energy Environ. 2013, 2, 548–570. [Google Scholar] [CrossRef]
- Golbazi, M.; Archer, C.L. Surface roughness for offshore wind energy. J. Phys. Conf. Ser. 2020, 1452, 012024. [Google Scholar] [CrossRef]
- Sathe, A.; Bierbooms, W. Influence of different wind profiles due to varying atmospheric stability on the fatigue life of wind turbines. J. Phys. Conf. Ser. 2007, 75, 012056. [Google Scholar] [CrossRef] [Green Version]
- Jung, C.; Schindler, D. The role of the power law exponent in wind energy assessment: A global analysis. Int. J. Energy Res. 2021, 45, 8484–8496. [Google Scholar] [CrossRef]
- Howland, M.F.; González, C.M.; Martínez, J.J.P.; Quesada, J.B.; Larrañaga, F.P.; Yadav, N.K.; Chawla, J.S.; Dabiri, J.O. Influence of atmospheric conditions on the power production of utility-scale wind turbines in yaw misalignment. J. Renew. Sustain. Energy 2020, 12, 063307. [Google Scholar] [CrossRef]
- Verelst, D.R.S.; Larsen, T.J.; van Wingerden, J.W. Wind tunnel tests of a free yawing downwind wind turbine. J. Phys. Conf. Ser. 2014, 555, 012103. [Google Scholar] [CrossRef] [Green Version]
- Geos, F. Wind and Wave Frequency Distributions for Sites around the British Isles; Offshore Technology Report; HSE Books: Norwich, UK, 2001. [Google Scholar]
- Leithead, W. Wind energy. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 957–970. [Google Scholar] [CrossRef] [PubMed]
- Dao, C.; Kazemtabrizi, B.; Crabtree, C. Wind turbine reliability data review and impacts on levelised cost of energy. Wind Energy 2019, 22, 1848–1871. [Google Scholar] [CrossRef] [Green Version]
- Müller, S.; Muhawenimana, V.; Wilson, C.A.; Ouro, P. Experimental investigation of the wake characteristics behind twin vertical axis turbines. Energy Convers. Manag. 2021, 247, 114768. [Google Scholar] [CrossRef]
- Dabiri, J.O. Potential order-of-magnitude enhancement of wind farm power density via counter-rotating vertical-axis wind turbine arrays. J. Renew. Sustain. Energy 2011, 3, 043104. [Google Scholar] [CrossRef] [Green Version]
- Abkar, M. Theoretical Modeling of Vertical-Axis Wind Turbine Wakes. Energies 2019, 12, 10. [Google Scholar] [CrossRef] [Green Version]
- Ouro, P.; Lazennec, M. Theoretical modelling of the three-dimensional wake of vertical axis turbines. Flow 2021, 1, E3. [Google Scholar] [CrossRef]
- Musial, W. Offshore wind energy facility characteristics. In Proceedings of the BOEM’s Offshore Wind and Maritime Industry Knowledge Exchange Workshop, Baltimore, MD, USA, 5–6 March 2018. [Google Scholar]
- MacKay, D. Sustainable Energy—Without the Hot Air; UIT Cambridge Ltd.: Cambridge, UK, 2008. [Google Scholar]
- Templin, R.J. Aerodynamic Performance Theory for the NRC Vertical-Axis Wind Turbine; Technical Report LTR-LA-160; National Aeronautical Establishment: Ottawa, ON, Canada, 1974. [Google Scholar]
- Strickland, J.H. A performance prediction model for the darrieus turbine. In Proceedings of the International Symposium on Wind Energy Systems, Cambridege, UK, 7–9 September 1976. [Google Scholar]
- Paraschivoiu, I. Double-Multiple Streamtube Model for Darrieus in Turbines; NASA Lewis Research Center Wind Turbine Dynamics: Cleveland, OH, USA, 1981. [Google Scholar]
- Madsen, H.; Larsen, T.; Vita, L.; Paulsen, U. Implementation of the Actuator Cylinder flow model in the HAWC2 code for aeroelastic simulations on Vertical Axis Wind Turbines. In Proceedings of the 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar] [CrossRef] [Green Version]
- Ning, A. Actuator cylinder theory for multiple vertical axis wind turbines. Wind Energy Sci. 2016, 1, 327–340. [Google Scholar] [CrossRef] [Green Version]
- Meng, F.; Schwarze, H.; Vorpahl, F.; Strobel, M. A free wake vortex lattice model for vertical axis wind turbines: Modeling, verification and validation. J. Phys. Conf. Ser. 2014, 555, 012072. [Google Scholar] [CrossRef] [Green Version]
- Giles, A.D. Wind Panel Manual: Modelling the Aerodynamics of Wind Turbines; University of Strathclyde: Glasgow, UK, 2017. [Google Scholar]
- Hirsch, I.H.; Mandal, A. A Cascade Theory for the Aerodynamic Performance of Darrieus Wind Turbines. Wind Eng. 1987, 11, 164–175. [Google Scholar]
- Bensason, D.; Fouest, S.L.; Young, A.; Mulleners, K. Greenberg’s force prediction for vertical-axis wind turbine blades. arXiv 2021, arXiv:2111.00871. [Google Scholar]
- Hansen, J.T.; Mahak, M.; Tzanakis, I. Numerical modelling and optimization of vertical axis wind turbine pairs: A scale up approach. Renew. Energy 2021, 171, 1371–1381. [Google Scholar] [CrossRef]
- Su, J.; Li, Y.; Chen, Y.; Han, Z.; Zhou, D.; Zhao, Y.; Bao, Y. Aerodynamic performance assessment of φ-type vertical axis wind turbine under pitch motion. Energy 2021, 225, 120202. [Google Scholar] [CrossRef]
- Collu, M.; Borg, M.; Shires, A.; Brennan, F.P. FloVAWT: Progress on the Development of a Coupled Model of Dynamics for Floating Offshore Vertical Axis Wind Turbines. In Proceedings of the 32nd International Conference on Offshore Mechanics and Arctic Engineering, Nantes, France, 9–14 June 2013. [Google Scholar] [CrossRef]
- Hand, B.; Cashman, A.; Kelly, G. A Low-Order Model for Offshore Floating Vertical Axis Wind Turbine Aerodynamics. IEEE Trans. Ind. Appl. 2017, 53, 512–520. [Google Scholar] [CrossRef]
- Cheng, Z.; Madsen, H.A.; Gao, Z.; Moan, T. A fully coupled method for numerical modeling and dynamic analysis of floating vertical axis wind turbines. Renew. Energy 2017, 107, 604–619. [Google Scholar] [CrossRef]
- LeBlanc, B.P.; Ferreira, C.S. Experimental Determination of Thrust Loading of a 2-Bladed Vertical Axis Wind Turbine. J. Phys. Conf. Ser. 2018, 1037, 022043. [Google Scholar] [CrossRef] [Green Version]
- Delafin, P.L.; Nishino, T.; Wang, L.; Kolios, A. Effect of the number of blades and solidity on the performance of a vertical axis wind turbine. J. Phys. Conf. Ser. 2016, 753, 022033. [Google Scholar] [CrossRef] [Green Version]
- Borg, M.; Collu, M. A comparison between the dynamics of horizontal and vertical axis offshore floating wind turbines. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140076. [Google Scholar] [CrossRef] [Green Version]
- Butterfield, S.; Musial, W.; Jonkman, J.; Sclavounos, P. Engineering Challenges for Floating Offshore Wind Turbines. In Proceedings of the Copenhagen Offshore Wind Conference, Copenhagen, Denmark, 26–28 October 2005. [Google Scholar]
- Seawind. Available online: https://seawindtechnology.com/ (accessed on 27 June 2021).
- Laura, C.S.; Vicente, D.C. Life-cycle cost analysis of floating offshore wind farms. Renew. Energy 2014, 66, 41–48. [Google Scholar] [CrossRef]
- Ultra-Deep Water Port: Feasibility Study. Available online: https://www.gov.scot/publications/ultra-deep-water-feasibility-study-report/pages/5/ (accessed on 3 September 2021).
- Next Step for Hywind Tampen. Available online: https://www.equinor.com/en/news/20210422-next-step-hywind-tampen.html (accessed on 3 September 2021).
- Tupper, E.C. Introduction to Naval Architecture, 5th ed.; Butterworth-Heinemann: Jersey City, NJ, USA, 2013. [Google Scholar]
- Martin, R.; Lazakis, I.; Barbouchi, S.; Johanning, L. Sensitivity analysis of offshore wind farm operation and maintenance cost and availability. Renew. Energy 2016, 85, 1226–1236. [Google Scholar] [CrossRef] [Green Version]
- Dinwoodie, I.; McMillan, D.; Quail, F. Analysis of offshore wind turbine operation and maintenance using a novel time domain meteo-ocean modeling approach. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012. [Google Scholar]
- Carroll, J.; McDonald, A.; McMillan, D. Failure rate, repair time and unscheduled O&M cost analysis of offshore wind turbines. Wind Energy 2016, 19, 1107–1119. [Google Scholar] [CrossRef] [Green Version]
- Artigao, E.; Martín-Martínez, S.; Honrubia-Escribano, A.; Gómez-Lázaro, E. Wind turbine reliability: A comprehensive review towards effective condition monitoring development. Appl. Energy 2018, 228, 1569–1583. [Google Scholar] [CrossRef]
- Kails, K.; Li, Q.; Mueller, M. A modular and cost-effective high-temperature superconducting generator for large direct-drive wind turbines. IET Renew. Power Gener. 2021, 15, 2022–2032. [Google Scholar] [CrossRef]
- Manning, P.T. The Environmental Impact of the Use of Large Wind Turbines. Wind Eng. 1983, 7, 1–11. [Google Scholar]
- Drewitt, A.L.; Langston, R.H.W. Assessing the impacts of wind farms on birds. Ibis 2006, 148, 29–42. [Google Scholar] [CrossRef]
- Islam, M.; Mekhilef, S.; Saidur, R. Progress and recent trends of wind energy technology. Renew. Sustain. Energy Rev. 2013, 21, 456–468. [Google Scholar] [CrossRef]
- Dabiri, J.O.; Greer, J.R.; Koseff, J.R.; Moin, P.; Peng, J. A new approach to wind energy: Opportunities and challenges. AIP Conf. Proc. 2015, 1652, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Santangeli, A.; Katzner, T. A call for conservation scientists to evaluate opportunities and risks from operation of vertical axis wind turbines. Front. Ecol. Evol. 2015, 3, 68. [Google Scholar] [CrossRef] [Green Version]
- Hüppop, O.; Dierschke, J.; Exo, K.M.; Fredrich, E.; Hill, R. Bird migration studies and potential collision risk with offshore wind turbines. Ibis 2006, 148, 90–109. [Google Scholar] [CrossRef]
- Marques, A.T.; Batalha, H.; Rodrigues, S.; Costa, H.; Pereira, M.J.R.; Fonseca, C.; Mascarenhas, M.; Bernardino, J. Understanding bird collisions at wind farms: An updated review on the causes and possible mitigation strategies. Biol. Conserv. 2014, 179, 40–52. [Google Scholar] [CrossRef]
- Wang, S.; Wang, S.; Smith, P. Ecological impacts of wind farms on birds: Questions, hypotheses, and research needs. Renew. Sustain. Energy Rev. 2015, 44, 599–607. [Google Scholar] [CrossRef]
- Tomaszewski, J.M.; Lundquist, J.K.; Churchfield, M.J.; Moriarty, P.J. Do wind turbines pose roll hazards to light aircraft? Wind Energy Sci. 2018, 3, 833–843. [Google Scholar] [CrossRef] [Green Version]
- Howell, R.; Qin, N.; Edwards, J.; Durrani, N. Wind tunnel and numerical study of a small vertical axis wind turbine. Renew. Energy 2010, 35, 412–422. [Google Scholar] [CrossRef] [Green Version]
- ACT Blade: The Lightest and Most Controllable Wind Turbine Blade. Available online: https://www.innoenergy.com/discover-innovative-solutions/product-portfolio/act-blade/ (accessed on 24 May 2021).
- Bank, L.C.; Arias, F.R.; Yazdanbakhsh, A.; Gentry, T.R.; Al-Haddad, T.; Chen, J.F.; Morrow, R. Concepts for Reusing Composite Materials from Decommissioned Wind Turbine Blades in Affordable Housing. Recycling 2018, 3, 3. [Google Scholar] [CrossRef] [Green Version]
- Blonk, D.L. Conceptual Design and Evaluation of Economic Feasibility of Floating Vertical Axis Wind Turbines. Master’s Thesis, TU Delft, Delft, The Netherlands, 2010. [Google Scholar]
- CATAPULT. Offshore Renewable Energy. Interactive Guide. Available online: https://guidetoanoffshorewindfarm.com/guide (accessed on 16 July 2021).
- EMEC. The European Marine Energy Centre LTD. Available online: http://www.emec.org.uk/services/pathway-to-emec/technology-readiness-levels/ (accessed on 16 July 2021).
- Gambuzza, S.; Ganapathisubramani, B. The effects of free-stream turbulence on the performance of a model wind turbine. J. Renew. Sustain. Energy 2021, 13, 023304. [Google Scholar] [CrossRef]
- Young, A.M.; Smyth, A.S.M. Gust–Airfoil Coupling with a Loaded Airfoil. AIAA J. 2021, 59, 773–785. [Google Scholar] [CrossRef]
- Jones, A.R.; Cetiner, O.; Smith, M.J. Physics and Modeling of Large Flow Disturbances: Discrete Gust Encounters for Modern Air Vehicles. Annu. Rev. Fluid Mech. 2022, 54, 469–493. [Google Scholar] [CrossRef]
- Salter, S.H.; Taylor, J.R.M. Vertical-axis tidal-current generators and the Pentland Firth. Proc. Inst. Mech. Eng. Part A J. Power Energy 2007, 221, 181–199. [Google Scholar] [CrossRef]
- Zhao, R.; Creech, A.C.W.; Borthwick, A.G.L.; Venugopal, V.; Nishino, T. Aerodynamic Analysis of a Two-Bladed Vertical-Axis Wind Turbine Using a Coupled Unsteady RANS and Actuator Line Model. Energies 2020, 13, 776. [Google Scholar] [CrossRef] [Green Version]
- Arredondo-Galeana, A.; Young, A.M.; Smyth, A.S.; Viola, I.M. Unsteady load mitigation through a passive trailing-edge flap. J. Fluids Struct. 2021, 106, 103352. [Google Scholar] [CrossRef]
- Hoerner, S.; Abbaszadeh, S.; Cleynen, O.; Bonamy, C.; Maître, T.; Thévenin, D. Passive flow control mechanisms with bioinspired flexible blades in cross-flow tidal turbines. Exp. Fluids 2021, 62, 104. [Google Scholar] [CrossRef]
- Pisetta, G.; Le Mestre, R.; Viola, I.M. Morphing blades for tidal turbines: A theoretical study. Renew. Energy 2021, in press. [Google Scholar] [CrossRef]




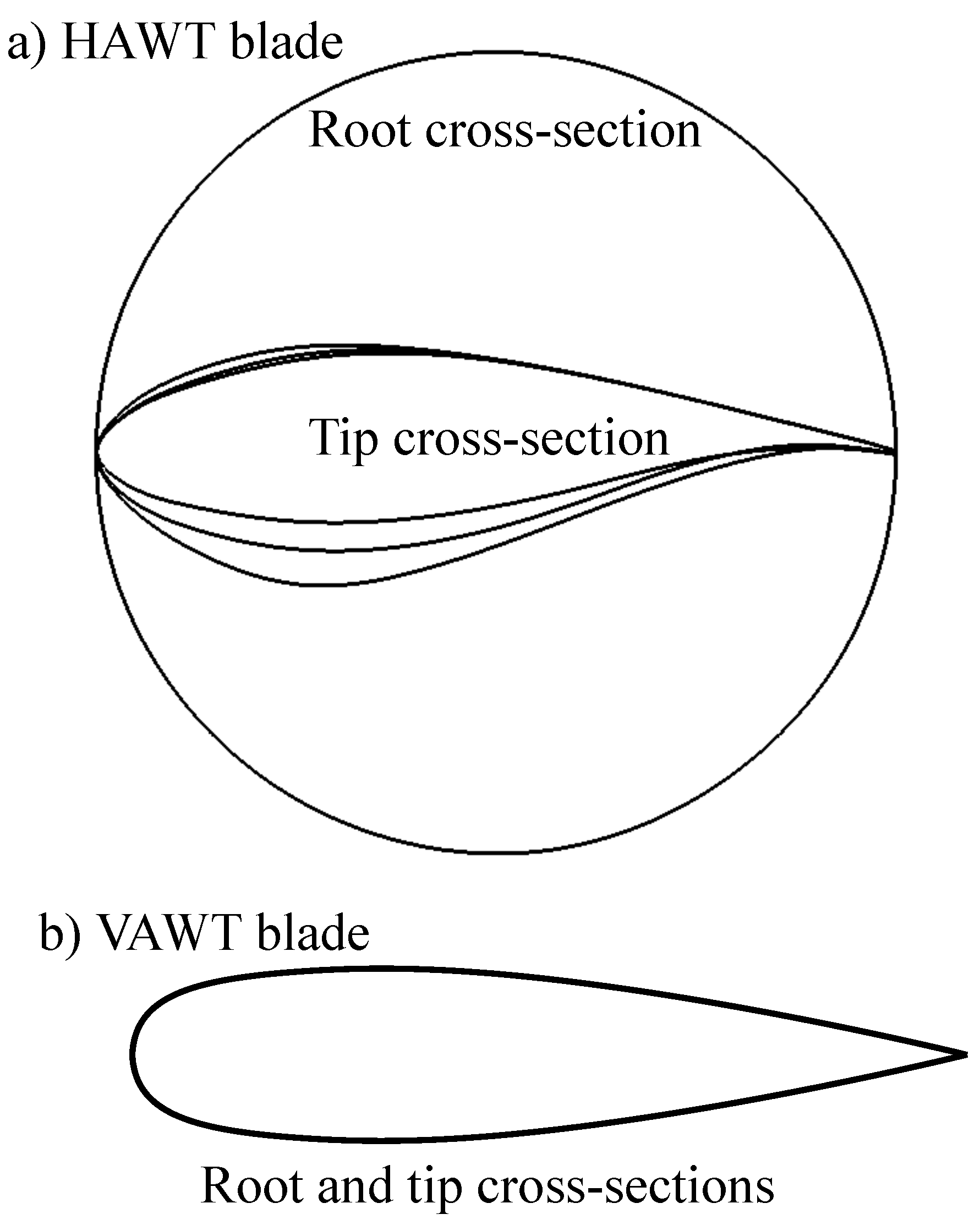

| Name of Turbine | Type of Turbine | Country | Years Active | Reference |
|---|---|---|---|---|
| Nova | V-shape VAWT | UK | 2009–2010 | [17,18] |
| Deepwind | Curved-bladed Darrieus | Denmark | 2010–2014 | [19] |
| Floating axis | Straight/curved-bladed Darrieus | Japan | 2011–ongoing | [23,24] |
| Skwid | Straight bladed Darrieus | Japan | 2013–2015 | [20] |
| Vertiwind | H-rotor | France | 2011–2018 | [21] |
| SeaTwirl | Straight-bladed Darrieus | Sweden | 2012–ongoing | [22] |
| Turbine | Power Rating | Type of Turbine | Data from | ||
|---|---|---|---|---|---|
| NREL | 5 MW | HAWT | 0.49 | 8.0 | Qblade simulation |
| NREL | 5 MW | HAWT | 0.48 | 7.9 | Zanon et al. [29] |
| Sandia 34 m | 500 KW | VAWT-Darrieus | 0.40 | 6.1 | Sandia report [30,31] |
| Musgrove | 100 KW | VAWT-H-rotor | 0.40 | 3.8 | Eriksson et al. [11] |
| HAWT Uniform Thrust | Suggested by Howland et al. [41] | VAWT Theoretical | |
|---|---|---|---|
| [] | |||
| ±5 | 0.99 | 0.99 | 1.00 |
| ±10 | 0.96 | 0.97 | 1.00 |
| ±15 | 0.90 | 0.93 | 1.00 |
| ±20 | 0.83 | 0.88 | 1.00 |
| ±25 | 0.74 | 0.82 | 1.00 |
| ±30 | 0.65 | 0.75 | 1.00 |
| Turbine Component | Subcomponent | Floating HAWT | Floating VAWT | ||
|---|---|---|---|---|---|
| 5 MW | 10 MW | 5 MW | 10 MW | ||
| Nacelle and hub | Bed plate | 8 | 7 | 6 | 6 |
| Main bearing | 8 | 7 | 3 | 3 | |
| Main shaft | 8 | 7 | 6 | 6 | |
| Gearbox | 8 | 7 | 6 | 6 | |
| Generator | 8 | 7 | 6 | 6 | |
| Power take-off | 8 | 7 | 3 | 3 | |
| Control system | 8 | 7 | 3 | 3 | |
| Yaw system | 8 | 7 | N/A | N/A | |
| Yaw bearing | 8 | 7 | N/A | N/A | |
| Spinner | 8 | 7 | N/A | N/A | |
| Blades | Blades | 8 | 7 | 6 | 6 |
| Blade bearings | 8 | 7 | 6 | 6 | |
| Pitch system | 8 | 7 | 6 | 6 | |
| Tower | Steel | 8 | 7 | 6 | 6 |
| Tower internals | 8 | 7 | 6 | 6 | |
| Full system | Turbine + floating structure | 8 | 7 | 3 | 2 |
| Area of Research | Subcategory | Specific Topics |
|---|---|---|
| Fluid and structure interactions | VAWT turbulence interactions | Turbulence scale and intensity |
| VAWT wave interactions | Directional waves, extreme waves | |
| VAWT gust encounters | Fatigue life, control strategies | |
| Mechanical design | Bearingless solutions | Salter’s turbine Akimoto’s turbine |
| Advanced materials | Morphing blades Variable stiffness moorings | Smart materials Smart materials |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arredondo-Galeana, A.; Brennan, F. Floating Offshore Vertical Axis Wind Turbines: Opportunities, Challenges and Way Forward. Energies 2021, 14, 8000. https://doi.org/10.3390/en14238000
Arredondo-Galeana A, Brennan F. Floating Offshore Vertical Axis Wind Turbines: Opportunities, Challenges and Way Forward. Energies. 2021; 14(23):8000. https://doi.org/10.3390/en14238000
Chicago/Turabian StyleArredondo-Galeana, Abel, and Feargal Brennan. 2021. "Floating Offshore Vertical Axis Wind Turbines: Opportunities, Challenges and Way Forward" Energies 14, no. 23: 8000. https://doi.org/10.3390/en14238000
APA StyleArredondo-Galeana, A., & Brennan, F. (2021). Floating Offshore Vertical Axis Wind Turbines: Opportunities, Challenges and Way Forward. Energies, 14(23), 8000. https://doi.org/10.3390/en14238000







