Electrohydrodynamic Enhancement of Phase Change Material Melting in Circular-Elliptical Annuli
Abstract
:1. Introduction
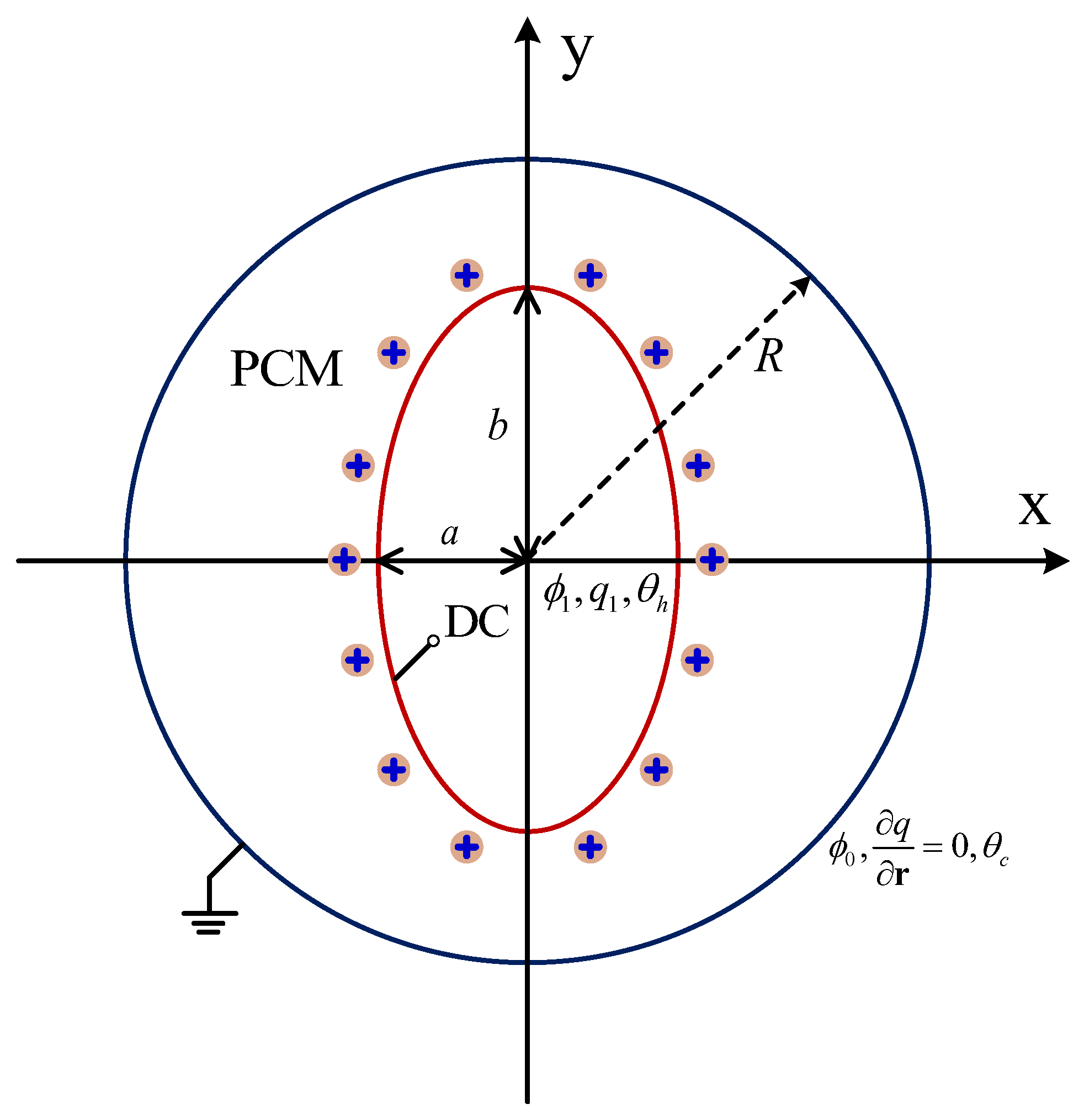
2. Physical Statement and Governing Equations
3. The Lattice Boltzmann Equations
3.1. Lattice Boltzmann Equation for Flow Field
3.2. Lattice Boltzmann Equation for Electric Potential
3.3. Lattice Boltzmann Equation for Charge Density
3.4. Lattice Boltzmann Equation for Temperature Field
3.5. Boundary Treatment
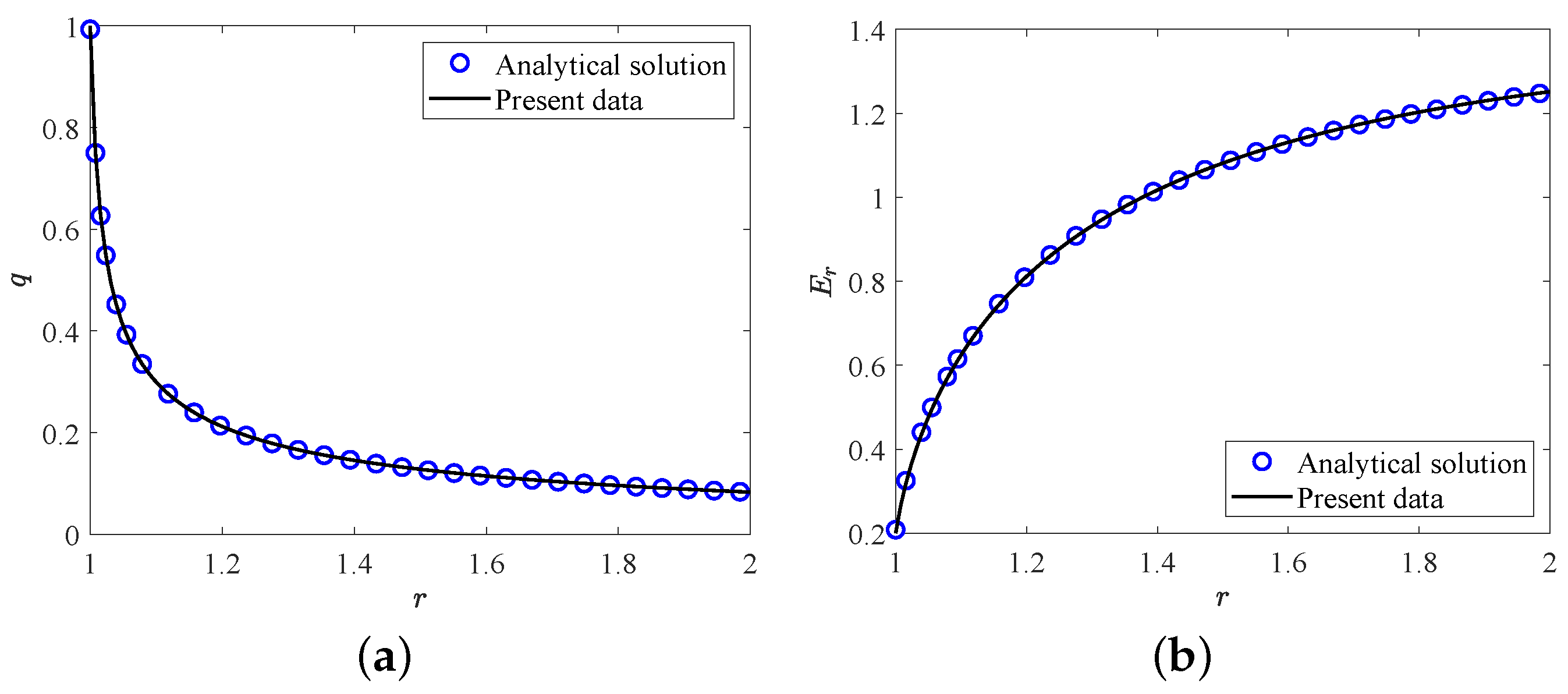
4. Code and Results Verifications
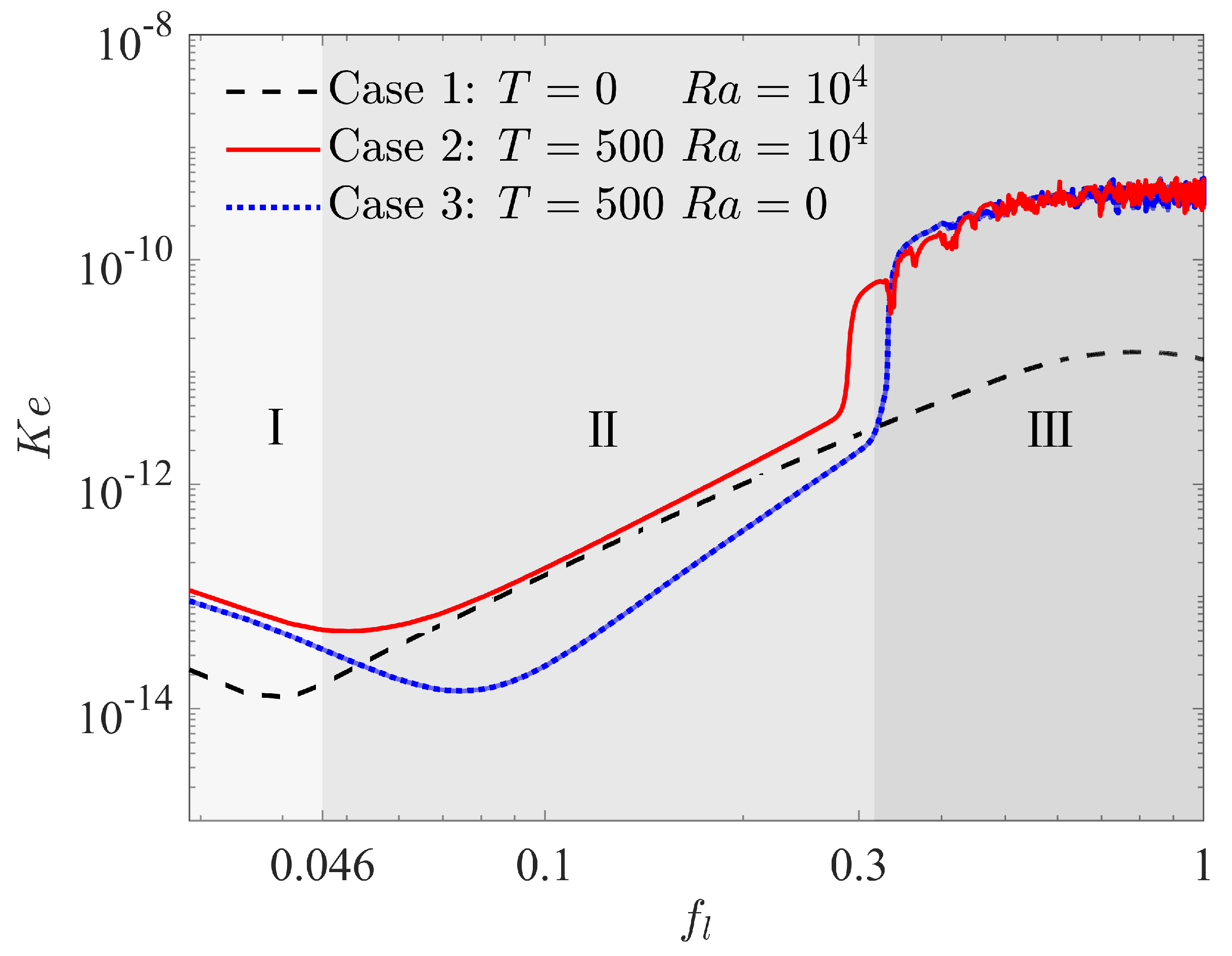
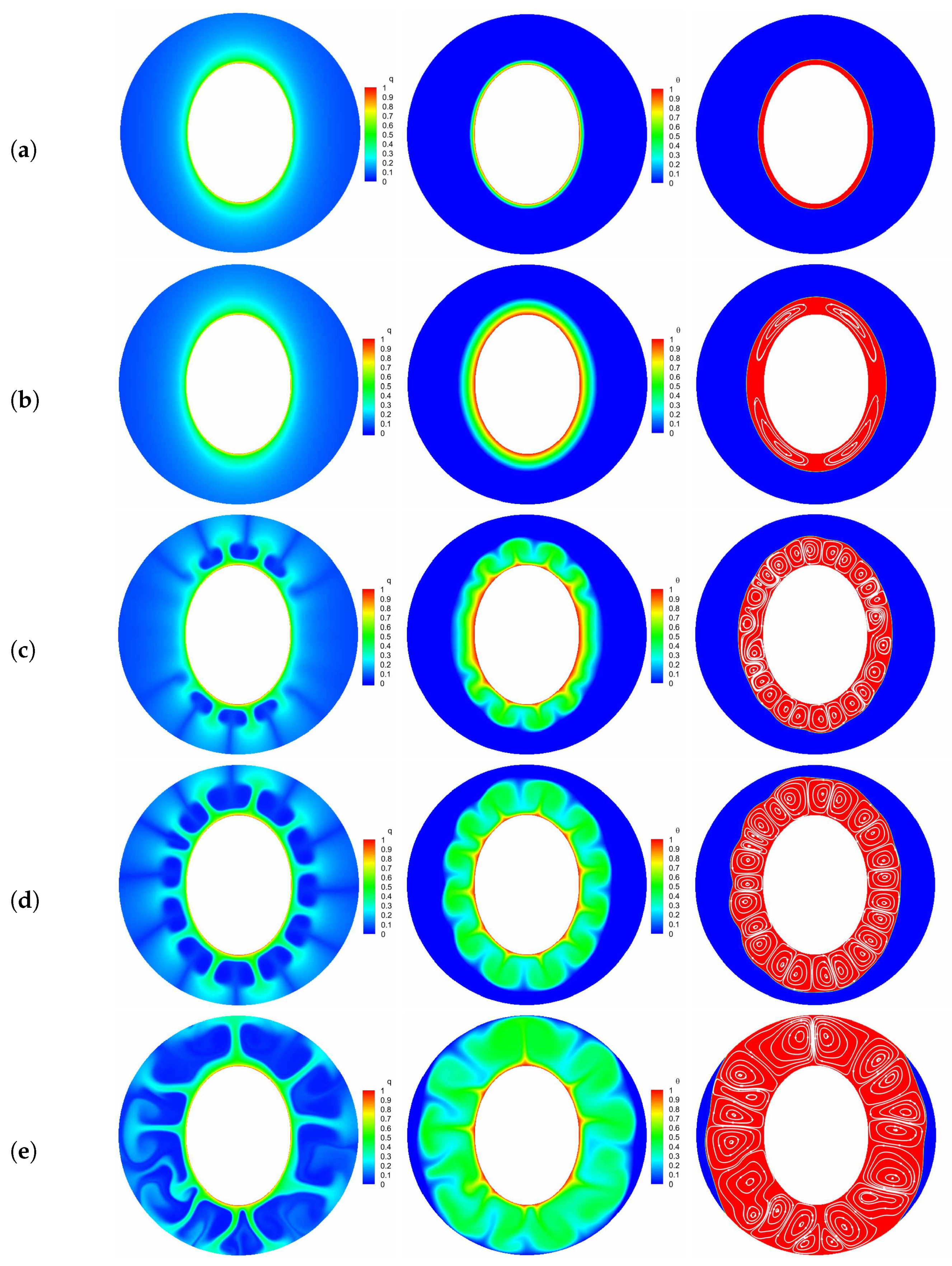
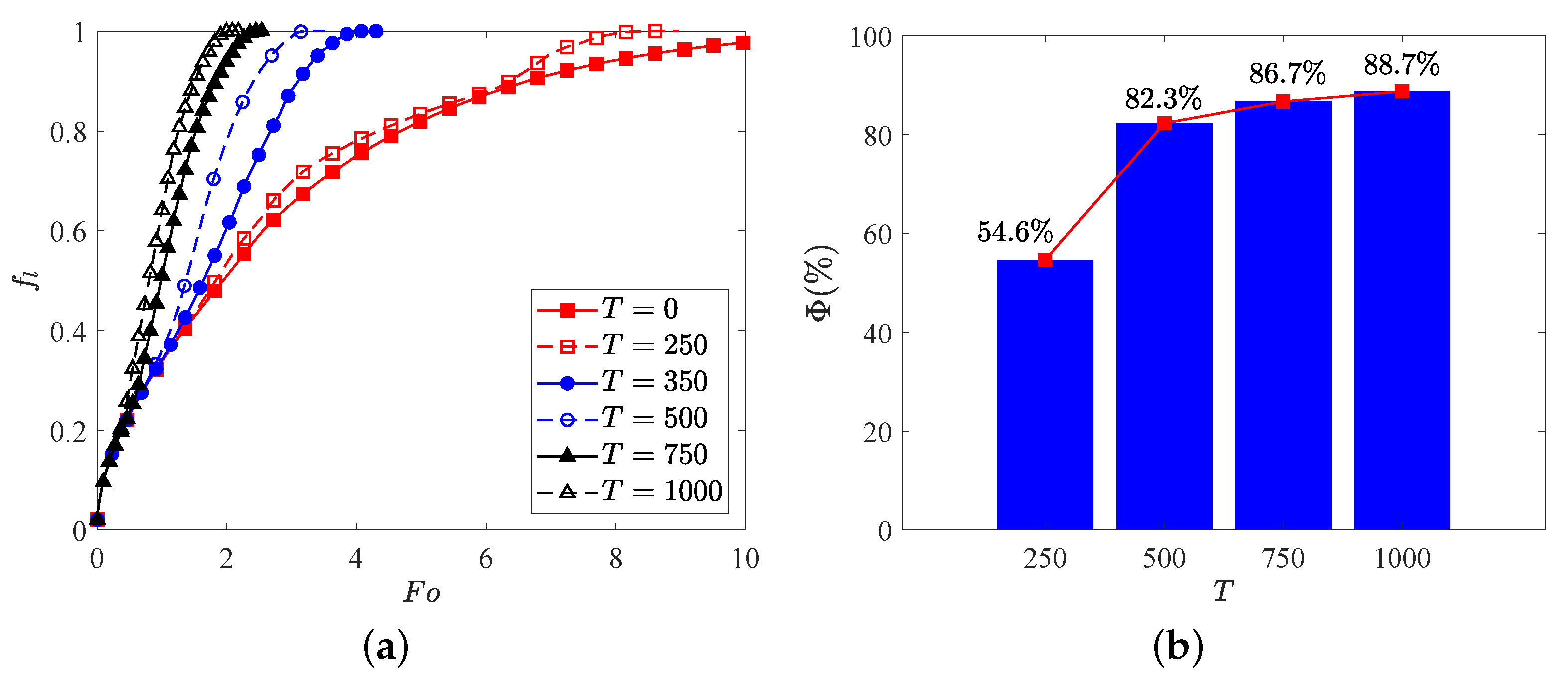
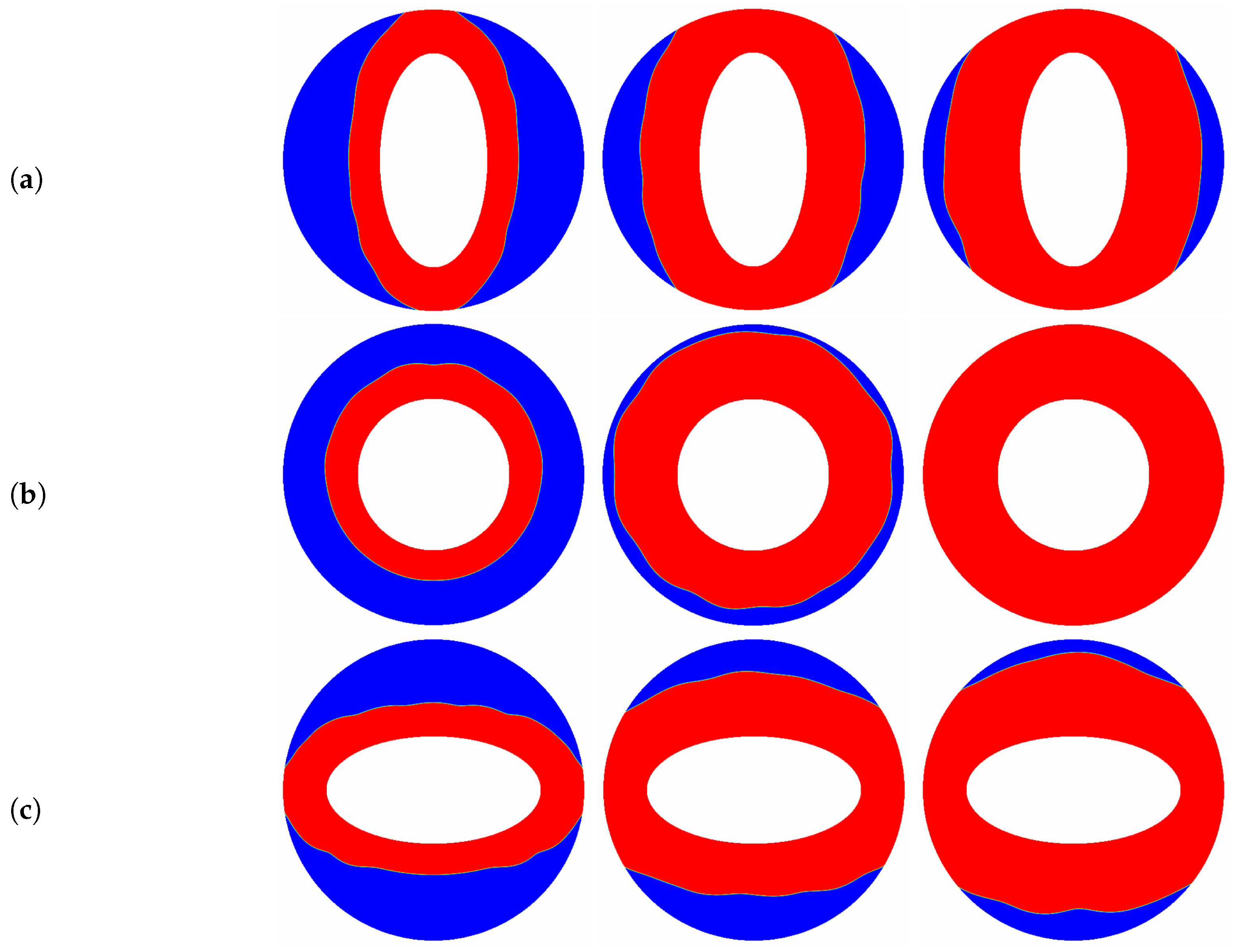
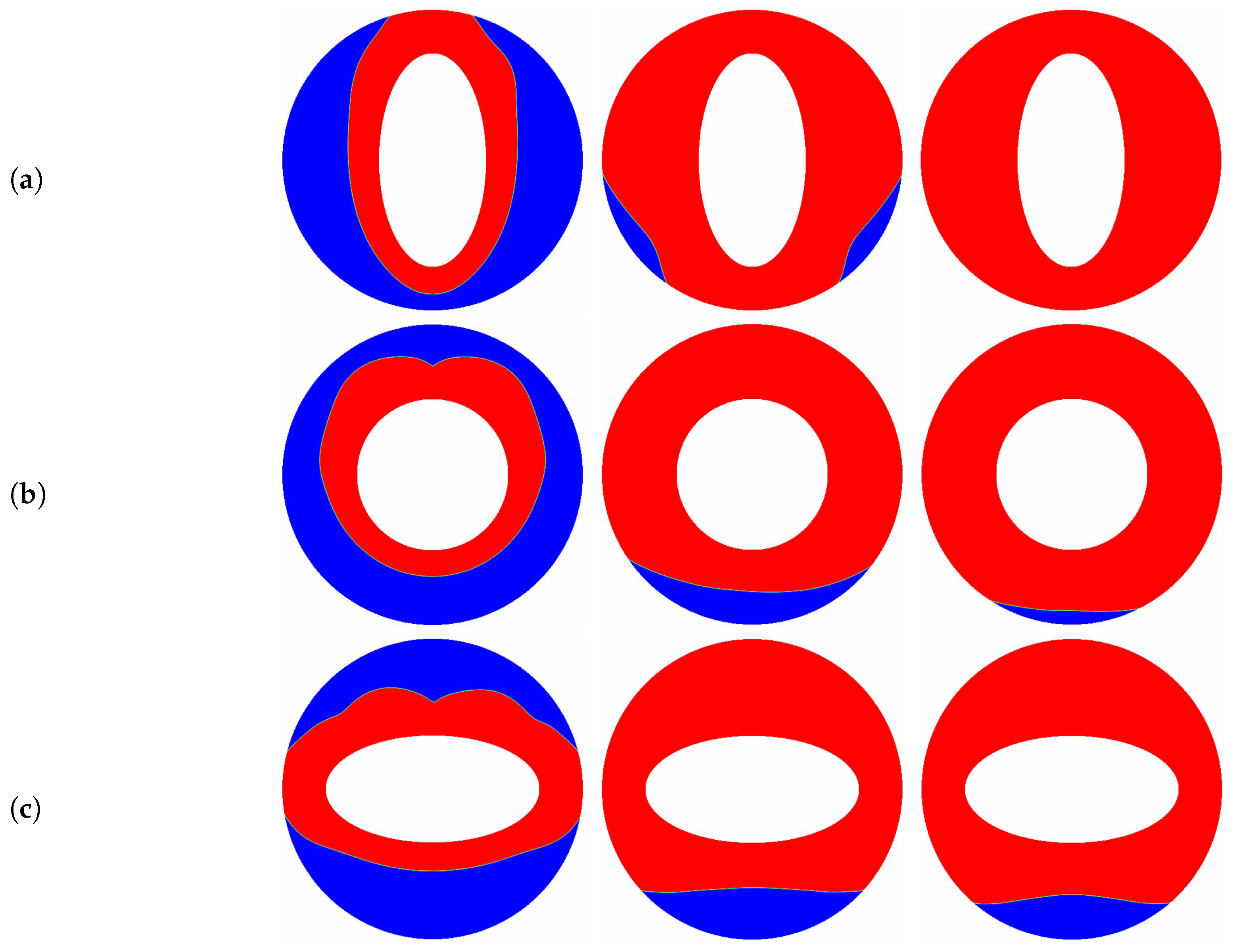
5. Results and Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Numerical Procedure for the Present Work
References
- Zalba, B.; Marın, J.M.; Cabeza, L.F.; Mehling, H. Review on thermal energy storage with phase change: Materials, heat transfer analysis and applications. Appl. Therm. Eng. 2003, 23, 251–283. [Google Scholar] [CrossRef]
- Kenisarin, M.; Mahkamov, K. Solar energy storage using phase change materials. Renew. Sustain. Energy Rev. 2007, 11, 1913–1965. [Google Scholar] [CrossRef]
- Sharma, A.; Tyagi, V.V.; Chen, C.; Buddhi, D. Review on thermal energy storage with phase change materials and applications. Renew. Sustain. Energy Rev. 2009, 13, 318–345. [Google Scholar] [CrossRef]
- Tomita, S.; Celik, H.; Mobedi, M. Thermal analysis of solid/liquid phase change in a cavity with one wall at periodic temperature. Energies 2021, 14, 5957. [Google Scholar] [CrossRef]
- Khudhair, A.M.; Farid, M.M. A review on energy conservation in building applications with thermal storage by latent heat using phase change materials. Energy Convers. Manag. 2004, 45, 263–275. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Jafaryar, M.; Shafee, A.; Babazadeh, H. Acceleration of discharge process of clean energy storage unit with insertion of porous foam considering nanoparticle enhanced paraffin. J. Clean. Prod. 2020, 261, 121206. [Google Scholar] [CrossRef]
- Kalbasi, R.; Salimpour, M.R. Constructal design of phase change material enclosures used for cooling electronic devices. Appl. Therm. Eng. 2015, 87, 339–349. [Google Scholar] [CrossRef]
- Atkin, P.; Farid, M.M. Improving the efficiency of photovoltaic cells using PCM infused graphite and aluminum fins. Sol. Energy 2015, 114, 217–228. [Google Scholar] [CrossRef]
- Mat, S.; Al-Abidi, A.A.; Sopian, K.; Sulaiman, M.Y.; Mohammad, A.T. Enhance heat transfer for PCM melting in triplex tube with internal-external fins. Energy Convers. Manag. 2013, 74, 223–236. [Google Scholar] [CrossRef]
- Darzi, A.A.R.; Jourabian, M.; Farhadi, M. Melting and solidification of PCM enhanced by radial conductive fins and nanoparticles in cylindrical annulus. Energy Convers. Manag. 2016, 118, 253–263. [Google Scholar] [CrossRef]
- Zeng, Y.; Fan, L.; Xiao, Y. An experimental investigation of melting of nanoparticle-enhanced phase change materials (NePCMs) in a bottom-heated vertical cylindrical cavity. Int. J. Heat Mass Transf. 2013, 66, 111–117. [Google Scholar] [CrossRef]
- Khodadadi, M.; Sheikholeslami, M. Heat transfer efficiency and electrical performance evaluation of photovoltaic unit under influence of NEPCM. Int. J. Heat Mass Transf. 2021, 122232. [Google Scholar] [CrossRef]
- Abdi, A.; Shahrooz, M.; Chiu, J.N.W. Experimental investigation of solidification and melting in a vertically finned cavity. Appl. Therm. Eng. 2021, 198, 117459. [Google Scholar] [CrossRef]
- Shatikian, V.; Ziskind, G.; Letan, R. Numerical investigation of a PCM-based heat sink with internal fins. Int. J. Heat Mass Transf. 2005, 48, 3689–3706. [Google Scholar] [CrossRef]
- Zhang, P.; Meng, Z.; Zhu, H. Experimental and numerical study of heat transfer characteristics of a paraffin/metal foam composite PCM. Energy Procedia 2015, 75, 3091–3097. [Google Scholar] [CrossRef] [Green Version]
- Velraj, R.; Seeniraj, R.V.; Hafner, B.; Faber, C.; Schwarzer, K. Heat transfer enhancement in a latent heat storage system. Sol. Energy 1999, 65, 171–180. [Google Scholar] [CrossRef]
- Nakhla, D.; Cotton, J.S. Effect of electrohydrodynamic (EHD) forces on charging of a vertical latent heat thermal storage module filled with octadecane. Int. J. Heat Mass Transf. 2021, 167, 120828. [Google Scholar] [CrossRef]
- Wu, W.; Liu, N.; Cheng, W.; Liu, Y. Study on the effect of shape-stabilized phase change materials on spacecraft thermal control in extreme thermal environment. Energy Convers. Manag. 2013, 69, 174–180. [Google Scholar] [CrossRef]
- Setareh, M.; Saffar-Avval, M.; Abdullah, A. Experimental and numerical study on heat transfer enhancement using ultrasonic vibration in a double-pipe heat exchanger. Appl. Therm. Eng. 2019, 159, 113867. [Google Scholar] [CrossRef]
- Shi, E.; Zonouzi, S.A.; Aminfar, H.; Mohammadpourfard, M. Enhancement of the performance of a NEPCM filled shell-and-multi tube thermal energy storage system using magnetic field: A numerical study. Appl. Therm. Eng. 2020, 178, 115604. [Google Scholar] [CrossRef]
- Al Omari, S.A.B.; Ghazal, A.M.; Elnajjar, E.; Qureshi, Z.A. Vibration-enhanced direct contact heat exchange using gallium as a solid phase change material. Int. Commun. Heat Mass Transf. 2021, 120, 104990. [Google Scholar] [CrossRef]
- Nakhla, D.; Sadek, H.; Cotton, J.S. Melting performance enhancement in latent heat storage module using solid extraction electrohydrodynamics (EHD). Int. J. Heat Mass Transf. 2015, 81, 695–704. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, X.; Xu, X.; Lin, X.; Liu, L. A review on the effect of external fields on solidification, melting and heat transfer enhancement of phase change materials. J. Energy Storage 2020, 31, 101567. [Google Scholar] [CrossRef]
- Seyed-Yagoobi, J.; Bryan, J.E. Enhancement of heat transfer and mass transport in single-phase and two-phase flows with electrohydrodynamics. Adv. Heat Transf. 1999, 33, 95–186. [Google Scholar]
- McCluskey, F.M.J.; Atten, P.; Perez, A.T. Heat transfer enhancement by electroconvection resulting from an injected space charge between parallel plates. Int. J. Heat Mass Transf. 1991, 34, 2237–2250. [Google Scholar] [CrossRef]
- Worraker, W.J.; Richardson, A.T. The effect of temperature-induced variations in charge carrier mobility on a stationary electrohydrodynamic instability. J. Fluid Mech. 1979, 93, 29–45. [Google Scholar] [CrossRef]
- Castellanos, A.; Velarde, M.G. Electrohydrodynamic stability in the presence of a thermal gradient. Phys. Fluids 1981, 24, 1784. [Google Scholar] [CrossRef]
- Wu, J.; Traoré, P.; Zhang, M.; Pérez, A.T.; Vázquez, P.A. Charge injection enhanced natural convection heat transfer in horizontal concentric annuli filled with a dielectric liquid. Int. J. Heat Mass Transf. 2016, 92, 139–148. [Google Scholar] [CrossRef]
- Hassen, W.; Oztop, H.F.; Kolsi, L.; Borjini, M.N.; Abu-Hamdeh, N. Analysis of the electro-thermo-convection induced by a strong unipolar injection between two concentric or eccentric cylinders. Numer. Heat Tranf. A Appl. 2017, 71, 789–804. [Google Scholar] [CrossRef]
- Rashidi, S.H.; Bafekr, R.; Masoodi, R.; Languri, E.M. EHD in thermal energy systems—A review of the applications, modelling, and experiments. J. Electrostat. 2017, 90, 1–14. [Google Scholar] [CrossRef]
- Heidarinejad, G.; Babaei, R. Numerical investigation of electrohydrodynamics (EHD) enhanced water evaporation using Large Eddy Simulation turbulent model. J. Electrostat. 2015, 77, 76–87. [Google Scholar] [CrossRef]
- Gao, M.; Cheng, P.; Quan, X. An experimental investigation on effects of an electric field on bubble growth on a small heater in pool boiling. Int. J. Heat Mass Transf. 2013, 67, 987–991. [Google Scholar] [CrossRef]
- Sadek, H.; Ching, C.Y.; Cotton, J. The effect of pulsed electric fields on horizontal tube side convective condensation. Int. J. Heat Mass Transfer. 2010, 53, 3721–3732. [Google Scholar] [CrossRef]
- Nakhla, D.; Thompson, E.; Lacroix, B.; Cotton, J.S. Measurement of heat transfer enhancement in melting of n-Octadecane under gravitational and electrohydrodynamics (EHD) forces. J. Electrostat. 2018, 92, 31–37. [Google Scholar] [CrossRef]
- Sun, Z.; Yang, P.; Luo, K.; Wu, J. Experimental investigation on the melting characteristics of n-octadecane with electric field inside macrocapsule. Int. J. Heat Mass Transfer. 2021, 173, 121238. [Google Scholar] [CrossRef]
- Luo, K.; Pérez, A.T.; Wu, J.; Yi, H.; Tan, H. Efficient lattice Boltzmann method for electrohydrodynamic solid-liquid phase change. Phys. Rev. E 2019, 100, 013306. [Google Scholar] [CrossRef] [PubMed]
- Selvakumar, R.D.; Qiang, L.; Luo, K.; Traoré, P.; Wu, J. Numerical modeling of solid-liquid phase change under the influence an external electric field. Int. J. Multiph. Flow 2021, 136, 103550. [Google Scholar] [CrossRef]
- He, K.; Guo, X.; Zhang, X.; Wang, L. Numerical investigation of electrohydrodynamic solid-liquid phase change in square enclosure. Acta Phys. Sin. 2021, 70, 149101. [Google Scholar]
- Dhaidan, N.S.; Khodadadi, J.M. Melting and convection of phase change materials in different shape containers: A review. Renew. Sustain. Energy Rev. 2015, 43, 449–477. [Google Scholar] [CrossRef] [Green Version]
- Hassen, W.; Elkhazen, M.I.; Traore, P.; Borjini, M.N. Charge injection in horizontal eccentric annuli filled with a dielectric liquid. Eur. J. Mech. B/Fluids 2018, 72, 691–700. [Google Scholar] [CrossRef]
- Lu, C.; Luo, K.; Zhou, P.; Yi, H. Lattice Boltzmann analysis for electro-thermo-convection with a melting boundary in horizontal concentric annuli. Phys. Fluids 2021, 33, 043605. [Google Scholar] [CrossRef]
- Schulenberg, F.J. Finned elliptical tubes and their application in air-cooled heat exchangers. ASME J. Eng. Ind. 1966, 88, 176–186. [Google Scholar] [CrossRef]
- Chang, T.; Yeh, W. Theoretical investigation into condensation heat transfer on horizontal elliptical tube in stationary saturated vapor with wall suction. Appl. Therm. Eng. 2011, 31, 946–953. [Google Scholar] [CrossRef]
- Wang, X.; Djakovic, U.; Bao, H. Experimental evaluation of heat transfer performance under natural and forced convection around a phase change material encapsulated in various shapes. Sustain. Energy Technol. Assess. 2021, 44, 101025. [Google Scholar] [CrossRef]
- Léal, L.; Miscevic, M.; Lavieille, P.; Amokrane, M.; Pigache, F.; Topin, F.; Nogarède, B.; Tadrist, L. An overview of heat transfer enhancement methods and new perspectives: Focus on active methods using electroactive materials. Int. J. Heat Mass Transf. 2013, 61, 505–524. [Google Scholar] [CrossRef]
- Huang, R.; Wu, H.; Cheng, P. A new lattice Boltzmann model for solid-liquid phase change. Int. J. Heat Mass Transf. 2013, 59, 295–301. [Google Scholar] [CrossRef]
- Li, Q.; Luo, K.; Kang, Q.; He, Y.; Chen, Q.; Liu, Q. Lattice boltzmann methods for multi-phase flow and phase-change heat transfer. Prog. Energy Combust. Sci. 2016, 52, 62–105. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; He, K.; Wang, L. Pore-Scale Investigation on Natural Convection Melting in a Square Cavity with Gradient Porous Media. Energies 2021, 14, 4274. [Google Scholar] [CrossRef]
- Luo, K.; Wu, J.; Yi, H.; Tan, H. Lattice Boltzmann model for Coulomb-driven flows in dielectric liquids. Phys. Rev. E 2016, 93, 023309. [Google Scholar] [CrossRef] [PubMed]
- Luo, K.; Wu, J.; Yi, H.; Tan, H. Lattice Boltzmann modelling of electro-thermo-convection in a planar layer of dielectric liquid subjected to unipolar injection and thermal gradient. Int. J. Heat Mass Transf. 2016, 103, 832–846. [Google Scholar] [CrossRef]
- He, K.; Chai, Z.; Wang, L.; Ma, B.; Shi, B. Numerical investigation of electro-thermo-convection with a solid-liquid interface via the lattice Boltzmann method. Phys. Fluids 2021, 33, 037128. [Google Scholar] [CrossRef]
- Wang, L.; Wei, Z.; Li, T.; Chai, Z.; Shi, B. A lattice Boltzmann modelling of electrohydrodynamic conduction phenomenon in dielectric liquids. Appl. Math. Model. 2021, 95, 361–378. [Google Scholar] [CrossRef]
- Guo, Z.; Shi, B.; Wang, N. Lattice BGK model for incompressible Navier–Stokes equation. J. Comput. Phys. 2000, 165, 288–306. [Google Scholar] [CrossRef]
- Lu, C.L.; Luo, K.; Zhou, P.C.; Yi, H.L. Rayleigh-Bénard convection in a dielectric fluid under an external electric field with a melting boundary. Phys. Rev. Fluids 2021, 6, 063504. [Google Scholar] [CrossRef]
- Kenisarin, M.M. Thermophysical properties of some organic phase change materials for latent heat storage. A review. Sol. Energy 2014, 107, 553–575. [Google Scholar] [CrossRef]
- Felici, N. Phénomènes hydro et aérodynamiques dans la conduction des diélectriques fluides. Rev. Gen. Electr. 1969, 78, 717–734. [Google Scholar]
- Atten, P. Electrohydrodynamic instability and motion induced by injected space charge in insulating liquids. IEEE Trans. Dielectr. Electr. Insul. 1996, 3, 1–17. [Google Scholar] [CrossRef]
- Qian, Y.; d’Humiéres, D.; Lallemand, P. Lattice BGK models for Navier-Stokes equation. Europhys. Lett. 1992, 17, 479. [Google Scholar] [CrossRef]
- Guo, Z.; Zheng, C.; Shi, B. Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys. Rev. E 2002, 65, 046308. [Google Scholar] [CrossRef] [PubMed]
- Chai, Z.; Shi, B. A novel lattice Boltzmann model for the Poisson equation. Appl. Math. Model. 2008, 32, 2050–2058. [Google Scholar] [CrossRef]
- Lu, J.; Lei, H.; Dai, C. An optimal two-relaxation-time lattice Boltzmann equation for solid-liquid phase change: The elimination of unphysical numerical diffusion. Int. J. Therm. Sci. 2019, 135, 17–29. [Google Scholar] [CrossRef]
- Huang, R.; Wu, H. Total enthalpy-based lattice Boltzmann method with adaptive mesh refinement for solid-liquid phase change. J. Comput. Phys. 2016, 315, 65–83. [Google Scholar] [CrossRef]
- Guo, Z.; Zheng, C.; Shi, B. An extrapolation method for boundary conditions in lattice Boltzmann method. Phys. Fluids 2002, 14, 2007–2010. [Google Scholar] [CrossRef]
- Mencinger, J. Numerical simulation of melting in two-dimensional cavity using adaptive grid. J. Comput. Phys. 2004, 198, 243–264. [Google Scholar] [CrossRef]
- Wu, J.; Vázquez, P.A.; Traoré, P.; Pérez, A.T. Finite amplitude electroconvection induced by strong unipolar injection between two coaxial cylinders. Phys. Fluids 2014, 26, 124105. [Google Scholar] [CrossRef]
- Bazai, H.; Moghimi, M.A.; Mohammed, H.I. Numerical study of circular-elliptical double-pipe thermal energy storage systems. J. Energy Storage 2020, 30, 101440. [Google Scholar] [CrossRef]




| Grid Resolution | |||
|---|---|---|---|
| Total melting time | 2.0407 | 1.9970 | 1.9894 |
| Averaged maximum velocity | 104.4851 | 97.7858 | 96.3265 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, K.; Wang, L.; Huang, J. Electrohydrodynamic Enhancement of Phase Change Material Melting in Circular-Elliptical Annuli. Energies 2021, 14, 8090. https://doi.org/10.3390/en14238090
He K, Wang L, Huang J. Electrohydrodynamic Enhancement of Phase Change Material Melting in Circular-Elliptical Annuli. Energies. 2021; 14(23):8090. https://doi.org/10.3390/en14238090
Chicago/Turabian StyleHe, Kun, Lei Wang, and Jiangxu Huang. 2021. "Electrohydrodynamic Enhancement of Phase Change Material Melting in Circular-Elliptical Annuli" Energies 14, no. 23: 8090. https://doi.org/10.3390/en14238090





