A Comparative Analysis of Energy Consumption by Conventional and Anchor Based Dynamic Positioning of Ship
Abstract
:1. Introduction
- The place of the test –> in this case it is the UPS switchboard,
- Determination what the test concerns –> 230 V UPS power rail,
- A section specifying the expected impact of a power failure on devices connected to the particular power rail, e.g., specifying that in the event of a power failure to the joystick system, no impact on the dynamic positioning system is expected.
- –
- wind speed,
- –
- the power of thrusters needed to cancel out the influence of the wind.
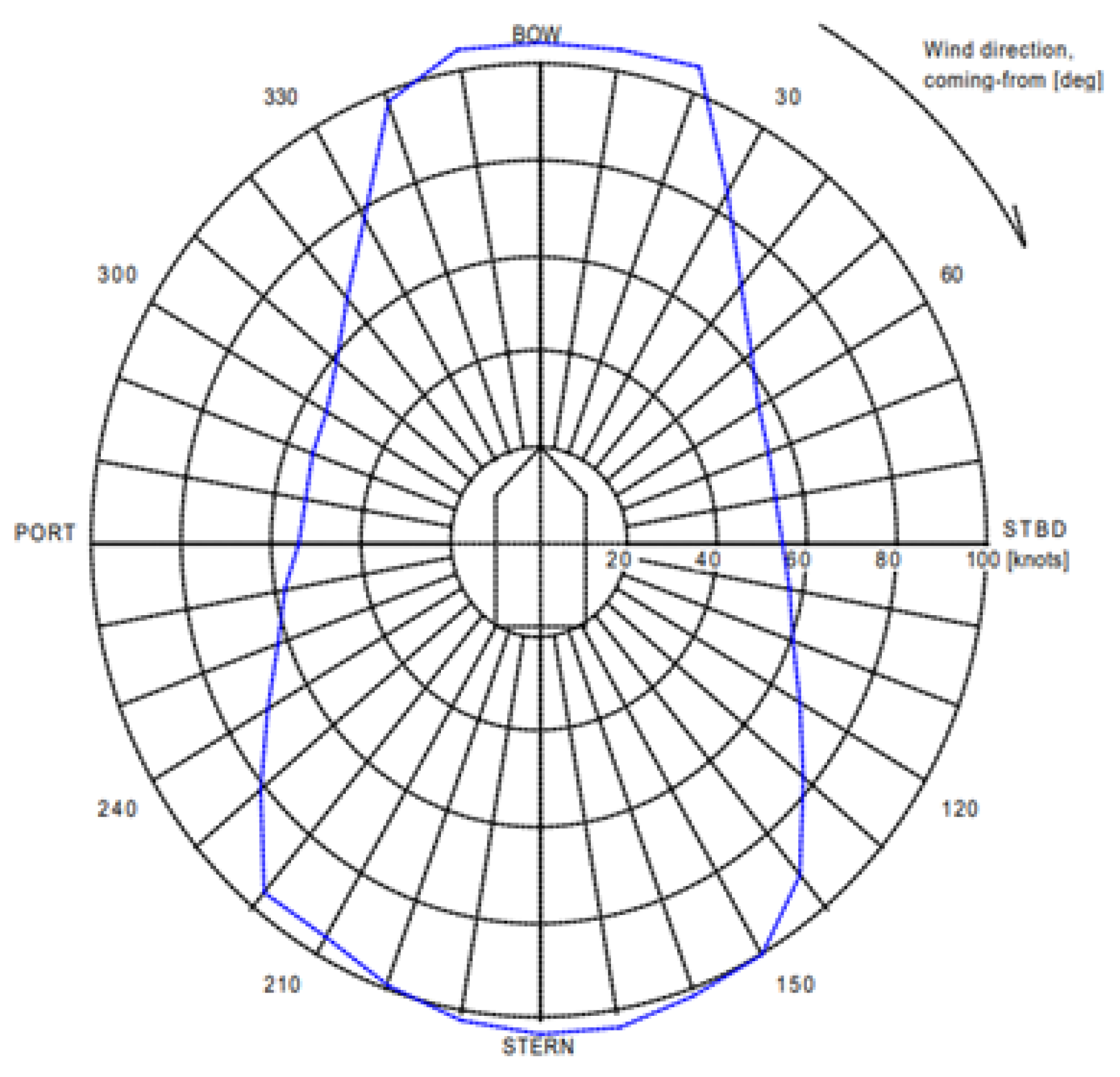
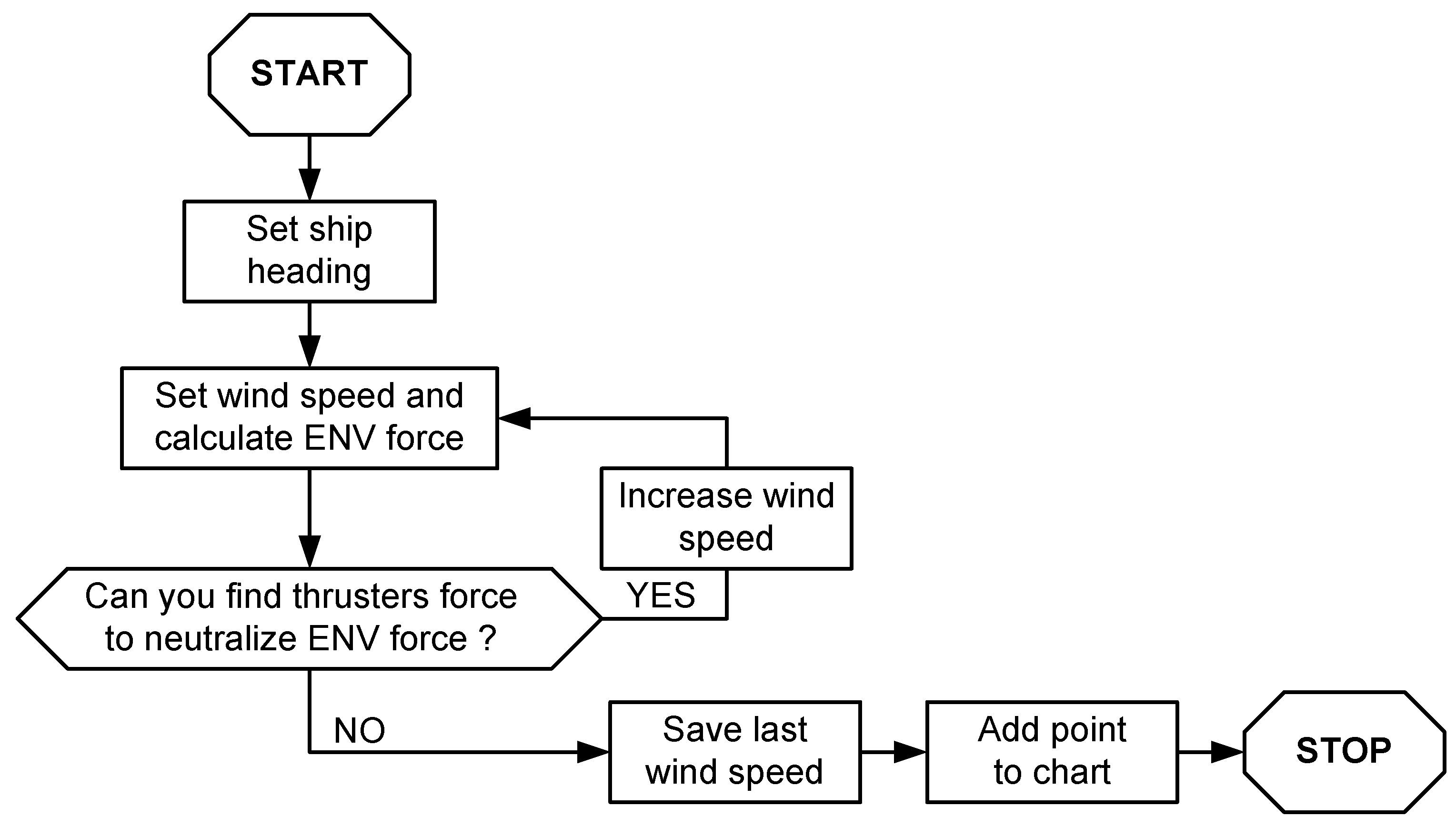
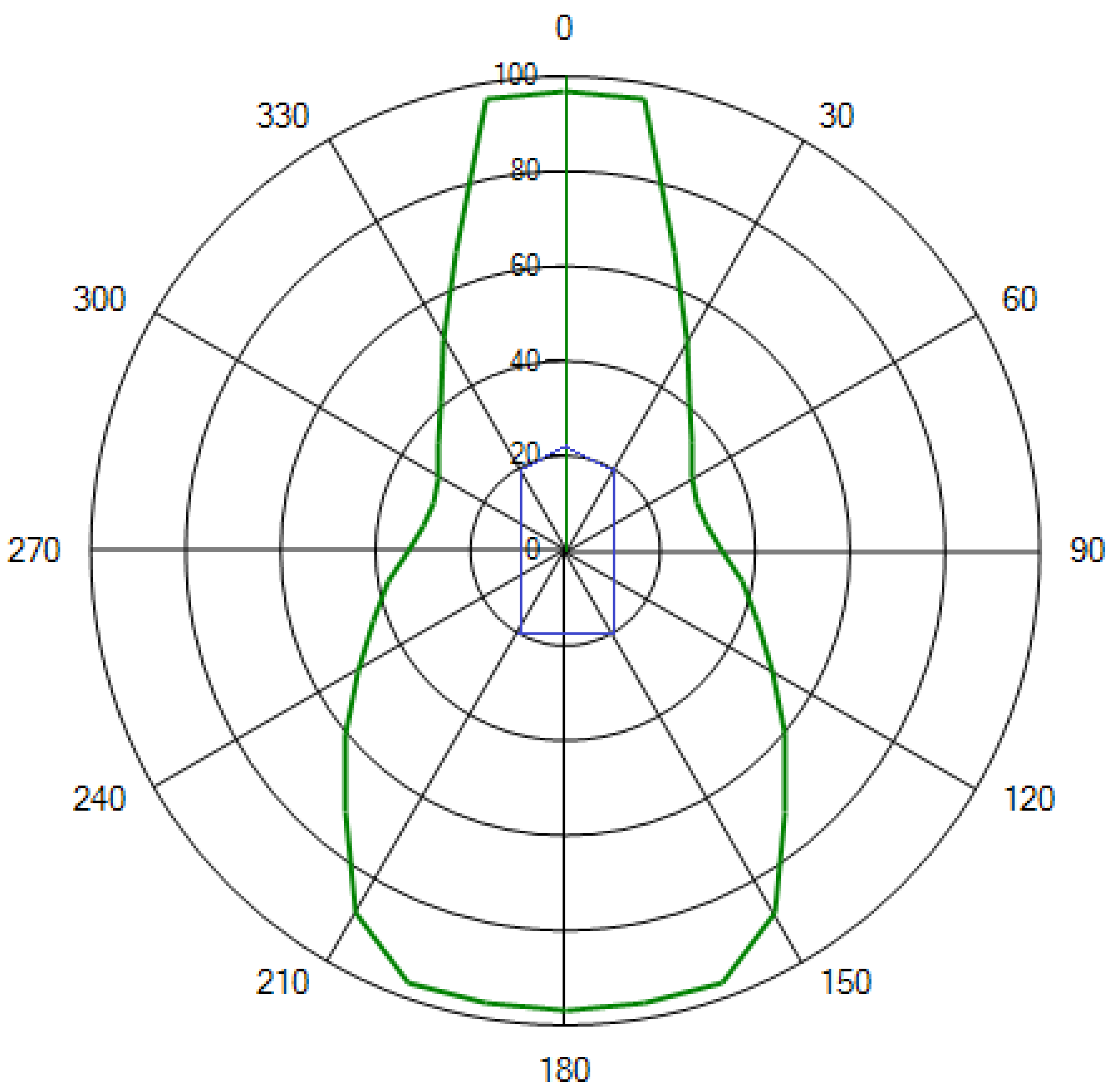
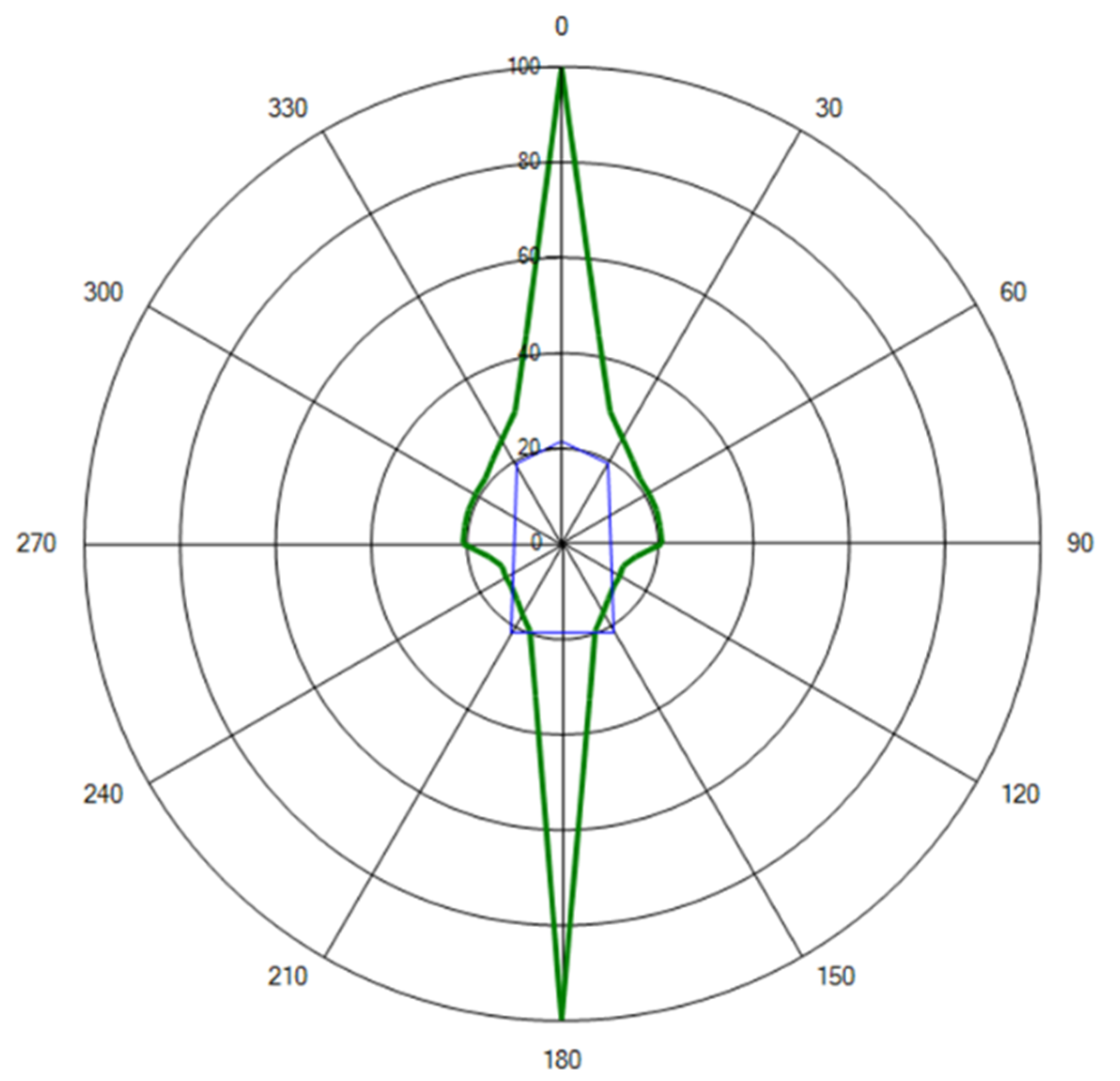
- The capability plot analysis.
- Based on the results of the analysis from point 1, the dependencies of the strength of individual thrusters on the wind speed were determined
- Using the dependencies given in [29], the individual thrusters’ forces were converted into power.
- The dependencies of the used thruster power on the wind speed were determined,
- Based on the characteristics from sub-point 4 and the graph of changes in wind speed during positioning, the power consumption over time was determined.
- Knowing the changes in power consumption and the positioning time, it was possible to determine the energy consumption.
2. Review of Existing Methods of Reducing Energy Consumption
- Methods related to control algorithms,
- Methods related to the structure of the ship
- Methods related to analysis during ship design process
2.1. Methods Related to Control Algorithms
2.2. Methods Related to the Structure of the Ship
2.3. Methods Related to Analysis during Ship Design Process
3. Research Methodology
3.1. Mathematical Model of Environmental Forces
- Wind force and resulting torque
- The strength of the sea current and the resulting torque
3.1.1. Wind Force and Torque
3.1.2. Sea Current and Torque
3.2. Mathematical Model of Thrusters
3.2.1. Tunnel Thruster
3.2.2. Azimuth Thruster
3.2.3. Main Screw
3.3. Determination of the Distribution of Forces on Propulsors
4. Simulation Studies of Energy Consumption in Various DP Systems
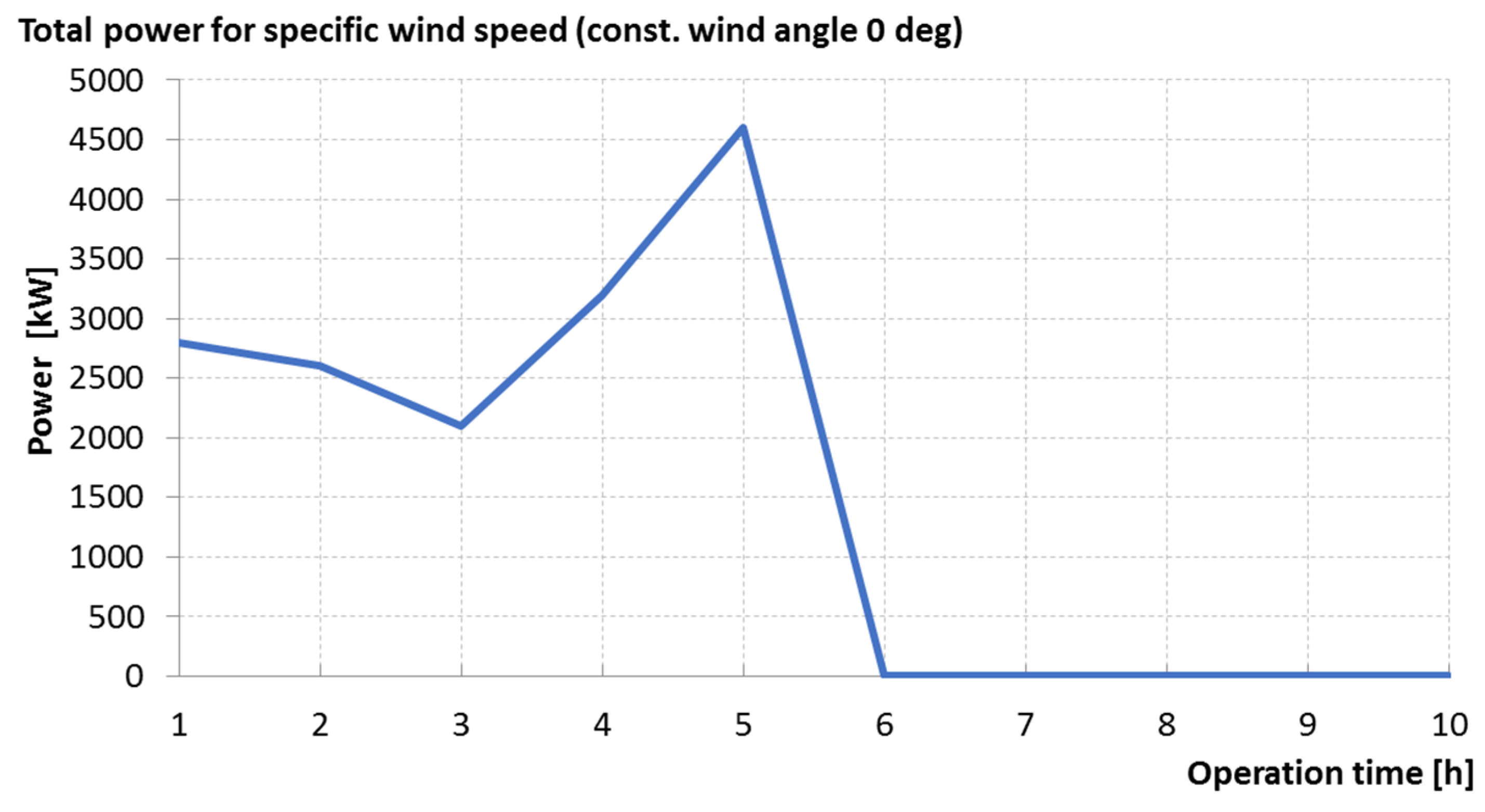
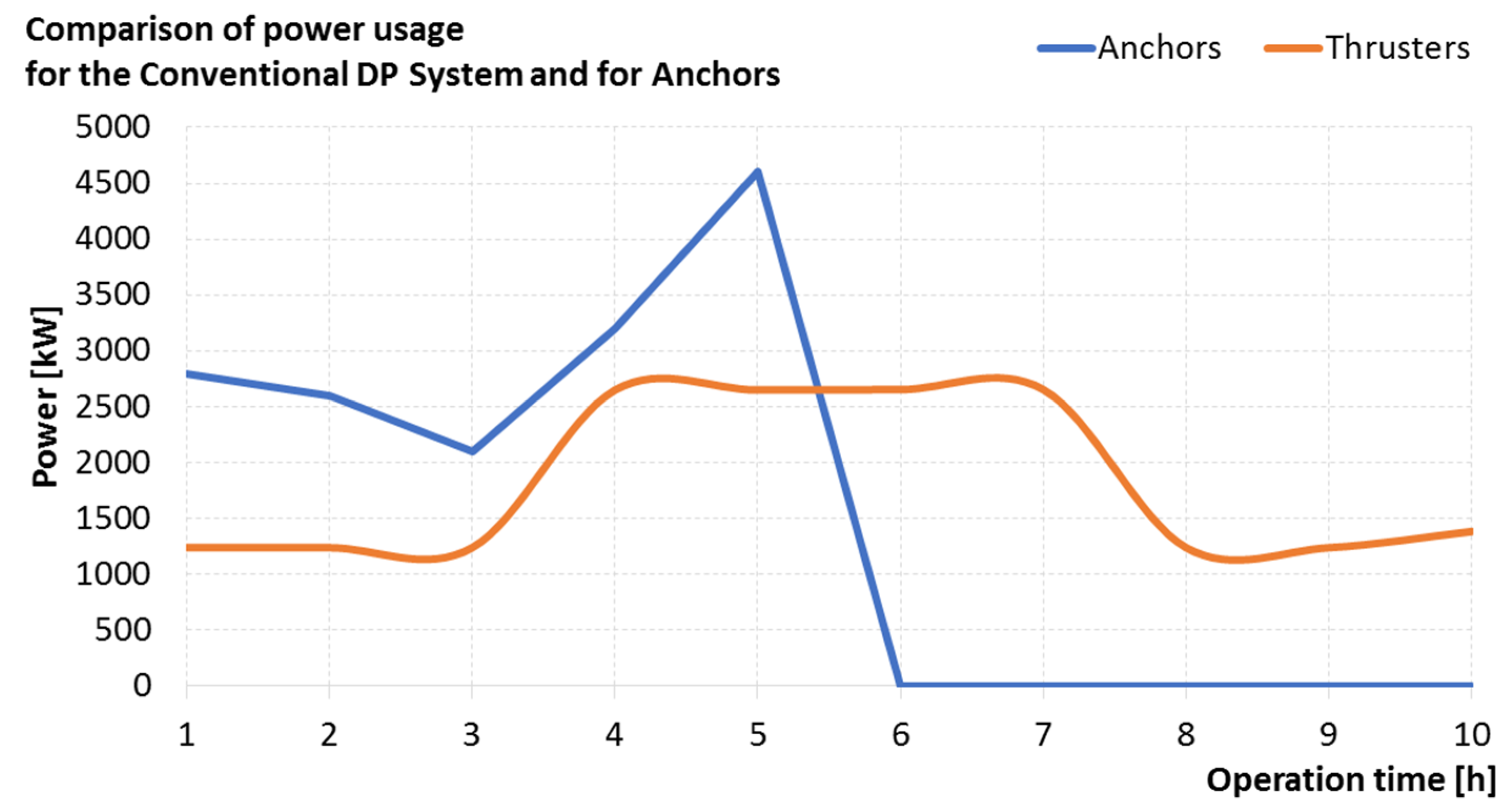
4.1. Conventional Dynamic Positioning System
4.2. Positioning System with a Set of Anchors
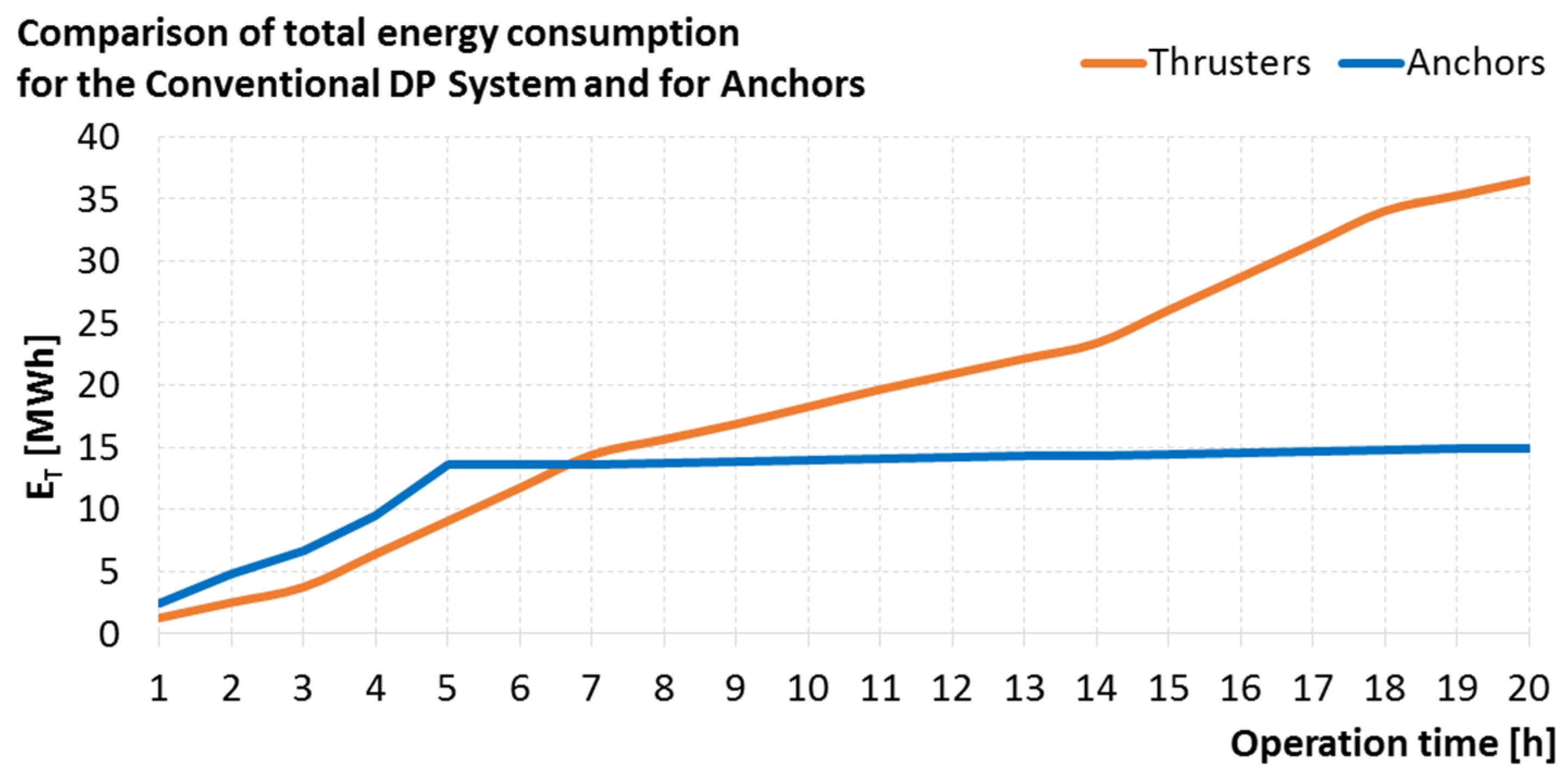
4.3. Comparison of Positioning Systems
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dynamic Positioning Committee. Available online: https://Dynamic-positioning.com/timeline/ (accessed on 6 October 2020).
- Kongsberg Website. Available online: https://www.kongsberg.com (accessed on 10 October 2020).
- Mehrzadi, M.; Terriche, Y.; Su, C.-L.; Othman, M.B.; Vasquez, J.C.; Guerrero, J.M. Review of Dynamic Positioning Control in Maritime Microgrid Systems. Energies 2020, 13, 3188. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control = Vademecum de Navium Motu Contra Aquas et de Motu Gubernando; John Wiley & Sons, Ltd.: Chichester, UK, 2014; ISBN 978-1-1199-9149-6. [Google Scholar]
- Kalman filtering for positioning and heading control of ships and offshore rigs. IEEE Control Syst. 2009, 29, 32–46. [CrossRef]
- Sørensen, A.J.; Sagatun, S.I.; Fossen, T.I. Design of a Dynamic Positioning system using model-based control. Control Eng. Pract. 1996, 4, 359–368. [Google Scholar] [CrossRef]
- Chin, C.S.; Dev, A.K. Modeling and Dynamic Positioning Simulation of OD21 Drill Ship. In Offshore Support Vessels, In Proceedings of the 4th International Conference on Technology and Operation of Offshore Support Vessels, Singapore, 16–17 August 2011; Dev, A.K., Aksu, S., Eds.; Research Publishing Services: Singapore, 2011; pp. 85–96. ISBN 978-981-08-9731-4. [Google Scholar]
- LePage, A.; Wide, P. Deep Diving From a Dynamically Positioned Drill Ship. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 28 April 1973. [Google Scholar] [CrossRef]
- Jung, C.-Y.; Yoo, S.-L. Optimal Rescue Ship Locations Using Image Processing and Clustering. Symmetry 2019, 11, 32. [Google Scholar] [CrossRef] [Green Version]
- Bruschi, R.; Vitali, L.; Marchionni, L.; Parrella, A.; Mancini, A. Pipe technology and installation equipment for frontier deep water projects. Ocean Eng. 2015, 108, 369–392. [Google Scholar] [CrossRef]
- Jensen, G.A.; Fossen, T.I. Mathematical Models for Model-Based Control in Offshore Pipelay Operations. In Volume 3: Pipeline and Riser Technology, In Proceedings of the ASME 2009 28th International Conference on Ocean, Offshore and Arctic Engineering, Honolulu, HI, USA, 1 May–5 June 2009; ASMEDC: Washington, DC, USA, 2019; pp. 269–276. ISBN 978-0-7918-4343-7. [Google Scholar]
- Jensen, G.A.; Safstrom, N.; Nguyen, T.D.; Fossen, T.I. Modeling and Control of Offshore Pipelay Operations Based on a Finite Strain Pipe Model. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 4717–4722, ISBN 978-1-4244-4523-3. [Google Scholar]
- Offshore Support Vessels. Available online: https://www.wartsila.com/encyclopedia/term/offshore-support-vessels-(osvs) (accessed on 25 October 2020).
- Erin Gill. Floating Hotels Advance Offshore Construction. Available online: https://www.windpowermonthly.com/article/1189367/floating-hotels-advance-offshore-construction (accessed on 5 November 2020).
- Floating Accomodations. Available online: https://floatingaccommodations.com/Our-Services/Offshore (accessed on 5 November 2020).
- WARTSILA. AZIPOD. Available online: https://www.wartsila.com/encyclopedia/term/azipod-(azimuthing-podded-drive) (accessed on 15 October 2020).
- Verhaar Omega, J.V. Channel Thrusters. Available online: https://verhaar.com/en/channel-thrusters/ (accessed on 15 November 2020).
- Wartsila. Exhaust gas Emissions from Ships. Available online: https://www.wartsila.com/encyclopedia/term/exhaust-gas-emissions-from-ships (accessed on 14 October 2020).
- DP Fmea/Fmeca Proving Trials. Available online: https://www.dpmarine.org/services/Dynamic-positioning/dp-fmea-fmeca-proving-trials/ (accessed on 15 October 2020).
- Herdzik, J. Remarks of the fmea procedures for ships with dynamic positioning systems. Sci. J. Gdyn. Marit. Univ. 2015, 91, 47–53. [Google Scholar]
- Dynamic Positioning Failure Mode Effects Analysis Assurance Framework Risk-Based Guidance. Available online: https://www.ocimf.org/media/159746/dp-failure-mode-effects-analysis-assurance-framework-risk-based-guidance.pdf (accessed on 15 October 2020).
- DNV GL. Available online: https://www.dnvgl.com/ (accessed on 6 October 2020).
- SEnControl. Available online: http://www.sencontrol.com/en/ (accessed on 1 September 2020).
- Wartsila.com. Wärtsilä—Enabling Sustainable Societies with Smart Technology. Available online: https://www.wartsila.com/ (accessed on 6 September 2020).
- Kongsberg, D.P. Capability Analysis. Available online: http://www.adamsoffshore.com/pdf/aqdpcapplot.pdf (accessed on 10 October 2020).
- Assessment of Station Keeping Capability of Dynamic Positioning Vessels. Available online: https://rules.dnvgl.com/docs/pdf/DNVGL/ST/2016-07/DNVGL-ST-0111.pdf (accessed on 8 October 2020).
- LocalSolver. Available online: https://www.localsolver.com/ (accessed on 10 January 2020).
- RIGZONE. How Does a Drillship Work? Available online: https://www.rigzone.com/training/insight.asp?insight_id=306&c_id= (accessed on 18 October 2020).
- Jurdzinski, M. Planning the energy efficiency on board the ships. Pr. Wydz. Nawig. 2013, 28, 5–10. [Google Scholar] [CrossRef] [Green Version]
- International Maritime Organization. International Convention for the Prevention of Pollution from Ships (MARPOL). Available online: https://www.imo.org/en/About/Conventions/Pages/International-Convention-for-the-Prevention-of-Pollution-from-Ships-(MARPOL).aspx (accessed on 20 October 2020).
- Wang, Q.; Wei, H.-H.; Xu, Q. A Solid Oxide Fuel Cell (SOFC)-Based Biogas-from-Waste Generation System for Residential Buildings in China: A Feasibility Study. Sustainability 2018, 10, 2395. [Google Scholar] [CrossRef] [Green Version]
- Chang, S.; Wang, Q.; Hu, H.; Ding, Z.; Guo, H. An NNwC MPPT-Based Energy Supply Solution for Sensor Nodes in Buildings and Its Feasibility Study. Energies 2019, 12, 101. [Google Scholar] [CrossRef] [Green Version]
- Tannuri, E.A.; Agostinho, A.C.; Morishita, H.M.; Moratelli, L. Dynamic Positioning systems: An experimental analysis of sliding mode control. Control Eng. Pract. 2010, 18, 1121–1132. [Google Scholar] [CrossRef]
- Chang, W. Fuzzy Control of Dynamic Positioning Systems for Ships. J. Mar. Sci. Technol. 2002, 47–53. [Google Scholar]
- Zhang, Z.; Wu, D. Operator Panel Design for Dynamic Positioning Simulator. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1020–1023, ISBN 978-1-7281-1312-8. [Google Scholar]
- Xu, L.; Liu, Z.-Q. Design of fuzzy PID controller for ship Dynamic Positioning. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 3130–3135, ISBN 978-1-4673-9714-8. [Google Scholar]
- Xie, D.; Han, X.; Jia, B.; Liu, Y.; Zheng, S. Research on improved PID Dynamic Positioning System Based on Nonlinear Observer. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 698–702, ISBN 978-1-7281-1312-8. [Google Scholar]
- Wu, G.; Atilla, I.; Tahsin, T.; Terziev, M.; Wang, L. Long-voyage route planning method based on multi-scale visibility graph for autonomous ships. Ocean Eng. 2020, 108242. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Z.; Zhu, Q.; Ma, S. Ship Route Planning Based on Double-Cycling Genetic Algorithm Considering Ship Maneuverability Constraint. IEEE Access 2020, 8, 190746–190759. [Google Scholar] [CrossRef]
- Kula, K.; Tomera, M. Control System of Training Ship Keeping the Desired Path Consisting of Straight-lines and Circular Arcs. TransNav 2017, 11, 711–719. [Google Scholar] [CrossRef] [Green Version]
- Tomera, M.; Alfuth, L. Waypoint Path Controller for Ships. TransNav 2020, 14, 375–383. [Google Scholar] [CrossRef]
- Rybczak, M.; Rak, A. Prototyping and Simulation Environment of Ship Motion Control System. TransNav 2020, 14, 367–374. [Google Scholar] [CrossRef]
- Lisowski, J.; Mohamed-Seghir, M. Comparison of Computational Intelligence Methods Based on Fuzzy Sets and Game Theory in the Synthesis of Safe Ship Control Based on Information from a Radar ARPA System. Remote Sens. 2019, 11, 82. [Google Scholar] [CrossRef] [Green Version]
- Lisowski, J. Multistage Dynamic Optimization with Different Forms of Neural-State Constraints to Avoid Many Object Collisions Based on Radar Remote Sensing. Remote Sens. 2020, 12, 1020. [Google Scholar] [CrossRef] [Green Version]
- Lisowski, J. Sensitivity of Safe Trajectory in a Game Environment to Determine Inaccuracy of Radar Data in Autonomous Navigation. Sensors 2019, 19, 1816. [Google Scholar] [CrossRef] [Green Version]
- Mohamed-Seghir, M. Methods based on fuzzy sets to solve problems of Safe Ship control. In Novel Algorithms and Techniques in Telecommunications and Networking; Springer: Dordrecht, The Netherlands, 2010; pp. 373–377. [Google Scholar]
- Chen, C.; Delefortrie, G.; Lataire, E. Experimental investigation of practical autopilots for maritime autonomous surface ships in shallow water. Ocean Eng. 2020, 218, 108246. [Google Scholar] [CrossRef]
- Jha, A.; Subedi, D.; Lovsland, P.-O.; Tyapin, I.; Reddy Cenkeramaddi, L.; Lozano, B.; Hovland, G. Autonomous Mooring towards Autonomous Maritime Navigation and Offshore Operations. In Proceedings of the 2020 15th IEEE Conference on Industrial Electronics and Applications (ICIEA), Kristiansand, Norway, 9–13 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1171–1175, ISBN 978-1-7281-5169-4. [Google Scholar]
- Peng, Z.; Wang, J.; Wang, D.; Han, Q.-L. An Overview of Recent Advances in Coordinated Control of Multiple Autonomous Surface Vehicles. IEEE Trans. Ind. Inf. 2021, 17, 732–745. [Google Scholar] [CrossRef]
- Lee, K.-J.; Shin, D.; Yoo, D.-W.; Choi, H.-K.; Kim, H.-J. Hybrid photovoltaic/diesel green ship operating in standalone and grid-connected mode—Experimental investigation. Energy 2013, 49, 475–483. [Google Scholar] [CrossRef]
- Tang, R. Large-scale photovoltaic system on green ship and its MPPT controlling. Sol. Energy 2017, 157, 614–628. [Google Scholar] [CrossRef]
- Fritz, F. Application of an Automated Kite System for Ship Propulsion and Power Generation. In Airborne Wind Energy; Ahrens, U., Diehl, M., Schmehl, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 359–372. ISBN 978-3-642-39964-0. [Google Scholar]
- Kim, J.; Park, C. Wind power generation with a parawing on ships, a proposal. Energy 2010, 35, 1425–1432. [Google Scholar] [CrossRef]
- Hein, K.; Xu, Y. Coordinated Optimal Voyage Planning and Energy Management of All-electric Ship with Hybrid Energy Storage System. IEEE Trans. Power Syst. 2020, 1. [Google Scholar] [CrossRef]
- Chen, W.; Tai, K.; Lau, M.; Abdelhakim, A.; Chan, R.R.; Kare Adnanes, A.; Tjahjowidodo, T. On the Modelling of Fuel Cell-Fed Power System in Electrified Vessels. In Proceedings of the 2020 IEEE 21st Workshop on Control and Modeling for Power Electronics (COMPEL), Aalborg, Denmark, 9–12 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–8, ISBN 978-1-7281-7160-9. [Google Scholar]
- Sun, Y.; Xu, Q.; Yuan, Y.; Yang, B. Optimal Energy Management of Fuel Cell Hybrid Electric Ships Considering Fuel Cell Aging Cost. In Proceedings of the 2020 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Weihai, China, 13–15 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 240–245, ISBN 978-1-7281-4303-3. [Google Scholar]
- Lele, A.; Rao, K.V.S. Net power generated by flettner rotor for different values of wind speed and ship speed. In Proceedings of the 2017 International Conference on Circuit, Power and Computing Technologies (ICCPCT), Kollam, India, 20–21 April 2017; Staff, I., Ed.; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6, ISBN 978-1-5090-4967-7. [Google Scholar]
- Abramowicz-Gerigk, T.; Burciu, Z. Design and Operational Innovations in Adapting the Existing Merchant River Fleet to Cost-Effective Shipping. Pol. Marit. Res. 2019, 26, 157–164. [Google Scholar] [CrossRef] [Green Version]
- Abramowicz-Gerigk, T.; Burciu, Z.; Jachowski, J. An Innovative Steering System for a River Push Barge Operated in Environmentally Sensitive Areas. Pol. Marit. Res. 2017, 24, 27–34. [Google Scholar] [CrossRef] [Green Version]
- Abramowicz-Gerigk, T.; Burciu, Z. Application of Ship Motion Simulation in Reliability Assessment of Ship Entrance into the Port. TransNav 2016, 10, 613–617. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Y.; Wu, L.; Zheng, X. Adaptive Risk-Averse Chance-Constrained Stochastic Coordination of Hybrid AC/DC Multi-Energy Ships Considering Renewable Energy and Ship Swinging. IEEE Trans. Power Syst. 2020, 1. [Google Scholar] [CrossRef]
- Nam, S.; Park, D.; Zadeh, M.K. Energy Storage System as Auxiliaries of Internal Combustion Engines in Hybrid Electric Ships. In Proceedings of the 2020 15th IEEE Conference on Industrial Electronics and Applications (ICIEA), Kristiansand, Norway, 9–13 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 431–436, ISBN 978-1-7281-5169-4. [Google Scholar]
- Belal, H.B.; Uddin, M.; Karim, T.; Nath, S. Design and Implementation of an Eco-Friendly Water Vehicle. In Proceedings of the 2019 International Conference on Robotics, Electrical and Signal Processing Techniques (ICREST), Dhaka, Bangladesh, 10–12 January 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 233–236, ISBN 978-1-5386-8012-4. [Google Scholar]
- Weintrit, A.; Neumann, T. Safety of Marine Transport Introduction; CRC Press-Taylor & Francis Group: Abingdon, UK; Gdynia Maritime University: Gdynia, Poland, 2015. [Google Scholar]
- Rindaroey, M.; Johansen, T.A. Fuel Optimal Thrust Allocation in Dynamic Positioning. Ifac Proc. Vol. 2013, 46, 43–48. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.; Wang, L.; Wang, X. Local optimization of thruster configuration based on a synthesized positioning capability criterion. Int. J. Nav. Archit. Ocean Eng. 2015, 7, 1044–1055. [Google Scholar] [CrossRef] [Green Version]
- Fossen, T.I. Handbook of Marine Craft HydroDynamics and Motion Control. IEEE Control Syst. 2016, 36, 78–79. [Google Scholar] [CrossRef]
- Johansen, T.A.; Fossen, T.I.; Berge, S.P. Constrained Nonlinear Control Allocation With Singularity Avoidance Using Sequential Quadratic Programming. IEEE Trans. Contr. Syst. Technol. 2004, 12, 211–216. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.; Wang, X.; Wang, L.; Meng, S. Applying the Bisection Search Method to Search the Maximum Environmental Conditions in DPCap Analysis for Marine Vessels. IJOPE 2015, 25, 104–111. [Google Scholar] [CrossRef]
- Xu, S.; Wang, X.; Wang, L.; Meng, S.; Li, B. A thrust sensitivity analysis based on a synthesized positioning capability criterion in DPCap/DynCap analysis for marine vessels. Ocean Eng. 2015, 108, 164–172. [Google Scholar] [CrossRef]
- Webster, W.C.; Sousa, J. Optimum Allocation for Multiple Thrusters. In Proceedings of the Ninth International Offshore and Polar Engineering Conference, Brest, France, 30 May 1999. [Google Scholar]
- DNV GL, Rules for Classification of Ships. Available online: https://rules.dnvgl.com/docs/pdf/DNV/rulesship/2012-01/ts607.pdf (accessed on 10 October 2020).
- Fay, H. Dynamic Positioning Systems. Principles, Design and Applications; Éditions Technip: Paris, France, 1990; ISBN 2710805804. [Google Scholar]
- You, Y.; Kim, S.; Kim, W. Development of a safe operation capability chart as the design basis of a rudder area. Int. J. Nav. Archit. Ocean Eng. 2018, 10, 529–544. [Google Scholar] [CrossRef]
- Wang, L.; Yang, J.-M.; Xu, S.-W. Dynamic Positioning Capability Analysis for Marine Vessels Based on a DPCap Polar Plot Program. China Ocean Eng. 2018, 32, 90–98. [Google Scholar] [CrossRef]
- Masnicki, R.; Mindykowski, J. Coordination of operations in registration channel of data from electrical power system. Measurement 2017, 99, 68–77. [Google Scholar] [CrossRef]
- Pilat, A.; Tarasiuk, T.; Jankowski, P. PSCAD Model of the Marine Sub-system with Nonlinear Load for Power Quality Assesment. In Proceedings of the 2018 20th European Conference on Power Electronics and Applications (EPE’18 ECCE Europe), Riga, Latvia, 17–21 September 2018. [Google Scholar]
- Jankowski, P.; Pilat, A.; Tarasiuk, T. The study of chaotic behaviour in the marine power system containing nonlinear varying load. In Proceedings of the 2018 International Conference and Exposition on Electrical and Power Engineering (EPE), Iasi, Romania, 18–19 October 2018; pp. 113–118. [Google Scholar]
- Gorniak, M.; Tarasiuk, T. Voltage spectrum in shipboard microgrid with the varying nonlinear load. In Proceedings of the 2018 20th European Conference on Power Electronics and Applications (EPE’18 ECCE Europe), Riga, Latvia, 17–21 September 2018. [Google Scholar]
- Tarasiuk, T.; Gorniak, M. Load Sharing in Ship Microgrids Under Nonsinusoidal Conditions—Case Study. IEEE Trans. Energy Convers. 2017, 32, 810–819. [Google Scholar] [CrossRef]
- Kasprowicz, A. Induction Generator with Three-Level Inverters and LCL Filter Connected to the Power Grid; Bulletin of the Polish Academy of Sciences. Tech. Sci. 2019, 67. [Google Scholar] [CrossRef]
- Masnicki, R. The Fluency of Data Flow in the Instrument for Measurement and Registration of Parameters of the Electrical Power Network. In Proceedings of the 2015 IEEE 15th International Conference on Environment and Electrical Engineering (EEEIC), Rome, Italy, 10–13 June 2015; pp. 2040–2044. [Google Scholar]
- Iwaszkiewicz, J.; Mysiak, P. Supply System for Three-Level Inverters Using Multi-Pulse Rectifiers with Coupled Reactors. Energies 2019, 12, 3385. [Google Scholar] [CrossRef] [Green Version]
- Iwaszkiewicz, J.; Muc, A. Trójfazowy trójpoziomowy falownik z obniżoną zawartością harmonicznych. Electrotech. Rev. 2019, 1, 128–133. [Google Scholar] [CrossRef] [Green Version]
- Hashad, M.; Iwaszkiewicz, J. A novel orthogonal-vectors-based topology of multilevel inverters. IEEE Trans. Ind. Electron. 2002, 49, 868–874. [Google Scholar] [CrossRef]
- Mysiak, P. Multipulse diode converters—Frequency domain analysis of operation of the applied coupled three-phase reactor. In Proceedings of the 6th International Conference-Workshop, 2009 Compatability and Power Electronics (CPE), Badajoz, Spain, 20–22 May 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 53–60, ISBN 978-1-4244-2855-7. [Google Scholar]
- Gnaciński, P.; Hallmann, D.; Pepliński, M.; Jankowski, P. The effects of voltage subharmonics on cage induction machine. Int. J. Electr. Power Energy Syst. 2019, 111, 125–131. [Google Scholar] [CrossRef]
- Gnaciński, P.; Pepliński, M.; Hallmann, D.; Jankowski, P. Induction cage machine thermal transients under lowered voltage quality. IET Electr. Power Appl. 2019, 13, 479–486. [Google Scholar] [CrossRef]
- Pettinger, T. Top CO2 Polluters and Highest per Capita—Economics Help. Available online: https://www.economicshelp.org/blog/10296/economics/top-co2-polluters-highest-per-capita/ (accessed on 6 October 2020).
- What are Nonrenewable Resources and How Do We Protect Them? Available online: https://www.rubicon.com/blog/nonrenewable-resources/ (accessed on 13 October 2020).
- Seckin Salvarli, M.; Salvarli, H. For Sustainable Development: Future Trends in Renewable Energy and Enabling Technologies. In Renewable Energy—Resources, Challenges and Applications; Al Qubeissi, M., El-kharouf, A., Serhad Soyhan, H., Eds.; IntechOpen: London, UK, 2020; ISBN 978-1-78984-283-8. [Google Scholar]
- Kula, K.S. An Overview of Roll Stabilizers and Systems for Their Control. TransNav 2015, 9, 405–414. [Google Scholar] [CrossRef] [Green Version]
- Kula, K.S. Heading Control System with limited Turning Radius based on IMC Structure. In Proceedings of the 21st International Conference Methods Models Automation Robotics (MMAR), Międzyzdroje, Poland, 29 August–1 September 2016; pp. 134–139. [Google Scholar] [CrossRef]
- Gupta, H.N. Fundamentals of Internal Combustion Engines, 2nd ed.; PHI Learning Private Limited: Delhi, India, 2014; ISBN 978-81-203-4680-2. [Google Scholar]




| C1—230V UPS Distribution Board Instrument Room | ||||
|---|---|---|---|---|
| Source: Main—230V UPS 1 Backup—230V MSB Bus A (Automatic Changeover) | ||||
| Ref. | Description | Notification | Primary Effect | Effect on DP |
| C1 1–14 | No DP related consumers | Loss of power supply | Not DP Related | No effect on position keeping capability. |
| C1 14 | AC/DC Converter | Loss of power supply | Not DP Related | No effect on position keeping capability. |
| C1 15 | IAS Servers | Loss of backup power to IAS servers, one on bridge and one in ECR | Servers remain operational on power from UPS No. 2 and 3 | No effect on position keeping capability. |
| C1 16–17 | No DP related consumers | Loss of power supply | Not DP Related | No effect on position keeping capability. |
| C1 18 | Independent Joystick system | Loss of power supply | Loss of independent joystick system | No effect on position keeping capability. Loss of backup system. |
| C1 19 | Loss of supply or Short Circuit | All of Above | All of Above | All of Above, |
| Parameter | Value |
|---|---|
| Length overall (LOA) [m]: | 90 |
| Length between perpendiculars (LPP) [m]: | 70 |
| Breadth [m]: | 22 |
| Draught [m]: | 5 |
| Displacement [T]: | 6400 |
| Distance between foremost and aft most point of the hull below the surface at design draft even keel [m]: | 82.8 |
| Water plane area [m2]: | 1390 |
| Projected longitudinal area above water [m2]: | 900 |
| Surge position of geometric center of the projected longitudinal area above water with respect to LPP/2 [m]: | 12.5 |
| Projected longitudinal area below water [m2]: | 420 |
| Surge position of geometric center of the projected longitudinal area below water with respect to LPP/2 [m]: | 5.5 |
| Surge position of water line center with respect to LPP/2 [m]: | −0.35 |
| Projected transverse area above water [m2]: | 430 |
| Projected transverse area below water [m2]: | 140 |
| Generator | Power [kW] | Connected to Switchboard |
|---|---|---|
| Generator 1 | 1500 | 1 |
| Generator 2 | 1500 | 2 |
| Generator 3 | 2000 | 1 |
| Generator 4 | 2000 | 2 |
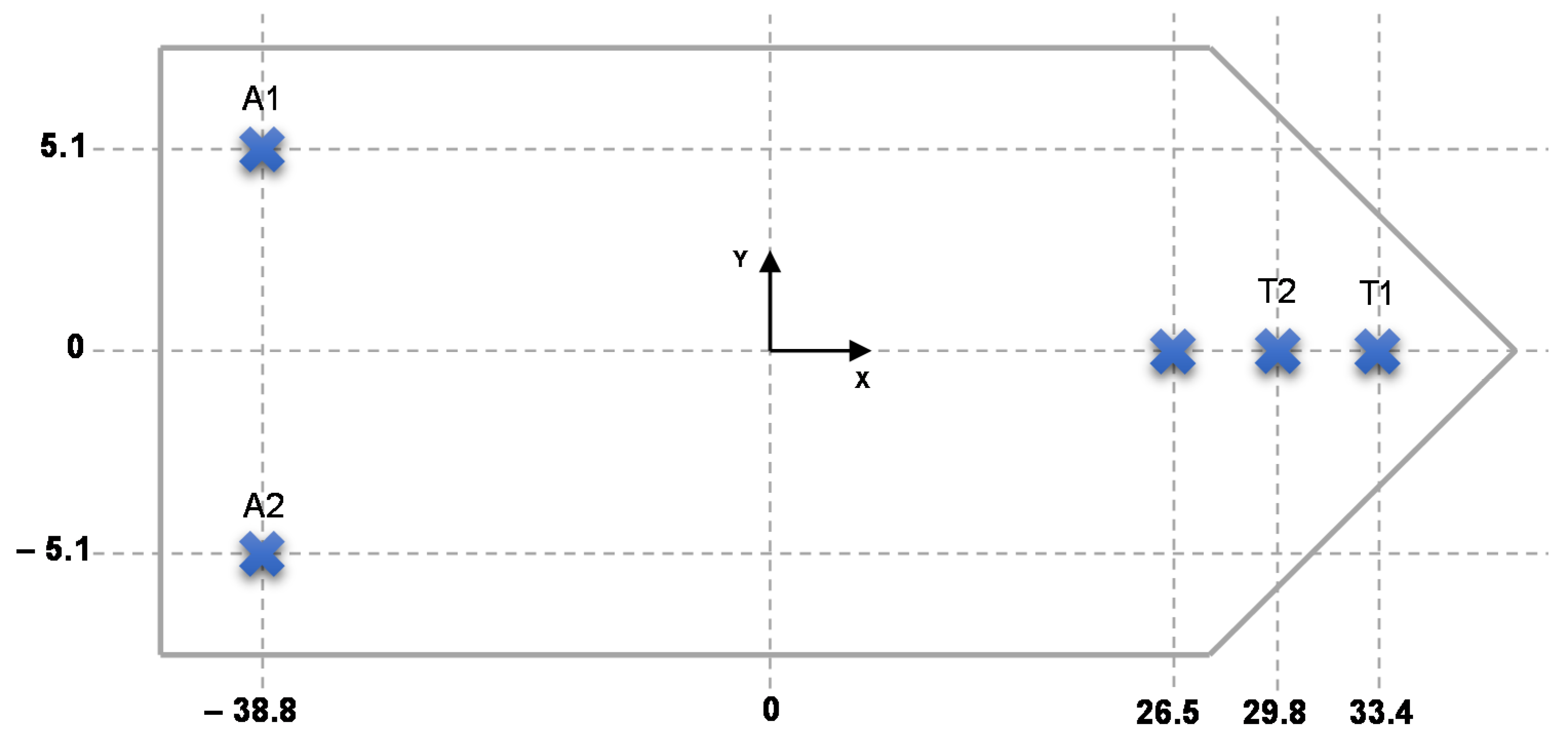
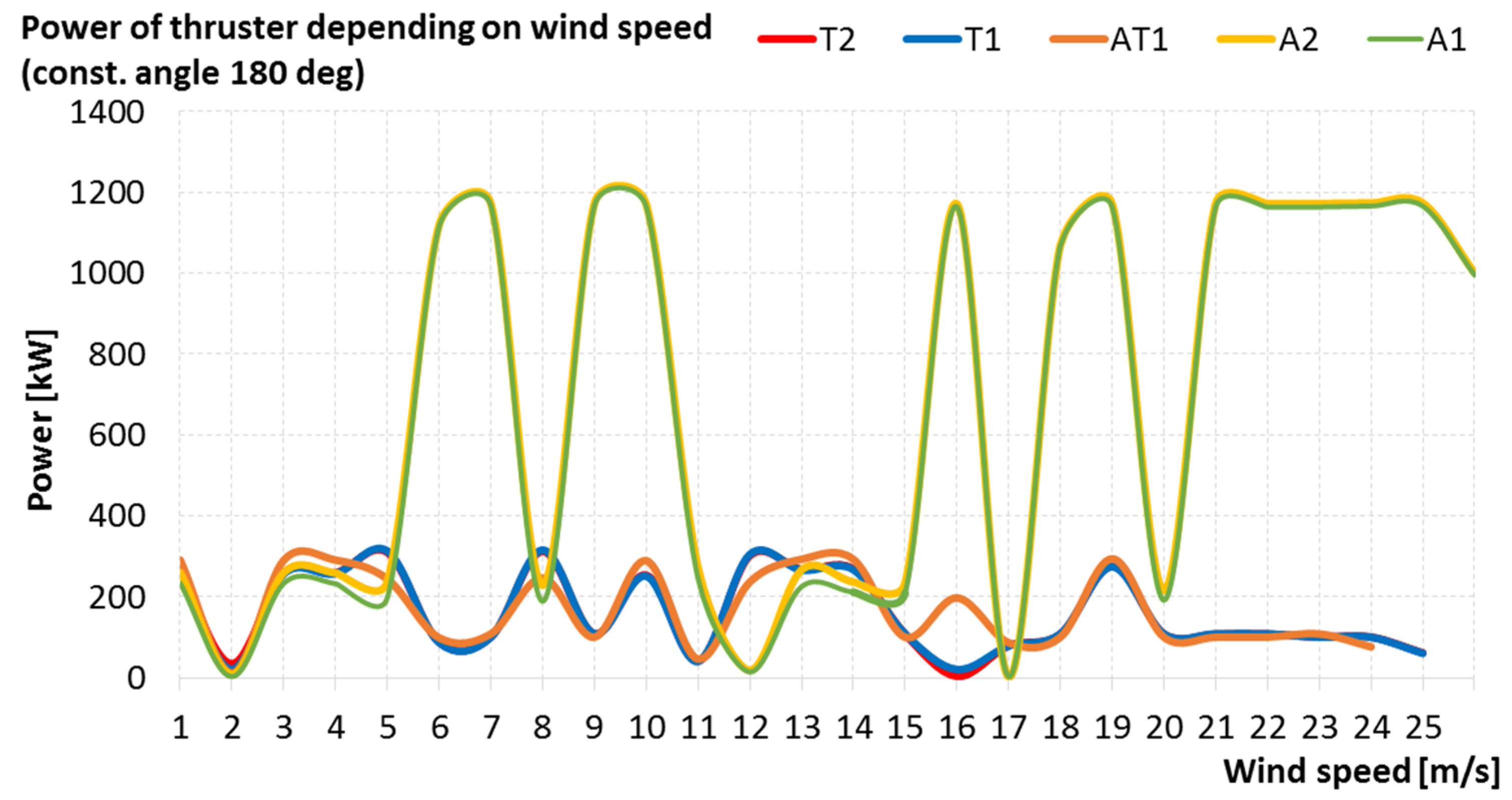
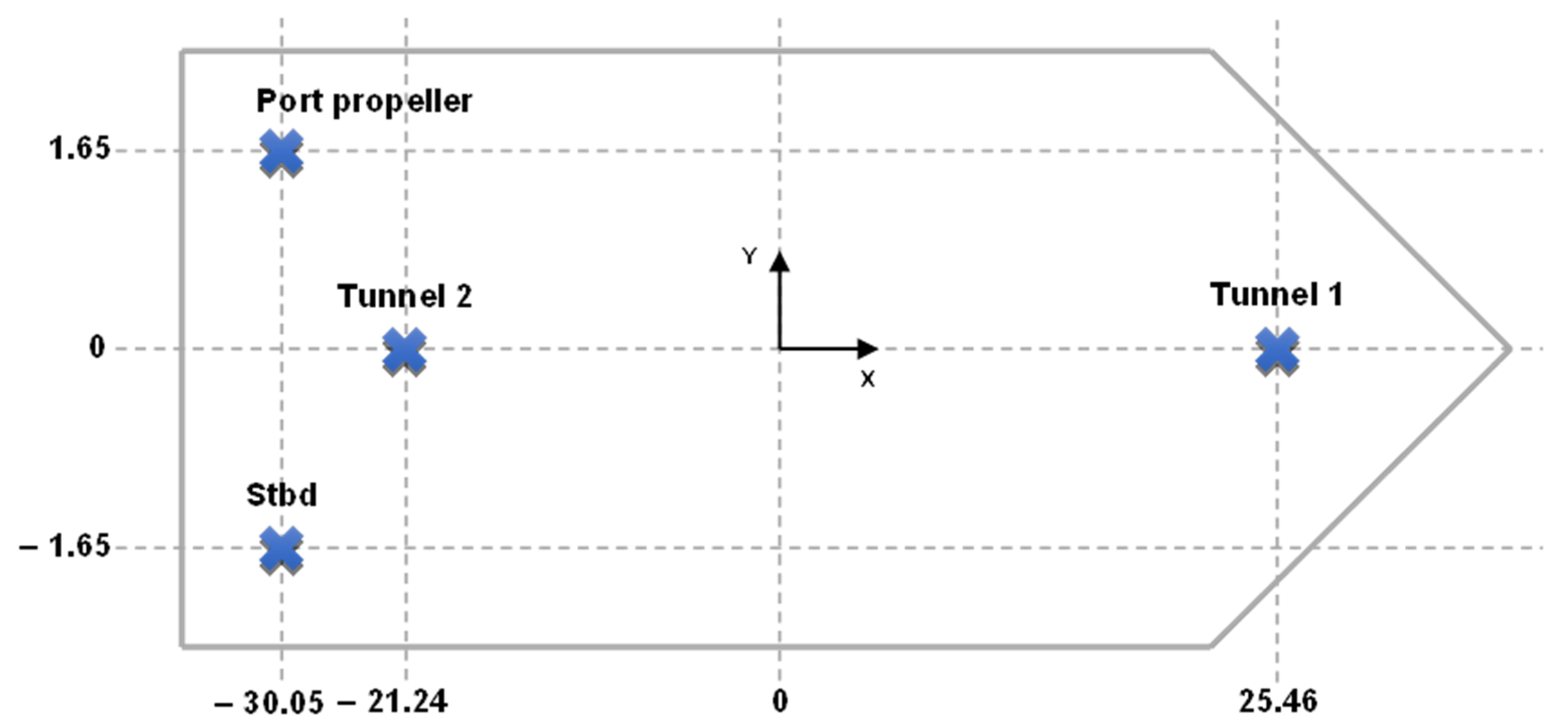
| Thruster | Thrust Max [kN] | Thrust Min [kN] | Power [kW] | X [m] | Y [m] |
|---|---|---|---|---|---|
| T1 | 118 | −118 | 588 | 33.4 | 0 |
| T2 | 118 | −118 | 588 | 29.8 | 0 |
| AT1 | 90 | −90 | 588 | 26.6 | 0 |
| A1 | 400 | −246 | 2000 | −38.8 | 5 |
| A2 | 400 | −246 | 2000 | −38.8 | −5 |
| Thruster | Switchboard 1 | Switchboard 2 |
|---|---|---|
| T1 | 100% | 0% |
| T2 | 0% | 100% |
| AT1 | 50% | 50% |
| A1 | 0% | 100% |
| A2 | 100% | 0% |
| Parameter | Value |
|---|---|
| Length overall (LOA) [m]: | 72.7 |
| Length between perpendiculars (LPP) [m]: | 64 |
| Breadth [m]: | 11.6 |
| Draught [m]: | 3.4 |
| Displacement [T]: | 1886 |
| Distance between foremost and aft most point of the hull below the surface at design draft even keel [m]: | 67.1 |
| Water plane area [m2]: | 639 |
| Projected longitudinal area above water [m2]: | 437 |
| Surge position of geometric center of the projected longitudinal area above water with respect to LPP/2 [m]: | 0.1 |
| Projected longitudinal area below water [m2]: | 223 |
| Surge position of geometric center of the projected longitudinal area below water with respect to LPP/2 [m]: | −2.9 |
| Surge position of water line center with respect to LPP/2 [m]: | −1.5 |
| Projected transverse area above water [m2]: | 140 |
| Projected transverse area below water [m2]: | 36 |
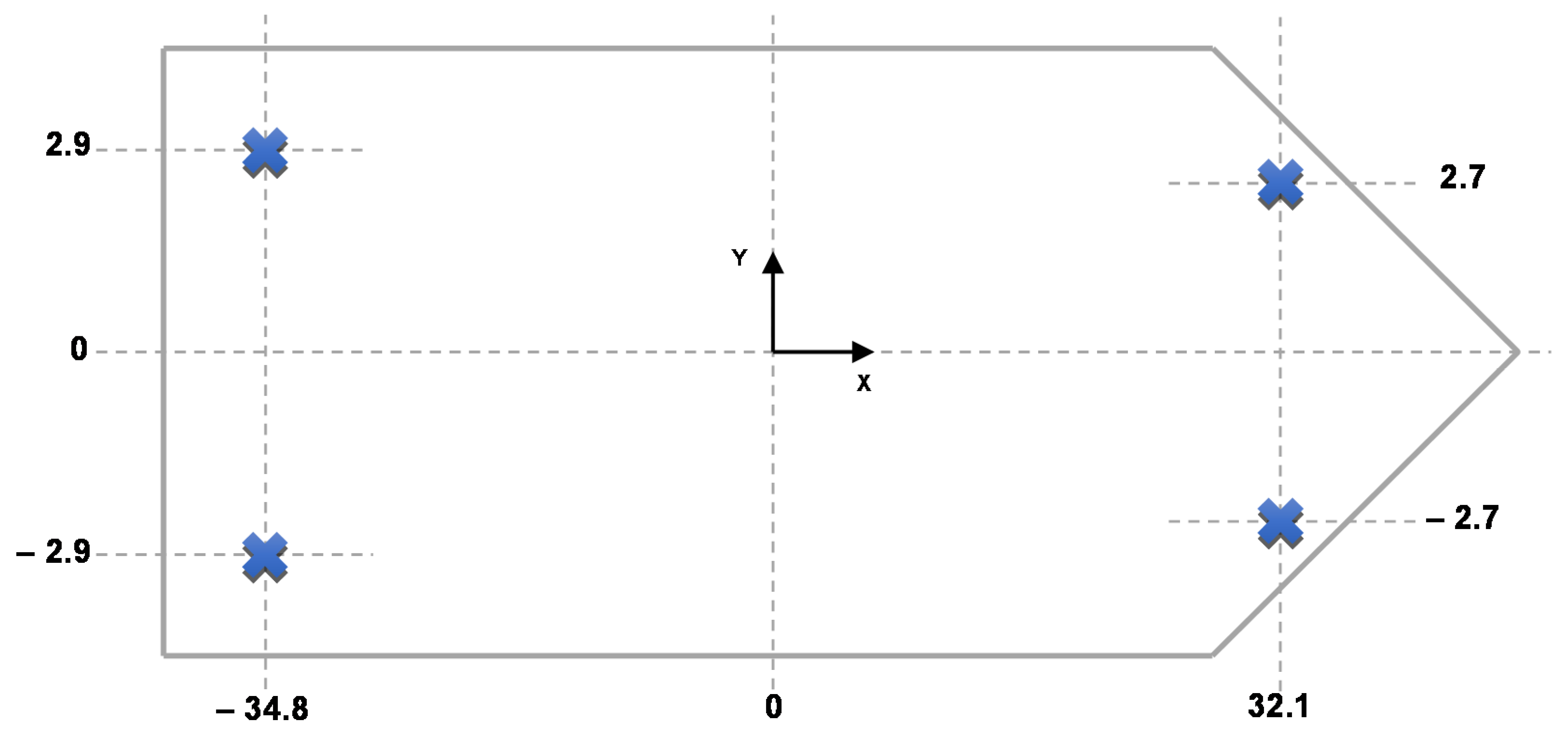
| Thruster | Thrust Max [kN] | Thrust Min [kN] | Power [kW] |
|---|---|---|---|
| Tunnel 1 | 24 | −24 | 250 |
| Tunnel 2 | 24 | −24 | 250 |
| Port propeller | 181 | −181 | 2000 |
| Stbd propeller | 181 | −181 | 2000 |
| Winch | Max Tension [kN] (500 m Chain) | Max Tension [kN] (750 m Chain) | Max Tension [kN] (1000 m Chain) |
|---|---|---|---|
| Port Winch 1 | 102.53 | 116.47 | 124.85 |
| Stbd Winch 1 | 102.53 | 116.47 | 124.85 |
| Port Winch 2 | 102.53 | 116.47 | 124.85 |
| Stbd Winch 2 | 102.53 | 116.47 | 124.85 |
| Conventional DP System | Anchor System | |
|---|---|---|
| Advantages |
|
|
| Disadvantages |
|
|
| Average hourly energy consumption (for 10 h of positioning) | 1825.7 [kWh] | 1390 [kWh] |
| Fuel consumption | 4258 [l] | 3241.6 [l] |
| 11.24 [t] | 8.56 [t] | |
| Application |
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Łebkowski, A.; Wnorowski, J. A Comparative Analysis of Energy Consumption by Conventional and Anchor Based Dynamic Positioning of Ship. Energies 2021, 14, 524. https://doi.org/10.3390/en14030524
Łebkowski A, Wnorowski J. A Comparative Analysis of Energy Consumption by Conventional and Anchor Based Dynamic Positioning of Ship. Energies. 2021; 14(3):524. https://doi.org/10.3390/en14030524
Chicago/Turabian StyleŁebkowski, Andrzej, and Jakub Wnorowski. 2021. "A Comparative Analysis of Energy Consumption by Conventional and Anchor Based Dynamic Positioning of Ship" Energies 14, no. 3: 524. https://doi.org/10.3390/en14030524







