A Comparative Study of the Scale Effect on the S-Shaped Characteristics of a Pump-Turbine Unit
Abstract
:1. Introduction
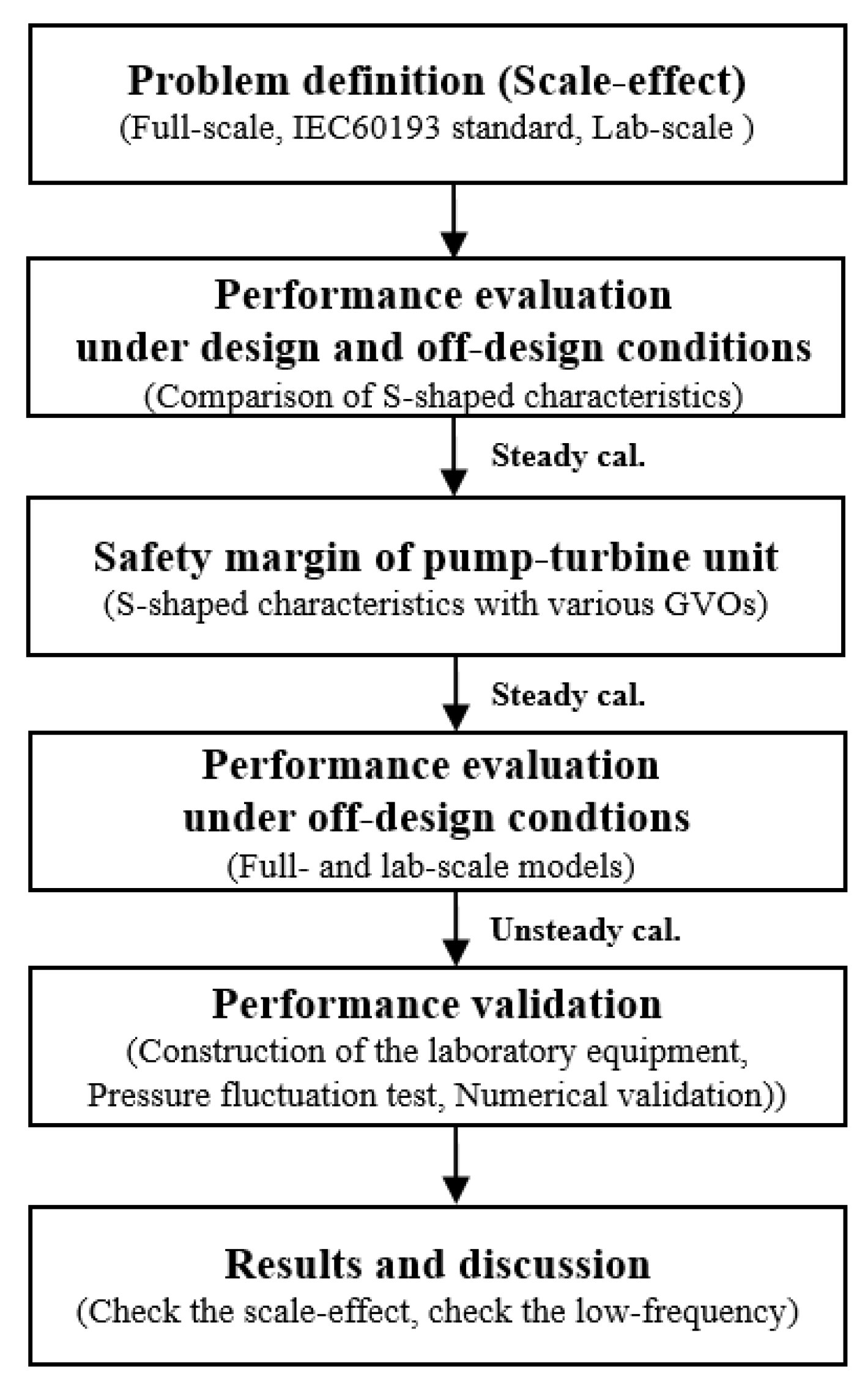
2. Research Procedure
3. Numerical Modeling and Schemes
3.1. Governing Equations
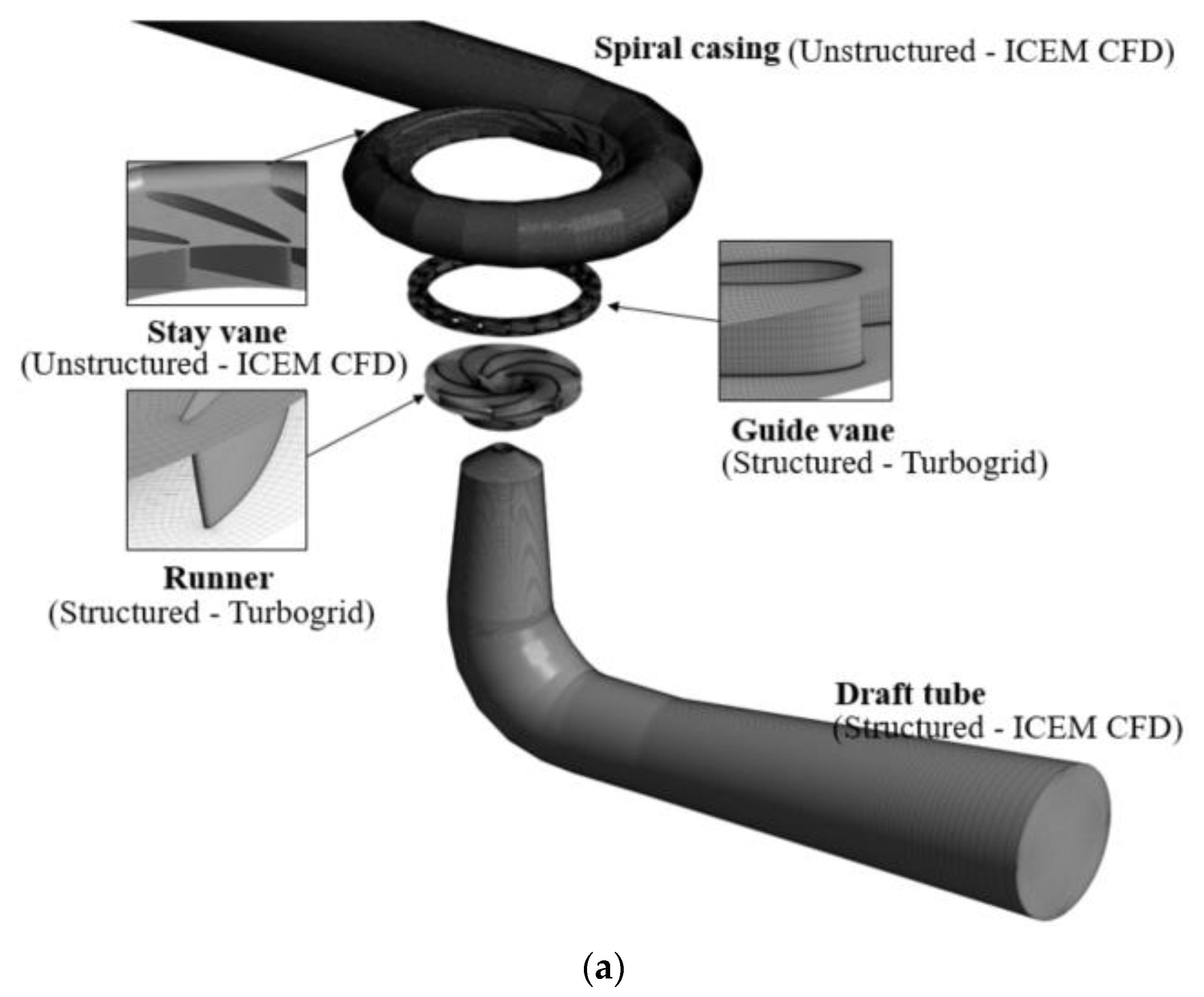
3.2. Computational Domain and Numerical Scheme
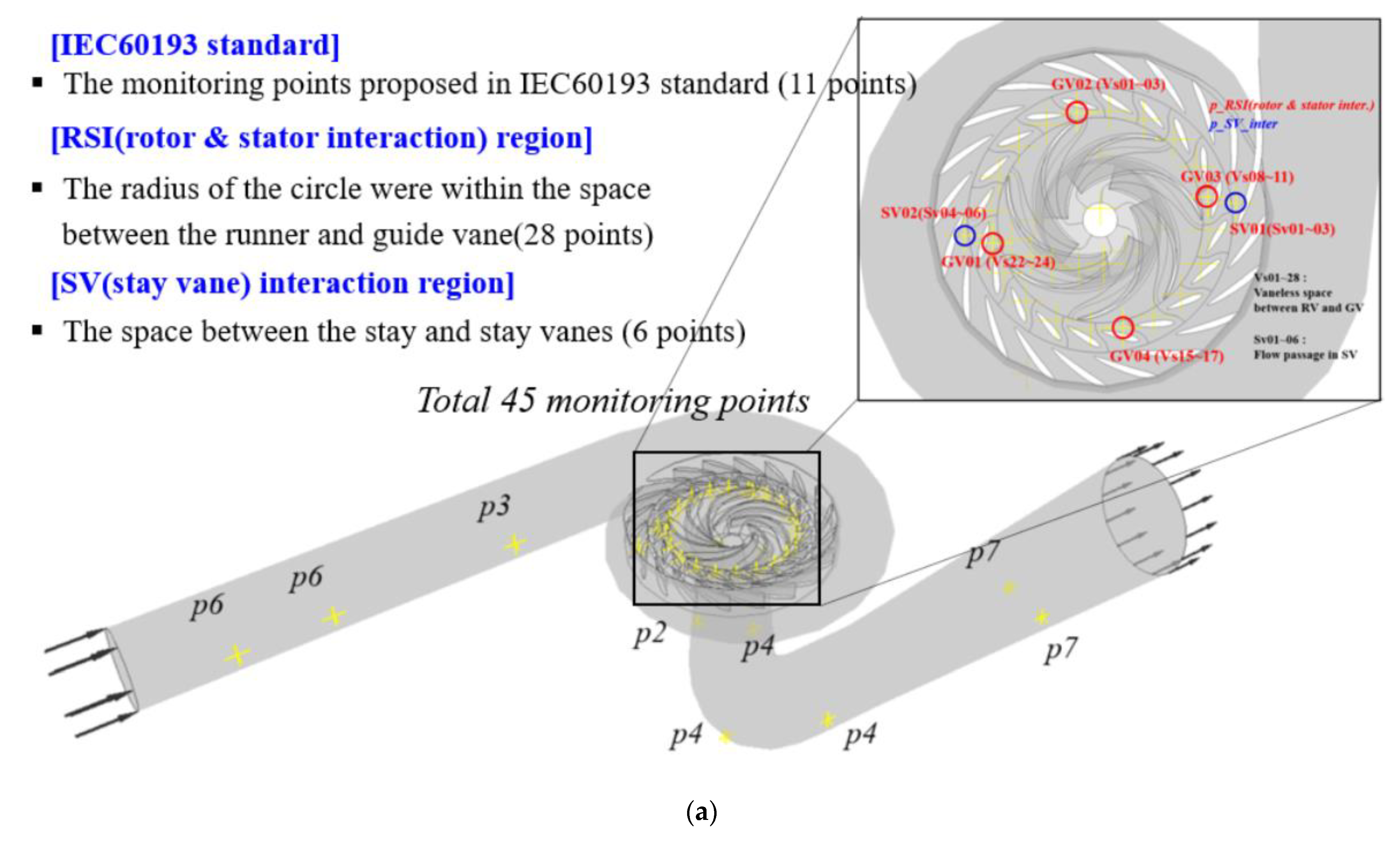
3.3. Schematic Diagram of Monitoring Points
4. Experimental Methods
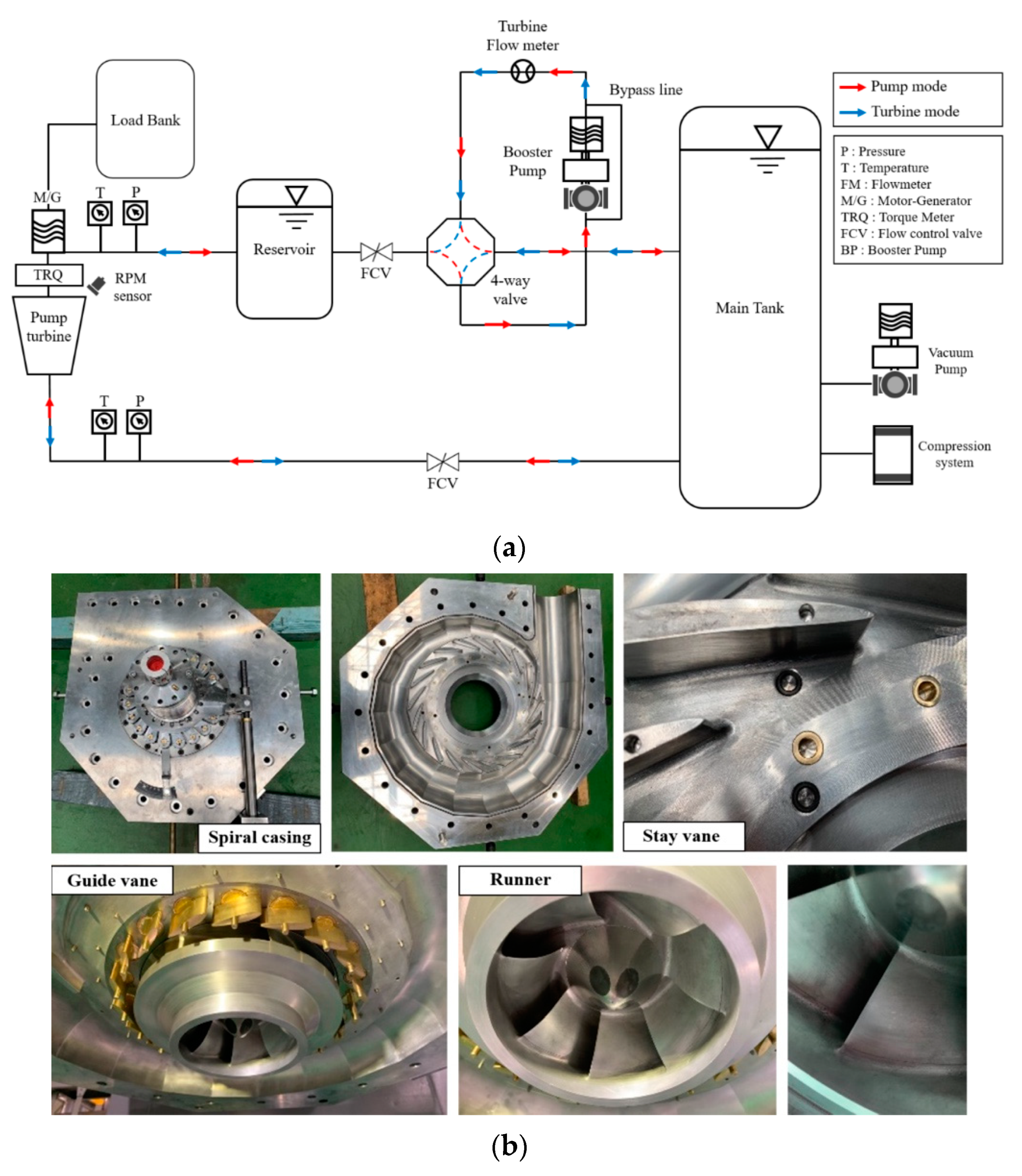
4.1. Experimental Methods of the Full-Scale Model
4.2. Experimental Methods of the Laboratory-Scale Model
5. Results and Discussion
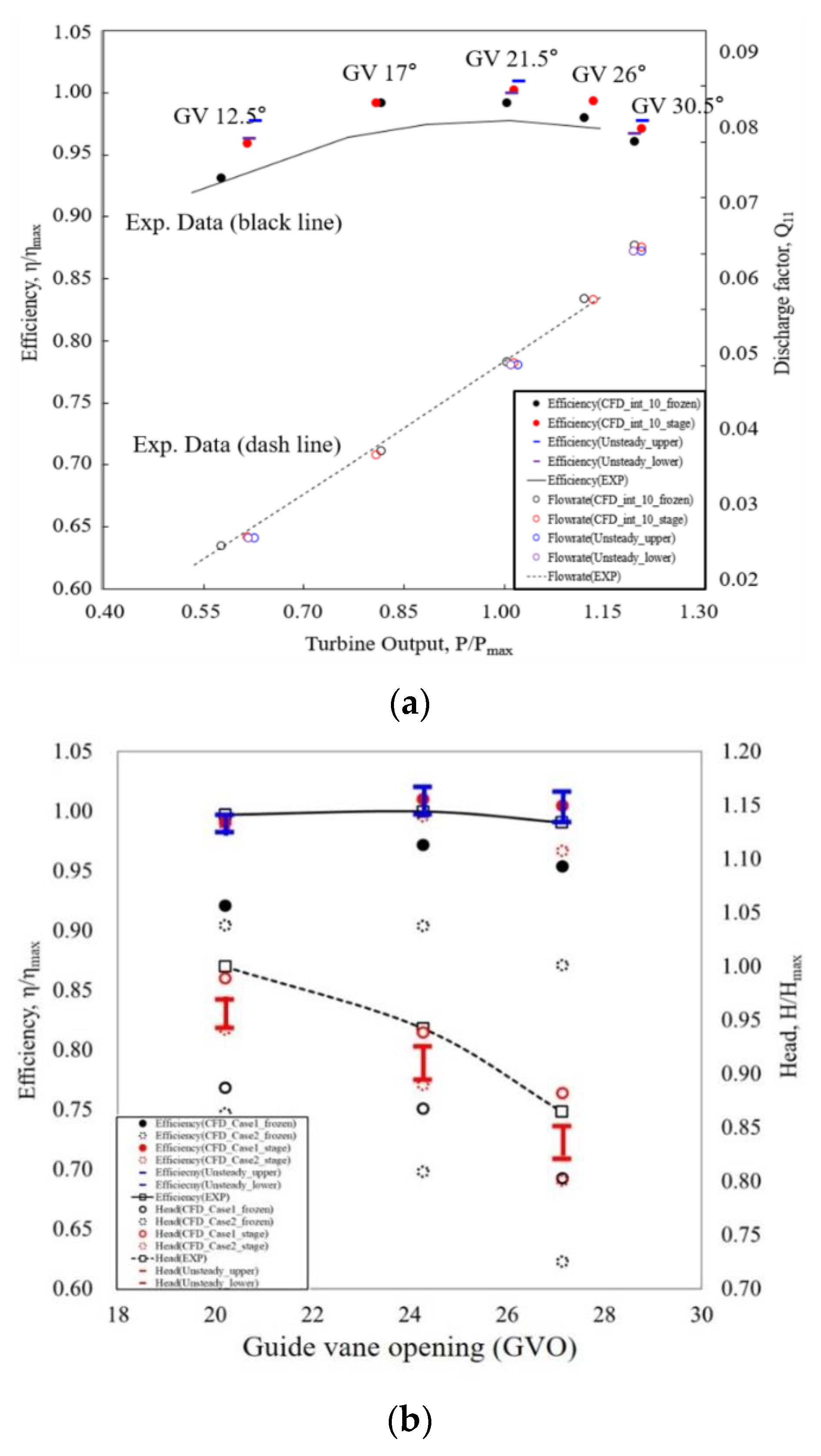
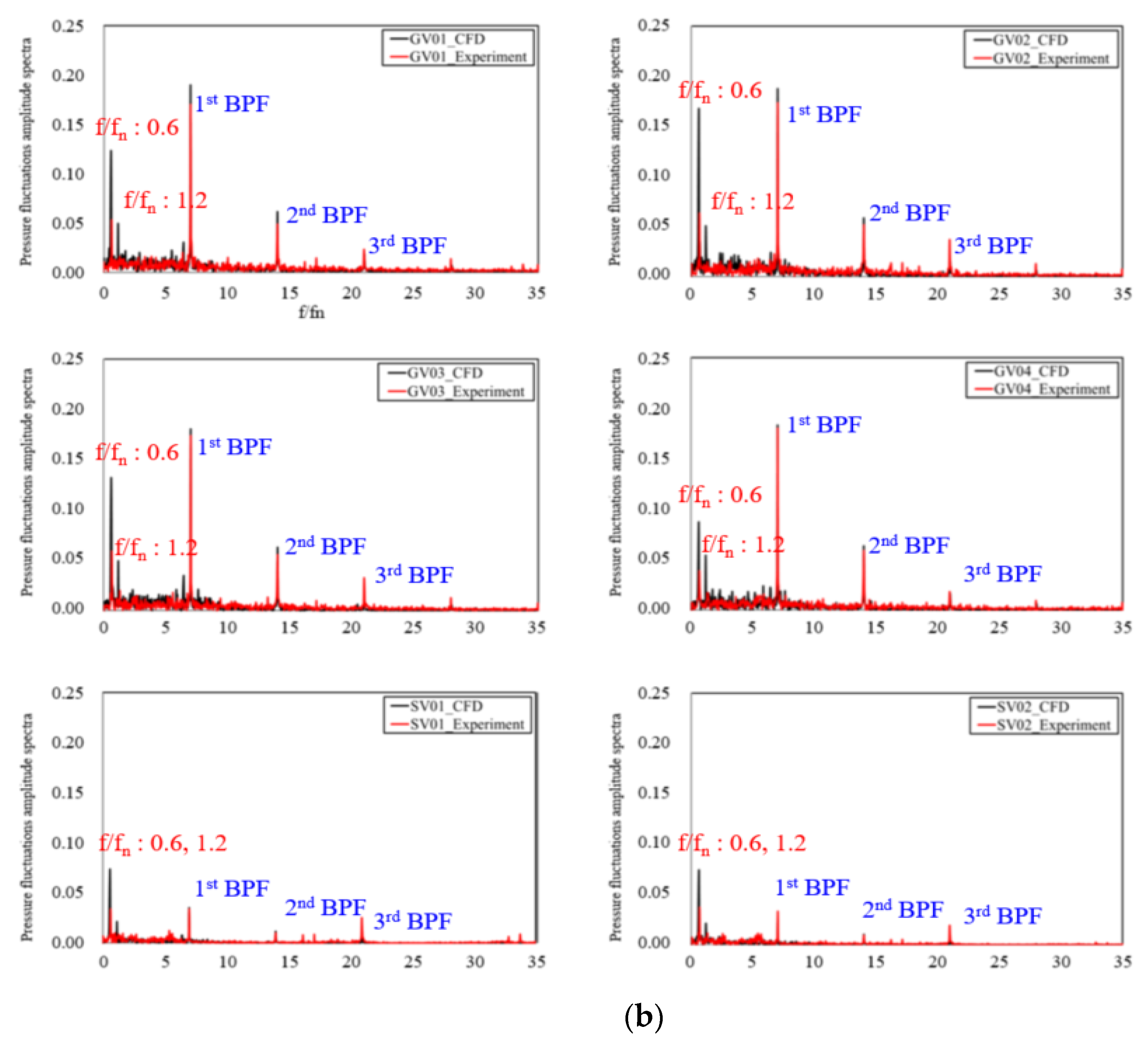
5.1. Validation of Numerical Results
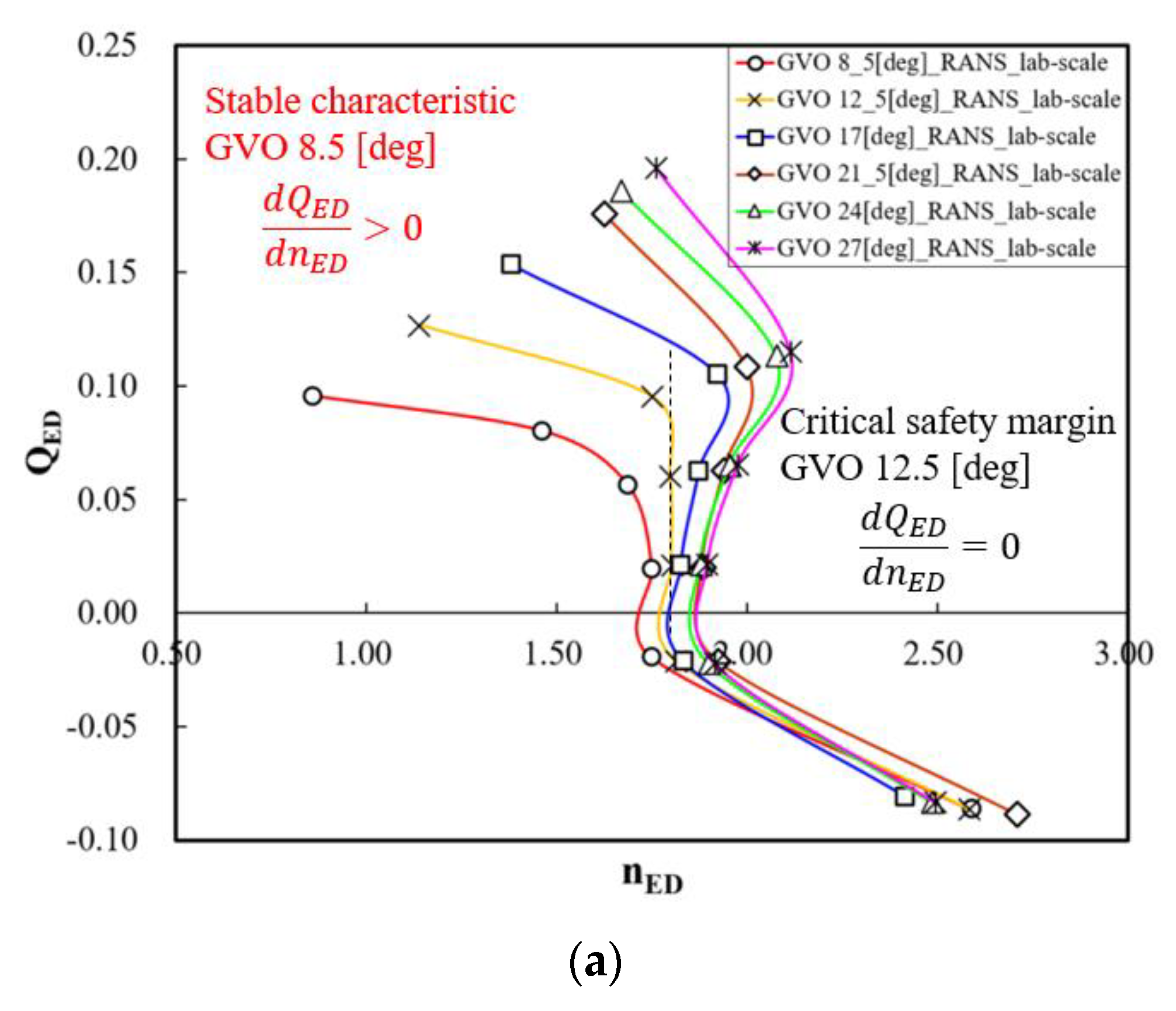
5.2. Predicting S-Shaped Characteristics between Model Scales
5.3. Safety Margin of S-Shaped Characteristics
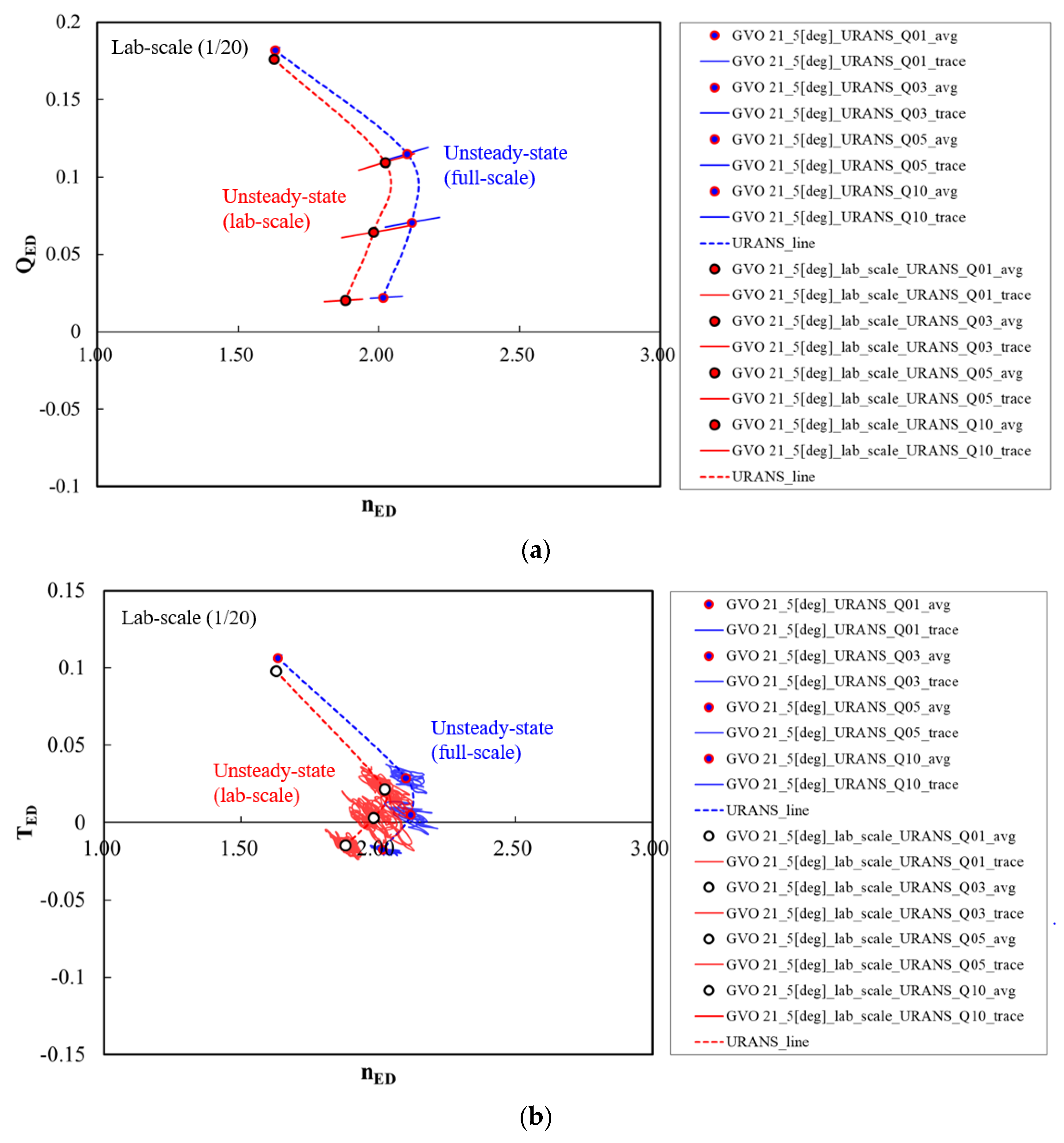
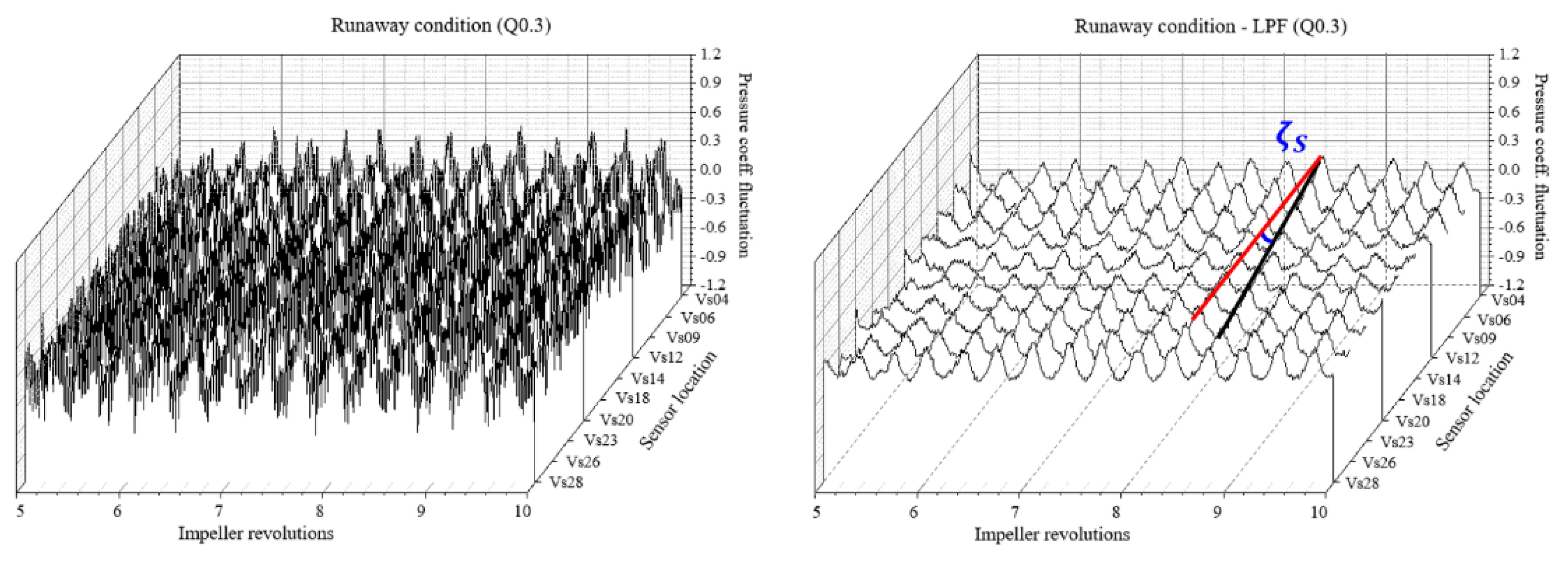
5.4. Comparison of Unsteady S-Shaped Characteristics
5.5. Unsteady Pressure and Internal Flow-Field Characteristics
6. Conclusions
- The S-shaped characteristics between model scales were compared to investigate the influence of the scale effect. For the results of both models, similar normalized values were predicted under normal operating conditions because the scale effect was not dominant. However, it is confirmed that the difference in the averaged-value increases as it went toward the transient region, and the variation of the speed and flow factors increases. The variations of pressure pulsation tended to peak and then decrease again in runaway conditions. Depending on the range of time and pulsation, the two models may be located at the same dimensionless value, or else the difference can be seen to be substantially greater. The slope of the speed and flow factors was similar for each operating point, as the function of the slope consists of mass flow rate, rotational speed, and reference diameter. The value of the head varies over time due to the flow blockage phenomena. Therefore, the averaged-value of each operating point is offset to a certain level.
- The numerical result was validated in comparison with experimental results. In the experiment of the full-scale model, transition conditions were difficult to perform in detail; therefore, steady and unsteady simulations were conducted under an optimal condition with various GVOs. The laboratory equipment was designed and manufactured for measuring the four-quadrant characteristic curve from the normal operating to the transition region. The numerical and experimental tendencies were well-matched in the overall operating and transition region. After comparing the values, the reliability of the numerical analysis was determined within 4%.
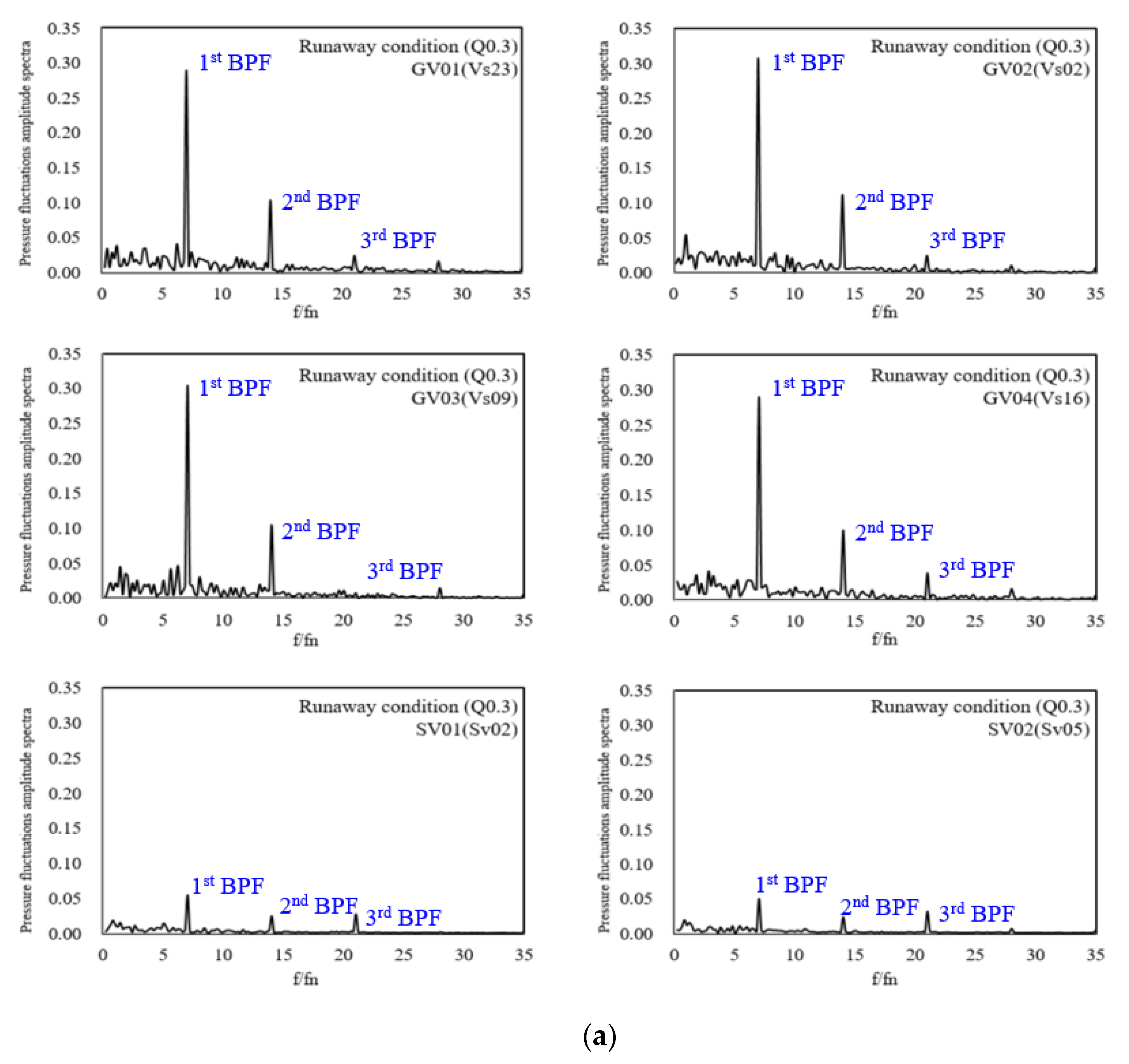
- The unsteady RANS equations in the SAS-SST model were discretized for a detailed analysis of the pressure characteristics. In the case of the full-scale model, there was no evidence of the RS. Therefore, the frequency spectra were only remarkable at f/fn = 7.0, 14.0, and 21.0 (representing the first, second, and third BPF harmonics). In the case of the laboratory-scale model, the frequency spectra were remarkable at f/fn = 0.6 (normalized frequency representing the RS) and at f/fn = 7, 14, and 21 (first, second, and third BPFs). These results indicate an RS with a frequency propagation approximately 60% of the rotational speed of the runner.
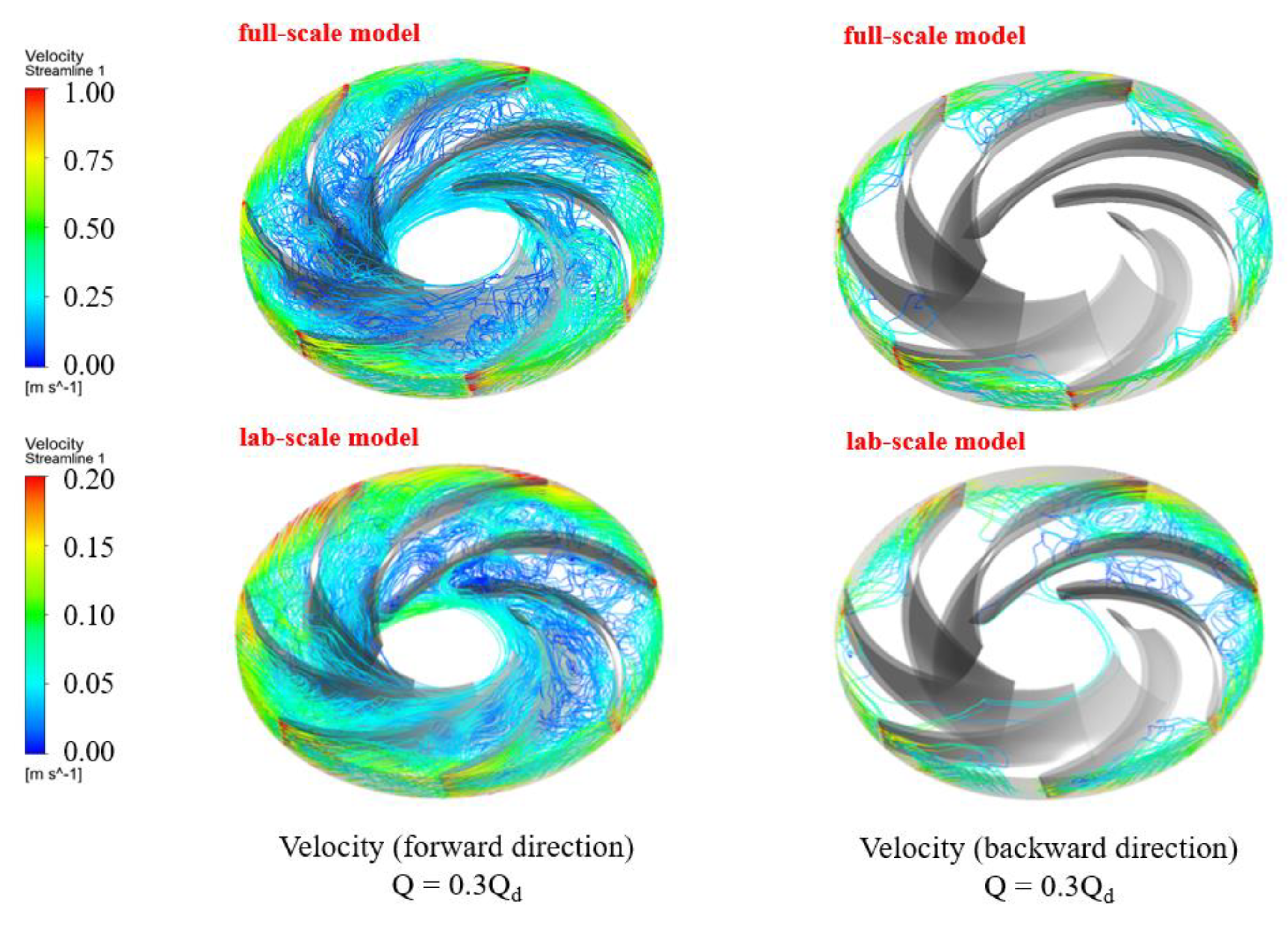
- The unsteady RANS equations in the SAS-SST model were discretized for a detailed analysis of the flow characteristics. Under the runaway condition of both models, the backflow became prominent. In the case of the full-scale model, the blade-loading distribution mostly showed a negative pattern. This means deflect flow from the flow blockage increasing the incidence angle whole the leading edge. As a result of checking the flow rate in and out of each flow passage, we found that there was no RS; therefore, the internal flow field was not completely blocked. In the case of the laboratory-scale model, some blade-loading distributions developed a positive shape, whereas others developed a negative shape. The characteristics of the passage adjacent to the stalled passage were also investigated.
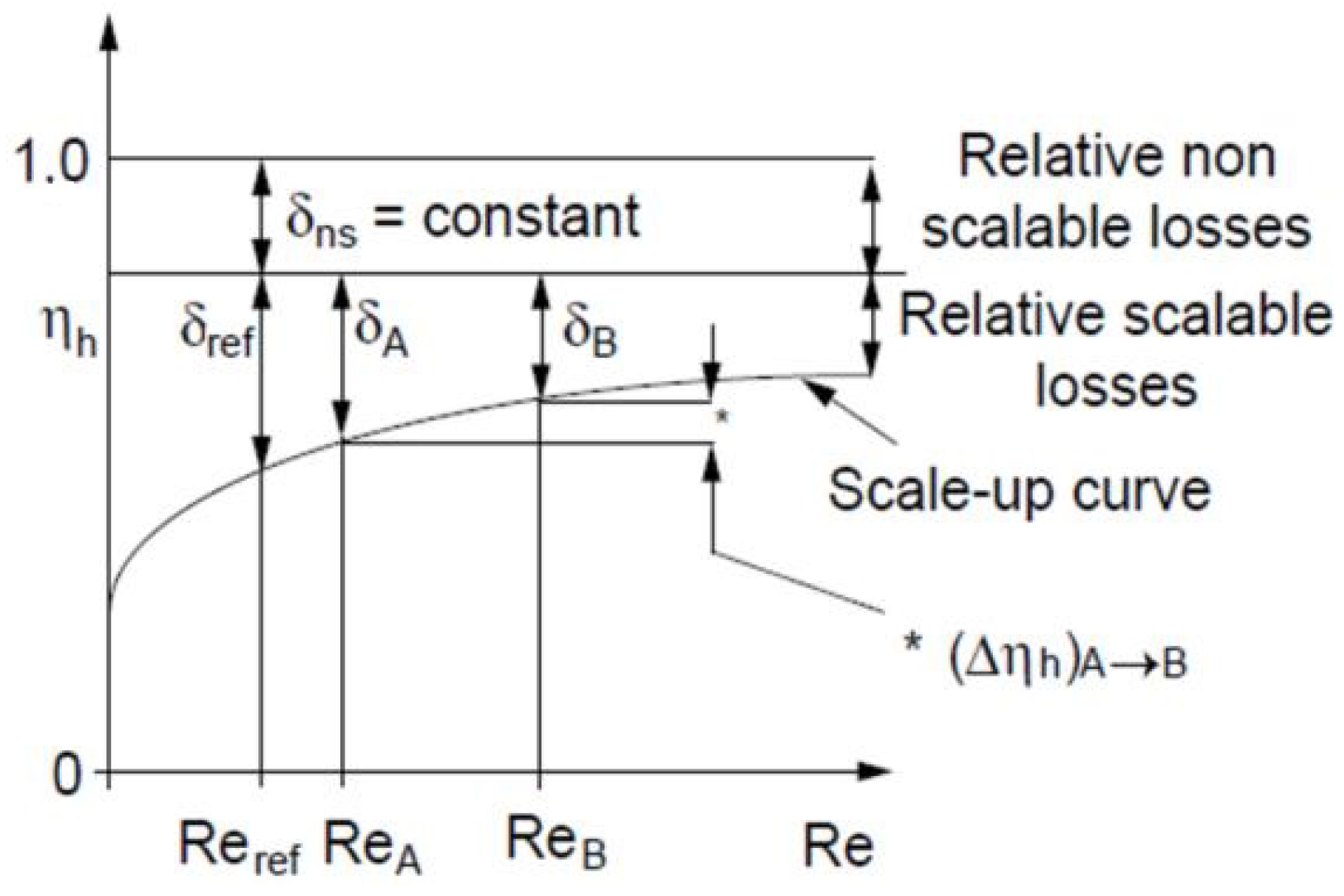
- The scale-up effect of the efficiency was calculated in hydraulically similar operating conditions having different Reynolds numbers. The numerical results obtained by calculating the hydraulic efficiency of the full- and laboratory-scale models were 95.15% and 91.38%, respectively. Based on the results of the scale-down model, the value calculated by predicting the hydraulic efficiency of the full-scale model by applying it to the formula was 94.61%. The scale-up effect between the models was found to be about 3.2%. The difference between the result calculated through numerical analysis and the value predicted through the calculation formula was 0.54%, confirming that the results obtained are fairly reliable.
- Predicting the efficiency and operating point of the scale effect through design is possible; however, slight variations occur in pressure and internal flow characteristics caused by hydrodynamic factors in the transition conditions. The reasons for these variations involve the composition of the grid system, turbulence model, surface roughness, and the development of an RS relative to the area of the flow passage, which require further investigation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| BPF | Blade-passing frequency |
| CFD | Computational fluid dynamics |
| DAQ | Data acquisition |
| FFT | Fast Fourier transform |
| FVM | Finite volume method |
| F1 | Blending function |
| GVO | Guide vane opening |
| G.V. | Guide vane |
| H | Head |
| L | Time length |
| Lvk | von Karman length scale |
| ΔP | Pressure rise |
| Q | Volume flow rate |
| QBEP | Volume flow rate at best efficiency point |
| Qd | Volume flow rate at design point |
| RANS | Reynolds-averaged Navier–Stokes |
| RMS | Root mean square |
| RSI | Rotor-stator interaction |
| RS | Rotating stall |
| R.V. | Runner vane |
| Rep | Reynolds number of prototype |
| ReM | Reynolds number of model |
| SAS | Scale-adaptive simulation |
| SST | Shear stress transport |
| Pressure coefficient fluctuation | |
| f | Frequency |
| fn | Rotating frequency |
| g | Acceleration of gravity |
| k | Turbulence kinetic energy |
| p | Instantaneously measured pressure |
| Time-averaged value of the pressure fluctuation | |
| t | Simulation time |
| ω | Angular velocity |
| y+ | Height of the first grid |
| ρ | Density |
| τ | Shear stress |
| τij | Specific Reynolds stress tensor |
| δref | Relative scalable losses at the point Reref |
References
- Lewi, N.S. Toward cost-effective solar energy use. Science 2017, 315, 798–801. [Google Scholar]
- Herbert, G.J.; Iniyan, S.; Sreevalsan, E.; Rajapandian, S. A review of wind energy technologies. Renew. Sustain. Energy Rev. 2005, 11, 1117–1145. [Google Scholar] [CrossRef]
- International Hydropower Association. Advancing Sustainable Hydropower, Activity and Strategy Report 2018–2019; International Hydropower Association: Paris, France, 2019. [Google Scholar]
- Widmer, C.; Staubli, T.; Ledergerber, N. Unstable characteristics and rotating stall in turbine brake operation of pump-turbines. J. Fluids Eng. 2011, 133, 041101. [Google Scholar] [CrossRef]
- Chen, W.M.; Kim, H.; Yamaguchi, H. Renewable energy in eastern Asia: Renewable energy policy review and comparative SWOT analysis for promoting renewable energy in Japan, South Korea, and Taiwan. Energy Policy 2014, 74, 319–329. [Google Scholar] [CrossRef]
- Hemmati, R.; Saboori, H. Emergence of hybrid energy storage systems in renewable energy and transport applications–A review. Renew. Sustain. Energy Rev. 2016, 65, 11–23. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. Hydraulic Turbines, Storage Pumps and Pump-Turbines e Model Acceptance Tests; Standard No, IEC 60193; International Electrotechnical Commission: Geneva, Switzerland, 1999. [Google Scholar]
- Zeng, W.; Yang, J.; Guo, W. Runaway instability of pump-turbines in S-shaped regions considering water compressibility. J. Fluids Eng. 2015, 137, 051401. [Google Scholar] [CrossRef]
- Martin, C.S. Stability of pump-turbines during transient operation. In Proceedings of the 5th Conference on Pressure Surges BHRA, Hannover, Germany, 22–24 September 1986. [Google Scholar]
- Hasmatuchi, V.; Farhat, M.; Roth, S.; Botero, F.; Avellan, F. Experimental evidence of rotating stall in a pump-turbine at off-design conditions in generating mode. J. Fluids Eng. 2011, 133, 051104. [Google Scholar] [CrossRef]
- Yin, J.L.; Wang, D.Z.; Wei, X.Z.; Wang, L.Q. Hydraulic improvement to eliminate S-shaped curve in pump turbine. J. Fluids Eng. 2013, 135, 071105. [Google Scholar] [CrossRef]
- Zuo, Z.; Liu, S.; Sun, Y.; Wu, Y. Pressure fluctuations in the vaneless space of high-head pump-turbines—A review. Renew. Sustain. Energy Rev. 2015, 41, 965–974. [Google Scholar] [CrossRef]
- Zuo, Z.; Fan, H.; Liu, S.; Wu, Y. S-shaped characteristics on the performance curves of pump-turbines in turbine mode–A review. Renew. Sustain. Energy Rev. 2016, 60, 836–851. [Google Scholar] [CrossRef]
- Cavazzini, G.; Houdeline, J.B.; Pavesi, G.; Teller, O.; Ardizzon, G. Unstable behavior of pump-turbines and its effects on power regulation capacity of pumped-hydro energy storage plants. Renew. Sustain. Energy Rev. 2018, 94, 399–409. [Google Scholar] [CrossRef]
- Favrel, A.; Junior, J.G.P.; Landry, C.; Alligne, S.; Andolfatto, L.; Nicolet, C.; Avellan, F. Prediction of hydro-acosutic resonances in hydropower plants by a new approach based on the concept of swirl number. J. Hydrualic Res. 2019, 58, 87–104. [Google Scholar] [CrossRef]
- Valentin, D.; Presas, A.; Valero, C.; Egusquiza, M.; Egusquiza, E.; Gomes, J.; Avellan, F. Transposition of the mechanical behaviour from model to prototype of Francis turbine. Renew. Energy 2020, 152, 1011–1023. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, Z.; Cheng, Y.; Zhang, X.; Liu, K.; Xia, L. Differences of flow patterns and pressure pulsations in four prototype pump-turbines during runaway Transient processes. Energies 2020, 152, 5269. [Google Scholar] [CrossRef]
- Chen, T.J.; Luo, X.Q.; Guo, P.C.; Wu, Y.L. 3-D Simulation of a prototype pump-turbine during starting period in turbine model. In IOP Conference Series: Materials Science and Engineering; IOPscience: Bristol, UK, 2013; Volume 52, p. 052028. [Google Scholar]
- Liu, J.T.; Liu, S.H.; Sun, Y.K.; Wu, Y.L.; Wang, L.Q. Numerical study of vortex rope during load rejection of a prototype pump-turbine. In IOP Conference Series: Earth and Environmental Science; IOPscience: Bristol, UK, 2012; Volume 15, p. 032044. [Google Scholar]
- Suh, J.W.; Kim, S.J.; Kim, J.H.; Yang, H.M.; Joo, W.G.; Hwang, T.G.; Lee, K.H.; Shrestha, U.; Chen, Z.; Cho, H.K.; et al. Establishment of Numerical analysis method of Pump-turbine for Pumped Storage. KSFM J. Fluid Mach. 2019, 22, 22–29. [Google Scholar] [CrossRef]
- Suh, J.W.; Kim, S.J.; Kim, J.H.; Joo, W.G.; Park, J.; Choi, Y.S. Effect of interface condition on the hydraulic characteristics of a pump-turbine at various guide vane opening conditions in pump mode. Renew. Energy 2020, 154, 986–1004. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A one-equation turbulence model for aerodynamic flows. In 30th Aerospace Sciences Meeting and Exhibit; National Aeronautics and Space Administration: Washington, DC, USA, 1992; p. 439. [Google Scholar]
- Jones, W.P.; Launder, B.E. The prediction of laminarization with a two-equation model of turbulence. Int. J. Heat Mass Transf. 1972, 15, 301–314. [Google Scholar] [CrossRef]
- Mohammadi, B.; Pironneau, O. Analysis of the K-Epsilon Turbulence Model; IAEA: Vienna, Austria, 1993. [Google Scholar]
- Chen, Y.S.; Kim, S.W. Computation of Turbulent Flows Using an Extended K-Epsilon Turbulence Closure Model; National Aeronautics and Space Administration: Washington, DC, USA, 1987.
- Rotta, J.C. Statistische theorie nichthomogener turbulenz. Z. Phys. 1951, 129, 547–572. [Google Scholar] [CrossRef]
- Rotta, J.C. Über eine methode zur Berechnung turbulenter Scherströmungen. Aerodyn. Vers. Rep. 1968, 69, A14. [Google Scholar]
- Menter, F.R.; Egorov, Y. The scale-adaptive simulation method for unsteady turbulent flow predictions. Part 1: Theory and model description. Flow Turbul. Combust. 2010, 85, 113–138. [Google Scholar] [CrossRef]
- ANSYS CFX-19.2. ANSYS CFX-Solver Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2019. [Google Scholar]
- Lee, Y.G.; Yuk, J.H.; Kang, M.H. Flow analysis of fluid machinery using CFX pressure-based coupled and various turbulence model. KSFM J. Fluid Mach. 2004, 7, 82–90. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Wu, Y. A review of rotating stall in reversible pump turbine. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 1181–1204. [Google Scholar] [CrossRef] [Green Version]
- International Electrotechnical Commission. Field Acceptance Tests to Determine the Hydraulic Performance of Hydraulic Turbines, Storage Pumps and Pump-Turbines; Standard No, IEC 60041; International Electrotechnical Commission: Geneva, Switzerland, 1991. [Google Scholar]
- OriginLab Corporation. Origin Pro 2019b, Origin Manual; OriginLab Corporation: Northampton, MA, USA, 2019. [Google Scholar]
- National Instruments Corporation. LabVIEW, LabVIEW User; National Instruments Corporation: Austin, TX, USA, 2000. [Google Scholar]
- Cavazzini, G.; Covi, A.; Pavesi, G.; Ardizzon, G. Analysis of the unstable behavior of a pump-turbine in turbine mode: Fluid-dynamical and spectral characterization of the S-shape characteristic. J. Fluids Eng. 2016, 138, 021105. [Google Scholar] [CrossRef]
- Brennen, C.E. Hydrodynamics of Pumps; Cambridge University Press: Cambridge, UK, 1994; pp. 146–148. [Google Scholar]



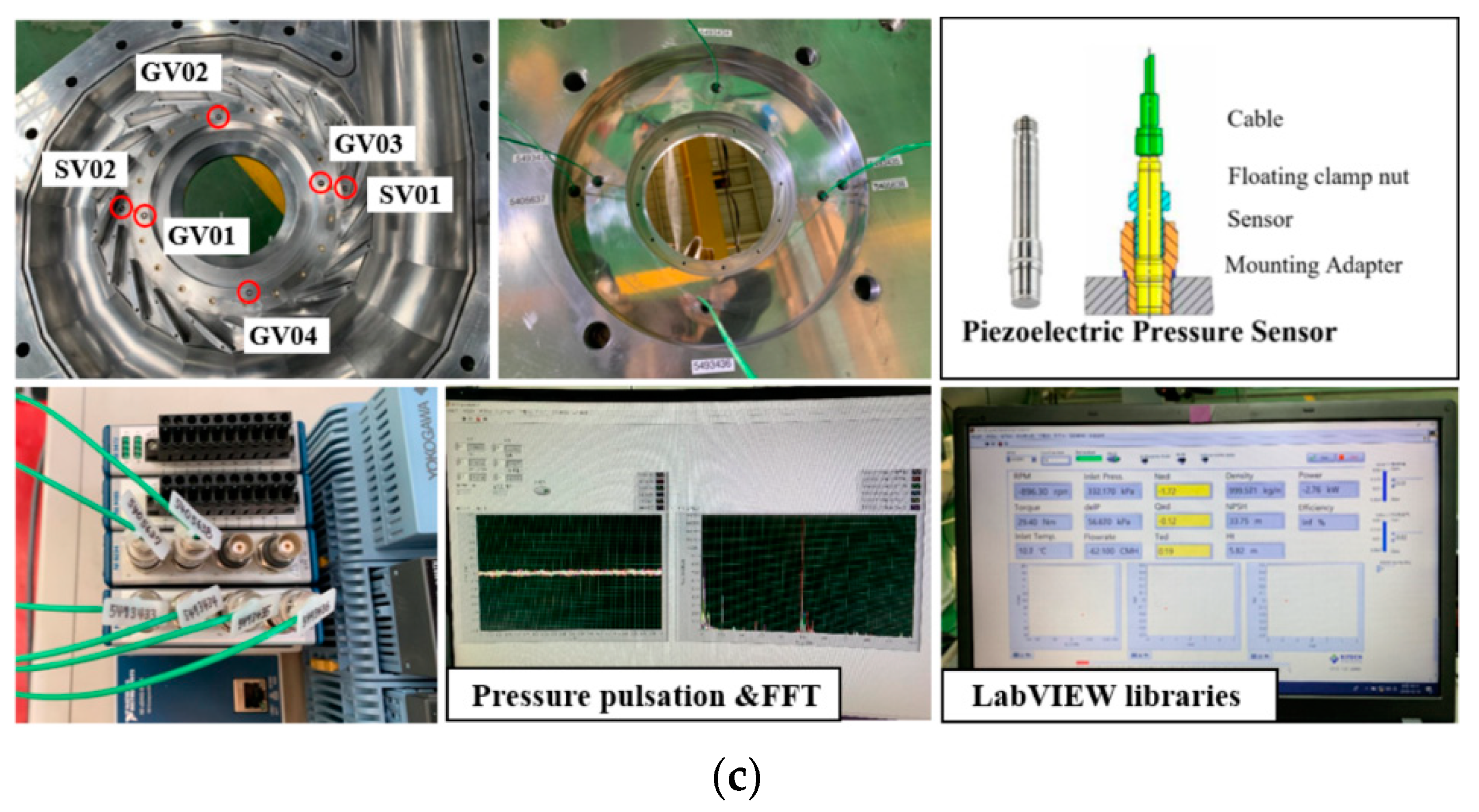







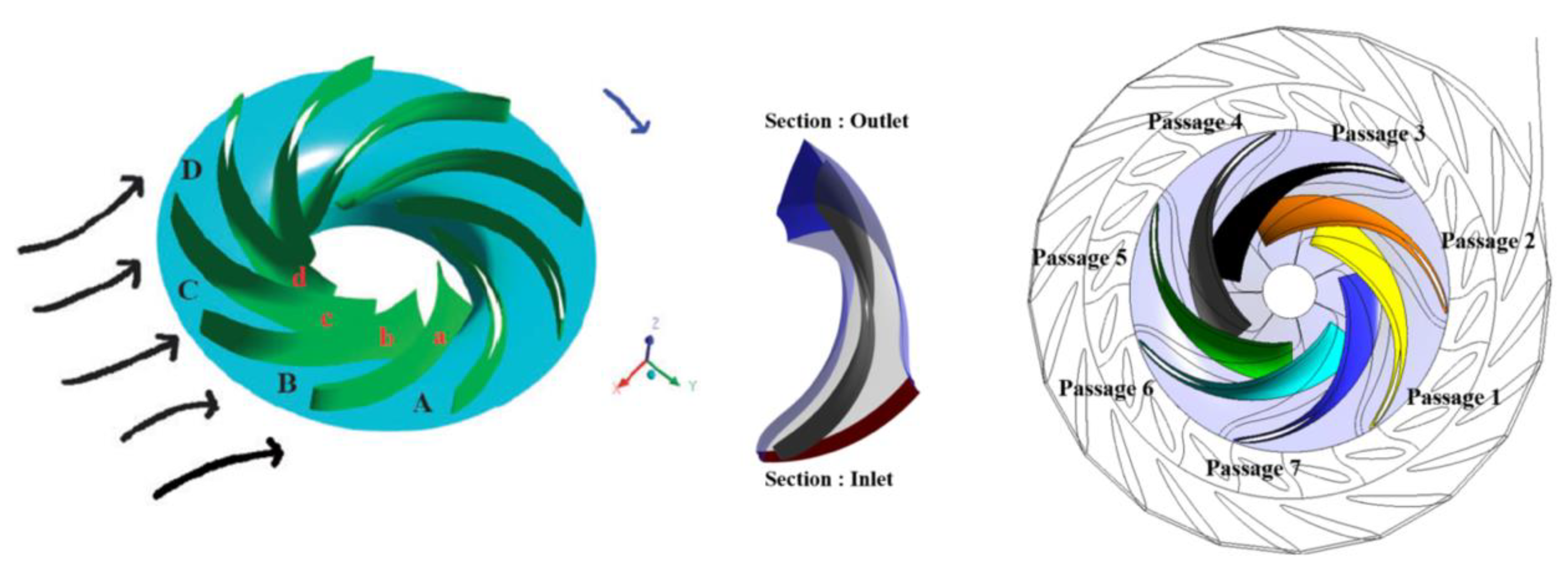

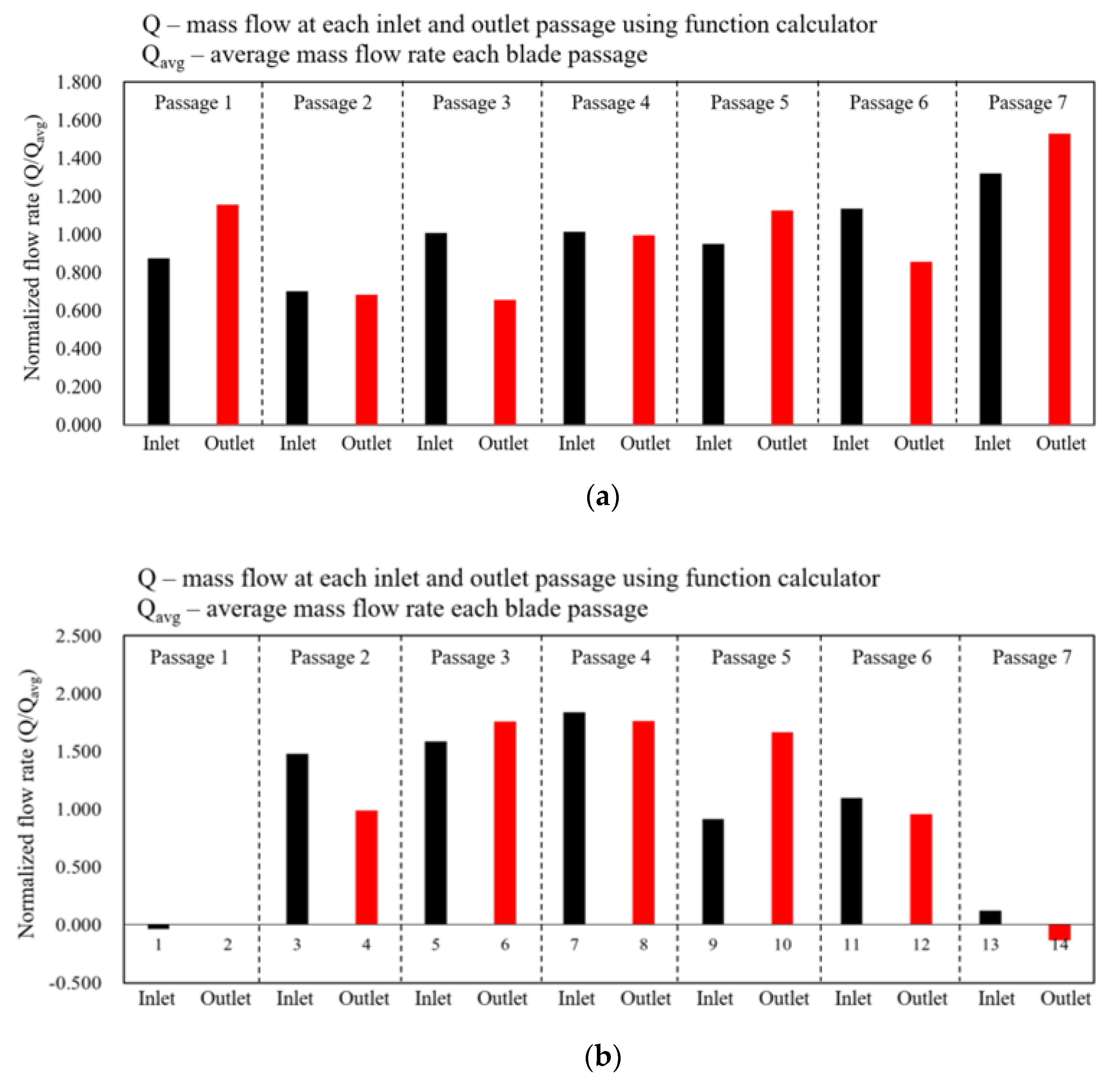
| Full-Scale (1) | IEC60193 Standard-Scale (1/11) | Laboratory-Scale (1/20) | |
|---|---|---|---|
| Reference diameter [m] | 2.77 | 0.25 | 0.1385 |
| Number of nodes | 1.0 × 107 | 1.0 × 107 | 1.0 × 107 |
| Value of y+ (RV/GV/SV/SP/DT) | y+ ≈ 100 (RV/GV) y+ ≈ 150 (SV/SP/DT) | y+ ≈ 2 (RV/GV) y+ ≈ 2 (SV/SP/DT) | y+ ≈ 1 (RV/GV) y+ ≈ 1 (SV/SP/DT) |
| Reynolds number | 1.4 × 108 | 7.2 × 106 | 3.6 × 105 |
| Turbulence model | SST high-Reynolds number | SST low-Reynolds number | SST low-Reynolds Number |
| Turbineand TurbineBrake | |
| Inlet (spiral casing) | Total pressure (energy coefficient, 0.117) |
| Outlet (draft tube) | Mass flow rate (1.0QBEP, 0.5QBEP, 0.3QBEP, 0.1QBEP) |
| Reverse pump (reverse flow direction) | |
| Inlet (draft tube) | Average static pressure (energy coefficient, 0.117) |
| Outlet (spiral casing) | Mass flow rate (0.2QBEP, 0.1QBEP) |
| Speed factor | 2.91 (360, 1200, 1800 rev/min) |
| Discharge factor | 0.065 (89, 0.21, 0.054 m3/s) |
| Turbulence model | SST high-Reynolds number (full-scale) SST low-Reynolds number (IEC60193 standard-scale, laboratory-scale) |
| Guide vane opening | 21.5° |
| Interface condition | Stage-average |
| Calculation type | Steady-state calculation |
| Turbineand TurbineBrake | |
| Inlet (spiral casing) | Total pressure (energy coefficient, 0.117) |
| Outlet (draft tube) | Mass flow rate (1.0QBEP,0.5QBEP,0.3QBEP,0.1QBEP) |
| Reverse pump (reverse flow direction) | |
| Inlet (draft tube) | Average static pressure (energy coefficient, 0.117) |
| Outlet (spiral casing) | Mass flow rate (0.2QBEP, 0.1QBEP) |
| Speed factor | 2.91 (1800 rev/min) |
| Discharge factor | 0.065 (0.054 m3/s) |
| Turbulence model | SST low-Reynolds number |
| Guide vane opening | 8.5°, 12.5°, 17°, 21.5°, 24°, 27° |
| Interface condition | Stage-average |
| Calculation type | Steady-state calculation |
| Turbine and Turbine Brake | |
|---|---|
| Guide vane opening | 21.5° |
| Total time | 1.667 [s]–10 revolutions |
| Time step | 0.00046305 [s], 1° |
| Initial condition | Result of steady-state calculation |
| Turbulence model | SAS-SST model |
| Interface condition | Transient rotor stator |
| Calculation type | Unsteady-state calculation |
| Operating Point | Factor | Experiments | Simulation (Steady-State) | Simulation (Steady State) |
|---|---|---|---|---|
| Normal operating (Q/Qd = 1.0) | ned | 1.5672 | 1.6234 | 1.6263 |
| Qed | 0.1697 | 0.1759 | 0.1762 | |
| Ted | 0.0952 | 0.0986 | 0.0978 | |
| Half-load condition (Q/Qd = 0.5) | ned | 2.0303 | 1.9979 | 2.0217 |
| Qed | 0.1107 | 0.1083 | 0.1095 | |
| Ted | 0.0146 | 0.0217 | 0.0217 | |
| Runaway condition (Q/Qd = 0.3) | ned | 2.0332 | 1.9368 | 1.9811 |
| Qed | 0.0645 | 0.0630 | 0.0644 | |
| Ted | −0.0067 | 0.0021 | 0.0033 | |
| Low-discharge condition (Q/Qd = 0.1) | ned | 1.9481 | 1.8797 | 1.8796 |
| Qed | 0.0211 | 0.0204 | 0.0203 | |
| Ted | −0.0276 | −0.0134 | −0.0145 |
| Operating Point | Factor | IEC60193 Standard-Scale (Steady State) | Laboratory-Scale (Steady State) |
|---|---|---|---|
| Normal operating condition | ned | 1.6282 | 1.6234 |
| Qed | 0.1765 | 0.1759 | |
| Ted | 0.0998 | 0.0986 | |
| Half-load condition | ned | 2.0030 | 1.9979 |
| Qed | 0.1086 | 0.1083 | |
| Ted | 0.0222 | 0.0217 | |
| Runaway condition | ned | 1.9340 | 1.9368 |
| Qed | 0.0630 | 0.0630 | |
| Ted | 0.0021 | 0.0021 | |
| Low-discharge condition | ned | 1.8822 | 1.8797 |
| Qed | 0.0204 | 0.0204 | |
| Ted | −0.0131 | −0.0134 | |
| Reverse pump condition | Ned | 1.9065 | 1.9199 |
| Qed | −0.0208 | −0.0209 | |
| Ted | −0.0423 | −0.0429 |
| Operating Point | Factor | Full-Scale (Averaged Value) | Laboratory-Scale (Averaged Value) |
|---|---|---|---|
| Normal operating condition | ned | 1.6317 | 1.6263 |
| Qed | 0.1819 | 0.1762 | |
| Ted | 0.1063 | 0.0978 | |
| Half-load condition | ned | 2.1001 | 2.0217 |
| Qed | 0.1150 | 0.1095 | |
| Ted | 0.0287 | 0.0217 | |
| Runaway condition | ned | 2.1201 | 1.9811 |
| Qed | 0.0708 | 0.0644 | |
| Ted | 0.0052 | 0.0033 | |
| Low-discharge condition | ned | 2.0148 | 1.8796 |
| Qed | 0.0221 | 0.0203 | |
| Ted | −0.0174 | −0.0145 |
| (Δηh)M*→P | δref | Vref | Reref | ReoptM | ReP | ReM* | ηhoptM |
|---|---|---|---|---|---|---|---|
| 0.0323 | 0.051579 | 0.7 | 7,000,000 | 1,800,682 | 144,054,539 | 1,800,682 | 0.9138 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suh, J.-W.; Kim, S.-J.; Yang, H.-M.; Kim, M.-S.; Joo, W.-G.; Park, J.; Kim, J.-H.; Choi, Y.-S. A Comparative Study of the Scale Effect on the S-Shaped Characteristics of a Pump-Turbine Unit. Energies 2021, 14, 525. https://doi.org/10.3390/en14030525
Suh J-W, Kim S-J, Yang H-M, Kim M-S, Joo W-G, Park J, Kim J-H, Choi Y-S. A Comparative Study of the Scale Effect on the S-Shaped Characteristics of a Pump-Turbine Unit. Energies. 2021; 14(3):525. https://doi.org/10.3390/en14030525
Chicago/Turabian StyleSuh, Jun-Won, Seung-Jun Kim, Hyeon-Mo Yang, Moo-Sung Kim, Won-Gu Joo, Jungwan Park, Jin-Hyuk Kim, and Young-Seok Choi. 2021. "A Comparative Study of the Scale Effect on the S-Shaped Characteristics of a Pump-Turbine Unit" Energies 14, no. 3: 525. https://doi.org/10.3390/en14030525
APA StyleSuh, J.-W., Kim, S.-J., Yang, H.-M., Kim, M.-S., Joo, W.-G., Park, J., Kim, J.-H., & Choi, Y.-S. (2021). A Comparative Study of the Scale Effect on the S-Shaped Characteristics of a Pump-Turbine Unit. Energies, 14(3), 525. https://doi.org/10.3390/en14030525







