Reduced-Order-VSM-Based Frequency Controller for Wind Turbines
Abstract
:1. Introduction
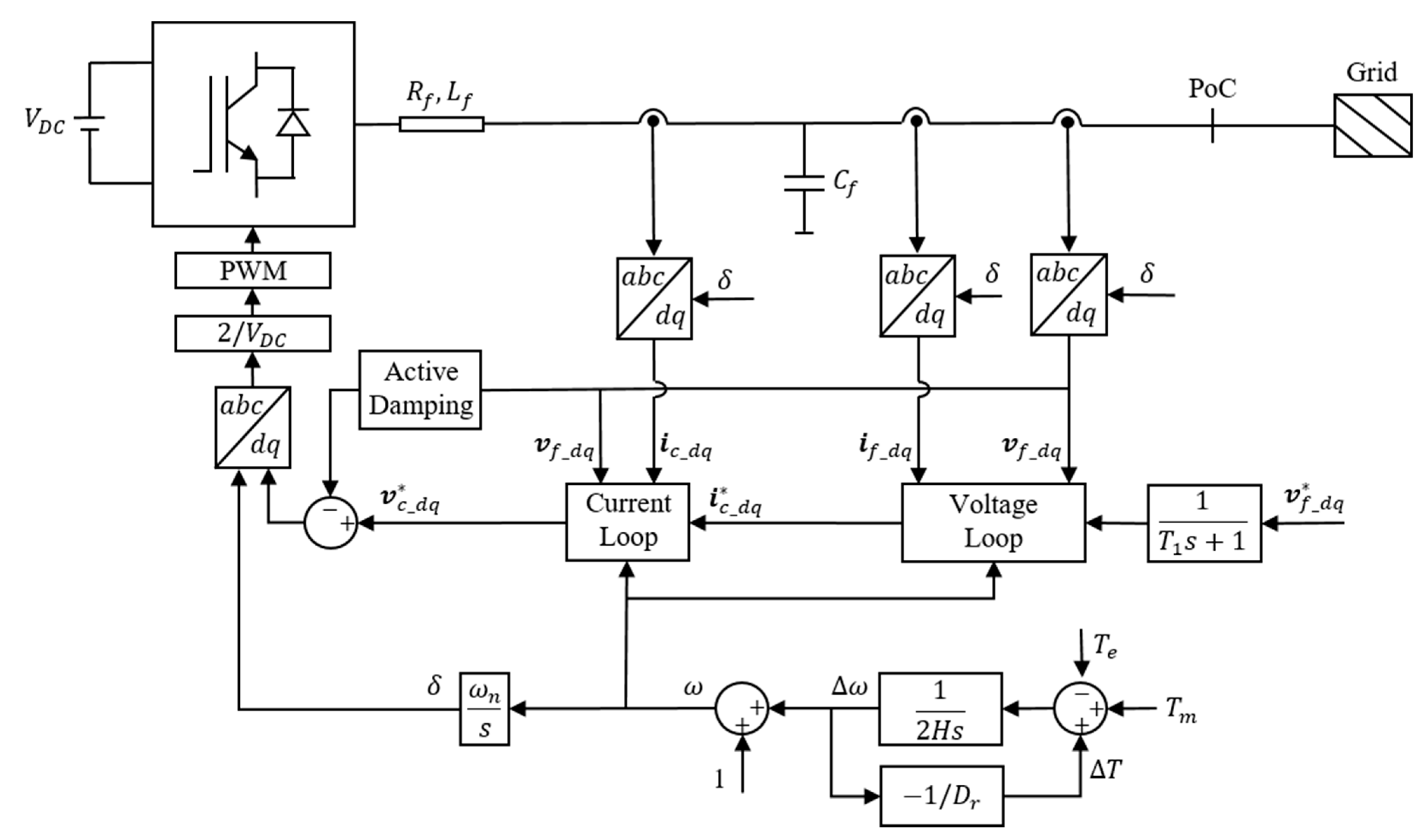
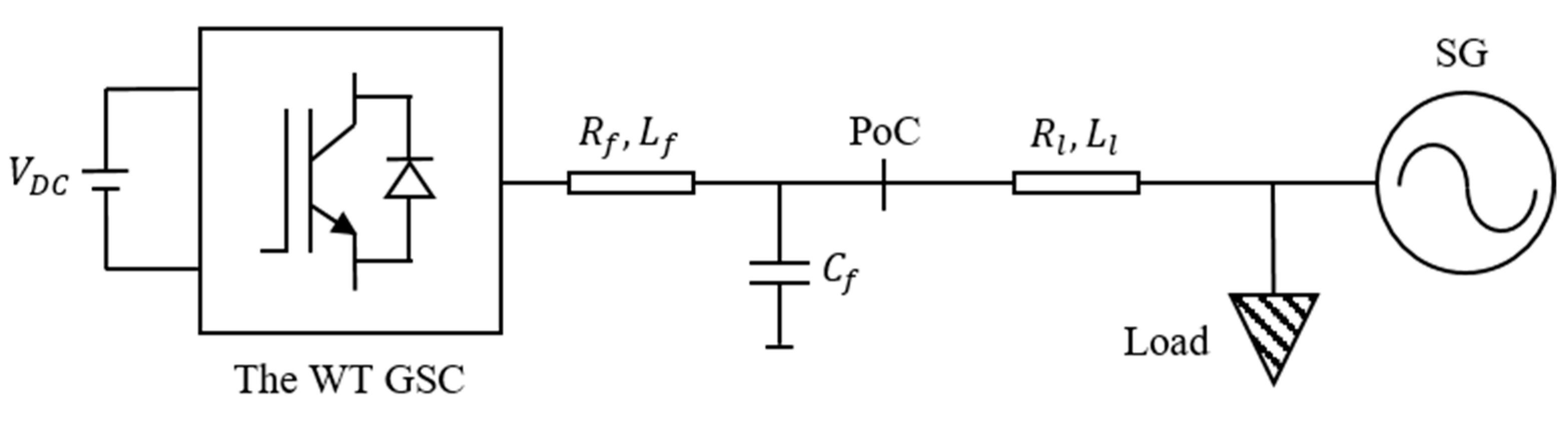
2. Modeling and Control of the GSC
Frequency Controller
- H = inertia constant in MW·s/MVA;
- = rated angular velocity in electrical rad/s;
- δ = angular position in electrical radians;
- t = time in s;
- = mechanical torque in per unit (pu);
- = electromagnetic torque in per unit (pu).
- = angular velocity in electrical rad/s;
- = deviation of angular velocity in pu
- =.
3. Simulation Results
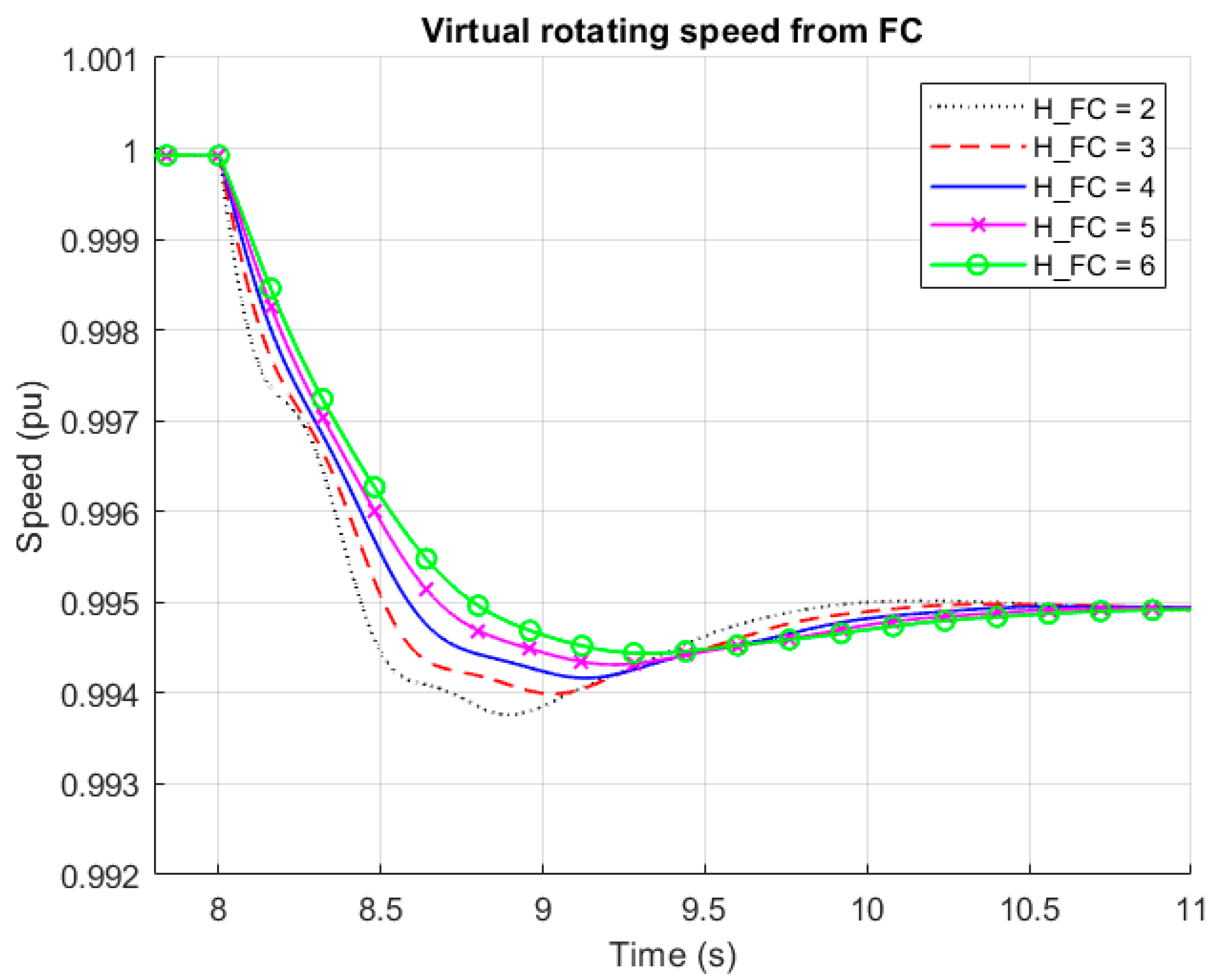
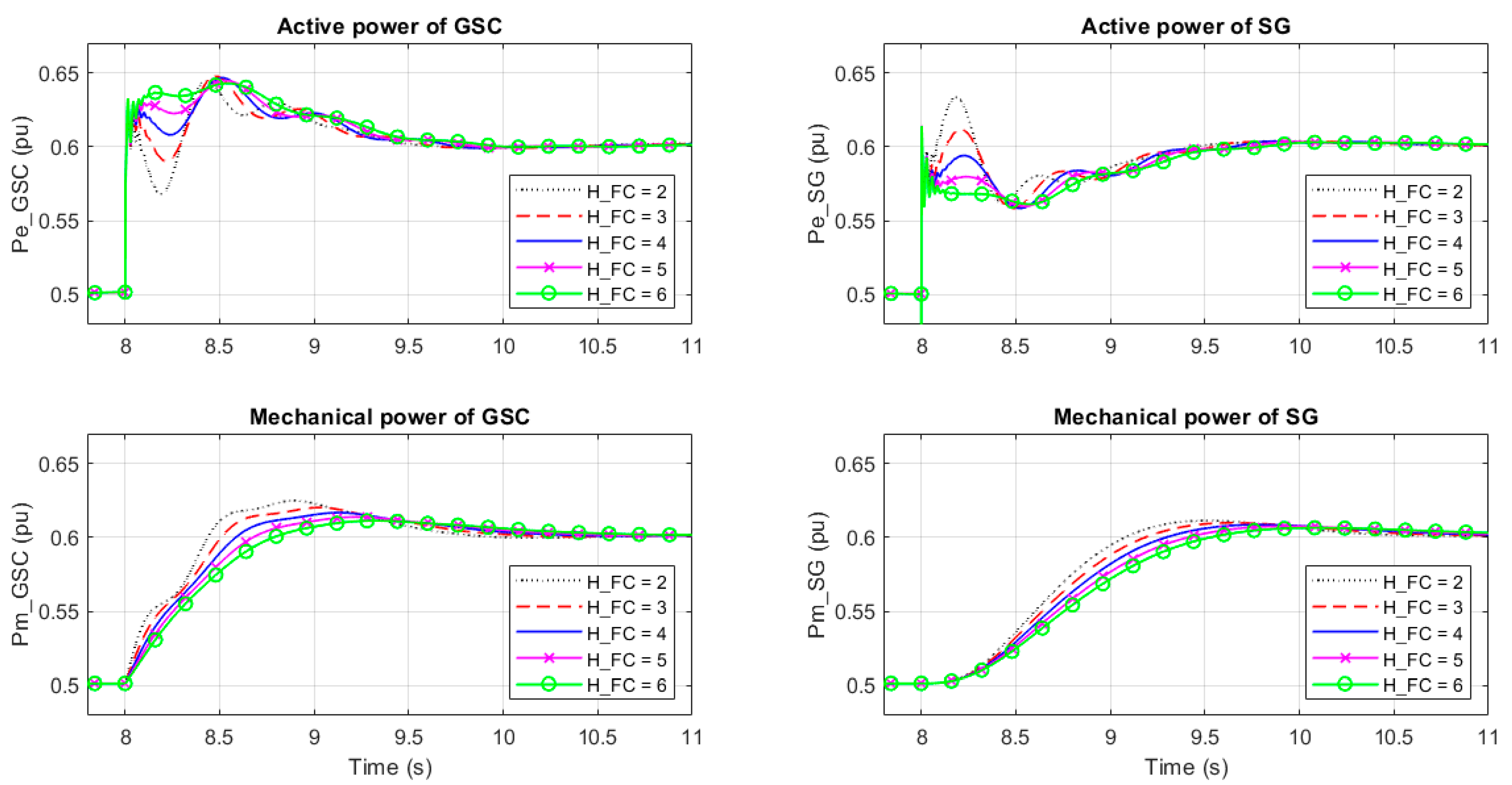
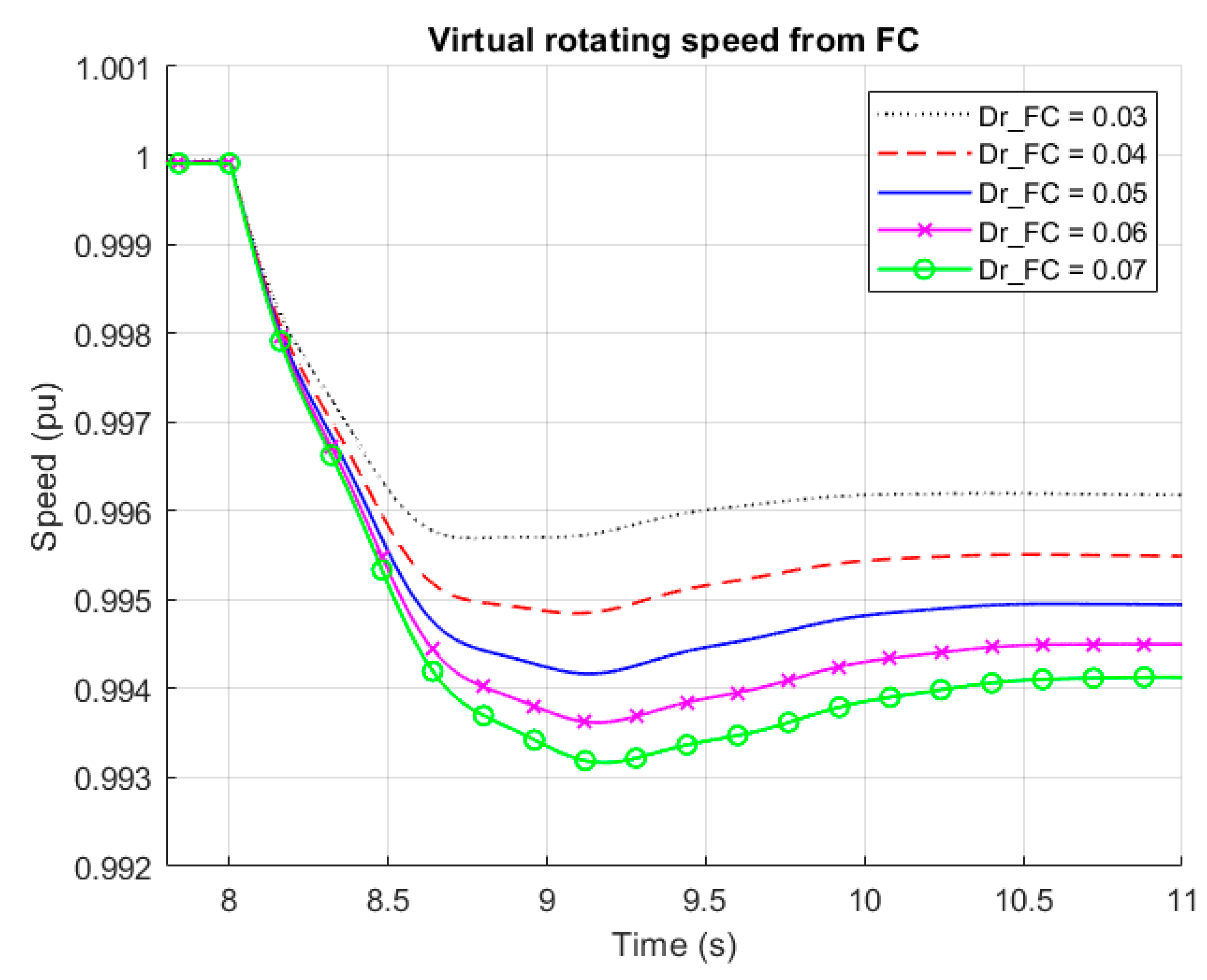
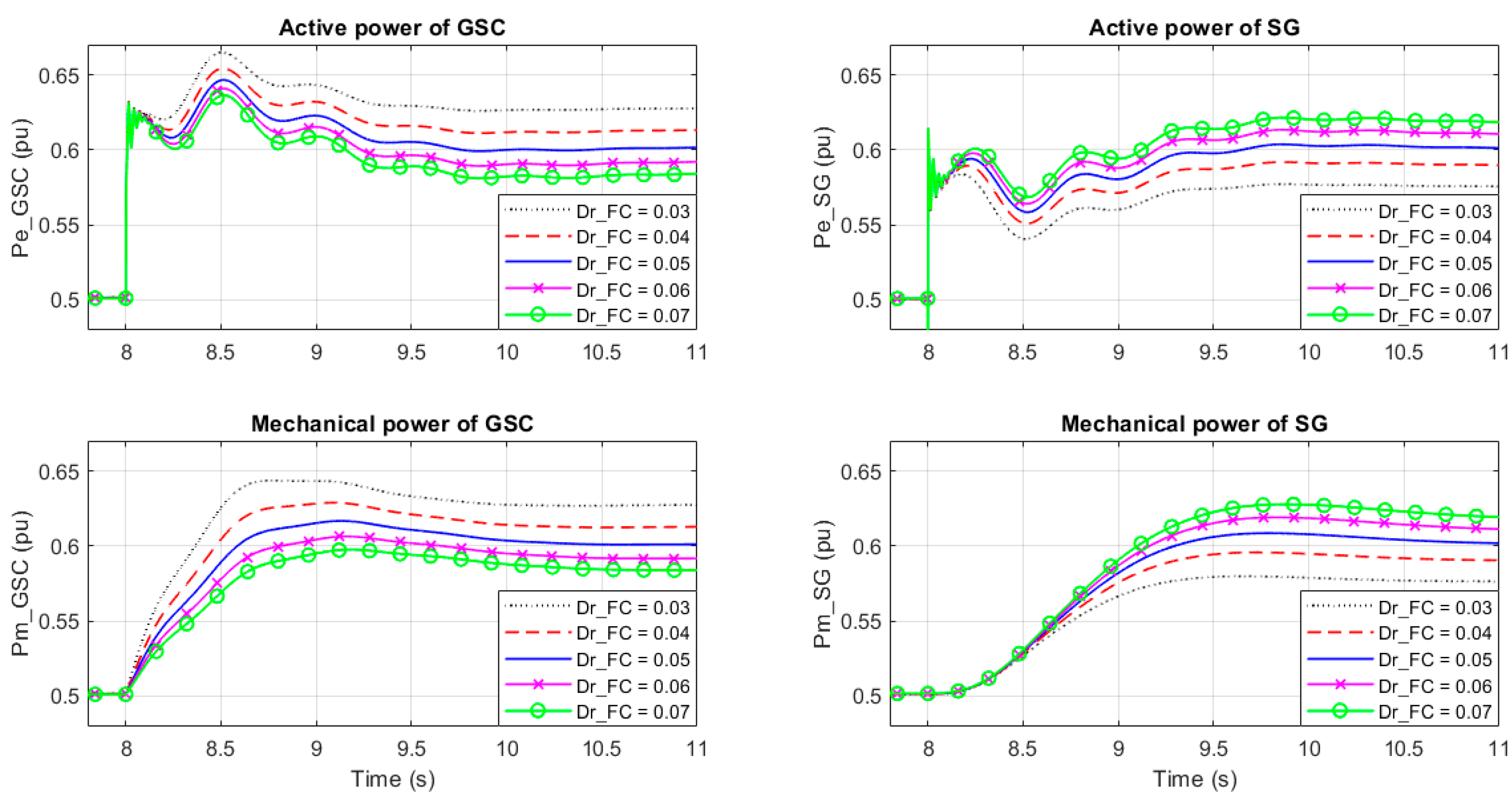
3.1. Influence on Dynamic Response
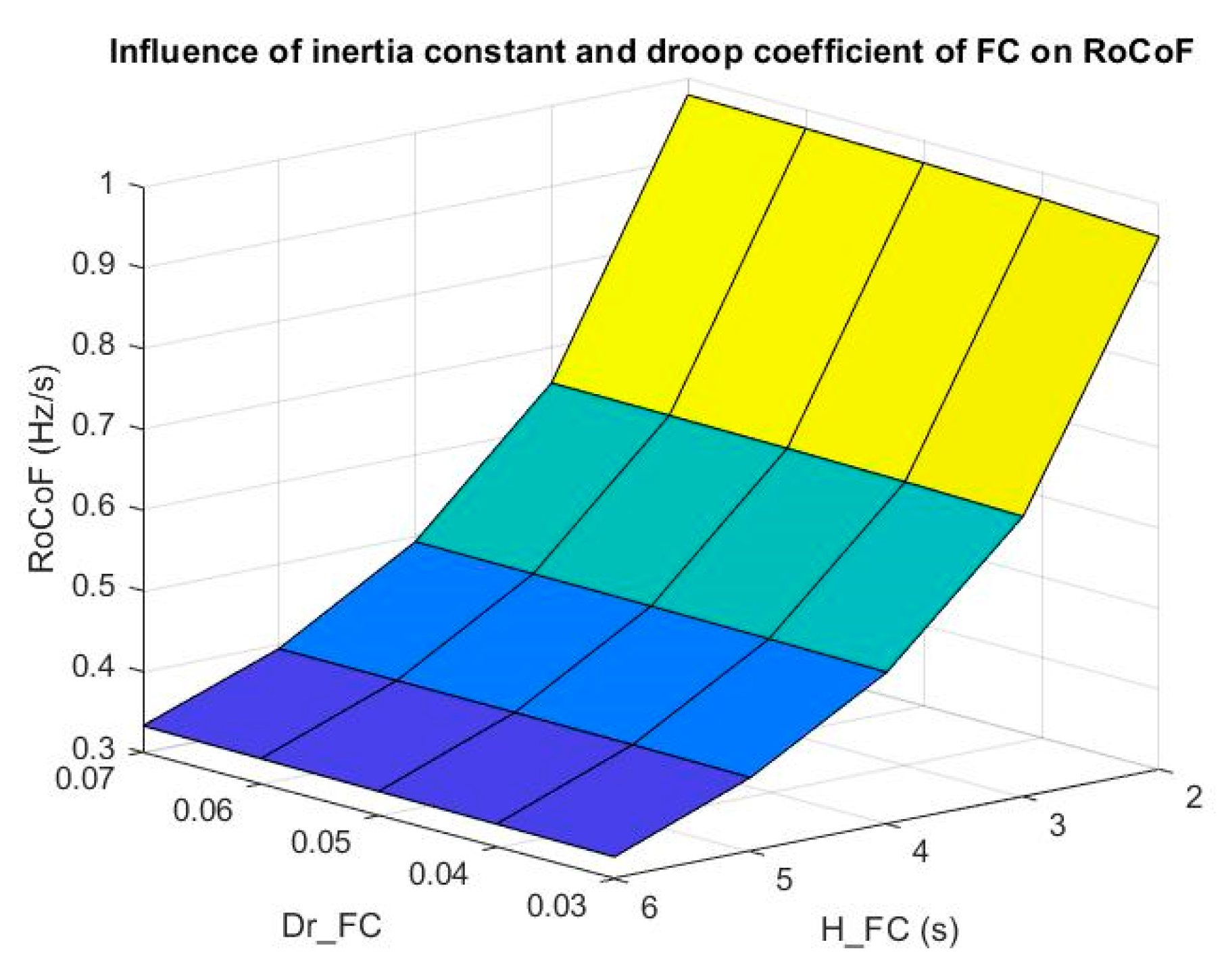
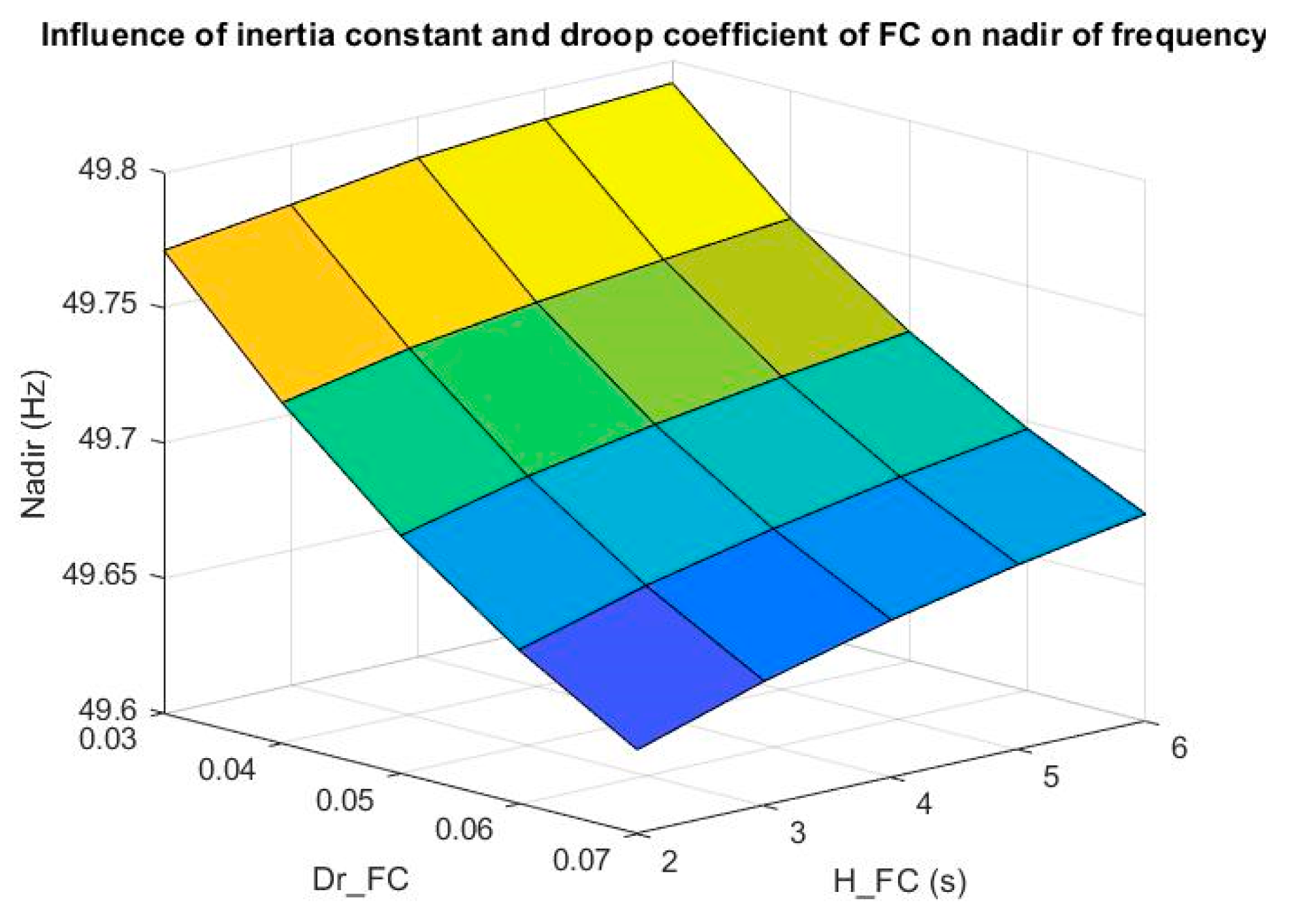
3.2. Influence on RoCoF and Frequency Nadir
- (1)
- An increase of inertia constant decreased RoCoF, which is desirable for frequency support.
- (2)
- Droop coefficient had little influence on RoCoF, which was slightly reduced with decreasing droop coefficient.
- (3)
- RoCoF was mainly influenced by inertia constant.
- (4)
- Inertia constant had little influence on nadir, which was slightly improved when increasing inertia constant. A higher nadir is desirable for frequency support.
- (5)
- A decrease of droop coefficient increased nadir.
- (6)
- Nadir of frequency was mainly influenced by droop coefficient.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Power base, | 10 kVA | Inductance base, | 0.0509 H |
| Voltage base (phase-to-ground, peak), | 326.5986 V | Capacitance base, | 1.9894 × 10−4 F |
| Current base, | 20.4124 A | Simulation time step, | 160 × 10−6 s |
| Impedance base, | 16 Ω | Initial power set point of GSC, | 0.5 pu |
| Frequency base, | 50 Hz | Initial power set point of SG, | 0.5 pu |
| Angular speed base, | 314.1593 rad/s |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Nominal active power, | 10 kW | Filter capacitance, | 0.05 pu |
| Nominal voltage (phase-to-phase, RMS), | 400 V | Current loop time constant, | 7.9577 × 10−4 s |
| Nominal current (RMS), | 14.43 A | Current loop proportional gain, | 0.4 |
| Nominal frequency, | 50 Hz | Current loop integral gain, | 0.1571 |
| DC-link voltage, | 800 V | Voltage loop proportional gain, | 0.0667 |
| Converter switch-on resistance, | 1× 10−3 Ω | Voltage loop reciprocal of integration time, z | 139.6263 |
| Filter resistance, | 1× 10−3 Ω | Inertia constant, H | 4 W·s/VA |
| Filter inductance, | 0.1 pu | Droop coefficient, | 0.05 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Capacity, | 10 kVA | d axis transient short-circuit time constant, | 1.01 s |
| Nominal voltage (phase-to-phase, RMS), | 400 V | d axis subtransient short-circuit time constant, | 0.053 s |
| Nominal current (RMS), | 14.43 A | q axis subtransient open-circuit time constant, | 0.1 s |
| Nominal frequency, | 50 Hz | Stator resistance, | 2.8544 × 10−3 pu |
| Number of pole pairs | 1 | Friction factor, F | 0 |
| d axis synchronous reactance, | 1.305 pu | Inertia constant, H | 4 W·s/VA |
| d axis transient reactance, | 0.296 pu | Droop coefficient, | 0.05 |
| d axis subtransient reactance, | 0.252 pu | Governor time constant, | 0.2 s |
| q axis synchronous reactance, | 0.474 pu | Steam turbine time constant, | 0.3 s |
| q axis subtransient reactance, | 0.243 pu | Line resistance, | 0.01 pu |
| Leakage reactance, | 0.18 pu | Line inductance, | 0.2 pu |
References
- Komusanac, I.; Brindley, G.; Fraile, D.; Walsh, C. Wind Energy in Europe in 2019—Trends and Statistics; Wind Europe: Brussels, Belgium, 2020. [Google Scholar]
- Gautam, D.; Goel, L.; Ayyanar, R.; Vittal, V.; Harbour, T. Control strategy to mitigate the impact of reduced inertia due to doubly fed induction generators on large power systems. IEEE Trans. Power Syst. 2011, 26, 214–224. [Google Scholar] [CrossRef]
- Mullane, A.; O’Malley, M. The inertial response of induction-machine-based wind turbines. IEEE Trans. Power Syst. 2005, 20, 1496–1503. [Google Scholar] [CrossRef]
- Holdsworth, L.; Ekanayake, J.B.; Jenkins, N. Power system frequency response from fixed speed and doubly fed induction generator-based wind turbines. Wind Energy 2004, 7, 21–35. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. On the Inertia of Future More-Electronics Power Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 2130–2146. [Google Scholar] [CrossRef]
- ENTSO-E. Rate of Change of Frequency (RoCoF) Withstand Capability; European Network of Transmission System Operation for Electricity: Brussels, Belgium, 2018. [Google Scholar]
- Uijlings, W. RoCoF An Independent Analysis on the Ability of Generators to Ride through Rate of Change of Frequency Values up to 2 Hz/s; DNV KEMA Energy & Sustainability: London, UK, February 2013. [Google Scholar]
- Tamrakar, U.; Shrestha, D.; Maharjan, M.; Bhattarai, B.P.; Hansen, T.M.; Tonkoski, R. Virtual Inertia: Current Trends and Future Directions. Appl. Sci. 2017, 7, 654. [Google Scholar] [CrossRef]
- Morren, J.; de Haan, S.W.H.; Kling, W.L.; Ferreira, J.A. Wind Turbines Emulating Inertia and Supporting Primary Frequency Control. IEEE Trans. Power Syst. 2006, 21, 433–434. [Google Scholar] [CrossRef]
- Durrant, M.; Werner, H.; Abbott, K. Model of a VSC HVDC terminal attached to a weak AC system. In Proceedings of the IEEE Conference on Control Applications, Istanbul, Turkey, 25 June 2003. [Google Scholar]
- Harnefors, L.; Bongiorno, M.; Lundberg, S. Input-admittance calculation and shaping for controlled voltage-source converters. IEEE Trans. Ind. Electron. 2007, 54, 3323–3334. [Google Scholar] [CrossRef]
- Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Small-Signal Stability Analysis of Three-Phase AC Systems in the Presence of Constant Power Loads Based on Measured d-q Frame Impedances. IEEE Trans. Power Electron. 2015, 30, 5952–5963. [Google Scholar] [CrossRef]
- Wang, X.; Taul, M.G.; Wu, H.; Liao, Y.; Blaabjerg, F.; Harnefors, L. Grid-Synchronization Stability of Converter-Based Resources—An Overview. IEEE Open J. Ind. Appl. 2020, 1, 115–134. [Google Scholar] [CrossRef]
- Beck, H.P.; Hesse, R. Virtual synchronous machine. In Proceedings of the 2007 9th International Conference on Electrical Power Quality and Utilisation, Barcelona, Spain, 9–11 October 2007. [Google Scholar]
- Zhong, Q.-C.; Weiss, G. Synchronverters: Inverters That Mimic Synchronous Generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Zhang, W.; Cantarellas, A.M.; Rocabert, J.; Luna, A.; Rodriguez, P. Synchronous Power Controller with Flexible Droop Characteristics for Renewable Power Generation Systems. IEEE Trans. Sustain. Energy 2016, 7, 1572–1582. [Google Scholar] [CrossRef]
- D’Arco, S.; Suul, J.A.; Fosso, O.B. A Virtual Synchronous Machine implementation for distributed control of power converters in SmartGrids. Electr. Power Syst. Res. 2015, 122, 180–197. [Google Scholar] [CrossRef]
- Qu, Z.; Yang, H.; Han, J.; Song, C.; Li, W.; Cai, Y. Effects analysis of excitation circuit on power control for VSG: A design-oriented study. IET Renew. Power Gener. 2020, 14, 803–810. [Google Scholar] [CrossRef]
- Kazmierkowski, M.P.; Malesani, L. Current control techniques for three-phase voltage-source pwm converters: A survey. IEEE Trans. Ind. Electron. 1998, 45, 691–703. [Google Scholar] [CrossRef]
- D’Arco, S.; Suul, J.A.; Fosso, O.B. Small-signal modelling and parametric sensitivity of a Virtual Synchronous Machine. In Proceedings of the 2014 Power Systems Computation Conference, PSCC 2014, Wroclaw, Poland, 18–22 August 2014. [Google Scholar]
- Mo, O.; Hernes, M.; Ljøkelsøy, K. Active damping of oscillations in LC-filter for line connected, current controlled, PWM voltage source converters. In Proceedings of the 10th European Conference on Power Electronics and Applications, Toulouse, France, 2–5 September 2003. [Google Scholar]
- Malinowski, M.; Kazmierkowski, M.P.; Bernet, S. New Simple Active Damping of Resonance in Three-Phase PWM Converter with LCL Filter. In Proceedings of the 2005 IEEE International Conference on Industrial Technology, Hong Kong, China, 14–17 December 2005. [Google Scholar]
- Kundur, P. Power System Stability And Control; McGraw-Hill, Inc.: New York, NY, USA, 1994; ISBN 0-07-035958-X. [Google Scholar]
- Alipoor, J.; Miura, Y.; Ise, T. Distributed Generation Grid Integration Using Virtual Synchronous Generator with Adoptive Virtual Inertia. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Oregon, Portland, 23–27 September 2018. [Google Scholar]
- Alipoor, J.; Miura, Y.; Ise, T. Power system stabilization using virtual synchronous generator with alternating moment of inertia. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 451–458. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, L.; Saborío-Romano, O.; Cutululis, N.A. Reduced-Order-VSM-Based Frequency Controller for Wind Turbines. Energies 2021, 14, 528. https://doi.org/10.3390/en14030528
Lu L, Saborío-Romano O, Cutululis NA. Reduced-Order-VSM-Based Frequency Controller for Wind Turbines. Energies. 2021; 14(3):528. https://doi.org/10.3390/en14030528
Chicago/Turabian StyleLu, Liang, Oscar Saborío-Romano, and Nicolaos A. Cutululis. 2021. "Reduced-Order-VSM-Based Frequency Controller for Wind Turbines" Energies 14, no. 3: 528. https://doi.org/10.3390/en14030528
APA StyleLu, L., Saborío-Romano, O., & Cutululis, N. A. (2021). Reduced-Order-VSM-Based Frequency Controller for Wind Turbines. Energies, 14(3), 528. https://doi.org/10.3390/en14030528







