Thermal Efficiency of Trombe Wall in the South Facade of a Frame Building
Abstract
:1. Introduction
- -
- active systems—in which installations and equipment are employed to obtain solar radiation energy;
- -
- passive systems—most often integrated into the structure of an external barrier, which will obtain solar radiation energy without additional equipment.
2. Materials and Methods
2.1. Research Site
2.2. Design of the Wall
2.3. Research Apparatus
- -
- Values of the global solar irradiance incident on the southern vertical plane (W/m2);
- -
- Values of the heat flux density flowing through the wall, measured on the inner surface of the wall (W/m2);
- -
- Temperature values of: external air, internal air in the chamber, on the surface of the absorber, on the inner surface of the wall and inside the storage layer (°C).
- Pyranometer (Figure 7a): measurement range—(0 to 2000 W/m2), operating temperature range—(−40 to +80 °C), measurement accuracy—(0.1 W/m2);
- Recorder saving measurement data from the pyranometer (Figure 7b).
- Multi-channel recorders (Figure 8a) for recording data from the heat flux density sensors;
- Probes for measuring the heat flux density (Figure 8b,c)—diameter 33 mm, measurement accuracy 6%;
- Temperature measurement sensor (Figure 9)—measuring range (−55 °C to + 125 °C), measuring accuracy 0.5 °C;
- Computer set recording data from temperature sensors.
2.4. Frequency of Data Recording from Experimental Tests
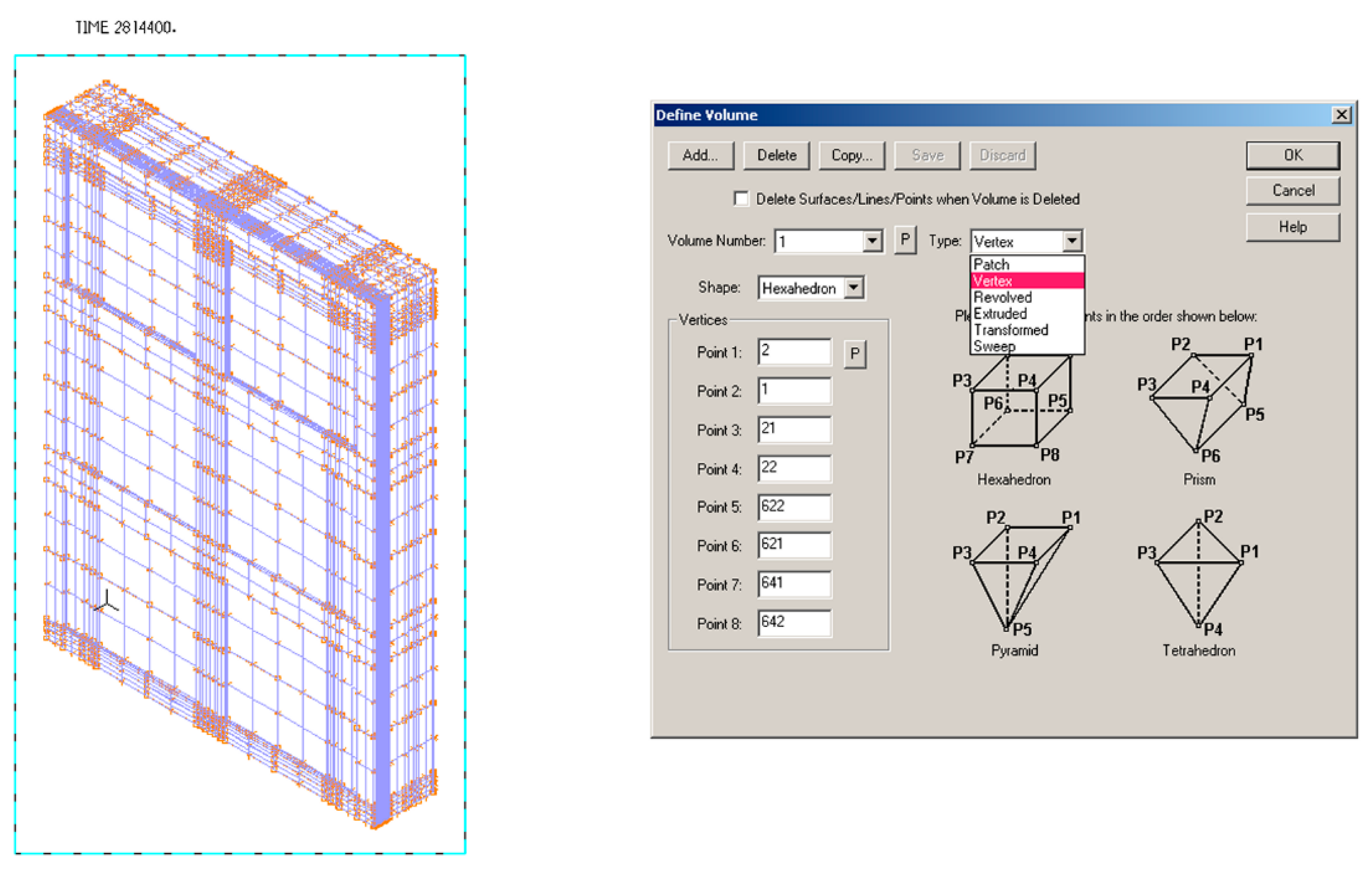
2.5. Numerical Simulations
- -
- convection boundary conditions:
- -
- radiation boundary conditions:
3. Results and Discussion
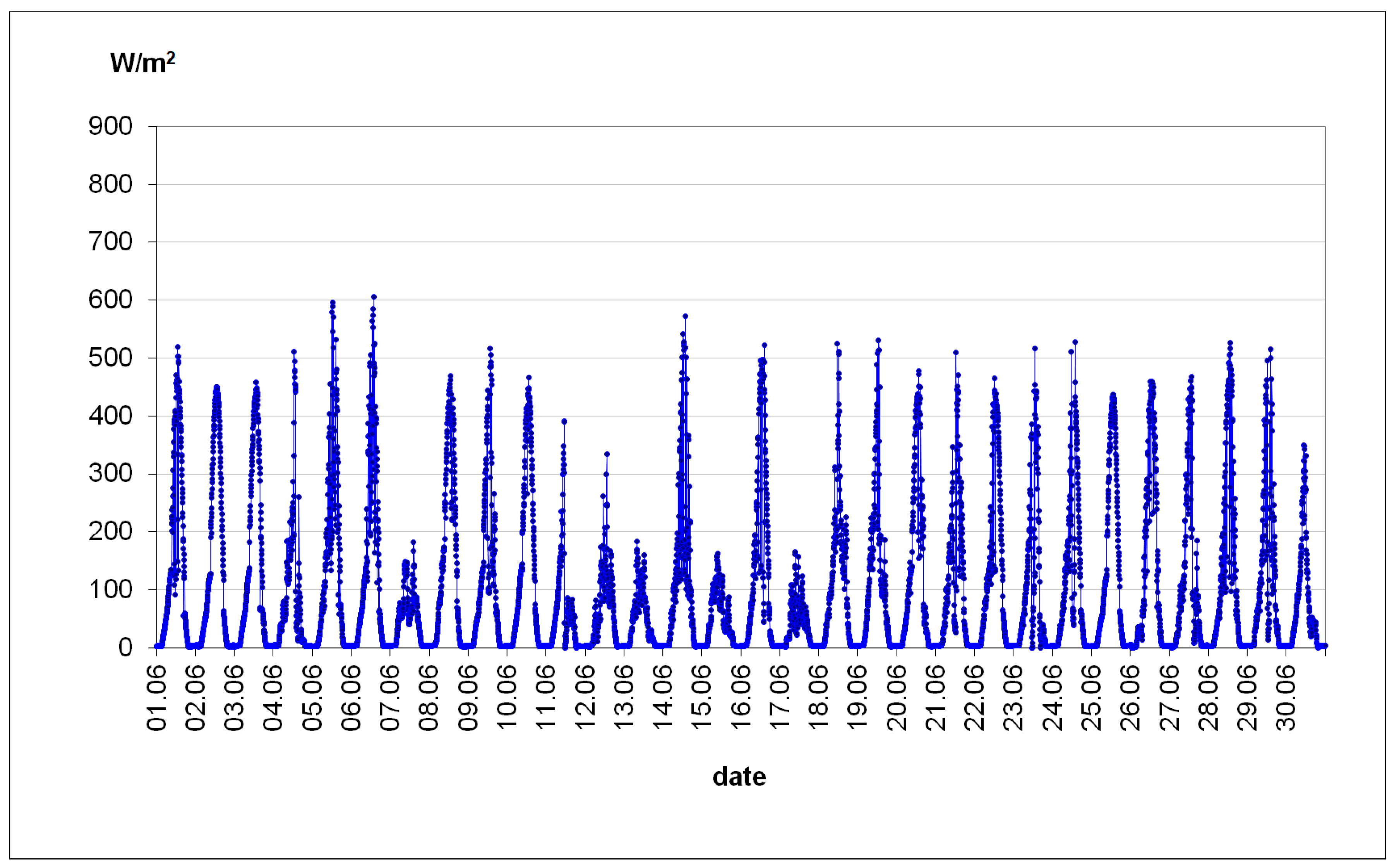
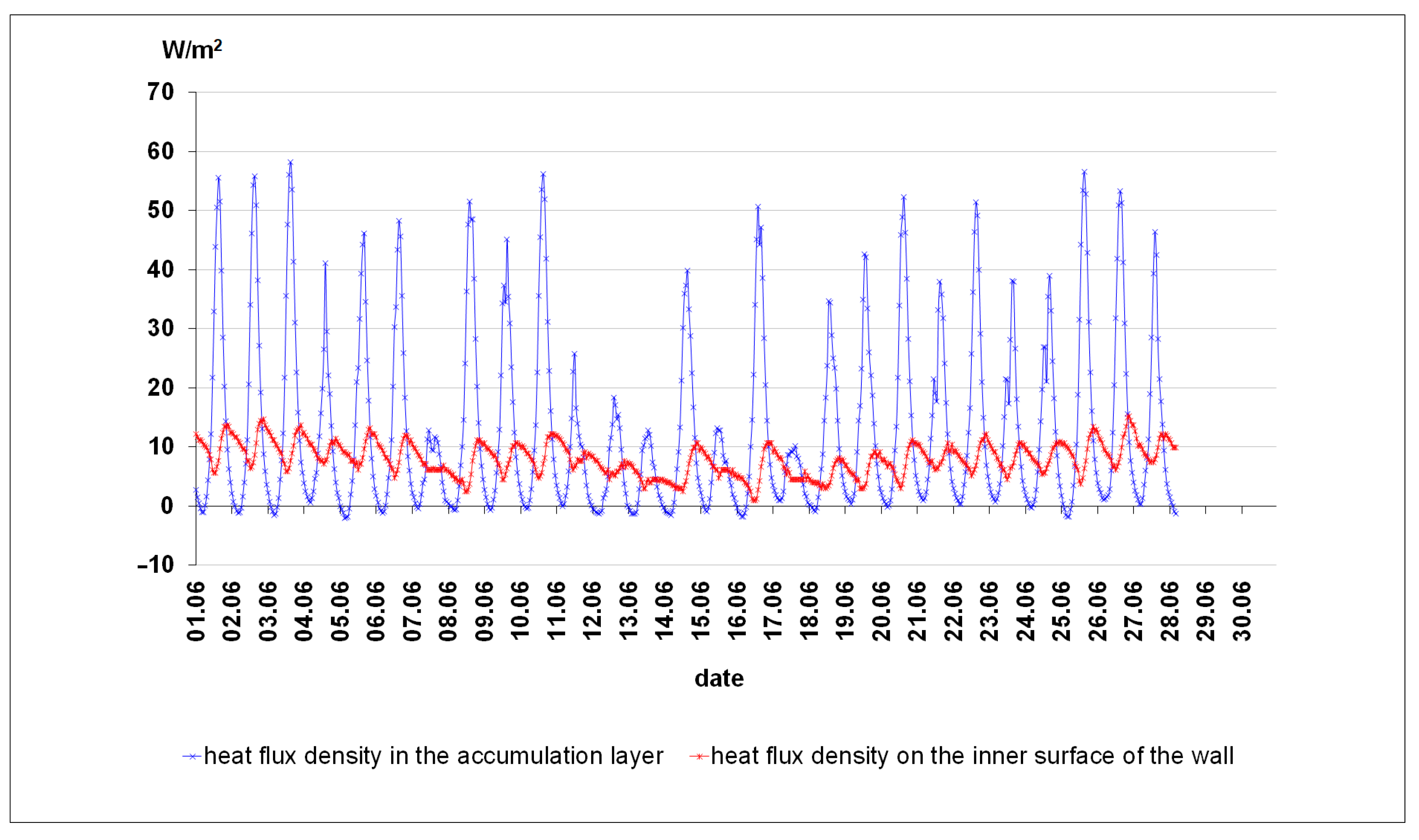
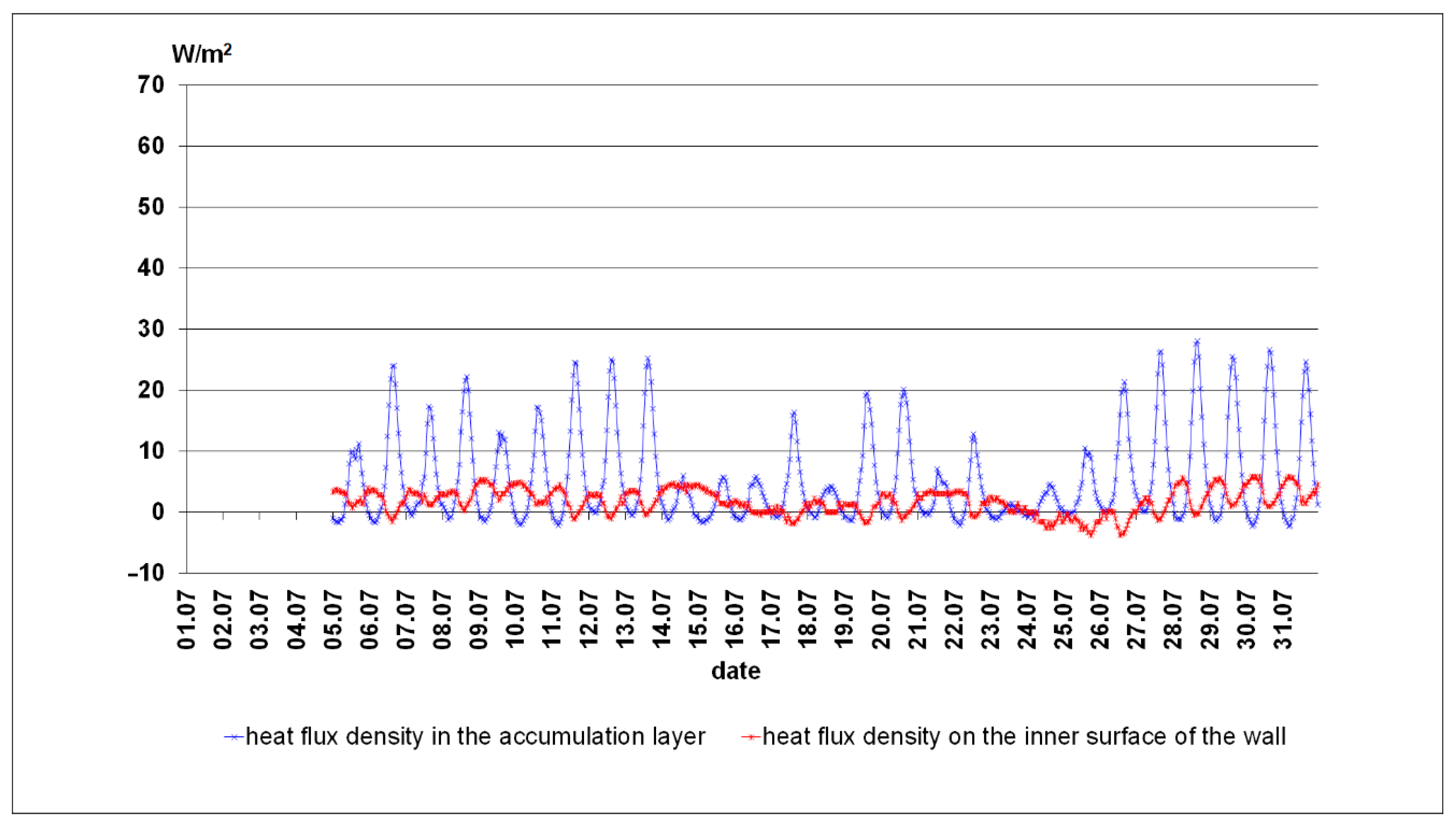
3.1. The Results of Empirical Research from the Summer Period
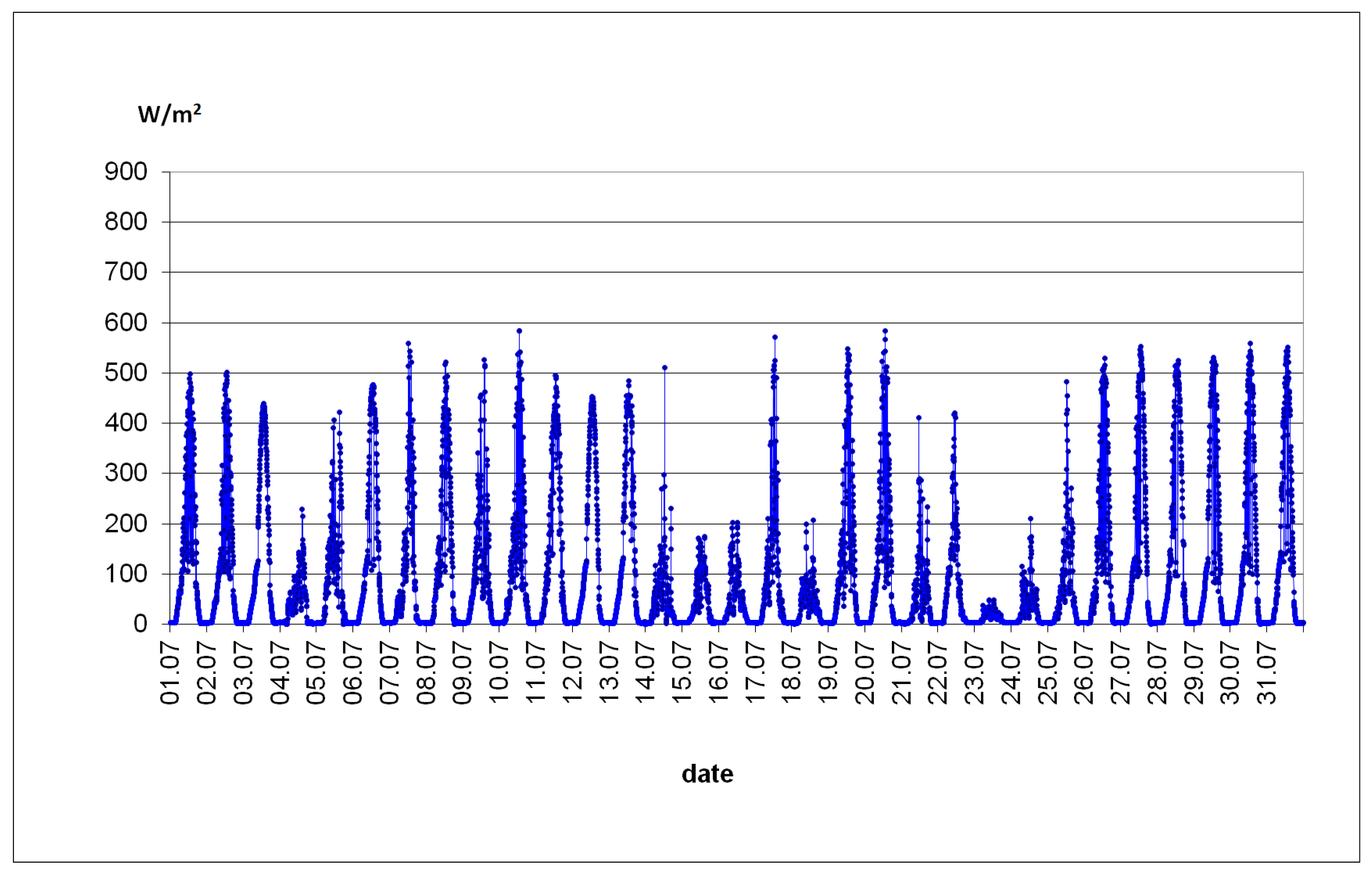
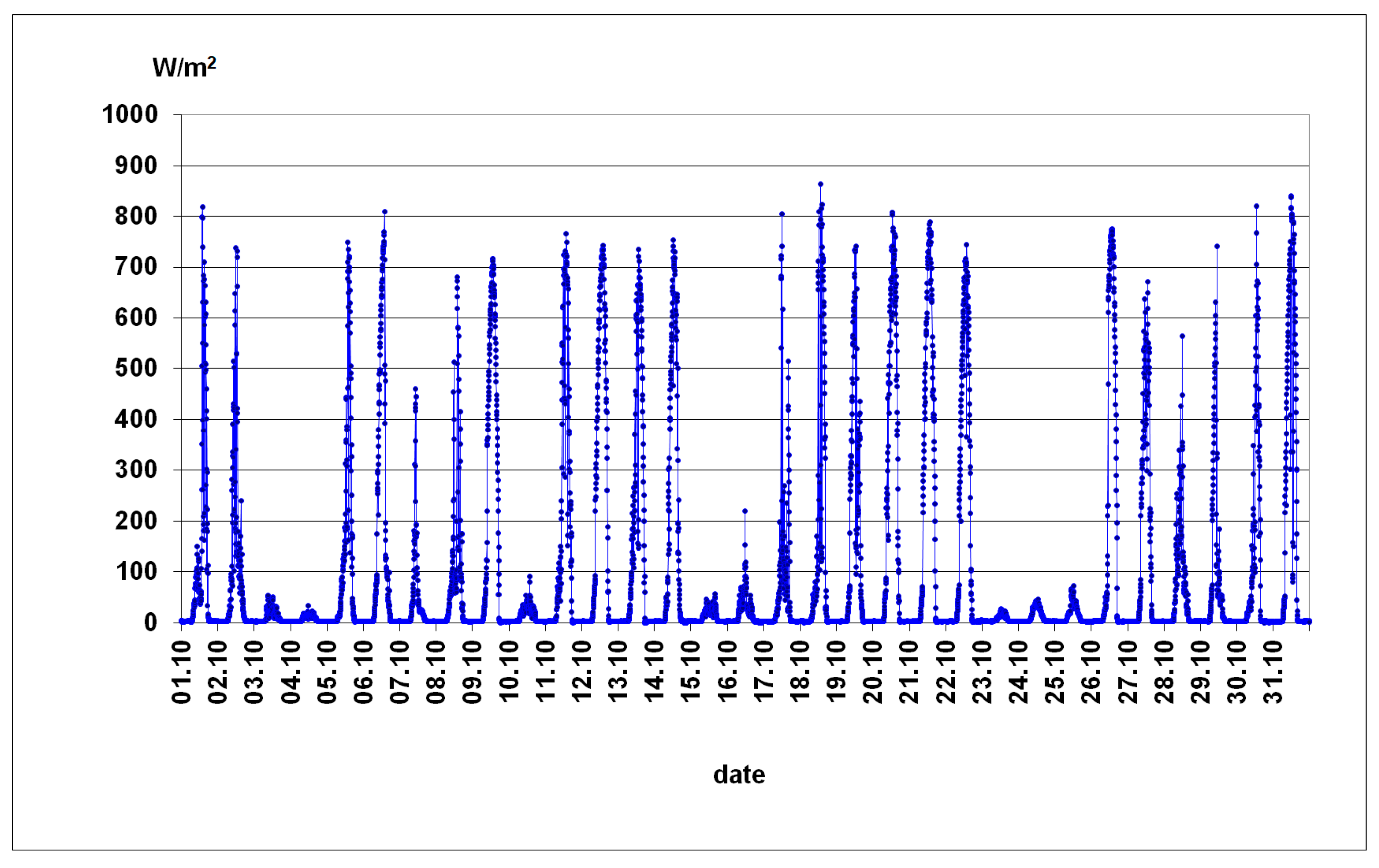
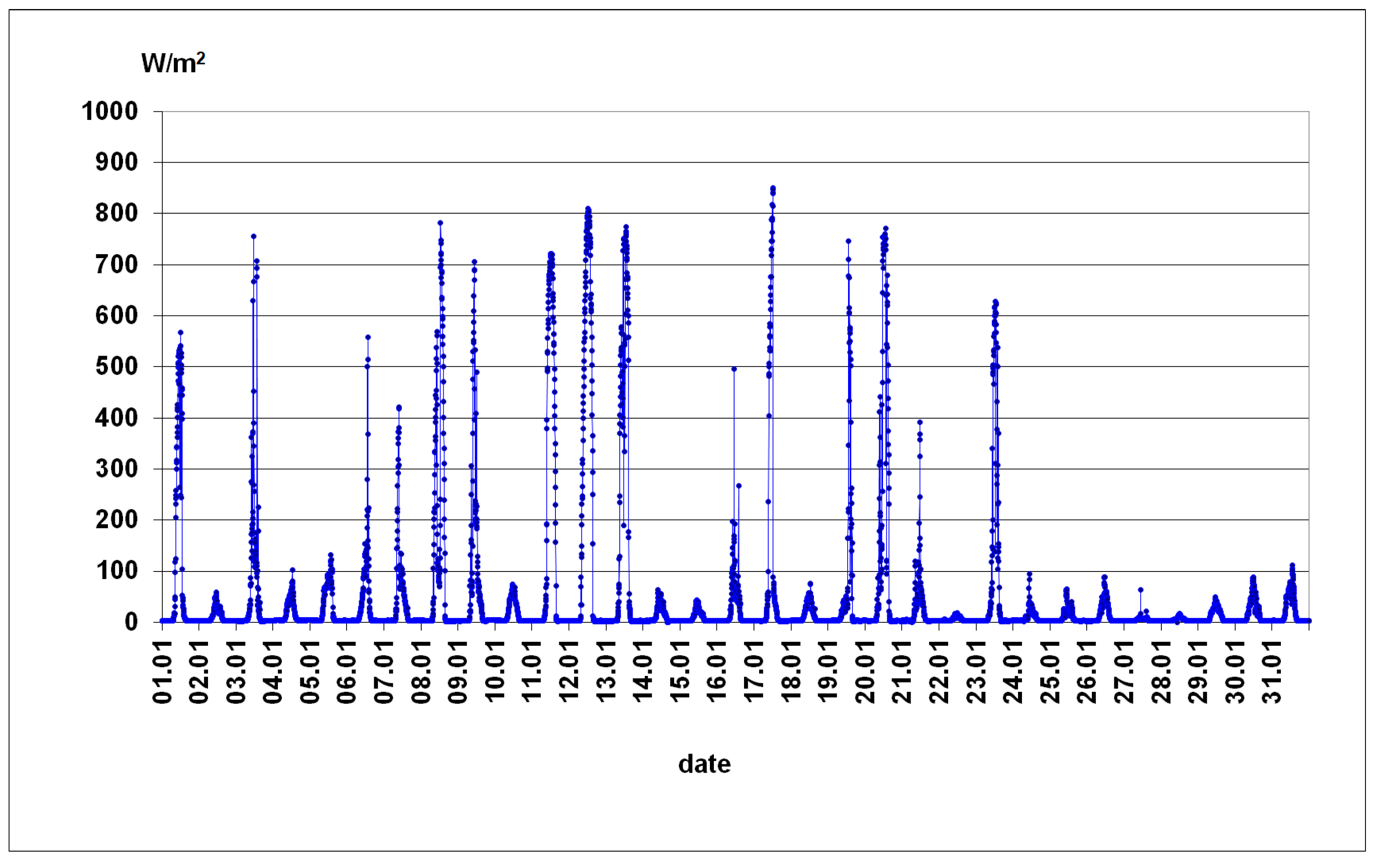
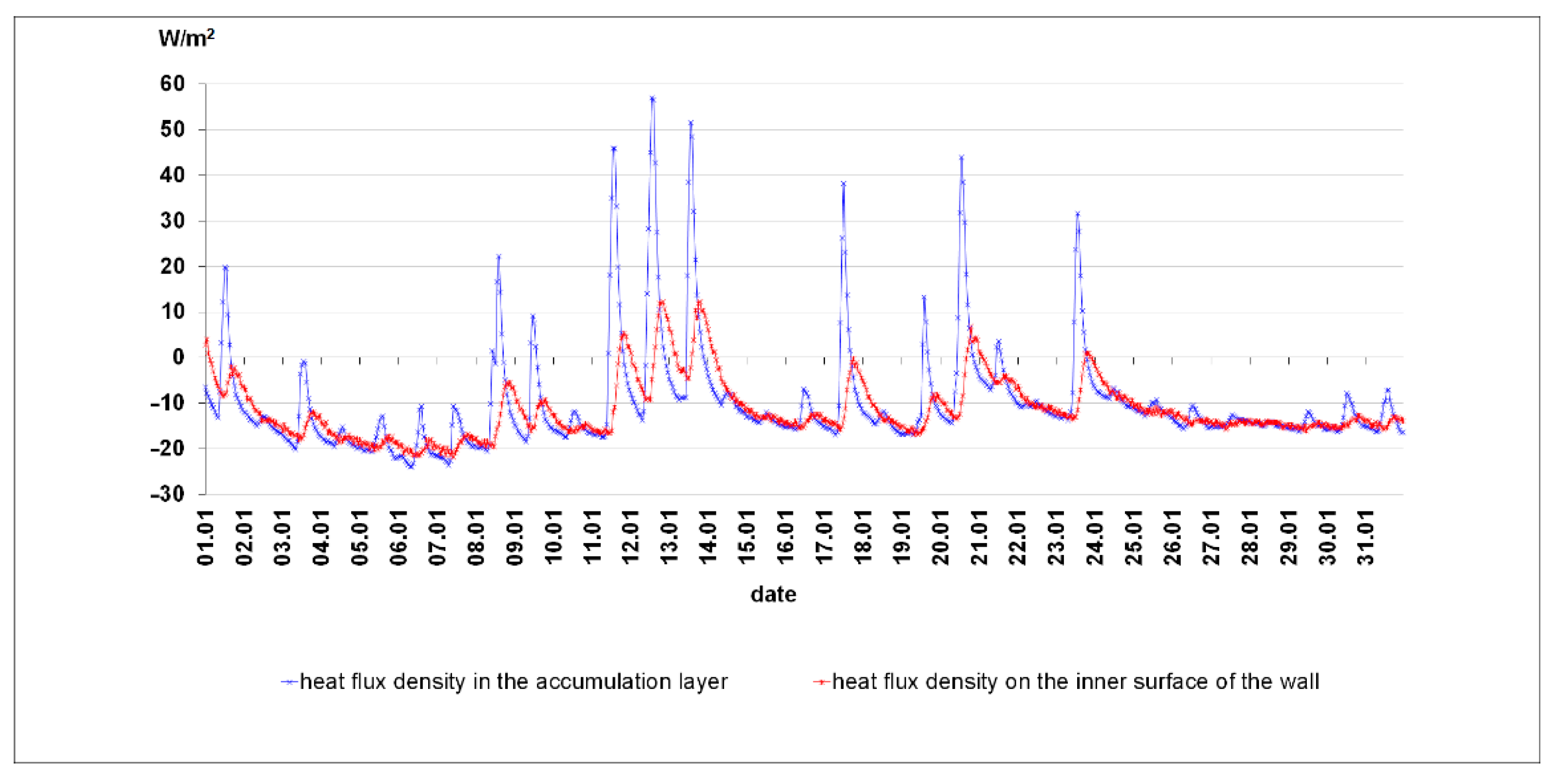
3.2. Results of Empirical Research from the Winter Period
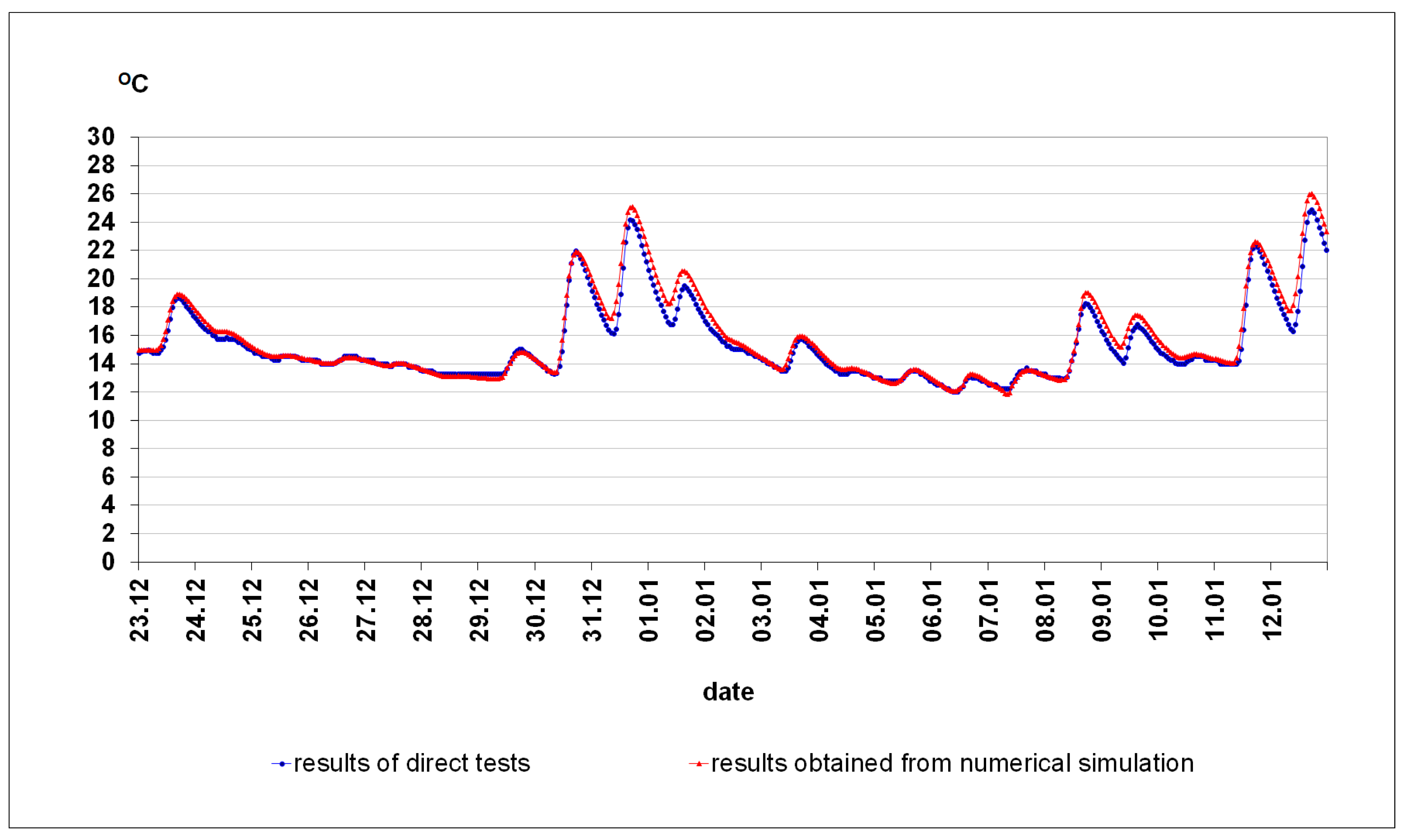
3.3. Comparison of the Results from the Numerical Model with the Empirical Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| G | global solar irradiance (W/m2) |
| S | surface (m2) |
| T | temperature (°C) |
| U | heat transfer coefficient (W/(m2·K)) |
| g | total energy transmittance of solar radiation (%) |
| h | convection coefficient (W/(m2·K)) |
| hr | radiation heat transfer coefficient (W/(m2·K)) |
| k | thermal conductivity (W/(m·K)) |
| q | heat flux density (W/m2) |
| qB | the rate of heat generated per unit volume (W/m3) |
| qS | heat transfer due to surface convection (W/m2) |
| Greek symbol | |
| θ | temperature (K) |
| θe | environmental (external) temperature (K) |
| θS | body surface temperature (K) |
| θr | temperature of the external radiation source (K) |
| ρ | density (kg/m3) |
References
- Saleh, M.A.; Kaseb, S.; El-Refaie, M.F. Glass–azimuth modification to reform direct solar heat gain. Build. Environ. 2004, 39, 653–659. [Google Scholar] [CrossRef]
- Barea, G.; Ganem, C.; Esteves, A. The multi-azimuthal window as a passive solar system: A study of heat gain for the rational use of energy. Energy Build. 2017, 144, 251–261. [Google Scholar] [CrossRef]
- Miąsik, P.; Krasoń, J. Thermal functioning of a transparent barrier equipped with a system of external thermal insulation shields. E3s Web. Conf. 2018, 49, 00071. [Google Scholar] [CrossRef]
- Saadatian, O.; Sopian, K.; Lim, C.H.; Asim, N.; Sulaiman, M.Y. Trombe walls: A review of opportunities and challenges in research and development. Renew. Sustain. Energy Rev. 2012, 16, 6340–6351. [Google Scholar] [CrossRef]
- Hu, Z.; He, W.; Ji, J.; Zhang, S. A review on the application of Trombe wall system in buildings. Renew. Sustain. Energy Rev. 2017, 70, 976–987. [Google Scholar] [CrossRef]
- Dabaieh, M.; Serageldin, A.A. Earth air heat exchanger, Trombe wall and green wall for passive heating and cooling in premium passive refugee house in Sweden. Energy Convers. Manag. 2020, 209, 112555. [Google Scholar] [CrossRef]
- Quesada, G.; Rousse, D.; Dutil, Y.; Badache, M.; Hallé, S. A comprehensive review of solar facades. Opaque solar facades. Renew. Sustain. Energy Rev. 2012, 16, 2820–2832. [Google Scholar] [CrossRef]
- Bojica, M.; Johannes, K.; Kuznik, F. Optimizing energy and environmental performance of passive Trombe wall. Energy Build. 2014, 70, 279–286. [Google Scholar] [CrossRef]
- Kostikov, S.; Chao, S.; Yiqiang, J. A review of the current work potential of a trombe wall. Renew. Sustain. Energy Rev. 2020, 130, 109947. [Google Scholar] [CrossRef]
- Wang, D.; Hu, L.; Du, H.; Liu, Y.; Huang, J.; Xu, Y.; Liu, J. Classification, experimental assessment, modeling methods and evaluation metrics of Trombe walls. Renew. Sustain. Energy Rev. 2020, 124, 109772. [Google Scholar] [CrossRef]
- Viegas, G.M.; Jodra, J.I.; Juan, G.A.S.; Díscoli, C.A. Heat storage wall made of concrete and encapsulated water applied to mass construction social housing in temperate climates. Energy Build. 2018, 159, 346–356. [Google Scholar] [CrossRef] [Green Version]
- Al-Tamimi, A.S.; Al-Amoudi, O.S.B.; Al-Osta, M.A.; Ali, M.R.; Ahmad, A. Effect of insulation materials and cavity layout on heat transfer of concrete masonry hollow blocks. Constr. Build. Mater. 2020, 254, 119300. [Google Scholar] [CrossRef]
- Rafidiarison, H.; Remond, R.; Mougel, E. Dataset for validating 1-D heat and mass transfer models within building walls with hygroscopic materials. Build. Environ. 2015, 89, 356–368. [Google Scholar] [CrossRef]
- Simo-Tagne, M.; Ndukwu, M.C.H.; Rogaume, Y. Modelling and numerical simulation of hygrothermal transfer through a building wall for locations subjected to outdoor conditions in Sub-Saharan Africa. J. Build. Eng. 2019, 26, 100901. [Google Scholar] [CrossRef]
- Simo-Tagne, M.; Remond, R.; Kharchi, R.; Bennamoun, L.; Ndukwu, M.C.; Rogaume, Y. Modeling, numerical simulation and validation of the hygrothermal transfer through a wooden building wall in Nancy, France. Sci. Eng. Prog. 2021, 22, 100808. [Google Scholar] [CrossRef]
- Szyszka, J.; Bevilacqua, P.; Bruno, R. An Innovative Trombe Wall for Winter Use: The Thermo-Diode Trombe Wall. Energies 2020, 13, 2188. [Google Scholar] [CrossRef]
- Duan, S.; Jing, C.; Zhao, Z. Energy and exergy analysis of different Trombe walls. Energy Build. 2016, 126, 517–523. [Google Scholar] [CrossRef]
- Corasaniti, S.; Manni, L.; Russo, F.; Gori, F. Numerical simulation of modified Trombe-Michel Walls with exergy and energy analysis. Int. Commun. Heat Mass Transf. 2017, 88, 269–276. [Google Scholar] [CrossRef]
- Briga-Sá, A.; Boaventura-Cunha, J.; Lanzinha, J.-C.; Paiva, A. Experimental and analytical approach on the Trombe wall thermal performance parameters characterization. Energy Build. 2017, 150, 262–280. [Google Scholar] [CrossRef]
- Mohamad, A.; Taler, J.; Ocłoń, P. Trombe Wall Utilization for Cold and Hot Climate Conditions. Energies 2019, 12, 285. [Google Scholar] [CrossRef] [Green Version]
- He, W.; Hong, X.; Wu, X.; Pei, G.; Hu, Z.; Tang, W.; Shen, Z.; Ji, J. Thermal and hydraulic analysis on a novel Trombe wall with venetian blind structure. Energy Build. 2016, 123, 50–58. [Google Scholar] [CrossRef]
- Yu, B.; Li, N.; Ji, J. Performance analysis of a purified Trombe wall with ventilation blinds based on photo-thermal driven purification. Appl. Energy 2019, 255, 113846. [Google Scholar] [CrossRef]
- Gracia de, A.; Navarro, L.; Castell, A.; Ruiz-Pardo, A.; Alvárez, S.; Cabeza, L.F. Experimental study of a ventilated facade with PCM during winter period. Energy Build. 2013, 58, 324–332. [Google Scholar] [CrossRef]
- Rabani, M.; Kalantar, V.; Rabani, M. Heat transfer analysis of a Trombe wall with a projecting channel design. Energy 2017, 134, 943–950. [Google Scholar] [CrossRef]
- Stazi, F.; Mastrucci, A.; di Perna, C. Trombe wall management in summer conditions: An experimental study. Sol. Energy 2012, 86, 2839–2851. [Google Scholar] [CrossRef]
- Jaber, S.; Ajib, S. Optimum design of Trombe wall system in mediterranean region. Sol. Energy 2011, 85, 1891–1898. [Google Scholar] [CrossRef]
- Ruiz-Pardo, A.; Dominguez, S.A.; Fernandez, J.A.S. Revision of the Trombe wall calculation method proposed by UNE-EN ISO 13790. Energy Build. 2010, 42, 763–773. [Google Scholar] [CrossRef]
- Fiorito, F. Trombe walls for lightweight buildings in temperate and hot climates. Exploring the use of phase-change materials for performances improvement. Energy Procedia 2012, 30, 1110–1119. [Google Scholar] [CrossRef] [Green Version]
- Szyszka, J.; Kogut, J.; Skrzypczak, I.; Kokoszka, W. Selective Internal Heat Distribution in Modified Trombe Wall. Iop Conf. Ser. Earth Environ. Sci. 2017, 95, 042018. [Google Scholar] [CrossRef]
- Krasoń, J.; Lichołai, L. Thermal efficiency of a modified thermal storage wall containing phase change material in comparative test periods. E3s Web Conf. 2018, 49, 00059. [Google Scholar] [CrossRef] [Green Version]
- Sun, D.; Wang, L. Research on heat transfer performance of passive solar collector-storage wall system with phase change materials. Energy Build. 2016, 119, 183–188. [Google Scholar] [CrossRef]
- Krasoń, J.; Miąsik, P.; Lichołai, L.; Dębska, B.; Starakiewicz, A. Analysis of the Thermal Characteristics of a Composite Ceramic Product Filled with Phase Change Material. Buildings 2019, 9, 217. [Google Scholar] [CrossRef] [Green Version]
- Zhou, G.; Pang, M. Experimental investigations on thermal performance of phase change material e Trombe wall system enhanced by delta winglet vortex generators. Energy 2015, 93, 758–769. [Google Scholar] [CrossRef]
- Kara, Y.A. Diurnal performance analysis of phase change material walls. Appl. Eng. 2016, 102, 1–8. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, L.; Yang, Y.; Feng, Y.; Yang, L.; Gao, Q. Effects of external insulation component on thermal performance of a Trombe wall with phase change materials. Sol. Energy 2020, 204, 115–133. [Google Scholar] [CrossRef]
- Li, S.; Zhu, N.; Hu, P.; Lei, F.; Deng, R. Numerical study on thermal performance of PCM Trombe Wall. Energy Procedia 2019, 158, 2441–2447. [Google Scholar] [CrossRef]
- Piotrowski, J.Z.; Stroy, A.; Olenets, M. Mathematical modelling of the steady state heat transfer processes in the convectional elements of passive solar heating systems. Arch. Civil. Mech. Eng. 2013, 13, 394–400. [Google Scholar] [CrossRef]
- Abbassi, F.; Dehmani, L. Experimental and numerical study on thermal performance of an unvented Trombe wall associated with internal thermal fins. Energy Build. 2015, 105, 119–128. [Google Scholar] [CrossRef]
- Leang, E.; Tittelein, P.; Zalewski, L.; Lassue, S. Numerical study of a composite Trombe solar wall integrating microencapsulated PCM. Energy Procedia 2017, 122, 1009–1014. [Google Scholar] [CrossRef]
- Abdeen, A.; Serageldin, A.A.; Ibrahim, M.G.E.; El-Zafarany, A.; Ookawara, S.; Murata, R. Experimental, analytical, and numerical investigation into the feasibility of integrating a passive Trombe wall into a single room. Appl. Eng. 2019, 154, 751–768. [Google Scholar] [CrossRef]
- Chwieduk, D. Impact of solar energy on the energy balance of attic rooms in high latitude countries. Appl. Eng. 2018, 136, 548–559. [Google Scholar] [CrossRef]
- Wieprzkowicz, A.; Heim, D. Modelling of thermal processes in a glazing structure with temperature dependent optical properties—An example of PCM-window. Renew. Energy 2020, 160, 653–662. [Google Scholar] [CrossRef]
- Hoes, P.; Hensen, J.L.M. The potential of lightweight low-energy houses with hybrid adaptable thermal storage: Comparing the performance of promising concepts. Energy Build. 2016, 110, 79–93. [Google Scholar] [CrossRef]
- Soares, N.; Santos, P.; Gervásio, H.; Costa, J.J.; Simões da Silva, L. Energy efficiency and thermal performance of lightweight steel-framed(LSF) construction: A review. Renew. Sustain. Energy Rev. 2017, 78, 194–209. [Google Scholar] [CrossRef]
- Lohmann, V.; Santos, P. Trombe Wall Thermal Behavior and Energy Efficiency of a Light Steel Frame Compartment: Experimental and Numerical Assessments. Energies 2020, 13, 2744. [Google Scholar] [CrossRef]
- PN-EN ISO 6946 Building Components and Building Elements—Thermal Resistance and Thermal Transmittance—Calculation Methods; Polish Committee for Standardization: Warsaw, Poland, 2017. (In Polish)
- Moore, W.I.; Donovan, E.S.; Powers, C.H.R. Thermal analysis of automotive lamps using the ADINA-F coupled specular radiation and natural convection model. Comput. Struct. 1999, 72, 17–30. [Google Scholar] [CrossRef]
- Adamus, J.; Pomada, M. Analysis of heat flow in composite structures used in window installation. Compos. Struct. 2018, 202, 127–135. [Google Scholar] [CrossRef]
- Dębska, B.; Lichołai, L.; Miąsik, P. Assessment of the Applicability of Sustainable Epoxy Composites Containing Waste Rubber Aggregates in Buildings. Buildings 2019, 9, 31. [Google Scholar] [CrossRef] [Green Version]
- Lichołai, L.; Miąsik, P.; Starakiewicz, A.; Krasoń, J. Analysis of the thermal characteristics of anti-icing driveway plates. Iop Conf. Ser. Earth Environ. Sci. 2019, 214, 012040. [Google Scholar] [CrossRef]

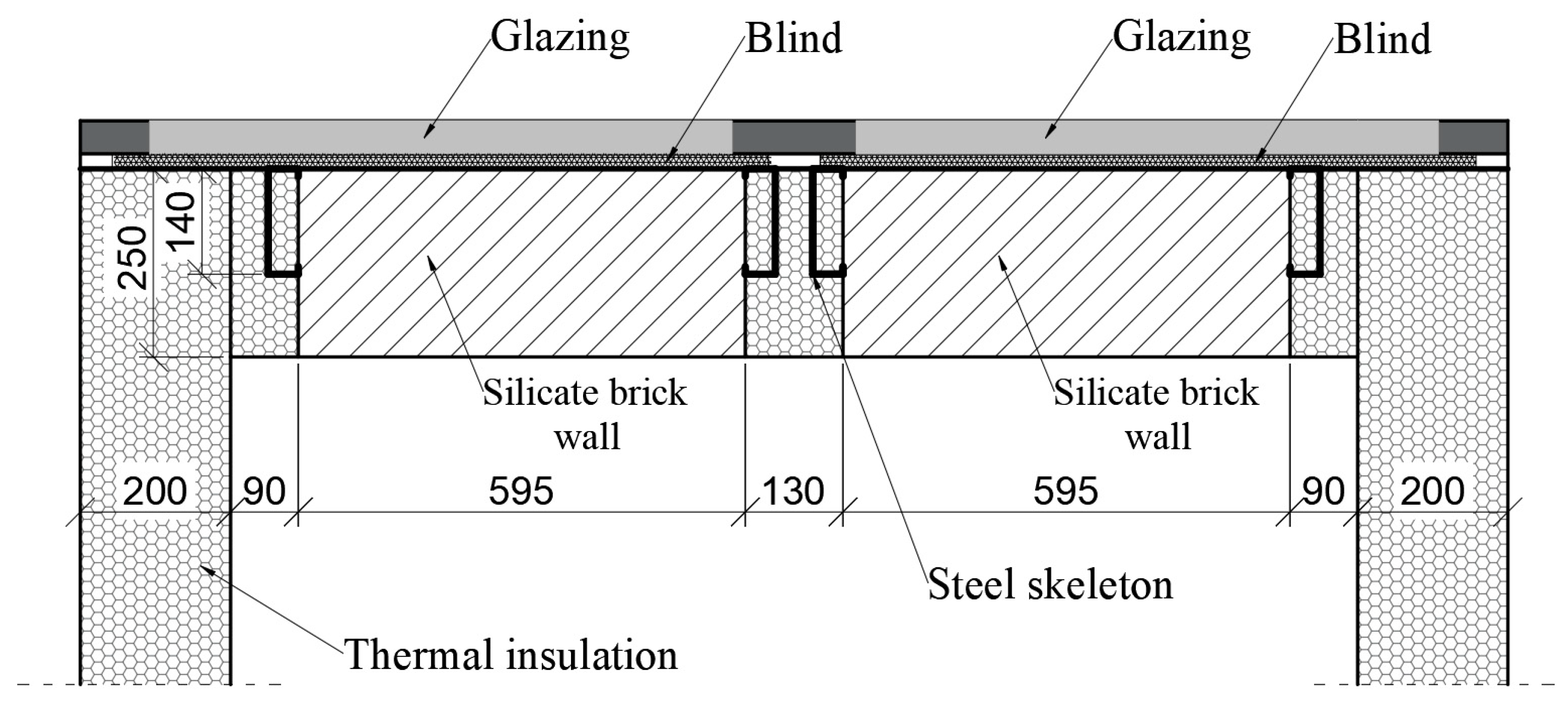









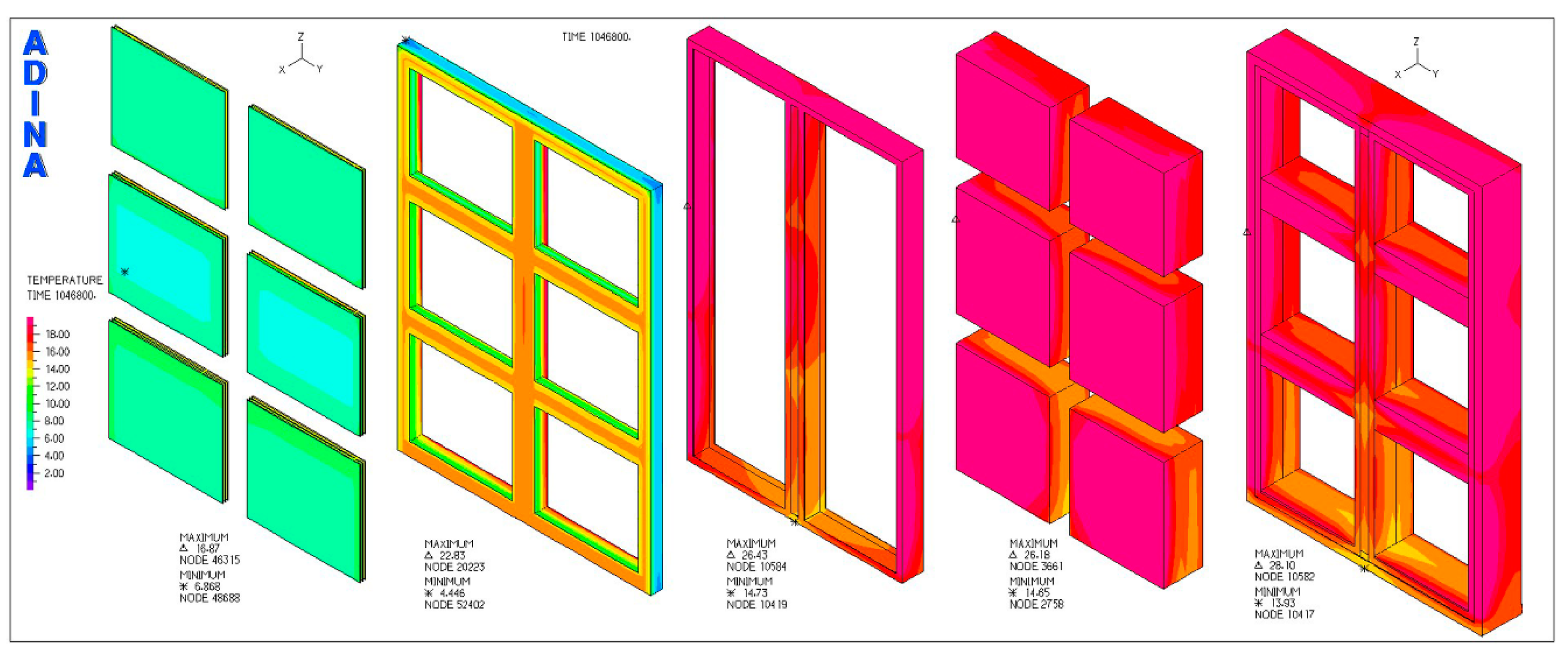
| Bulk Density kg/m3 | Thermal Conductivity W/(m·K) | Heat Transfer Coefficient W/(m2·K) | Total Energy Transmittance of Solar Radiation % | |
|---|---|---|---|---|
| Glazing | - | - | 1.1 | 61 |
| Steel skeleton + absorber | 7850 | 58 | - | - |
| Silicate brick wall | 1900 | 0.9 | - | - |
| Thermal insulation | 30 | 0.045 | - | - |
| Time Interval h | Average Value of the Global Solar Irradiance Incident on the Vertical Plane W/m2 | Heat Flux Density on the Inner Wall Surface W/m2 | Average Temperature Value °C | |||||
|---|---|---|---|---|---|---|---|---|
| External Air | Absorber | at a Distance from the Absorber Equal to 1/3 of the Width of the Storage Layer | at a Distance from the Absorber Equal to 2/3 of the Width of the Storage Layer | on the Inner Surface of the Wall | Air Inside the Chamber | |||
| 0:00–3:00 | 3.33 | 9.36 | 16.17 | 28.19 | 31.05 | 31.04 | 29.64 | 28.10 |
| 3:00–6:00 | 24.59 | 8.32 | 14.98 | 26.72 | 29.63 | 29.80 | 28.63 | 27.26 |
| 6:00–9:00 | 95.54 | 7.23 | 17.18 | 27.59 | 28.57 | 28.60 | 27.55 | 26.36 |
| 9:00–12:00 | 227.47 | 5.89 | 22.82 | 32.88 | 28.73 | 28.05 | 26.95 | 25.98 |
| 12:00–15:00 | 279.66 | 5.25 | 24.57 | 41.16 | 30.87 | 28.78 | 27.24 | 26.38 |
| 15:00–18:00 | 133.43 | 7.63 | 24.52 | 41.59 | 33.76 | 30.84 | 28.58 | 27.33 |
| 18:00–21:00 | 12.22 | 9.98 | 21.59 | 34.44 | 33.90 | 32.22 | 29.97 | 28.33 |
| 21:00–24:00 | 3.27 | 10.20 | 18.16 | 30.52 | 32.45 | 31.96 | 30.21 | 28.54 |
| average value | 97.44 | 7.98 | 20.00 | 32.89 | 31.12 | 30.16 | 28.60 | 27.29 |
| Time Interval, h | Average Value of the Global Solar Irradiance Incident on the Vertical Plane W/m2 | Heat Flux Density on the Inner Wall Surface W/m2 | Average Temperature Value °C | |||||
|---|---|---|---|---|---|---|---|---|
| External Air | Absorber | at a Distance from the Absorber Equal to 1/3 of the Width of the Storage Layer | at a Distance from the Absorber Equal to 2/3 of the Width of the Storage Layer | on the Inner Surface of the Wall | Air Inside the Chamber | |||
| 0:00–3:00 | 3.26 | −0.06 | 17.00 | 25.35 | 26.66 | 26.71 | 26.10 | 25.66 |
| 3:00–6:00 | 17.84 | −0.95 | 15.82 | 24.45 | 25.93 | 26.11 | 25.55 | 25.07 |
| 6:00–9:00 | 75.57 | 0.26 | 17.35 | 24.55 | 25.28 | 25.44 | 24.91 | 24.44 |
| 9:00–12:00 | 202.96 | 4.30 | 22.20 | 26.46 | 25.07 | 24.97 | 24.44 | 24.15 |
| 12:00–15:00 | 276.55 | 12.45 | 24.97 | 30.42 | 25.84 | 25.09 | 24.51 | 24.46 |
| 15:00–18:00 | 144.95 | 15.28 | 25.01 | 31.74 | 27.28 | 26.02 | 25.20 | 25.16 |
| 18:00–21:00 | 9.41 | 8.78 | 22.16 | 29.10 | 27.89 | 26.98 | 26.11 | 25.93 |
| 21:00–24:00 | 3.31 | 2.52 | 18.85 | 26.74 | 27.52 | 27.22 | 26.51 | 26.17 |
| average value | 91.73 | 5.32 | 20.42 | 27.35 | 26.43 | 26.07 | 25.42 | 25.13 |
| Month | Average Value of the Global Solar Irradiance Incident on the Vertical Plane W/m2 | Average Value of the External Air Temperature °C | Average Temperature Value on the Surface of the Absorber °C | Average Value of the Internal Air Temperature °C |
|---|---|---|---|---|
| April | 89.05 | 10.66 | 27.35 | 28.05 |
| May | 94.32 | 14.87 | 28.49 | 29.17 |
| June | 97.44 | 20.00 | 32.89 | 27.29 |
| July | 91.73 | 20.42 | 27.35 | 25.13 |
| August | 116.50 | 21.25 | 30.85 | 27.80 |
| September | 76.62 | 14.58 | 24.40 | 22.74 |
| first stage | 93.61 | 15.17 | 29.57 | 28.18 |
| second stage | 95.15 | 18.80 | 27.57 | 25.25 |
| Time Interval, h | Average Value of the Global Solar Irradiance Incident on the Vertical Plane, W/m2 | Heat Flux Density on the Inner Wall Surface, W/m2 | Average Temperature Value, °C | |||||
|---|---|---|---|---|---|---|---|---|
| External Air | Absorber | at a Distance from the Absorber Equal to 1/3 of the Width of the Storage Layer | at a Distance from the Absorber Equal to 2/3 of the Width of the Storage Layer | on the Inner Surface of the Wall | Air Inside the Chamber | |||
| 0:00–3:00 | 3.04 | 7.52 | 10.50 | 22.22 | 24.44 | 24.38 | 23.47 | 22.24 |
| 3:00–6:00 | 3.04 | 6.26 | 10.01 | 21.05 | 23.25 | 23.33 | 22.71 | 21.68 |
| 6:00–9:00 | 32.13 | 4.69 | 10.23 | 20.66 | 22.21 | 22.34 | 21.97 | 21.20 |
| 9:00–12:00 | 240.25 | 3.37 | 13.76 | 28.09 | 22.16 | 21.70 | 21.35 | 20.79 |
| 12:00–15:00 | 342.14 | 3.54 | 16.32 | 37.91 | 24.95 | 22.60 | 21.56 | 20.98 |
| 15:00–18:00 | 131.09 | 6.60 | 14.89 | 33.55 | 27.86 | 24.91 | 22.92 | 21.84 |
| 18:00–21:00 | 2.89 | 9.26 | 12.34 | 26.26 | 27.31 | 25.95 | 24.05 | 22.53 |
| 21:00–24:00 | 2.98 | 9.20 | 11.22 | 23.72 | 25.76 | 25.36 | 24.00 | 22.49 |
| average value | 94.70 | 6.31 | 12.41 | 26.68 | 24.74 | 23.82 | 22.75 | 21.72 |
| Time Interval, h | Average Value of the Global Solar Irradiance Incident on the Vertical Plane, W/m2 | Heat Flux Density on the Inner Wall Surface, W/m2 | Average Temperature Value, °C, | |||||
|---|---|---|---|---|---|---|---|---|
| External Air | Absorber | at a Distance from the Absorber Equal to 1/3 of the Width of the Storage Layer | at a Distance from the Absorber Equal to 2/3 of the Width of the Storage Layer | on the Inner Surface of the Wall | Air Inside the Chamber | |||
| 0:00–3:00 | 3.16 | −10.56 | −1.74 | 11.87 | 14.89 | 15.91 | 17.55 | 19.28 |
| 3:00–6:00 | 3.18 | −11.89 | −1.62 | 11.40 | 14.33 | 15.43 | 17.27 | 19.22 |
| 6:00–9:00 | 17.54 | −12.94 | −1.44 | 11.07 | 13.90 | 15.05 | 17.06 | 19.18 |
| 9:00–12:00 | 164.22 | −13.75 | 0.18 | 15.77 | 14.02 | 14.86 | 16.89 | 19.14 |
| 12:00–15:00 | 166.97 | −12.91 | 1.16 | 19.90 | 15.81 | 15.56 | 17.08 | 19.20 |
| 15:00–18:00 | 12.6 | −10.21 | −0.22 | 15.21 | 16.66 | 16.64 | 17.68 | 19.33 |
| 18:00–21:00 | 3.00 | −8.96 | −1.24 | 13.21 | 16.00 | 16.68 | 17.87 | 19.34 |
| 21:00-24:00 | 3.11 | −9.78 | −1.58 | 12.26 | 15.27 | 16.23 | 17.69 | 19.30 |
| average value | 46.73 | −11.37 | −0.81 | 13.84 | 15.11 | 15.80 | 17.39 | 19.25 |
| Month | Monthly Average Value of the Heat Flux Density | Thermal Energy Consumption during the Heating Season | ||
|---|---|---|---|---|
| for the Tested Wall | for a Traditional Wall with a Heat Transfer Coefficient U = 0.30 W/(m2K) | for the Tested Wall | for a Traditional Wall with a Heat Transfer Coefficient U = 0.30 W/(m2K) | |
| October | 6.31 | −2.79 | −4.69 | 2.08 |
| November | −0.26 | −3.63 | 0.19 | 2.61 |
| December | −10.60 | −5.14 | 7.89 | 3.82 |
| January | −11.37 | −6.02 | 8.46 | 4.48 |
| February | −8.73 | −5.59 | 5.86 | 3.75 |
| March | −3.76 | −5.46 | 2.80 | 4.06 |
| ∑ | −28.42 | −28.62 | 20.51 | 20.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miąsik, P.; Krasoń, J. Thermal Efficiency of Trombe Wall in the South Facade of a Frame Building. Energies 2021, 14, 580. https://doi.org/10.3390/en14030580
Miąsik P, Krasoń J. Thermal Efficiency of Trombe Wall in the South Facade of a Frame Building. Energies. 2021; 14(3):580. https://doi.org/10.3390/en14030580
Chicago/Turabian StyleMiąsik, Przemysław, and Joanna Krasoń. 2021. "Thermal Efficiency of Trombe Wall in the South Facade of a Frame Building" Energies 14, no. 3: 580. https://doi.org/10.3390/en14030580





