A Combined Experimental and Numerical Characterization of the Flowfield and Heat Transfer around a Multiperforated Plate with Compound Angle Injection
Abstract
1. Introduction
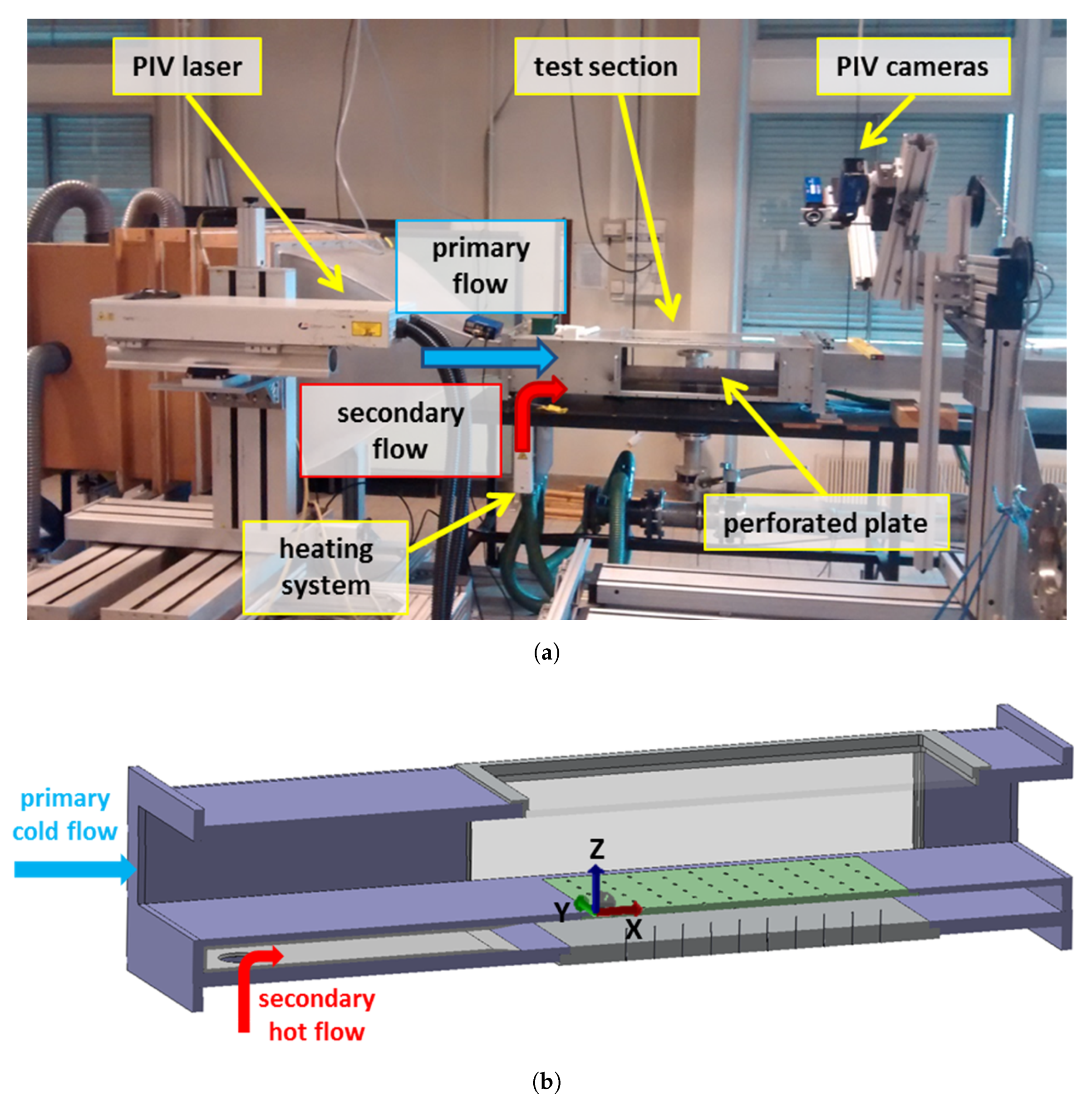
2. Description of the Experiment
2.1. Experimental Set-Up
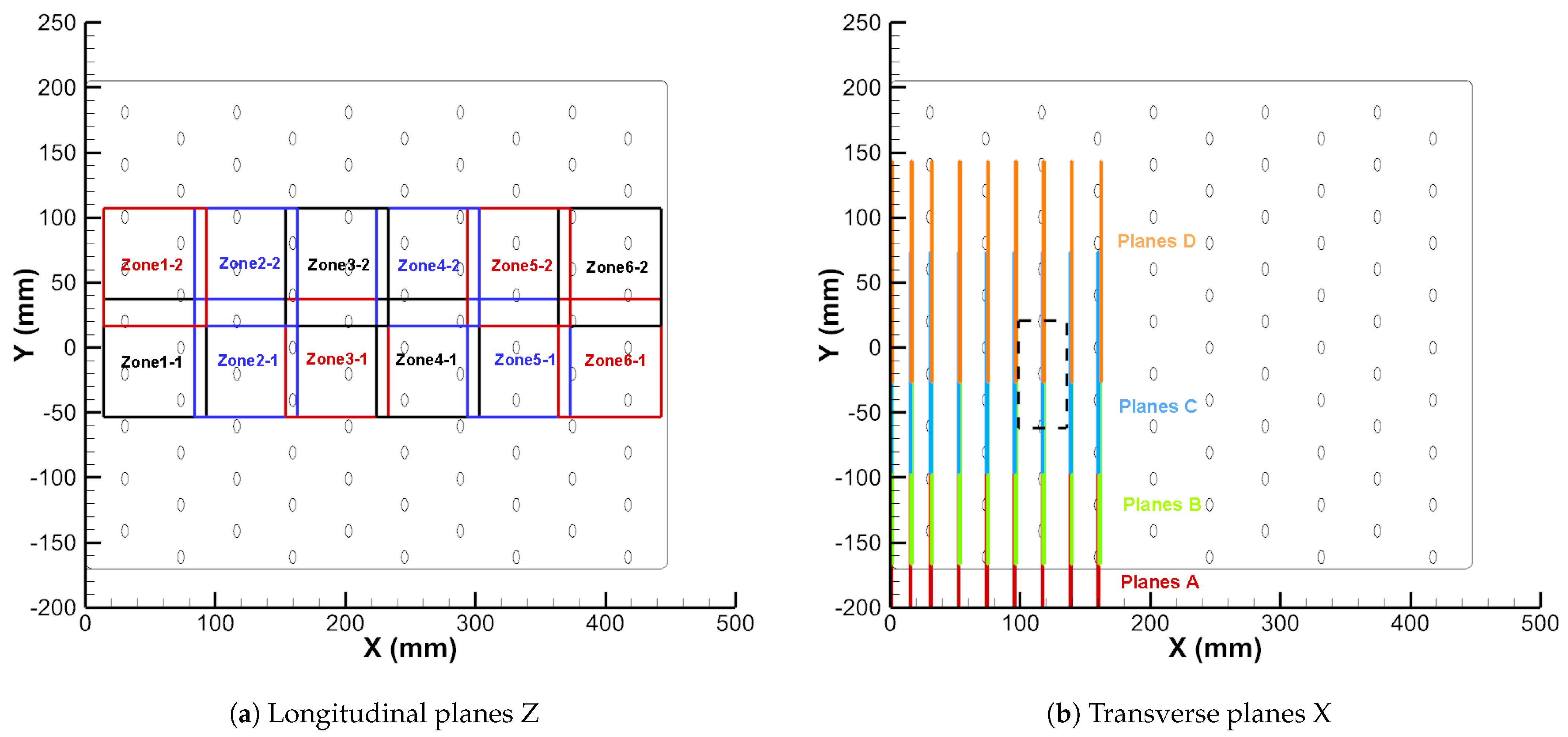
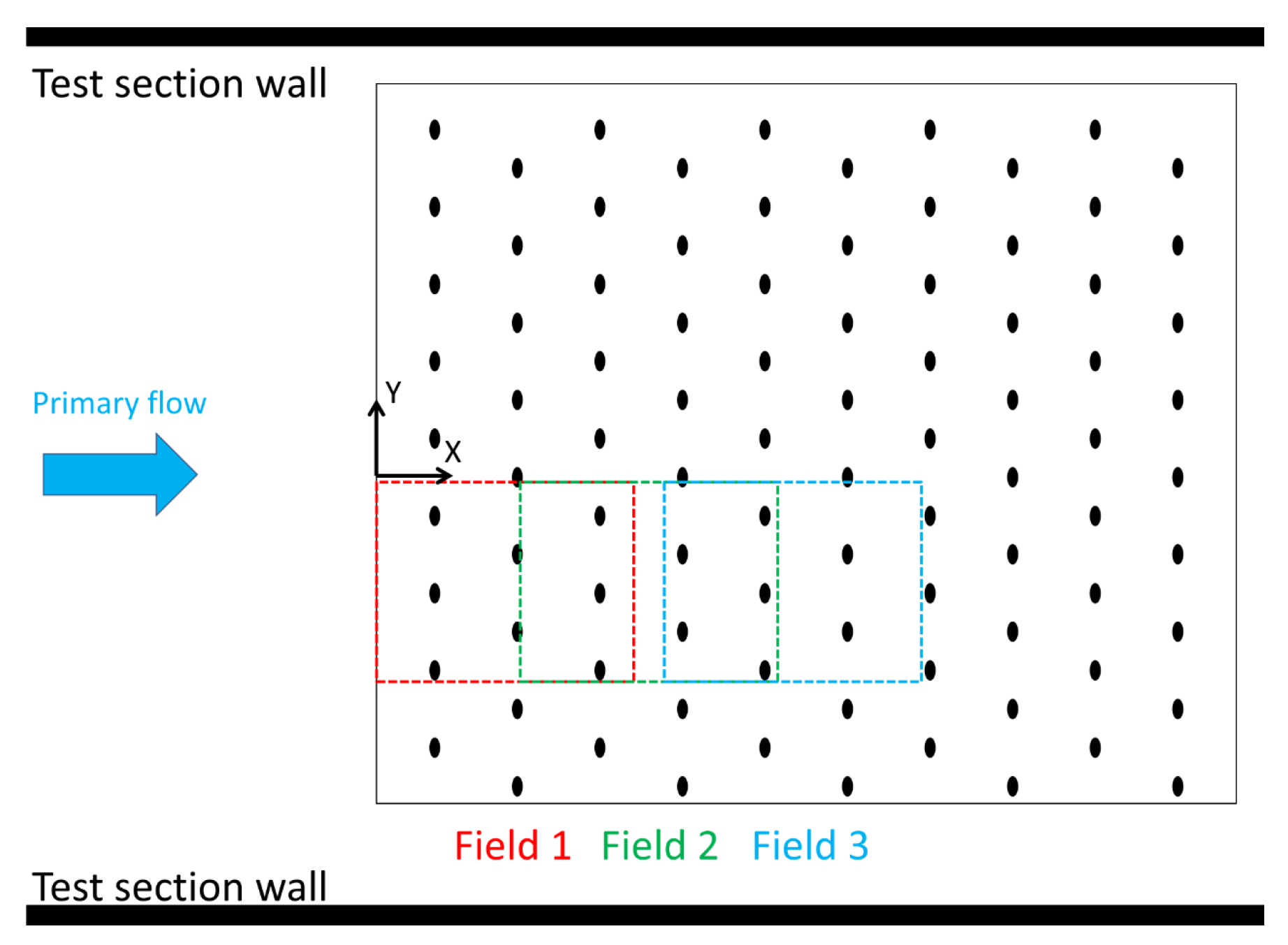
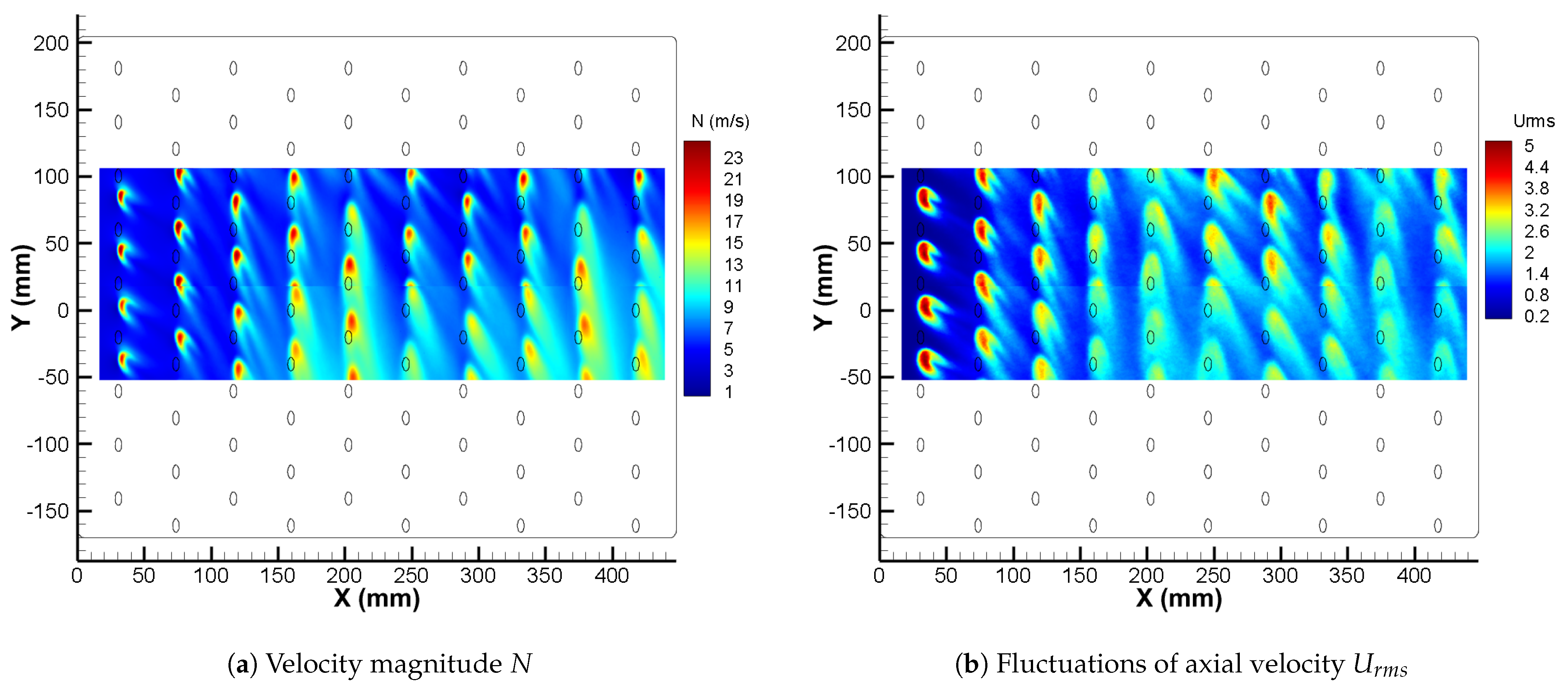
2.2. Aerodynamic Measurements
2.3. Thermal Measurements
2.3.1. Flow Temperature Measurements
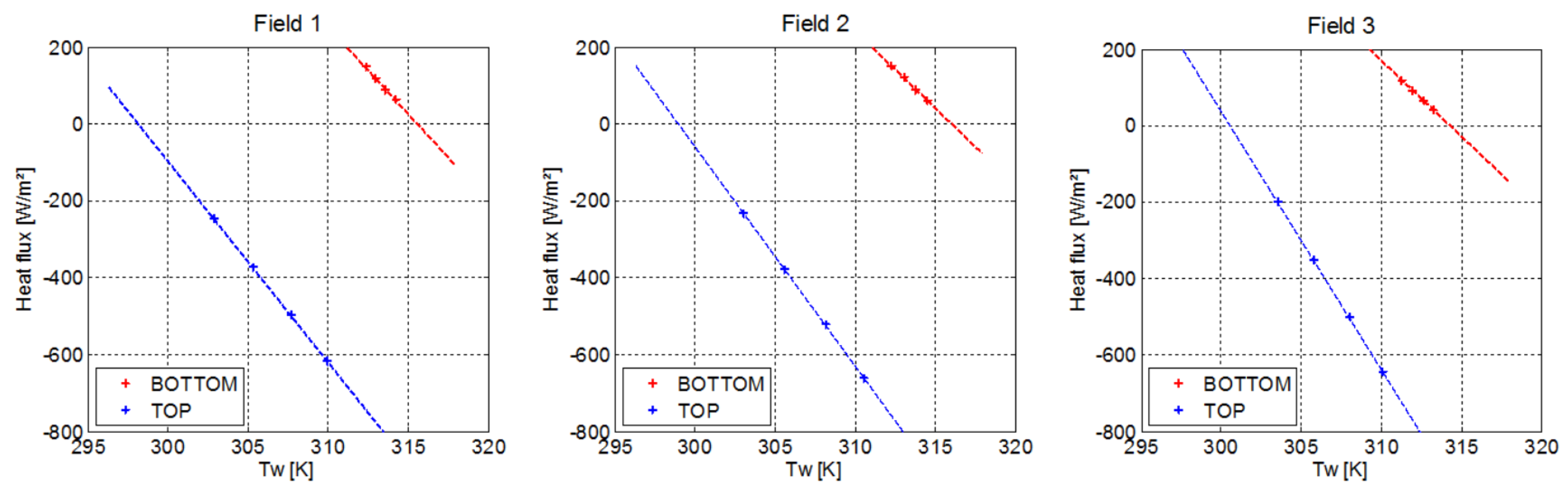
2.3.2. Characterization of the Wall Heat Transfer
3. Numerical Model
4. Discussion
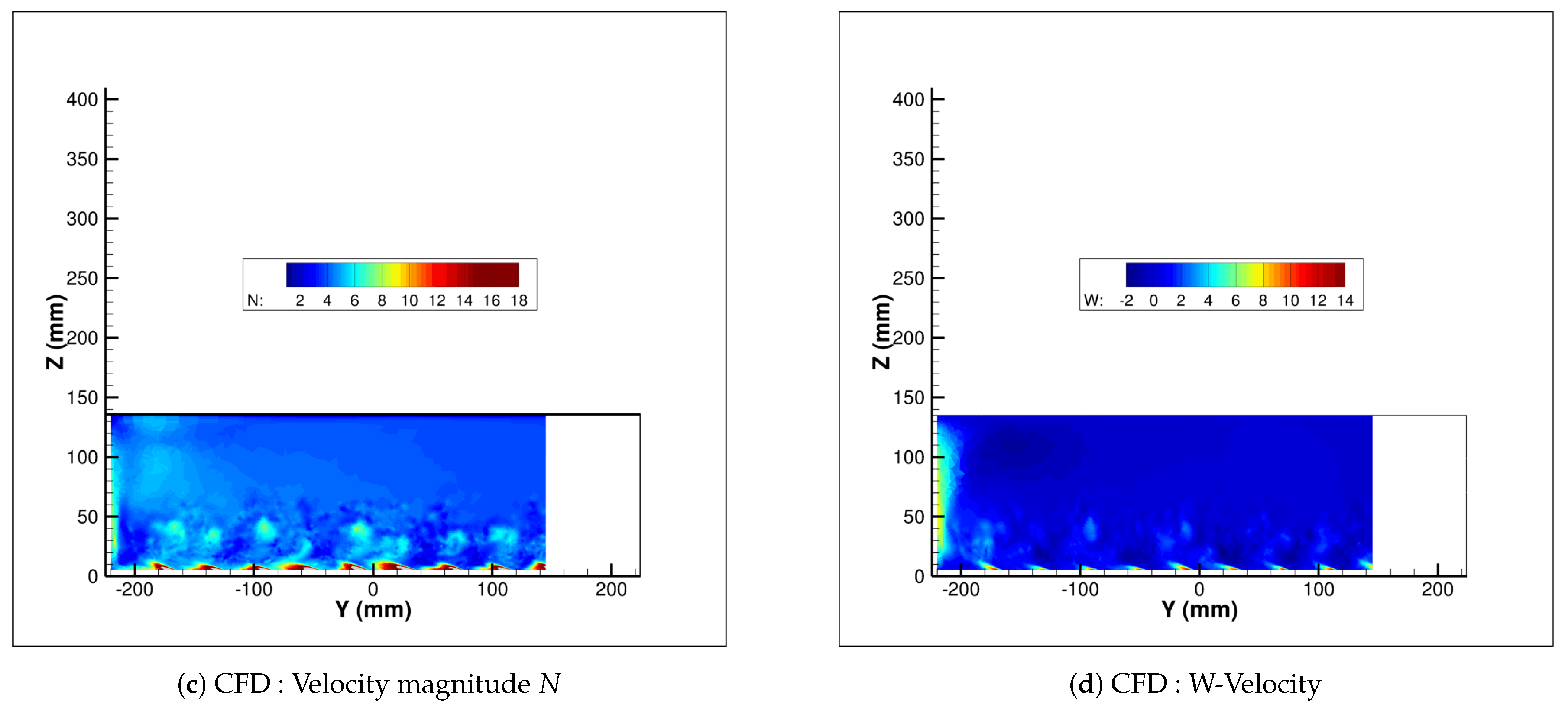
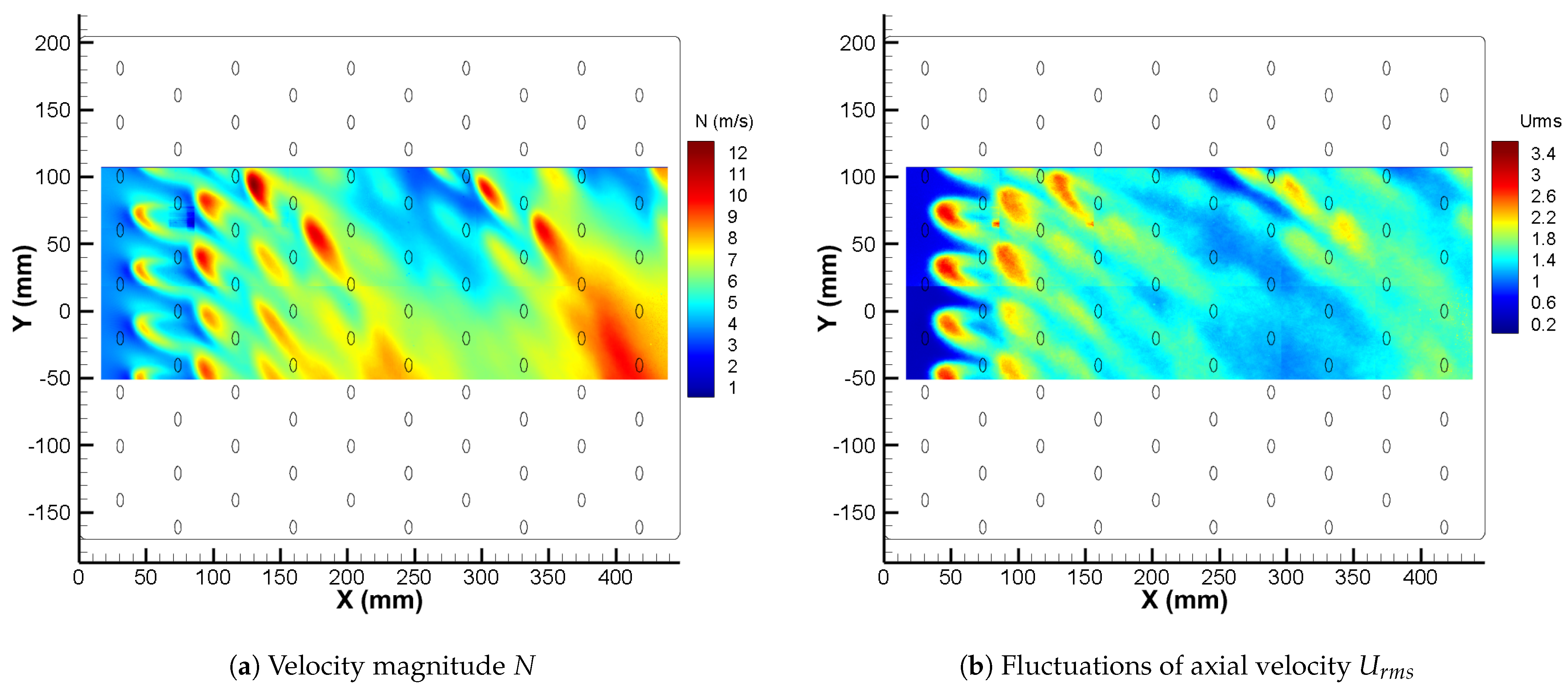
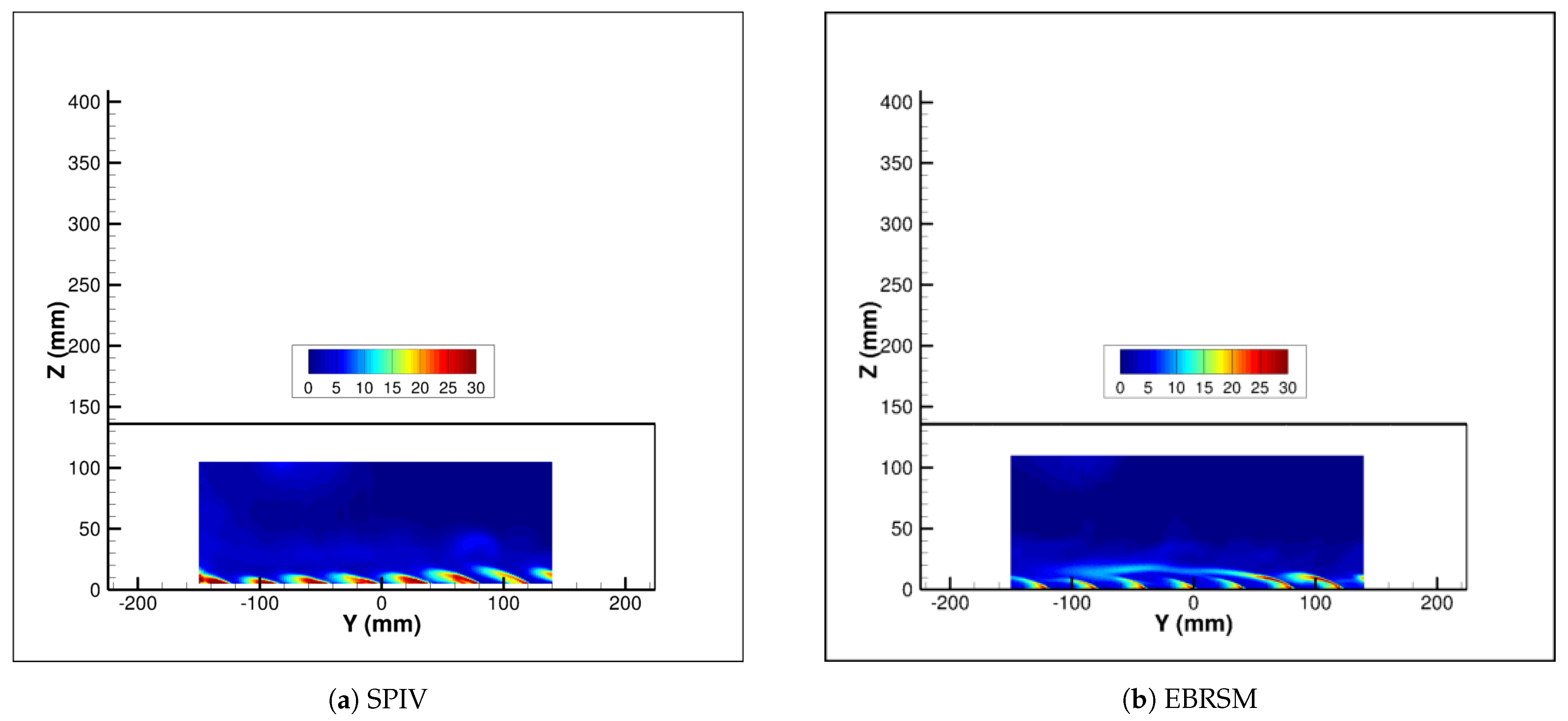
4.1. Dynamics of the Flow
4.2. Heat Transfer Characterization
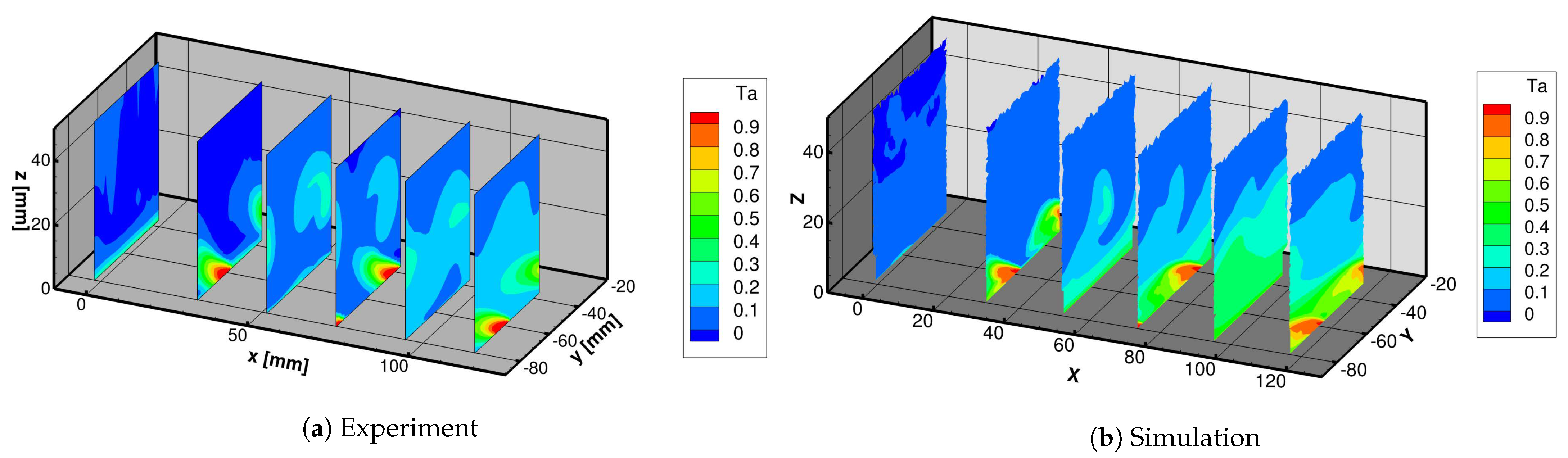
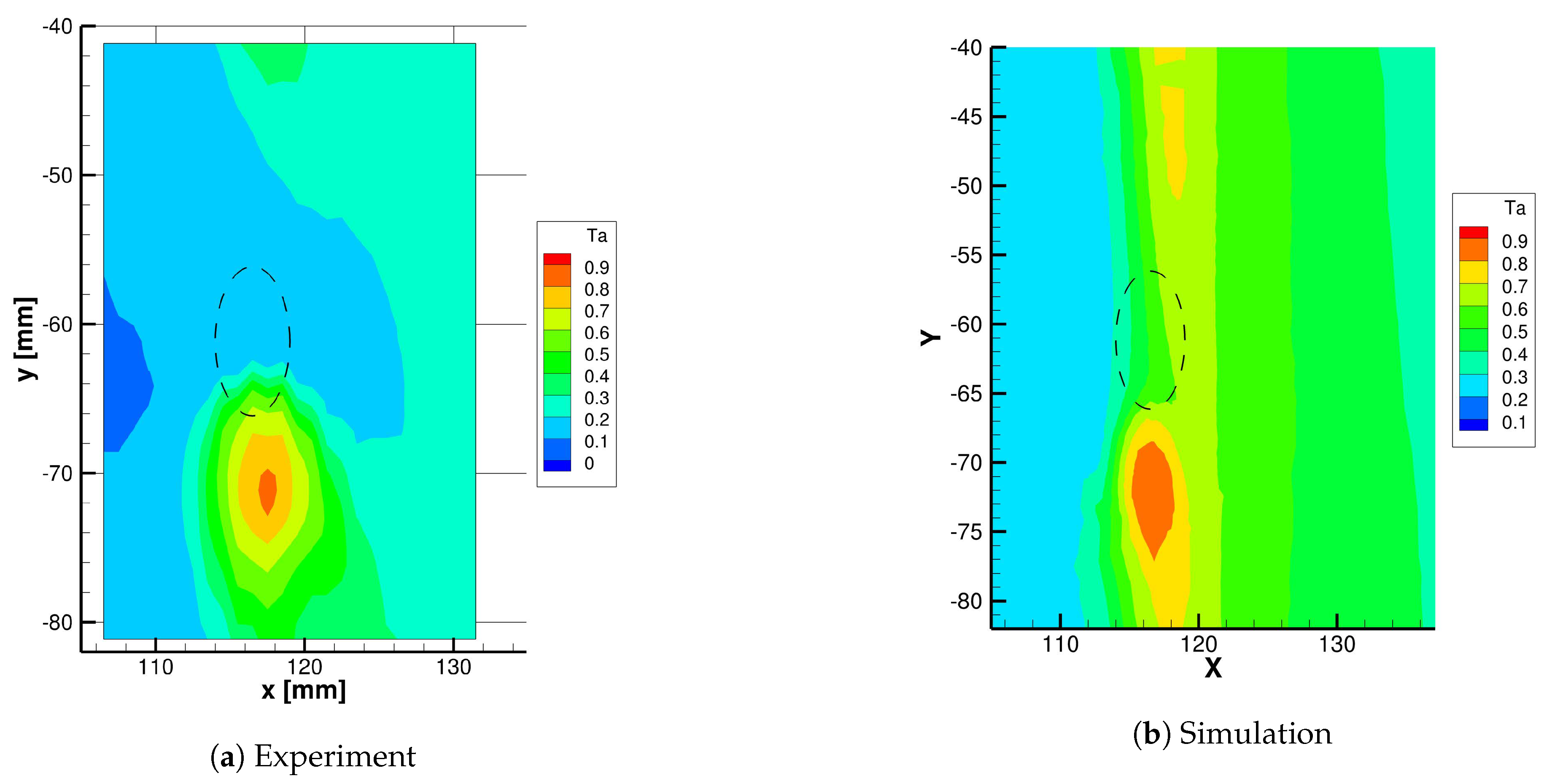
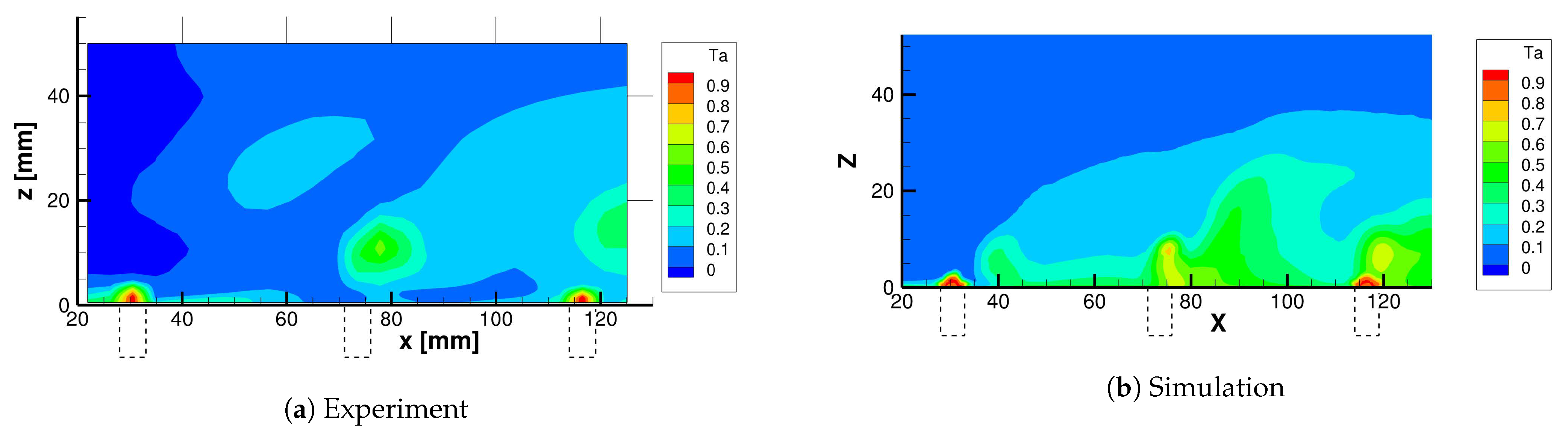
4.2.1. Primary Flow Temperature
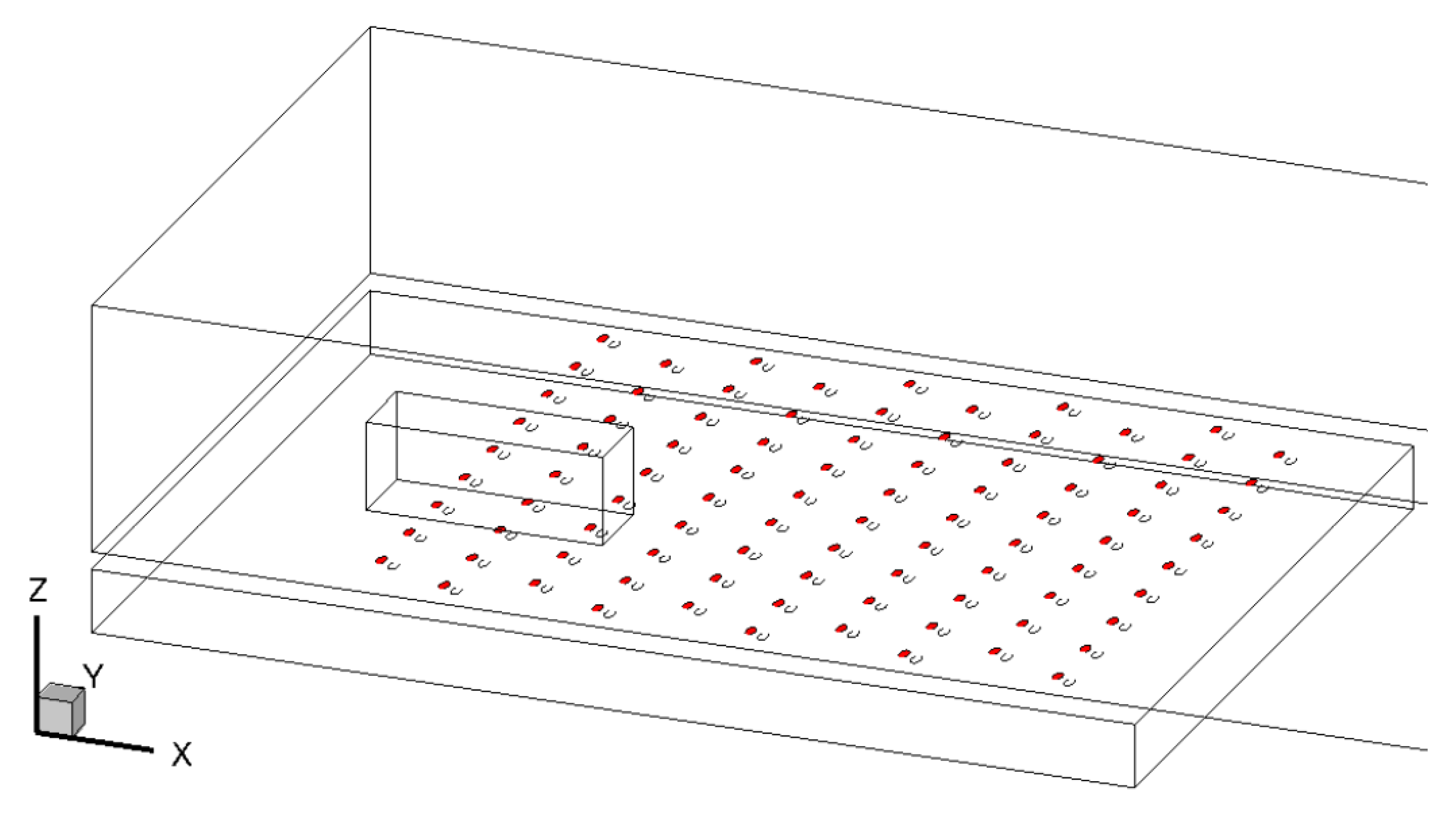
- 6 constant-X planes: (inlet conditions, 32 mm upstream 1st row), (1st row), , (2nd row), , (3rd row)
- 1 constant-Y plane: at the center of one hole in 1st and 3rd rows
- 1 constant-Z plane: above the center of one hole in 3rd row
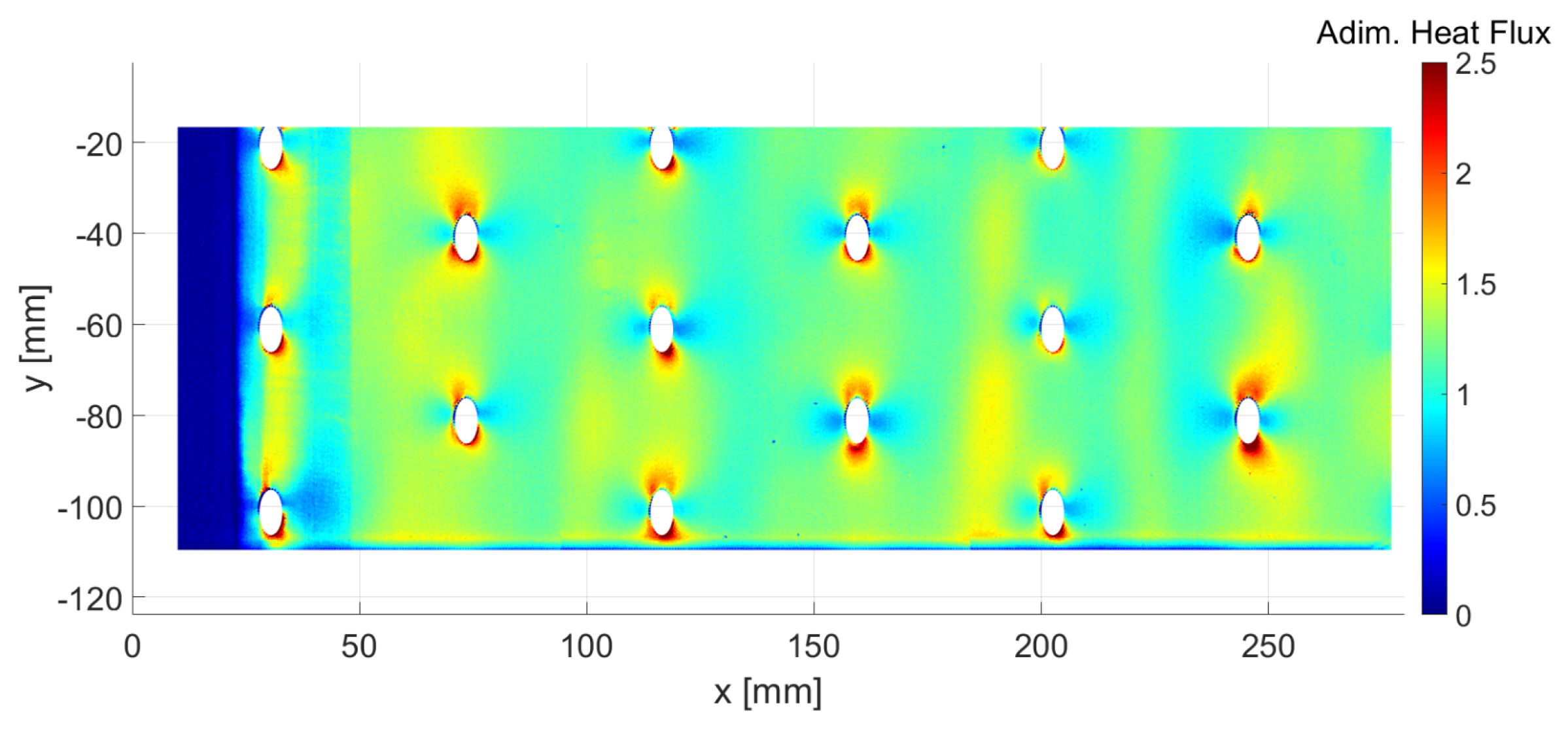
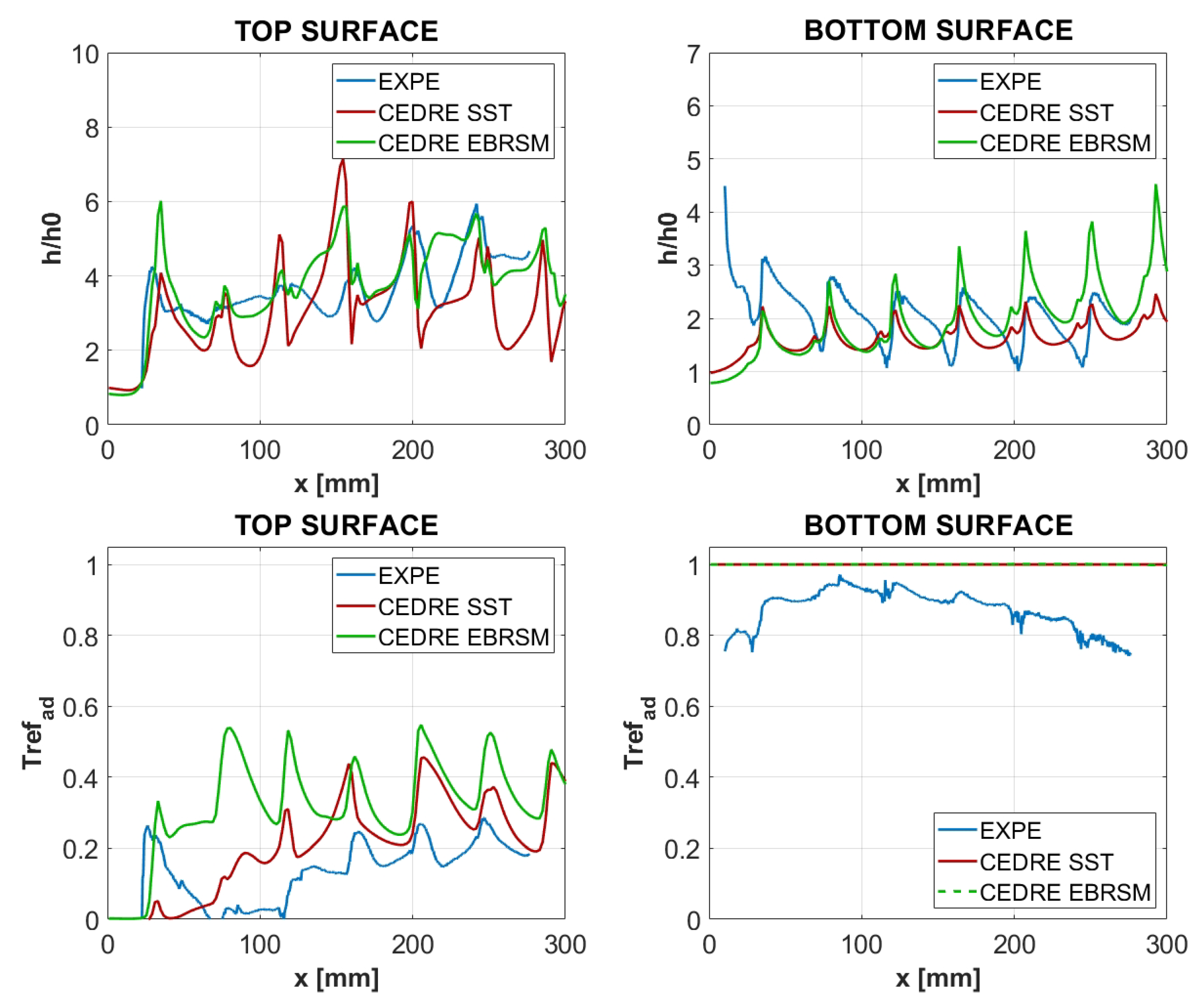
4.2.2. Wall Heat Transfer
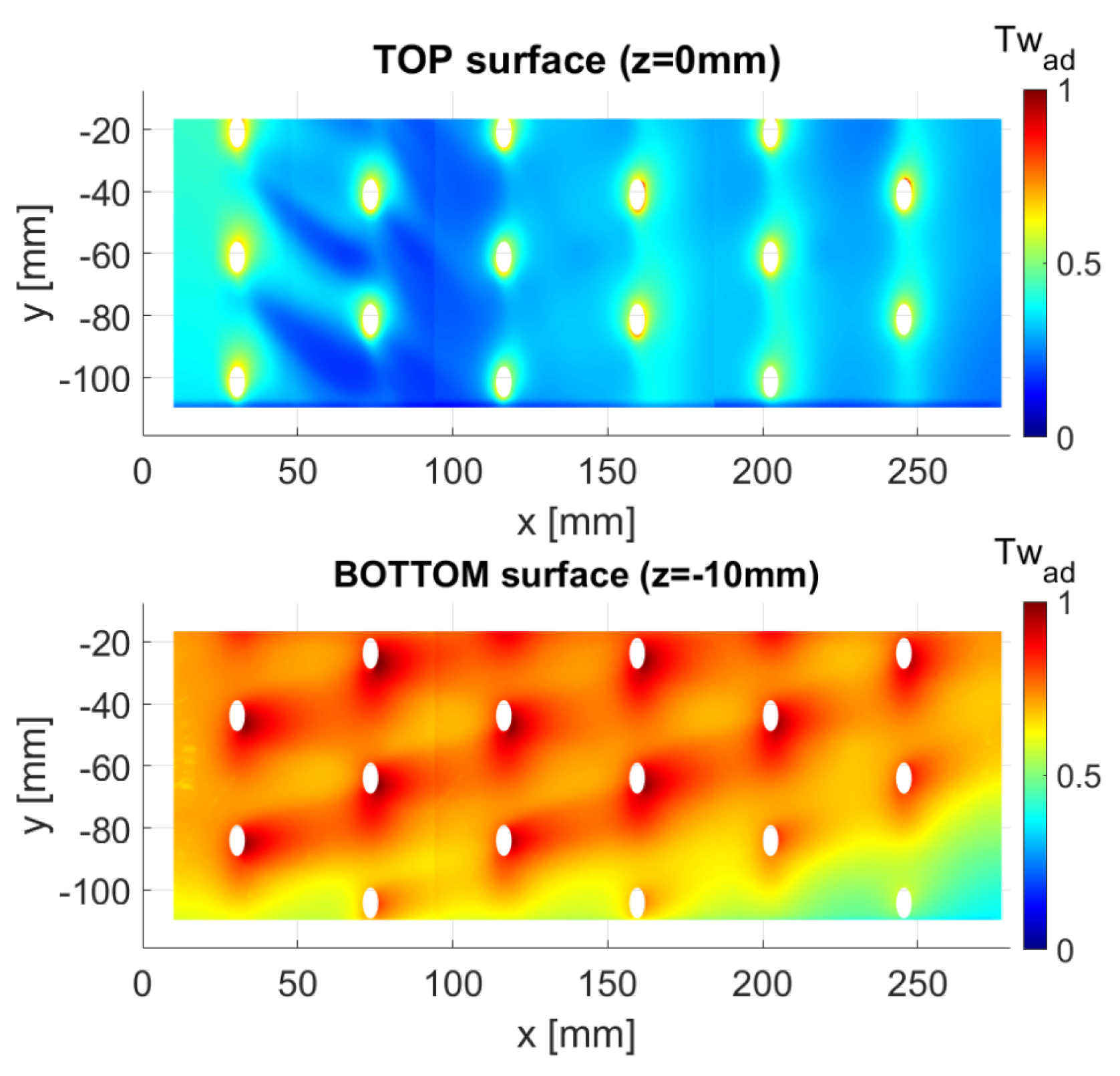
Wall Temperature Distribution
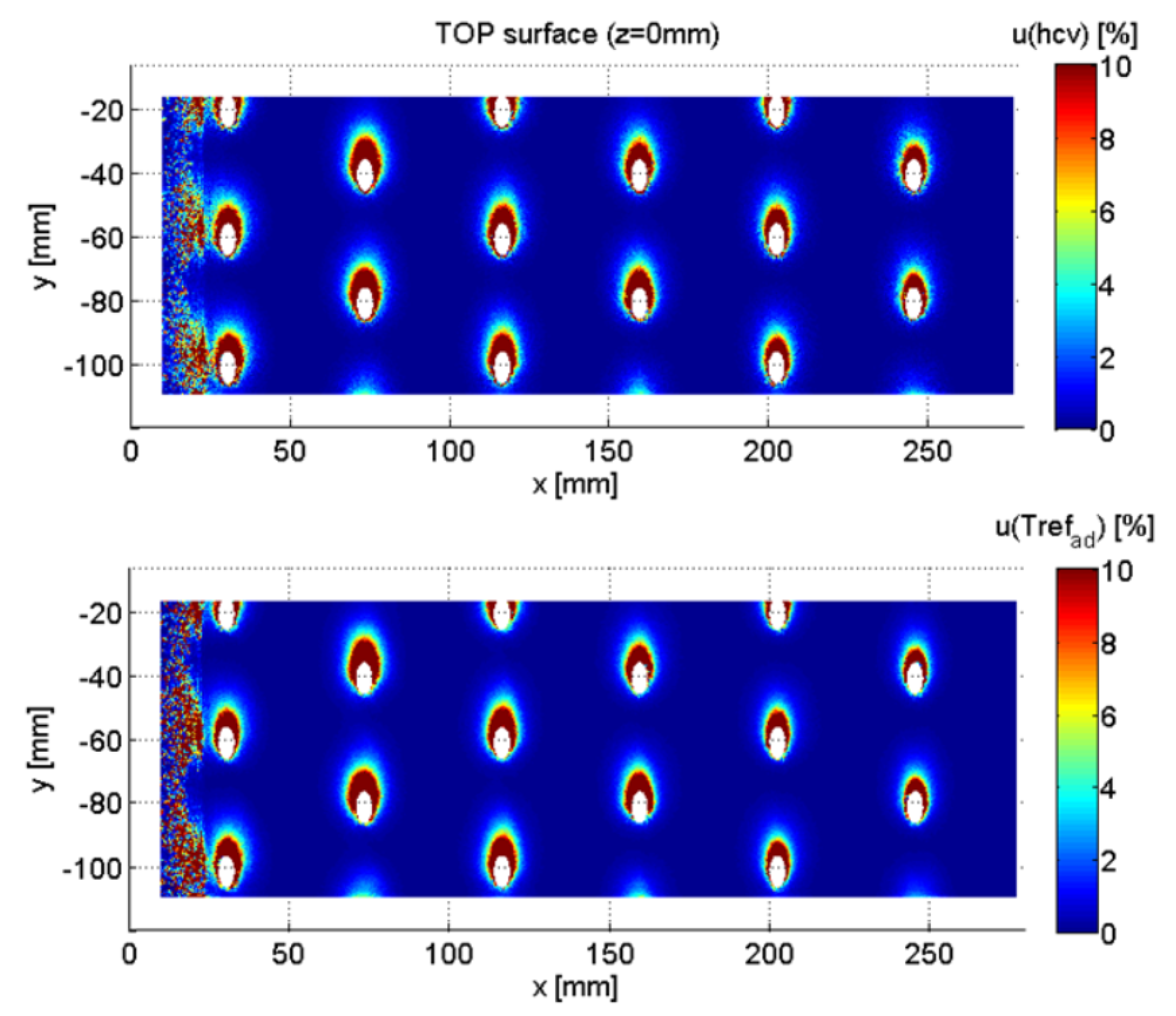
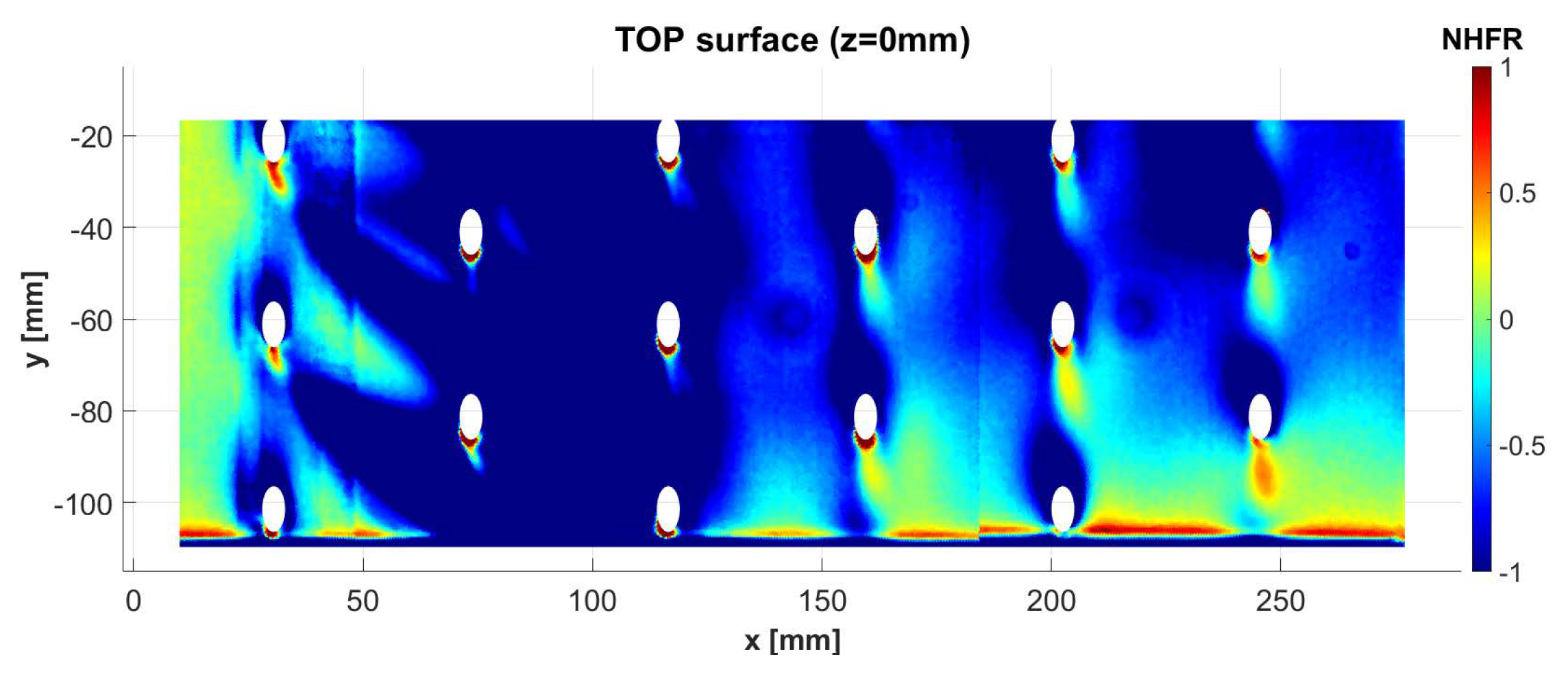
Wall Heat Transfer Coefficient and Adiabatic Wall Temperature
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Acronyms | |
| IRTh | Infrared Thermography |
| HTC | Heat Transfer Coefficient |
| NHFR | Net Heat Flux Reduction |
| RANS | Reynolds Averaged Navier-Stokes |
| RSM | Reynolds Stress Model |
| SPIV | Stereo Particle Image Velocimetry |
| Subscripts | |
| non-dimensional | |
| adiabatic | |
| primary channel (cold flow) | |
| convection | |
| electrical | |
| h | hole |
| secondary channel (hot flow) | |
| reference | |
| t | turbulent |
| w | wall |
| Nomenclature | ||
| specific heat | [J·kgK] | |
| h | heat transfer coefficient | [W·mK] |
| k | turbulent kinetic energy | [ms] |
| N | velocity magnitude | [m·s] |
| p | axial spacing of hole rows | [m] |
| Prandtl number | [−] | |
| Reynolds number | [−] | |
| s | lateral spacing of hole rows | [m] |
| S | surface area | [m] |
| T | temperature | [K] |
| spatial coordinates | [m] | |
| velocity components | [m·s] | |
| velocity fluctuation components | [m·s] | |
| Greeks | ||
| pitch angle | [] | |
| yaw angle | [] | |
| effectiveness | [−] | |
| thermal conductivity | [W·mK] | |
| heat flux density | [W·m] | |
| density | [kg·m] | |
References
- Mayle, R.; Camarata, F. Multihole Cooling Film Effectiveness and Heat Transfer. ASME J. Propul. Power 1975, 97, 534–538. [Google Scholar] [CrossRef]
- Schmidt, D.L.; Sen, B.; Bogard, D.G. Film Cooling with Compound Angle Holes: Adiabatic Effectiveness. ASME J. Turbomach. 1996, 118, 807–813. [Google Scholar] [CrossRef]
- Sen, B.; Schmidt, D.L.; Bogard, D.G. Film Cooling with Compound Angle Holes: Heat Transfer. ASME J. Turbomach. 1996, 118, 800–806. [Google Scholar] [CrossRef]
- Ligrani, P.; Ramsey, A. Film Cooling from Spanwise-Oriented Holes in Two Staggered Rows. ASME J. Turbomach. 1997, 119, 562–567. [Google Scholar] [CrossRef]
- Andrews, G.; Khalifa, I.; Asere, A.; Bazdidi-Tehrani, F. Full coverage effusion film cooling with inclined holes. In Proceedings of the International Gas Turbine and Aeroengine Congress and Exposition, Houston, TX, USA, 5–8 June 1995. [Google Scholar] [CrossRef]
- Scrittore, J.J.; Thole, K.A.; Burd, S.W. Investigation of Velocity Profiles for Effusion Cooling of a Combustor Liner. ASME J. Turbomach. 2007, 129, 518–526. [Google Scholar] [CrossRef]
- Michel, B. Caractérisation Aérodynamique d’un Écoulement Avec Injection Pariétale de Type Dilution Giratoire en vue de sa Modélisation. Ph.D. Thesis, L’Institut Supérieur de l’Aéronautique et de l’Espace, Toulouse, France, 2008. [Google Scholar]
- Zhang, C.; Lin, Y.; Xu, Q.; Liu, G.; Song, B. Cooling Effectiveness of Effusion Walls with Deflection Hole Angles Measured by Infrared Imaging. Appl. Therm. Eng. 2009, 29, 966–972. [Google Scholar] [CrossRef]
- Leylek, J.H.; Zerkle, R.D. Discrete-Jet Film Cooling: A Comparison of Computational Results With Experiments. J. Turbomach. 1994, 116, 358–368. [Google Scholar] [CrossRef]
- Bergeles, G.; Gosman, A.D.; Launder, B.E. The Turbulent Jet in a Cross Stream at Low Injection Rates: A Three-Dimensional Numerical Treatment. Numer. Heat Transf. Part B Fundam. 1978, 1, 217–242. [Google Scholar] [CrossRef]
- Lakehal, D.; Theodoridis, G.; Rodi, W. Three-dimensional flow and heat transfer calculations of film cooling at the leading edge of a symmetrical turbine blade model. Int. J. Heat Fluid Flow 2001, 22, 113–122. [Google Scholar] [CrossRef]
- Arroyo-Callejo, G.; Laroche, E.; Millan, P.; Leglaye, F.; Chedevergne, F. Numerical Investigation of Compound Angle Effusion Cooling Using Differential Reynolds Stress Model and Zonal Detached Eddy Simulation Approaches. ASME J. Turbomach. 2016, 138. [Google Scholar] [CrossRef]
- Andreini, A.; Caciolli, G.; Facchini, B.; Tarchi, L.; Coutandin, D.; Peschiulli, A.; Taddei, S. Density ratio effects on the cooling performances of a combustor liner cooled by a combined slot/ effusion system. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012. [Google Scholar] [CrossRef]
- Crouzy, G.; Desarnaud, F.; Laroche, E.; Millan, P. Numerical modelling of a realistic annular effusion cooling system. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019. [Google Scholar] [CrossRef]
- Bizzari, R.; Lahbib, D.; Dauptain, A.; Duchaine, F.; Richard, S.; Nicoud, F. Low order modeling method for assessing the temperature of multi-perforated plates. Int. J. Heat Mass Transf. 2018, 127, 727–742. [Google Scholar] [CrossRef]
- Champagnat, F.; Plyer, A.; Le Besnerais, G.; Davoust, S.; Le Sant, Y. Experiments on a turbulent jet in cross flow. Exp. Fluids 2011, 50, 1169–1182. [Google Scholar] [CrossRef]
- Lee, S.K.; Giacobello, M.; Manovski, P.; Kumar, C. Optimising Camera Arrangement for Stereoscopic Particule Image Velocimetry. In Proceedings of the 19th Australasian Fluid Mechanics Conference, Melbourne, Australia, 8–12 December 2014. [Google Scholar]
- Johnson, B.; Tian, W.; Zhang, K.; Hu, H. An experimental study of density ratio effects on the film cooling injection from discrete holes by using PIV and PSP techniques. Int. J. Heat Mass Transf. 2014, 76, 337–349. [Google Scholar] [CrossRef]
- RESCOLL Society Website. 2020. Available online: http://rescoll.fr/fabrication/peintures/ (accessed on 22 January 2021).
- Cottin, G. Contribution à la Modélisation Thermique d’une Paroi Mlutiperforée. Ph.D. Thesis, L’Institut Supérieur de l’Aéronautique et de l’Espace, Toulouse, France, 2013. [Google Scholar]
- Roux, S.; Fénot, M.; Lalizel, G.; Brizzi, L.; Dorignac, E. Experimental investigation of the flow and heat transfer of an impinging jet under acoustic excitation. Int. J. Heat Mass Transf. 2011, 54, 3277–3290. [Google Scholar] [CrossRef]
- Hruska, Z.; Guesnet, P.; Salin, C.; Couchoud, J.J. Polychlorure de Vinyle ou PVC; Techniques de L’Ingénieur; AM3325 V3; Editions T.I.: Paris, France, 2007. [Google Scholar]
- Centaur Software, Computational Grids for Advanced Modelling. Available online: http://www.centaursoft.com (accessed on 22 January 2021).
- Refloch, A.; Courbet, B.; Murrone, A.; Villedieu, P.; Laurent, C.; Gilbank, P.; Troyes, J.; Tessé, L.; Chaineray, G.; Dargaud, J.; et al. CEDRE software. Aerosp. Lab J. 2011. Available online: https://aerospacelab.onera.fr/sites/www.aerospacelab-journal.org/files/AL2-11.pdf (accessed on 22 January 2021).
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Manceau, R. Recent progress in the development of the Elliptic Blending Reynolds-stress model. Int. J. Heat Fluid Flow 2015, 51, 195–220. [Google Scholar] [CrossRef]
- Kays, W.M. Turbulent Prandtl Number—Where Are We? J. Heat Transf. 1994, 116, 284–295. [Google Scholar] [CrossRef]
- Daly, B.J.; Harlow, F.H. Transport Equations in Turbulence. Phys. Fluids 1970, 13, 2634–2649. [Google Scholar] [CrossRef]
- Laroche, E.; Reulet, P.; Donjat. A Combined Experimental and Numerical Characterization of the Flowfield and Heat Transfer Around a Multiperforated Plate With Compound Angle Injection. In Proceedings of the ASME Turbo Expo 2020, London, UK, 22–26 June 2020. [Google Scholar] [CrossRef]
- Byerley, A.; Joners, T.; Ireland, P. Internal Cooling Passage Heat Transfer Near the Entrance to a Film Cooling Hole: Experimental and Computational Results. In Proceedings of the International Gas Turbine and Aeroengine Congress and Exposition, Cologne, Germany, 1–4 June 1992. [Google Scholar] [CrossRef]
- Ling, J.; Ryan, K.J.; Bodart, J.; Eaton, J.K. Analysis of Turbulent Scalar Flux Models for a Discrete Hole Film Cooling Flow. J. Turbomach. 2016, 138. [Google Scholar] [CrossRef]











| Primary Flow | Secondary Flow | |
|---|---|---|
| HTC | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laroche, E.; Donjat, D.; Reulet, P. A Combined Experimental and Numerical Characterization of the Flowfield and Heat Transfer around a Multiperforated Plate with Compound Angle Injection. Energies 2021, 14, 613. https://doi.org/10.3390/en14030613
Laroche E, Donjat D, Reulet P. A Combined Experimental and Numerical Characterization of the Flowfield and Heat Transfer around a Multiperforated Plate with Compound Angle Injection. Energies. 2021; 14(3):613. https://doi.org/10.3390/en14030613
Chicago/Turabian StyleLaroche, Emmanuel, David Donjat, and Philippe Reulet. 2021. "A Combined Experimental and Numerical Characterization of the Flowfield and Heat Transfer around a Multiperforated Plate with Compound Angle Injection" Energies 14, no. 3: 613. https://doi.org/10.3390/en14030613
APA StyleLaroche, E., Donjat, D., & Reulet, P. (2021). A Combined Experimental and Numerical Characterization of the Flowfield and Heat Transfer around a Multiperforated Plate with Compound Angle Injection. Energies, 14(3), 613. https://doi.org/10.3390/en14030613






