Control Configurations for Reactive Power Compensation at the Secondary Side of the Low Voltage Substation by Using Hybrid Transformer
Abstract
1. Introduction
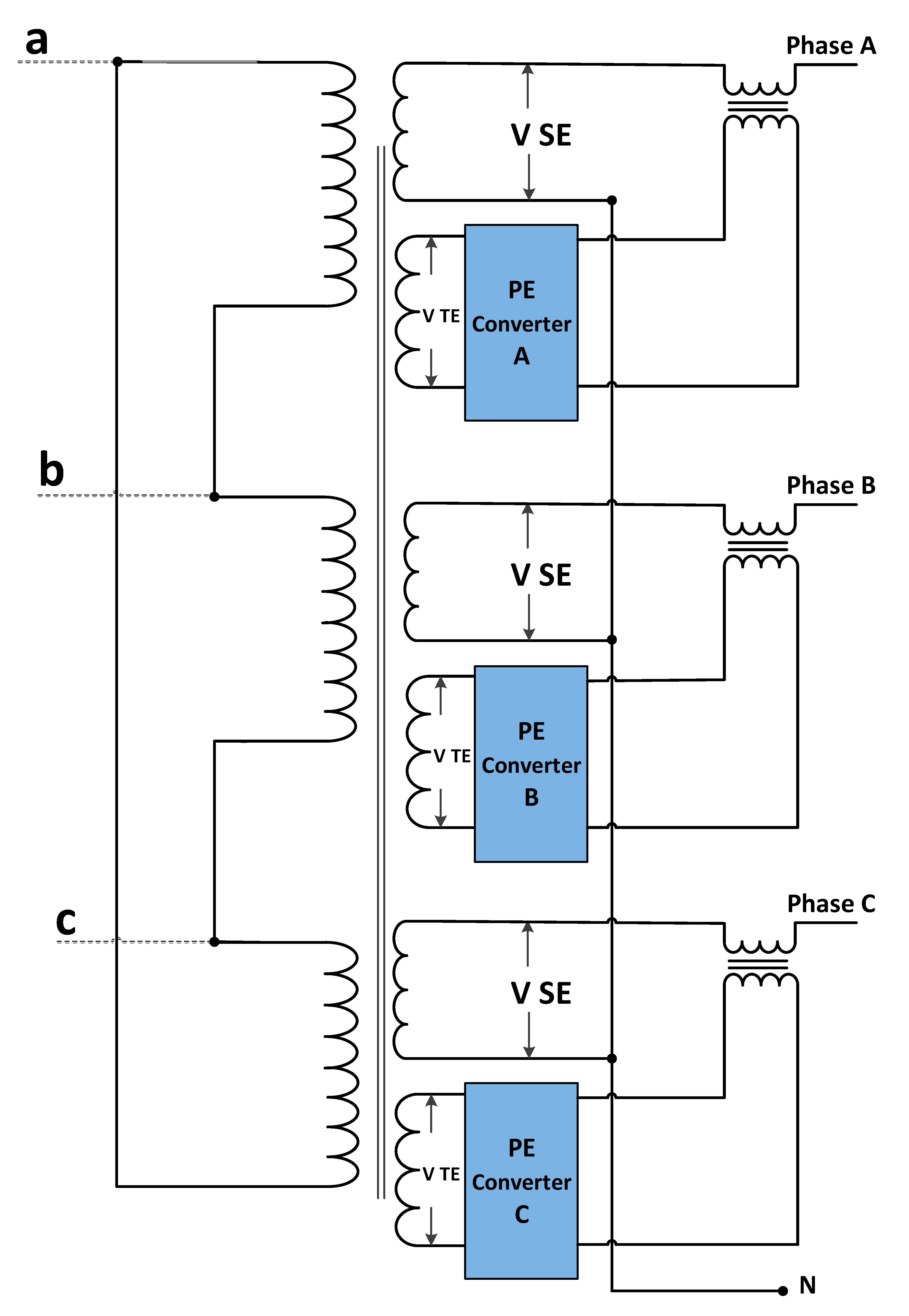
2. Proposed HT Approach
- High reliability, but low cost when compared to full rated converts.
- Reducing switching losses due to operating within lower switches’ ratings.
- Exploiting the latent advantages of one of the most reliable devices in the network, i.e., the transformer.
- The system partially tastes the flexibility of the PE and its functionalities that could be bypassed in case of PE failure.
2.1. HT Design
- Voltage regulation of up to ±30% of the nominal value.
- RP control of up to ±30% of the nominal value.
- It performs fast control for power flow.
- If the power at the DC link from the rectifier and inverter sides is balanced, the variations in the DC voltage at the DC link can be avoided [33]. In this way, the current level at the DC link is not distorted.
- A DC output can be supplied in case of further modifications.
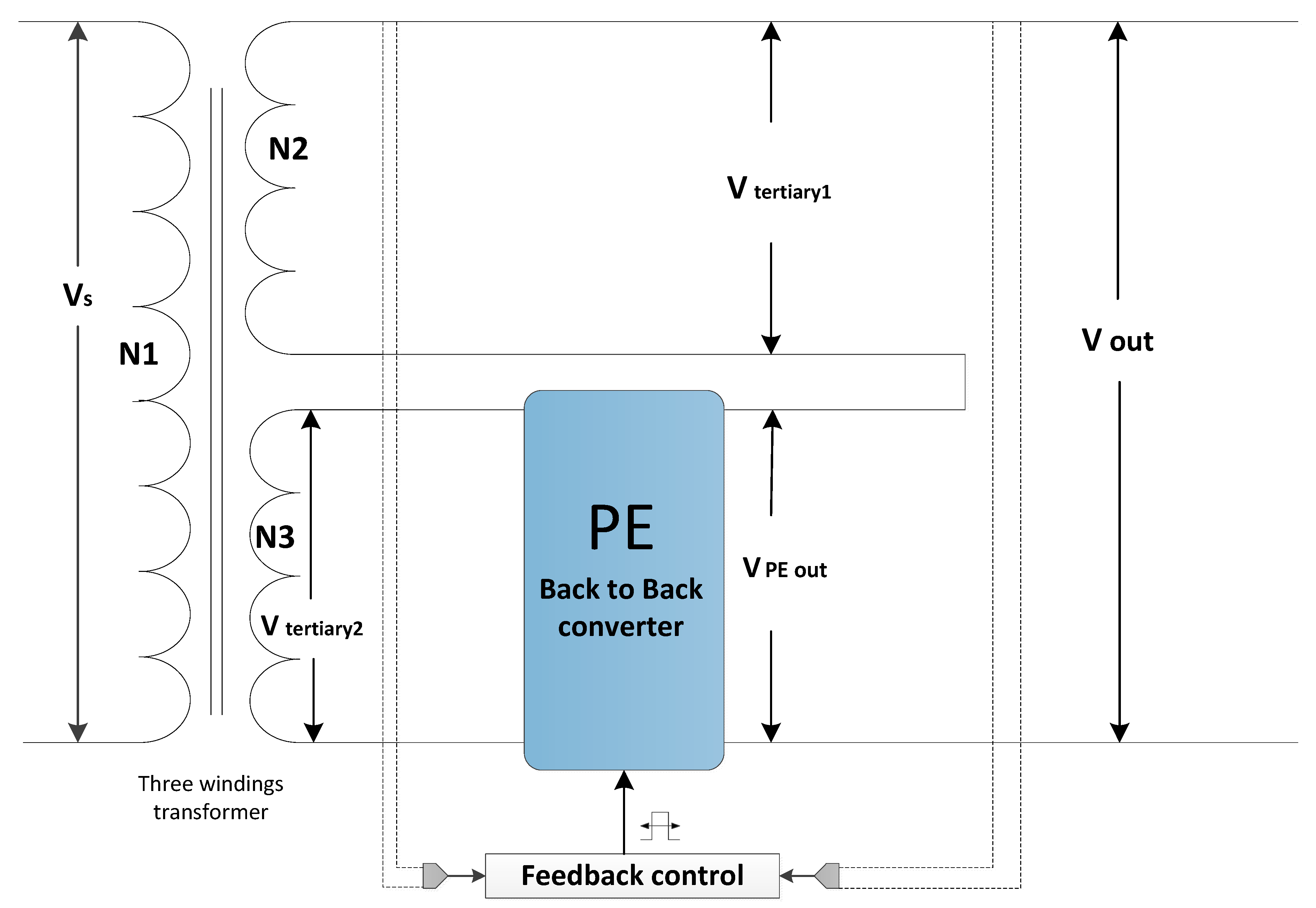
2.2. HT Topology
- It provides a fast control for the power flow.
- It avoids variations in the DC voltage at the DC link.
- It keeps the current level undistorted when the power at the DC link from the rectifier and inverter sides is balanced [33].
2.3. HT Implementation
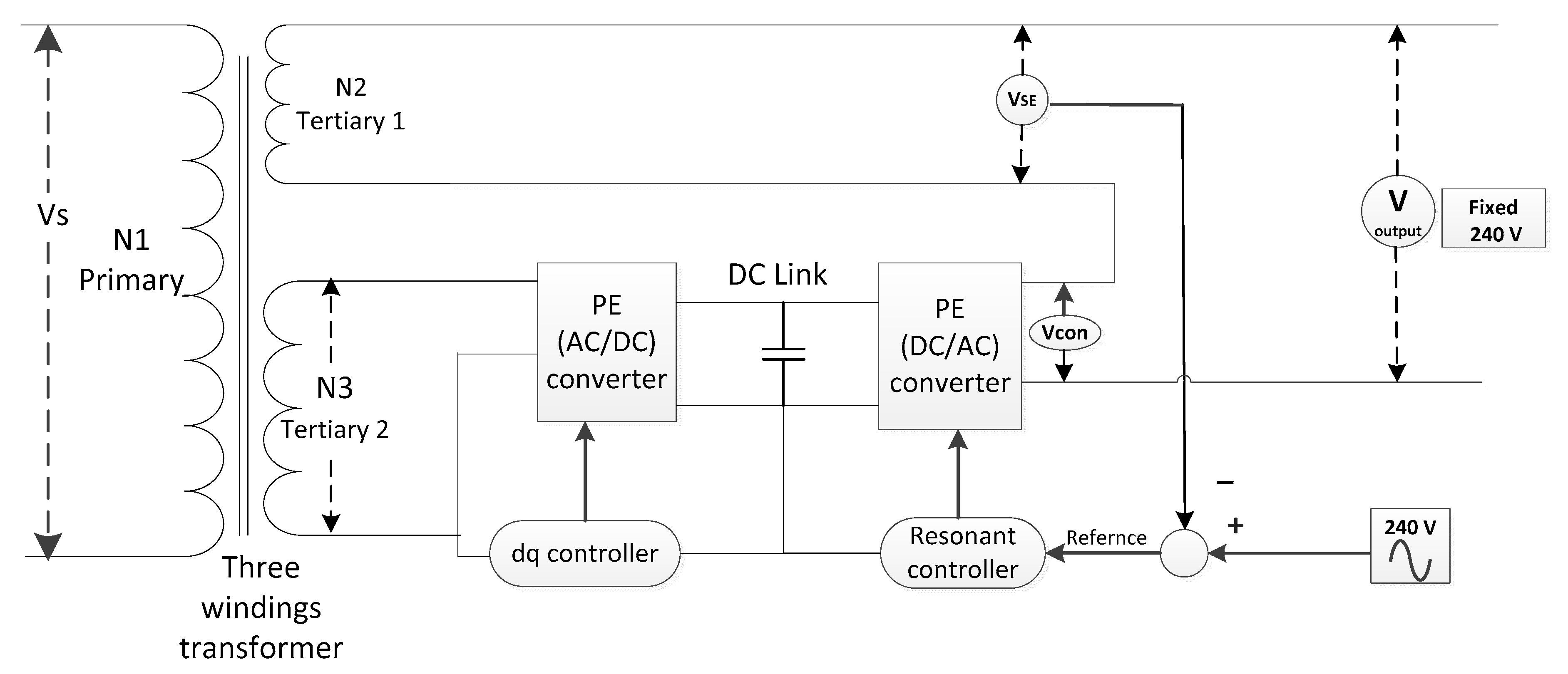
3. Proposed HT Control Approach
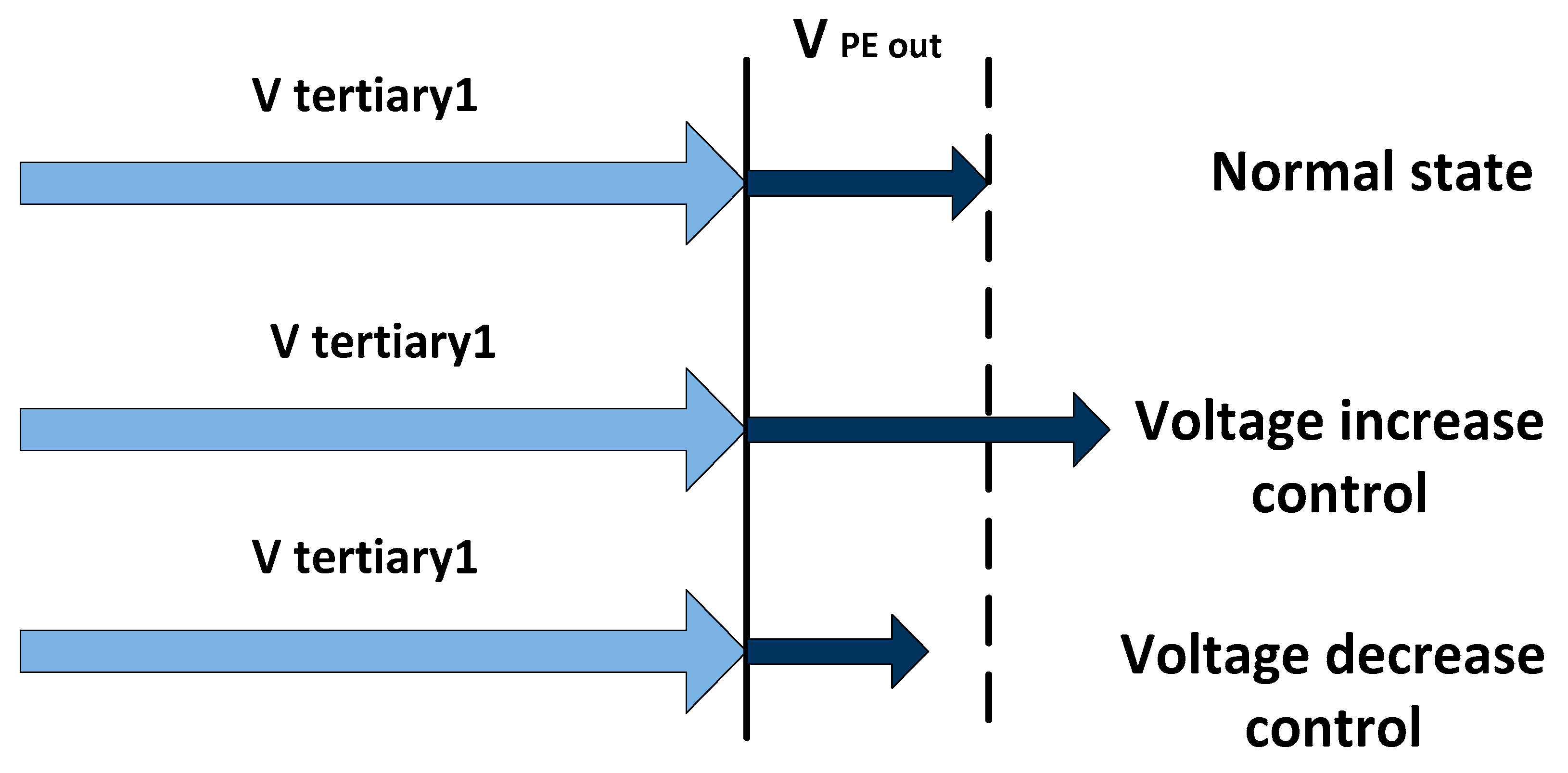
3.1. Voltage Control Approach
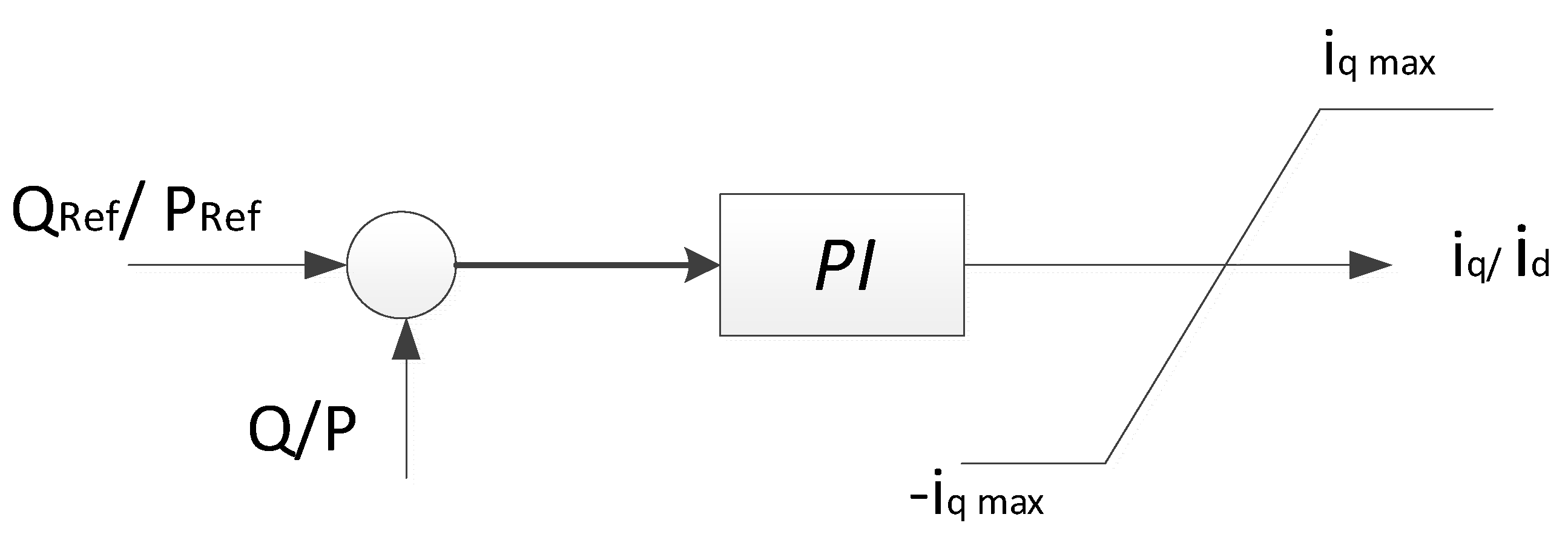
3.2. Reactive and Active Power Control
3.3. DC Link Control Using Power Control Principle
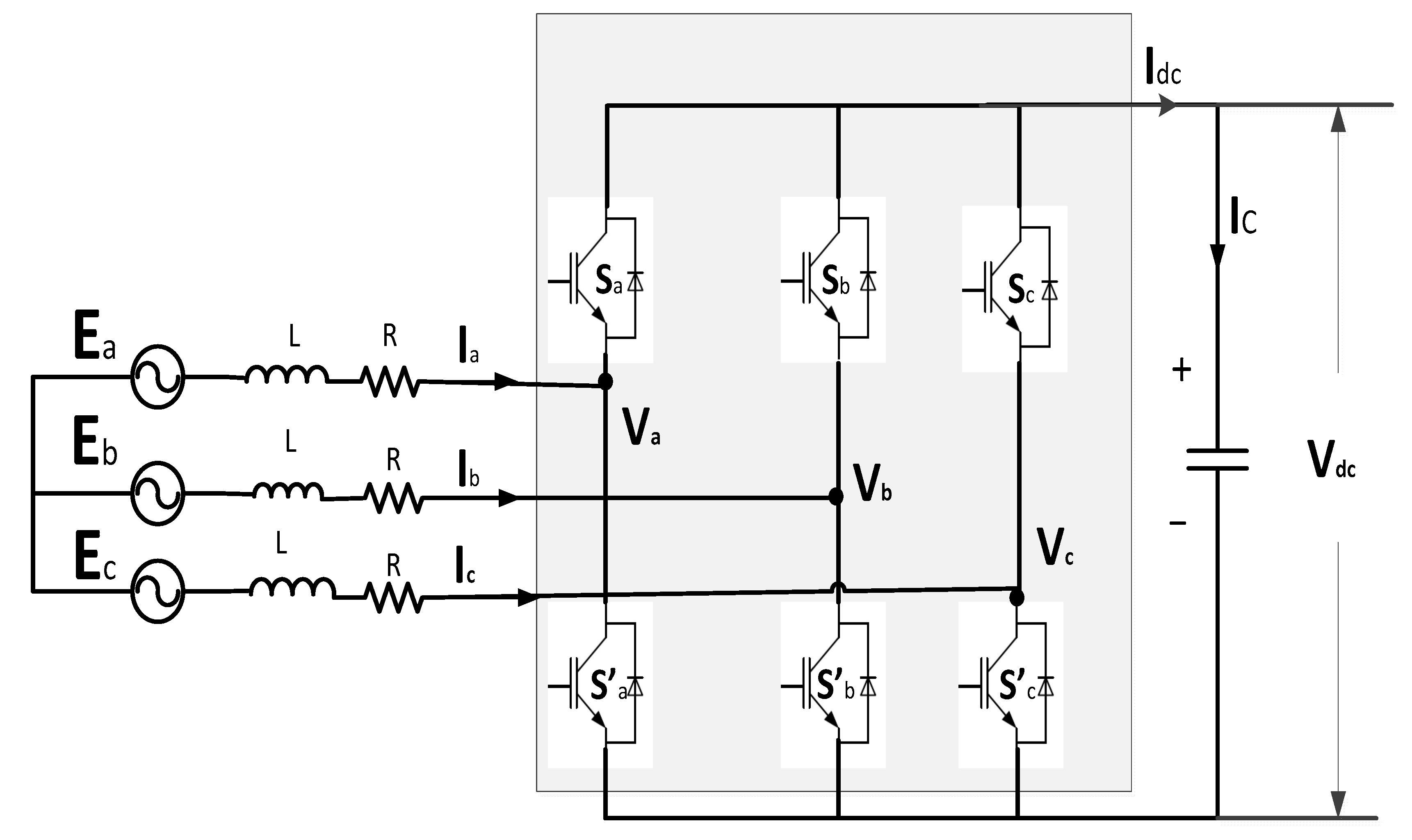
3.4. Inverter and Rectifier Power Dynamics
3.4.1. Inverter Dynamics
3.4.2. Inverter Dynamics
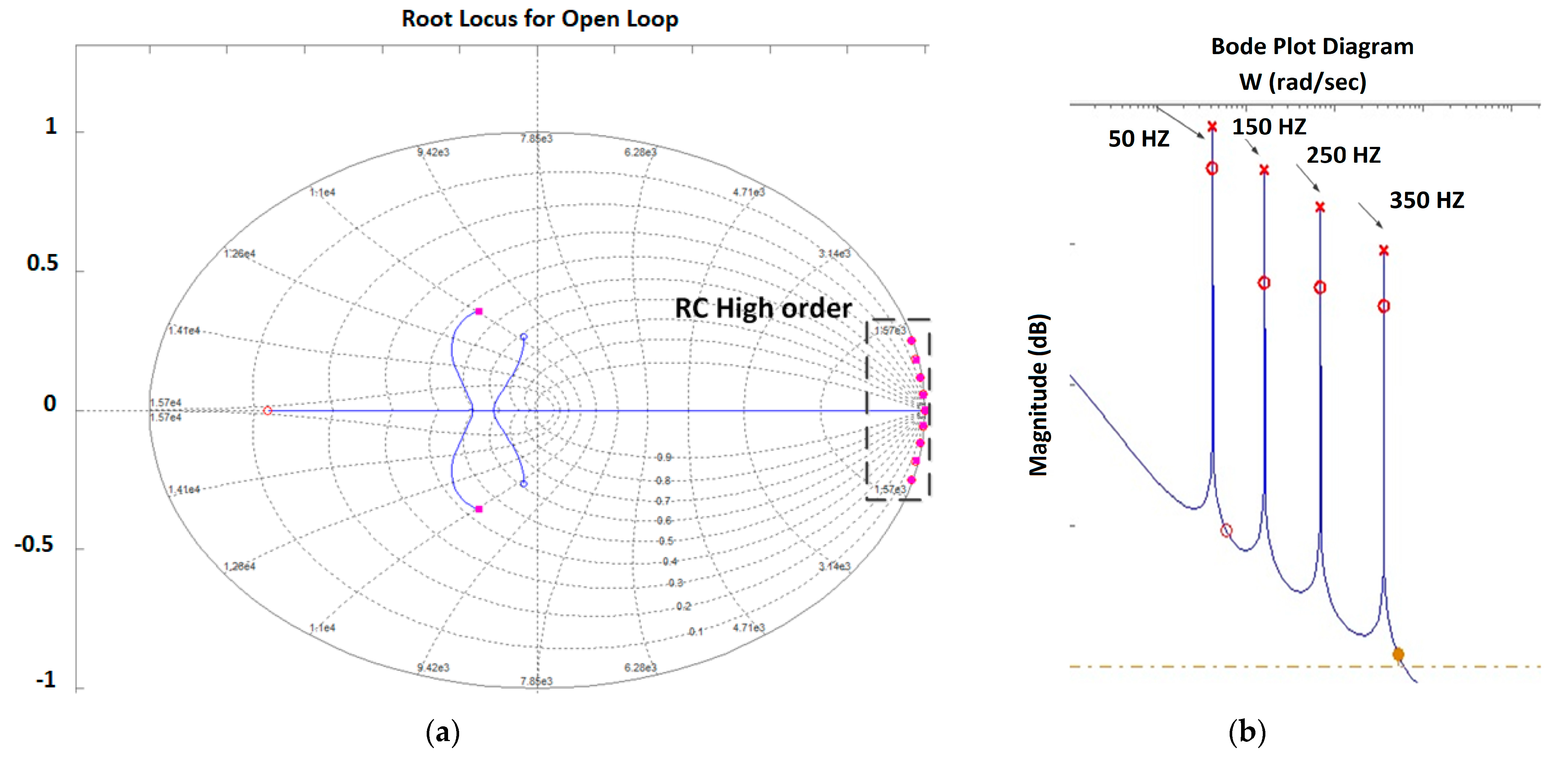
3.5. Transfer Function for Power Control
4. Results and Discussion
4.1. Voltage Control Results
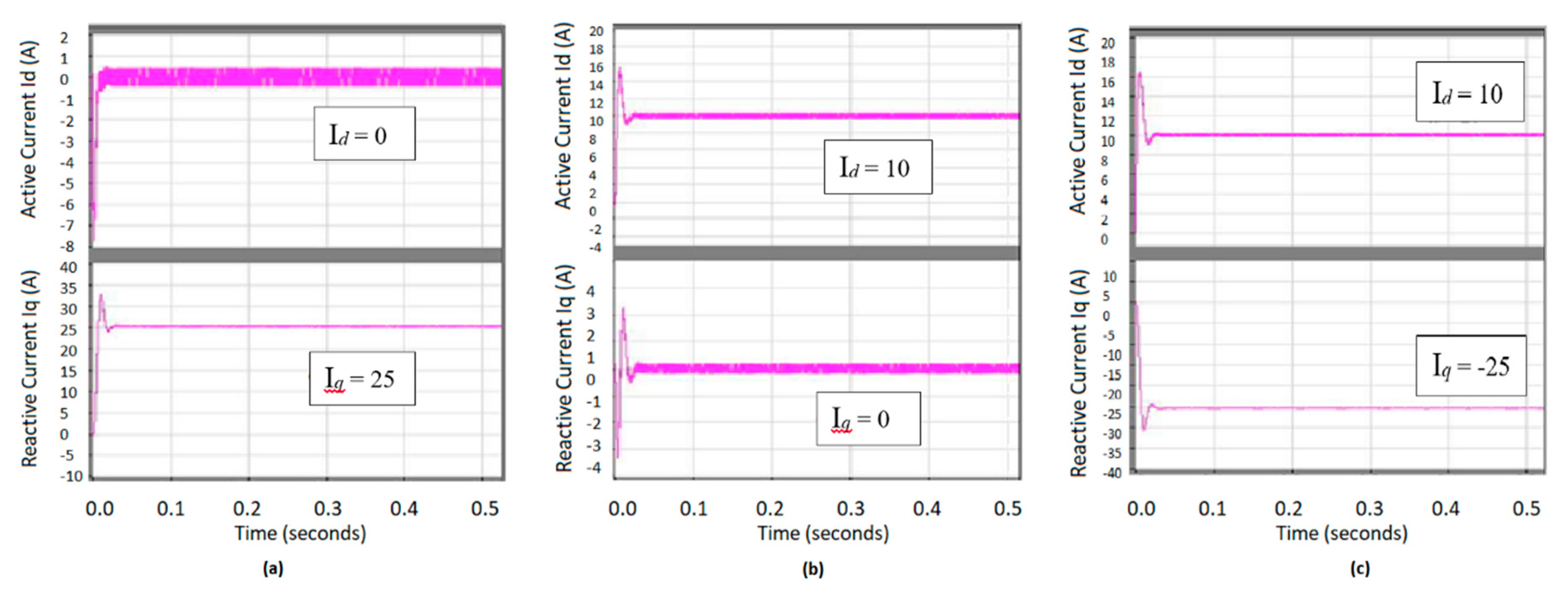
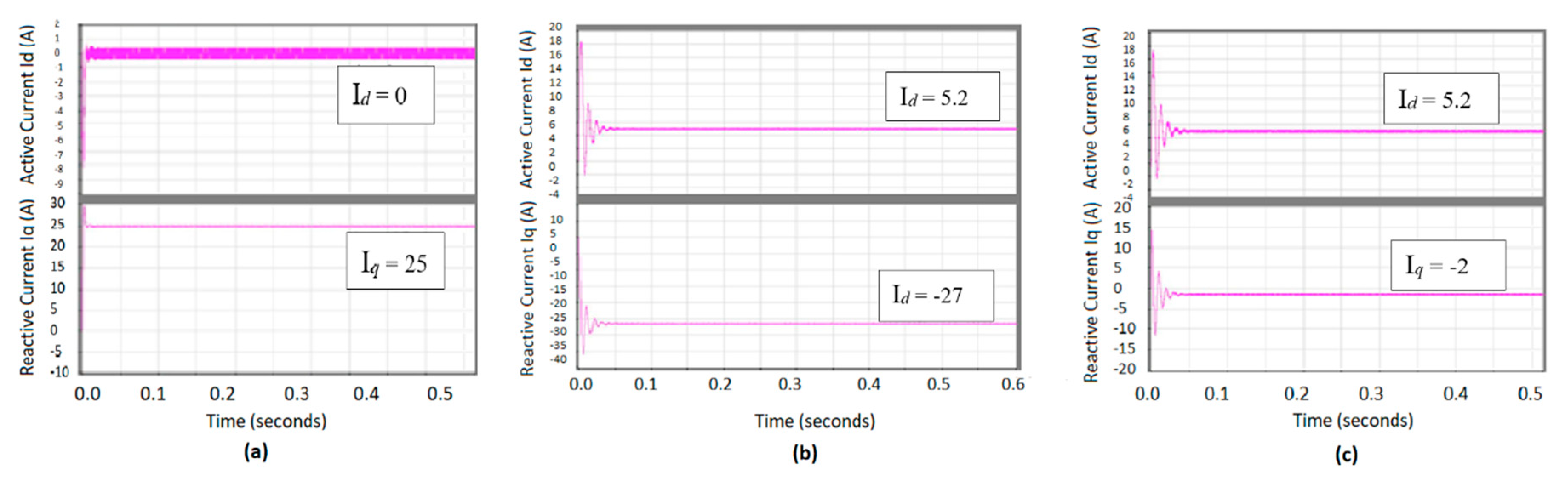
4.2. RP Compensation Results
4.2.1. Loading Scenario (L1)
4.2.2. Loading Scenario (L2)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Muttaqi, K.M.; Islam, M.R.; Sutanto, D. Future Power Distribution Grids: Integration of Renewable Energy, Energy Storage, Electric Vehicles, Superconductor, and Magnetic Bus. IEEE Trans. Appl. Supercond. 2019, 29, 1–5. [Google Scholar] [CrossRef]
- Qian, K.; Zhou, C.; Allan, M.; Yuan, Y. Modeling of load demand due to EV battery charging in distribution systems. IEEE Trans. Power Syst. 2011, 26, 802–810. [Google Scholar] [CrossRef]
- Green, R.C.; Wang, L.; Alam, M. The impact of plug-in hybrid electric vehicles on distribution networks: A review and outlook. Renew. Sustain. Energy Rev. 2011, 15, 544–553. [Google Scholar] [CrossRef]
- Boglou, V.; Karavas, C.; Arvanitis, K.; Karlis, A. A Fuzzy Energy Management Strategy for the Coordination of Electric Vehicle Charging in Low Voltage Distribution Grids. Energies 2020, 13, 3709. [Google Scholar] [CrossRef]
- Coignard, J.; MacDougall, P.; Stadtmueller, F.; Vrettos, E. Will Electric Vehicles Drive Distribution Grid Upgrades?: The Case of California. IEEE Electrif. Mag. 2019, 7, 46–56. [Google Scholar] [CrossRef]
- Anastasiadis, A.G.; Kondylis, G.P.; Polyzakis, A.; Vokas, G. Effects of Increased Electric Vehicles into a Distribution Network. Energy Procedia 2019, 157, 586–593. [Google Scholar] [CrossRef]
- Spitzer, M.; Schlund, J.; Apostolaki-Iosifidou, E.; Pruckner, M. Optimized Integration of Electric Vehicles in Low Voltage Distribution Grids. Energies 2019, 12, 4059. [Google Scholar] [CrossRef]
- Caramanis, M.; Ntakou, E.; Hogan, W.W.; Chakrabortty, A.; Schoene, J. Co-Optimization of Power and Reserves in Dynamic T&D Power Markets With Nondispatchable Renewable Generation and Distributed Energy Resources. Proc. IEEE 2016, 104, 807–836. [Google Scholar] [CrossRef]
- Sarimuthu, C.R.; Ramachandaramurthy, V.K.; Mokhlis, H.; Agileswari, K.R. Impact of distributed generation on voltage profile in radial feeder. Indones. J. Electr. Eng. Comput. Sci. 2017, 6, 583–590. [Google Scholar] [CrossRef]
- Chamandoust, H.; Derakhshan, G.; Hakimi, S.M.; Bahramara, S. Tri-objective scheduling of residential smart electrical distribution grids with optimal joint of responsive loads with renewable energy sources. J. Energy Storage 2020, 27, 101112. [Google Scholar] [CrossRef]
- Reshikeshan, S.S.M.; Matthiesen, S.L.; Illindala, M.S. Autonomous Voltage Regulation by Distributed PV Inverters with Minimal Inter-Node Interference. In Proceedings of the 2020 IEEE/IAS 56th Industrial and Commercial Power Systems Technical Conference (I&CPS), Las Vegas, NV, USA, 29 June–28 July 2020; pp. 1–8. [Google Scholar]
- Zhiqun, W.; Shouzhen, Z.; Shuangxi, Z.; Renle, H.; Liangui, W. Impacts of distributed generation on distribution system voltage profile. Autom. Electr. Power Syst. 2004, 16, 014. [Google Scholar]
- Kaloudas, C.G.; Ochoa, L.F.; Marshall, B.; Majithia, S.; Fletcher, I. Assessing the future trends of reactive power demand of distribution networks. IEEE Trans.Power Syst. 2017, 32, 4278–4288. [Google Scholar] [CrossRef]
- Swami, S.; Wagle, S. Addressing Last Mile Electricity Distribution Problems: Study of Performance of SHGs in Odisha. In Proceedings of the 7th International Conference on Advances in Energy Research; Springer: Singapore; pp. 515–523.
- Gao, D.; Lu, Q.; Luo, J. A New Scheme for on-Load Tap-Changer of Transformers. In Proceedings of the PowerCon 2002—2002 International Conference on Power System Technology, Proceedings, Kunming, China, 13–17 October 2002; Volume 2, pp. 1016–1020. [Google Scholar]
- Shamshuddin, M.A.; Rojas, F.; Cardenas, R.; Pereda, J.; Diaz, M.; Kennel, R. Solid State Transformers: Concepts, Classification, and Control. Energies 2020, 13, 2319. [Google Scholar] [CrossRef]
- Farnesi, S.; Marchesoni, M.; Passalacqua, M.; Vaccaro, L. Solid-State Transformers in Locomotives Fed through AC Lines: A Review and Future Developments. Energies 2019, 12, 4711. [Google Scholar] [CrossRef]
- Radi, M.A.; Darwish, M. Var Control Considerations for the Design of Hybrid Distribution Transformers. In Proceedings of the 11th IET International Conference on AC and DC Power Transmission, Birmingham, UK, 10–12 February 2015; pp. 1–9. [Google Scholar]
- Lim, J.-W.; Cho, Y.; Lee, H.-S.; Cho, K.-Y. Design and control of a 13.2 kV/10 kVA single-phase solid-state-transformer with 1.7 kV SiC devices. Energies 2018, 11, 201. [Google Scholar] [CrossRef]
- Martin-Arnedo, J.; González-Molina, F.; Martinez-Velasco, J.; Adabi, E. EMTP model of a bidirectional cascaded multilevel solid state transformer for distribution system studies. Energies 2017, 10, 521. [Google Scholar] [CrossRef]
- Radi, M.A.; Darwish, M.; Alqarni, M. Voltage Regulation Considerations for the Design of Hybrid Distribution Transformers. In Proceedings of the 2014 49th International Universities Power Engineering Conference (UPEC), Cluj-Napoca, Romania, 2–5 September 2014; pp. 1–6. [Google Scholar]
- Szcześniak, P.; Tadra, G.; Kaniewski, J.; Fedyczak, Z. Model predictive control algorithm of AC voltage stabilizer based on hybrid transformer with a matrix converter. Electr. Power Syst. Res. 2019, 170, 222–228. [Google Scholar] [CrossRef]
- Rodrigues, W.A.; De Oliveira, T.; Morais, L.M.F.; Rosa, A. Voltage and Power Balance Strategy without Communication for a Modular Solid State Transformer Based on Adaptive Droop Control. Energies 2018, 11, 1802. [Google Scholar] [CrossRef]
- Yun, C.; Cho, Y. Active Hybrid Solid State Transformer Based on Multi-Level Converter Using SiC MOSFET. Energies 2019, 12, 66. [Google Scholar] [CrossRef]
- Bala, S.; Das, D.; Aeloiza, E.; Maitra, A.; Rajagopalan, S. Hybrid Distribution Transformer: Concept Development and Field Demonstration. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 4061–4068. [Google Scholar]
- Sastry, J.; Bala, S. Considerations for the Design of Power Electronic Modules for Hybrid Distribution Transformers. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 1422–1428. [Google Scholar]
- Zhao, J.; Zirka, S.E.; Moroz, Y.I.; Arturi, C.M. Structure and properties of the hybrid and topological transformer models. Int. J. Electr. Power Energy Syst. 2020, 118, 105785. [Google Scholar] [CrossRef]
- Foti, S.; Caro, S.D.; Testa, A.; Tornello, L.D.; Scelba, G.; Cacciato, M. An Open-End Winding Hybrid Transformer. In Proceedings of the 2020 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Sorrento, Italy, 24–26 June 2020; pp. 173–177. [Google Scholar]
- Yamaguchi, K.; Lee, K.; Kurokawa, K. Study on Voltage Regulation Method in the Power Distribution System. In Proceedings of the 2007 7th Internatonal Conference on Power Electronics, Daegu, Korea, 22–26 October 2007; pp. 488–492. [Google Scholar]
- Purgat, P.; Prakoso, R.A.; Mackay, L.; Qin, Z.; Ramirez-Elizondo, L.; Bauer, P. A Partially Rated DC-DC Converter for Power Flow Control in Meshed LVDC Distribution Grids. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 1591–1596. [Google Scholar]
- Radi, M.A.M. Power Electronics Considerations for Voltage Regulation and VAR Control Approaches in LV Distribution Networks–Hybrid Power Electronic Modules By. Ph.D. Thesis, Brunel University London, Uxbridge, UK, 2016. [Google Scholar]
- Silva, S.M.; Lopes, B.M.; Filho, B.J.C.; Campana, R.P.; Bosventura, W.C. Performance Evaluation of PLL Algorithms for Single-phase Grid-Connected Systems. In Proceedings of the Conference Record of the 2004 IEEE Industry Applications Conference, 2004. 39th IAS Annual Meeting, Seattle, WA, USA, 3–7 October 2004; Volume 4, pp. 2259–2263. [Google Scholar]
- Hur, N.; Jung, J.; Nam, K. A fast dynamic DC-link power-balancing scheme for a PWM converter-inverter system. IEEE Trans. Ind. Electron. 2001, 48, 794–803. [Google Scholar]
- Felber, L.; Arango, H.; Bonatto, B.; Gouvea, M. Voltage Regulation in Electric Energy Distribution Substations. In Proceedings of the 2010 IEEE/PES Transmission and Distribution Conference and Exposition: Latin America (T&D-LA), Sao Paulo, Brazil, 8–10 November 2010; pp. 846–852. [Google Scholar]
- Sen, K.K. SSSC-static synchronous series compensator: Theory, modeling, and application. IEEE Trans. Power Deliv. 1998, 13, 241–246. [Google Scholar] [CrossRef]
- Kumar, S.S.; Subbiah, V.; Kandaswaray, A.; Kumar, G.D.; Sujay, R.; Manoharan, S. A State of the Art STATCON for Instantaneous VAr Compensation and Harmonic Suppression to Enhance Power Quality. In Proceedings of the CIGRE/IEEE PES International Symposium Quality and Security of Electric Power Delivery Systems, Montreal, QC, Canada, 8–10 October 2003; pp. 86–90. [Google Scholar]
- Van, T.L.; Lee, D. Developing function models of back-to-back PWM converters for simplified simulation. J. Power Electron. 2011, 11, 51–58. [Google Scholar] [CrossRef][Green Version]
- Meier, S. Novel Voltage Source Converter based HVDC Transmission System for Offshore Wind Farms. Ph.D. Thesis, KTH, Stockholm, Sweden, 2005; p. 112. [Google Scholar]
- Zhang, L.; Harnefors, L.; Nee, H.P. Modeling and control of VSC-HVDC links connected to island systems. IEEE Trans. Power Syst. 2011, 26, 783–793. [Google Scholar] [CrossRef]
- Kalitjuka, T. Control of Voltage Source Converters for Power System Applications. Master Sci. Electr. Power Eng. 2011, 1, 13–45. [Google Scholar]
- Malesani, L.; Rossetto, L.; Tenti, P.; Tomasin, P. AC/DC/AC PWM converter with reduced energy storage in the DC link. IEEE Trans. Ind. Appl. 1995, 31, 287–292. [Google Scholar] [CrossRef]
- de Oliveira Filho, M.E.; Gazoli, J.R.; Sguarezi Filho, A.J.; Ruppert Filho, E. A Control Method for Voltage Source Inverter without Dc Link Capacitor. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 4432–4437. [Google Scholar]
- Richardson, B.C. Sustainable transport: Analysis frameworks. J. Transp. Geogr. 2005, 13, 29–39. [Google Scholar] [CrossRef]
- Roshan, A.; Burgos, R.; Baisden, A.C.; Wang, F.; Boroyevich, D. A DQ Frame Controller for a Full-Bridge Single Phase Inverter Used in Small Distributed Power Generation Systems. In Proceedings of the APEC 07-Twenty-Second Annual IEEE Applied Power Electronics Conference and Exposition, Anaheim, CA, USA, 25 February–1 March 2007; pp. 641–647. [Google Scholar]
- Dursun, B.; Doğan, M. FPGA Based Linear Sweep Controller Implementation for FMCW Radar Applications. In Proceedings of the 2012 20th Signal Processing and Communications Applications Conference (SIU), Mugla, Turkey, 18–20 April 2012; pp. 1–4. [Google Scholar]
- Mouli, G.R.C.; Bauer, P.; Wijekoon, T.; Panosyan, A.; Bärthlein, E. Design of a Power-Electronic-Assisted OLTC for Grid Voltage Regulation. IEEE Trans. Power Deliv. 2015, 30, 1086–1095. [Google Scholar] [CrossRef]
- Bugade, V. Automatic Voltage Control of Load using on Load Tap Changer. Int. J. Res. Appl. Sci. Eng. Technol. 2018, 6, 3158–3162. [Google Scholar] [CrossRef]
- Rasool, E.; Darwish, M. High Frequency Inverter Circuit for UPS Systems. In Proceedings of the 2012 47th International Universities Power Engineering Conference (UPEC), London, UK, 4–7 September 2012; pp. 1–4. [Google Scholar]













| Conceptual Schematics | Functionality and Ability |
|---|---|
| Figure 3a Conceptual 1 | This configuration allows correcting the PF for both the distortion and displacement PF. In addition, the DC source can be charged and discharged through the bidirectional converter. |
| Figure 3b Conceptual 2 | This configuration functions similarly to the Static Synchronous Series Compensator (SSSC) [35]. In particular, it has a separate DC source, where the converter can take the power to inject it as voltage in the line, either in a capacitive or inductive mode. |
| Figure 3c Conceptual 3 | This configuration allows injecting the RP as voltage by using a back-to-back converter. |
| Figure 3d Conceptual 4 | This configuration operates similarly to the Static Synchronous Compensator (STATCOM) [36]. It injects the RP through a parallel restricted rated transformer. |
| Figure 3e Conceptual 5 | This configuration includes the secondary side of the DT. It compensates the RP at the secondary side with lower ratings for the SSSs that operate high voltage and lower current ratings. |
| Components | Ratings |
|---|---|
| Rated power | 200 KVA |
| DC voltage Vdc | 800 V |
| AC voltage | 48 V |
| Frequency | 50 Hz |
| ) | (0.01 + j0.26) pu, L = 0.00047 H, R = 0.06 ῼ |
| Switching frequency ƒs | 5 KHz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radi, M.; Darwish, M.; Taylor, G.; Pisica, I. Control Configurations for Reactive Power Compensation at the Secondary Side of the Low Voltage Substation by Using Hybrid Transformer. Energies 2021, 14, 620. https://doi.org/10.3390/en14030620
Radi M, Darwish M, Taylor G, Pisica I. Control Configurations for Reactive Power Compensation at the Secondary Side of the Low Voltage Substation by Using Hybrid Transformer. Energies. 2021; 14(3):620. https://doi.org/10.3390/en14030620
Chicago/Turabian StyleRadi, Mohammed, Mohamed Darwish, Gareth Taylor, and Ioana Pisica. 2021. "Control Configurations for Reactive Power Compensation at the Secondary Side of the Low Voltage Substation by Using Hybrid Transformer" Energies 14, no. 3: 620. https://doi.org/10.3390/en14030620
APA StyleRadi, M., Darwish, M., Taylor, G., & Pisica, I. (2021). Control Configurations for Reactive Power Compensation at the Secondary Side of the Low Voltage Substation by Using Hybrid Transformer. Energies, 14(3), 620. https://doi.org/10.3390/en14030620






