Reviewing the Exergy Analysis of Solar Thermal Systems Integrated with Phase Change Materials

Abstract

The application of thermal storage materials in solar systems involves materials that utilize sensible heat energy, thermo-chemical reactions or phase change materials, such as hydrated salts, fatty acids paraffin and non-paraffin like glycerol. This article reviews the various exergy approaches that were applied for several solar systems including hybrid solar water heating, solar still, solar space heating, solar dryers/heaters and solar cooking systems. In fact, exergy balance was applied for the different components of the studied system with a particular attention given to the determination of the exergy efficiency and the calculation of the exergy during charging and discharging periods. The influence of the system configuration and heat transfer fluid was also emphasized. This review shows that not always the second law of thermodynamics was applied appropriately during modeling, such as how to consider heat charging and discharging periods of the tested phase change material. Accordingly, the possibility of providing with inappropriate or not complete results, was pointed.

1. Introduction

A major challenge encountered by the application of solar heating systems is the continuity of their operation when there is no sunshine, i.e., during off-sunshine periods [1,2,3]. In response, researchers have either adopted supplementary heating systems using electric heaters or biomass furnace [4] or have integrated thermal storage materials [4]. The application of thermal storage materials involves materials (rocks, bricks, water, concretes, etc.) that utilize their sensible heat energy, thermo-chemical reactions and those that apply both sensible and latent heat energy (phase change materials) such as hydrated salts, fatty acid paraffins and non-paraffins like glycerol, etc. [3,5,6]. The advantage of phase change materials (PCM) is that they evolve large energy density over a narrow temperature range as the material changes from liquid to solid or vice versa [4] as shown in Figure 1. Kenesarin and Mahkamov [5] and Sharma and Sagara [7] have comprehensively reviewed available PCMs and their applications as thermal storage in solar energy system and their application as thermal storage materials in energy storage systems in housing, spacecraft, vehicles, space heating, desalination, solar dryers, water heating, etc. In their discussion they classified the PCMs as organic materials, mainly present as fatty acids with melting temperatures of −5 to 71 °C and inorganic materials present mostly as hydrated salts. They also analyzed the structural compatibility of the PCM chemical composition and concluded that research on inorganic PCMs needed time for commercial application. This is because PCMs, especially hydrated salts, suffer from the problem of super cooling (“phase irreversibility”) and phase segregation in thermal process [8]. This has been observed for sodium sulfate decahydrate (Na₂SO₄·10H₂O) when used in solar drying [9], though researchers have suggested adding nucleating agents, thickening agents, direct contact heat transfer, encapsulation, rotating storage and rotary storage devices [8] to address this issue.

Despite this shortcoming, the large energy density carrier of PCMs has made them attractive in solar heating systems while researchers are working to overcome the problems associated with hydrated salts [5,11]. However, the performance of solar systems adopting PCMs as thermal storage can only be assessed if the thermal behavior of the PCM while in the system is known. Several studies dealing with this aspect have considered different configurations and positions of the PCM in the system. This thermal behavior of the PCM has been established in relationship with its position within the system. For example, Ndukwu et al. [4] placed the PCM on the solar collector chamber during charging and moved it into the drying chamber during discharging in a solar dryer, while Ortega and Carmona [12] and Ghiami et al. [13] placed their PCMs under the collector as shown in Figure 2. Nkwetta, and Haghighat [14] encapsulated the PCM in the solar system while Li et al. [15] placed the PCM in a storage tank. Abdulmunen et al. [16] embedded the solar fin into a PCM in a solar collector.

Recent reviews in the literature have also presented the thermal behavior of PCM in solar heaters in terms of their thermo-physical properties [4], sensible and latent heat energy [17], thermal storage abilities [18,19], application in buildings [20], application in solar absorption refrigeration systems [21], integration of nano-fluids [22,23,24], progress in thermal storage and recovery of industrial waste heat [25] and application in cold storage [26,27]. However, to properly understand the thermodynamic performance of the system units, energy and exergy analysis approach has always been adopted. Many researchers are of the opinion that exergy analysis provides a better understanding of the thermodynamic performance of energy systems and it is the future of research if the efficiency of energy systems is to be improved [3,4,13]. Jegadheeswaran et al. [28] have emphasized the need of exergy studies based on the analysis and continuous update on exergy evaluation techniques for different system applications. The analysis was based on the configuration of the heat flow, the position or method of integration of the latent heat storage material in the system and the heat carrying fluids. Elucidating exergy analysis methods is vital in improving the operation of the thermodynamic systems and designing energy systems to obtain higher efficiency. Therefore, this study is intended to present a review of the exergy based thermodynamic analysis for some solar system configurations that have adopted PCMs as thermal storage. This is to present a guide for further studies on this area.

Thermodynamic Performance of Energy Systems

The evaluation of the thermodynamic performance of energy systems can be performed using the energy conservation principle which is based on the first law of thermodynamics or the concept of exergy based on the second law [29]. Exergy is the maximum extractable amount of work from a thermodynamic system as it equilibrates with the surroundings [30,31]. Obtaining higher energy output from a thermodynamic system makes the operation attractive. During energy flow, losses occurring within the system components which affects the total energy output from these systems. The magnitude of these losses varies from one component to another and at different points along the energy streams. Accounting for these losses based on individual components as embodied in the concept of exergy helps to know the components that requires improvement for better optimization and design of the energy systems, which the first law does not give room for. In a properly insulated solar system integrated with a PCM, the energy analysis during the PCM cycle will give 100% efficiency because the latent heat of solidification and melting which is equal to the output and input energy is the same [13]. However, there is irreversibility which will lead to energy destruction. Exergy does not only identify irreversibility (therefore cannot be conserved) but also where it occurs and the degree of this irreversibility. This will lower the output exergy which is why the exergy efficiency is lower than energy efficiency since both is expressed as a ratio of output to input of each adopted principle. The more exergy is destroyed within the system, the more entropy is generated, which indicates the unavailability of thermal energy for conversion into mechanical work. Consequently, exergy is proportional to the produced entropy, as the system approaches equilibrium with the surroundings, which decreases the efficiency of the system to zero.

Most importantly, exergy is related to the concept of environmental sustainability. Minimizing system losses (increased exergy efficiency) will limit energy waste into the surroundings. Ndukwu et al. [4] have reported that exergy waste might upstage the thermodynamic equilibrium of the environment by interfering with the presence of atmospheric CO_2, which can lead to solar re-radiation. Thus, exergy analysis evaluates energy both quantitatively and qualitatively [32,33]. In the analysis of the exergy of most solar heating systems with or without sensible heat, three exergy streams have always been identified, viz: exergy of the solar radiation, exergy of the heat transfer fluid and exergy exchange within the product of which the stream is applied to in the case of drying as shown in Equations (1)–(3) below [34,35]:

$${\mathrm{Ex}}_{\mathrm{R}}={\mathrm{I}\mathsf{\tau }\mathsf{\alpha }}_{\mathrm{p}}{\mathrm{A}}_{\mathrm{s}}\left(1-\frac{{\mathrm{T}}_{\mathrm{a}}}{{\mathrm{T}}_{\mathrm{s}}}\right)$$

(1)

$$\begin{array}{c}{\mathrm{E}}_{\mathrm{xf}}={\dot{\mathrm{m}}}_{\mathrm{f}}\{{\mathrm{C}}_{\mathrm{p},\mathrm{f}}\left(\mathrm{T}-{\mathrm{T}}_0-{\mathrm{T}}_0\mathrm{In}\frac{\mathrm{T}}{{\mathrm{T}}_0}\right)+{\mathrm{R}}_{\mathrm{a}}{\mathrm{T}}_0\\ \times \left[\left(1+\frac{{\mathrm{M}}_{\mathrm{f}}}{{\mathrm{M}}_{\mathrm{v}}}\mathrm{H}\right)\mathrm{In}\frac{1+\frac{{\mathrm{M}}_{\mathrm{f}}}{{\mathrm{M}}_{\mathrm{v}}}{\mathrm{H}}_0}{1+\frac{{\mathrm{M}}_{\mathrm{f}}}{{\mathrm{M}}_{\mathrm{v}}}\mathrm{H}}+1+\frac{{\mathrm{M}}_{\mathrm{f}}}{{\mathrm{M}}_{\mathrm{v}}}\mathrm{HIn}\frac{\mathrm{H}}{{\mathrm{H}}_0}\right]\}\end{array}$$

(2)

$$\begin{array}{l}{\mathrm{X}}_{\mathrm{w}}={\mathrm{m}}_{\mathrm{w}}[\left({\mathrm{h}}_{\mathrm{f}}\left(\mathrm{T}\right)-{\mathrm{h}}_{\mathrm{f}}\left({\mathrm{T}}_0\right)\right)+{\mathrm{v}}_{\mathrm{f}}\left(\mathrm{P}-{\mathrm{P}}_{\mathrm{g}}\left(\mathrm{T}\right)\right)-{\mathrm{T}}_0\left({\mathrm{S}}_{\mathrm{f}}\left(\mathrm{T}\right)-{\mathrm{S}}_{\mathrm{g}}\left({\mathrm{T}}_0\right)\right)\\ +{\mathrm{T}}_0{\mathrm{R}}_{\mathrm{w}}\mathrm{In}\left(\frac{{\mathrm{P}}_{\mathrm{g}}\left({\mathrm{T}}_0\right)}{{\mathrm{P}}_0{\mathrm{X}}_{\mathrm{v}}^0}\right)]\end{array}$$

(3)

However, when a PCM is applied in a solar heating system, the exergy analysis includes the phase change exergy. In most exergy analysis of solar systems involving the solar collector (receiver) and PCM storage, researchers have separated the two components and analyzed their respective exergy streams [15]. Pertaining to the exergy analysis for PCMs factors such as thermal storage, mass ratio, melting (charging) temperature, discharging (solidification) temperature, mass flow rate and the number of transfer units are taken into consideration, assuming that the PCM is a reservoir of thermal energy with constant melting temperature while the temperature of flowing air varies along with its flow path [15,32]. This is because the process of charging and discharging of a PCM involves the receiver transferring the high temperature into the heat transfer fluid which was at low temperature. This temperature mix raises the temperature of the heat transfer fluid (HTF), partly absorbed by the PCM [4]. The PCM melts at its melting temperature. As the HTF exhausts and returns-back to the receiver or the ambient depending on the system design to complete the charging cycle, the PCM cools by releasing the latent heat of fusion. Hence, the exergy analysis is evaluated during both the charging and discharging periods [12]. The assessment of thermodynamic performance of any system integrated with PCM requires the operational configuration of the system, including the trajectory of the HTF, point of heat contact of the PCM, geometric and other design parameters of the system. Exergy efficiency is carried out to determine the maximum recoverable energy from the system since entropy generation destroys efficiency of the system. Nevertheless, adoption of the PCM though helps the functionality of the system, however, it generates entropy (Equations (4) and (5)) in the heat storage process during the charging and discharging of the PCM and also due to HTF flow across the heat exchanger. Li et al. [15] expressed the entropy generated for PCM as follows:

$${\mathrm{S}}_{\mathrm{gen}}=\mathrm{m}\left({\mathrm{S}}_{\mathrm{l}}-{\mathrm{S}}_{\mathrm{s}}\right)+{\dot{\mathrm{m}}}_{\mathrm{a}}\left({\mathrm{S}}_{\mathrm{aout}}-{\mathrm{S}}_{\mathrm{ain}}\right)\Delta \mathrm{t}$$

(4)

El-Dessouky and Faisal [36] gave the entropy of PCM during charging as:

$$\mathrm{m}\left({\mathrm{S}}_{\mathrm{l}}-{\mathrm{S}}_{\mathrm{s}}\right)=\frac{\mathrm{M}{ʎ}_{\mathrm{p}}}{{\mathrm{T}}_{\mathrm{m}}}$$

(5)

2. Application of Exergy Analysis in PCM for Solar Systems

Solar collectors or solar thermal systems (heliostats, concentrators and receivers) have been widely utilized in capturing solar radiation for heating purposes. The operating temperature range is useful in low temperature heat applications but suffers from temperature fluctuations due to the vagaries of weather. Nevertheless, the intermittent nature of solar radiation requires the system to be assisted with supplementary heat sources. The arrangement is such that the transport medium, mostly air, flows past the collector from the inlet into the process chamber or the product placed directly on the collector before exiting or recycled. This same fluid heats up the PCM raising the temperature during the charging period before it discharges as it cools during the off-sunshine hours.

Exergy analysis involving thermal storage materials is progressively increasing. The earlier approaches considered that the exergy destroyed for any process is a function of the entropy changes of all the components that make up the exergy stream and the surrounding temperature [37,38,39]. Bejan [40] presented the exergy of a PCM as sensible thermal storage material only, based on a lump sum analysis where two optimum conditions of charging temperature and number of transfer unit were considered. Accordingly, beyond this optimum the dominant exergy loss is as a result of convention in the surrounding gas and friction in the working fluid. Therefore, the source of irreversibility, were, temperature change between the surrounding fluid and the thermal storage material, rejection of work to the surrounding at dead state and frictional loss in the gaseous fluid [20]. However, Bjurström and Carlson [41] extended the exergy analysis of PCM thermal storage to include the sensible and latent heat storage periods. In their analysis they neglected the friction of the gaseous fluid and assumed a uniform temperature through the PCM while the melting temperature was taken as a square root of the product of the ambient temperature and the inlet charging temperature. Using a single transfer unit, they obtained a 12% exergy efficiency claiming that the heavy loss was generated due to the temperature transition as the PCM temperature increases during the charging and cools during the discharging process. However, since the work of Bjurström and Carlson [41], many researchers have evaluated exergy efficiency of PCMs as thermal storage in energy systems involving several transfer units [42]. Nevertheless, the application of PCM has become part of component design for several solar energy systems and exergy analysis of these systems are carried out with the integration of the exergy contribution of the PCM. Heat is transferred to the PCM by the heat transfer fluid (HTF) as it flows past the PCM position.

2.1. Evaluation of Exergy Equations

2.1.1. Water Heating

Solar energy has been converted to heat for heating water using collectors or solar concentrators [43,44]. They can operate as hybrid systems or independently [44]. Consequently, various configurations of solar water heaters have been designed and commercialized and are available in different cost ranges. Solar water heaters can use only water or a PCM to store energy before making use of it. To evaluate the thermodynamic efficiency of the system, various analyses based on the concept exergy have been proposed for the hybrid mode integrated with PCM.

Table 1. Results of some of the studies presented on water heating and the PCM used.

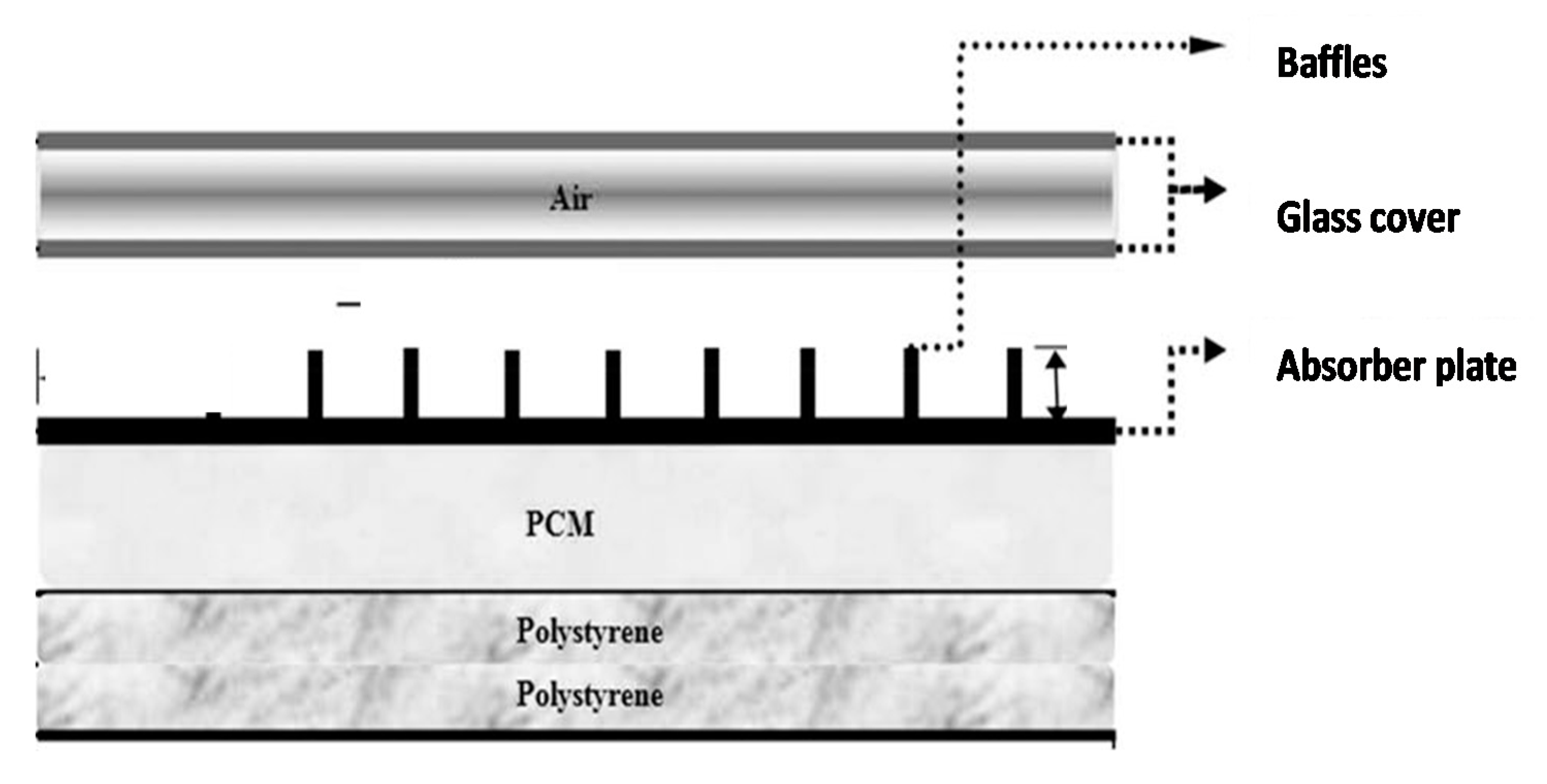
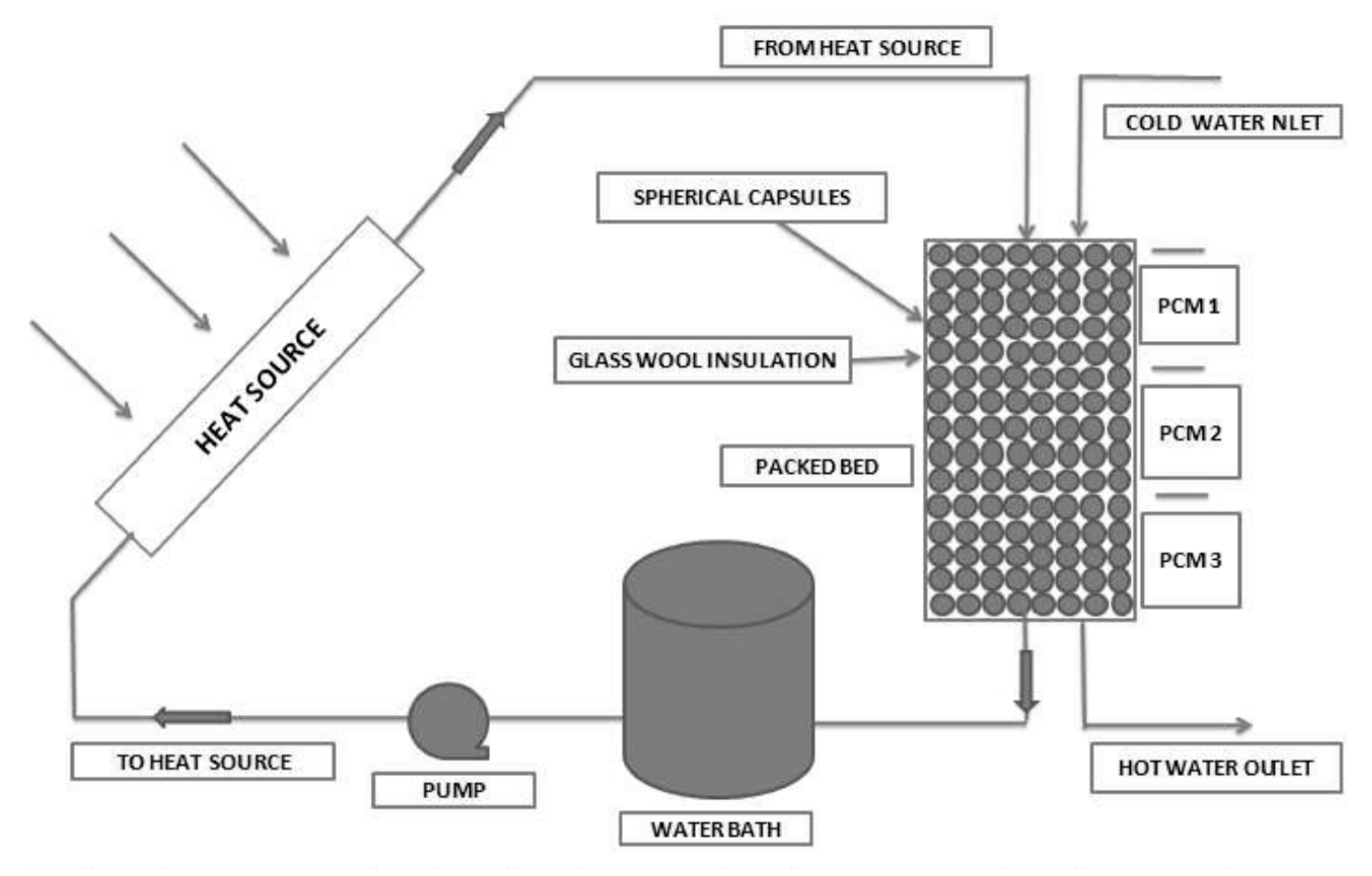
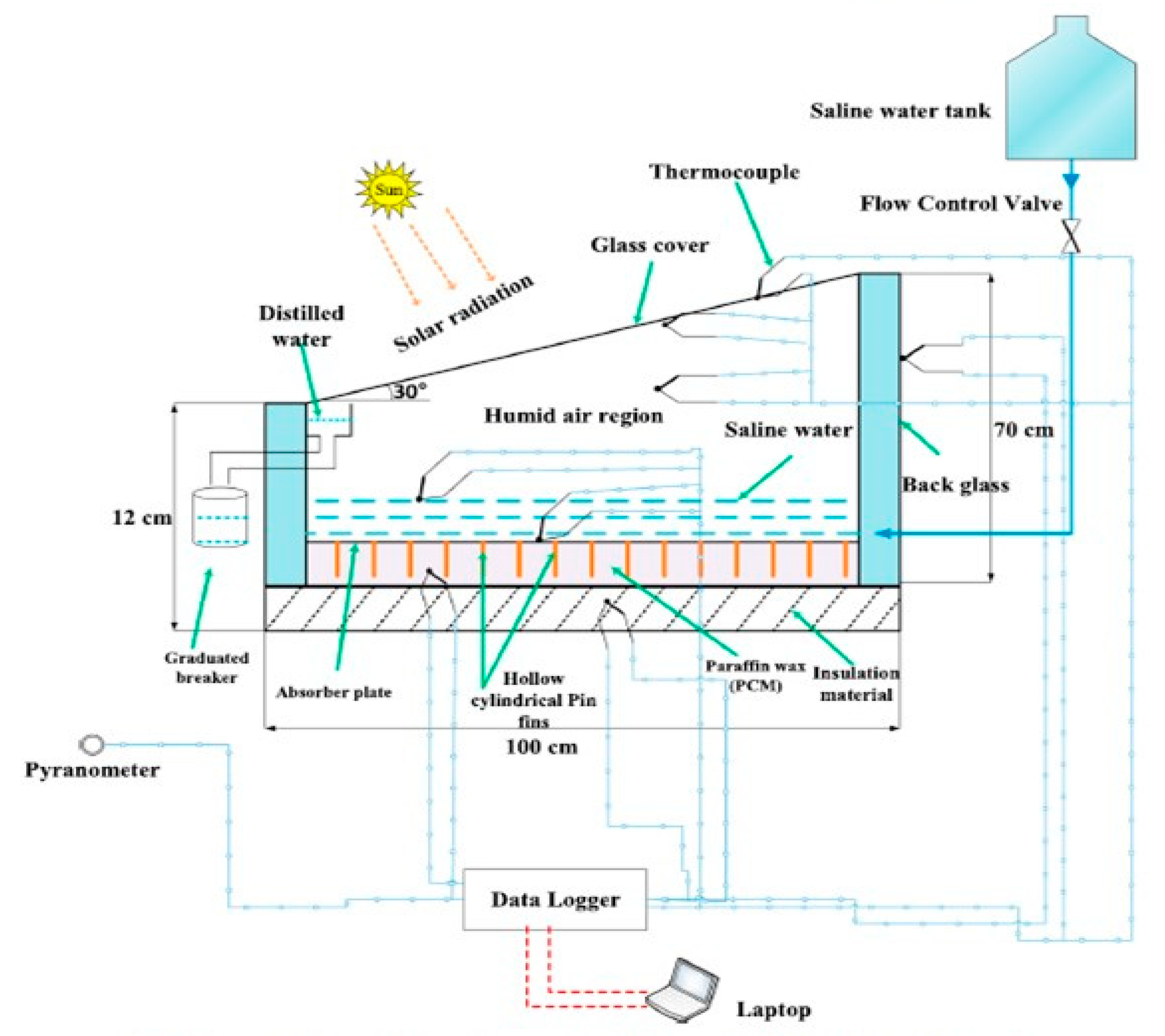
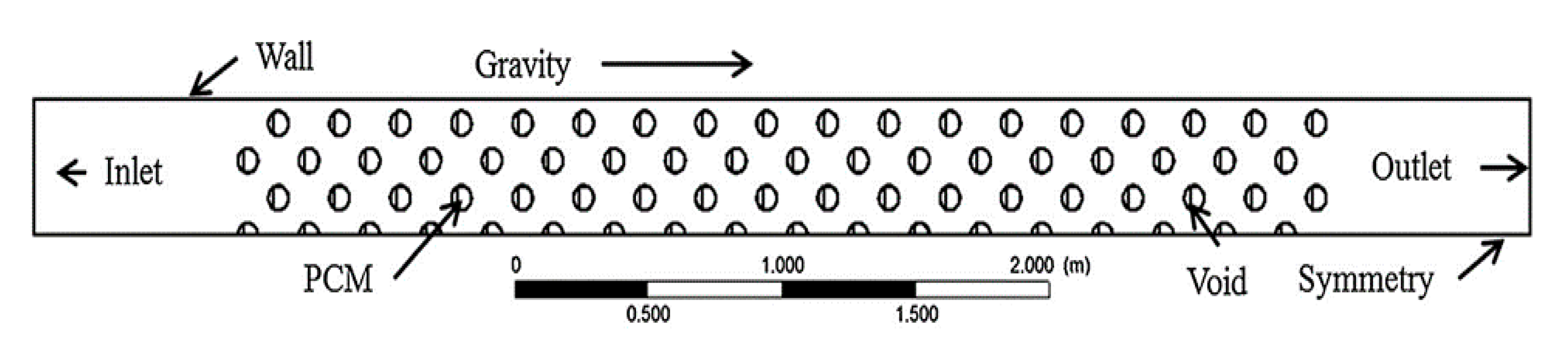
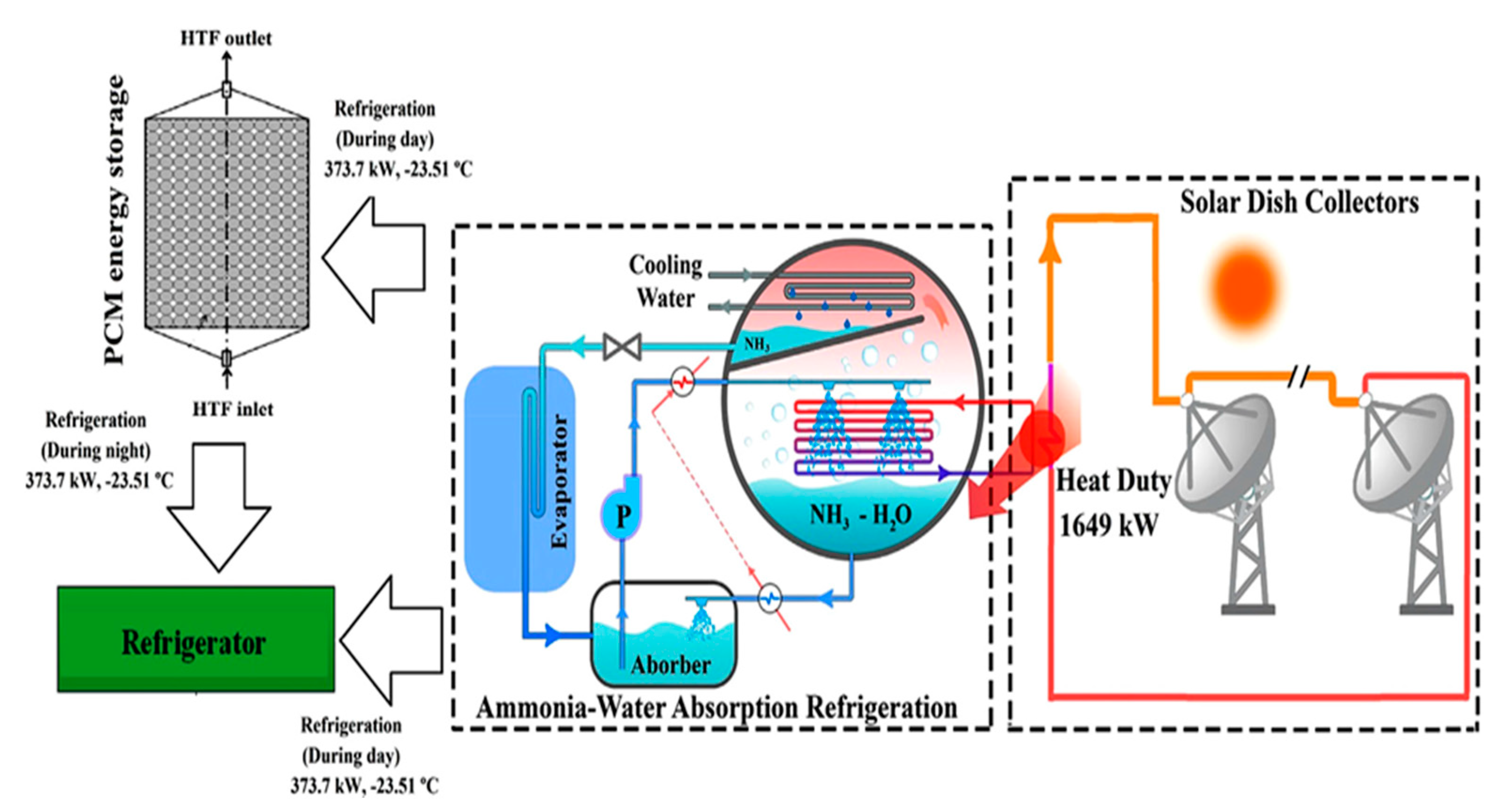
Authors [Reference]	Nature of Studies	Aim	PCM Type	HTF	Results
Aghbasolou et al. [21]	Theoretical studies	Optimization of thermodynamic performance of solar thermal energy storage system with PCM slabs based on exergy analysis	Rubi-therm	Water	Melting temperature affected Irreversibility with lower value at higher melting point and lower value at lower melting point which gave better quality energy
Koca et al. [45]	Experimental studies	Analysis of the energy and exergy of a latent heat storage system with PCM for a solar collector	CaCl2.6H2O	Water	Low exergy efficiency of 2.2% was recorded due to the small area occupied by PCM compared to the collector which resulted in low outlet temperature
Singh and Singh [48]	Theoretical studies	numerical investigation of stuffed bed utilizing a stratified PCM	Paraffin, Hybrid wax, Bee wax	Water	Not validated
Ortega and Carmona [12]	Experimental studies	Performance of exergy analysis to determine the potential for the useful work presented by used PCM	paraffin wax	air	13.2% average exergetic efficiency was obtained for of low radiation days, 20.56% was recorded for medium radiation days, and 18.6% was obtained for high radiation days
Yang and Zhan [47]	Theoretical studies	To presents a theoretical study of a packed bed using a stratified PCM	C21H44, C22H46, C24H50	Water	The PCM bed presented lower irreversibility compared to single packed bed. Higher efficiency was recorded in the simultaneous charging and discharging for stratified packed bed compared to single packed bed
Omara et al. [46]	Experimental studies	Investigation of the thermodynamic performance of solar water heating system incorporated with PCM	Parafin wax	Water	Addition of PCM increase the exergy output which led to lower exergy destruction. Therefore, the PCM improved the exergy efficiency
Gürtürk et al. [49]	Comparative experimental studies	To compare exergetic and energetic efficiency with and without the PCM	Mixture of Na2HPO4·12H2O) and NH4, Al(SO4)·6H2O) to form a eutectic PCM	Water	exergy analysis recorded highest efficiency of 22% for the heat storage tank integrated with the PCM

presents a summary of some studies on exergy analysis applied to solar water heating systems, the PCM adopted and the key results obtained.

Koca et al. [45] presented an exergy analysis of a solar water heater for a city water network, where a PCM-filled tank was located under the solar collector and copper pipe used as heat exchanger. Conservation of energy and mass with the second law of thermodynamics in the exergy analysis were applied to the system. Based on the configuration of the solar system and the input of the thermal storage, five exergy stream balances were considered, which include exergy of inlet energy ($E_{x,}{}_{H_i}$), exergy losses during heat transfer between water and heat stored in the collector ($E_x{Q}_t$), exergy of outlet energy from the collector ($E_{x,}{}_{H_o}$), exergy of solar energy ($E_x{Q}_i$) and exergy losses of energy in the collector ($E_x{Q}_{t^l}$). The general exergy balance was given as expressed by [45] as follows:

$$E_{x,}{}_{{\dot{Q}}_i}=E_{x,}{}_{{\dot{Q}}_t}+E_x{}_{{\dot{Q}}_{t^l}}+E_{x,}{}_{H_o}-E_{x,}{}_{H_i}+Irr$$

(6)

$$E_{x,}{}_{{\dot{Q}}_t}=\left(1-\frac{T_{env}}{T_{av}}\right){\dot{Q}}_l$$

(7)

$$E_x{}_{{\dot{Q}}_{t^l}}=\left(1-\frac{T_{env}}{T_{av}}\right){\dot{Q}}_{l^l}$$

(8)

$${\dot{Q}}_l=\frac{\Delta V_s{\rho }_{s}h}{\Delta t}$$

(9)

This exergy contribution of PCM compared to overall exergy of the system was found to be low [45]

The general entropy balance for the system was expressed under the following equation:

$$S_{gen}=m\left(S_o-S_i\right)-\frac{{\dot{Q}}_i}{T_{ev}}-\frac{{\dot{Q}}_l}{T_{av}}+\frac{{\dot{Q}}_s}{T_{av}}-\frac{{\dot{Q}}_{l^1}}{T_{av}}$$

(10)

where $\dot{Q}$_s is the heat transfer rate given as

$${\dot{Q}}_l=M{C}_p\frac{dT}{dt}$$

(11)

The irreversibility or exergy destroyed was given as function of the entropy generated as follows:

$$Irr=T_{env}{S}_{gen}$$

(12)

Therefore, the net exergy efficiency for both the thermal storage and solar heating was expressed as a ratio of exergy recovery from the system and input exergy as follows:

$${\eta }_{ex}=\frac{E_{x,}{}_{H_o}-E_{x,}{}_{H_i}}{E_{x,}{}_{{\dot{Q}}_i}}\times 100$$

(13)

Omara et al. [46] considered only the charging period in the exergy analysis of a solar heated water tank with the PCM contained in a cylindrical steel container, though, this might lead to serious errors, since the complete cycle was not considered [42]. The design of the water tank was done in a such manner that the water flows by gravity since no electricity is used to power the pump. Exergy balance of the considered components are presented in Equations (14)–(16), where the input exergy (E_xin) was as a result of the heat absorbed by the water tank which is partly transferred to the PCM, exergy stored in the PCM (E_xst) during the charging periods and Exergy output from the water (E_xout):

$$E_{x,in}=C_{pw}\left[\left(T_{in}-T_{tank}\right)-T_{0}ln\frac{T_{in}}{T_{tank}}\right]$$

(14)

$$E_{xst}=C_{pw}\left(T_{in}-T_{out}\right)\left[1-\frac{T_0}{T_{pcm}}\right]$$

(15)

$$E_{x,out}=C_{pw}\left[\left(T_{tank}-T_{out}\right)-T_{0}ln\frac{T_{tank}}{T_{out}}\right]$$

(16)

The numerical investigation of exergetic performance of a solar water heater using PCM as thermal storage has been presented [47,48]. The design was in a manner that three different PCMs were placed in series and randomly encapsulated inside a steel cylinder (thermal storage tank). The hot air from the solar receiver is driven through the PCM with the help of a fan as shown in Figure 3. The fluid carrying the hot air and water to be heated flows concurrently through the cylinder with the hot water discharging some of its heat to the PCM while the air is recycled. The net exergy efficiency of the cycle was given in terms of charging and discharging periods as the heat is transferred from the heat transfer fluid to the PCM and vice versa. From the presented configuration water flows from top to bottom, therefore they expressed the charged exergy consisting of liquid, solid and phase transition as Equation (17):

$$E_{xpcm}={{\displaystyle \sum }}_i{m}_{pcm,i}{C}_{p,l}\left(T_{p,i}-T_{l,i}-T_{0}ln\frac{T_{p,i}}{T_{l,i}}\right)+ {{\displaystyle \sum }}_i{m}_{pcm,i}{C}_{p,s}\left(T_{s,i}-T_{p,ini}-T_{0}ln\frac{T_{s,i}}{T_{p,ini}}\right)+{{\displaystyle \sum }}_i{m}_{pcm,i}{C}_{p,l}\left(T_{l,i}-T_{s,i}-T_{0}ln\frac{T_{l,i}}{T_{s,i}}\right)$$

(17)

The charged exergy at the heat transfer fluid was expressed as follows:

$$E_{xhtf}={{\displaystyle \sum }}_i{m}_{htf,i}{C}_f\left(T_{f,i}-T_{f,ini}-T_{0}ln\frac{T_{f,i}}{T_{f,ini}}\right)$$

(18)

The exergy efficiency in the charging process was expressed as the ratio of the net exergy of the charging periods to the exergy supplied as follows:

$${\eta }_{exchg}=\frac{E_{x,}{}_{htf}+E_{x,}{}_{pcm}}{E_{x,}{}_{sup}}\times 100$$

(19)

The exergy supply (E_xsup) was expressed as follows:

$$E{x}_{sup}={{\displaystyle \int }}_0^t{m}_f{C}_f\left(T_{f,in}-T_{f,out}-T_{0}ln\frac{T_{f,in}}{T_{f,out}}\right)dt$$

(20)

In the discharging process the exergy efficiency was expressed as the ratio of the exergy of the discharging period to the exergy of the charging process which serves as the inlet exergy. Singh and Singh [48] stated that the remaining exergy after charging kept decreasing to zero. Thus, the discharging exergy was expressed as:

$$E_{x,}{}_{disch}={{\displaystyle \int }}_0^t{m}_f{C}_f\left(T_{f,out}-T_{f,in}-T_{0}ln\frac{T_{f,out}}{T_{f,in}}\right)dt$$

(21)

Moreover, the exergy efficiency for discharging period was expressed as:

$${\eta }_{exdishg}=\frac{E_{x,}{}_{disch}}{E_{x,}{}_{htf}+E_{x,}{}_{pcm}}\times 100$$

(22)

They gave the net exergy efficiency of the cycle as follows:

$${\eta }_{excycle}={\eta }_{exdishg}\times {\eta }_{exchg}$$

(23)

Analytic solutions, which allo obtaining optimum calculation of exergy (work) for a solar water tank embedded with PCM distributed in an assembly of slabs, have been reported [21]. The analysis utilized both the conduction and convention heat transfer in both the PCM and the solar water tank and also the melting temperature of the PCM. To determine the exergy of the system (the maximum power) and optimum melting temperature of the PCM, solar energy storage tank was considered as a Carnot engine where heat exits at the melting temperature of the PCM into the Carnot engine to perform work. Exchange of heat was between hot water coming from the solar collector and the PCM. Exergy in this case was defined as the maximum work which is the best energy quality expressed in Equation (24) considering the hot stream flow rate, melting temperature (T_m) of the PCM, the initial water temperature (T_L), number of transfer units (N_tu) and the net efficiency of the solar energy storage tank:

$$W={\dot{m}}_w{C}_{pw}\left(T_{in}-T_m\right)\left(1-e^{-N_{tu}}\right)\left(1-\frac{T_L}{T_m}\right)$$

(24)

The melting temperature (presented in Equation (25)) was established as a function of the number of transfer units (presented in Equation (26)) following the assumption that the hot water flows from the collector at a temperature T_in and gets in contact with the PCM, releasing part of its energy to the PCM that lowers the temperature of the hot stream of water (T_out):

$$T_m=T_{out}-\left(T_{in}-T_m\right)e^{-N_{tu}}$$

(25)

$${\mathrm{N}}_{tu}=\frac{UA}{{\dot{m}}_w{C}_{pw}}$$

(26)

Gurturk et al. [49] analyzed a solar water heater with PCM thermal storage based on the concept of exergy. The phase change materials were embedded inside a storage water tank. The total exergy efficiency was calculated for only the charging periods with Equation (27):

$${\eta }_{ex}=\frac{\left[v\rho C_p\left(T_i-T_0\right)-T_{a}v\rho C_{p}ln\left(\frac{T_i}{T_0}\right)\right]-\left[{\dot{Q}}_l\left(1-\frac{T_a}{T_{pcm}}\right)\right]}{v\rho C_p\left(T_i-T_0\right)-T_{a}v\rho C_{p}ln\left(\frac{T_i}{T_0}\right)}$$

(27)

where v is volumetric flow rate, m³/s, ρ is density, kg/m³, T_pcm is the temperature of phase change materials, $\dot{Q}$ is the rate of heat transfer in W.

2.1.2. Solar Green House

A greenhouse is an enclosure with walls and glass covering where the temperature is regulated for plant growth. Plants require a warmer environment than the normal ambient condition as they are exposed to sunlight [50]. To maintain this condition greenhouses have been equipped with PCMs as thermal storage with thermodynamic analysis being carried out. The exergy cost approach has been used to conduct thermo-economic analysis of adopting PCM in a solar greenhouse because the feasibility of the system depends partly on the cost rate of the exergy of the system. Damirel and Ozturk [51] and Damirel [52] integrated a technical grade paraffin wax as a PCM stored inside a steel tank insulated with fiberglass. Mixture of the air from the green house and the solar receiver occurs through perforated spiral coils embedded inside the PCM. The profile of the charging and discharging of the PCM is shown in Figure 4 with some key results presented in

Table 2. Results of some of the studies presented on solar greenhouses and the PCM used.

Authors [Reference]	Nature of Studies	Aim	PCM Type	HTF	Results
Demirel and Ozturk [51]	Theoretical and experimental studies	Thermo economic analysis for a seasonal PCM for heating a Greenhouse	Paraffin wax	Air	Thermo-economic analysis was used to obtain feasible design which was accounted for by the cost of exergy within

. The warm air from the solar receiver heats the PCM with initial temperature, T_sc and it melts at temperature T_s reaching its sensible temperature T_sh.

The exergy of the system was analyzed during the charging and discharging periods. However, the exergy efficiency was expressed as a ratio of exergy stored in the PCM to the exergy supplied by the solar receiver. This implied that they assumed that the PCM completely melts and reached the sensible temperature and did not consider irreversibility. Therefore, the PCM was treated as sensible heat storage material only without considering the latent heat storage. The same method was adopted by Ortega and Carmona [12] for a solar system where paraffin was located in a container under the solar collector used for water heating. The net exergy efficiency was the product of exergy efficiency during charging (η_ch) and discharging (η_disch) periods as shown below:

$${\eta }_{net}={\eta }_{ch}\times {\eta }_{disch}$$

(28)

The exergy efficiencies were expressed in terms of temperatures as follows:

$${\eta }_{ch}=\frac{exergyofPCM}{exergyofHTF}=\frac{\left(T_{ci}-T_{c0}\right)\left(1-\frac{T_0}{T_{sh}}\right)}{\left(T_{ci}-T_{c0}\right)-T_{o}ln\left(\frac{T_{ci}}{T_{c0}}\right)}$$

(29)

$${\eta }_{disch}=\frac{exergygiventodischargeHTF}{ExergyofPCM}=\frac{\left(T_{di}-T_{d0}\right)-T_{o}ln\left(\frac{T_{ci}}{T_{c0}}\right)}{\left(T_{di}-T_{d0}\right)\left(1-\frac{T_0}{T_{sl}}\right)}$$

(30)

2.1.3. Power Generation

Table 3. Results of some of the studies presented on solar power generation and the PCM used.

Authors [Reference]	Nature of Studies	Aim	PCM Type	HTF	Results
Manfrida et al. [54]	parametric studies	Modelling of a PCM spheres filled storage tank for power generation	Erythritol	water	Simulated result obtained with mixed TRNSYS/EES software was in good agreement with experimental data obtained from literature. The Exergy efficiency obtained was 68% for mutually operational phases with the net efficiency of 3.9%
Li et al. [15]	Theoretical studies	Development of a theoretical model to obtain the net exergetic efficiency of serially placed double PCM storage system based on finite-time thermodynamics	Not indicated	air	The overall exergetic efficiency was improved with double PCM placed in series than single PCM. Melting temperature had different effects on the net exergetic efficiency
Mahfuz et al. [53]	Comparation of experimental and theoretical studies	thermodynamic performance analysis for a solar thermal power plant located in Shiraz, Iran	H190, H220, H230, H250	oil	About 30% net higher exergy efficiency can be obtained for using PCM storage along with the solar collector

presents a summary of some studies on exergy analysis applied for solar power generation integrating a PCM as heat reservoir and the results obtained. Exergy analysis of solar thermal system equipped with two PCM storage tank in series has been proposed based on finite time thermodynamics [15] for a solar concentrator used for power generation. During the charging process, the heat transfer carrier, which in this case is air, flows through the two PCMs that absorb part of the heat to melt while the low temperature fluids return back to the receiver to compete the charging process. In the analysis part, both melting temperature and the number of transfers were considered, and exergy efficiency deduced based on lump sum and distributed model. In developing the exergy model, the authors assumed that the phase change material is a reservoir of heat, where the temperature of the reservoir is constant and equivalent to the melting temperature of the PCM, and the air temperature changes as air moves along its path. Consequently, the balance of the exergy flow is the sum of exergy due to heat absorbed by the PCM, exergy loss by the PCM due to phase change (E_xp1 and E_xp2 for the two PCM respectively) and exergy loss from the components of the thermal system (heliostat, concentrator and receiver). The exergy efficiency of the PCM was expressed as a function of useful exergy of the system (E_u) and exergy loss by the PCM due to phase change as expressed in Equation (31). Increasing the number of transfer units for each PCM was found to increase the exergy efficiency:

$${ɳ}_{\mathrm{ex}}=1-\frac{{\mathrm{E}}_{\mathrm{xp}1}+{\mathrm{E}}_{\mathrm{xp}2}}{{\mathrm{E}}_{\mathrm{u}}}$$

(31)

$${\mathrm{E}}_{\mathrm{xp}1}={\mathrm{T}}_{\mathrm{e}}\left[\frac{{\mathrm{M}}_{\mathrm{p}1}{\mathsf{\lambda }}_{\mathrm{p}1}}{{\mathrm{T}}_{\mathrm{m}1}}+{\mathrm{m}}_{\mathrm{a}}{\mathrm{t}}_{\mathrm{p}1}\left({\mathrm{C}}_{\mathrm{p}}\ln \frac{{\mathrm{T}}_{\mathrm{a}2}}{{\mathrm{T}}_{\mathrm{a}1}}-{\mathrm{R}}_{\mathrm{g}}\ln \frac{{\mathrm{P}}_{\mathrm{a}2}}{{\mathrm{P}}_{\mathrm{a}1}}\right)\right]$$

(32)

$${\mathrm{E}}_{\mathrm{xp}2}={\mathrm{T}}_{\mathrm{e}}\left[\frac{{\mathrm{M}}_{\mathrm{p}2}{\mathsf{\lambda }}_{\mathrm{p}2}}{{\mathrm{T}}_{\mathrm{m}2}}+{\mathrm{m}}_{\mathrm{a}}{\mathrm{t}}_{\mathrm{p}2}\left({\mathrm{C}}_{\mathrm{p}}\ln \frac{{\mathrm{T}}_{\mathrm{a}3}}{{\mathrm{T}}_{\mathrm{a}2}}-{\mathrm{R}}_{\mathrm{g}}\ln \frac{{\mathrm{P}}_{\mathrm{a}3}}{{\mathrm{P}}_{\mathrm{a}2}}\right)\right]$$

(33)

Mahfuz et al. [53] showed that the exergy efficiency of a solar power plant can be enhanced by the application of a PCM connected in parallel to the collector field made of multiple concentrators as shown in Figure 5. The PCM was charged during the day by passing a fluid through it as shown in Figure 5. During the night, the oil flow from the field is stopped while the fluid is pumped through the PCM thermal storage. However, there was no consideration of the transition temperature of the PCM in the calculation, which may lead to some errors in the results.

The exergy efficiency was calculated as exergy recovered from the PCM (X_o.pcm) and the exergy input to the PCM (X_in,pcm) as follows:

$${\eta }_{ex}=\frac{X_{o.pcm}}{X_{in,pcm}}$$

(34)

The total output exergy of the system was calculates using:

$$outputexergy=X_u+X_{o.pcm}$$

(35)

The overall exergy efficiency of the solar plant was presented as follows:

$${\eta }_{ex}=\frac{outputexergy}{inputexergyofsolar}$$

(36)

$$X_u=N.\dot{m}.\left[\left(h_a-h_b\right)-T_o\left(s_a-s_b\right)\right]$$

(37)

where N is the number of collectors.

$$X_{in,pcm}={\dot{m}}_{HTF}{C}_{P,HTF}\left[\left(T_2-T_1\right)-T_{o}ln\left(\frac{T_1}{T_2}\right)\right]$$

(38)

$$X_{o,pcm}={\dot{m}}_{HTF}{C}_{P,HTF}\left[\left(T_1-T_2\right)-T_{o}ln\left(\frac{T_2}{T_1}\right)\right]$$

(39)

Equations (40) and (41) were also used by Manfrida et al. [54] to calculate the exergy efficiency and stored exergy of cylindrical tank filled with spherical PCM capsules integrated in a solar-powered organic Rankin cycle. In the charging phase, the air flows through the encapsulated porous PCM. Unlike Thomas et al. [55], they considered the time step in charging and discharging periods to determine the exergy stored by the PCM using numerical solution:

$$d{\dot{Q}}_{stored}=\{\begin{array}{c}\left(T_p<T_{melt}\right)\Lambda \left(\varphi =0\right)\Rightarrow m_p.C_{ps}.\left(T_{ps,fin}-T_{ps,ini}\right).\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\Delta t$}\right.\right)\\ \left(T_p=T_{melt}\right)\Lambda \left(0<\varphi <1\right)\Rightarrow m_p.\lambda .\left({\varphi }_{,fin}-{\varphi }_{,ini}\right).\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\Delta t$}\right.\right)\\ \left(T_p>T_{melt}\right)\Lambda \left(\varphi =1\right)\Rightarrow m_p.C_{pl}.\left(T_{pl,fin}-T_{pl,ini}\right).\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\Delta t$}\right.\right)\end{array}$$

(40)

The storage exergy efficiency was calculated as follows:

$${ɳ}_{ex-st}=\frac{{{\displaystyle \int }}_0^x{{\displaystyle \int }}_0^{\tau }d{\dot{E}}_{stored}dxdt}{{{\displaystyle \int }}_0^x{{\displaystyle \int }}_0^{\tau }d{\dot{E}}_{in}-d{\dot{E}}_{out}dxdt}$$

(41)

$$d{\dot{E}}_{in}-d{\dot{E}}_{out}={\dot{m}}_{HTF}{C}_{P,HTF}\left[\left(T_{HTF,in}-T_{0ut}\right)-T_{o}ln\left(\frac{T_{HTF,out}}{T_{in}}\right)\right]$$

(42)

2.1.4. Solar Dryers/Air Heaters

Several authors (

Table 4. Results of some of the studies presented on solar space heating and the PCM used.

Authors [Reference]	Nature of Studies	Aim	PCM Type	HTF	Results
Ndukwu et al. [4]	Experimental studies	Comparative performance analysis based on exergy efficiency of a solar dryer integrated with or without wind powered fan and PCM	Glycerol	air	Lower exergy efficiency was obtained for solar dryers with PCM
Ghiami et al. [13]	Experimental and theoretical studies	Experimental investigation a single-pass double-glazed solar air heater with the use of packed bed PCM	Paraffin wax	air	The dailyExergy efficiency varied between 10.7% and 19.5%
Bouadila et al. [57]	Experimental studies	To experimentally investigate the amount of PCM heat for a night use with Solar Air Heater with Latent Sto) using spherically encapsulate PCM as a packed-bed under the absorber	Capsule (AC27)	air	The exergy efficiency of the system varied between 13% and 25% daily
Edalatpour et al. [56]	Experimental and theoretical studies	To present and thermodynamic evaluate solar air heater device with special configuration and PCM placed under the absorber	Paraffin wax	Air	The exergy efficiency varied between 14.45% and 26.34% daily
Ndukwu et al. [4]	Experimental and theoretical studies	To build cheap solar dryers with available local building materials incorporating a PCM	Na2SO4.10H2O	Air	The exergy efficiency the system using PCM during the off-sunshine hours and net exergy-efficiency of the entire drying duration were 81.19 and 66.82% for the two process

) have separated the exergy computation of the solar systems, especially in solar dryers where the PCM is utilized during off sunshine periods with the air flow completely isolated from the environment. It is assumed that during this period there is zero air flow across the PCM [4], therefore exergy loss in Equations (32) or (33) is reduced to Equation (43):

$${\mathrm{E}}_{\mathrm{xpcm}}={\mathrm{T}}_{\mathrm{e}}\left[\frac{{\mathrm{M}}_{\mathrm{p}}{\mathsf{\lambda }}_{\mathrm{p}}}{{\mathrm{T}}_{\mathrm{m}}}\right]$$

(43)

The exergy efficiency of the PCM was calculated as follows:

$${\mathrm{E}}_{\mathrm{pcmxef}}=1-\frac{{\mathrm{Ex}}_{\mathrm{pcm}}}{{\mathrm{E}}_{\mathrm{xin}}}$$

(44)

$${\mathrm{E}}_{\mathrm{xin}}={\dot{\mathrm{m}}}_{\mathrm{a}}{\mathrm{C}}_{\mathrm{p}}\left[\left({\mathrm{T}}_{\mathrm{in}}-{\mathrm{T}}_{\mathrm{a}}\right)-{\mathrm{T}}_{\mathrm{a}}\mathrm{In}\frac{{\mathrm{T}}_{\mathrm{in}}}{{\mathrm{T}}_{\mathrm{a}}}\right]$$

(45)

Ndukwu et al. [4] did not consider the melting temperature or the charging period in the exergy analysis of a PCM used in solar drying of potato chips. According to them the solidification temperature of the PCM was not attained, therefore there was no phase change. They calculated the exergy efficiency of the dryer using Equation (45) for inlet and outlet temperature from the system excluding the exergy of PCM. Nevertheless, when the PCM is embedded directly under the solar collector as shown in Figure 2, the inlet and outlet are mostly closed to allow charging the PCM and opened for the PCM when it discharges to support the heating operation during the off-sunshine periods [13,56]. The exergy efficiency is expressed in terms of exergy discharge by the PCM and the exergy absorbed by the collector as shown in Equation (46):

$${ɳ}_{\mathrm{ex}}=\frac{\left({{\displaystyle \int }}_{\mathrm{disch}}^0{\mathrm{E}}_{\mathrm{xdisch}}\right)}{\left({{\displaystyle \int }}_{\mathrm{ch}}^0\mathrm{Exin}\left(\mathrm{absorbed}\right)\right)}$$

(46)

$${\mathrm{E}}_{\mathrm{xdisch}}=\left[\begin{array}{c}{\mathrm{m}}_{\mathrm{p}}{\mathrm{C}}_{\mathrm{pl}}\left({\mathrm{T}}_{\mathrm{m}}-{\mathrm{T}}_{\mathrm{fin},\mathrm{disch}}-{\mathrm{T}}_{\mathrm{a}}\ln \left(\frac{{\mathrm{T}}_{\mathrm{m}}}{{\mathrm{T}}_{\mathrm{fin},\mathrm{disch}}}\right)+{\mathrm{m}}_{\mathrm{p}}\mathrm{L}\left(1-\left(\frac{{\mathrm{T}}_{\mathrm{a}}}{{\mathrm{T}}_{\mathrm{m}}}\right)\right)\right)\\ +{\mathrm{m}}_{\mathrm{p}}{\mathrm{C}}_{\mathrm{p},\mathrm{s}}\left({\mathrm{T}}_{\mathrm{ini},\mathrm{disch},\mathrm{p}}-{\mathrm{T}}_{\mathrm{m}}-{\mathrm{T}}_{\mathrm{a}}\ln \left(\frac{{\mathrm{T}}_{\mathrm{ini},\mathrm{disch},\mathrm{p}}}{{\mathrm{T}}_{\mathrm{m}}}\right)\right)\end{array}\right]/\Delta {\mathrm{T}}_{\mathrm{disch}}$$

(47)

The E_{xin(absorbed)} is given by Bouadilia et al. [57] as follows:

$${\mathrm{E}}_{\mathrm{xin}\left(\mathrm{absorbed}\right)}={\mathsf{\eta }}_0{\mathrm{I}}_{\mathrm{T}}{\mathrm{A}}_{\mathrm{c}}\left(1-\frac{{\mathrm{T}}_{\mathrm{a}}}{{\mathrm{T}}_{\mathrm{sun}}}\right)$$

(48)

where T_ini,disch and T_fin,disch are the initial and final discharge temperature and exergy absorbed is as expressed in Equation (16), ∆t is the change in time, I_T is the solar radiation (W/m⁻²), A_c is the surface area of the collector (m²), Ta is ambient temperature, η_o is optical yield and T_sun is sun temperature.

Equation (47) was also used by Bouadilia et al. [57] in a packed bed solar collector with an encapsulated PCM which formed part of a solar heater.

2.1.5. Solar Stills

A very efficient method of desalination of saline seawater is the use of solar stills. Latent heat energy storage has been integrated to improve freshwater yield and some of the results of the thermodynamic analysis obtained through exergy analysis is presented in

Table 5. Results of some of the studies presented on solar still and the PCM used.

Authors [Reference]	Nature of Studies	Aim	PCM Type	HTF	Results
Sarhaddi et al. [64]	Theoretical analysis	Comparative performance of thermodynamic performance of two weir type cascade solar stills integrated with and without PCM thermal storage for different cloudy conditions	Paraffin wax	water	The highest exergy efficiencies obtained with PCM was 8.59% during the semi-cloudy day and therefore preferred due to high exergy efficiencies. The irreversibility rate of collector absorber was is 83.1% and 78.8% of the whole systems on a typical hot day for the two considered configurations
Asbik et al. [58]	Theoretical studies	Exergy analysis of a passive solar still equipped with PCM thermal storage	Paraffin wax	water	The PCM increases the water yield and lowers the exergy efficiency. the instantaneous exergy efficiency of the system was less than 5%, but can increase to over 80% during the night
Yousef and Hassan [59]	Comparative Experimental studies	Thermodynamic evaluation of enhancement of solar still incorporated with PCMs	Paraffin wax		Solar still with PCM has higher exergetic efficiency

. Abesik et al. [58] presented an exergy analysis of a solar still where the PCM was embedded under the collector absorber plate and evaporation of water was induced by the temperature variation between the water surface and inner glass cover of the collector as water flows into the basin from the feeding tank. They presented a numerical solution of the exergy balance of the system including the PCM. Charging and discharging period were considered by implementing the exergy balance of the PCM. The destroyed exergy (E_xd,ch) for the charging periods includes the received exergy (E_xrc) from the basin liner on top of the PCM, the stored exergy (E_xs) by the PCM and exergy loss (E_xl) within the insulation as follows:

$${\mathrm{E}}_{\mathrm{xd},\mathrm{ch}}={\mathrm{E}}_{\mathrm{xrc}}+{\mathrm{E}}_{\mathrm{xs}}-{\mathrm{E}}_{\mathrm{xl}}$$

(49)

$${\mathrm{E}}_{\mathrm{xrc}}=\frac{{\mathsf{\lambda }}_{\mathrm{b}}}{{\varrho }_{\mathrm{b}}}\left({\mathrm{T}}_{\mathrm{b}}-{\mathrm{T}}_{\mathrm{pcm}}\right)\left(1-\frac{{\mathrm{T}}_{\mathrm{amb}}}{{\mathrm{T}}_{\mathrm{b}}}\right)$$

(50)

$${\mathrm{E}}_{\mathrm{xs}}={\mathrm{Q}}_{\mathrm{ch}}\left(1-\frac{{\mathrm{T}}_{\mathrm{amb}}}{{\mathrm{T}}_{\mathrm{pcm}}}\right)$$

(51)

$${\mathrm{E}}_{\mathrm{xl}}={\mathrm{h}}_{\mathrm{ins}}\left({\mathrm{T}}_{\mathrm{pcm}}-{\mathrm{T}}_{\mathrm{ins}}\right)\left(1-\frac{{\mathrm{T}}_{\mathrm{amb}}}{{\mathrm{T}}_{\mathrm{pcm}}}\right)$$

(52)

where T is temperature, b is basin, h is over all heat transfer coefficient, ʎ is thermal conductivity (Wm⁻¹K⁻¹), is thickness (m).

For the discharging period the exergy destroyed (E_xd,disch) components consists of exergy loss (E_xrdisch) by the PCM during the discharge process and the exergy absorbed by the insulation (E_xa), as represented by the following equations:

$${\mathrm{E}}_{\mathrm{xd},\mathrm{disch}}={\mathrm{E}}_{\mathrm{a}}-{\mathrm{E}}_{\mathrm{xrdisch}}$$

(53)

$${\mathrm{E}}_{\mathrm{xrdisch}}={\mathrm{Q}}_{\mathrm{disch}}\left(1-\frac{{\mathrm{T}}_{\mathrm{amb}}}{{\mathrm{T}}_{\mathrm{pcm}}}\right)$$

(54)

$${\mathrm{E}}_{\mathrm{xa}}=-{\mathrm{E}}_{\mathrm{xl}}$$

(55)

Q is heat flux density (Wm⁻²), ch represents charging, disch represents discharging,

The exergy efficiency was expressed in terms of exergy out and input taking into considering the charging and discharging periods.

The thermodynamic performance of two similar sloping solar stills (Figure 6) were also tested by Yousef and Hassan [59] under four design methods with an integrated PCM. In the first approach, a pin fins heat sink was embedded into the PCM while in the second method black steel mesh fibers were employed in the basin dotted with PCM. Also, the solar still was tested without PCM and PCM placed under the collector. The authors did not consider the exergy of the PCM in determination of the exergy balance.

The exergy efficiency of the solar still was deduced in terms of output as evaporative exergy and input the exergy from the sun [60,61]:

$${\mathsf{\eta }}_{\mathrm{ex}}=\frac{{\mathrm{E}}_{\mathrm{x},}{}_{\mathrm{evap}}}{{\mathrm{E}}_{\mathrm{x},}{}_{\mathrm{sun}}}$$

(56)

The exergy of the Sun was calculated following the method used also by Deniz [62]:

$${\mathrm{E}}_{\mathrm{x},}{}_{\mathrm{sun}}={\mathrm{A}}_{\mathrm{b}}{\mathrm{I}}_{\mathrm{i}}\left[1-\frac{4}{3}\left(\frac{{\mathrm{T}}_{\mathrm{a}}+273}{{\mathrm{T}}_{\mathrm{s}}}\right)+\frac{1}{3}{\left(\frac{{\mathrm{T}}_{\mathrm{a}}+273}{{\mathrm{T}}_{\mathrm{s}}}\right)}^4\right]$$

(57)

The evaporative exergy was calculated as follows:

$${\mathrm{E}}_{\mathrm{x},}{}_{\mathrm{evap}}=\frac{{\dot{\mathrm{m}}}_{\mathrm{cw}}{\mathsf{\lambda }}_{\mathrm{fg}}}{3600}\left[1-\left(\frac{{\mathrm{T}}_{\mathrm{a}}+273}{{\mathrm{T}}_{\mathrm{w}}+273}\right)\right]$$

(58)

$${\mathsf{\lambda }}_{\mathrm{fg}}=3.1615\left({10}^6-761.6{\ast \mathrm{T}}_{\mathrm{i}}\right),{\mathrm{T}}_{\mathrm{i}}>70$$

(59)

$${\mathsf{\lambda }}_{\mathrm{fg}}=3.1615\left({10}^6-947.79{\ast \mathrm{T}}_{\mathrm{i}}+0.13132{\ast \mathrm{T}}_{\mathrm{i}}^2-0.00047974{\ast \mathrm{T}}_{\mathrm{i}}^3\right),{\mathrm{T}}_{\mathrm{i}}<70$$

(60)

$${\mathrm{T}}_{\mathrm{i}}=\frac{{\mathrm{T}}_{\mathrm{w}}-{\mathrm{T}}_{\mathrm{g}}}{2}$$

(61)

The same method has been used by several authors in similar studies dealing with exergy analysis of solar stills with PCMs as thermal storage [62,63,64]. This process of exergy of a system is irreversible due to the generated entropy and the exergy can only be preserved if the process is reversed. To reduce the irreversibility, effects of this last have to be determined. However, in solar still with PCM embedded under the absorber plate, the PCM stores the transferred exergy input from the absorber plate with some losses to the environment through the insulations. The exergy transfer rate from the absorber plate to the PCM has been deduced [64] as follows:

$${\mathrm{E}}_{\mathrm{x},}{}_{\mathrm{loss}}=\frac{{\mathrm{k}}_{\mathrm{pcm}}}{{\mathrm{t}}_{\mathrm{pcm}}}{\mathrm{A}}_{\mathrm{p}}\left({\mathrm{T}}_{\mathrm{p}}-{\mathrm{T}}_{\mathrm{pcm}}\right)\left[1-\left(\frac{{\mathrm{T}}_{\mathrm{a}}+273}{{\mathrm{T}}_{\mathrm{p}}+273}\right)\right]$$

(62)

The exergy loss rate from the PCM to the surroundings:

$${\mathrm{E}}_{\mathrm{x},}{}_{\mathrm{loss}}=\frac{{\mathrm{k}}_{\mathrm{ins}}}{{\mathrm{t}}_{\mathrm{ins}}}{\mathrm{A}}_{\mathrm{p}}\left({\mathrm{T}}_{\mathrm{pcm}}-{\mathrm{T}}_{\mathrm{a}}\right)\left[1-\left(\frac{{\mathrm{T}}_{\mathrm{a}}+273}{{\mathrm{T}}_{\mathrm{pcm}}+273}\right)\right]$$

(63)

2.1.6. Space Conditioning

Most space conditioners apply electricity or fossil fuels during the heating or cooling season. However, the application of solar energy reduces the energy bill. The methods of heat distribution in building spaces using solar space heaters can be based on radiant or slab heating, hot water baseboard heaters or central force air systems [65] while desiccant cooling can be adopted in the cooling process [66]. Solar space heating can be designed with thermal storage unit that captures and stores the energy from the sun before gradually distributing it to the space. Based on the above designs, thermodynamic analysis has been carried out to determine the exergy efficiencies of various designs and some of the obtained results is summarized in

Table 6. Results of some of the studies presented on space heating and the PCM used.

Authors [Reference]	Nature of Studies	Aim	PCM Type	HTF	Results
Thomas et al. [55]	Experimental studies	Thermodynamic evaluation of simulated solar space heating	Sodium thiosulfate pentahydrate	Air	Exergy efficiency of the system decreased with air flow rate and was very low
Solomon and Oztekin [68]	Comparative theoretical Studies	To determine the benefit of a system equipped with a multiple PCM	NaNO3, NaNO2, and KNO3	air	The difference between the melting point of the PCMs and the inlet temperatures during charging and discharging greatly affected the performance of the system
Mehla and Yadav [69]	Experimental studies	To produce hot air for space heating in consecutive and simultaneous charging and discharging of the PCM using evacuated tube solar air collector	Acetamide	Water	The maximum average efficiency of 17.9% was obtained for the collector at a high air flow rate during simultaneously charging and discharging of the PCM
Abdulmunem et al. [16]	Comparative experimental studies	To analyze the thermodynamic performance of flat plate solar air collector with PCM and the effect of embedding fins into the PCM on the collector performance	Paraffin wax	Air	Compared with the collector without PCM, using of PCM reduces the losses of exergy of the collector
Arul Kumar et al. [67]	Experimental and theoretical studies	To compare the performance of a forced convention solar heater using different configuration (pin-fin, triangular and circular)of packed bed PCM thermal storage	Paraffin wax	air	Packed bed absorber plate configurations using PCM has 2-20% higher exergy efficiency when compared to flat absorber plate

. Kumar et al. [67] considered the charging and discharging process in energy analysis but not in the exergy analysis of solar heater with pin-fin, circular and triangular absorber plate filled with PCM as thermal storage. The same method was used by Abdulmunem et al. [16]. The overall exergy efficiency was calculated in terms of net output of the system considering only the exergy input of the air. Therefore, they expressed the exergy efficiency as it is represented by Equation (64):

$${\mathsf{\eta }}_{\mathrm{ex}}=1-\frac{{\mathrm{T}}_{\mathrm{o}}{\mathrm{S}}_{\mathrm{g}}}{\left(1-\frac{{\mathrm{T}}_{\mathrm{o}}}{{\mathrm{T}}_{\mathrm{s}}}\right){\dot{\mathrm{Q}}}_{\mathrm{s}}}$$

(64)

The benefit of employing encapsulated cascaded multi-PCMs in solar space heating with the inlet and outlet of the void symmetry (Figure 7) reversed for the discharging process was presented by Solomon and Oztekin [68]. The exergy calculation was deduced by assuming uniform temperature distribution in the capsule and the melting of the PCM to be incongruent, therefore the liquid and solid temperature were assumed the same. The overall exergy efficiency was calculated using the following equations:

$${\mathsf{\eta }}_{\mathrm{ex}}=\frac{{\mathrm{E}}_{\mathrm{x},}{}_{\mathrm{released}}}{{\mathrm{E}}_{\mathrm{x},}{}_{\mathrm{stored}}}$$

(65)

$${\mathrm{E}}_{\mathrm{x},\mathrm{stored}}=\{\begin{array}{cc}{\mathrm{m}}_{\mathrm{i}}{\mathrm{c}}_{\mathrm{pi}}^{\mathrm{s}}\left[\left(\mathrm{T}-{\mathrm{T}}_{\mathrm{i}}\right)-{\mathrm{T}}_0\ln \left(\frac{\mathrm{T}}{{\mathrm{T}}_{\mathrm{i}}}\right)\right]& \mathrm{T}<{\mathrm{T}}_{\mathrm{si}}\\ {\mathrm{m}}_{\mathrm{i}}{\mathrm{c}}_{\mathrm{pi}}^{\mathrm{s}}\left[\left(\mathrm{T}-{\mathrm{T}}_{\mathrm{i}}\right)-{\mathrm{T}}_0\ln \left(\frac{\mathrm{T}}{{\mathrm{T}}_{\mathrm{i}}}\right)\right]+{\mathrm{m}}_{\mathrm{i}}{\gamma \mathrm{L}}_{\mathrm{i}}\left[1-\left(\frac{{\mathrm{T}}_0}{\mathrm{T}}\right)\right]& {\mathrm{T}}_{\mathrm{si}}<\mathrm{T}<{\mathrm{T}}_{\mathrm{li}}\hspace{1em}\\ {\mathrm{m}}_{\mathrm{i}}{\mathrm{c}}_{\mathrm{pi}}^s\left[\left(\mathrm{T}-{\mathrm{T}}_{\mathrm{i}}\right)-{\mathrm{T}}_0\ln \left(\frac{\mathrm{T}}{{\mathrm{T}}_{\mathrm{i}}}\right)\right]+{\mathrm{m}}_{\mathrm{i}}{\gamma \mathrm{L}}_{\mathrm{i}}\left[1-\left(\frac{{\mathrm{T}}_0}{\mathrm{T}}\right)\right]+{\mathrm{m}}_{\mathrm{i}}{\mathrm{c}}_{\mathrm{pi}}^{\mathrm{l}}\left[\left(\mathrm{T}-{\mathrm{T}}_{\mathrm{mi}}\right)-{\mathrm{T}}_0\ln \left(\frac{\mathrm{T}}{{\mathrm{T}}_{\mathrm{mi}}}\right)\right]& \mathrm{T}>{\mathrm{T}}_{\mathrm{li}}\end{array}$$

(66)

$${\mathrm{E}}_{\mathrm{x},\mathrm{sreleased}}=\{\begin{array}{cc}{\mathrm{m}}_{\mathrm{i}}{\mathrm{c}}_{\mathrm{pi}}^{\mathrm{l}}\left[\left({\mathrm{T}}_{\mathrm{char}}-{\mathrm{T}}_{\mathrm{i}}\right)-{\mathrm{T}}_0\ln \left(\frac{{\mathrm{T}}_{\mathrm{char}}}{\mathrm{T}}\right)\right]& \mathrm{T}>{\mathrm{T}}_{\mathrm{si}}\\ {\mathrm{m}}_{\mathrm{i}}{\mathrm{c}}_{\mathrm{pi}}^{\mathrm{l}}\left[\left({\mathrm{T}}_{\mathrm{char}}-{\mathrm{T}}_{\mathrm{mi}}\right)-{\mathrm{T}}_0\ln \left(\frac{{\mathrm{T}}_{\mathrm{char}}}{{\mathrm{T}}_{\mathrm{mi}}}\right)\right]+{\mathrm{m}}_{\mathrm{i}}{\gamma \mathrm{L}}_{\mathrm{i}}\left[1-\left(\frac{{\mathrm{T}}_0}{\mathrm{T}}\right)\right]& {\mathrm{T}}_{\mathrm{si}}<\mathrm{T}<{\mathrm{T}}_{\mathrm{li}}\hspace{1em}\\ {\mathrm{m}}_{\mathrm{i}}{\mathrm{c}}_{\mathrm{pi}}^{\mathrm{l}}\left[\left({\mathrm{T}}_{\mathrm{char}}-{\mathrm{T}}_{\mathrm{mi}}\right)-{\mathrm{T}}_0\ln \left(\frac{{\mathrm{T}}_{\mathrm{char}}}{{\mathrm{T}}_{\mathrm{mi}}}\right)\right]+{\mathrm{m}}_{\mathrm{i}}{\gamma \mathrm{L}}_{\mathrm{i}}\left[1-\left(\frac{{\mathrm{T}}_0}{{\mathrm{T}}_{\mathrm{mi}}}\right)\right]+{\mathrm{m}}_{\mathrm{i}}{\mathrm{c}}_{\mathrm{pi}}^{\mathrm{l}}\left[\left({\mathrm{T}}_{\mathrm{mi}}-\mathrm{T}\right)-{\mathrm{T}}_0\ln \left(\frac{{\mathrm{T}}_{\mathrm{mi}}}{\mathrm{T}}\right)\right]& \mathrm{T}<{\mathrm{T}}_{\mathrm{li}}\end{array}$$

(67)

The exergy efficiency of the charging process was calculated with Equation (68):

$${\mathsf{\eta }}_{\mathrm{ex}}=\frac{{\mathrm{E}}_{\mathrm{x},}{}_{\mathrm{stored}}}{{\mathrm{E}}_{\mathrm{x},}{}_{\mathrm{input}}}$$

(68)

$${\mathrm{E}}_{\mathrm{x},}{}_{\mathrm{input}}={\dot{\mathrm{m}}}_{\mathrm{HTF}}{\mathrm{C}}_{\mathrm{P},\mathrm{HTF}}\left[\left({\mathrm{T}}_{\mathrm{HTF},\mathrm{in}}-{\mathrm{T}}_0\right)-{\mathrm{T}}_{\mathrm{o}}\ln \left(\frac{{\mathrm{T}}_{\mathrm{HTF},\mathrm{in}}}{{\mathrm{T}}_0}\right)\right]\times \Delta \mathrm{t}$$

(69)

Thomas et al. [55] used Equation (69) to calculate the exergy input of PCM for an electrically simulated solar heater without considering the charging and discharging time. The PCM was stored in an aluminum tube arranged in parallel. The air was allowed flowing through the storage tank with the help of a blower. The exergy efficiency was determined using Equation (67), however the exergy stored was calculated with Equation (70) [56] as follows:

$${\mathrm{E}}_{\mathrm{xstored}}={\mathrm{Q}}_{\mathrm{stored}}\ast \left[1-\frac{{\mathrm{T}}_0}{{\mathrm{T}}_{\mathrm{pcm}}}\right]$$

(70)

$$\mathrm{Energy}\mathrm{stored}\left({\mathrm{Q}}_{\mathrm{stored}}\right)=\mathrm{Energy}\mathrm{in}-\mathrm{Energy}\mathrm{loss}$$

(71)

Energy inlet was calculated as follows:

$$\mathrm{Energy}\mathrm{in}={\dot{\mathrm{m}}}_{\mathrm{HTF}}{\mathrm{C}}_{\mathrm{P},\mathrm{HTF}\left({\mathrm{T}}_{\mathrm{HTF},\mathrm{in}}-{\mathrm{T}}_{\mathrm{HTF},0\mathrm{ut}}\right)}$$

(72)

Energy loss was calculated as:

$$\mathrm{Energy}\mathrm{loss}=\frac{{\mathrm{T}}_{\mathrm{m}}-{\mathrm{T}}_0}{{\mathrm{R}}_{\mathrm{total}}}$$

(73)

T_m is the mean temperature, R_total is the tube resistance deduced with Equation (74) as follows:

$${\mathrm{R}}_{\mathrm{total}}=\frac{1}{2\mathsf{\pi }\mathrm{l}}\left(\frac{1}{{\mathrm{h}}_{\mathrm{i}}{\mathrm{r}}_{\mathrm{i}}}+\frac{1}{{\mathrm{k}}_{\mathrm{p}}\mathrm{vc}}+\ln \left(\frac{{\mathrm{r}}_{\mathrm{o}}}{{\mathrm{r}}_{\mathrm{i}}}\right)+\frac{\mathrm{i}}{{\mathrm{h}}_{\mathrm{o}}{\mathrm{r}}_{\mathrm{o}}}\right)$$

(74)

where k is the thermal conductivity of the heat transfer fluid, h_i is the inside heat transfer coefficient, h_o is the outside heat transfer coefficient, r_o is the outer radius of the storage tank, r_i is the inner radius of the storage tank, v is the kinematic viscosity, l is the length of storage tank and c is the specific heat capacity.

Mehla and Yadav [69] evaluated the exergy analyses of a solar space heater with an evacuated tube solar collector integrated with a PCM considering the consecutive and simultaneous charging and discharging modes of the PCM. Description of the system shows that heated water is used to charge the PCM contained in a rectangular inner box at the extreme of the tubes. The water flows around the rectangular box housing the PCM contained in the inner rectangular box. The presented exergy efficiency in terms of exergy out-flow and exergy in-flow by the following expressions:

$${\mathsf{\eta }}_{\mathrm{ex}}=\frac{{\mathrm{E}}_{\mathrm{xout}}}{{\mathrm{E}}_{\mathrm{xin}}}$$

(75)

$${\mathrm{E}}_{\mathrm{xout}}=\frac{\left\{{\mathrm{m}}_{\mathrm{pcm}}{\mathrm{C}}_{\mathrm{pcm}}{{\displaystyle \int }}_0^{\mathrm{t}}\left[\left({\mathrm{T}}_{\mathrm{in},\mathrm{pcm}}-{\mathrm{T}}_{\mathrm{out},\mathrm{pcm}}\right)-{\mathrm{T}}_{\mathrm{o}}\ln \left(\frac{{\mathrm{T}}_{\mathrm{in},\mathrm{pcm}}}{{\mathrm{T}}_{\mathrm{out},\mathrm{pcm}}}\right)\right]\mathrm{dt}\right\}}{3600}$$

(76)

$${\mathrm{E}}_{\mathrm{x},\mathrm{in}}=\frac{\left\{{\mathrm{m}}_{\mathrm{w}}{\mathrm{C}}_{\mathrm{p},\mathrm{w}}{{\displaystyle \int }}_0^{\mathrm{t}}\left[\left({\mathrm{T}}_{\mathrm{in},\mathrm{w}}-{\mathrm{T}}_{\mathrm{out},\mathrm{w}}\right)-{\mathrm{T}}_{\mathrm{o}}\ln \left(\frac{{\mathrm{T}}_{\mathrm{in},\mathrm{w}}}{{\mathrm{T}}_{\mathrm{out},\mathrm{w}}}\right)\right]\mathrm{dt}\right\}}{3600}$$

(77)

Their analysis demonstrated the importance and the influence of using high air flow rate during the simultaneous charging and discharging modes.

2.1.7. Solar Cooker

Different designs of solar cookers abound in the literature. A typical design with PCM as thermal storage was presented by Sharma et al. [70] and Pal and Chaun [71] as shown in Figure 8 and the key results obtained presented in

Table 7. Results of some of the studies presented on solar cooking and the PCM used.

Authors [Reference]	Nature of Studies	Aim	PCM Type	HTF	Results
Pal and Chauhan [71]	Comparative Experimental studies	Experiment investigation for solar cooking with parabolic solar concentrator and PCM to check their feasibility	paraffin wax	Air	The exergy efficiency of the system with PCM storage was higher than the system without PCM storage.

. Considering a parabolic solar water boiler where the PCM was filled in the gap between pot in pot steel pots (Figure 8). Pal and Chaun [71] presented the exergy efficiency of the system in terms of availability input and availability output exergy as follows:

$${\mathsf{\eta }}_{\mathrm{ex}}=\frac{\mathrm{Availability}\mathrm{output}}{\mathrm{Availability}\mathrm{input}}$$

(78)

$$\mathrm{Availability}\mathrm{input}={\mathrm{Q}}_{\mathrm{i}}\left(1-\frac{{\mathrm{T}}_0}{{\mathrm{T}}_{\mathrm{sun}}}\right)$$

(79)

$$\begin{array}{cc}\hfill \mathrm{vailability}\mathrm{output}& ={\mathrm{m}}_{\mathrm{p}}{\mathrm{C}}_{\mathrm{ps}}\left({\mathrm{T}}_2-{\mathrm{T}}_1\right)-{\mathrm{m}}_{\mathrm{p}}{\mathrm{C}}_{\mathrm{ps}}{\mathrm{T}}_0\ln \left(\frac{{\mathrm{T}}_2}{{\mathrm{T}}_1}\right)+{\mathrm{m}}_{\mathrm{p}}{\mathrm{L}}_{\mathrm{p}}-{\mathrm{m}}_{\mathrm{p}}{\mathrm{L}}_{\mathrm{p}}\frac{{\mathrm{T}}_0}{\mathrm{T}}+{\mathrm{m}}_{\mathrm{p}}{\mathrm{C}}_{\mathrm{pl}}\left({\mathrm{T}}_2-{\mathrm{T}}_1\right)-{\mathrm{m}}_{\mathrm{p}}{\mathrm{C}}_{\mathrm{pl}}{\mathrm{T}}_0\ln \left(\frac{{\mathrm{T}}_2}{{\mathrm{T}}_1}\right)\\ & +{\mathrm{m}}_{\mathrm{w}}{\mathrm{C}}_{\mathrm{w}}\left({\mathrm{T}}_2-{\mathrm{T}}_1\right)-{\mathrm{m}}_{\mathrm{w}}{\mathrm{C}}_{\mathrm{w}}{\mathrm{T}}_0\ln \left(\frac{{\mathrm{T}}_2}{{\mathrm{T}}_1}\right)\hfill \end{array}$$

(80)

2.1.8. Solar Refrigeration

Thermal driven coolers have the advantage of operating at low temperatures and they can be powered using heat recovery from other heat engines, solar heaters or even geothermal systems [72]. Thermal systems can be operated as absorption or adsorption cycles [73]. However, Miyazaki and Akisawa [74] noted that adsorption refrigeration cycles operate at lower temperature, with fewer moving parts compared to absorption refrigeration cycles. Nevertheless, a thorough search of literature reveals very little information on any integrated refrigerated structures using a solar cycle incorporated with a PCM. A typical sketch of a solar refrigerator device integrated with a PCM is presented by Ghorbani and Mehrpooy [75] as shown in Figure 9. The PCM was added to aid refridgeration during the off-sunshine hours. Their irreversibility (I) of the system was evaluated based on absolute value of the reversible work (W_rev) and real work (W_real) as follows:

$$\mathrm{I}=\left|{\dot{\mathrm{W}}}_{\mathrm{rev}}-{\dot{\mathrm{W}}}_{\mathrm{real}}\right|$$

(81)

3. Discussion

The reviewed papers showed different heat flow designs within the system to improve the heat transfer rate. Some of the researchers improved the heat transfer rate by using fins, multiple PCMs, evacuated tubes and microencapsulation of PCMs [15,59,67,68] and these designs were considered in the exergy analysis. However, the evaluation of various reviewed papers reveals that the research all broadly falls into experimental analysis and parametric research studies. For all the papers, generic input and output exergy equations of the exergy streams were used to compute the exergy efficiency for most experimental analysis without considering the system configuration. For the parametric studies, theoretical exergy equations for each heating systems considered the choice of PCM and its thermo-physical properties, the storage configuration of the PCM, heat transfer fluid, method of PCM storage and point of contact and HTF in the system as a determinant for equation coupling to derive the exergy efficiency of each system. The heat transfer mode for the melting of PCM is dominated by convection, though conduction dominates the solidification process [13].

The major observations from most of the equations presented was the non-inclusion of the dimensions of the PCM compartment or units in the analysis. It is expected that the amount of heat stored is a function of the quantity of the PCM because the melting of the PCM is dominated by convention heat transfer, therefore the dimensions of the containing unit is expected to affect the heat transfer rate [13]. Increases in natural convention as a result of increases in the PCM unit size are likely to decrease the entropy generation which affects the destroyed exergy. Also, the pressure of heat transfer fluid can be lowered or increased if the dimensions of the heat transfer unit are altered which can also affect the entropy generated, but this aspect was lacking in all the reviewed articles.

The exergy evaluations and equations used or derived for various heating systems involve the exergy of heat transfer fluids which are either water or air and the exergy of the PCM which has been evaluated separately. Various studies focused on heat transfer rate [21], energy released or stored [45] and the charging and discharging periods [47]. Therefore, for a complete cycle, the components of the exergy equations include the exergy stored during the melting of the PCM, the exergy stored during heating and melting, respectively, for the sensible periods. The analysis of various exergy equations shows two broad methods have been adopted. In the first case the temperature of the PCM is taken as the melting temperature whereby the authors neglect the sensible heat. In this case only the charging cycle is considered. This is not an appropriate approach because the PCM first gains heat during charging before melting and after super cooling it has its own temperature. Therefore, the temperature of PCM is different from the melting temperature. In this case the temperature of the PCM is computed as an average temperature between the initial and the final value [68].

It is important to identify that the temperature of the HTF varies as it moves around to complete its cycle that is why some researchers have employed multiple PCM storage units with decreasing order of latent heat storage [48], while in the second case some authors computed the exergy efficiency for a complete cycle by including the charging and discharging time interval in the calculation of exergy equations leading to the determination of the exergy efficiencies. The implications of not considering the charging and discharging time will be the presentation of erroneous exergy efficiencies compared to those that considered the time intervals. This will lead to presentation of inappropriate results by undervaluing the exergy efficiency [13]. Generally, the exergy input was expressed as the change in the flow of exergy produced by the heat transfer fluid or the exergy input from the solar radiation while the exergy output can be calculated as the energy stored or released, exergy of the evaporation of water in the case of solar still. Therefore, the efficiencies were presented as charging or discharging efficiencies, PCM efficiencies, and system efficiencies, net or overall efficiencies. It was observed in most approaches related to determination of the efficiency of the system, the destroyed exergy was not taken into consideration. Destroyed exergy is important in calculating the exergy efficiency of the system because it helps the calculation of the generated entropy. This is more pronounced depending on the method of introducing the PCM. If it is encapsulated the generated entropy can be neglected [76]. However, in other design considerations like the tubular heat exchanger or when the PCM is embedded in fins to increase the heat transfer rate or if the heat transferred to the PCM is by convention, entropy variations between the separating surfaces need to be included in the exergy analysis [77,78].

4. Conclusions

The exergy equations for various configurations of hybrid solar heating systems integrated with PCMs as thermal storage is reviewed in this paper. Exergy computation is very important for the design and thermo-economic analysis of solar systems. Several numbers of exergy efficiency method based on exergy recovery, energy stored, system exergy input and out and exergy availability and evaporative exergy have been presented in this paper for solar heating systems. Most research on solar stills ignores the exergy contribution of PCM in the overall exergy efficiency of the system while focusing on the exergy of evaporation of water. A review of literature shows that most of the systems did not consider entropy generation in the calculation of exergy efficiency. However, the inclusion of a PCM increased the exergy efficiency of most of the systems but this requires more complex logic control to determine the overall true effect on the exergy flux. This is because a PCM produces its own entropy that ought to have reduced the exergy efficiency. Therefore, real time software computing models are required to the show temperature profile of the heat transfer fluid from the inlet through the complete cycle of the process based on each system configuration. Future exergy models therefore should focus on the contribution of melting temperature in controlling exergy flux of each system.