An Improved Variational Mode Decomposition and Its Application on Fault Feature Extraction of Rolling Element Bearing
Abstract
:1. Introduction
2. Basic Theory
2.1. Variational Mode Decomposition
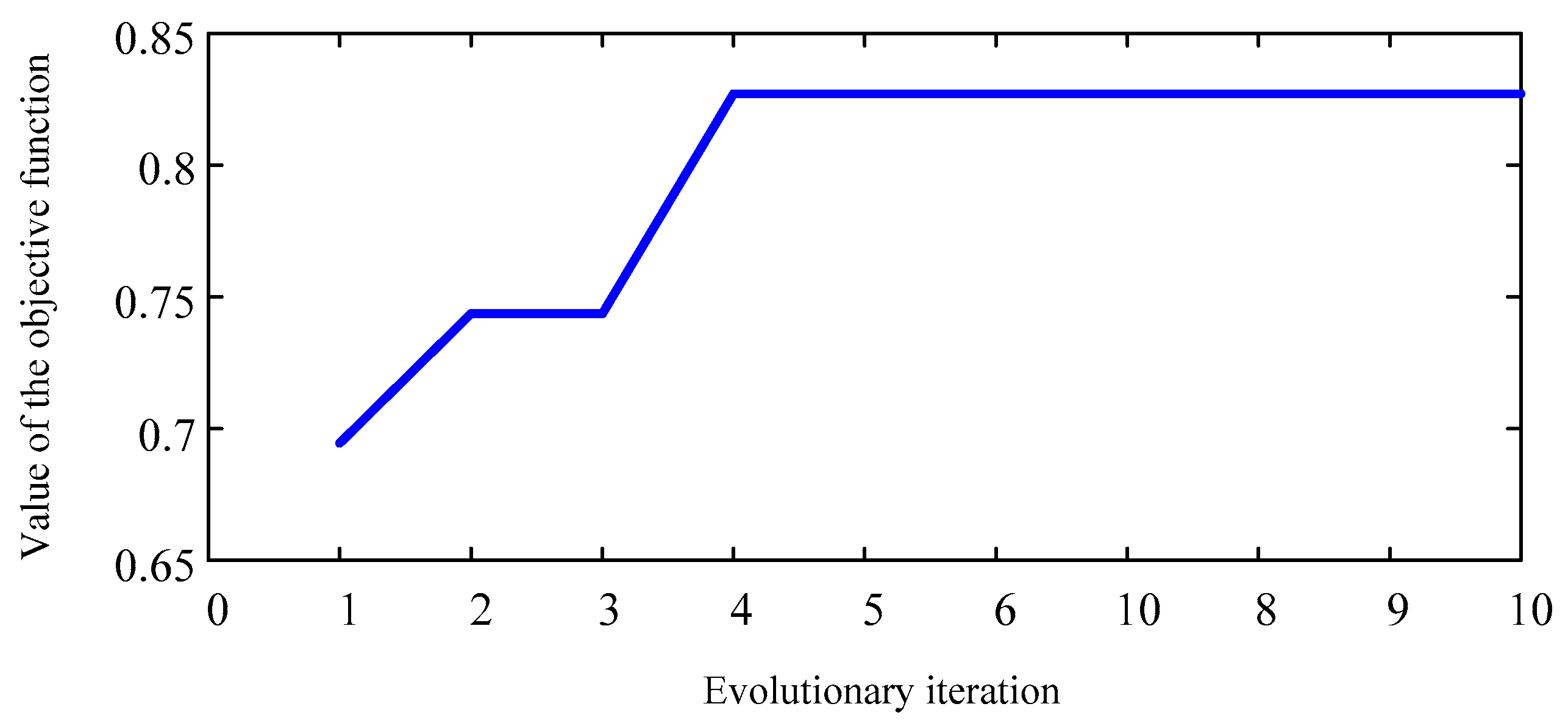
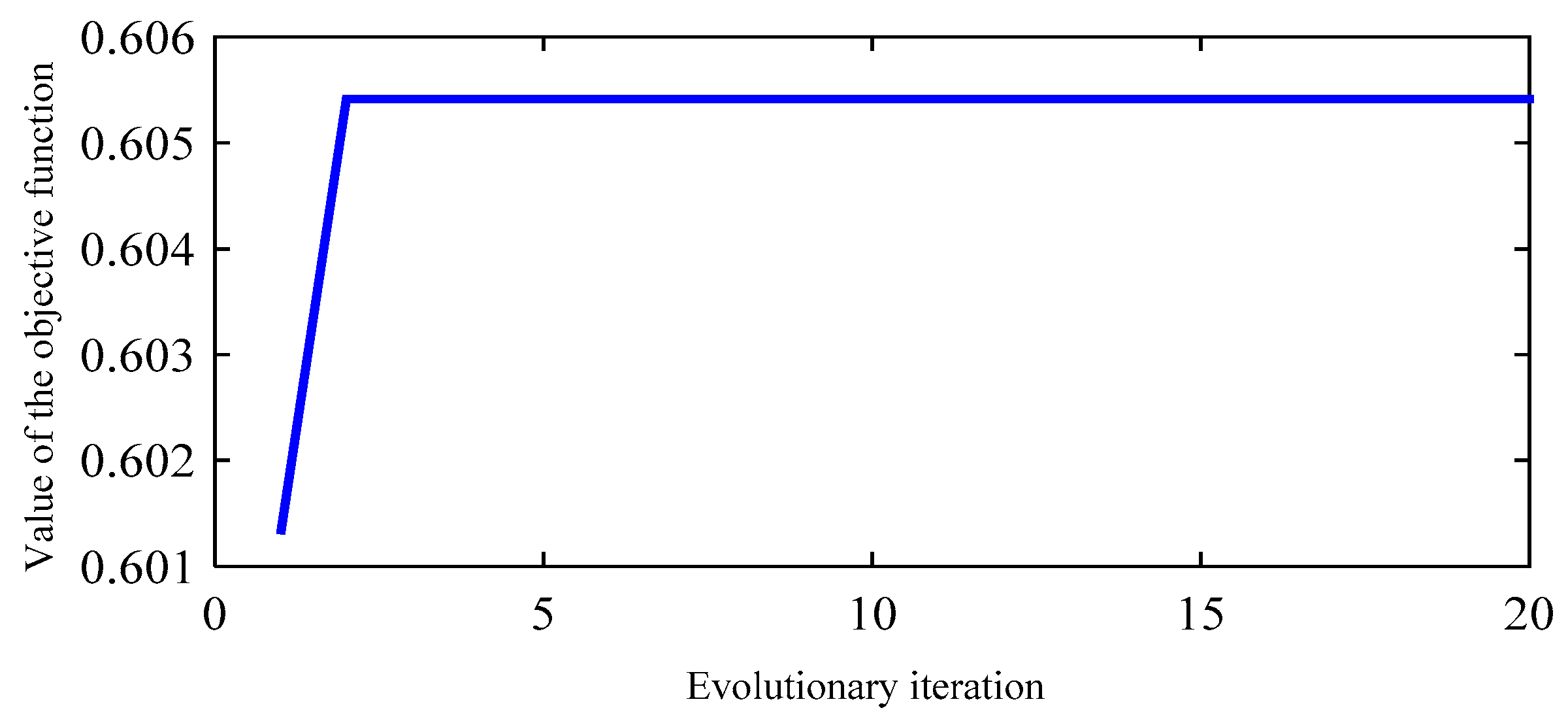
2.2. Shuffled Frog Leaping Algorithm
- The relative change in the fitness of the global frog within a number of consecutive shuffling iterations is less than a pre-specified tolerance.
- The maximum predefined number of shuffling iterations has been obtained.
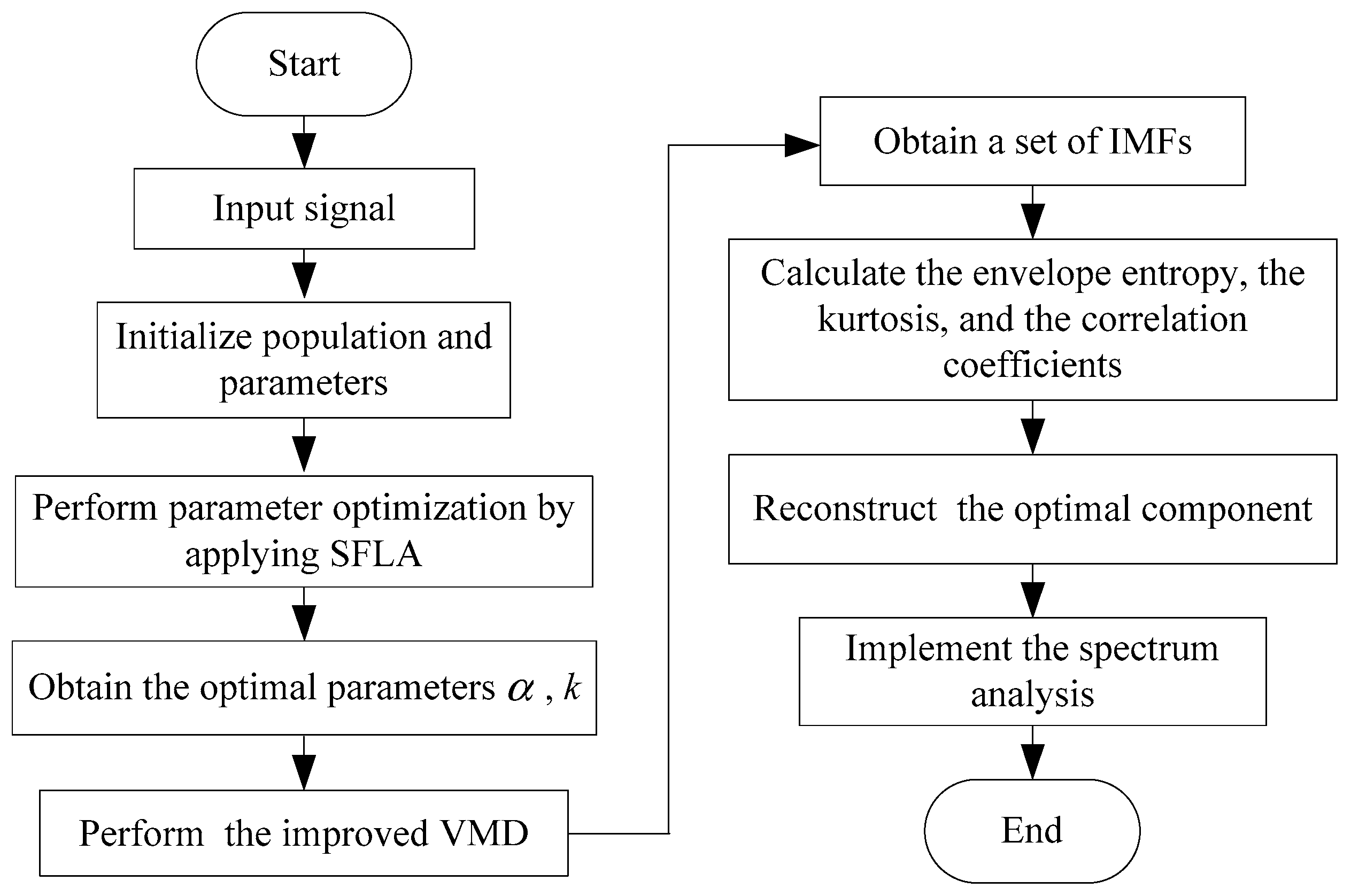
3. Improved VMD Algorithm
- Initialize the parameters: total number of frogs , number of subgroups , number of each group frogs , maximal number of iterations , random initialization of frog individuals, initialize the population;
- Implement VMD, and obtain a set of IMFs;
- Construct the global fitness function based on the envelope entropy, the kurtosis, and the correlation coefficients;
- Calculate the fitness value of each frog;
- Rank the frogs according to their fitness values;
- Divided the sorted frogs into subgroups according to the descending order of the objective function. The first frog goes to the first memeplex, the second frog goes to the second memeplex, frog m goes to the m-th memeplex, and frog goes to the first memeplex, and so on.
- Determine the best individual of the subgroup , the worst individual and the optimal solutions in the population , the worst solution is improved by the Equation (12) in evolutional iterations ;
- Update the worst individual and descend the order to the individual to form a new group;
- Judge whether the algorithm satisfies the terminating condition, outputs the optimum solution when the algorithm satisfies the termination condition, otherwise moves on to step 6.
4. Fault Feature Extraction by IVMD
- Initialize population and parameters: the numbers of subgroup , the numbers of each group frogs , the numbers of iteration within a group , the numbers of evolutional iteration ;
- Optimize VMD parameters by applying SFLA and obtain global optimal parameter k and ;
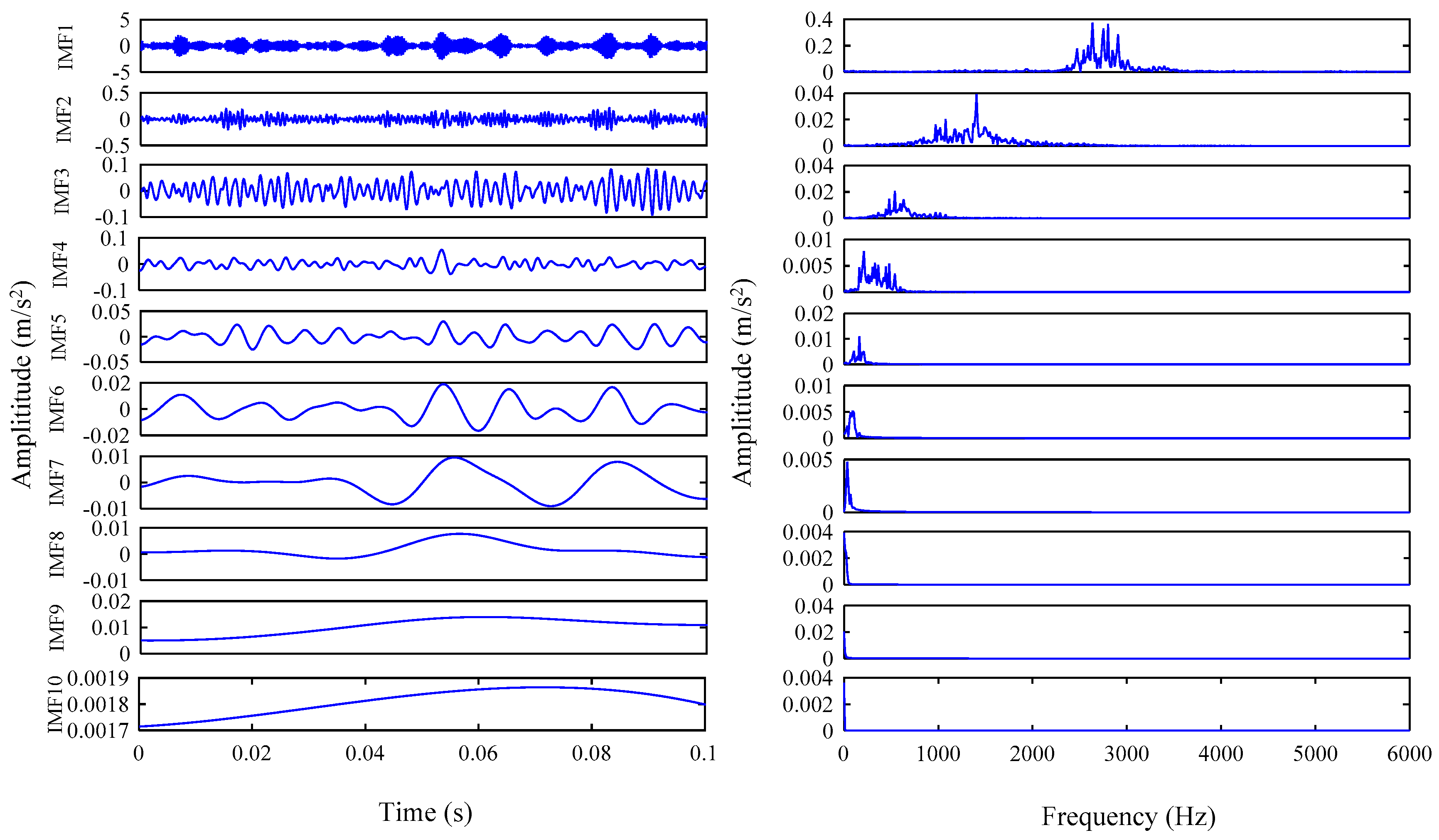
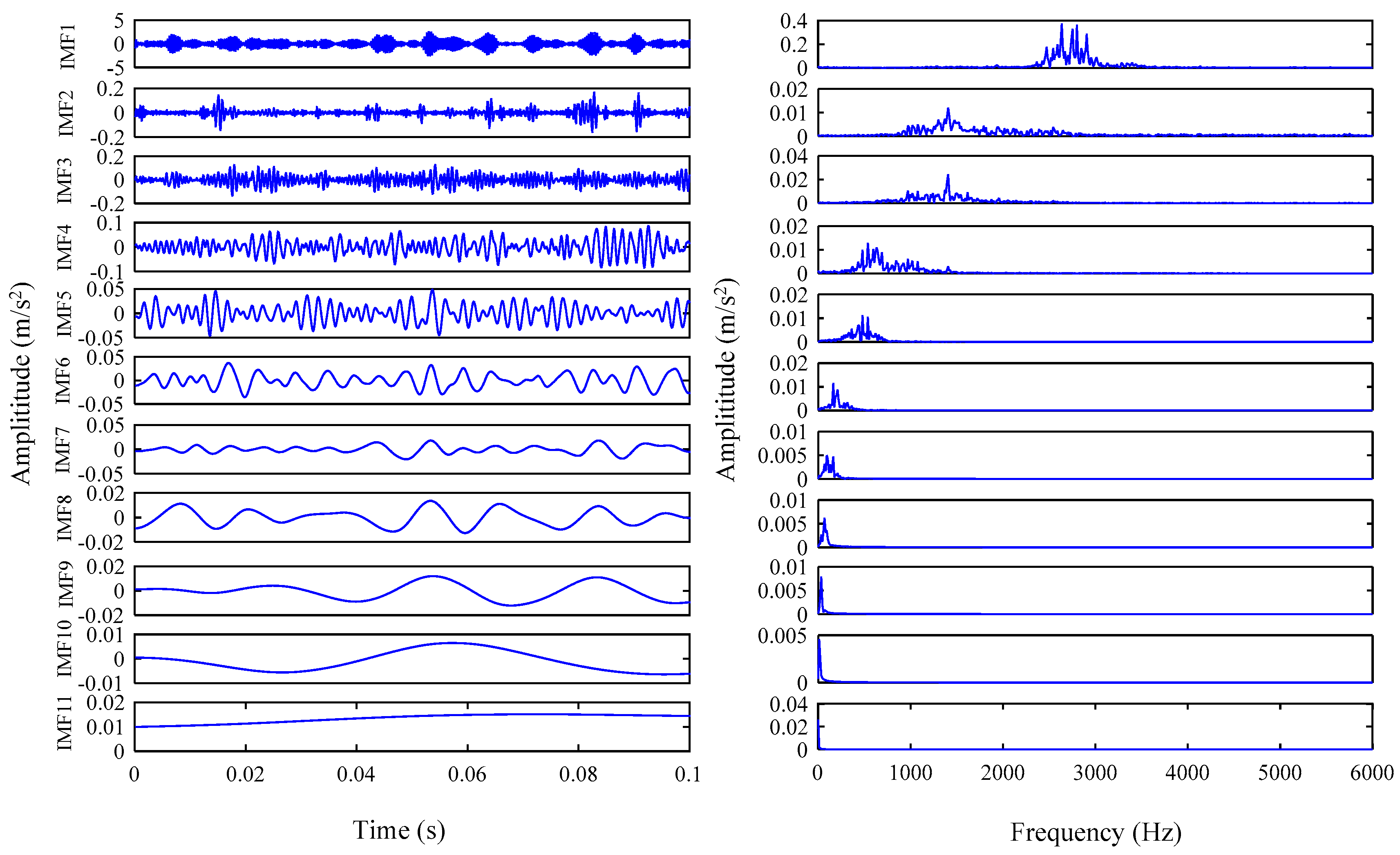
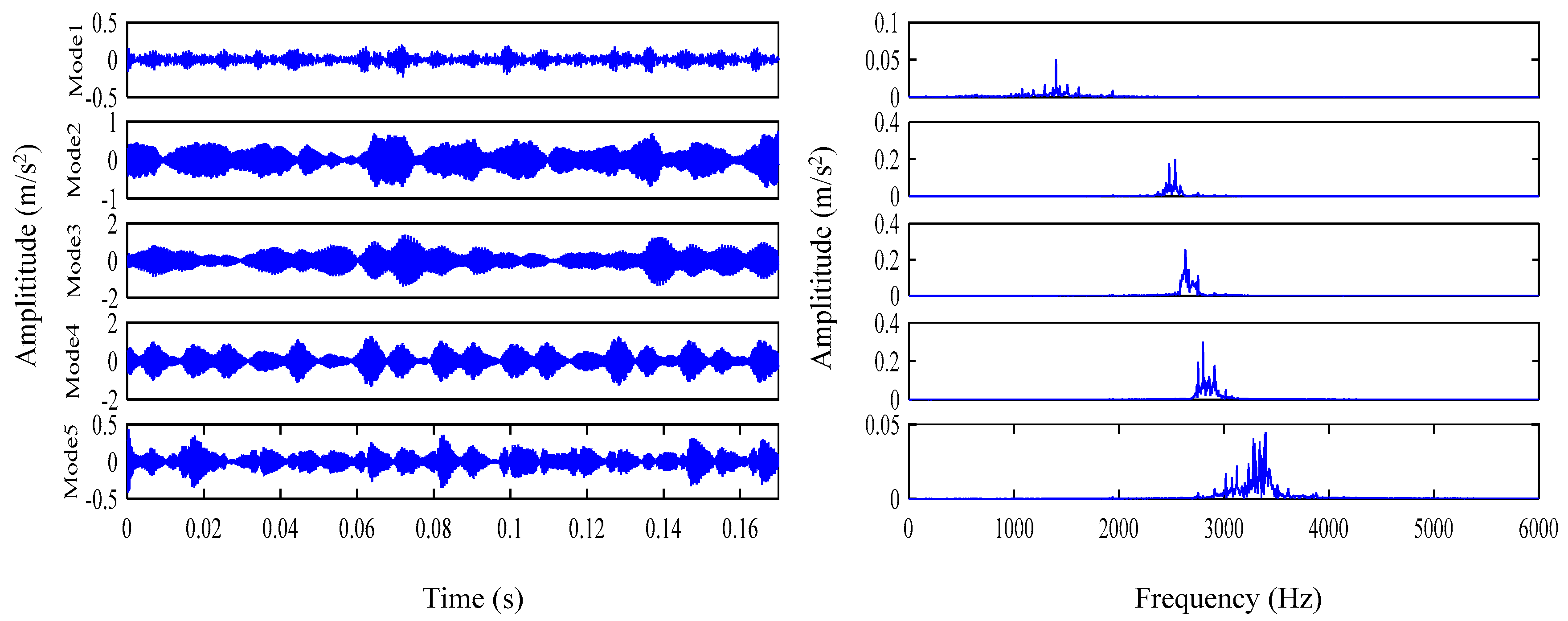
- Decompose the original vibration signal into a set of the IMFs by the improved VMD;
- Calculate the envelope entropy, kurtosis and correlation coefficients of all IMF components;
- Select the reconstructed IMF component with the largest kurtosis value, the highest correlation and the smallest envelope entropy as the optimal component;
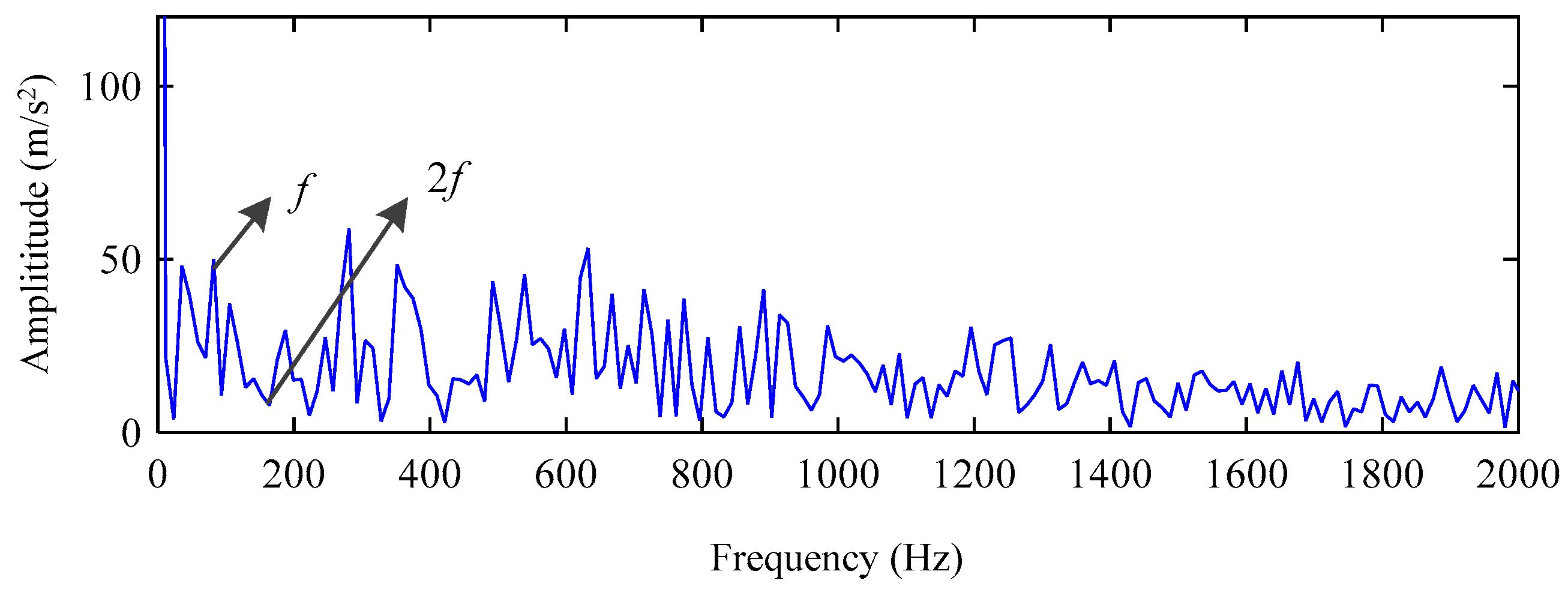
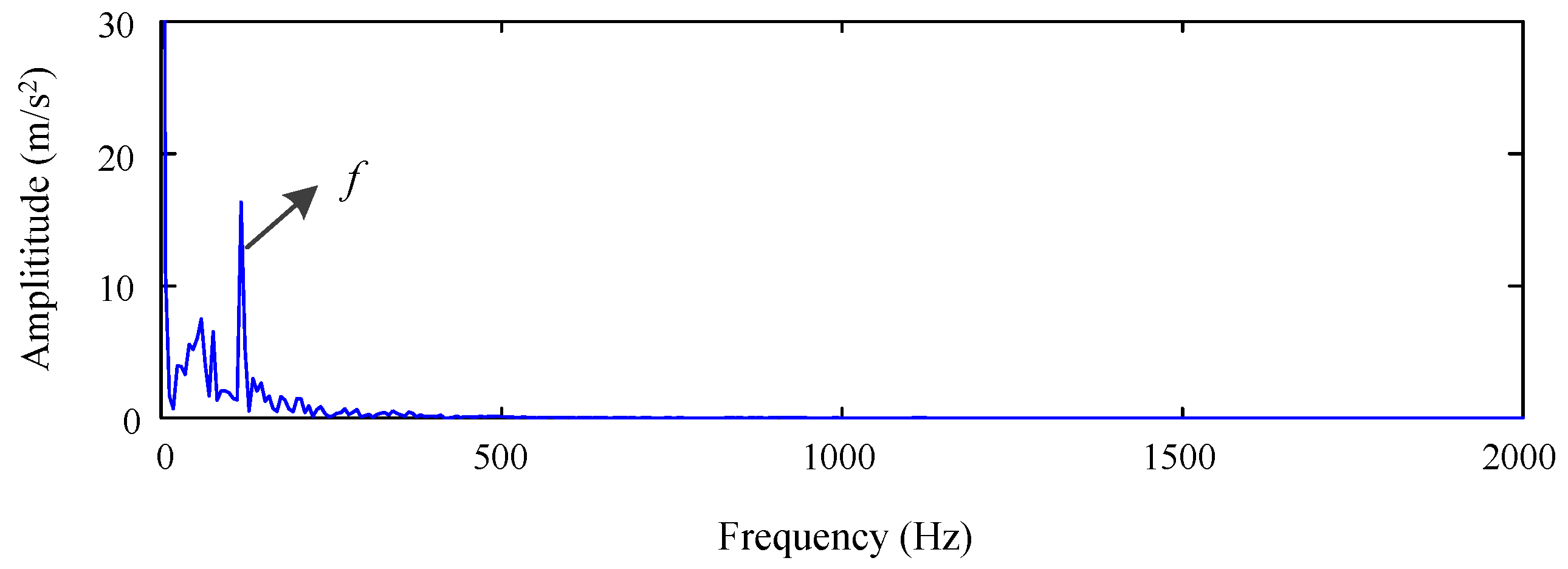
- Implement the spectrum analysis and compare the fault feature frequency in the envelope spectrum with the theoretical value of the bearing fault and determine the fault.
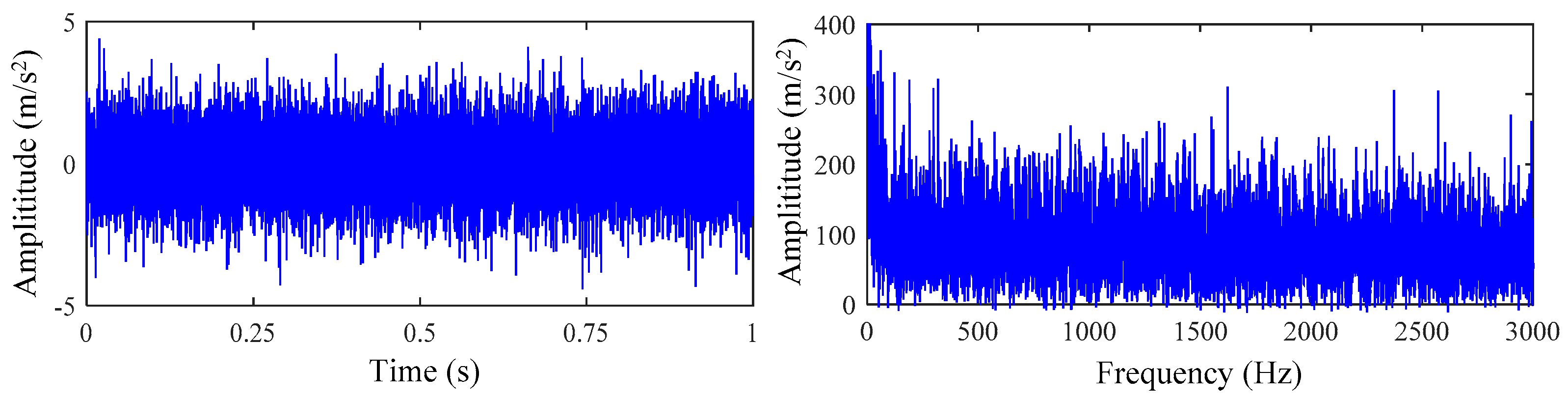
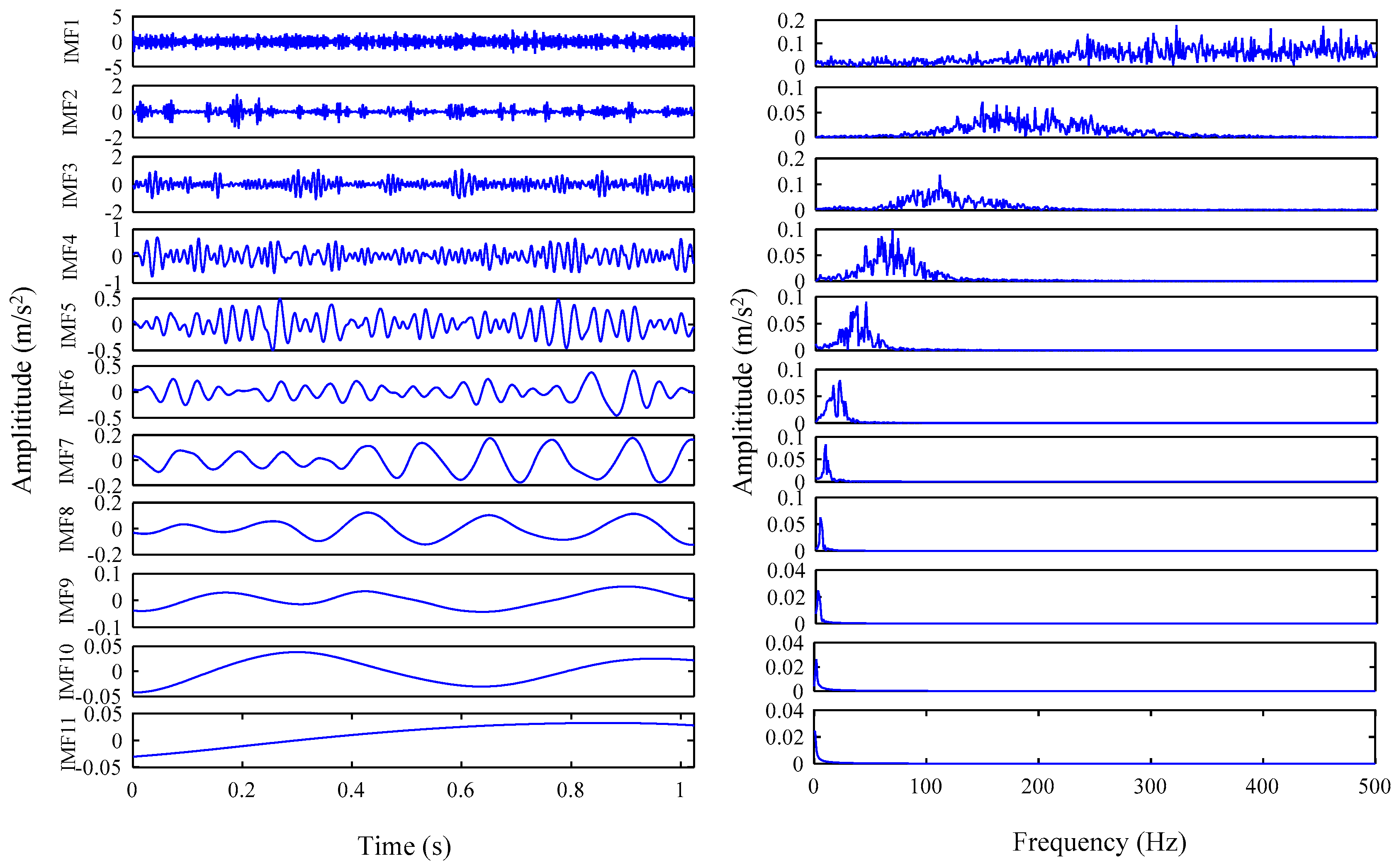
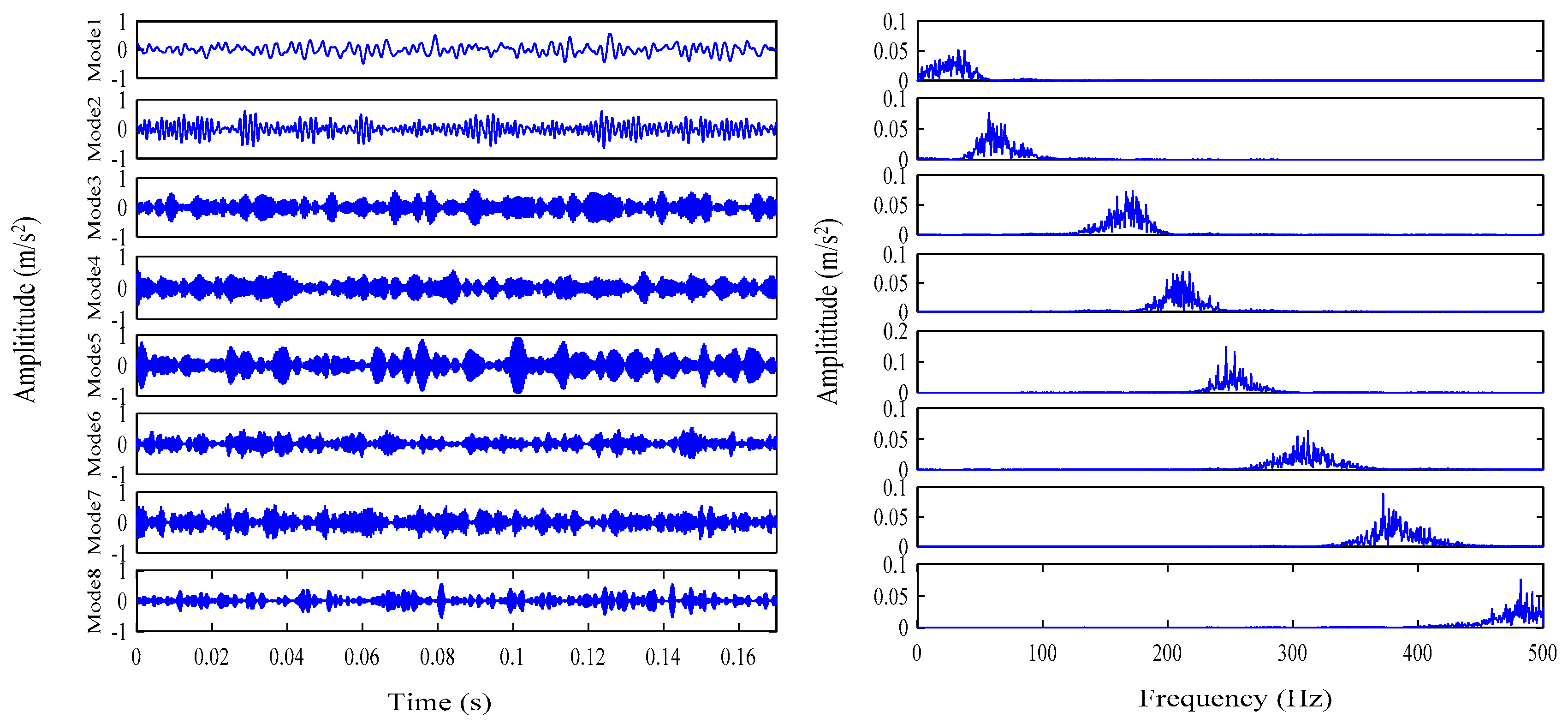
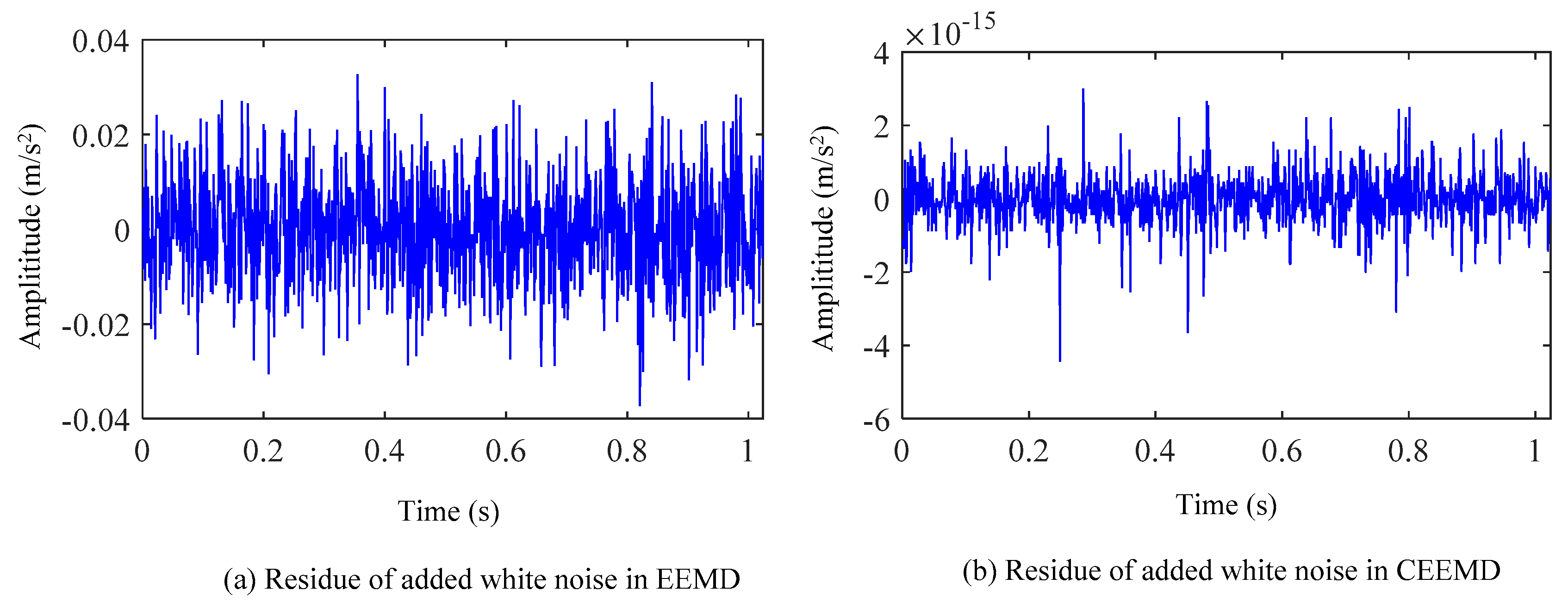
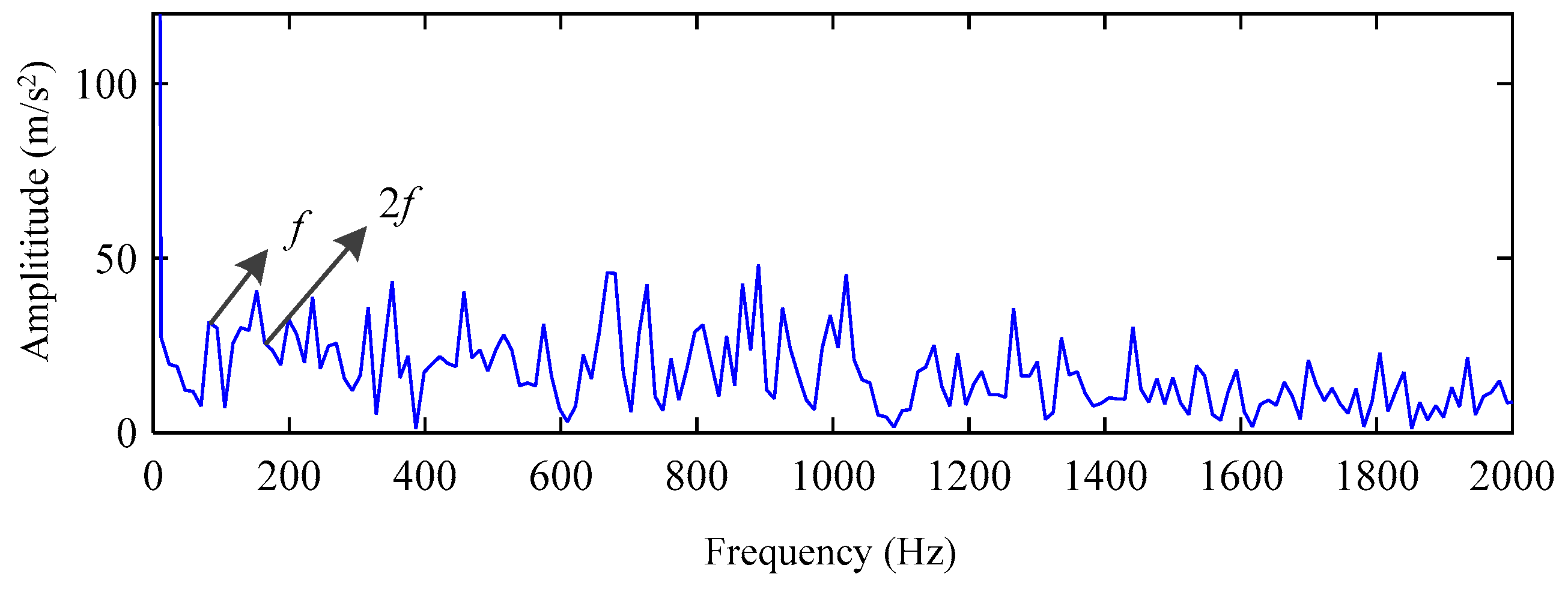
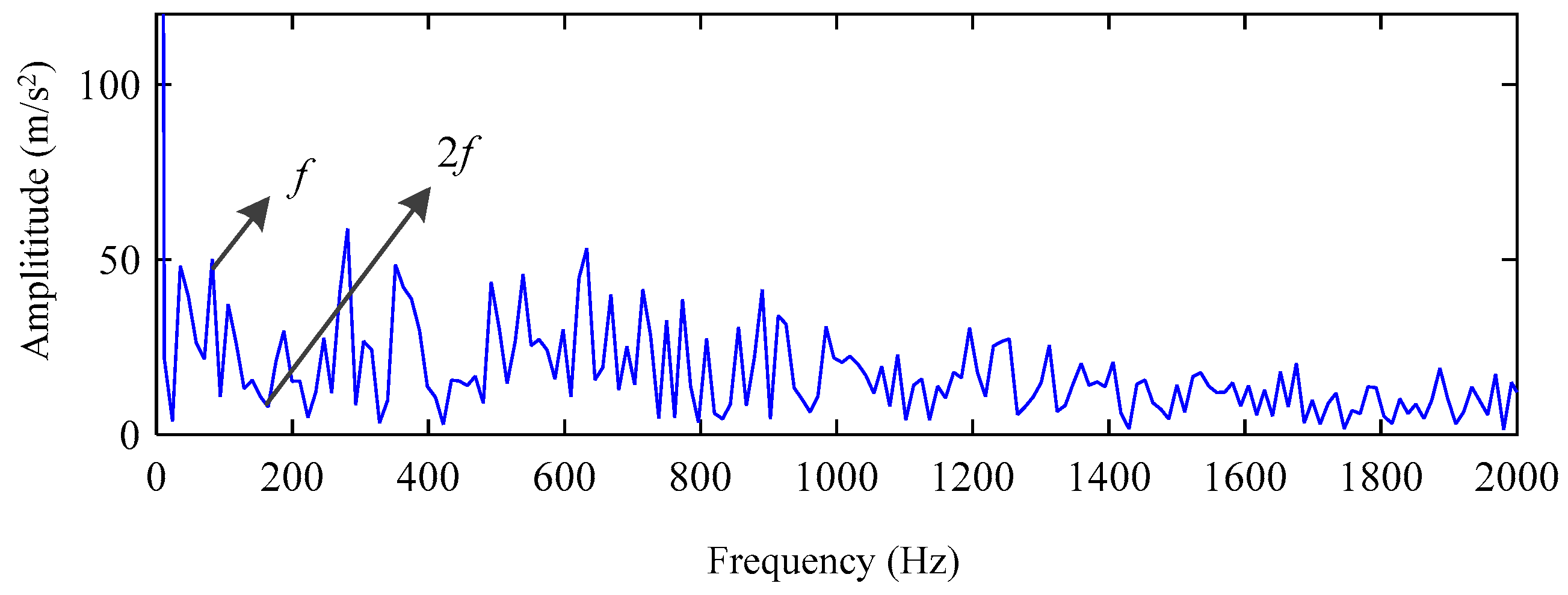
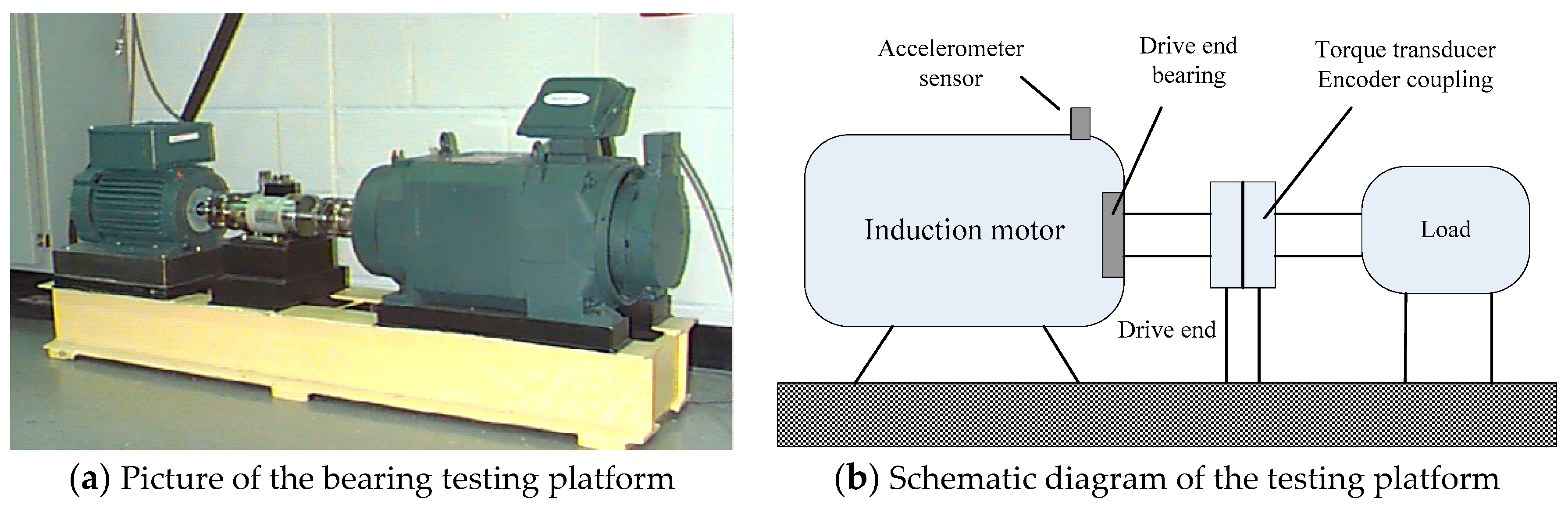
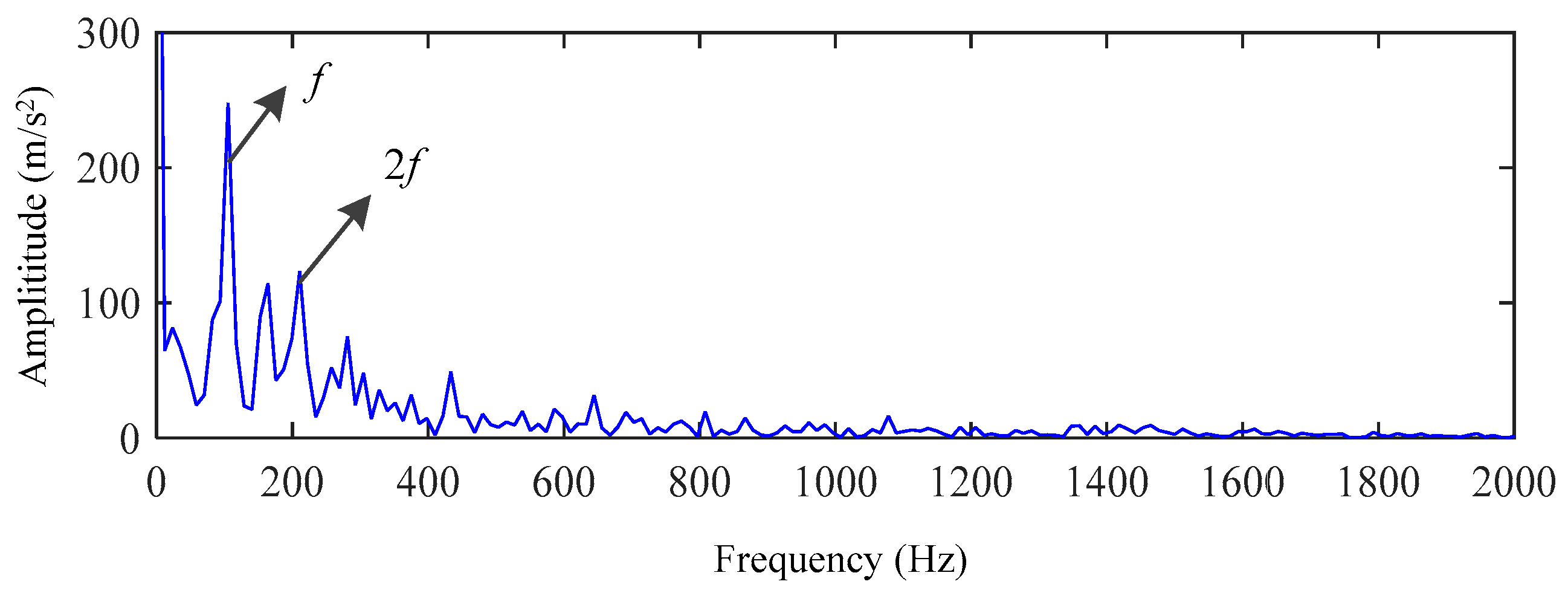
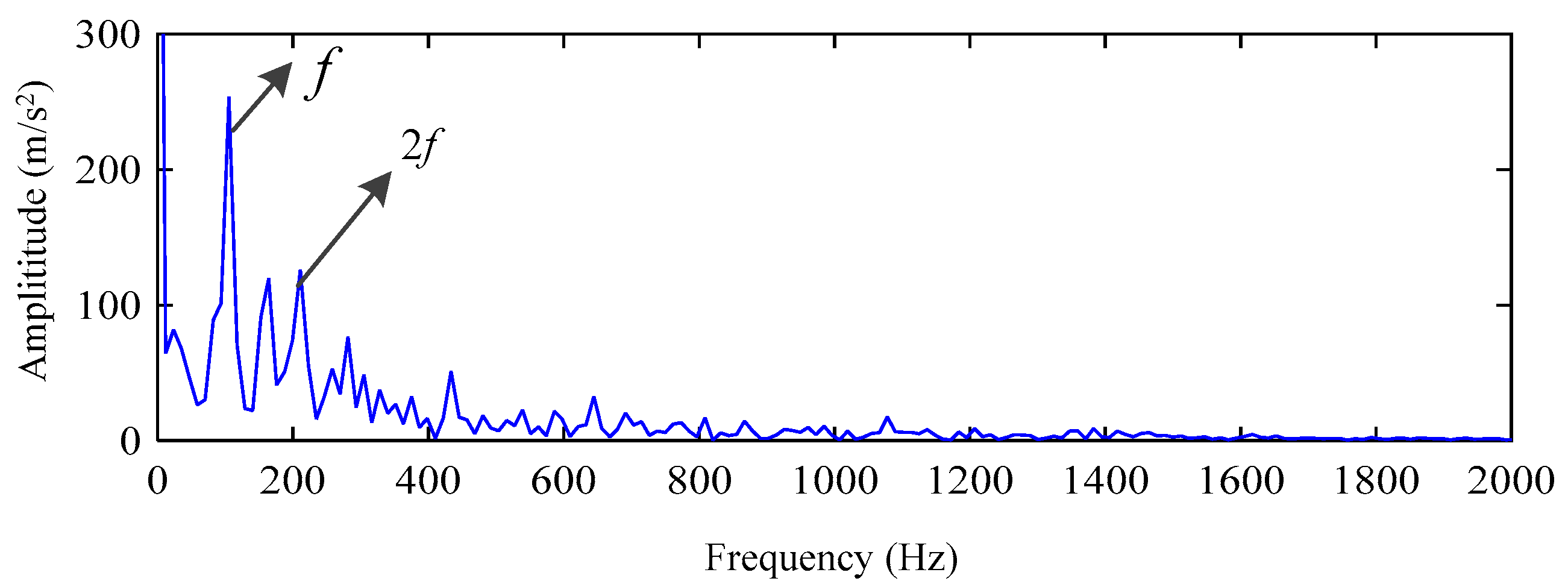
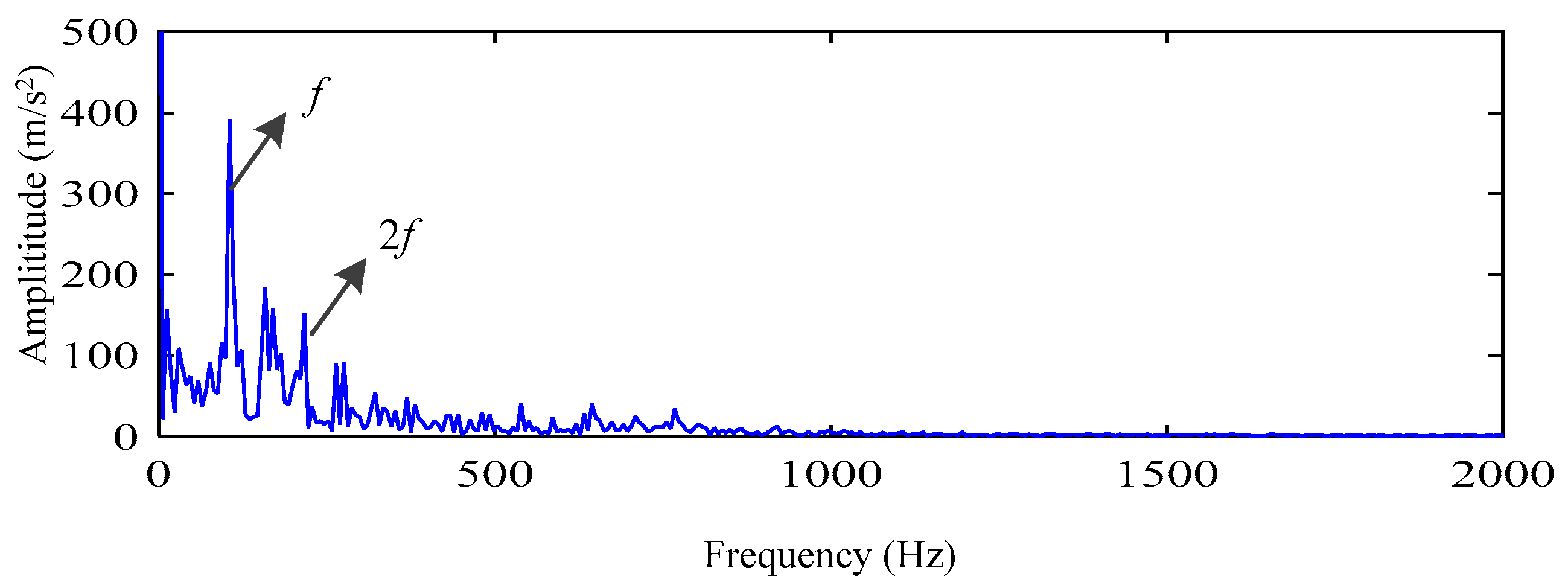
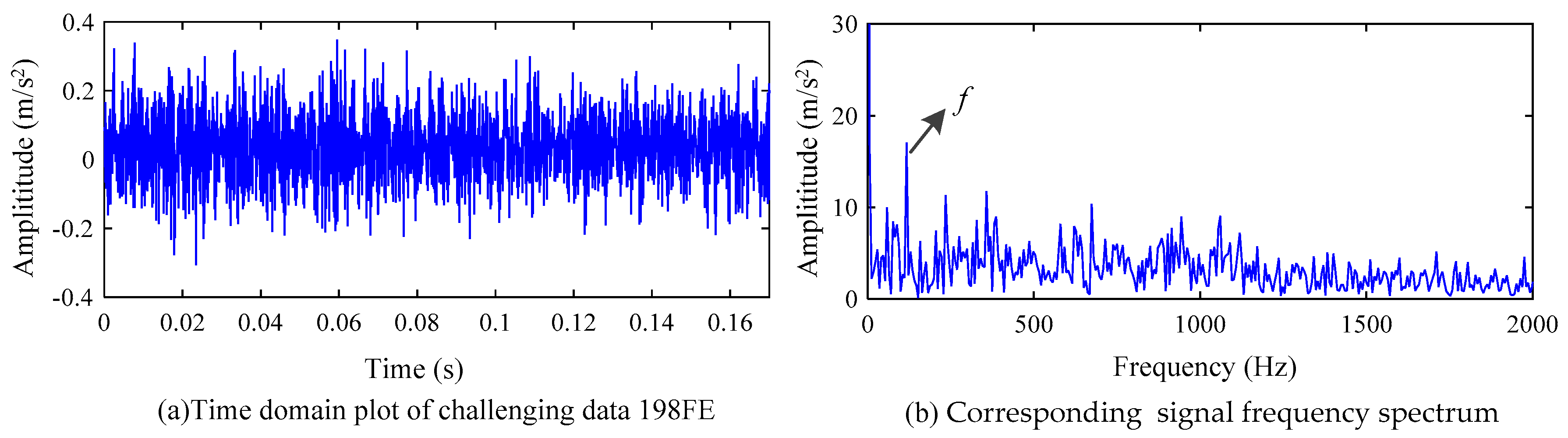
5. Experimental Results and Analysis
5.1. Simulation Analysis Using IVMD Algorithm
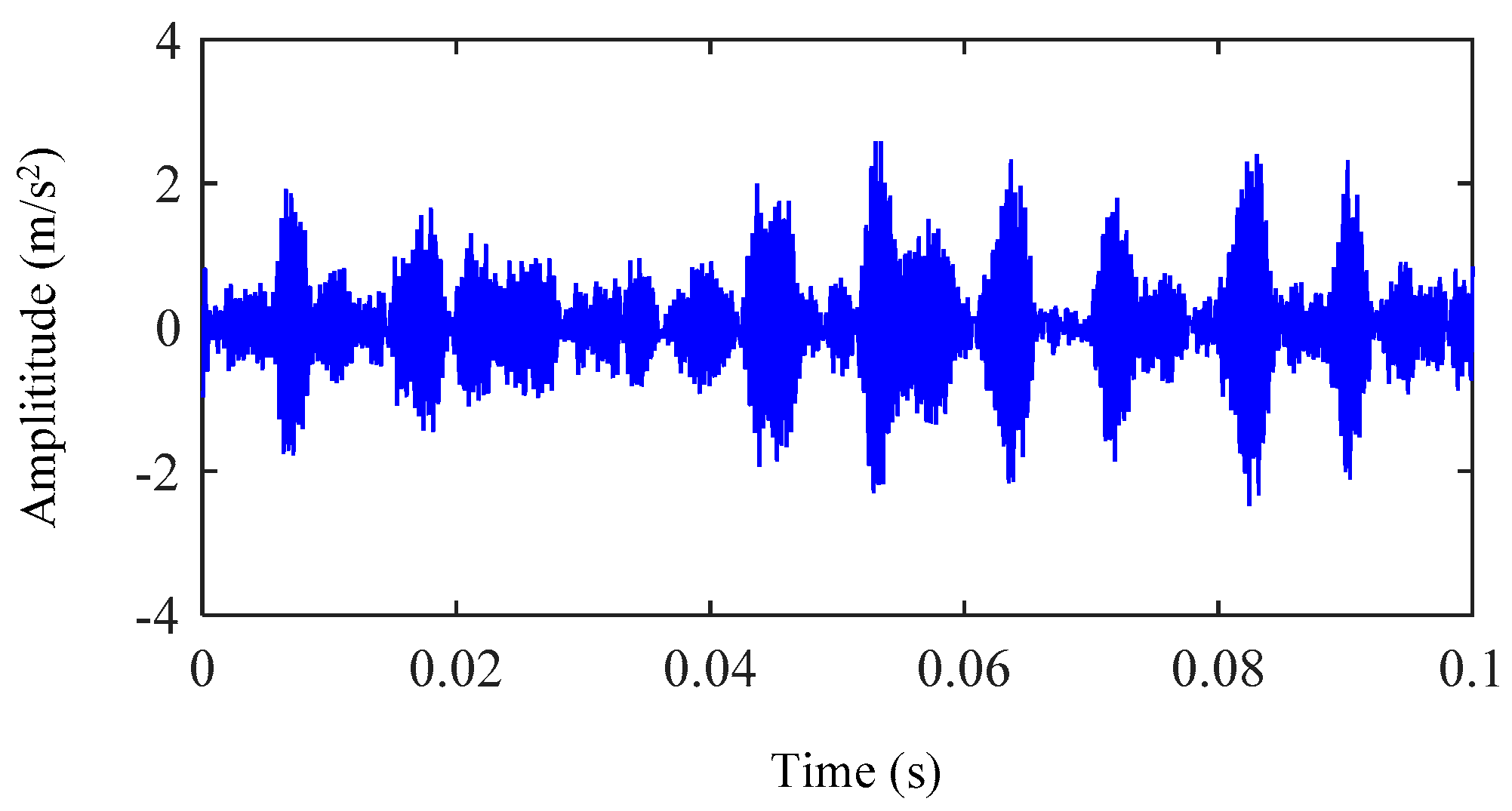
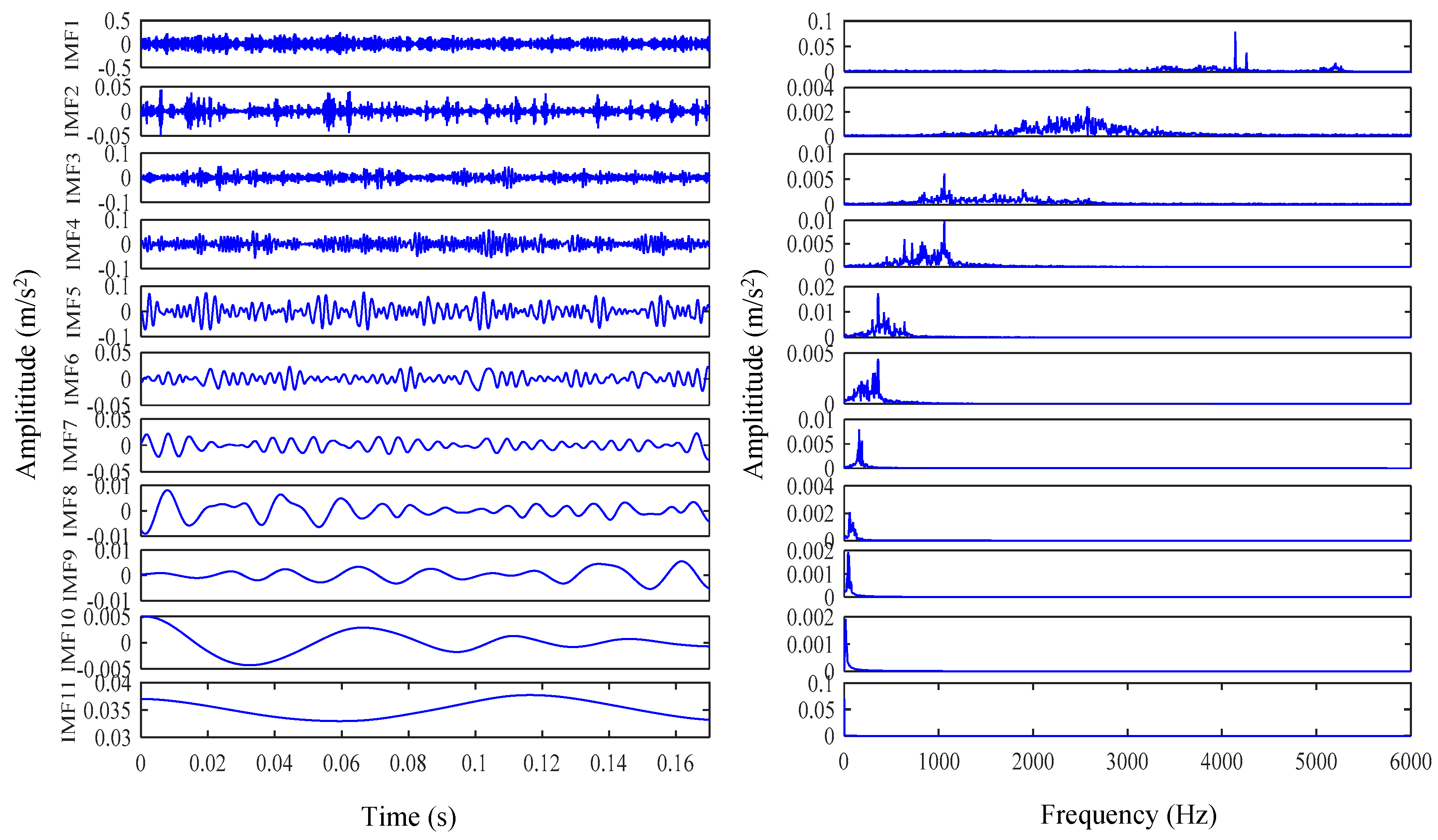
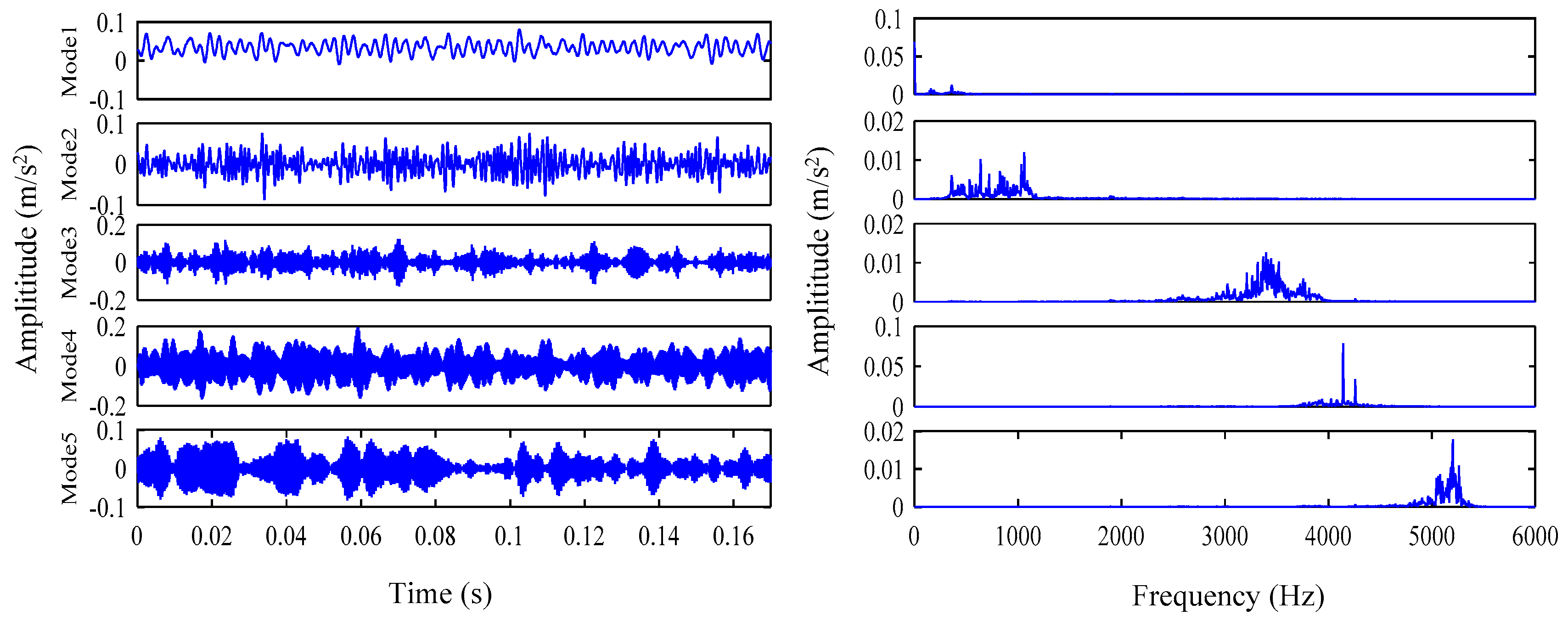
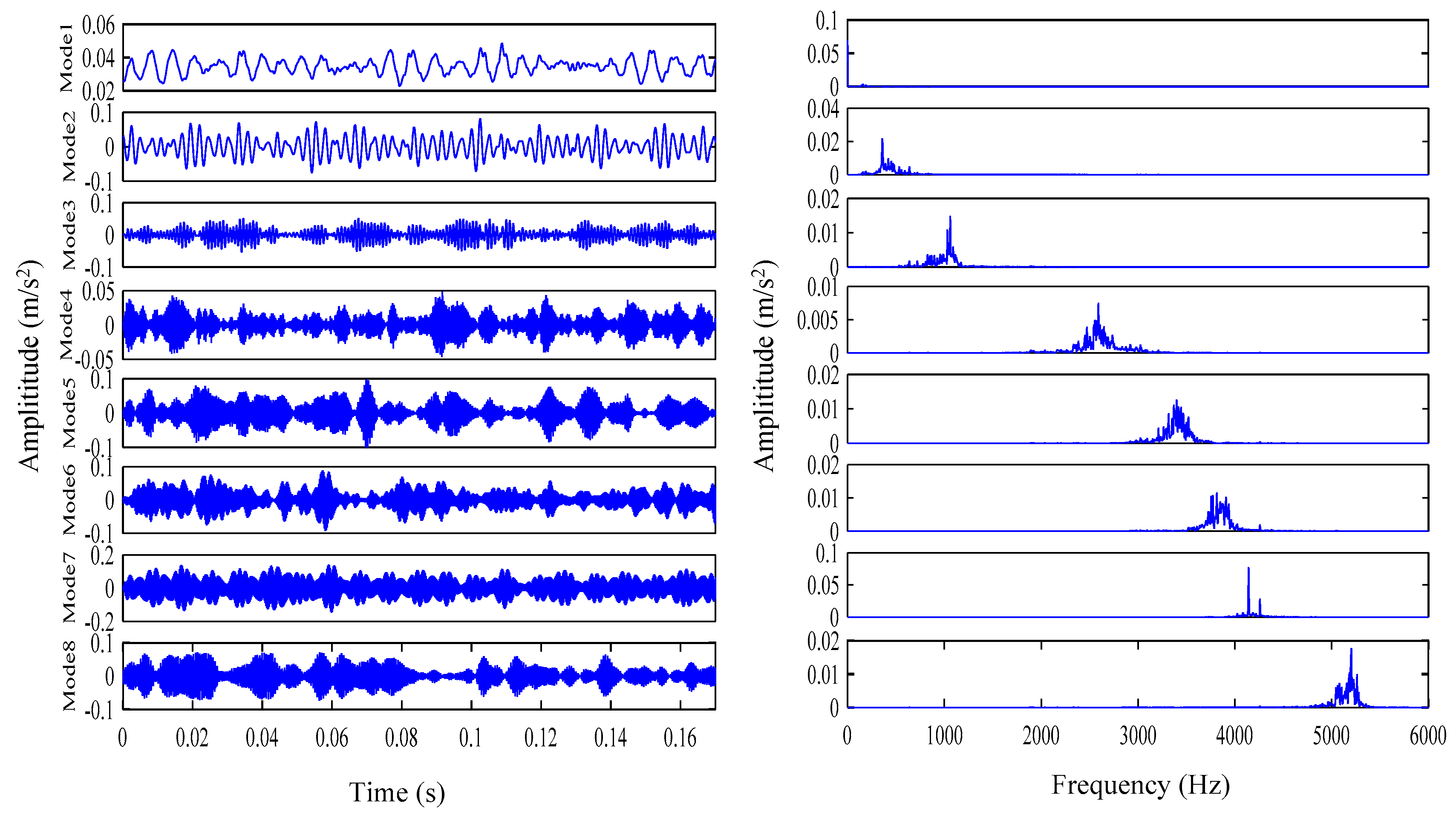
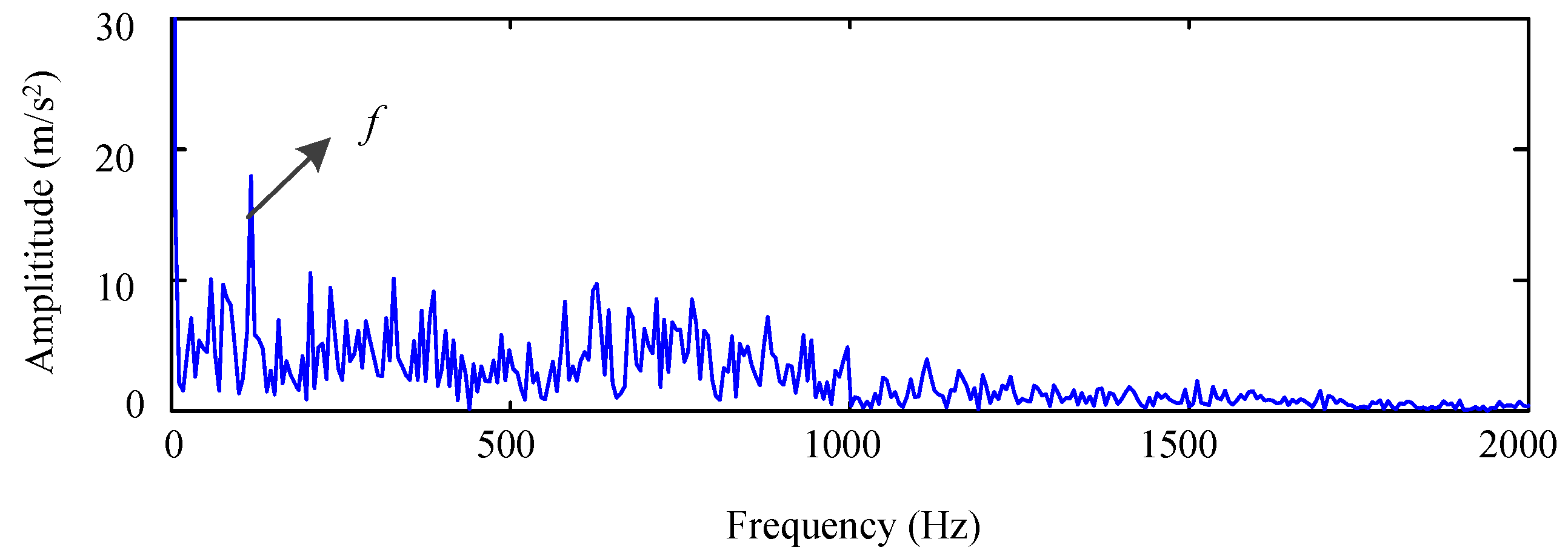
5.2. Actual Vibration Signal Analysis
5.3. Challenging Data Analysis
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Jiang, H.; Li, X.; Shao, H.; Zhao, K. Intelligent fault diagnosis of rolling bearings using an improved deep recurrent neural network. Meas. Sci. Technol. 2018, 29, 065107. [Google Scholar] [CrossRef]
- Xiong, S.; Zhou, H.; He, S.; Zhang, L.; Xia, Q.; Xuan, J.; Shi, T. A novel end-to-end fault diagnosis approach for rolling bearings by integrating wavelet packet transform into convolutional neural network structures. Sensors 2020, 20, 4965. [Google Scholar] [CrossRef] [PubMed]
- Yan, X.; Liu, Y.; Jia, M.; Zhu, Y. A multi-stage hybrid fault diagnosis approach for rolling element bearing under various working conditions. IEEE Access 2019, 7, 138426–138441. [Google Scholar] [CrossRef]
- Chen, F.; Cheng, M.; Tang, B.; Xiao, W.; Chen, B.; Shi, X. A novel optimized multi-kernel relevance vector machine with selected sensitive features and its application in early fault diagnosis for rolling bearings. Measurement 2020, 156, 107583. [Google Scholar] [CrossRef]
- Zhao, X.; Jia, M. Fault diagnosis of rolling bearing based on feature reduction with global-local margin Fisher analysis. Neurocomputing 2018, 315, 447–464. [Google Scholar] [CrossRef]
- Chaabi, L.; Lemzadmi, A.; Djebala, A.; Bouhalais, M.L.; Ouelaa, N. Fault diagnosis of rolling bearings in non-stationary running conditions using improved CEEMDAN and multivariate denoising based on wavelet and principal component analyses. Int. J. Adv. Manuf. Technol. 2020, 107, 3859–3873. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Dong, G.; Chen, J. Noise resistant time frequency analysis and application in fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2012, 33, 212–236. [Google Scholar] [CrossRef]
- Guo, J.; Zhen, D.; Li, H.; Shi, Z.; Gu, F.; Ball, A.D. Fault feature extraction for rolling element bearing diagnosis based on a multi-stage noise reduction method. Measurement 2019, 139, 226–235. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Zhao, Y.; Yi, C.; Tsui, K.L.; Lin, J. Sparsity guided empirical wavelet transform for fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2018, 101, 292–308. [Google Scholar] [CrossRef]
- Singh, J.; Darpe, A.K.; Singh, S.P. Rolling element bearing fault diagnosis based on over-complete rational dilation wavelet transform and auto-correlation of analytic energy operator. Mech. Syst. Signal Process. 2018, 100, 662–693. [Google Scholar] [CrossRef]
- Wang, C.; Gan, M. Fault feature extraction of rolling element bearings based on wavelet packet transform and sparse representation theory. J. Intell. Manuf. 2018, 29, 937–951. [Google Scholar] [CrossRef]
- Tong, Q.; Cao, J.; Han, B.; Zhang, X.; Nie, Z.; Wang, J.; Lin, Y.; Zhang, W. A fault diagnosis approach for rolling element bearings based on RSGWPT-LCD bilayer screening and extreme learning machine. IEEE Access 2017, 5, 5515–5530. [Google Scholar] [CrossRef]
- Huang, W.; Kong, F.; Zhao, X. Spur bevel gearbox fault diagnosis using wavelet packet transform and rough set theory. J. Intell. Manuf. 2018, 29, 1257–1271. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, N.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Xu, Y.; Cai, Z.; Ding, K. An enhanced bearing fault diagnosis method based on TVF-EMD and a high-order energy operator. Meas. Sci. Technol. 2018, 29, 095108. [Google Scholar] [CrossRef]
- Wang, J.; Du, G.; Zhu, Z.; Shen, C.; He, Q. Fault diagnosis of rotating machines based on the EMD manifold. Mech. Syst. Signal Process. 2020, 135, 106443. [Google Scholar] [CrossRef]
- Abdelkader, R.; Kaddour, A.; Derouiche, Z. Enhancement of rolling bearing fault diagnosis based on improvement of empirical mode decomposition denoising method. Int. J. Adv. Manuf. Technol. 2018, 97, 3099–3117. [Google Scholar] [CrossRef]
- Ye, X.; Hu, Y.; Shen, J.; Feng, R.; Zhai, G. An improved empirical mode decomposition based on adaptive weighted rational quartic spline for rolling bearing fault diagnosis. IEEE Access 2020, 8, 123813–123827. [Google Scholar] [CrossRef]
- Fan, H.; Shao, S.; Zhang, X.; Wan, X.; Cao, X.; Ma, H. Intelligent fault diagnosis of rolling bearing using FCM clustering of EMD-PWVD vibration images. IEEE Access 2020, 8, 145194–145206. [Google Scholar] [CrossRef]
- Mohanty, S.; Gupta, K.K.; Raju, K.S. Hurst based vibro-acoustic feature extraction of bearing using EMD and VMD. Measurement 2018, 117, 200–220. [Google Scholar] [CrossRef]
- Niu, Y.; Fei, J.; Li, Y.; Wu, D. A novel fault diagnosis method based on EMD, cyclostationary, SK and TPTSR. J. Mech. Sci. Technol. 2020, 34, 1925–1935. [Google Scholar] [CrossRef]
- Han, D.; Zhao, N.; Shi, P. Gear fault feature extraction and diagnosis method under different load excitation based on EMD, PSO-SVM and fractal box dimension. J. Mech. Sci. Technol. 2019, 33, 487–494. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Jiang, F.; Zhu, Z.; Li, W.; Ren, Y.; Zhou, G.; Chang, Y. A fusion feature extraction method using EEMD and correlation coefficient analysis for bearing fault diagnosis. Appl. Sci. 2018, 8, 1621. [Google Scholar] [CrossRef] [Green Version]
- Han, T.; Liu, Q.; Zhang, L.; Tan, A.C. Fault feature extraction of low speed roller bearing based on Teager energy operator and CEEMD. Measurement 2019, 138, 400–408. [Google Scholar] [CrossRef]
- Liu, F.; Gao, J.; Liu, H. The feature extraction and diagnosis of rolling bearing based on CEEMD and LDWPSO-PNN. IEEE Access 2020, 8, 19810–19819. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Wang, Y.; Markert, R.; Xiang, J.; Zheng, W. Research on variational mode decomposition and its application in detecting rub-impact fault of the rotor system. Mech. Syst. Signal Process. 2015, 60, 243–251. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, H.; Xu, J.; Guo, C.; Deng, W. Research on a fault diagnosis method of rolling bearings using variation mode decomposition and deep belief network. J. Mech. Sci. Technol. 2019, 33, 4165–4172. [Google Scholar] [CrossRef]
- Eusuff, M.; Lansey, K.; Pasha, F. Shuffled frog-leaping algorithm: A memetic meta-heuristic for discrete optimization. Eng. Optimiz. 2006, 38, 129–154. [Google Scholar] [CrossRef]
- Eusuff, M.M.; Lansey, K.E. Optimization of water distribution network design using the shuffled frog leaping algorithm. J. Water. Res. Plan. Manag. 2003, 129, 210–225. [Google Scholar] [CrossRef]
- Pérez-Delgado, M.L. Color image quantization using the shuffled-frog leaping algorithm. Eng. Appl. Artif. Intel. 2019, 79, 142–158. [Google Scholar] [CrossRef]
- Venkatesan, T.; Sanavullah, M.Y. SFLA approach to solve PBUC problem with emission limitation. Int. J. Elec. Power 2013, 46, 1–9. [Google Scholar] [CrossRef]
- Sun, J.; Xiao, Q.; Wen, J.; Wang, F. Natural gas pipeline small leakage feature extraction and recognition based on LMD envelope spectrum entropy and SVM. Measurement 2014, 55, 434–443. [Google Scholar] [CrossRef]
- Sawalhi, N.; Randall, R.; Endo, H. The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis. Mech. Syst. Signal Process. 2007, 21, 2616–2633. [Google Scholar] [CrossRef]
- Wang, S.; Huang, W.; Zhu, Z.K. Transient modeling and parameter identification based on wavelet and correlation filtering for rotating machine fault diagnosis. Mech. Syst. Signal Process. 2011, 25, 1299–1320. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, C.; Wen, P.; Wang, M.; Zhao, J. Comprehensive performance evaluation of low-carbon modified asphalt based on efficacy coefficient method. J. Clean. Prod. 2018, 203, 633–644. [Google Scholar] [CrossRef]
- Case Western Reserve University Bearing Data Center. Seeded Fault Test Data. 2012. Available online: https://csegroups.case.edu/bearingdatacenter/home (accessed on 18 January 2019).
- Li, X.; Zhang, W.; Ding, Q. Cross-domain fault diagnosis of rolling element bearings using deep generative neural networks. IEEE Trans. Ind. Electron. 2018, 66, 5525–5534. [Google Scholar] [CrossRef]
- Smith, W.A.; Randall, R.B. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mech. Syst. Signal Process. 2015, 64, 100–131. [Google Scholar] [CrossRef]

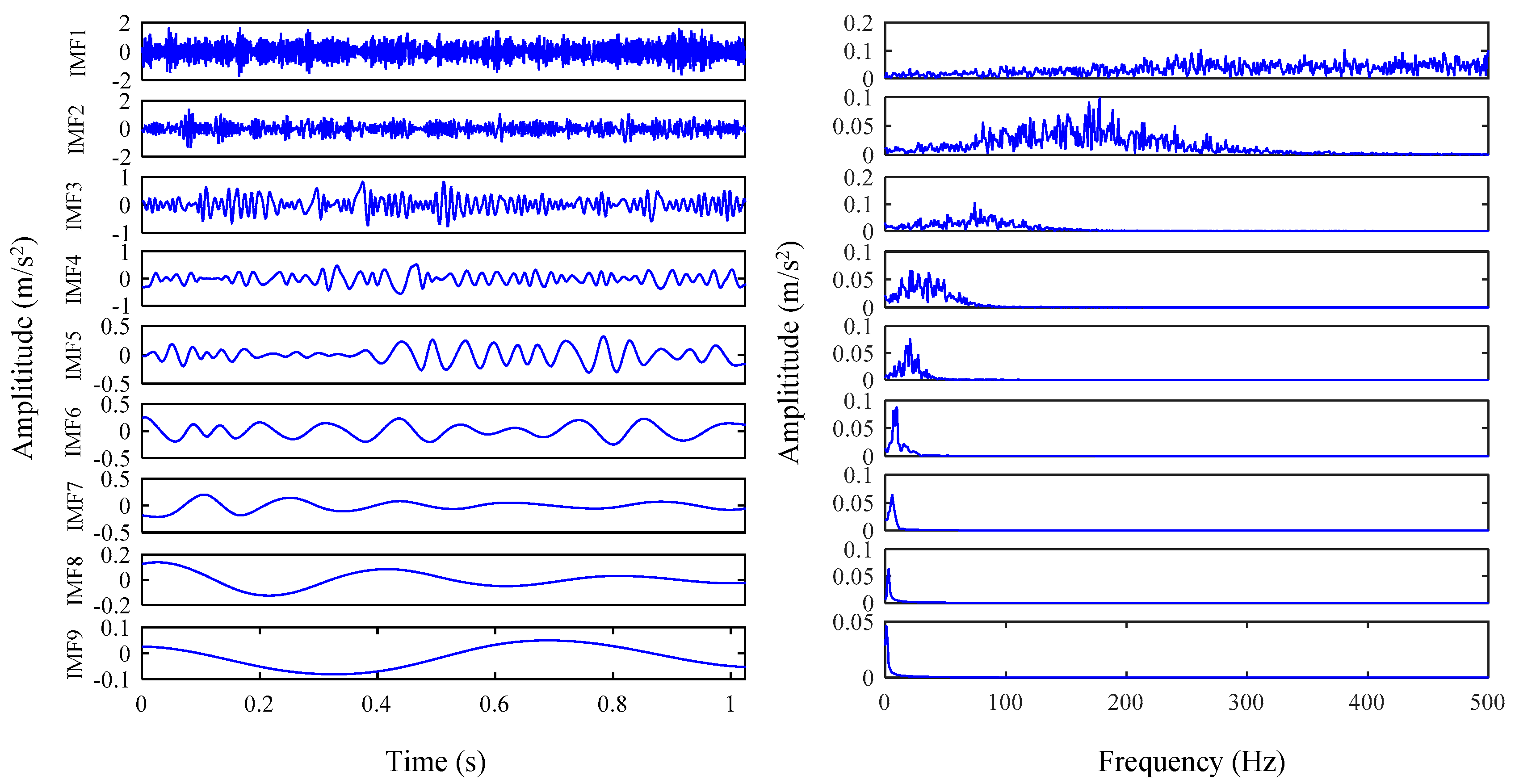
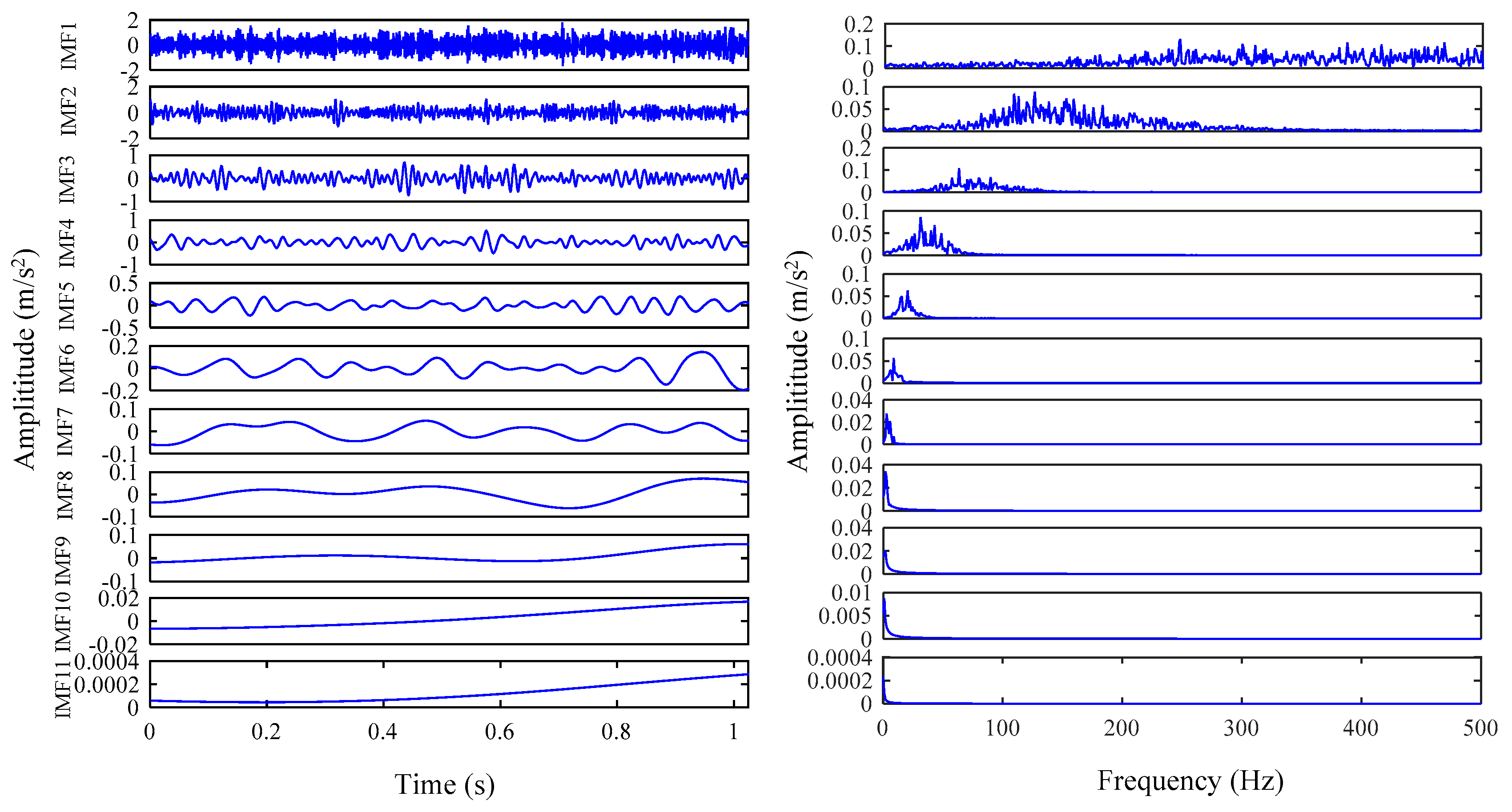








| Mode Number | Efficacy Coefficient | ||
|---|---|---|---|
| ηK (Kurtosis) | ηC (Correlation Degree) | ηE (Envelope Entropy) | |
| 1 | 3.4182 | 0.3075 | 3.2476 |
| 2 | 3.2029 | 0.3560 | 3.2406 |
| 3 | 2.6970 | 0.4076 | 3.2577 |
| 4 | 2.4257 | 0.4114 | 3.2703 |
| 5 | 3.6255 | 0.4880 | 3.2486 |
| 6 | 2.8788 | 0.3777 | 3.2474 |
| 7 | 2.6286 | 0.4042 | 3.2588 |
| 8 | 3.2790 | 0.3026 | 3.2443 |
| Mode Number | Efficacy Coefficient | ||
|---|---|---|---|
| ηK (Kurtosis) | ηC (Correlation Degree) | ηE (Envelope Entropy) | |
| 1 | 3.5669 | 0.1121 | 3.2413 |
| 2 | 2.6746 | 0.4765 | 3.2577 |
| 3 | 3.1393 | 0.7161 | 3.2524 |
| 4 | 3.1648 | 0.6993 | 3.2296 |
| 5 | 3.8560 | 0.2220 | 3.2358 |
| Mode Number | Efficacy Coefficient | ||
|---|---|---|---|
| ηK (Kurtosis) | ηC (Correlation Degree) | ηE (Envelope Entropy) | |
| 1 | 2.4683 | 0. 0910 | 3.3077 |
| 2 | 2.4792 | 0.1832 | 3.2730 |
| 3 | 2.9384 | 0.0134 | 3.2527 |
| 4 | 3.6555 | 0.0885 | 3.2390 |
| 5 | 2.7657 | 0.2204 | 3.2524 |
| 6 | 2.7522 | 0.2287 | 3.2509 |
| 7 | 1.8823 | 0.6227 | 3.2961 |
| 8 | 2.8763 | 0.2941 | 3.2673 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, G.; Tong, Q.; Zhang, Y.; Liu, R.; Li, W.; Cao, J.; Lin, Y. An Improved Variational Mode Decomposition and Its Application on Fault Feature Extraction of Rolling Element Bearing. Energies 2021, 14, 1079. https://doi.org/10.3390/en14041079
An G, Tong Q, Zhang Y, Liu R, Li W, Cao J, Lin Y. An Improved Variational Mode Decomposition and Its Application on Fault Feature Extraction of Rolling Element Bearing. Energies. 2021; 14(4):1079. https://doi.org/10.3390/en14041079
Chicago/Turabian StyleAn, Guoping, Qingbin Tong, Yanan Zhang, Ruifang Liu, Weili Li, Junci Cao, and Yuyi Lin. 2021. "An Improved Variational Mode Decomposition and Its Application on Fault Feature Extraction of Rolling Element Bearing" Energies 14, no. 4: 1079. https://doi.org/10.3390/en14041079
APA StyleAn, G., Tong, Q., Zhang, Y., Liu, R., Li, W., Cao, J., & Lin, Y. (2021). An Improved Variational Mode Decomposition and Its Application on Fault Feature Extraction of Rolling Element Bearing. Energies, 14(4), 1079. https://doi.org/10.3390/en14041079






