Dual Two-Level Voltage Source Inverter Virtual Inertia Emulation: A Comparative Study
Abstract
:1. Introduction
2. Model Description
2.1. DTL VSI Configuration
2.2. VSG Method
3. State-Space Modeling of the System
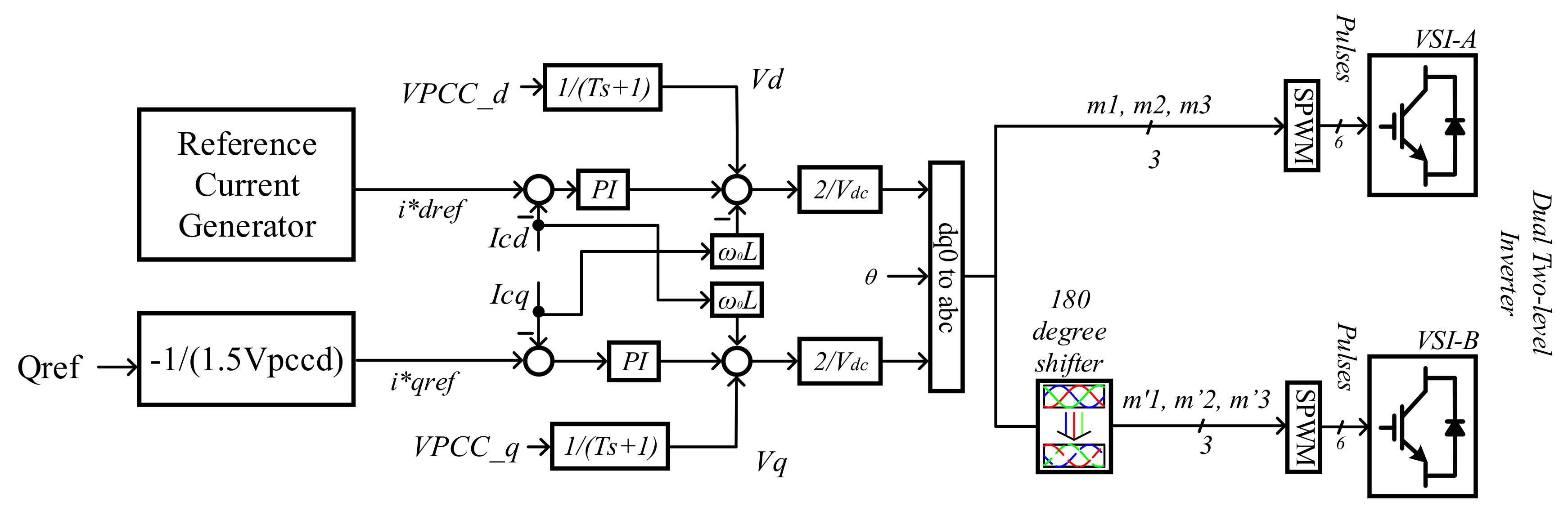
3.1. Current Controller Model
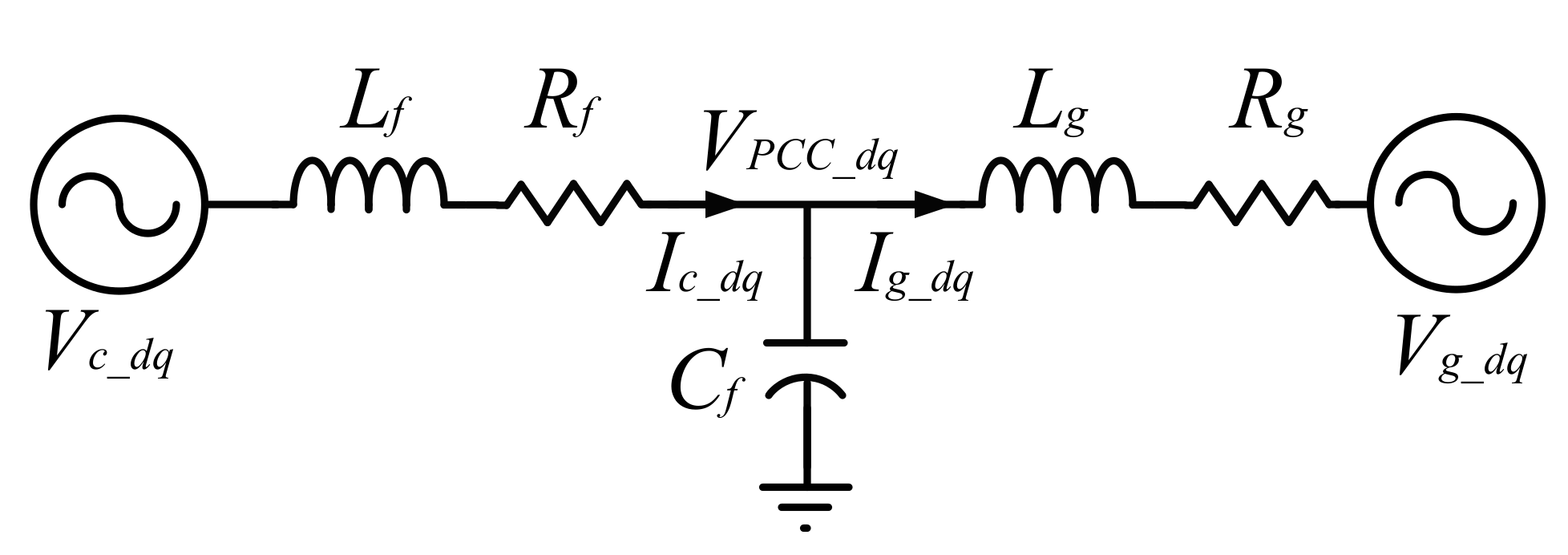
3.2. Equations of the Equivalent Circuit of the TL VSI
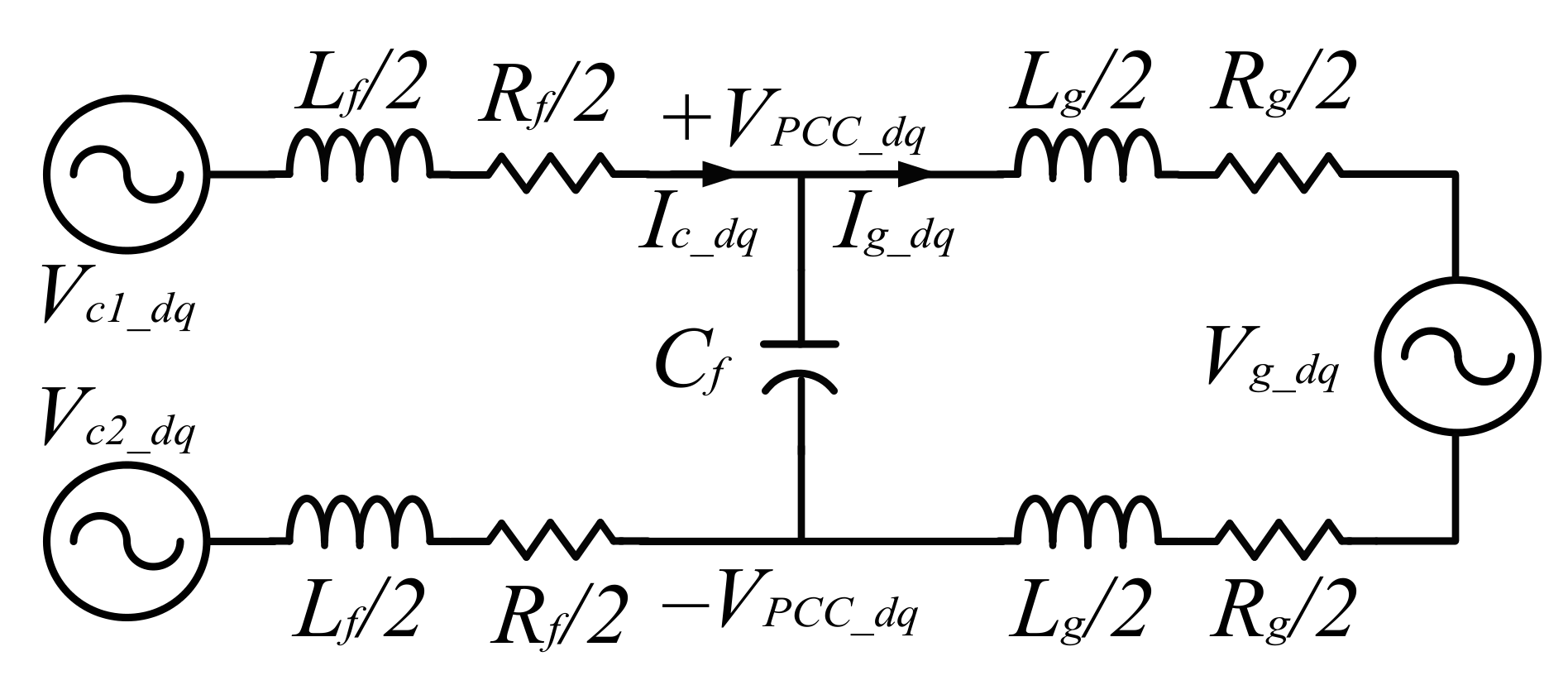
3.3. Equations of the Equivalent Circuit of the DTL VSI
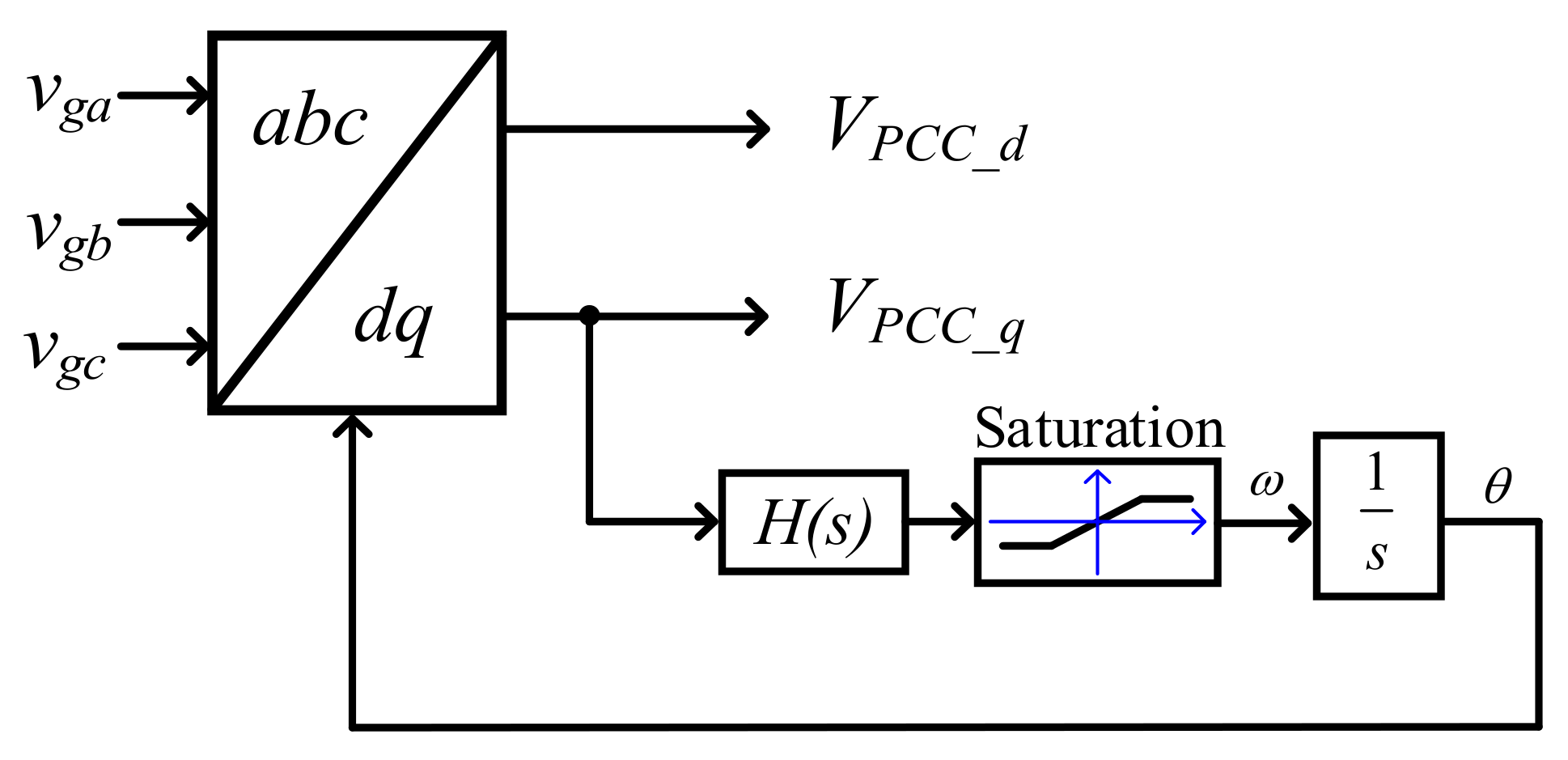
3.4. Phase-Locked Loop
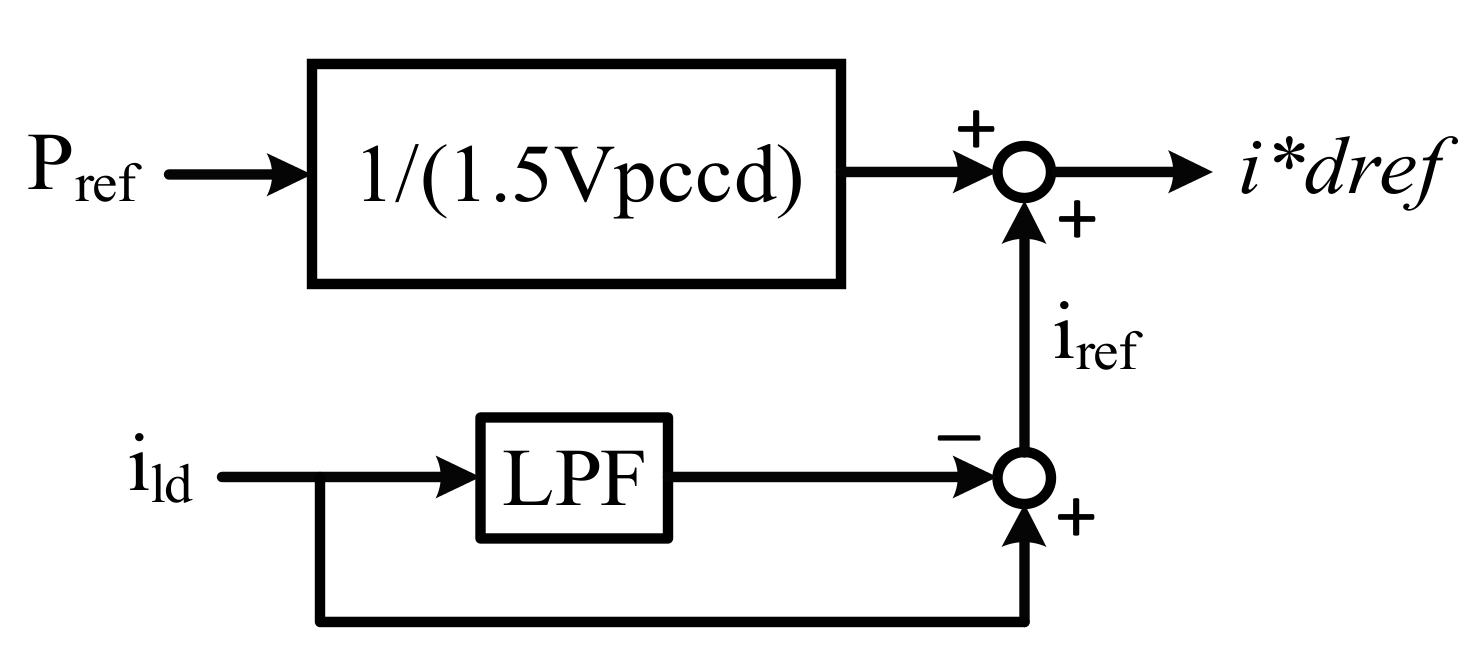
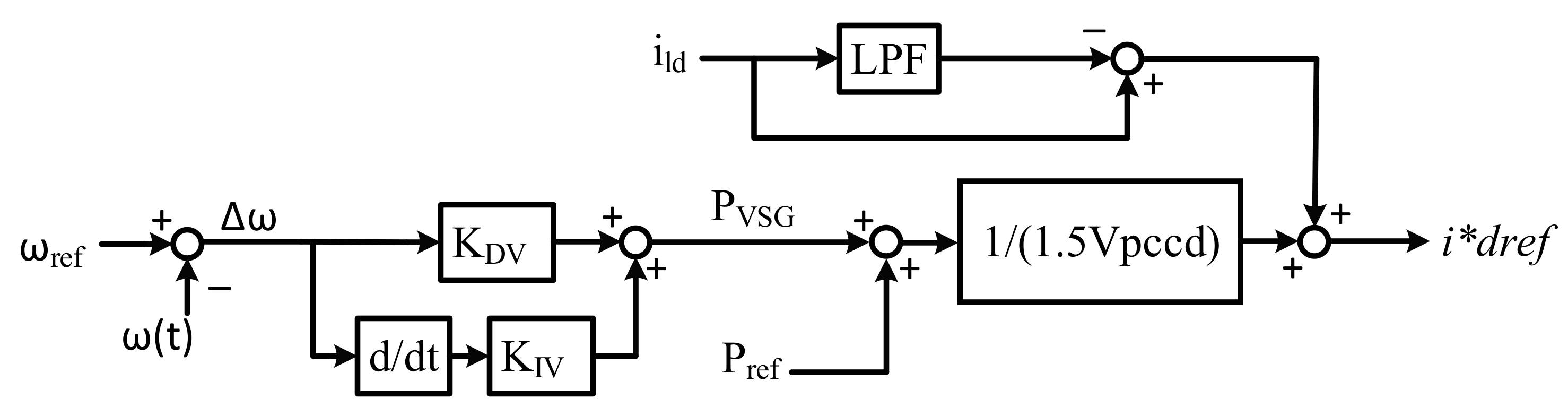
3.5. VSG Controller
4. Small-Signal Modelling and Simulation Verifications
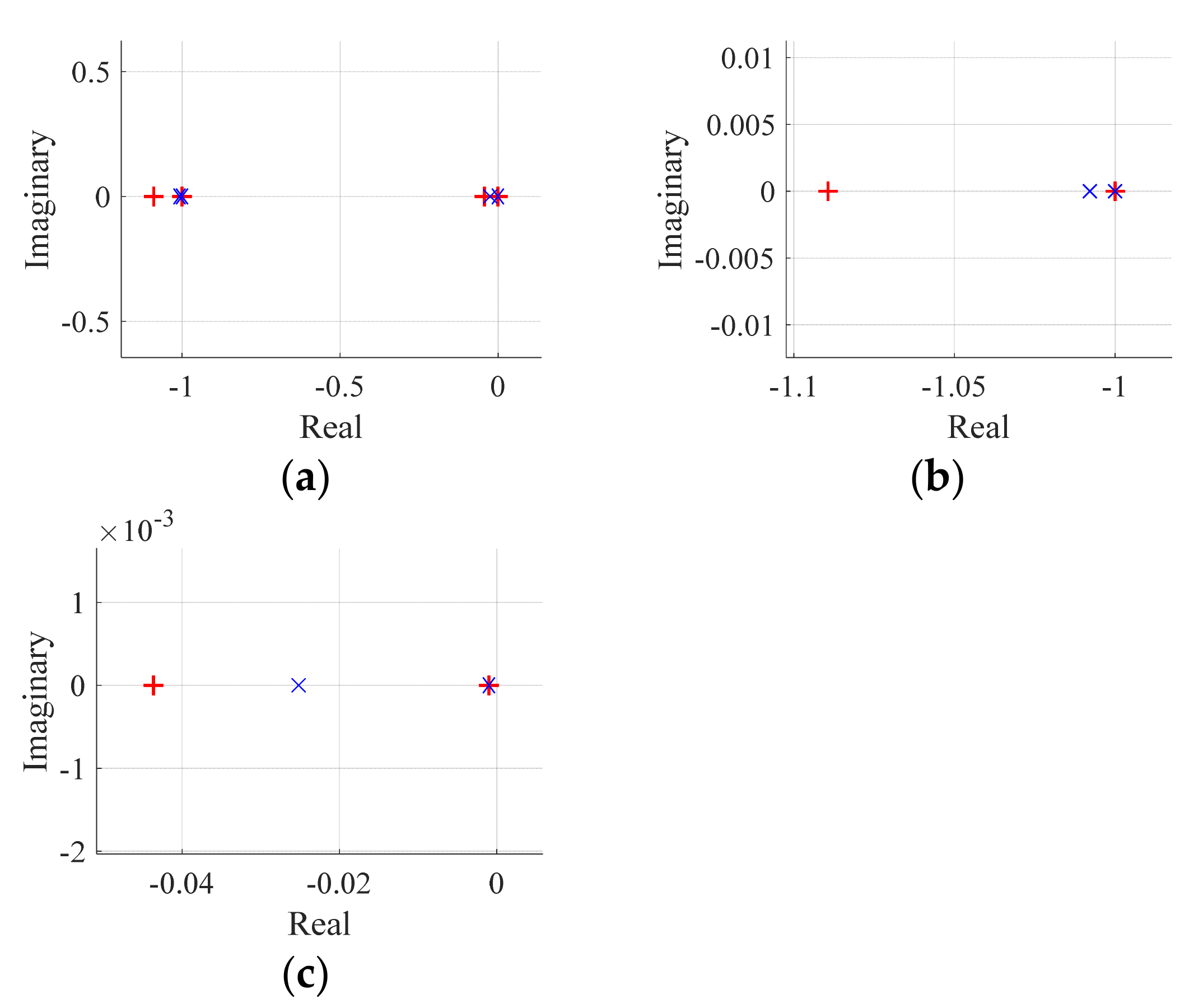
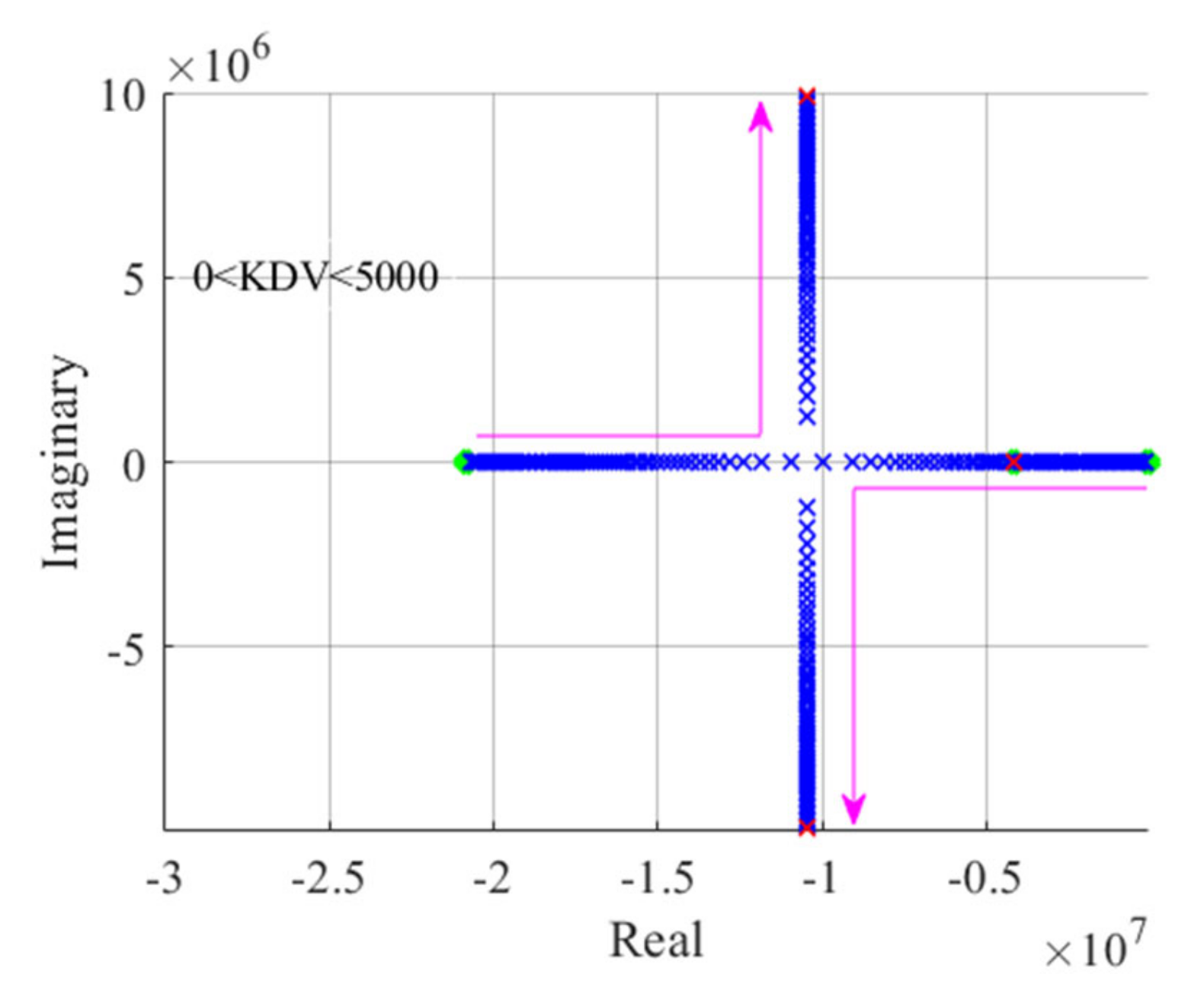
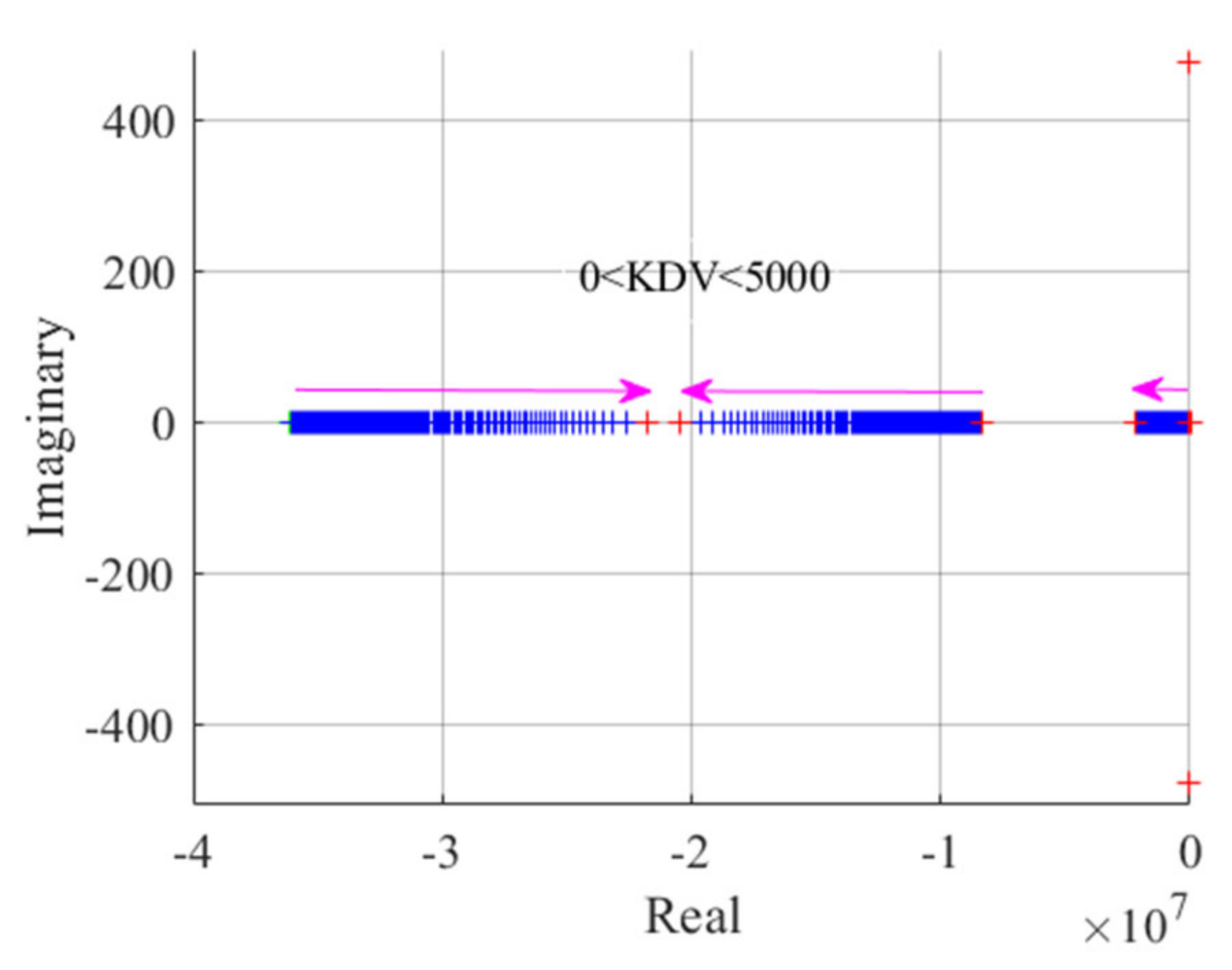
4.1. Dominant Eigenvalues Analysis of the TL VSI and the DTL VSI
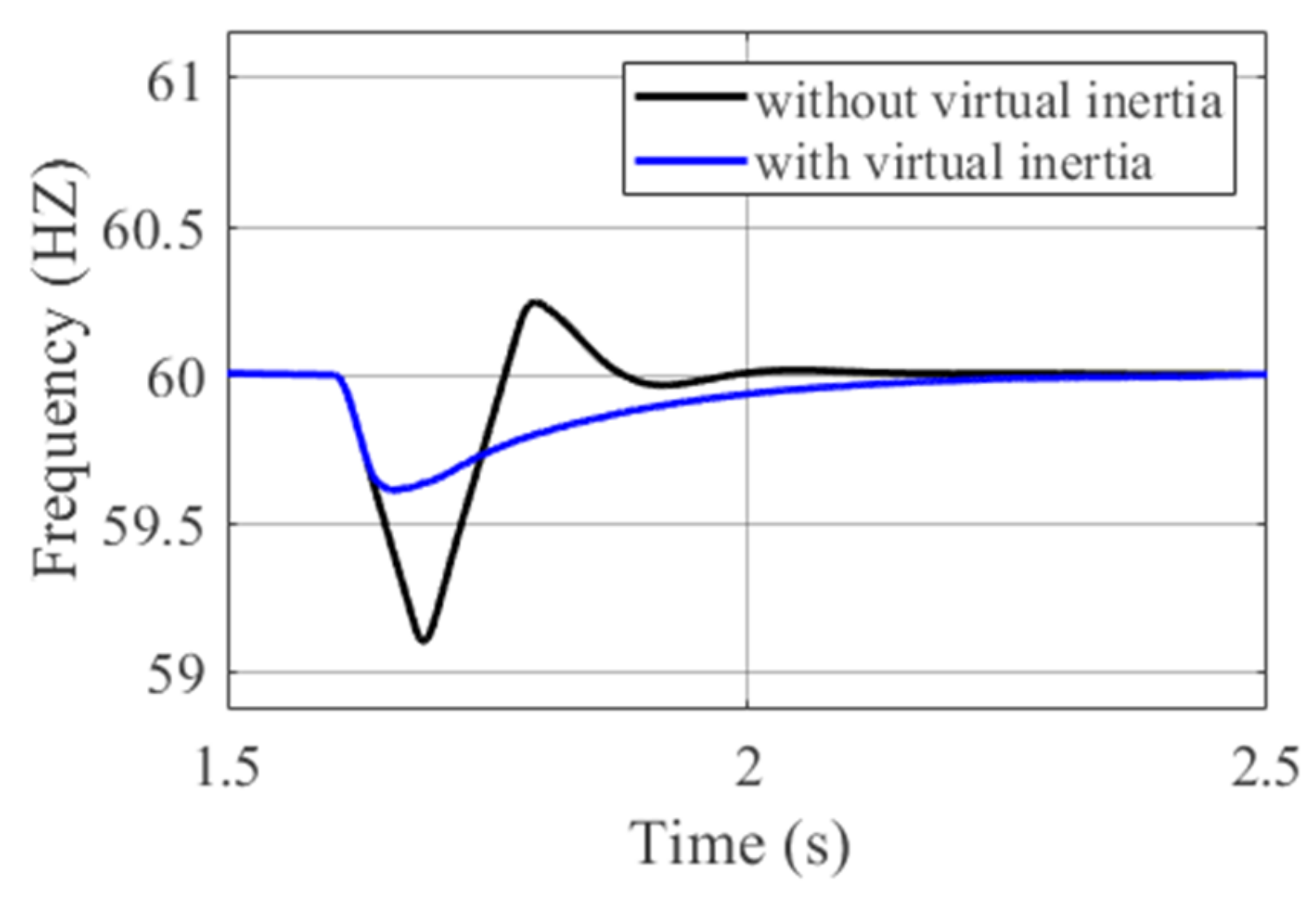
4.2. Oscillation Damping Ability of the DTL VSI and the TL VSI
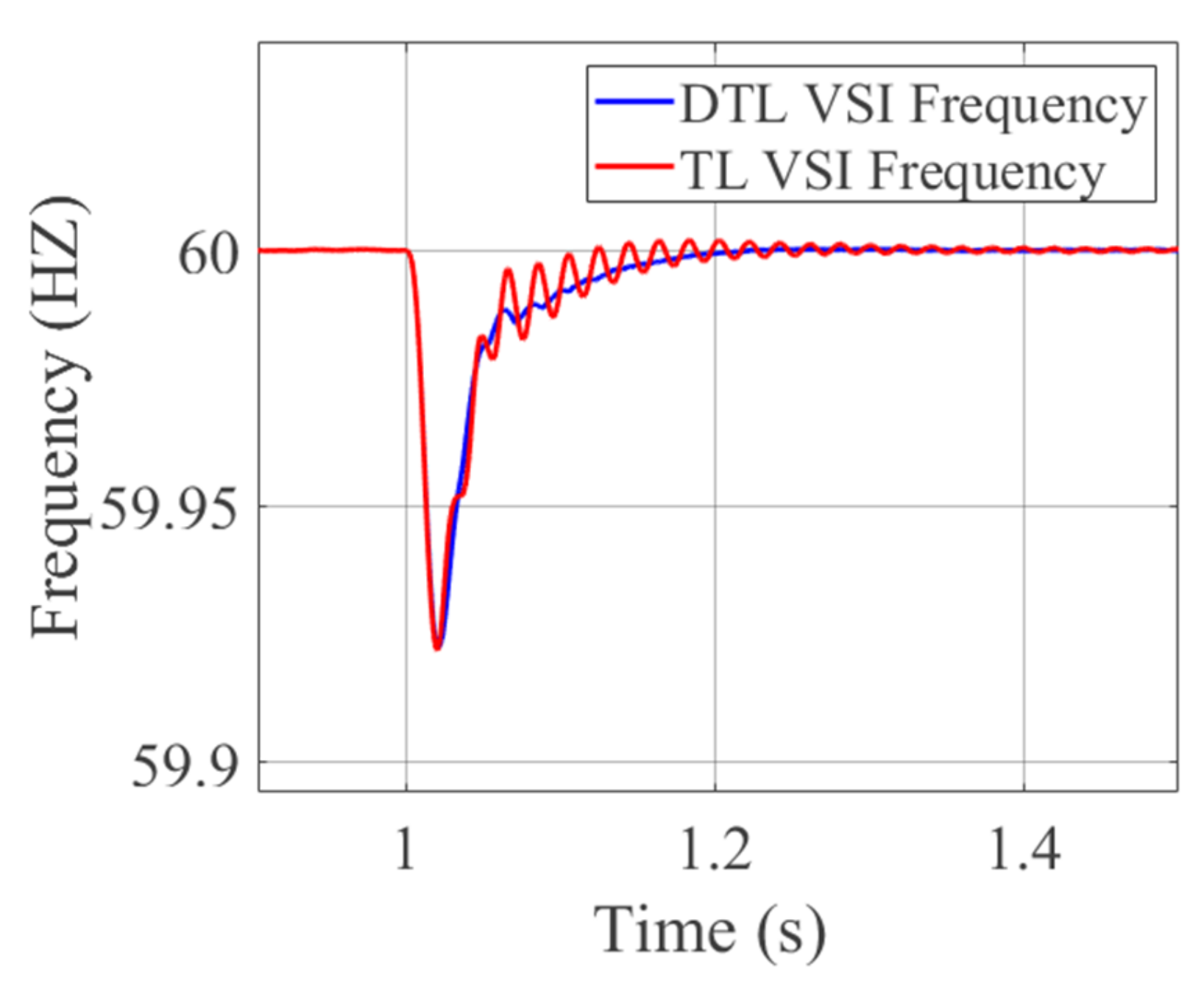
4.3. Simulation Results
5. Grid Current THD Reduction in the DTL VSI Topology
Simulation Results and the Grid Current Analysis
6. Performance Comparison Between the TL VSI and the DTL VSI
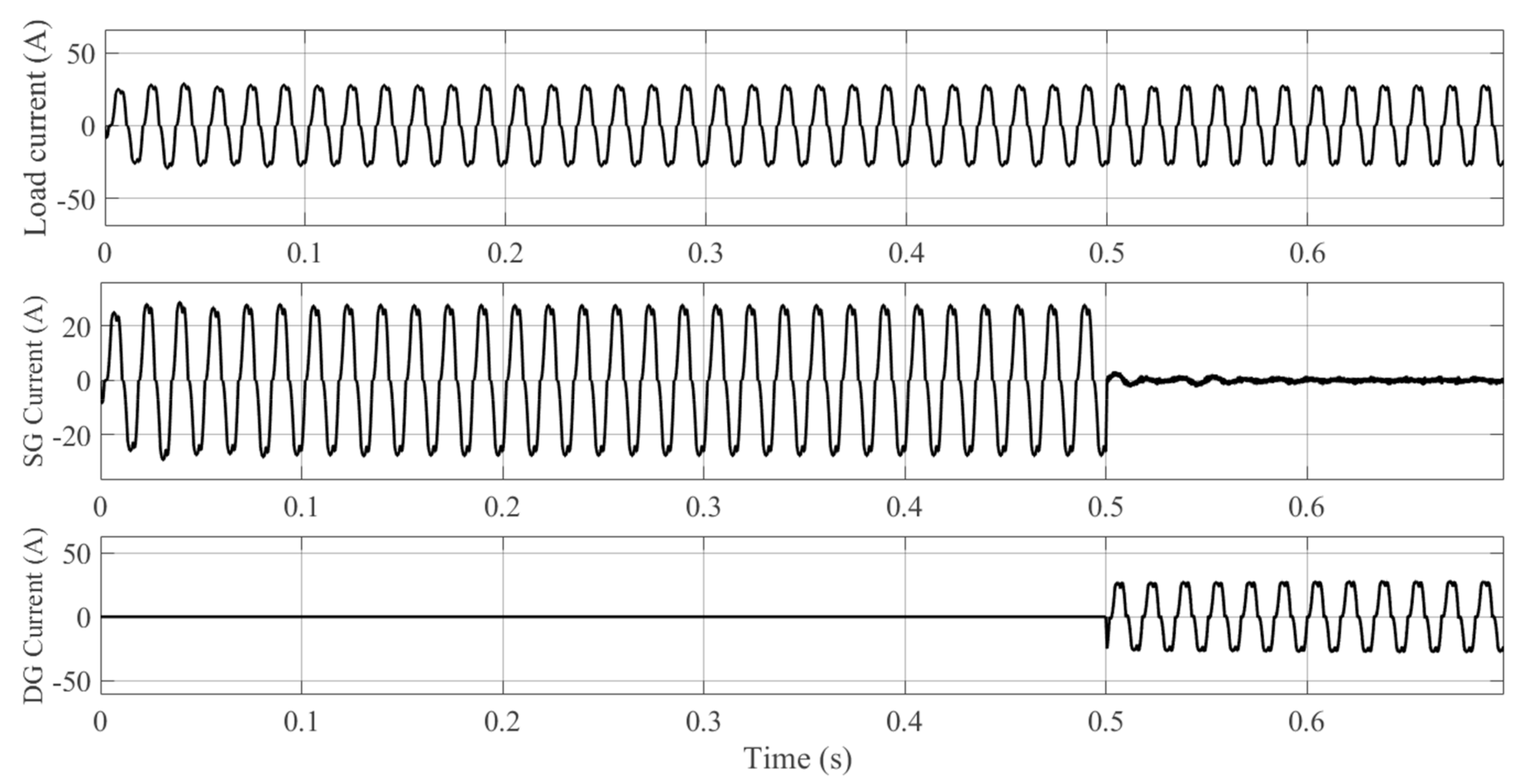
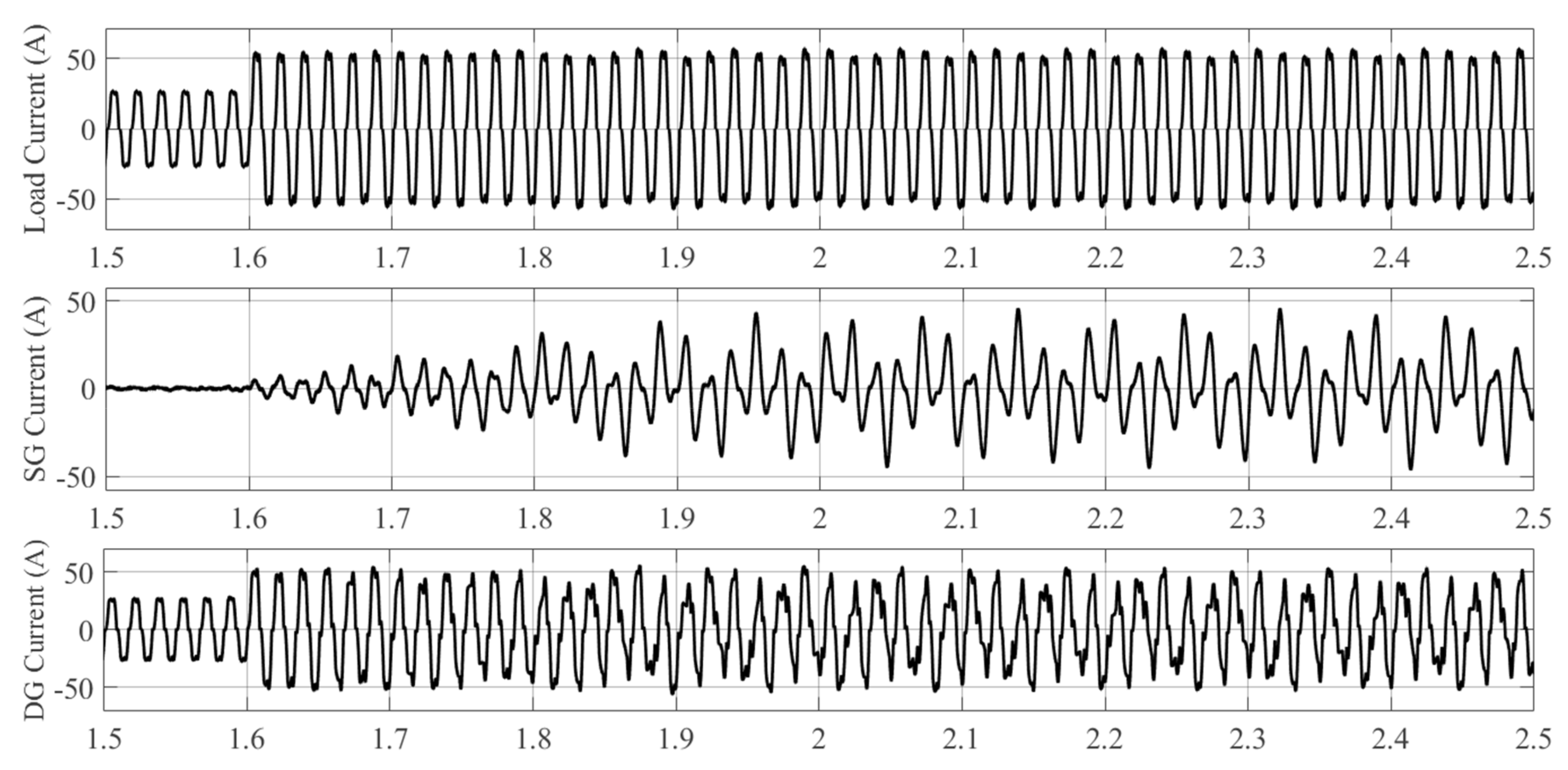
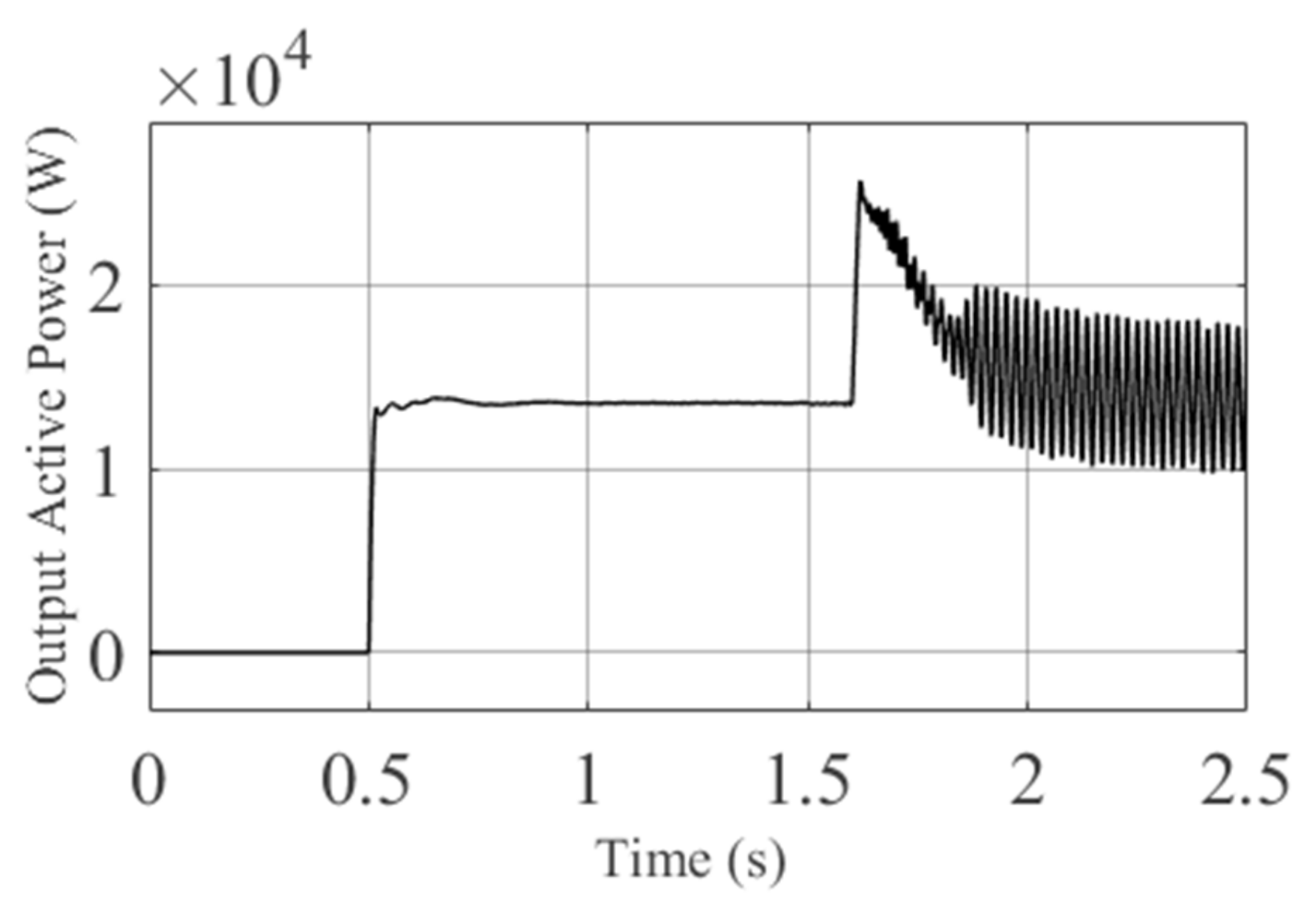
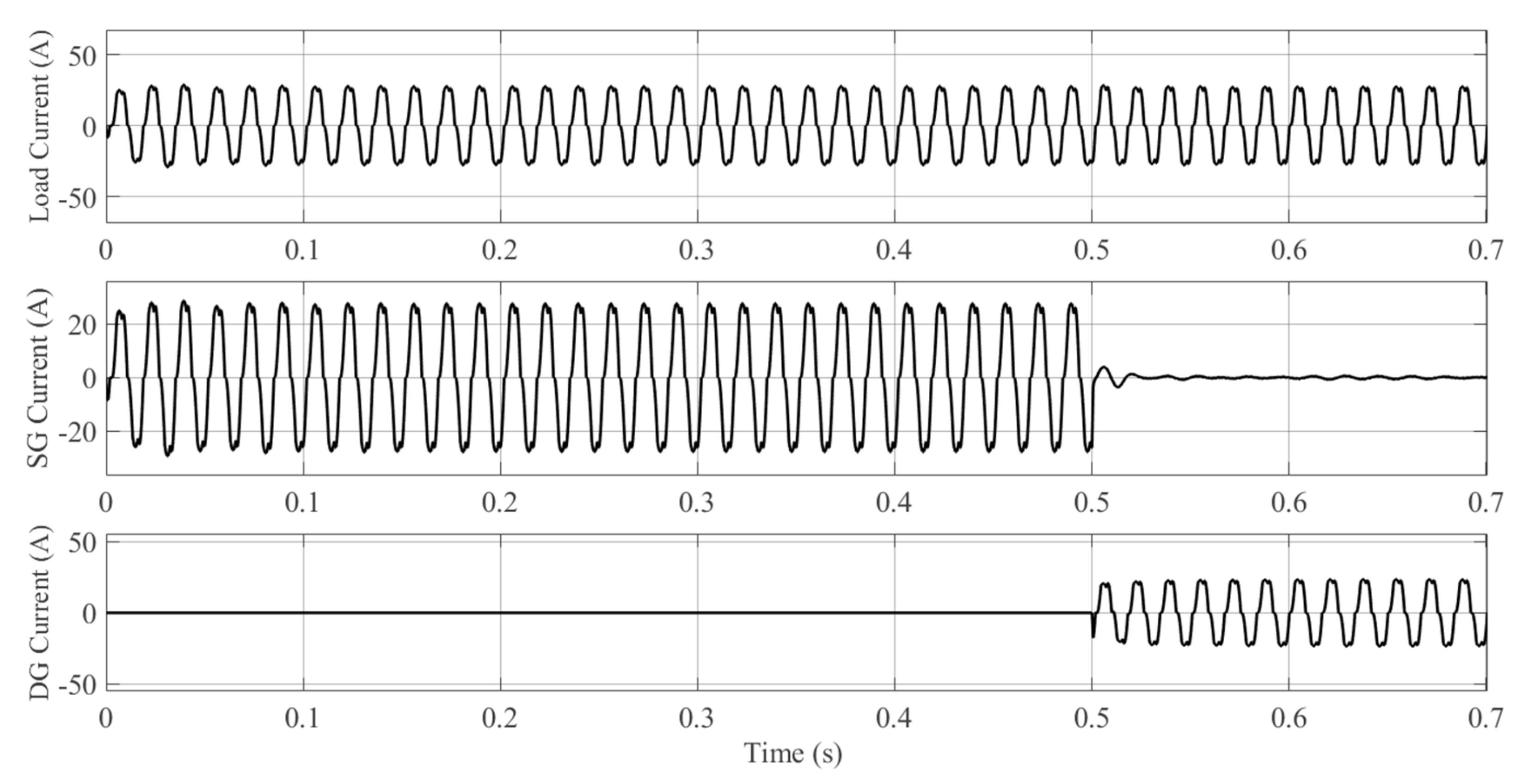
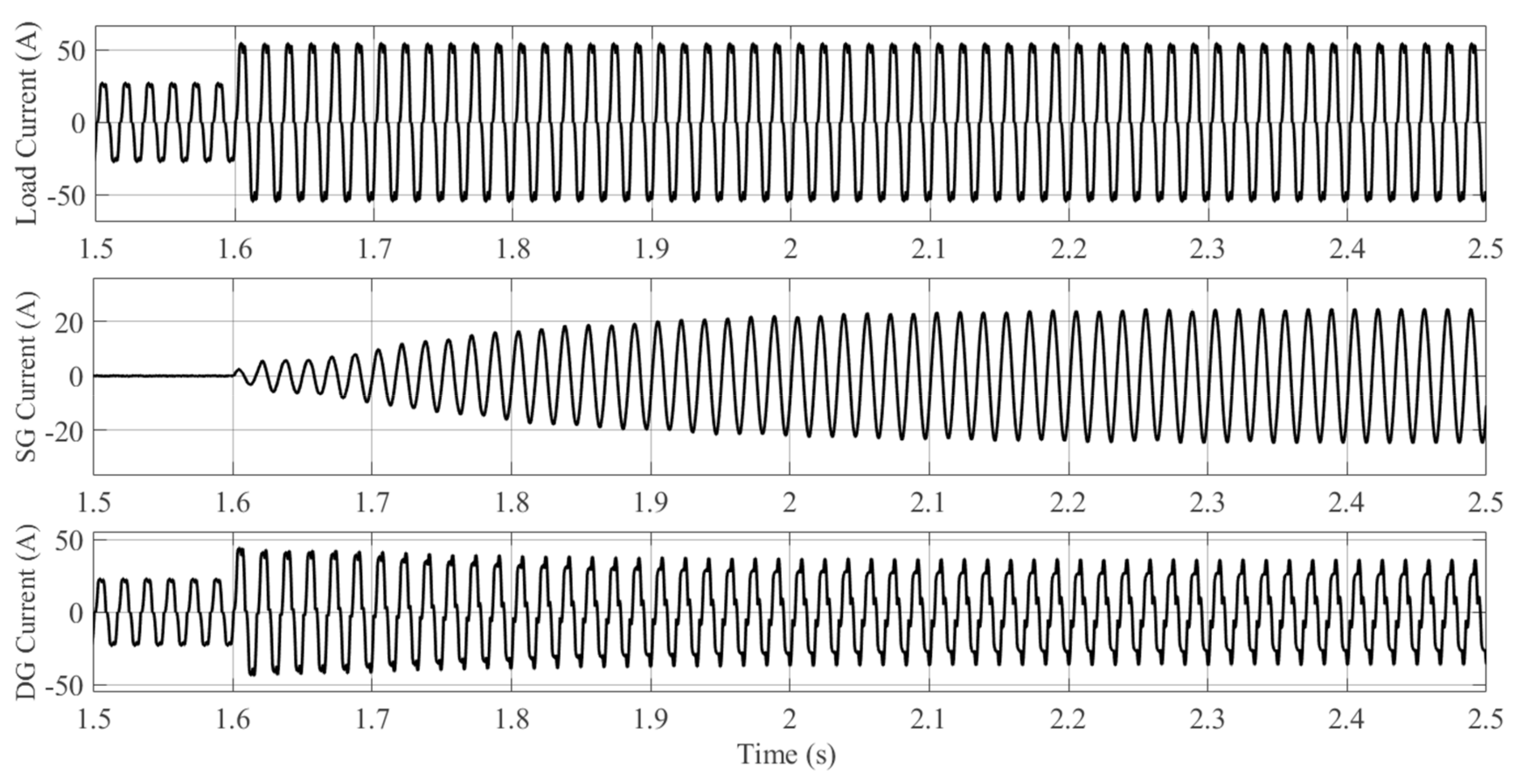
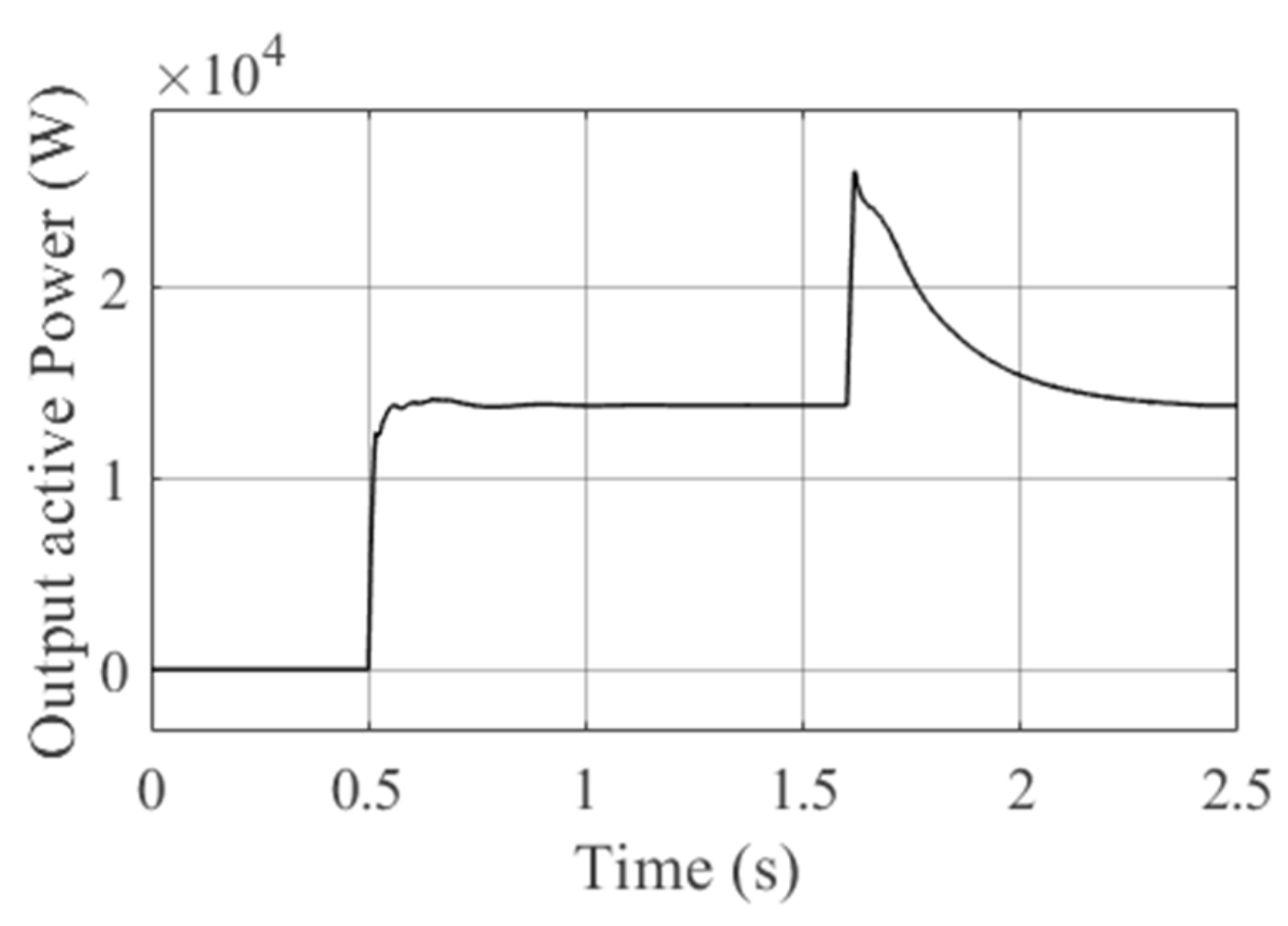
6.1. Simulation Results of the Proposed Controller
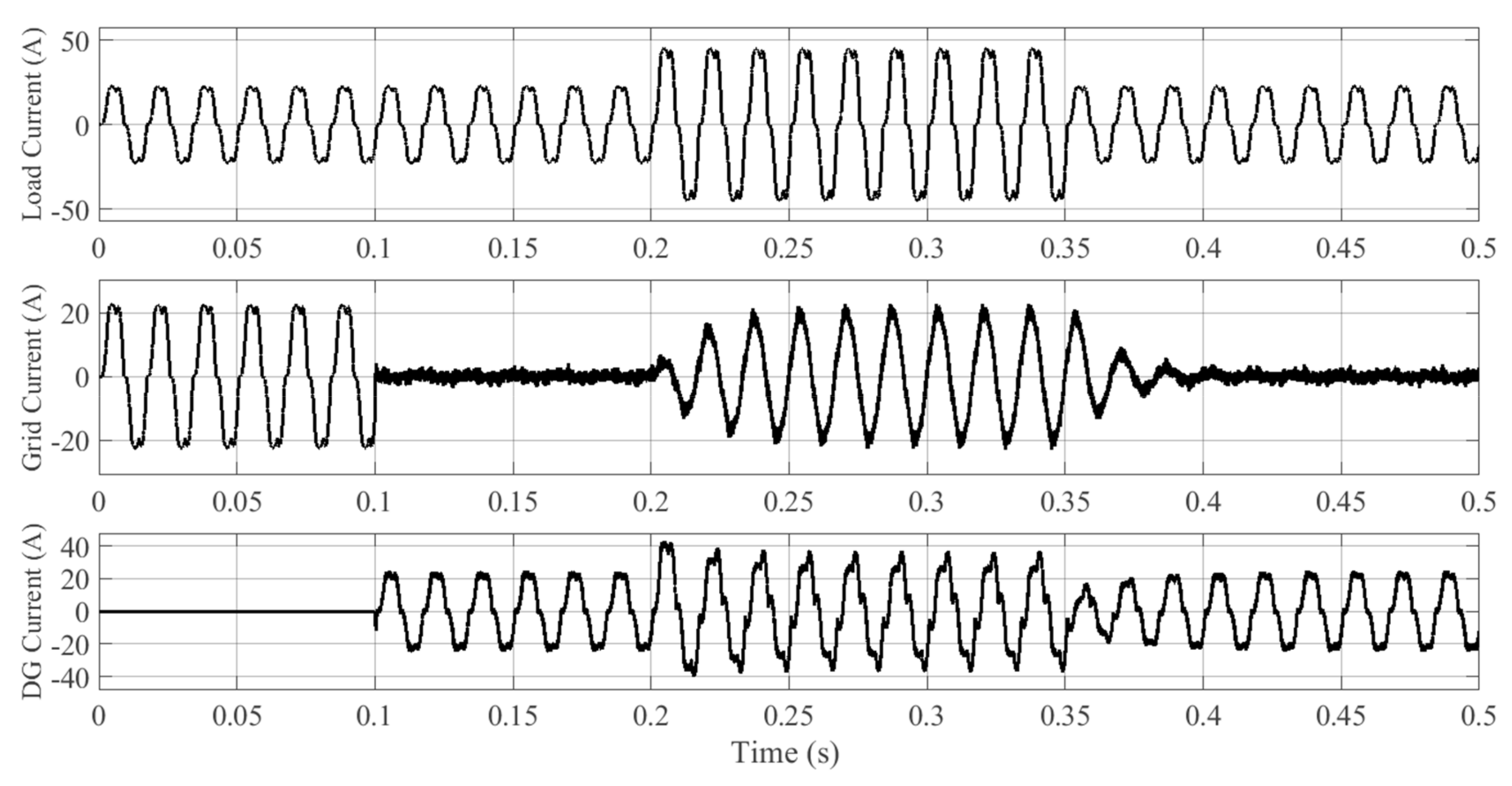
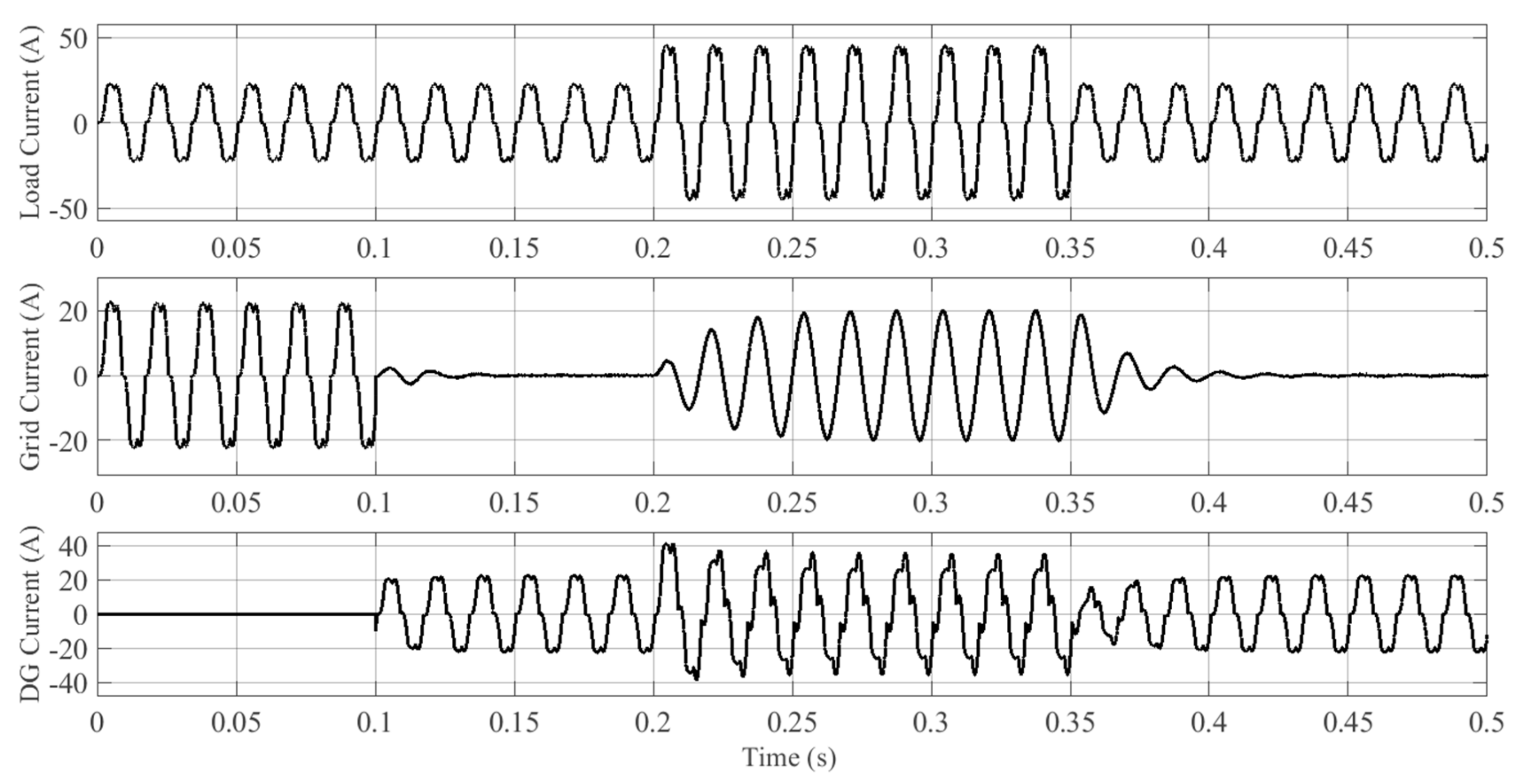
6.1.1. Case A: Grid-Connected TL VSI
6.1.2. Case B: Grid-Connected DTL VSI
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter | Value |
|---|---|
| PID controller of the PLL coefficients (KP/KI/KD) | 180/3200/1 |
| DC link voltage (VDC) | 500 V |
| RLC filter resistance, inductance and capacitance (Rf/Lf/Cf) | 0.01 Ω/0.0024 H/10−6 F |
| Line to line rms voltage (VLLrms) | 25,000 V |
| Nominal frequency (f0) | 60 HZ |
| C1/C2 | 0.001/0.001 |
| Switching frequency | 8000 HZ |
| Transformer ratio | 1:96.15 |
| Nonlinear loads inductance and resistance | 0.01 H/20 Ω |
| PI Current controller (Kpi/Kii) | 1000/30 |
| The low-pass filter time constant (T) | 0.05 |
| The grid inductance and resistance (Lg/Rg) | H/ Ω |
| SCCR | 10 |
| Nominal rated power of the inverter | 30 kVA |
References
- Tamrakar, U.; Shrestha, D.; Maharjan, M.; Bhattarai, B.P.; Hansen, T.M.; Tonkoski, R. Virtual Inertia: Current Trends and Future Directions. Appl. Sci. 2017, 7, 654. Available online: https://www.mdpi.com/2076-3417/7/7/654#cite (accessed on 19 February 2021). [CrossRef]
- Driesen, J.; Visscher, K. Virtual synchronous generators. In Proceedings of the IEEE Power and Energy Society 2008 General Meeting: Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008. [Google Scholar]
- Loix, T.; De Breucker, S.; Vanassche, P.; Van Den Keybus, J.; Driesen, J.; Visscher, K. Layout and performance of the power electronic converter platform for the VSYNC project. In Proceedings of the 2009 IEEE Bucharest PowerTech: Innovative Ideas Toward the Electrical Grid of the Future, Bucharest, Romania, 28 June–2 July 2009. [Google Scholar]
- Zhong, Q.C.; Weiss, G. Synchronverters: Inverters that mimic synchronous generators. IEEE Trans. Ind. Electron. 2011. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Nguyen, P.L.; Ma, Z.; Sheng, W. Self-synchronized synchronverters: Inverters without a dedicated synchronization unit. IEEE Trans. Power Electron. 2014. [Google Scholar] [CrossRef]
- Ashabani, M.; Mohamed, Y.A.R.I. Integrating VSCs to weak grids by nonlinear power damping controller with self-synchronization capability. IEEE Trans. Power Syst. 2014. [Google Scholar] [CrossRef]
- Huang, L.; Xin, H.; Wang, Z.; Wu, K.; Wang, H.; Hu, J.; Lu, C. A Virtual Synchronous Control for Voltage-Source Converters Utilizing Dynamics of DC-Link Capacitor to Realize Self-Synchronization. IEEE J. Emerg. Sel. Top. Power Electron. 2017. [Google Scholar] [CrossRef]
- Mishra, S.; Pullaguram, D.; Buragappu, S.A.; Ramasubramanian, D. Single-phase synchronverter for a gridconnected roof top photovoltaic system. IET Renew. Power Gener. 2016. [Google Scholar] [CrossRef]
- Yap, K.Y.; Sarimuthu, C.R.; Lim, J.M.Y. Grid Integration of Solar Photovoltaic System Using Machine Learning-Based Virtual Inertia Synthetization in Synchronverter. IEEE Access. 2020. [Google Scholar] [CrossRef]
- Shuai, Z.; Huang, W.; Shen, Z.J.; Luo, A.; Tian, Z. Active Power Oscillation and Suppression Techniques between Two Parallel Synchronverters during Load Fluctuations. IEEE Trans. Power Electron. 2020. [Google Scholar] [CrossRef]
- Rosso, R.; Engelken, S.; Liserre, M. Robust stability analysis of synchronverters operating in parallel. IEEE Trans. Power Electron. 2019. [Google Scholar] [CrossRef]
- Sakimoto, K.; Miura, Y.; Ise, T. Stabilization of a power system with a distributed generator by a Virtual Synchronous Generator function. In Proceedings of the 8th International Conference on Power Electronics—ECCE Asia, Jeju, Korea, 29 May–2 June 2011; pp. 1498–1505. Available online: https://ieeexplore.ieee.org/document/5944492 (accessed on 19 February 2021).
- Soni, N.; Doolla, S.; Chandorkar, M.C. Improvement of transient response in microgrids using virtual inertia. IEEE Trans. Power Deliv. 2013. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Ise, T. Comparison of Dynamic Characteristics Between Virtual Synchronous Generator and Droop Control in Inverter-Based Distributed Generators. IEEE Trans. Power Electron. 2016, 31, 3600–3611. Available online: https://ieeexplore.ieee.org/document/7182342 (accessed on 19 February 2021). [CrossRef]
- Torres, L.M.A.A.; Lopes, L.A.C.; Morán, T.L.A.A.; Espinoza, C.J.R. Self-tuning virtual synchronous machine: A control strategy for energy storage systems to support dynamic frequency control. IEEE Trans. Energy Convers. 2014. [Google Scholar] [CrossRef]
- Alipoor, J.; Miura, Y.; Ise, T. Power system stabilization using virtual synchronous generator with alternating moment of inertia. IEEE J. Emerg. Sel. Top. Power Electron. 2015. [Google Scholar] [CrossRef]
- Li, D.; Zhu, Q.; Lin, S.; Bian, X.Y. A Self-Adaptive Inertia and Damping Combination Control of VSG to Support Frequency Stability. IEEE Trans. Energy Convers. 2017. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. Distributed Power System Virtual Inertia Implemented by Grid-Connected Power Converters. IEEE Trans. Power Electron. 2018. [Google Scholar] [CrossRef] [Green Version]
- Fang, J.; Lin, P.; Li, H.; Yang, Y.; Tang, Y. An improved virtual inertia control for three-phase voltage source converters connected to a weak grid. IEEE Trans. Power Electron. 2019. [Google Scholar] [CrossRef] [Green Version]
- Saeedian, M.; Eskandari, B.; Taheri, S.; Hinkkanen, M.; Pouresmaeil, E. A Control Technique Based on Distributed Virtual Inertia for High Penetration of Renewable Energies Under Weak Grid Conditions. IEEE Syst. J. 2020. [Google Scholar] [CrossRef]
- Ashabani, M.; Freijedo, F.D.; Golestan, S.; Guerrero, J.M. Inducverters: PLL-Less Converters With Auto-Synchronization and Emulated Inertia Capability. IEEE Trans. Smart Grid 2016. [Google Scholar] [CrossRef]
- Yan, X.; Mohamed, S.Y.A.; Li, D.; Gadalla, A.S. Parallel operation of virtual synchronous generators and synchronous generators in a microgrid. J. Eng. 2019. [Google Scholar] [CrossRef]
- Zhao, H.; Yang, Q.; Zeng, H. Multi-loop virtual synchronous generator control of inverter-based DGs under microgrid dynamics. IET Gener. Transm. Distrib. 2017. [Google Scholar] [CrossRef]
- Dashtaki, M.A.; Nafisi, H.; Pouresmaeil, E.; Khorsandi, A. Virtual Inertia Implementation in Dual Two-Level Voltage Source Inverters. In Proceedings of the 2020 11th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tehran, Iran, 4–6 February 2020; pp. 1–6. Available online: https://ieeexplore.ieee.org/document/9088389 (accessed on 19 February 2021). [CrossRef]
- Aghazadeh, A.; Jafari, M.; Khodabakhshi-Javinani, N.; Nafisi, H.; Jabbari Namvar, H. Introduction and advantage of space opposite vectors modulation utilized in dual two-level inverters with isolated DC sources. IEEE Trans. Ind. Electron. 2019. [Google Scholar] [CrossRef]
- Manoj Kumar, M.V.; Mishra, M.K.; Kumar, C. A Grid-Connected Dual Voltage Source Inverter with Power Quality Improvement Features. IEEE Trans. Sustain. Energy 2015. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, X.; Song, C.; Cao, R. Research on the filters for dual-inverter fed open-end winding transformer topology in photovoltaic grid-tied applications. Energies 2019, 2338. [Google Scholar] [CrossRef] [Green Version]
- Gohil, G.; Bede, L.; Teodorescu, R.; Kerekes, T.; Blaabjerg, F. Dual-Converter-Fed Open-End Transformer Topology with Parallel Converters and Integrated Magnetics. IEEE Trans. Ind. Electron. 2016. [Google Scholar] [CrossRef] [Green Version]
- Pouresmaeil, E.; Miguel-Espinar, C.; Massot-Campos, M.; Montesinos-Miracle, D.; Gomis-Bellmunt, O. A control technique for integration of DG units to the electrical networks. IEEE Trans. Ind. Electron. 2013. [Google Scholar] [CrossRef]
- Aghazadeh, A.; Davari, M.; Nafisi, H.; Blaabjerg, F. Grid Integration of a Dual Two-Level Voltage-Source Inverter considering Grid Impedance and Phase-Locked Loop. IEEE J. Emerg. Sel. Top. Power Electron. 2019. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dashtaki, M.A.; Nafisi, H.; Khorsandi, A.; Hojabri, M.; Pouresmaeil, E. Dual Two-Level Voltage Source Inverter Virtual Inertia Emulation: A Comparative Study. Energies 2021, 14, 1160. https://doi.org/10.3390/en14041160
Dashtaki MA, Nafisi H, Khorsandi A, Hojabri M, Pouresmaeil E. Dual Two-Level Voltage Source Inverter Virtual Inertia Emulation: A Comparative Study. Energies. 2021; 14(4):1160. https://doi.org/10.3390/en14041160
Chicago/Turabian StyleDashtaki, Mohammad Ali, Hamed Nafisi, Amir Khorsandi, Mojgan Hojabri, and Edris Pouresmaeil. 2021. "Dual Two-Level Voltage Source Inverter Virtual Inertia Emulation: A Comparative Study" Energies 14, no. 4: 1160. https://doi.org/10.3390/en14041160
APA StyleDashtaki, M. A., Nafisi, H., Khorsandi, A., Hojabri, M., & Pouresmaeil, E. (2021). Dual Two-Level Voltage Source Inverter Virtual Inertia Emulation: A Comparative Study. Energies, 14(4), 1160. https://doi.org/10.3390/en14041160







