Multi-Objective Optimisation-Based Design of an Electric Vehicle Cabin Heating Control System for Improved Thermal Comfort and Driving Range
Abstract
:1. Introduction
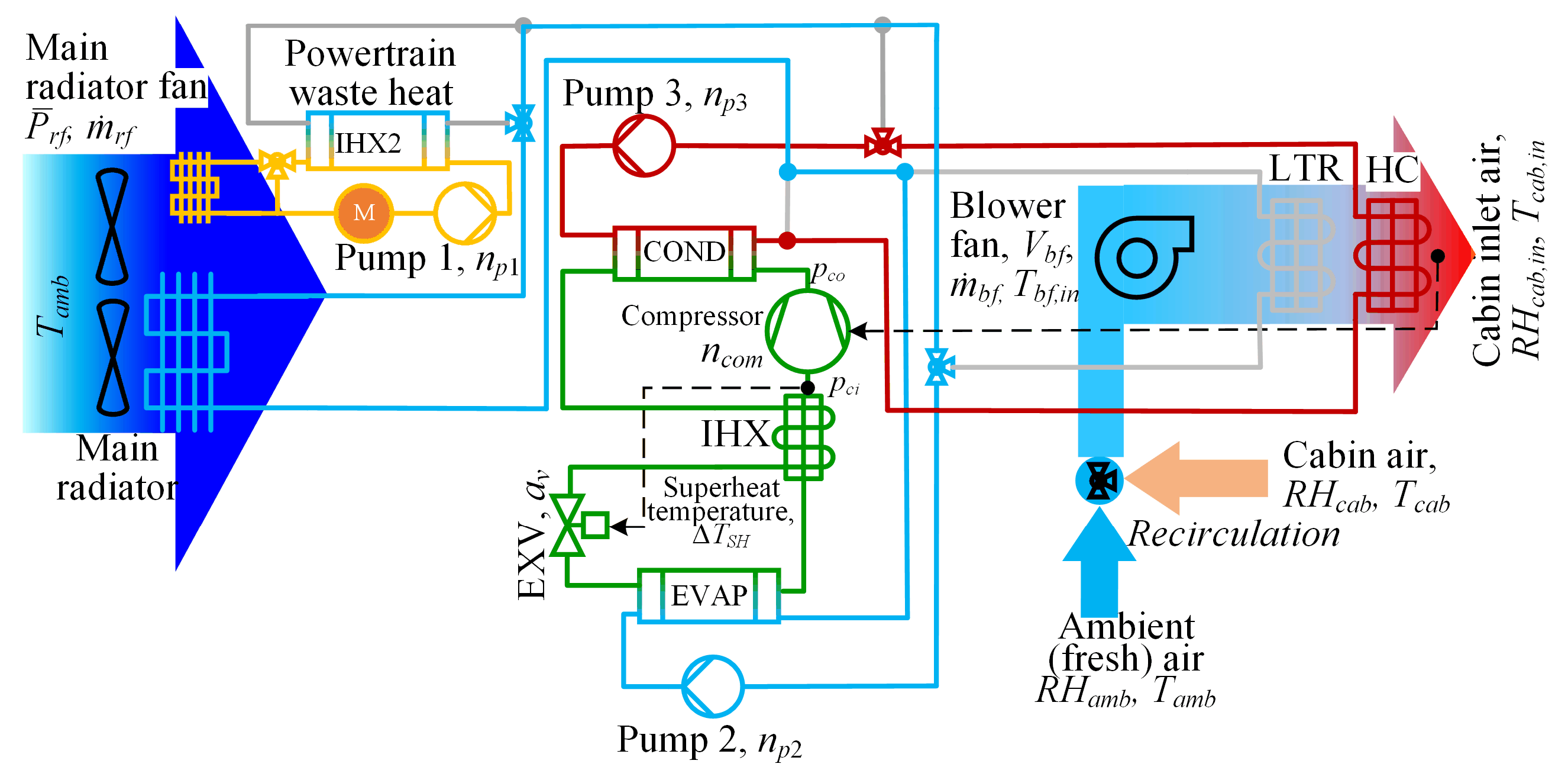
2. HVAC System Model
2.1. HVAC System Configuration
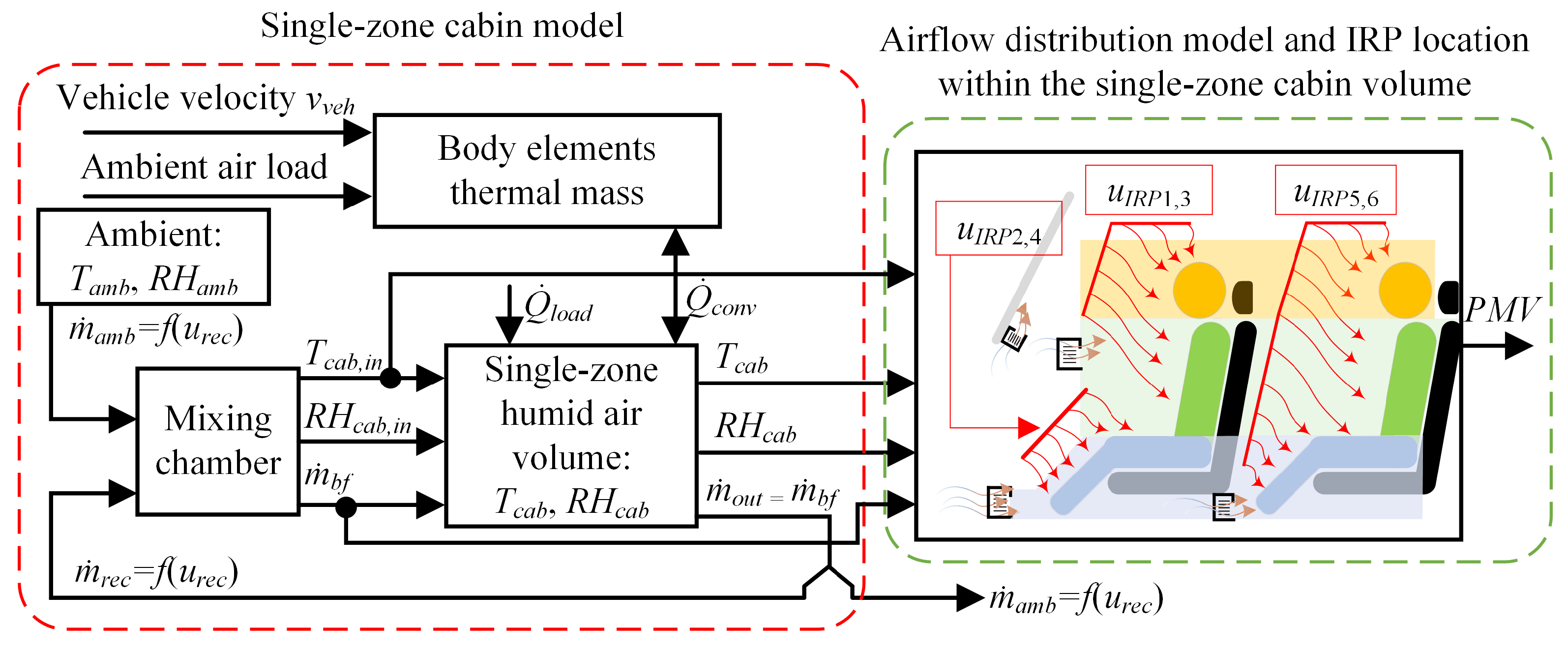
2.2. Dymola-Based HVAC and Cabin Air Flow Distribution Models
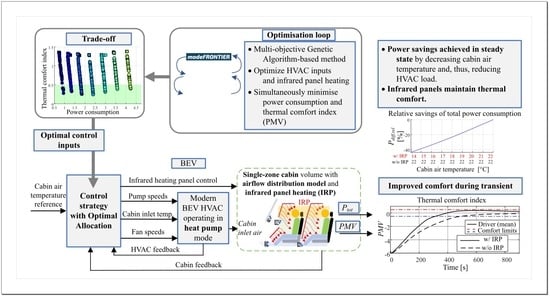
3. Control Input Optimisation Framework
3.1. General Aim
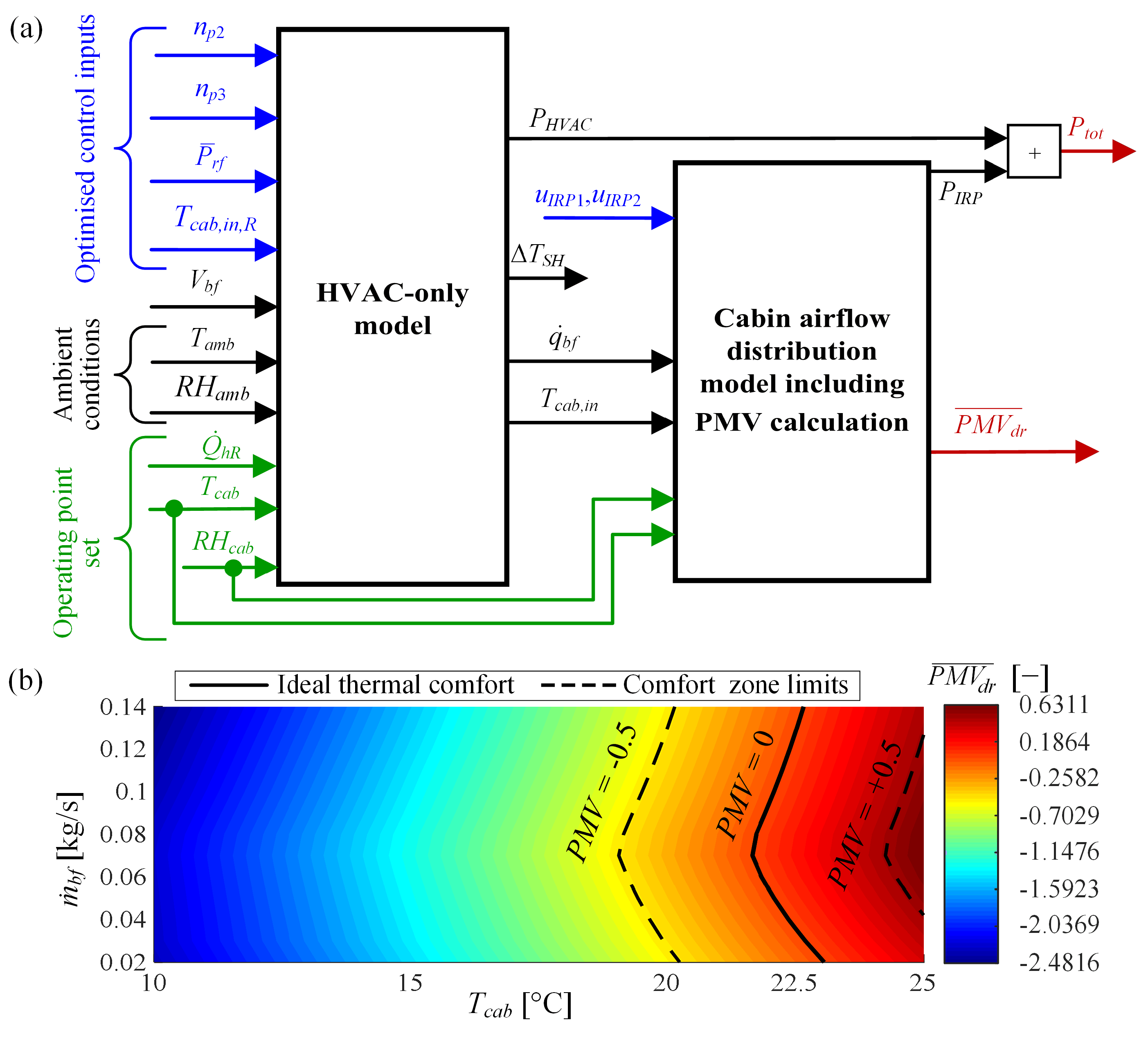
3.2. Objectives and Constraints
3.3. Optimisation Method
4. Optimisation Results and Related Power Consumption Reduction Analysis
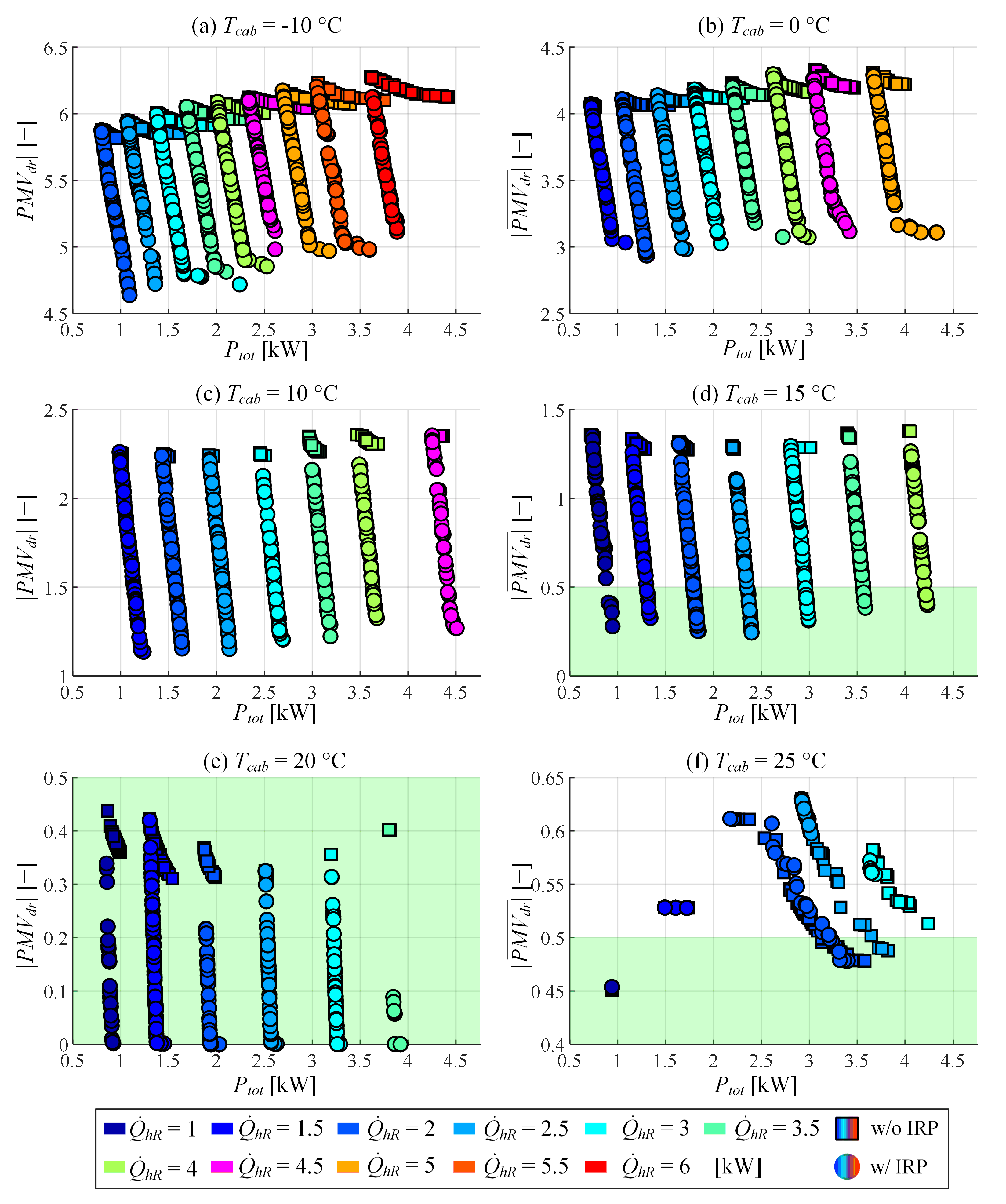
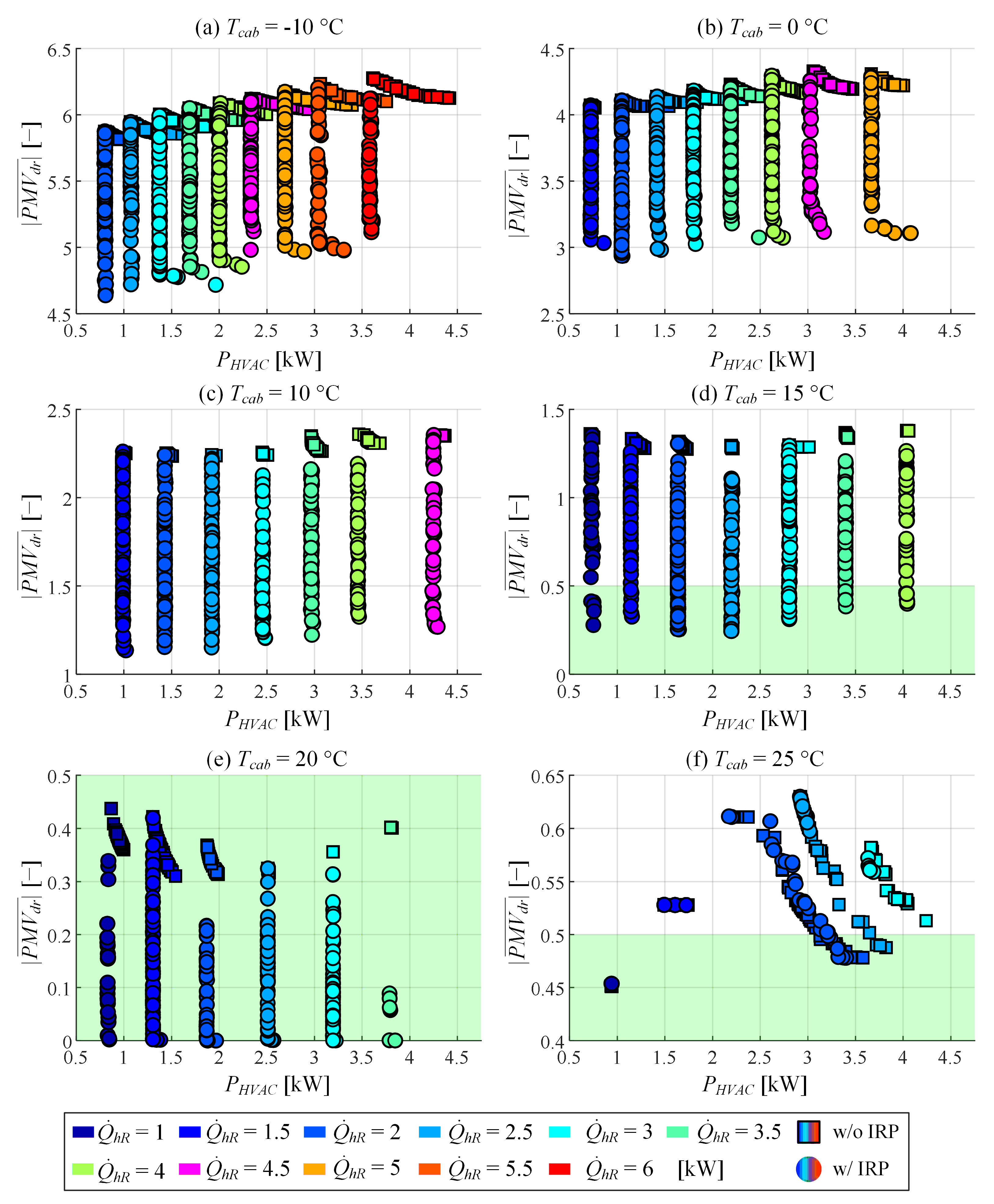
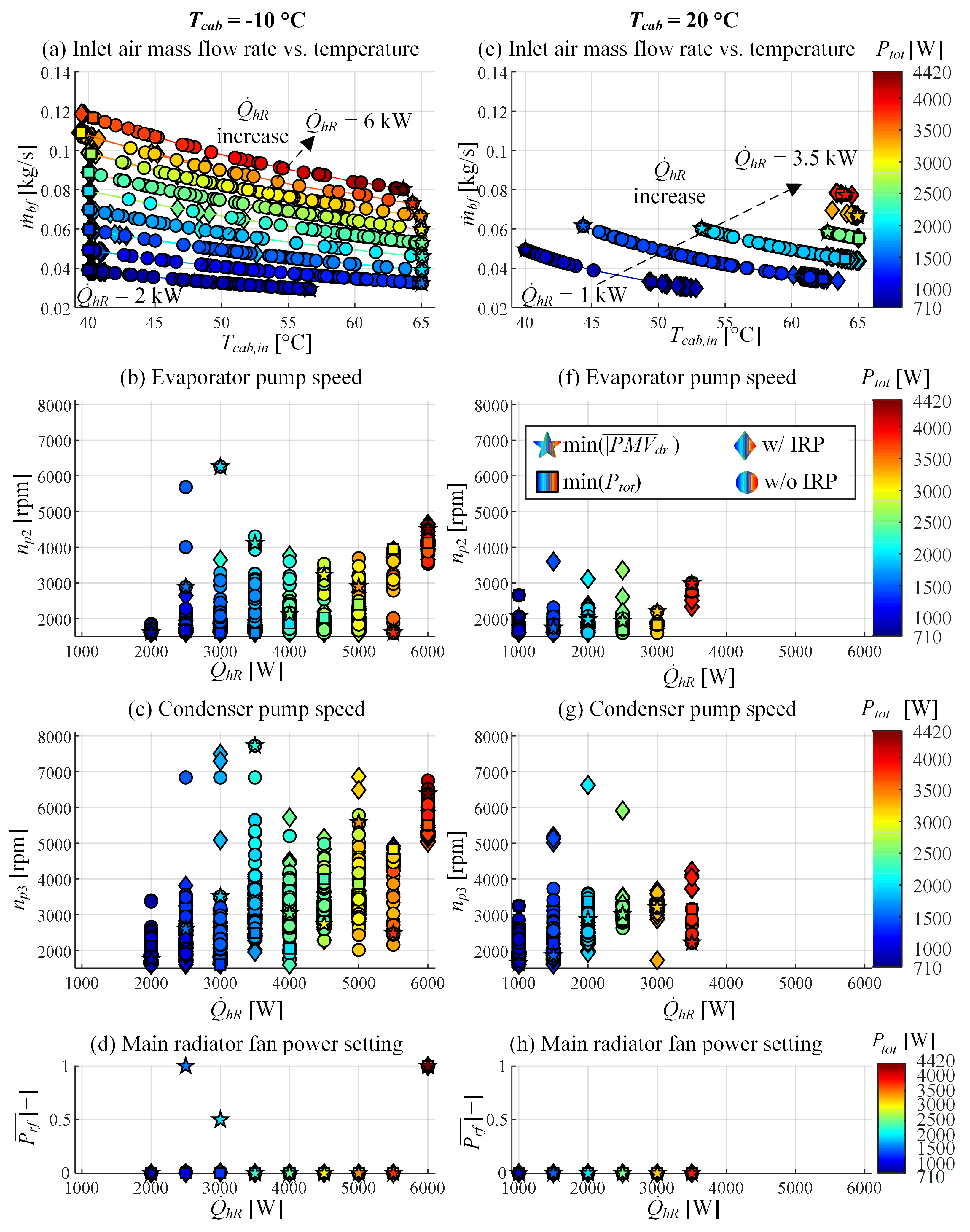
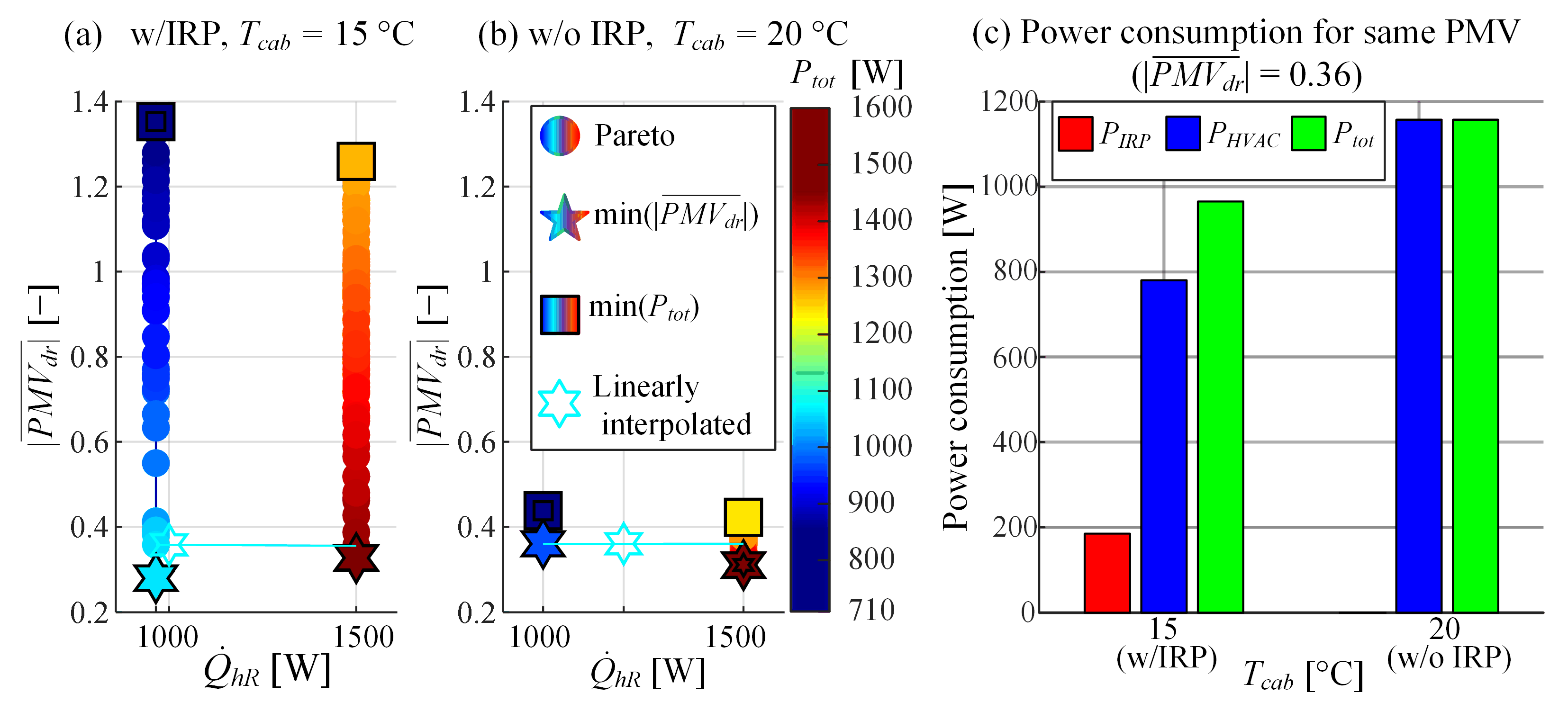
4.1. Optimisation Results
4.2. Power Consumption Reduction Analysis
5. Simulation Results
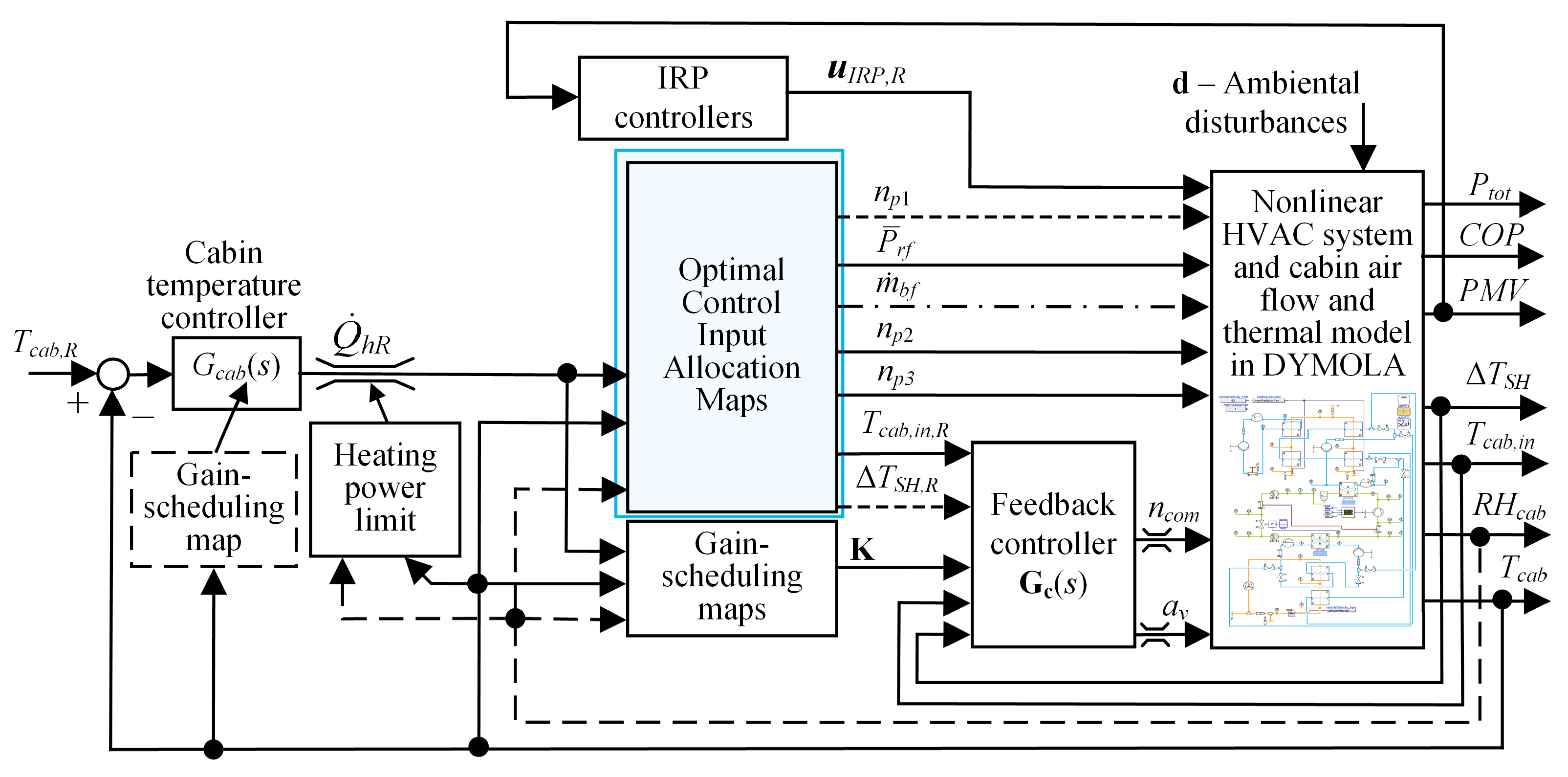
5.1. Control Strategy
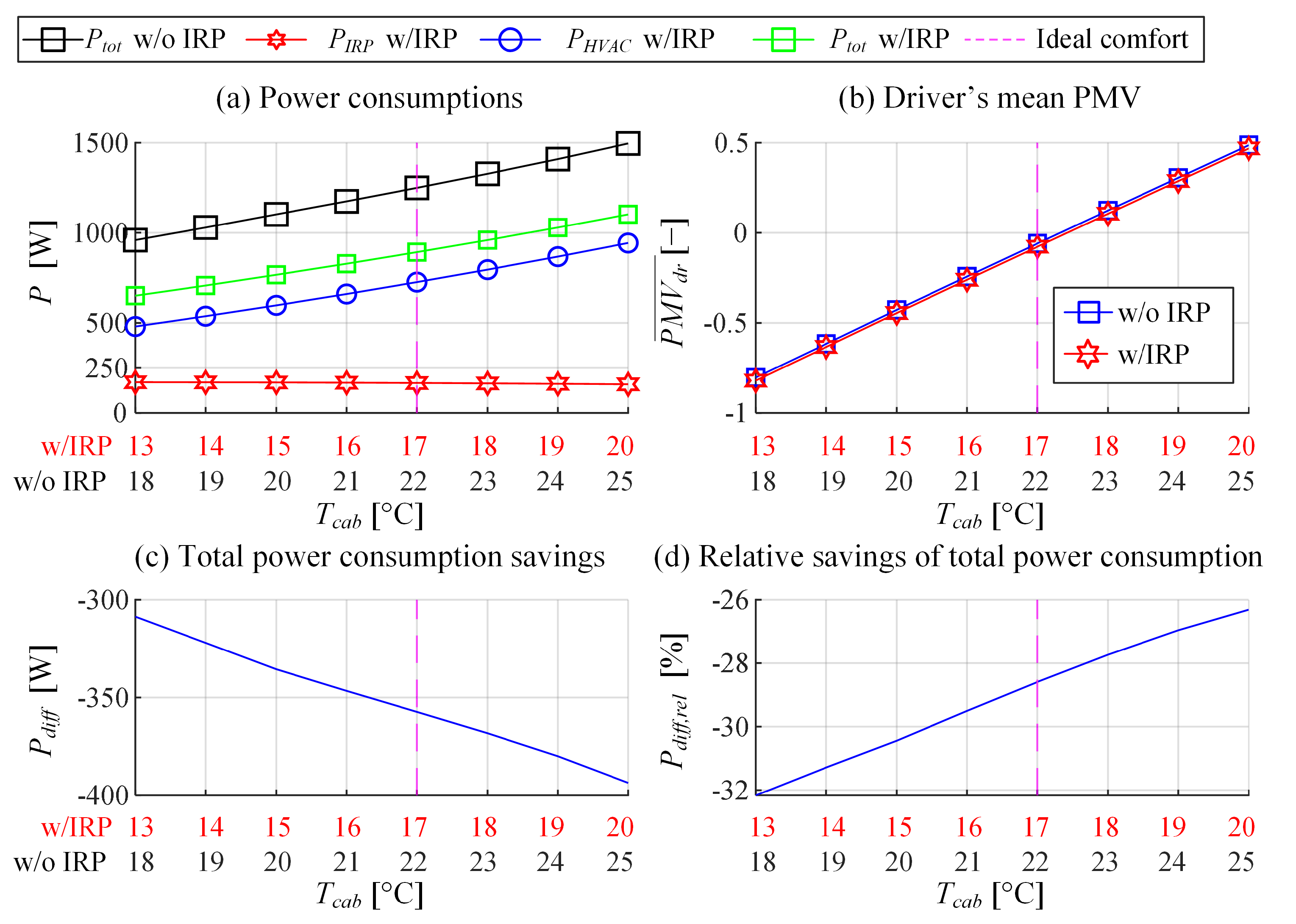
5.2. Simulation Analysis of IRP-Based Steady-State Power Consumption Reduction Potential
5.3. Heat-Up Scenario Simulation Results
- Total energy consumed (Eel);
- Two thermal comfort indices: (i) time to reach the comfortable range defined by |dr | < 0.5 (tPMV,05), and (ii) integral of absolute value of mean PMV in uncomfortable range C2 [min] = ∫|dr|/60 dt, if |dr| > 0.5 [20].
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Description |
| HVAC | Heating, ventilation and air conditioning |
| VCC | Vapour-compression cycle |
| A/C | Air conditioning |
| EXV | Electronic expansion valve |
| CFD | Computational fluid dynamics |
| HC | Heater core |
| LTR | Low temperature radiator |
| IRP | Infra-red panel |
| PMV | Predictive mean vote |
| MOGA | Multi-objective genetic algorithm |
Nomenclature
| Symbols | Unit | Description | |
| RH | % | Air relative humidity | |
| T | °C | Temperature | |
| kg/s | Fluid mass flow rate | ||
| n | rpm | Rotational speed | |
| P | W | Power consumption | |
| - | Discrete actuator power setting | ||
| V | V | Voltage | |
| av | - | Electronic expansion valve steps | |
| W | Heat flow | ||
| - | Mean PMV index | ||
| cp | Jkg−1K−1 | Isobaric specific mass capacity | |
| e | - | Control error | |
| k | - | PMV Controller proportional gain | |
| Eel | Wh | Total energy consumption | |
| Subscripts | Description | Subscripts | Description |
| amb | Ambient | SH | superheat |
| cab | Cabin | IRP | Infra-red panel |
| in | Inlet | veh | Vehicle |
| out | Outlet | met | Metabolic |
| rf | Main radiator fan | sol | Solar |
| bf | Blower fan | rec | Recirculation |
| p | Coolant pump | dr | Driver |
| com | Compressor | h | Heating |
| R | reference | ||
Appendix A
- The air recirculation is set to 100%. This means that the blower fan inlet air temperature and the relative humidity correspond to the cabin air conditions, i.e., Tin = Tcab and RHin = RHcab.
- The ambient air temperature is set to 40 °C and the relative humidity is 60%.
- The air distribution vents are set to “VENT” mode, where the air is only distributed at chest-height positioned air vents (see [25] for details).
- The lower limit of cabin inlet air temperature is set to 5 °C, while the upper limit is equated with the cabin air temperature to prevent heating, i.e., 5 °C < Tcab,in,R < Tcab.
- The control inputs are allocated with respect to three inputs: the cooling power demand cR, the cabin air temperature Tcab, and the cabin relative humidity RHcab, where the latter is relevant in the A/C mode due to the dehumidification effect.

References
- Global EV Outlook 2020—Analysis—IEA. Available online: https://www.iea.org/reports/global-ev-outlook-2020 (accessed on 7 December 2020).
- Council of the European Union Council. Decision (EU) 2017/710 of 3 April 2017 on the Position to Be Adopted, on Behalf of the European Union, within the EEA Joint Committee Concerning an Amendment to Annex XX (Environment) to the EEA Agreement (CO2 Emissions). Available online: https://eur-lex.europa.eu/eli/dec/2017/710/oj (accessed on 23 June 2020).
- Yang, D.X.; Qiu, L.S.; Yan, J.J.; Chen, Z.Y.; Jiang, M. The government regulation and market behavior of the new energy automotive industry. J. Clean. Prod. 2019, 210, 1281–1288. [Google Scholar] [CrossRef]
- Pouladi, J.; Bannae Sharifian, M.B.; Soleymani, S. Determining charging load of PHEVs considering HVAC system and ana-lyzing its probabilistic impacts on residential distribution network. Electr. Power Syst. Res. 2016, 141, 300–312. [Google Scholar] [CrossRef]
- Vatanparvar, K.; Al Faruque, M.A. Battery lifetime-aware automotive climate control for electric vehicles. In Proceedings of the 52nd ACM/EDAC/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 8–12 June 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, T.; Gao, C.; Gao, Q.; Wang, G.; Liu, M.H.; Guo, Y.; Xiao, C.; Yan, Y.Y. Status and development of electric vehicle integrated thermal management from BTM to HVAC. Appl. Therm. Eng. 2015, 88, 398–409. [Google Scholar] [CrossRef]
- Paffumi, E.; Otura, M.; Centurelli, M.; Casellas, R.; Brenner, A.; Jahn, S. Energy consumption, driving range and cabin tem-perature performances at different ambient conditions in support to the design of a user-centric efficient electric vehicle: The QUIET Project. In Proceedings of the 14th SDEWES Conference, Dubrovnik, Croatia, 1–6 October 2019; p. 18. [Google Scholar]
- Park, M.H.; Kim, S.C. Heating Performance Characteristics of High-Voltage PTC Heater for an Electric Vehicle. Energies 2017, 10, 1494. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Wang, J.; Feng, X.; Chang, L.; Chen, Y.; Wang, X. The solutions to electric vehicle air conditioning systems: A review. Renew. Sustain. Energy Rev. 2018, 91, 443–463. [Google Scholar] [CrossRef]
- Feng, L.; Hrnjak, P. Performance characteristics of a mobile heat pump system at low ambient temperature. In SAE Technical Paper; SAE Interational: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef]
- Okamoto, K.; Aikawa, H.; Ohmikawa, M.; Hayashi, K. Thermal management of a hybrid vehicle using a heat pump. In SAE Technical Paper; SAE Interational: Warrendale, PA, USA, 2019. [Google Scholar] [CrossRef]
- Menken, J.C.; Strasser, K.; Anzenberger, T.; Rebinger, C. Evaluation of the Energy Consumption of a Thermal Management System of a Plug-In Hybrid Electric Vehicle Using the Example of the Audi Q7 e-tron. SAE Int. J. Passeng. Cars Mech. Syst. 2018, 11, 203–212. [Google Scholar] [CrossRef]
- Chowdhury, S.; Leitzel, L.; Zima, M.; Santacesaria, M.; Titov, G.; Lustbader, J.; Rugh, J.; Winkler, J.; Khawaja, A.; Go-vindarajalu, M. Total Thermal management of battery electric vehicles (BEVs). In SAE Technical Paper; SAE Interational: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef] [Green Version]
- Drage, P.; Hinteregger, M.; Zotter, G.; Šimek, M. Cabin Conditioning for Electric Vehicles. ATZ Worldw. 2019, 121, 44–49. [Google Scholar] [CrossRef]
- Oi, H.; Yanagi, K.; Tabat, K.; Tochihar, Y. Effects of heated seat and foot heater on thermal comfort and heater energy con-sumption in vehicle. Ergonomics 2011, 54, 690–699. [Google Scholar] [CrossRef] [PubMed]
- Bauml, T.; Dvorak, D.; Frohner, A.; Simic, D. Simulation and measurement of an energy efficient infrared radiation heating of a full electric vehicle. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Coimbra, Portugal, 27–30 October 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Steiner, A.; Rauch, A.; Larrañaga, J.; Izquierdo, M.; Ferraris, W.; Piovano, A.A.; Gyoeroeg, T.; Huenemoerder, W.; Backes, D.; Trenktrog, M. Energy Efficient and Comfortable Cabin Heating. In Future Interior Concepts; Fuchs, A., Brandstätter, B., Eds.; Springer: Cham, Switzerland, 2021; pp. 89–100. [Google Scholar] [CrossRef]
- Farzaneh, Y.; Tootoonchi, A.A. Controlling automobile thermal comfort using optimized fuzzy controller. Appl. Therm. Eng. 2008, 28, 1906–1917. [Google Scholar] [CrossRef]
- Yan, X.; Fleming, J.; Lot, R. A/C Energy Management and Vehicle Cabin Thermal Comfort Control. IEEE Trans. Veh. Technol. 2018, 67, 11238–11242. [Google Scholar] [CrossRef]
- Cvok, I.; Škugor, B.; Deur, J. Control trajectory optimisation and optimal control of an electric vehicle HVAC system for favourable efficiency and thermal comfort. Optim. Eng. 2020. [CrossRef]
- Amini, M.R.; Wang, H.; Gong, X.; Liao-Mcpherson, D.; Kolmanovsky, I.; Sun, J. Cabin and battery thermal management of connected and automated hevs for improved energy efficiency using hierarchical model predictive control. IEEE Trans. Control Syst. Technol. 2020, 28, 1711–1726. [Google Scholar] [CrossRef]
- Schaut, S.; Sawodny, O. Thermal Management for the Cabin of a Battery Electric Vehicle Considering Passengers’ Comfort. IEEE Trans. Control Syst. Technol. 2020, 28, 1476–1492. [Google Scholar] [CrossRef]
- Cvok, I.; Ratković, I.; Deur, J. Optimisation of Control Input Allocation Maps for Electric Vehicle Heat Pump-based Cabin Heating Systems. Energies 2020, 13, 5131. [Google Scholar] [CrossRef]
- Qi, Z. Advances on air conditioning and heat pump system in electric vehicles—A review. Renew. Sustain. Energy Rev. 2014, 38, 754–764. [Google Scholar] [CrossRef]
- Dvorak, D.; Basciotti, D.; Gellai, I. Demand-Based Control Design for Efficient Heat Pump Operation of Electric Vehicles. Energies 2020, 13, 5440. [Google Scholar] [CrossRef]
- Basciotti, D.; Dvorak, D.; Gellai, I. A Novel Methodology for Evaluating the Impact of Energy Efficiency Measures on the Cabin Thermal Comfort of Electric Vehicles. Energies 2020, 13, 3872. [Google Scholar] [CrossRef]
- ASHRAE. ANSI/ASHRAE Standar Thermal Environmental Conditions for Human Occupancy; ASHRAE: Atlanta, GA, USA, 2017; Volume 2017. [Google Scholar]
- Poles, S. MOGA-II an Improved Multi-Objective Genetic Algorithm: Technical Report; ESTECO: Trieste, Italy, 2003. [Google Scholar]
- Cvok, I.; Ratković, I.; Deur, J. Optimization of control parameters of vehicle air-conditioning system for maximum efficiency. In SAE Technical Paper; SAE Interational: Warrendale, PA, USA, 2020. [Google Scholar] [CrossRef]
- Esteco ModeFrontier. Available online: https://www.esteco.com/modefrontier (accessed on 28 August 2020).
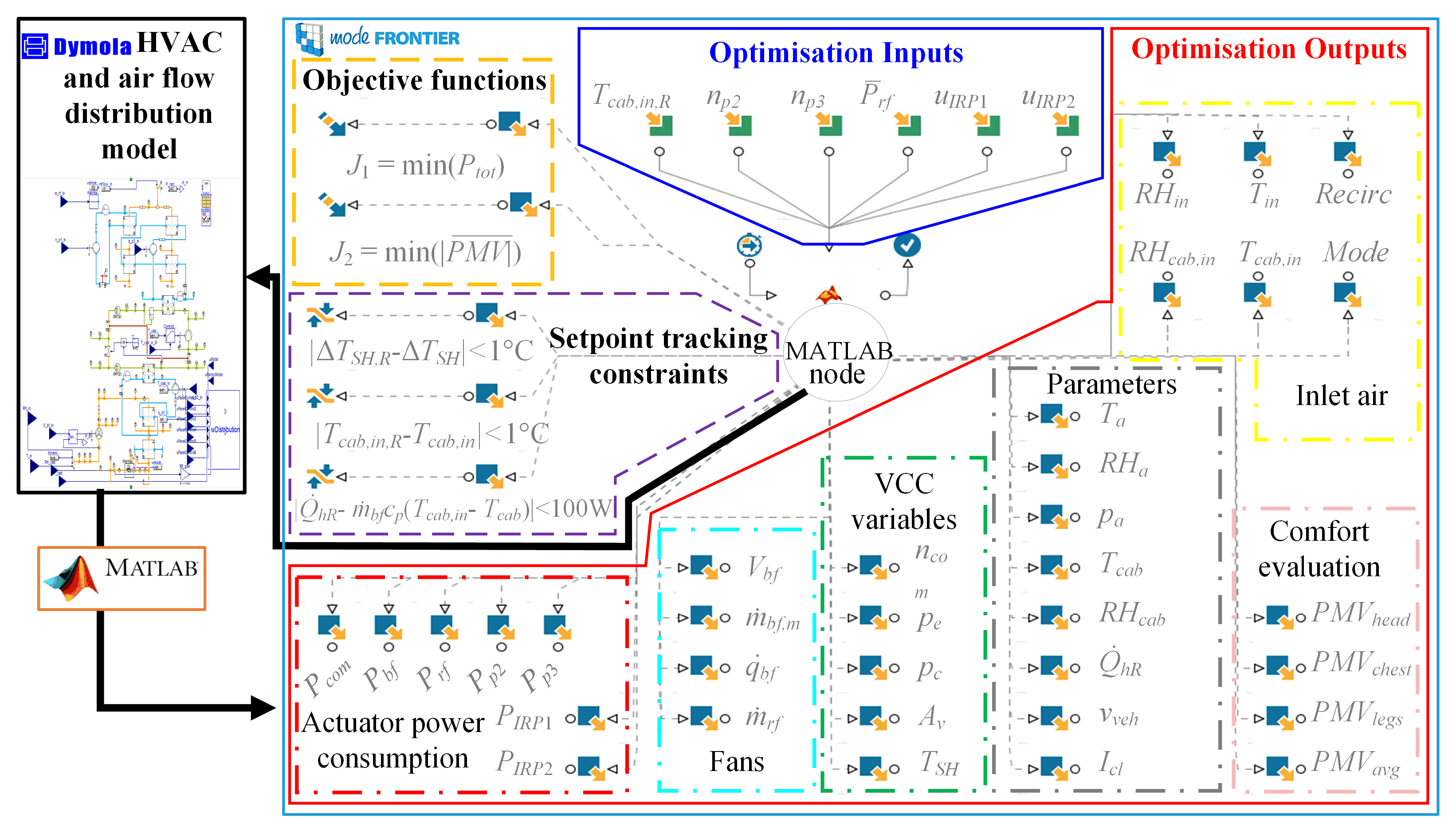



| Control Input Constraints | Setpoint Tracking Constraints |
|---|---|
| Parameter | Value |
|---|---|
| Heating power demand grid | hR ∈ {1:0.5:6} kW |
| Cabin air temperature grid | Tcab ∈ {−10:5:25} °C |
| Cabin relative humidity | RHcab = 10% |
| Ambient conditions | Tamb = −10 °C, RHamb = 60%, pamb = 101.3 kPa |
| Dassl solver tolerance | 0.0001 |
| Case | Tcab,R [degC] | IRP | Eel [Wh] | tPMV,05 [s] | C2 [min] |
|---|---|---|---|---|---|
| 1 | 22.5 | w/o IRP | 433.4 | 493 | 23 |
| (0%) | (0%) | (0%) | |||
| 2 | 22.5 | w/IRP | 473.1 | 314 | 17.8 |
| (+9%) | (−36%) | (−23%) | |||
| 3 | 17.5 | w/o IRP | 341.1 | N/A | 31.0 |
| (−21%) | (+35%) | ||||
| 4 | 17.5 | w/IRP | 407.9 | 315 | 15.9 |
| (−6%) | (−36%) | (−31%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cvok, I.; Ratković, I.; Deur, J. Multi-Objective Optimisation-Based Design of an Electric Vehicle Cabin Heating Control System for Improved Thermal Comfort and Driving Range. Energies 2021, 14, 1203. https://doi.org/10.3390/en14041203
Cvok I, Ratković I, Deur J. Multi-Objective Optimisation-Based Design of an Electric Vehicle Cabin Heating Control System for Improved Thermal Comfort and Driving Range. Energies. 2021; 14(4):1203. https://doi.org/10.3390/en14041203
Chicago/Turabian StyleCvok, Ivan, Igor Ratković, and Joško Deur. 2021. "Multi-Objective Optimisation-Based Design of an Electric Vehicle Cabin Heating Control System for Improved Thermal Comfort and Driving Range" Energies 14, no. 4: 1203. https://doi.org/10.3390/en14041203
APA StyleCvok, I., Ratković, I., & Deur, J. (2021). Multi-Objective Optimisation-Based Design of an Electric Vehicle Cabin Heating Control System for Improved Thermal Comfort and Driving Range. Energies, 14(4), 1203. https://doi.org/10.3390/en14041203