Dynamic Performance of Planetary Gear Joint for Satellite Antenna Driving Mechanism Considering Multi-Clearance Coupling
Abstract
:1. Introduction
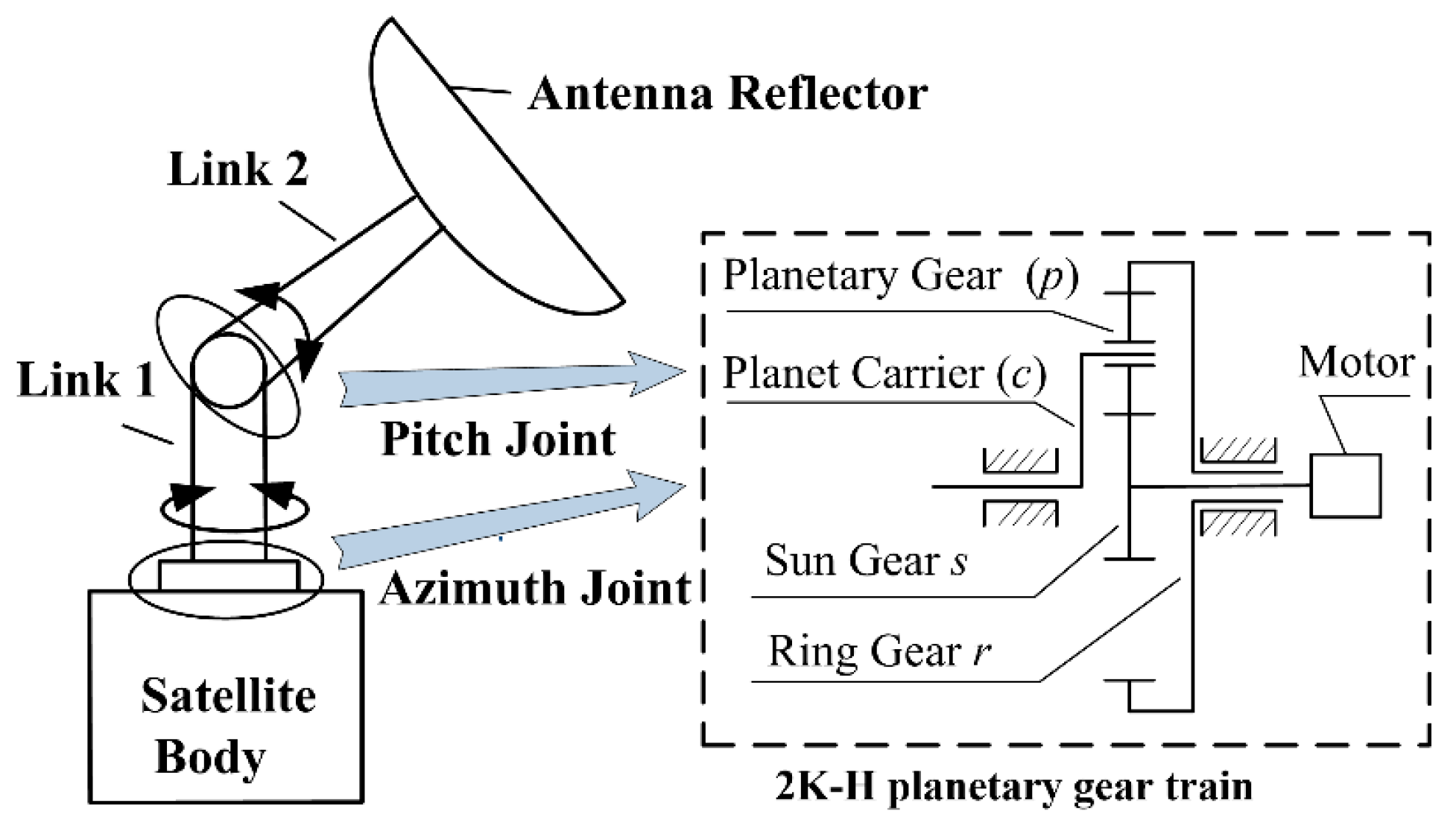
2. Dynamic Model of the Dual-Axis Driving Mechanism for Satellite Antenna with Planetary Gear Joint Considering Multi-Clearance Coupling
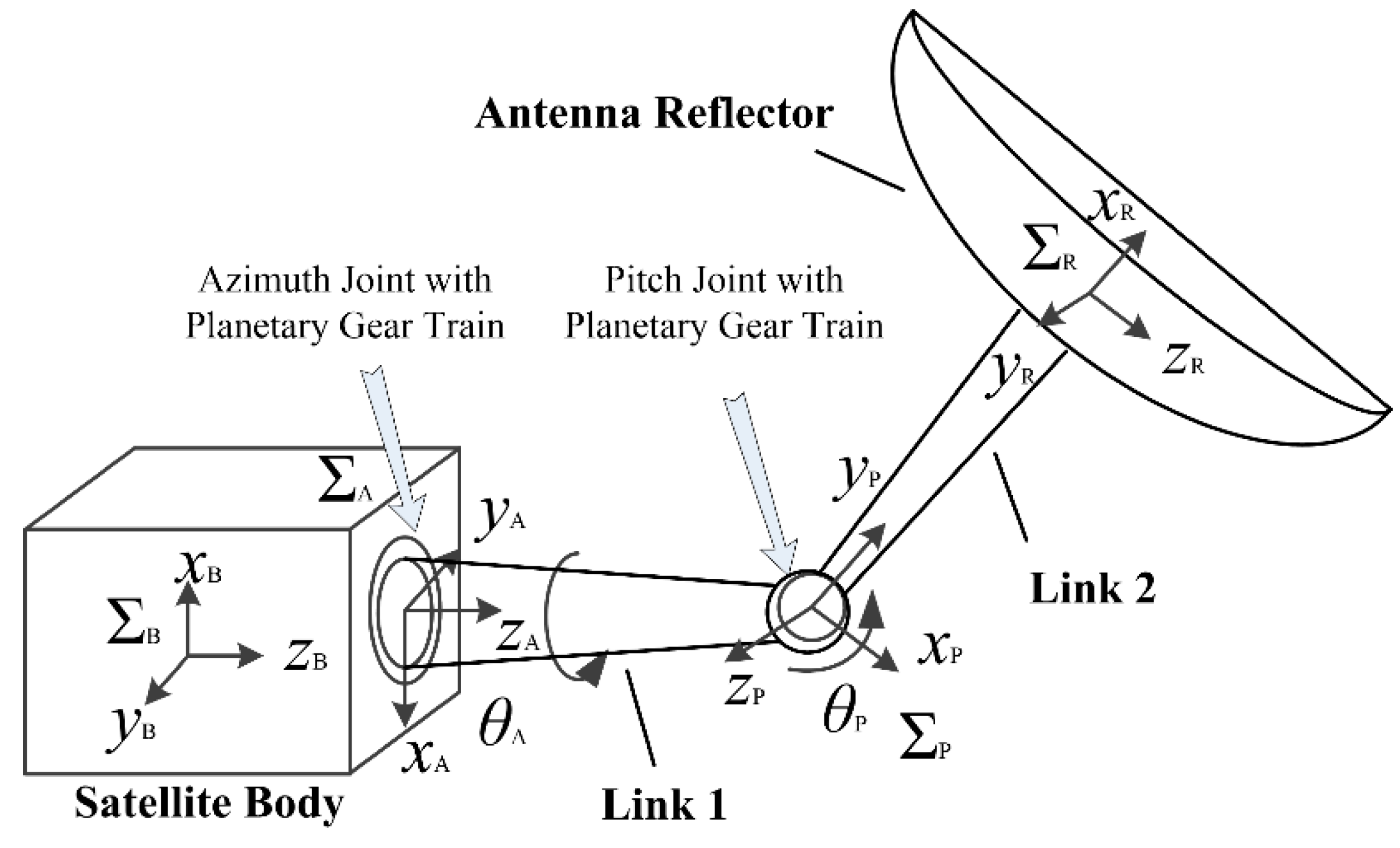
2.1. The Simplification of Joints
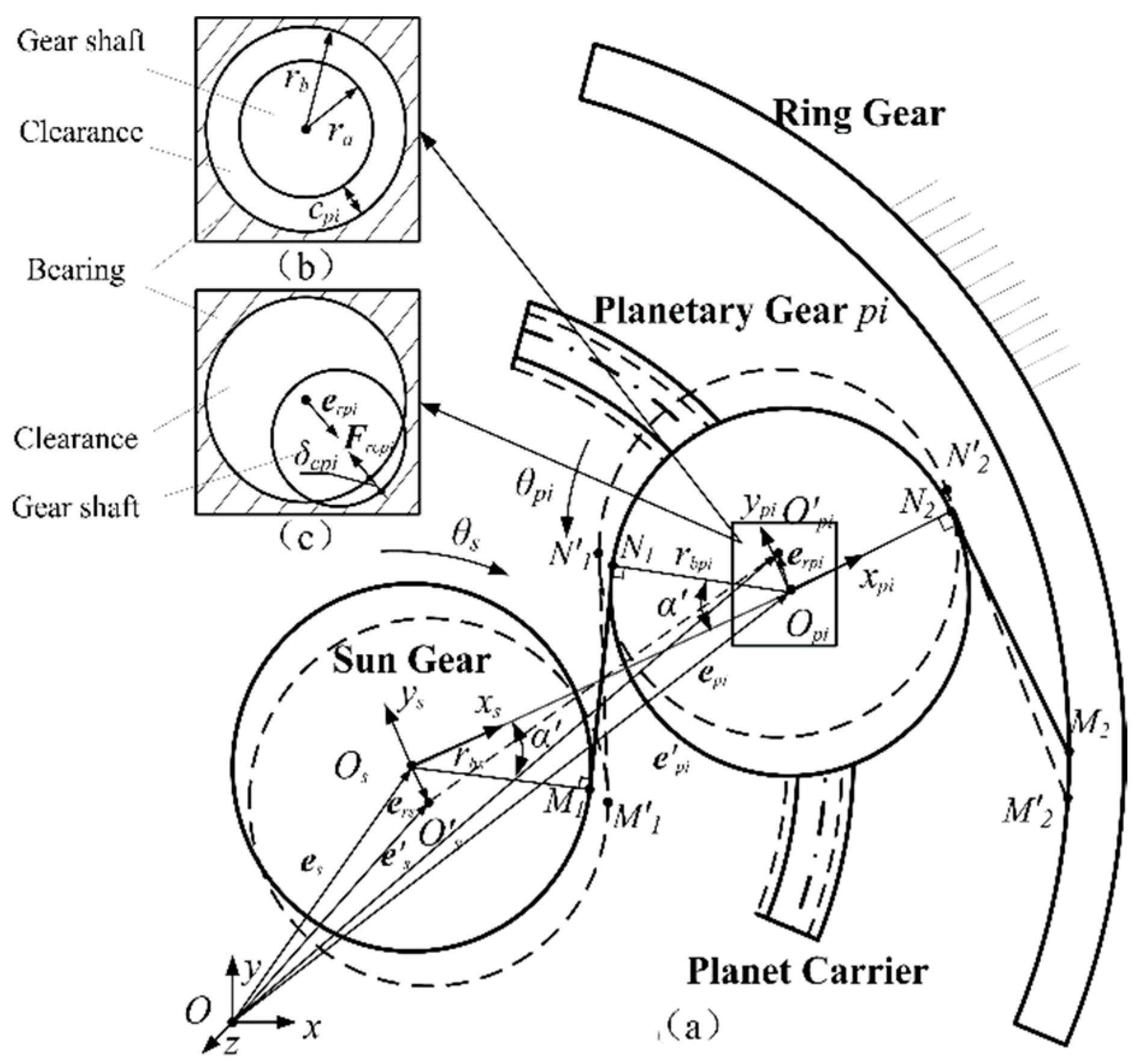
2.2. Contact Force Model of Planetary Gear Pair
2.2.1. Calculation of the Meshing Force
2.2.2. Calculation of the Radial Contact Force
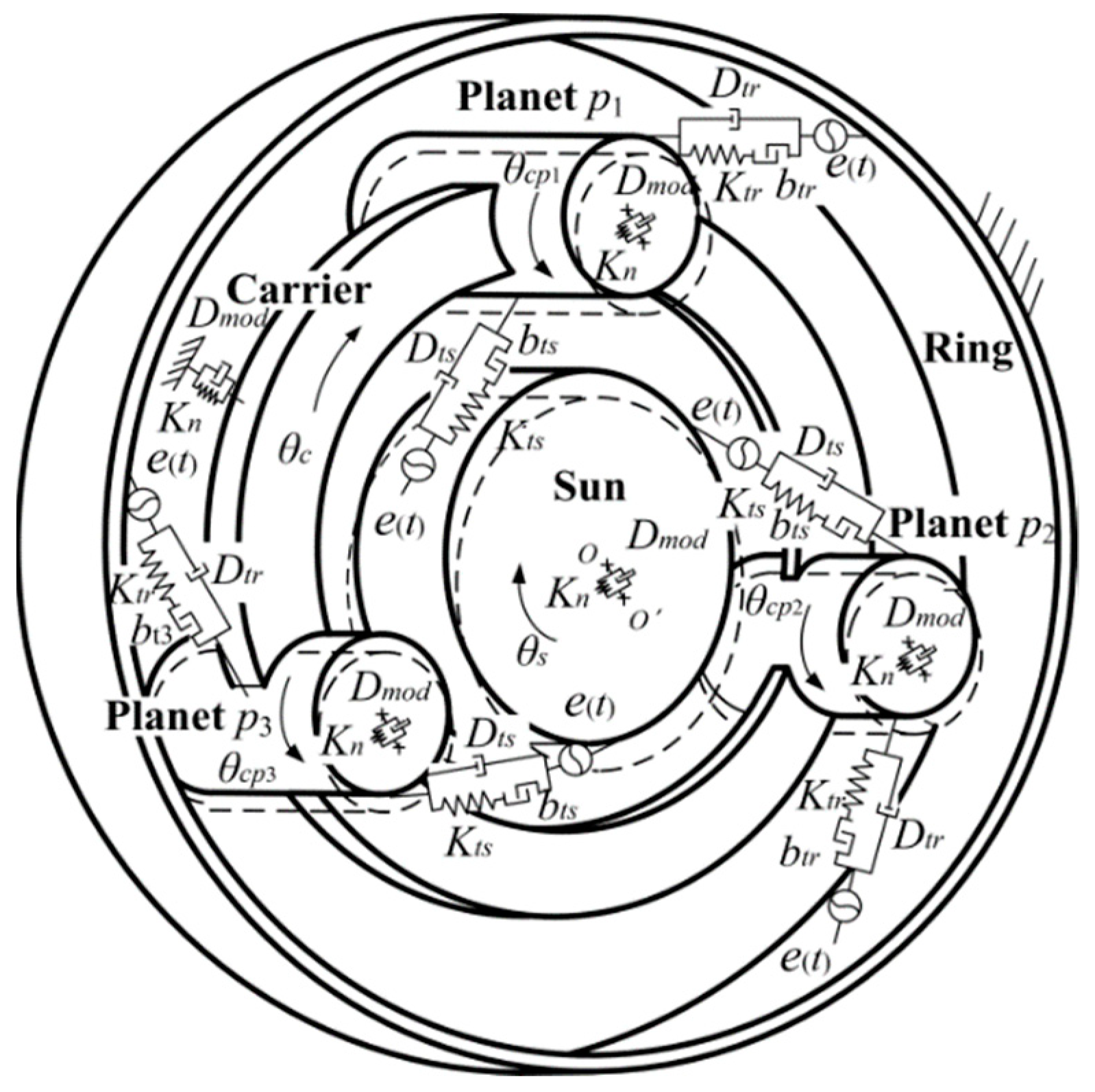
2.3. The Modified Dynamic Model of 2K-H Planetary Gear Joint
2.4. System Dynamic Model
3. Numerical Simulation and Dynamic Performance Analysis
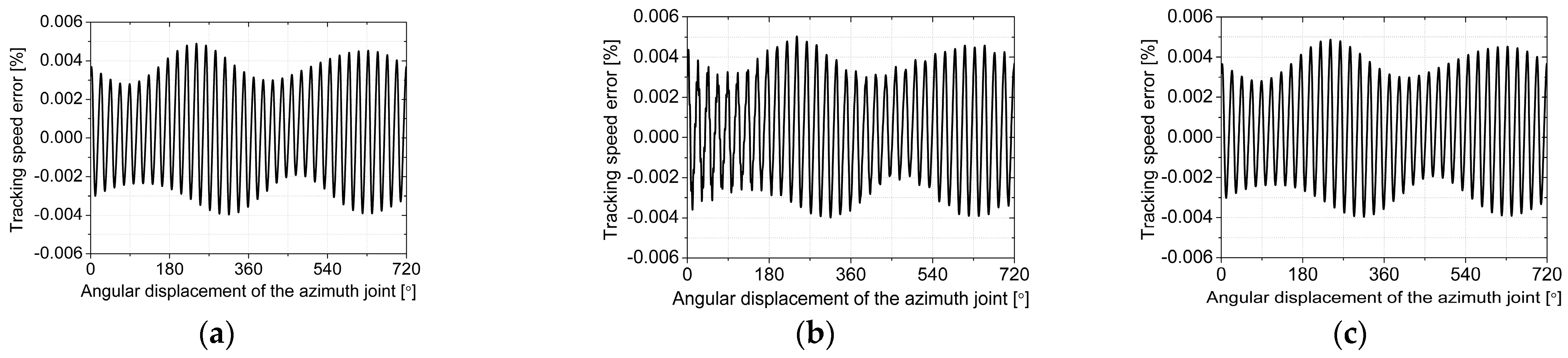
3.1. Simulations of Dual-Axis Driving Mechanism with Multi-Clearance Coupling in Single-Axis Driving Mode
3.1.1. Effects of Rotational Speed
3.1.2. Effects of Radial Clearance
3.1.3. Effects of Backlash
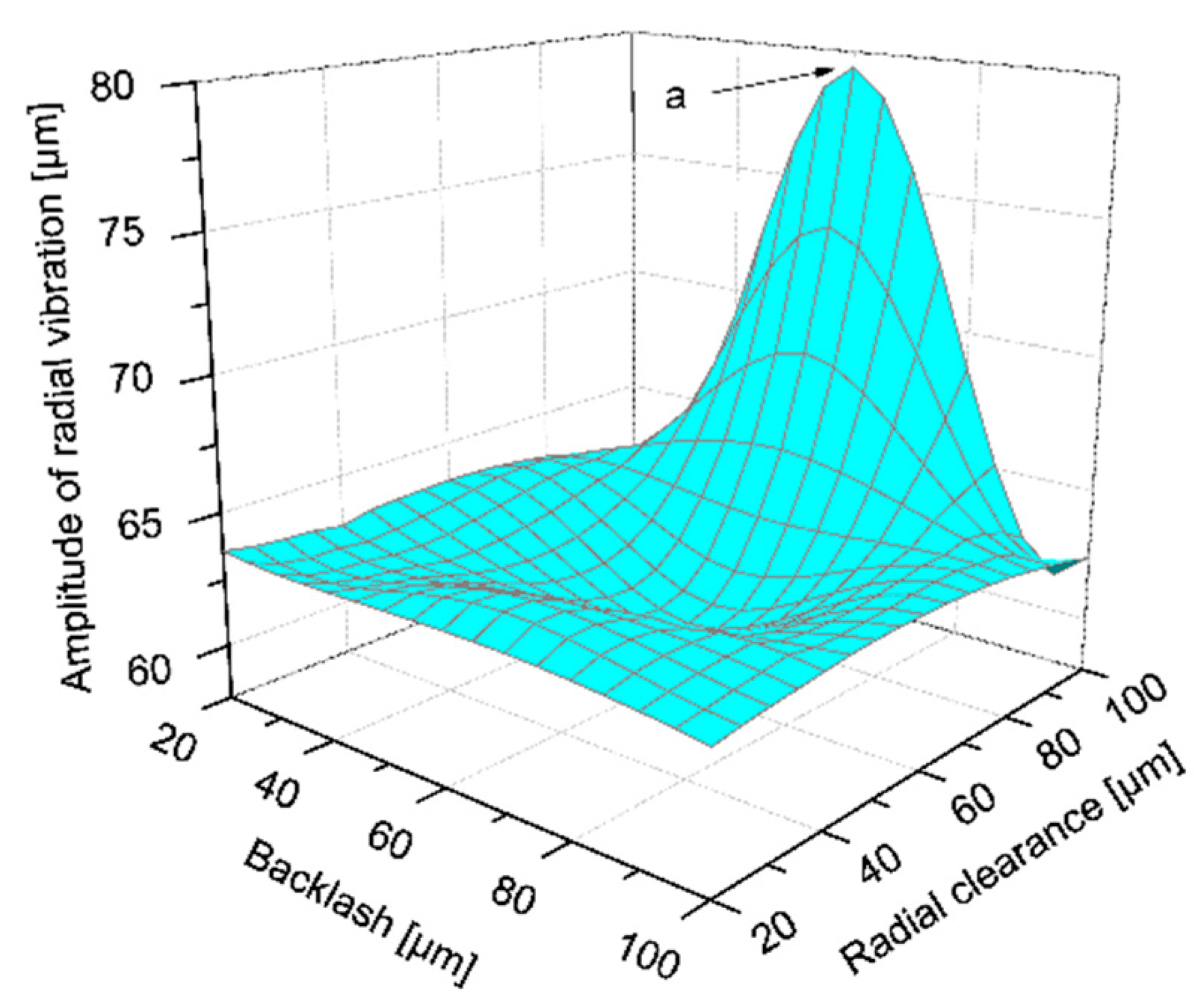
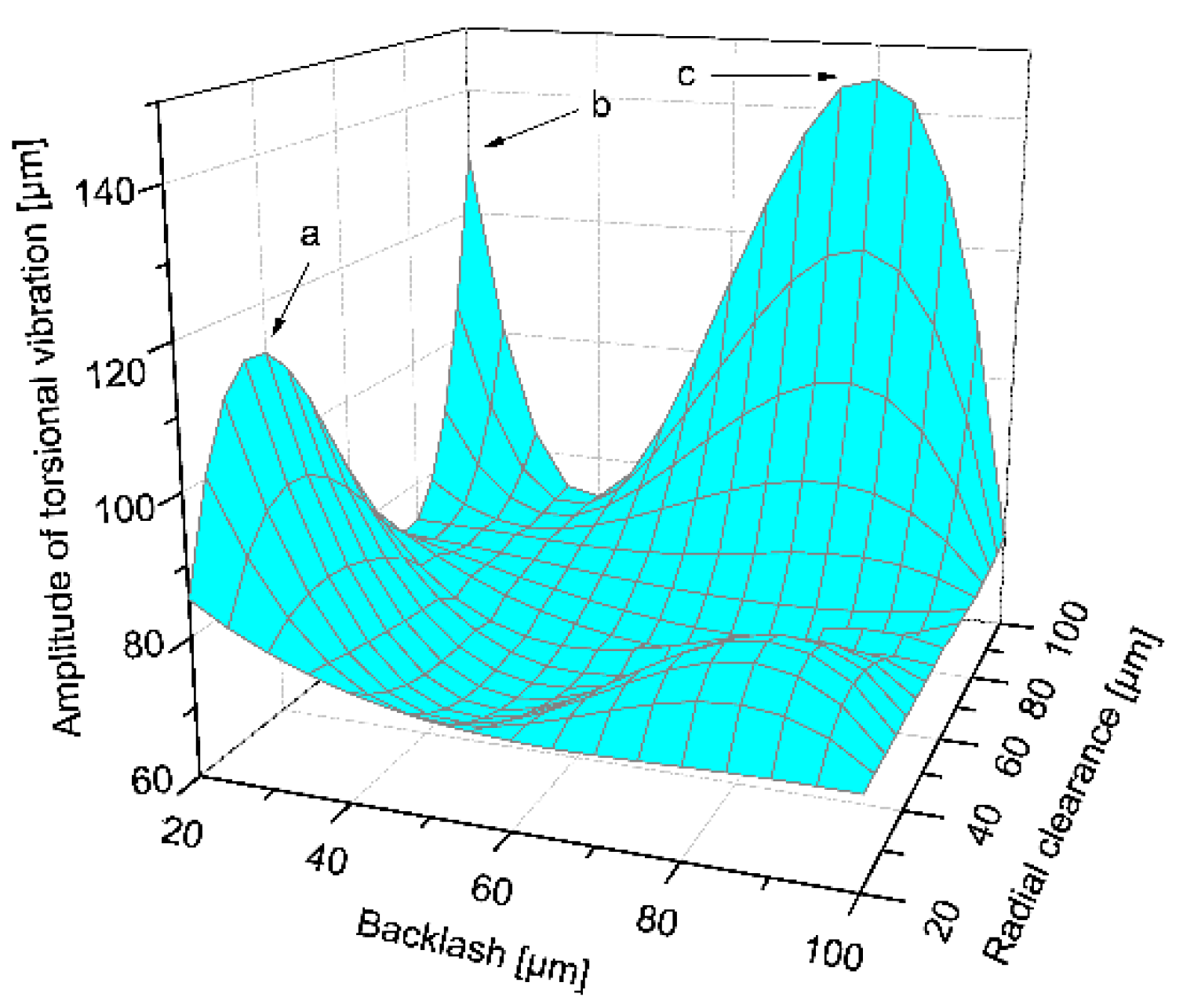
3.1.4. Effects of Coupling between Radial Clearance and Backlash
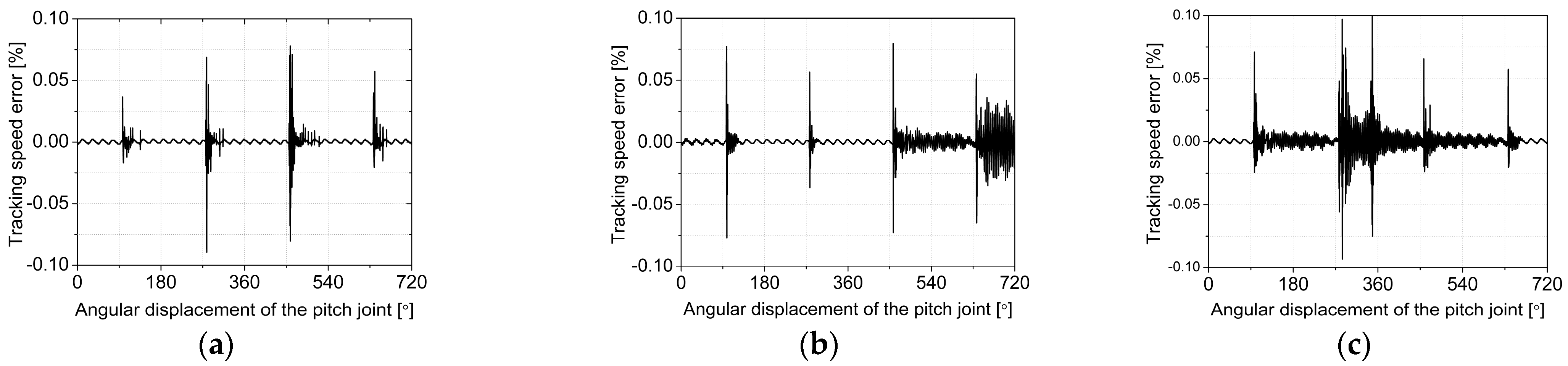
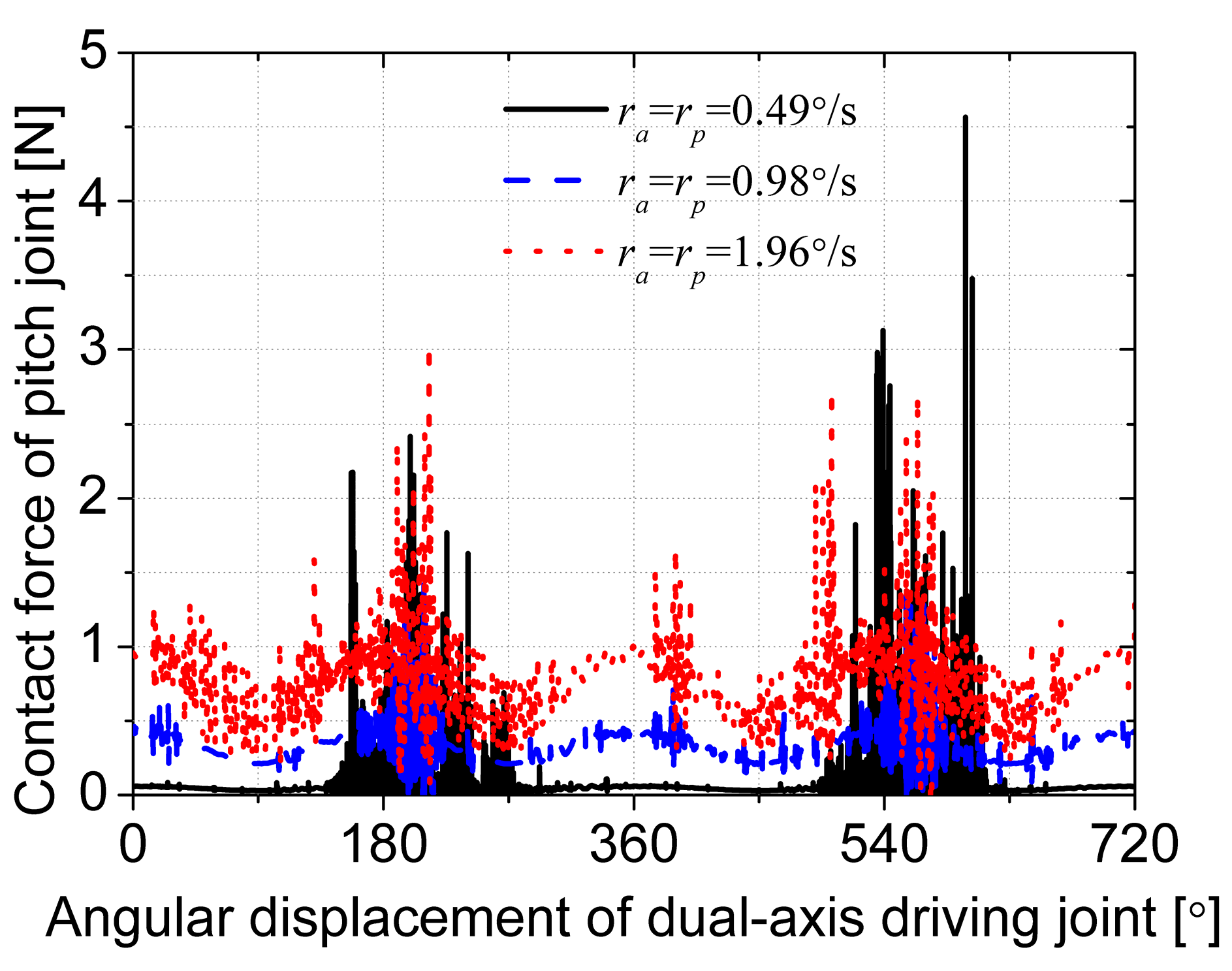
3.2. Simulations of Dual-Axis Driving Mechanism with Multi-Clearance Coupling in Dual-Axis Driving Mode
4. Conclusions
- The coupling effect of the multi-clearance on the dynamic behavior of the dual-axis drive mechanism cannot be ignored. The radial clearance and the backlash in the planetary gear joints have a complex coupling relationship, which is the main factor causing the radial vibration and torsional vibration of the planetary gear joint;
- In a certain clearance size, the vibration of the planetary gear joint is aggravated, which further affects the stability and accuracy of the dual-axis drive mechanism. Reasonable clearance design can improve the dynamic pointing accuracy and tracking accuracy of the dual-axis driving mechanism, and the analysis data in this article can be used for further reference;
- The coupling between rotational speed and clearance will cause uncertainty in the dynamic performance of the multibody system. In a certain range, increasing the rotational speed properly can make the joint output shaft and the bearing in a continuous contact mode and make the system run more smoothly, but the contact force also increases, which will increase the joint wear and make the clearance larger in the long-term operation. Higher size of clearance causes greater impact dynamic load and high frequency shakes of the joint, which makes the dynamic performance of the multibody system worse;
- For the dual-axis driving mechanism, different positions of planetary gear joints have different effects on the dynamic performance of the system. In addition, the dynamic performance of the joints affects each other, which makes the dynamic performance of the system nonlinear such as the contact force of the pitch joint quite different in both driving modes. Compared with the pitch joint, the azimuth joint has a greater impact on the tracking speed accuracy of the system, while the pitch has a greater impact on the radial and torsional vibration of the system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, J.; Ma, X.; Yu, D. Pointing accuracy analyses of a satellitic two-axes antenna pointing mechanism. J. Astronaut. 2007, 28, 545–550. [Google Scholar]
- You, B.; Zhang, H.; Li, W.; Zhao, Z.; Chen, J. Dynamic analysis of satellite antenna system with joint clearance and reflector flexibility. J. Aerosp. Eng. 2014, 27, 297–307. [Google Scholar] [CrossRef]
- Pan, B.; Zhang, D.; Shi, W.; Lin, T. Modeling and analysis on pointing accuracy of antenna in satellite. Spacecr. Eng. 2011, 20, 49–54. [Google Scholar]
- Bai, Z.; Liu, Y.; Sun, Y. Investigation on dynamic responses of dual-axis positioning mechanism for satellite antenna considering joint clearance. J. Mech. Sci. Technol. 2015, 29, 453–460. [Google Scholar] [CrossRef]
- Tian, Q.; Flores, P.; Lankarani, H.M. A comprehensive survey of the analytical, numerical and experimental methodologies for dynamics of multibody mechanical systems with clearance or imperfect joints. Mech. Mach. Theory 2018, 122, 1–57. [Google Scholar] [CrossRef]
- Alves, J.; Peixinho, N.; da Silva, M.T.; Flores, P.; Lankarani, H.M. A comparative study of the viscoelastic constitutive models for frictionless contact interfaces in solids. Mech. Mach. Theory 2015, 85, 172–188. [Google Scholar] [CrossRef]
- Yan, S.; Xiang, W.; Zhang, L. Comprehensive model for 3D revolute joints with clearances in mechanical systems. Nonlinear Dyn. 2015, 80, 309–328. [Google Scholar] [CrossRef]
- Lankarani, H.M.; Nikravesh, P.E. Contact force model with hysteresis damping for impact analysis of multibody systems. ASME J. Mech. Des. 1990, 112, 369–376. [Google Scholar] [CrossRef]
- Yan, S.; Xiang, W.; Huang, T. Advances in modeling of clearance joints and dynamics of mechanical systems with clearances. Acta Sci. Nat. Univ. Pekin. 2016, 52, 741–755. [Google Scholar]
- Flores, P.; Ambrósio, J. Revolute joints with clearance in multibody systems. Comput. Struct. 2004, 82, 1359–1369. [Google Scholar] [CrossRef] [Green Version]
- Flores, P.; Ambrósio, J.; Claro, J.C.P.; Lankarani, H.M. Translational joints with clearance in rigid multibody systems. J. Comput. Nonlinear Dyn. 2008, 3, 011007. [Google Scholar] [CrossRef] [Green Version]
- Flores, P.; Koshy, C.S.; Lankarani, H.M.; Ambrósio, J.; Claro, J.C.P. Numerical and experimental investigation on multibody systems with revolute clearance joints. Nonlinear Dyn. 2011, 65, 383–398. [Google Scholar] [CrossRef] [Green Version]
- Erkaya, S.; Uzmay, B. Investigation on effect of joint clearance on dynamics of four-bar mechanism. Nonlinear Dyn. 2009, 58, 179–198. [Google Scholar] [CrossRef]
- Erkaya, S. Trajectory optimization of a walking mechanism having revolute joints with clearance using ANFIS approach. Nonlinear Dyn. 2013, 71, 75–91. [Google Scholar] [CrossRef]
- Erkaya, S. Effects of joint clearance on the motion accuracy of robotic manipulators. Stroj. Vestn. J. Mech. Eng. 2018, 64, 82–94. [Google Scholar]
- Koshy, C.S.; Flores, P.; Lankarani, H.M. Study of the effect of contact force model on the dynamic response of mechanical systems with dry clearance joints: Computational and experimental approaches. Nonlinear Dyn. 2013, 73, 325–338. [Google Scholar] [CrossRef]
- Marques, F.; Isaac, F.; Dourado, N.; Flores, P. An enhanced formulation to model spatial revolute joints with radial and axial clearance. Mech. Mach. Theory 2017, 116, 123–144. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, K.; Yang, L. Normal force-displacement relationship of spherical joints with clearances. J. Comput. Nonlinear Dyn. 2006, 1, 160–167. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, K.; Yang, L. The FEM analysis and approximate model for cylindrical joints with clearances. Mech. Mach. Theory 2007, 42, 183–197. [Google Scholar] [CrossRef]
- Bai, Z.; Zhao, Y. Dynamic behaviour analysis of planar mechanical systems with clearance in revolute joints using a new hybrid contact force model. Int. J. Mech. Sci. 2012, 54, 190–205. [Google Scholar] [CrossRef]
- Bai, Z.; Zhao, Y. A hybrid contact force model of revolute joint with clearance for planar mechanical systems. Int. J. Nonlinear Mech. 2013, 48, 15–36. [Google Scholar] [CrossRef]
- Tian, Q.; Liu, C.; Machado, M.; Flores, P. A new model for dry and lubricated cylindrical joints with clearance in spatial flexible multibody systems. Nonlinear Dyn. 2011, 64, 25–47. [Google Scholar] [CrossRef]
- Liu, C.; Tian, Q.; Hu, H. Dynamics and control of a spatial rigid-flexible multibody system with multiple cylindrical clearance joints. Mech. Mach. Theory 2012, 52, 106–129. [Google Scholar] [CrossRef]
- Wang, Z.; Tian, Q.; Hu, H.; Flores, P. Nonlinear dynamics and chaotic control of a flexible multibody system with uncertain joint clearance. Nonlinear Dyn. 2011, 86, 1571–1597. [Google Scholar] [CrossRef]
- Li, J.; Huang, H.; Yan, S.; Yang, Y. Kinematic accuracy and dynamic performance of a simple planar space deployable mechanism with joint clearance considering parameter uncertainty. Acta Astronaut. 2017, 136, 34–45. [Google Scholar] [CrossRef]
- Herisanu, N.; Marinca, V. An efficient analytical approach to investigate the dynamics of a misaligned multirotor system. Mathematics 2020, 8, 1083. [Google Scholar] [CrossRef]
- Fan, W.; Yang, Y.; Su, X. Dynamic modeling and vibration characteristics analysis of transmission process for dual-motor coupling drive system. Symmetry 2020, 12, 1171. [Google Scholar] [CrossRef]
- Liu, X.; Wang, J.; Li, W. Dynamic analytical solution of a piezoelectric stack utilized in an actuator and a generator. Appl. Sci. 2018, 8, 1779. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Qin, D.; Liu, C.; Yi, Y.; Jia, H. Dynamic modeling of multistage gearbox and analysis method of resonance danger path. IEEE Access 2019, 7, 154796–154807. [Google Scholar] [CrossRef]
- Kahraman, A.; Singh, R. Non-linear dynamics of a spur gear pair. J. Sound Vib. 1990, 142, 49–75. [Google Scholar] [CrossRef]
- Al-shyyab, A.; Kahraman, A. Non-linear dynamic analysis of a multi-mesh gear train using multi-term harmonic balance method: Period-one motions. J. Sound Vib. 2005, 284, 151–172. [Google Scholar] [CrossRef]
- Al-shyyab, A.; Kahraman, A. A non-linear dynamic model for planetary gear sets. Proc. Inst. Mech. Eng. Part K J. Mul. 2007, 221, 567–576. [Google Scholar] [CrossRef]
- Al-shyyab, A.; Alwidyan, K.; Jawarneh, A.; Tlilan, H. Non-linear dynamic behaviour of compound planetary gear trains: Model formulation and semi-analytical solution. Proc. Inst. Mech. Eng. Part K J. Mul. 2009, 223, 199–210. [Google Scholar] [CrossRef]
- Kahraman, A.; Vijayakar, S. Effect of internal gear flexibility on the quasi-static behavior of a planetary gear set. J. Mech. Des. 2001, 123, 408–415. [Google Scholar] [CrossRef]
- Tian, Q.; Xiao, Q.; Sun, Y.; Hu, H.; Liu, H.; Flores, P. Coupling dynamics of a geared multibody system supported by ElastoHydroDynamic lubricated cylindrical joints. Multibody Syst. Dyn. 2015, 33, 259–284. [Google Scholar] [CrossRef] [Green Version]
- Ambarisha, V.K.; Parker, R.G. Nonlinear dynamics of planetary gears using analytical and finite element models. J. Sound Vib. 2007, 302, 577–595. [Google Scholar] [CrossRef]
- Bahk, C.J.; Parker, R.G. Analytical solution for the nonlinear dynamics of planetary gears. J. Comput. Nonlinear Dyn. 2011, 6, 21007. [Google Scholar] [CrossRef]
- Bahk, C.J.; Parker, R.G. Analytical investigation of tooth profile modification effects on planetary gear dynamics. Mech. Mach. Theory 2013, 70, 298–319. [Google Scholar] [CrossRef]
- Cooley, C.G.; Parker, R.G. A frequency domain finite element approach for three-dimensional gear dynamics. J. Vib. Acoust. 2011, 133, 41004. [Google Scholar] [CrossRef]
- Li, X.; You, B.; Zhang, H.; Zhao, Y. Dynamic analysis of gear-rotor system coupled with radial clearance and dynamic backlash. J. Vib. Eng. Technol. 2016, 4, 271–281. [Google Scholar]
- Zhang, H.; Qi, C.; Fan, J.; Dai, S.; You, B. Vibration characteristics analysis of planetary gears with a multi-clearance coupling in space mechanism. Energies 2018, 11, 2687. [Google Scholar] [CrossRef] [Green Version]
- Wei, J.; Zhang, A.; Qin, D.; Lim, T.C.; Shu, R.; Lin, X.; Meng, F. A coupling dynamics analysis method for a multistage planetary gear system. Mech. Mach. Theory 2017, 110, 27–49. [Google Scholar] [CrossRef]
- Yang, T.; Yan, S.; Han, Z. Nonlinear model of space manipulator joint considering time-variant stiffness and backlash. J. Sound Vib. 2015, 341, 246–259. [Google Scholar] [CrossRef]
- Yang, T.; Yan, S.; Ma, W.; Han, Z. Joint dynamic analysis of space manipulator with planetary gear train transmission. Robotica 2016, 34, 1042–1058. [Google Scholar] [CrossRef]
- Bai, Z.; Zhao, J.; Chen, J.; Zhao, Y. Design optimization of dual-axis driving mechanism for satellite antenna with two planar revolute clearance joints. Acta Astronaut. 2018, 144, 80–89. [Google Scholar] [CrossRef]
- Xiang, L.; Zhang, Y.; Gao, N.; Hu, A.J. Nonlinear dynamics of a multistage gear transmission system with multi-clearance. Int. J. Bifurc. Chaos 2018, 28, 1850034. [Google Scholar] [CrossRef]
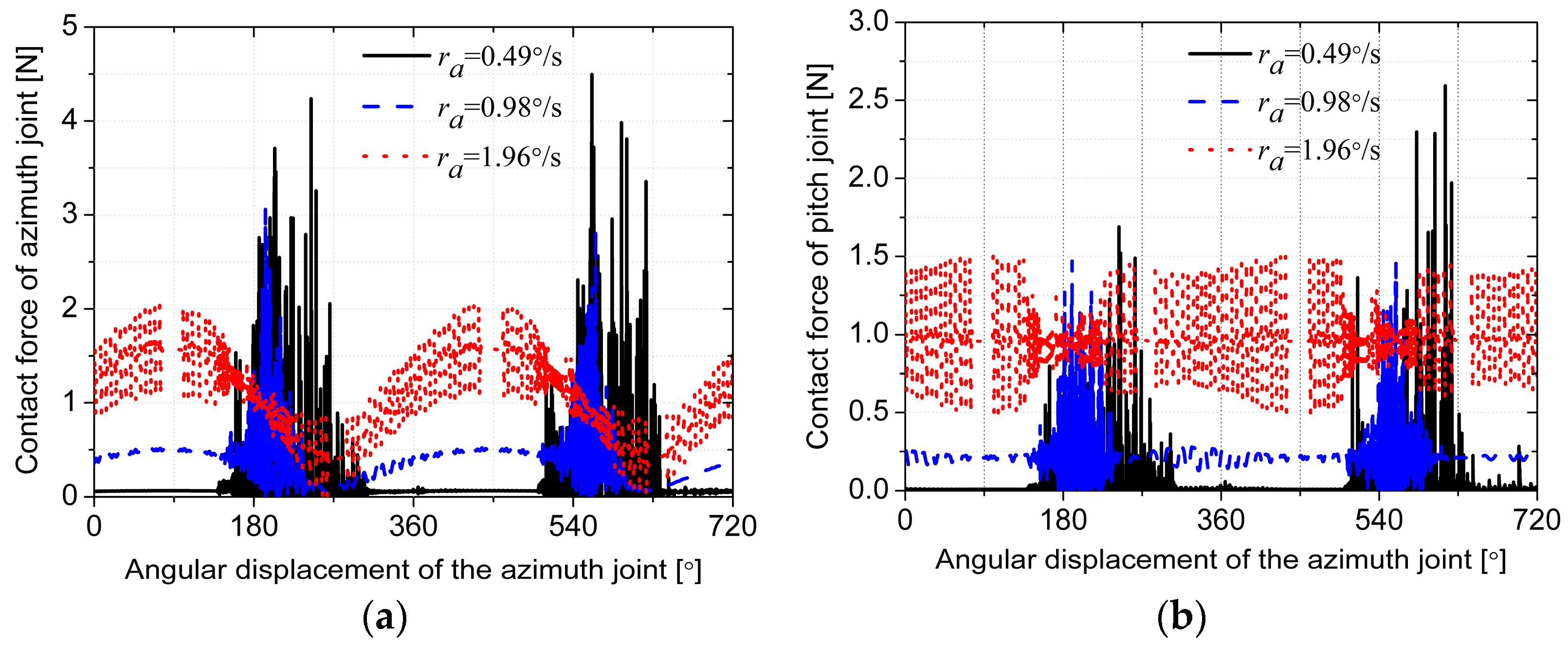

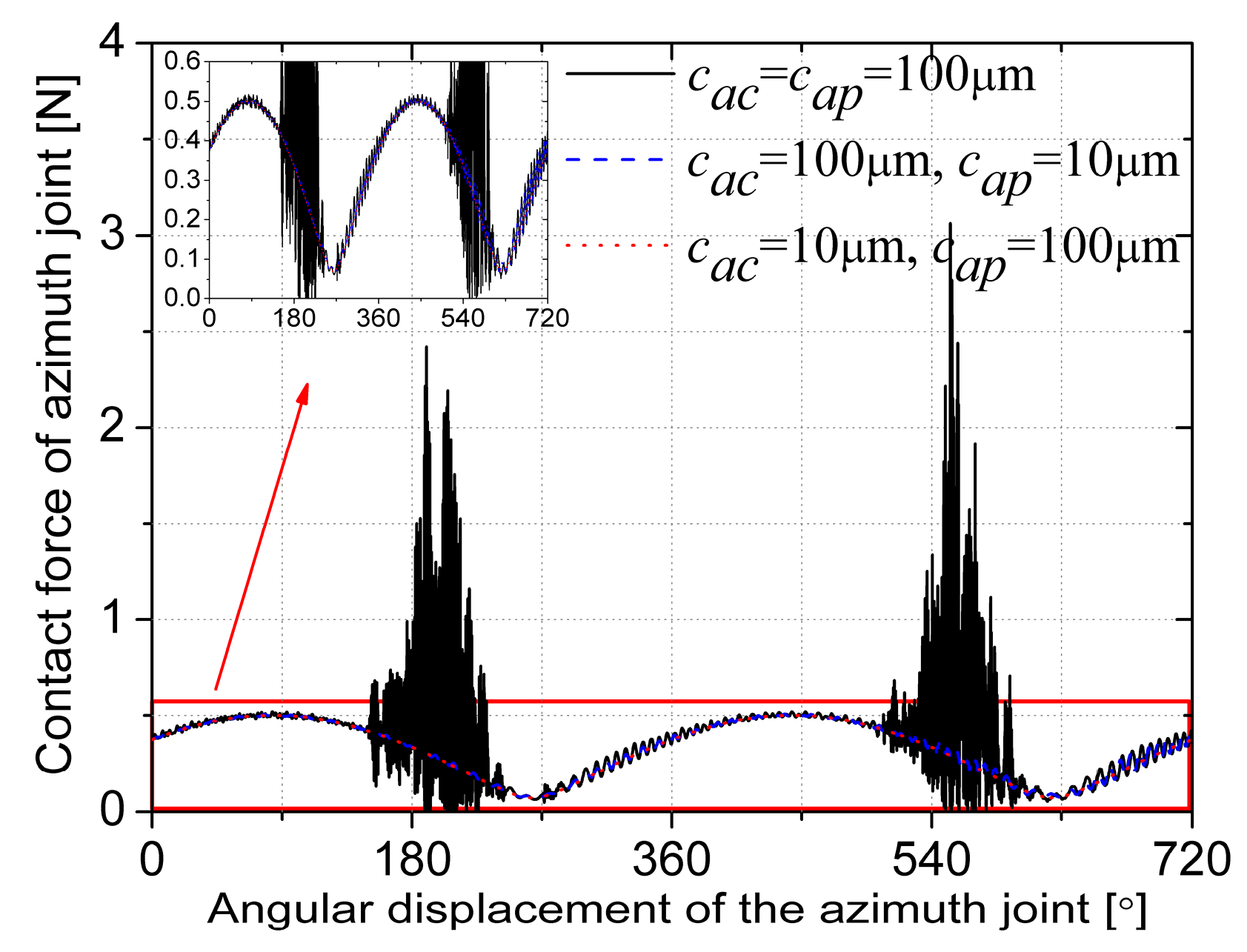


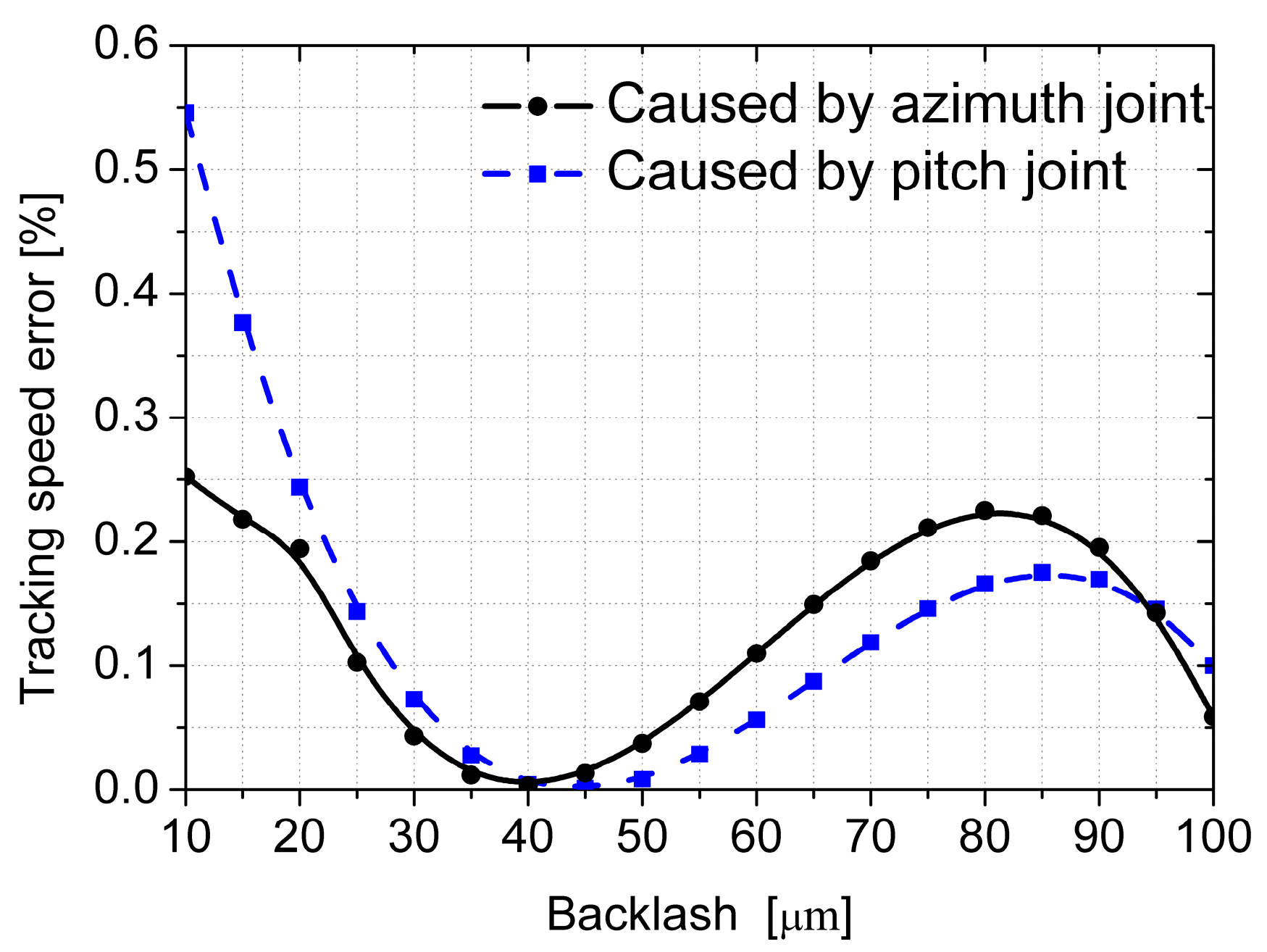
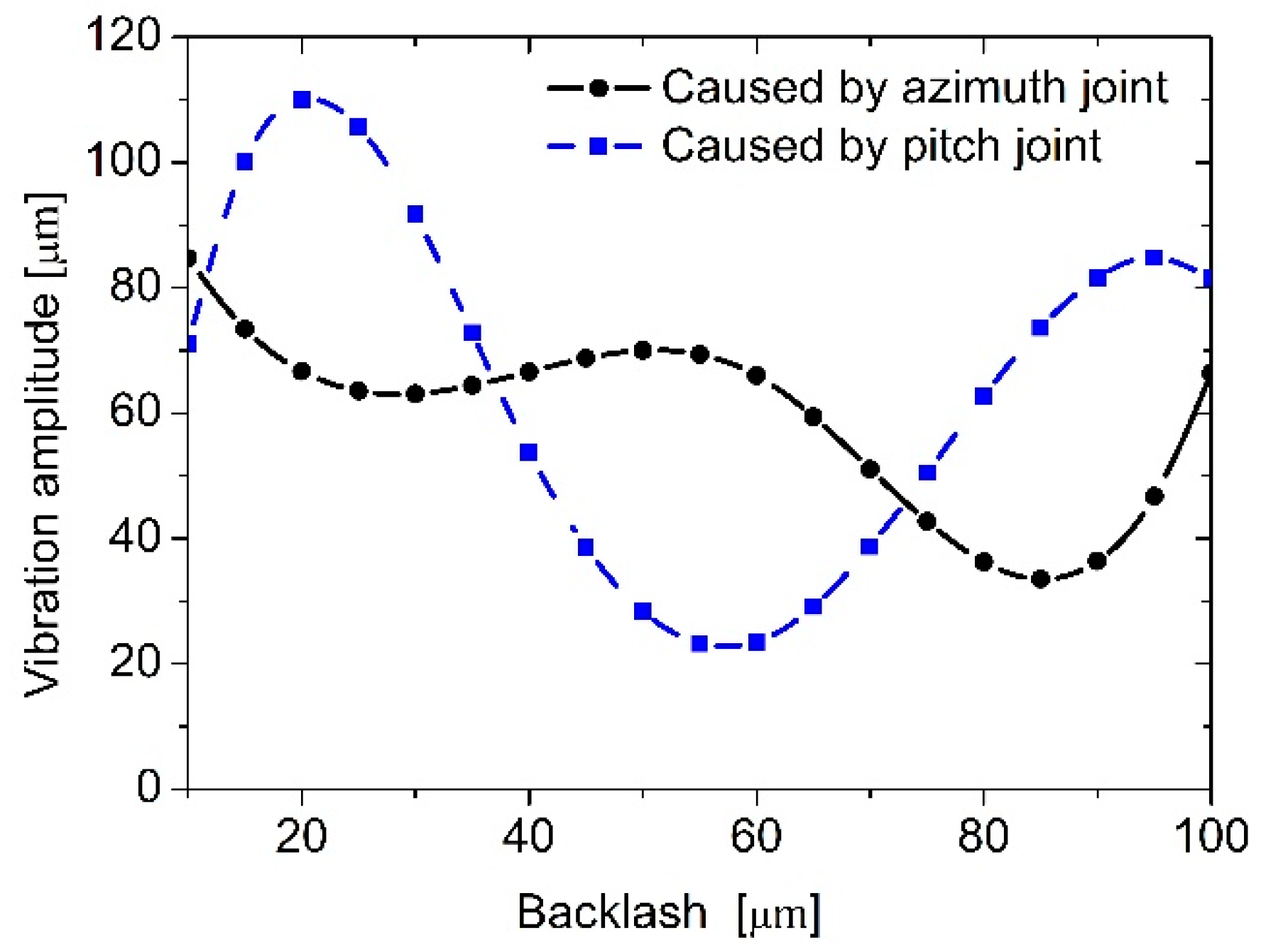




| Rigid Body | Mass/kg | Ixx/kg·m2 | Iyy/kg·m2 | Izz/kg·m2 |
|---|---|---|---|---|
| Spacecraft body | 1500 | 2100 | 1700 | 2400 |
| Azimuth joint | 3.77 | 0.11545 | 0.11545 | 0.004712 |
| Pitch joint | 3.77 | 0.11545 | 0.11545 | 0.004712 |
| Antenna reflector | 8.005 | 0.68297 | 1.05956 | 0.68297 |
| Parameter | Value |
|---|---|
| Driving moment of the azimuth axis, Ta (N·m) | 1.5 cos (2 πt) |
| Driving moment of the pitch axis, Tp (N·m) | 0.8 cos (2 πt) |
| Contact stiffness coefficient, K (N/m) | 1 × 107 |
| Damping coefficient, D (Ns/m) | 100 |
| Step size (s) | 0.0001 |
| Driving Joint | Non-Driving Join | Backlash of Driving Joint | Radial Clearance of Driving Joint |
|---|---|---|---|
| Azimuth joint, and ra = 0.98°/s | Pitch joint, and cp = 100 μm | ba = 10 μm | (a) cac= cap = 100 μm |
| (b) cac = 100 μm, cap =10 μm | |||
| (c) cac = 10 μm, cap =100 μm | |||
| Pitch joint, and rp = 0.98°/s | Azimuth joint, and ca = 100 μm | bp = 10 μm | (a) cpc= cpp = 100 μm |
| (b) cpc =100 μm, cpp =10 μm | |||
| (c) cpc =10 μm, cpp =100 μm |
| Peak Point | Radial Clearance of Planet Carrier cac (μm) | Radial Clearance of Planetary Gear cap (μm) | Vibration Amplitude (μm) |
|---|---|---|---|
| a | 35 | 100 | 19.5 |
| b | 40 | 35 | 20 |
| c | 100 | 30 | 22.5 |
| d | 100 | 100 | 21 |
| Peak Point | Radial Clearance of Planet Carrier cpc (μm) | Radial Clearance of Planetary Gear cpp (μm) | Vibration Amplitude (μm) |
|---|---|---|---|
| a | 85 | 85 | 75 |
| b | 20 | 85 | 125 |
| c | 35 | 35 | 56 |
| Driving Joint | Non-Driving Joint | Radial Clearance of Driving Joint | Backlash of Driving Joint |
|---|---|---|---|
| Azimuth joint, and ra = 0.98°/s | Pitch joint, and cp = 100 μm | cac = cap = 10 μm | ba = 10–100 μm |
| Pitch joint, and rp = 0.98°/s | Azimuth joint, and ca = 100 μm | cpc = cpp = 10 μm | bp = 10–100 μm |
| Driving Joint | Non-Driving Joint | Radial Clearance of Driving Joint | Backlash of Driving Joint | Other Clearance of Driving |
|---|---|---|---|---|
| Azimuth joint, and ra = 0.98°/s | Pitch joint, and cp = 100 μm | (a) cap = 100 μm, | (a) basp = barp = 100 μm; | 10 μm |
| (b) cap = 100 μm, | (b) basp = barp = 10 μm; | |||
| (c) cap = 10 μm, | (c) basp = barp = 100 μm | |||
| Pitch joint, and rp = 0.98°/s | Azimuth joint, and ca = 100 μm | (a) cpp = 100 μm, | (a) bpsp = bprp = 100 μm; | 10 μm |
| (b) cpp = 100 μm, | (b) bpsp = bprp = 10 μm; | |||
| (c) cpp = 10 μm, | (c) bpsp = bprp = 100 μm |
| Peak Point | Radial Clearance of Planetary Gear cpp (μm) | Backlash of Planetary Gear bpsp and bprp (μm) | Vibration Amplitude (μm) |
|---|---|---|---|
| a | 100 | 30 | 78.5 |
| Peak Point | Radial Clearance of Planetary Gear cpp (μm) | Backlash of Planetary Gear bpsp and bprp (μm) | Vibration Amplitude (μm) |
|---|---|---|---|
| a | 40 | 20 | 112 |
| b | 100 | 20 | 130 |
| c | 100 | 80 | 145 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, J.; Liang, L.; Zhao, Y. Dynamic Performance of Planetary Gear Joint for Satellite Antenna Driving Mechanism Considering Multi-Clearance Coupling. Energies 2021, 14, 815. https://doi.org/10.3390/en14040815
Han J, Liang L, Zhao Y. Dynamic Performance of Planetary Gear Joint for Satellite Antenna Driving Mechanism Considering Multi-Clearance Coupling. Energies. 2021; 14(4):815. https://doi.org/10.3390/en14040815
Chicago/Turabian StyleHan, Jianchao, Lei Liang, and Yang Zhao. 2021. "Dynamic Performance of Planetary Gear Joint for Satellite Antenna Driving Mechanism Considering Multi-Clearance Coupling" Energies 14, no. 4: 815. https://doi.org/10.3390/en14040815





