Load Frequency Regulator in Interconnected Power System Using Second-Order Sliding Mode Control Combined with State Estimator
Abstract
:1. Introduction
- The integral sliding surface (ISS) and the decentralized controller are designed based on the estimated system state variables (SSV) so that we do not need to measure the power SSV to achieve LFC. Therefore, the limitation of measuring the power system state variables to achieve LFC in [32,33] has been solved.
- A new LMI technique is proposed to ensure the stability of MAPS via the Lyapunov theory.
- SOSMC combined with state estimator is designed to improve the system performance due to a decrease in chattering in the control input.
- The simulation results indicate the proposed approach has a better performance in terms of settling time and under/overshoots. Thus, this provides evidence of the new controller application for large MAPS.
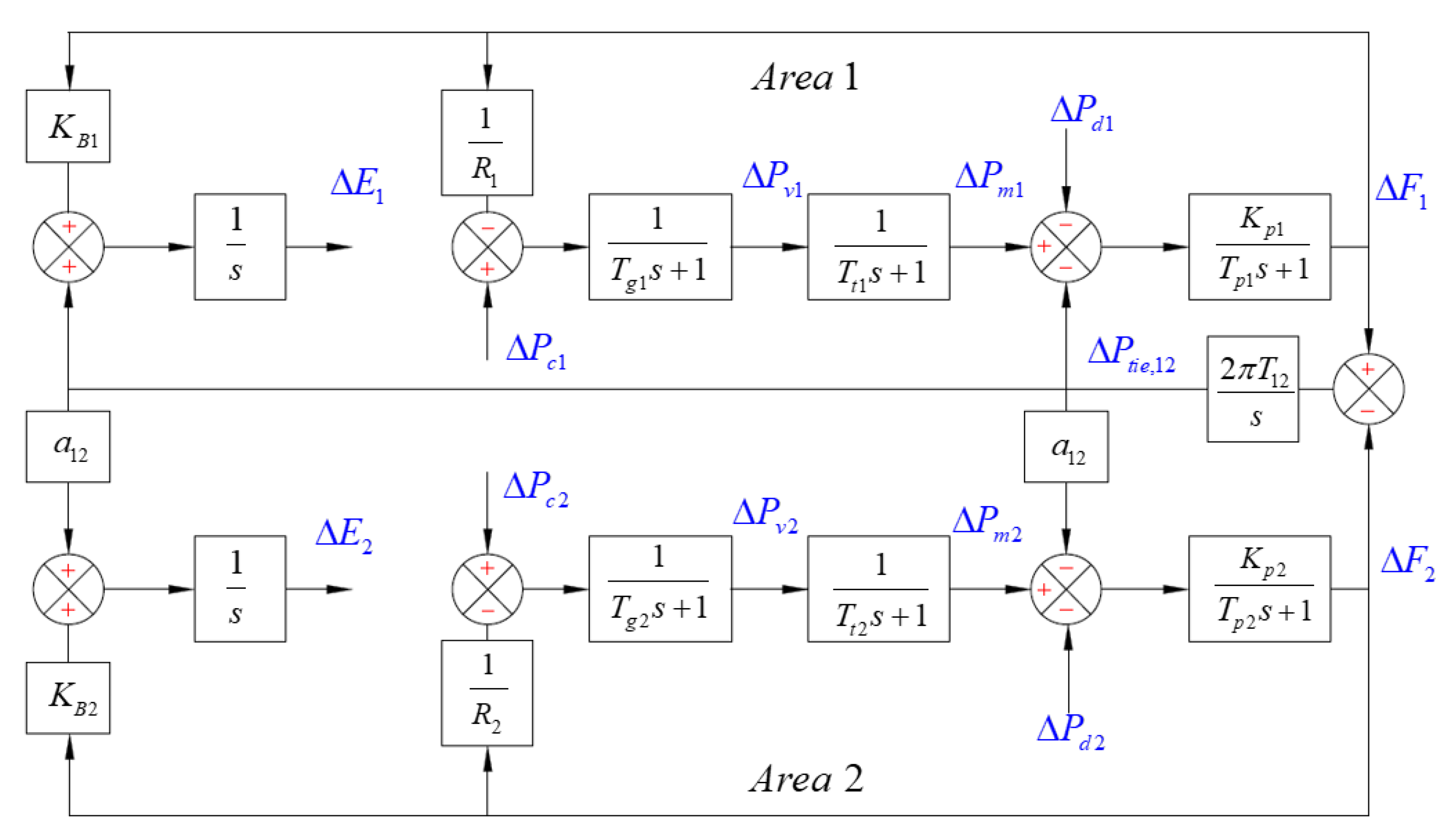
2. Model of Two-Area Power System (TAPS) in State Space Form
3. New Second Order-Sliding Mode Control Based Observer Design
3.1. Design of Observer
3.2. Integral Sliding Surface (ISS) with State Observer
3.3. Design of Second-Order Sliding Mode Controller Based on State Estimator
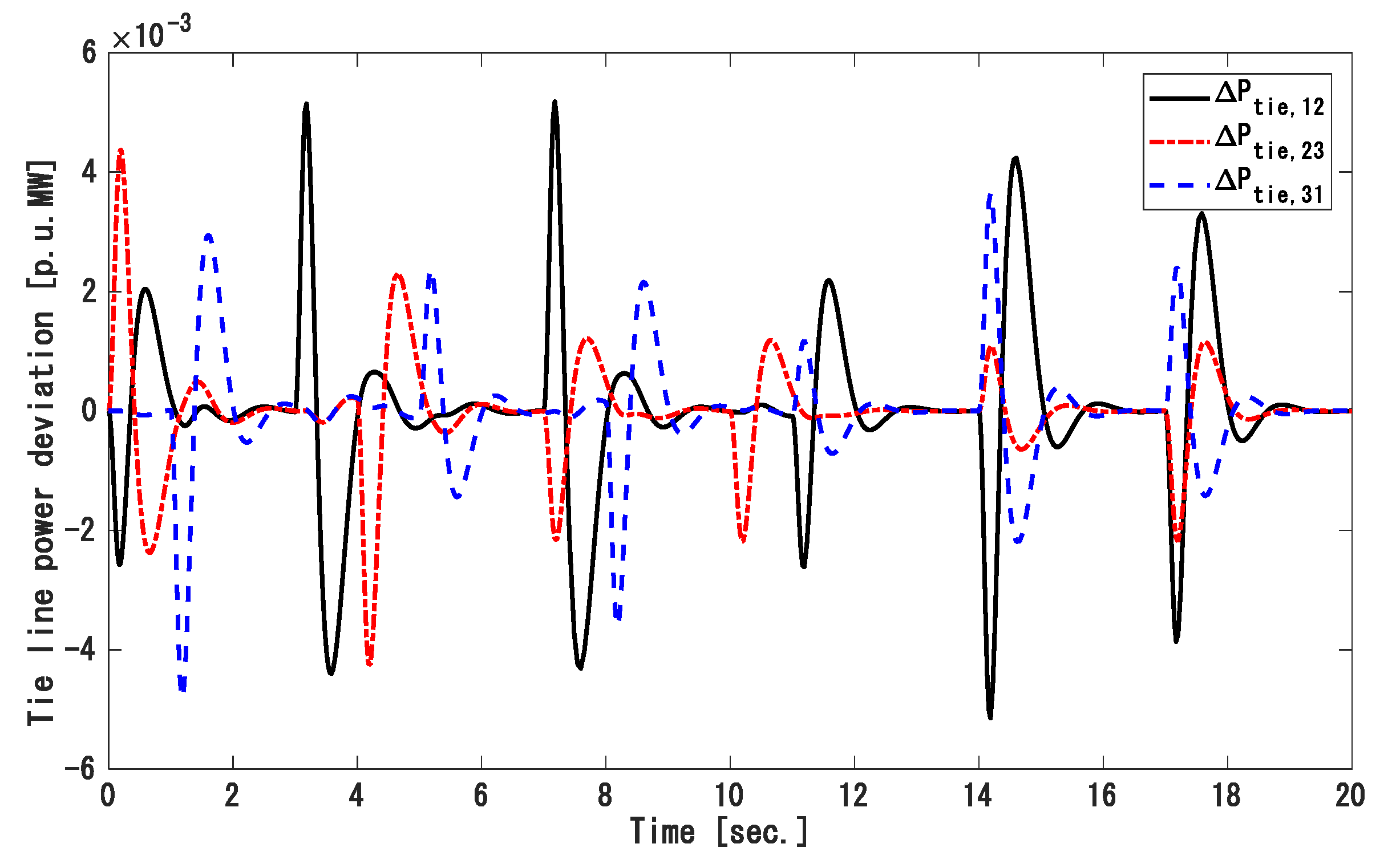
4. Results and Discussions
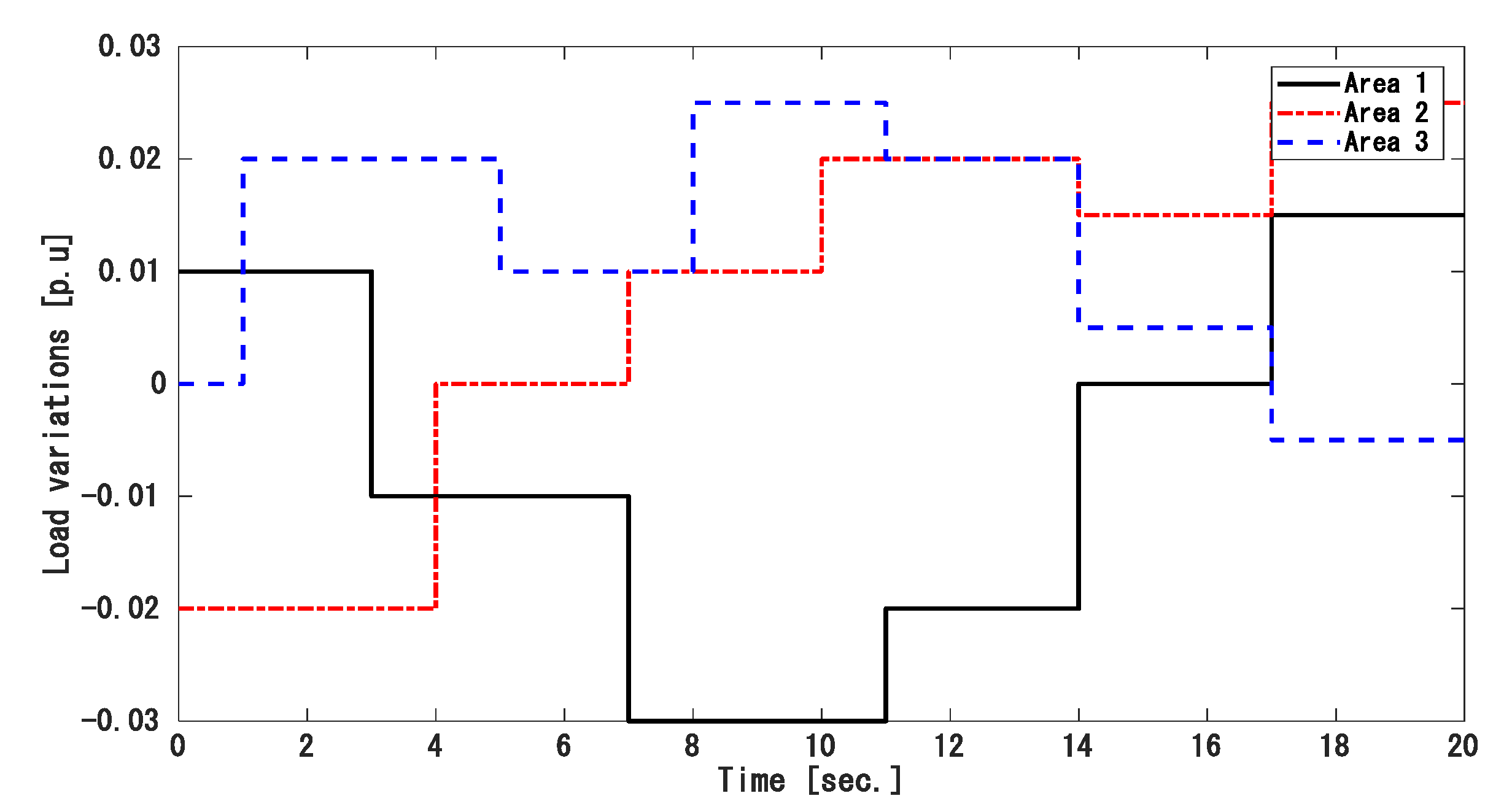
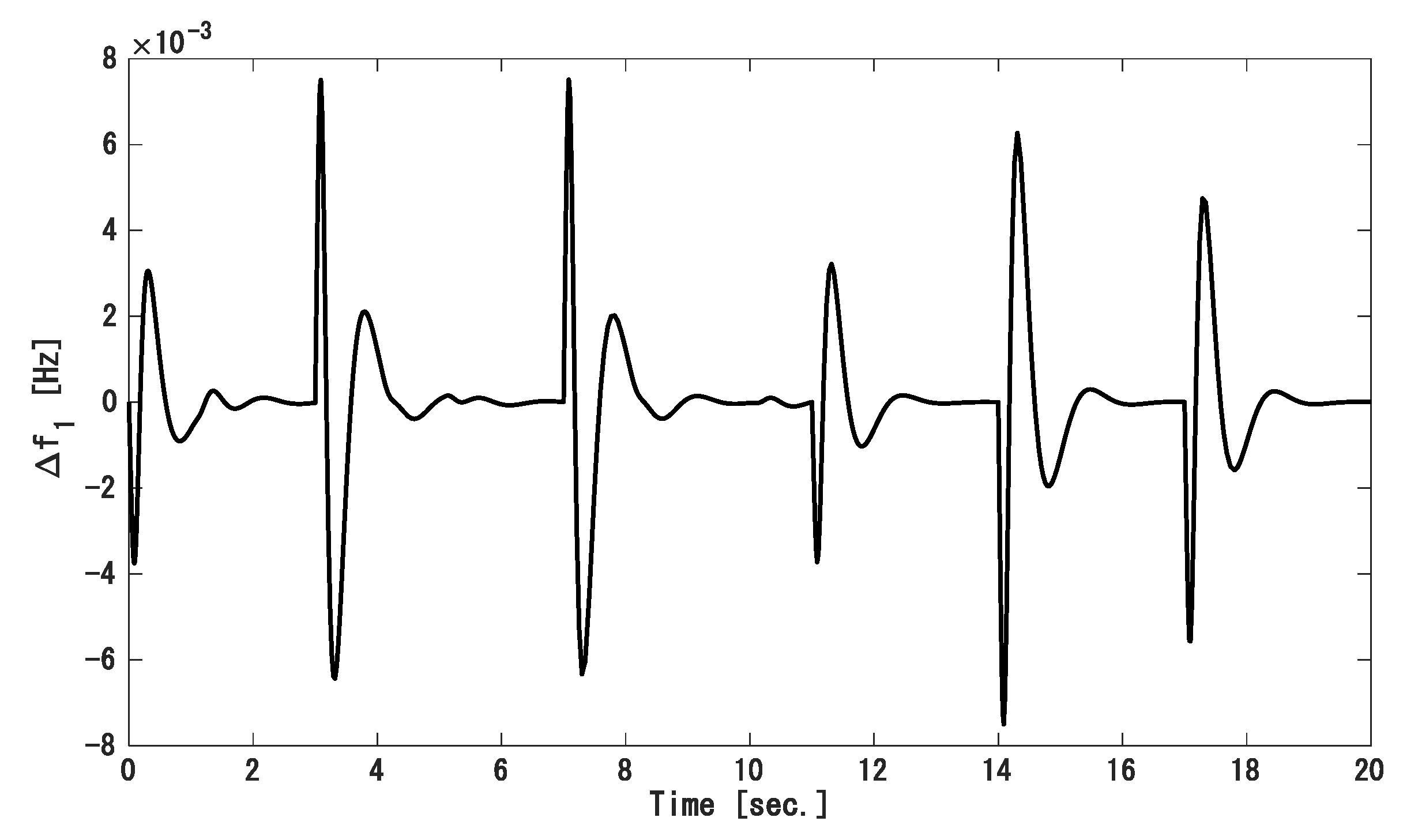
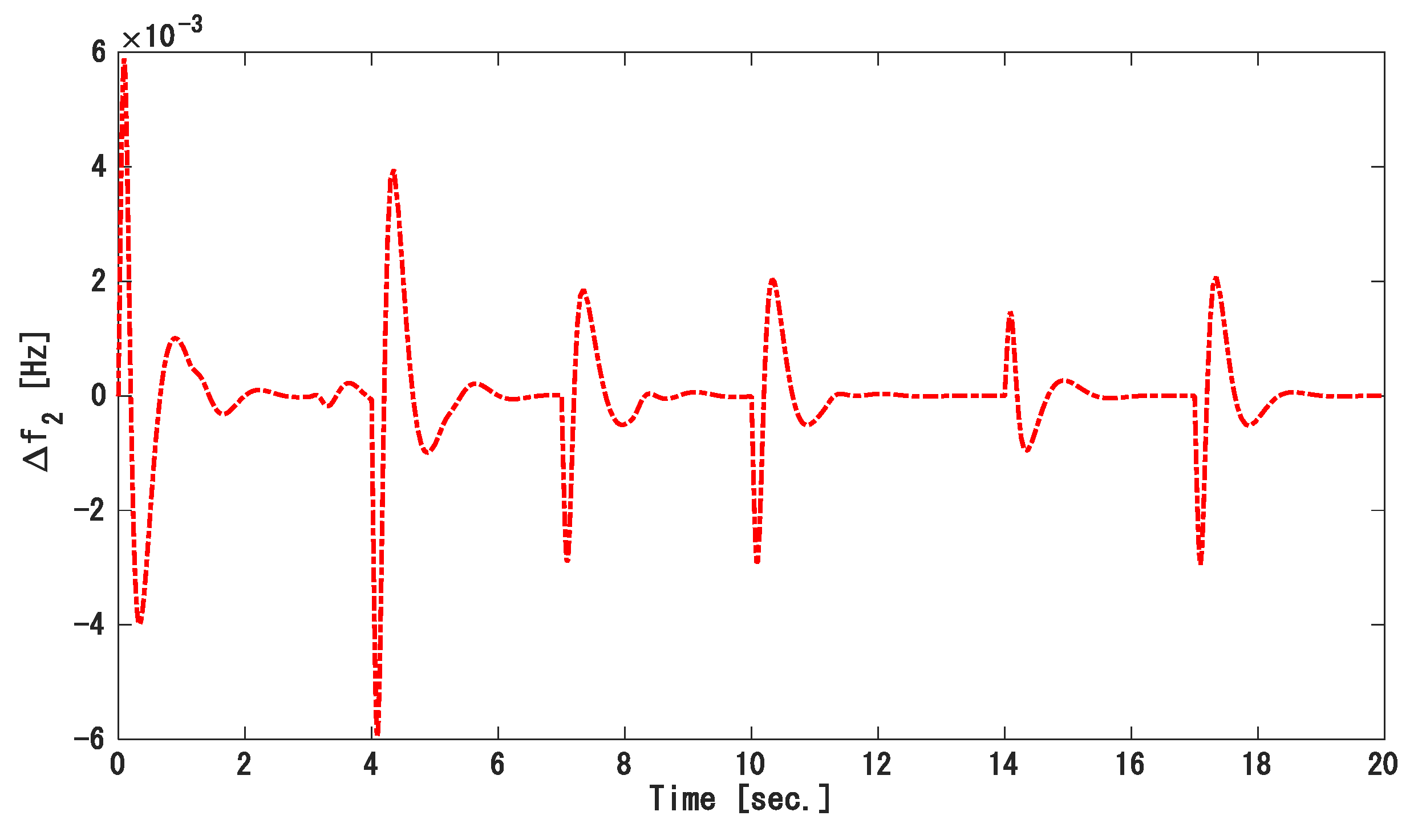
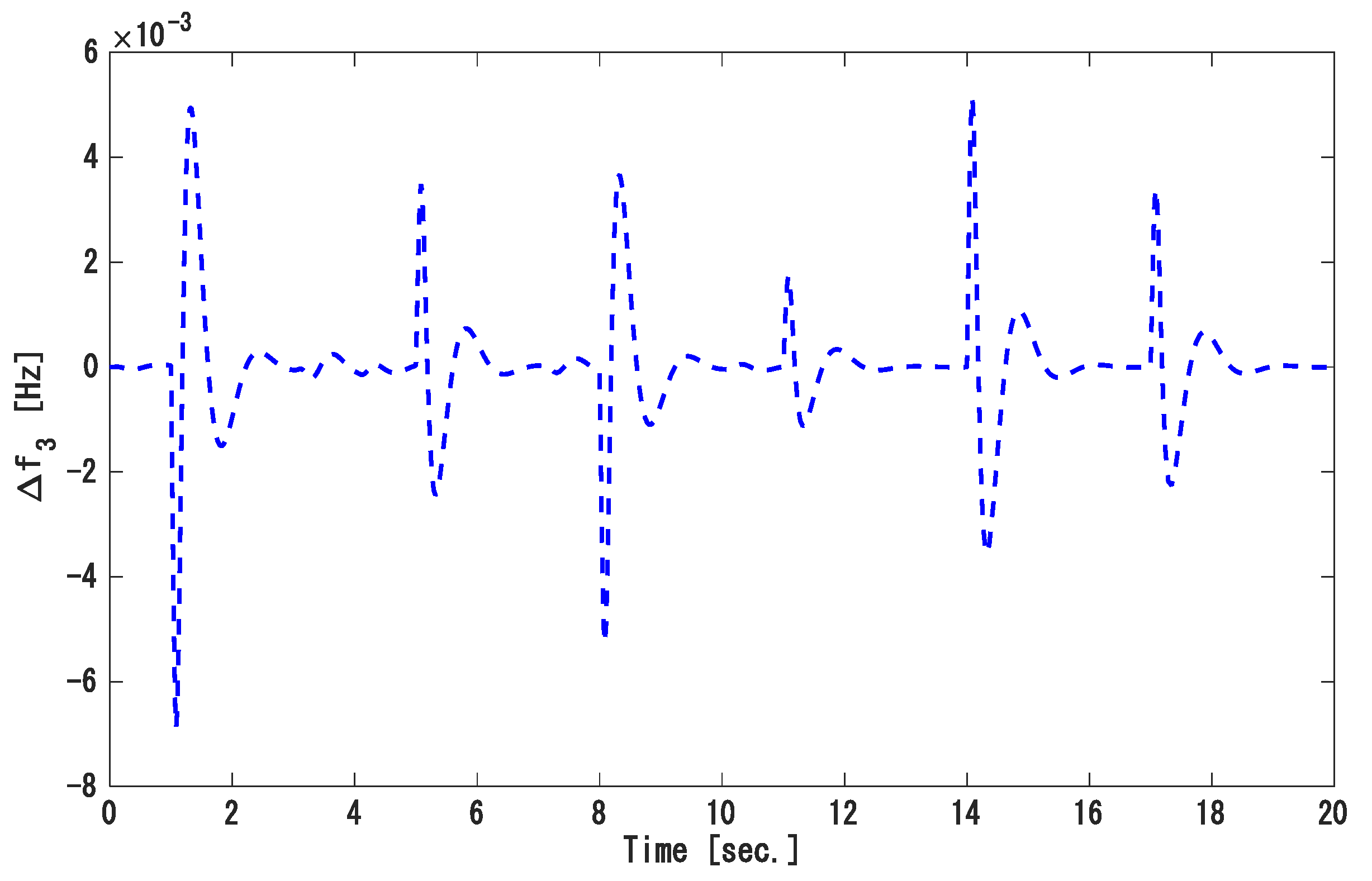
4.1. Simulation 1: Two-Area Power System (TAPS)
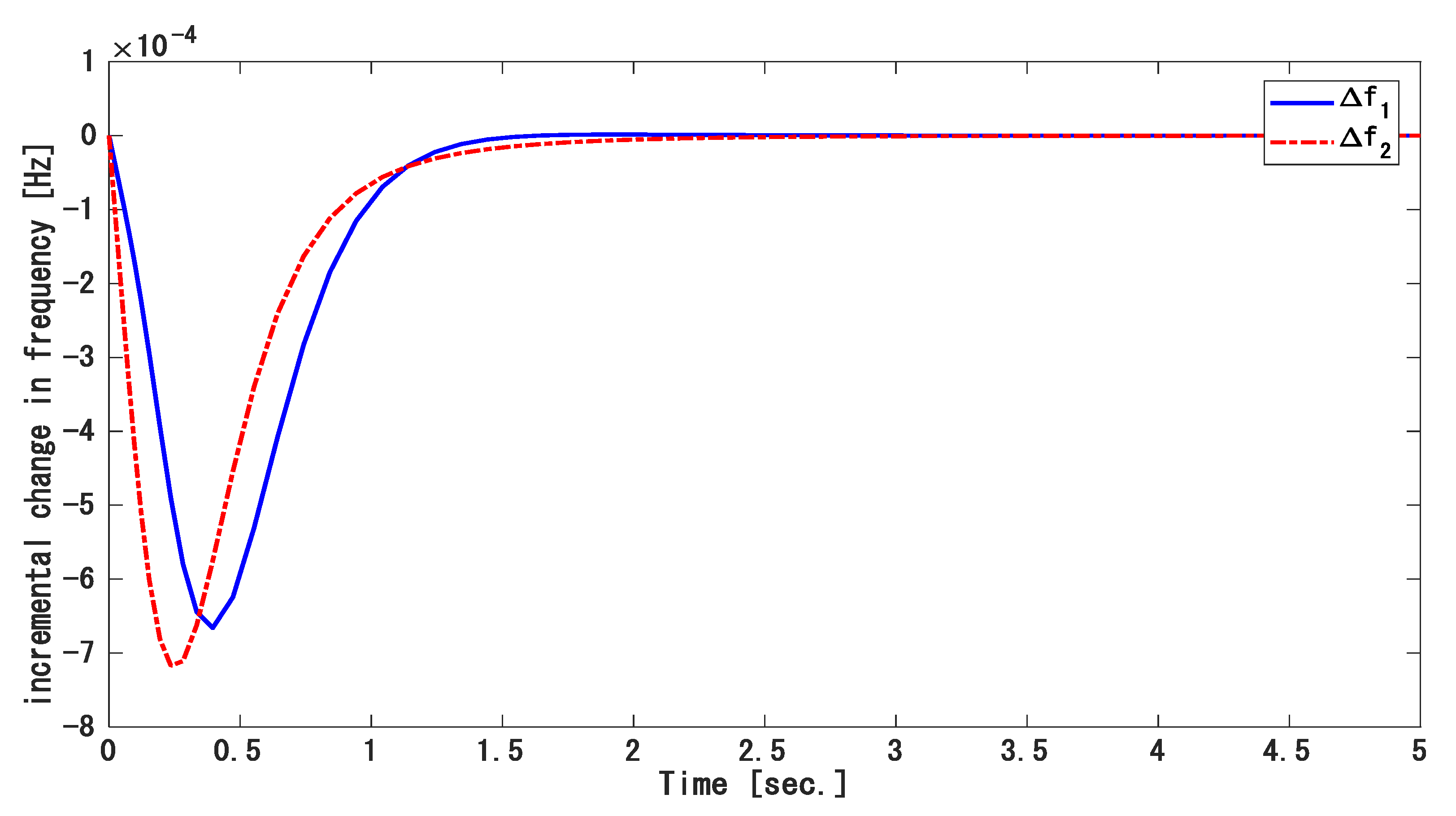
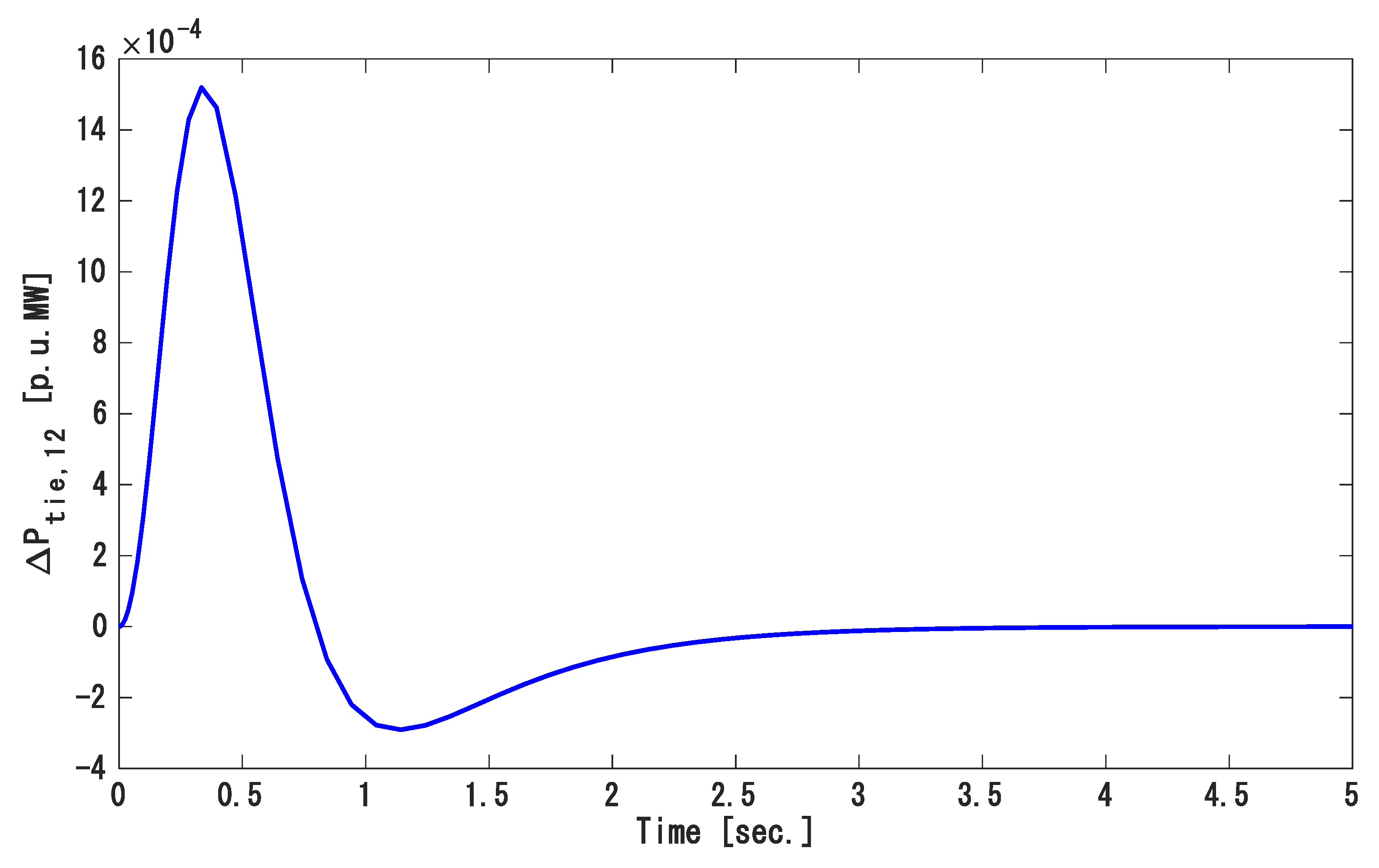
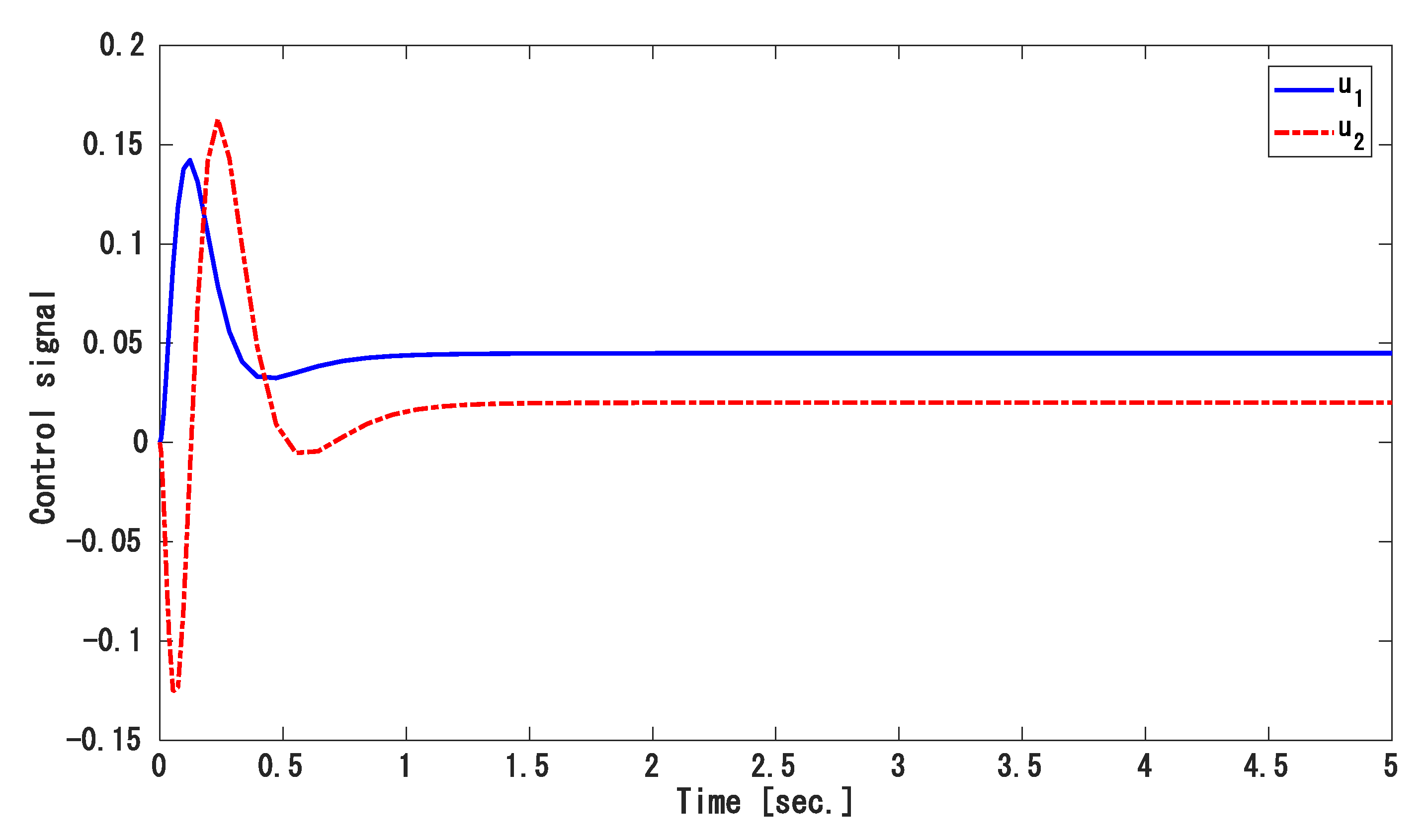
- Case 1: Step load disturbance under a nominal condition.
- Case 2: Step load disturbance under mismatched uncertainty.
- Case 3: Random load disturbance under mismatched uncertainty.
- Case 1: Step load disturbance with nominal conditions
- Case 2. Step load disturbance under the mismatched uncertainty.
- Case 3. Random load disturbance under mismatched uncertainty
4.2. Simulation 2: England 10 Generation 39 Bus Power System
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Parmar, K.P.S.; Majhi, S.; Kothari, D.P. Load frequency control of a realistic power system with multi-source power generation. Int. J. Electr. Power Energy Syst. 2012, 42, 426–433. [Google Scholar] [CrossRef]
- Liu, X.; Nong, H.; Xi, K.; Yao, X. Robust Distributed Model Predictive Load Frequency Control of Interconnected Power System. Math. Probl. Eng. 2013, 15, 10–20. [Google Scholar] [CrossRef]
- Vittal, V.; Mc Calley, J.D.; Anderson, P.M.; Fouad, A.A. Power System Control and Stability, 3rd ed.; Electric Power Systems: Richardson, TX, USA, 2019; pp. 19–400. [Google Scholar]
- Tan, W.; Hao, Y.; Li, D. Load frequency control in deregulated environments via active disturbance rejection. Int. J. Electr. Power Energy Syst. 2015, 66, 166–177. [Google Scholar] [CrossRef]
- Pandey, S.K.; Mohanty, S.R.; Kishor, N. A literature survey on load–frequency control for conventional and distribution generation power systems. Renew. Sustain. Energy Rev. 2013, 25, 318–334. [Google Scholar] [CrossRef]
- Tan, W.; Zhou, H.; Fu, C. Linear active disturbance rejection control for load frequency control of power systems. Control Theory Appl. 2013, 30, 1607–1615. [Google Scholar]
- Lu, X.; Yu, X.; Lai, J.; Guerrero, J.M.; Zhou, H. Distributed Secondary Voltage and Frequency Control for Islanded Microgrids with Uncertain Communication Links. IEEE Trans. Ind. Inform. 2017, 13, 448–460. [Google Scholar] [CrossRef] [Green Version]
- Lim, K.Y.; Wang, Y.; Zhou, R. Robust decentralised load-frequency control of multi-area power systems. IEEE Proc.-Gener. Transm. Distrib. 1996, 143, 377–386. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, Y.; Gao, Z. A robust decentralized load frequency controller for interconnected power systems. ISA Trans. 2012, 51, 410–419. [Google Scholar] [CrossRef] [Green Version]
- Alrifai, M.; Hassan, M.; Zribi, M. Decentralized load frequency controller for a multi-area interconnected power system. Int. J. Electr. Power Energy Syst. 2011, 33, 198–209. [Google Scholar] [CrossRef]
- Pappachen, A.; Fathima, A.P. Critical research areas on load frequency control issues in a deregulated power system: A state-of-the-art-of-review. Renew. Sustain. Energy Rev. 2017, 72, 163–177. [Google Scholar] [CrossRef]
- Sharma, J.; Hote, Y.V.; Prasad, R. Robust PID Load Frequency Controller Design with Specific Gain and Phase Margin for Multi-area Power Systems. IFAC Pap. 2018, 51, 627–632. [Google Scholar] [CrossRef]
- Aditya. Design of Load Frequency Controllers Using Genetic Algorithm for Two Area Interconnected Hydro Power System. Electr. Power Compon. Syst. 2010, 31, 81–94. [Google Scholar] [CrossRef]
- Ramachandran, R.; Madasamy, B.; Veerasamy, V.; Saravanan, L. Load frequency control of a dynamic interconnected power system using generalized Hopfield neural network based self-adaptive PID controller. IET Gener. Transm. Distrib. 2018, 12, 5713–5722. [Google Scholar] [CrossRef]
- Bevrani, H.; Daneshmand, P.R. Fuzzy logic-based load-frequency control concerning high penetration of wind turbines. IEEE Syst. J. 2012, 6, 173–180. [Google Scholar] [CrossRef]
- Yousef, H.A.; AL-Kharusi, K.; Albadi, M.H.; Hossetinzadeh, N. Load frequency control of a multi-area power system: An adaptive fuzzy logic approach. IEEE Trans. Power Syst. 2014, 29, 1822–1830. [Google Scholar] [CrossRef]
- Sinha, S.; Patel, R.; Prasad, R. Application of GA and PSO Tuned Fuzzy Controller for AGC of Three Area Thermal-Thermal-Hydro Power System. Int. J. Comput. Theory Eng. 2010, 2, 238–244. [Google Scholar] [CrossRef]
- Daneshfar, F.; Bevrani, H. Multiobjective design of load frequency control using genetic algorithms. Int. J. Electr. Power Energy Syst. 2012, 42, 257–263. [Google Scholar] [CrossRef]
- Rahman, M.M.; Chowdhury, A.H.; Hossain, M.A. Improved load frequency control using a fast acting active disturbance rejection controller. Energies 2017, 10, 1718. [Google Scholar] [CrossRef] [Green Version]
- Vijaya Chandrakala, K.R.M.; Balamurugan, S.; Sankaranarayanan, K. Variable structure fuzzy gain scheduling based load frequency controller for multi area hydro thermal system. Int. J. Electr. Power Energy Syst. 2013, 53, 375–381. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Shu, H.; Yao, W.; Jiang, L. Sliding-mode perturbation observer-based sliding-mode control design for stability enhancement of multi-machine power systems. Trans. Inst. Meas. Control 2018, 41, 1418–1434. [Google Scholar] [CrossRef]
- Pradhan, S.K.; Das, D.K. H∞ Load Frequency Control Design Based on Delay Discretization Approach for Interconnected Power Systems with Time Delay. J. Mod. Power Syst. Clean Energy 2020. [CrossRef]
- Sun, Y.; Wang, Y.; Wei, Z.; Sun, G.; Wu, X. Robust H∞ Load Frequency Control of Multi-Area Power System with Time Delay: A Sliding Mode Control Approach. IEEE/Caa J. Autom. Sin. 2018, 5, 610–617. [Google Scholar] [CrossRef]
- Mi, Y.; Fu, Y.; Wang, C.; Wang, P. Decentralized Sliding Mode Load Frequency Control for Multi-Area Power Systems. IEEE Trans. Power Syst. 2013, 28, 4301–4309. [Google Scholar] [CrossRef]
- Huynh, V.V.; Minh, B.L.N.; Amaefule, E.N.; Tran, A.-T.; Tran, P.T. Highly Robust Observer Sliding Mode Based Frequency Control for Multi Area Power Systems with Renewable Power Plants. Electronics 2021, 10, 274. [Google Scholar] [CrossRef]
- Huynh, V.V.; Tran, P.T.; Minh, B.L.N.; Tran, A.-T.; Tuan, D.H.; Nguyen, T.M.; Vu, P.T. New Second-Order Sliding Mode Control Design for Load Frequency Control of a Power System. Energies 2020, 13, 6509. [Google Scholar] [CrossRef]
- Wei, Z.; Dong, G.; Zhang, X.; Pou, J.; Quan, Z.; He, H. Noise-Immune Model Identification and State-of-Charge Estimation for Lithium-Ion Battery Using Bilinear Parameterization. IEEE Trans. Ind. Electron. 2020, 68, 312–323. [Google Scholar] [CrossRef]
- Wei, Z.; He, H.; Pou, J.; Tsui, K.L.; Quan, Z.; Li, Y. Signal-Disturbance Interfacing Elimination for Unbiased Model Parameter Identification of Lithium-Ion Battery. IEEE Trans. Ind. Inform. 2020. [CrossRef]
- Chen, C.; Zhang, K.; Yuan, K.; Wang, W. Extended partial states observer based load frequency control scheme design for multi-area power system considering wind energy integration. IFAC Pap. 2017, 50, 4388–4393. [Google Scholar] [CrossRef]
- Mi, Y.; Fu, Y.; Li, D.; Wang, C.; Loh, P.C.; Wang, P. The sliding mode load frequency control for hybrid power system based on disturbance observer. Int. J. Electr. Power Energy Syst. 2016, 74, 446–452. [Google Scholar] [CrossRef]
- Prasad, S.; Purwar, S.; Kishor, N. Load frequency regulation using observer based non-linear sliding mode control. Int. J. Electr. Power Energy Syst. 2019, 104, 178–193. [Google Scholar] [CrossRef]
- Dev, A.; Sarkar, M.K. Robust higher order observer based non-linear super twisting load frequency control for multi area power systems via sliding mode. Int. J. Control Autom. Syst. 2019, 17, 1814–1825. [Google Scholar] [CrossRef]
- Liao, K.; Xu, Y. A robust load frequency control scheme for power systems based on second-order sliding mode and extended disturbance observer. IEEE Trans. Ind. Inform. 2017, 14, 3076–3086. [Google Scholar] [CrossRef]
- Tsai, Y.W.; Huynh, V.V. A multitask sliding mode control for mismatched uncertain large-scale systems. Int. J. Control 2015, 88, 1911–1923. [Google Scholar] [CrossRef]

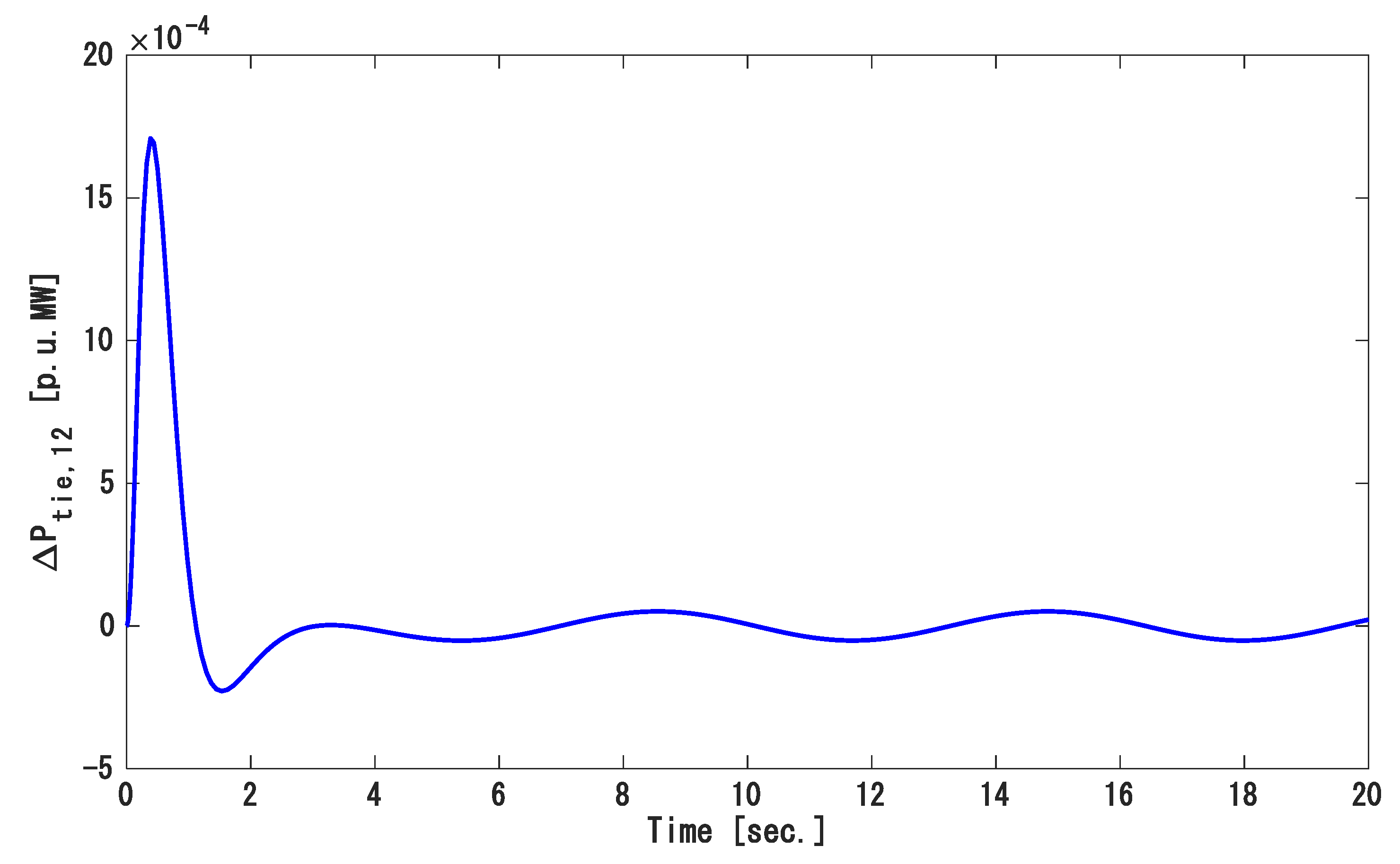

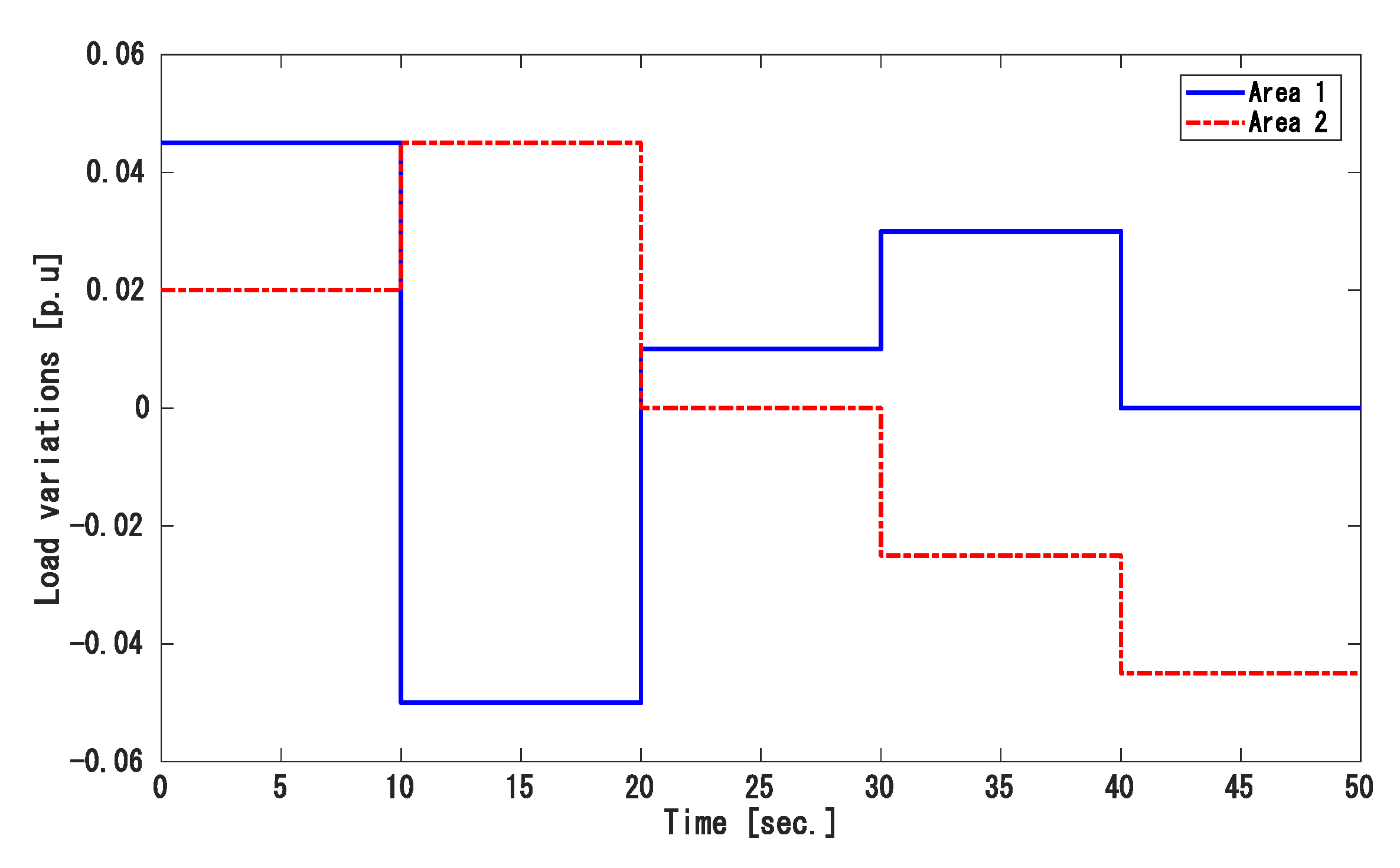
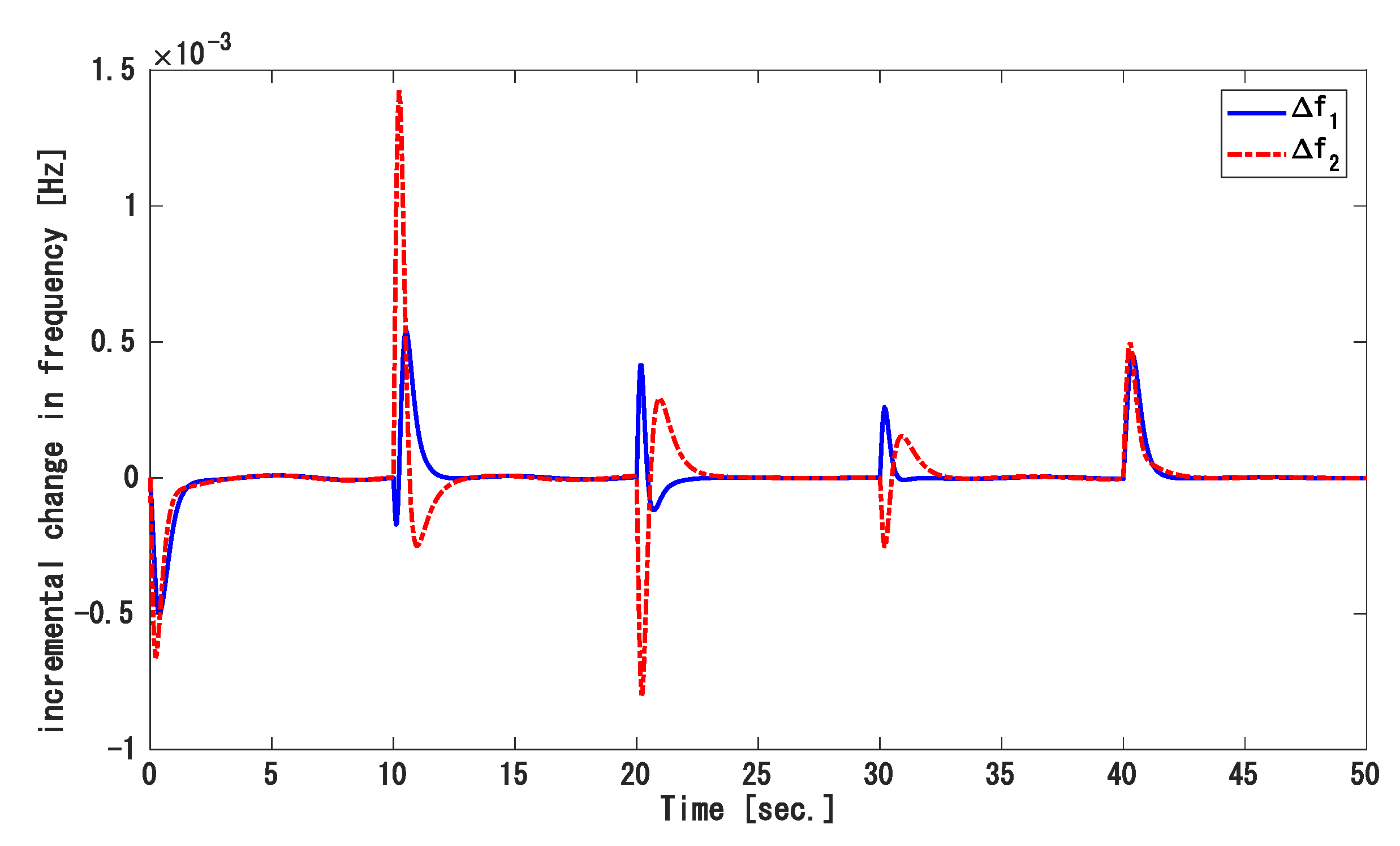

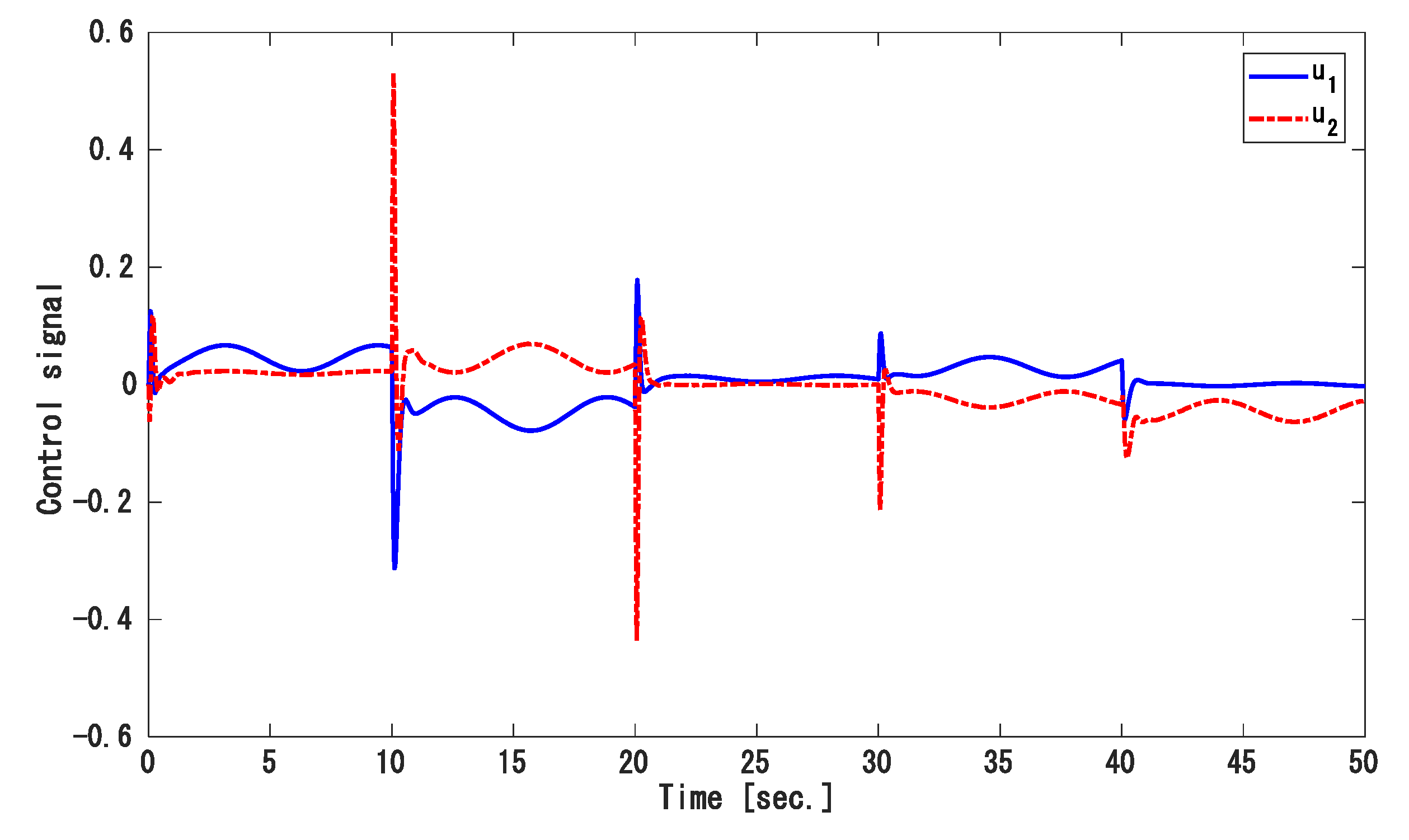

| Areas | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 8 | 0.67 | 81.5 | 0.05 | 0.4 | 0.17 | 0.5 | 3.77 |
| 2 | 10 | 1.00 | 41.5 | 0.1 | 0.30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, A.-T.; Minh, B.L.N.; Huynh, V.V.; Tran, P.T.; Amaefule, E.N.; Phan, V.-D.; Nguyen, T.M. Load Frequency Regulator in Interconnected Power System Using Second-Order Sliding Mode Control Combined with State Estimator. Energies 2021, 14, 863. https://doi.org/10.3390/en14040863
Tran A-T, Minh BLN, Huynh VV, Tran PT, Amaefule EN, Phan V-D, Nguyen TM. Load Frequency Regulator in Interconnected Power System Using Second-Order Sliding Mode Control Combined with State Estimator. Energies. 2021; 14(4):863. https://doi.org/10.3390/en14040863
Chicago/Turabian StyleTran, Anh-Tuan, Bui Le Ngoc Minh, Van Van Huynh, Phong Thanh Tran, Emmanuel Nduka Amaefule, Van-Duc Phan, and Tam Minh Nguyen. 2021. "Load Frequency Regulator in Interconnected Power System Using Second-Order Sliding Mode Control Combined with State Estimator" Energies 14, no. 4: 863. https://doi.org/10.3390/en14040863






