A Robust Nonlinear Controller for PMSG Wind Turbines †
Abstract
:1. Introduction
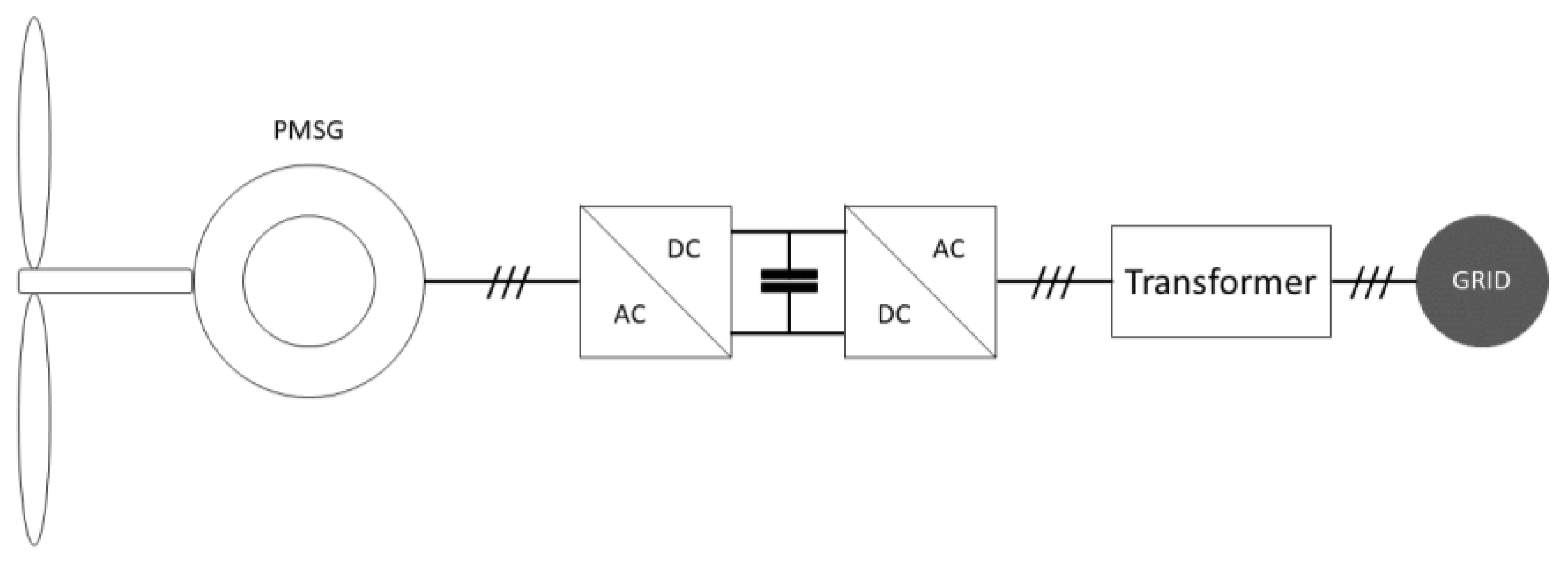
2. System Model
3. Proposed Controller
3.1. Speed Error Dynamics
3.2. Current Error Dynamics
4. Validation
4.1. Stability Analysis
4.2. Simulation Platform
4.3. Linear Controller Setup
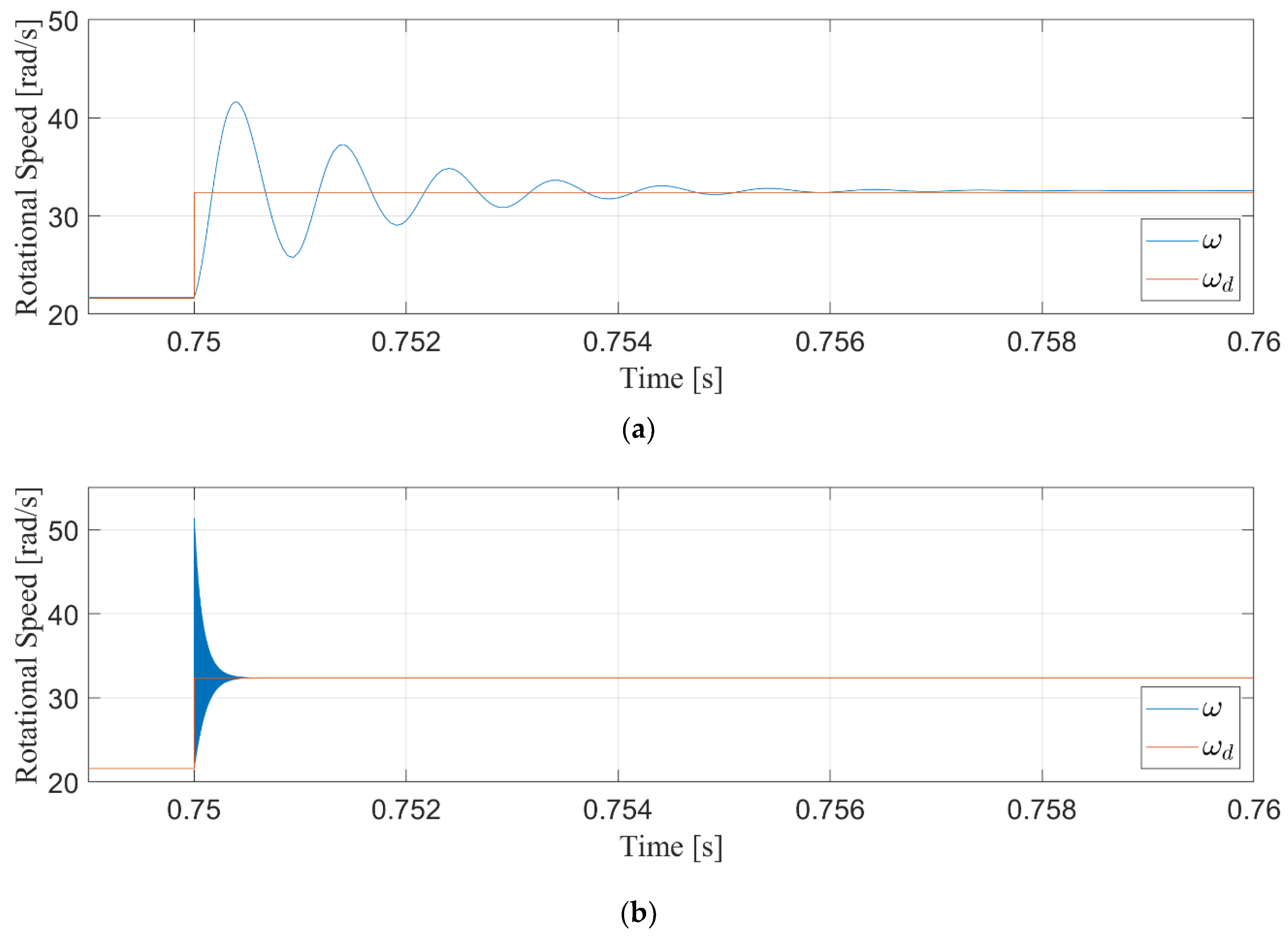
4.4. Wind Step Results
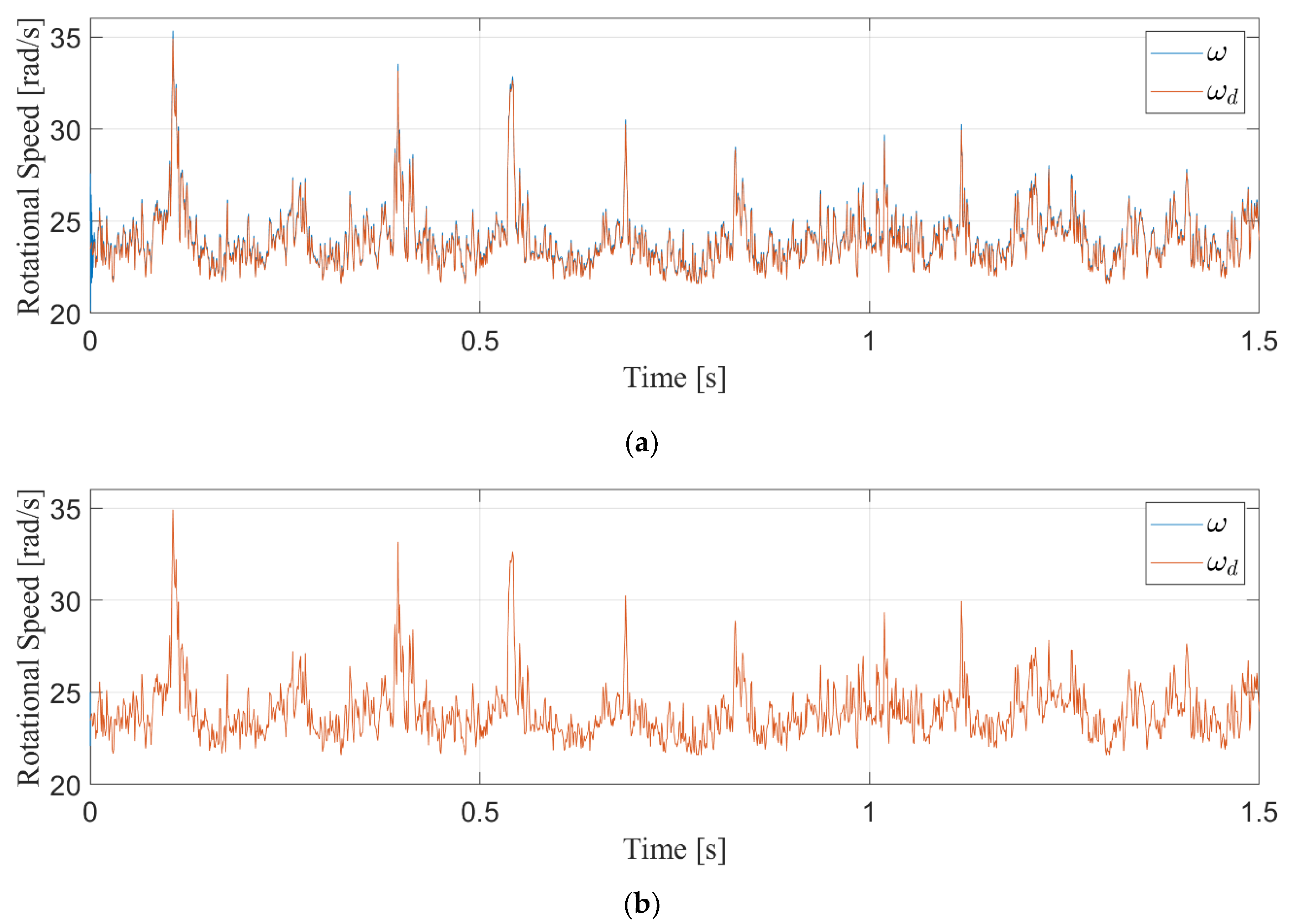
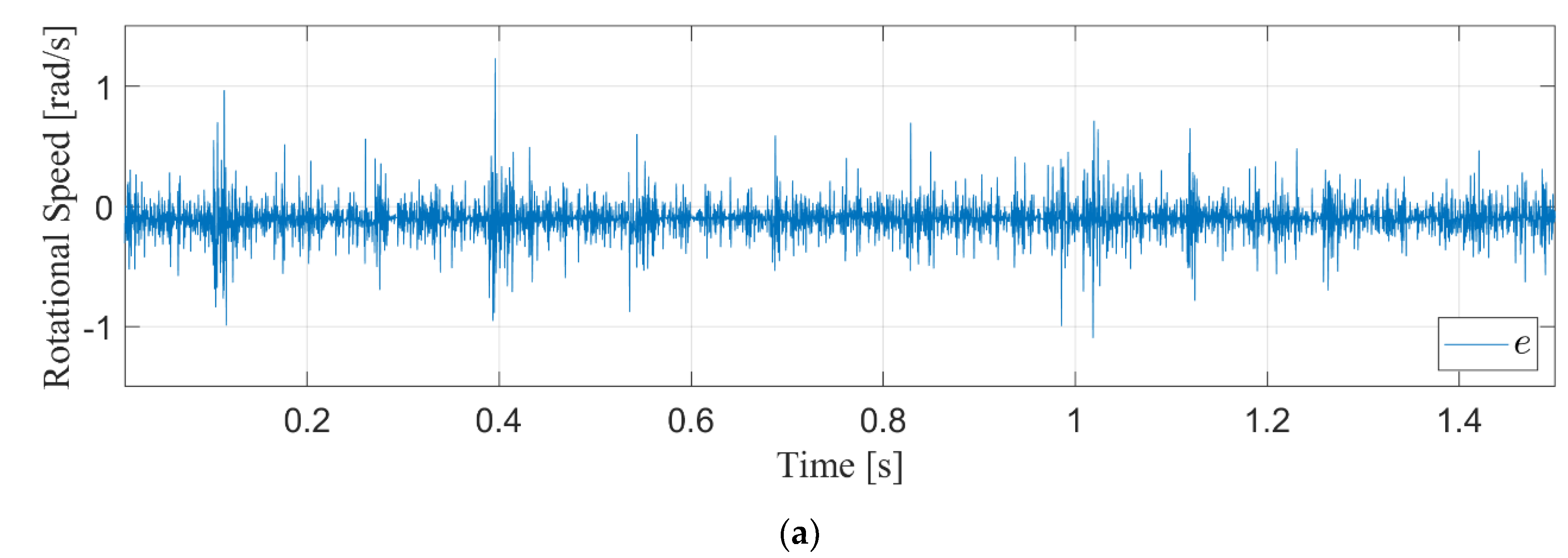
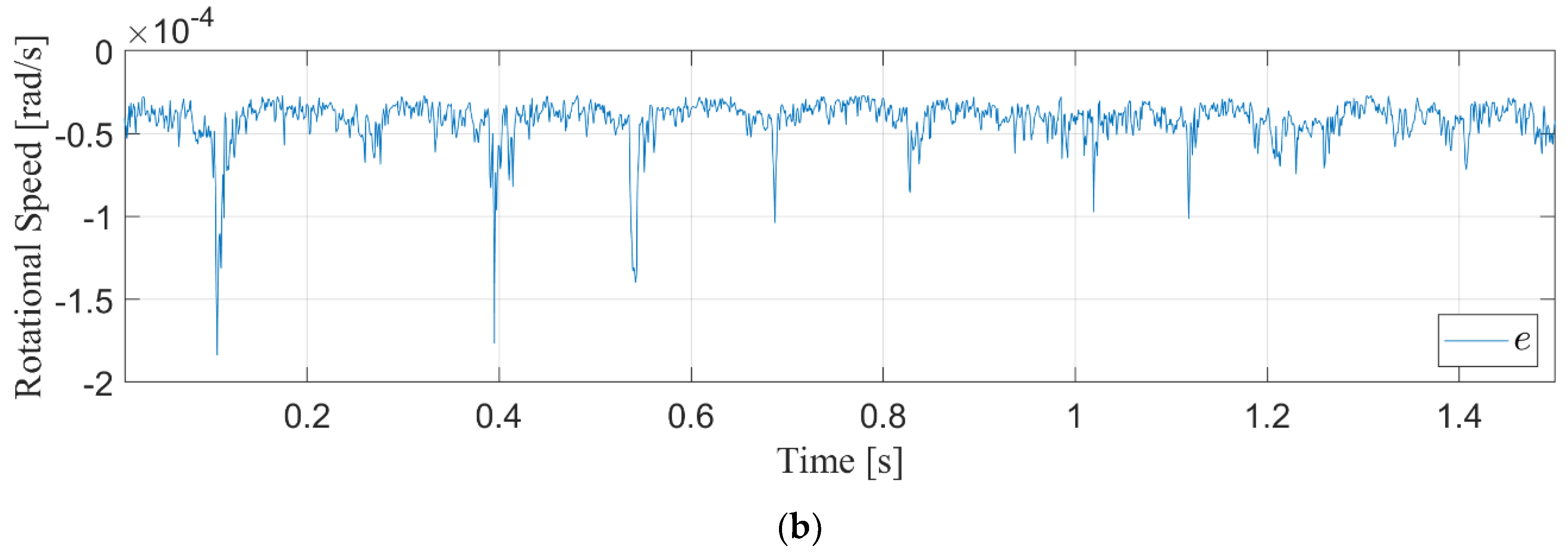
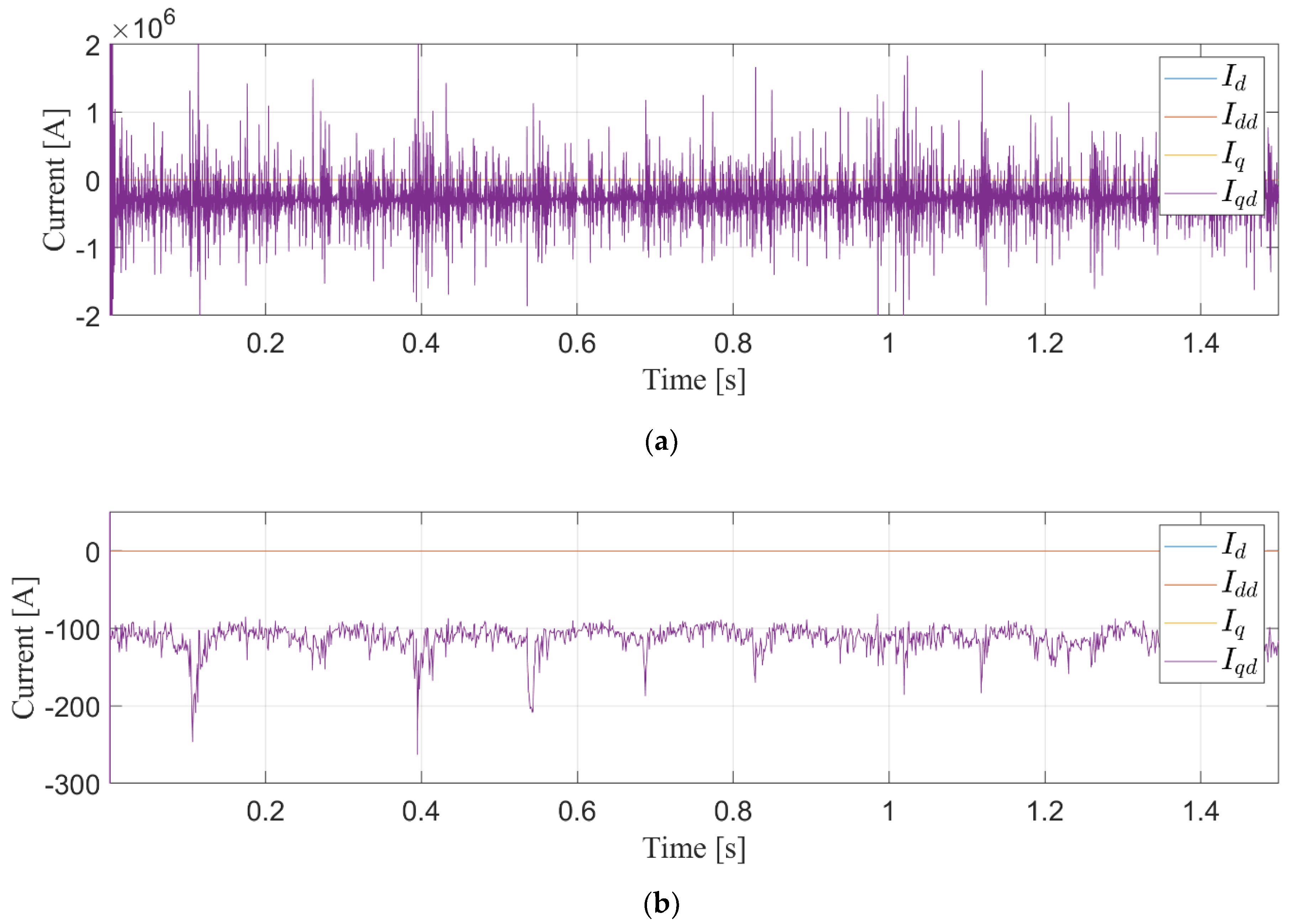
4.5. Turbulent Wind Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Z.; Guerrero, J.M.; Blaabjerg, F. A review of the state of the art of power electronics for wind turbines. IEEE Trans. Power Electron. 2009, 24, 1859–1875. [Google Scholar] [CrossRef]
- Yaramasu, V.; Wu, B.; Sen, P.C.; Kouro, S.; Narimani, M. High-power wind energy conversion systems: State-of-the-art and emerging technologies. Proc. IEEE 2015, 103, 740–788. [Google Scholar] [CrossRef]
- IRENA. Wind Energy. 2018. Available online: https://irena.org/wind (accessed on 17 November 2019).
- U. E. I. Administration. Table 10.1 Renewable Energy Production and Consumption by Source; US Department of Energy: Washington, DC, USA, 2018.
- U.S. Department of Energy. Wind Vision: A New Era for Wind Power in the United States; US Department of Energy: Washington, DC, USA, 2015.
- Fateh, F.; White, W.N.; Gruenbacher, D. A Maximum Power Tracking Technique for Grid-Connected DFIG-Based Wind Turbines. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 957–966. [Google Scholar] [CrossRef]
- Haque, M.E.; Negnevitsky, M.; Muttaqi, K.M. A Novel Control Strategy for a Variable-Speed Wind Turbine with a Permanent-Magnet Synchronous Generator. IEEE Trans. Ind. Appl. 2010, 46, 331–339. [Google Scholar] [CrossRef] [Green Version]
- Goudarzi, N.; Zhu, W.D. A review on the development of wind turbine generators across the world. Int. J. Dyn. Control 2013, 1, 192–202. [Google Scholar] [CrossRef] [Green Version]
- Han, K.; Chen, G.-Z. A novel control strategy of wind turbine MPPT implementation for direct-drive PMSG wind generation imitation platform. In Proceedings of the IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009. [Google Scholar]
- Uehara, A.; Pratap, A.; Goya, T.; Senjyu, T.; Yona, A.; Urasaki, N.; Funabashi, T. A Coordinated Control Method to Smooth Wind Power Fluctuations of a PMSG-Based WECS. IEEE Trans. Energy Convers. 2011, 26, 550–558. [Google Scholar] [CrossRef]
- Torki, W.; Grouz, F.; Sbita, L. Vector control of a PMSG direct-drive wind turbine. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017. [Google Scholar]
- Sahu, S.; Panda, G.; Yadav, S.P. Dynamic Modelling and Control of PMSG based Stand-alone Wind Energy Conversion System. In Proceedings of the 2018 Recent Advances on Engineering, Technology and Computational Sciences (RAETCS), Allahabad, India, 6–8 February 2018. [Google Scholar]
- Wen, C.; Lu, G.; Wang, P.; Li, Z.; Liu, X.; Fan, Z. Vector control strategy for small-scale grid-connected PMSG wind turbine converter. In Proceedings of the 2011 2nd IEEE PES International Conference and Exhibition on Innovative Smart Grid Technologies, Manchester, UK, 5–7 December 2011. [Google Scholar]
- Errami, Y.; Maaroufi, M.; Ouassaid, M. Modelling and control strategy of PMSG based variable speed wind energy conversion system. In Proceedings of the 2011 International Conference on Multimedia Computing and Systems, Ouarzazate, Morocco, 7–9 April 2011. [Google Scholar]
- Davoodnezhad, R.; Holmes, D.G.; McGrath, B.P.; Vahidnia, A. Self-synchronising stator terminal control of permanent magnet synchronous generators for wind energy conversion systems. In Proceedings of the IEEE 7th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Vancouver, BC, Canada, 7–30 June 2016. [Google Scholar]
- Boobalan, M.; Vijayalakshmi, S.; Brindha, R. A fuzzy-PI based power control of wind energy conversion system using PMSG. In Proceedings of the 2013 International Conference on Energy Efficient Technologies for Sustainability, Nagercoil, India, 10–12 April 2013. [Google Scholar]
- Rhaili, S.; Abbou, A.; Ziouh, A.; Elidrissi, R. Comparative study between PI and FUZZY logic controller in vector controlled five-phase PMSG based variable-speed wind turbine. In Proceedings of the 2018 IEEE 12th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG 2018), Doha, Qatar, 10–12 April 2018. [Google Scholar]
- Dixon, W.E.; Behal, A.; Dawson, D.M.; Nagarkatti, S.P. Nonlinear Control of Engineering Systems: A Lyapunov-Based Approach; Springer: New York, NY, USA, 2012. [Google Scholar]
- Djagarov, N.; Grozdev, Z.; Bonev, M.; Djagarova, J.; Pazderin, A.V.; Kokin, S. Adaptive control of wind PMSG. In Proceedings of the 2016 17th International Scientific Conference on Electric Power Engineering (EPE), Prague, Czech Republic, 16–18 May 2016. [Google Scholar]
- Kchaou, A.; Naamane, A.; Koubaa, Y.; M’Sirdi, N.K. Nonlinear control of a permanent magnet synchronous generator in wind energy conversion system with maximum power extraction. In Proceedings of the 18th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Monastir, Tunisia, 21–13 December 2017. [Google Scholar]
- Torki, W.; Grouz, F.; Sbita, L. A sliding mode model reference adaptive control of PMSG wind turbine. In Proceedings of the International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017. [Google Scholar]
- Lee, S.-W.; Chun, K.-H. Adaptive Sliding Mode Control for PMSG Wind Turbine Systems. Energies 2019, 12, 595. [Google Scholar] [CrossRef] [Green Version]
- Gajewski, P.; Pienkowski, K. Analysis of Sliding Mode Control of variable speed wind turbine system with PMSG. In Proceedings of the 2017 International Symposium on Electrical Machines (SME), Naleczow, Poland, 18–21 June 2017. [Google Scholar]
- Jena, N.K.; Mohanty, K.B.; Pradhan, H.; Sanyal, S.K. A comparison between PI & SMC used for decoupled control of PMSG in a variable speed wind energy system. In Proceedings of the 2015 International Conference on Energy, Power and Environment: Towards Sustainable Growth (ICEPE), Shillong, India, 12–13 June 2015. [Google Scholar]
- Kim, K.-H.; Jeung, Y.-C.; Lee, D.-C.; Kim, H.-G. Robust control of PMSG wind turbine systems with back-to-back PWM converters. In Proceedings of the 2nd International Symposium on Power Electronics for Distributed Generation Systems, Hefei, China, 16–18 June 2010. [Google Scholar]
- Ali, M.; Guo, F.; Gou, B.; Ali, M. Nonlinear control design using exact linearization for permanent magnet synchronous generator. In Proceedings of the IEEE International Conference on Electro-Information Technology, EIT 2013, Rapid City, SD, USA, 9–11 May 2013. [Google Scholar]
- Li, X.-C.; Zhao, Y.-N.; Zui-Bing, X. Nonlinear control of permanent magnet wind turbine generation (PSMG). In Proceedings of the 2013 International Conference on Power, Energy and Control (ICPEC), Sri Rangalatchum Dindigul, India, 6–8 February 2013. [Google Scholar]
- Abir, A.; Mehdi, D.; Lassaad, S. Pitch angle control of the variable speed wind turbine. In Proceedings of the 2016 17th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Sousse, Tunisia, 19–21 December 2016. [Google Scholar]
- Zhou, J.; Li, S.; Li, J.; Zhang, J. A combined control strategy of wind energy conversion system with direct-driven PMSG. In Proceedings of the 2016 31st Youth Academic Annual Conference of Chinese Association of Automation (YAC), Wuhan, China, 11–13 November 2016. [Google Scholar]
- Zhang, X.; Wang, K. Model predictive current control for the semi-controlled open winding PMSG. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, Australia, 11–14 August 2017. [Google Scholar]
- Chang, Y.-C.; Tsai, C.-T.; Lu, Y.-L. Current Control of the Permanent-Magnet Synchronous Generator Using Interval Type-2 T-S Fuzzy Systems. Energies 2019, 12, 2953. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Tao, L.; Zhou, X.; Li, W.; Shi, X. Analysis and Control of Wind Power Grid Integration Based on a Permanent Magnet Synchronous Generator Using a Fuzzy Logic System with Linear Extended State Observer. Energies 2019, 12, 2862. [Google Scholar] [CrossRef] [Green Version]
- Jisha, L.; Thomas, A.A.P. A comparative study on scalar and vector control of Induction motor drives. In Proceedings of the 2013 International conference on Circuits, Controls and Communications (CCUBE), Bengaluru, India, 27–28 December 2013. [Google Scholar]
- Horch, M.; Boumédiène, A.; Baghli, L. Backstepping approach for nonlinear super twisting sliding mode control of an induction motor. In Proceedings of the 2015 3rd International Conference on Control, Engineering & Information Technology (CEIT), Tlemcen, Algeria, 25–27 May 2015. [Google Scholar]
- Hawkins, N.; Alqatamin, M.; Bhagwat, B.; McIntyre, M.L. Nonlinear Control and Observation of a PMSG Wind Turbine through Unknown Wind Torque Characteristics. In Proceedings of the American Controls Conference, Denver, CO, USA, 1–3 July 2020. [Google Scholar]
- Li, M.; Smedley, K. One-cycle control of PMSG for wind power generation. In Proceedings of the IEEE Power Electronics and Machines in Wind Applications, Lincoln, NE, USA, 24–26 June 2009. [Google Scholar]
- Li, H.; Shi, K.; McLaren, P. Neural-network-based sensorless maximum wind energy capture with compensated power coefficient. IEEE Trans. Ind. Appl. 2005, 41, 1548–1556. [Google Scholar] [CrossRef]
- Fdaili, M.; Essadki, A.; Nadour, M.; Nasser, T. Comparative Study of MPPT and Pitch Angle Control Strategies for a Wind Energy Conversion System. In Proceedings of the 2017 International Renewable and Sustainable Energy Conference (IRSEC), Tangier, Morocco, 4–7 December 2017. [Google Scholar]




| Parameter | Value | Units |
|---|---|---|
| 0.0078 | ||
| 0 | ||
| 8 | # poles | |
| 0.36 | ||
| 0.42 | Ω | |
| 6.9 | mH | |
| 1.225 | ||
| 3 | m | |
| 8.0977 | - |
| Parameter | Value |
|---|---|
| 100 | |
| 50 | |
| 5 | |
| 1 |
| Parameter | Value |
|---|---|
| 10,000 | |
| 0.01 | |
| 1000 | |
| 100 | |
| 1 | |
| 500 |
| Controller | Settling Time (s) |
|---|---|
| Linear | 0.006 |
| Nonlinear | 0.0006 |
| Controller | RMS Error (rad/s) |
|---|---|
| Linear | 0.185994 |
| Nonlinear | 0.005751 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hawkins, N.; McIntyre, M.L. A Robust Nonlinear Controller for PMSG Wind Turbines. Energies 2021, 14, 954. https://doi.org/10.3390/en14040954
Hawkins N, McIntyre ML. A Robust Nonlinear Controller for PMSG Wind Turbines. Energies. 2021; 14(4):954. https://doi.org/10.3390/en14040954
Chicago/Turabian StyleHawkins, Nicholas, and Michael L. McIntyre. 2021. "A Robust Nonlinear Controller for PMSG Wind Turbines" Energies 14, no. 4: 954. https://doi.org/10.3390/en14040954
APA StyleHawkins, N., & McIntyre, M. L. (2021). A Robust Nonlinear Controller for PMSG Wind Turbines. Energies, 14(4), 954. https://doi.org/10.3390/en14040954






