CFD Analysis of the Performance of a Double Decker Turbine for Wave Energy Conversion
Abstract
:1. Introduction
2. Non-Dimensional Analysis
3. Numerical CFD Model
4. Validation and Results
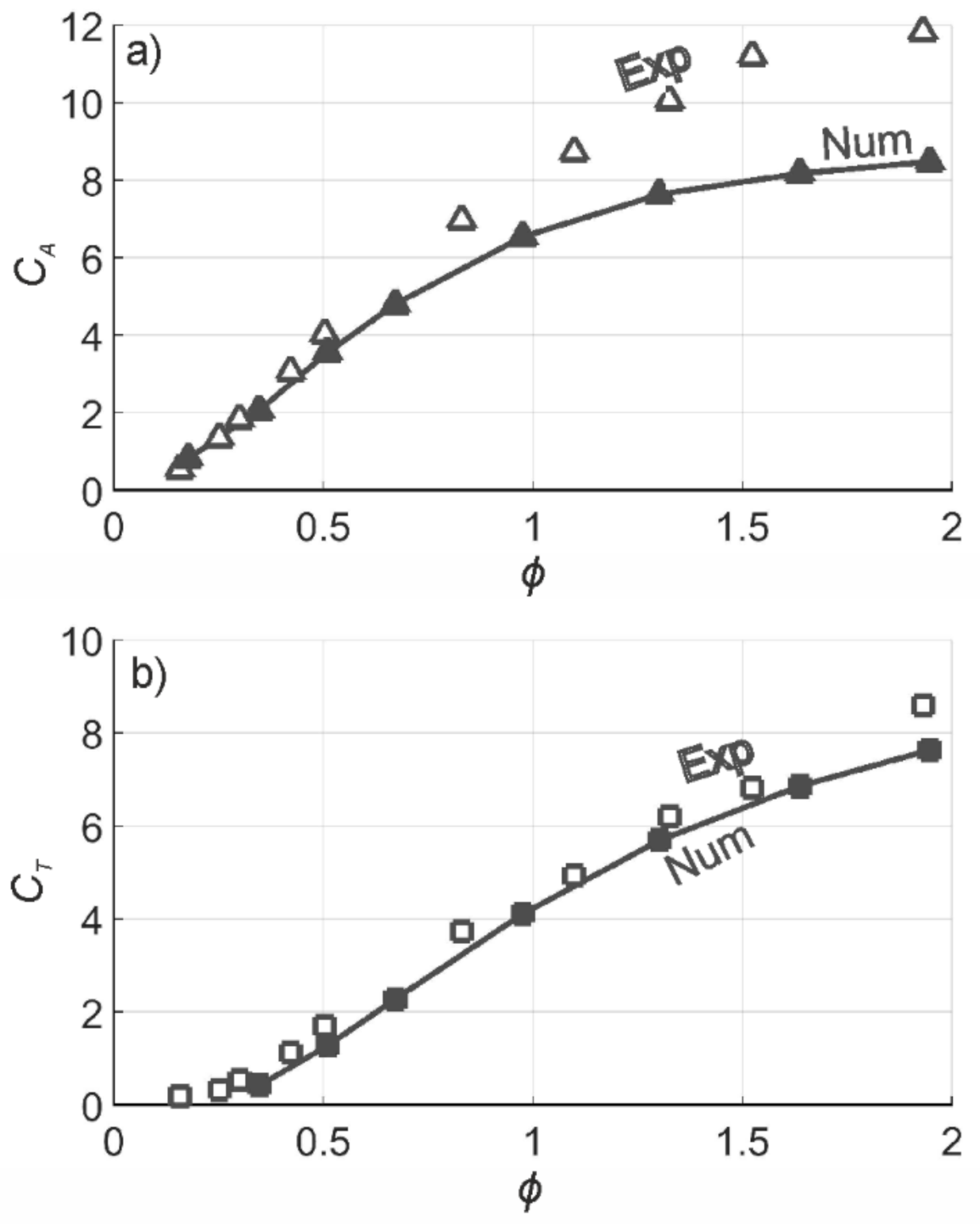
4.1. Validation
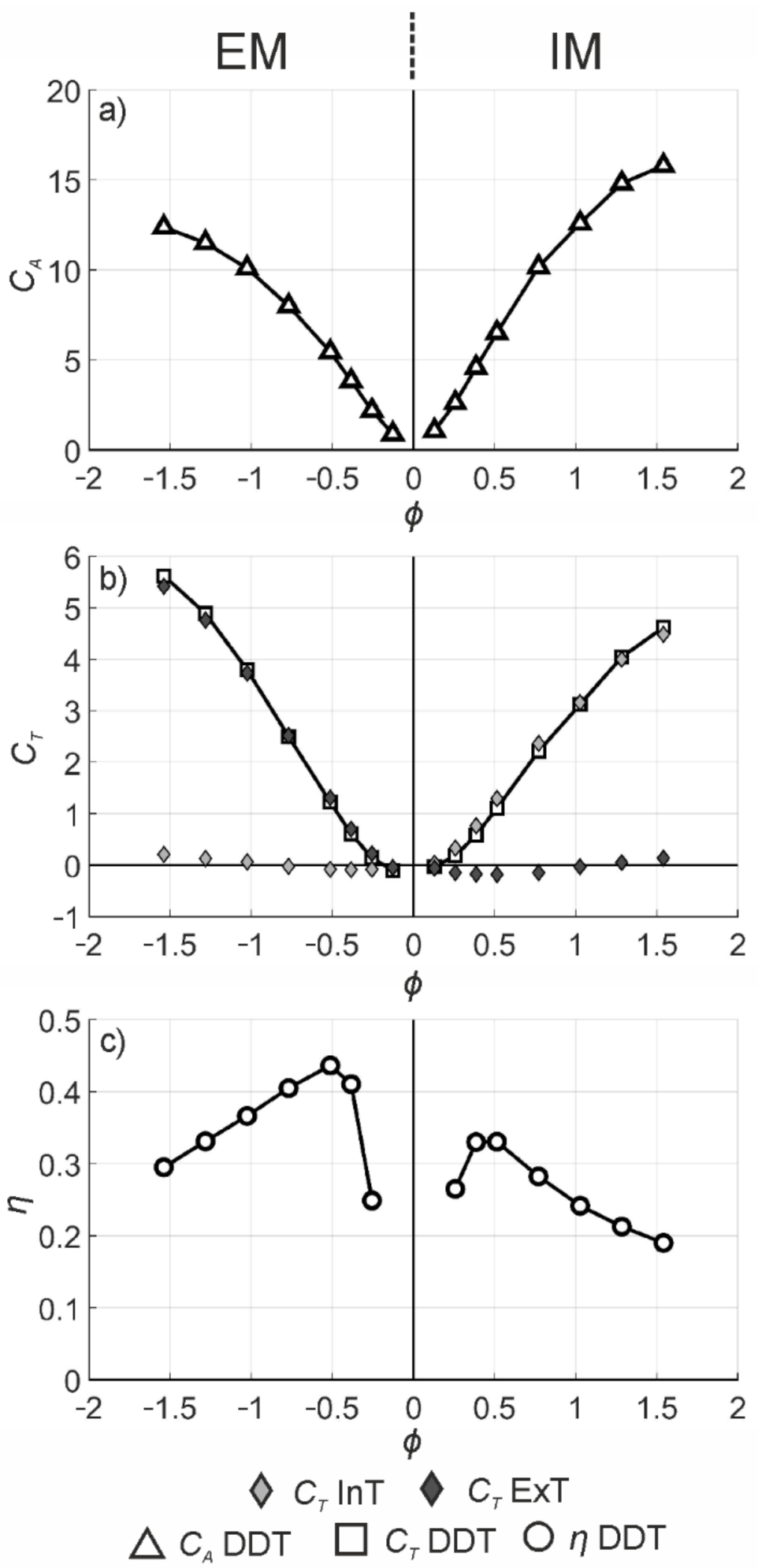
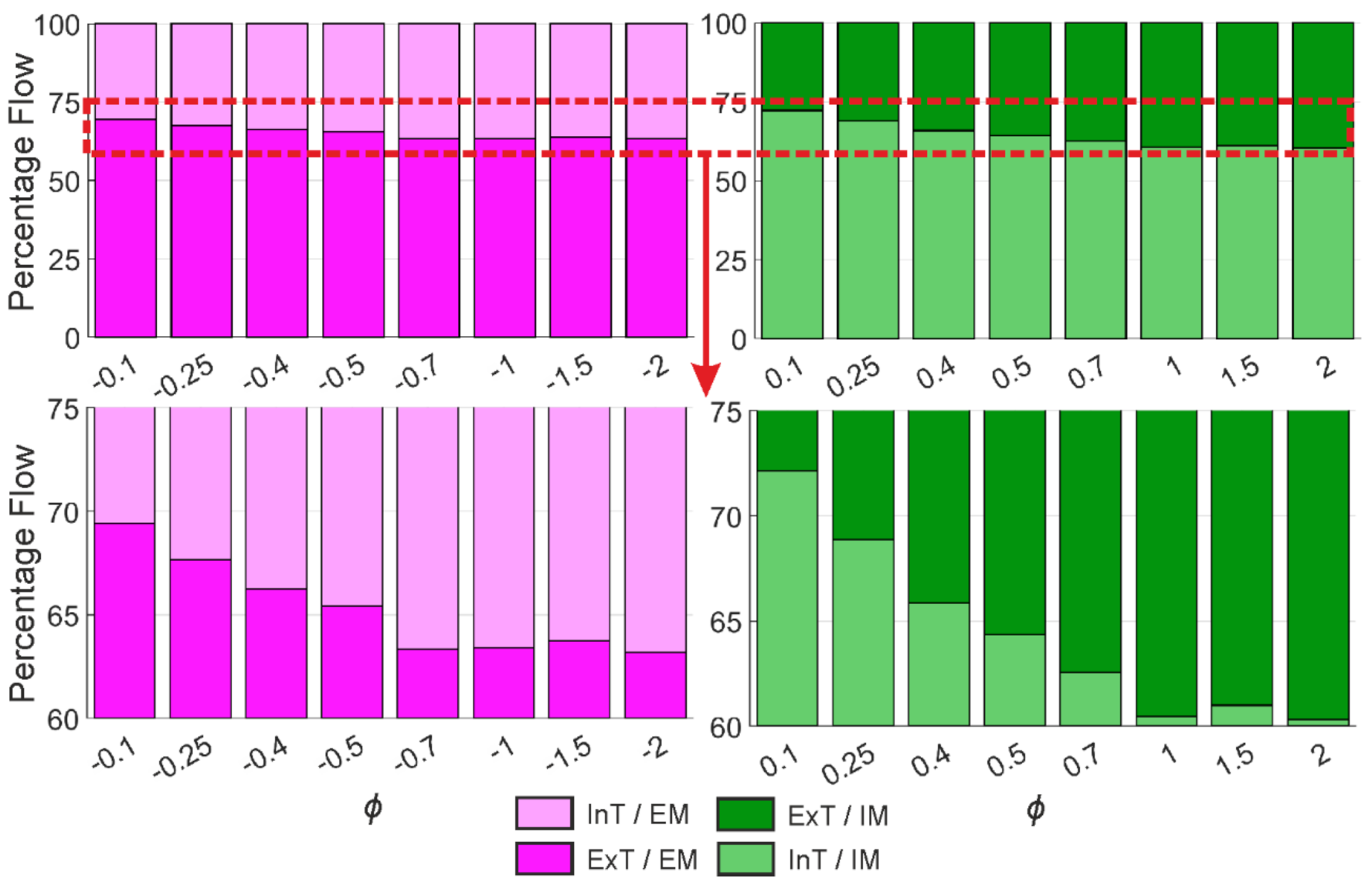
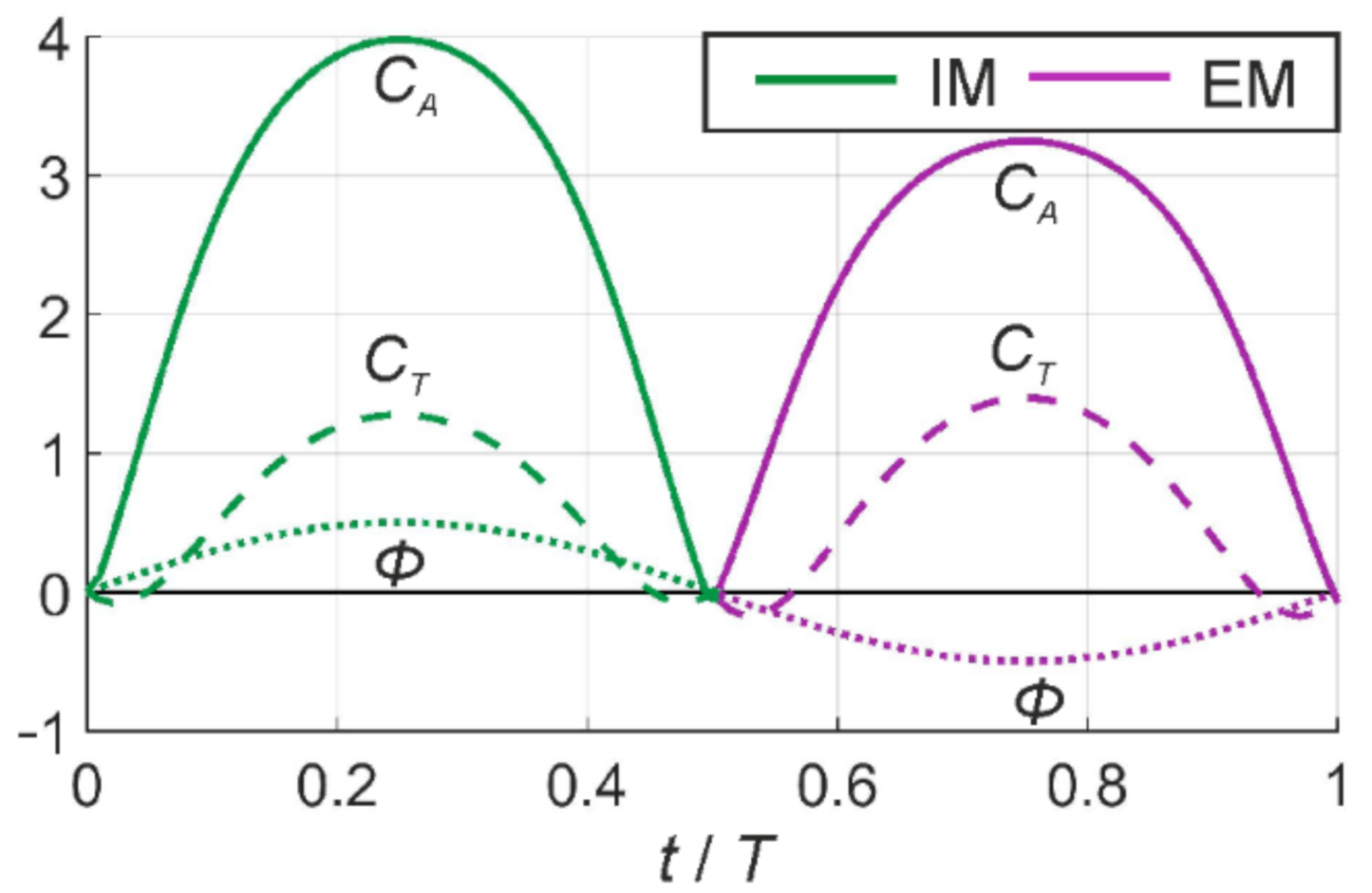
4.2. Performance Curves and Flow Rate Distribution
4.3. Pressure Losses Diagram
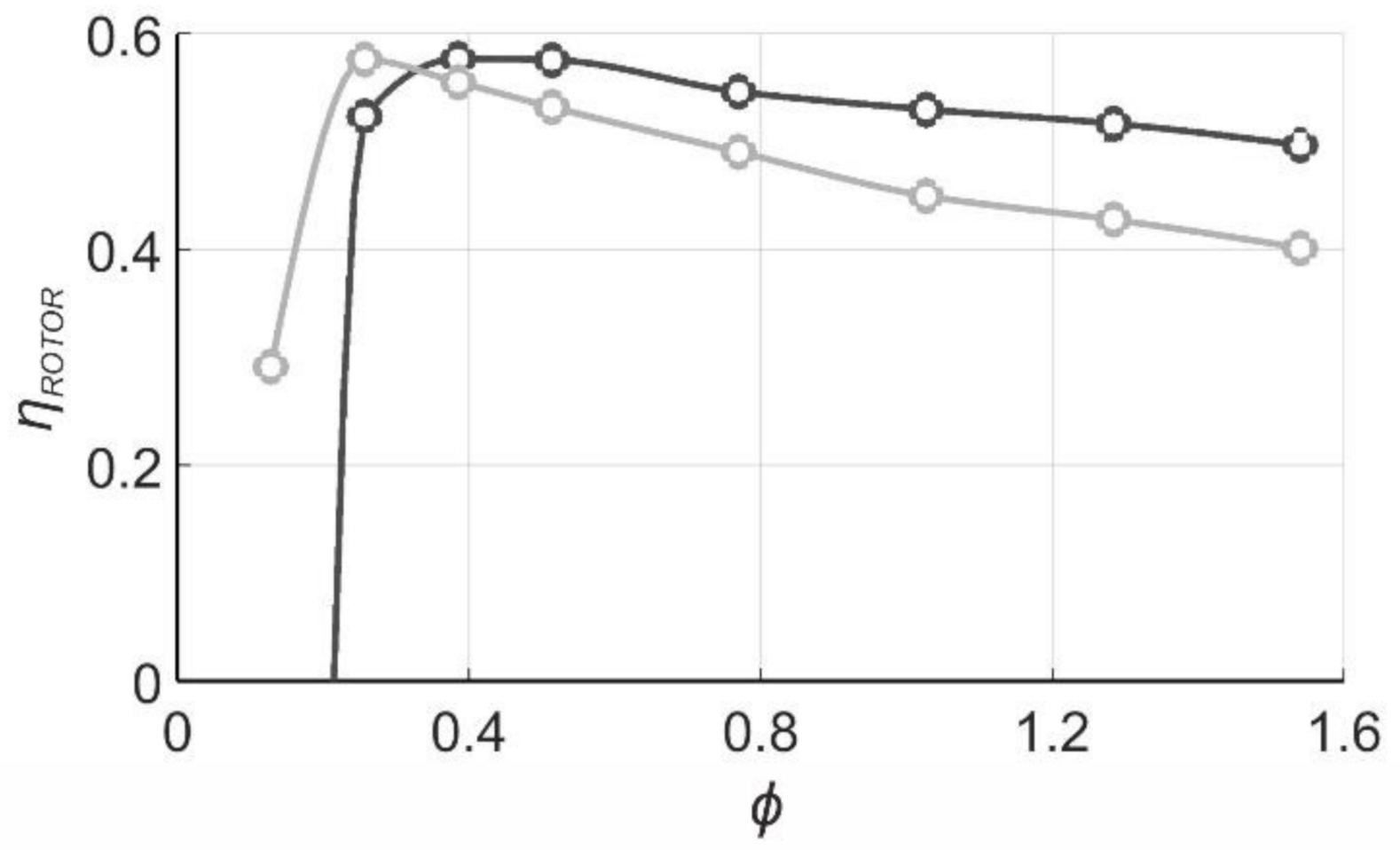
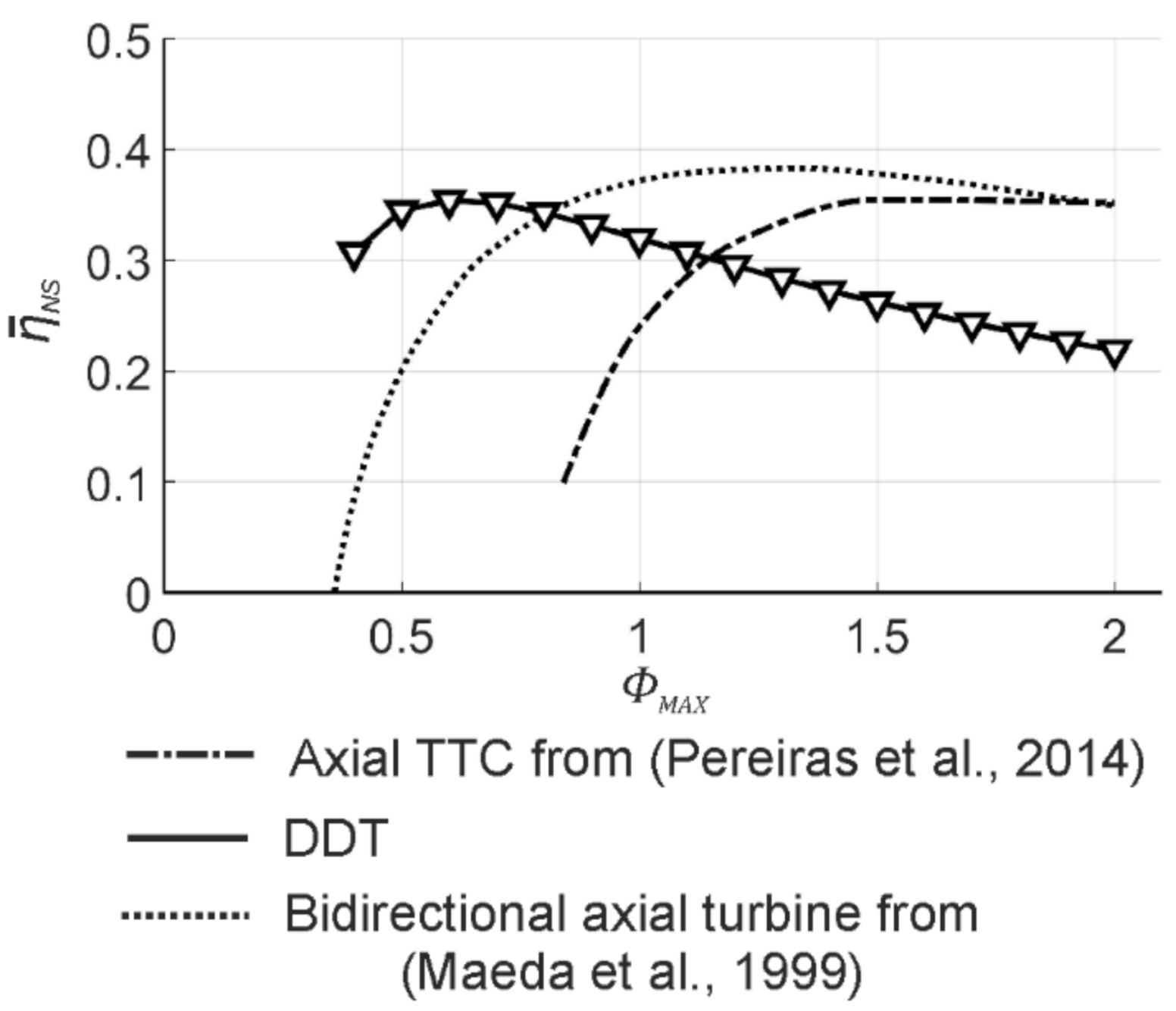
4.4. Rotor Efficiency
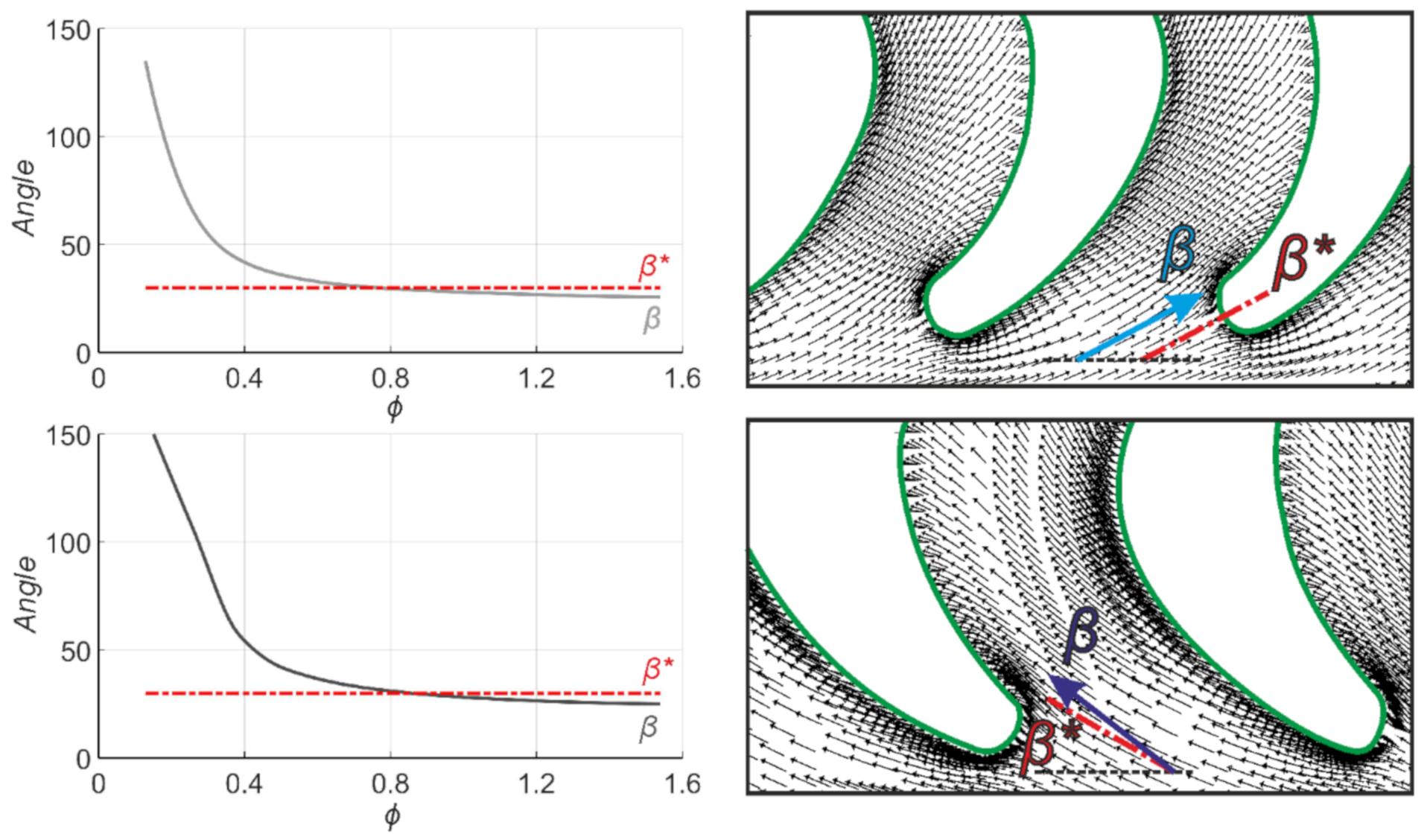
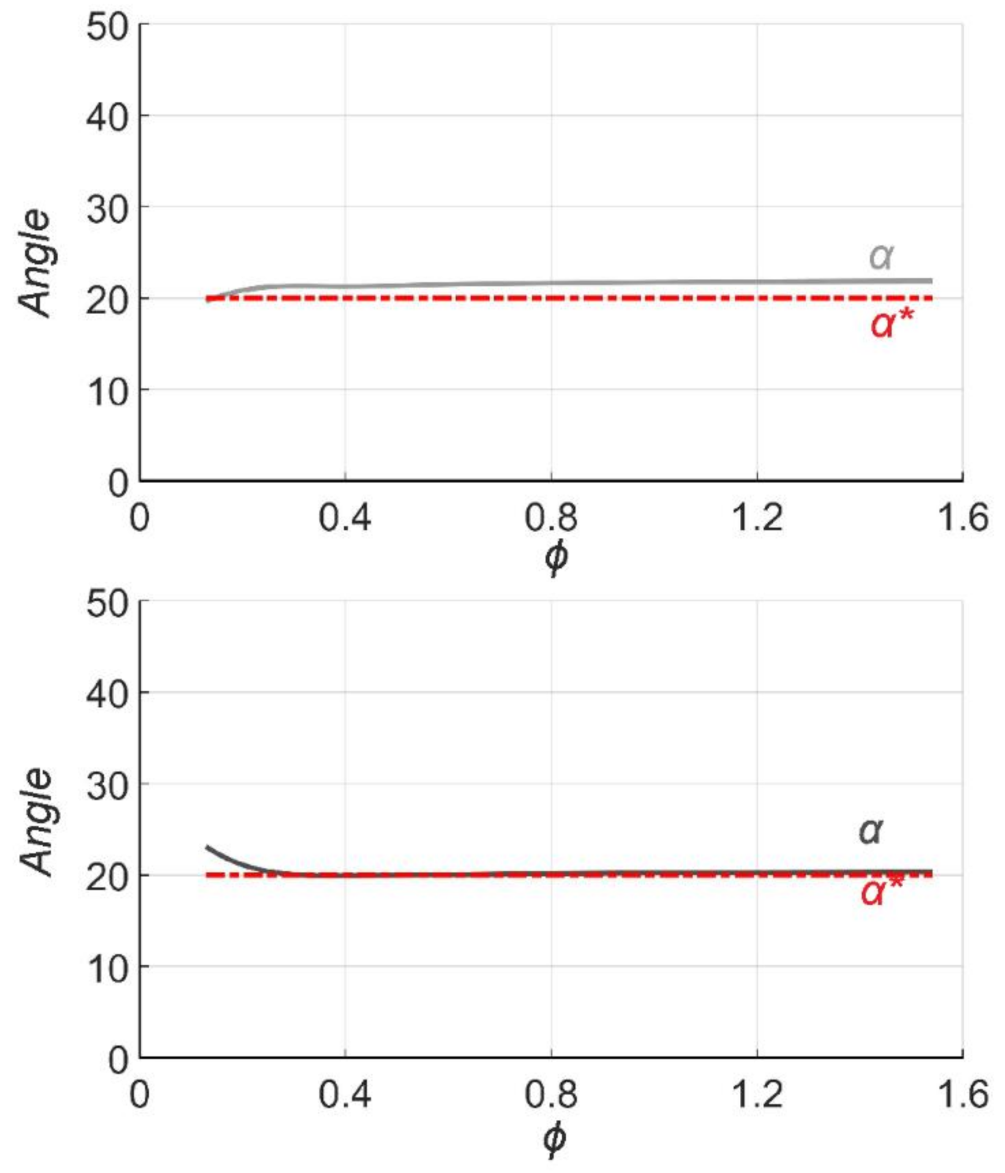
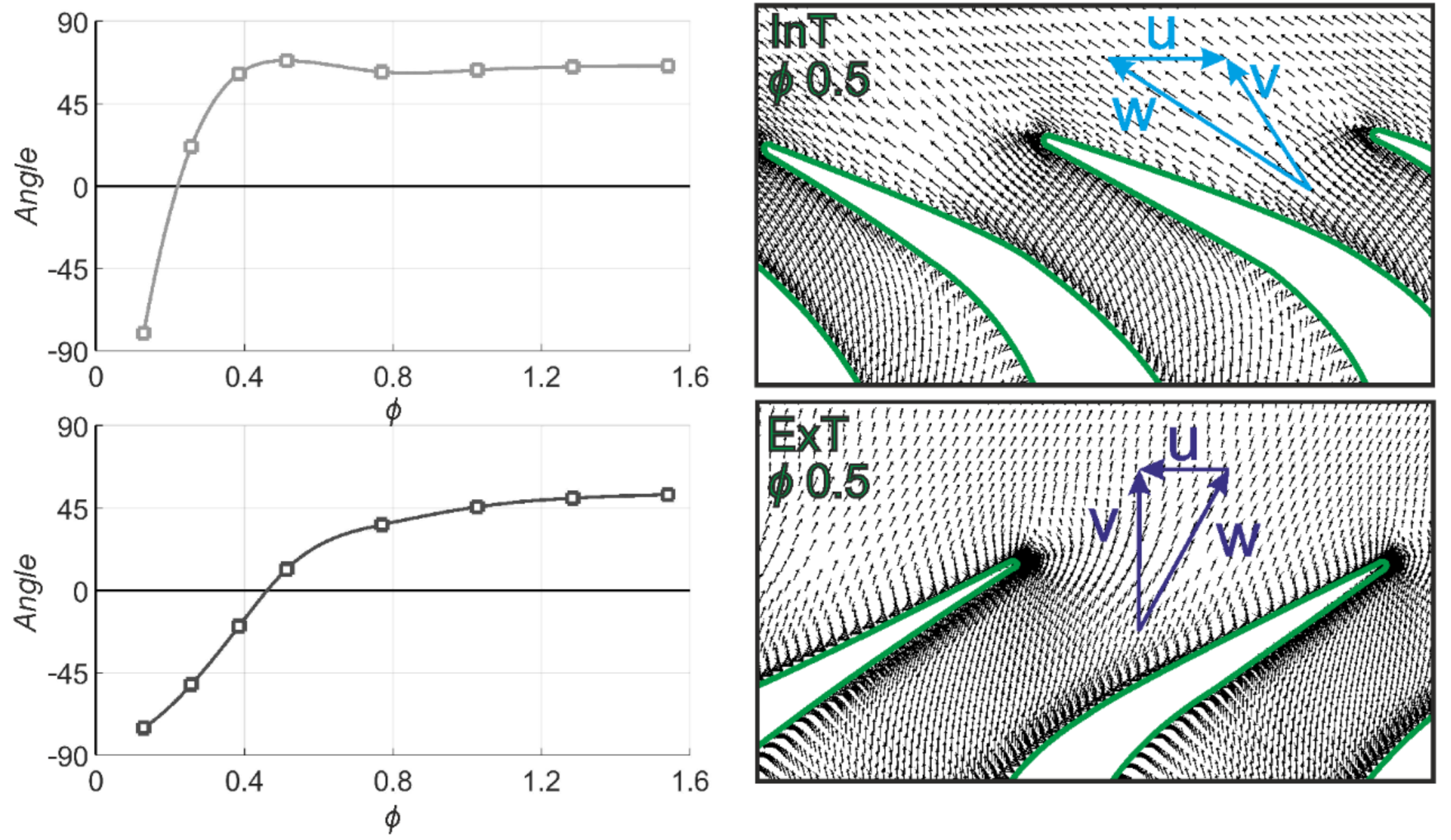
4.5. Rotor Entry and Exit Angles
4.6. Non-Steady Efficiency
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| AR = π·(rEX2 − rIN2) | Cross-Flow Area | (m2) |
| c | Blade Chord | (m) |
| CA | Dimensionless Input Coefficient | (-) |
| CT | Dimensionless Torque Coefficient | (-) |
| D | Diameter | (m) |
| DREF | Reference Diameter | (m) |
| N | Number of Blades | (-) |
| ΔP | Total to Static Pressure Difference | (Pa) |
| Q | Flow Rate | (m3s−1) |
| QExT | Flow Rate across the ExT | (m3s−1) |
| QInT | Flow Rate across the InT | (m3s−1) |
| QTOT | Total Flow Rate across the DDT | (m3s−1) |
| rm | Mean Radius | (m) |
| rREF | Reference Radius | (m) |
| rEX | External Radius of the ExT | (m) |
| rIN | Internal Radius of the InT | (m) |
| T | Wave Period | (s) |
| t | Time | (s) |
| T0 | Torque | (Nm) |
| TExT | Torque of the ExT | (Nm) |
| TInT | Torque of the InT | (Nm) |
| TTOT | Torque of the DDT | (Nm) |
| uR | Tangential Velocity at rREF | (ms−1) |
| va | Velocity at AR | (ms−1) |
| ω | Rotational Speed | (rads−1) |
| ρ | Air Density | (kgm−3) |
| ɸ | Steady Dimensionless Flow Coefficient | (-) |
| η | Total-to-Static Steady Efficiency | (-) |
| NS | Non-Steady Efficiency | (-) |
| Input | Input efficiency | (-) |
| tg | Net efficiency of the DDT | (-) |
| Φ | Non-steady Dimensionless Flow Coefficient | (-) |
| ΦMAX | Maximum value of Φ | (-) |
| BEP | Best Efficiency Point | (-) |
| DDT | Double Decker Turbine | (-) |
| ExT | External Turbine | (-) |
| GV | Guide Vanes | (-) |
| InT | Internal Turbine | (-) |
| NRMSE | Normalized Root-Mean Squared Error | (-) |
| OWC | Oscillating Water Column | (-) |
| PTO | Power-Take-Off | (-) |
| RMSE | Root-Mean Squared Error | (-) |
| TTC | Twin Turbines Configuration | (-) |
| WEC | Wave Energy Converter | (-) |
References
- Astariz, S.; Iglesias, G. The economics of wave energy: A review. Renew. Sustain. Energy Rev. 2015, 45, 397–408. [Google Scholar] [CrossRef]
- Melikoglu, M. Current status and future of ocean energy sources: A global review. Ocean Eng. 2018, 148, 563–573. [Google Scholar] [CrossRef]
- Falcão, A.F.O.; Gato, L.M.C. Chapter 8.5: Air Turbines. In Comprehensive renewable energy; Sayigh, A., Ed.; Elsevier: Amsterdam, The Netherlands, 2012; Volume 8, pp. 1–39. ISBN 9780080878737. [Google Scholar]
- Setoguchi, T.; Takao, M. Current status of self-rectifying air turbines for wave energy conversion. Energy Convers. Manag. 2006, 47, 2382–2396. [Google Scholar] [CrossRef]
- Takao, M.; Setoguchi, T. Air turbines for wave energy conversion. Int. J. Rotating Mach. 2012, 2012, 10. [Google Scholar] [CrossRef] [Green Version]
- Ansarifard, N.; Kianejad, S.S.; Fleming, A.; Chai, S. A radial inflow air turbine design for a vented oscillating water column. Energy 2019, 166, 380–391. [Google Scholar] [CrossRef]
- Okuhara, S.; Takao, M.; Sato, H.; Takami, A.; Setoguchi, T. A Twin Impulse Turbine for Wave Energy Conversion—Effect of Fluidic Diode Geometry on the Performance. Open J. Fluid Dyn. 2014, 4, 433–439. [Google Scholar] [CrossRef] [Green Version]
- Bruschi, D.L.; Fernandes, J.C.S.; Falcão, A.F.O.; Bergmann, C.P. Analysis of the degradation in the Wells turbine blades of the Pico oscillating-water-column wave energy plant. Renew. Sustain. Energy Rev. 2019, 115, 109368. [Google Scholar] [CrossRef]
- Wells, A.A. Fluid driven rotary transducer. Br. Pat. spec 1976, 1, 595–700. [Google Scholar]
- Raghunathan, S. the Wells Air Turbine for Wave Energy Conversion. Prog. Aerosp. Sci. 1995, 31, 335–386. [Google Scholar] [CrossRef]
- Ibarra-Berastegi, G.; Sáenz, J.; Ulazia, A.; Serras, P.; Esnaola, G.; Garcia-Soto, C. Electricity production, capacity factor, and plant efficiency index at the Mutriku wave farm (2014–2016). Ocean Eng. 2018, 147, 20–29. [Google Scholar] [CrossRef] [Green Version]
- Kumar, P.M.; Halder, P.; Husain, A.; Samad, A. Performance enhancement of Wells turbine: Combined radiused edge blade tip, static extended trailing edge, and variable thickness modifications. Ocean Eng. 2019, 185, 47–58. [Google Scholar] [CrossRef]
- Babintsev, I.A. Apparatus for Converting Sea Wave Energy into Electrical Energy. Patent No. US3922739A, 12 February 1975. [Google Scholar]
- López, I.; Andreu, J.; Ceballos, S.; Martínez De Alegría, I.; Kortabarria, I. Review of wave energy technologies and the necessary power-equipment. Renew. Sustain. Energy Rev. 2013, 27, 413–434. [Google Scholar] [CrossRef]
- Jayashankar, V.; Anand, S.; Geetha, T.; Santhakumar, S.; Jagadeesh Kumar, V.; Ravindran, M.; Setoguchi, T.; Takao, M.; Toyota, K.; Nagata, S. A twin unidirectional impulse turbine topology for OWC based wave energy plants. Renew. Energy 2009, 34, 692–698. [Google Scholar] [CrossRef]
- Falcão, A.F.O.; Henriques, J.C.C. Oscillating-water-column wave energy converters and air turbines: A review. Renew. Energy 2016, 85, 1391–1424. [Google Scholar] [CrossRef]
- Falcão, A.F.O.; Gato, L.M.C.; Henriques, J.C.C.; Borges, J.E.; Pereiras, B.; Castro, F. A novel twin-rotor radial-inflow air turbine for oscillating-water-column wave energy converters. Energy 2015, 93, 2116–2125. [Google Scholar] [CrossRef]
- Falcao, A.F.O.; Gato, L.M.C. Turbine with radial inlet and outlet rotor for use in bidirectional flows. Patent No. EP2538070B1, 12 February 1975. [Google Scholar]
- Ansarifard, N.; Fleming, A.; Henderson, A.; Kianejad, S.S.; Chai, S.; Orphin, J. Comparison of inflow and outflow radial air turbines in vented and bidirectional OWC wave energy converters. Energy 2019, 182, 159–176. [Google Scholar] [CrossRef]
- Rodríguez, L.; Pereiras, B.; Fernández-Oro, J.; Castro, F. Optimization and experimental tests of a centrifugal turbine for an owc device equipped with a twin turbines configuration. Energy 2019, 171, 710–720. [Google Scholar] [CrossRef] [Green Version]
- Lopes, B.S.; Gato, L.M.C.; Falcão, A.F.O.; Henriques, J.C.C. Test results of a novel twin-rotor radial inflow self-rectifying air turbine for OWC wave energy converters. Energy 2019, 170, 869–879. [Google Scholar] [CrossRef]
- García Díaz, M.; Rodriguez, L.; Pereiras, B. Turbina para aprovechamiento de flujo bidireccional. Patent No. ES2729207B2, 2018. [Google Scholar]
- Garcia-Diaz, M.; Pereiras, B.; Miguel-Gonzalez, C.; Rodriguez, L.; Fernandez-Oro, J. Design of a new turbine for OWC Wave Energy Converters: The DDT concept. Renew. Energy 2021. accepted for publication. [Google Scholar] [CrossRef]
- Rodríguez, L.; Pereiras, B.; Fernández-Oro, J.; Castro, F. Viability of unidirectional radial turbines for twin-turbine configuration of OWC wave energy converters. Ocean Eng. 2018, 154, 288–297. [Google Scholar] [CrossRef]
- Takao, M.; Takami, A.; Okuhara, S.; Setoguchi, T. A twin unidirectional impulse turbine for wave energy conversion. J. Therm. Sci. 2011, 20, 394–397. [Google Scholar] [CrossRef]
- Pereiras, B.; Valdez, P.; Castro, F. Numerical analysis of a unidirectional axial turbine for twin turbine configuration. Appl. Ocean Res. 2014, 47, 1–8. [Google Scholar] [CrossRef]
- Thakker, A.; Dhanasekaran, T.S. Computed effects of tip clearance on performance of impulse turbine for wave energy conversion. Renew. Energy 2004, 29, 529–547. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, Z.; Zhang, X.; Xu, C. Review of CFD studies on axial-flow self-rectifying turbines for OWC wave energy conversion. Ocean Eng. 2019, 175, 80–102. [Google Scholar] [CrossRef]
- Cho, S.Y.; Choi, S.K. Experimental study of the incidence effect on rotating turbine blades. Proc. Inst. Mech. Eng. Part A J. Power Energy 2004, 218, 669–676. [Google Scholar] [CrossRef]
- Thakker, A.; Jarvis, J.; Sahed, A. Quasi-steady analytical model benchmark of an impulse turbine for wave energy extraction. Int. J. Rotat. Mach. 2008, 2008, 12. [Google Scholar] [CrossRef] [Green Version]
- Maeda, H.; Santhakumar, S.; Setoguchi, T.; Takao, M.; Kinoue, Y.; Kaneko, K. Performance of an impulse turbine with fixed guide vanes for wave power conversion. Renew. Energy 1999, 17, 533–547. [Google Scholar] [CrossRef]
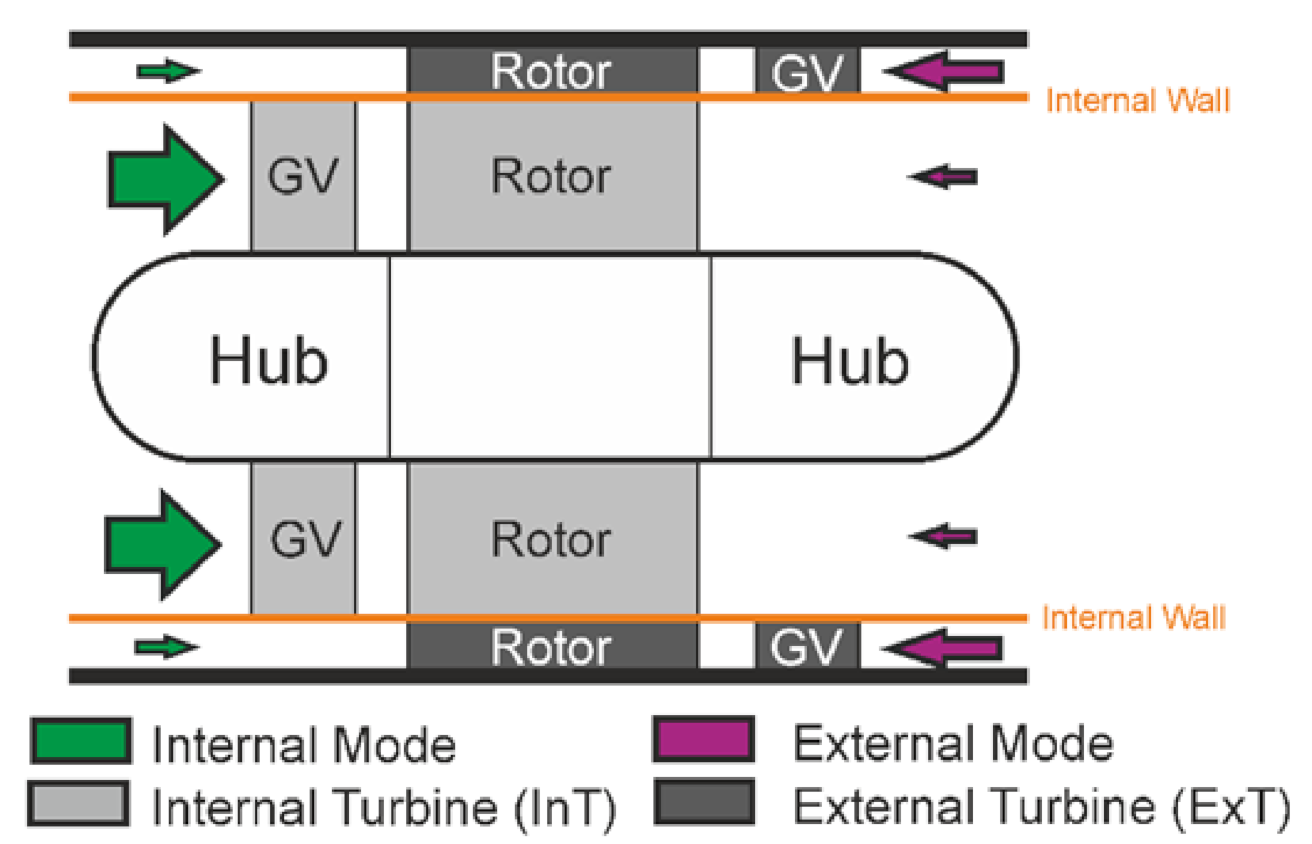
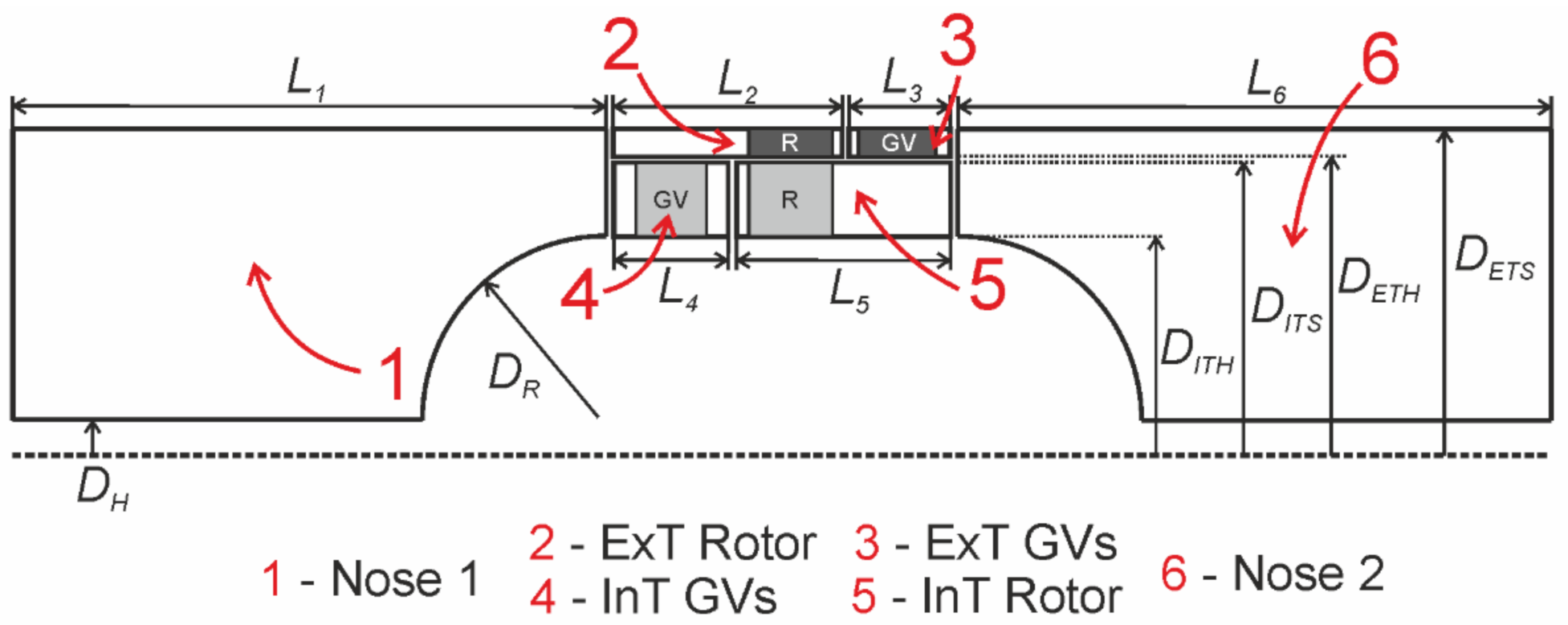
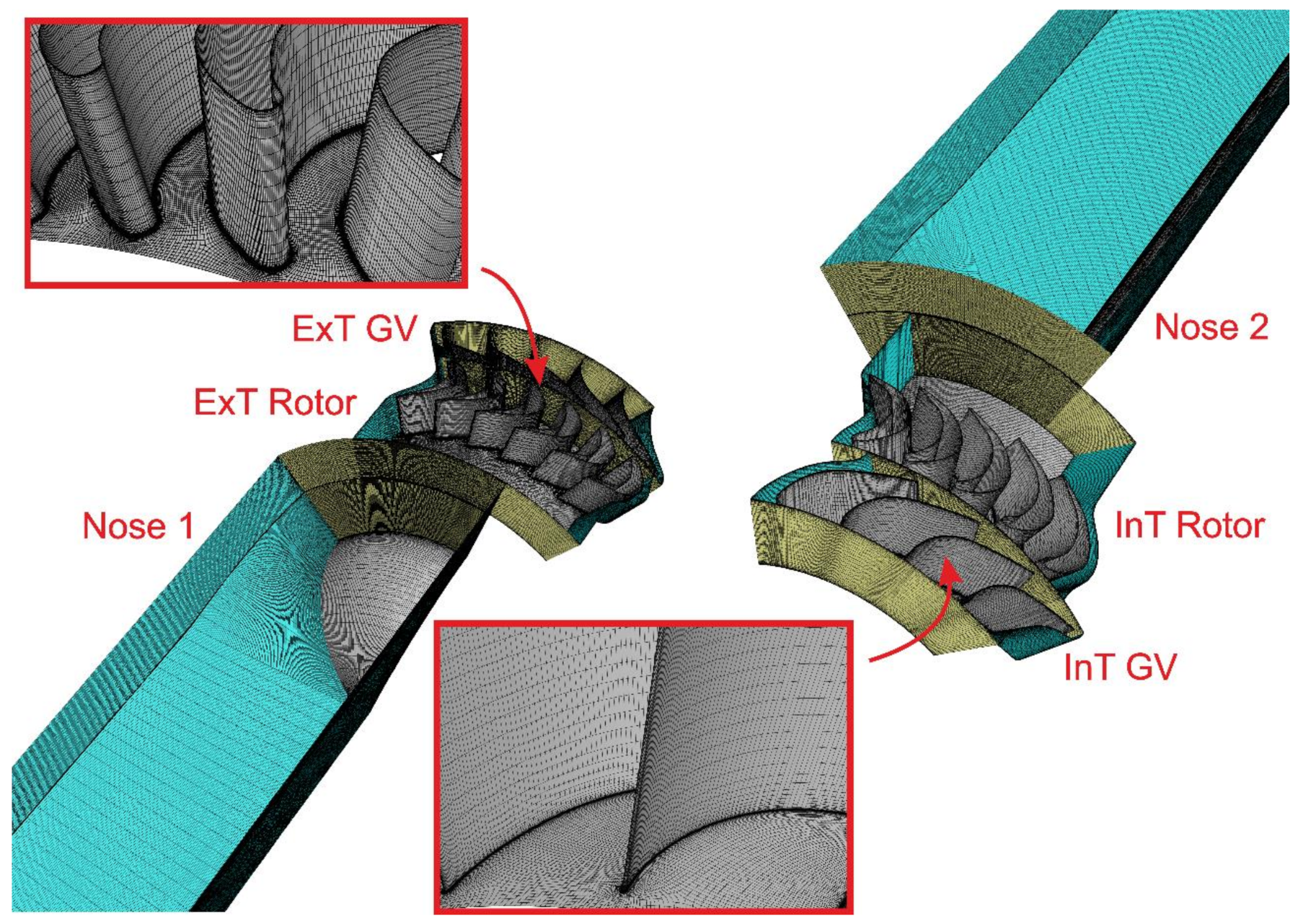


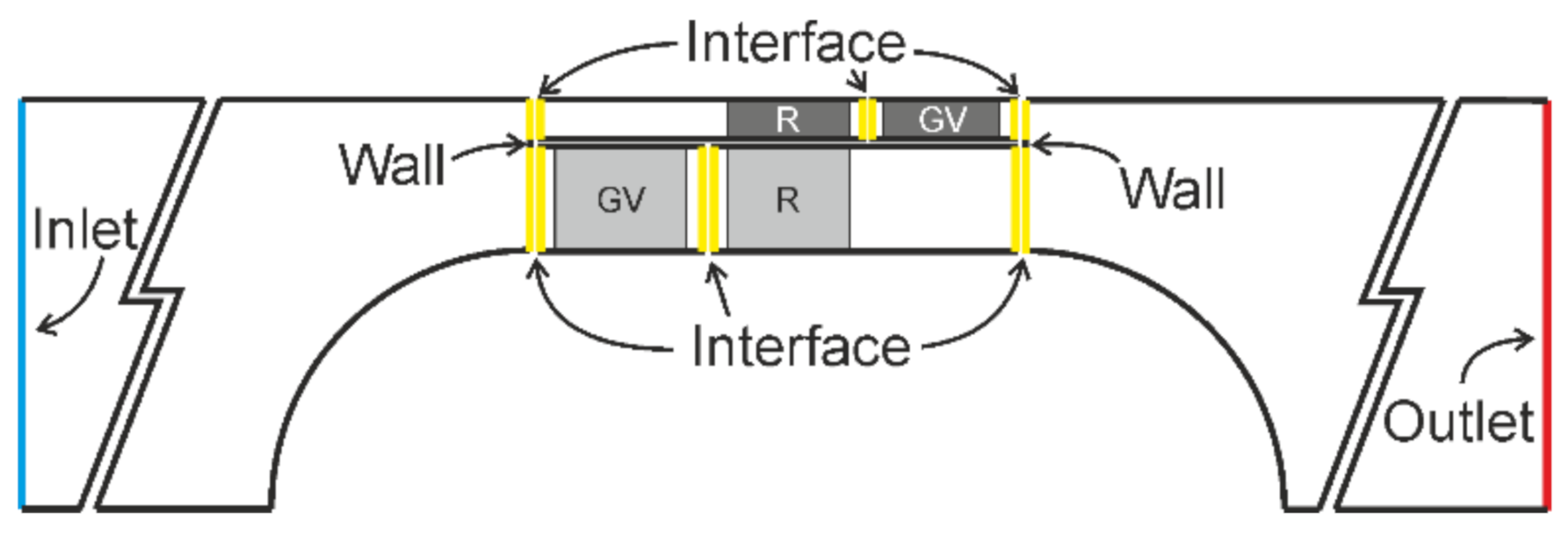

| L1 | 734 mm |
| L2 | 120 mm |
| L3 | 55 mm |
| L4 | 55 mm |
| L5 | 120 mm |
| L6 | 734 mm |
| DH | 10 mm |
| DR | 190 mm |
| DITH | 210 mm |
| DITS /DREF | 298 mm |
| DETH | 300 mm |
| DETS | 367 mm |
| Number of ExT rotor blades | 36 |
| Number of ExT guide vanes | 30 |
| Number of InT rotor blades | 24 |
| Number of InT guide vanes | 30 |
| Turbulence Model | Realizable k-ε with Enhanced Wall Treatment |
|---|---|
| Pressure-velocity coupling | SIMPLE Scheme |
| Transient formulation | Second order implicit |
| Spatial Discretization | |
| Gradient | Green-Gauss cell based |
| Pressure | Body force weighted |
| Momentum | Third-order MUSCL |
| Turbulent kinetic energy | Third-order MUSCL |
| Turbulent dissipation rate | Third-order MUSCL |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Díaz, M.; Pereiras, B.; Miguel-González, C.; Rodríguez, L.; Fernández-Oro, J. CFD Analysis of the Performance of a Double Decker Turbine for Wave Energy Conversion. Energies 2021, 14, 949. https://doi.org/10.3390/en14040949
García-Díaz M, Pereiras B, Miguel-González C, Rodríguez L, Fernández-Oro J. CFD Analysis of the Performance of a Double Decker Turbine for Wave Energy Conversion. Energies. 2021; 14(4):949. https://doi.org/10.3390/en14040949
Chicago/Turabian StyleGarcía-Díaz, Manuel, Bruno Pereiras, Celia Miguel-González, Laudino Rodríguez, and Jesús Fernández-Oro. 2021. "CFD Analysis of the Performance of a Double Decker Turbine for Wave Energy Conversion" Energies 14, no. 4: 949. https://doi.org/10.3390/en14040949
APA StyleGarcía-Díaz, M., Pereiras, B., Miguel-González, C., Rodríguez, L., & Fernández-Oro, J. (2021). CFD Analysis of the Performance of a Double Decker Turbine for Wave Energy Conversion. Energies, 14(4), 949. https://doi.org/10.3390/en14040949






