Autonomous Operation of Stationary Battery Energy Storage Systems—Optimal Storage Design and Economic Potential
Abstract
:1. Introduction
2. Approach
2.1. Model
2.2. Optimization
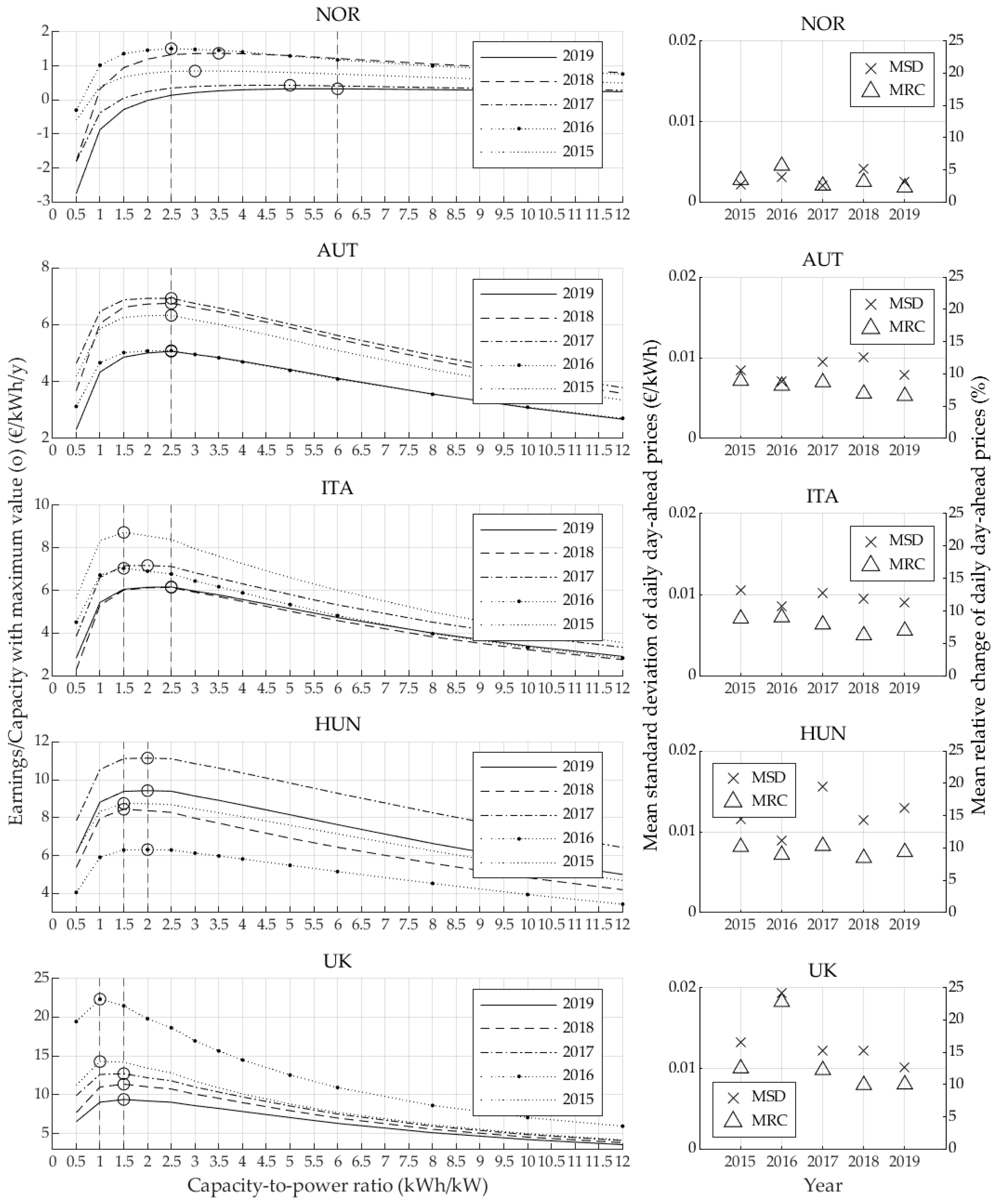
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature and Abbreviations
| AC | Alternating current |
| AUT | Austria |
| BESS | Battery energy storage system |
| Incentive (€/MWh) | |
| DC | Direct current |
| ENTSO-E | European network of transmission system operators for electricity |
| Electrical energy content (J) | |
| Electric vehicle | |
| EXAA | Energy exchange Austria |
| HUN | Hungary |
| ITA | Italy |
| MRC | Mean relative change (%) |
| MSD | Mean standard deviation (€/kWh) |
| NOR | Norway |
| N2EX | Power market in the United Kingdom |
| Alternating charging/discharging power (W) | |
| Direct charging/discharging power (W) | |
| Linearized battery losses (W) | |
| SOC | State of charge (%) |
| Time (s) | |
| Decision variable on DC side (–) | |
| UK | United Kingdom |
| Charging selected (–) | |
| Discharging selected (–) | |
| Battery efficiency (–) | |
| Converter efficiency (–) |
References
- Letcher, T.M. Why do we have global warming? In Managing Global Warming; Elsevier: Amsterdam, The Netherlands, 2019; pp. 3–15. ISBN 978-0-12-814104-5. [Google Scholar]
- Kung, C.-C.; McCarl, B. Sustainable Energy Development under Climate Change. Sustainability 2018, 10, 3269. [Google Scholar] [CrossRef] [Green Version]
- Moriarty, P.; Honnery, D. Energy Efficiency or Conservation for Mitigating Climate Change? Energies 2019, 12, 3543. [Google Scholar] [CrossRef] [Green Version]
- Sugiyama, M. Climate Change Mitigation and Electrification. Energy Policy 2012, 44, 464–468. [Google Scholar] [CrossRef]
- European Commission. The European Green Deal; European Commission: Brussels, Belgium, 2019; p. 2. [Google Scholar]
- Heide, D.; von Bremen, L.; Greiner, M.; Hoffmann, C.; Speckmann, M.; Bofinger, S. Seasonal Optimal Mix of Wind and Solar Power in a Future, Highly Renewable Europe. Renew. Energy 2010, 35, 2483–2489. [Google Scholar] [CrossRef]
- Blonsky, M.; Nagarajan, A.; Ghosh, S.; McKenna, K.; Veda, S.; Kroposki, B. Potential Impacts of Transportation and Building Electrification on the Grid: A Review of Electrification Projections and Their Effects on Grid Infrastructure, Operation, and Planning. Curr. Sustain. Energy Rep. 2019, 6, 169–176. [Google Scholar] [CrossRef]
- Langniß, O.; Diekmann, J.; Lehr, U. Advanced Mechanisms for the Promotion of Renewable Energy—Models for the Future Evolution of the German Renewable Energy Act. Energy Policy 2009, 37, 1289–1297. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Bremner, S.; Menictas, C.; Kay, M. Battery Energy Storage System Size Determination in Renewable Energy Systems: A Review. Renew. Sustain. Energy Rev. 2018, 91, 109–125. [Google Scholar] [CrossRef]
- Madlener, R.; Specht, J.M. An Exploratory Economic Analysis of Underground Pumped-Storage Hydro Power Plants in Abandoned Coal Mines. SSRN Electron. J. 2013, 2. [Google Scholar] [CrossRef] [Green Version]
- Faessler, B.; Kepplinger, P.; Petrasch, J. Field Testing of Repurposed Electric Vehicle Batteries for Price-Driven Grid Balancing. J. Energy Storage 2019, 21, 40–47. [Google Scholar] [CrossRef]
- Canals Casals, L.; Barbero, M.; Corchero, C. Reused Second Life Batteries for Aggregated Demand Response Services. J. Clean. Prod. 2019, 212, 99–108. [Google Scholar] [CrossRef]
- Musio, M.; Damiano, A. Analysis of Vehicle to Grid and Energy Storage Integration in a Virtual Power Plant. In Proceedings of the IECON 2014—40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 3094–3100. [Google Scholar]
- Steber, D.; Bazan, P.; German, R. SWARM—Strategies for Providing Frequency Containment Reserve Power with a Distributed Battery Storage System. In Proceedings of the 2016 IEEE International Energy Conference (ENERGYCON), Leuven, Belgium, 4–8 April 2016; pp. 1–6. [Google Scholar]
- Deconinck, G. An Evaluation of Two-Way Communication Means for Advanced Metering in Flanders (Belgium). In Proceedings of the 2008 IEEE Instrumentation and Measurement Technology Conference, Victoria, BC, Canada, 12–15 May 2008; pp. 900–905. [Google Scholar]
- Kepplinger, P.; Huber, G.; Petrasch, J. Autonomous Optimal Control for Demand Side Management with Resistive Domestic Hot Water Heaters Using Linear Optimization. Energy Build. 2015, 100, 50–55. [Google Scholar] [CrossRef]
- Hesse, H.; Schimpe, M.; Kucevic, D.; Jossen, A. Lithium-Ion Battery Storage for the Grid—A Review of Stationary Battery Storage System Design Tailored for Applications in Modern Power Grids. Energies 2017, 10, 2107. [Google Scholar] [CrossRef] [Green Version]
- Müller, M.; Viernstein, L.; Truong, C.N.; Eiting, A.; Hesse, H.C.; Witzmann, R.; Jossen, A. Evaluation of Grid-Level Adaptability for Stationary Battery Energy Storage System Applications in Europe. J. Energy Storage 2017, 9, 1–11. [Google Scholar] [CrossRef]
- Zeh, A.; Müller, M.; Naumann, M.; Hesse, H.; Jossen, A.; Witzmann, R. Fundamentals of Using Battery Energy Storage Systems to Provide Primary Control Reserves in Germany. Batteries 2016, 2, 29. [Google Scholar] [CrossRef] [Green Version]
- Stephan, A.; Battke, B.; Beuse, M.D.; Clausdeinken, J.H.; Schmidt, T.S. Limiting the Public Cost of Stationary Battery Deployment by Combining Applications. Nat. Energy 2016, 1, 16079. [Google Scholar] [CrossRef]
- European Commission Passenger Cars|EAFO. Available online: https://www.eafo.eu/vehicles-and-fleet/m1 (accessed on 7 July 2020).
- IEA. Global EV Outlook 2020; IEA: Paris, France, 2020; p. 276. [Google Scholar]
- Opitz, A.; Badami, P.; Shen, L.; Vignarooban, K.; Kannan, A.M. Can Li-Ion Batteries Be the Panacea for Automotive Applications? Renew. Sustain. Energy Rev. 2017, 68, 685–692. [Google Scholar] [CrossRef] [Green Version]
- Casals, L.C.; Amante García, B.; Canal, C. Second Life Batteries Lifespan: Rest of Useful Life and Environmental Analysis. J. Environ. Manag. 2019, 232, 354–363. [Google Scholar] [CrossRef] [PubMed]
- Reinhardt, R.; Domingo, S.G.; Garcia, B.A.; Christodoulou, I. Macro Environmental Analysis of the Electric Vehicle Battery Second Use Market. In Proceedings of the 2017 14th International Conference on the European Energy Market (EEM), Dresden, Germany, 6–9 June 2017; pp. 1–6. [Google Scholar]
- Mirzaei Omrani, M.; Jannesari, H. Economic and Environmental Assessment of Reusing Electric Vehicle Lithium-Ion Batteries for Load Leveling in the Residential, Industrial and Photovoltaic Power Plants Sectors. Renew. Sustain. Energy Rev. 2019, 116, 109413. [Google Scholar] [CrossRef]
- Ahmadi, L.; Young, S.B.; Fowler, M.; Fraser, R.A.; Achachlouei, M.A. A Cascaded Life Cycle: Reuse of Electric Vehicle Lithium-Ion Battery Packs in Energy Storage Systems. Int. J. Life Cycle Assess. 2017, 22, 111–124. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Y.; Pang, B.; Sun, B.; Kokko, A. Second Use Value of China’s New Energy Vehicle Battery: A View Based on Multi-Scenario Simulation. Sustainability 2020, 12, 341. [Google Scholar] [CrossRef] [Green Version]
- Bobba, S.; Mathieux, F.; Ardente, F.; Blengini, G.A.; Cusenza, M.A.; Podias, A.; Pfrang, A. Life Cycle Assessment of Repurposed Electric Vehicle Batteries: An Adapted Method Based on Modelling Energy Flows. J. Energy Storage 2018, 19, 213–225. [Google Scholar] [CrossRef]
- Fäßler, B.; Kepplinger, P.; Kolhe, M.L.; Petrasch, J. Decentralized On-Site Optimization of a Battery Storage System Using One-Way Communication. In Proceedings of the International Conference on Renewable Power Generation (RPG 2015), Beijing, China, 17–18 October 2015; pp. 1–6. [Google Scholar]
- Faessler, B.; Kepplinger, P.; Petrasch, J. Decentralized Price-Driven Grid Balancing via Repurposed Electric Vehicle Batteries. Energy 2017, 118, 446–455. [Google Scholar] [CrossRef]
- Faessler, B.; Schuler, M.; Preißinger, M.; Kepplinger, P. Battery Storage Systems as Grid-Balancing Measure in Low-Voltage Distribution Grids with Distributed Generation. Energies 2017, 10, 2161. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Rincon-Mora, G.A. Accurate Electrical Battery Model Capable of Predicting Runtime and I-V Performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Jakobsen, A.B. Autonomous Operation of a Second-Use Battery Storage System. Bachelor’s Thesis, University of Agder, Grimstad, Norway, 2020. [Google Scholar]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Mohamed, A. A Review of Lithium-Ion Battery State of Charge Estimation and Management System in Electric Vehicle Applications: Challenges and Recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- Zdyb, A.; Gulkowski, S. Performance Assessment of Four Different Photovoltaic Technologies in Poland. Energies 2020, 13, 196. [Google Scholar] [CrossRef] [Green Version]
- Khatib, T. Optimization of a Grid-Connected Renewable Energy System for a Case Study in Nablus, Palestine. Int. J. Low-Carbon Technol. 2014, 9, 311–318. [Google Scholar] [CrossRef] [Green Version]
- Nord Pool Historical Market Data. Available online: https://www.nordpoolgroup.com/historical-market-data/ (accessed on 11 December 2020).
- ENTSO-E ENTSO-E Transparency Platform. Available online: https://transparency.entsoe.eu/ (accessed on 23 October 2020).
- Energy Exchange Austria Historische Daten. Available online: https://www.exaa.at/de/marktdaten/historische-daten (accessed on 11 December 2020).
- Muhammad, M.; Attidekou, P.S.; Ahmeid, M.; Milojevic, Z.; Lambert, S. Sorting of Spent Electric Vehicle Batteries for Second Life Application. In Proceedings of the 2019 IEEE 7th International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 12–14 August 2019; pp. 325–329. [Google Scholar]
- Farhad, S.; Nazari, A. Introducing the Energy Efficiency Map of Lithium-Ion Batteries. Int. J. Energy Res. 2019, 43, 931–944. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faessler, B.; Bogunović Jakobsen, A. Autonomous Operation of Stationary Battery Energy Storage Systems—Optimal Storage Design and Economic Potential. Energies 2021, 14, 1333. https://doi.org/10.3390/en14051333
Faessler B, Bogunović Jakobsen A. Autonomous Operation of Stationary Battery Energy Storage Systems—Optimal Storage Design and Economic Potential. Energies. 2021; 14(5):1333. https://doi.org/10.3390/en14051333
Chicago/Turabian StyleFaessler, Bernhard, and Aleksander Bogunović Jakobsen. 2021. "Autonomous Operation of Stationary Battery Energy Storage Systems—Optimal Storage Design and Economic Potential" Energies 14, no. 5: 1333. https://doi.org/10.3390/en14051333
APA StyleFaessler, B., & Bogunović Jakobsen, A. (2021). Autonomous Operation of Stationary Battery Energy Storage Systems—Optimal Storage Design and Economic Potential. Energies, 14(5), 1333. https://doi.org/10.3390/en14051333






