Figure 1.
Geometry of how a 1D slab reactor may be split into five domains with a reflective boundary condition on the left-hand side and a bare boundary condition on the right-hand side.
Figure 1.
Geometry of how a 1D slab reactor may be split into five domains with a reflective boundary condition on the left-hand side and a bare boundary condition on the right-hand side.
Figure 2.
Geometry of a 1D slice taken through a fuel assembly. Regions A, B, C, D and E contain guide-tubes that can have control rods inserted. All other regions contain fuel rods with fissionable material.
Figure 2.
Geometry of a 1D slice taken through a fuel assembly. Regions A, B, C, D and E contain guide-tubes that can have control rods inserted. All other regions contain fuel rods with fissionable material.
Figure 3.
vs. iteration number for all methods and the High-Fidelity Model (HFM).
Figure 3.
vs. iteration number for all methods and the High-Fidelity Model (HFM).
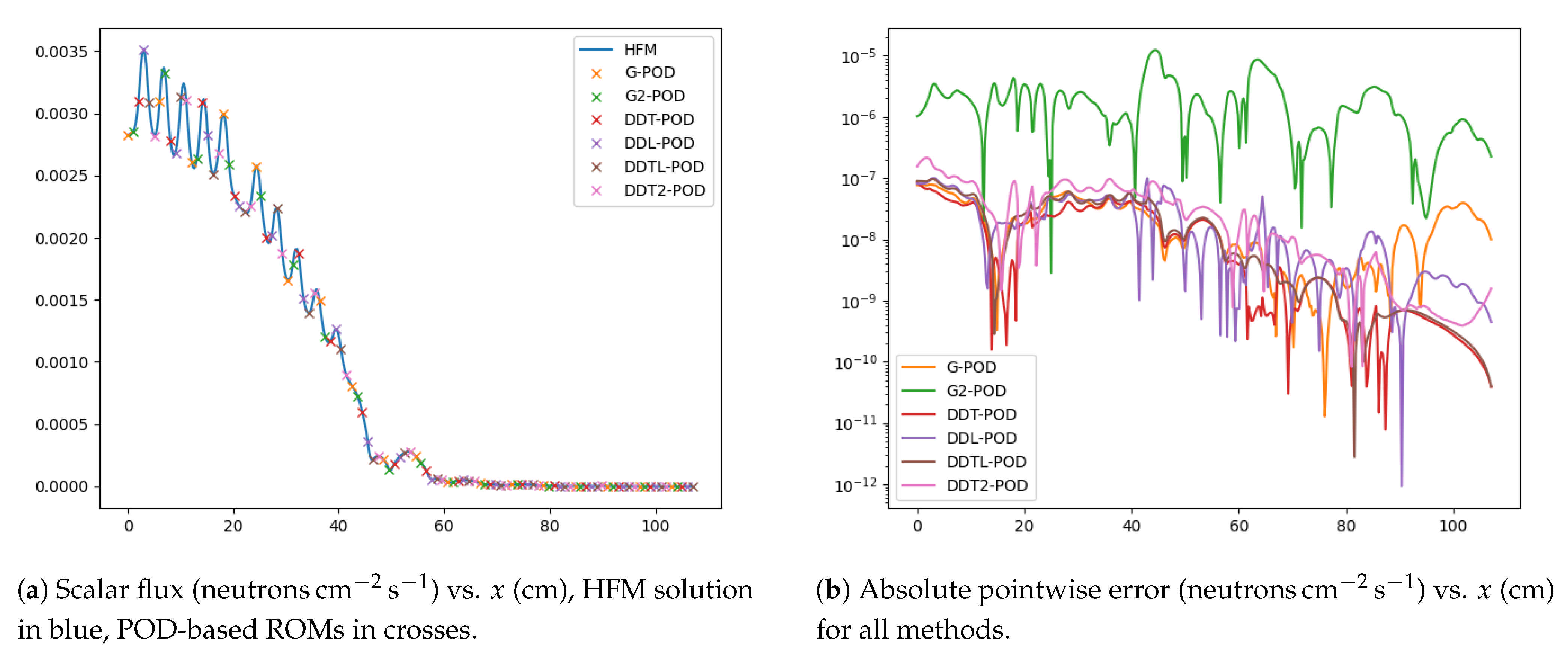
Figure 4.
Scalar flux for Energy Group 1 for the HFM (blue) and POD methods and the pointwise error between them with parameters .
Figure 4.
Scalar flux for Energy Group 1 for the HFM (blue) and POD methods and the pointwise error between them with parameters .
Figure 5.
Scalar flux for Energy Group 5 for the HFM (blue) and POD methods and the pointwise error between them with parameters .
Figure 5.
Scalar flux for Energy Group 5 for the HFM (blue) and POD methods and the pointwise error between them with parameters .
Figure 6.
Scalar flux for Energy Group 9 for the HFM (blue) and POD methods and the pointwise error between them with parameters .
Figure 6.
Scalar flux for Energy Group 9 for the HFM (blue) and POD methods and the pointwise error between them with parameters .
Figure 7.
Scalar flux for Energy Group 13 for the HFM (blue) and POD methods and the pointwise error between them with parameters .
Figure 7.
Scalar flux for Energy Group 13 for the HFM (blue) and POD methods and the pointwise error between them with parameters .
Figure 8.
Scalar flux for Energy Group 17 for the HFM (blue) and POD methods and the pointwise error between them with parameters .
Figure 8.
Scalar flux for Energy Group 17 for the HFM (blue) and POD methods and the pointwise error between them with parameters .
Figure 9.
Scalar flux for Energy Group 21 for the HFM (blue) and POD methods and the pointwise error between them with parameters .
Figure 9.
Scalar flux for Energy Group 21 for the HFM (blue) and POD methods and the pointwise error between them with parameters .
Figure 10.
Boxplots showing the errors for all six methods. The median is given by the orange line, the interquartile ranges by the box and the minimum and maximum values by whiskers.
Figure 10.
Boxplots showing the errors for all six methods. The median is given by the orange line, the interquartile ranges by the box and the minimum and maximum values by whiskers.
Figure 11.
vs. iteration number for the HFM and the three methods with limited (lim) number of snapshots or smart selection of number of basis functions.
Figure 11.
vs. iteration number for the HFM and the three methods with limited (lim) number of snapshots or smart selection of number of basis functions.
Figure 12.
Scalar flux for Energy Group 1 for the HFM (blue) and POD-based ROMs, with limited number of snapshots or smart selection of number of basis functions, in crosses, and the pointwise error between them with parameters .
Figure 12.
Scalar flux for Energy Group 1 for the HFM (blue) and POD-based ROMs, with limited number of snapshots or smart selection of number of basis functions, in crosses, and the pointwise error between them with parameters .
Figure 13.
Scalar flux for Energy Group 1 for the HFM (blue) and POD-based ROMs, with the limited number of snapshots or smart selection of the number of basis functions, in crosses, and the pointwise error between them with parameters .
Figure 13.
Scalar flux for Energy Group 1 for the HFM (blue) and POD-based ROMs, with the limited number of snapshots or smart selection of the number of basis functions, in crosses, and the pointwise error between them with parameters .
Figure 14.
Scalar flux for Energy Group 1 for the HFM (blue) and POD-based ROMs, with the limited number of snapshots or smart selection of the number of basis functions, in crosses, and the pointwise error between them with parameters .
Figure 14.
Scalar flux for Energy Group 1 for the HFM (blue) and POD-based ROMs, with the limited number of snapshots or smart selection of the number of basis functions, in crosses, and the pointwise error between them with parameters .
Figure 15.
Scalar flux for Energy Group 1 for the HFM (blue) and POD-based ROMs, with the limited number of snapshots or smart selection of the number of basis functions, in crosses, and the pointwise error between them with parameters .
Figure 15.
Scalar flux for Energy Group 1 for the HFM (blue) and POD-based ROMs, with the limited number of snapshots or smart selection of the number of basis functions, in crosses, and the pointwise error between them with parameters .
Figure 16.
Scalar flux for Energy Group 1 for the HFM (blue) and POD-based ROMs, with the limited number of snapshots or smart selection of the number of basis functions, in crosses, and the pointwise error between them with parameters .
Figure 16.
Scalar flux for Energy Group 1 for the HFM (blue) and POD-based ROMs, with the limited number of snapshots or smart selection of the number of basis functions, in crosses, and the pointwise error between them with parameters .
Figure 17.
Scalar flux for Energy Group 1 for the HFM (blue) and POD-based ROMs, with the limited number of snapshots or smart selection of the number of basis functions, in crosses, and the pointwise error between them with parameters .
Figure 17.
Scalar flux for Energy Group 1 for the HFM (blue) and POD-based ROMs, with the limited number of snapshots or smart selection of the number of basis functions, in crosses, and the pointwise error between them with parameters .
Figure 18.
Boxplots showing the errors for methods with the limited number of snapshots and smart selection of the number of basis functions. The median is given by the orange line, the interquartile ranges by the box and the minimum and maximum values by whiskers.
Figure 18.
Boxplots showing the errors for methods with the limited number of snapshots and smart selection of the number of basis functions. The median is given by the orange line, the interquartile ranges by the box and the minimum and maximum values by whiskers.
Table 1.
Table showing possible domains within a system. The rows represent the material type of domain, and the columns represent the location within the system. UOX, Uranium Oxide; MOX, Mixed Oxide.
Table 1.
Table showing possible domains within a system. The rows represent the material type of domain, and the columns represent the location within the system. UOX, Uranium Oxide; MOX, Mixed Oxide.
| | 1 | 2 | 3 | 4 | 5 |
|---|
| UOX | Yes | Yes | Yes | Yes | Yes unless 4 = Reflector |
| MOX | Yes | Yes | Yes | Yes | Yes unless 4 = Reflector |
| Reflector | No | No | No | Yes | Yes |
Table 2.
Table showing possible systems within the smaller data set. The rows represent the material type of domain, and the columns represent the location and how many domains are used in the solution.
Table 2.
Table showing possible systems within the smaller data set. The rows represent the material type of domain, and the columns represent the location and how many domains are used in the solution.
| | | | | | | | | |
|---|
| | 1 | 2 | 3 | | 1 | 2 | | 1 |
| UOX | Yes | Yes | Yes unless 2 = Reflector | | Yes | Yes | | Yes |
| MOX | Yes | Yes | Yes unless 2 = Reflector | | Yes | Yes | | Yes |
| Reflector | No | Yes | Yes | | Yes | No | | No |
Table 3.
Table showing the six methods, how many sets of basis functions are retained and the data from which they are constructed. POD, Proper Orthogonal Decomposition.
Table 3.
Table showing the six methods, how many sets of basis functions are retained and the data from which they are constructed. POD, Proper Orthogonal Decomposition.
| Name | Sets of Basis Functions | Data Used to Construct Basis Functions |
|---|
| G-POD | 1 | Global data: , 250 basis functions retained |
| G2-POD | 1 | Global data: , 50 basis functions retained |
| DDT-POD | 3 | Type of domain: |
| DDL-POD | 5 | Location of domain: |
| DDTL-POD | 12 | Location and type of domain: |
| DDT2-POD | 3 | Type of domain from alternate data set: |
Table 4.
Mean absolute maximum errors in the flux profile and for solutions using POD-based reduced-order models.
Table 4.
Mean absolute maximum errors in the flux profile and for solutions using POD-based reduced-order models.
| | G-POD | G2-POD | DDT-POD | DDL-POD | DDTL-POD | DDT2-POD |
|---|
| Flux Error | 1.2286 × 10−3 | 2.7860 × 10−2 | 1.2391 × 10−3 | 1.7601 × 10−3 | 1.6563 × 10−3 | 1.6593 × 10−3 |
| Error | 2.2952 × 10−5 | 4.3557 × 10−3 | 2.3154 × 10−5 | 2.3901 × 10−5 | 2.6866 × 10−5 | 5.6589 × 10−5 |
Table 5.
Mean absolute maximum errors in the flux profile and for solutions using POD-based reduced-order models with the limited number of snapshots and smart selection of the number of basis functions.
Table 5.
Mean absolute maximum errors in the flux profile and for solutions using POD-based reduced-order models with the limited number of snapshots and smart selection of the number of basis functions.
| | G-POD-Lim | DDT-POD-Lim | DDL-POD-Lim | G-POD-Basis | DDT-POD-Basis | DDL-POD-Basis |
|---|
| Flux Error | 2.4846 × 10−1 | 7.5716 × 10−3 | 2.1496 × 10−3 | 1.2416 × 10−3 | 1.2375 × 10−3 | 3.1000 × 10−3 |
| Error | 2.3198 × 10−2 | 1.3405 × 10−3 | 7.5412 × 10−5 | 2.5474 × 10−5 | 2.4721 × 10−5 | 6.1249 × 10−5 |