Simulation Studies of Control Systems for Doubly Fed Induction Generator Supplied by the Current Source Converter
Abstract
:1. Introduction
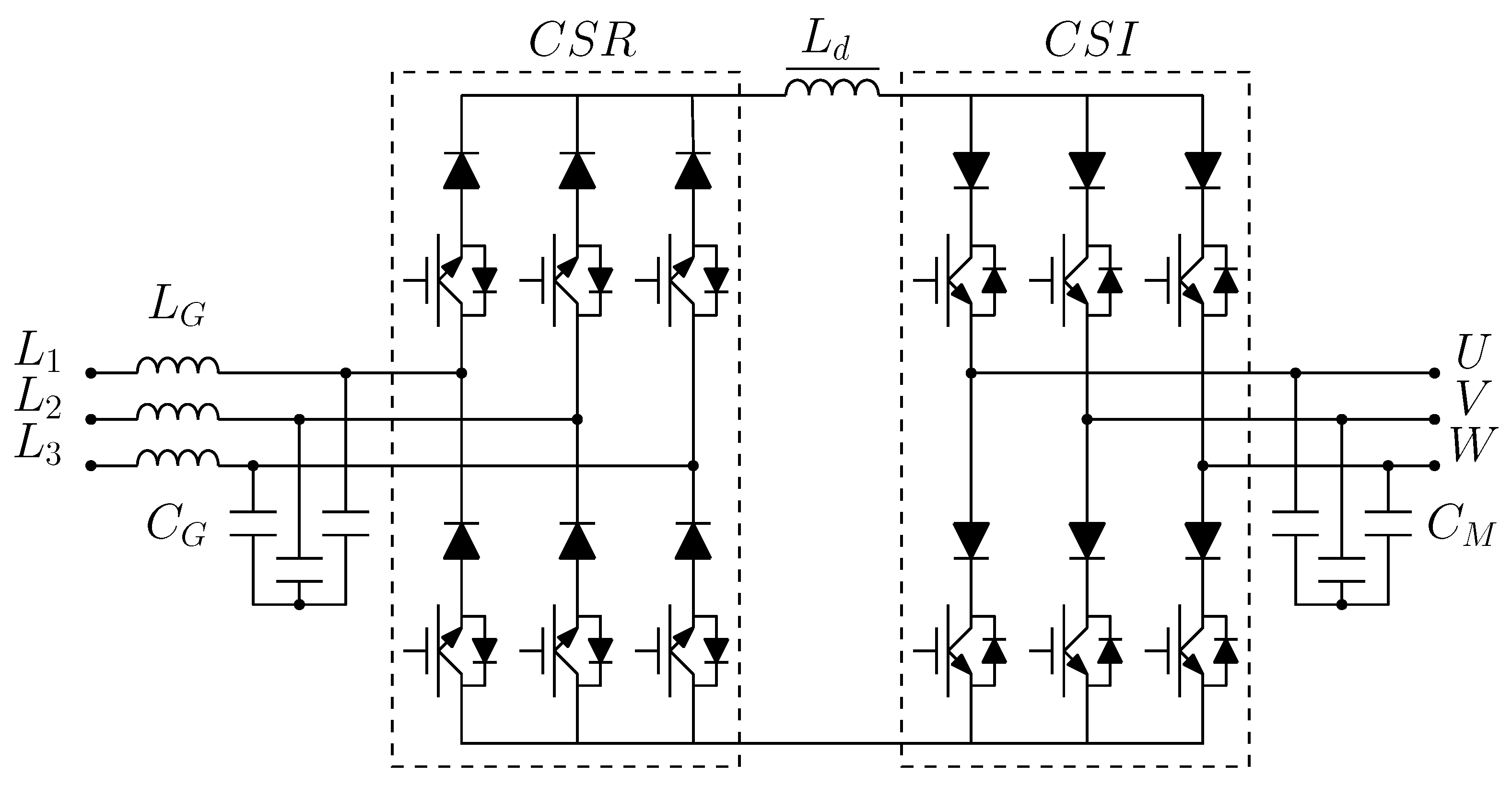
2. Doubly Fed Induction Generator System Model
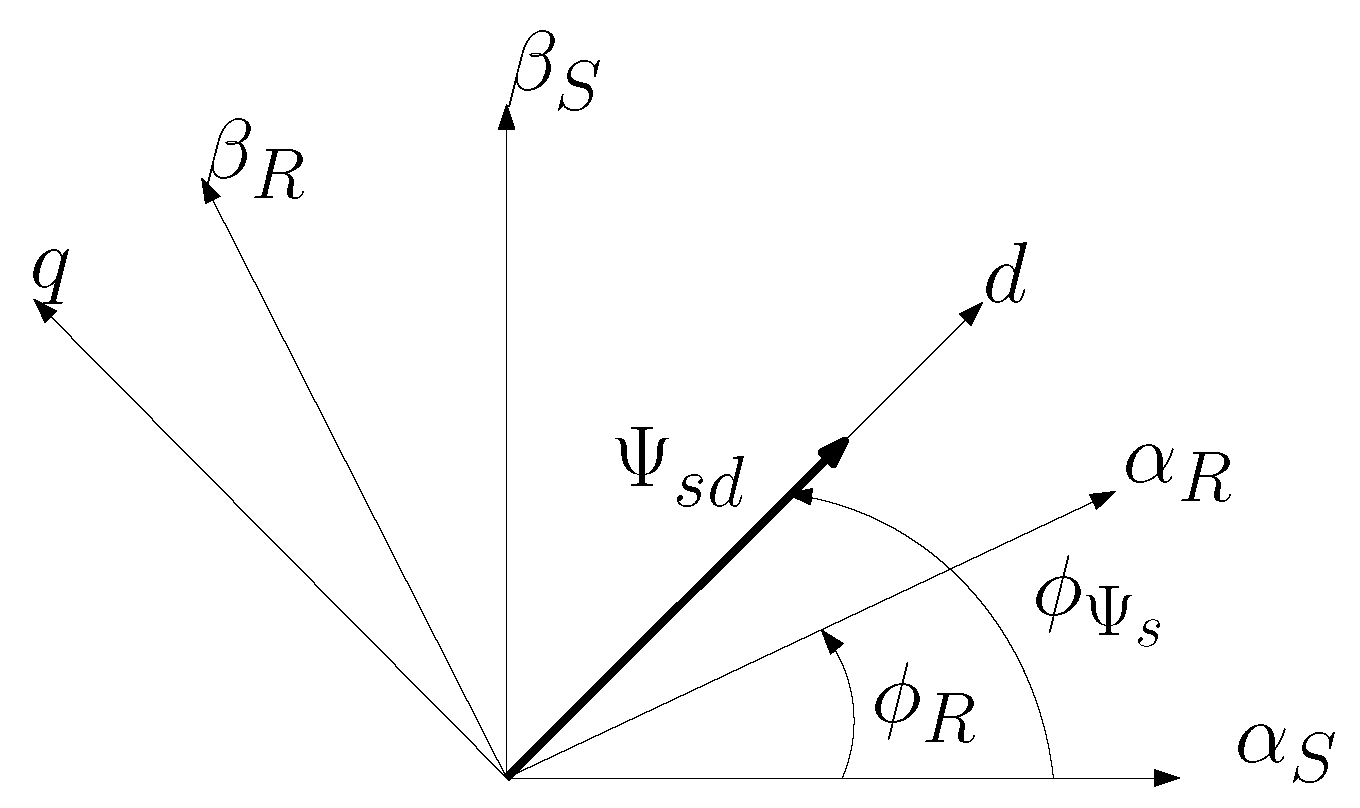
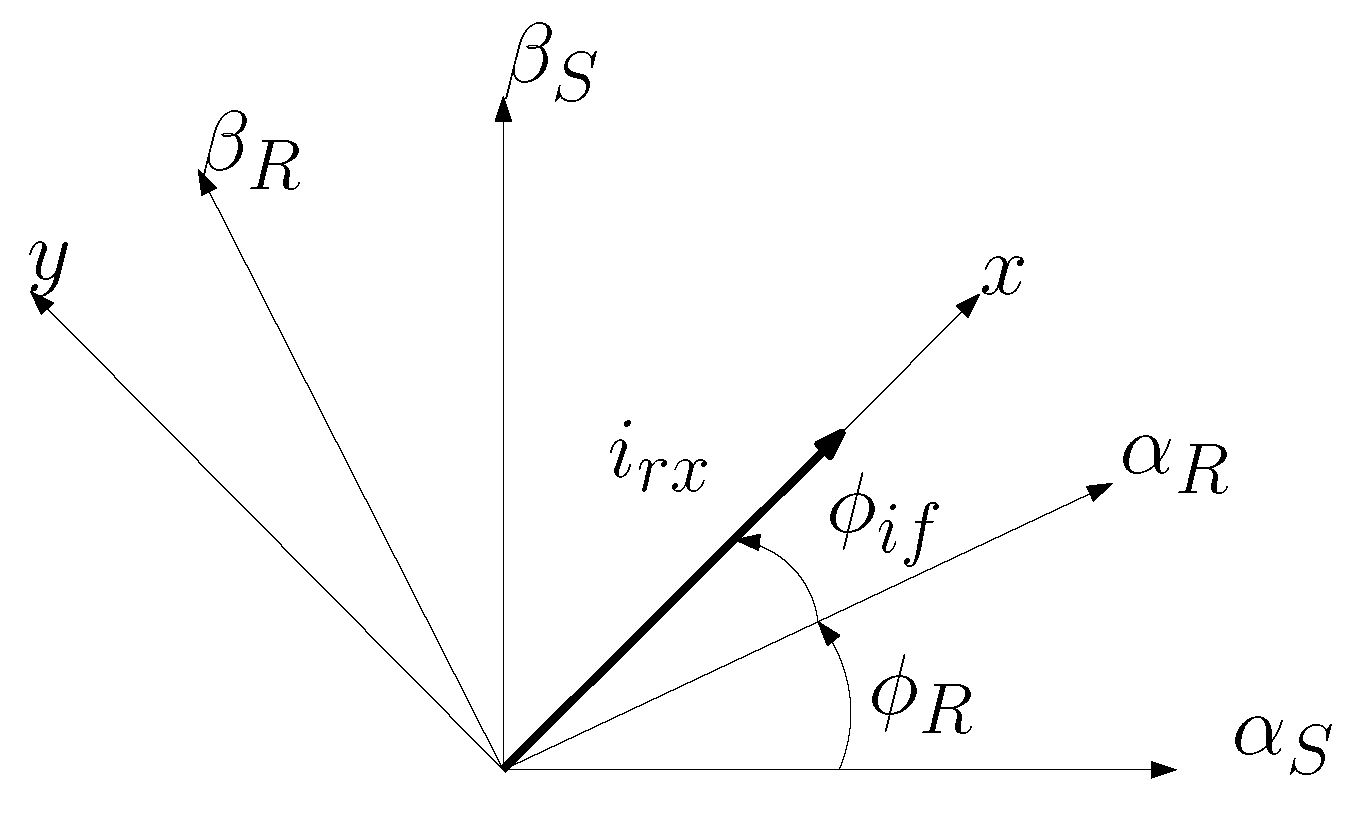
2.1. Field-Oriented Control
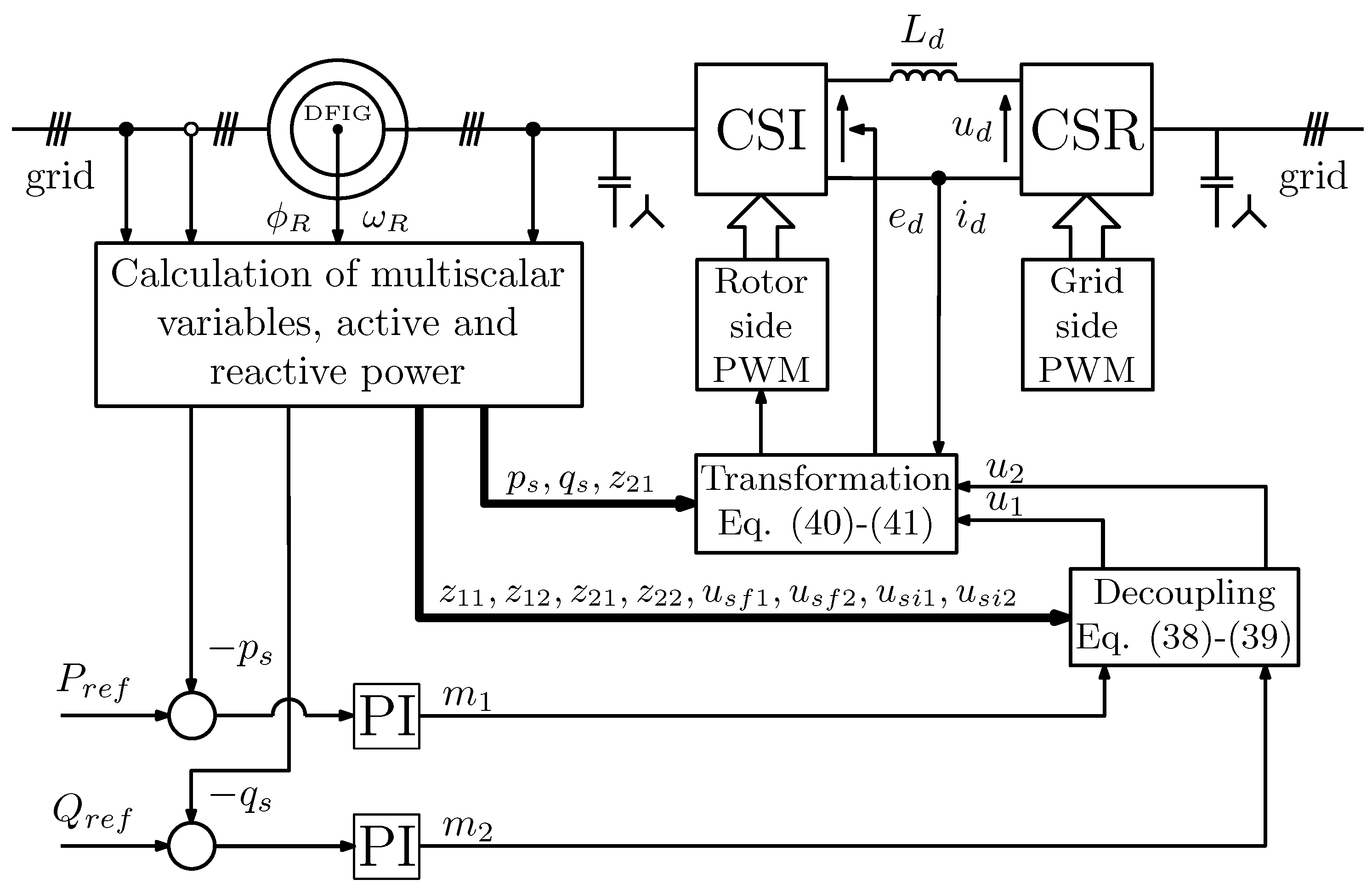
2.2. DFIG Control System Based on Active and Reactive Powers
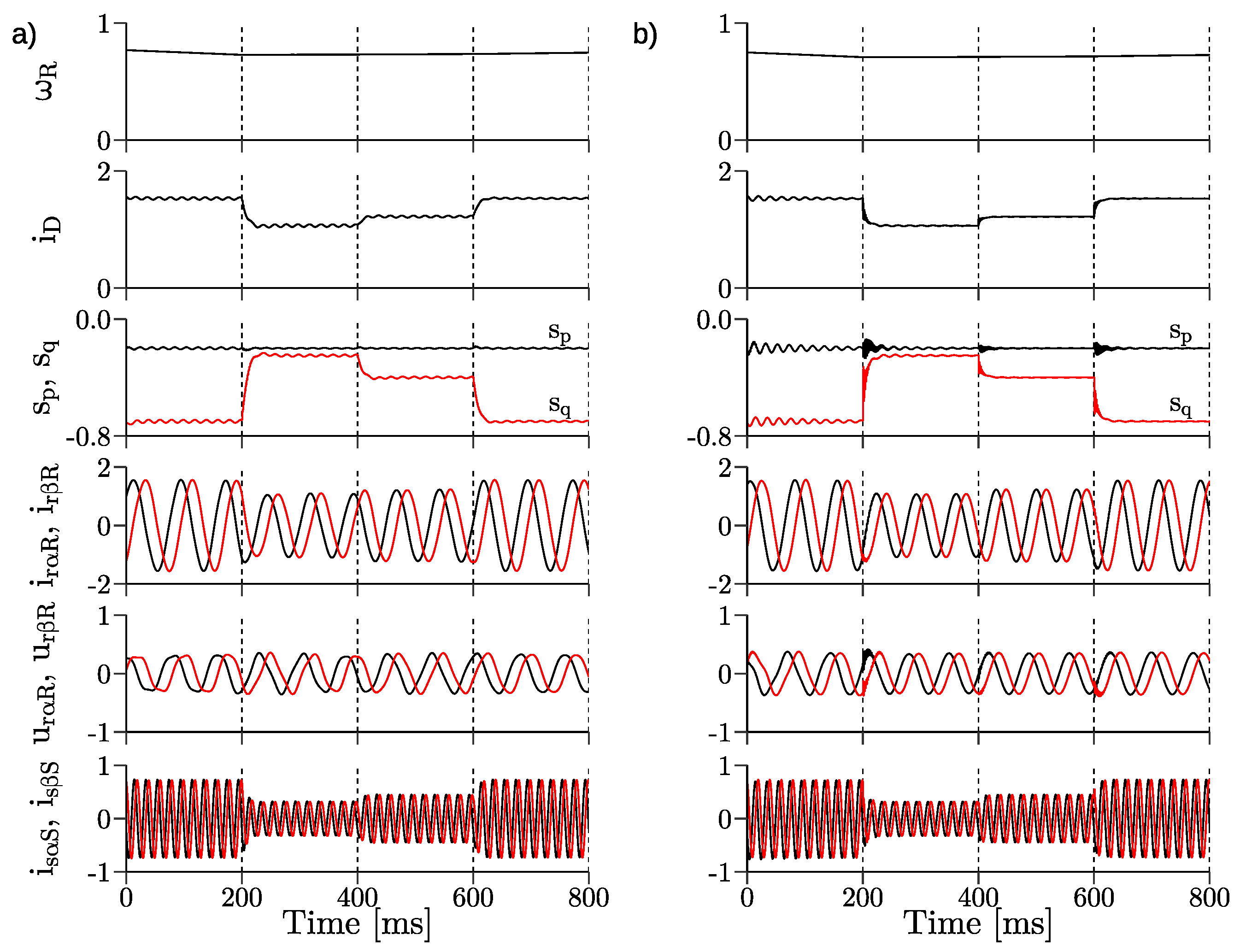
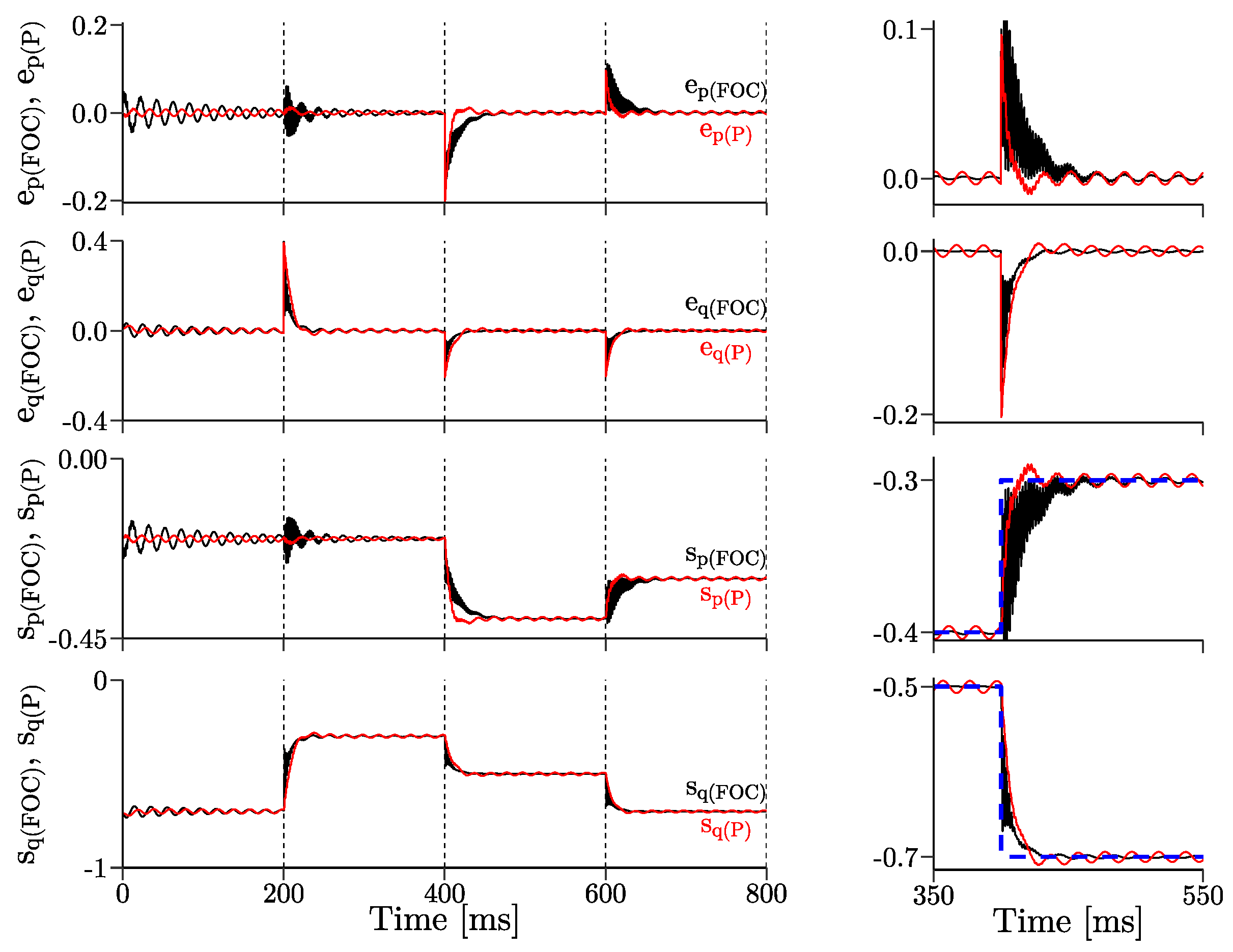
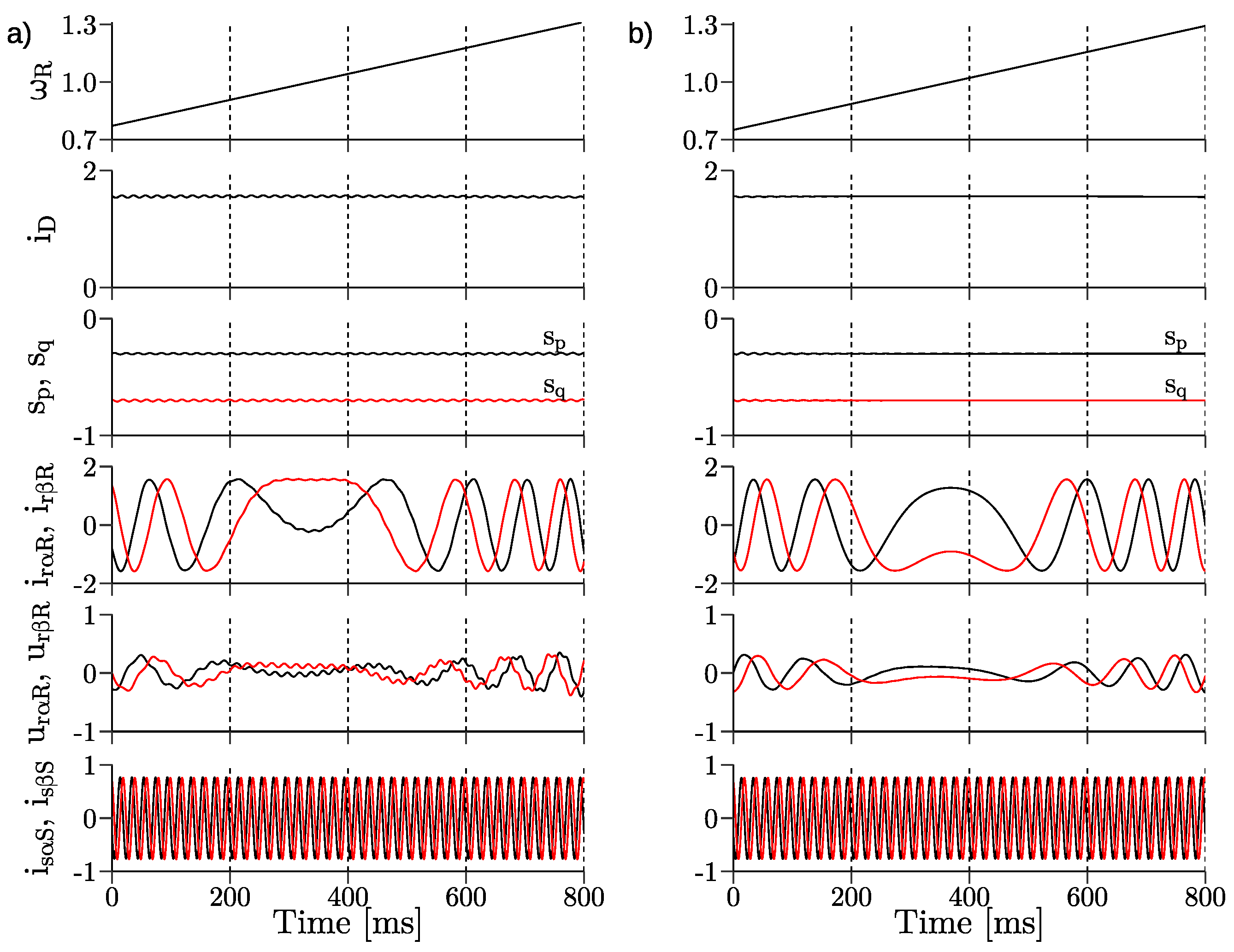
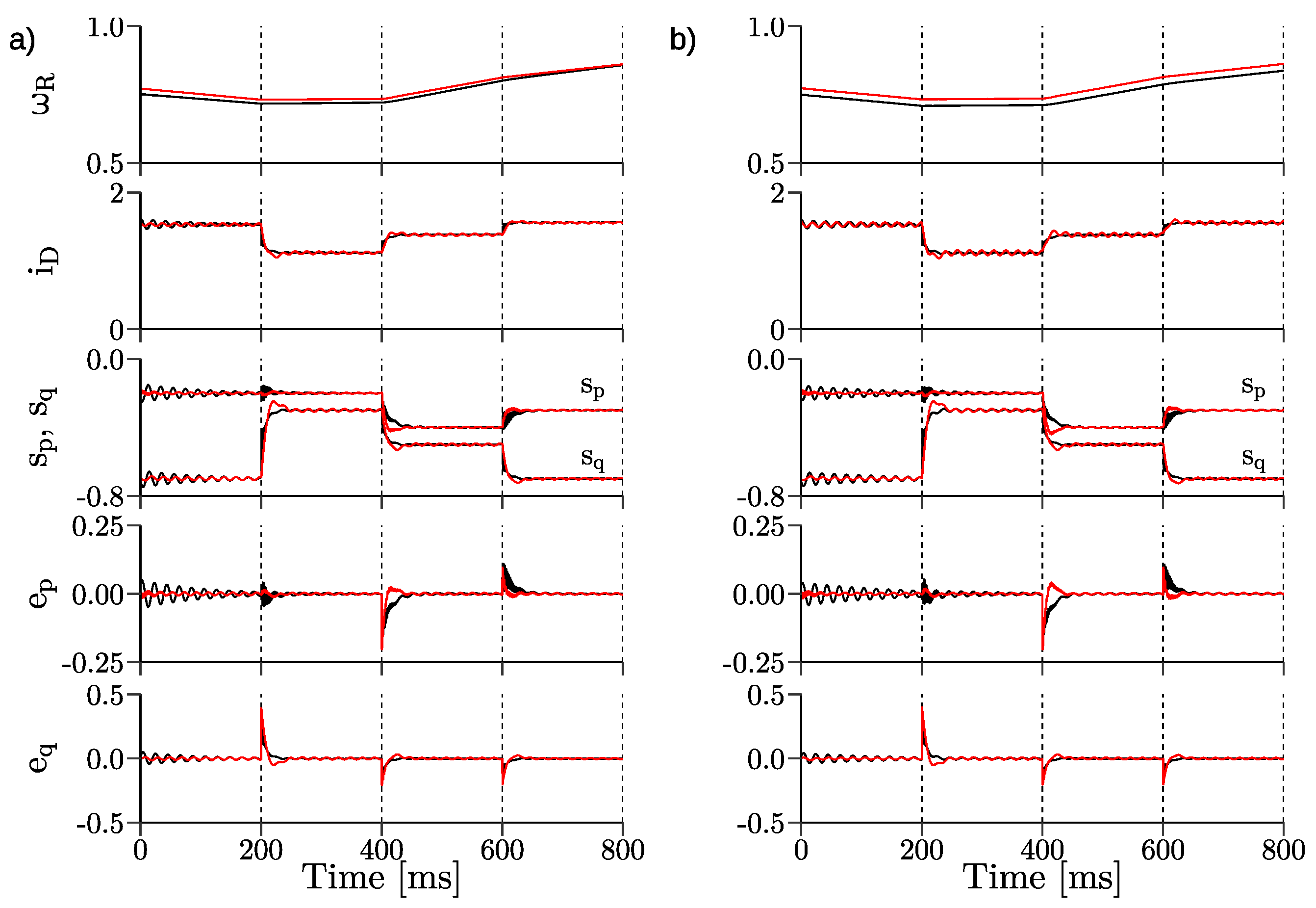
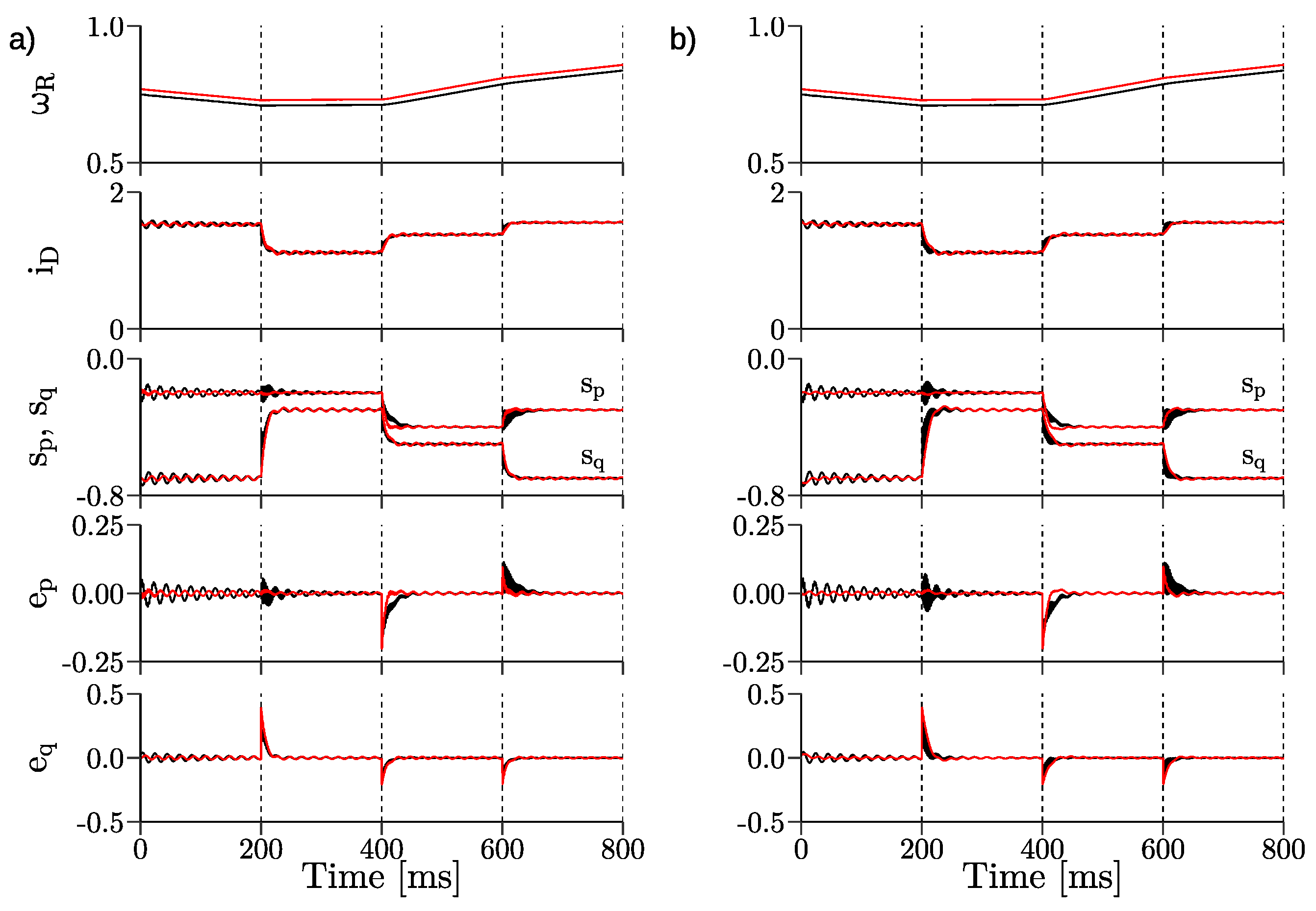
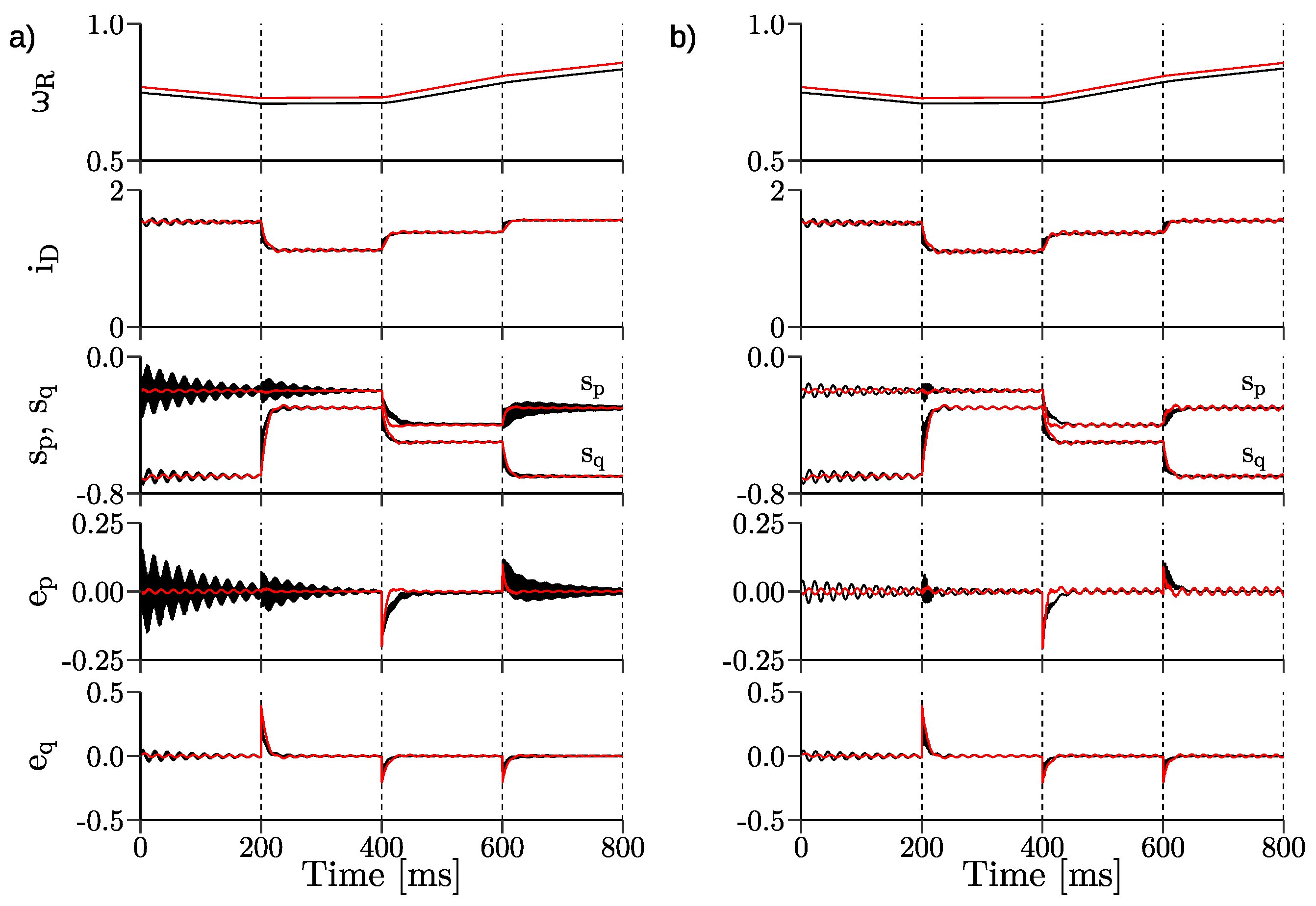
3. Simulation Results
- changes of the reference active power;
- changes of the reference reactive power;
- simultaneous changes of the reference active and reactive powers;
- changes of the rotor speed from under-synchronous to over-synchronous speed with constant reference active and reactive powers;
- uncertainties of DFIG nominal parameters for both control systems.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Burton, T.; Sharpe, D.; Jenkins, N.; Bossanyi, E. Wind Energy Handbook; John Wiley & Sons Ltd.: Chichester, UK, 2001. [Google Scholar]
- Fortmann, J. Modeling of Wind Turbines with Doubly Fed Generator System; Springer: Duisburg, Germany, 2014. [Google Scholar]
- Pillai, S.K.; Desai, K.M. A static scherbius drive with chopper. IEEE Trans. Ind. Electron. Control Instrum. 1977, 24, 24–29. [Google Scholar] [CrossRef]
- Smith, G.A.; Nigim, K.A. Wind-energy recovery by a static Scherbius induction generator. IEE Proc. C 1981, 128, 317–324. [Google Scholar] [CrossRef]
- Prasad, R.M.; Mulla, M.A. A Novel Position-Sensorless Algorithm for Field-Oriented Control of DFIG With Reduced Current Sensors. IEEE Trans. Sustain. Energy 2019, 10, 1098–1108. [Google Scholar] [CrossRef]
- Kakosimos, P.; Sarigiannidis, A.G.; Beniakar, M.; Kladas, A.; Gerada, C. Induction Motors Versus Permanent-Magnet Actuators for Aerospace Applications. IEEE Trans. Ind. Electron. 2014, 61, 4315–4325. [Google Scholar] [CrossRef]
- Aydin, E.; Polat, A.; Ergene, L.T. Vector Control of DFIG in Wind Power Applications. In Proceedings of the 5th International Conference on Renewable Energy Research and Applications, Birmingham, UK, 20–23 November 2016; pp. 478–483. [Google Scholar]
- Ihedrane, Y.; El Bekkali, C. Direct and Indirect Field Oriented Control Of DFIG-Generators for Wind Turbines Variable-Speed. In Proceedings of the 14th International Multi-Conference on Systems, Signals & Devices (SSD), Marrakech, Morocco, 28–31 March 2017; pp. 27–32. [Google Scholar]
- Erazo-Damián, I.; Apsley, J.M.; Perini, R.; Iacchetti, M.F.; Marques, G.D. Stand-Alone DFIG FOC Sensitivity and Stability Under Mismatched Inductances. IEEE Trans. Energy Convers. 2019, 34, 860–869. [Google Scholar] [CrossRef]
- Koczara, W.; Przybylski, J.; Drechsler, H. Oriented Control in the Drive System Double-Fed Machine (DFM). IFAC Proc. Vol. 1987, 20, 381–385. [Google Scholar] [CrossRef]
- Miller, N.W.; Sanchez-Gasca, J.J.; Price, W.W. Dynamic modeling of ge 1.5 and 3.6 mw wind turbine-generators for stability simulations. In Proceedings of the Power Engineering Society General Meeting, Toronto, ON, Canada, 13–17 July 2003; Volume 7, pp. 1977–1983. [Google Scholar]
- Benbouhenni, H.; Boudjema, Z. Two-level DTC based on ANN controller of DFIG using 7-level hysteresis command to reduce flux ripple comparing with traditional command. In Proceedings of the 2018 International Conference on Applied Smart Systems (ICASS), Medea, Algeria, 24–25 November 2018; pp. 1–8. [Google Scholar]
- Bakou, Y.; Abid, M.; Harrouz, A.; Yaichi, I.; Colak, I.; Kayisli, K.; Aissaoui, A. DTC Control of the DFIG, Application to the Production of Electrical Energy. In Proceedings of the 2019 8th International Conference on Renewable Energy Research and Applications (ICRERA), Brasov, Romania, 3–6 November 2019; pp. 910–915. [Google Scholar]
- Li, Y.; Hang, L.; Li, G.; Guo, Y.; Zou, Y.; Chen, J.; Li, J.; Zhuang, J.; Li, S. An improved DTC controller for DFIG-based wind generation system. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 1423–1426. [Google Scholar]
- Ouezgan, K.; Bossoufi, B.; Bargach, M.N. DTC Control of DFIG-Generators for Wind Turbines: FPGA Implementation Based. In Proceedings of the 2017 International Renewable and Sustainable Energy Conference (IRSEC), Tangier, Morocco, 4–7 December 2017; pp. 1–6. [Google Scholar]
- Singh, P.; Kaur, A. Power control of Doubly Fed Induction Generator (DFIG) using back to back converters (PWM technique). In Proceedings of the 2014 IEEE International Conference on Advanced Communications, Control and Computing Technologies, Ramanathapuram, India, 8–10 May 2014; pp. 73–77. [Google Scholar]
- Demirbas, S.; Bayhan, S. Active and reactive power control of doubly fed induction generator using direct power control technique. In Proceedings of the 4th International Conference on Power Engineering, Energy and Electrical Drives, Istanbul, Turkey, 13–17 May 2013; pp. 41–45. [Google Scholar]
- Soares Pereira, B.S.; Luis Maia Santos, T. Speed and Reactive Power Regulation of Doubly-fed Induction Generator using Model Predictive Control. In Proceedings of the 2018 Workshop on Communication Networks and Power Systems (WCNPS), Brasília, Brazil, 7–9 November 2018. [Google Scholar]
- Alaya, J.B.; Khedher, A.; Mimouni, M.F. Nonlinear vector control strategy applied to a variable speed DFIG generation system. In Proceedings of the Eighth International Multi-Conference on Systems, Signals & Devices, Sousse, Tunisia, 22–25 March 2011; pp. 1–8. [Google Scholar]
- Mestri, M.N.; Kumar, B.S. Design of 9-Switch Converter for DFIG System for Active and Reactive Power Control by PID and Fuzzy Logic Controller. In Proceedings of the 2019 3rd International conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 12–14 June 2019. [Google Scholar]
- Ramadan, A.; Kamel, S.; Rashad, A.; Yu, J. Design of Fuzzy Logic Control for Direct and Quadratic Components of DFIG’s Rotor and Grid Side Control System Based Wind Turbines. In Proceedings of the 2018 Twentieth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 18–20 December 2018; pp. 655–659. [Google Scholar]
- Geniusz, A.; Krzemiński, Z. Control System Based on the Modified Multiscalar Model for the Double Fed Machine; Centrum Usług Informatycznych Politechniki Gdańskiej: Gdańsk, Poland, 2005. [Google Scholar]
- Bogalecka, E. Power control of a double fed induction generator without speed or position sensor. In Proceedings of the Fifth European Conference on Power Electronics and Applications, Brighton, UK, 13–16 September 1993; pp. 224–228. [Google Scholar]
- Krzemiński, Z. Sensorless multiscalar control of double fed machine for wind power generators. In Proceedings of the Power Conversion Conference-Osaka 2002, Osaka, Japan, 2–5 April 2002; pp. 334–339. [Google Scholar]
- Bogalecka, E.; Krzemiński, Z. Control systems of doubly-fed induction machine supplied by current controlled voltage source inverter. In Proceedings of the Sixth International Conference on Electrical Machines and Drives, Oxford, UK, 8–10 September 1993; pp. 168–172. [Google Scholar]
- Hailemariam, Z.M.; Leidhold, R.; Tesfamariam, G.T. Real-Time Speed Control of a PMSM for Wind Turbine Application. In Proceedings of the 2019 IEEE PES/IAS PowerAfrica, Abuja, Nigeria, 20–23 August 2019; pp. 396–401. [Google Scholar]
- Gang, Y.; Yichang, G.; Lidan, Z.; Dongdong, L.; Xing, L. Multi-Phase Permanent Magnet Synchronous Generator Variable Speed Constant Frequency Offshore Wind System Based on Modular Multilevel Converter. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies - Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 2127–2132. [Google Scholar]
- Djagarov, N.; Grozdev, Z.; Enchev, G.; Djagarova, J. Study of Low-Voltage Ride Through of Wind Permanent Magnet Synchronous Generator by means of STATCOM. In Proceedings of the 2019 20th International Scientific Conference on Electric Power Engineering (EPE), Kouty nad Desnou, Czech Republic, 15–17 May 2019; pp. 1–6. [Google Scholar]
- Solomon, O. The Design, Control and Dynamic Performance of an Interior Permanent Magnet Synchronous Generator for Wind Power System. In Proceedings of the IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 714–718. [Google Scholar]
- Klumpner, C.; Blaabjerg, F. Using reverse-blocking IGBTs in power converters for adjustable-speed drives. IEEE Trans. Ind. Appl. 2006, 42, 807–816. [Google Scholar] [CrossRef]
- Takei, M.; Harada, Y.; Ueno, K. 600 V-IGBT with reverse blocking capability. In Proceedings of the Proceedings of the 13th International Symposium on Power Semiconductor Devices & ICs. IPSD ’01 (IEEE Cat. No.01CH37216), Osaka, Japan, 7 June 2001; pp. 413–416. [Google Scholar]
- Xu, Y.; Wang, Z.; Liu, P.; Song, Q.; Tang, C.; Cheng, M. Zero-Voltage Switching Current-Source-Inverter Motor Drives Based on Silicon Carbide Devices. In Proceedings of the 22nd Inter. Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019. [Google Scholar]
- Barth, H.; Hofmann, W. Potentials and Boundaries of Discrete SiC-Transistors in AC Drives. In Proceedings of the 2018 20th European Conference on Power Electronics and Applications (EPE’18 ECCE Europe), Riga, Latvia, 17–21 September 2018. [Google Scholar]
- Villagrán-Valencia, L.J.; Ramírez-Hernández, J.; Mondragón-Escamilla, N.; Araujo-Vargas, I. Analysis of Bidirectional Switching of SiC Transistors in a Matrix Converter Leg. In Proceedings of the 2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Nottingham, UK, 7–9 November 2018; pp. 1–5. [Google Scholar]
- Sahan, B.; Araújo, S.V.; Noding, C.; Zacharias, P. Comparative evaluation of three-phase current source inverters for grid interfacing of distributed and renewable energy systems. IEEE Trans. Power Electron. 2011, 26, 2304–2318. [Google Scholar] [CrossRef]
- Ryndzionek, R.; Sienkiewicz, Ł. Evolution of the HVDC Link Connecting Offshore Wind Farms to Onshore Power Systems. Energies 2020, 13, 1914. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.; Zhao, D.; Yao, L.; Qian, M.; Yamashita, K.; Zhu, L. Analysis on application of a current-source based DFIG wind generator model. CSEE J. Power Energy Syst. 2018, 4, 352–361. [Google Scholar] [CrossRef]
- Blecharz, K.; Morawiec, M. Nonlinear control of a doubly fed generator supplied by a current source inverter. Energies 2019, 12, 2335. [Google Scholar] [CrossRef] [Green Version]
- Abobkr, A.H.; El-Hawary, M.E. Fault ride-through capability of doubly-fed induction generators based wind turbines. In Proceedings of the 2015 IEEE Electrical Power and Energy Conference, London, ON, Canada, 26–28 October 2015; pp. 8–15. [Google Scholar]


| Gain Name | Field-Oriented Control (Value) | Nonlinear Control (Value) |
|---|---|---|
| 0.45 | 1.5 | |
| 0.3 | 0.6 | |
| 0.8 | 1.25 | |
| 0.7 | 0.4 |
| Symbol | Name | Values |
|---|---|---|
| stator resistance | 2.741 /0.0649 p.u. | |
| rotor resistance | 3.212 /0.0762 p.u. | |
| magnetizing inductance | 0.17 H/1.2733 p.u. | |
| stator and rotor inductance | 0.195 H/1.3378 p.u. | |
| nominal power | 2 kW | |
| nominal stator current | 5.5 A | |
| nominal rotor current | 3.4 A | |
| nominal stator voltage | 400 V | |
| n | nominal rotor speed | 910 rpm |
| f | nominal frequency | 50 Hz |
| r | turn ratio / | 1 |
| DC choke inductance | 12.4 mH/0.1 p.u. | |
| output filter capacitance | 100 µF/0.125 p.u. | |
| reference voltage | 400 V | |
| reference current | 9.52 A | |
| reference power | 3.81 kVA | |
| converters PWM period | 150 ms |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kroplewski, P.; Morawiec, M.; Jąderko, A.; Odeh, C. Simulation Studies of Control Systems for Doubly Fed Induction Generator Supplied by the Current Source Converter. Energies 2021, 14, 1511. https://doi.org/10.3390/en14051511
Kroplewski P, Morawiec M, Jąderko A, Odeh C. Simulation Studies of Control Systems for Doubly Fed Induction Generator Supplied by the Current Source Converter. Energies. 2021; 14(5):1511. https://doi.org/10.3390/en14051511
Chicago/Turabian StyleKroplewski, Paweł, Marcin Morawiec, Andrzej Jąderko, and Charles Odeh. 2021. "Simulation Studies of Control Systems for Doubly Fed Induction Generator Supplied by the Current Source Converter" Energies 14, no. 5: 1511. https://doi.org/10.3390/en14051511
APA StyleKroplewski, P., Morawiec, M., Jąderko, A., & Odeh, C. (2021). Simulation Studies of Control Systems for Doubly Fed Induction Generator Supplied by the Current Source Converter. Energies, 14(5), 1511. https://doi.org/10.3390/en14051511







