A Numerical Study on Hydrodynamic Energy Conversions of OWC-WEC with the Linear Decomposition Method under Irregular Waves
Abstract
:1. Introduction
2. Numerical Methods
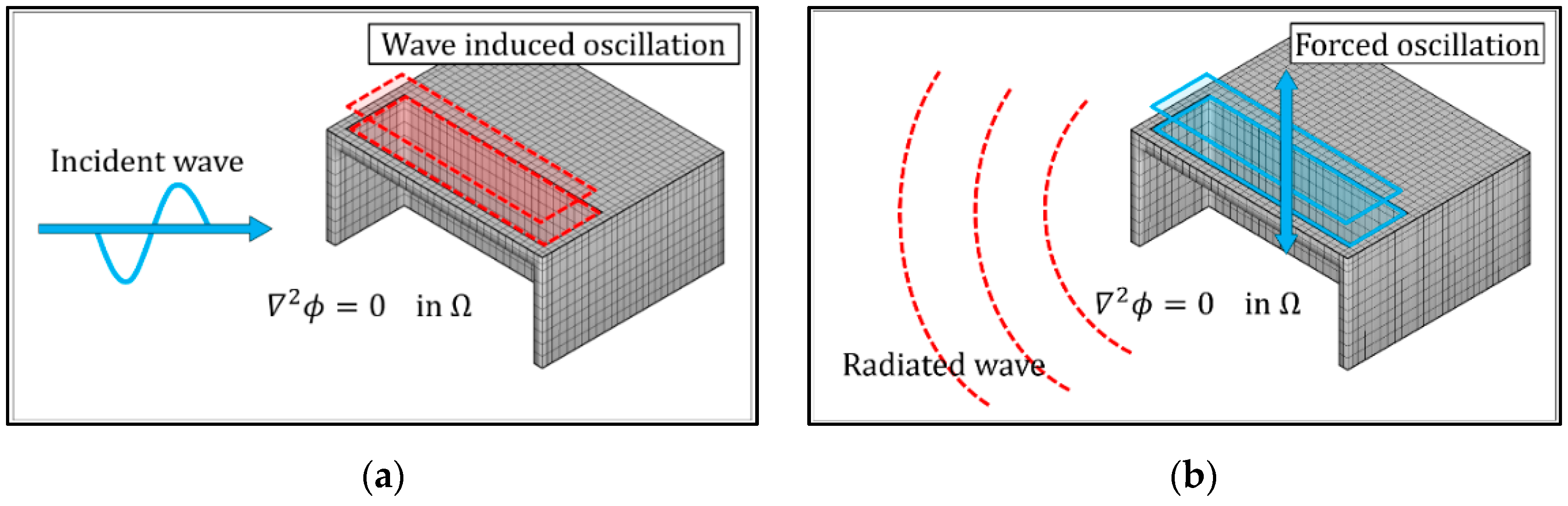
2.1. Linear Decomposition Method
2.2. Boundary Value Problem
| (12) | ||
| (13) | ||
| (14) | ||
| (15) |
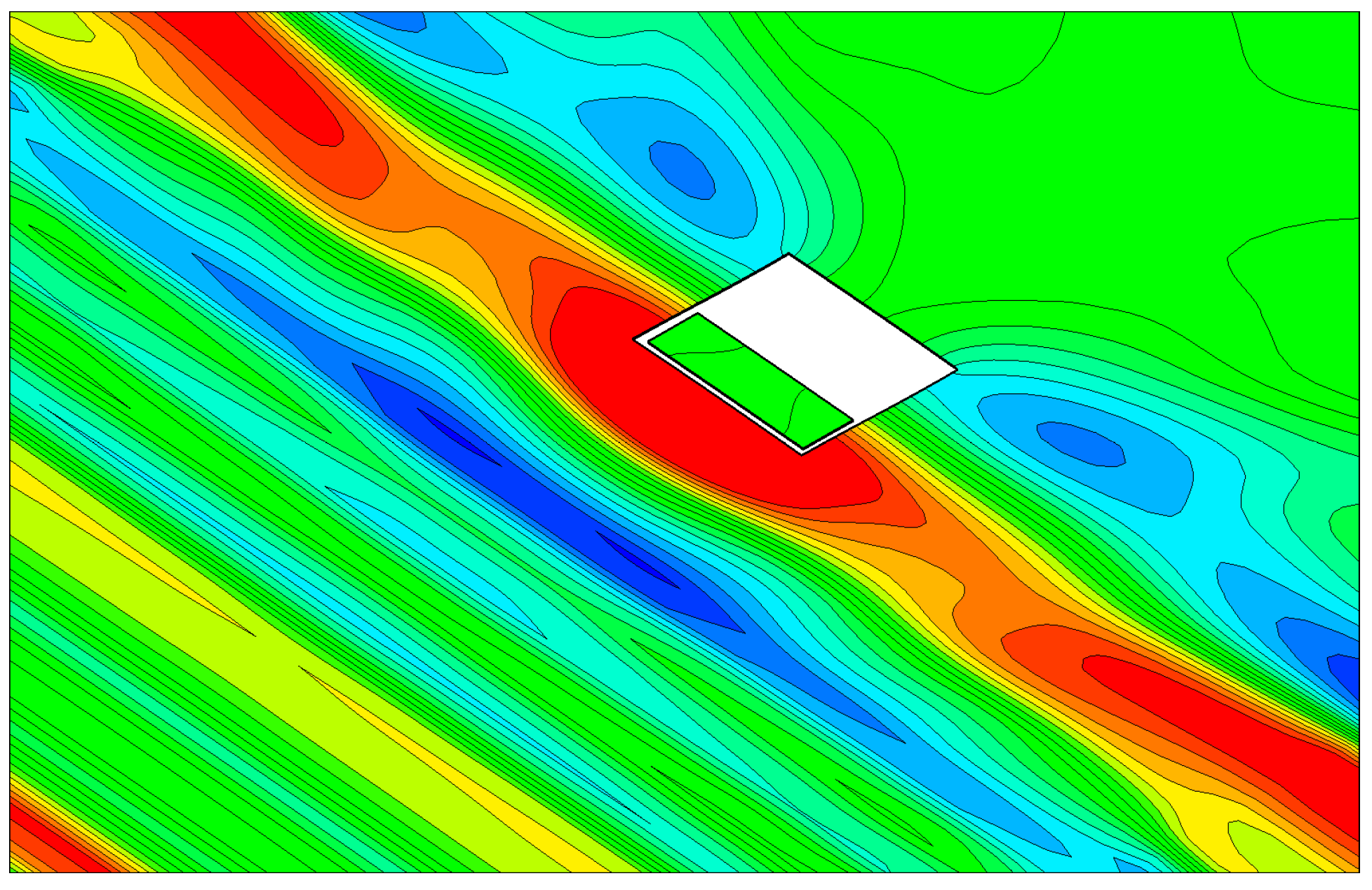
2.3. Finite Element Method
3. Results and Discussions
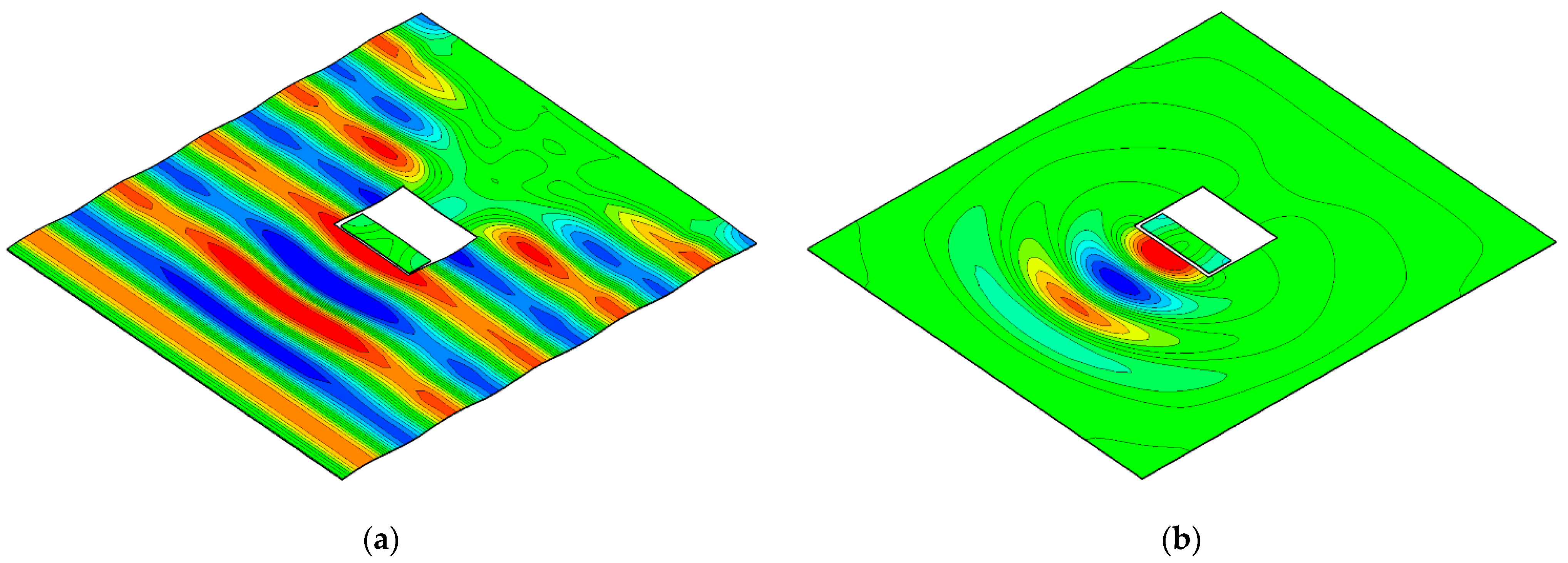
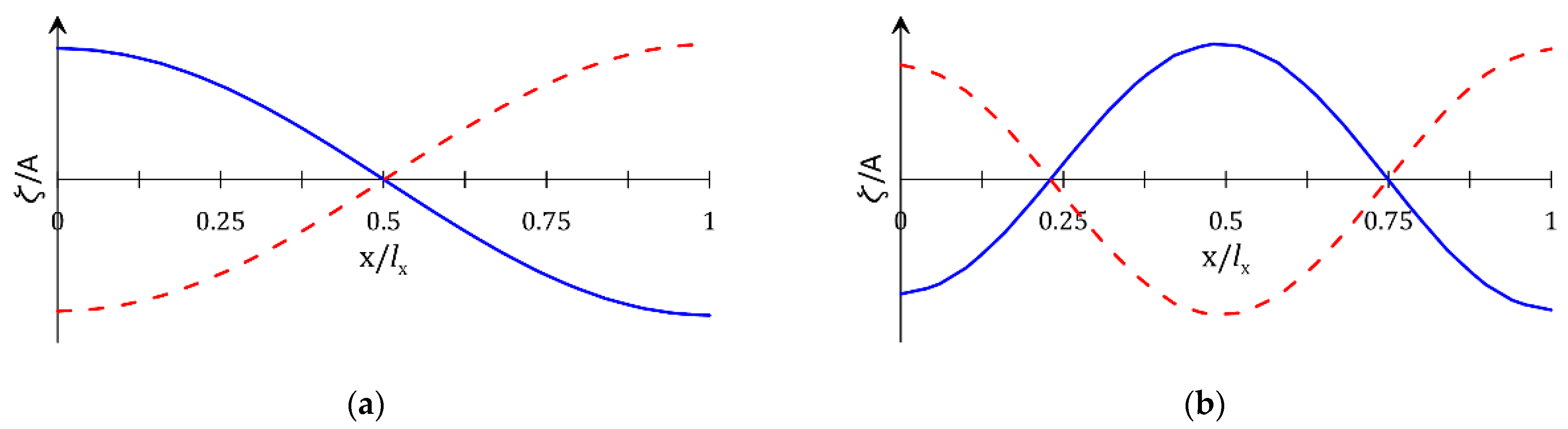
3.1. Linear Decomposition Method (LDM) for OWC’s Hydrodynamic Energy Conversion
- : phase difference from pressure drop to airflow in the forced radiation case;
- : phase difference from wave excitation airflow to forced radiation airflow.
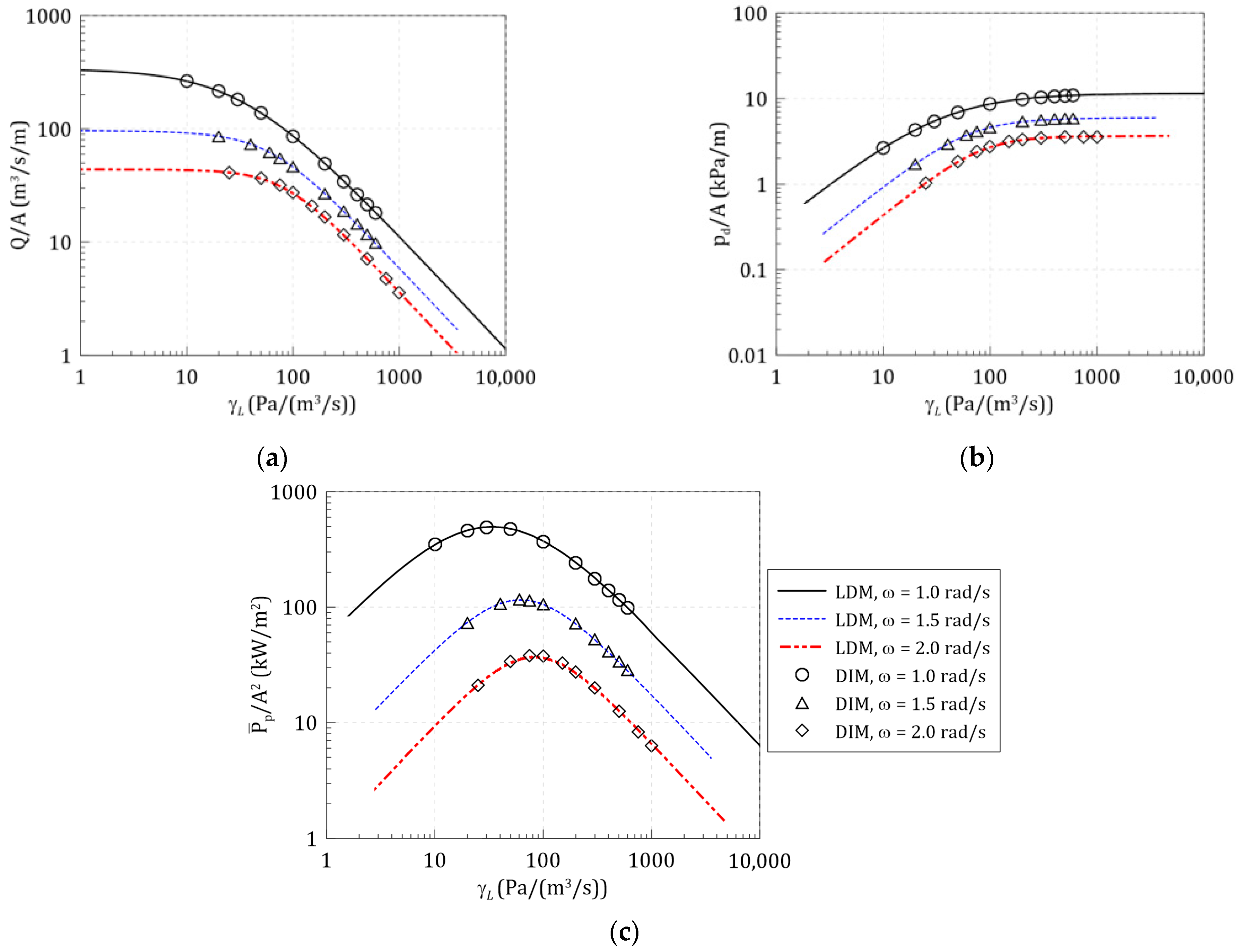
3.2. Comparison of Linear Decomposition Method (LDM) and Direct Interaction Method (DIM)
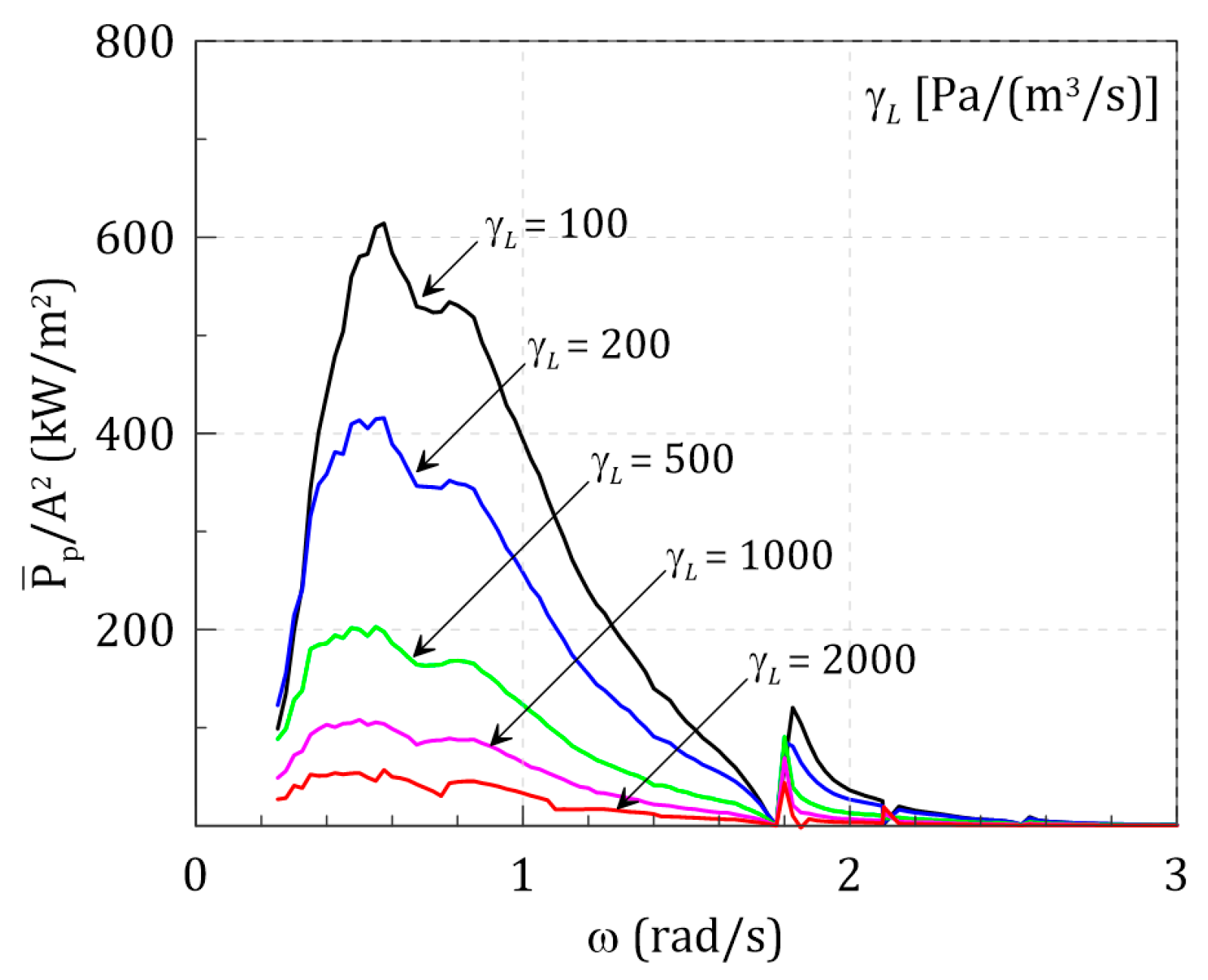
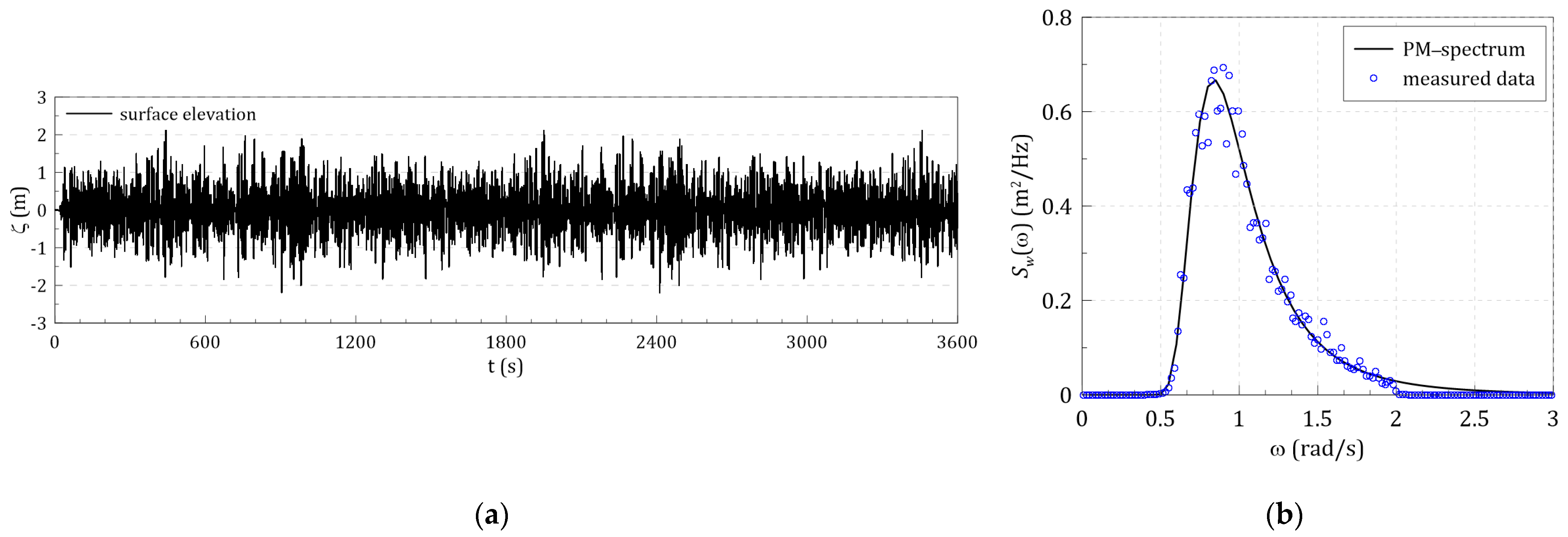
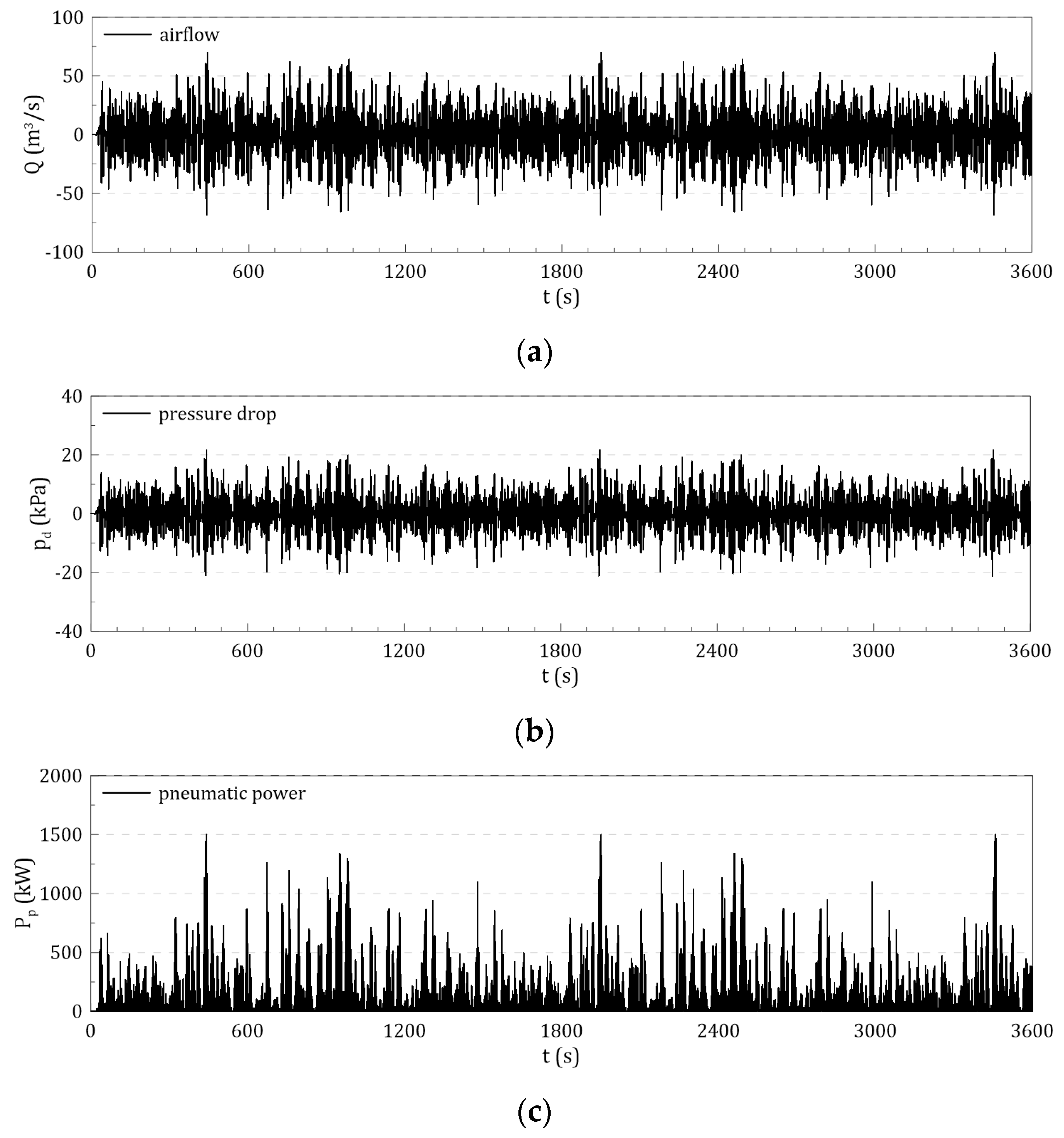
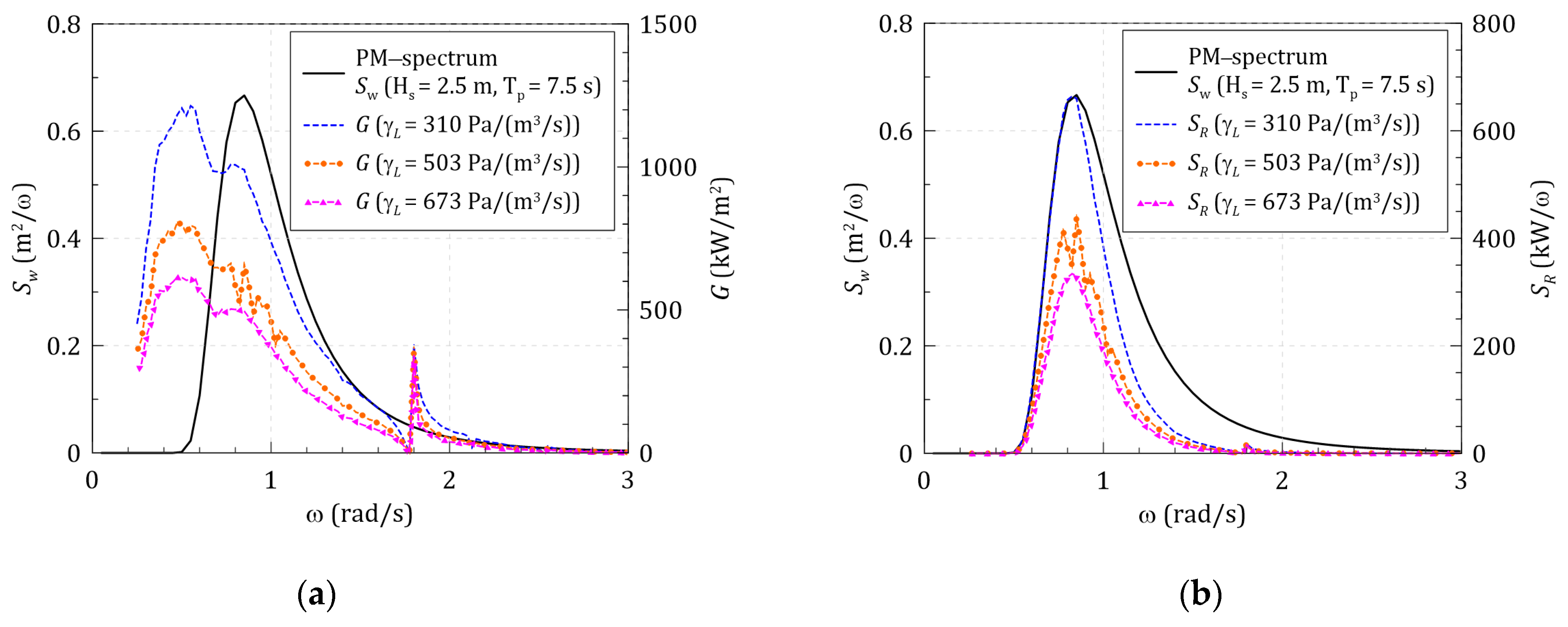
3.3. LDM-based Response Spectrum Method (RSM) for OWC’s Hydrodynamic Energy Conversion under Irregular Waves
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yemm, R.; Pizer, D.; Retzler, C.; Henderson, R. Pelamis: Experience from concept to connection. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 365–380. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y.; Yu, Y.H. A synthesis of numerical methods for modeling wave energy converter-point absorbers. Renew. Sustain. Energy Rev. 2012, 16, 4352–4364. [Google Scholar] [CrossRef]
- Contestabile, P.; Crispino, G.; Di Lauro, E.; Ferrante, V.; Gisonni, C.; Vicinanza, D. Overtopping breakwater for wave Energy Conversion: Review of state of art, recent advancements and what lies ahead. Renew. Energy 2020, 147, 705–718. [Google Scholar] [CrossRef]
- Falcão, A.F.; Henriques, J.C. Oscillating-water-column wave energy converters and air turbines: A review. Renew. Energy 2016, 85, 1391–1424. [Google Scholar] [CrossRef]
- Kim, J.-S.; Nam, B.W.; Kim, K.-H.; Park, S.; Shin, S.H.; Hong, K. A Numerical Study on Hydrodynamic Performance of an Inclined OWC Wave Energy Converter with Nonlinear Turbine–Chamber Interaction Based on 3D Potential Flow. J. Mar. Sci. Eng. 2020, 8, 176. [Google Scholar] [CrossRef] [Green Version]
- Pawitan, K.A.; Dimakopoulos, A.S.; Vicinanza, D.; Allsop, W.; Bruce, T. A loading model for an OWC caisson based upon large-scale measurements. Coast. Eng. 2019, 145, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Vicinanza, D.; Lauro, E.D.; Contestabile, P.; Gisonni, C.; Lara, J.L.; Losada, I.J. Review of innovative harbor breakwaters for wave-energy conversion. J. Waterw. Port Coast. Ocean Eng. 2019, 145, 03119001. [Google Scholar] [CrossRef]
- Kim, K.H.; Nam, B.W.; Park, S.; Kim, J.S. Initial design of OWC WEC Applicable to Breakwater in Remote Island. In Proceedings of the 4th Asian Wave Tidal Energy Conference, Taipei, Taiwan, 9–13 September 2018. [Google Scholar]
- Park, S.; Kim, K.H.; Nam, B.W.; Kim, J.S.; Hong, K. A Study on Effects of Breakwater on Performance of OWC. In Proceedings of the 13th ISOPE Pacific/Asia Offshore Mechanics Symposium, Jeju, Korea, 14–17 October 2018. [Google Scholar]
- Kim, J.-S.; Nam, B.W.; Kim, K.-H.; Park, S.; Hong, K. Numerical study of an inclined OWC chamber combined breakwater and turbine interaction under waves. In Proceedings of the 13th European Wave and Tidal Energy Conference, Napoli, Italy, 1–6 September 2019. ID No. 1285. [Google Scholar]
- Evans, D.V. Wave-power absorption by systems of oscillating surface pressure distributions. J. Fluid Mech. 1982, 114, 481–499. [Google Scholar] [CrossRef]
- Falnes, J.; McIver, P. Surface wave interactions with systems of oscillating bodies and pressure distributions. Appl. Ocean Res. 1985, 7, 225–234. [Google Scholar] [CrossRef]
- Falnes, J. Ocean Waves and Oscillating Systems: Linear Interactions Including Wave-Energy Extraction; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Evans, D.V.; Porter, R. Hydrodynamic characteristics of an oscillating water column device. Appl. Ocean Res. 1995, 17, 155–164. [Google Scholar] [CrossRef]
- Brito-Melo, A.; Sarmento, A.J.N.A. Numerical modelling of OWC wave-power plants of the oscillating water column type. WIT Trans. Model. Simul. 2002, 32, 25–34. [Google Scholar]
- Josset, C.; Clément, A.H. A time-domain numerical simulator for oscillating water column wave power plants. Renew. Energy 2007, 32, 1379–1402. [Google Scholar] [CrossRef]
- Koo, W.; Kim, M.H. Nonlinear time-domain simulation of a land-based oscillating water column. J. Waterw. Port Coast. Ocean Eng. 2010, 136, 276–285. [Google Scholar] [CrossRef]
- Wang, R.Q.; Ning, D.Z.; Zhang, C.W.; Zou, Q.P.; Liu, Z. Nonlinear and viscous effects on the hydrodynamic performance of a fixed OWC wave energy converter. Coast. Eng. 2018, 131, 42–50. [Google Scholar] [CrossRef]
- Koley, S.; Trivedi, K. Mathematical modeling of oscillating water column wave energy converter devices over the undulated sea bed. Eng. Anal. Bound. Elem. 2020, 117, 26–40. [Google Scholar] [CrossRef]
- Rezanejad, K.; Bhattacharjee, J.; Soares, C.G. Analytical and numerical study of dual-chamber oscillating water columns on stepped bottom. Renew. Energy 2015, 75, 272–282. [Google Scholar] [CrossRef]
- Ning, D.-Z.; Shi, J.; Zou, Q.P.; Teng, B. Investigation of hydrodynamic performance of an OWC (oscillating water column) wave energy device using a fully nonlinear HOBEM (higher-order boundary element method). Energy 2015, 83, 177–188. [Google Scholar] [CrossRef]
- Ning, D.-Z.; Wang, R.-Q.; Zou, Q.-P.; Teng, B. An experimental investigation of hydrodynamics of a fixed OWC Wave Energy Convert. Appl. Energy 2016, 168, 636–648. [Google Scholar] [CrossRef]
- Kim, J.-S. Numerical Study on Fully Coupled Hydrodynamic Energy Conversion Problem of OWC-WEC System. Ph.D. Thesis, Korea Maritime and Ocean University, Busan, Korea, 2021. [Google Scholar]
- Det Norske Veritas. DNV-RP-H103 Modelling and Analysis of Marine Operation; Det Norske Veritas: Høvik, Norway, 2011. [Google Scholar]
- Journée, J.M.J.; Massie, W.W. Offshore Hydromechanics; Delft University of Technology: Delft, The Netherlands, 2001. [Google Scholar]










| Wave ID | |||
|---|---|---|---|
| W#1 | 0.75 | 5.0 | 310, 503, 673 |
| W#2 | 1.50 | 6.0 | 310, 503, 673 |
| W#3 | 2.50 | 7.5 | 310, 503, 673 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.-S.; Kim, K.-H.; Park, J.; Park, S.; Shin, S.H. A Numerical Study on Hydrodynamic Energy Conversions of OWC-WEC with the Linear Decomposition Method under Irregular Waves. Energies 2021, 14, 1522. https://doi.org/10.3390/en14061522
Kim J-S, Kim K-H, Park J, Park S, Shin SH. A Numerical Study on Hydrodynamic Energy Conversions of OWC-WEC with the Linear Decomposition Method under Irregular Waves. Energies. 2021; 14(6):1522. https://doi.org/10.3390/en14061522
Chicago/Turabian StyleKim, Jeong-Seok, Kyong-Hwan Kim, Jiyong Park, Sewan Park, and Seung Ho Shin. 2021. "A Numerical Study on Hydrodynamic Energy Conversions of OWC-WEC with the Linear Decomposition Method under Irregular Waves" Energies 14, no. 6: 1522. https://doi.org/10.3390/en14061522





