Metaheuristic Based Solution for the Non‐Linear Controller of the Multiterminal High‐Voltage Direct Current Networks
Abstract
1. Introduction
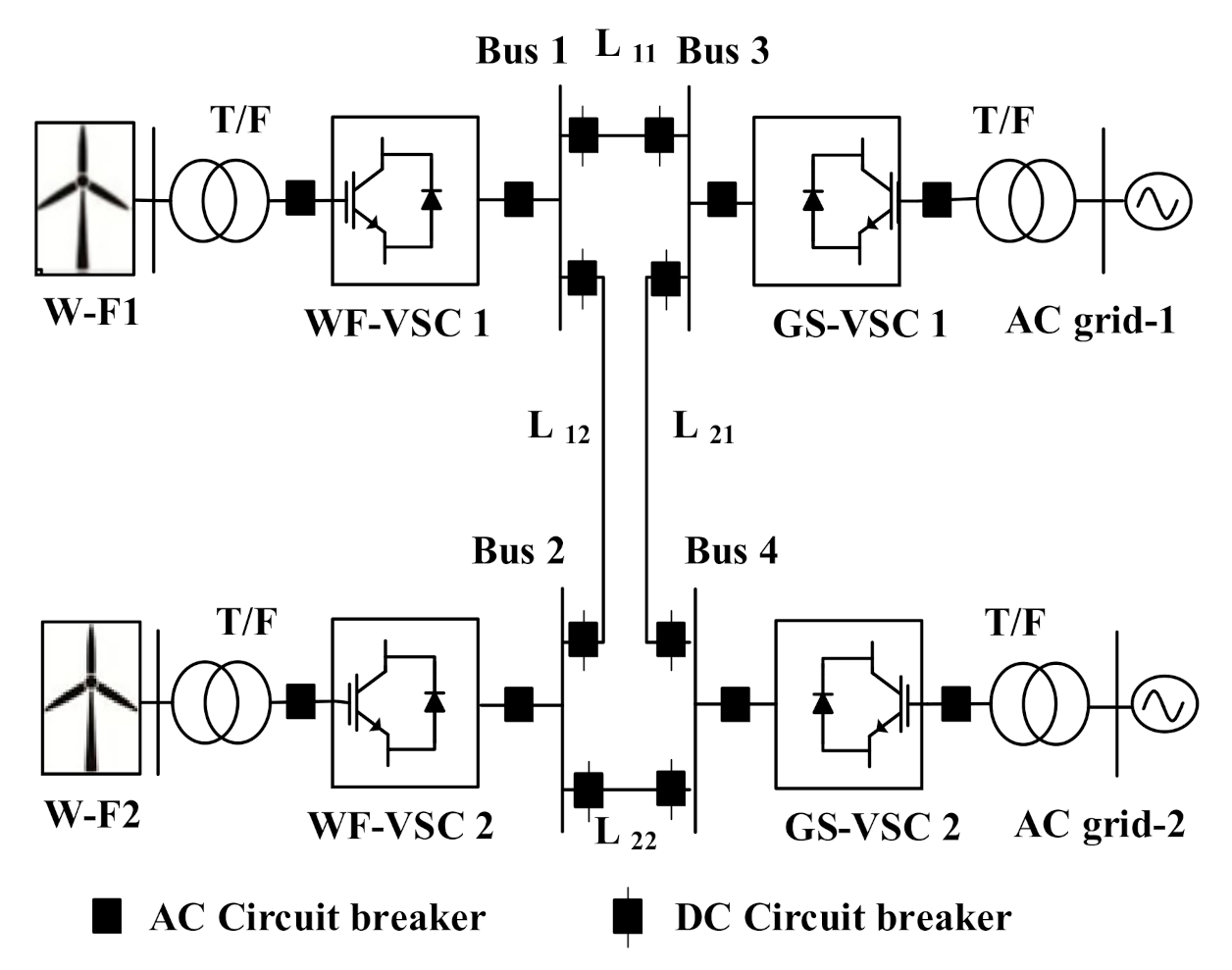
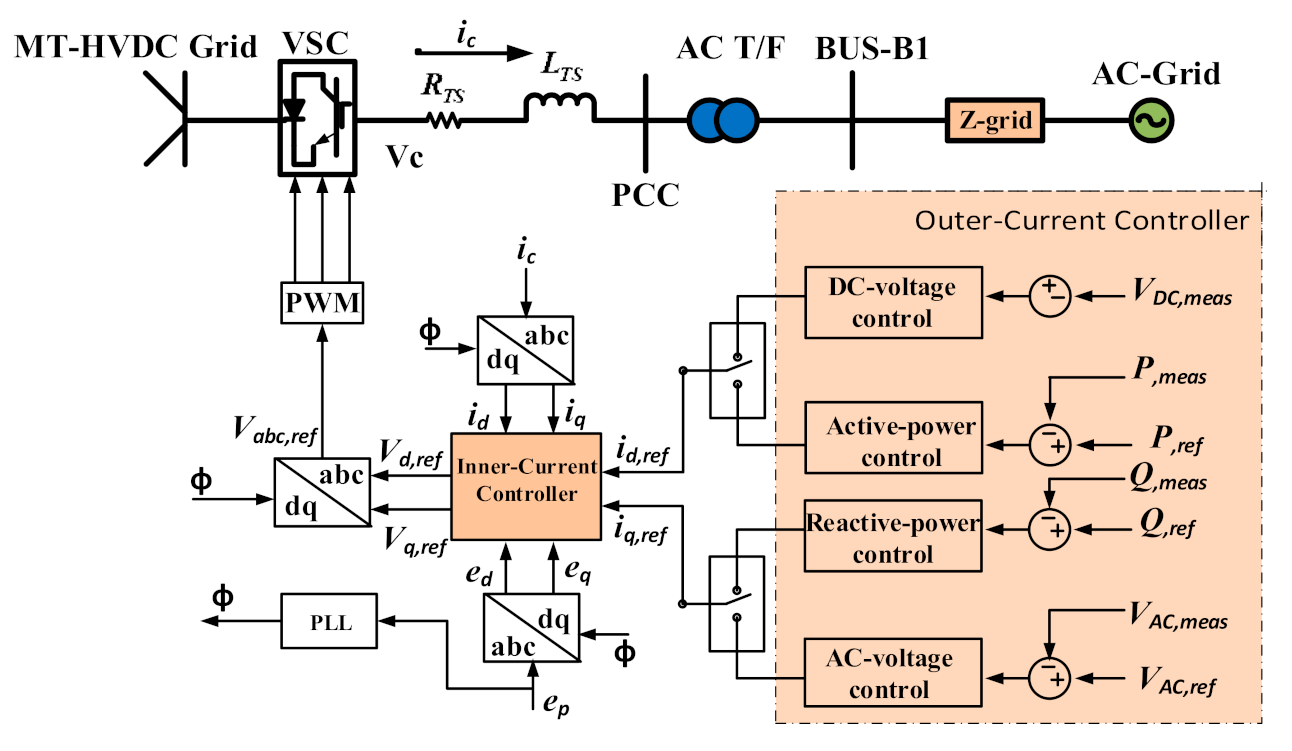
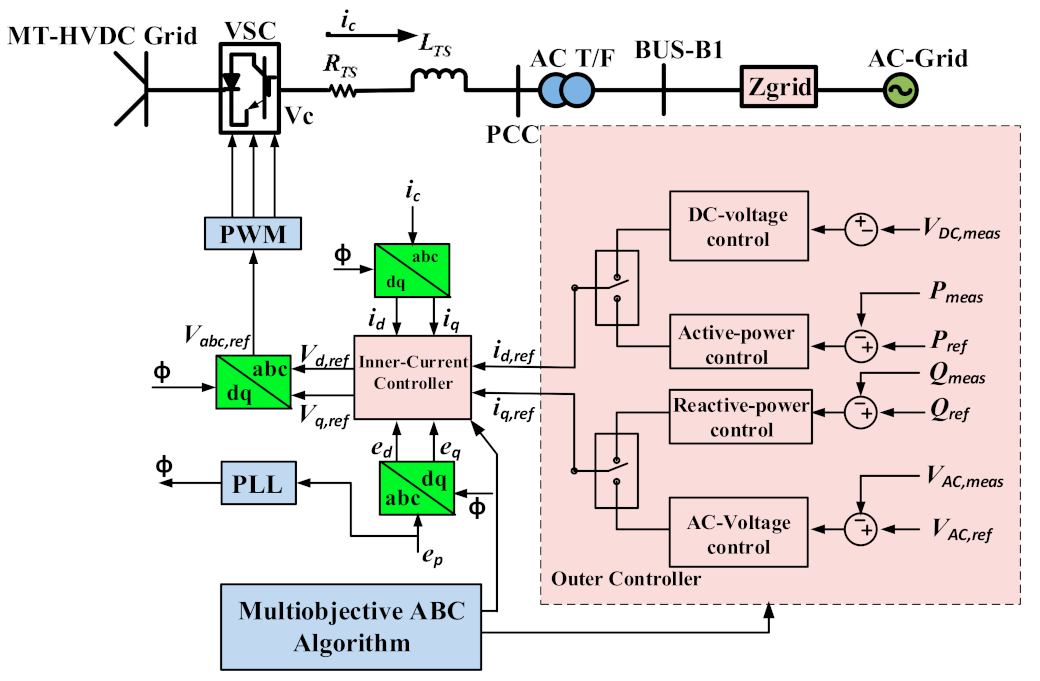
2. Control of Voltage-Source Converters (VSC) Based Multiterminal High Voltage Direct-Current (MT-HVDC) Grids
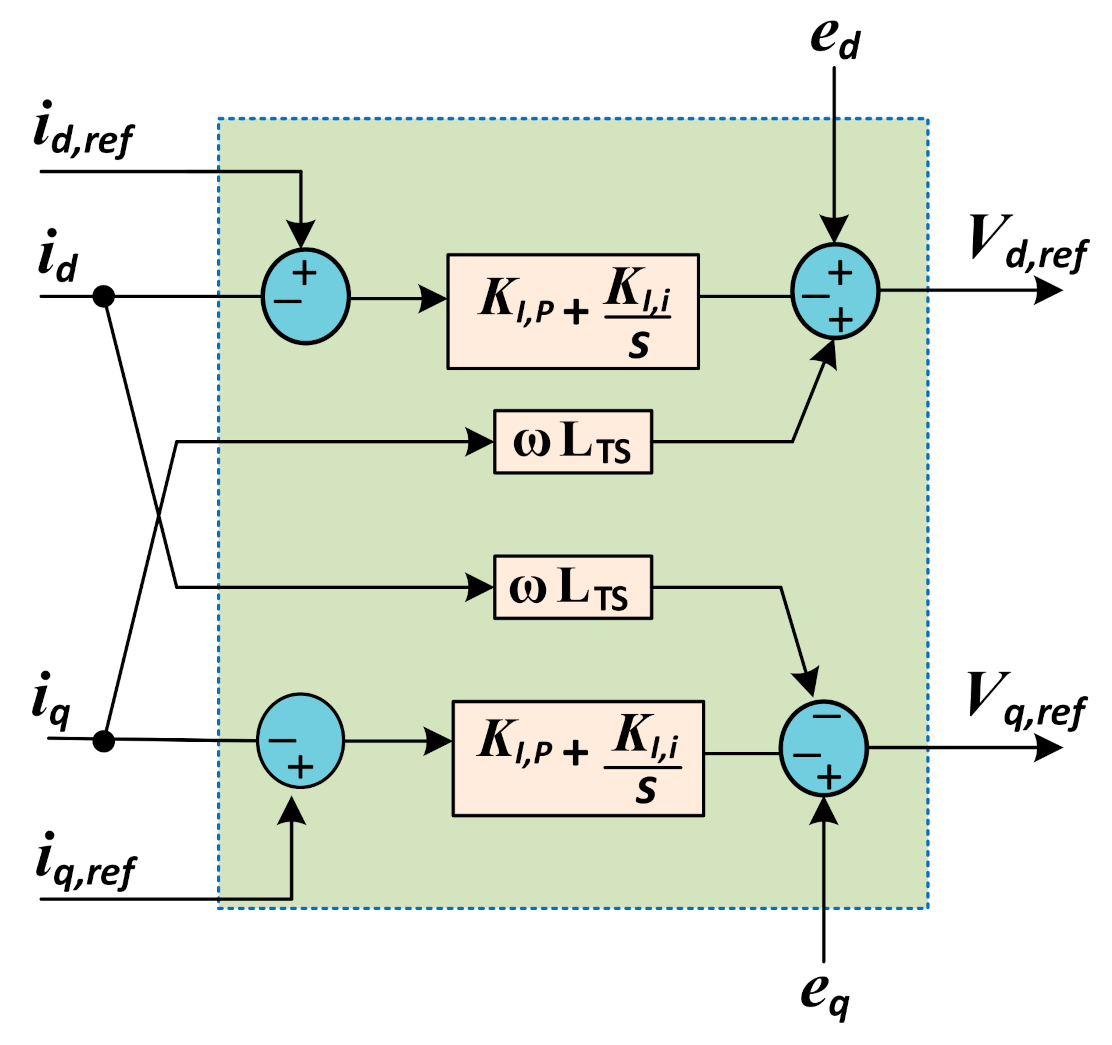
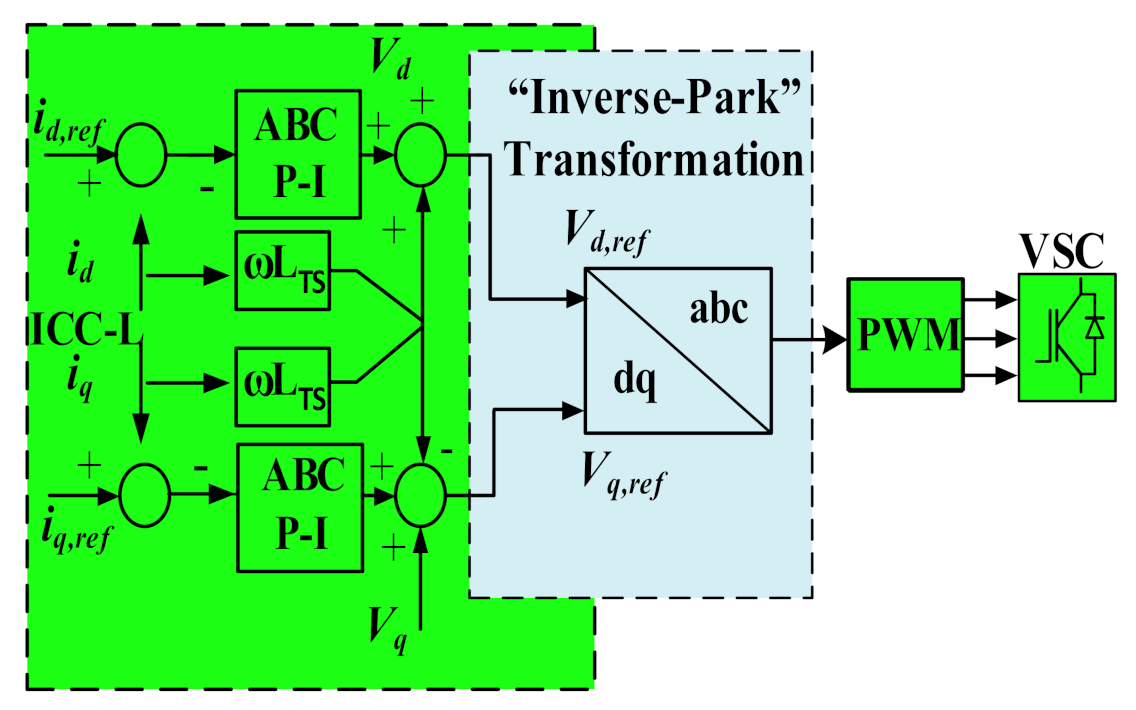
2.1. Inner Current Control Loop
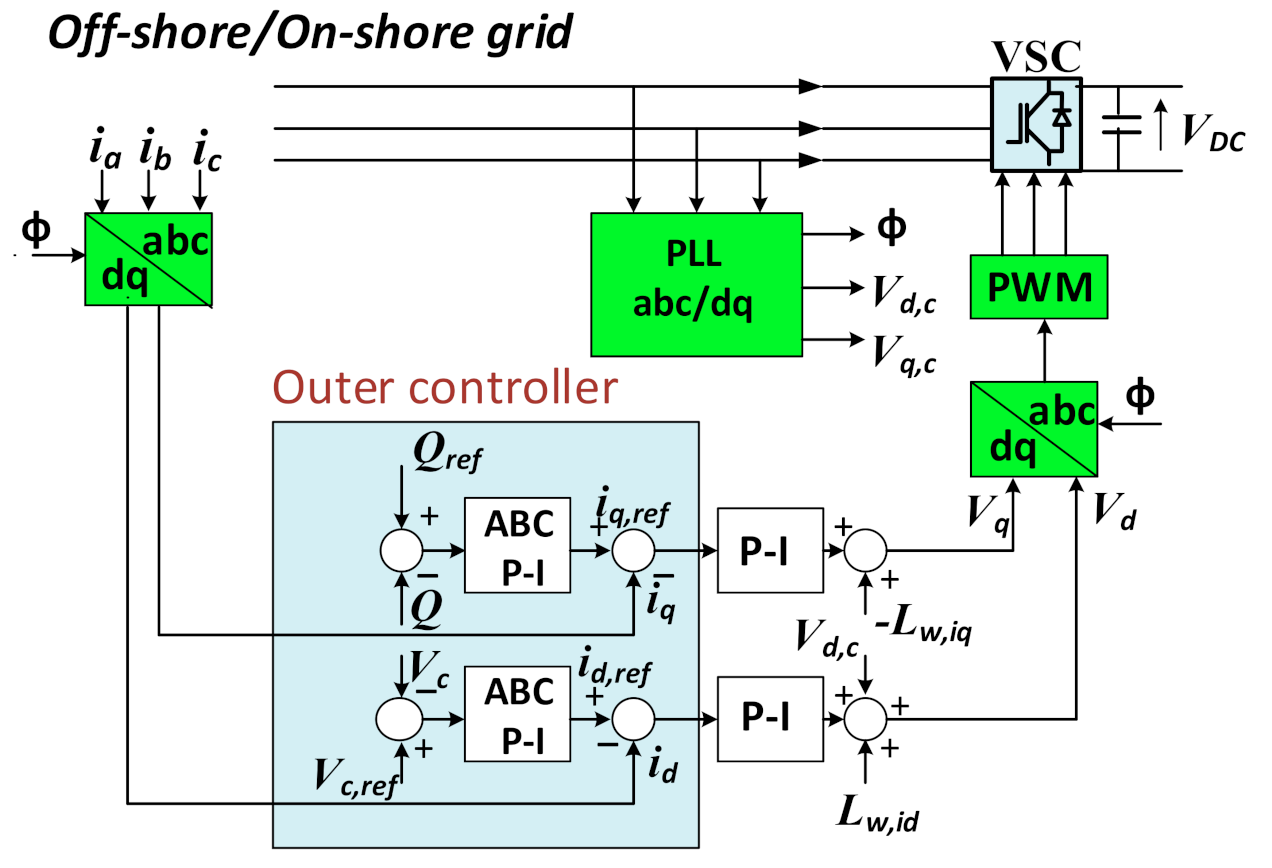
2.2. Outer Current Control Loop
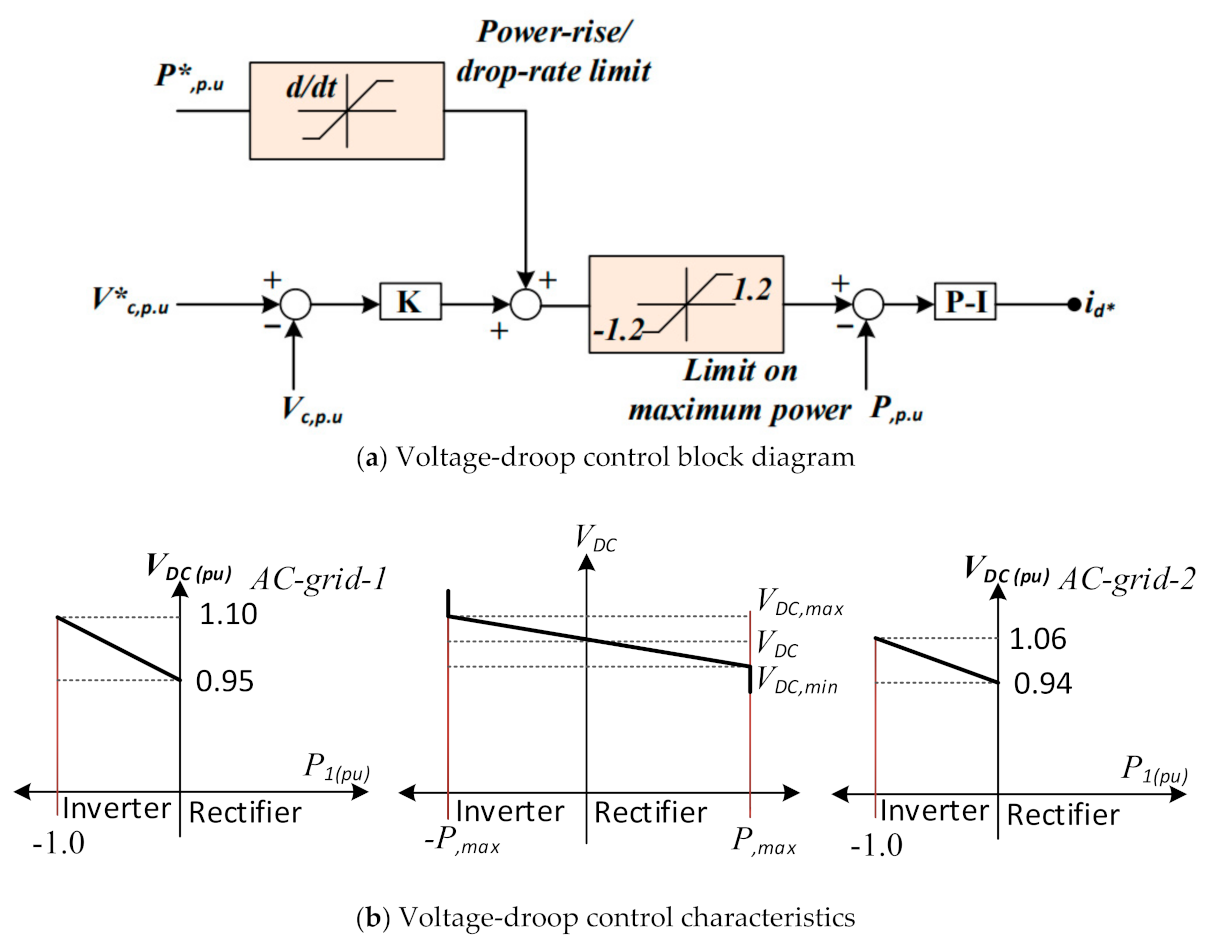
2.3. Voltage-Droop Control
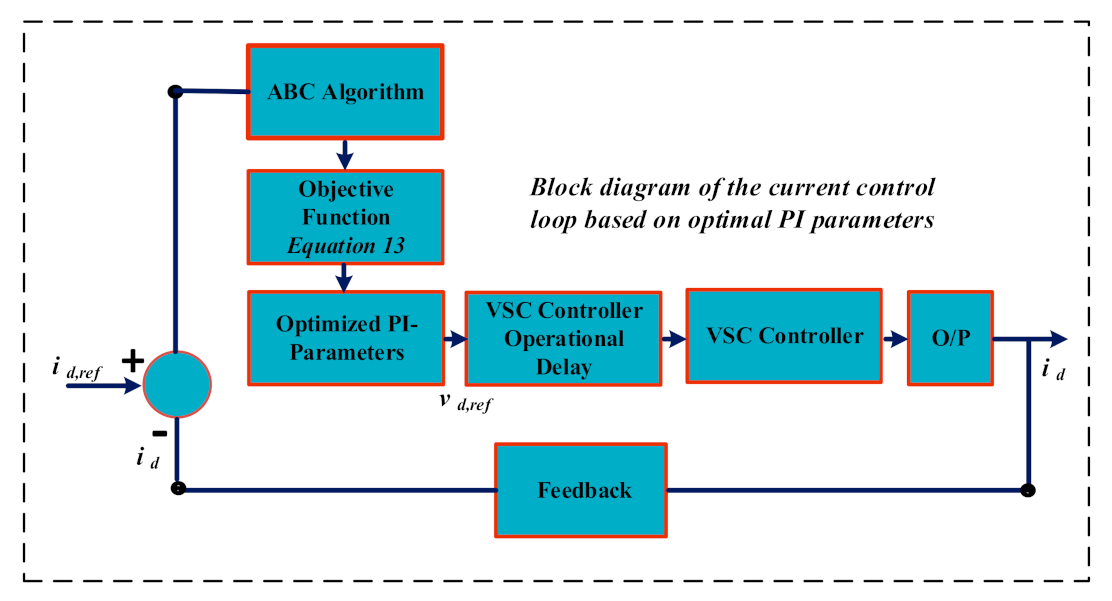
3. Optimization Technique Based Artificial Bee Colony Algorithm
3.1. Initial Population
- represent parametric numbers,
- indicate the lower limit of the initial population’s parameters,
- indicate the upper limit, respectively.
3.2. Employee Bees
- is a random number between [−1, 1],
- is the new source position,
- is the previous source position.
3.3. On-Looker Bees
- where shows the improved fitness of the solution and can be written as:
- shows the fitness value of the solution.
3.4. Scout Bees
3.5. Tuning of Inner-Current Control Loop (ICC-L)
- whereas represent corresponding d-axis current,
- represent referenced-axis current.
3.6. Tuning of Outer-Current Control Loop (OCC-L)
4. Execution of the Multiobjective Functions
- shows the nonzero weights. Here, the user-defined set of values describe the preferred criteria of weights.
- , represent the allocated weights and associated with each other as , whereas variate between 0 and 1.
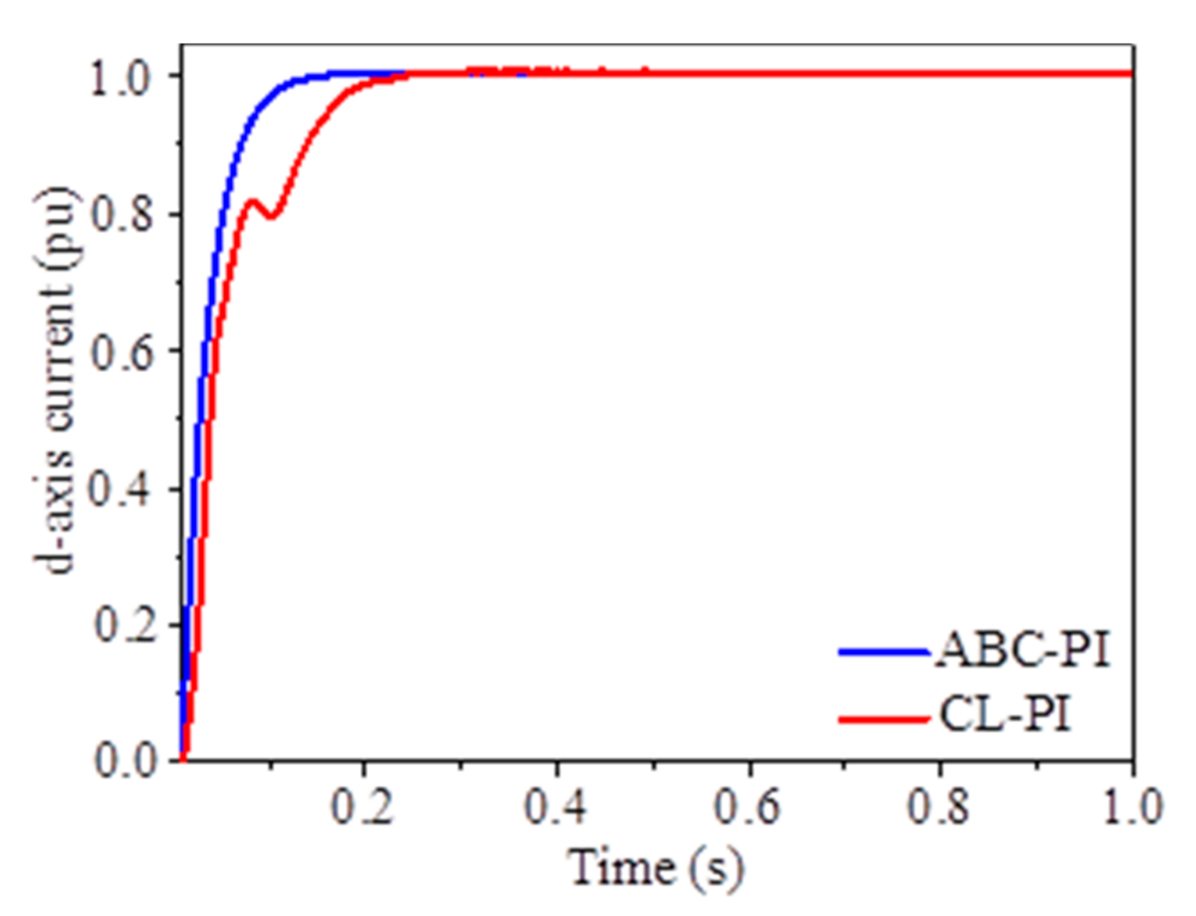
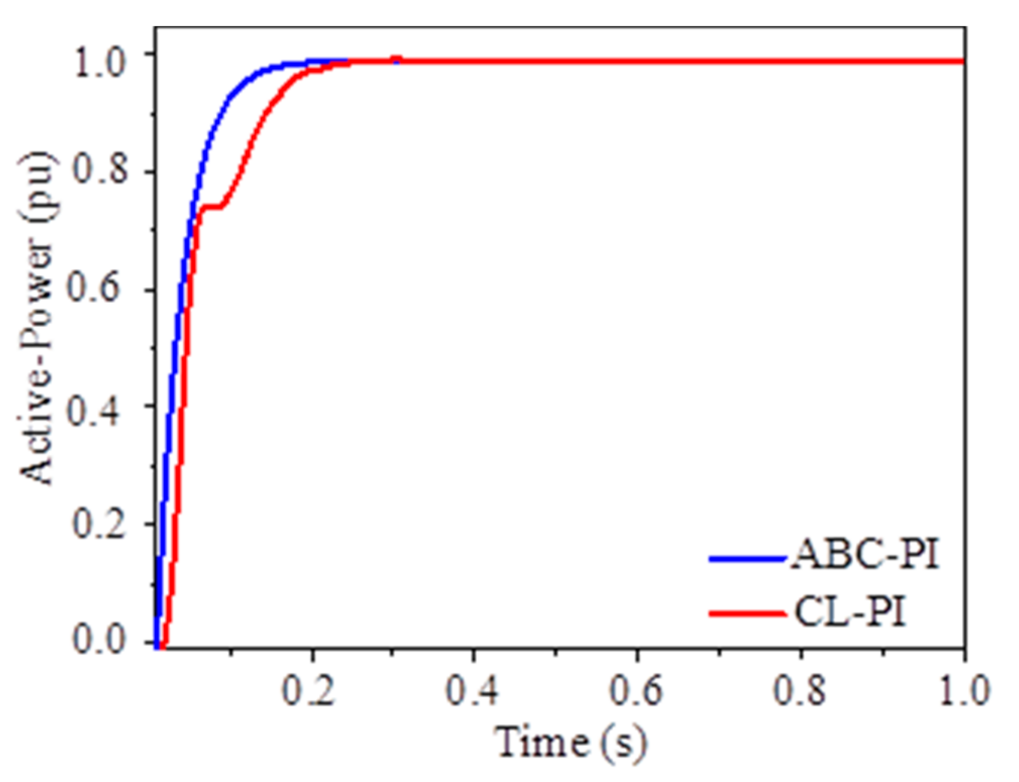
4.1. Comparative Analysis of the Controller’s Efficiency
4.2. Tuning of ICC-L Based on the Classical Optimization Method
- The ICC-L’s closed-loop bandwidth must be 1/5 times lower than the angular switching- frequency to attain adequate efficiency.
- The inner current controllers must be ten times faster than outer controllers to achieve a closed-loop system free from the oscillating response.
4.3. Tuning of ICC-L Based on the Classical Optimization Method
4.4. Multiobjective Optimization of ICC-L and OCC-L Based on ABC Algorithm
5. Simulation Results
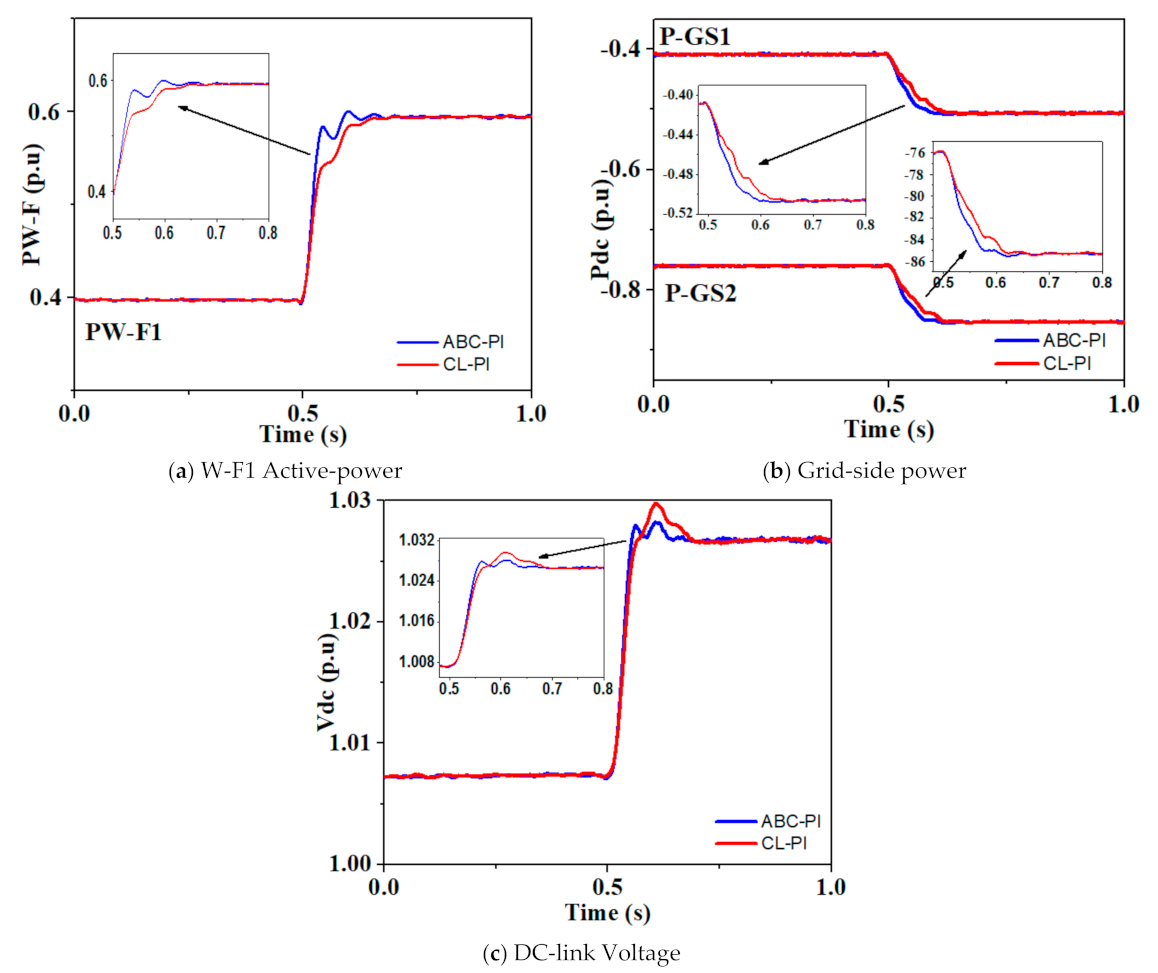
- Unbalance wind power,
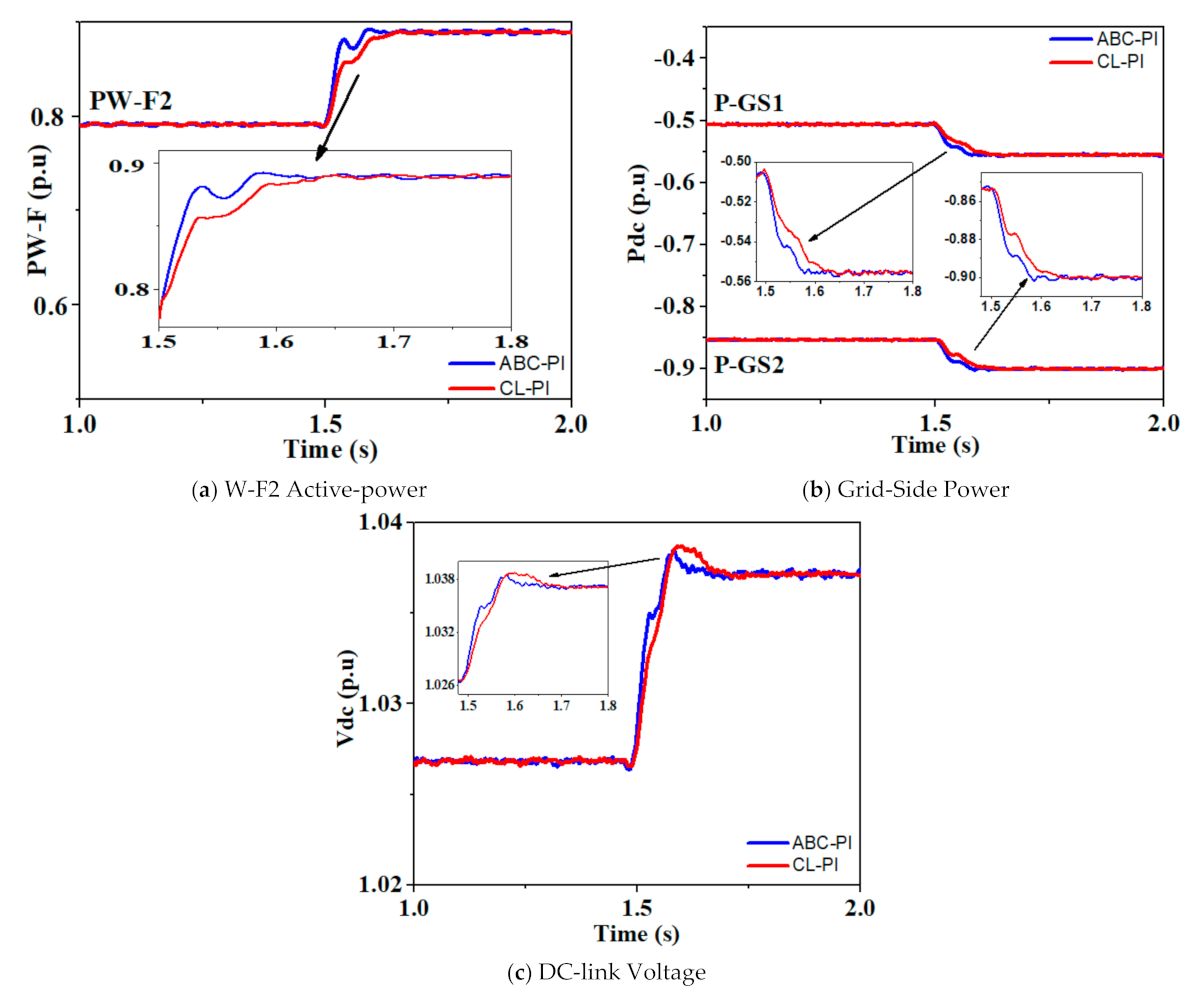
- Unbalanced power demand at the AC grids side,
- Eventual VSC disconnection.
5.1. Unbalance Wind Power
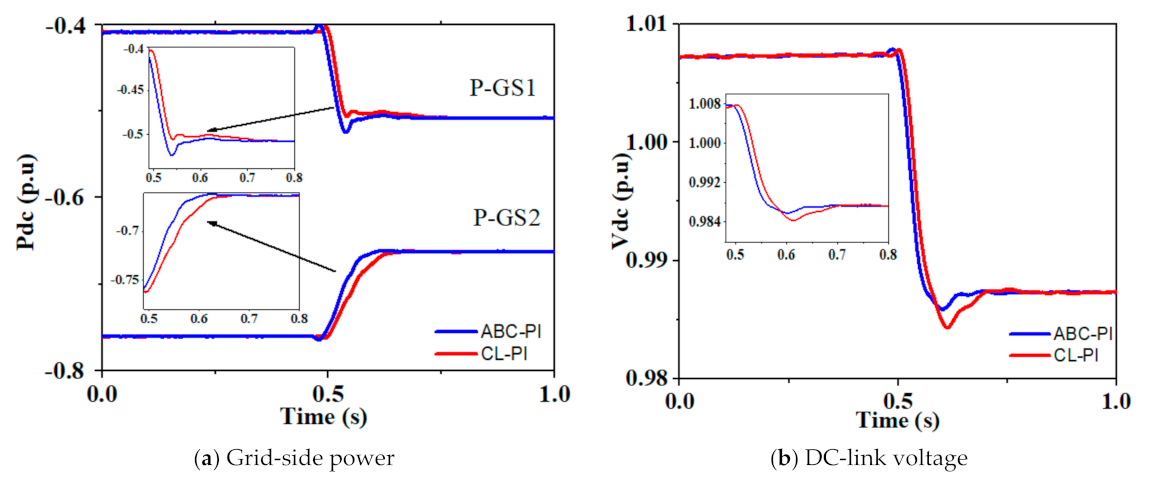
5.2. Unbalanced Load Demand at AC Grids
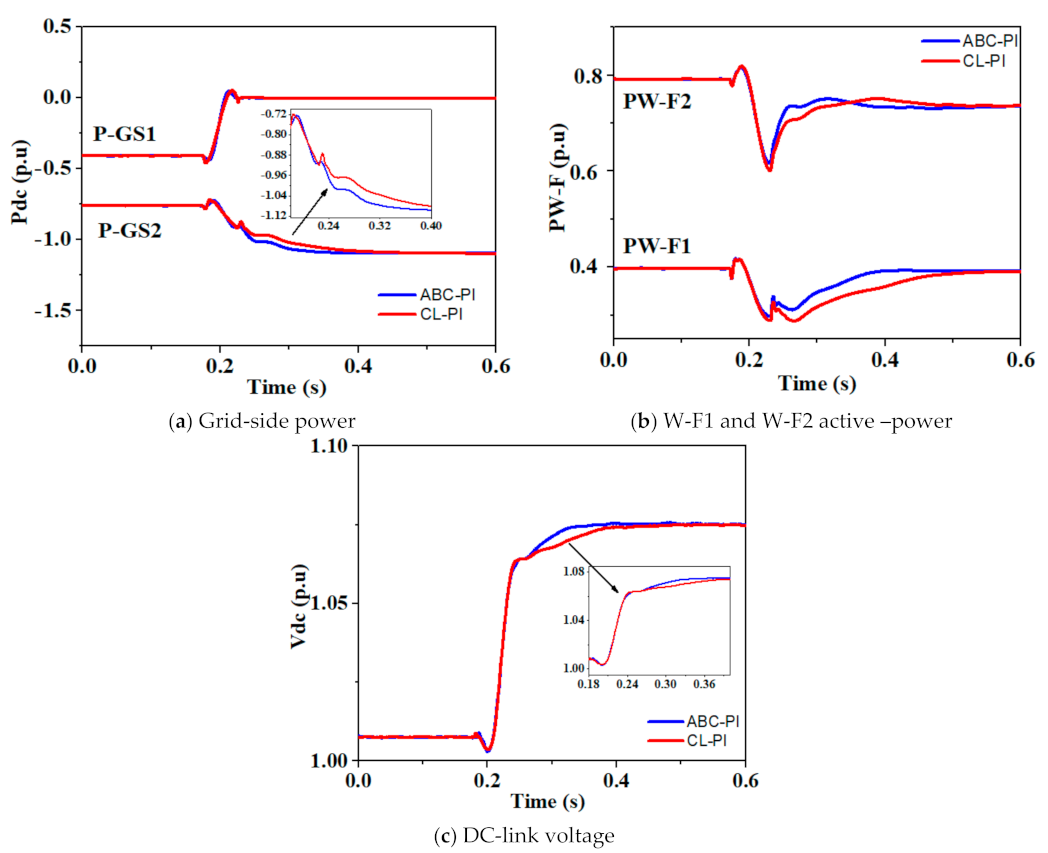
5.3. Eventual VSC Disconnection
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| ABC Algorithm Pseudo-Code |
| Initialization (1) C (cycle number) = 1 (2) Initialize a random population (solutions) (Wi,j), , (3) Evaluate the population (fitness function based on Equation (12) (4) Repeat (5) Employee Bee Phase For each employee bee Generate a new population (food source) Calculate the fitness values and If new solution is better than the previous solution Then memorize the new solution and apply the greedy selection End for. (6) Evaluate the probability of the solution (7) On-looker Bees Phase For each on-looker bee Select a solution depends on Generate the new solution Evaluate the fitness values and If new solution is better than the previous solution Then memorize the new solution and apply greed selection End for (8) Scout Bees Phase If there is an employee bee becomes a scout Then replace it with a new random population (9) Memorizing the best solution (10) C = C +1 (11) Until C = Maximum cycle number (i.e., 120 in our case) and satisfy minimization of objective function = |
References
- Liang, J.; Jing, T.; Gomis-Bellmunt, O.; Ekanayake, J.; Jenkins, N. Operation and control of multiterminal HVDC transmission for offshore wind farms. IEEE Trans. Power Deliv. 2011, 26, 2596–2604. [Google Scholar] [CrossRef]
- Rao, H. Architecture of Nan’ao multi-terminal VSC-HVDC system and its multi-functional control. CSEE J. Power Energy Syst. 2015, 1, 9–18. [Google Scholar] [CrossRef]
- Hannan, M.; Hussin, I.; Ker, P.J.; Hoque, M.M.; Lipu, M.H.; Hussain, A.; Rahman, M.A.; Faizal, C.; Blaabjerg, F. Advanced control strategies of VSC based HVDC transmission system: Issues and potential recommendations. IEEE Acces 2018, 6, 78352–78369. [Google Scholar] [CrossRef]
- Mobarrez, M.; Kashani, M.G.; Bhattacharya, S. A novel control approach for protection of multiterminal VSC-based HVDC transmission system against DC faults. IEEE Trans. Ind. Appl. 2016, 52, 4108–4116. [Google Scholar] [CrossRef]
- Zhang, S.; Zou, G.; Huang, Q.; Xu, B.; Li, J. Single-ended line protection for MMC-MTDC grids. IET Gener. Transm. Distrib. 2019, 13, 4331–4338. [Google Scholar] [CrossRef]
- Liu, Y.; Xie, S.; Liang, H.; Cui, H. Coordinated control strategy of multi-terminal VSC-HVDC system considering frequency stability and power sharing. IET Gener. Transm. Distrib. 2019, 13, 5188–5196. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.; Xiong, L.; Jia, K.; Song, G. DC fault analysis and transient average current based fault detection for radial MTDC system. IEEE Trans. Power Deliv. 2019, 35, 1310–1320. [Google Scholar] [CrossRef]
- Wu, G.; Liang, J.; Zhou, X.; Li, Y.; Egea-Alvarez, A.; Li, G.; Peng, H.; Zhang, X. Analysis and design of vector control for VSC-HVDC connected to weak grids. CSEE J. Power Energy Syst. 2017, 3, 115–124. [Google Scholar] [CrossRef]
- Lu, S.; Xu, Z.; Xiao, L.; Jiang, W.; Bie, X. Evaluation and enhancement of control strategies for VSC stations under weak grid strengths. IEEE Trans. Power Syst. 2017, 33, 1836–1847. [Google Scholar] [CrossRef]
- Rouzbehi, K.; Miranian, A.; Candela, J.I.; Luna, A.; Rodriguez, P. A generalized voltage droop strategy for control of multiterminal DC grids. IEEE Trans. Ind. Appl. 2014, 51, 607–618. [Google Scholar] [CrossRef]
- Yang, X.; Hu, H.; Ge, Y.; Aatif, S.; He, Z.; Gao, S. An improved droop control strategy for VSC-based MVDC traction power supply system. IEEE Trans. Ind. Appl. 2018, 54, 5173–5186. [Google Scholar] [CrossRef]
- Rouzbehi, K.; Miranian, A.; Candela, J.I.; Luna, A.; Rodriguez, P. A hierarchical control structure for multi-terminal VSC-based HVDC grids with GVD characteristics. In Proceedings of the 2013 International Conference on Renewable Energy Research and Applications (ICRERA), Madrid, Spain, 20–23 October 2013; pp. 996–1001. [Google Scholar]
- Raza, A.; Dianguo, X.; Yuchao, L.; Xunwen, S.; Williams, B.; Cecati, C. Coordinated operation and control of VSC based multiterminal high voltage DC transmission systems. IEEE Trans. Sustain. Energy 2015, 7, 364–373. [Google Scholar] [CrossRef]
- Yousaf, M.Z.; Liu, H.; Raza, A.; Baig, M. Primary and backup fault detection techniques for multi-terminal HVdc systems: A review. IET Gener. Transm. Distrib. 2020, 14, 5261–5276. [Google Scholar] [CrossRef]
- Seng, T.L.; Khalid, M.B.; Yusof, R. Tuning of a neuro-fuzzy controller by genetic algorithm. IEEE Trans. Syst. Man Cybern. Part B 1999, 29, 226–236. [Google Scholar] [CrossRef] [PubMed]
- Song, E.; Lynch, A.F.; Dinavahi, V. Experimental validation of nonlinear control for a voltage source converter. IEEE Trans. Control Syst. Technol. 2009, 17, 1135–1144. [Google Scholar] [CrossRef]
- Gaing, Z.-L. A particle swarm optimization approach for optimum design of PID controller in AVR system. IEEE Trans. Energy Convers. 2004, 19, 384–391. [Google Scholar] [CrossRef]
- Krohling, R.A.; Rey, J.P. Design of optimal disturbance rejection PID controllers using genetic algorithms. IEEE Trans. Evol. Comput. 2001, 5, 78–82. [Google Scholar] [CrossRef]
- Hassan, L.H.; Moghavvemi, M.; Almurib, H.A.; Muttaqi, K.M. A coordinated design of PSSs and UPFC-based stabilizer using genetic algorithm. IEEE Trans. Ind. Appl. 2014, 50, 2957–2966. [Google Scholar] [CrossRef]
- Lotfy, M.E.; Senjyu, T.; Farahat, M.A.; Abdel-Gawad, A.F.; Yona, A. Enhancement of a small power system performance using multi-objective optimization. IEEE Access 2017, 5, 6212–6224. [Google Scholar] [CrossRef]
- Dierckxsens, C.; Srivastava, K.; Reza, M.; Cole, S.; Beerten, J.; Belmans, R. A distributed DC voltage control method for VSC MTDC systems. Electr. Power Syst. Res. 2012, 82, 54–58. [Google Scholar] [CrossRef]
- Pinto, R.T.; Bauer, P.; Rodrigues, S.F.; Wiggelinkhuizen, E.J.; Pierik, J.; Ferreira, B. A novel distributed direct-voltage control strategy for grid integration of offshore wind energy systems through MTDC network. IEEE Trans. Ind. Electron. 2012, 60, 2429–2441. [Google Scholar] [CrossRef]
- Bajracharya, C.; Molinas, M.; Suul, J.A.; Undeland, T.M. Understanding of tuning techniques of converter controllers for VSC-HVDC. In Proceedings of the Nordic Workshop on Power and Industrial Electronics (NORPIE/2008), Espoo, Finland, 9–11 June 2008; Helsinki University of Technology: Espoo, Finland, 2008. [Google Scholar]
- Akagi, H.; Watanabe, E.H.; Aredes, M. Instantaneous Power Theory and Applications to Power Conditioning; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical report-tr06; Erciyes University, Faculty of Engineering, Department of Computer Engineering: Kayseri, Turkey, 2005. [Google Scholar]
- Ayan, K.; KILIÇ, U. Solution of transient stability-constrained optimal power flow using artificial bee colony algorithm. Turk. J. Electr. Eng. Comput. Sci. 2013, 21, 360–372. [Google Scholar]
- Şahin, A.Ş.; Kılıç, B.; Kılıç, U. Design and economic optimization of shell and tube heat exchangers using Artificial Bee Colony (ABC) algorithm. Energy Convers. Manag. 2011, 52, 3356–3362. [Google Scholar] [CrossRef]
- Kılıç, U.; Ayan, K. Optimizing power flow of AC–DC power systems using artificial bee colony algorithm. Int. J. Electr. Power Energy Syst. 2013, 53, 592–602. [Google Scholar] [CrossRef]
- Karaboga, N. A new design method based on artificial bee colony algorithm for digital IIR filters. J. Frankl. Inst. 2009, 346, 328–348. [Google Scholar] [CrossRef]
- Holland, J. Adaptation in Natural and Artificial Systems; MI University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Tareen, W.U.K.; Aamir, M.; Mekhilef, S.; Nakaoka, M.; Seyedmahmoudian, M.; Horan, B.; Memon, M.A.; Baig, N.A.J.E. Mitigation of power quality issues due to high penetration of renewable energy sources in electric grid systems using three-phase APF/STATCOM technologies: A review. Energies 2018, 11, 1491. [Google Scholar] [CrossRef]
- Marler, R.T.; Arora, J.S. The weighted sum method for multi-objective optimization: New insights. Struct. Multidiscip. Optim. 2010, 41, 853–862. [Google Scholar] [CrossRef]
- Rouzbehi, K.; Miranian, A.; Luna, A.; Rodriguez, P. Optimized control of multi-terminal DC GridsUsing particle swarm optimization. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–9. [Google Scholar]
- Rodrigues, S.; Bauer, P.; Bosman, P.A.J.R.; Reviews, S.E. Multi-objective optimization of wind farm layouts–Complexity, constraint handling and scalability. Renew. Sustain. Energy Rev. 2016, 65, 587–609. [Google Scholar] [CrossRef]
- Rodrigues, S.M.F.; Pinto, R.T.; Bauer, P. Dynamic Modeling and Control of VSC-based Multiterminal DC networks. Inst. Super. Técnico 2011. [Google Scholar]
- Faisal, S.F.; Beig, A.R.; Thomas, S.J.E. Time domain particle swarm optimization of PI controllers for bidirectional VSC HVDC light system. Energies 2020, 13, 866. [Google Scholar] [CrossRef]
- Beerten, J.; Cole, S.; Belmans, R. Modeling of multi-terminal VSC HVDC systems with distributed DC voltage control. IEEE Trans. Power Syst. 2013, 29, 34–42. [Google Scholar] [CrossRef]


| Specifications | Number of Food-Source | Bees (Employeed + On-Looker Bees) | Iterations |
|---|---|---|---|
| Values | 20 | 20 | 60 |
| Controllers | CL P-I | ABC P-I | ||
|---|---|---|---|---|
| ICC-L | 0.48 | 16.7500 | 0.87 | 21.6535 |
| OCC-L | 0.12 | 35.0050 | 0.87 | 76.2550 |
| Controllers | ITAE | |
|---|---|---|
| CL P-I | ABC P-I | |
| ICC-L | 4.82208 × 10−4 | 9.5642 × 10−5 |
| Active power | 1.6402 × 10−3 | 4.8640 × 10−4 |
| MO-F | 5.1532 × 10−5 |
| Component | Nominal-Voltage (kV) | Impedance | Description |
|---|---|---|---|
| Wind-farms | 33 | 0.002 + j0.012 (p.u) | 1000 MVA |
| AC grids | 220 | 0.001 + j0.0125 (p.u) | 1000 MVA |
| Phase-reactor | 180 | 0.02 + 0.15 (p.u) | |
| DC-capacitor | ±250 | 1200 µF, two capacitors in series | |
| DC link | ±250 | R = 0.20 × 10−2 10 Ω/km L = 0.55 × 10−4 H/km C = 2.2 × 10−7 F/km | 100 km b/w all terminals |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, M.A.; Li, X.; Yousaf, M.Z.; Mustafa, A.; Wei, M. Metaheuristic Based Solution for the Non‐Linear Controller of the Multiterminal High‐Voltage Direct Current Networks. Energies 2021, 14, 1578. https://doi.org/10.3390/en14061578
Khan MA, Li X, Yousaf MZ, Mustafa A, Wei M. Metaheuristic Based Solution for the Non‐Linear Controller of the Multiterminal High‐Voltage Direct Current Networks. Energies. 2021; 14(6):1578. https://doi.org/10.3390/en14061578
Chicago/Turabian StyleKhan, Muhammad Ahmad, Xiaocong Li, Muhammad Zain Yousaf, Ali Mustafa, and Mingshuo Wei. 2021. "Metaheuristic Based Solution for the Non‐Linear Controller of the Multiterminal High‐Voltage Direct Current Networks" Energies 14, no. 6: 1578. https://doi.org/10.3390/en14061578
APA StyleKhan, M. A., Li, X., Yousaf, M. Z., Mustafa, A., & Wei, M. (2021). Metaheuristic Based Solution for the Non‐Linear Controller of the Multiterminal High‐Voltage Direct Current Networks. Energies, 14(6), 1578. https://doi.org/10.3390/en14061578







