A Study on Common Mode Voltage Reduction Strategies According to Modulation Methods in Modular Multilevel Converter
Abstract
1. Introduction
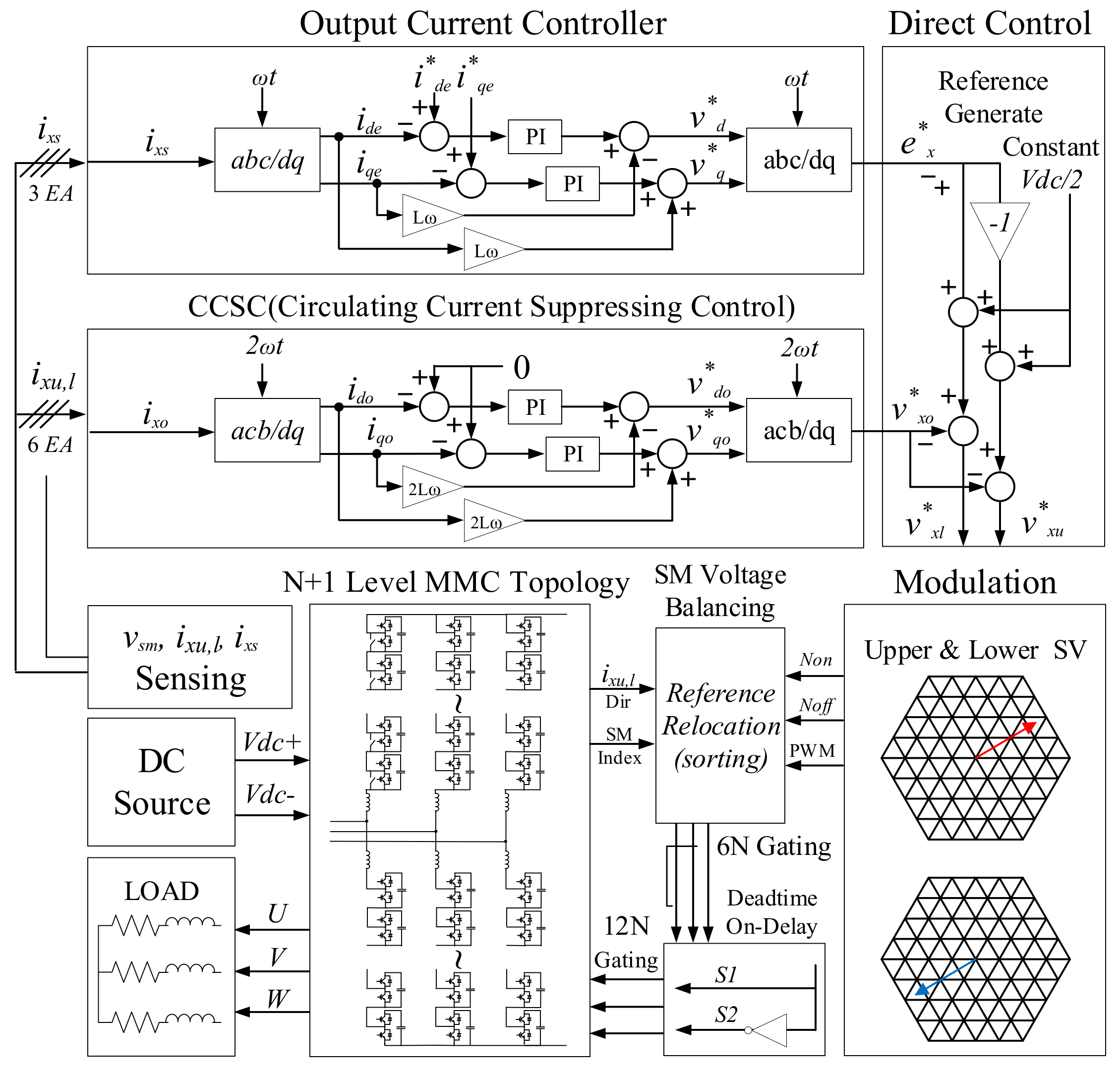
2. Basics of MMC
3. Analysis of CMV in Three Phases N + 1 Level MMC
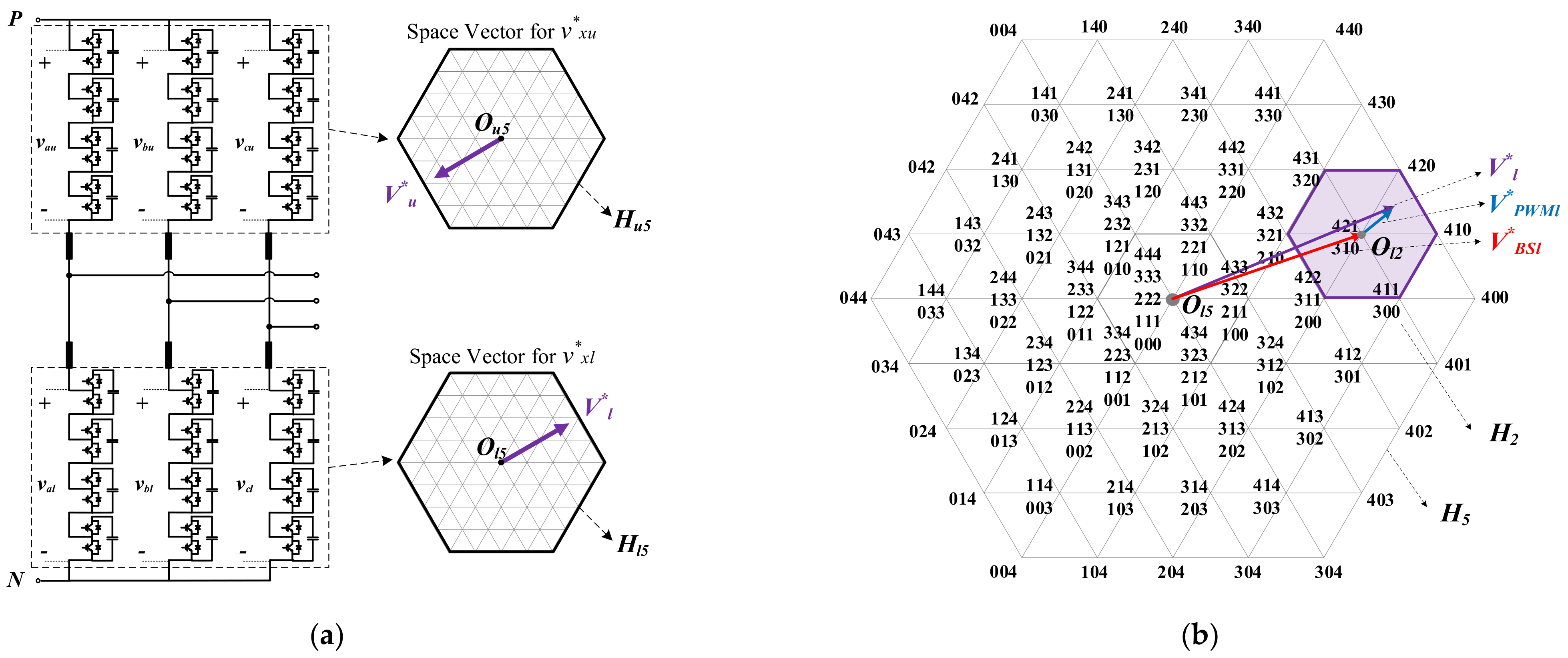
3.1. Definition of CMV
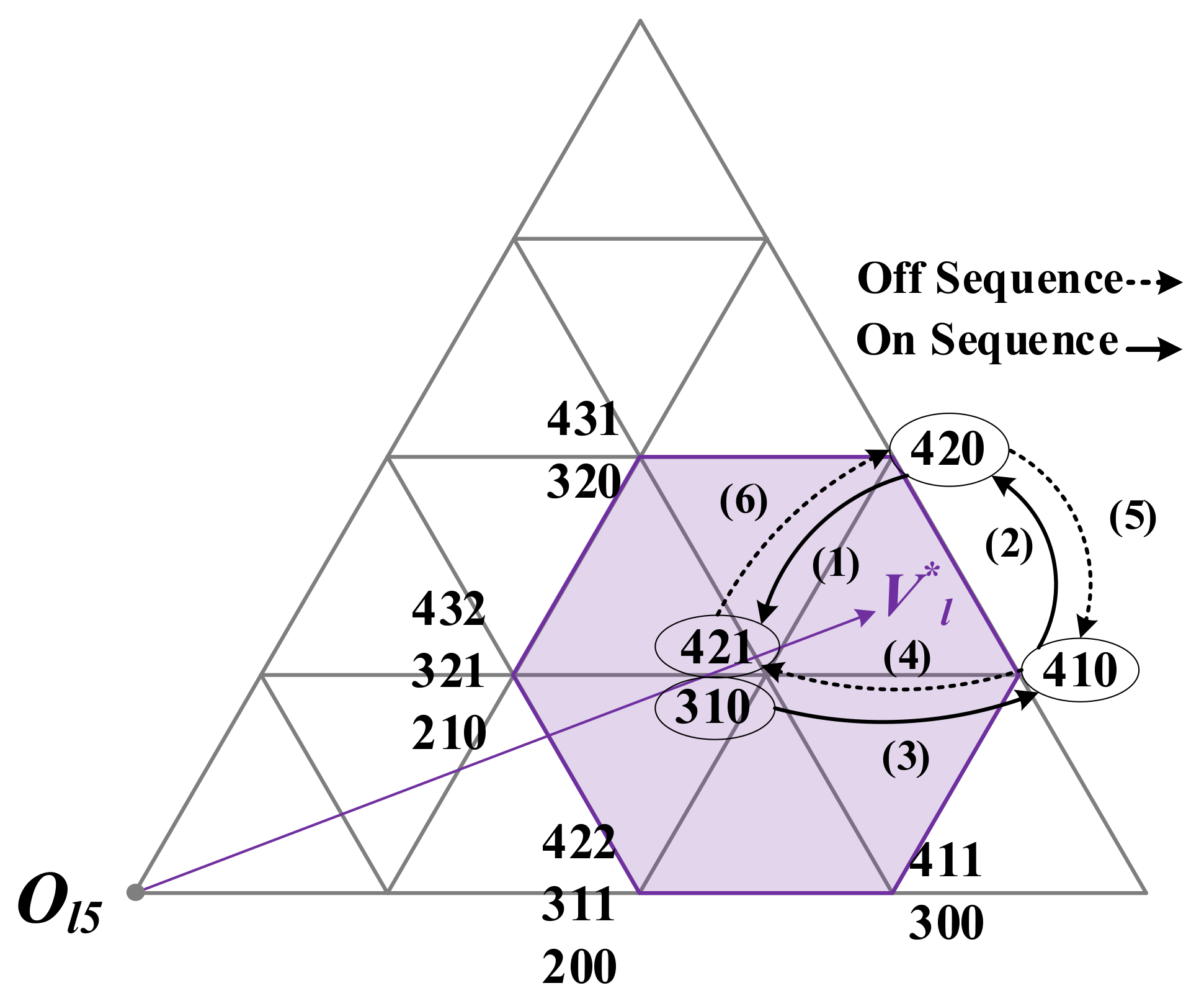
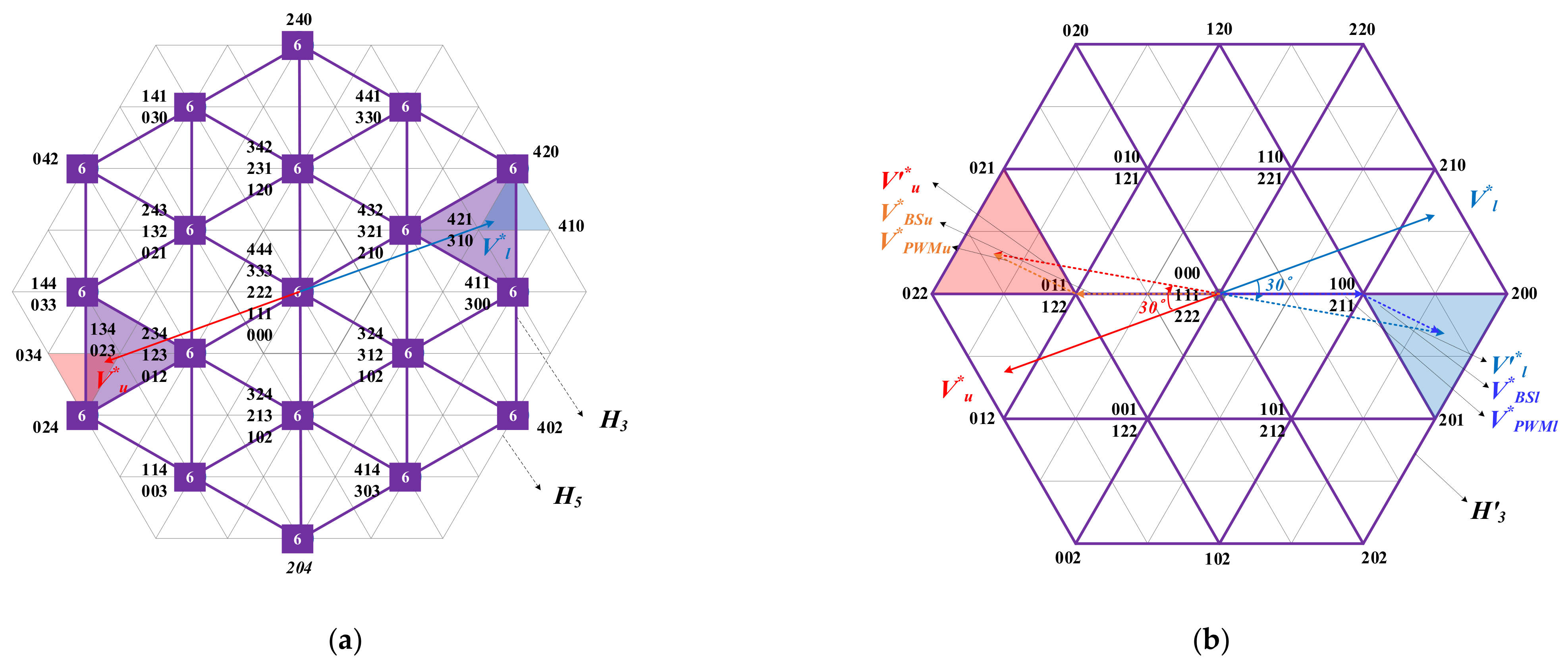
3.2. CMV Anlaysis on Space Vector
4. CMV Reduction in MMC
4.1. Complete CMV Reduction (CCR) Method
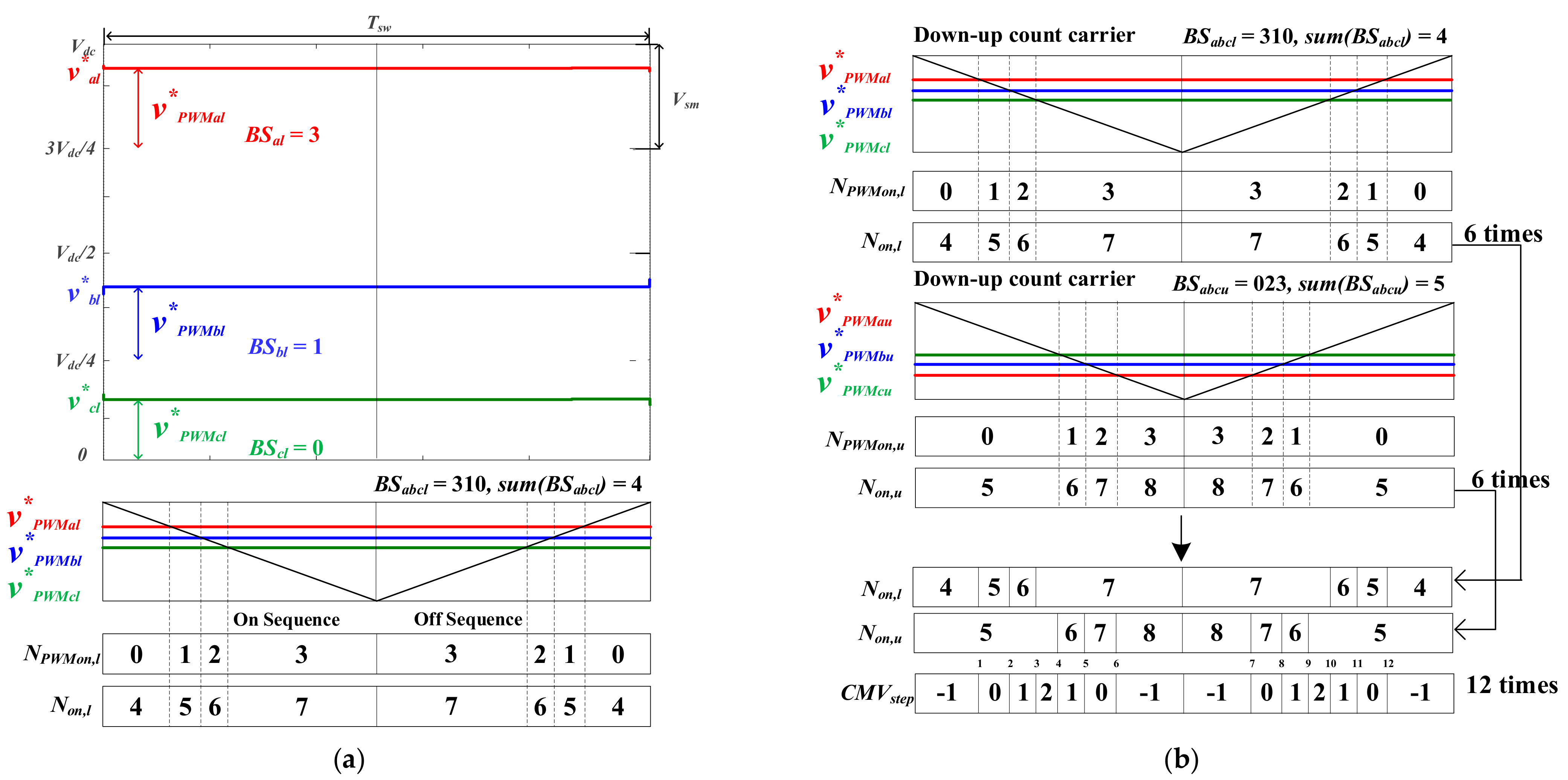
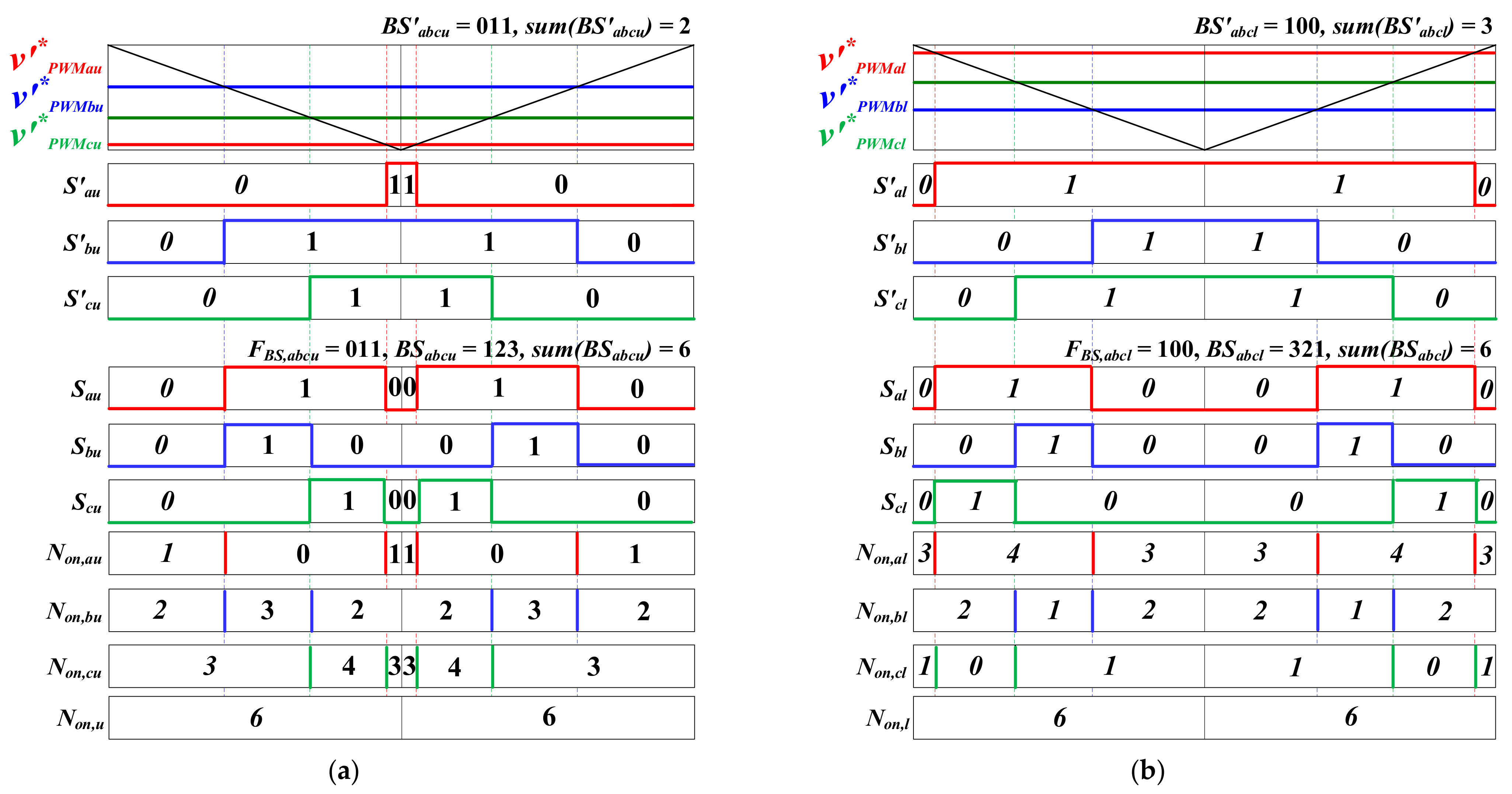
4.2. DPWM CMV Reduction (DCR) Method
4.3. Partial CMV Reduction (PCR) Method
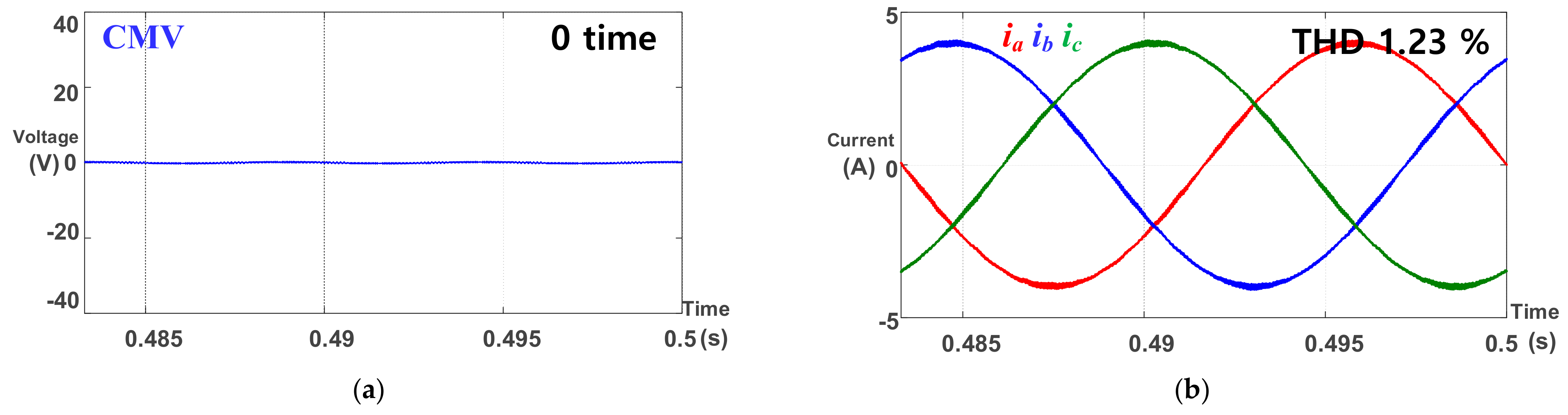
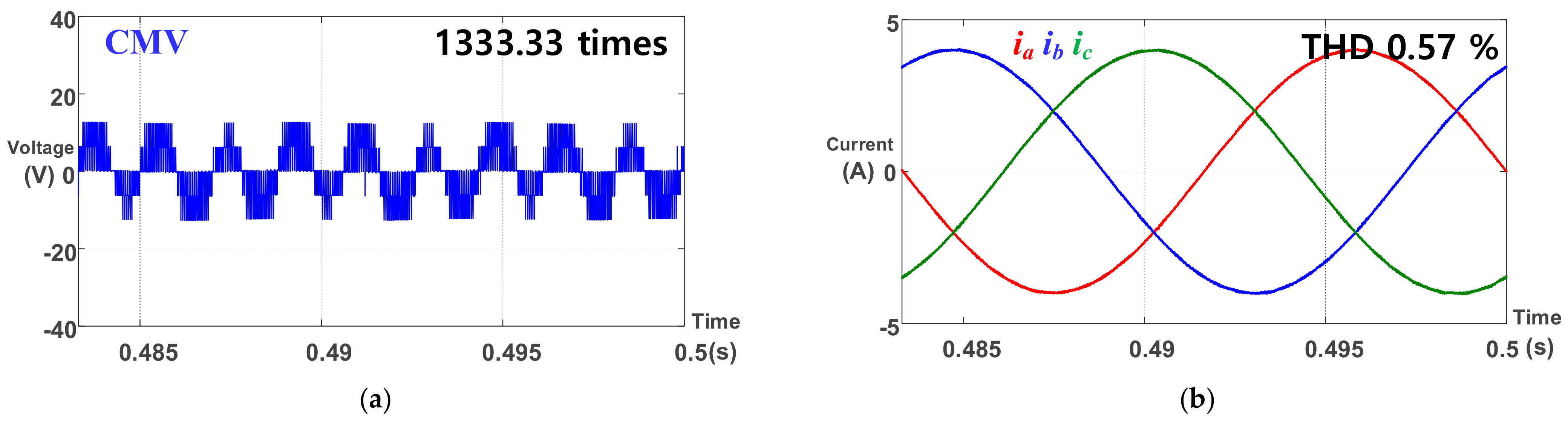
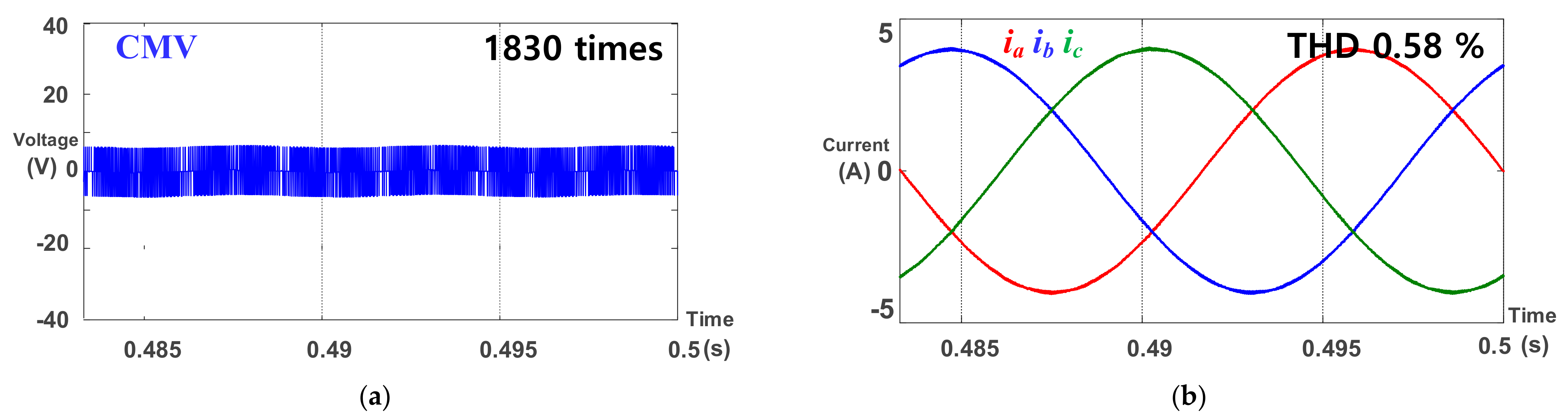
5. Simulation
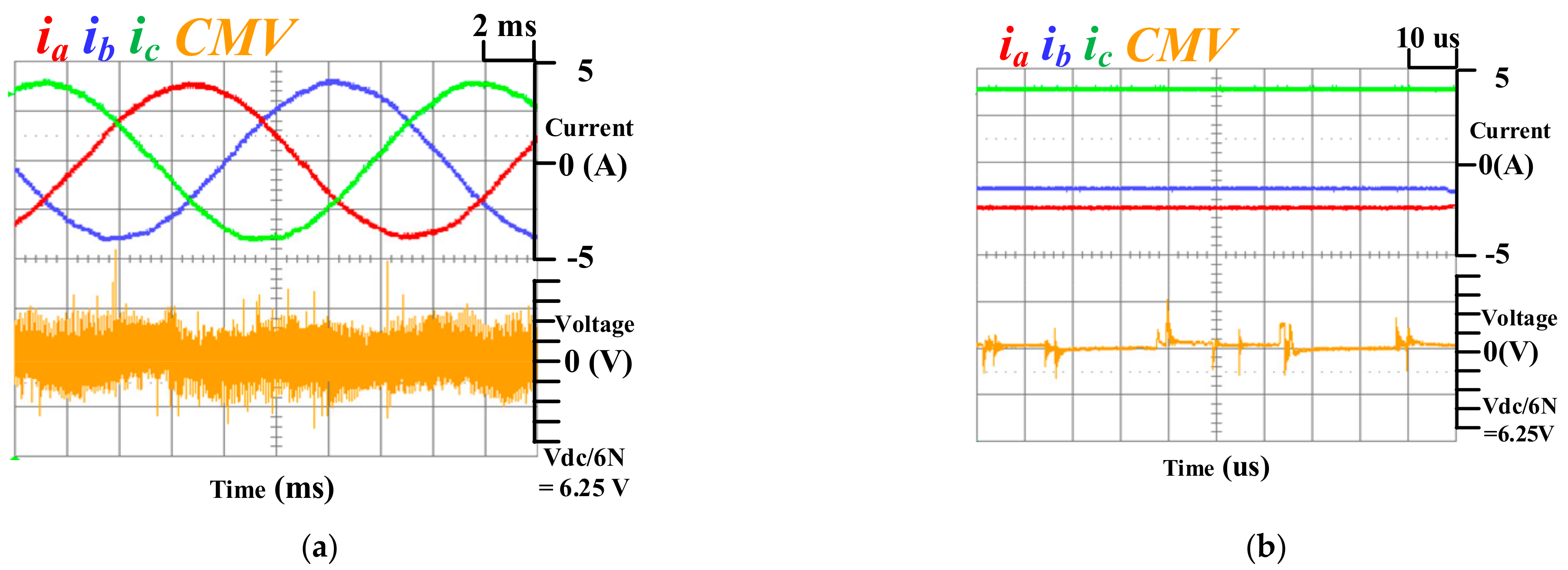
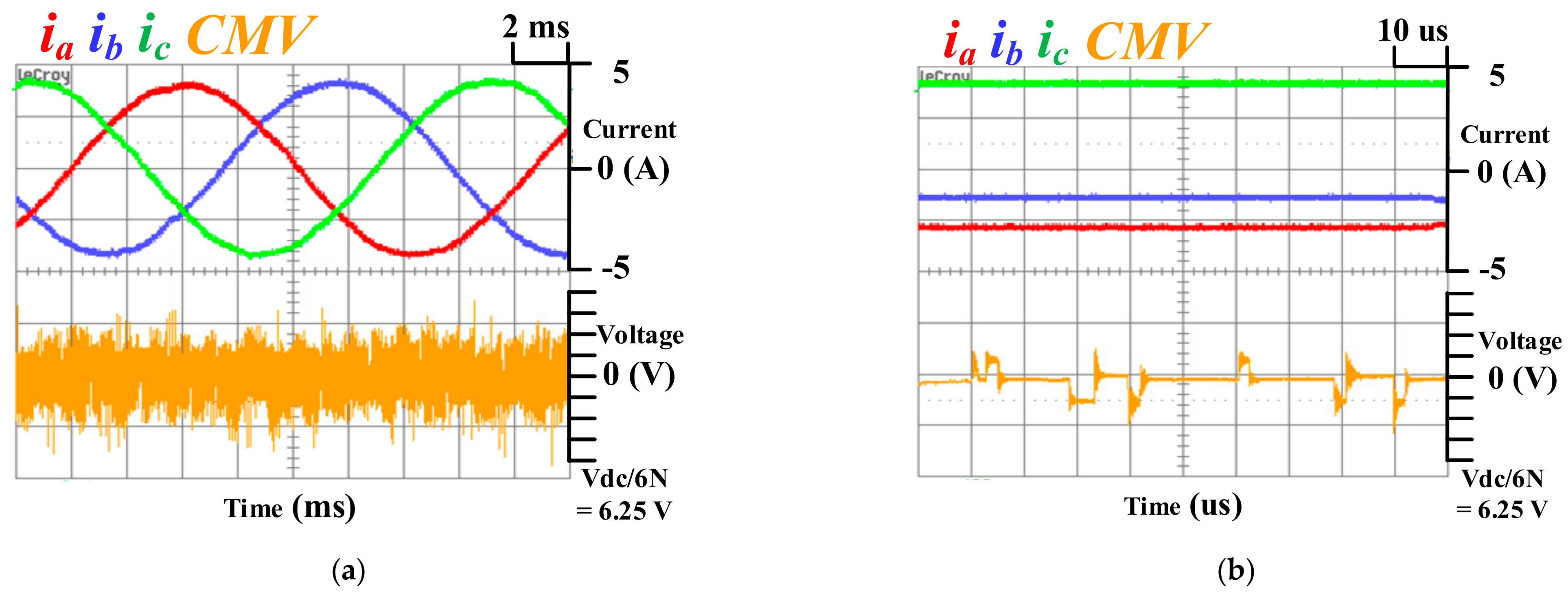
6. Experiment
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Allebrod, S.; Hamerski, R.; Marquardt, R. New Transformerless, Scalable Modular Multilevel Converters for HVDC-Transmission. In Proceedings of the 2017 International Conference on Innovations in Information, Embedded and Communication Systems (ICIIECS), Coimbatore, India, 17–18 March 2017. [Google Scholar]
- Gemmell, B.; Dorn, J.; Retzmann, D.; Soerangr, D. Prospects of Multilevel VSC Technologies for Power Transmission. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008. [Google Scholar]
- Marquardt, R. Modular Multilevel Converter: An universal concept for HVDC-Networks and extended DC-Bus-applications. In Proceedings of the 2010 International Power Electronics Conference—ECCE ASIA, Sapporo, Japan, 21–24 June 2010. [Google Scholar]
- Chen, Y.; Li, Z.; Zhao, S.; Wei, X.; Kang, Y. Design and Implementation of a Modular Multilevel Converter with Hierarchical Redundancy Ability for Electric Ship MVDC System. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 189–202. [Google Scholar] [CrossRef]
- Jung, J.J.; Lee, H.J.; Sul, S.K. Control Strategy for Improved Dynamic Performance of Variable-Speed Drives with Modular Multilevel Converter. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 371–380. [Google Scholar] [CrossRef]
- Akagi, H. New Trends in Medium-Voltage Power Converters and Motor Drives. In Proceedings of the IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011. [Google Scholar]
- Hagiwara, M.; Nishimura, K.; Akagi, H. A Medium-Voltage Motor Drive with a Modular Multilevel PWM Inverter. IEEE Trans. Power Electron. 2010, 25, 1786–1799. [Google Scholar] [CrossRef]
- Spichartz, M.; Staudt, V.; Steimel, A. Modular Multilevel Converter for propulsion system of electric ships. In Proceedings of the IEEE Electric Ship Technologies Symposium (ESTS), Arlington, VA, USA, 22–24 April 2013. [Google Scholar]
- Lesnicar, A.; Marquardt, R. A new modular voltage source inverter topology. In Proceedings of the 10th European Conference on Power Electronics and Applications, Toulouse, France, 2–4 September 2003. [Google Scholar]
- Lesnicar, A.; Marquardt, R. An Innovative Modular Multilevel Converter Topology Suitable for a Wide Power Range. In Proceedings of the IEEE Bologna Power Tech Conference, Bologna, Italy, 23–26 June 2003. [Google Scholar]
- Debnath, S.; Qin, J.; Bahrani, B.; Saeedifard, M.; Barbosa, P. Operation, Control, and Applications of the Modular Multilevel Converter: A Review. IEEE Trans. Power Electron. 2015, 30, 37–53. [Google Scholar] [CrossRef]
- Moranchel, M.; Bueno, E.J.; Rodriguez, F.J.; Sanz, I. Implementation of Nearest Level Modulation for Modular Multilevel Converter. In Proceedings of the IEEE 6th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aachen, Germany, 22–25 June 2015. [Google Scholar]
- Meshram, P.M.; Borghate, V.B. A Simplified Nearest Level Control (NLC) Voltage Balancing Method for Modular Multilevel Converter (MMC). IEEE Trans. Power Electron. 2015, 30, 450–462. [Google Scholar] [CrossRef]
- Tu, Q.; Xu, Z. Impact of Sampling Frequency on Harmonic Distortion for Modular Multilevel Converter. IEEE Trans. Power Electron. 2011, 26, 298–306. [Google Scholar] [CrossRef]
- Franquelo, L.G.; Rodriguez, J.; Leon, J.I.; Kouro, S.; Portillo, R.; Prats, M.A.M. The age of multilevel converters arrives. IEEE Ind. Electron. Mag. 2008, 2, 28–39. [Google Scholar] [CrossRef]
- Rodriguez, J.; Lai, J.S.; Peng, F.Z. Multilevel Inverters: A Survey of Topologies, Controls, and Applications. IEEE Trans. Ind. Electron. 2002, 49, 724–738. [Google Scholar] [CrossRef]
- Rodriguez, J.; Franquelo, L.G.; Kouro, S.; Leon, J.I.; Portillo, R.C.; Prats, M.Á.M.; Perez, M.A. Multilevel Converters: An Enabling Technology for High-Power Applications. Proc. IEEE 2009, 97, 1786–1817. [Google Scholar] [CrossRef]
- Agelidis, V.G.; Calais, M. Application specific harmonic performance evaluation of multicarrier PWM techniques. In Proceedings of the 29th Annual IEEE Power Electronics Specialists Conference, Fukuoka, Japan, 22 May 1998. [Google Scholar]
- Konstantinou, G.S.; Agelidis, V.G. Performance Evaluation of Half-Bridge Cascaded Multilevel Converters Operated with Multicarrier Sinusoidal PWM Techniques. In Proceedings of the 4th IEEE Conference on Industrial Electronics and Applications, Xi’an, China, 25–27 May 2009. [Google Scholar]
- Konstantinou, G.S.; Ciobotaru, M.; Agelidis, V.G. Analysis of Multi-carrier PWM Methods for Back-to-back HVDC Systems based on Modular Multilevel Converters. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011. [Google Scholar]
- Mahatom, B.; Kumari, R.; Raushan, R.; Jana, K.C.; Thakura, P.; Singh, S.K. Comparative Analysis of Different PWM Techniques in Multilevel Inverters. Int. J. Eng. Technol. 2016, 4, 2. [Google Scholar]
- Wang, Y.; Hu, C.; Ding, R.; Xu, L.; Fu, C.; Yang, E. A Nearest Level PWM Method for the MMC in DC Distribution Grids. IEEE Trans. Power Electron. 2018, 33, 9209–9218. [Google Scholar] [CrossRef]
- Deng, Y.; Harle, R.G. Space-Vector Versus Nearest-Level Pulse Width Modulation for Multilevel Converters. IEEE Trans. Power Electron. 2015, 30, 2962–2974. [Google Scholar] [CrossRef]
- Chen, S.; Lipo, T.A.; Fitzgerald, D. Modeling of motor bearing currents in PWM inverter drives. IEEE Trans. Ind. Appl. 1996, 32, 1365–1370. [Google Scholar] [CrossRef]
- Julian, A.L.; Oriti, G.; Lipo, T.A. Elimination of common-mode voltage in three-phase sinusoidal power converters. IEEE Trans. Power Electron. 1999, 14, 982–989. [Google Scholar] [CrossRef]
- Ogasawara, S.; Ayano, H.; Akagi, H. An active circuit for cancellation of common-mode voltage generated by a PWM inverter. IEEE Trans. Power Electron. 1998, 13, 835–841. [Google Scholar] [CrossRef]
- Jouanne, A.V.; Zhang, H.; Wallace, A.K. An evaluation of mitigation techniques for bearing currents, EMI and over voltages in ASD applications. IEEE Trans. Ind. Appl. 1998, 34, 1113–1122. [Google Scholar] [CrossRef]
- Hadden, T.; Jiang, J.W.; Bilgin, B.; Yang, Y.; Sathyan, A.; Dadkhah, H.; Emadi, A. A Review of Shaft Voltage and Bearing Currents in EV and HEV Motors. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016. [Google Scholar]
- Guttowski, S.; Weber, S.; Schinkel, M.; John, W.; Reichl, H. Troubleshooting and Fixing of Inverter Driven Induction Motor Bearing Currents in Existing Plants of Large Size—An Evaluation of Possible Mitigation Techniques in Practical Applications. In Proceedings of the 21st Annual IEEE Applied Power Electronics Conference and Exposition, Dallas, TX, USA, 19–23 March 2006. [Google Scholar]
- Du, S.; Wu, B.; Zargari, N.R. Common-Mode Voltage Elimination for Variable-Speed Motor Drive Based on Flying-Capacitor Modular Multilevel Converter. IEEE Trans. Power Electron. 2018, 33, 5621–5628. [Google Scholar] [CrossRef]
- Du, S.; Wu, B.; Zargari, N.R. Common-mode voltage minimization for grid-tied modular multilevel converter. IEEE Trans. Ind. Electron. 2019, 66, 7480–7487. [Google Scholar] [CrossRef]
- Edpuganti, A.; Rathore, A.K. Optimal Pulsewidth Modulation for Common-Mode Voltage Elimination Scheme of Medium-Voltage Modular Multilevel Converter-Fed Open-End Stator Winding Induction Motor Drives. IEEE Trans. Ind. Electron. 2017, 64, 848–856. [Google Scholar] [CrossRef]
- Adam, G.P.; Abdelsalam, I.; Fletcher, J.E.; Burt, G.M.; Holliday, D.; Finney, S.J. New Efficient Submodule for a Modular Multilevel Converter in Multiterminal HVDC Networks. IEEE Trans. Power Electron. 2017, 32, 4258–4278. [Google Scholar] [CrossRef]
- Akagi, H. Classification, Terminology, and Application of the Modular Multilevel Cascade Converter (MMCC). IEEE Trans. Power Electron. 2011, 26, 3119–3130. [Google Scholar] [CrossRef]
- Liu, M.; Li, Z.; Yang, X. A Universal Mathematical Model of Modular Multilevel Converter with Half-Bridge. Energies 2020, 13, 4464. [Google Scholar] [CrossRef]
- Tu, Q.; Xu, Z.; Zhang, J. Circulating current suppressing controller in modular multilevel converter. In Proceedings of the IECON 2010—36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010. [Google Scholar]
- Loh, P.C.; Holmes, D.G.; Fukuta, Y.; Lipo, T.A. Reduced common-mode modulation strategies for cascaded multilevel inverters. IEEE Trans. Ind. Appl. 2003, 39, 1386–1395. [Google Scholar]
- Tu, Q.; Xu, Z.; Huang, H.; Zhang, J. Parameter design principle of the arm inductor in modular multilevel converter based HVDC. In Proceedings of the International Conference on Power System Technology, Zhejiang, China, 24–28 October 2010. [Google Scholar]










| S | S = 1 | S = 0 | |
|---|---|---|---|
| Positive | Charge | Charge | |
| Negative | Discharge | No change | |
| PD, NLC + PWM | PSC, POD, APOD | |
|---|---|---|
| Carriers between the upper and lower arms | In-phase carriers | 180° out of phase carriers |
| Switching pattern | Shifted pattern | In-phase pattern |
| Maximum | 4 steps | steps |
| Number of changes in CMV (One switching period) | 12 times | 6 times |
| Arm voltage level | 5 levels (N + 1) | 5 levels (N + 1) |
| Output voltage level | 11 levels (2N + 1) |
| Parameter | Value |
|---|---|
| DC source | 150 (V) |
| SMs per arm | 4 (EA) |
| SM Capacitor | 2200 (uF) |
| Arm Inductor | 5 (mH) |
| AC output frequency | 60 (Hz) |
| Switching frequency | 10 (kHz) |
| Load | 15 (Ohm) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, C.-H.; Seo, I.-K.; Negesse, B.B.; Yoon, J.-s.; Kim, J.-M. A Study on Common Mode Voltage Reduction Strategies According to Modulation Methods in Modular Multilevel Converter. Energies 2021, 14, 1607. https://doi.org/10.3390/en14061607
Park C-H, Seo I-K, Negesse BB, Yoon J-s, Kim J-M. A Study on Common Mode Voltage Reduction Strategies According to Modulation Methods in Modular Multilevel Converter. Energies. 2021; 14(6):1607. https://doi.org/10.3390/en14061607
Chicago/Turabian StylePark, Chang-Hwan, In-Kyo Seo, Belete Belayneh Negesse, Jong-su Yoon, and Jang-Mok Kim. 2021. "A Study on Common Mode Voltage Reduction Strategies According to Modulation Methods in Modular Multilevel Converter" Energies 14, no. 6: 1607. https://doi.org/10.3390/en14061607
APA StylePark, C.-H., Seo, I.-K., Negesse, B. B., Yoon, J.-s., & Kim, J.-M. (2021). A Study on Common Mode Voltage Reduction Strategies According to Modulation Methods in Modular Multilevel Converter. Energies, 14(6), 1607. https://doi.org/10.3390/en14061607






