A Parametrical Study on Convective Heat Transfer between High-Temperature Gas and Regenerative Cooling Panel
Abstract
:1. Introduction
2. Numerical Methods
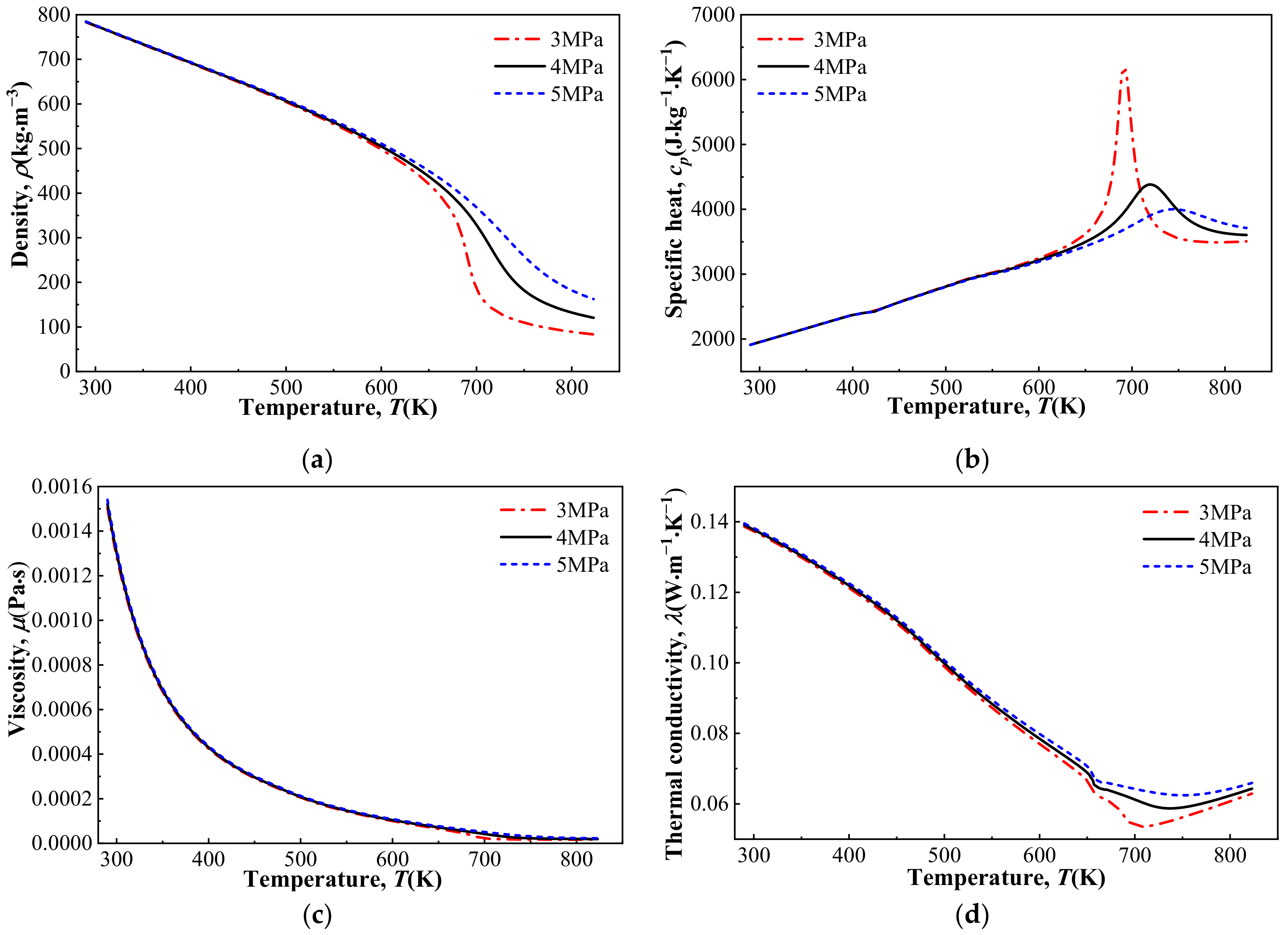
2.1. Governing Equations
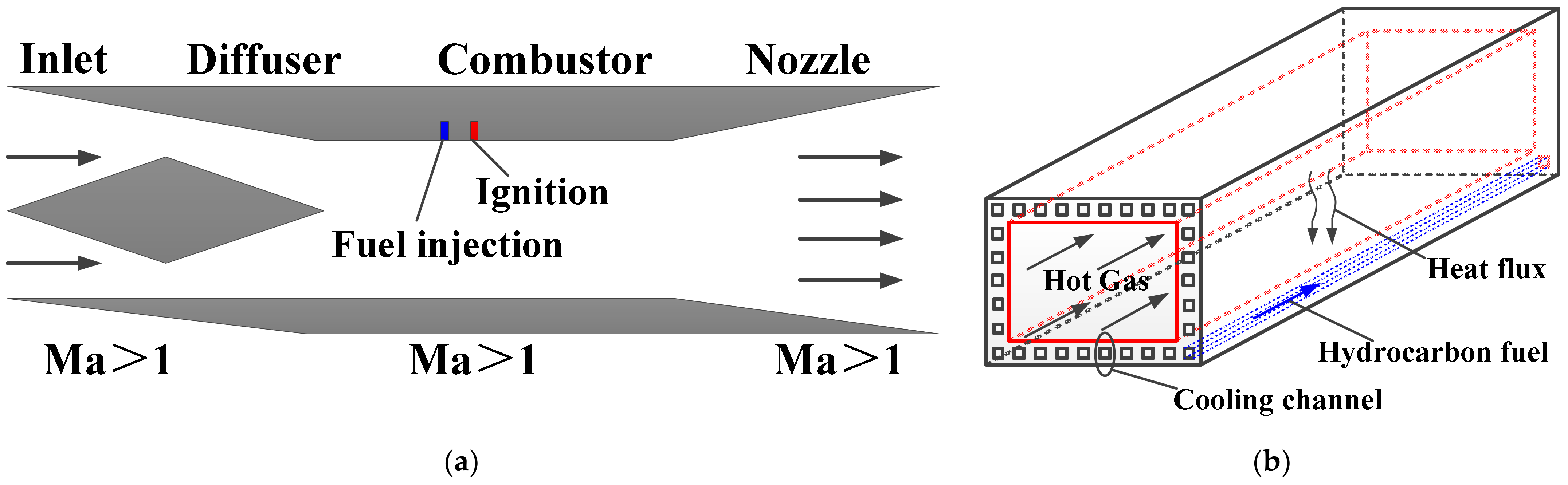
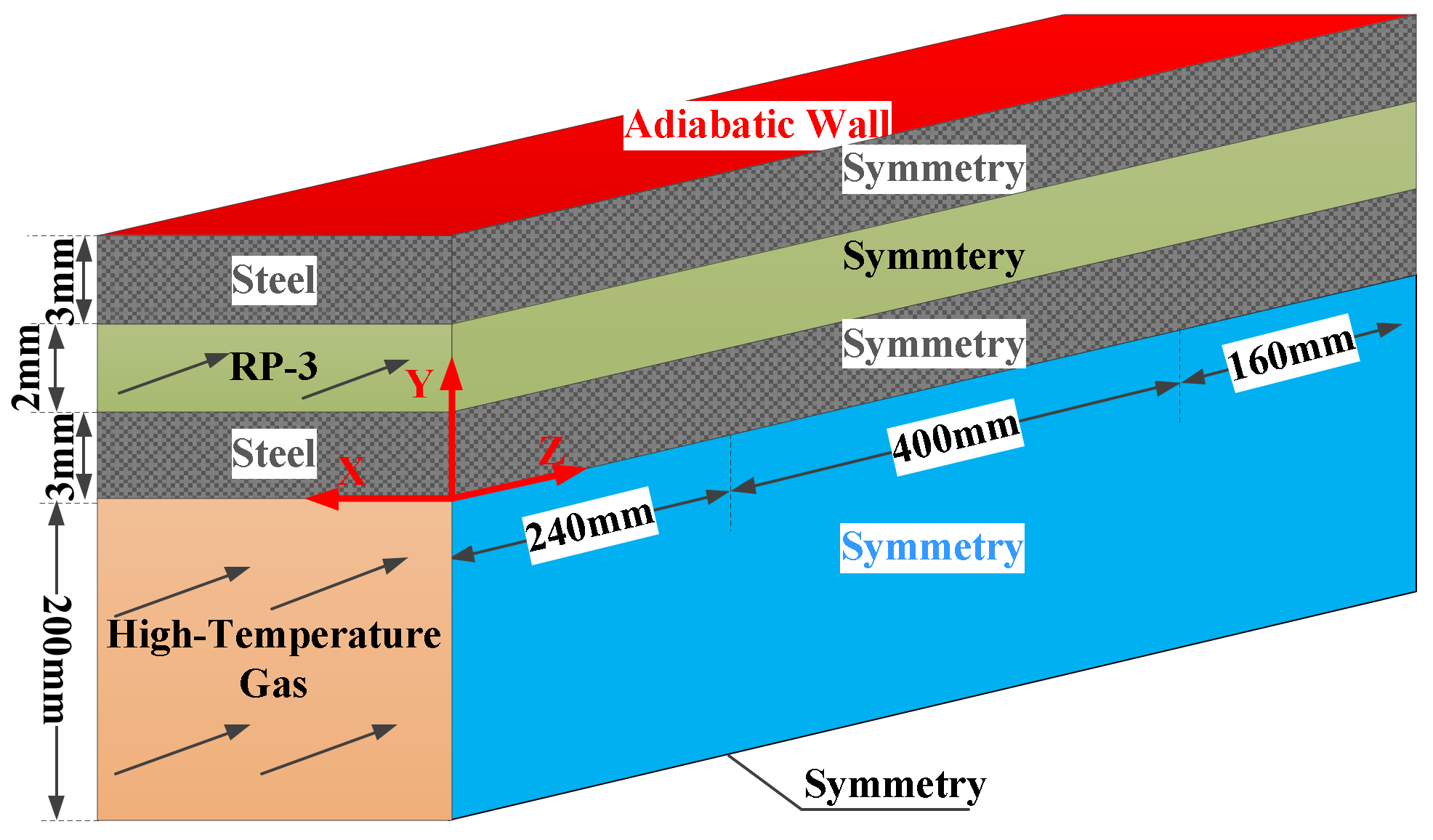
2.2. Physical Model
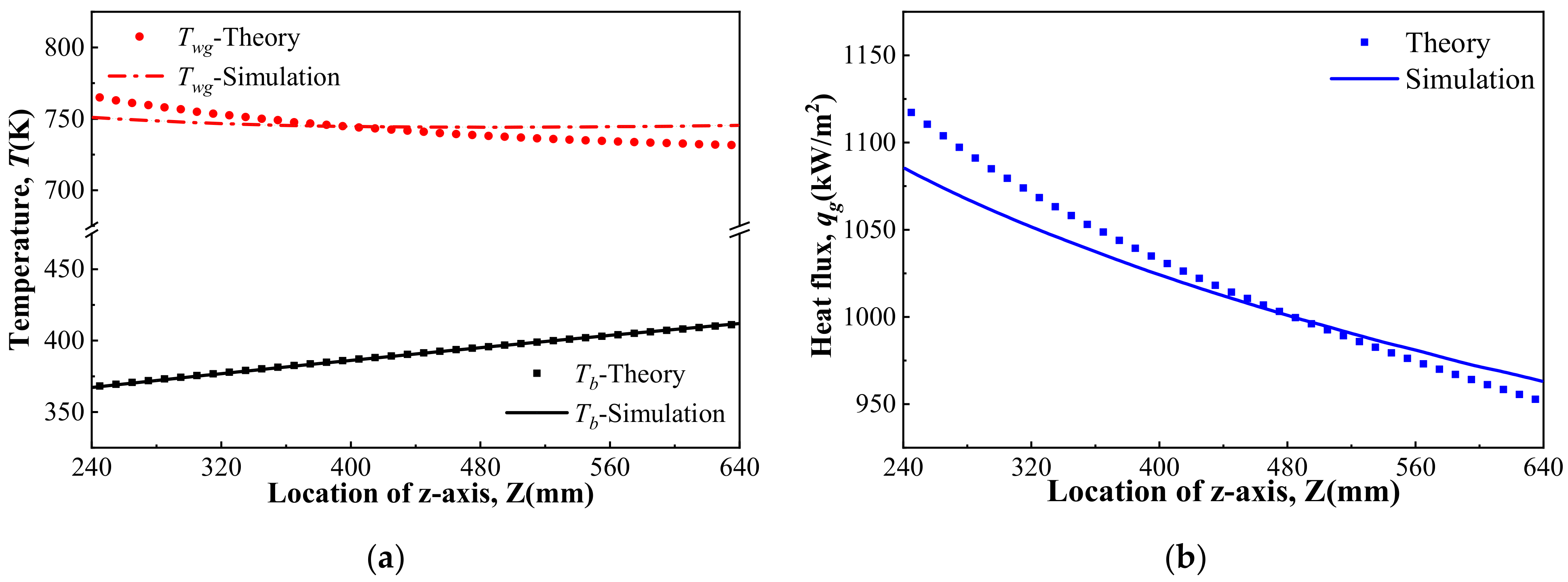
2.3. Validation
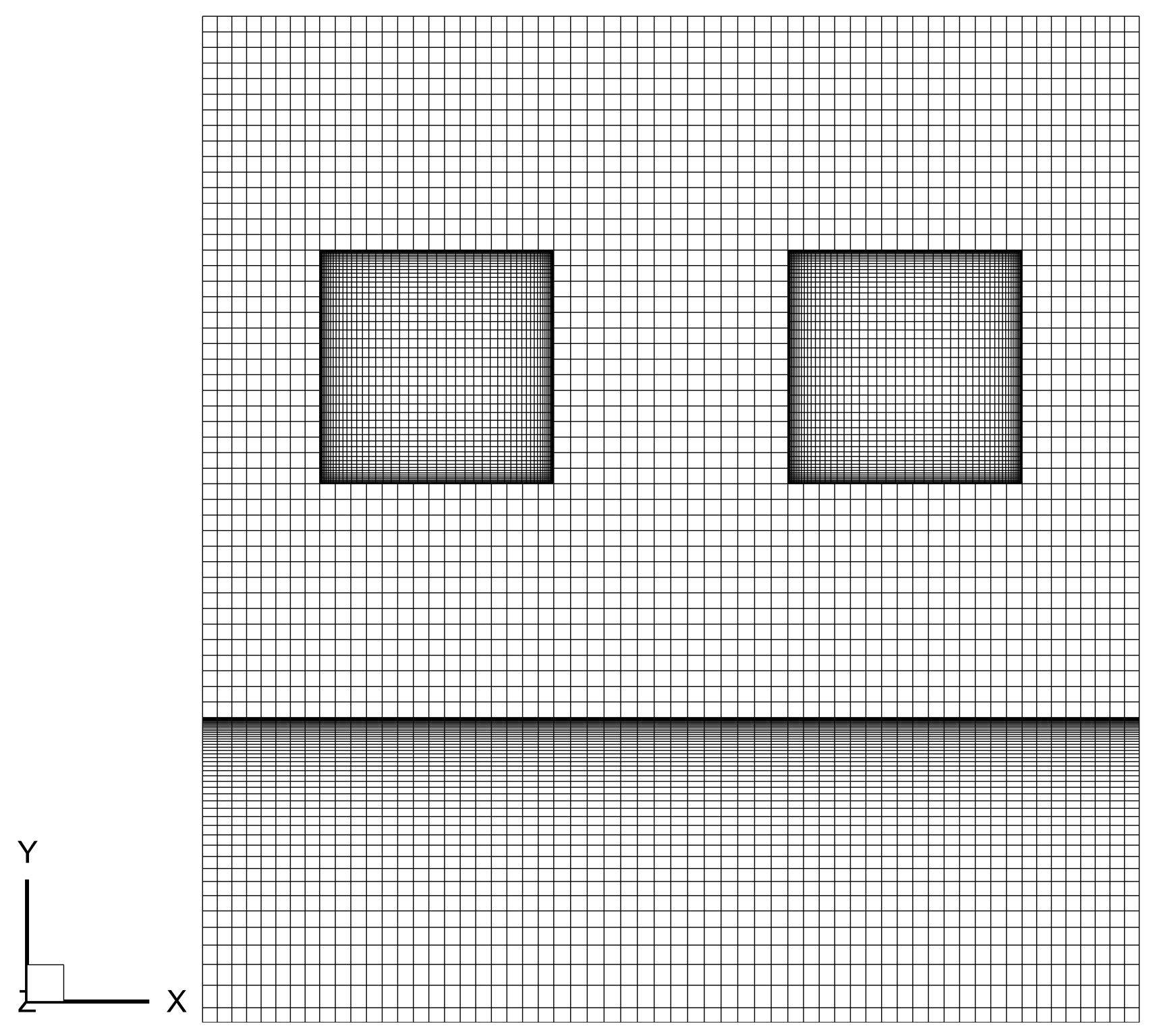
2.4. Mesh Sensitivity
3. Results and Discussion
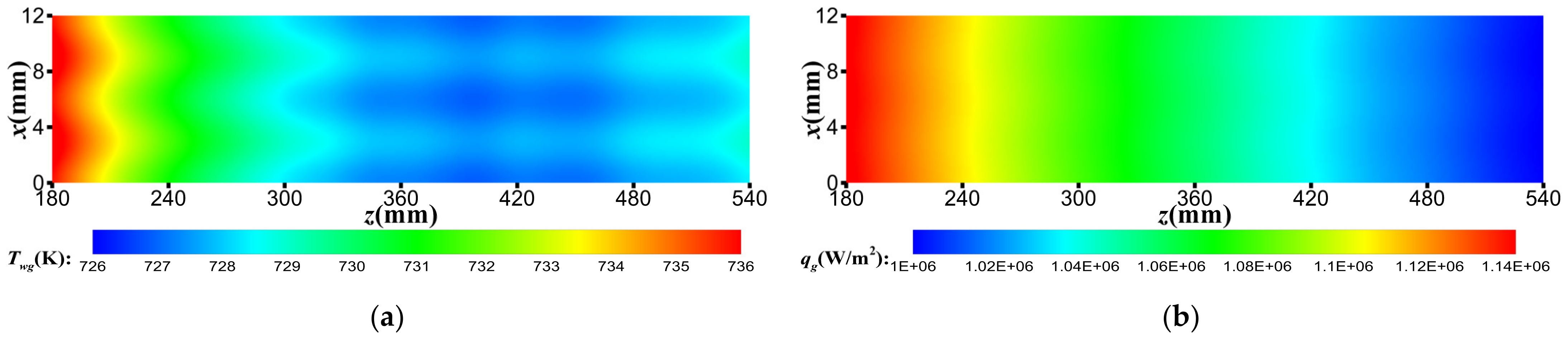
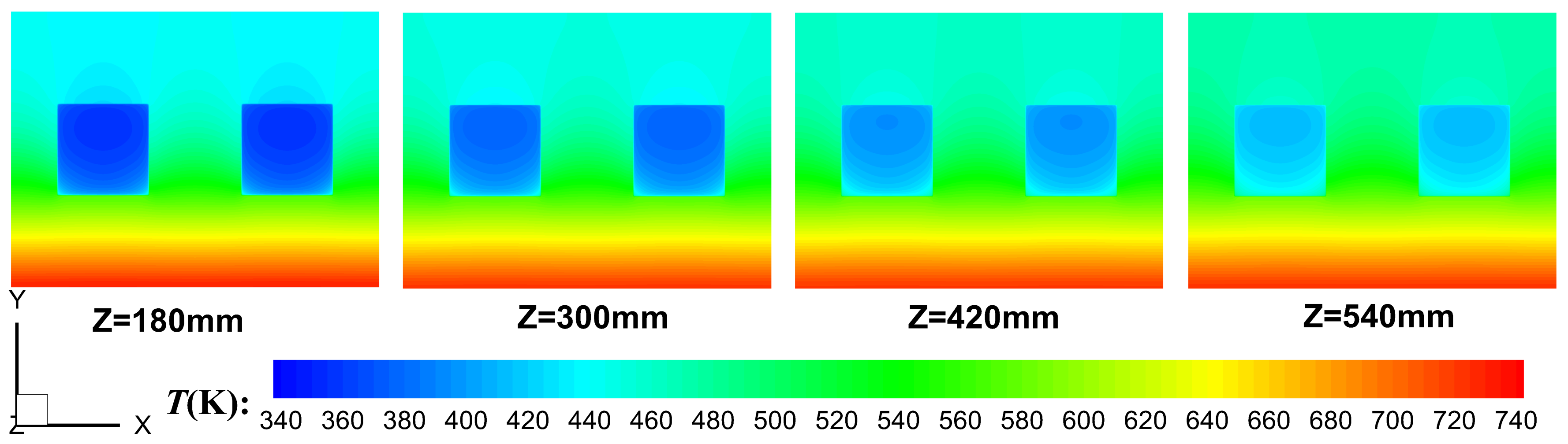
3.1. Primary Characteristics of Regenerative Cooling
3.2. Influencing Factors of Coupled Heat Transfer
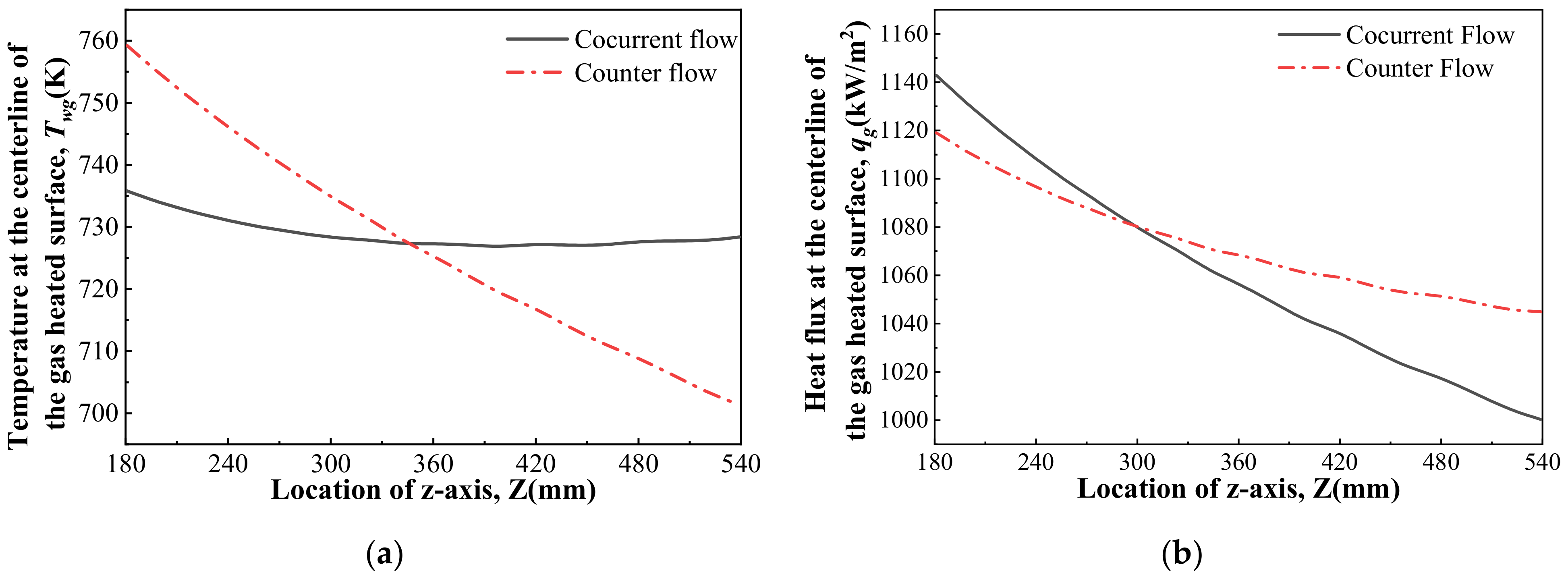
3.2.1. Flowing Direction of Kerosene
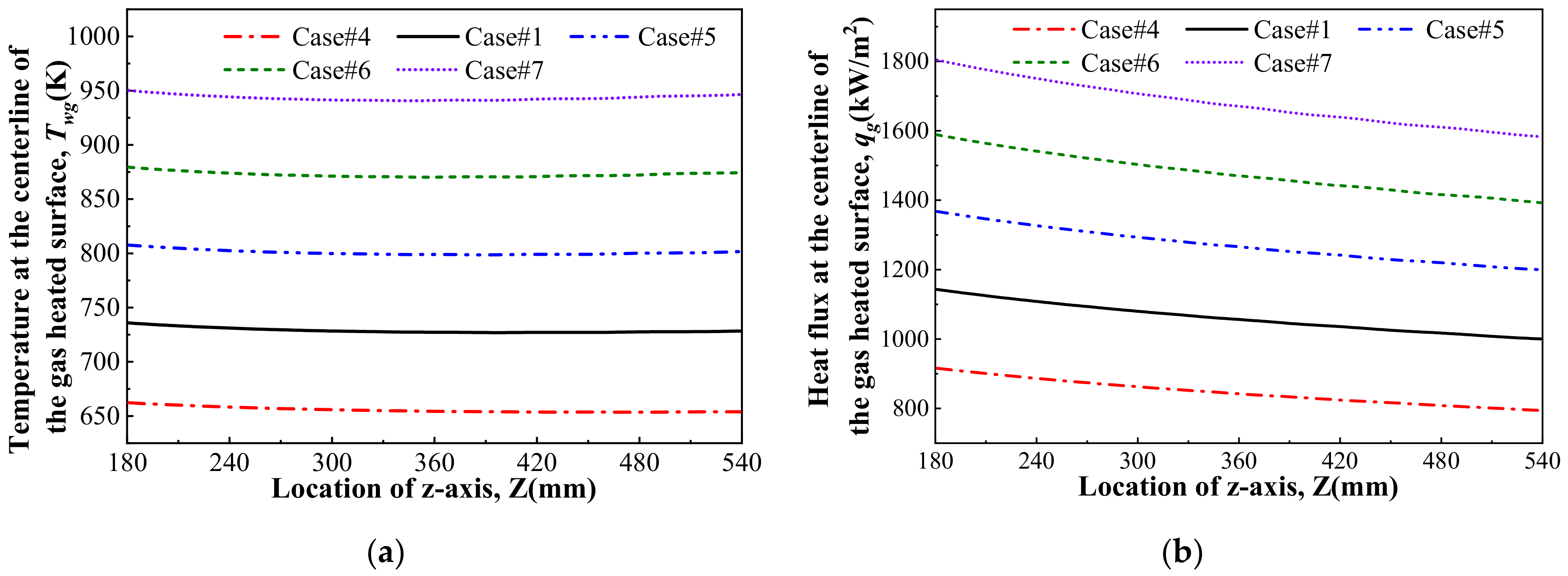
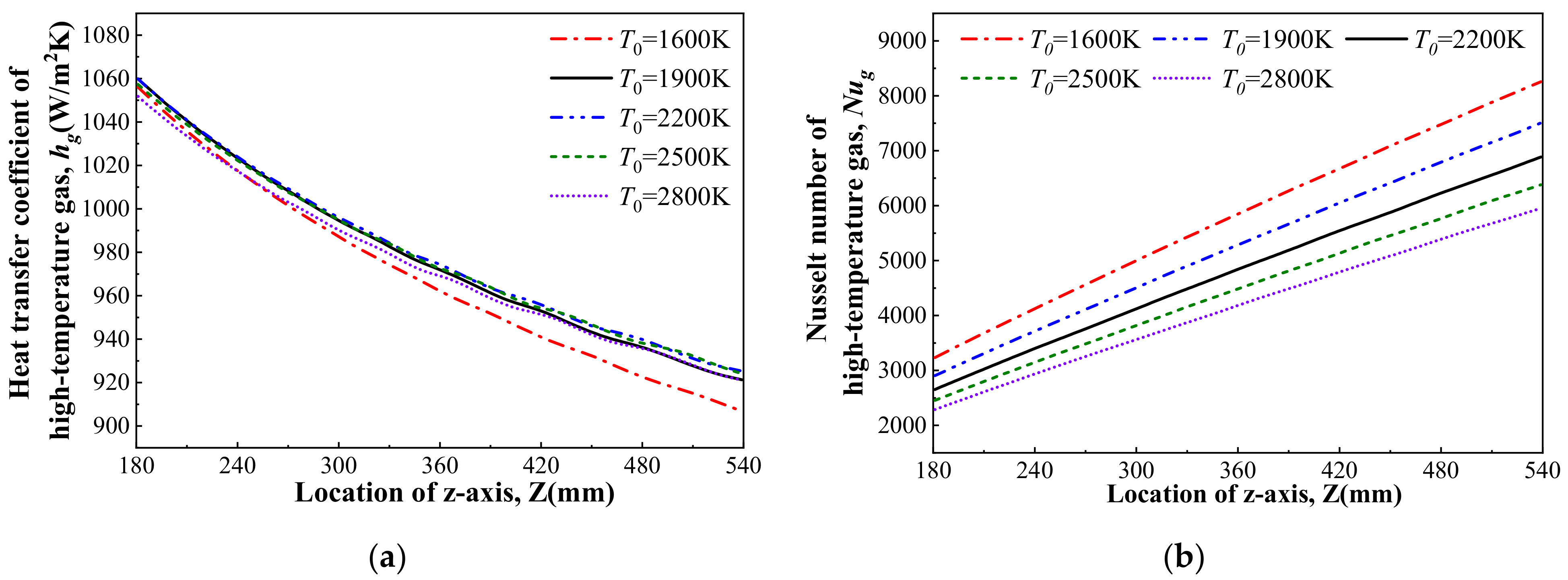
3.2.2. Flowing Parameters of High-Temperature Gas
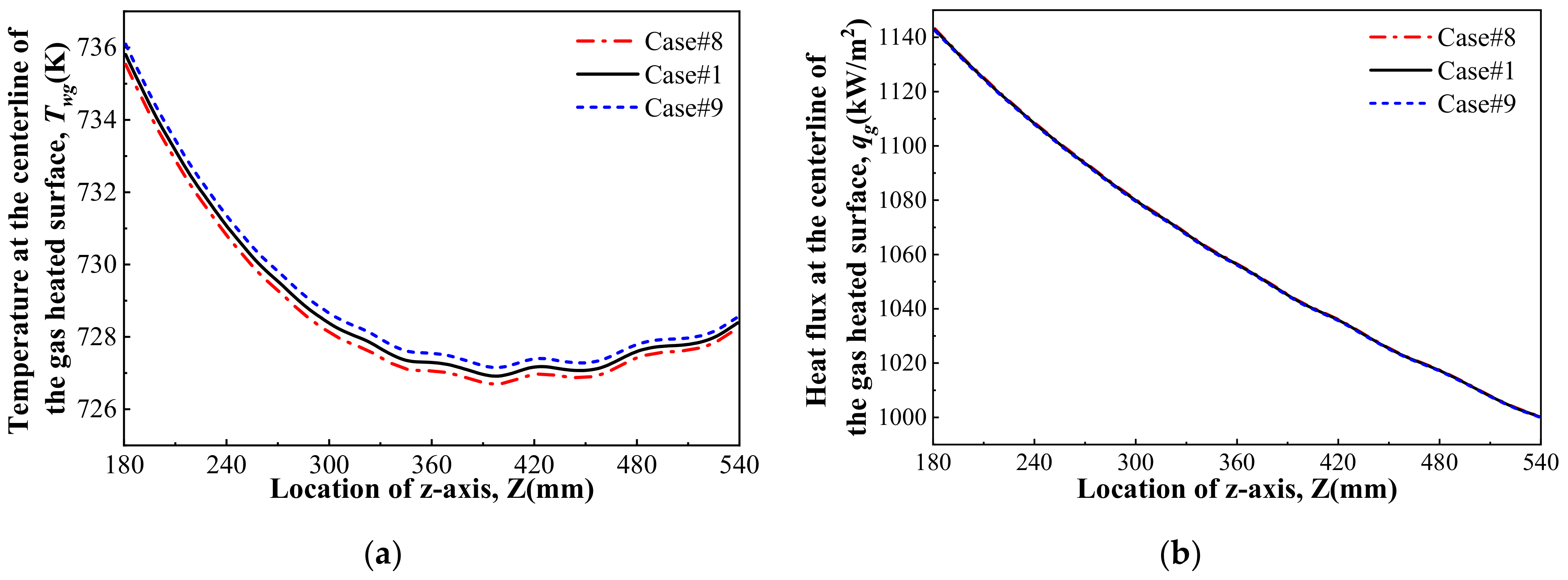
3.2.3. Flowing Parameters of Kerosene
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| cp | Isobaric specific heat capacity (J·kg−1·K−1) |
| E | Total energy of fluid (J) |
| h | Heat transfer coefficient (W·K−1·m−2) |
| k | Turbulent kinetic energy (m2·s−2) |
| m | Mass flow rate (kg·s−1) |
| Ma | Mach number |
| N | Number of elements |
| Nu | Nusselt number |
| P | Pressure (Pa) |
| Pr | Prandtl number |
| q | Heat flux (W·m−2) |
| Re | Reynolds number |
| T | Temperature (K) |
| ui, (i, j, k) | Velocities in x, y, z directions (m·s−1) |
| , (i, j, k) | Deviation of ui from its average amplitude (m·s−1) |
| xi, (i, j, k) | Cartesian coordinate |
| x, y, z | axis |
| δ | Thickness (m) |
| δij | Kronecker delta |
| λ | Thermal conductivity (W·K−1·m−1) |
| μ | Dynamic viscosity (kg·m−1·s−1) |
| ρ | Density (kg·m−3) |
| τ | Time (s) |
| ω | Specific dissipation rate (s−1) |
| Subscripts | |
| a | adiabatic |
| b | bulk |
| c | coolant |
| eq | equivalent |
| g | gas |
| in | inlet |
| p | panel |
| s | static |
| t | turbulent |
| tot | total |
| w | wall |
References
- Bertin, J.J.; Cummings, R.M. Fifty years of hypersonics: Where we’ve been, where we’re going. Prog. Aerosp. Sci. 2003, 39, 511–536. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.L.; Li, X.; Zuo, J.Y.; Qin, J.; Cheng, K.L.; Feng, Y.; Bao, W. Research progress on active thermal protection for hypersonic vehicles. Prog. Aerosp. Sci. 2020, 119, 100646. [Google Scholar] [CrossRef]
- Zhu, Y.H.; Wei, P.; Xu, R.N.; Jiang, P.X. Review on active thermal protection and its heat transfer for airbreathing hypersonic vehicles. Chin. J. Aeronaut. 2018, 31, 1929–1953. [Google Scholar] [CrossRef]
- Zhang, S.L.; Qin, J.; Zhou, W.X.; Bao, W. Review on regenerative cooling for hypersonic propulsion. J. Propuls. Technol. 2018, 39, 23–36. (In Chinese) [Google Scholar]
- Kilkovský, B. Review of design and modeling of regenerative heat exchangers. Energies 2020, 13, 759. [Google Scholar] [CrossRef] [Green Version]
- Gou, J.J.; Chang, Y.; Yan, Z.W.; Chen, B.; Gong, C.L. The design of thermal management system for hypersonic launch vehicles based on active cooling networks. Appl. Therm. Eng. 2019, 159, 113938. [Google Scholar] [CrossRef]
- Kennedy, P.J.; Donbar, J.M.; Trelewicz, J.R.; Gouldstone, C.; Longtin, J.P. Heat flux measurements in a scramjet combustor using direct write technology. In Proceedings of the 17th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, San Francisco, CA, USA, 11–14 April 2011. [Google Scholar]
- Trelewicz, J.R.; Longtin, J.P.; Gouldstone, C.; Kennedy, P.J.; Donbar, J.M. Heat flux measurements in a scramjet combustor using embedded direct-write sensors. J. Propul. Power. 2015, 31, 1003–1013. [Google Scholar] [CrossRef]
- Li, L.; Fan, X.J.; Wang, J. Measurements of wall heat flux and temperature in a supersonic model combustor. In Proceedings of the 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, San Diego, CA, USA, 31 July–3 August 2011. [Google Scholar]
- Cheng, D.; Wang, J.; Lu, Y.; Li, L.; Yao, W.; Fan, X.J. Wall heat flux measurements for a kerosene-fueled supersonic combustor. J. Aerosp. Eng. 2019, 32, 04019080. [Google Scholar] [CrossRef] [Green Version]
- Cui, M.; Mei, J.; Zhang, B.-W.; Xu, B.-B.; Zhou, L.; Zhang, Y. Inverse identification of boundary conditions in a scramjet combustor with a regenerative cooling system. Appl. Therm. Eng. 2018, 134, 555–563. [Google Scholar] [CrossRef]
- Wang, X.; Zhong, F.Q.; Gu, H.B.; Zhang, X.Y. Numerical study of combustion and convective heat transfer of a Mach 2.5 supersonic combustor. Appl. Therm. Eng. 2015, 89, 883–896. [Google Scholar] [CrossRef] [Green Version]
- Cheng, L.W.; Zhong, F.Q.; Gu, H.B.; Zhang, X.Y. Application of conjugate gradient method for estimation of the wall heat flux of a supersonic combustor. Int. J. Heat Mass Transf. 2016, 96, 249–255. [Google Scholar] [CrossRef]
- Sobel, D.R.; Spadaccini, L.J. Hydrocarbon fuel cooling technologies for advanced propulsion. J. Eng. Gas Turb. Power 1997, 119, 344–351. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Y.; Liang, C.; Zhang, Q.Y.; Li, X.Y. Heat transfer analysis of n-decane with variable heat flux distributions in a mini-channel. Appl. Therm. Eng. 2018, 144, 695–701. [Google Scholar] [CrossRef]
- Lv, L.L.; Wen, J.; Fu, Y.C.; Quan, Y.K.; Zhu, J.Q.; Xu, G.Q. Numerical investigation on convective heat transfer of supercritical aviation kerosene in a horizontal tube under hyper gravity conditions. Aerosp. Sci. Technol. 2020, 105, 105962. [Google Scholar] [CrossRef]
- Wang, Y.H.; Lu, Y.N.; Li, S.F.; Dong, M. Numerical study on non-uniform heat transfer deterioration of supercritical RP-3 aviation kerosene in a horizontal tube. Chin. J. Chem. Eng. 2020, 28, 1542–1557. [Google Scholar] [CrossRef]
- Sun, X.; Meng, H.; Zheng, Y. Asymmetric heating and buoyancy effects on heat transfer of hydrocarbon fuel in a horizontal square channel at supercritical pressures. Aerosp. Sci. Technol. 2019, 93, 105358. [Google Scholar] [CrossRef]
- Sun, X.; Meng, H. Large eddy simulations and analyses of hydrocarbon fuel heat transfer in vertical upward flows at supercritical pressures. Int. J. Heat Mass Transf. 2021, 170, 120988. [Google Scholar] [CrossRef]
- Lei, Z.L.; He, K.; Huang, Q.; Bao, Z.W.; Li, X.Y. Numerical study on supercritical heat transfer of n-decane during pyrolysis in rectangular tubes. Appl. Therm. Eng. 2020, 170, 115002. [Google Scholar] [CrossRef]
- Lei, Z.L.; Liu, B.; Huang, Q.; He, K.; Bao, Z.W.; Zhu, Q.; Li, X.Y. Thermal cracking characteristics of n-decane in the rectangular and circular tubes. Chinese J. Chem. Eng. 2019, 27, 2876–2883. [Google Scholar] [CrossRef]
- Li, Z.Z.; Wang, H.Y.; Jing, K.; Wang, L.M.; Li, Y.; Zhang, X.W.; Liu, G.Z. Kinetics and modeling of supercritical pyrolysis of endothermic hydrocarbon fuels in regenerative cooling channels. Chem. Eng. Sci. 2019, 207, 202–214. [Google Scholar] [CrossRef]
- Li, Z.Z.; Liu, G.Z.; Zhang, R.L. Heat transfer to supercritical hydrocarbon fuel in horizontal tube: Effects of near-wall pyrolysis at high heat flux. Chem. Eng. Sci. 2021, 229, 115994. [Google Scholar] [CrossRef]
- Xu, K.K.; Sun, X.; Meng, H. Conjugate heat transfer, endothermic fuel pyrolysis and surface coking of aviation kerosene in ribbed tube at supercritical pressure. Int. J. Therm. Sci. 2018, 132, 209–218. [Google Scholar] [CrossRef]
- Zhao, W.Z.; Song, Z.C.; Li, H.Z.; Gu, H.F.; Tuo, X.B.; Zheng, Y.L.; Wang, H.J. Research on heat transfer characteristics of kerosene at supercritical pressure in circular tubes. Exp. Therm. Fluid Sci. 2018, 96, 507–515. [Google Scholar] [CrossRef]
- Wang, Y.H.; Li, S.F.; Dong, M. Experimental investigation on heat transfer deterioration and thermoacoustic instability of supercritical-pressure aviation kerosene within a vertical upward circular tube. Appl. Therm. Eng. 2019, 157, 113707. [Google Scholar] [CrossRef]
- Sun, X.; Xu, K.K.; Meng, H.; Zheng, Y. Buoyancy effects on supercritical-pressure conjugate heat transfer of aviation kerosene in horizontal tubes. J. Supercrit. Fluids 2018, 139, 105–113. [Google Scholar] [CrossRef]
- Jiao, S.; Li, S.F.; Pu, H.; Dong, M.; Shang, Y. Investigation of pyrolysis effect on convective heat transfer characteristics of supercritical aviation kerosene. Acta Astronaut. 2020, 171, 55–68. [Google Scholar] [CrossRef]
- Tao, Z.; Cheng, Z.Y.; Zhu, J.Q.; Li, H.W. Effect of turbulence models on predicting convective heat transfer to hydrocarbon fuel at supercritical pressure. Chin. J. Aeronaut. 2016, 29, 1247–1261. [Google Scholar] [CrossRef] [Green Version]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Goyne, C.P.; Hall, C.D.; O’Brien, W.F.; Schetz, J.A. The Hy-V scramjet flight experiment. In Proceedings of the 14th AIAA/AHI Space Planes and Hypersonic Systems and Technologies Conference, Canberra, ACT, Australia, 6–9 November 2006. [Google Scholar]
- Ai, Q.; Xia, X.L.; Sun, F.X. Influences of wall thermal characteristics on thermal environment in supercritical combustors. J. Eng. Thermophys. 2009, 30, 1373–1375. (In Chinese) [Google Scholar]
- Deng, H.W.; Zhu, K.; Xu, G.Q.; Tao, Z.; Zhang, C.B.; Liu, G.Z. Isobaric specific heat capacity measurement for kerosene rp-3 in the near-critical and supercritical regions. J. Chem. Eng. Data 2012, 57, 263–268. [Google Scholar] [CrossRef]
- Deng, H.W.; Zhang, C.B.; Xu, G.Q.; Zhang, B.; Tao, Z.; Zhu, K. Viscosity measurements of endothermic hydrocarbon fuel from (298 to 788) K under supercritical pressure conditions. J. Chem. Eng. Data 2012, 57, 358–365. [Google Scholar] [CrossRef]
- Deng, H.W.; Zhang, C.B.; Xu, G.Q.; Tao, Z.; Zhang, B.; Liu, G.Z. Density measurements of endothermic hydrocarbon fuel at sub- and supercritical conditions. J. Chem. Eng. Data 2012, 56, 2980–2986. [Google Scholar] [CrossRef]
- Zhong, F.Q.; Fan, X.J.; Yu, G.; Li, J.G. Heat transfer of aviation kerosene at supercritical conditions. J. Thermophys. Heat Tr. 2009, 23, 543–550. [Google Scholar] [CrossRef] [Green Version]
- Huber, M.L. NIST Thermophysical Properties of Hydrocarbon Mixtures Database (SUPERTRAPP); Version 3.2, User’ Guide NIST Standard Reference Database; NIST: Gaithersburg, MD, USA, 2007. [Google Scholar]
- Eckert, E.R.G. Survey of Boundary Layer Heat Transfer at High Velocities and High Temperatures; WADC Technical Report, No. 59-624; Wright Air Development Center: Dayton, OH, USA, 1960. [Google Scholar]
- Sieder, E.N.; Tate, C.E. Heat Transfer and Pressure drop of Liquids in Tubes. Ind. Eng. Chem. 1936, 28, 1429–1435. [Google Scholar] [CrossRef]







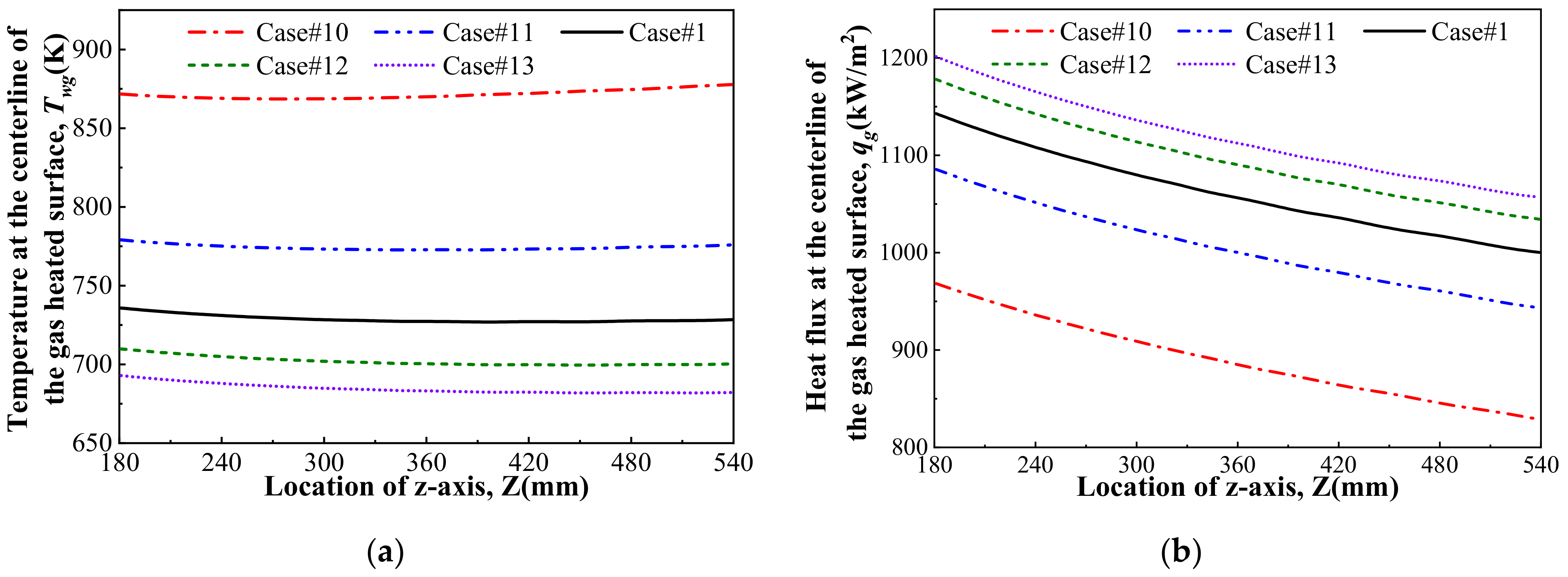
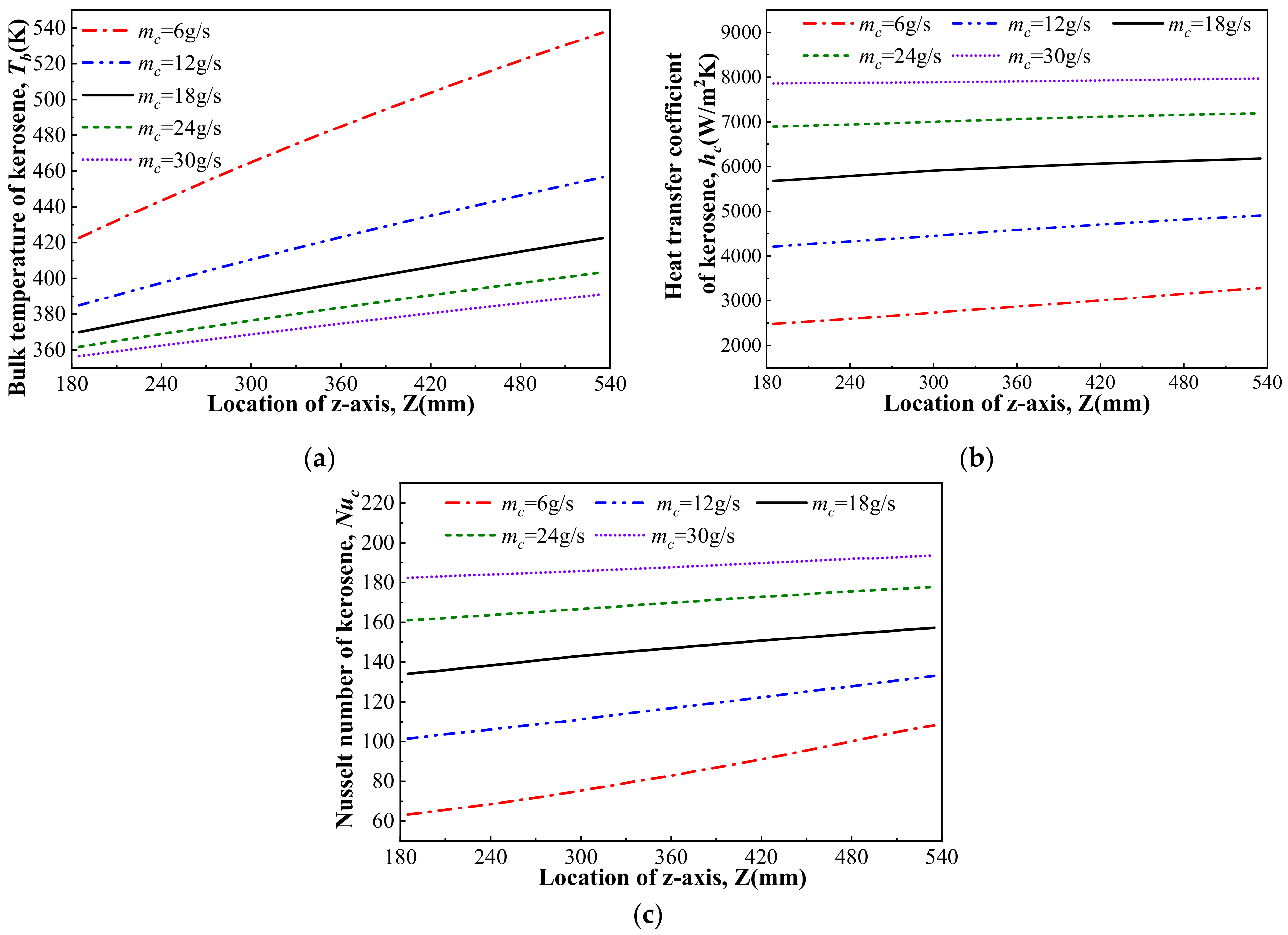
| Case ID | Tin/K | Pc/MPa | mc/(kg/s) | Rec,in | mg/ (kg/s) | T0/K | Pg,s/kPa | Ma |
|---|---|---|---|---|---|---|---|---|
| Case#1 | 333 | 4 | 0.018 | 7200 | 1.2 | 1900 | 75 | 2.76 |
| Case#2 | 333 | 4 | 0.018 | 7200 | 0.8 | 1900 | 50 | 2.76 |
| Case#3 | 333 | 4 | 0.018 | 7200 | 1.6 | 1900 | 100 | 2.76 |
| Case#4 | 333 | 4 | 0.018 | 7200 | 1.2 | 1600 | 75 | 2.60 |
| Case#5 | 333 | 4 | 0.018 | 7200 | 1.2 | 2200 | 75 | 2.91 |
| Case#6 | 333 | 4 | 0.018 | 7200 | 1.2 | 2500 | 75 | 3.03 |
| Case#7 | 333 | 4 | 0.018 | 7200 | 1.2 | 2800 | 75 | 3.15 |
| Case#8 | 333 | 3 | 0.018 | 7200 | 1.2 | 1900 | 75 | 2.76 |
| Case#9 | 333 | 5 | 0.018 | 7200 | 1.2 | 1900 | 75 | 2.76 |
| Case#11 | 333 | 4 | 0.006 | 2400 | 1.2 | 1900 | 75 | 2.76 |
| Case#11 | 333 | 4 | 0.012 | 4800 | 1.2 | 1900 | 75 | 2.76 |
| Case#12 | 333 | 4 | 0.024 | 9600 | 1.2 | 1900 | 75 | 2.76 |
| Case#13 | 333 | 4 | 0.030 | 12000 | 1.2 | 1900 | 75 | 2.76 |
| Mesh ID | Nc | Np | Ng | Ntot |
|---|---|---|---|---|
| Mesh#1 | 324,000 | 180,000 | 576,000 | 1,080,000 |
| Mesh#2 | 576,000 | 405,000 | 1,080,000 | 2,061,000 |
| Mesh#3 | 1,400,000 | 630,000 | 1,680,000 | 3,710,000 |
| Mesh#4 | 2,016,000 | 1,120,000 | 3,584,000 | 6,720,000 |
| Mesh#5 | 3,584,000 | 1,120,000 | 4,032,000 | 8,736,000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Wang, N.; Zhou, J.; Pan, Y. A Parametrical Study on Convective Heat Transfer between High-Temperature Gas and Regenerative Cooling Panel. Energies 2021, 14, 1784. https://doi.org/10.3390/en14061784
Hu J, Wang N, Zhou J, Pan Y. A Parametrical Study on Convective Heat Transfer between High-Temperature Gas and Regenerative Cooling Panel. Energies. 2021; 14(6):1784. https://doi.org/10.3390/en14061784
Chicago/Turabian StyleHu, Jiangyu, Ning Wang, Jin Zhou, and Yu Pan. 2021. "A Parametrical Study on Convective Heat Transfer between High-Temperature Gas and Regenerative Cooling Panel" Energies 14, no. 6: 1784. https://doi.org/10.3390/en14061784
APA StyleHu, J., Wang, N., Zhou, J., & Pan, Y. (2021). A Parametrical Study on Convective Heat Transfer between High-Temperature Gas and Regenerative Cooling Panel. Energies, 14(6), 1784. https://doi.org/10.3390/en14061784





