Impacts of Mooring-Lines Hysteresis on Dynamic Response of Spar Floating Wind Turbine
Abstract
:1. Introduction
2. Governing Equations and Numerical Approach
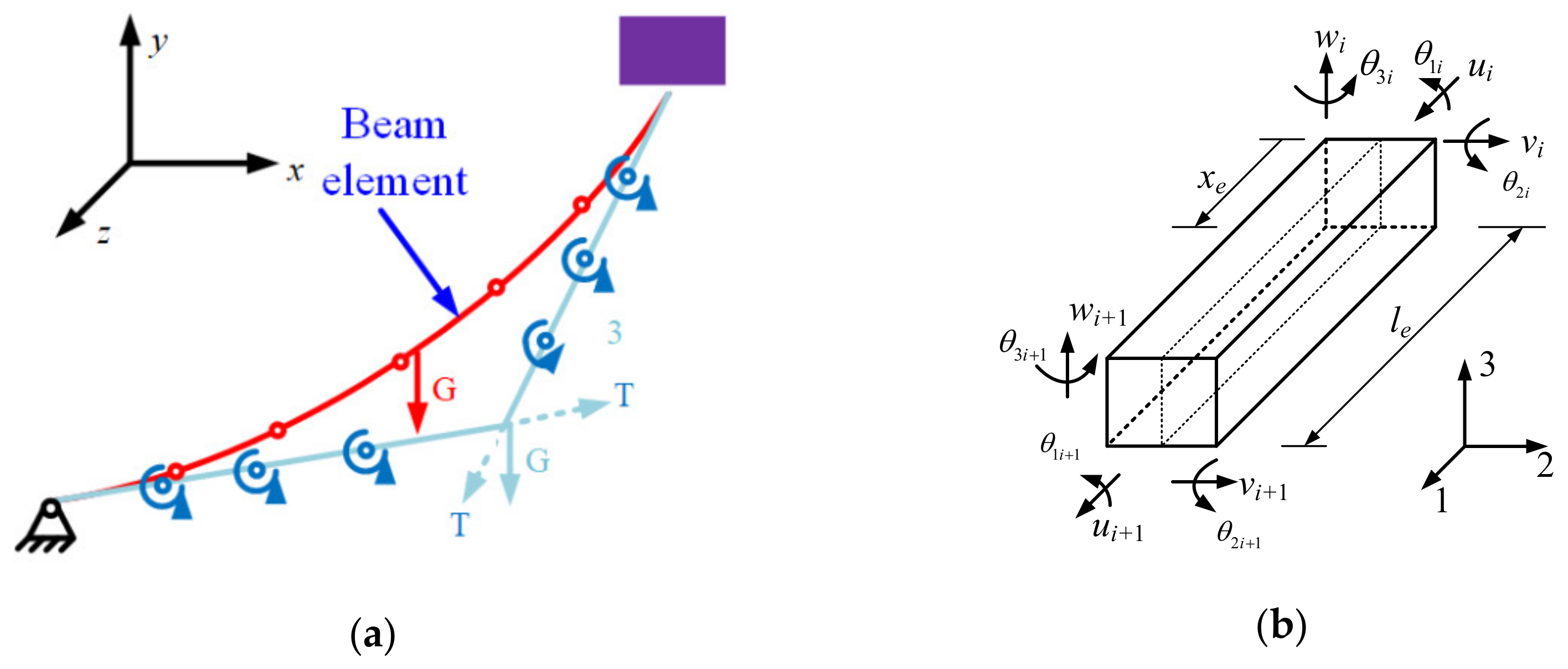
2.1. Governing Equations
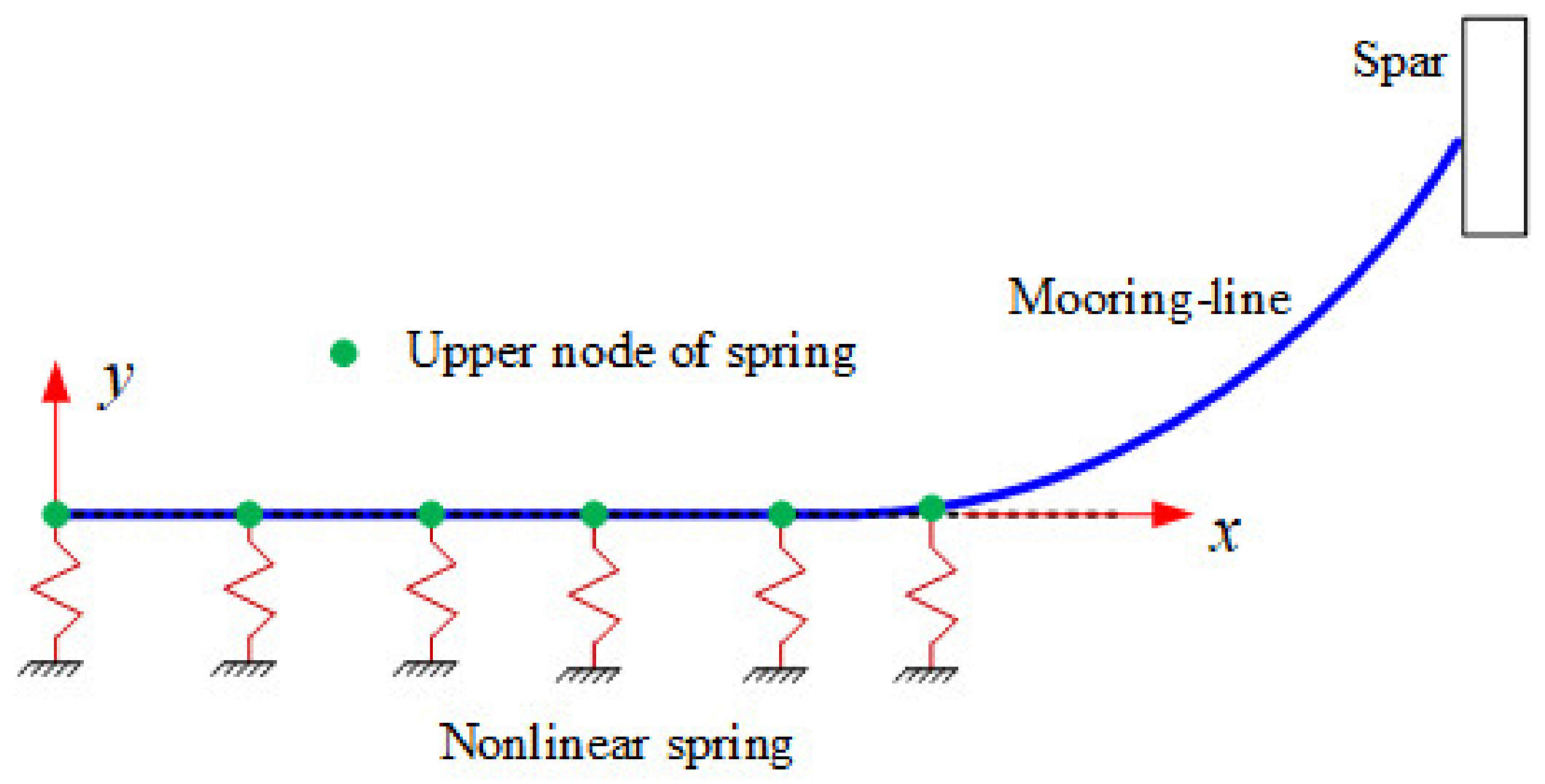
2.2. Non-Linear Mooring-Lines Model
2.3. Iteration Scheme during Dynamic Response
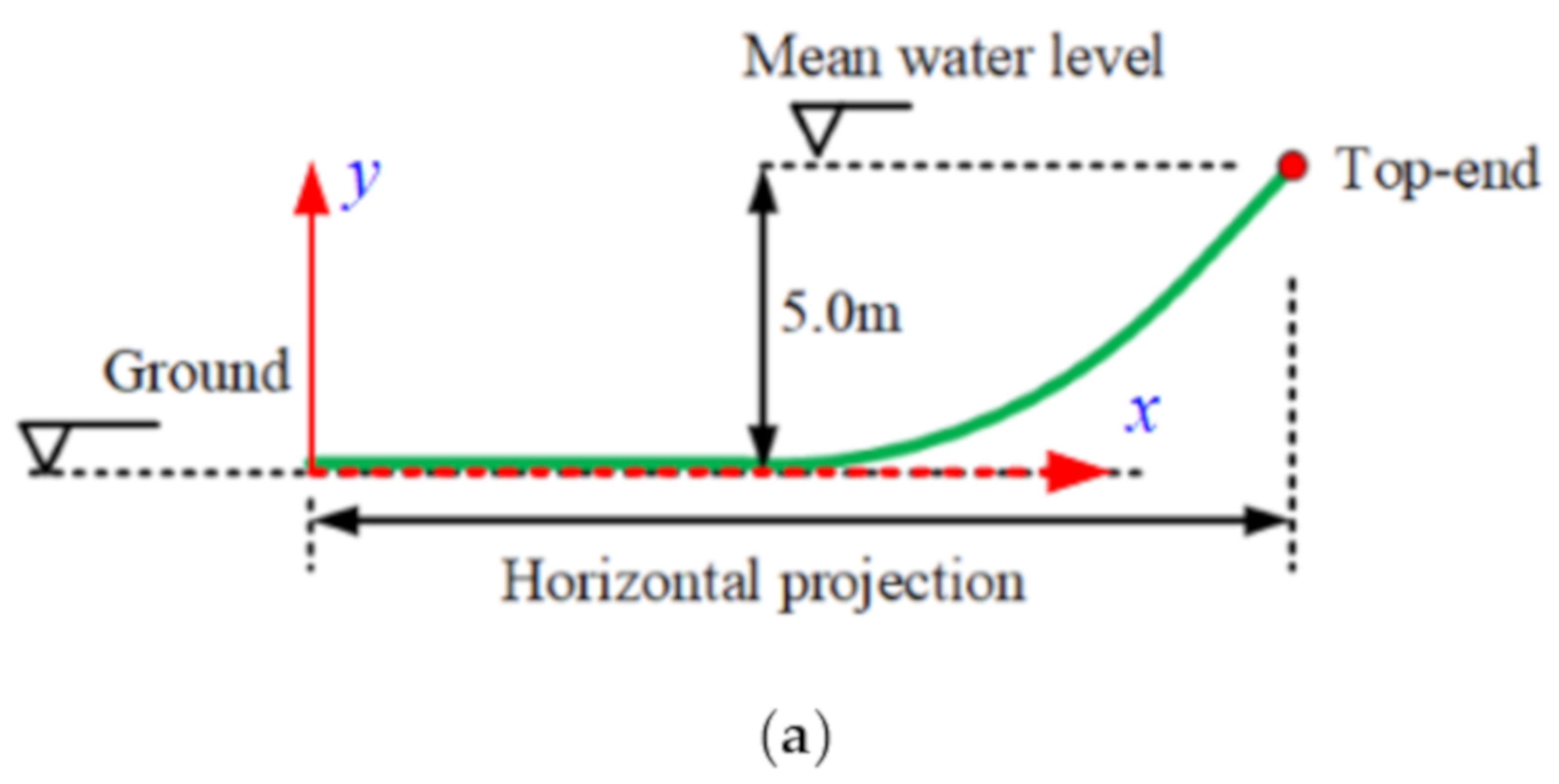
3. Model Verifications
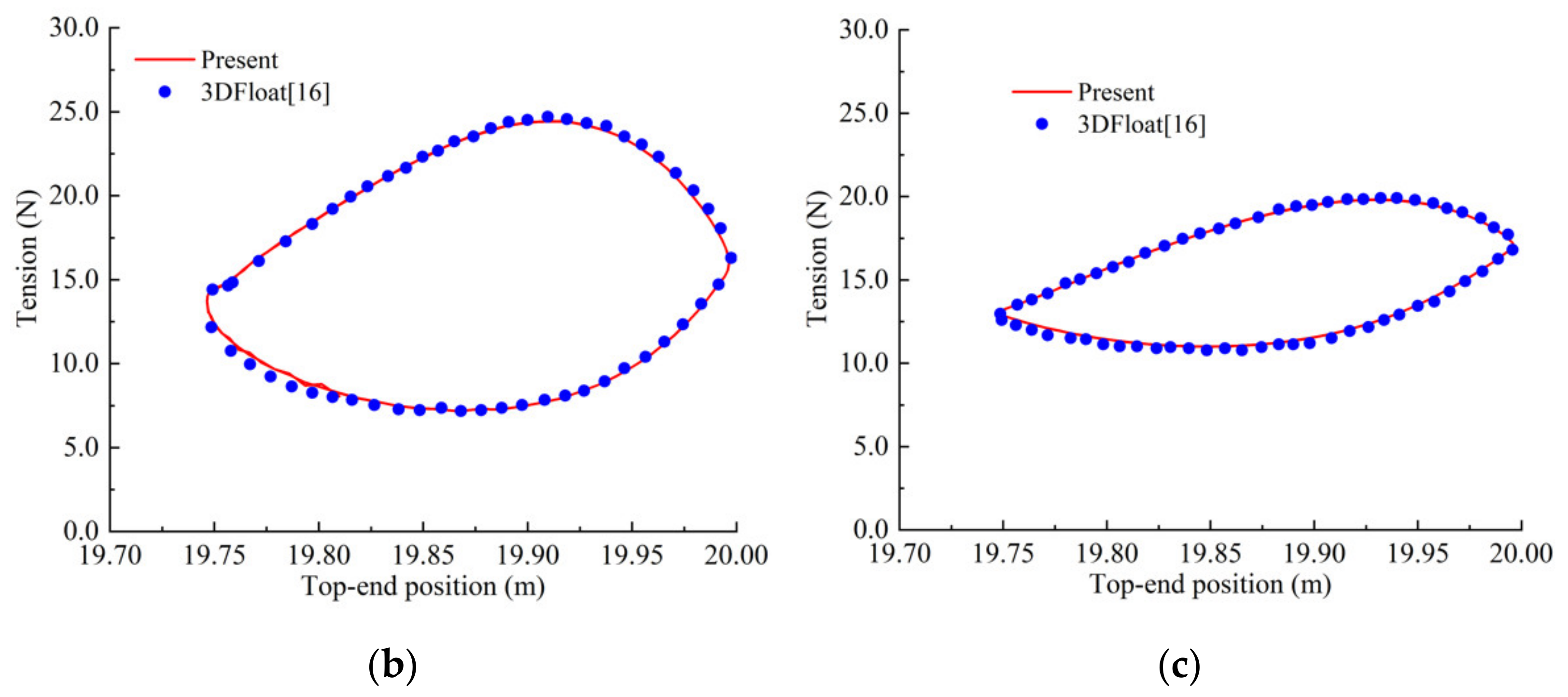
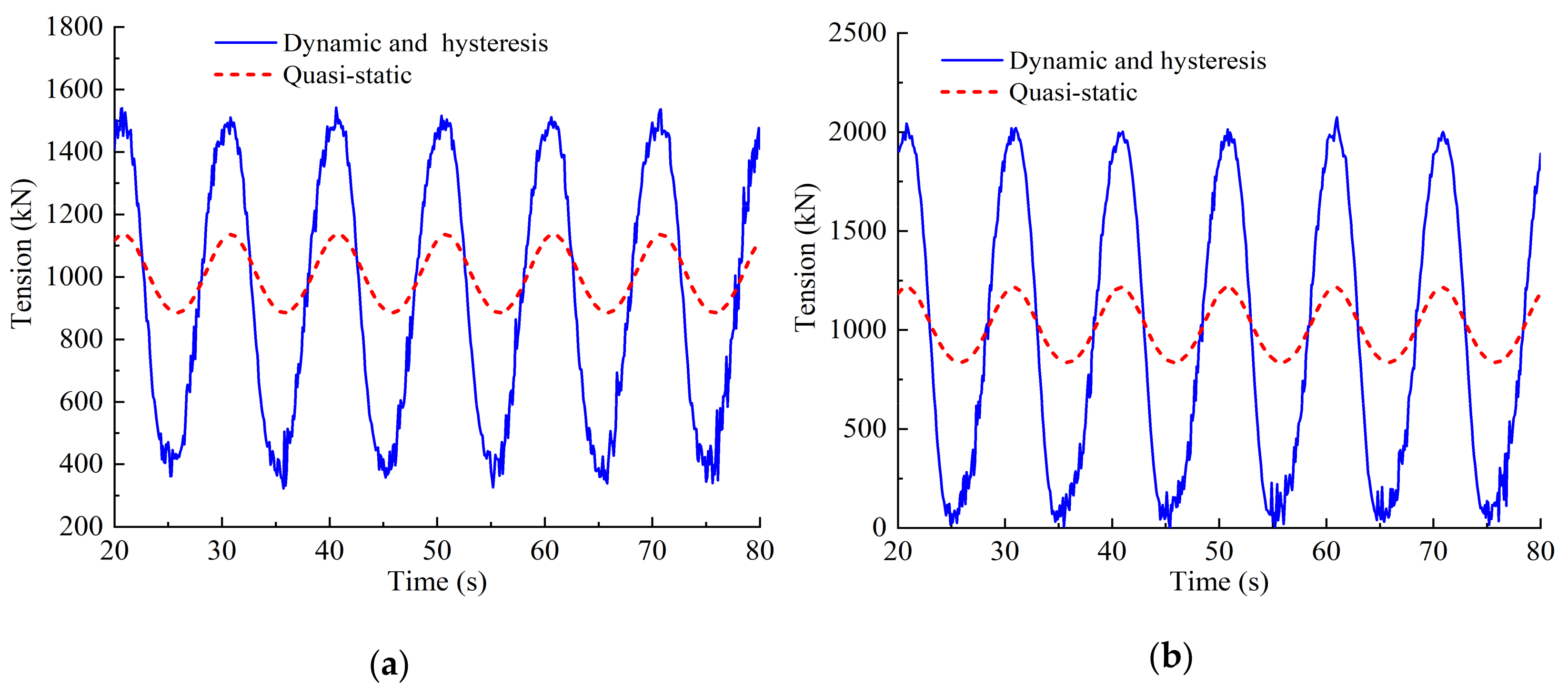
3.1. Comparisons of Top Tension
3.2. Verifications of the Coupled FEM Model
4. Structural Response and Result Discussions
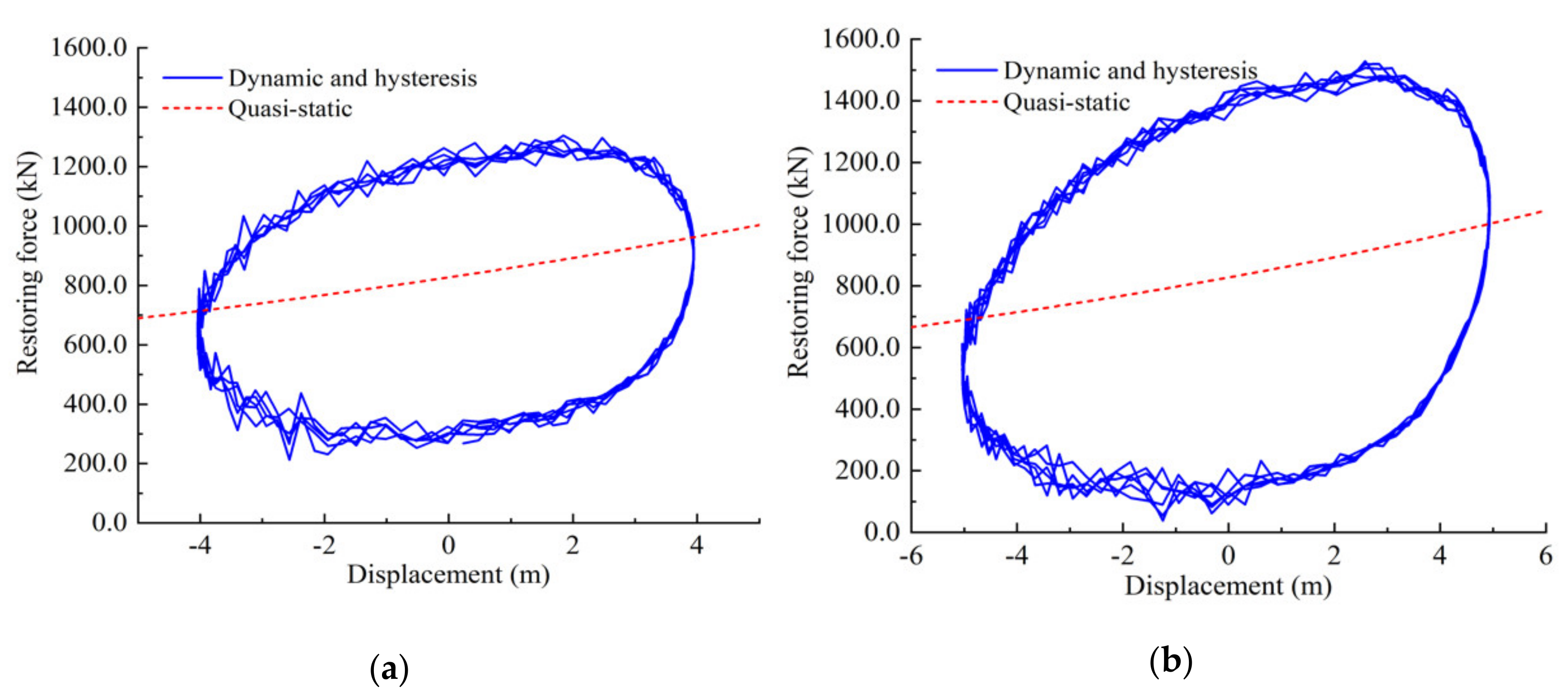
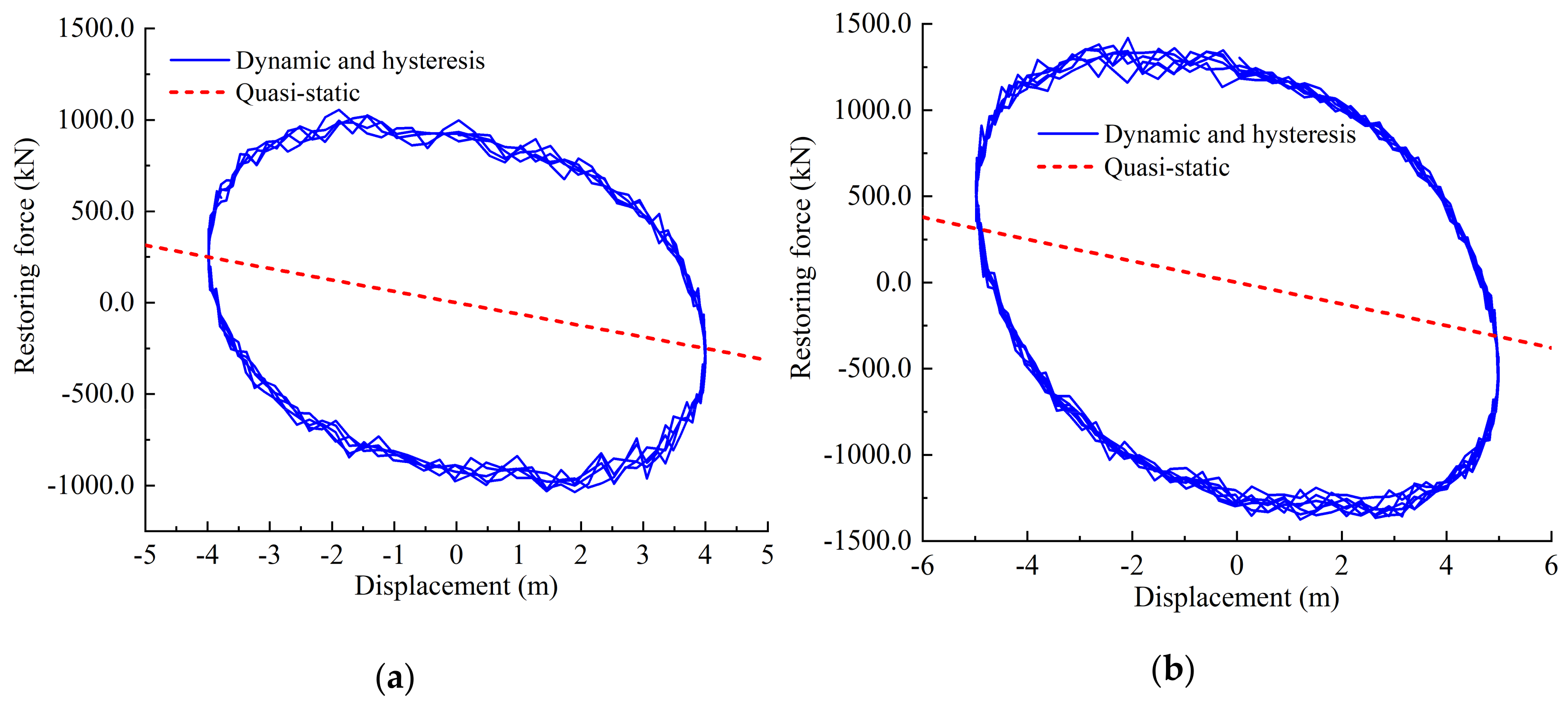
4.1. Hysteresis Behavior of Dynamic Mooring-Lines
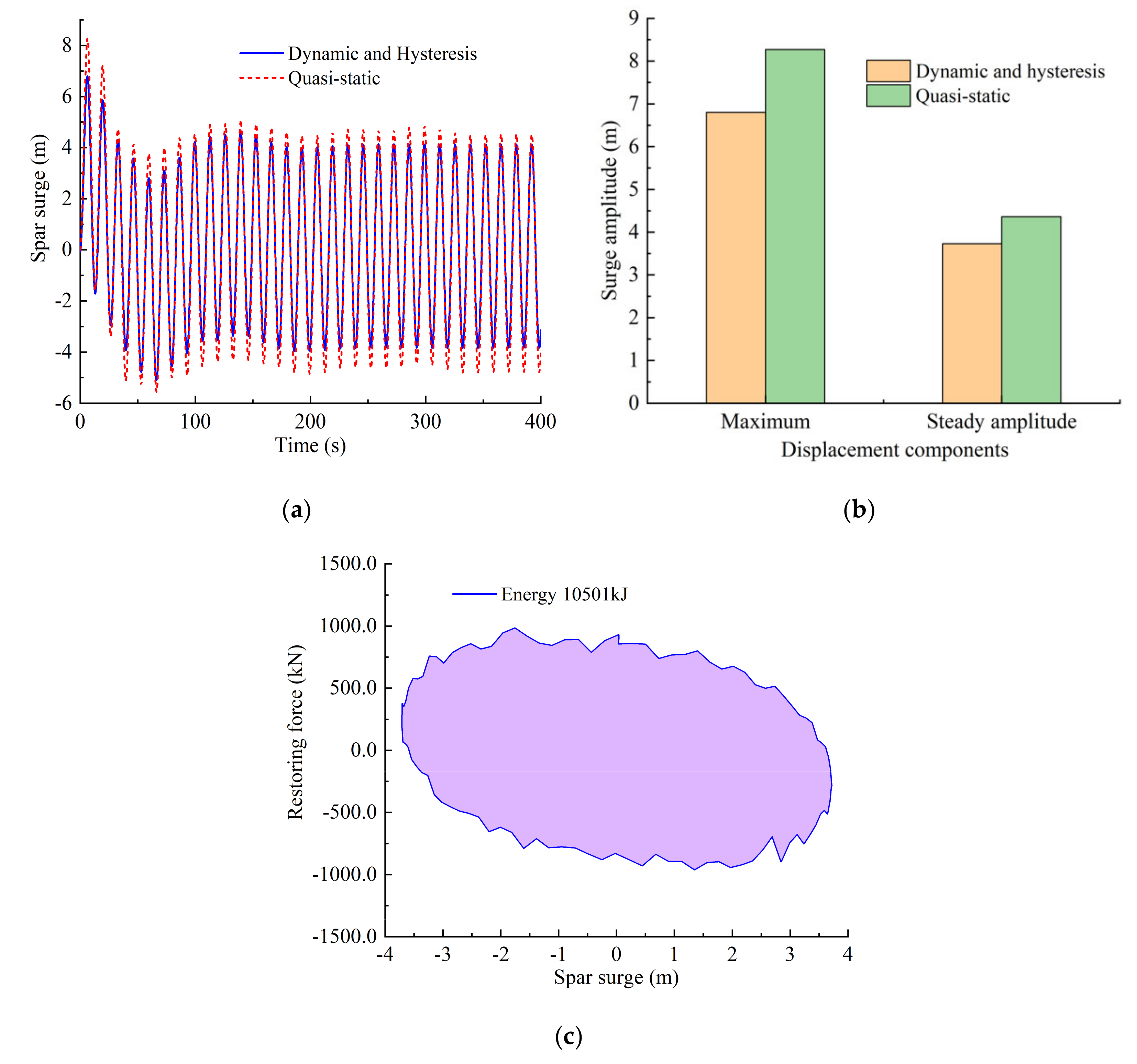
4.2. Impact of Restoring Hysteresis on Wind Turbine Response
5. Conclusions
- (1)
- The tensions with dynamic and hysteresis under consideration get larger with the increase of the spar surge amplitude, and the maximum tension and tension amplitude are, respectively, 1.6 and 5.3 times larger than the quasi-static one.
- (2)
- The restoring stiffness of the mooring-lines exhibits hysteresis behavior, and the restoring force is directionally dependent.
- (3)
- Due to the hysteresis behavior of the restoring performance, under extreme wave load conditions, the spar surge gets about 14.4% smaller compared with the quasi-static cases.
Author Contributions
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Global Wind Report. Global Wind Energy Council. 2020. Available online: https://wfo-global.org/wp-content/uploads/2020/08/WFO_Global-Offshore-Wind-Report-HY1-2020.pdf (accessed on 1 December 2020).
- Han, Y.; Le, C.; Ding, H.; Cheng, Z.; Zhang, P. Stability and dynamic response analysis of a submerged tension leg platform for offshore wind turbines. Ocean Eng. 2017, 129, 68–82. [Google Scholar] [CrossRef]
- Zhang, H.; Liang, F.; Zheng, H. Dynamic impedance of monopiles for offshore wind turbines considering scour-hole dimensions. Appl. Ocean Res. 2021, 107, 102493. [Google Scholar] [CrossRef]
- Cao, G.; Chen, Z.; Wang, C.; Ding, X. Dynamic responses of offshore wind turbine considering soil nonlinearity and wind-wave load combinations. Ocean Eng. 2020, 217, 108155. [Google Scholar] [CrossRef]
- Chen, D.; Gao, P.; Huang, S.; Li, C.; Yu, X. Static and dynamic loading behavior of a hybrid foundation for offshore wind turbines. Mar. Struct. 2020, 71, 102727. [Google Scholar] [CrossRef]
- Kim, H.G.; Kim, B.J. Design Optimization of Conical Concrete Support Structure for Offshore Wind Turbine. Energies 2020, 13, 4876. [Google Scholar] [CrossRef]
- Zhang, R.; Tang, Y.; Hu, J.; Ruan, S.; Chen, C. Dynamic response in frequency and time domains of a floating foundation for offshore wind turbines. Ocean Eng. 2013, 60, 115–123. [Google Scholar] [CrossRef]
- Jeon, S.H.; Cho, Y.U.; Seo, M.W.; Cho, J.R.; Jeong, W.B. Dynamic response of floating substructure of spar-type offshore wind turbine with catenary mooring cables. Ocean Eng. 2013, 72, 356–364. [Google Scholar] [CrossRef]
- Tanaka, K.; Sato, I.; Utsunomiya, T.; Kakuya, H. Validation of dynamic response of a 2-MW hybrid-spar floating wind turbine during typhoon using full-scale field data. Ocean Eng. 2020, 218, 108262. [Google Scholar] [CrossRef]
- Ishihara, T.; Liu, Y. Dynamic Response Analysis of a Semi-Submersible Floating Wind Turbine in Combined Wave and Current Conditions Using Advanced Hydrodynamic Models. Energies 2020, 13, 5820. [Google Scholar] [CrossRef]
- Ferri, G.; Marino, E.; Borri, C. Optimal Dimensions of a Semisubmersible Floating Platform for a 10 MW Wind Turbine. Energies 2020, 13, 3092. [Google Scholar] [CrossRef]
- Matha, D.; Bischoff, O.; Fechter, U. Non-Linear Multi-Body Mooring System Model for Floating Offshore Wind Turbines. In Proceedings of the EWEA Offshore, Amsterdam, The Netherlands, 29 November–1 December 2011. [Google Scholar]
- Azcona, J.; Palacio, D.; Munduate, X.; González, L.; Nygaard, T.A. Impact of mooring lines dynamics on the fatigue and ultimate loads of three offshore floating wind turbines computed with IEC 61400-3 guideline. Wind Energy 2017, 20, 797–813. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Guo, S.; Chen, W.; Yan, D.; Song, J. Analysis on restoring stiffness and its hysteresis behavior of slender catenary mooring-line. Ocean Eng. 2020, 209, 107521. [Google Scholar] [CrossRef]
- Li, Y.; Guo, S.; Kong, Y.; Li, M.; Chen, W. Non-Linearly Restoring Performance and its Hysteresis Behavior of Dynamic Catenary. In Proceedings of the ASME2019, International Conference on Ocean, Offshore and Arctic Engineering, Scotland, UK, 9–14 June 2019; Volume 58806, p. V05AT04A016. [Google Scholar]
- Azcona, J.; Munduate, X.; González, L.; Nygaard, T.A. Experimental validation of a dynamic mooring lines code with tension and motion measurements of a submerged chain. Ocean Eng. 2017, 129, 415–427. [Google Scholar] [CrossRef] [Green Version]
- Jonkman, J.M. Definition of the Floating System for Phase IV of OC3; National Renewable Energy Laboratory: Golden, CO, USA, 2010. [Google Scholar]
- Jonkman, J.M.; Butterfield, S.; Musial, W. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Laboratory: Golden, CO, USA, 2009. [Google Scholar]
- Karimirad, M. Modeling aspects of a floating wind turbine for coupled wave-wind-induced dynamic analyses. Renew. Energy 2013, 53, 299–305. [Google Scholar] [CrossRef]


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Total length | 21.0 m | Equivalent hydrodynamic diameter | 0.0034 m |
| Initial horizontal projection | 19.872 m | Mass per unit length | 0.069 kg/m |
| Initial vertical projection | 5.0 m | Wet weight per unit length | 0.5872 N/m |
| Axial stiffness | 3.4 × 105 N |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Tower height above water | 87.6 m | Mooring-line length | 904.0 m |
| Material density of tower | 8500.0 kg/m3 | Rotor diameter | 126.0 m |
| Depth to spar base below water | 120.0 m | Blade length | 61.5 m |
| Spar total mass | 7,466,330.0 kg | Hub diameter | 3.0 m |
| Equivalent mooring-line weight in water | 698.1 N/m | Rated wind speed | 11.4 m/s |
| Depth to anchors below water | 320.0 m | Blade mass | 17,740.0 kg |
| Horizontal projection mooring-lines | 853.0 m |
| Wind Turbine Modes | Predicted Value (s) | Ref. [19] (s) | Difference/% |
|---|---|---|---|
| Surge | 129.0 | 125.6 | 2.7 |
| Sway | 129.0 | 125.6 | 2.7 |
| Pitch | 28.0 | 28.5 | 1.79 |
| Roll | 28.0 | 28.5 | 1.79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Guo, S.; Li, Y.; Shen, Y. Impacts of Mooring-Lines Hysteresis on Dynamic Response of Spar Floating Wind Turbine. Energies 2021, 14, 2109. https://doi.org/10.3390/en14082109
Chen W, Guo S, Li Y, Shen Y. Impacts of Mooring-Lines Hysteresis on Dynamic Response of Spar Floating Wind Turbine. Energies. 2021; 14(8):2109. https://doi.org/10.3390/en14082109
Chicago/Turabian StyleChen, Weimin, Shuangxi Guo, Yilun Li, and Yijun Shen. 2021. "Impacts of Mooring-Lines Hysteresis on Dynamic Response of Spar Floating Wind Turbine" Energies 14, no. 8: 2109. https://doi.org/10.3390/en14082109





