Virtual Simulations of a New Construction of the Artificial Shaft Bottom (Shaft Safety Platform) for Use in Mine Shafts

Abstract

The deepening of a mine shaft is a difficult and dangerous operation. Moreover, it requires the continuous operation of the shaft during the process of deepening. Because of this, it is necessary to leave the plug on the shaft bottom or install an artificial shaft bottom. The main task of an artificial shaft bottom is to provide safety from falling objects for the employees working on the shaft bottom. Many solutions for shaft safety platforms have been used in Polish mines over the years. A new construction of the artificial shaft bottom consists of using layers of highly durable net. It allows a reduction in the construction weight as well as the installation time. This article presents a new construction of an artificial shaft bottom and the simulations and calculations that confirm the possibility of its application to mine shafts during their deepening.

1. Introduction

Mine shaft deepening requires continuous operation. This means that it is necessary to separate the mine shaft into two different zones. In one of them, the typical operation of the shaft, e.g., the transport of people or materials, is carried out, and in the other one, shaft deepening is conducted. A separation of these zones is realized by leaving the plug or by the installation of a specially constructed shaft safety platform (or artificial shaft bottom). The artificial shaft bottom’s main task is to provide safety for the employees working underneath the platform by consuming the energy of falling objects. It is important, especially in mine shafts equipped with hoisting systems, because in such cases, the energy to be consumed by the artificial shaft bottom is extremely high. This high energy results from the great weight of potential falling objects, which sometimes weigh more than 20 tonnes, and the distance that they can fall down the shaft, which can be greater than 1000 m [1,2,3,4]. Years of experience in shaft deepening in Poland have brought numerous solutions to shaft safety platforms, which are basically horizontal partitions attached to the shaft lining [5,6].

The construction of the artificial shaft bottom, presented in the patent description PL 140,124 [7], consists of a moveable safety platform connected by friction braking units to vertical friction guides, which are attached to the shaft lining. The top surface of the lattice construction, which is responsible for receiving an impact, has properties of an elastic plane. It is a plate, suspended on steel ropes and connected radially to the top rim of the lattice construction of the platform. An amortization of the impact is insufficient and can lead to significant damages and a significant transfer of energy to the platform, which is caused by friction braking.

Another construction of the artificial shaft bottom was presented in the patent description PL 140,124 [8]. It consists of a lattice platform that is rigidly attached to the shaft lining, covered with an amortizing deck, and consists of a few layers of steel pipes. The pipes in the neighboring layers are arranged perpendicularly. The gaps between the pipes are filled with a bulky material, e.g., sand. An impact causes huge deformations of the pipes, which result in the loss of the cushioning properties of the artificial shaft bottom.

An innovative solution of the artificial shaft bottom was presented in the patent description PL 12309U1 [9]. This construction is equipped with a moveable safety platform of lattice construction, connected with friction braking units to vertical guides, attached to the shaft lining. The key feature of this construction is the cushioning layer placed on the moveable platform. It comprises a few layers of steel pipes. The pipes in the neighboring layers are arranged perpendicularly, and the gaps between the pipes are filled with a bulky material. The combination of the two previously presented solutions allowed an increase in the effectiveness of the impact energy consumption and increased the durability of the construction. The presented construction of the artificial shaft bottom is able to consume 200 MJ of energy.

A cross section of the artificial shaft bottom described above is shown in Figure 1.

The advantage of this construction of the artificial shaft bottom is its relatively low weight and high potential to consume energy. Moreover, a modular construction allows for the assembly of the elements of the platform on the surface, which leads to a reduction in the cost and time of assembly and disassembly of the artificial shaft bottom in the shaft [10].

2. A New Solution for the Artificial Shaft Bottom

The Department of Projects, Innovations, and Development of the Shaft Sinking Company (PBSz SA) designed a new artificial shaft bottom, which is able to absorb 35,300 kJ of energy. This construction was designed to absorb the energy of a fully loaded mine car, weighing 3500 kg and falling from a height of 950 m. A distinctive feature of the new construction of the artificial shaft bottom is the application of materials that had never been used in such constructions, and a modular construction [11].

The artificial shaft bottom is designed as a construction consisting of five layers of highly durable net supported by steel ropes. The steel ropes are attached to the braking elements, which are able to consume 696 kJ (120 kN × 5.8 m) of kinetic energy within 0.3 s. Each layer of the net is attached to the shaft lining with 12 braking elements. The distances between the layers are:

• 1.0 m between the first and second layers;
• 0.5 m between the second and third, third and fourth, and fourth and fifth layers.

The total height of the new construction of the artificial shaft lining, containing the height of the ropes and net, is equal to 11.38 m (full variant) or 18.56 m (half variant). Figure 2 presents a virtual model of the new construction of the artificial shaft bottom.

The main load-bearing elements are attachments anchored to the shaft lining and connected to the braking elements that hold the supporting ropes. The vertical rope is connected to the braking element on the top of the construction. The rope’s bottom end connects the supporting ropes to the braking elements.

Layer no. 1 (Figure 3) consists of:

• double brakes 120 kN Geobrugg, absorbing the energy of the impact from a distance of 5855 mm in a period of time equal to 0.3 s with a roll;
• Geobinex Ø22 ropes of braking force 400.6 kN;
• rope holders;
• Rocco 19/3/300 rings (ring diameter Ø300 mm, wire diameter Ø3 mm, 19 coils, energy class 5000 kJ) suitable for Ø22 mm ropes;
• a braided net, 40 × 40 mm, made of 5-millimeter-thick wires;
• 300-millimeter-thick reinforced and segmented concrete of class 2.5 MPa, placed on the wooden formwork;
• 5 mm steel sheets covering the concrete.

Layer no. 2 (Figure 4) consists of:

• single brakes 120 kN Geobrugg, absorbing the energy of the impact from a distance of 5855 mm in a period of time equal to 0.3 s with a roll;
• Geobinex Ø22 ropes of braking force 400.6 kN;
• rope holders;
• Rocco 19/3/300 rings (ring diameter Ø300 mm, wire diameter Ø3 mm, 19 coils, energy class 5000 kJ) suitable for Ø22 mm ropes;
• a braided net 40 × 40 mm, made of 5-millimeter-thick wires.

Layer no. 3 (Figure 3) consists of:

• single brakes 120 kN Geobrugg, absorbing the energy of the impact from a distance of 5855 mm in a period of time equal to 0.3 s with a roll;
• Geobinex Ø22 ropes of braking force 400.6 kN;
• rope holders;
• Rocco 19/3/300 rings (ring diameter Ø300 mm, wire diameter Ø3 mm, 19 coils, energy class 5000 kJ) suitable for Ø22 mm ropes;
• a braided net 40 × 40 mm, made of 5-millimeter-thick wires;
• 300-millimeter-thick reinforced and segmented concrete of class 2.5 MPa, placed on the wooden formwork.

Layer no. 4 (Figure 4) consists of:

• single brakes 120 kN Geobrugg, absorbing the energy of the impact from a distance of 5855 mm in a period of time equal to 0.3 s with a roll;
• Geobinex Ø22 ropes of braking force 400.6 kN;
• rope holders;
• Rocco 19/3/300 rings (ring diameter Ø300 mm, wire diameter Ø3 mm, 19 coils, energy class 5000 kJ) suitable for Ø22 mm ropes;
• a braided net 40 × 40 mm, made of 5-millimeter-thick wires.

Layer no. 5 (Figure 3) consists of:

• single brakes 120 kN Geobrugg, absorbing the energy of the impact from a distance of 5855 mm in a period of time equal to 0.3 s with a roll;
• Geobinex Ø22 ropes of braking force 400.6 kN;
• rope holders;
• Rocco 19/3/300 rings (ring diameter Ø300 mm, wire diameter Ø3 mm, 19 coils, energy class 5000 kJ) suitable for Ø22 mm ropes;
• a braided net 40 × 40 mm, made of 5-millimeter-thick wires.

The design of the presented solution of the artificial shaft bottom allows for its quick assembly, which is its major advantage. There is no need to assemble the huge steel elements in the shaft, which could cause numerous problems with their transport (because of their weight and size) or with their assembly. The assembly of the anchors is quicker by far. Thus, the time needed to stop the regular shaft’s operation, which is required for the assembly of the artificial shaft bottom, can be significantly reduced. The shorter time of assembly and the lower cost of the materials used make the presented construction of the artificial shaft bottom cheaper and quicker to build than the traditional construction.

The design of the layers allows for the assembly of the artificial shaft bottom to cover the whole area of the cross-section of the shaft (full variant) or half of this area (half variant). The full variant of the artificial shaft bottom is usually used in case of a shaft deepening or other reasons for a vertical shaft partition, such as shortening the hoisting system to the mid-level. The half variant is used when only one of the shaft’s hoisting systems is shortened or, on the other hand, when only one is extended. In such situations, the artificial shaft bottom has to be constructed under the other hoist.

In the full variant, the ropes are assembled symmetrically on the whole shaft’s perimeter. In the half variant, the ropes are assembled in the idle half of the shaft and the central ropes are suspended using hangers. Each layer of the full variant uses 12 supporting ropes, connected to 120 kN brakes, either single or double. The task of the brakes is to suspend the whole construction in the shaft and, in the event of an impact, to consume its energy. The braking units are connected to the attachment that is anchored to the shaft lining. In the full variant, 72 braking units, cooperating with 60 supporting ropes, are used. They are able to absorb 50,400 kJ of energy. The safety factor in this variant is k_c ≈ 1.47.

Each layer of the half variant uses 11 supporting ropes, connected to 120 kN brakes. In total, 66 braking units are used in the half variant, cooperating with 55 supporting ropes. The brakes are able to absorb 46,200 kJ of energy. The safety factor in the half variant is k_p ≈ 1.35.

Before it is used in real-life conditions, the new construction of the artificial shaft bottom needs to be verified via tests and simulations. As it is crucial to provide safety for the people working in the shaft, the construction has to be investigated thoroughly. The following sections present virtual simulations of the artificial shaft bottom’s behavior as well as calculations of the braking elements, which are its vital elements.

3. Calculations

3.1. Dynamic Testing

The crucial part of the design process of the new construction of the artificial shaft bottom was the verification of the assumptions of the energy to be absorbed. It is vital to provide a proper level of safety for the employees working under the construction. Numerous approaches were used for the purpose of such verifications in the past. Nowadays, numerical methods and simulations [12,13] are the most popular approaches. The calculations, conducted for a verification of assumptions made for the new construction of the artificial shaft bottom, are presented below [14,15,16,17].

As it was stated before, the artificial shaft bottom consists of five layers of highly durable net, supported by steel ropes. These ropes are connected to braking elements, which can absorb 696 kJ (120 kN × 5.8 m) of kinetic energy in a period of time equal to 0.3 s. The full variant of the artificial shaft bottom consists of 12 braking elements per layer, while in the half version there are 11 braking elements for each layer.

Moreover, the first and the third layers are covered with a 0.3-meter-thick layer of concrete. The upper concrete layer is covered with a 5-millimeter-thick steel sheet. The task of the artificial shaft bottom is to protect the employees working underneath from an object weighing 3500 kg falling from a height of 950 m. All of the elements described above were modeled using the Working Model software and dynamic simulations were conducted. Because of the 2D environment of the software, the following assumptions were made:

• the weight of the falling object is 1/6 of the initial weight, so it is equal to 583.3 kg;
• the initial velocity of the falling object is 136.5 m/s;
• the ropes are weightless and nonstretchable;
• the layers of concrete and the steel sheets are replaced with rectangles of relevant weight and parameters corresponding to the tensile strength of concrete, and the steel joint is replaced with cylinders;
• after the specified extension of the cylinders, steel sheets and concrete, they are excluded from the simulation, which corresponds to the destruction of the material.

During the simulations, the following parameters are displayed in real-time:

• time;
• the velocity, position, and kinetic energy of the falling object;
• the forces and extension of the brakes.

3.1.1. The Full Variant Simulation

Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 present the stages of the simulation for the full variant.

The simulation revealed that:

• after 0.1092 s, the falling object decelerated from 136.5 to 0 m/s;
• the top layer of the steel sheets was destroyed;
• both of the concrete layers were destroyed;
• the maximal extension of the braking units was 1 m;
• the deformation of the artificial shaft bottom in its lower part was less than 2.0 m.

3.1.2. The Simulation of the Full Variant with Partial Concrete Layers

Figure 13 and Figure 14 present the stages of the simulation conducted for the full variant of the artificial shaft bottom with partial layers of concrete. These layers cover only half of the platform area.

The simulation revealed that:

• after 0.1092 s, the falling object decelerated from 136.5 to 0 m/s;
• the top layer of the steel sheets was destroyed;
• both of the concrete layers were destroyed;
• the maximal extension of the braking units was 1 m;
• the deformation of the artificial shaft bottom in its lower part was less than 2.0 m.

3.1.3. The Half Variant Simulation

Figure 15 and Figure 16 present the stages of the simulation conducted for the half variant.

The simulation revealed that:

• after 0.07721 s, the falling object decelerated from 136.5 to 0 m/s;
• the top layer of the steel sheets was destroyed;
• both of the concrete layers were destroyed;
• the maximal extension of the braking units was 0.3 m;
• the deformation of the artificial shaft bottom in its lower part was less than 1.0 m.

3.1.4. A Summary of the Simulations

A summary and a comparison of the obtained simulations’ results are presented in

Table 1. The results of the simulations carried out for the different artificial shaft bottom constructions.

Full Variant	Full Variant with Partial Concrete Layers	Half Variants
after 0.1092 s, the falling object decelerated from 136.5 to 0 m/s the top layer of steel sheets was destroyed both concrete layers were destroyed maximal extension of braking units was 1 m the deformation of the artificial shaft bottom in its lower part was less than 2.0 m.	after 0.1092 s, the falling object decelerated from 136.5 to 0 m/s the top layer of steel sheets was destroyed both concrete layers were destroyed maximal extension of braking units was 1 m the deformation of the artificial shaft bottom in its lower part was less than 2.0 m.	after 0.07721 s, the falling object decelerated from 136.5 to 0 m/s top layer of steel sheets was destroyed both concrete layers were destroyed maximal extension of braking units was 0.3 m the deformation of the artificial shaft bottom in its lower part was less than 1.0 m.

.

3.2. Static Calculations of the Artificial Shaft Bottom Attachments

Strength calculations of the artificial shaft bottom attachments are presented below. The 120 kN and 240 kN attachments are joined with the 120 kN GEOBRUGG braking units. The 240 kN attachment is used only in the first layer, while the 120 kN attachment is used in the other layers. The 240 kN attachment cooperates with the 240 kN double braking unit and the 120 kN attachment cooperates with the 120 kN single braking unit. In addition to the attachments and braking units, roll holders are used. A task of the roll holders is to level the layers.

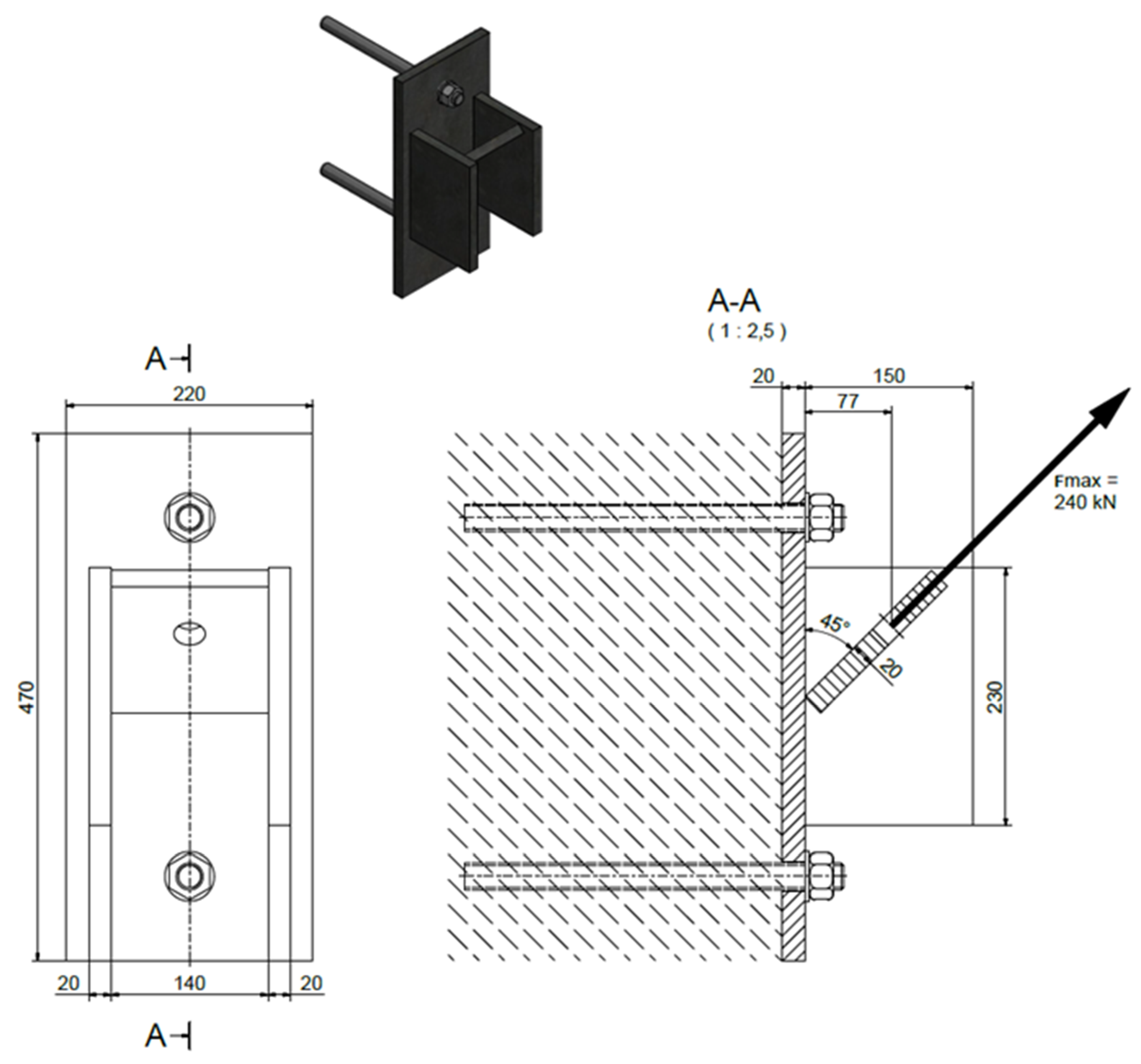
3.2.1. Calculations of the 240 kN Attachment

The attachment, presented in Figure 17, consists of welded steel sheets and anchors. The main anchor is M39 L = 780 kN, and the stabilizing anchor is M24 L = 300 mm. The attachment is made of 235JR steel.

R_m = 340 MPa

W_x = 357.5 cm³

M_g = 124,000 Nm

σ = 67.13 Mpa

n = 3.35 > 2 – OK

The task of the braking unit is to cushion the impact of 240 kN. An impact of a greater value causes the destruction of the braking unit. The required safety factor of the attachment has to be greater than n = 1.0, so its assumed value is n_min = 2.0.

3.2.2. Calculations of the 120 kN attachment

The attachment, presented in Figure 18, consists of welded steel sheets and anchors. The main anchor is M39 L = 780 kN, and the stabilizing anchor is M24 L = 300 mm. The attachment is made of 235JR steel.

Rm = 340 MPa

Wx = 228.33 cm³

Mg = 12,000 Nm

σ = 52.55 Mpa

n = 6.47 > 2 – OK

The task of the braking unit is to cushion the impact of 120 kN. An impact of a greater value causes the destruction of the braking unit. The required safety factor of the attachment has to be greater than n = 1.0, so its assumed value is n_min = 2.0.

3.2.3. Calculations of the Roll Holder

The roll holder, presented in Figure 19, consists of welded steel sheets and anchors M24 L = 300 mm. The attachment is made of 235JR steel. The task of the roll holder and the anchors is to support the construction. They do not take part in the cushioning of the impact.

Rm = 340 MPa

Wx = 240.67 cm³

Mg = 18.480 Nm

σ = 76.76 Mpa

n = 4.43 > 2 – OK

4. Conclusions

The artificial shaft bottom is crucial for providing safety for people working in the shaft during its deepening. An analysis of the existing solutions allowed employees of the Shaft Sinking Company to develop a new idea for the artificial shaft bottom and then to design such a solution. The presented construction can help increase the level of safety and reduce the installation time of the safety platform in the shaft.

The concept of the artificial shaft bottom presented above, based on its construction with highly durable nets, can become a safe and reliable solution and can be used routinely during shaft-deepening operations. The presented solution complies with the requirements of Polish laws.

The new construction of the artificial shaft bottom is characterized by a high durability and an ability to absorb the energy of an object falling from a height of 950 m. The destruction and deformations of the elements are on the acceptable level, and they have a lower value than the artificial shaft bottoms used nowadays.

The demand for artificial shaft bottoms is still high. The solution presented above can lead to a reduction in the costs spent on shaft deepening. The use of anchors instead of huge steel elements makes the assembly of the designed solution much quicker, safer, and cheaper. This construction also requires less space in the shaft than traditional solutions. Thus, it can reduce the time and the cost of the long and expensive process of shaft deepening.

Simulations and calculations carried out by designers led to the determination that this approach also provides a proper level of safety for the people working in the shaft heading. It allows a falling element to be caught with deformations less than 2.0 m. However, it is necessary to test the new construction of the artificial shaft bottom in real-life conditions. This is needed in order to verify the results of the conducted simulations and to confirm the proper level of safety achieved due to the implementation of this innovative solution.