Remaining Useful Life Prediction of MOSFETs via the Takagi–Sugeno Framework
Abstract
:1. Introduction
- Development of a Takagi–Sugeno framework for modeling MOSFET degradation modeling based on run-to-failure historical data. Thus, instead of a large amount of historical data, parameters of the historical models are stored.
- Development of an on-line estimation and inference scheme selecting a historical model that is used for RUL prediction purposes.
- Development of an on-line approach for estimating an analytical exponential model along with RUL prediction.
- Merging together Takagi–Sugeno data-driven and analytical approaches to form an interval of RUL instead of a point prediction.
- Experimental validation of the proposed approach based on the NASA Ames Prognostics Data Repository [23].
2. RUL Prediction of Power MOSFETs
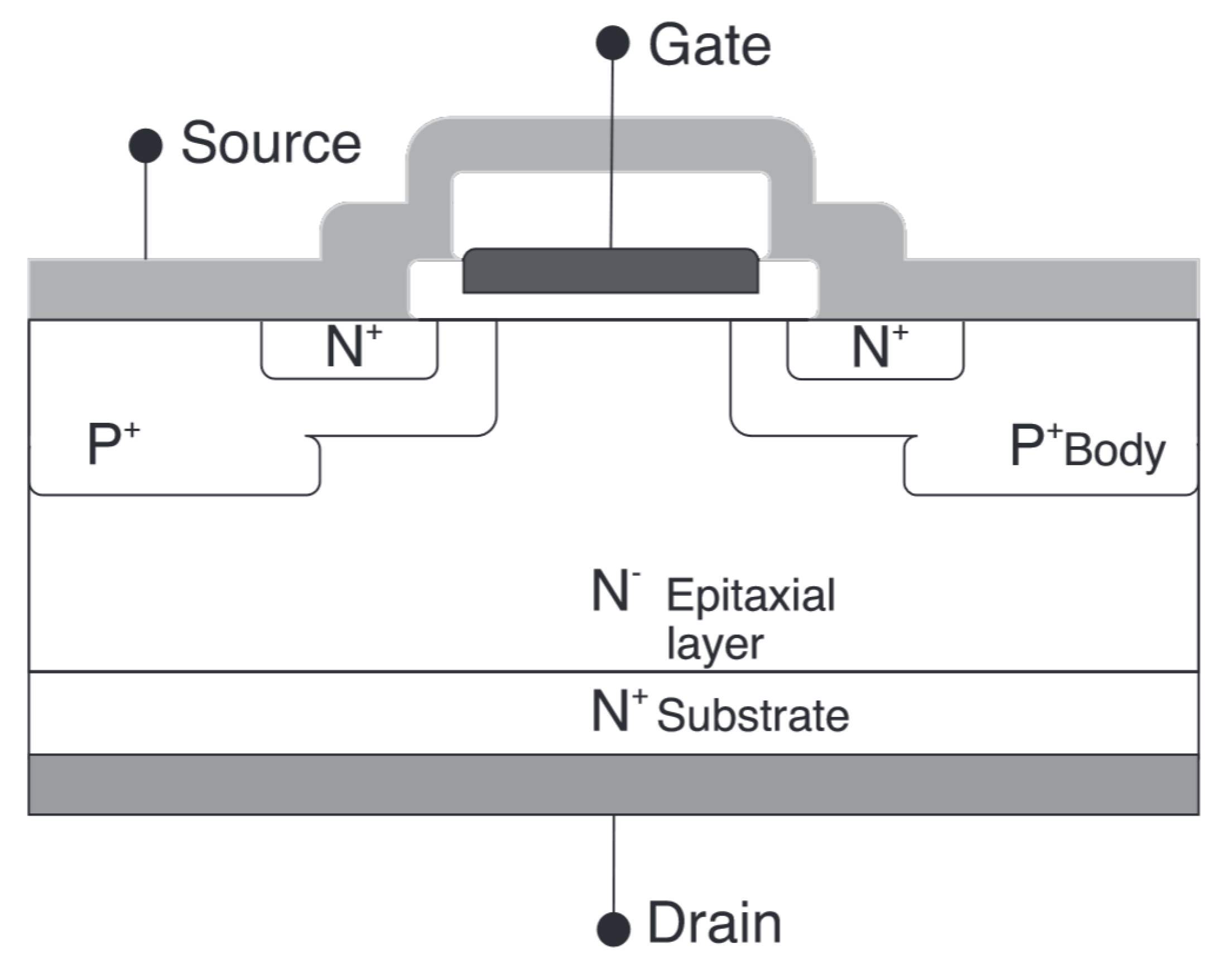
2.1. MOSFETs
- Maximum drain to source voltage: a nominal parameter of MOSFETs; exceeding the limit voltage results in an uncontrolled mode conduction.
- Maximum drain current: in general, a drain current should not reach a border value. However, there are momentary increases in the current, which are called a pulse of drain current.
- Maximum temperature: specifies the maximum temperature of the junction, which does not affects changes of functionality.
- Gate oxide breakdown: a decrease in gate dielectric thickness causes an increased frequency of switching. A significant reduction of lifetime is noticeable when the nominal gate voltage is exceeded, which possibly results in a failure.
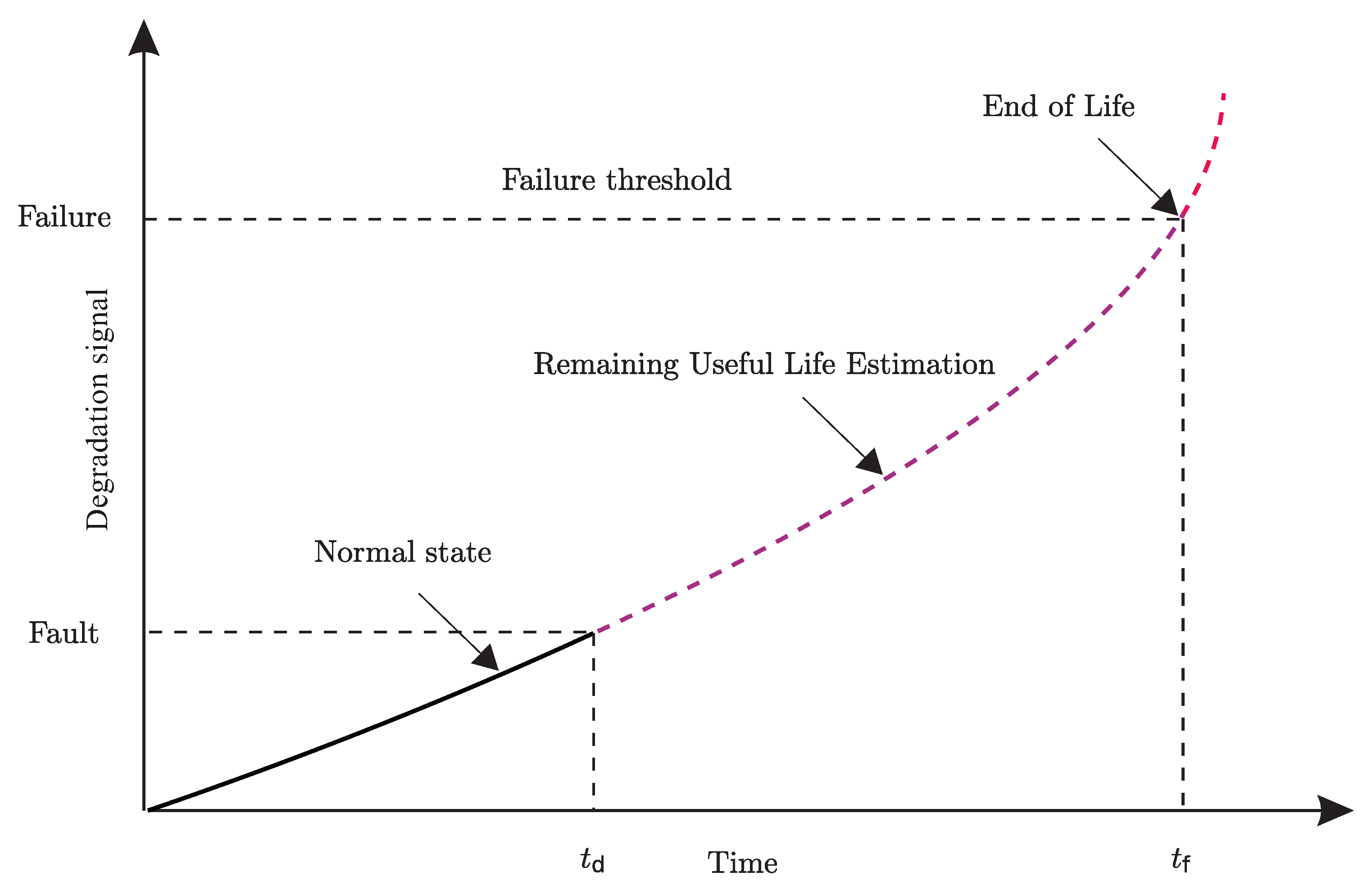
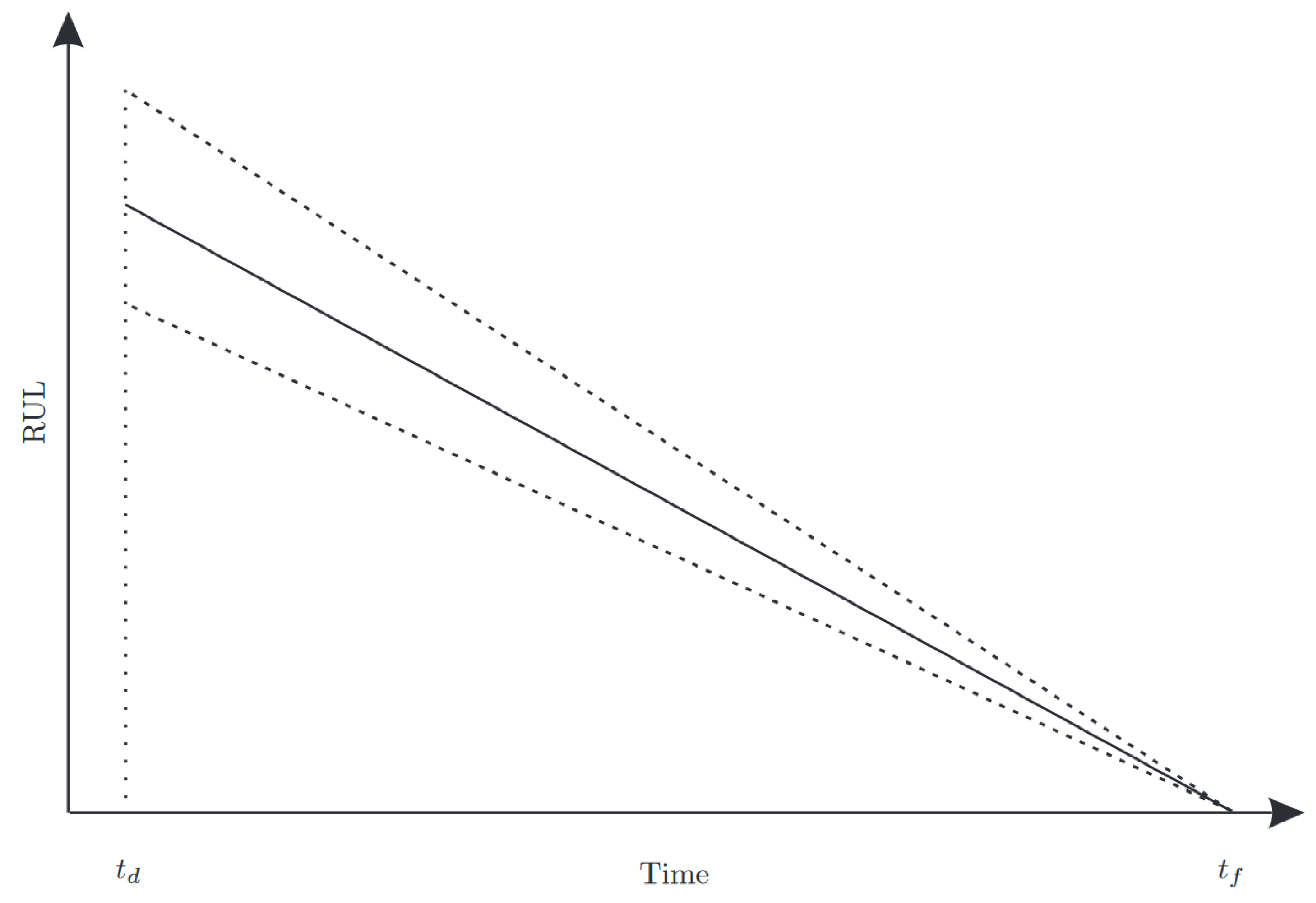
2.2. RUL Prediction Concept
2.3. Methods of Modeling MOSFET Degradation Process
3. Multiple Model-Based T-S Framework MOSFET Degradation Modeling
- Q1:
- How to provide on-line updating rules for (3) with the possibly less restrictive assumptions on the uncertainty terms? They should be assumed bounded but it is unrealistic to assume that they obey any particular distribution.
- Q2:
- How to introduce (3) within the RUL prediction scheme for a currently performing MOSFET?
- Q3:
- How to use historical data to support fault diagnostics and assessment of the state of the currently operating MOSFET?
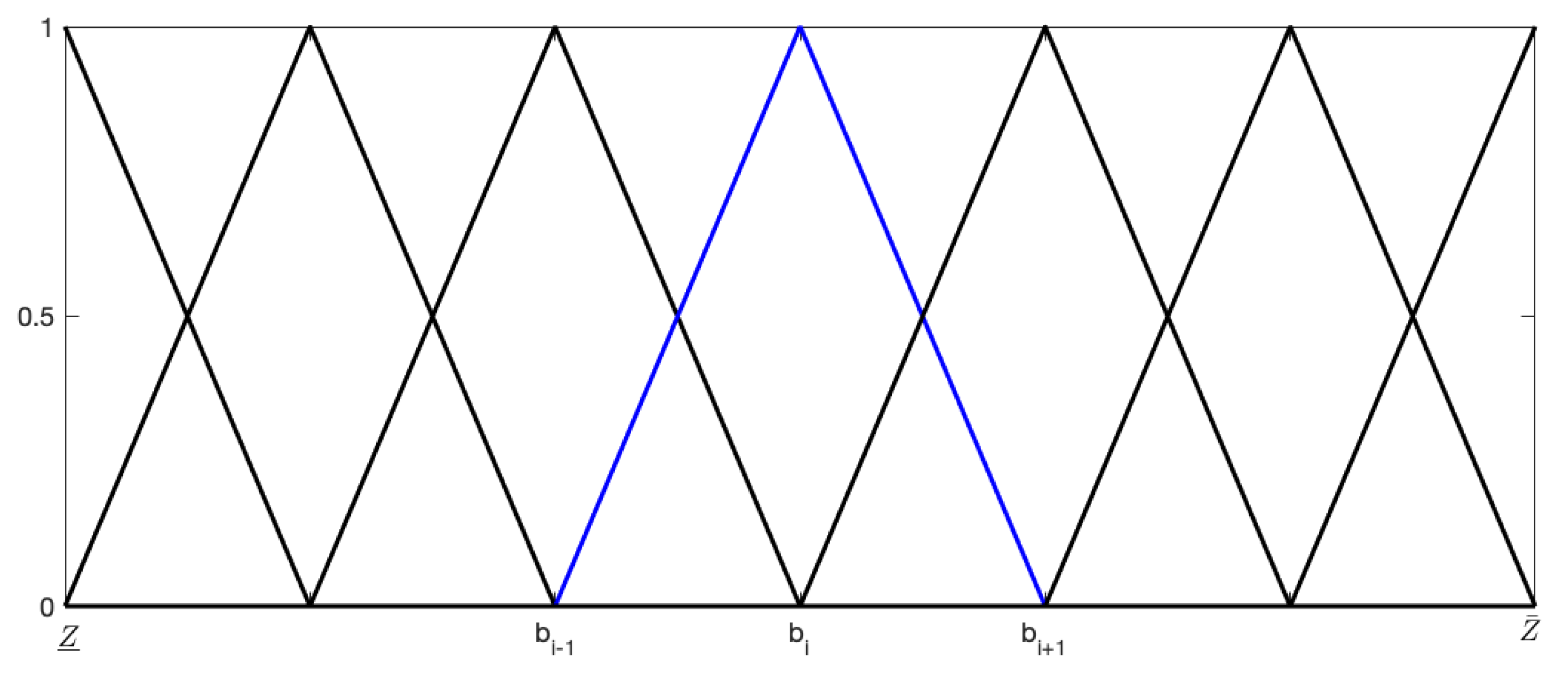
3.1. T-S-Based Historical Data Approach
- Step 0:
- Assume the initial parameters: , for , moreover for , wherein .
- Step 1:
- Obtain a set of active sub-models:
- Step 2:
- Assume:
- Step 3:
- Obtain:
- Step 4:
- If , then calculate:else:
- Step 5:
- Set and go to Step 1.
- Step 0:
- Assume the initial parameters: , , , and .
- Step 1:
- Obtain:
- Step 2:
- If then calculate:else:
- Step 3:
- Set and go to Step 1.
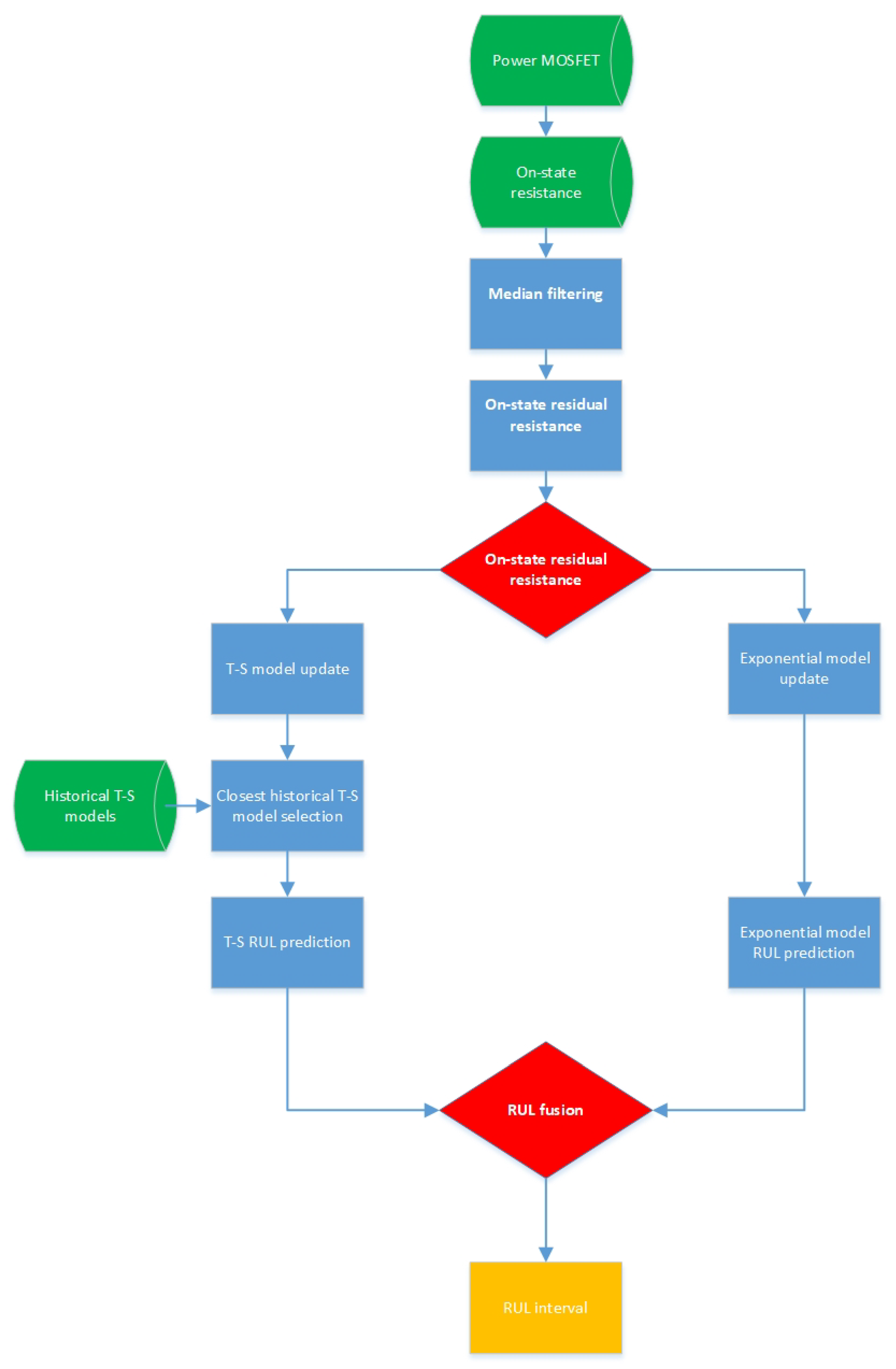
- Perform Closest historical T-S model selection.
- Introduce the run-to-failure-based Historical T-S models repository for obtaining the RUL of a currently operating MOSFET.
- Use an exponential model (3) for obtaining an alternative RUL prediction.
- Perform an RUL fusion resulting in an RUL interval.
4. Validation of the RUL Prediction Framework
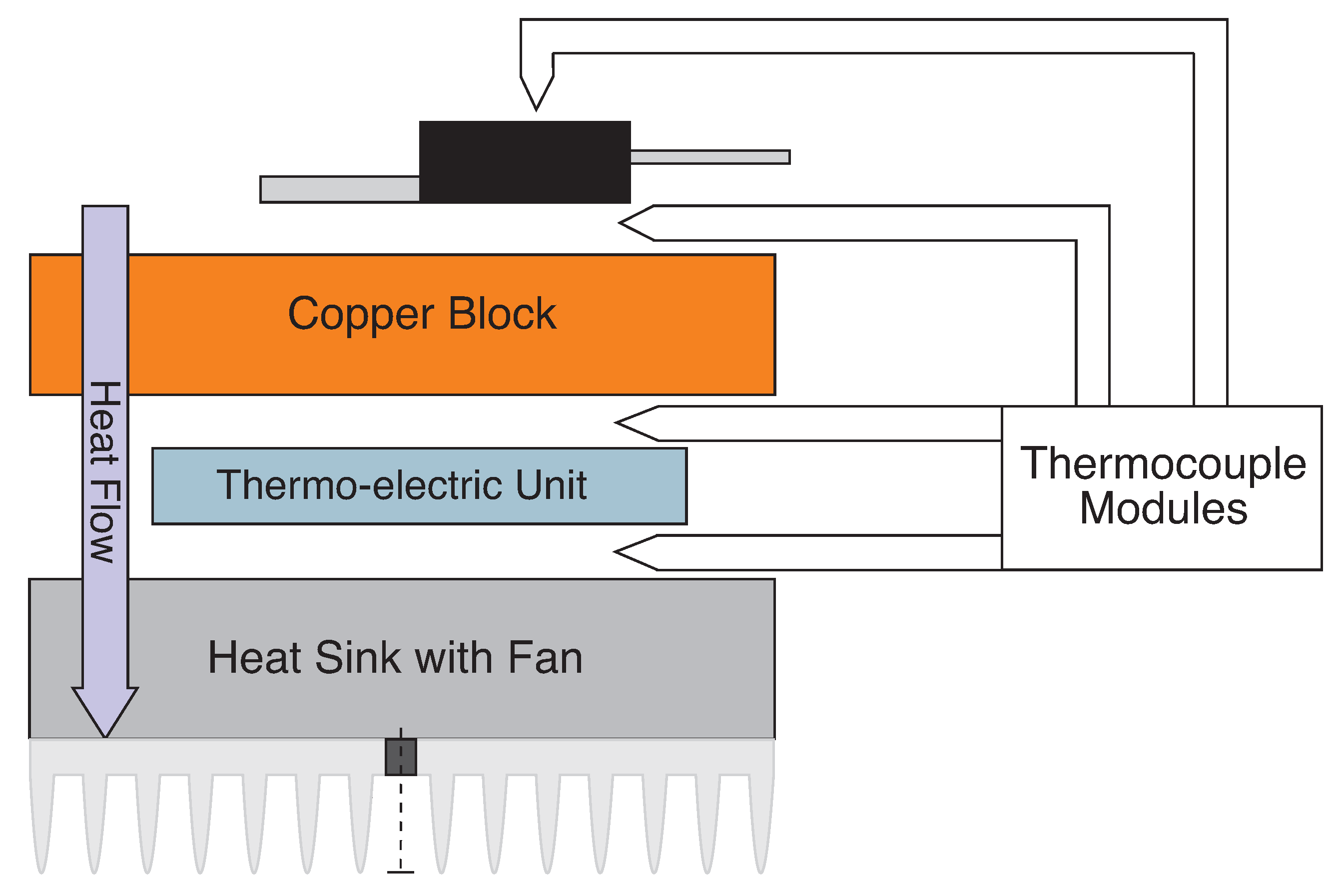
4.1. Power MOSFETs Data Processing
- Drain-to-source leakage current of −25 A;
- Maximum continuous drain voltage of −100 V;
- Continuous drain current of −9.7 A;
- Minimum gate threshold voltage of −2 V;
- Maximum gate threshold voltage of −4 V;
- Internal drain inductance of −4.5 nH;
- Internal source inductance of −7.5 nH.
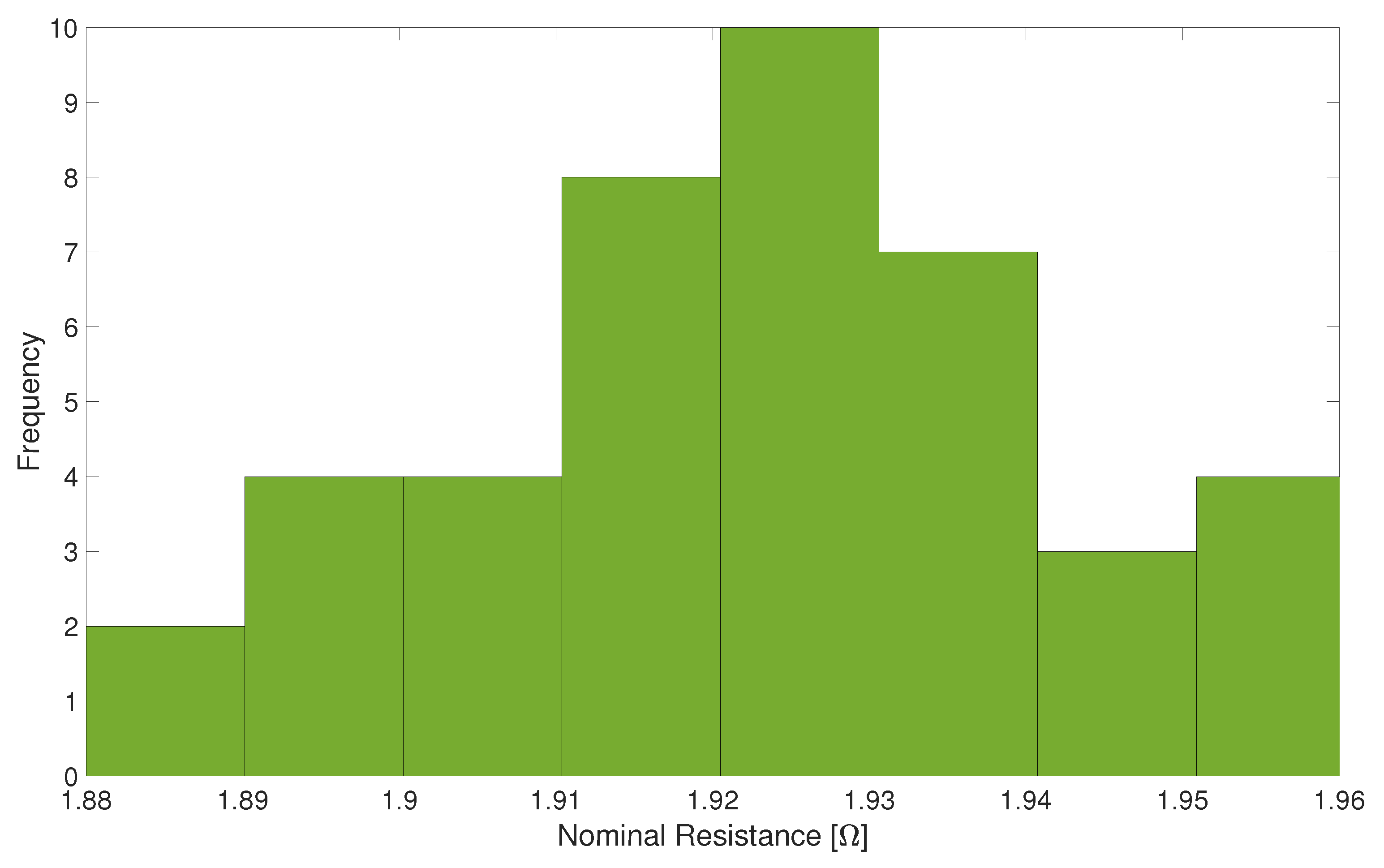
4.2. Design of Historical Model Repository
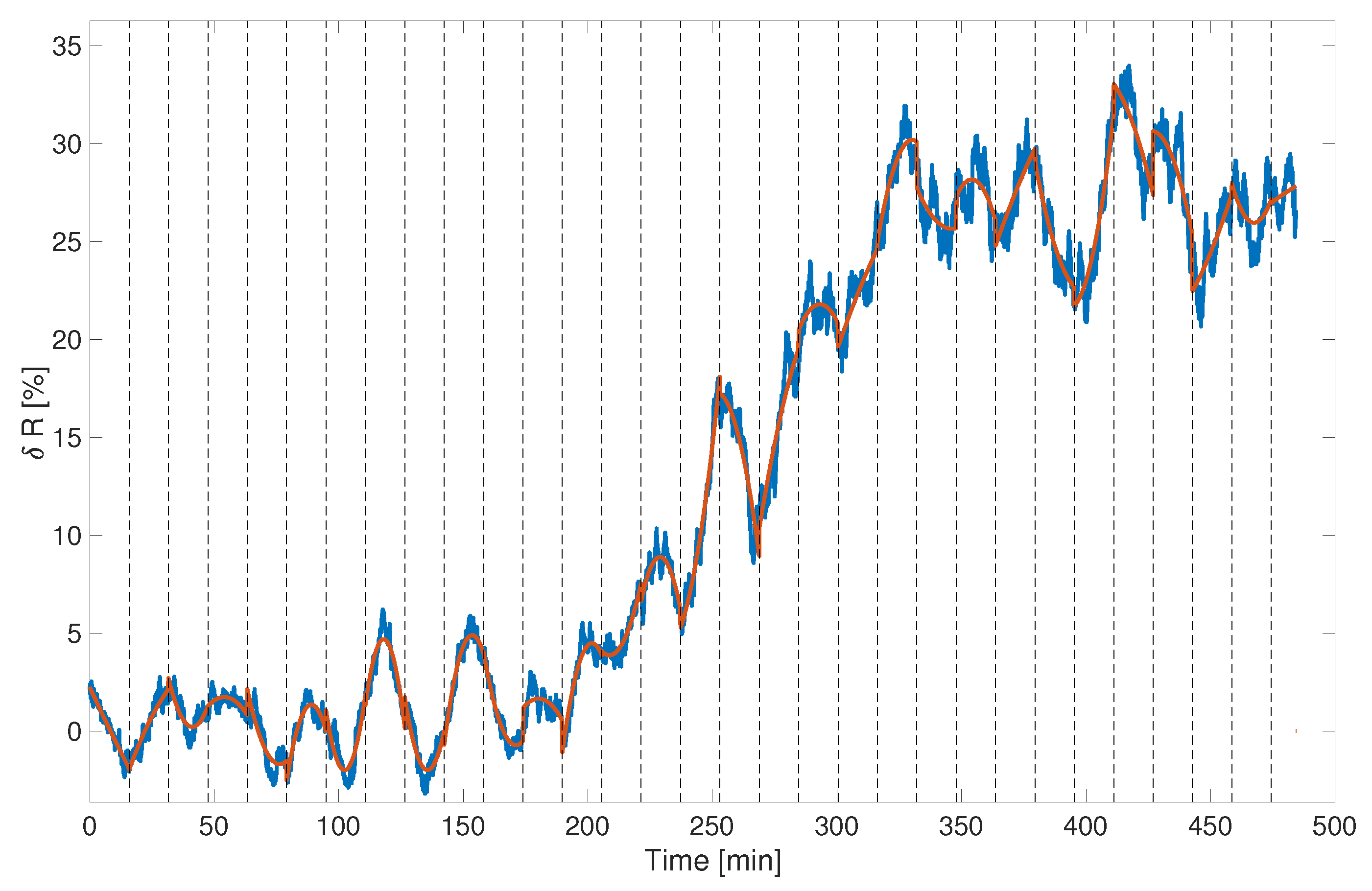
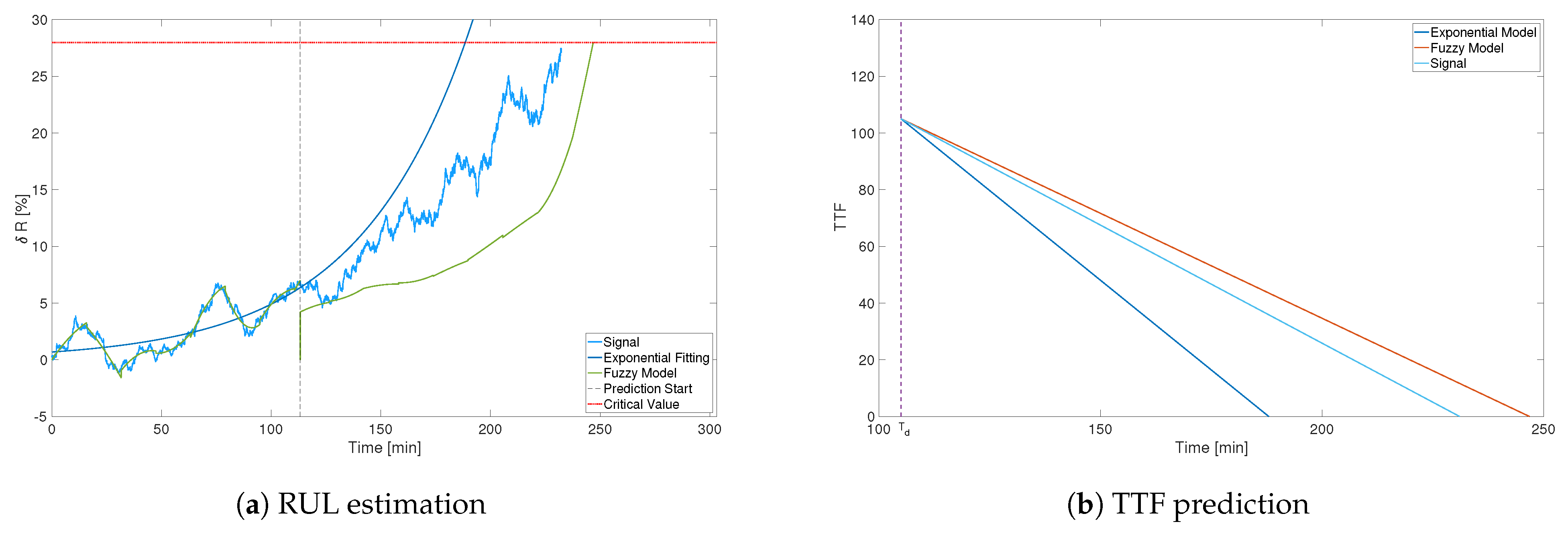
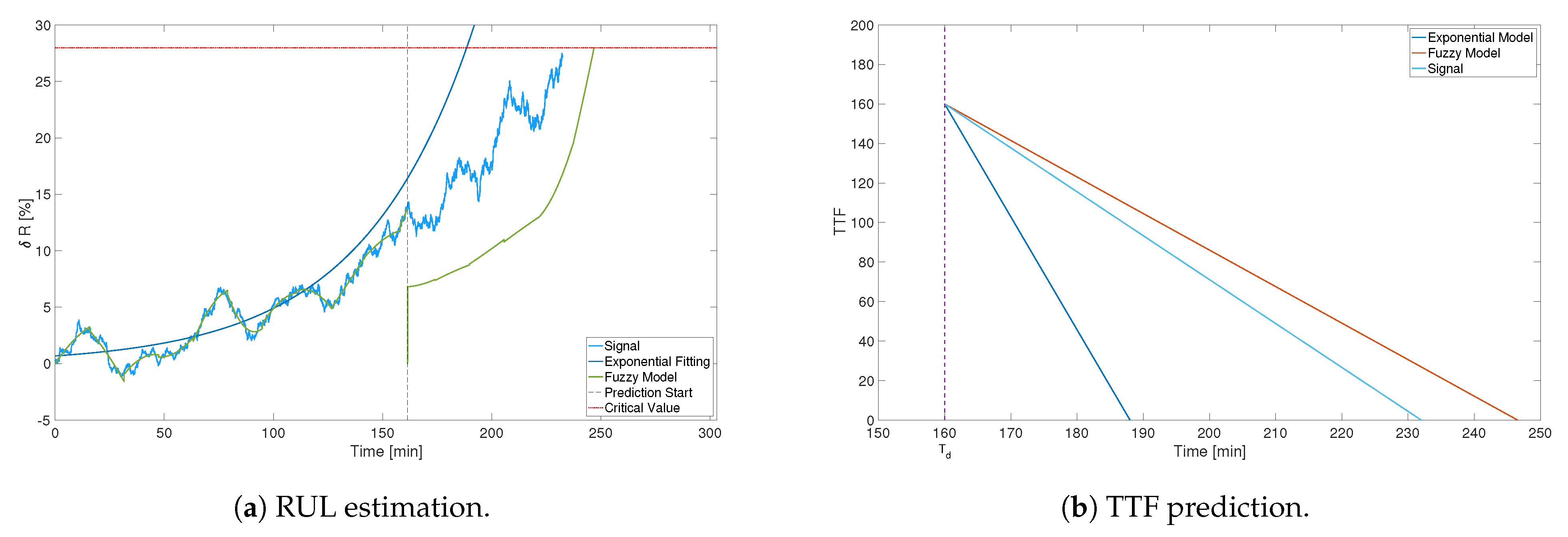
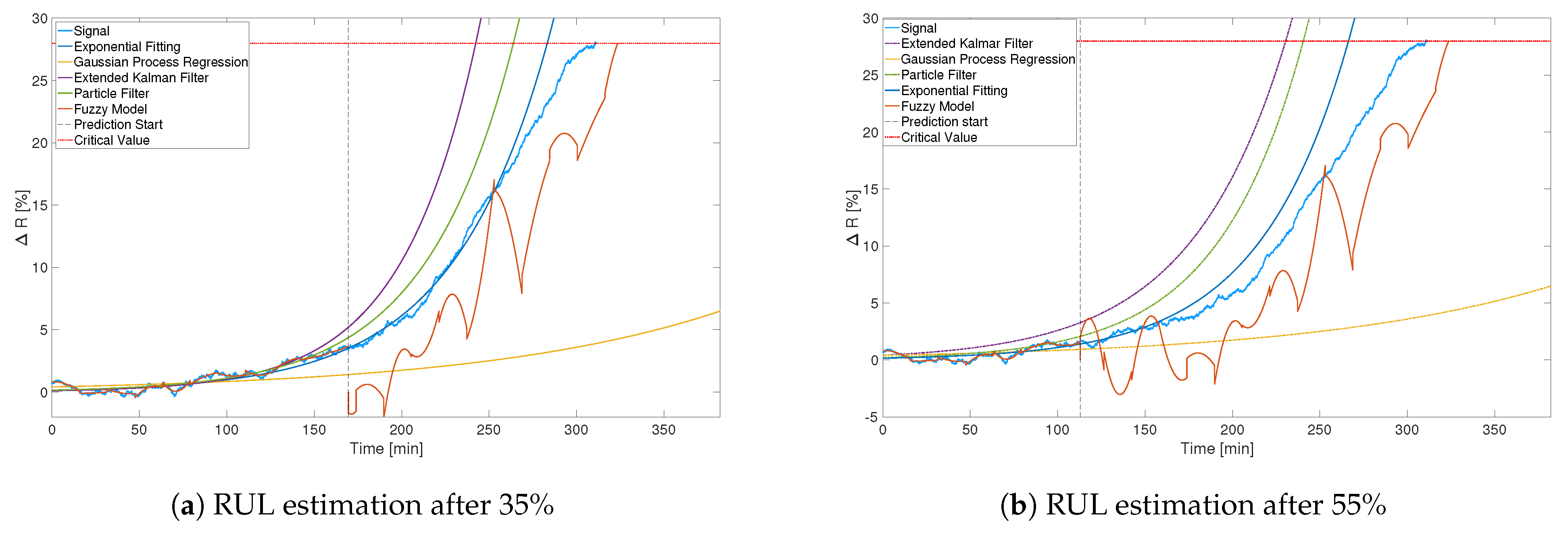
4.3. RUL Estimation and Prediction
- Gaussian process regression;
- Extended Kalman filter;
- Particle filter.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ARMA | Autoregressive-Moving Average Model |
| ANN | Artificial Neural Network |
| EoL | End of Life |
| FPT | First Prediction Time |
| MOSFET | Metal-Oxide Semiconductor Field-Effect Transistor |
| On-State Resistance | |
| RLS | Recursive Least-Square |
| RUL | Remaining Useful Life |
| PHM | Prognostics and Health Management |
| TTF | Time-To-Failure |
| T-S | Takagi–Sugeno model |
| QOBE | Quasi-Outer Bounding Ellipsoid algorithm |
References
- Wu, Y.; Yin, S.; Li, H.; Dong, M. Modeling and Experimental Investigation of Electromagnetic Interference (EMI) for SiC-Based Motor Drive. Energies 2020, 13, 5173. [Google Scholar] [CrossRef]
- Cha, K.H.; Ju, C.T.; Kim, R.Y. Analysis and Evaluation of WBG Power Device in High Frequency Induction Heating Application. Energies 2020, 13, 5351. [Google Scholar] [CrossRef]
- Okilly, A.; Kim, N.; Baek, J. Inrush Current Control of High Power Density DC–DC Converter. Energies 2020, 13, 4301. [Google Scholar] [CrossRef]
- Li, H.; Liao, X.; Hu, Y.; Huang, Z.; Wang, K. Analysis of voltage variation in silicon carbide MOSFETs during turn-on and turn-off. Energies 2017, 10, 1456. [Google Scholar] [CrossRef] [Green Version]
- Zuev, A.; Zhirabok, A.; Filaretov, V. Fault identification in underwater vehicle thrusters via sliding mode observers. Int. J. Appl. Math. Comput. Sci. 2020, 30. [Google Scholar] [CrossRef]
- Zhou, D.; Ji, H.; He, X.; Shang, J. Fault detection and isolation of the brake cylinder system for electric multiple units. IEEE Trans. Control Syst. Technol. 2017, 26, 1744–1757. [Google Scholar] [CrossRef]
- Zhang, H.; Tolbert, L. Efficiency impact of silicon carbide power electronics for modern wind turbine full scale frequency converter. IEEE Trans. Ind. Electron. 2010, 58, 21–28. [Google Scholar] [CrossRef]
- Simani, S.; Farsoni, S.; Castaldi, P. Data–Driven Techniques for the Fault Diagnosis of a Wind Turbine Benchmark. Int. J. Appl. Math. Comput. Sci. 2018, 28, 247–268. [Google Scholar] [CrossRef] [Green Version]
- Tsai, W.C. Optimization of Operating Parameters for Stable and High Operating Performance of a GDI Fuel Injector System. Energies 2020, 13, 2405. [Google Scholar] [CrossRef]
- Tsai, C.T.; Chen, W.M. Buck converter with soft-switching cells for PV panel applications. Energies 2016, 9, 148. [Google Scholar] [CrossRef] [Green Version]
- Pang, X.; Huang, R.; Wen, J.; Shi, Y.; Jia, J.; Zeng, J. A lithium-ion battery RUL prediction method considering the capacity regeneration phenomenon. Energies 2019, 12, 2247. [Google Scholar] [CrossRef] [Green Version]
- Salazar, J.C.; Sanjuan, A.; Nejjari, F.; Sarrate, R. Health–Aware and Fault–Tolerant Control of an Octorotor UAV System Based on Actuator Reliability. Int. J. Appl. Math. Comput. Sci. 2020, 30, 47–59. [Google Scholar]
- Do, N.V.; Nguyen, H.D.; Selamat, A. Knowledge-based model of expert systems using rela-model. Int. J. Softw. Eng. Knowl. Eng. 2018, 28, 1047–1090. [Google Scholar] [CrossRef]
- Chudnovsky, B.H. Electrical Equipment Life Expectancy, Aging, and Failures. In Electrical Power Transmission and Distribution; CRC Press: Boca Raton, FL, USA, 2017; pp. 269–308. [Google Scholar]
- Wang, C.; Lu, N.; Wang, S.; Cheng, Y.; Jiang, B. Dynamic long short-term memory neural-network-based indirect remaining-useful-life prognosis for satellite lithium-ion battery. Appl. Sci. 2018, 8, 2078. [Google Scholar] [CrossRef] [Green Version]
- Sun, B.; Li, Y.; Wang, Z.; Ren, Y.; Feng, Q.; Yang, D.; Lu, M.; Chen, X. Remaining useful life prediction of aviation circular electrical connectors using vibration-induced physical model and particle filtering method. Microelectron. Reliab. 2019, 92, 114–122. [Google Scholar] [CrossRef]
- Gebraeel, N.; Lawley, M.; Li, R.; Ryan, J. Residual-life distributions from component degradation signals: A Bayesian approach. IIE Trans. 2005, 37, 543–557. [Google Scholar] [CrossRef]
- Li, N.; Lei, Y.; Lin, J.; Ding, S. An improved exponential model for predicting remaining useful life of rolling element bearings. IEEE Trans. Ind. Electron. 2015, 62, 7762–7773. [Google Scholar] [CrossRef]
- Tanaka, K.; Sugeno, M. Stability analysis and design of fuzzy control systems. Fuzzy Sets Syst. 1992, 45, 135–156. [Google Scholar] [CrossRef]
- Witczak, M. Fault Diagnosis and Fault-Tolerant Control Strategies for Non-Linear Systems; Lectures Notes in Electrical Engineering; Springer International Publisher: Berlin/Heidelberg, Germany, 2014; Volume 266. [Google Scholar]
- Salcedo, J.V.; Martínez, M.; García-Nieto, S.; Hilario, A. T–S Fuzzy Bibo Stabilisation of Non–Linear Systems Under Persistent Perturbations Using Fuzzy Lyapunov Functions and Non–PDC Control Laws. Int. J. Appl. Math. Comput. Sci. 2020, 30, 529–550. [Google Scholar]
- Li, M.; Yu, D.; Chen, Z.; Xiahou, K.; Ji, T.; Wu, Q. A data-driven residual-based method for fault diagnosis and isolation in wind turbines. IEEE Trans. Sustain. Energy 2018, 10, 895–904. [Google Scholar] [CrossRef]
- Celaya, J.; Saxena, A.; Saha, S.; Goebel, K. MOSFET Thermal Overstress Aging Data Set. NASA AMES Prognostics Data Repository. 2007. Available online: https://ti.arc.nasa.gov/c/37/ (accessed on 10 April 2021).
- Wahle, P.; Schrimpf, R.; Galloway, K. Simulated space radiation effects on power MOSFETs in switching power supplies. IEEE Trans. Ind. Appl. 1990, 26, 798–802. [Google Scholar] [CrossRef]
- Dupont, L.; Lefebvre, S.; Bouaroudj, M.; Khatir, Z.; Faugières, J.C. Failure modes on low voltage power MOSFETs under high temperature application. Microelectron. Reliab. 2007, 47, 1767–1772. [Google Scholar] [CrossRef]
- Chen, Y.; Peng, G.; Zhu, Z.; Li, S. A novel deep learning method based on attention mechanism for bearing remaining useful life prediction. Appl. Soft Comput. 2020, 86, 105–919. [Google Scholar] [CrossRef]
- Li, X.; Ding, Q.; Sun, J.Q. Remaining useful life estimation in prognostics using deep convolution neural networks. Reliab. Eng. Syst. Saf. 2018, 172, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Wagner, W.P. Trends in expert system development: A longitudinal content analysis of over thirty years of expert system case studies. Expert Syst. Appl. 2017, 76, 85–96. [Google Scholar] [CrossRef]
- Mrugalska, B. A bounded-error approach to actuator fault diagnosis and remaining useful life prognosis of Takagi–Sugeno fuzzy systems. ISA Trans. 2018, 80, 257–266. [Google Scholar] [CrossRef] [PubMed]
- Chu, A.; Allam, A.; Arenas, A.C.; Rizzoni, G.; Onori, S. Stochastic capacity loss and remaining useful life models for lithium-ion batteries in plug-in hybrid electric vehicles. J. Power Sources 2020, 478, 228991. [Google Scholar] [CrossRef]
- Ossai, C.I.; Raghavan, N. Statistical characterization of the state-of-health of lithium-ion batteries with Weibull distribution function—A consideration of random effect model in charge capacity decay estimation. Batteries 2017, 3, 32. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Tsui, K.L. Statistical modeling of bearing degradation signals. IEEE Trans. Reliab. 2017, 66, 1331–1344. [Google Scholar] [CrossRef]
- Benker, M.; Furtner, L.; Semm, T.; Zaeh, M.F. Utilizing uncertainty information in remaining useful life estimation via Bayesian neural networks and Hamiltonian Monte Carlo. J. Manuf. Syst. 2020. [Google Scholar] [CrossRef]
- Li, W.; Liu, T. Time varying and condition adaptive hidden Markov model for tool wear state estimation and remaining useful life prediction in micro-milling. Mech. Syst. Signal Process. 2019, 131, 689–702. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Y.; Xia, T.; Pan, E. Hidden Markov model with auto-correlated observations for remaining useful life prediction and optimal maintenance policy. Reliab. Eng. Syst. Saf. 2019, 184, 123–136. [Google Scholar] [CrossRef]
- Nielsen, J.S.; Sørensen, J.D. Bayesian estimation of remaining useful life for wind turbine blades. Energies 2017, 10, 664. [Google Scholar] [CrossRef] [Green Version]
- Mosallam, A.; Medjaher, K.; Zerhouni, N. Data-driven prognostic method based on Bayesian approaches for direct remaining useful life prediction. J. Intell. Manuf. 2016, 27, 1037–1048. [Google Scholar] [CrossRef]
- Baptista, M.; Henriques, E.M.; de Medeiros, I.P.; Malere, J.P.; Nascimento, C.L., Jr.; Prendinger, H. Remaining useful life estimation in aeronautics: Combining data-driven and Kalman filtering. Reliab. Eng. Syst. Saf. 2019, 184, 228–239. [Google Scholar] [CrossRef]
- Cui, L.; Wang, X.; Xu, Y.; Jiang, H.; Zhou, J. A novel switching unscented Kalman filter method for remaining useful life prediction of rolling bearing. Measurement 2019, 135, 678–684. [Google Scholar] [CrossRef]
- Sikorska, J.; Hodkiewicz, M.; Ma, L. Prognostic modeling options for remaining useful life estimation by industry. Mech. Syst. Signal Process. 2011, 25, 1803–1836. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Lin, J. A new method based on stochastic process models for machine remaining useful life prediction. IEEE Trans. Instrum. Meas. 2016, 65, 2671–2684. [Google Scholar] [CrossRef]
- Li, N.; Lei, Y.; Guo, L.; Yan, T.; Lin, J. Remaining useful life prediction based on a general expression of stochastic process models. IEEE Trans. Ind. Electron. 2017, 64, 5709–5718. [Google Scholar] [CrossRef]
- Baptista, M.; Sankararaman, S.; de Medeiros, I.P.; Nascimento, C., Jr.; Prendinger, H.; Henriques, E.M. Forecasting fault events for predictive maintenance using data-driven techniques and ARMA modeling. Comput. Ind. Eng. 2018, 115, 41–53. [Google Scholar] [CrossRef]
- Long, Y.; Luo, H.; Zhi, Y.; Wang, X. Remaining Useful Life Estimation of Solder joints using an ARMA Model Optimized by Genetic Algorithm. In Proceedings of the 2018 19th International Conference on Electronic Packaging Technology (ICEPT), Shanghai, China, 8–11 August 2018; pp. 1108–1111. [Google Scholar]
- Xia, M.; Li, T.; Liu, L.; Xu, L.; Gao, S.; De Silva, C.W. Remaining useful life prediction of rotating machinery using hierarchical deep neural network. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; pp. 2778–2783. [Google Scholar]
- Mrugalski, M. Advanced Neural Network-Based Computational Schemes for Robust Fault Diagnosis; Springer International Publishing: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Witczak, M.; Mrugalski, M.; Korbicz, J. Towards Robust Neural-Network-Based Sensor and Actuator Fault Diagnosis: Application to a Tunnel Furnace. Neural Process. Lett. 2015, 42, 71–87. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Su, Y.; Cheng, Y.; Shao, X.; Deng, C.; Liu, C. Multi-sensor information fusion for remaining useful life prediction of machining tools by adaptive network based fuzzy inference system. Appl. Soft Comput. 2018, 68, 13–23. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Gontarz, S.; Lin, J.; Radkowski, S.; Dybala, J. A model-based method for remaining useful life prediction of machinery. IEEE Trans. Reliab. 2016, 65, 1314–1326. [Google Scholar] [CrossRef]
- Zhang, L.; Mu, Z.; Sun, C. Remaining useful life prediction for lithium-ion batteries based on exponential model and particle filter. IEEE Access 2018, 6, 17729–17740. [Google Scholar] [CrossRef]
- Anis, M.D. Towards Remaining Useful Life Prediction in Rotating Machine Fault Prognosis: An Exponential Degradation Model. In Proceedings of the 2018 Condition Monitoring and Diagnosis (CMD), Perth, Australia, 23–26 September 2018; pp. 1–6. [Google Scholar]
- Lu, C.J.; Meeker, W.O. Using degradation measures to estimate a time-to-failure distribution. Technometrics 1993, 35, 161–174. [Google Scholar] [CrossRef]
- Zadeh, L.A. Knowledge representation in fuzzy logic. In Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers by Lotfi a Zadeh; World Scientific: Singapore, 1996; pp. 764–774. [Google Scholar]
- Söderström, T.; Stoica, P. System Identification; Prentice-Hall International: Hoboken, NJ, USA, 1989. [Google Scholar]
- Cowan, C.F.; Grant, P.M. Adaptive Filters; Prentice-Hall: Englewood Cliffs, NJ, USA, 1985; Volume 152. [Google Scholar]
- Arablouei, R.; Doğançay, K. Modified quasi-OBE algorithm with improved numerical properties. Signal Process. 2013, 93, 797–803. [Google Scholar] [CrossRef]
- Kraus, T.; Mandour, G.I.; Joachim, D. Estimating the error bound in QOBE Vowel classification. In Proceedings of the 2007 50th Midwest Symposium on Circuits and Systems, Montreal, QC, Canada, 5–8 August 2007; pp. 369–372. [Google Scholar]
- Bottomley, G.; Alexander, S. A theoretical basis for divergence of conventional recursive least squares filters. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Glasgow, UK, 23–26 May 1989; pp. 908–911. [Google Scholar]
- Celaya, J.; Saxena, A.; Saha, S.; Goebel, K.F. Prognostics of power MOSFETs under thermal stress accelerated aging using data-driven and model-based methodologies. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, Denver, CO, USA, 20–23 June 2011. [Google Scholar]
- Mosfet TO220AB Datasheet. Available online: http://pdf.datasheetcatalog.com/datasheets2/73/73619_1.pdf (accessed on 17 March 2021).
- Celaya, J.R.; Saxena, A.; Wysocki, P.; Saha, S.; Goebel, K. Towards Prognostics of Power MOSFETs: Accelerated Aging and Precursors of Failure; Technical Report; National Aeronautics and Space Administrations Moffett Field CA AMES Research: Mountain View, CA, USA, 2010.
- Patil, N.; Celaya, J.; Das, D.; Goebel, K.; Pecht, M. Precursor parameter identification for insulated gate bipolar transistor (IGBT) prognostics. IEEE Trans. Reliab. 2009, 58, 271–276. [Google Scholar] [CrossRef]
- Saha, S.; Celaya, J.R.; Vashchenko, V.; Mahiuddin, S.; Goebel, K.F. Accelerated aging with electrical overstress and prognostics for power MOSFETs. In Proceedings of the IEEE 2011 EnergyTech, Cleveland, OH, USA, 25–26 May 2011; pp. 1–6. [Google Scholar]
- Celaya, J.R.; Wysocki, P.; Vashchenko, V.; Saha, S.; Goebel, K. Accelerated aging system for prognostics of power semiconductor devices. In Proceedings of the 2010 IEEE Autotestcon, Orlando, FL, USA, 13–16 September 2010; pp. 1–6. [Google Scholar]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Witczak, M.; Mrugalski, M.; Lipiec, B. Remaining Useful Life Prediction of MOSFETs via the Takagi–Sugeno Framework. Energies 2021, 14, 2135. https://doi.org/10.3390/en14082135
Witczak M, Mrugalski M, Lipiec B. Remaining Useful Life Prediction of MOSFETs via the Takagi–Sugeno Framework. Energies. 2021; 14(8):2135. https://doi.org/10.3390/en14082135
Chicago/Turabian StyleWitczak, Marcin, Marcin Mrugalski, and Bogdan Lipiec. 2021. "Remaining Useful Life Prediction of MOSFETs via the Takagi–Sugeno Framework" Energies 14, no. 8: 2135. https://doi.org/10.3390/en14082135
APA StyleWitczak, M., Mrugalski, M., & Lipiec, B. (2021). Remaining Useful Life Prediction of MOSFETs via the Takagi–Sugeno Framework. Energies, 14(8), 2135. https://doi.org/10.3390/en14082135






