Thermodynamic and Kinetic Considerations Regarding the Prospects for a Dual-Purpose Hydrogen Extraction and Separation Membrane
Abstract
1. Introduction
2. Methods
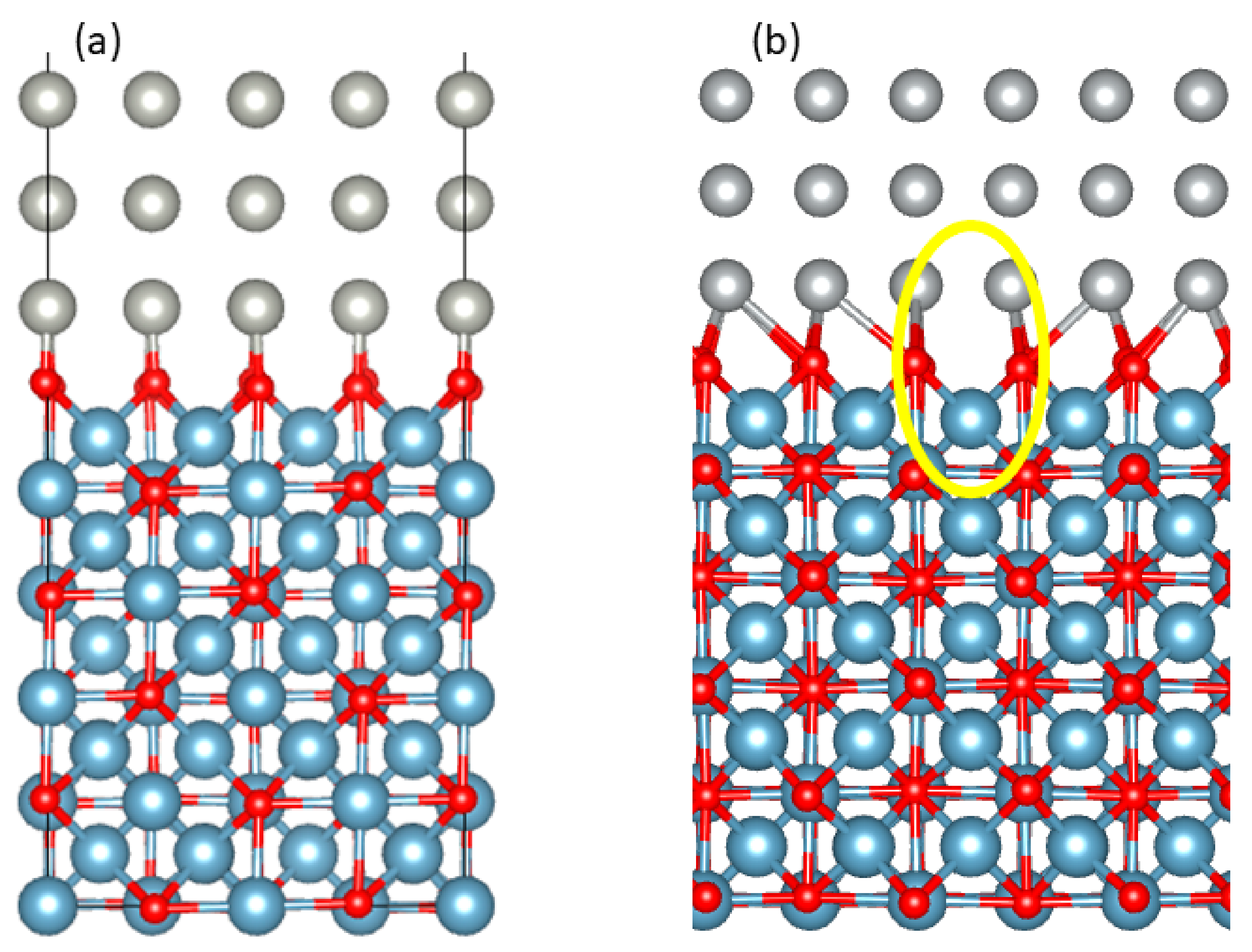
2.1. Extraction of Energetic Data from the Literature
2.1.1. Step 1
2.1.2. Step 2
2.1.3. Step 3
2.1.4. Step 4
2.1.5. Step 5
2.1.6. Step 6
2.2. Discussion of Thermodynamic Considerations
2.3. Kinetic Analysis
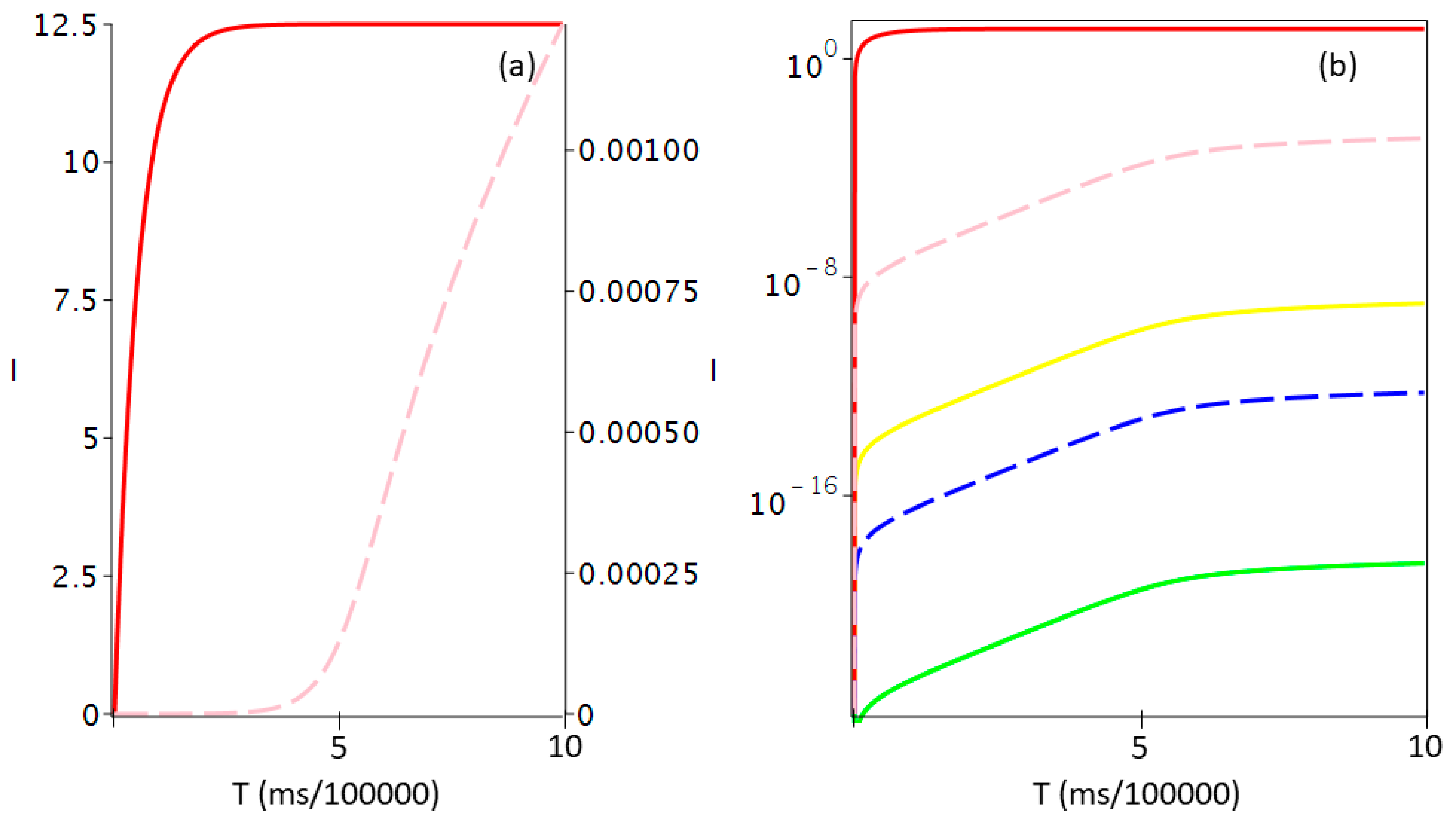
2.3.1. Steady-State Analysis
2.3.2. Time-Dependent Analysis
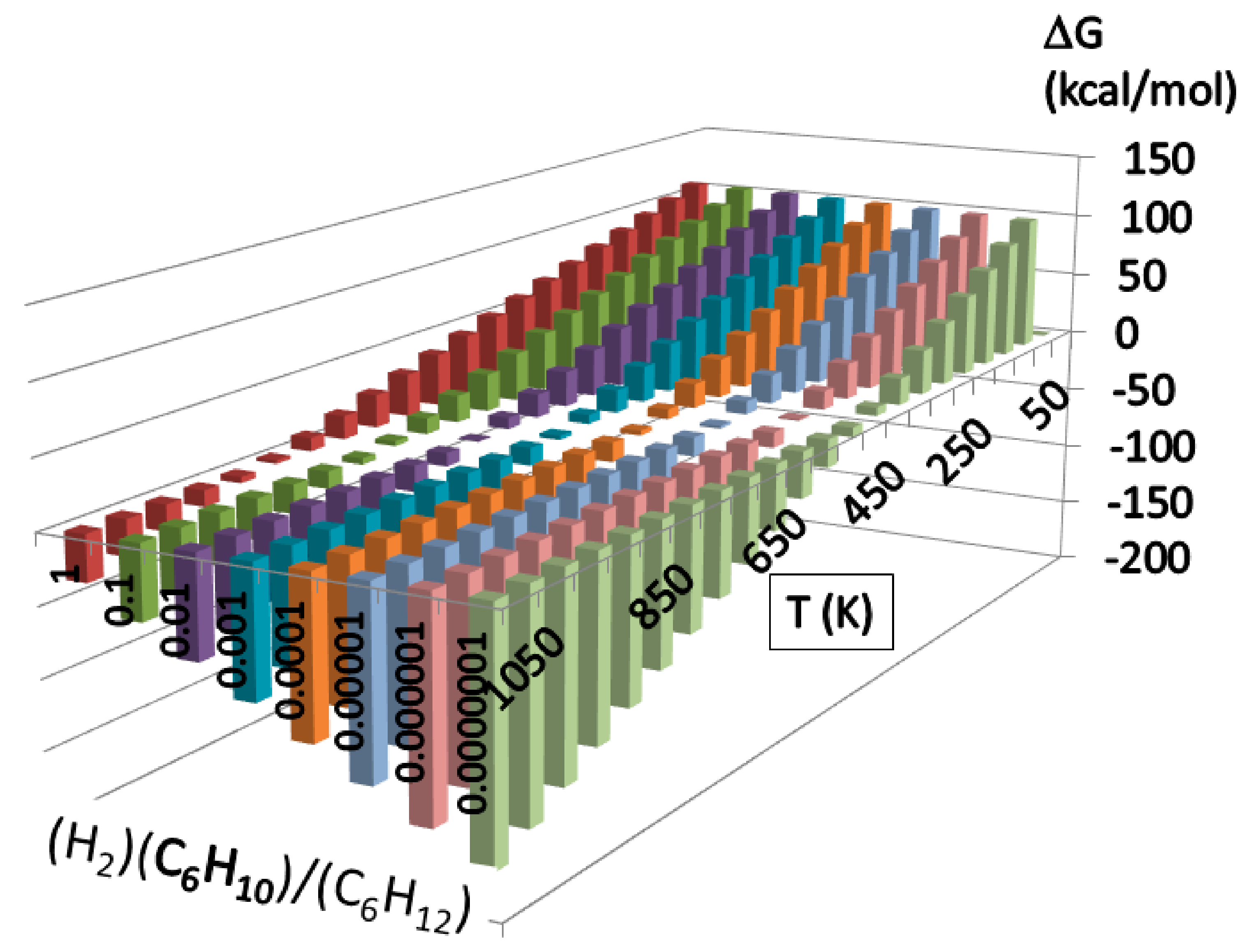
3. Results
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- García, L. 4—Hydrogen Production by Steam Reforming of Natural Gas and Other Nonrenewable Feedstocks. In Compendium of Hydrogen Energy; Subramani, V., Basile, A., Veziroğlu, T.N., Eds.; Woodhead Publishing: Oxford, UK, 2015; pp. 83–107. [Google Scholar]
- Hydrogen Production: Natural Gas Reforming; US Department of Energy, Office of Energy Efficiency and Renewable Energy: Washington, DC, USA, 2018.
- Papadias, D.D.; Lee, S.H.; Ferrandon, M.; Ahmed, S. An analytical and experimental investigation of high-pressure catalytic steam reforming of ethanol in a hydrogen selective membrane reactor. Int. J. Hydrogen Energy 2010, 35, 2004–2017. [Google Scholar] [CrossRef]
- Sattler, J.J.H.B.; Ruiz-Martinez, J.; Santillan-Jimenez, E.; Weckhuysen, B.M. Catalytic Dehydrogenation of Light Alkanes on Metals and Metal Oxides. Chem. Rev. 2014, 114, 10613–10653. [Google Scholar] [CrossRef]
- Trombetta, M.; Busca, G.; Rossini, S.; Piccoli, V.; Cornaro, U.; Guercio, A.; Catani, R.; Willey, R.J. FT-IR Studies on Light Olefin Skeletal Isomerization Catalysis. J. Catal. 1998, 179, 581–596. [Google Scholar] [CrossRef]
- Burkhanov, B.G.S.; Gorina, N.B.; Kolchugina, N.B.; Roshan, N.R.; Slovetsky, D.I.; Chistov, E.M. Palladium-Based Alloy Membranes for Separation of High Purity Hydrogen from Hydrogen-Containing Gas Mixtures. Platin. Met. Rev. 2011, 55, 3–12. [Google Scholar] [CrossRef]
- Airaksinen, S.M.K.; Harlin, M.E.; Krause, A.O.I. Kinetic Modeling of Dehydrogenation of Isobutane on Chromia/Alumina Catalyst. Ind. Eng. Chem. Res. 2002, 41, 5619–5626. [Google Scholar] [CrossRef]
- Gielens, F.C.; Tong, H.D.; Vorstman, M.A.G.; Keurentjes, J.T.F. Measurement and modeling of hydrogen transport through high-flux Pd membranes. J. Membr. Sci. 2007, 289, 15–25. [Google Scholar] [CrossRef]
- Ono, S.; Uchikoshi, T.; Hayashi, Y.; Kitagawa, Y.; Yeh, G.; Yamaguchi, E.; Tanabe, K. A Heterothermic Kinetic Model of Hydrogen Absorption in Metals with Subsurface Transport. Metals 2019, 9, 1131. [Google Scholar] [CrossRef]
- Deveau, N.D.; Ma, Y.H.; Datta, R. Beyond Sieverts’ law: A comprehensive microkinetic model of hydrogen permeation in dense metal membranes. J. Membr. Sci. 2013, 437, 298–311. [Google Scholar] [CrossRef]
- Spitzer, R.; Huffman, H.M. The Heats of Combustion of Cyclopentane, Cyclohexane, Cycloheptane and Cyclooctane. J. Am. Chem. Soc. 1947, 69, 211–213. [Google Scholar] [CrossRef]
- Steele, W.V.; Chirico, R.D.; Knipmeyer, S.E.; Nguyen, A.; Smith, N.K.; Tasker, I.R. Thermodynamic Properties and Ideal-Gas Enthalpies of Formation for Cyclohexene, Phthalan (2,5-Dihydrobenzo-3,4-furan), Isoxazole, Octylamine, Dioctylamine, Trioctylamine, Phenyl Isocyanate, and 1,4,5,6-Tetrahydropyrimidine. J. Chem. Eng. Data 1996, 41, 1269–1284. [Google Scholar] [CrossRef]
- Abdulwahed, M. Thermodynamic Analysis of Isobutane Dehydrogenation Reaction. Int. J. Thermodyn. 2015, 18, 213. [Google Scholar] [CrossRef][Green Version]
- Cai, S.; Chihaia, V.; Sohlberg, K. Interactions of methane, ethane and pentane with the (110C) surface of γ-alumina. J. Mol. Catal. A: Chem. 2007, 275, 63–71. [Google Scholar] [CrossRef]
- Sohlberg, K.; Pennycook, S.J.; Pantelides, S.T. The Bulk and Surface Structure of γ-alumina. Chem. Eng. Commun. 2000, 181, 107–135. [Google Scholar] [CrossRef]
- Rashkeev, S.N.; Sohlberg, K.W.; Zhuo, S.; Pantelides, S.T. Hydrogen-Induced Initiation of Corrosion in Aluminum. J. Phys. Chem. C 2007, 111, 7175–7178. [Google Scholar] [CrossRef]
- Knözinger, H.; Ratnasamy, P. Catalytic Aluminas: Surface Models and Characterization of Surface Sites. Catal. Rev. 1978, 17, 31–70. [Google Scholar] [CrossRef]
- Weckhuysen, B.M.; Schoonheydt, R.A. Alkane dehydrogenation over supported chromium oxide catalysts. Catal. Today 1999, 51, 223–232. [Google Scholar] [CrossRef]
- Korhonen, S.T.; Airaksinen, S.M.; Bañares, M.A.; Krause, A.O.I. Isobutane dehydrogenation on zirconia-, alumina-, and zirconia/alumina-supported chromia catalysts. Appl. Catal. A Gen. 2007, 333, 30–41. [Google Scholar] [CrossRef]
- Sattler, J.J.H.B.; González-Jiménez, I.D.; Mens, A.M.; Arias, M.; Visser, T.; Weckhuysen, B.M. Operando UV-Vis spectroscopy of a catalytic solid in a pilot-scale reactor: Deactivation of a CrOx/Al2O3 propane dehydrogenation catalyst. Chem. Commun. 2013, 49, 1518–1520. [Google Scholar] [CrossRef] [PubMed]
- Ostrovskii, V.E.; Kadyshevich, E.A.; Gostev, B.V.; Lapidus, A.L. An adsorption and calorimetric study of the interaction of hydrogen with chromium oxide. Russ. J. Phys. Chem. A 2008, 82, 1626–1632. [Google Scholar] [CrossRef]
- Borisevich, A.Y.; Wang, S.; Rashkeev, S.N.; Glazoff, M.; Pennycook, S.J.; Pantelides, S.T. Dual Nanoparticle/Substrate Control of Catalytic Dehydrogenation. Adv. Mater. 2007, 19, 2129–2133. [Google Scholar] [CrossRef]
- Sohlberg, K.; Pennycook, S.J.; Pantelides, S.T. Hydrogen Mobility in Catalytic Aluminas: Theory and Implications. Recent Res. Dev. Phys. Chem. 2000, 4, 71–81. [Google Scholar]
- Zhang, W.; Smith, J.; Evans, A. The connection between ab initio calculations and interface adhesion measurements on metal/oxide systems: Ni/Al2O3 and Cu/Al2O3. Acta Mater. 2002, 50, 3803–3816. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Yokogawa Corporation of America. Application Note: Hydrogen Permeation, PROD #: 2018-01-2361; Yokogawa Corporation: Sugar Land, TX, USA, 2018. [Google Scholar]
- Nace, D.M.; Aston, J.G. Palladium Hydride. I. The Thermodynamic Properties of Pd2H between 273 and 345°K.1. J. Am. Chem. Soc. 1957, 79, 3619–3623. [Google Scholar] [CrossRef]
- Sholl, D.S. Using density functional theory to study hydrogen diffusion in metals: A brief overview. J. Alloy. Compd. 2007, 446–447, 462–468. [Google Scholar] [CrossRef]
- Christmann, K. Kinetics, energetics and structure of hydrogen adsorbed on transition metal single crystal surfaces. Bull. Sociétés Chim. Belg. 2010, 88, 519–539. [Google Scholar] [CrossRef]
- Wilke, S.; Scheffler, M. Potential-energy surface forH2dissociation over Pd(100). Phys. Rev. B 1996, 53, 4926–4932. [Google Scholar] [CrossRef]
- Peachey, N.M.; Snow, R.C.; Dye, R.C. Composite PdTa metal membranes for hydrogen separation. J. Membr. Sci. 1996, 111, 123–133. [Google Scholar] [CrossRef]
- Amano, M.; Komaki, M.; Nishimura, C. Hydrogen permeation characteristics of palladium-plated V-Ni alloy membranes. J. Less Common Met. 1991, 172–174, 727–731. [Google Scholar] [CrossRef]
- Shu, J.; Grandjean, B.P.A.; Van Neste, A.; Kaliaguine, S. Catalytic palladium-based membrane reactors: A review. Can. J. Chem. Eng. 1991, 69, 1036–1060. [Google Scholar] [CrossRef]
- Holleck, G.L. Diffusion and solubility of hydrogen in palladium and palladium-silver alloys. J. Phys. Chem. 1970, 74, 503–511. [Google Scholar] [CrossRef]
- Edlund, D.J.; Pledger, W.A.; Studebaker, T. Hydrogen-Permeable Metal Membrane and Hydrogen Purification Assemblies Containing the Same; IdaTech, LCC: Bend, OR, USA, 2003. [Google Scholar]
- Bromberg, J.P. Physcial Chemistry; Allyn and Bacon Inc.: Boston, MA, USA, 1980. [Google Scholar]
- Tsyganenko, A.A.; Filimonov, V.N. Infrared Spectra of Surface Hydroxyl Groups and Crystalline Structure of Oxides. J. Mol. Struct. 1973, 19, 579. [Google Scholar] [CrossRef]
- Tsyganenko, A.; Smirnov, K.; Rzhevskij, A.; Mardilovich, P. Infrared spectroscopic evidence for the structural OH groups of spinel alumina modifications. Mater. Chem. Phys. 1990, 26, 35. [Google Scholar] [CrossRef]
- Tsyganenko, A.A.; Mardilovich, P.P. Structure of alumina surfaces. J. Chem. Soc. Faraday Trans. 1996, 92, 4843. [Google Scholar] [CrossRef]
- Pelmenschikov, V.; Gee, L.B.; Wang, H.; MacLeod, K.C.; McWilliams, S.F.; Skubi, K.L.; Cramer, S.P.; Holland, P.L. High-Frequency Fe-H Vibrations in a Bridging Hydride Complex Characterized by NRVS and DFT. Angew. Chem. Int. Ed. 2018, 57, 9367–9371. [Google Scholar] [CrossRef] [PubMed]
- Rosenbrock, H.H. Some general implicit processes for the numerical solution of differential equations. Comput. J. 1963, 5, 329–330. [Google Scholar] [CrossRef]
- Maple. Maplesoft, a Division of Waterloo; Maple Inc.: Waterloo, ON, Canada, 2020. [Google Scholar]
- Sakintuna, B.; Lamari-Darkrim, F.; Hirscher, M. Metal hydride materials for solid hydrogen storage: A review. Int. J. Hydrog. Energy 2007, 32, 1121–1140. [Google Scholar] [CrossRef]
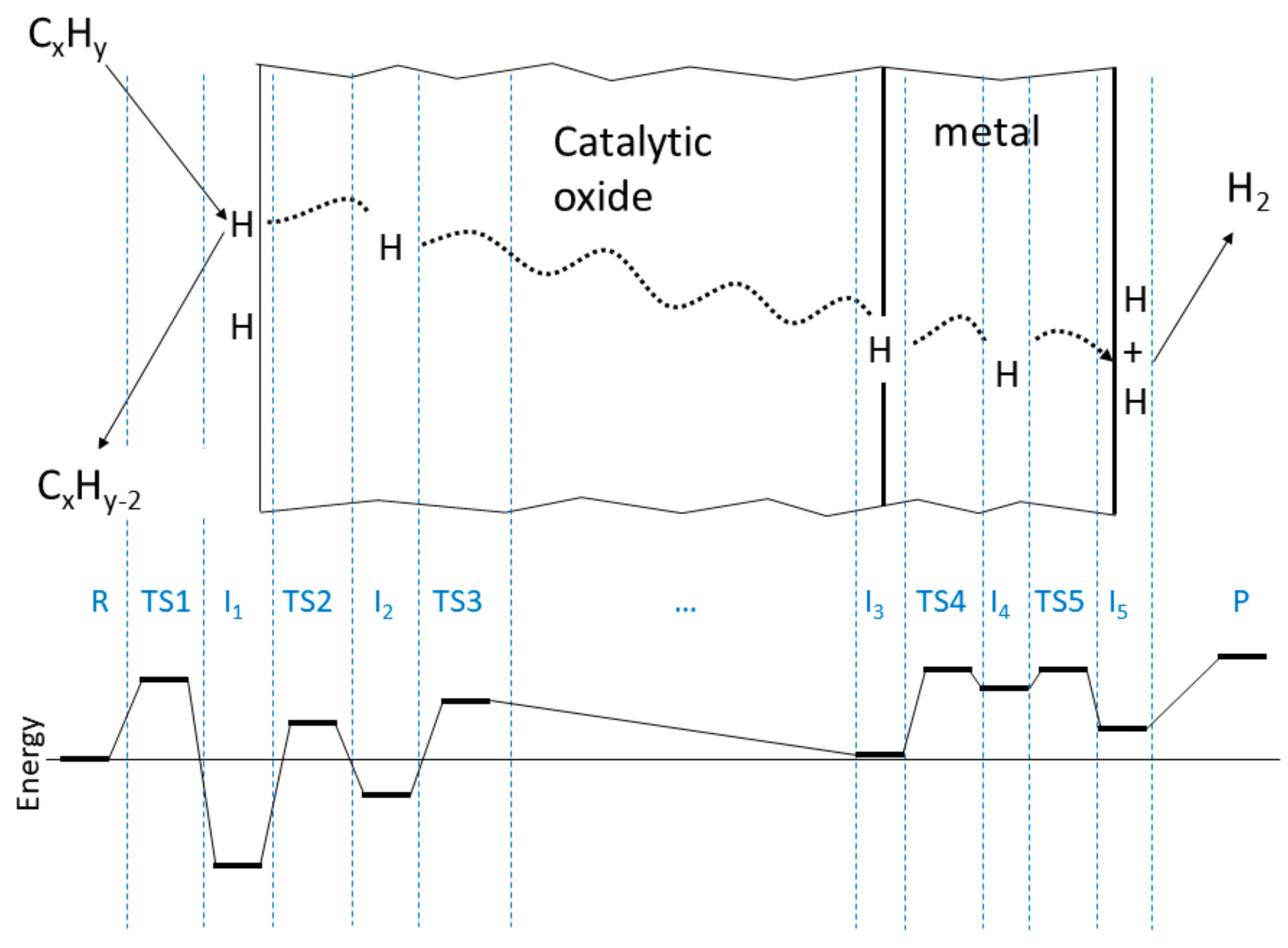
| R | TS1 | I1 | TS2 | I2 | TS3 | I3 | TS4 | I4 | TS5 | I5 | P |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 1.1 | −1.45(0.45) | 0.55 | −0.55 | 0.85 | 0.05(−1.95) | 1.25 | 1.03 | 1.25 | 0.41 | 1.42 |
| Species | ΔH (kJ/mol) | ΔH (eV) | Reference |
|---|---|---|---|
| C2H6 | 137 | 1.42 | [4] |
| C3H6 | 124.3 | 1.29 | [4] |
| C6H12 | 120.3 | 1.25 | [11,12] |
| C4H10 (isobutane) | 122 (@773 K) | 1.26 | [13] |
| Rate Constant | Frequency Factor | |
|---|---|---|
| 2.97 × 105 nm−2.ms−1 | 1.1 | |
| 9.89 × 1010 ms−1 (3300 cm−1) | 2.55 | |
| 9.89 × 1010 ms−1 (3300 cm−1) | 2.0 | |
| 9.89 × 1010 ms−1 (3300 cm−1) | 1.1 | |
| 9.89 × 1010 ms−1 (3300 cm−1) | 1.4 | |
| 9.89 × 1010 ms−1 (3300 cm−1) | 0.8 | |
| 9.89 × 1010 ms−1 (3300 cm−1) | 1.2 | |
| 4.20 × 1010 ms−1 (1400 cm−1) | 0.22 | |
| 4.20 × 1010 ms−1 (1400 cm−1) | 0.22 | |
| 4.20 × 1010 ms−1 (1400 cm−1) | 0.84 | |
| 4.20 × 1010 ms−1 (1400 cm−1) | 1.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sohlberg, K. Thermodynamic and Kinetic Considerations Regarding the Prospects for a Dual-Purpose Hydrogen Extraction and Separation Membrane. Energies 2021, 14, 2136. https://doi.org/10.3390/en14082136
Sohlberg K. Thermodynamic and Kinetic Considerations Regarding the Prospects for a Dual-Purpose Hydrogen Extraction and Separation Membrane. Energies. 2021; 14(8):2136. https://doi.org/10.3390/en14082136
Chicago/Turabian StyleSohlberg, Karl. 2021. "Thermodynamic and Kinetic Considerations Regarding the Prospects for a Dual-Purpose Hydrogen Extraction and Separation Membrane" Energies 14, no. 8: 2136. https://doi.org/10.3390/en14082136
APA StyleSohlberg, K. (2021). Thermodynamic and Kinetic Considerations Regarding the Prospects for a Dual-Purpose Hydrogen Extraction and Separation Membrane. Energies, 14(8), 2136. https://doi.org/10.3390/en14082136






