Simulation Research on Regenerative Braking Control Strategy of Hybrid Electric Vehicle
Abstract
:1. Introduction
2. System Analysis and Modelling
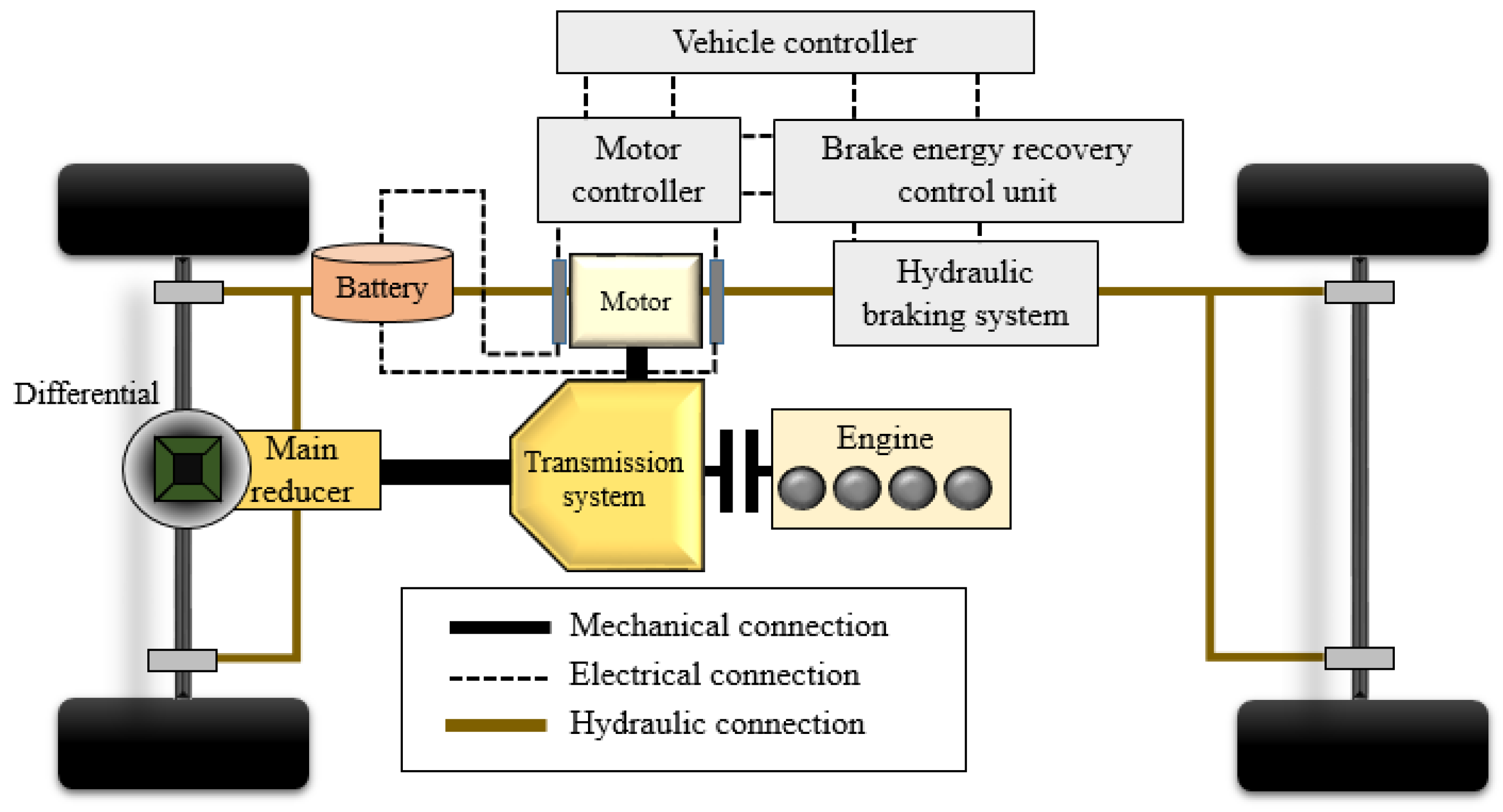
2.1. Structure of Braking Energy Recovery System
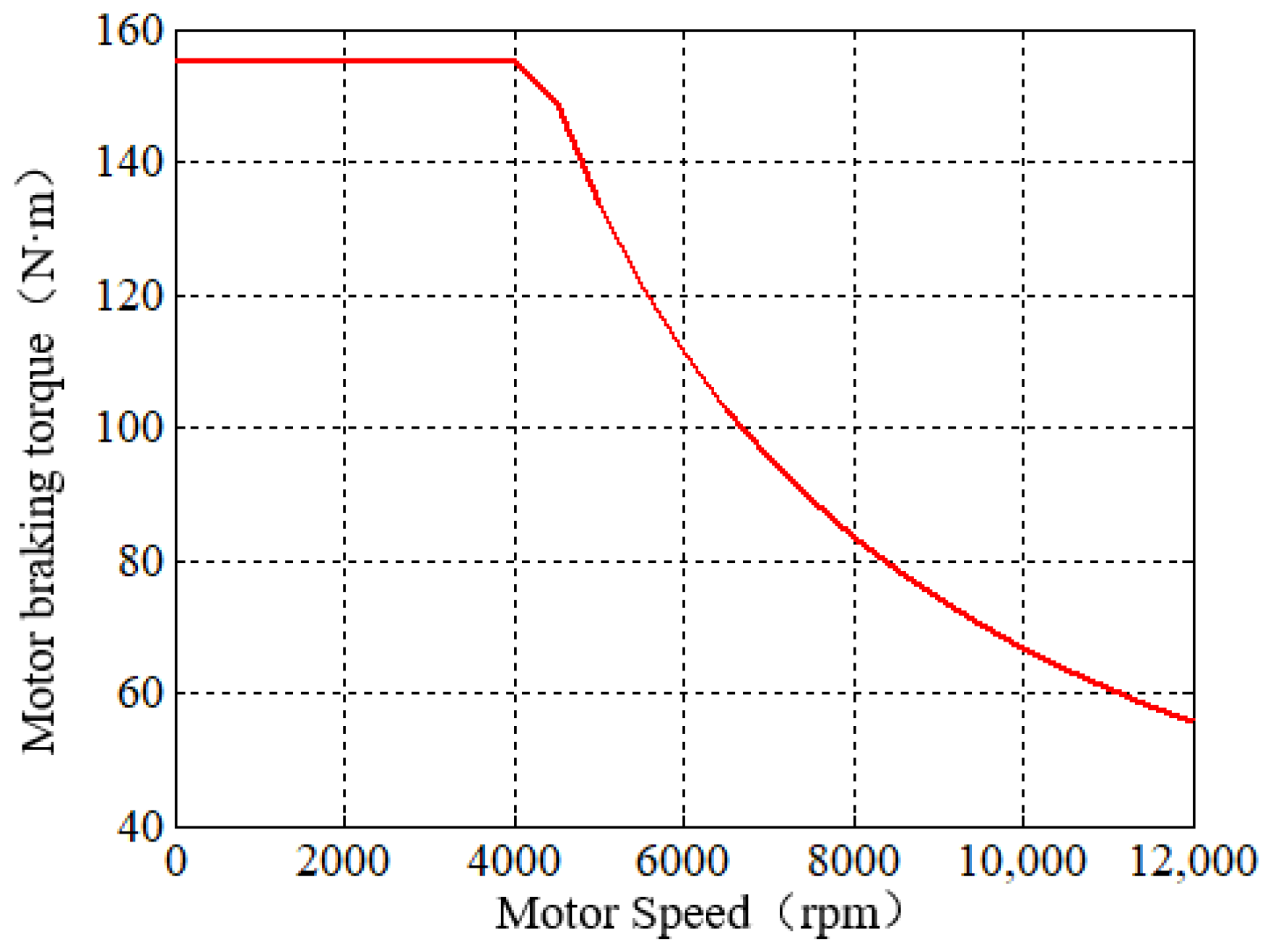
2.2. Motor Model
2.3. Power Battery Model
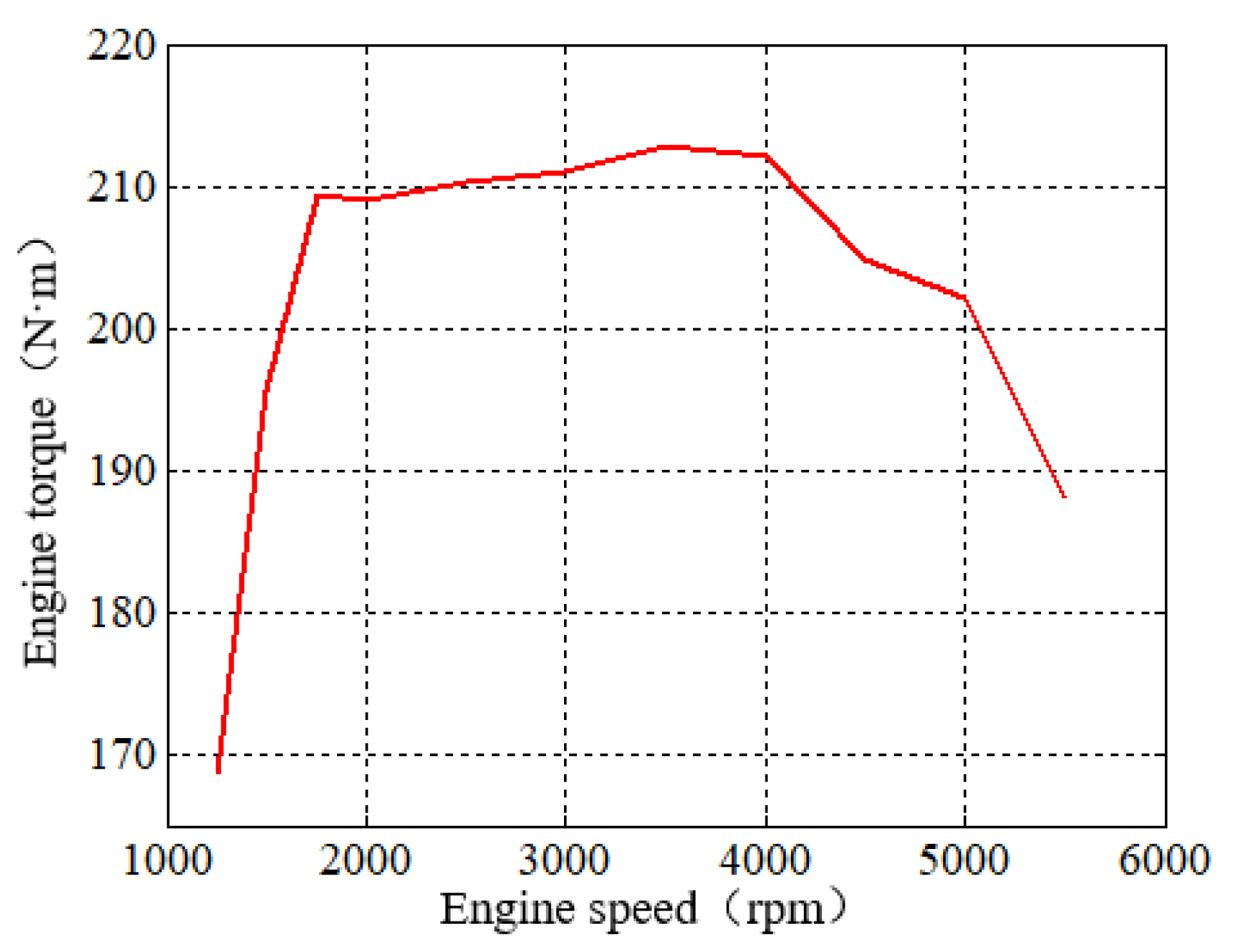
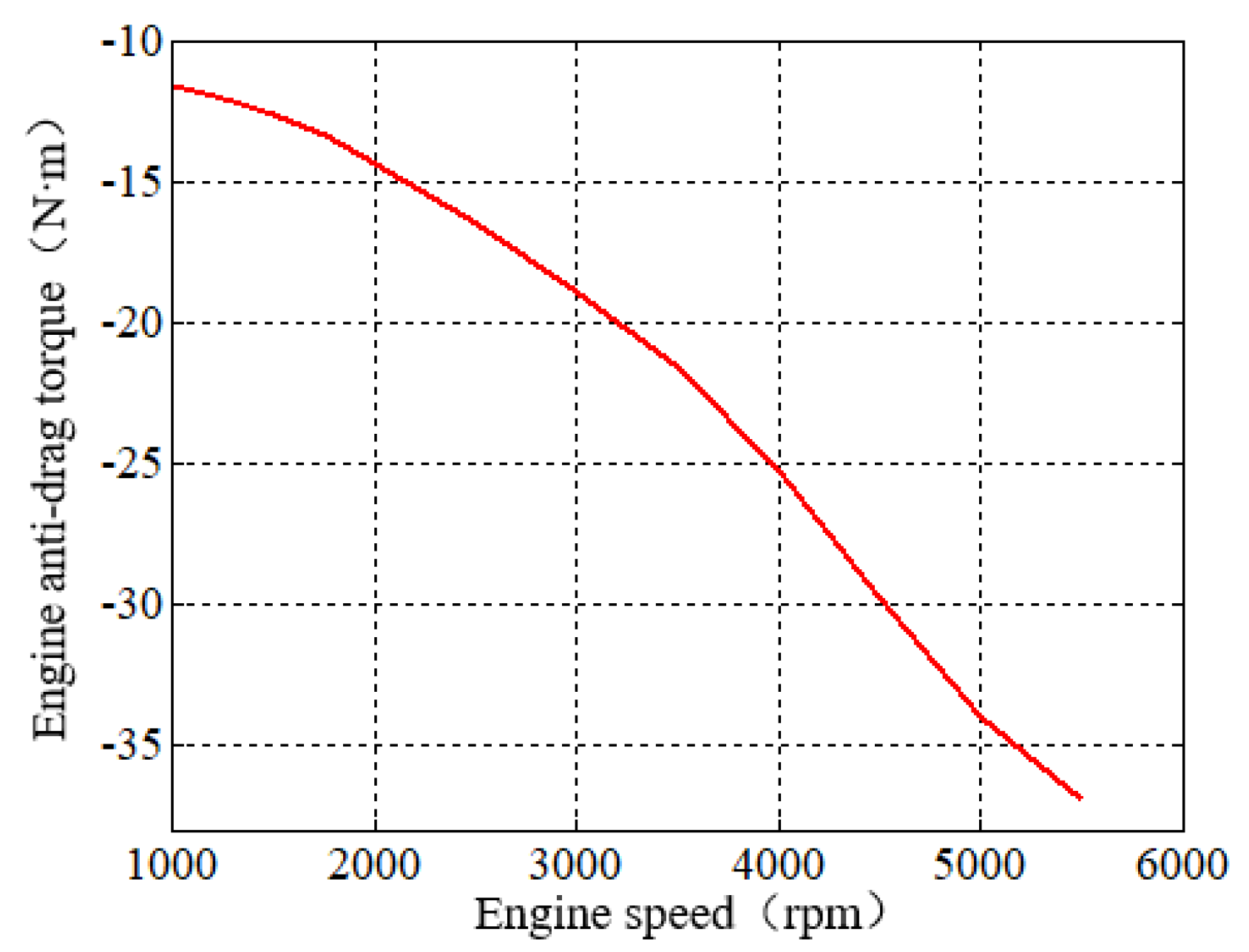
2.4. Engine Model
2.5. Vehicle Parameters
2.6. Braking Energy Recovery Control Strategy
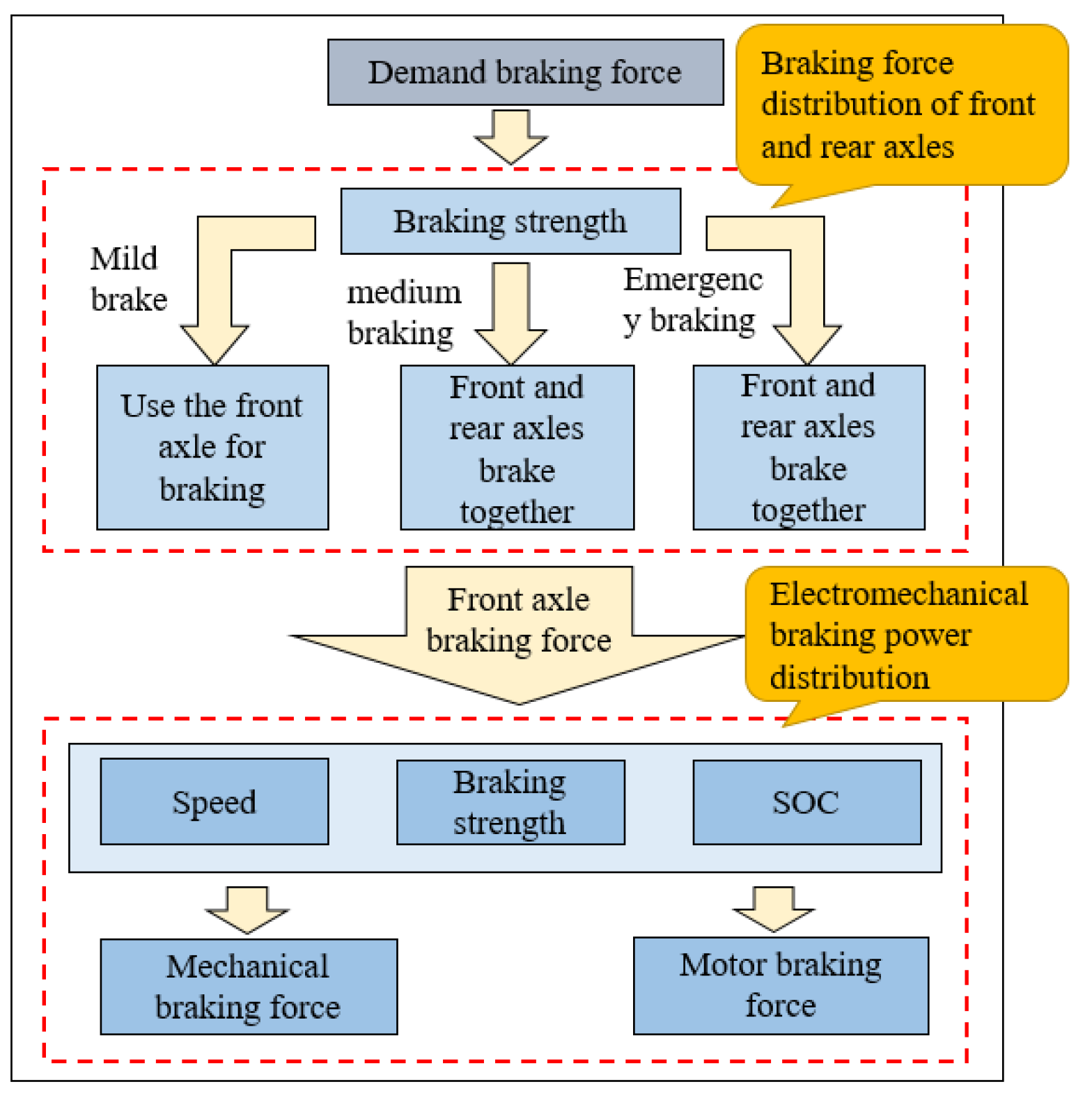
3. Control Strategy of Braking Force Distribution for Front and Rear Axles
3.1. Relationship between Braking Strength and Braking Force Distribution Coefficient
- The braking strength should satisfy for the biaxial vehicle with an adhesion coefficient of 0.2~0.8;
- when the braking strength z is 0.15~0.80, the adhesion coefficient utilization curve of the front axle should be above the adhesion coefficient utilization curve of the rear axle under various loads;
- when the braking strength z is 0.30~0.45, if the adhesion coefficient utilization curve of the rear axle does not exceed 0.05 above the straight line determined by the formula , the adhesion coefficient utilization curve of the rear axle can be above the adhesion coefficient utilization curve of the front axle.
3.2. Braking Mode Division and Braking Force Distribution
4. Control Strategy of Electromechanical Braking Force Distribution for Front Axle
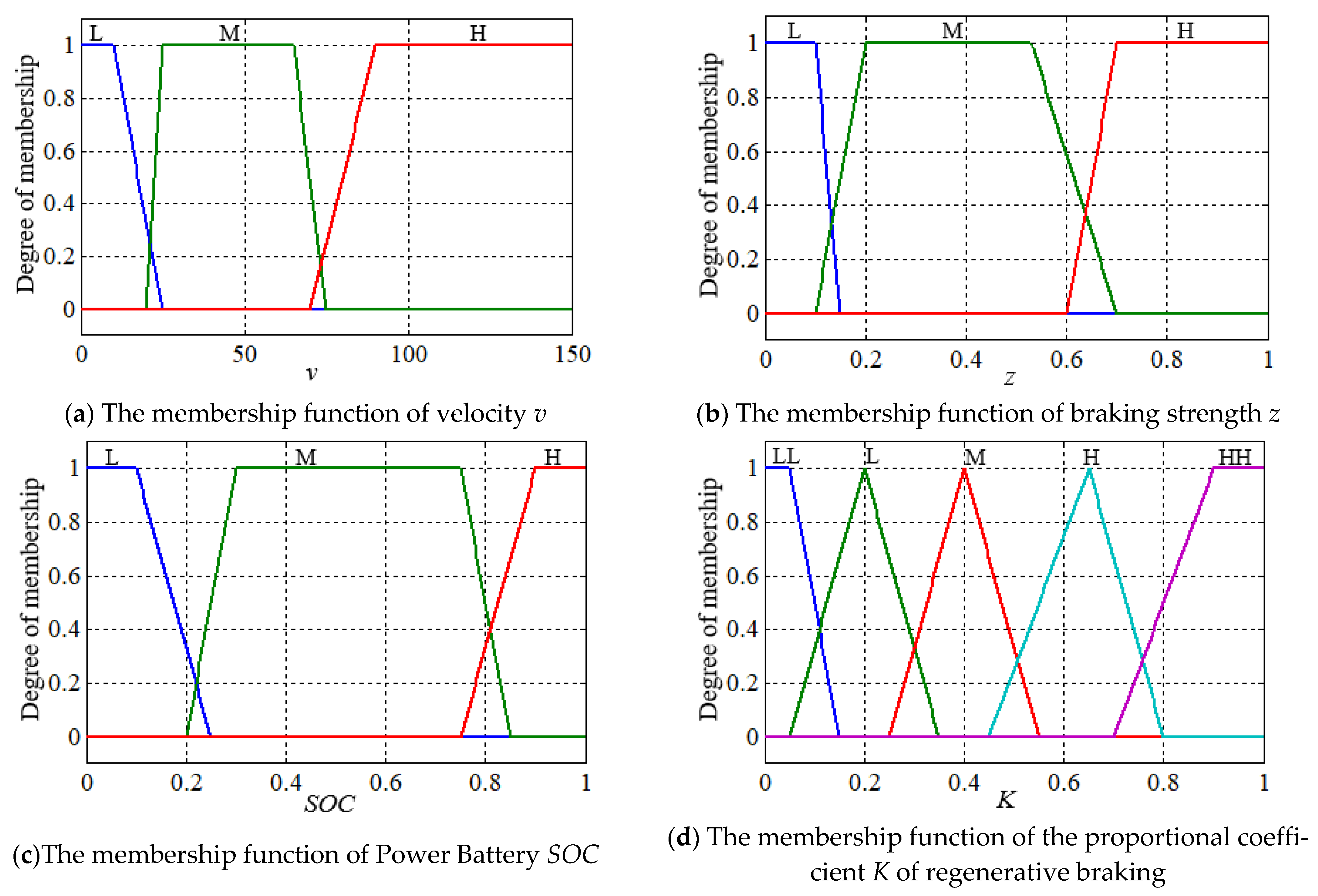
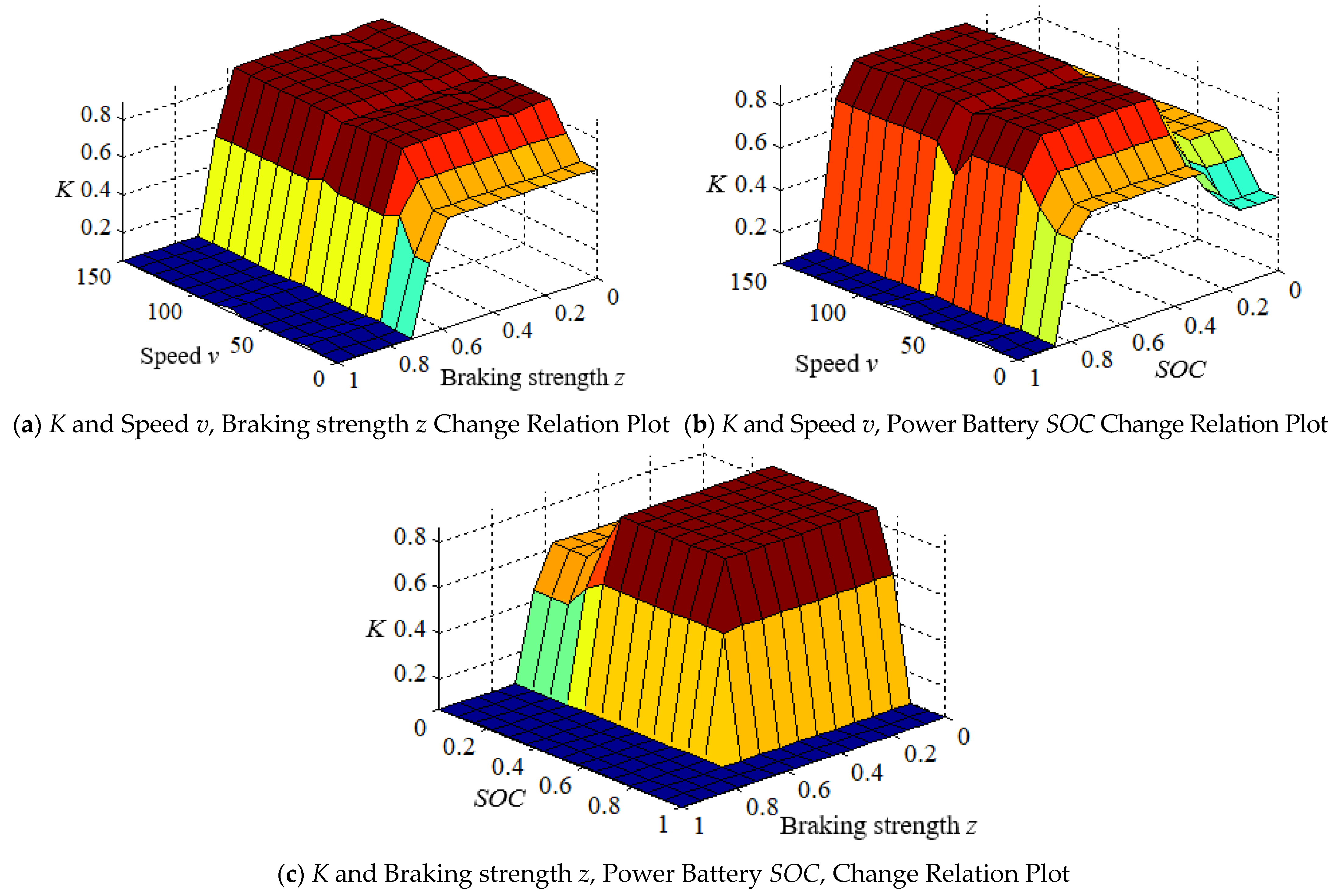
4.1. Design of Fuzzy Controller
4.2. Fuzzy Rules
4.3. Defuzzification
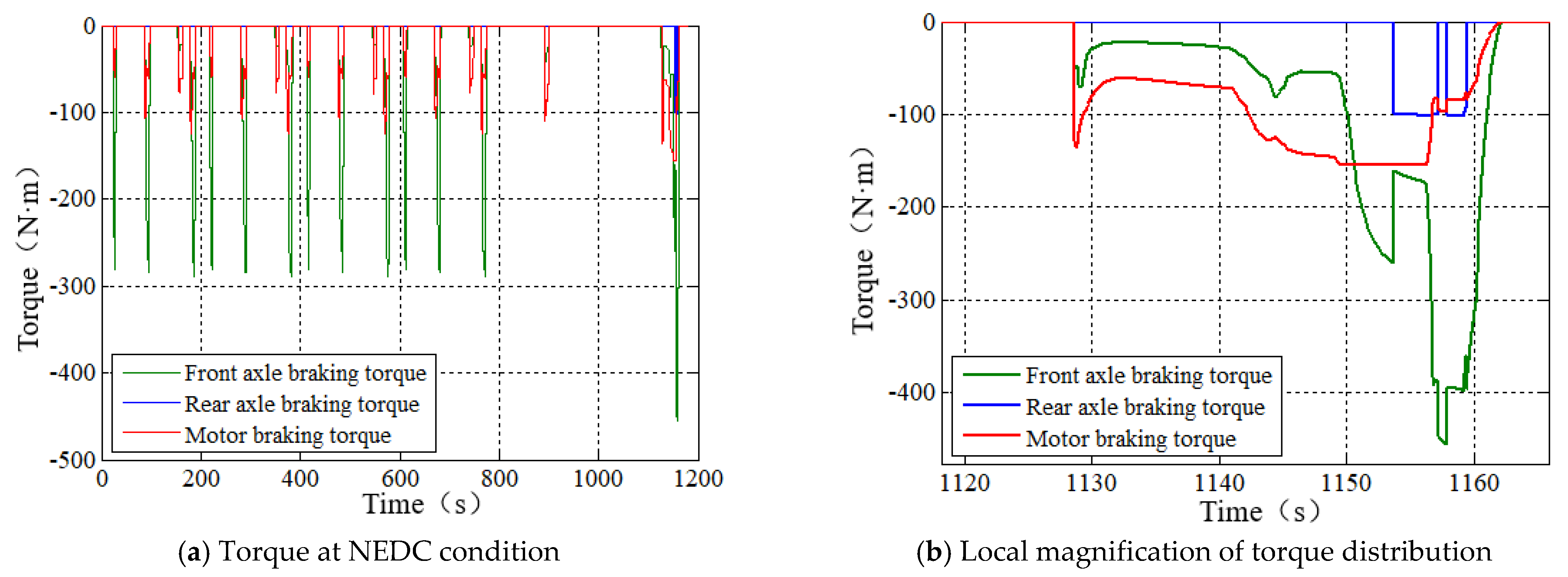
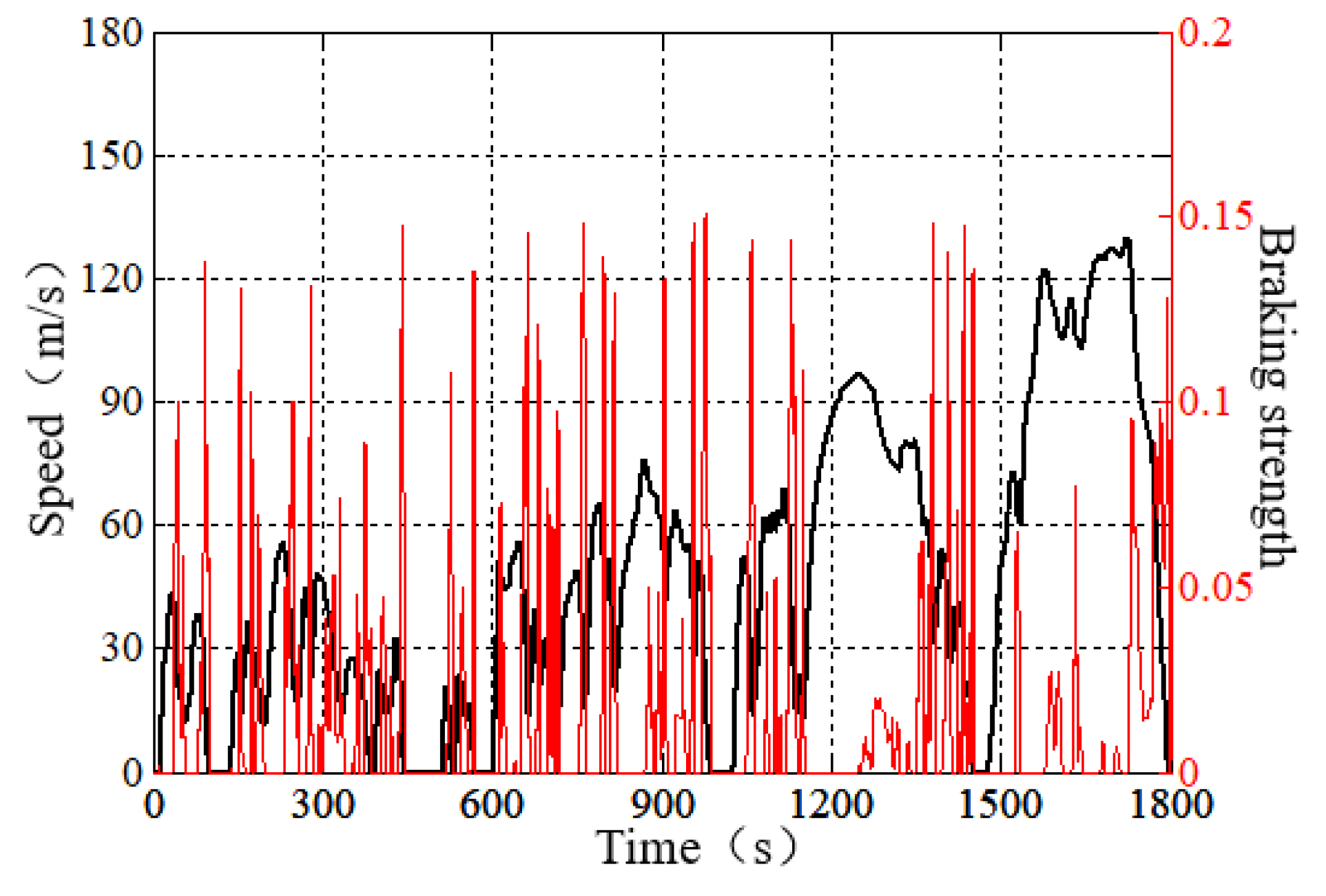
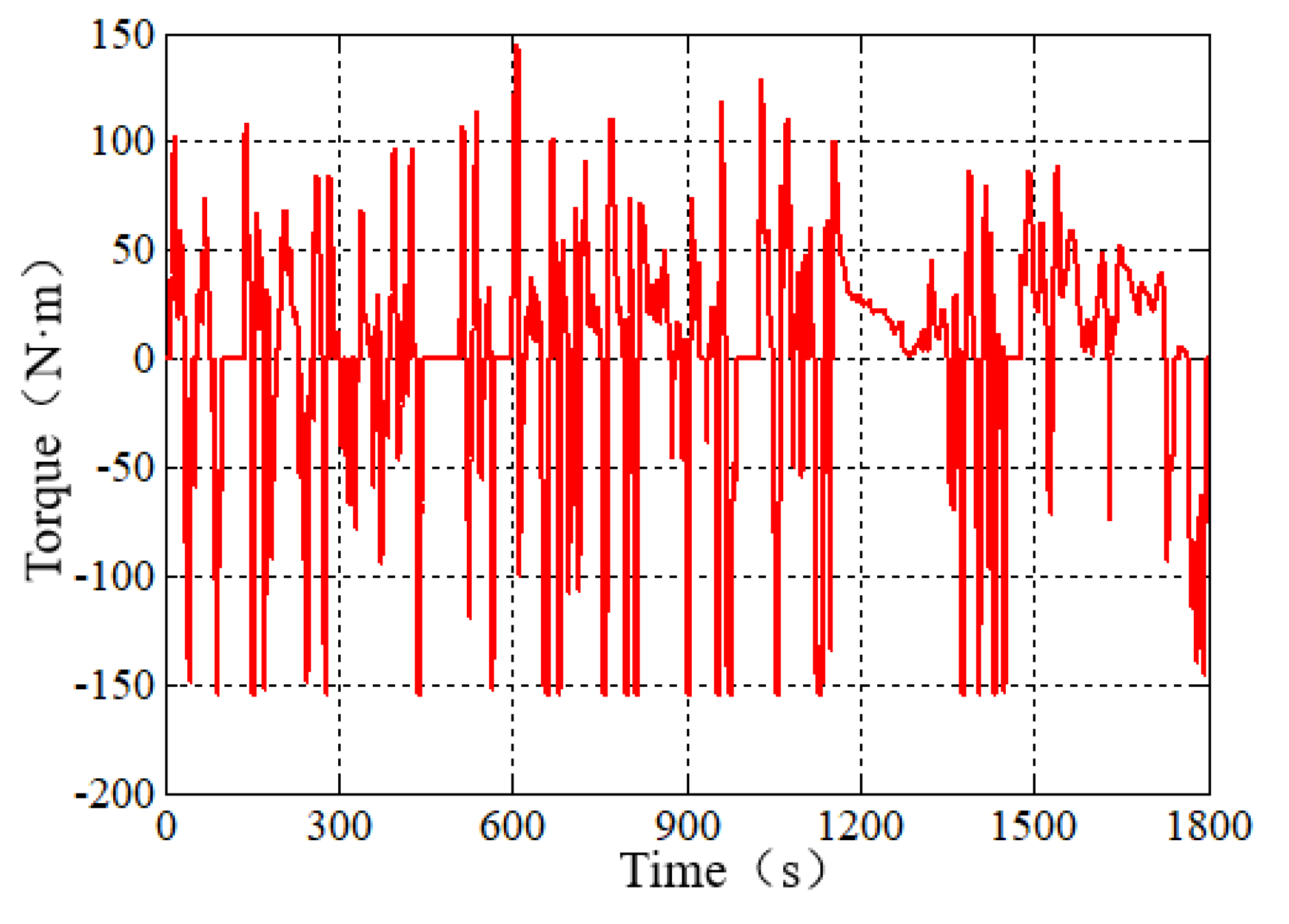
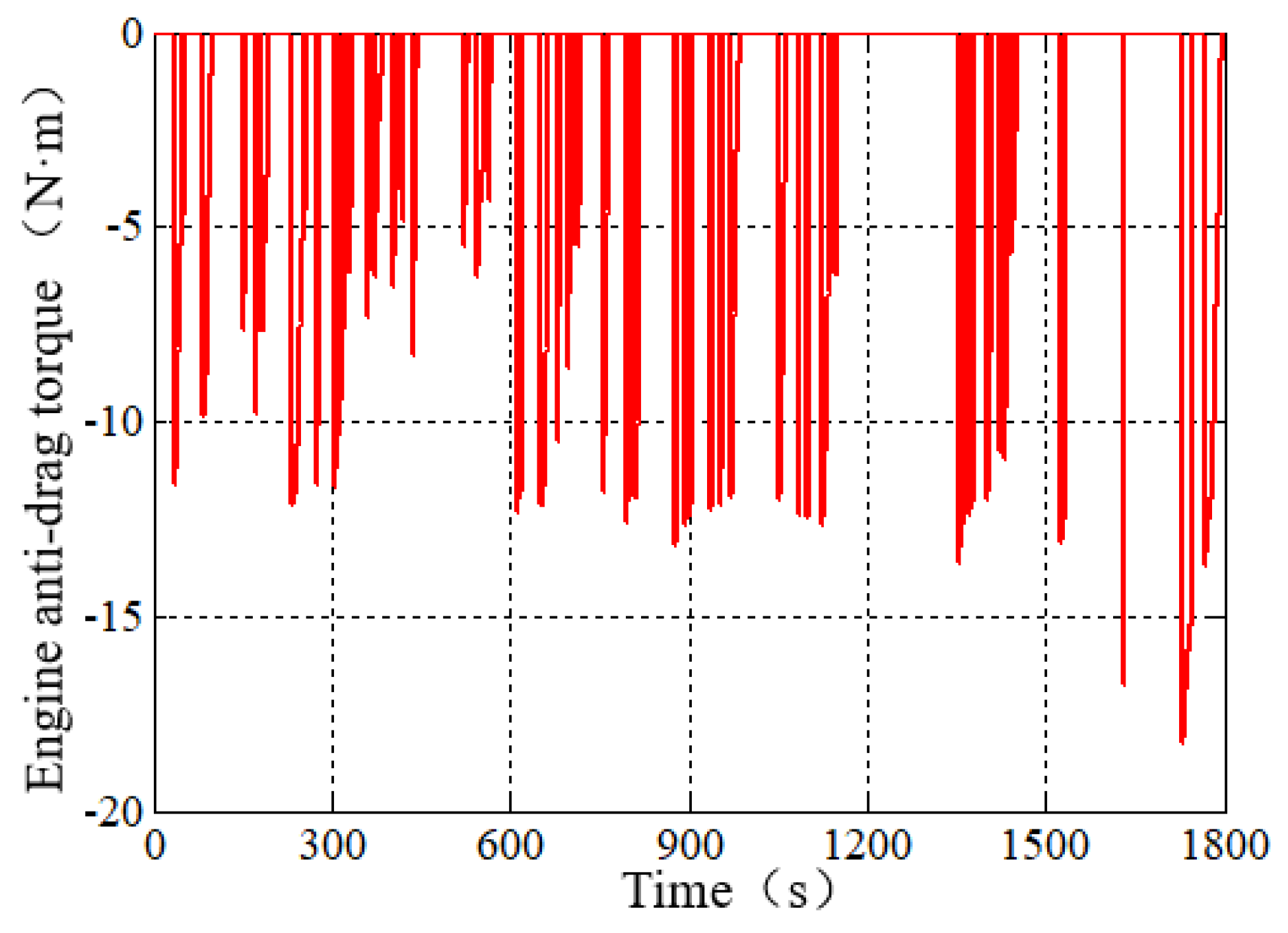
5. Simulation Results and Analysis
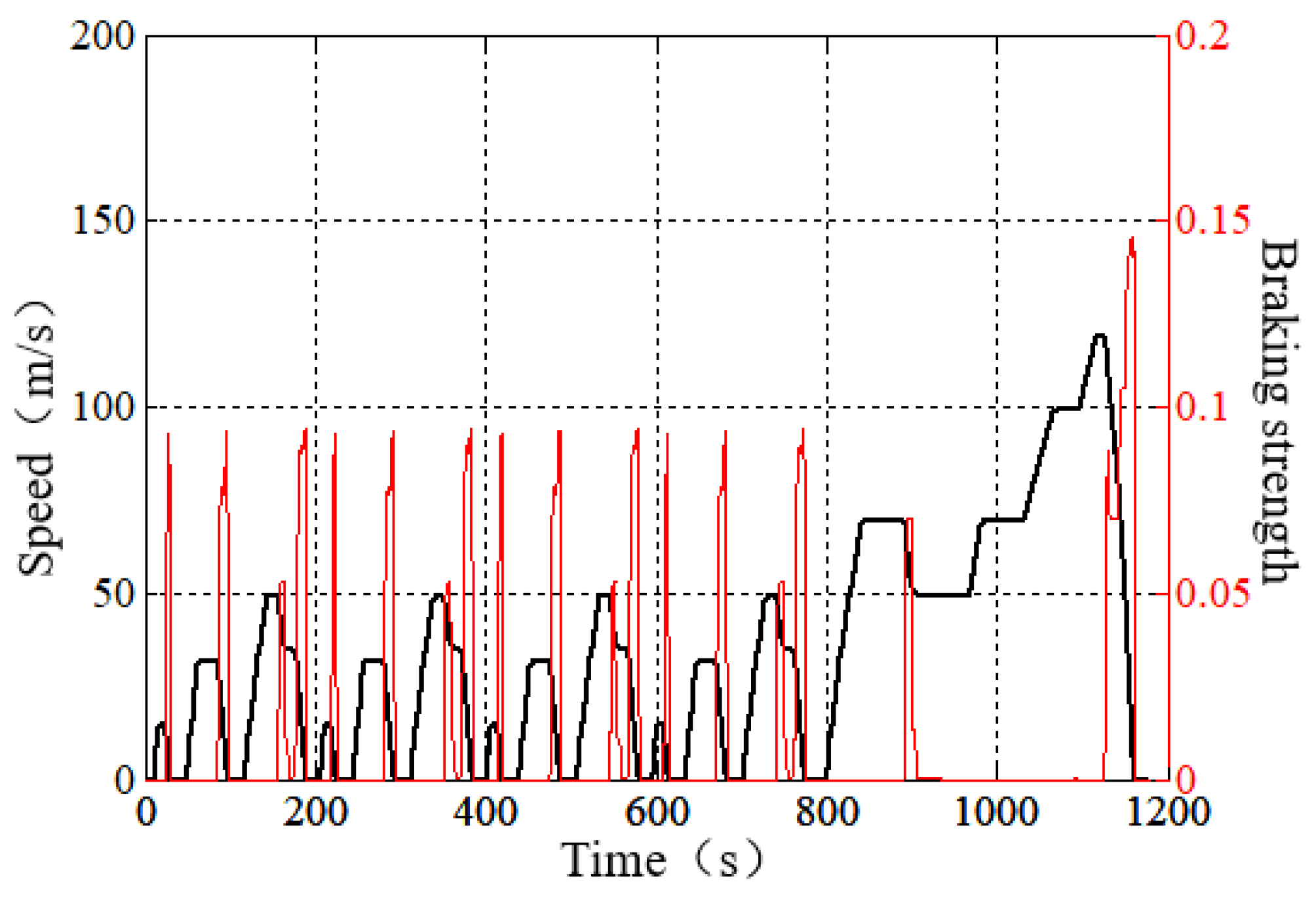
5.1. Simulation Analysis of Braking Energy Recovery Control Strategy for Hybrid Electric Vehicle
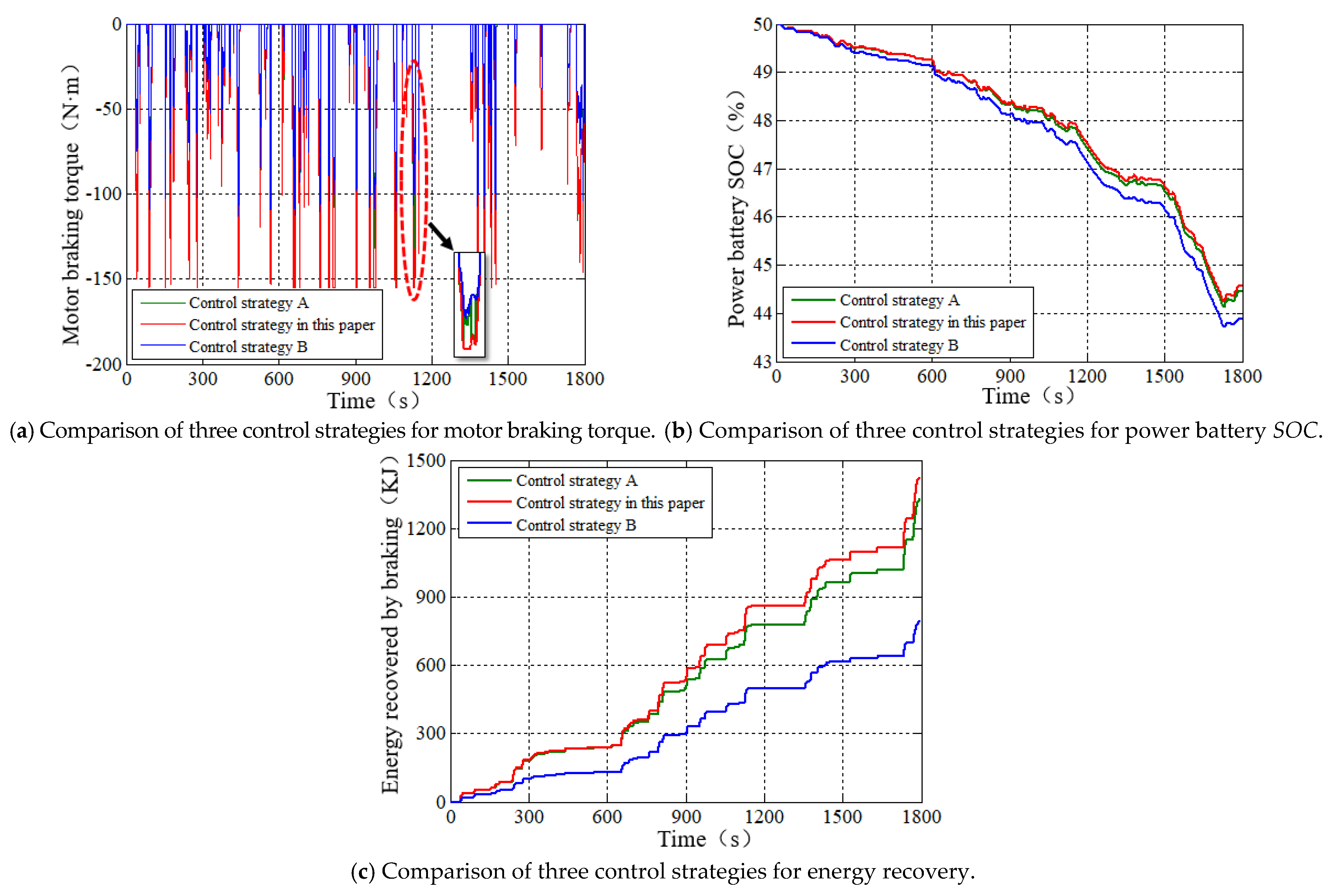
5.2. Comparative Analysis of Simulation Results of Different Braking Energy Recovery Control Strategies
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Enang, W.; Bannister, C. Modelling and control of hybrid electric vehicles (A comprehensive review). Renew. Sustain. Energy Rev. 2017, 74, 1210–1239. [Google Scholar] [CrossRef] [Green Version]
- Sharma, M.; Singh, A.N.; Yadav, R.; Jha, A.; Vanshaj, K.; Fahim, M. Regenerative Braking System. J. Trend Sci. Res. Dev. 2019, 3, 298–300. [Google Scholar] [CrossRef]
- Xu, L.; He, X.; Shen, X. Improving Energy Recovery Rate of the Regenerative Braking System by Optimization of Influencing Factors. Appl. Sci. 2019, 9, 3807. [Google Scholar] [CrossRef] [Green Version]
- Zhao, D.; Chu, L.; Xu, N.; Sun, C.; Xu, Y. Development of a Cooperative Braking System for Front-Wheel Drive Electric Vehicles. Energies 2018, 11, 378. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.; Zhang, H.; Xin, Y.; Salman, S. Research on Control Strategy of Hydraulic Regenerative Braking of Electrohydraulic Hybrid Electric Vehicles. Math. Probl. Eng. 2021, 2021, 5391351. [Google Scholar] [CrossRef]
- He, H.; Wang, C.; Jia, H. A single-pedal regenerative braking control strategy of accelerator pedal for electric vehicles based on adaptive fuzzy control algorithm. Energy Procedia 2018, 152, 624–629. [Google Scholar]
- Qiu, C.; Wang, G.; Meng, M.; Shen, Y. A novel control strategy of regenerative braking system for electric vehicles under safety critical driving situations. Energy 2018, 149, 329–340. [Google Scholar] [CrossRef]
- Wu, Y.; Shu, M.; Ge, H. Research on Brake Force Distribution Control Strategy of Electric Vehicle Subtitle as needed. Iop Conf. Ser. Mater. Sci. Eng. 2018, 452, 032054. [Google Scholar] [CrossRef]
- Xin, Y.; Zhang, T.; Zhang, H.; Zhao, Q.; Zheng, J.; Wang, C.; Pace, R.D. Fuzzy Logic Optimization of Composite Brake Control Strategy for Load-Isolated Electric Bus. Math. Probl. Eng. 2019, 2019, 9735368. [Google Scholar] [CrossRef]
- Liu, H.; Lei, Y.; Fu, Y.; Li, X. An Optimal Slip Ratio-Based Revised Regenerative Braking Control Strategy of Range-Extended Electric Vehicle. Energies 2020, 13, 1526. [Google Scholar] [CrossRef] [Green Version]
- Xu, W.; Chen, H.; Zhao, H.; Ren, B. Torque optimization control for electric vehicles with four in-wheel motors equipped with regenerative braking system. Mechatronics 2019, 57, 95–108. [Google Scholar] [CrossRef]
- Wu, J.; Wang, X.; Li, L.; Qin, C.; Du, Y. Hierarchical control strategy with battery aging consideration for hybrid electric vehicle regenerative braking control. Energy 2018, 145, 301–312. [Google Scholar] [CrossRef]
- Yang, Y.; He, Q.; Chen, Y.; Fu, C. Efficiency Optimization and Control Strategy of Regenerative Braking System with Dual Motor. Energies 2020, 13, 711. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Yu, B.; Feng, X. Research on braking energy recovery strategy of electric vehicle based on ECE regulation and I curve. Sci. Prog. 2020, 103, 36850419877762. [Google Scholar] [CrossRef] [PubMed]
- Xiao, B.; Lu, H.; Wang, H.; Ruan, J.; Zhang, N. Enhanced Regenerative Braking Strategies for Electric Vehicles: Dynamic Performance and Potential Analysis. Energies 2017, 10, 1875. [Google Scholar]
- Zhou, M.; Wang, J.; Chen, Q. Research on vehicle controller and control strategy for pure electric vehicle with composite power. Int. J. Electr. Hybrid Veh. 2019, 11, 170–193. [Google Scholar] [CrossRef]
- Ma, K.; Wang, Z.; Liu, H.; Yu, H.; Wei, C. Numerical Investigation on Fuzzy Logic Control Energy Management Strategy of Parallel Hybrid Electric Vehicle. Energy Procedia 2019, 158, 2643–2648. [Google Scholar] [CrossRef]
- Pei, X.; Pan, H.; Chen, Z.; Guo, X.; Yang, B. Coordinated control strategy of electro-hydraulic braking for energy regeneration. Control Eng. Pract. 2020, 96, 104324. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, Y.; Zhu, R.; Geng, R.; Zhang, J.; Fan, D.; Wang, H. Study on the Control Strategy of Regenerative Braking for the Hybrid Electric Vehicle under Typical Braking Condition. IOP Conf. Ser. Mater. Sci. Eng. 2018, 452, 032092. [Google Scholar] [CrossRef]







| Parameters | Numerical Value | |
|---|---|---|
| Windward area (m2) | 2.638 | |
| Wheelbase (m) | 2.710 | |
| Vehicle fit-up quality (kg) | 1545 | |
| Vehicle parameters | Rolling radius of tire (m) | 0.347 |
| Height center of mass (m) | 0.650 | |
| Drive Mode (FWD/AWD/RWD) | FWD (front drive) | |
| Transmission ratio | 3.12 | |
| Maximum Motor Power (kw) | 70 | |
| Motor parameters | Maximum torque of motor (N·m) | 155 |
| Maximum speed of motor (rpm) | 12,000 | |
| Battery parameter | Battery capacity (Ah) | 75 |
| Voltage Range (V) | 260~420 |
| V | SOC | z | K | v | SOC | z | K | ||
|---|---|---|---|---|---|---|---|---|---|
| 1 | L | H | L | VL | 15 | M | M | H | VL |
| 2 | L | H | M | VL | 16 | H | M | L | VH |
| 3 | L | H | H | VL | 17 | H | M | M | H |
| 4 | M | H | L | VL | 18 | H | M | H | VL |
| 5 | M | H | M | VL | 19 | L | L | L | M |
| 6 | M | H | H | VL | 20 | L | L | M | M |
| 7 | H | H | L | VL | 21 | L | L | H | VL |
| 8 | H | H | M | VL | 22 | M | L | L | H |
| 9 | H | H | H | VL | 23 | M | L | M | H |
| 10 | L | M | L | L | 24 | M | L | H | VL |
| 11 | L | M | M | M | 25 | H | L | L | VH |
| 12 | L | M | H | VL | 26 | H | L | M | H |
| 13 | M | M | L | VH | 27 | H | L | H | VL |
| 14 | M | M | M | VH |
| Control Strategy | Control Strategy A | Control Strategy B | Control Strategy Proposed in This Paper | |||
|---|---|---|---|---|---|---|
| NEDC | WLTC | NEDC | WLTC | NEDC | WLTC | |
| Total energy consumption of vehicles (KJ) | 4212.36 | 12,141.2 | 4201.19 | 12,043.53 | 4224.82 | 12,131.13 |
| Total braking energy (KJ) | 1640.81 | 3677.4 | 1632.72 | 3646.52 | 1676.80 | 3681.21 |
| Energy recovered by braking (KJ) | 603.25 | 1324.61 | 344.51 | 790.20 | 656.90 | 1420.34 |
| Effective energy recovery rate (%) | 14.32 | 10.91 | 8.20 | 6.56 | 15.55 | 11.71 |
| Braking energy recovery rate (%) | 36.76 | 36.02 | 21.10 | 21.67 | 39.18 | 38.58 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, C.; Ning, D.; Guo, L.; Xue, Q.; Mei, S. Simulation Research on Regenerative Braking Control Strategy of Hybrid Electric Vehicle. Energies 2021, 14, 2202. https://doi.org/10.3390/en14082202
Geng C, Ning D, Guo L, Xue Q, Mei S. Simulation Research on Regenerative Braking Control Strategy of Hybrid Electric Vehicle. Energies. 2021; 14(8):2202. https://doi.org/10.3390/en14082202
Chicago/Turabian StyleGeng, Cong, Dawen Ning, Linfu Guo, Qicheng Xue, and Shujian Mei. 2021. "Simulation Research on Regenerative Braking Control Strategy of Hybrid Electric Vehicle" Energies 14, no. 8: 2202. https://doi.org/10.3390/en14082202
APA StyleGeng, C., Ning, D., Guo, L., Xue, Q., & Mei, S. (2021). Simulation Research on Regenerative Braking Control Strategy of Hybrid Electric Vehicle. Energies, 14(8), 2202. https://doi.org/10.3390/en14082202







