Alternating Current Loss of Superconductors Applied to Superconducting Electrical Machines
Abstract
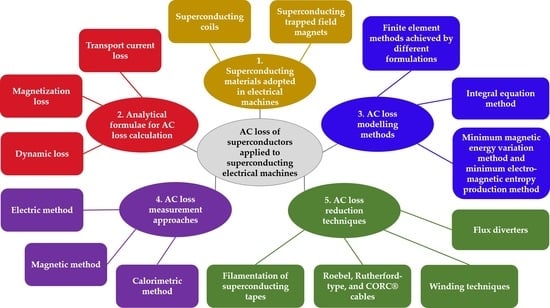
:1. Introduction
2. Superconducting Materials Applied to Electrical Machines
3. Analytical Formulae for AC Loss Calculation
4. Modelling Methods
- (1)
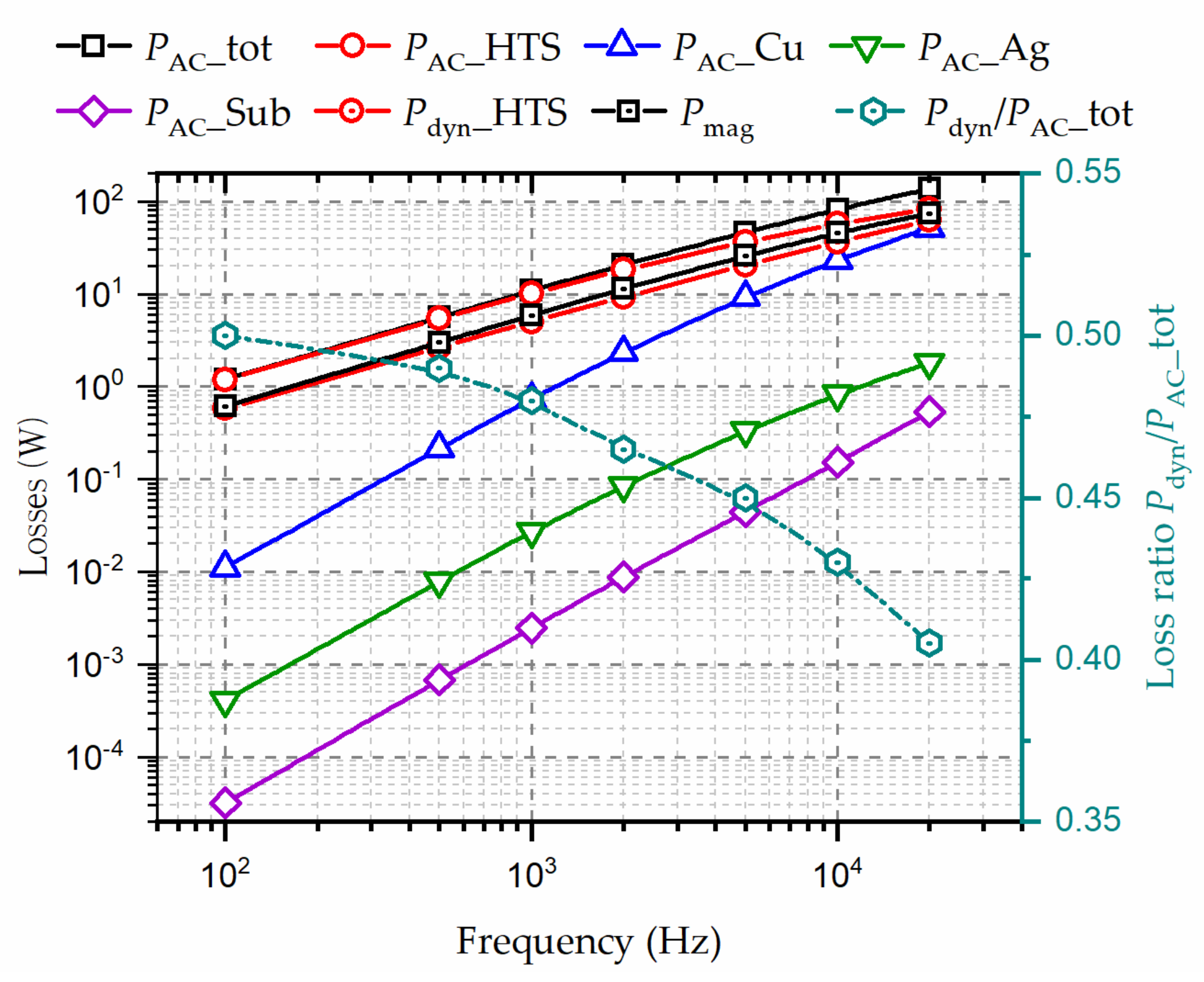
- Aerospace electrical machines work at very high speeds (7–50 krpm), and accordingly the adopted HTS materials in superconducting machines ought to be capable of operating in a high-frequency electromagnetic environment (~0.2–2 kHz) [15]. Until now, the vast majority of numerical models are based on the thin film approximation and only the HTS layer is considered, which has been proven inapplicable for high frequencies beyond 100 Hz for the first time by our previous research work [22,23,24]. Therefore, the multilayer physical structure of the commercial HTS CC needs to be taken into account, typically composed of the copper stabilizers, silver overlayer, and substrate, in addition to the HTS layer, as shown in Figure 2b. In [23], Zhang et al. have analyzed the magnetization loss and dynamic loss of HTS CCs, stacks, circular coils as well as racetrack coils over a wide frequency band from 50 Hz to 20 kHz using the H-formulation-based multilayer numerical models. The modelled losses in different layers of the studied 2 × 12 double pancake racetrack coil in [23] are shown in Figure 6. It can be found that the loss in the copper layer increases fast and it will be approaching the magnetization loss and the total AC loss with increasing frequency. Musso et al. have also studied the AC loss distributions in various layers of HTS CCs by use of the A−V formulation and found that the contribution to the total losses of the non-superconducting parts is strengthened when the field frequency surpasses 1 kHz [126]. However, the electromagnetic interaction among different layers can largely increase the number of DOF and computational complexity, especially for the 3D modelling of racetrack coils.
- (2)
- The electromagnetic environment in electrical machines is quite complex, composed of high-frequency harmonics. Therefore, the electromagnetic signals are not purely sinusoidal. The vast majority of numerical models concentrate on the AC loss with standard sinusoidal AC transport current or magnetic fields. Although some simulation work of AC loss has considered both the DC background field, AC ripple field, and non-sinusoidal currents [127,128,129,130], the input signals for simulation are not real synthetic signals generated inside practical electrical machines. Consequently, the performance of HTS CCs under a complex synthetic electromagnetic environment deserves further exploration.
- (3)
- The magnetic field distribution inside HTS machines is determined by both the superconducting and non-superconducting parts; thus, just modelling the superconductors is not sufficient to reflect the overall power dissipation of the machine that decides the design of cryogenic systems. The non-superconducting parts can contain conventional conductors, iron cores, and permanent magnets; thus, their electromagnetic interaction with the superconductors has to be considered. However, the existing numerical models have rarely considered the influence of non-superconducting parts.
- (4)
- 3D numerical models of superconducting machines are still lacking due to a large number of DOF and high computation complexity. Studies on convergence and computational speed in 3D models have to be thoroughly conducted to improve simulation efficiency.
- (5)
- Besides the electromagnetic properties, the thermal characteristics of superconductors should also be investigated because they directly affect the design of cryocoolers and quench protection. An electro-thermal numerical model for high-speed superconducting machines needs to be developed.
- (6)
- The stability of superconducting materials is critical to the normal functioning of the machine. The high centrifugal force in high-speed electrical machines brings a big challenge to the design of rotating field coils. Apart from the necessary mechanical simulation, online monitoring and fault detection methods of HTS machines have not been studied due to the lack of superconducting machine demonstrators.
5. AC Loss Measurement Approaches
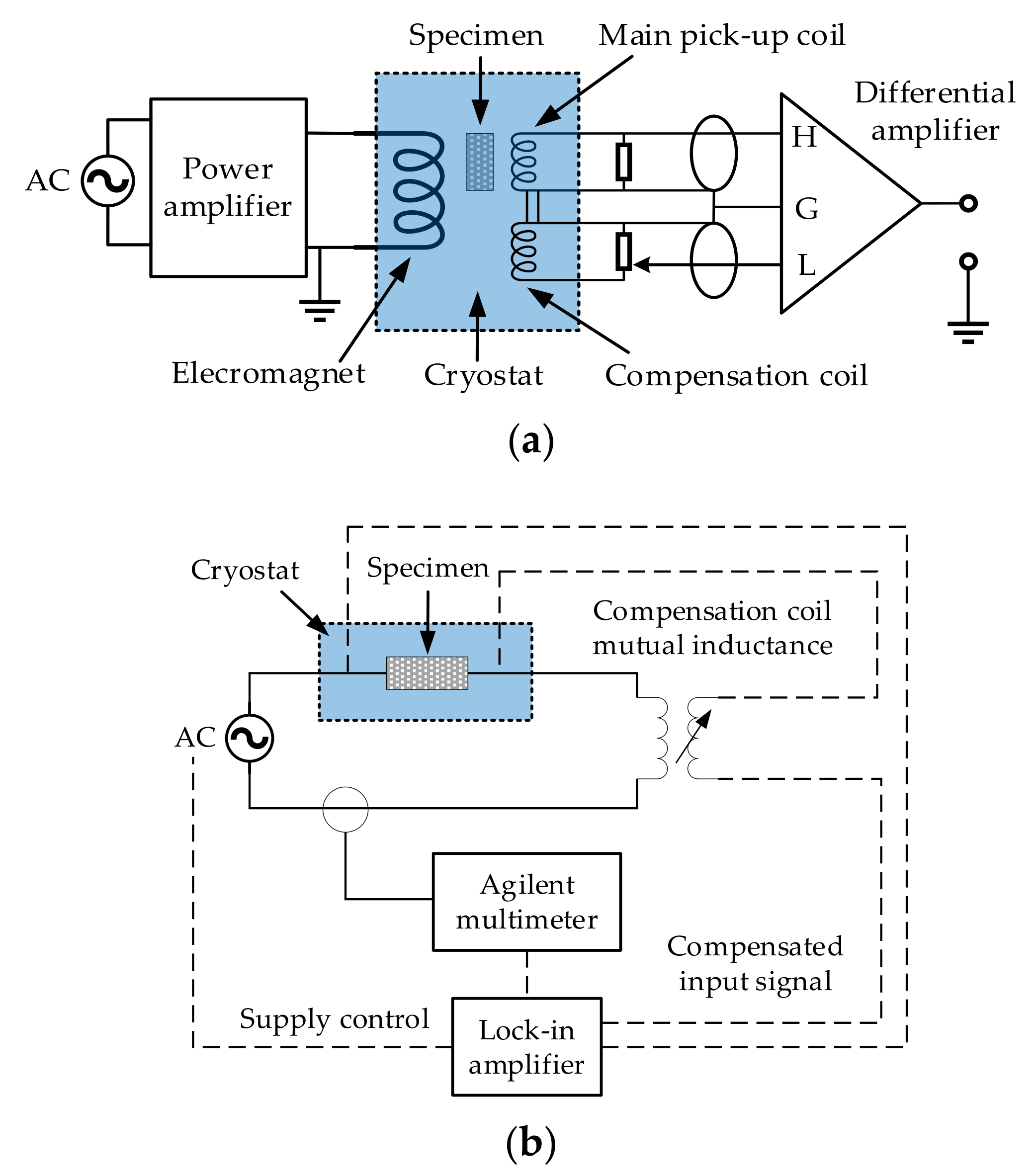
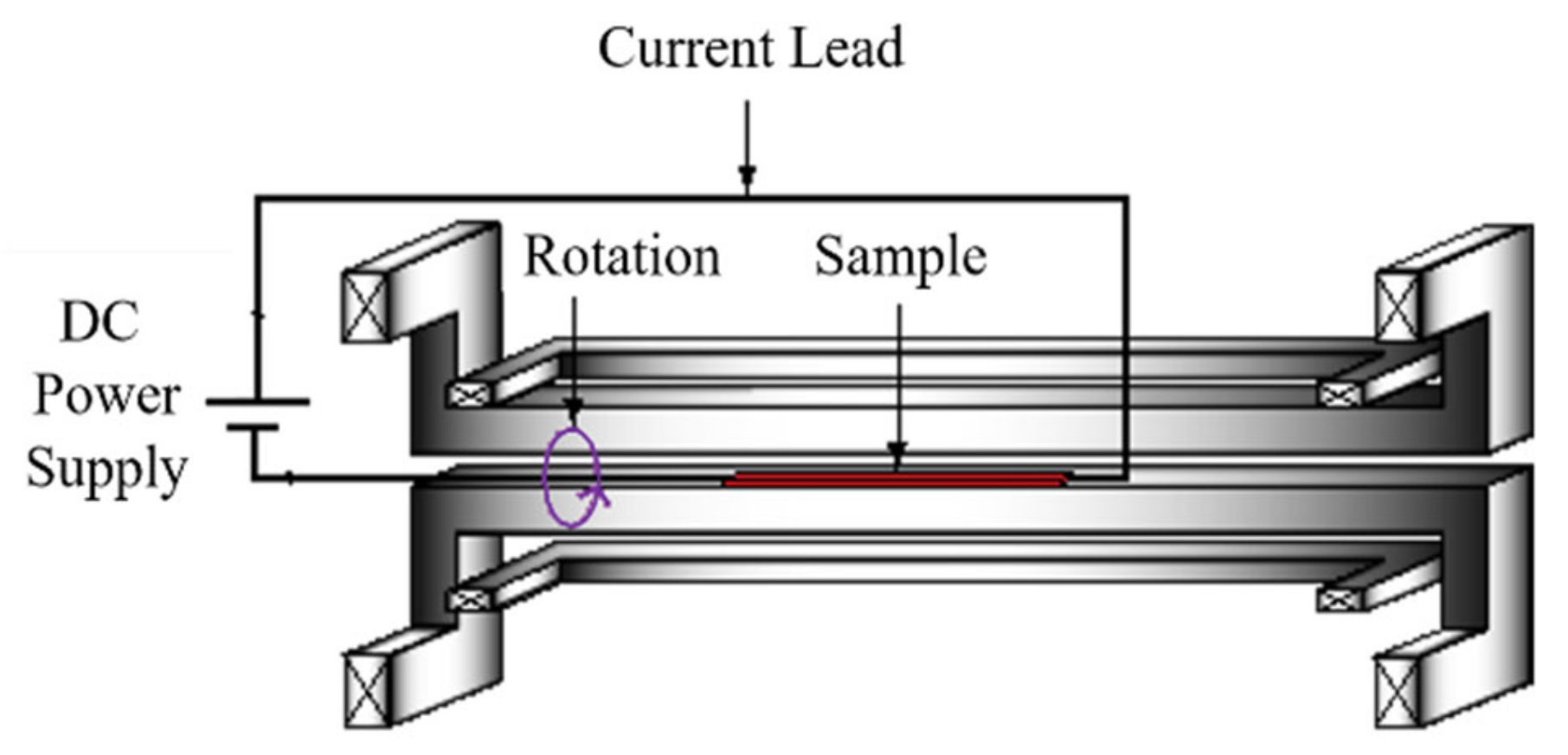
5.1. Electric Method
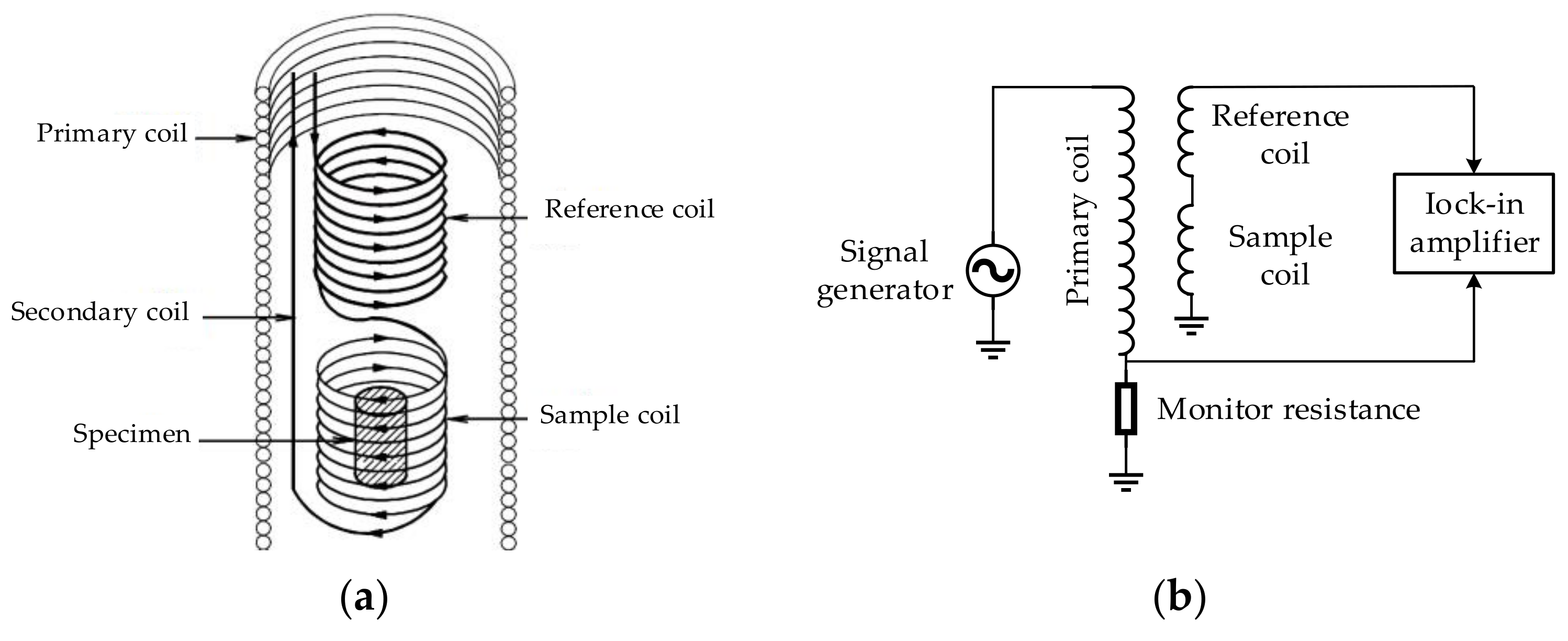
5.2. Magnetic Method
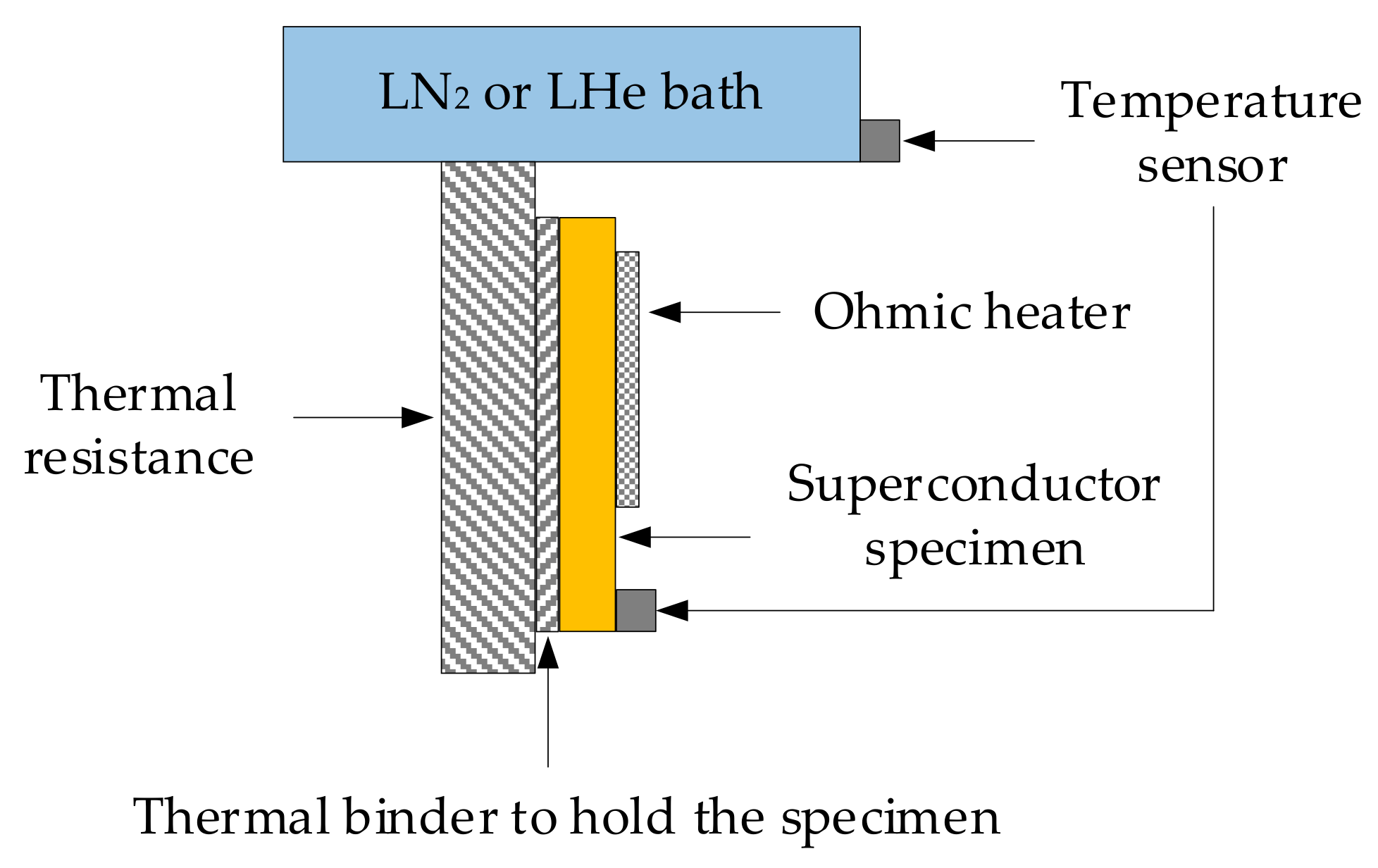
5.3. Calorimetric Method
5.3.1. Measurement of the Temperature Rise
5.3.2. Measurement of the Cryogen Evaporation
6. AC Loss Reduction Techniques
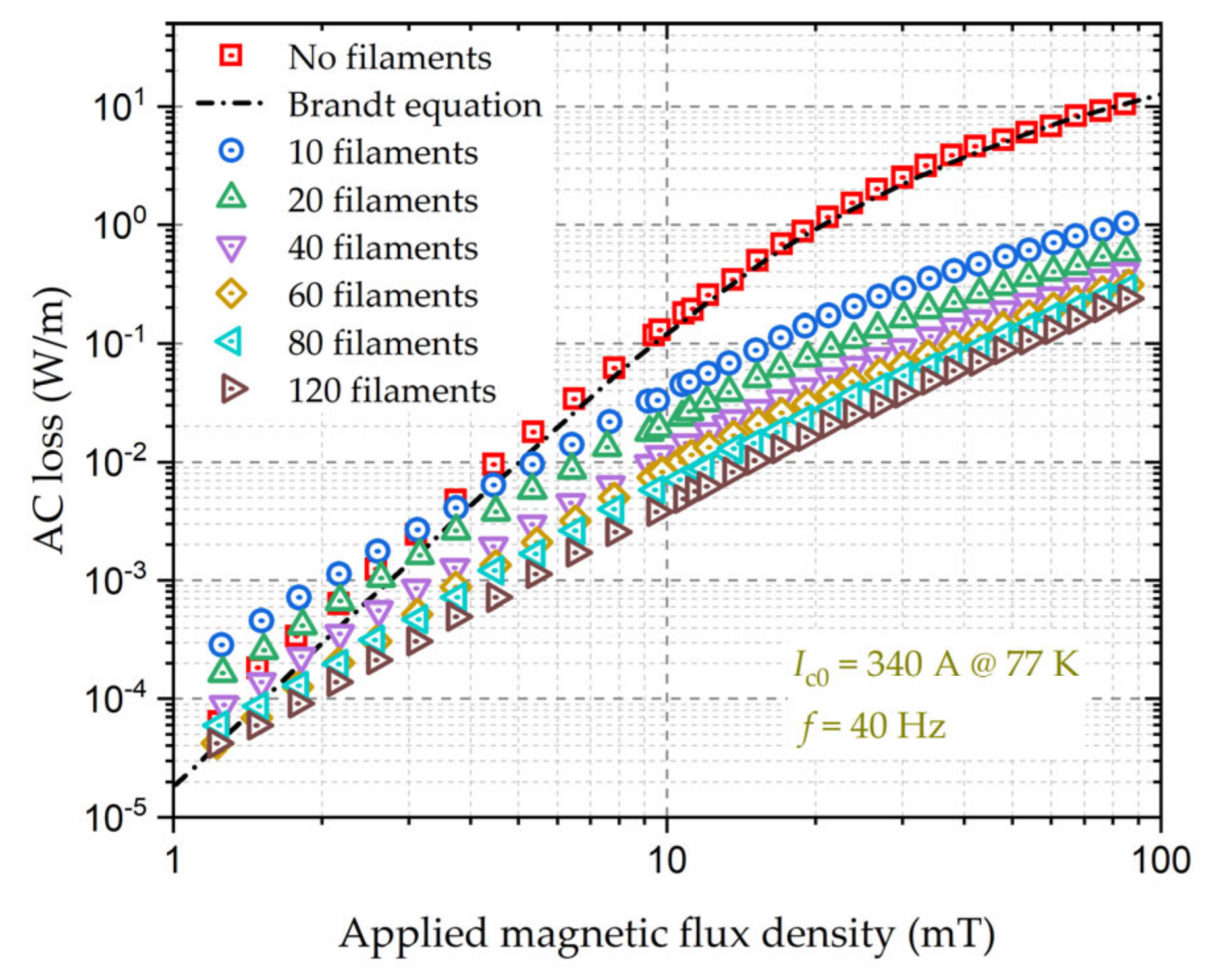
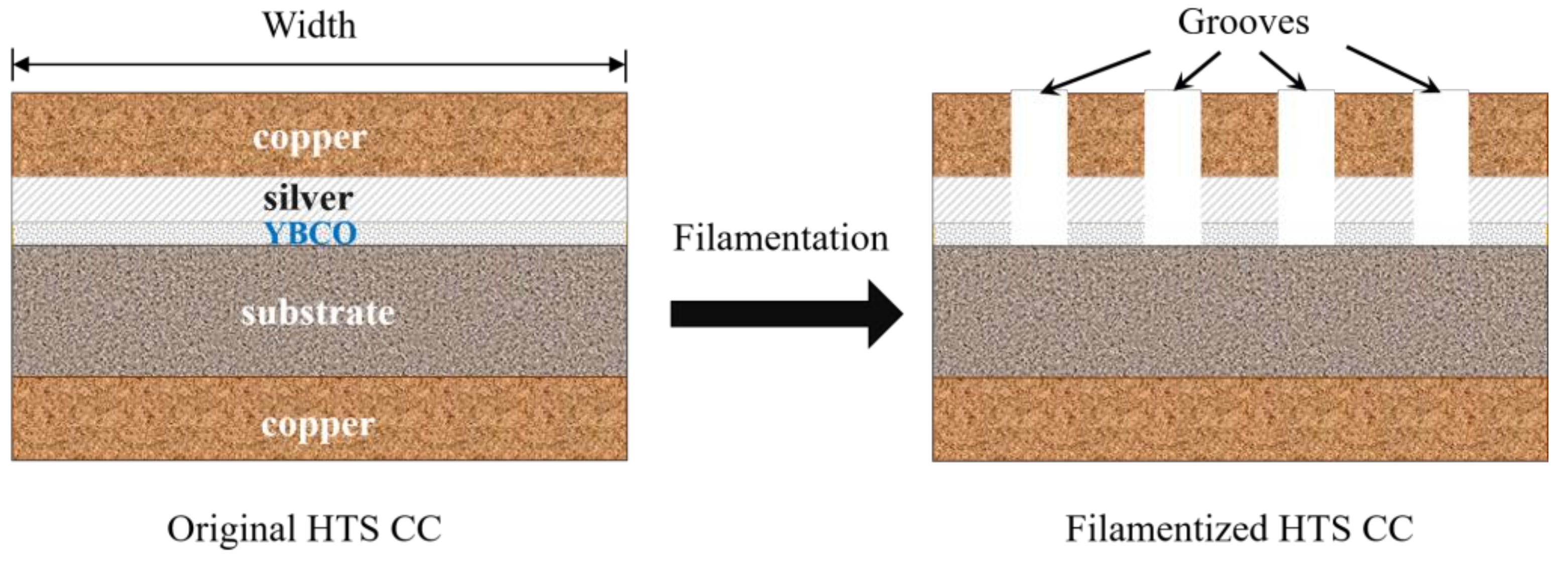
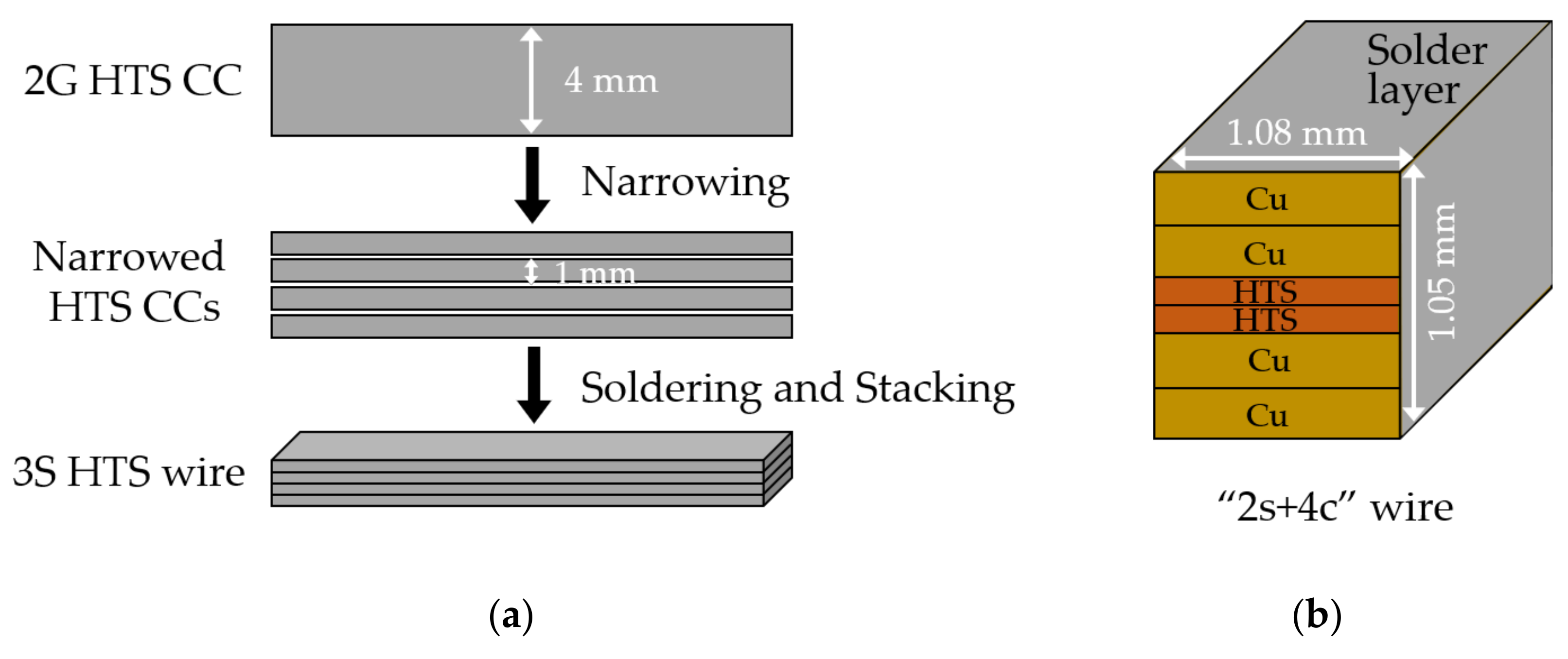
6.1. Filamentation of HTS CCs
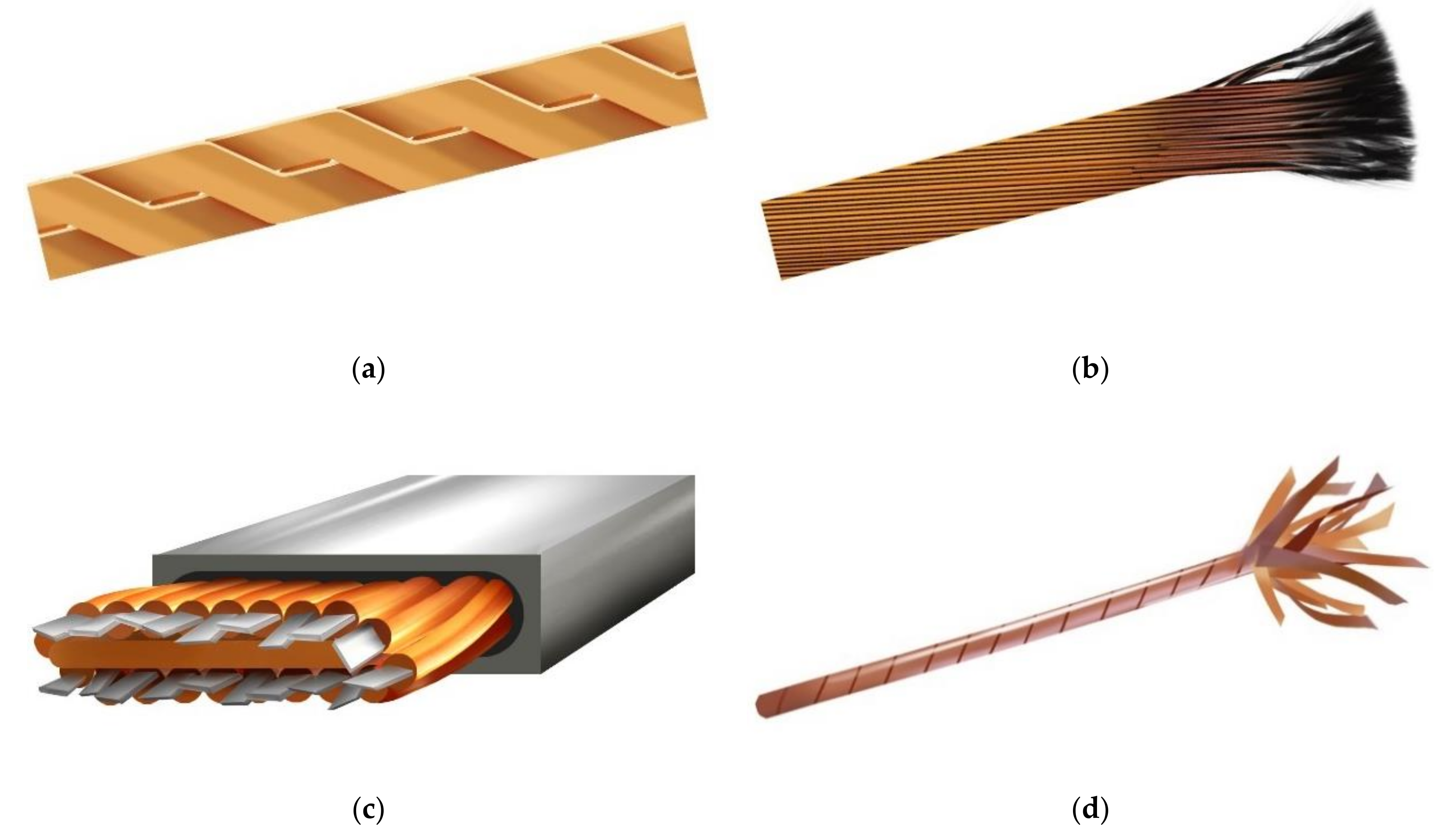
6.2. Roebel, Rutherford-Type, and CORC® Cables
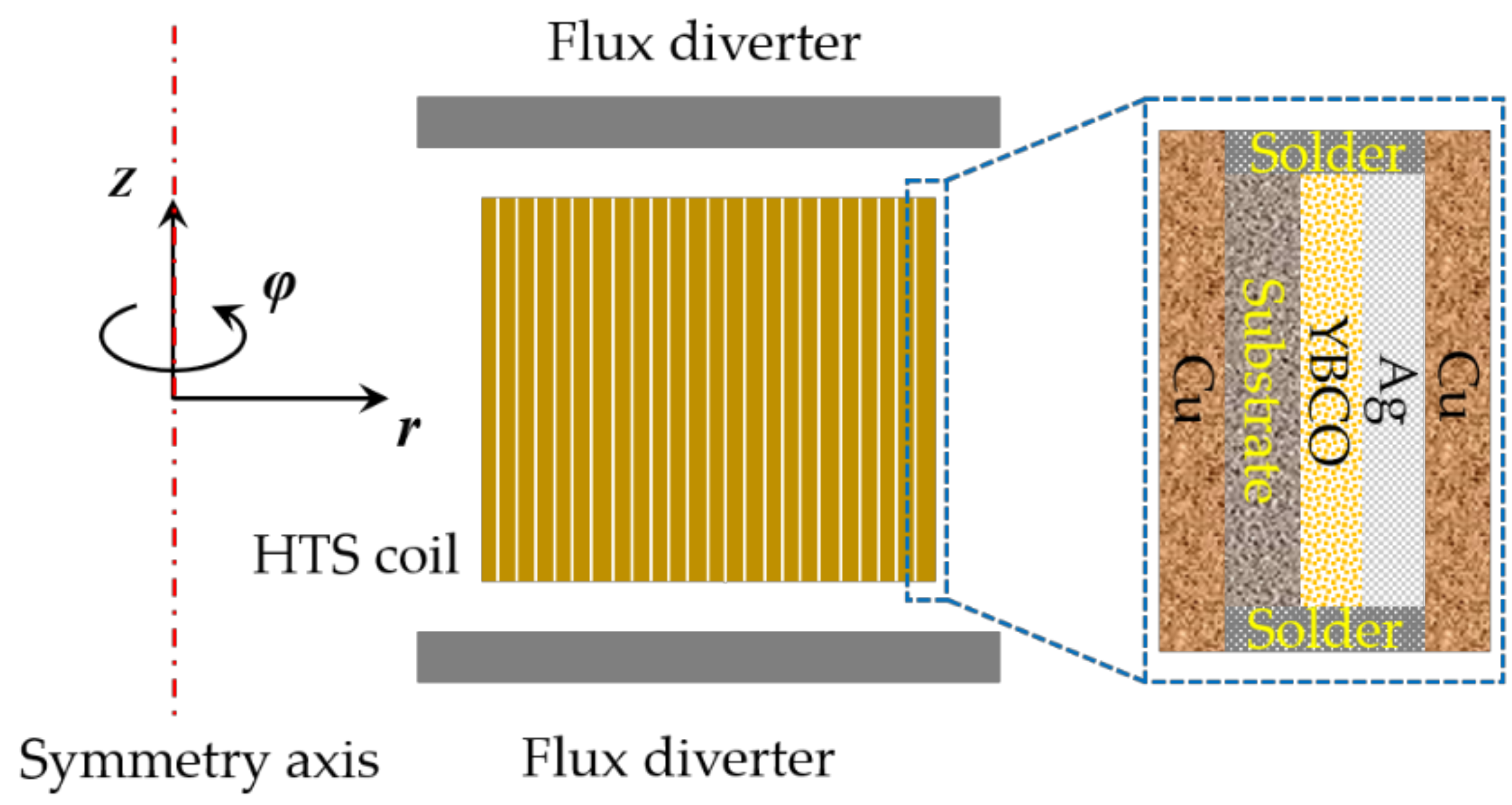
6.3. Flux Diverters
6.4. Winding Techniques
- (1)
- The filamentation of HTS CCs, the Roebel, the Rutherford as well as the CORC cables can help with the reduction of AC loss. However, their electro-thermal performance under the skin effect and coupling effect between filaments in the practical machine environment (especially at high frequencies for high-speed rotating machines) is still unclear; therefore, their loss reduction effectiveness needs to be further explored.
- (2)
- Flux diverters have been proven to be useful to decrease the AC loss of superconductors, but this effectiveness gets weaker with the increase in the number of turns in a coil. Besides, the hysteresis loss in ferromagnetic flux diverters increases rapidly with increasing frequency. In this way, the flux diverter at high frequencies can become a severe heat load itself. Therefore, the contribution of flux diverters to the total loss distribution at high frequencies inside superconducting machines needs more investigation.
- (3)
- Winding techniques appear to be a useful alternative for the AC loss reduction of HTS coils. When the coils are implemented into rotating machines, besides the electromagnetic performance, their mechanical strength, thermal characteristics, as well as processing difficulty also need to be considered. A balance needs to be reached between the AC loss reduction and total mass augmentation for the design of superconducting machines.
7. Conclusions and Future Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lei, G.; Zhu, J.; Guo, Y.; Liu, C.; Ma, B. A Review of Design Optimization Methods for Electrical Machines. Energies 2017, 10, 1962. [Google Scholar] [CrossRef] [Green Version]
- Wildi, T. Electrical Machines Drives and Power Systems; Prentice-Hall: Englewood Cliffs, NJ, USA, 2005. [Google Scholar]
- Saidur, R. A review on electrical motors energy use and energy savings. Renew. Sustain. Energy Rev. 2010, 14, 877–898. [Google Scholar] [CrossRef]
- Hossain, M.S. Panel estimation for CO2 emissions, energy consumption, economic growth, trade openness and urbaniza-tion of newly industrialized countries. Energy Policy 2011, 39, 6991–6999. [Google Scholar] [CrossRef]
- Cheng, M.; Sun, L.; Buja, G.; Song, L. Advanced Electrical Machines and Machine-Based Systems for Electric and Hybrid Vehicles. Energies 2015, 8, 9541–9564. [Google Scholar] [CrossRef] [Green Version]
- Cheng, M.; Zhu, Y. The state of the art of wind energy conversion systems and technologies: A review. Energy Convers. Manag. 2014, 88, 332–347. [Google Scholar] [CrossRef]
- Wrobel, R.; Mecrow, B.C. A Comprehensive Review of Additive Manufacturing in Construction of Electrical Machines. IEEE Trans. Energy Convers. 2020, 35, 1054–1064. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Zhang, S.; Habetler, T.G.; Harley, R.G. Modeling, Design Optimization, and Applications of Switched Reluctance Machines—A Review. IEEE Trans. Ind. Appl. 2019, 55, 2660–2681. [Google Scholar] [CrossRef]
- Lee, D.; Park, G.; Son, B.K.; Jung, H. Efficiency improvement of IPMSG in the electric power generating system of a range-extended electric vehicle. IET Electr. Power Appl. 2019, 13, 943–950. [Google Scholar] [CrossRef]
- Sun, X.; Shi, Z.; Lei, G.; Guo, Y.; Zhu, J. Analysis and Design Optimization of a Permanent Magnet Synchronous Motor for a Campus Patrol Electric Vehicle. IEEE Trans. Veh. Technol. 2019, 68, 10535–10544. [Google Scholar] [CrossRef]
- Sahoo, S.; Zhao, X.; Kyprianidis, K. A Review of Concepts, Benefits, and Challenges for Future Electrical Propulsion-Based Aircraft. Aerospace 2020, 7, 44. [Google Scholar] [CrossRef] [Green Version]
- Jlassi, I.; Cardoso, A.J.M. Fault-Tolerant Back-to-Back Converter for Direct-Drive PMSG Wind Turbines Using Direct Torque and Power Control Techniques. IEEE Trans. Power Electron. 2019, 34, 11215–11227. [Google Scholar] [CrossRef]
- Taherian-Fard, E.; Sahebi, R.; Niknam, T.; Izadian, A.; Shasadeghi, M. Wind Turbine Drivetrain Technologies. IEEE Trans. Ind. Appl. 2020, 56, 1729–1741. [Google Scholar] [CrossRef]
- Grilli, F.; Benkel, T.; H¨anisch, J.; Lao, M.; Reis, T.; Berberich, E.; Wolfst¨adter, S.; Schneider, C.; Miller, P.; Palmer, C.; et al. Superconducting motors for aircraft propulsion: The Advanced Superconducting Motor Experimental Demonstrator project. J. Phys. Conf. Ser. 2020, 1590, 012051. [Google Scholar] [CrossRef]
- Haran, K.S.; Kalsi, S.; Arndt, T.; Karmaker, H.; Badcock, R.; Buckley, B.; Haugan, T.; Izumi, M.; Loder, D.; Bray, J.W.; et al. High power density superconducting rotating machines—development status and technology roadmap. Supercond. Sci. Technol. 2017, 30, 123002. [Google Scholar] [CrossRef]
- Ainslie, M.D.; Bumby, C.W.; Jiang, Z.; Toyomoto, R.; Amemiya, N. Numerical modelling of dynamic resistance in high-temperature superconducting coated-conductor wires. Supercond. Sci. Technol. 2018, 31, 074003. [Google Scholar] [CrossRef]
- Feddersen, M.; Haran, K.S.; Berg, F. AC Loss Analysis of MgB2-Based Fully Superconducting Machines. IOP Conf. Ser. Mater. Sci. Eng. 2017, 279, 012026. [Google Scholar] [CrossRef] [Green Version]
- Fair, R.; Lewis, C.; Eugene, J.; Ingles, M. Development of an HTS hydroelectric power generator for the hirschaid power station. J. Phys. Conf. Ser. 2010, 234, 032008. [Google Scholar] [CrossRef]
- Corduan, M.; Boll, M.; Bause, R.; Oomen, M.P.; Filipenko, M.; Noe, M. Topology Comparison of Superconducting AC Machines for Hybrid Electric Aircraft. IEEE Trans. Appl. Supercond. 2020, 30, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Demencik, E.; Vojenciak, M.; Kario, A.; Nast, R.; Jung, A.; Goldacker, W.; Grilli, F. AC Loss and Coupling Currents in YBCO Coated Conductors With Varying Number of Filaments. IEEE Trans. Appl. Supercond. 2014, 24, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Grilli, F.; Pardo, E.; Stenvall, A.; Nguyen, D.N.; Yuan, W.; Gomory, F. Computation of Losses in HTS Under the Action of Varying Magnetic Fields and Currents. IEEE Trans. Appl. Supercond. 2014, 24, 78–110. [Google Scholar] [CrossRef]
- Zhang, H.; Yao, M.; Kails, K.; Machura, P.; Mueller, M.; Jiang, Z.; Xin, Y.; Li, Q. Modelling of electromagnetic loss in HTS coated conductors over a wide frequency band. Supercond. Sci. Technol. 2019, 33, 025004. [Google Scholar] [CrossRef]
- Zhang, H.; Machura, P.; Kails, K.; Chen, H.; Mueller, M. Dynamic loss and magnetization loss of HTS coated conductors, stacks, and coils for high-speed synchronous machines. Supercond. Sci. Technol. 2020, 33, 084008. [Google Scholar] [CrossRef]
- Kails, K.; Zhang, H.; Machura, P.; Mueller, M.; Li, Q. Dynamic loss of HTS field windings in rotating electric machines. Supercond. Sci. Technol. 2020, 33, 045014. [Google Scholar] [CrossRef]
- Miura, S.; Iwakuma, M.; Izumi, T. Lightweight Design of Tens-MW Fully-Superconducting Wind Turbine Generators With High-Performance REBa 2 Cu 3 O y Wires. IEEE Trans. Appl. Supercond. 2020, 30, 9028170. [Google Scholar] [CrossRef]
- Stautner, W. Cryocoolers for Superconducting Generators. In Thermal Properties of Solids at Room and Cryogenic Temperatures; Metzler, J.B., Ed.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 121–154. [Google Scholar]
- Sun, J.; Neumann, H.; Sanz, S.; Sarmiento, G.; Tropeano, M.; Marino, I.; Pujana, A.; Merino, J.M. Design and Construction of the Cryogenic Cooling System for the Rotating Magnetic Validator of the 10 MW SUPRAPOWER Offshore Superconducting Wind Turbine. IEEE Trans. Appl. Supercond. 2018, 28, 1–5. [Google Scholar] [CrossRef]
- Tomsic, M.; Rindfleisch, M.; Yue, J.; McFadden, K.; Phillips, J.; Sumption, M.D.; Bhatia, M.; Bohnenstiehl, S.; Collings, E.W. Overview of MgB2Superconductor Applications. Int. J. Appl. Ceram. Technol. 2007, 4, 250–259. [Google Scholar] [CrossRef]
- Nam, G.-D.; Sung, H.-J.; Go, B.-S.; Park, M.; Yu, I.-K. Design and Comparative Analysis of MgB2 and YBCO Wire-Based-Superconducting Wind Power Generators. IEEE Trans. Appl. Supercond. 2018, 28, 1–5. [Google Scholar] [CrossRef]
- Lin, F.; Qu, R.; Li, D.; Cheng, Y.; Sun, J. Electromagnetic Design of 13.2 MW Fully Superconducting Machine. IEEE Trans. Appl. Supercond. 2018, 28, 1–5. [Google Scholar] [CrossRef]
- Song, X.; Mijatovic, N.; Jensen, B.B.; Holboll, J. Design Study of Fully Superconducting Wind Turbine Generators. IEEE Trans. Appl. Supercond. 2015, 25, 1–5. [Google Scholar] [CrossRef]
- Saruwatari, M.; Yun, K.; Iwakuma, M.; Tamura, K.; Hase, Y.; Sasamori, Y.; Izumi, T. Design Study of 15-MW Fully Superconducting Generators for Offshore Wind Turbine. IEEE Trans. Appl. Supercond. 2016, 26, 1–5. [Google Scholar] [CrossRef]
- Gomory, F.; Souc, J.; Pardo, E.; Seiler, E.; Soloviov, M.; Frolek, L.; Skarba, M.; Konopka, P.; Pekarčíková, M.; Janovec, J. AC Loss in Pancake Coil Made From 12 mm Wide REBCO Tape. IEEE Trans. Appl. Supercond. 2013, 23, 5900406. [Google Scholar] [CrossRef]
- Hayashi, K. Commercialization of Bi-2223 Superconducting Wires and Their Applications. Sei Tech. Rev. 2020, 91, 68–74. Available online: https://global-sei.com/technology/tr/bn91/pdf/E91-12.pdf (accessed on 10 January 2021).
- Ku, M.-H.; Kang, M.-H.; Lee, H.-J.; Cha, G.-S. The Critical Current Characteristics and n-value Measurement of HTS Tapes. Pro-gress Supercond. Cryog. 2010, 12, 12–16. [Google Scholar]
- Ishmael, S.A.; Rogers, S.; Hunte, F.; Naderi, G.; Roach, C.; Straka, W.; Schwartz, J. Current Density and Quench Behavior of MgB 2/Ga Composite Wires. IEEE Trans. Appl. Supercond. 2015, 25, 1–8. [Google Scholar] [CrossRef]
- Park, M. Realization of a Large-Scale Superconducting Generator for a Wind Power Generation System; ESAS Summer School on HTS Technology for Sustainable Energy and Transport System. Available online: http://www.die.ing.unibo.it/pers/morandi/didattica/Temporary-ESAS-summer-school-Bologna-2016/Park.pdf (accessed on 20 December 2020).
- Haught, D. Recent HTS activities in the US. In Proceedings of the IEA HTS Executive Committee Meeting, Milan, Italy, 19 June 2014; pp. 1–47. Available online: http://www.superpower-inc.com/system/files/2014_0619_Haught+IEA+HTS+ExCo.pdf (accessed on 20 December 2020).
- Yagai, T.; Mizuno, S.; Okubo, T.; Mizuochi, S.; Kamibayashi, M.; Jimbo, M.; Takao, T.; Hirano, N.; Makida, Y.; Shintomi, T.; et al. Development of design for large scale conductors and coils using MgB2 for superconducting magnetic energy storage device. Cryogenics 2018, 96, 75–82. [Google Scholar] [CrossRef]
- Elsherif, M.; Taylor, P.; Blake, S. Investigating the potential impact of superconducting distribution networks. In Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution (CIRED 2013), Stockholm, Sweden, 10–13 June 2013; p. 816. [Google Scholar]
- Rammah, Y.; Salama, A.; Elkhatib, M. Magnetic Moment and its Correlation with the Critical Temperature in YBCO. Int. Ceram. Rev. 2019, 68, 34–41. [Google Scholar] [CrossRef]
- Tsuchiya, K.; Kikuchi, A.; Terashima, A.; Norimoto, K.; Uchida, M.; Tawada, M.; Masuzawa, M.; Ohuchi, N.; Wang, X.; Takao, T.; et al. Critical current measurement of commercial REBCO conductors at 4.2 K. J. Cryog. 2017, 85, 1–7. [Google Scholar] [CrossRef]
- Jensen, B.B.; Mijatovic, N.; Abrahamsen, A.B. Development of superconducting wind turbine generators. J. Renew. Sustain. Energy 2013, 5, 23137. [Google Scholar] [CrossRef] [Green Version]
- Bykovskiy, N.; Kaal, S.; Dudarev, A.; Mentink, M.; Kate, H.H.J.T. Demonstration of engineering current density exceeding 1 kA mm−2 in ultra-thin no-insulation, soldered coil windings using NbTi/Cu wires with CuNi cladding. Supercond. Sci. Technol. 2020, 33, 114001. [Google Scholar] [CrossRef]
- Patel, A.; Baskys, A.; Mitchell-Williams, T.B.; McCaul, A.; Coniglio, W.; Haenisch, J.; Lao, M.L.; A Glowacki, B. A trapped field of 17.7 T in a stack of high temperature superconducting tape. Supercond. Sci. Technol. 2018, 31, 09LT01. [Google Scholar] [CrossRef]
- Durrell, J.H.; Dennis, A.R.; Jaroszynski, J.; Ainslie, M.D.; Palmer, K.G.B.; Shi, Y.-H.; Campbell, A.M.; Hull, J.R.; Strasik, M.; E Hellstrom, E.; et al. A trapped field of 17.6 T in melt-processed, bulk Gd-Ba-Cu-O reinforced with shrink-fit steel. Supercond. Sci. Technol. 2014, 27, 082001. [Google Scholar] [CrossRef]
- Hirano, T.; Takahashi, Y.; Namba, S.; Naito, T.; Fujishiro, H. A record-high trapped field of 1.61 T in MgB2 bulk comprised of copper plates and soft iron yoke cylinder using pulsed-field magnetization. Supercond. Sci. Technol. 2020, 33, 085002. [Google Scholar] [CrossRef]
- Kurbatova, E.; Kurbatov, P.; Dergachev, P.; Molokanov, O. Electromagnetic Analysis of HTS Generator with Bulk Superconductor. In 2018 20th International Symposium on Electrical Apparatus and Technologies (SIELA); Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2018; pp. 1–4. [Google Scholar]
- Zhang, Y.; Zhou, D.; Ida, T.; Miki, M.; Izumi, M. Melt-growth bulk superconductors and application to an axial-gap-type rotating machine. Supercond. Sci. Technol. 2016, 29, 044005. [Google Scholar] [CrossRef]
- Colle, A.; Lubin, T.; Ayat, S.; Gosselin, O.; Leveque, J. Analytical Model for the Magnetic Field Distribution in a Flux Modulation Superconducting Machine. IEEE Trans. Magn. 2019, 55, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Patel, A.; Filar, K.; Nizhankovskii, V.I.; Hopkins, S.C.; Glowacki, B.A. Trapped fields greater than 7 T in a 12 mm square stack of commercial high-temperature superconducting tape. Appl. Phys. Lett. 2013, 102, 102601. [Google Scholar] [CrossRef]
- Patel, A.; Climente-Alarcon, V.; Baskys, A.; A Glowacki, B.; Reis, T. Design considerations for fully superconducting synchronous motors aimed at future electric aircraft. In Proceedings of the 2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Railway, Nottingham, UK, 7–9 November 2018; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2018; pp. 1–6. [Google Scholar]
- Kapolka, M.; Pardo, E.; Grilli, F.; Baskys, A.; Climente-Alarcon, V.; Dadhich, A.; A Glowacki, B. Cross-field demagnetization of stacks of tapes: 3D modelling and measurements. Supercond. Sci. Technol. 2019, 33, 044019. [Google Scholar] [CrossRef] [Green Version]
- Ainslie, M.D. Transport AC Loss in High Temperature Superconducting Coils. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2012. [Google Scholar] [CrossRef]
- Brandt, E.H.; Indenbom, M. Type-II-superconductor strip with current in a perpendicular magnetic field. Phys. Rev. B 1993, 48, 12893–12906. [Google Scholar] [CrossRef] [PubMed]
- Halse, M.R. AC face field losses in a type II superconductor. J. Phys. D Appl. Phys. 1970, 3, 717–720. [Google Scholar] [CrossRef]
- Zeldov, E.; Clem, J.R.; McElfresh, M.; Darwin, M. Magnetization and transport currents in thin superconducting films. Phys. Rev. B 1994, 49, 9802–9822. [Google Scholar] [CrossRef]
- Norris, W.T. Calculation of hysteresis losses in hard superconductors carrying ac: Isolated conductors and edges of thin sheets. J. Phys. D Appl. Phys. 1970, 3, 489–507. [Google Scholar] [CrossRef]
- Farinon, S.; Fabbricatore, P.; Grilli, F.; Krüger, P.A.C. Applicability of the Adaptive Resistivity Method to Describe the Critical State of Complex Superconducting Systems. J. Supercond. Nov. Magn. 2012, 25, 2343–2350. [Google Scholar] [CrossRef]
- Mikitik, G.P.; Mawatari, Y.; Wan, A.T.S.; Sirois, F. Analytical Methods and Formulas for Modeling High Temperature Superconductors. IEEE Trans. Appl. Supercond. 2013, 23, 8001920. [Google Scholar] [CrossRef]
- Mawatari, Y. Critical state of superconducting strip array systems in perpendicular magnetic fields. IEEE Trans. Appl. Supercond. 1997, 7, 1216–1219. [Google Scholar] [CrossRef]
- Mawatari, Y. Critical state of periodically arranged superconducting-strip lines in perpendicular fields. Phys. Rev. B 1996, 54, 13215–13221. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Yao, M.; Jiang, Z.; Xin, Y.; Li, Q. Dependence of Dynamic Loss on Critical Current and n-Value of HTS Coated Conductors. IEEE Trans. Appl. Supercond. 2019, 29, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Chen, H.; Jiang, Z.; Yang, T.; Xin, Y.; Mueller, M.; Li, Q. A full-range formulation for dynamic loss of high-temperature superconductor coated conductors. Supercond. Sci. Technol. 2020, 33, 05LT01. [Google Scholar] [CrossRef]
- Rabbers, J.; Haken, B.T.; Shevchenko, O.; Kate, H.T. An engineering formula to describe the AC loss of BSCCO/Ag tape. IEEE Trans. Appl. Supercond. 2001, 11, 2623–2626. [Google Scholar] [CrossRef]
- Amemiya, N.; Murasawa, S.; Banno, N.; Miyamoto, K. Numerical modelings of superconducting wires for AC loss calculations. Phys. C Supercond. 1998, 310, 16–29. [Google Scholar] [CrossRef]
- Sugita, S.; Ohsaki, H. Numerical analysis of AC losses in REBCO thin film for coated conductor and fault current limiter. Phys. C Supercond. 2003, 392–396, 1150–1155. [Google Scholar] [CrossRef]
- Sirois, F.; Grilli, F. Potential and limits of numerical modelling for supporting the development of HTS devices. Supercond. Sci. Technol. 2015, 28, 043002. [Google Scholar] [CrossRef]
- Brandt, E.H. Superconductors of finite thickness in a perpendicular magnetic field: Strips and slabs. Phys. Rev. B 1996, 54, 4246–4264. [Google Scholar] [CrossRef] [Green Version]
- Otten, S.; Grilli, F. Simple and Fast Method for Computing Induced Currents in Superconductors Using Freely Available Solvers for Ordinary Differential Equations. IEEE Trans. Appl. Supercond. 2019, 29, 1–8. [Google Scholar] [CrossRef]
- Website of the HTS Modelling Workgroup. 2019. Available online: http://www.htsmodelling.com (accessed on 10 January 2021).
- Nibbio, N.; Stavrev, S.; Dutoit, B. Finite element method simulation of AC loss in HTS tapes with B-dependent E-J power law. IEEE Trans. Appl. Supercond. 2001, 11, 2631–2634. [Google Scholar] [CrossRef]
- Costa, M.; Martínez, E.; Beduz, C.; Yang, Y.; Grilli, F.; Dutoit, B.; Vinot, E.; Tixador, P. 3D modeling of coupling between superconducting filaments via resistive matrix in AC magnetic field. IEEE Trans. Appl. Supercond. 2003, 13, 3634–3637. [Google Scholar] [CrossRef]
- Stenvall, A.; Tarhasaari, T. Programming finite element method based hysteresis loss computation software using non-linear superconductor resistivity andT− ϕ formulation. Supercond. Sci. Technol. 2010, 23, 075010. [Google Scholar] [CrossRef]
- Stenvall, A.; Tarhasaari, T. An eddy current vector potential formulation for estimating hysteresis losses of superconductors with FEM. Supercond. Sci. Technol. 2010, 23, 125013. [Google Scholar] [CrossRef]
- Lahtinen, V.; Lyly, M.; Stenvall, A.; Tarhasaari, T. Comparison of three eddy current formulations for superconductor hysteresis loss modelling. Supercond. Sci. Technol. 2012, 25, 115001. [Google Scholar] [CrossRef]
- Vinot, E.; Meunier, G.; Tixador, P. Different formulations to model superconductors. IEEE Trans. Magn. 2000, 36, 1226–1229. [Google Scholar] [CrossRef]
- Grilli, F. Numerical modeling of HTS applications. IEEE Trans. Appl. Supercond. 2016, 26, 1. [Google Scholar] [CrossRef]
- Shen, B.; Grilli, F.; Coombs, T. Review of the AC loss computation for HTS using H formulation. Supercond. Sci. Technol. 2020, 33, 033002. [Google Scholar] [CrossRef] [Green Version]
- Shen, B.; Grilli, F.; Coombs, T. Overview of H -Formulation: A Versatile Tool for Modeling Electromagnetics in High-Temperature Superconductor Applications. IEEE Access 2020, 8, 100403–100414. [Google Scholar] [CrossRef]
- Lahtinen, V.; Stenvall, A. Scientific Research in the Field of Mesh Method Based Modeling of AC Losses in Superconductors: A Review. J. Supercond. Nov. Magn. 2014, 27, 641–650. [Google Scholar] [CrossRef]
- Arsenault, A.; Sirois, F.; Grilli, F. Implementation of the H-$\phi$ Formulation in COMSOL Multiphysics for Simulating the Magnetization of Bulk Superconductors and Comparison With the H-Formulation. IEEE Trans. Appl. Supercond. 2021, 31, 1–11. [Google Scholar] [CrossRef]
- Nguyen, D.N.; Ashworth, S.P.; Willis, J.O.; Sirois, F.; Grilli, F. A new finite-element method simulation model for computing AC loss in roll assisted biaxially textured substrate YBCO tapes. Supercond. Sci. Technol. 2010, 23, 025001. [Google Scholar] [CrossRef]
- Ainslie, M.D.; Rodriguez-Zermeno, V.M.; Hong, Z.; Yuan, W.; Flack, T.J.; Coombs, T.A. An improved FEM model for computing transport AC loss in coils made of RABiTS YBCO coated conductors for electric machines. Supercond. Sci. Technol. 2011, 24, 045005. [Google Scholar] [CrossRef]
- Liu, Y.; Ou, J.; Grilli, F.; Schreiner, F.; Zermeno, V.M.R.; Zhang, M.; Noe, M. Comparison of 2D simulation models to estimate the critical current of a coated superconducting coil. Supercond. Sci. Technol. 2018, 32, 014001. [Google Scholar] [CrossRef] [Green Version]
- Liang, F.; Venuturumilli, S.; Zhang, H.; Zhang, M.; Kvitkovic, J.; Pamidi, S.; Wang, Y.; Yuan, W. A finite element model for simulating second generation high temperature superconducting coils/stacks with large number of turns. J. Appl. Phys. 2017, 122, 043903. [Google Scholar] [CrossRef]
- Machura, P.; Zhang, H.; Kails, K.; Li, Q. Loss characteristics of superconducting pancake, solenoid and spiral coils for wireless power transfer. Supercond. Sci. Technol. 2020, 33, 074008. [Google Scholar] [CrossRef]
- Zou, S.; Zermeno, V.M.R.; Grilli, F. Simulation of Stacks of High-Temperature Superconducting Coated Conductors Magnetized by Pulsed Field Magnetization Using Controlled Magnetic Density Distribution Coils. IEEE Trans. Appl. Supercond. 2016, 26, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Zubko, V.V.; Fetisov, S.S.; Zanegin, S.Y.; Vysotsky, V.S. AC Losses Analysis in stack of 2G HTS tapes in a coil. J. Physics Conf. Ser. 2020, 1559, 012115. [Google Scholar] [CrossRef]
- Benkel, T.; Lao, M.; Liu, Y.; Pardo, E.; Wolfstadter, S.; Reis, T.; Grilli, F. T–A-Formulation to Model Electrical Machines With HTS Coated Conductor Coils. IEEE Trans. Appl. Supercond. 2020, 30, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Zheng, J.; Song, Y.; Wan, Y. Multiscale Model for Simulation of Large-Scale YBCO Solenoid Coils With J Infinite-Turn. IEEE Trans. Appl. Supercond. 2019, 29, 1–5. [Google Scholar] [CrossRef]
- Berrospe-Juarez, E.; Zermeno, V.M.R.; Trillaud, F.; Grilli, F. Real-time simulation of large-scale HTS systems: Multi-scale and homogeneous models using the T–A formulation. Supercond. Sci. Technol. 2019, 32, 065003. [Google Scholar] [CrossRef] [Green Version]
- Sotelo, G.G.; Carrera, M.; Lopez-Lopez, J.; Granados, X. H-Formulation FEM Modeling of the Current Distribution in 2G HTS Tapes and Its Experimental Validation Using Hall Probe Mapping. IEEE Trans. Appl. Supercond. 2016, 26, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Kapek, J.; Berger, K.; Koblischka, M.R.; Trillaud, F.; Leveque, J. 2-D Numerical Modeling of a Bulk HTS Magnetization Based on H Formulation Coupled with Electrical Circuit. IEEE Trans. Appl. Supercond. 2019, 29, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Ru, Y.; Yong, H.; Zhou, Y.-H. Numerical simulation of dynamic fracture behavior in bulk superconductors with an electromagnetic-thermal model. Supercond. Sci. Technol. 2019, 32, 074001. [Google Scholar] [CrossRef]
- Brambilla, R.; Grilli, F.; Martini, L.; Bocchi, M.; Angeli, G. A Finite-Element Method Framework for Modeling Rotating Machines With Superconducting Windings. IEEE Trans. Appl. Supercond. 2018, 28, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Yong, H.; Zhang, X.; Zhou, Y. Numerical Simulation of Superconducting Generator Based on the T—A Formulation. IEEE Trans. Appl. Supercond. 2020, 30, 1–11. [Google Scholar] [CrossRef]
- Huang, X.; Huang, Z.; Xu, X.; Wang, L.; Li, W.; Jin, Z. A Fully Coupled Numerical Method for Coated Conductor HTS Coils in HTS Generators. IEEE Trans. Appl. Supercond. 2020, 30, 1–6. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, W.; Wang, X.; Ye, H.; Zhang, Y.; Zeng, Y.; Huang, Z.; Zhou, Q.; Liu, X.; Zhu, Y.; et al. Design, Fabrication, and Testing of a YBCO Racetrack Coil for an HTS Synchronous Motor With HTS Flux Pump. IEEE Trans. Appl. Supercond. 2020, 30, 1–5. [Google Scholar] [CrossRef]
- Vargas-Llanos, C.R.; Lengsfeld, S.; Grilli, F. T-A Formulation for the Design and AC Loss Calculation of a Superconducting Generator for a 10 MW Wind Turbine. IEEE Access 2020, 8, 208767–208778. [Google Scholar] [CrossRef]
- Numerical Modelling of Superconductors and Components. Available online: http://www.itep.kit.edu/english/67.php (accessed on 10 January 2021).
- Dular, P.; Geuzaine, C. GetDP Reference Manual: The Documentation for GetDP—A General Environment for the Treatment of Discrete Problems; University of Liège: Liège, Belgium, 2019; Available online: http://getdp.info/doc/texinfo/getdp.pdf (accessed on 10 January 2021).
- Burger, L.; Geuzaine, C.; Henrotte, F.; Vanderheyden, B. Modelling the penetration of magnetic flux in thin superconducting films with shell transformations. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2019, 38, 1441–1452. [Google Scholar] [CrossRef]
- Zermeno, V.M.R.; Abrahamsen, A.B.; Mijatovic, N.; Jensen, B.B.; Sørensen, M.P. Calculation of alternating current losses in stacks and coils made of second generation high temperature superconducting tapes for large scale applications. J. Appl. Phys. 2013, 114, 173901. [Google Scholar] [CrossRef] [Green Version]
- Zermeno, V.M.R.; Grilli, F. 3D modeling and simulation of 2G HTS stacks and coils. Supercond. Sci. Technol. 2014, 27, 44025. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Li, Q.; Ubani, O.; Mueller, M. High Temperature Superconducting Halbach Array Topology for Air-cored Electrical Machines. J. Phys. Conf. Ser. 2020, 1559, 012140. [Google Scholar] [CrossRef]
- Zermeno, V.M.R.; Mijatovic, N.; Traeholt, C.; Zirngibl, T.; Seiler, E.; Abrahamsen, A.B.; Pedersen, N.F.; Sørensen, M.P. Towards Faster FEM Simulation of Thin Film Superconductors: A Multiscale Approach. IEEE Trans. Appl. Supercond. 2010, 21, 3273–3276. [Google Scholar] [CrossRef]
- Quéval, L.; Zermeño, V.M.R.; Grilli, F. Numerical models for ac loss calculation in large-scale applications of HTS coated conductors. Supercond. Sci. Technol. 2016, 29, 024007. [Google Scholar] [CrossRef] [Green Version]
- Berrospe-Juarez, E.; Trillaud, F.; Zermeño, V.M.R.; Grilli, F. Advanced electromagnetic modeling of large-scale high-temperature superconductor systems based on H and T-A formulations. Supercond. Sci. Technol. 2021, 34, 044002. [Google Scholar] [CrossRef]
- Mykola, S.; Fedor, G. A–V formulation for numerical modelling of superconductor magnetization in true 3D geometry. Supercond. Sci. Technol. 2019, 32, 115001. [Google Scholar] [CrossRef]
- Zhang, H.; Mueller, M. Electromagnetic properties of curved HTS trapped field stacks under high-frequency cross fields for high-speed rotating machines. Supercond. Sci. Technol. 2021, 34, 045018. [Google Scholar] [CrossRef]
- Zermeno, V.M.R.; Grilli, F.; Sirois, F. A full 3D time-dependent electromagnetic model for Roebel cables. Supercond. Sci. Technol. 2013, 26, 052001. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, M.; Yuan, W. An efficient 3D finite element method model based on the T–A formulation for superconducting coated conductors. Supercond. Sci. Technol. 2017, 30, 024005. [Google Scholar] [CrossRef]
- Zhang, M.; Coombs, T.A. 3D modeling of high- T c superconductors by finite element software. Supercond. Sci. Technol. 2012, 25, 015009. [Google Scholar] [CrossRef]
- Kapolka, M.; Pardo, E. 3D modelling of macroscopic force-free effects in superconducting thin films and rectangular prisms. Supercond. Sci. Technol. 2019, 32, 054001. [Google Scholar] [CrossRef] [Green Version]
- Hu, D.; Ainslie, M.; Rush, J.P.; Durrell, J.; Zou, J.; Raine, M.J.; Hampshire, D. DC characterization and 3D modelling of a triangular, epoxy-impregnated high temperature superconducting coil. Supercond. Sci. Technol. 2015, 28, 065011. [Google Scholar] [CrossRef] [Green Version]
- Sheng, J.; Vojenciak, M.; Terzioglu, R.; Frolek, L.; Gomory, F. Numerical Study on Magnetization Characteristics of Superconducting Conductor on Round Core Cables. IEEE Trans. Appl. Supercond. 2017, 27, 1–5. [Google Scholar] [CrossRef]
- Hu, D.; Ainslie, M.; Zou, J.; Cardwell, D. 3D Modelling of All-Superconducting Synchronous Electric Machines by the Finite Element Method. 2014. Available online: https://www.comsol.com/paper/download/199173/hu_paper.pdf (accessed on 20 December 2020).
- Brambilla, R.; Grilli, F.; Martini, L.; Sirois, F. Integral equations for the current density in thin conductors and their solution by the finite-element method. Supercond. Sci. Technol. 2008, 21, 105008. [Google Scholar] [CrossRef]
- Pardo, E.; Gömöry, F.; Šouc, J.; Ceballos, J.M. Current distribution and ac loss for a superconducting rectangular strip with in-phase alternating current and applied field. Supercond. Sci. Technol. 2007, 20, 351–364. [Google Scholar] [CrossRef]
- Pardo, E.; Šouc, J.; Frolek, L. Electromagnetic modelling of superconductors with a smooth current–voltage relation: Variational principle and coils from a few turns to large magnets. Supercond. Sci. Technol. 2015, 28, 044003. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Kováč, J.; Pardo, E. Coupling loss at the end connections of REBCO stacks: 2D modelling and measurement. Supercond. Sci. Technol. 2020, 33, 075014. [Google Scholar] [CrossRef]
- Farinon, S.; Fabbricatore, P.; Gömöry, F. Critical state and magnetization loss in multifilamentary superconducting wire solved through the commercial finite element code ANSYS. Supercond. Sci. Technol. 2010, 23, 115004. [Google Scholar] [CrossRef]
- Zhang, K.; Hellmann, S.; Calvi, M.; Schmidt, T. Magnetization simulation of ReBCO tape stack with a large number of layers using the ANSYS A-V-A formulation. IEEE Trans. Appl. Supercond. 2020, 30, 1. [Google Scholar] [CrossRef]
- AC Losses in a Superconducting Magnet in the Presence of a Time-Dependent Transport Current (ANSYS 15.0). Available online: http://www.htsmodelling.com/?page_id=748 (accessed on 5 February 2021).
- Musso, A.; Breschi, M.; Ribani, P.L.; Grilli, F. Analysis of AC Loss Contributions From Different Layers of HTS Tapes Using the A−V Formulation Model. IEEE Trans. Appl. Supercond. 2021, 31, 1–11. [Google Scholar] [CrossRef]
- Hong, Z.; Yuan, W.; Ainslie, M.; Yan, Y.; Pei, R.; Coombs, T.A. AC Losses of Superconducting Racetrack Coil in Various Magnetic Conditions. IEEE Trans. Appl. Supercond. 2010, 21, 2466–2469. [Google Scholar] [CrossRef]
- Lahtinen, V.; Pardo, E.; Šouc, J.; Solovyov, M.; Stenvall, A. Ripple field losses in direct current biased superconductors: Simulations and comparison with measurements. J. Appl. Phys. 2014, 115, 113907. [Google Scholar] [CrossRef] [Green Version]
- Kails, K.; Yao, M.; Zhang, H.; Machura, P.; Mueller, M.; Li, Q. T-formulation based numerical modelling of dynamic loss with a DC background field. J. Phys. Conf. Ser. 2020, 1559, 012145. [Google Scholar] [CrossRef]
- De Bruyn, B.J.H.; Jansen, J.W.; A Lomonova, E. AC losses in HTS coils for high-frequency and non-sinusoidal currents. Supercond. Sci. Technol. 2017, 30, 095006. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.S.; Guan, X.J.; Shu, J. Review of AC loss measuring methods for HTS tape and unit. In Proceedings of the 2013 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices, Beijing, China, 25–27 October 2013; pp. 560–566. [Google Scholar]
- Kawabata, S.; Tsuzura, H.; Fukuda, Y.; Funaki, K.; Osamura, K. Standardization of the pickup coil method for AC loss measurement of three-component superconducting wires. Phys. C Supercond. 2003, 392–396, 1129–1133. [Google Scholar] [CrossRef]
- Yang, Y.; Martínez, E.; Norris, W.T. Configuration and calibration of pickup coils for measurement of ac loss in long superconductors. J. Appl. Phys. 2004, 96, 2141–2149. [Google Scholar] [CrossRef]
- Šouc, J.; Pardo, E.; Vojenčiak, M.; Gömöry, F. Theoretical and experimental study of AC loss in high temperature superconductor single pancake coils. Supercond. Sci. Technol. 2009, 22, 015006. [Google Scholar] [CrossRef] [Green Version]
- Ogawa, J.; Zushi, Y.; Fukushima, M.; Tsukamoto, O.; Suzuki, E.; Hirakawa, M.; Kikukawa, K. AC losses in a HTS coil carrying DC current in AC external magnetic field. Phys. C Supercond. 2003, 392-396, 1145–1149. [Google Scholar] [CrossRef]
- Amemiya, N.; Tominaga, N.; Toyomoto, R.; Nishimoto, T.; Sogabe, Y.; Yamano, S.; Sakamoto, H. Coupling time constants of striated and copper-plated coated conductors and the potential of striation to reduce shielding-current-induced fields in pancake coils. Supercond. Sci. Technol. 2017, 31, 025007. [Google Scholar] [CrossRef]
- Kajikawa, K.; Iwakuma, M.; Funaki, K.; Wada, M.; Takenaka, A. Influences of geometrical configuration on AC loss measurement with pickup-coil method. IEEE Trans. Appl. Supercond. 1999, 9, 746–749. [Google Scholar] [CrossRef]
- Šouc, J.; Gömöry, F.; Vojenčiak, M. Calibration free method for measurement of the AC magnetization loss. Supercond. Sci. Technol. 2005, 18, 592–595. [Google Scholar] [CrossRef]
- Messina, G.; Morici, L.; Vetrella, U.B.; Celentano, G.; Marchetti, M.; Viola, R.; Sabatino, P. AC Loss Measurements of a Trapezoidal Shaped HTS Coil Using an Electrical Method. Int. J. Supercond. 2014, 2014, 391329. [Google Scholar] [CrossRef]
- Zhou, P.; Ma, G.; Queval, L. Transition frequency of transport ac losses in high temperature superconducting coated conductors. J. Appl. Phys. 2019, 126, 063901. [Google Scholar] [CrossRef]
- Majoros, M.; Ye, L.; Velichko, A.V.; A Coombs, T.; Sumption, M.D.; Collings, E.W. Transport AC losses in YBCO coated conductors. Supercond. Sci. Technol. 2007, 20, S299–S304. [Google Scholar] [CrossRef]
- Šouc, J.; Gömöry, F.; Vojenčiak, M.; Frolek, L.; Isfort, D.; Ehrenberg, J.; Bock, J.; Usoskin, A.; Rutt, A. AC loss of the short coaxial superconducting cable model made from ReBCO coated tapes. J. Phys. Conf. Ser. 2008, 97, 012198. [Google Scholar] [CrossRef]
- Hu, D.; Ainslie, M.D.; Kvitkovic, J.; Kim, J.; Kim, C.; Pamidi, S.; Zhou, D.; Rush, J.P.; Durrell, J.H. Transport AC Loss Measurements of a Triangular Epoxy-Impregnated High-Temperature Superconducting Coil. IEEE Trans. Appl. Supercond. 2017, 27, 1–6. [Google Scholar] [CrossRef]
- Pappas, D.P.; David, D.E.; Lake, R.E.; Bal, M.; Goldfarb, R.B.; Hite, D.A.; Kim, E.; Ku, H.-S.; Long, J.L.; McRae, C.R.H.; et al. Enhanced superconducting transition temperature in electroplated rhenium. Appl. Phys. Lett. 2018, 112, 182601. [Google Scholar] [CrossRef] [Green Version]
- Pei, R.; Velichko, A.; Jiang, Y.; Hong, Z.; Katayama, M.; Coombs, T. High-precision digital lock-in measurements of critical current and AC loss in HTS 2G-tapes. In Proceedings of the 2008 SICE Annual Conference, Chofu, Japan, 20–22 August 2008; pp. 3147–3150. [Google Scholar]
- Šouc, J.; Gömöry, F. New approach to the ac loss measurement in the superconducting secondary circuit of an iron-core transformer. Supercond. Sci. Technol. 2002, 15, 927–932. [Google Scholar] [CrossRef]
- Liao, Y.; Tang, Y.; Shi, J.; Shi, X.; Ren, L.; Li, J.; Wang, Z.; Xia, Z. An Automatic Compensation Method for Measuring the AC loss of a Superconducting Coil. IEEE Trans. Appl. Supercond. 2016, 26, 1–5. [Google Scholar] [CrossRef]
- Pei, X.; Smith, A.C.; Barnes, M. AC Losses Measurement and Analysis for a 2G YBCO Coil in Metallic Containment Vessels. IEEE Trans. Appl. Supercond. 2017, 27, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Shen, L.; Liu, C.; Zhang, X.; Zhou, Y. A distinct method to eliminate the induced voltage in AC loss determination without phase control. AIP Adv. 2020, 10, 105111. [Google Scholar] [CrossRef]
- Breschi, M.; Filicori, F.; Musso, A.; Pasini, G. An electromagnetic method for measuring AC losses in HTS tapes without lock-in amplifier. J. Phys. Conf. Ser. 2020, 1559, 012066. [Google Scholar] [CrossRef]
- Sytnikov, V.; Shutov, K.; Polyakova, N.; Fetisov, S.; Nosov, A.; Vysotsky, V. The AC Loss Analysis in the 5 m HTS Power Cables. IEEE Trans. Appl. Supercond. 2009, 19, 1706–1709. [Google Scholar] [CrossRef]
- Lee, S.-J.; Kang, S.Y.; Park, M.; Won, D.; Yoo, J.; Yang, H.S. Performance Analysis of Real-Scale 23 kV/60 MVA Class Tri-Axial HTS Power Cable for Real-Grid Application in Korea. Energies 2020, 13, 2053. [Google Scholar] [CrossRef]
- Rabbers, J.J.; ten Haken, B.; ten Kate, H.H.J. Advanced ac loss measurement methods for high-temperature superconducting tapes. Rev. Sci. Instrum. 2001, 72, 2365–2373. [Google Scholar] [CrossRef]
- Jiang, Z.; Amemiya, N. An experimental method for total AC loss measurement of high T c superconductors. Supercond. Sci. Technol. 2004, 17, 371–379. [Google Scholar] [CrossRef]
- Pamidi, S.; Nguyen, D.; Guomin, Z.; Knoll, D.; Trociewitz, U.; Schwartz, J. Variable Temperature Total AC Loss and Stability Characterization Facility. IEEE Trans. Appl. Supercond. 2007, 17, 3179–3182. [Google Scholar] [CrossRef]
- Vojenciak, M.; Grilli, F.; Stenvall, A.; Kling, A.; Goldacker, W. Influence of the voltage taps position on the self-field DC and AC transport characterization of HTS superconducting tapes. J. Cryog. 2013, 57, 189–194. [Google Scholar] [CrossRef] [Green Version]
- Zhu, K.; Guo, S.; Ren, L.; Xu, Y.; Wang, F.; Yan, S.; Liang, S.; Tang, Y.; Shi, J.; Li, J. AC loss measurement of HTS coil under periodic current. Phys. C Supercond. 2020, 569, 1353562. [Google Scholar] [CrossRef]
- Jiang, Z.; Toyomoto, R.; Amemiya, N.; Zhang, X.; Bumby, C.W. Dynamic resistance of a high- T c coated conductor wire in a perpendicular magnetic field at 77 K. Supercond. Sci. Technol. 2017, 30, 03LT01. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, Z.; Sidorov, G.; Bumby, C.W.; Badcock, R.A.; Fang, J. Dynamic resistance measurement in a YBCO wire under perpendicular magnetic field at various operating temperatures. J. Appl. Phys. 2019, 126, 243904. [Google Scholar] [CrossRef]
- Jiang, Z.; Toyomoto, R.; Amemiya, N.; Bumby, C.W.; Badcock, R.A.; Long, N.J. Dynamic resistance measurements in a GdBCO coated conductor. IEEE Trans. Appl. Supercond. 2016, 27, 1. [Google Scholar] [CrossRef]
- Zhang, H.; Hao, C.; Xin, Y.; Mueller, M. Demarcation Currents and Corner Field for Dynamic Resistance of HTS-Coated Conductors. IEEE Trans. Appl. Supercond. 2020, 30, 1–5. [Google Scholar] [CrossRef]
- Oomen, M.P. AC Loss in Superconducting Tapes and Cables. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2000. Available online: https://www.elibrary.ru/item.asp?id=5312717 (accessed on 20 December 2020).
- University of Florida-Department of Physics, PHY4803L-Advanced Physics Laboratory. AC Susceptibility Measurements in High-Tc Superconductors. Available online: https://www.phys.ufl.edu/courses/phy4803L/group_II/high_Tc/hightc.pdf (accessed on 20 December 2020).
- Pardo, E.; Souc, J.; Vojenciak, M.; Gomory, F. AC Loss and Voltage Signal in a Pancake Coil Made of Coated Conductor with Ferromagnetic Substrate. IEEE Trans. Appl. Supercond. 2009, 19, 2223–2227. [Google Scholar] [CrossRef]
- Gömöry, F. Characterization of high-temperature superconductors by AC susceptibility measurements. Supercond. Sci. Technol. 1997, 10, 523–542. [Google Scholar] [CrossRef]
- Kajikawa, K.; Nishimura, M.; Moriyama, H.; Iwakuma, M.; Funaki, K. A new experimental technique to evaluate perpendicular-field losses of superconducting tape wires with meter-class length. Phys. C Supercond. 2001, 357-360, 1201–1204. [Google Scholar] [CrossRef]
- Iwakuma, M.; Funaki, K.; Kajikawa, K.; Tanaka, H.; Bohno, T.; Tomioka, A.; Yamada, H.; Nose, S.; Konno, M.; Yagi, Y.; et al. AC loss properties of a 1 MVA single-phase HTS power transformer. IEEE Trans. Appl. Supercond. 2001, 11, 1482–1485. [Google Scholar] [CrossRef]
- Iwakuma, M.; Nanri, M.; Fukui, M.; Fukuda, Y.; Kajikawa, K.; Funaki, K. Theoretical investigation on the detection ratio of the magnetization in superconducting wires by a saddle-shaped pick-up coil. Supercond. Sci. Technol. 2003, 16, 545–556. [Google Scholar] [CrossRef]
- Funaki, K.; Kurawaki, M.; Sato, S.; Kajikawa, K.; Iwakuma, M.; Hayashi, T.; Kato, T.; Fujino, K. Transport AC Loss Properties of a Bi-2223 Superconducting Coil From 0.1 Hz to 10 Hz. IEEE Trans. Appl. Supercond. 2012, 23, 4700804. [Google Scholar] [CrossRef]
- Sasa, H.; Miura, S.; Iwakuma, M.; Izumi, T.; Machi, T.; Ibi, A. Estimation Method for AC Loss of Perpendicularly Stacked REBa2Cu3O Superconducting Tapes under Magnetic Field. Phys. C Supercond. Appl. 2021, 580, 1353801. [Google Scholar] [CrossRef]
- Muzzi, L.; Spadoni, M. Magnetic method for AC losses measurement of coil wound CICCs in pulsed regimes. Supercond. Sci. Technol. 2003, 16, 19–23. [Google Scholar] [CrossRef]
- Fisher, L.M.; Kalinov, A.V.; Voloshin, I.F. Simple calibration free method to measure ac magnetic moment and losses. J. Phys. Conf. Ser. 2008, 97, 012032. [Google Scholar] [CrossRef] [Green Version]
- Chiletti, M. Coupling Losses in Large Superconducting Cable in Conduit Conductors for Fusion Reactors: Analytical Modelling and Experimental Investigations. Ph.D. Thesis, Aix Marseille Université, Provence, France, 2020. [Google Scholar]
- Anvar, V.; Qin, J.; Wu, Y.; Bagni, T.; Devred, A.; Haugan, T.; Hossain, M.; Zhou, C.; Nijhuis, A. AC loss and contact resistance of different CICC cable patterns: Experiments and numerical modeling. Fusion Eng. Des. 2020, 161, 111898. [Google Scholar] [CrossRef]
- Nguyen, D.N.; Sastry, P.V.P.S.S.; Zhang, G.M.; Knoll, D.C.; Schwartz, J. AC Loss Measurement With a Phase Difference Between Current and Applied Magnetic Field. IEEE Trans. Appl. Supercond. 2005, 15, 2831–2834. [Google Scholar] [CrossRef]
- Vojenčiak, M.; Šouc, J.; Ceballos, J.M.; Gömöry, F.; Klinčok, B.; Pardo, E.; Grilli, F. Study of ac loss in Bi-2223/Ag tape under the simultaneous action of ac transport current and ac magnetic field shifted in phase. Supercond. Sci. Technol. 2006, 19, 397–404. [Google Scholar] [CrossRef]
- McConnell, R.D.; Critchlow, P.R. Variable temperature apparatus using a thermal conductivity measurement technique for the determination of superconducting ac power loss. Rev. Sci. Instrum. 1975, 46, 511–516. [Google Scholar] [CrossRef]
- Schmidt, C.; Specht, E. ac loss measurements on superconductors in the microwatt range. Rev. Sci. Instruments 1990, 61, 988–992. [Google Scholar] [CrossRef]
- Dolez, P.; Aubin, M.; Willén, D.; Nadi, R.; Cave, J. Calorimetric ac loss measurements of silver sheathed Bi-2223 superconducting tapes. Supercond. Sci. Technol. 1996, 9, 374–378. [Google Scholar] [CrossRef]
- Dolez, P.; Cave, J.; Willén, D.; Zhu, W.; Aubin, M. Improvements and validation of the null calorimetric method for a.c. loss measurements in superconductors. Cryogenics (Guildf) 1998, 38, 429–434. [Google Scholar] [CrossRef]
- Ashworth, S.; Suenaga, M. The calorimetric measurement of losses in HTS tapes due to ac magnetic fields and transport currents. Phys. C Supercond. 1999, 315, 79–84. [Google Scholar] [CrossRef]
- See, K.W.; Cook, C.D.; Dou, S.X. Innovative Calorimetric AC Loss Measurement of HTSC for Power Applications. IEEE Trans. Appl. Supercond. 2010, 21, 3261–3264. [Google Scholar] [CrossRef]
- See, K.W.; Xu, X.; Horvat, J.; Cook, C.D.; Dou, S.X. Calorimetric AC loss measurement of MgB2superconducting tape in an alternating transport current and direct magnetic field. Supercond. Sci. Technol. 2012, 25, 115016. [Google Scholar] [CrossRef]
- Ghoshal, P.K.; Coombs, T.; Campbell, A.M. Calorimetric method of ac loss measurement in a rotating magnetic field. Rev. Sci. Instruments 2010, 81, 74702. [Google Scholar] [CrossRef]
- Hartwig, J.; New Test Rig to Measure Alternating Current Losses of both Low and High Critical Temperature Super-conductors. NASA/TM—2019-220046. Available online: https://ntrs.nasa.gov/api/citations/20190025926/downloads/20190025926.pdf (accessed on 16 January 2021).
- Dai, J.S.; Wang, Y.S.; Zhao, W.J.; Xia, L.M.; Sun, D. A novel calorimetric method for measurement of AC losses of HTS tapes by optical fiber Bragg grating. In Proceedings of the 2013 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices, Beijing, China, 25–27 October 2013; pp. 124–127. [Google Scholar]
- Jones, C.H.; Schenk, H.L. AC Losses in Hard Superconductors. In Advances in Cryogenic Engineering; Plenum: New York, NY, USA, 1963; pp. 579–584. [Google Scholar]
- Kuroda, K. ac losses of superconducting solenoidal coils. J. Appl. Phys. 1982, 53, 578–583. [Google Scholar] [CrossRef]
- Kuroda, K. Modified boil-off method for measuring a.c. losses of superconducting composites. Cryogenics 1986, 26, 566–568. [Google Scholar] [CrossRef]
- Okamoto, H.; Sumiyoshi, F.; Miyoshi, K.; Suzuki, Y. The Nitrogen Boil-Off Method for Measuring AC Losses in HTS Coils. IEEE Trans. Appl. Supercond. 2006, 16, 105–107. [Google Scholar] [CrossRef]
- Yuan, W.; Coombs, T.A.; Kim, J.-H.; Han Kim, C.; Kvitkovic, J.; Pamidi, S. Measurements and calculations of transport AC loss in second generation high temperature superconducting pancake coils. J. Appl. Phys. 2011, 110, 113906. [Google Scholar] [CrossRef] [Green Version]
- Murphy, J.P.; Mullins, M.J.; Barnes, P.N.; Haugan, T.J.; Levin, G.A.; Majoros, M.; Sumption, M.D.; Collings, E.W.; Polak, M.; Mozola, P. Experiment Setup for Calorimetric Measurements of Losses in HTS Coils Due to AC Current and External Magnetic Fields. IEEE Trans. Appl. Supercond. 2013, 23, 4701505. [Google Scholar] [CrossRef]
- Iwakuma, M.; Toyota, K.; Nigo, M.; Kiss, T.; Funaki, K.; Iijima, Y.; Saitoh, T.; Yamada, Y.; Shiohara, Y. AC loss properties of YBCO superconducting tapes fabricated by IBAD–PLD technique. Phys. C Supercond. 2004, 412–414, 983–991. [Google Scholar] [CrossRef]
- Jiang, Z.; Amemiya, N.; Kakimoto, K.; Iijima, Y.; Saitoh, T.; Suzuki, K.; Shiohara, Y. Total AC Loss Characteristics in a Stacked YBCO Conductor. IEEE Trans. Appl. Supercond. 2007, 17, 2442–2445. [Google Scholar] [CrossRef]
- Shen, B.; Li, J.; Geng, J.; Fu, L.; Zhang, X.; Zhang, H.; Li, C.; Grilli, F.; A Coombs, T. Investigation of AC losses in horizontally parallel HTS tapes. Supercond. Sci. Technol. 2017, 30, 075006. [Google Scholar] [CrossRef]
- Ainslie, M.D.; Yuan, W.; Hong, Z.; Pei, R.; Flack, T.J.; Coombs, T.A. Modeling and Electrical Measurement of Transport AC Loss in HTS-Based Superconducting Coils for Electric Machines. IEEE Trans. Appl. Supercond. 2010, 21, 3265–3268. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, W.; Huang, Z.; Baghdadi, M.; Yuan, W.; Kvitkovic, J.; Pamidi, S.; Coombs, T.A. AC Loss Measurements for 2G HTS Racetrack Coils With Heat-Shrink Tube Insulation. IEEE Trans. Appl. Supercond. 2014, 24, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.-H.; Kim, C.H.; Iyyani, G.; Kvitkovic, J.; Pamidi, S. Transport AC Loss Measurements in Superconducting Coils. IEEE Trans. Appl. Supercond. 2010, 21, 3269–3272. [Google Scholar] [CrossRef]
- Zhang, M.; Kvitkovic, J.; Pamidi, S.V.; A Coombs, T. Experimental and numerical study of a YBCO pancake coil with a magnetic substrate. Supercond. Sci. Technol. 2012, 25, 125020. [Google Scholar] [CrossRef]
- Liu, B.; Wang, S.; Zhao, B.; Wang, X.; Fang, J. Research on AC losses of racetrack superconducting coils applied to high-temperature superconducting motors. Supercond. Sci. Technol. 2019, 32, 115010. [Google Scholar] [CrossRef]
- Zhang, M.; Yuan, W.; Kvitkovic, J.; Pamidi, S. Total AC loss study of 2G HTS coils for fully HTS machine applications. Supercond. Sci. Technol. 2015, 28, 115011. [Google Scholar] [CrossRef]
- Weng, F.; Zhang, M.; Lan, T.; Wang, Y.; Yuan, W. Fully superconducting machine for electric aircraft propulsion: Study of AC loss for HTS stator. Supercond. Sci. Technol. 2020, 33, 104002. [Google Scholar] [CrossRef]
- Amemiya, N.; Kasai, S.; Yoda, K.; Jiang, Z.; A Levin, G.; Barnes, P.N.; E Oberly, C. AC loss reduction of YBCO coated conductors by multifilamentary structure. Supercond. Sci. Technol. 2004, 17, 1464–1471. [Google Scholar] [CrossRef] [Green Version]
- Sumption, M.; Barnes, P.; Collings, E. AC Losses of Coated Conductors in Perpendicular Fields and Concepts for Twisting. IEEE Trans. Appl. Supercond. 2005, 15, 2815–2818. [Google Scholar] [CrossRef]
- Marchevsky, M.; Zhang, E.; Xie, Y.; Selvamanickam, V.; Ganesan, P.G. AC Losses and Magnetic Coupling in Multifilamentary 2G HTS Conductors and Tape Arrays. IEEE Trans. Appl. Supercond. 2009, 19, 3094–3097. [Google Scholar] [CrossRef]
- Grilli, F.; Kario, A. How filaments can reduce AC losses in HTS coated conductors: A review. Supercond. Sci. Technol. 2016, 29, 083002. [Google Scholar] [CrossRef]
- Godfrin, A.; Kario, A.; Gyuraki, R.; Demencik, E.; Nast, R.; Scheiter, J.; Mankevich, A.; Molodyk, A.; Goldacker, W.; Grilli, F.; et al. Influence of the Striation Process and the Thickness of the Cu-Stabilization on the AC Magnetization Loss of Striated REBCO Tape. IEEE Trans. Appl. Supercond. 2017, 27, 1–9. [Google Scholar] [CrossRef]
- Herrmann, J.; Müller, K.-H.; Savvides, N.; Gnanarajan, S.; Thorley, A.; Katsaros, A. AC losses of YBCO strips on YSZ/hastelloy substrates. Phys. C Supercond. 2000, 341–348, 2493–2494. [Google Scholar] [CrossRef]
- Cobb, C.B.; Barnes, P.N.; Haugan, T.J.; Tolliver, J.; Lee, E.; Sumption, M.; Collings, E.; Oberly, C.E. Hysteretic loss reduction in striated YBCO. Phys. C Supercond. 2002, 382, 52–56. [Google Scholar] [CrossRef]
- Majoros, M.; Tomov, R.; Glowacki, B.; Campbell, A.; Oberly, C. Hysteresis losses in YBCO coated conductors on textured metallic substrates. IEEE Trans. Appl. Supercond. 2003, 13, 3626–3629. [Google Scholar] [CrossRef]
- Majoros, M.; Glowacki, B.; Campbell, A.; Levin, G.; Barnes, P.; Polak, M. AC Losses in Striated YBCO Coated Conductors. IEEE Trans. Appl. Supercond. 2005, 15, 2819–2822. [Google Scholar] [CrossRef]
- Zhang, Y.; Duckworth, R.C.; Ha, T.T.; List, F.A.; Gouge, M.J.; Chen, Y.; Xiong, X.; Selvamanickam, V.; Polyanskii, A. AC Loss Reduction in Filamentized YBCO Coated Conductors With Virtual Transverse Cross-Cuts. IEEE Trans. Appl. Supercond. 2010, 21, 3301–3306. [Google Scholar] [CrossRef]
- Ashworth, S.P.; Grilli, F. A strategy for the reduction of ac losses in YBCO coated conductors. Supercond. Sci. Technol. 2006, 19, 227–232. [Google Scholar] [CrossRef]
- Abraimov, D.; Gurevich, A.; Polyanskii, A.; Cai, X.Y.; Xu, A.; Pamidi, S.; Larbalestier, D.; Thieme, C.L.H. Significant reduction of AC losses in YBCO patterned coated conductors with transposed filaments. Supercond. Sci. Technol. 2008, 21, 082004. [Google Scholar] [CrossRef] [Green Version]
- Prestigiacomo, J.C.; Auyeung, R.C.Y.; Charipar, K.; Claassen, J.; Bassim, N.; Pique, A.; Osofsky, M.S.; Rupich, M.W.; Kvitkovic, J.; Hatwar, R.; et al. Use of Laser Lithography for Striating 2G HTS Conductors for AC Loss Reduction. IEEE Trans. Appl. Supercond. 2017, 27, 1–5. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, M.; Song, M.; Li, Z.; Dong, F.; Hong, Z.; Jin, Z. An effective way to reduce AC loss of second-generation high temperature superconductors. Supercond. Sci. Technol. 2019, 32, 01LT01. [Google Scholar] [CrossRef]
- Hussennether, V.; Oomen, M.; Leghissa, M.; Neumüller, H.-W. DC and AC properties of Bi-2223 cabled conductors designed for high-current applications. Phys. C Supercond. 2004, 401, 135–139. [Google Scholar] [CrossRef]
- Goldacker, W.; Grilli, F.; Pardo, E.; Kario, A.; I Schlachter, S.; Vojenčiak, M. Roebel cables from REBCO coated conductors: A one-century-old concept for the superconductivity of the future. Supercond. Sci. Technol. 2014, 27, 093001. [Google Scholar] [CrossRef] [Green Version]
- Long, N.J.; Badcock, R.; Beck, P.; Mulholl, M.; Ross, N.; Staines, M.; Sun, H.; Hamilton, J.; Buckley, R.G. Narrow strand YBCO Roebel cable for lowered AC loss. J. Phys. Conf. Ser. 2008, 97, 012280. [Google Scholar] [CrossRef]
- Hull, J.R.; Wilson, M.N.; Bottura, L.; Rossi, L.; Green, M.A.; Iwasa, Y.; Hahn, S.; Duchateau, J.-L.; Kalsi, S.S. Superconducting Magnets; Wiley: Hoboken, NJ, USA, 2015; pp. 403–602. [Google Scholar]
- Oberly, C.; Razidlo, B.; Rodriguez, F. Conceptual Approach to the Ultimate Low AC Loss YBCO Superconductor. IEEE Trans. Appl. Supercond. 2005, 15, 1643–1646. [Google Scholar] [CrossRef]
- Van der Laan, D.C. YBa 2 Cu 3 O 7−δ coated conductor cabling for low ac-loss and high-field magnet applications. Supercond. Sci. Technol. 2009, 22, 065013. [Google Scholar] [CrossRef]
- Weiss, J.D.; Mulder, T.; Kate, H.J.T.; Van Der Laan, D.C. Introduction of CORC®wires: Highly flexible, round high-temperature superconducting wires for magnet and power transmission applications. Supercond. Sci. Technol. 2017, 30, 014002. [Google Scholar] [CrossRef] [Green Version]
- Van Der Laan, D.C.; Weiss, J.D.; McRae, D. Status of CORC® cables and wires for use in high-field magnets and power systems a decade after their introduction. Supercond. Sci. Technol. 2019, 32, 033001. [Google Scholar] [CrossRef] [Green Version]
- Glasson, N.; Staines, M.; Buckley, R.; Pannu, M.; Kalsi, S. Development of a 1 MVA 3-Phase Superconducting Transformer Using YBCO Roebel Cable. IEEE Trans. Appl. Supercond. 2010, 21, 1393–1396. [Google Scholar] [CrossRef]
- LHC Machine Outreach: Super Conducting Cable. Available online: http://lhc-machine-outreach.web.cern.ch/components/cable.htm (accessed on 18 January 2021).
- Takayasu, M.; Chiesa, L.; Bromberg, L.; Minervini, J.V. HTS twisted stacked-tape cable conductor. Supercond. Sci. Technol. 2011, 25, 014011. [Google Scholar] [CrossRef]
- Uglietti, D.; Bykovsky, N.; Wesche, R.; Bruzzone, P. Development of HTS Conductors for Fusion Magnets. IEEE Trans. Appl. Supercond. 2014, 25, 1–6. [Google Scholar] [CrossRef]
- Uglietti, D.; Bykovsky, N.; Sedlak, K.; Stepanov, B.; Wesche, R.; Bruzzone, P. Test of 60 kA coated conductor cable prototypes for fusion magnets. Supercond. Sci. Technol. 2015, 28, 124005. [Google Scholar] [CrossRef]
- Vojenčiak, M.; Kario, A.; Ringsdorf, B.; Nast, R.; Van Der Laan, D.C.; Scheiter, J.; Jung, A.; Runtsch, B.; Gömöry, F.; Goldacker, W. Magnetization ac loss reduction in HTS CORC®cables made of striated coated conductors. Supercond. Sci. Technol. 2015, 28, 104006. [Google Scholar] [CrossRef] [Green Version]
- Terzioğlu, R.; Vojenčiak, M.; Sheng, J.; Gömöry, F.; Çavuş, T.F.; Belenli, İ. AC loss characteristics of CORC ® cable with a Cu former. Supercond. Sci. Technol. 2017, 30, 085012. [Google Scholar] [CrossRef]
- Yagotintsev, K.; A Anvar, V.; Gao, P.; Dhalle, M.J.; Haugan, T.J.; Van Der Laan, D.C.; Weiss, J.D.; A Hossain, M.S.; Nijhuis, A. AC loss and contact resistance in REBCO CORC®, Roebel, and stacked tape cables. Supercond. Sci. Technol. 2020, 33, 085009. [Google Scholar] [CrossRef]
- Gömöry, F.; Vojenčiak, M.; Pardo, E.; Šouc, J. Magnetic flux penetration and AC loss in a composite superconducting wire with ferromagnetic parts. Supercond. Sci. Technol. 2009, 22, 034017. [Google Scholar] [CrossRef]
- Safran, S.; Gömöry, F.; Gencer, A. AC loss in stacks of Bi-2223/Ag tapes modified with ferromagnetic covers at the edges. Supercond. Sci. Technol. 2010, 23, 105003. [Google Scholar] [CrossRef]
- Krüger, P.; Grilli, F.; Vojenčiak, M.; Zermeño, V.M.R.; Demencik, E.; Farinon, S. Superconductor/ferromagnet heterostructures exhibit potential for significant reduction of hysteretic losses. Appl. Phys. Lett. 2013, 102, 202601. [Google Scholar] [CrossRef] [Green Version]
- Pardo, E.; Šouc, J.; Vojenčiak, M. AC loss measurement and simulation of a coated conductor pancake coil with ferromagnetic parts. Supercond. Sci. Technol. 2009, 22, 075007. [Google Scholar] [CrossRef]
- Ainslie, M.D.; Yuan, W.; Flack, T.J. Numerical Analysis of AC Loss Reduction in HTS Superconducting Coils Using Magnetic Materials to Divert Flux. IEEE Trans. Appl. Supercond. 2013, 23, 4700104. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, G.; Jing, L.; Yu, H. Numerical study on AC loss reduction of stacked HTS tapes by optimal design of flux diverter. Supercond. Sci. Technol. 2017, 30, 125014. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, G.; Jing, L.; Ai, L.; Yu, H.; Li, W.; Liu, Q. Study on the AC Loss Reduction of REBCO Double Pancake Coil. IEEE Trans. Appl. Supercond. 2018, 28, 1–6. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, G.; Jing, L. Experimental and numerical study of the frequency-dependent transport ac losses of the YBa2Cu3O7−δ coil with and without flux diverters. Supercond. Sci. Technol. 2019, 32, 055002. [Google Scholar] [CrossRef]
- Kawagoe, A.; Sumiyoshi, F.; Nakanishi, M.; Mito, T.; Kawashima, T. A new winding method to reduce AC losses in stable LTS pulse coils. IEEE Trans. Appl. Supercond. 2003, 13, 2404–2407. [Google Scholar] [CrossRef]
- Heydari, H.; Faghihi, F.; Aligholizadeh, R. A new approach for AC loss reduction in HTS transformer using auxiliary windings, case study: 25 kA HTS current injection transformer. Supercond. Sci. Technol. 2007, 21, 015009. [Google Scholar] [CrossRef]
- Kim, J.; Kim, Y.; Hong, S.; Park, S.; Kim, H.; Choi, Y.; Lee, H.; Kim, J.; Kim, J. Investigation about the effects of metal-clad winding on the electromagnetic characteristics of the GdBCO racetrack coils in a time-varying magnetic field. Results Phys. 2018, 11, 400–405. [Google Scholar] [CrossRef]
- Wang, Y.; Weng, F.; Li, J.; Souc, J.; Gomory, F.; Zou, S.; Zhang, M.; Yuan, W. No-Insulation High-Temperature Superconductor Winding Technique for Electrical Aircraft Propulsion. IEEE Trans. Transp. Electrification 2020, 6, 1613–1624. [Google Scholar] [CrossRef]
- Simpson, N.; Mellor, P.H. Additive Manufacturing of Shaped Profile Windings for Minimal AC Loss in Electrical Machines. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 5765–5772. [Google Scholar]
- Jiang, Z.; Song, W.; Pei, X.; Fang, J.; A Badcock, R.; Wimbush, S.C. 15% reduction in AC loss of a 3-phase 1 MVA HTS transformer by exploiting asymmetric conductor critical current. J. Phys. Commun. 2021, 5, 025003. [Google Scholar] [CrossRef]
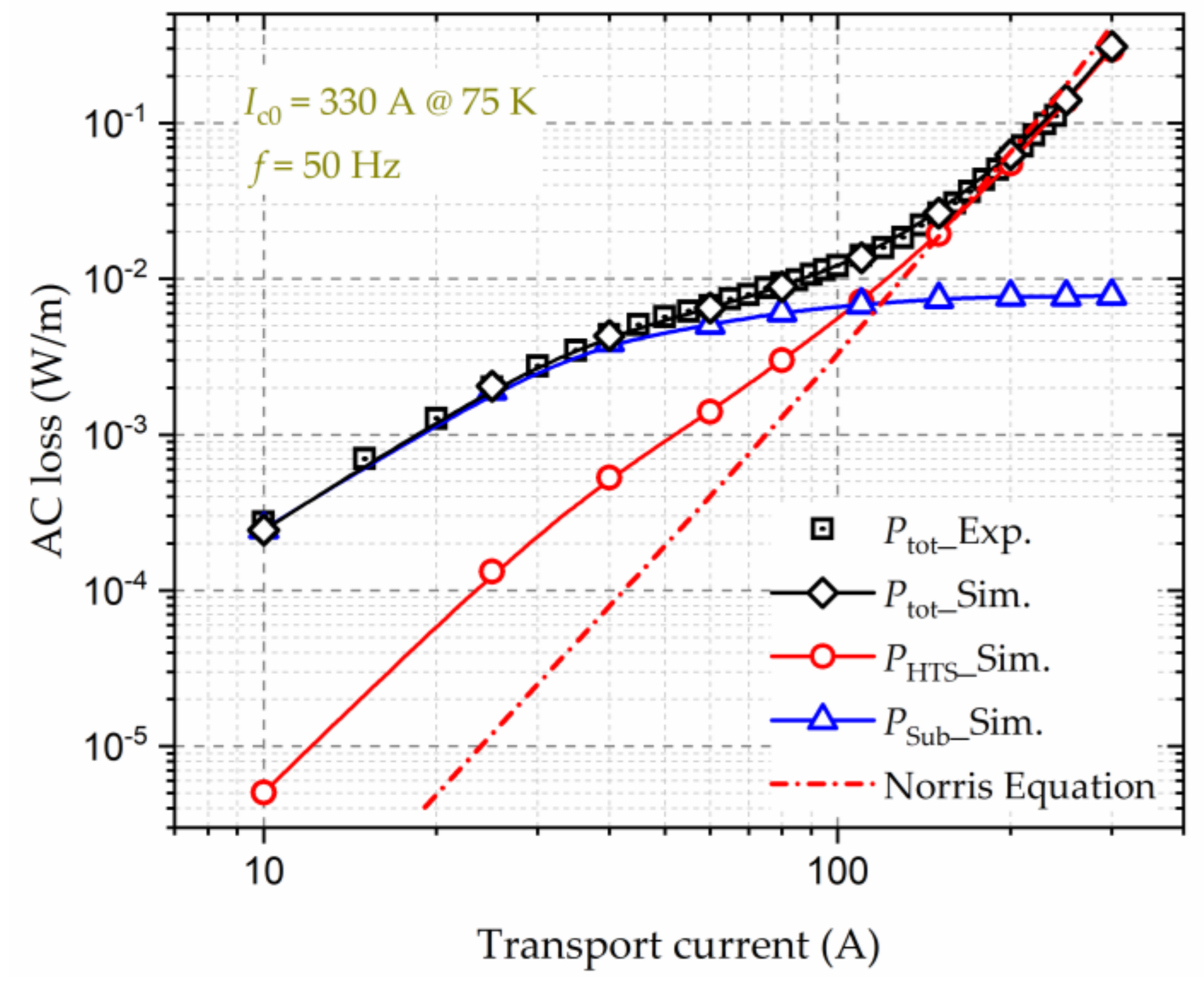
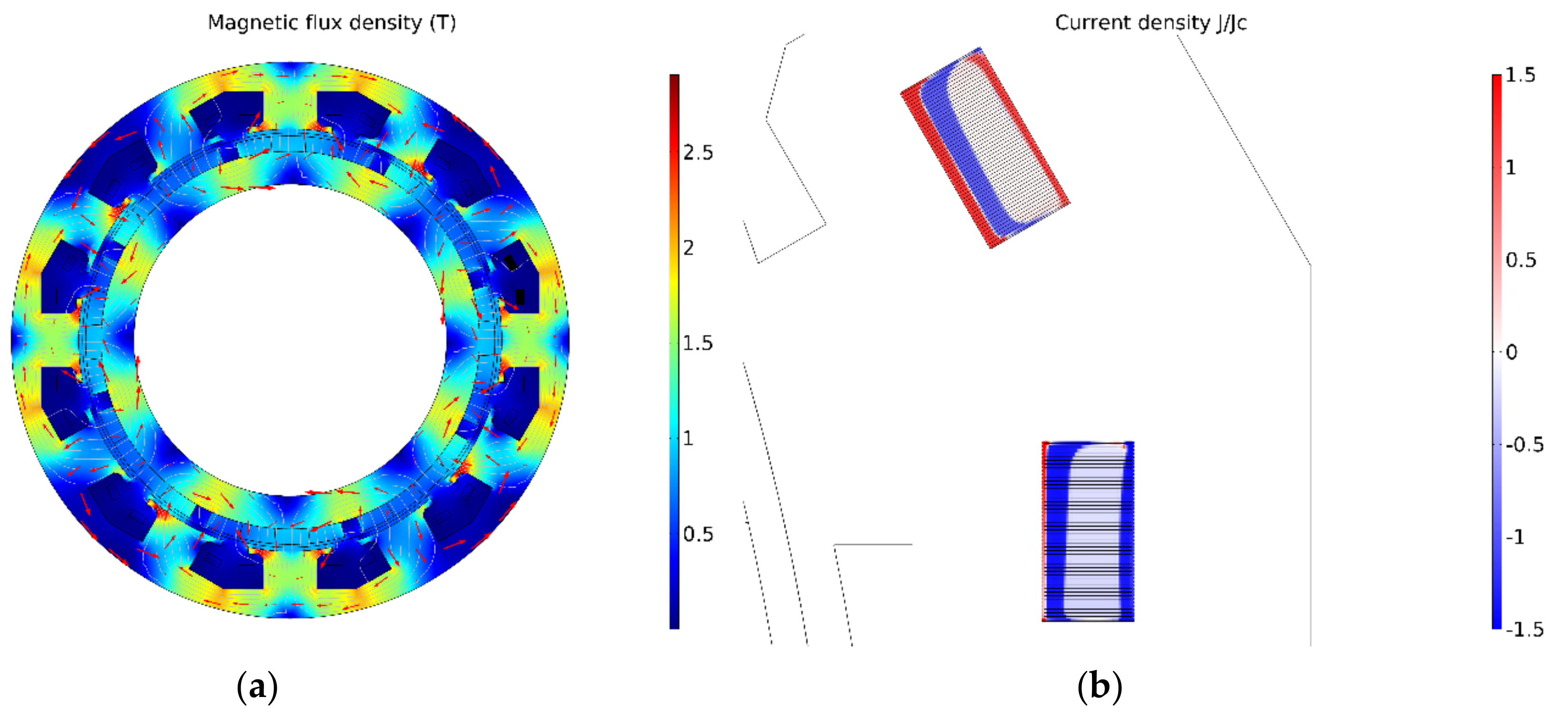




| HTS Machines | Power Level | BSCCO Heat Load | YBCO Heat Load |
|---|---|---|---|
| Generators | 10–500 MW | 100–500 W at 25–40 K | 100–500 W at 50–65 K |
| Motors | 1–10 MW | 50–200 W at 25–40 K | 50–200 W at 50–65 K |
| Working Temperature (K) | Ideal Carnot Specific Power (W) | Practical Carnot Specific Power (W) (When Heat Load > 100 W) |
|---|---|---|
| 273 | 0.11 | 0.4 |
| 77 | 2.94 | 12–20 |
| 50 | 5.06 | 25–35 |
| 20 | 14.15 | 100–200 |
| 4.2 | 71.14 | 11,000 |
| Material | Unit Cost | Tc | Ic0 |
|---|---|---|---|
| REBCO (12 mm-width) | ~227 $/(kA·m) | up to 119 K | 400–600 A (SuperPower, 77 K) |
| REBCO (4 mm-width) | ~230 $/(kA·m) | up to 119 K | >100 A (SuperOX, 77 K) min. 88-min. 152 A (SuperPower, 77 K) min. 130 A (AMSC, enhanced pinning, 77 K) >165 A (Fujikura, 77 K) >150 A (SuNAM, 77 K) ~150 A (Shanghai SC, 77 K) >100 A (SWCC, 77 K) |
| Bi-2223 | 17.4 $/(kA·m) | 110 K | ~170–~200 A (SEI, 77 K) |
| NbTi (LTS) | 0.8 $/(kA·m) | 9.5 K | Up to 3 kA (SuperCon, 4.2 K) |
| MgB2 | 20 $/(kA·m) | 39 K | ~157 A (MgB2/Ga(30), 4.2 K) |
| NdFeB (PM) | 28.9 $/kg | / | / |
| Copper | 11.6 $/kg | / | / |
| Iron (Silicon steel) | 1.6 $/kg | / | / |
| Measurement Methods | Main Purpose | Advantages | Disadvantages |
|---|---|---|---|
| Electric method | Transport current loss; total AC loss | Fast; high sensitivity; high accuracy; able to measure low AC loss | Compensation coil needed; lock-in amplifier can only work with pure sinusoidal signals; easy introduction of harmonics. |
| Magnetic method | Magnetization loss | Fast; high sensitivity; high accuracy; able to measure low AC loss | Limited to static measurement; pick-up coils easily interfered by external magnetic fields; |
| Calorimetric method | Total loss | Disregarding object shape; disregarding working conditions; able to measure large-scale specimen | Poor sensitivity; weak accuracy; long time consumption; possible disturbance from thermal effects of non-superconductors. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Wen, Z.; Grilli, F.; Gyftakis, K.; Mueller, M. Alternating Current Loss of Superconductors Applied to Superconducting Electrical Machines. Energies 2021, 14, 2234. https://doi.org/10.3390/en14082234
Zhang H, Wen Z, Grilli F, Gyftakis K, Mueller M. Alternating Current Loss of Superconductors Applied to Superconducting Electrical Machines. Energies. 2021; 14(8):2234. https://doi.org/10.3390/en14082234
Chicago/Turabian StyleZhang, Hongye, Zezhao Wen, Francesco Grilli, Konstantinos Gyftakis, and Markus Mueller. 2021. "Alternating Current Loss of Superconductors Applied to Superconducting Electrical Machines" Energies 14, no. 8: 2234. https://doi.org/10.3390/en14082234
APA StyleZhang, H., Wen, Z., Grilli, F., Gyftakis, K., & Mueller, M. (2021). Alternating Current Loss of Superconductors Applied to Superconducting Electrical Machines. Energies, 14(8), 2234. https://doi.org/10.3390/en14082234