Abstract
The article presents an original simulation model of a wind farm (WF) consisting of 30 wind turbine-generator units connected to the electrical power system (EPS) through power converters. The model is dedicated to the evaluation of the WF capabilities to participate in frequency and voltage regulation services in the power system. A system that allows for frequency and voltage control is proposed and implemented in the presented model. The system includes primary frequency regulation with synthetic inertia and secondary regulation available on request from the system operator. The concept of a reference power generation unit was introduced, according to which only one wind generator unit was modeled in detail, and the other units were replaced with simple current sources. Such a solution allowed for the reduction of size and complexity of the model as well as shortened the simulation time. Simulation tests were conducted in the PSCAD/EMTDC environment for an electrical power system composed of the wind farm, a synchronous generator, and a dummy load. The performance of the wind farm control system was analyzed in different operation conditions, and the control capabilities of the farm were assessed. Selected simulation results are presented and discussed in the paper. They illustrate the regulatory properties of the WF and confirm the correctness of the developed model.
1. Introduction
Basic regulation processes in conventional electrical power systems (EPSs) are provided by synchronous generators to maintain the power balance between production and demand and the required quality of the energy delivered to consumers. The growth in the power of renewable energy sources (RESs) installed in EPSs increases the possibilities of power balancing, but at the same time, it extends the area of power generation that can be regarded as excluded from the central control due to unstable power generation and the low inertia of the system. Maintaining the tendency of the growing share of RESs in an overall power and energy balance will make it necessary for system operators to change the method of controlling the operation of the whole power system and to include these sources in the provision of system regulation services [1].
The ability of individual RESs to participate in system regulation depends on the technology that is used to produce energy. It includes the type of primary energy, the presence of rotating components, the method of evacuating power from the source into the system, and the structure of regulatory systems [2].
At present, wind farms (WFs) are regarded as the most promising technology, owing to the presence of rotating components that constitute the source of natural inertia [3,4,5,6]. Wind power plants that are currently used in Polish EPSs are characterized by the inertial response at the level from 2 to 3.5 s, i.e., a value that is ca. half as high as the value characteristic for conventional steam units with inertia constant from 5 to 8 s [7,8,9,10,11,12,13]. However, compared to other RESs, such as photovoltaic systems (PVs) that have no inertia, it is quite a significant value.
In accordance with the current Polish Grid Code [14], WFs with the power equal to or exceeding 50 MW should be equipped with a system for controlling and regulating active power, making it possible for the farm to operate within the limitations defined by the system operator and to participate in frequency regulation, as well as a system for controlling reactive power, ensuring the possibility of cooperating with primary voltage regulation systems [15]. Similar technical requirements are specified for WFs in other countries’ grid codes [16]. Thus, it can be claimed that WFs participation in frequency and voltage regulation is not only justified by the need to raise the level of system services, but it should also be technically possible provided that the requirements resulting from the current regulations are fulfilled.
Owing to the degree of complexity of EPSs and the specific character of WFs, it can be stated that an analysis of wind farm participation in the provision of system regulatory services is a difficult issue and an interesting research problem. It becomes necessary to develop methods and tools of assessing the impact of WFs operation on the power system, and, in particular, of verifying their regulatory capabilities. In the case of a power system, performing direct tests is limited; therefore, a simulation method based on the system models is the most effective and sometimes the only one to apply.
Extensive studies are conducted worldwide to assess the possibility of providing system services by WFs [17]. This subject is discussed in numerous articles and concerns both simulation studies [18,19] and studies conducted on real WFs [6,20,21,22], whereby various aspects of their operation are analyzed. The key directions of research concern the comparison of various types of generators used in wind power plants [5,23] in terms of manufacturing technology, the impact of farms on the power system operation, and the power quality as well as maximizing energy production in WFs.
Various simulation models are used in the studies, the features of which depend on the specific application. The models dedicated to closed loop on-line control to optimize the power production of wind turbines [24,25,26,27,28,29] belong to the class of control-oriented dynamic models and differ in terms of the degree of fidelity. Other models are used for the WFs layout optimization. It is especially useful at the farm design stage to help WFs produce as much power as possible while minimizing the wake impact that can disturb the flow of the wind inside a wind farm [30,31]. The awakening of one or more turbines causes the wind to become turbulent and the wind speed to decrease, which can significantly reduce the energy production of the wind farm. Such optimization is carried out with the use of advanced optimization algorithms (e.g., genetic algorithms), and its aim is to maximize the power production in the farm and to limit the mutual influence of turbines on each other [32,33,34].
Some publications deal with the regulatory capabilities of wind generators and WFs in terms of voltage regulation in medium voltage distribution networks [35,36,37]. They describe an indirect method of regulation through the control of reactive power by an interface converter. In [37], a simulated study was performed to compare using reactive power for voltage regulation and for losses reduction in the network.
Numerous papers [38,39,40,41,42,43,44] concern the issue of frequency control. In [38], a control strategy for an islanded system with a WF and a hydrogenerator is presented. A modification of the control algorithm applied for the real WF was proposed to improve the control quality. A detailed review on the frequency response of WFs with different types of generators is presented in [39]. A simulation study showing the behavior of the real WF during the event of frequency nadir is discussed in [40]. Frequency control in an islanded system with drop characteristics applied in WTs is the subject of paper [41]. In [42], the contribution of WFs equipped with DFIG generators in secondary frequency control in the power system is analyzed. In the control system described, the PID (proportional–integral–differential) controller was used, which reduced overshooting in the frequency response. In [43], an extended study of applying WFs for primary frequency control in the power system is presented. A method based on rootlocus analysis was applied for tuning control parameters. In [44], the NREL simulation model of a WF with DFIG generators was used to study the participation of the farm in the frequency secondary regulation. The active power control was designed using adaptive pole placement control and fuzzy gain-scheduled PI (proportional–integral) controller.
Models used for the analysis in the literature differ in the structure of the power grid, the type of WFs generators, and a different share of WFs in the power balance. The presented results indicate that including proper frequency controls in the wind turbines can significantly improve the frequency response of the power system.
This paper presents a comprehensive simulation model of a WF connected to the EPS through power converters and participating in frequency and voltage regulation. The model has been developed using the PSCAD software and consists of wind turbine-generator units and their control systems allowing them to react to frequency and voltage changes in the power system. As the model is dedicated to studying the power system behavior under regulation (the cooperation of the WF with the power system), the authors focused on the electrical part of the system. Component modules from the PSCAD library were used in the model, such as the wind turbine model. It enables programming variables for various types of winds (blasts, turbulences) as an input and regulates the turbine power by changing the attack angle of the blades; however, it does not take into account the wake effect. The model, firstly presented in [45], has been extended and modified. Virtual inertia was introduced to the frequency control, which improved the behavior of the system under the violation of the power balance. The frequency regulation encompasses primary regulation with virtual inertia and secondary regulation on request of the system operator. Based on the simulation tests conducted using the PSCAD software, an analysis of the WF response to a change in operating conditions and to the limitations imposed by the operator was conducted. The reaction of the farm to the input signals applied to control systems was also shown, illustrating its capability to participate in the system regulation.
The paper is organized as follows: Section 2 describes the basic principles of regulating frequency and voltage in power systems. Particular attention was paid to the analysis of the WF potential in terms of providing regulatory services depending on the type of generator used in the wind power unit. Section 3 presents the power system for which simulation studies were carried out. Section 4 describes the models of individual elements of the tested system. The electromechanical elements and the algorithm of the wind turbine are presented in detail. Section 5 contains the results of the simulation tests. The conclusions from the tests and the evaluation of the created model are included in Section 6.
2. Principles of Frequency and Voltage Regulation in the EPS
2.1. Frequency Control
Frequency regulation is performed basically by the conventional power and is aimed at controlling active power production during frequency changes. In a steady state, the power generated by energy sources is equal to the power consumed by loads; i.e., the EPS is in an equilibrium point. Any change in the generated or consumed power results in the violation of the power balance. Then, the primary frequency regulation is carried out locally by the speed governors of synchronous generators according to their static f-P characteristic, which leads to a new equilibrium point but for a different frequency. To restore frequency to the value before a disturbance, secondary regulation is accomplished. Secondary regulation results from a coordinated impact of the central control system on selected generators.
The capabilities of WFs to participate in frequency control as well as the applied control methods depend on the type of a generator unit. Various types of generators are used in wind power plants. Currently, the double-feed induction generators (DFIGs) and two types of synchronous generators (SG and PMSG) are most commonly used in WFs [46]. The SG has an excitation circuit, while in the PSMG generator, the source of excitation are permanent magnets. All these types are connected to the network through power electronic converters. In the case of the DFIG generator, the converter is located in the rotor circuit, which means partial separation from the network. The synchronous generators are completely separated from the grid because the converter is located in the stator circuit.
As the generators are electromechanically isolated from the grid, they cannot provide the primary frequency control by means of a rotational speed governor, unlike synchronous generators in conventional power plants. The control system is located in the power converter. Its characteristic feature is a small inertia and immediate response after disturbing the power balance.
The frequency regulation in wind power plants with synchronous generators can be performed by means of controlling the pitch angle of the turbine blades, so called pitch control. [47]. It affects the turbine mechanical torque and, as a result, changes the active power generation. To obtain regulatory capabilities in terms of both positive and negative frequency variations, it is necessary to maintain a power regulatory reserve, i.e., limit the power generation in the WF.
An additional service that can be provided by WFs is the imitation of the responses of conventional generators through virtual inertia and thus damping power oscillations. The purpose of virtual inertia is to make a portion of energy accumulated in the turbine rotating elements available for control purposes. A system with greater inertia is less sensitive to frequency fluctuations in case of sudden changes in the power balance.
To increase the capabilities of frequency control in systems with a significant number of WFs, a feedback loop with a frequency-dependent signal is added to the WF active power control system [10,11,48]. To enhance this effect, WFs are also combined with energy storage [49,50,51,52]. The existing systems make it possible to obtain additional active power for control purposes with a value of even 5–10% of the rated power for a time dependent on the value of the inertia constant [53,54]. The value of the additional active power in primary regulation depends on the amplitude of the frequency change (Δf) and the rate of this change (df/dt). There are many publications in the literature describing the method of selecting the gain coefficient of the virtual inertia algorithm [55]. The gain value can be selected experimentally as a constant value or vary according to the amplitude of frequency change [56].
2.2. Voltage Control
Direct and indirect methods for voltage regulation are used in the EPS. Direct methods involve changing the voltage level at the generators’ terminals or the transformation ratio of power transformers. Indirect methods include the change of reactive power flow in the system.
Voltage regulation is possible for all types of turbine-generator units and entire WFs by modifying the control system or connecting additional devices. Three operating modes of WF control system are defined [26]: operation with a constant power factor tgφ, direct voltage regulation at the point of WF connection to the EPS (the Point of Common Coupling, PCC) and the control of the reactive power fed into the grid as a function of voltage. All these modes of operation may be implemented for DFIG and PMSG generators. They can work with a set value of reactive power, voltage, or power factor. This requires a modification of the control system by adding an additional control loop to the voltage control system [57,58]. An additional increase in the range of the reactive power generated by the farm is possible through the use of dedicated devices for reactive power compensation, e.g., static compensators (STATCOM) [59,60]. Such a combination is used in the case of very poor connection to the network and to improve Low Voltage Ride-Through (LVRT) [61].
Based on the analysis of the literature, it can be concluded that the capabilities of a WF to participate in frequency or/and regulation processes may be associated with the necessity of modifying the control system or the installation of additional equipment.
3. System under Study
3.1. System Layout
A diagram showing the analyzed system is presented in Figure 1. It consists of three basic components: a WF with 60 MW installed capacity, a conventional power plant with a synchronous generator of 360 MW rated power, and an equivalent network load with defined voltage characteristics.
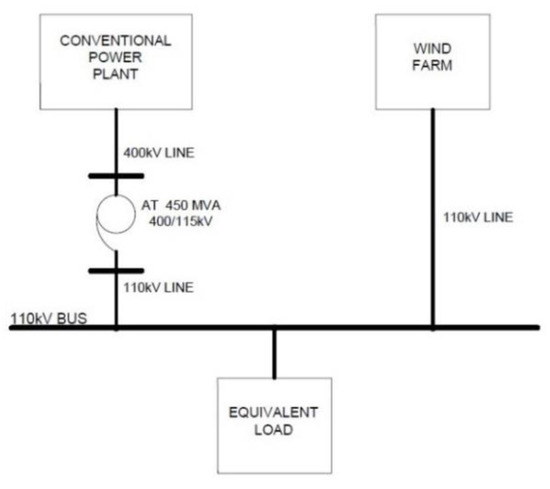
Figure 1.
A scheme of the considered system.
The wind farm consists of thirty E70 wind turbine-generator units with synchronous generators of 2 MW rated power. The generators are connected to the farm internal power network of 30 kV using power electronic converters and 0.4/30 kV transformers. The WF is connected to an external power grid through a 110/30 kV substation with a transformer of 63 MVA rated power and a cable line of 110 kV voltage.
An equivalent generator and a 22/400 kV block transformer were used in the “Conventional power plant” block. The parameters of the generator correspond to the GTHW-360 bipolar generator, which is most frequently used in the Polish national EPS. Power output from the power plant is transmitted using a 400 kV overhead line. A connection with the 110 kV power grid was implemented using a 450 MVA autotransformer with the ratio of 400/115 kV and Yd11 winding connections.
3.2. Assumptions for WF Control
For the participation of the WF in system regulation services, the control system of wind turbines should allow for the active power control when the power balance or frequency set value is violated and reactive power control when the voltage exceeds the required range. To accomplish these tasks, two modes of operation were assumed for the turbine-generator units:
- Normal operation mode with available power or power limitations,
- Intervention mode, operation with performing voltage and/or frequency regulation services.
In the first mode, power generation results from the available wind energy. If there are no limitations imposed by the operator, the usage of renewable energy is maximal. The system operator may limit the power generation below the level that is possible to obtain in given weather conditions in order to obtain a reserve of regulatory power. In such a case, the WF can contribute to power balancing in the system when frequency changes due to a disturbance. Participating in power balancing in the power system corresponds to primary frequency regulation. The second mode is called interventional and is activated on the request of the system operator. In this mode, secondary frequency and/or voltage regulation service is performed.
4. System Model
4.1. The Wind Farm Model
The model of the analyzed system was created in the PSCAD™/EMTDC™ program environment using modules from the program library [62].
A wind farm model includes individual wind turbine-generator units, the farm internal network, and the main 110/30 kV power substation. Due to limitations in the number of computing nodes, only one turbine-generator unit, called the reference wind generator, was fully modeled. The remaining units were modeled as controlled current sources. Assuming that all turbine-generator units of the WF are of the same type as the reference one, it was accepted that reference currents of the sources correspond to the currents of the reference wind generator. Owing to that, simulation computations were conducted considerably faster.
A model of the reference wind-generator unit consists of the following main blocks: wind turbine, synchronous generator, electronic power converter system, and an interface transformer, as shown in Figure 2. The control system was modeled separately and is described in detail in the next section.
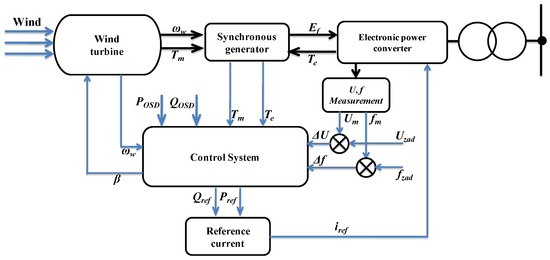
Figure 2.
A block diagram of the reference turbine-generator unit model.
The wind turbine was modeled using a “Wind Source” block, which enables programming variables for various types of winds (blasts, turbulences). A modified power curve corresponding to the characteristics given by the manufacturer for the E70 turbine was used in it [63]. The turbine power is regulated by changing the attack angle of the blades.
A low-speed multi-polar (36 pole pairs) generator, operating with a variable rotational speed in the range from 8 to 21.5 rpm was used in the model. The generator was connected to the power network using a power electronic converter consisting of a rectifier, voltage stabilization system, and an inverter.
The wind farm data correspond to the real WF installed in the Polish EPS.
4.2. The Wind Farm Control
The WF control system was designed to meet the requirements specified in Section 3.2.
The following signals are supplied to the control system module:
- The angle speed of the turbine-generator unit ωw,
- The values of the mechanical and electromagnetic torque Te, Tm,
- The values of active and reactive power set by the operator, divided equally between individual turbine-generator units POSD, QOSD,
- Measured active power Pm,
- Measured deviations of frequency and voltage Δf, ΔU.
The output signals from the block are the attack angle of turbine blades β (pitch control) and reference values of active power Pref and reactive power Qref that should be supplied to the power network.
A diagram of the turbine-generator unit active power control is presented in Figure 3. Basic regulation results from the balance of mechanical and electromagnetic torques described by the following equation [64].
where J—moment of inertia of the generator rotor, ω—rotational speed of the rotor, Tm—mechanical torque, Te—electromagnetic torque, T0—loss torque.
J × (dω/dt) = (Tm − T0) − Te
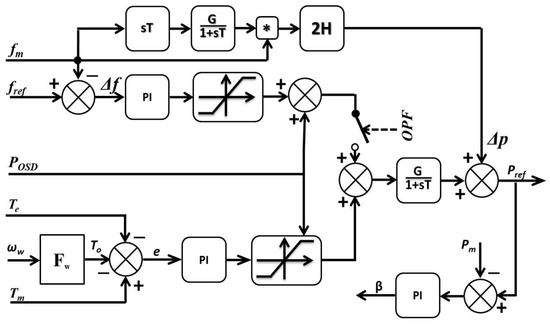
Figure 3.
The active power control of the turbine-generator unit.
Block Fω allows for considering the dependence of the loss torque on the generator angle speed.
An additional path introducing the virtual inertia of the turbine has been added to the control system in order for the WF to be able to take part in power balancing and the first moment of a disturbance [65,66,67]. This part of the system reacts to frequency deviations resulting from the violation of power balance in the electric power system. Additional power obtained due to virtual inertia is described by the following equation [68,69,70].
where H—inertia constant [s], and fm—measured system frequency (p.u.).
Δp = 2H × fm × (dfm/dt)
Using virtual inertia, the WF can contribute to reducing frequency variations dynamics in the initial state after a disturbance. However, to have this functionality, the wind farm should operate with some power reserve to be able to contribute to power balancing in case of load increase. The system operator may limit the power generation below the level that is possible to obtain in given weather conditions using the signal POSD. Power reserve is also needed if the WF is to participate in frequency secondary regulation. This regulation starts after the OPF control signal is supplied. Then, the WF power is corrected depending on the frequency deviation so that the frequency returns to its nominal value.
The control processes in turbine-generation units are conducted by means of the pitch control, which causes a limitation of the turbine mechanical torque to the required value Tm. The β angle control system is activated when there is any change in the reference value of active power due to the operation of the control system or the power system operator’s decision. The regulation of the β angle also protects the wind turbines against mechanical overloads that may occur when the permissible wind speed is exceeded. In the simulation model, power PMAX corresponds to the rated turbine rotational speed equal to 2.3 rad/s.
A diagram of the turbine-generator unit reactive power control is presented in Figure 4. The control system allows the farm to generate reactive power with the value QOSD set by the operator (when no value is set by the operator, the generated reactive power is equal to zero) or to operate in the voltage regulation mode obtained after the OPV control signal is supplied.
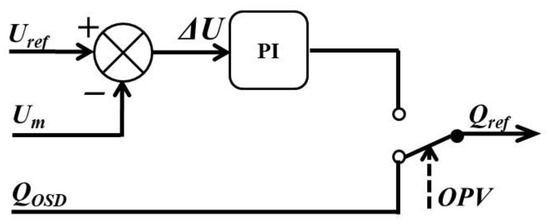
Figure 4.
The wind farm reactive power control system.
The inverter of the reference turbine-generator unit is current-controlled. The reference currents iref are determined on the basis of the Pref and Qref power signals obtained from the active and reactive power control systems.
4.3. The Conventional Power Plant Model
In the considered system, the conventional power plant with an equivalent synchronous generator constitutes an element that balances power and energy, so that it takes on a role of the equivalent EPS. The turbine-generator unit model was built using the following modules from the PSCAD library: “Synchronous Machine”, “Exciter”, “Power System Stabilizer”, and “Steam Governor”. The steam governor controls the influx of steam to the turbine. A static excitation system maintains a constant voltage value on the generator terminals. In order to limit the oscillation of the output power, the authors used a power system stabilizer that impacts on the excitation system, depending on the changes in the rotational speed of the generator shaft. A block diagram of the turbine-generator system is shown in Figure 5.
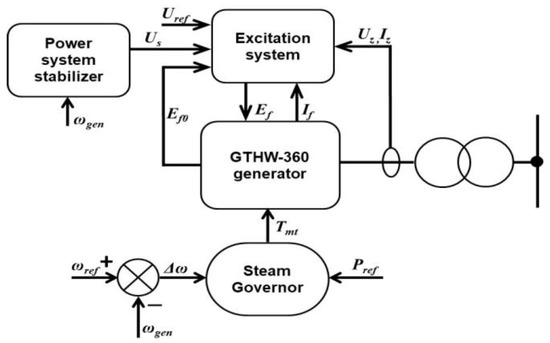
Figure 5.
A block diagram of the equivalent turbine-generator unit.
Connecting a single generator to a network with loads makes it rotate at a speed corresponding to the mechanical torque of the turbine, counterbalancing the electromagnetic torque. The change in the rotational speed of the turbine results in the change in the power output as a result of the steam governor activation, which is in accordance with its static control characteristics [71].
A diagram of the turbine power control system is shown in Figure 6 [72]. The input signals are the reference turbine speed ωref and measured speeds ωgen and the reference power Pref that determines the operating point on the P = f(ω) characteristics. The speed error is fed to the block 1/R, which is the slope of the P(f) characteristic.
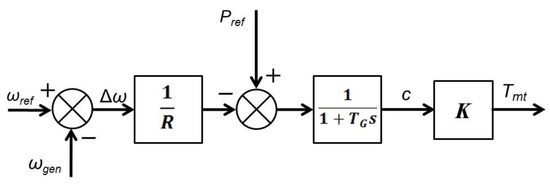
Figure 6.
The steam turbine power regulation system.
The output signal is the turbine mechanical torque, which depends on the degree of opening steam supply valves c. Level c = 0 corresponds to closed valves, and c = 1 corresponds to completely open valves. The slope of generation characteristics can be regulated by changing the coefficient 1/R, where statism R is the setting of the control system. The basic actuator, i.e., the hydraulic actuator, is presented as a first-order inert element.
4.4. The Load Model
A model of the equivalent load was built using the “FixedLoad” module from the PSCAD library. The model makes it possible to define the load active and reactive power in a grid node on the basis of known voltage characteristics:
where PL, QL—rated phase load, U,UN—measured and rated voltage, NP, NQ,KPP, KQF—coefficients.
P = PL × (U/UN)^NP. × (1 + KPP × df)
Q = QL × (U/UN)^NQ × (1 + KQP × df)
5. System Model
Simulation tests were performed to study the operation of the WF in the EPS in different operating conditions. Some simulation cases that illustrate the WF control abilities are presented below.
5.1. Participation of the WF in Frequency Regulation
The participation of the WF in frequency regulation requires maintaining a reserve of active power, which means that the generated power is lower than the power that it is able to generate under given conditions.
In the discussed scenario, it was assumed that the WF operates with the power limited by the operator to the value of 15 MW, at the set reactive power equal to 5 Mvarind. In the 2nd second of the simulation, the load was increased by 30 MW and 10.5 Mvarind and after a steady state was reached, the frequency regulator was switched on in the 7th second of the simulation (Figure 7 and Figure 8).
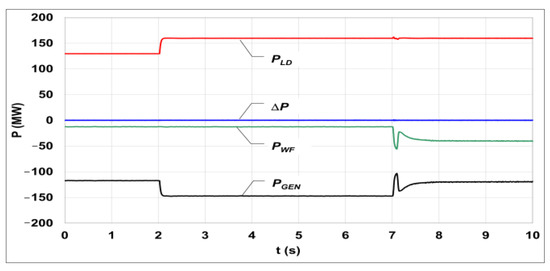
Figure 7.
Changes in the active power balance in the system, resulting from the operation of the farm in the frequency regulation mode: PLD—active equivalent load power, PWF—active WF power, PGEN—active generator power, ΔP—active power losses in the network.
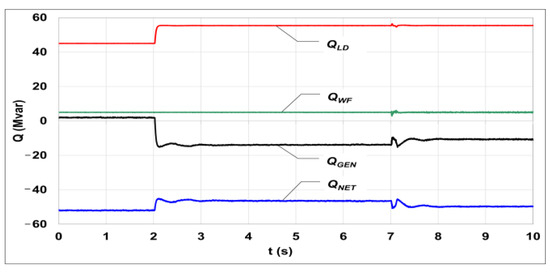
Figure 8.
Changes in the reactive power balance in the system, resulting from the farm operation in the frequency regulation mode: QLD—reactive power of the equivalent load, QWF—reactive WF power, QGEN—reactive generator power, QNET—network capacitive reactive power.
In accordance with the active power balance shown in Figure 7, the demand power was mainly met using the conventional power plant generator at the initial stage of the simulation. Under those conditions, the value of the supply voltage was 115 kV (Figure 9), and the frequency was equal to 50 Hz (Figure 10).
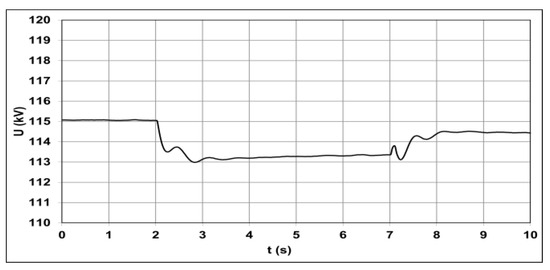
Figure 9.
Changes in the voltage value in the receiving node, resulting from the farm operation in the frequency regulation mode.
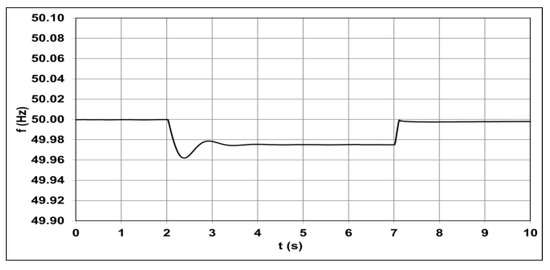
Figure 10.
Frequency changes in the receiving node, resulting from the operation of the farm in the frequency regulation mode.
In reaction to the increased load, the generator power rose, which resulted in a decrease in frequency to 49.98 Hz. The active and reactive power generated in the WF did not change, while voltage decreased to 113.3 kV at the point of load connection.
When the wind power plant began operating in the frequency regulation mode, the active power generation rose to 40 MW as the attack angle of the wind turbine blades decreased to 12° (Figure 11). At the same time, there was a decrease in the power of the synchronous generator as a balancing source (Figure 7).
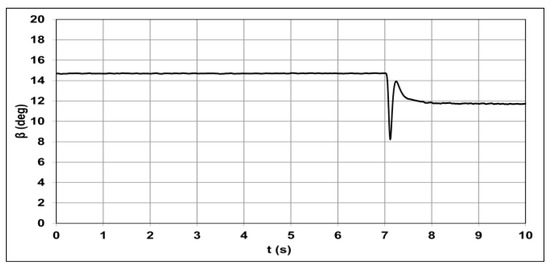
Figure 11.
Changes in the attack angle of the blades after including the farm in frequency regulation.
A change in the active load distribution between energy-generating units in the system resulted in a change of the reactive power flow in the system (Figure 8) and thus in a change of the voltage value in the load node (Figure 9).
The operation of the frequency control system in the WF resulted in an increase of the power generated by the farm and a rise in frequency to the reference value equal to 50 Hz (Figure 10).
This confirms the effectiveness of operation of the applied WF frequency and the active power regulation system.
5.2. WF Frequency Response Using Virtual Inertia
In the next part of the research, the frequency response of the WF was analyzed with increasing and decreasing the load. The inertia coefficients for the WF were 0, 0.5, 1, and 2, respectively. During the tests, the farm worked with the secondary frequency control mode turned off (the OPF control in Figure 3). The activation of the virtual inertia algorithm took place after setting the inertia constant greater than zero. The frequency response analysis was performed while increasing the system load from 180 MW to 210 MW. Figure 12 shows the course of frequency changes depending on the set inertia coefficients. Before the load change, the frequency in the system was close to 50 Hz. After increasing the load, its value decreased to 49.977 Hz. According to Equation (2), the maximum reaction of the virtual inertia algorithm occurs in the first moment after the disturbance, when the derivative of frequency changes in time achieves the highest value. In the analyzed case, the maximum frequency deviation with the load increase by 30 MW and inertia switched off was approximately 13 mHz. The maximum overshoot for all inertia coefficients occurred about 40 msec after the disturbance.
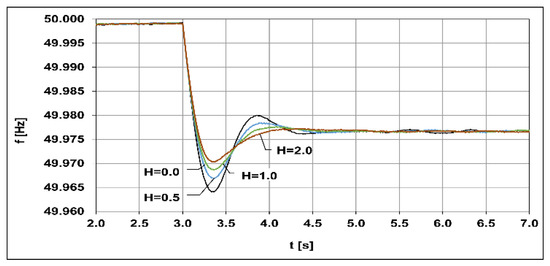
Figure 12.
Frequency changes during load increase for selected inertia coefficients.
Along with the increase of the inertia coefficient, the overshoot amplitudes and their number are reduced. In the case of constant inertia equal to H = 2 s, the first maximum overshoot was smaller by half and amounted to ca. 6 mHz, while the second overshoot (upwards) practically did not occur.
The second of the analyzed cases, i.e., the reduction of the system load from 210 to 180 MW, resulted in an increase in frequency from 49.977 to 50.001 Hz. The course of frequency changes in the system is aperiodic, which results from the system inertia. In the absence of virtual inertia in the frequency course, there are three overshoots with the maximum value of the first of them at the level of 13 mHz (Figure 13). When the virtual inertia was increased to the value of H = 2 s, there was only one overshoot of the maximum value of 3 mHz.
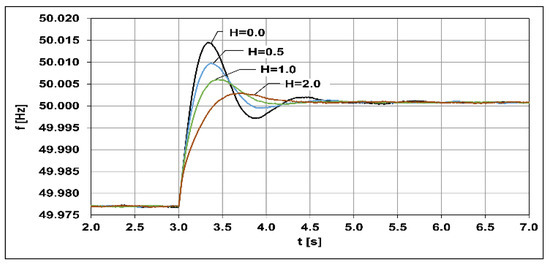
Figure 13.
Frequency changes during load reduction for selected inertia coefficients.
5.3. Participation of the WF in Voltage Regulation
The reactive power generation capacity of WFs makes it possible to use them in the process of voltage regulation in a network. In order to illustrate the regulation effect, the results of simulation are shown below, where the starting point corresponded to the voltage and frequency values obtained at the previous stage of the calculations (frequency—50 Hz, voltage—115 kV). In the 2nd second, the network load was increased by 30 MW and 10.5 Mvarind, and then, in the 7th second, a voltage regulation system was activated. Power balances in the system are shown in Figure 14 and Figure 15.
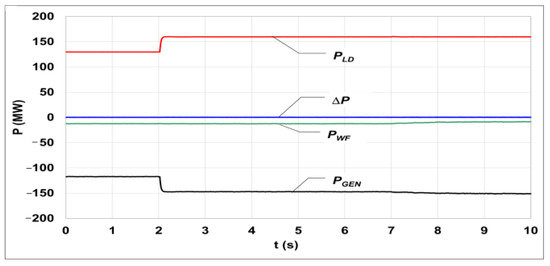
Figure 14.
Changes in active power in the system, resulting from the farm operation in the voltage regulation mode (the symbols used correspond to those in Figure 8).
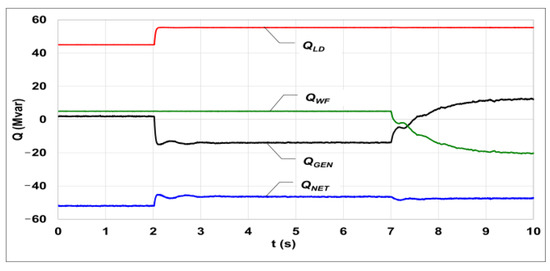
Figure 15.
Reactive power changes in the system, resulting from the farm operation in the voltage regulation mode (the symbols used correspond to those in Figure 9).
After a short-lasting transient state, the system was balanced again. The values of the active and reactive power generated by the farm did not change owing to the operator limitations, while the power balance in the system was ensured by appropriately increasing the generator output to 149 MW of active power and 16 Mvarcap of reactive power.
As a result of changes in the reactive power flow, there was a decrease in voltage at the load busses (Figure 16), and thus, the capacitive reactive power of the network also decreased (Figure 15). The increasing generator active power caused frequency reduction to the level of 49.98 Hz (Figure 17).
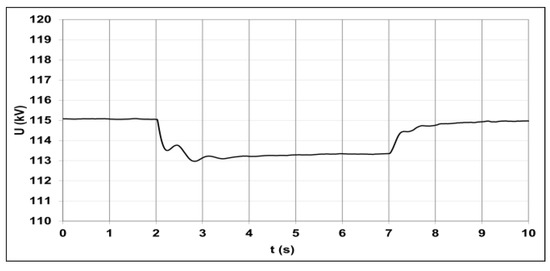
Figure 16.
Changes in voltage at the point of the WF connection, resulting from including the farm in voltage regulation.
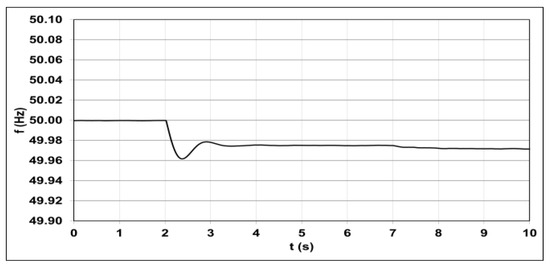
Figure 17.
Frequency changes resulting from including the farm in voltage regulation.
Switching on the voltage regulator in the WF in the 7th second of the simulation resulted in a change of the value and character of the reactive power generated by the WF (Figure 15). As a result, the character and value of the reactive power generated in the conventional generator also changed.
As a result of the regulator operation, the voltage at the load connection node rose from 113.3 kV to the set value equal to 115 kV (Figure 16). The voltage regulation process had a negligible effect on frequency, which stabilized again after a transient state at a slightly lower level of 49.97 Hz (Figure 17).
6. Conclusions
Due to the complexity of the EPS and the specific character of RESs, the investigation of WFs capabilities to participate in system regulation services is an interesting and important issue, taking into account the continuous increase in the number and power of WFs in the system. This paper proposes a simulation tool that makes it possible to assess the operation of control systems of cooperating sources and to analyze the regulatory process under different operating conditions.
Participation in frequency regulation requires the creation of a regulatory reserve of active power and operation of the WF with active power below the value that could be obtained in given wind conditions. The implementation of an additional control loop reflecting the inertia of conventional generators significantly improves the WFs response during short-term frequency control. The ability to generate reactive power enables WFs to be used in voltage regulation.
The WF model presented in the paper makes it possible to study the dynamic characteristics of power systems including large wind farms. Due to the concept of one so-called reference power generation unit modeled in detail and other units replaced with simple current sources, the size and complexity of the model were reduced and the simulation time was shortened.
The simulation results presented in the paper illustrate the regulatory properties of the WF and confirm the correctness of the developed model. Taking into account their control capabilities, it can be stated that WFs could be effectively used for providing system services in terms of frequency and voltage regulation, thus contributing to an increase in the safety of operation of electrical power systems.
It can be concluded that the selection of the appropriate model, solution technique, and proper algorithms for a particular application is important for efficient modeling and can contribute significantly to developing a reliable and efficient wind-energy based power system.
Author Contributions
Conceptualization, H.B. and R.P.; methodology, H.B., R.P. and I.W.; modelling, H.B. and R.P.; validation, I.W.; investigation, H.B. and R.P.; writing—original draft preparation, H.B. and I.W.; supervision, R.P. and I.W.; schemes and charts, H.B. and R.P.; writing—review and editing, I.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Szablicki, M.; Rzepka, P. Analysis of technical possibilities of photovoltaic and wind sources playing in an ancillary service of frequency and power regulation. Acta Energetica 2016, 4, 112–119. [Google Scholar] [CrossRef]
- Czarnecki, B. Possibilities for regulation of wind farms in the context of ancillary services. Defined in PolishGridCode. In Proceedings of the XVIII Scientific Conference Advances in Power Engineering, Jastrzębia Góra, Poland, 7–9 July 2017. [Google Scholar]
- Klempke, H.; McCulloch, C.B.; Piekutowski, M.; Wong, A. Impact of high wind generation penetration on frequency control. In Proceedings of the 20th Australasian Universities Power Engineering Conference, Christchurch, New Zealand, 5–8 December 2010. [Google Scholar]
- Ulbig, A.; Borsche, T.; Andersson, G. Impact of low rotational inertia on power system stability and operation. In Proceedings of the IFAC, Cape Town, South Africa, 24–29 August 2014; pp. 7290–7297. [Google Scholar] [CrossRef]
- Muljadi, E.; Singh, M. Understanding inertial and frequency response of wind power plants. In Proceedings of the IEEE Conference: Power Electronics and Machines in Wind Applications (PEMWA), Denver, CO, USA, 16–18 July 2012. [Google Scholar] [CrossRef]
- Miller, N.W.; Clark, K.; Shao, M. Frequency responsive wind plant controls: Impacts on grid performance. In Proceedings of the IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011. [Google Scholar] [CrossRef]
- Wasilewski, J.; Lubośny, Z. Analysis of annual rotational mass inertia variability in the synchronous power system of continental Europe in the context of RES development and operation. Electrotech. News 2017, 85, 8–14. [Google Scholar] [CrossRef]
- Keung, P.K.; Li, P.; Banakar, H.; Ooi, B.T. Kinetic Energy of Wind-Turbine Generators for System Frequency Support. IEEE Trans. Power Syst. 2009, 24, 279–287. [Google Scholar] [CrossRef]
- Ma, H.T.; Chowdhury, B.H. Working towards frequency regulation with wind plants: Combined control approaches. IET Renew. Power Gener. 2010, 4, 308–316. [Google Scholar] [CrossRef]
- Wang, D.; Gao, X.; Meng, K.; Qiu, J.; Lei Lai, L.; Gao, S. Utilisation of kinetic energy from wind turbine for grid connections: A review paper. IET Renew. Power Gener. 2018, 12, 615–624. [Google Scholar] [CrossRef]
- Akbari, M.; Madani, S.M. Analytical evaluation of control strategies for participation of doubly fed induction generator-based wind farms in power system short-term frequency regulation. IET Renew. Power Gener. 2014, 8, 324–333. [Google Scholar] [CrossRef]
- Mujcinagic, A.; Kusljugic, M.; Nukic, E. Wind inertial response based on the center of inertia frequency of a control area. Energies 2020, 13, 6177. [Google Scholar] [CrossRef]
- Morren, J.; Pierik, J.; de Haan, S.W.H. Inertial response of variable speed wind turbines. Electr. Power Syst. Res. 2006, 76, 980–987. [Google Scholar] [CrossRef]
- Polish Grid Code. Instruction of Transmission System operations and Maintenance Version 1.2; Polish Power System: Warsaw, Poland, 15 December 2011; Available online: https://www.pse.pl/web/pse-eng/documents (accessed on 23 February 2020).
- Regulation of the Minister of Economy of 4 May 2007 regarding detailed conditions for the functioning of the electrical energy system. Pol. J. Laws 2007, 93, 623.
- Tsili, M.; Papathanassiou, S. A review of grid code technical requirements for wind farms. IET Renew. Power Gener. 2009, 3, 308–332. [Google Scholar] [CrossRef]
- Van de Vyver, J.; Vandoorn, T.; De Kooning, J.; Meersman, B.; Vandevelde, L. Provision of ancillary services with variable speed wind turbines. In Proceedings of the IEEE Young Researchers Symposium, Ghent, Belgium, 24–25 April 2014; EESA: Ghent, Belgium, 2014; pp. 1–6. [Google Scholar]
- Anca, D.; Blaabjerg, F.; Iov, F.; Sorensen, P. Modeling of wind farm controllers. In Proceedings of the European Wind Energy Conference and Exhibition 2006, Athens, Greece, 27 February–2 March 2006; pp. 2377–2385. [Google Scholar]
- Bao, Y.Q.; Li, Y. On deloading control strategies of wind generators for system frequency regulation. Int. Trans. Electr. Energy Syst. 2015, 25, 623–635. [Google Scholar] [CrossRef]
- Fischer, M.; Mendonca, A.; Engelken, S.; Mihov, N. Operational experiences with inertial response provided by type 4 wind turbines. IET Renew. Power Gener. 2016, 10, 17–24. [Google Scholar] [CrossRef]
- Margaris, I.D.; Papathanassiou, S.A.; Hatziargyriou, N.D.; Hansen, A.D.; Sorensen, P. Frequency control in autonomous power systems with high wind power penetration. IEEE Trans. Power Syst. 2012, 32, 189–199. [Google Scholar] [CrossRef]
- Rebello, E.; Watson, D.; Rodgers, M. Performance analysis of a 10 MW wind farm in providing secondary frequency regulation: Experimental aspects. IEEE Trans. Power Syst. 2019, 34, 3090–3097. [Google Scholar] [CrossRef]
- Mullane, A.; Bryans, G.; O’Malley, M. Kinetic energy and frequency response comparison for renewable generation systems. In Proceedings of the International Conference on Future Power Systems, Amsterdam, The Netherlands, 18 November 2005. [Google Scholar] [CrossRef]
- Boersma, S.; Doekemeijer, B.M.; Siniscalchi-Minna, S.; Wingerden, J.W. A constrained wind farm controller providing secondary frequency regulation: An LES study. Renew. Energy 2019, 134, 639–652. [Google Scholar] [CrossRef]
- Shapiro, C.; Meyers, J.; Meneveau, C.; Dennice, G. Wind farms providing secondary frequency regulation: Evaluating the performance of model-based receding horizon control. Wind Energy Sci. 2008, 3, 11–24. [Google Scholar] [CrossRef]
- Rebello, E.; Watson, D.; Rodgers, M. Ancillary services from wind turbines: Automatic generation control (AGC) from a single Type 4 turbine. Wind Energy Sci. 2020, 5, 225–236. [Google Scholar] [CrossRef]
- EU. Horizon 2020 Project Closed Loop Wind Farm Control; Deliverable No. 4.1. Classification of Control-Oriented Models for Wind Farm Control Applications; EU: Stuttgart, Germany, 2018. [Google Scholar]
- Kanev, S.K.; Savenije, F.J.; Soleimanzadeh, M.; Wiggelinkhuizen, E. Wind Farm Modeling and Control: An Inventory ECN-E–13-058; ECN: Le Petten, The Netherlands, December 2013. [Google Scholar]
- Boersma, S.; Doekemeijer, B.; Vali, M.; Meyers, J.; van Wingerden, J.-W. A control-oriented dynamic wind farm model: WFSim. Wind Energy Sci. 2018, 3, 75–95. [Google Scholar] [CrossRef]
- Silva, J.E.; Danao, L.A.M. Varying VAWT cluster configuration and the effect on individual rotor and overall cluster performance. Energies 2021, 14, 1567. [Google Scholar] [CrossRef]
- Haces-Fernandez, F.; Li, H.; Ramirez, D. Improving wind farm power output through deactivating selected wind turbines. Energy Convers. Manag. 2019, 187, 407–422. [Google Scholar] [CrossRef]
- Liu, F.; Ju, X.; Wang, N.; Wang, L.; Lee, W.J. Wind farm macro-siting optimization with insightful bi-criteria identification and relocation mechanism in genetic algorithm. Energy Convers. Manag. 2020, 217. [Google Scholar] [CrossRef]
- Ju, H.; Liu, F.; Wang, L.; Lee, W.J. Wind farm layout optimization based on support vector regression guided genetic algorithm with consideration of participation among landowners. Energy Convers. Manag. 2019, 196, 1267–1281. [Google Scholar] [CrossRef]
- Ju, X.; Liu, F. Wind farm layout optimization using self-informed genetic algorithm with information guided exploitation. Appl. Energy 2019, 248, 429–445. [Google Scholar] [CrossRef]
- Chirapongsananurak, P.; Santoso, S.; Dugan, R.C.; Smith, J. Voltage regulation in distribution circuits with wind power. In Proceedings of the IEEE Power and Energy Society General Meeting 2012, San Diego, CA, USA, 22–26 July 2012. [Google Scholar] [CrossRef]
- Kłosowski, Z. The analysis of the possible use of wind turbines for voltage stabilization in the power node of MV Line with use of a real-time simulator. Przegląd Elektrotechniczny 2015, 91, 20–27. [Google Scholar] [CrossRef]
- Fandi, G.; Igbinovia, F.O.; Tlusty, J.; Mahmoud, R. Voltage regulation and power losses reduction in a wind farm integrated MV distribution network. J. Electr. Eng. 2018, 69, 85–92. [Google Scholar] [CrossRef]
- Josefsson, R.; Mehmedovic, H.; Wang-Hansen, M. Frequency controlling wind power modeling of control strategies. IEEE Trans. Sustain. Energy 2013, 4, 954–959. [Google Scholar] [CrossRef]
- Wu, Z.; Gao, W.; Gao, T.; Yan, W.; Zhang, H.; Yan, S.; Wang, X. State-of-the-art review on frequency response of wind power plants in power systems. J. Mod. Power Syst. Clean Energy 2018, 6, 1–16. [Google Scholar] [CrossRef]
- Asmine, M.; Langlois, C.-E.; Aubut, N. Inertial response from wind power plants during a frequency disturbance on the Hydro-Quebec system—Event analysis and validation. IET Renew. Power Gener. 2018, 12, 515–522. [Google Scholar] [CrossRef]
- Vidyanandan, K.V.; Sneroy, N. Primary frequency regulation by deloaded wind turbines using variable droop. IEEE Trans. Power Syst. 2013, 28, 837–846. [Google Scholar] [CrossRef]
- Oshnoei, A.; Khezri, R.; Muyeen, S.; Blaabjerg, F. On the contribution of wind farms in automatic generation control: Review and new control approach. Appl. Sci. 2018, 8, 1848. [Google Scholar] [CrossRef]
- Wilches-Bernal, F.; Chow, J.H.; Sanchez-Gasca, J.J. A fundamental study of applying wind turbines for power system frequency control. IEEE Trans. Power Syst. 2016, 31, 1496–1505. [Google Scholar] [CrossRef]
- Badihi, H.; Zhang, Y.; Hong, H. Active power control design for supporting grid frequency regulation in wind farms. Annu. Rev. Control. 2015, 40, 70–81. [Google Scholar] [CrossRef]
- Białas, H.; Pawełek, R.; Wasiak, J. A simulation model for the analysis of wind farm usage in frequency and voltage regulation in an electrical power system. In Proceedings of the 12th International Conference and Exhibition on Electrical Power Quality and Utilisation, Krakow, Poland, 14–15 September 2020; IEEE Publisher: New York, NY, USA, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, A.; Matveev, A.; Nilssen, R.; Nysveen, A. High-power generators for offshore wind turbines. Energy Proc. 2013, 35, 52–61. [Google Scholar] [CrossRef]
- Attya, A.; Luis Dominguez-Garcia, J. Provision of ancillary services by wind power generators. In Advances in Modelling and Control of Wind and Hydrogenerators; Ebrahimi, A., Ed.; IntechOpen: London, UK, 2020; Available online: https://www.intechopen.com/books/advances-in-modelling-and-control-of-wind-and-hydrogenerators/provision-of-ancillary-services-by-wind-power-generators (accessed on 23 February 2020). [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Mitani, Y. Virtual inertia control application to enhance frequency stability of interconnected power systems with high renewable energy penetration. Energies 2018, 11, 981. [Google Scholar] [CrossRef]
- Yuan, T.; Wang, J.; Guan, Y.; Liu, Z.; Song, X.; Che, Y.; Cao, W. Virtual inertia adaptive control of a doubly fed induction generator (DFIG) wind power system with hydrogen energy storage. Energies 2018, 11, 904. [Google Scholar] [CrossRef]
- Díaz-González, F.; Sumper, A.; Gomis-Bellmunt, O.; Villafáfila-Robles, R. A review of energy storage technologies for wind power applications. Renew. Sustain. Energy Rev. 2012, 16, 2154–2171. [Google Scholar] [CrossRef]
- Zhaoxia, X.; Yu, H.; Guerrero, J.M.; Hongwei, F. Frequency participation by using virtual inertia in wind turbines including energy storage. In Proceedings of the 43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017. [Google Scholar] [CrossRef]
- Canbulat, S.; Balci, K.; Canbulat, O.; Bayram, I.S. Techno-economic analysis of on-site energy storage units to mitigate wind energy curtailment: A case study in scotland. Energies 2021, 14, 1691. [Google Scholar] [CrossRef]
- Ullah, N.; Thiringer, T.; Karlsson, D. Temporary primary frequency control support by variable speed wind turbines—Potential and applications. IEEE Trans. Power Syst. 2008, 23, 601–612. [Google Scholar] [CrossRef]
- Beltran, O.; Peña, R.; Segundo, J.; Esparza, A.; Muljadi, E.; Wenzhong, D. Inertia estimation of wind power plants based on the swing equation and phasor measurement units. Appl. Sci. 2018, 8, 2413. [Google Scholar] [CrossRef]
- Zhang, Z.S.; Sun, Y.Z.; Lin, J.; Li, G.J. Coordinated frequency regulation by doubly fed induction generator-based wind power plants. IET Renew. Power Gener. 2012, 6, 38–47. [Google Scholar] [CrossRef]
- Eto, J.H.; Undrill, J.; Mackin, P.; Daschmans, R.; Williams, B.; Haney, B.; Hunt, R.; Ellis, J.; Illian, H.; Martinez, C.; et al. Use of Frequency Response Metrics to Asses the Planning and Operating Requirements for Reliable Integration of Variable Renewable Generation; The Ernest Orlando Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2010. [Google Scholar] [CrossRef]
- Matos, K.N.V.; Londero, R.R.; de M. Affonso, C.; Vieira, A.P.A. Secondary voltage control applied to DFIG-based wind park and its effect on long-term voltage stability. Electr. Power Syst. Res. 2019, 175. [Google Scholar] [CrossRef]
- Chiandone, M.; Campaner, R.; Arcidiacono, V.; Sulligoi, G.; Milano, F. Automatic voltage and reactive power regulator for wind farms participating to TSO voltage regulation. In Proceedings of the IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015. [Google Scholar] [CrossRef]
- Pathak, A.K.; Sharma, M.P.; Bundele, M. A critical review of voltage and reactive power managementof wind farms. Renew. Sustain. Energy Rev. 2015, 51, 460–471. [Google Scholar] [CrossRef]
- Bena, L.; Kut, P. Wind farms in the process of voltage regulation in the power system. Przegląd Elektrotechniczny 2019, 8, 20–27. [Google Scholar] [CrossRef]
- Al-Majed, S.I. Secondary voltage control: Enhancing power system voltage profile. In Proceedings of the 2nd IEEE International Conference on Power and Energy, Johor Baharu, Malaysia, 1–3 December 2008. [Google Scholar] [CrossRef]
- PSCAD—Power Systems Computer Aided Design. User’s Guide on the Use of PSCAD; Manitoba Research Centre: Winnipeg, MB, Canada, 2003; Available online: https://www.pscad.com/uploads/ck/files/reference_material/PSCAD_User_Guide_v4_3_1.pdf (accessed on 23 February 2020).
- ENERCON GmbH. ENERCON Wind Energy Converters. Technology & Service; ENERCON GmbH: Aurich, Germany, June 2015; Available online: https://www.enercon.de/fileadmin/Redakteur/Medien-Portal/broschueren/pdf/en/ENERCON_TuS_en_06_2015.pdf (accessed on 23 February 2020).
- Eriksson, R.; Modig, N.; Elkington, K. Synthetic inertia versus fast frequency response: A definition. IET Renew. Power Gener. 2018, 12, 507–514. [Google Scholar] [CrossRef]
- Dharmawardena, H.; Uhlen, K.; Gjerde, S. Modeling wind farm with synthetic inertia for power system dynamic studies. In Proceedings of the IEEE International Energy Conference, Leuven, Belgium, 4–8 April 2016. [Google Scholar] [CrossRef]
- Gonzalez-Longatt, F.M. Effects of the synthetic inertia from wind power on the total system inertia: Simulation study. In Proceedings of the 2nd International Symposium on Environment Friendly Energies and Applications, Newcastle Upon Tyne, UK, 25–27 June 2012. [Google Scholar] [CrossRef]
- Wasilewski, J.; Karkoszka, K.; Lubośny, Z.; Rzepka, P.; Szablicki, M. Investigation of the impact of synthetic inertia coming from wind sources on the dynamics of a domestics power system working asynchronously in relation to the neighbouring transmission systems. Power Eng. 2018, 4, 209–213. [Google Scholar]
- Liu, Z.; Liu, F.; Shen, C.; Mei, S.; Yao, Y. Speed recovery strategy for the inertia response control of DFIGs: Extended state observer based approach. IET Renew. Power Gener. 2017, 11, 1110–1120. [Google Scholar] [CrossRef]
- Shang, L.; Hu, J.; Yuan, X.; Chi, Y. Understanding inertial response of variable-speed wind turbines by defined internal potential vector. Energies 2017, 10, 22. [Google Scholar] [CrossRef]
- Hu, J.; Sun, L.; Yuan, X.; Wang, S.; Chi, Y. Modeling of type 3 wind turbines with df/dt inertia control for system frequency response study. IEEE Trans. Power Syst. 2017, 32, 2799–2809. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control, 6th ed.; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Machowski, J.; Bialek, J.W.; Bumby, J.R. Power System Dynamics: Stability and Control, 2nd ed.; John Wiley: Oxford, UK, 2008. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).