A Fibonacci Wavelet Method for Solving Dual-Phase-Lag Heat Transfer Model in Multi-Layer Skin Tissue during Hyperthermia Treatment
Abstract
:1. Introduction
2. Mathematical Formulation of the Model
3. Fibonacci Wavelets and Operational Matrices of Integration
3.1. Fibonacci Wavelets and Function Approximation
3.2. Operational Matrices of Fibonacci Wavelets
4. Solution of the Dual-Phase Model
4.1. Discretizing the Space Variable
4.2. Implementation of the Fibonacci Wavelets
5. Numerical Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| T | Temperature (C) |
| Arterial blood temperature (C) | |
| Tissue wall temperature (C) | |
| t | Time (s) |
| r | Space coordinate (m) |
| T | Temperature (C) |
| Arterial blood temperature (C) | |
| Tissue wall temperature (C) | |
| t | Time (s) |
| r | Space coordinate (m) |
| r | Tumor position |
| Specific heat of tissue (J kgC) | |
| L | Length of tissue (m) |
| Mass flow rate of blood (kg m s) | |
| Water diffusion in tissue (m s) | |
| Molar mass of water (g mol) | |
| Vapor pressure of water (Pa) | |
| Universal gas constant (J mol) | |
| RH | Relative humidity (%) |
| Tissue density (kg m) | |
| k | Thermal conductivity of tissue (Wm C) |
| Specific heat of blood (J kg C) | |
| Phase lag of heat flux (s) | |
| Phase lag of temperature gradient (s) | |
| Heat generation due to metabolism in the skin tissue (Wm) | |
| Heat loss due to water diffusion in the tissue (Wm) | |
| Heat loss due to water vaporization in the tissue (Wm) | |
| External heat source (Wm) | |
| S | Antenna constant (m) |
| P | Antenna power (W) |
| m | Water vaporization rate of skin surface (g m s) |
| Enthalpy of water vaporization (J kg) | |
| c | Average distance of momentum boundary layer (m) |
| Dimensionless variables | |
| Space coordinate | |
| Fourier number or time | |
| Phase-lag due to heat flux | |
| Phase-lag due to temperature grad. | |
| Local tissue temperature | |
| Arterial blood temperature | |
| Tissue wall temperature | |
| Blood perfusion coefficient | |
| External heat source coefficient | |
| Metabolic heat source coefficient | |
| Kirchhoff number | |
| Biot number | |
| Location of tumor | |
References
- Blecher, E.; Chaney-Graves, K.; DeSantis, C.; Edwards, B.; Ferlay, J.; Forman, D.; Grey, N.; Harford, J.; Kramer, J.; McMikel, A. Global Cancer Facts and Figures; American Cancer Society: Atlanta, GA, USA, 2011. [Google Scholar]
- Dewhirst, M.W.; Samulski, T.V. Hyperthermia in the Treatment for Cancer; Upjohn: Kalamazoo, MI, USA, 1988. [Google Scholar]
- Xu, F.; Lu, T.-J.; Seffen, K.A. Bio-thermomechanics of skin tissues. J. Mech. Phys. Solids. 2008, 56, 1852–1884. [Google Scholar] [CrossRef]
- Espinosa, S.; Asproulis, N.; Drikakis, D. Chemotherapy efficiency increase via shock wave interaction with biological membranes: A molecular dynamics study. Microfluid Nanofluid 2014, 16, 613–622. [Google Scholar] [CrossRef]
- Romano, M.R.; Romano, V.; Mauro, A.; Angi, M.; Costagliola, C.; Ambrosone, L. The effect of temperature changes in vitreoretinal surgery. Transl. Vis. Sci. Technol. 2016, 5, 4. [Google Scholar] [CrossRef] [Green Version]
- Wulff, W. The energy conservation equation for living tissues. IEEE Trans. Biomed. Eng. 1974, 21, 494–495. [Google Scholar] [CrossRef]
- Klinger, H.G. Heat transfer in perfused biological tissue. I. Bull. Math. Biol. 1974, 36, 403–415. [Google Scholar]
- Gao, F.; Yang, X.-J.; Srivastava, H.M. Exact travelling-wave solutions for linear and non-linear heat transfer equations. Thermal Sci. 2017, 21, 2307–2311. [Google Scholar] [CrossRef]
- Chen, M.-M.; Holmes, M.M. Microvascular contributions in tissue heat transfer. Ann. N. Y. Acad. Sci. 1980, 335, 137–150. [Google Scholar] [CrossRef]
- Weinbaum, S.; Jiji, L.M.; Lemons, D.E. Theory and experiment for the effect of vascular microstructure on surface tissue heat transfer. I. ASME J. Biomech. Eng. 1984, 106, 321–330. [Google Scholar] [CrossRef]
- Nakayama, F.; Kuwahar. A general bioheat transfer model based on the theory of porous media. Int. J. Heat Mass Transf. 2008, 51, 3190–3199. [Google Scholar] [CrossRef] [Green Version]
- Pennes, H.H. Analysis of tissue and arterial blood temperature in the resting forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef]
- Cattaneo, C. A form of heat conduction equation which eliminates the paradox of instantaneous propagation. C. R. Acad. Sci. Paris. 1958, 247, 431–433. [Google Scholar]
- Vernotte, P. Les paradoxes de la théorie continue de I équation de l a chleur. C. R. Acad. Sci. Paris 1958, 246, 3154–3155. [Google Scholar]
- Tzou, D.Y. Macro-to Micro-Scale Heat Transfer: The Lagging Behavior; Taylor & Francis: Washington, DC, USA, 1996. [Google Scholar]
- Zhou, J.; Chen, J.-K.; Zhang, Y. Dual-phase lag effects on thermal damage to biological tissues caused by laser irradiation. Comput. Biol. Med. 2009, 39, 286–293. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Rai, K.N. Analysis of classical Fourier, SPL and DPL heat transfer model in biological tissues in presence of metabolic and external heat source. Heat Mass Transf. 2016, 52, 1089–1107. [Google Scholar] [CrossRef]
- Mohamed, A.F. Boundary element algorithm for modeling and simulation of dual phase lag bioheat transfer and biomechanics of anisotropic soft tissues. Int. J. Appl. Mech. 2018, 10, 1850108. [Google Scholar]
- Gupta, P.K.; Singh, J.; Rai, K.N.; Rai, S.K. Solution of the heat transfer problem in tissues during hyperthermia by finite difference-decomposition method. Appl. Math. Comput. 2013, 219, 6882–6892. [Google Scholar] [CrossRef]
- Noroozi, M.; Saedodin, S.; Ganji, D. A new solution for nonlinear dual phase lagging heat conduction problem. Alex. Eng. J. 2016, 55, 1745–1752. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, A.F. Shape design sensitivity and optimization of anisotropic functionally graded smart structures using bicubic B-splines DRBEM. Eng. Anal. Bound. Elem. 2018, 87, 27–35. [Google Scholar]
- Lepik, U.; Hein, H. Haar Wavelets with Applications; Springer: New York, NY, USA, 2014. [Google Scholar]
- Debnath, L.; Shah, F.A. Wavelet Transforms and Their Applications; Birkhäuser: New York, NY, USA, 2015. [Google Scholar]
- Sabermahani, S.; Ordokhani, Y.; Yousefi, S.A. Fibonacci wavelets and their applications for solving two classes of time-varying delay problems. Optim. Control Appl. Meth. 2020, 41, 395–416. [Google Scholar] [CrossRef]
- Sabermahani, S.; Ordokhani, Y. Fibonacci wavelets and Galerkin method to investigate fractional optimal control problems with bibliometric analysis. J. Vib. Control 2020, 26, 1–15. [Google Scholar] [CrossRef]
- Falcon, S.; Plaza, A. On k-Fibonacci sequences and polynomials and their derivatives. Chaos Solitons Fractals 2009, 39, 1005–1019. [Google Scholar] [CrossRef]
- Chen, C.-F.; Hsiao, C.-H. Haar wavelet method for solving lumped and distributed-parameter systems. IEE Proc. Control Theory Appl. 1997, 144, 87–94. [Google Scholar] [CrossRef] [Green Version]
- Shah, F.A.; Awana, M.I. A computational wavelet method for solving dual-phase-lag model of bioheat transfer during hyperthermia treatment. Comp. Math. Methods 2020, 2, e1095. [Google Scholar] [CrossRef] [Green Version]
- Kumari, T.; Kumar, D.; Rai, K.N.; Singh, S.K. Numerical solution of DPL heat transfer model in multi-layer biological skin tissue of the living body during hyperthermia treatment. Mech. Based Des. Struct. Mach. 2020. [Google Scholar] [CrossRef]
- Ming, F.; Weng, W.; Yuan, H. Numerical simulation of the effects of blood perfusion, water diffusion, and vaporization on the skin temperature and burn injuries. Numer. Heat Transf. Part A 2014, 65, 1187–1203. [Google Scholar]
- Liu, K.-C. Nonlinear behavior of thermal lagging in concentric living tissues with Gaussian distribution source. Int. J. Heat Mass Transf. 2011, 54, 13–14. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, D.; Rai, K.N. A numerical study on dual-phase-lag model of bio-heat transfer during hyperthermia treatment. J. Therm. Biol. 2015, 49, 98–105. [Google Scholar] [CrossRef]
- Scheid, F. Schaum’s Outline of Theory and Problems in Numerical Analysis; McGraW-Hill: New York, NY, USA, 1989. [Google Scholar]


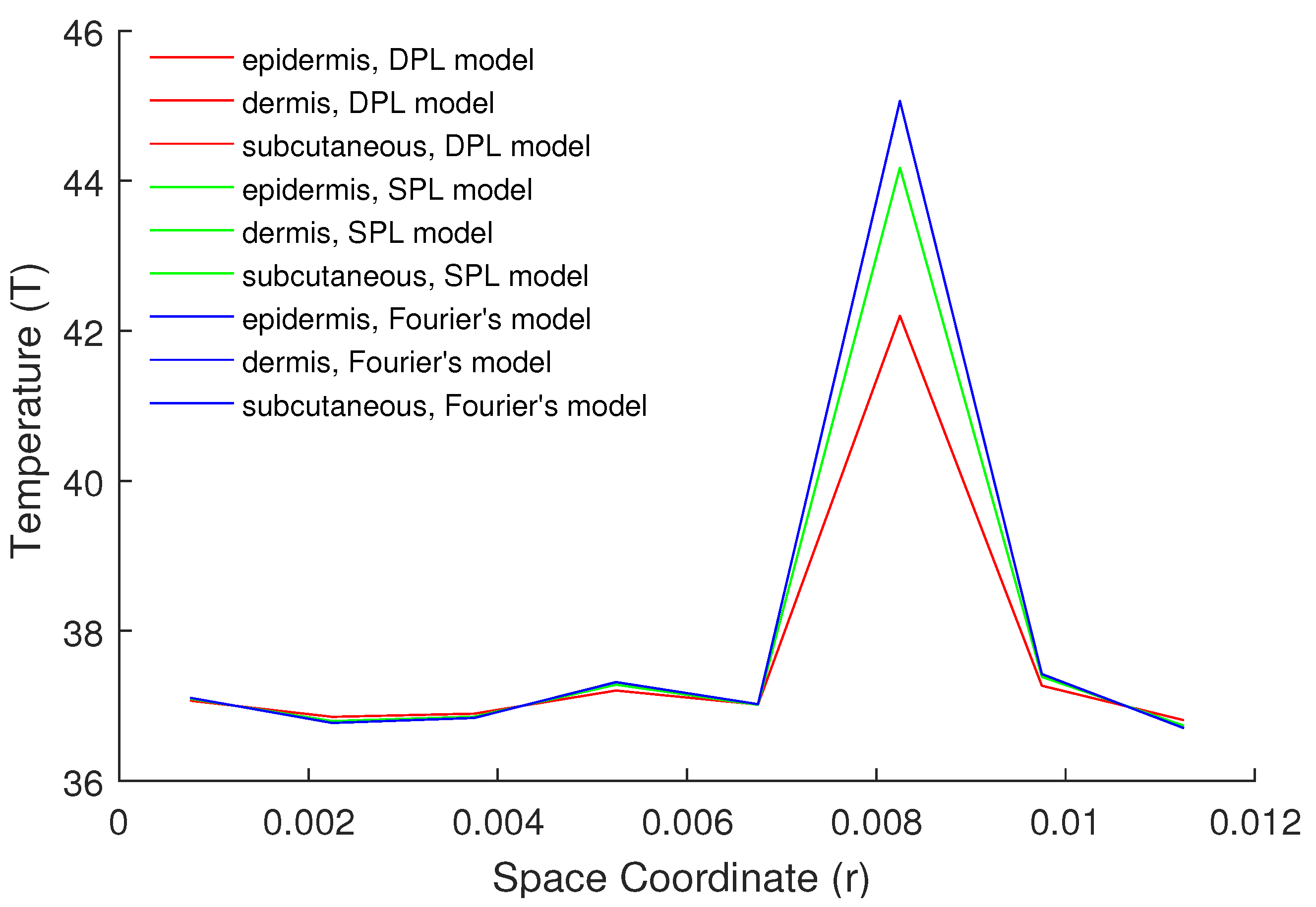

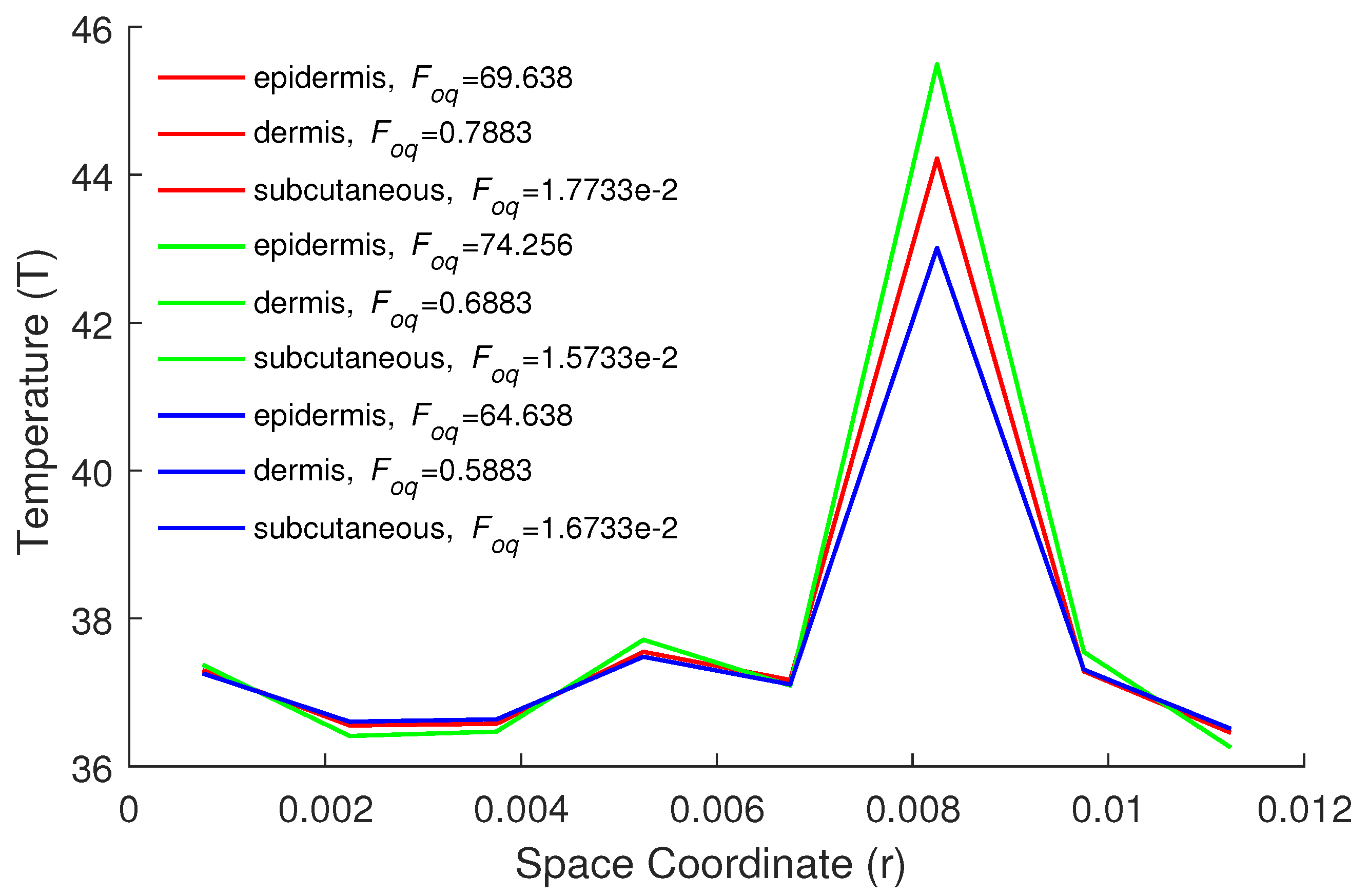


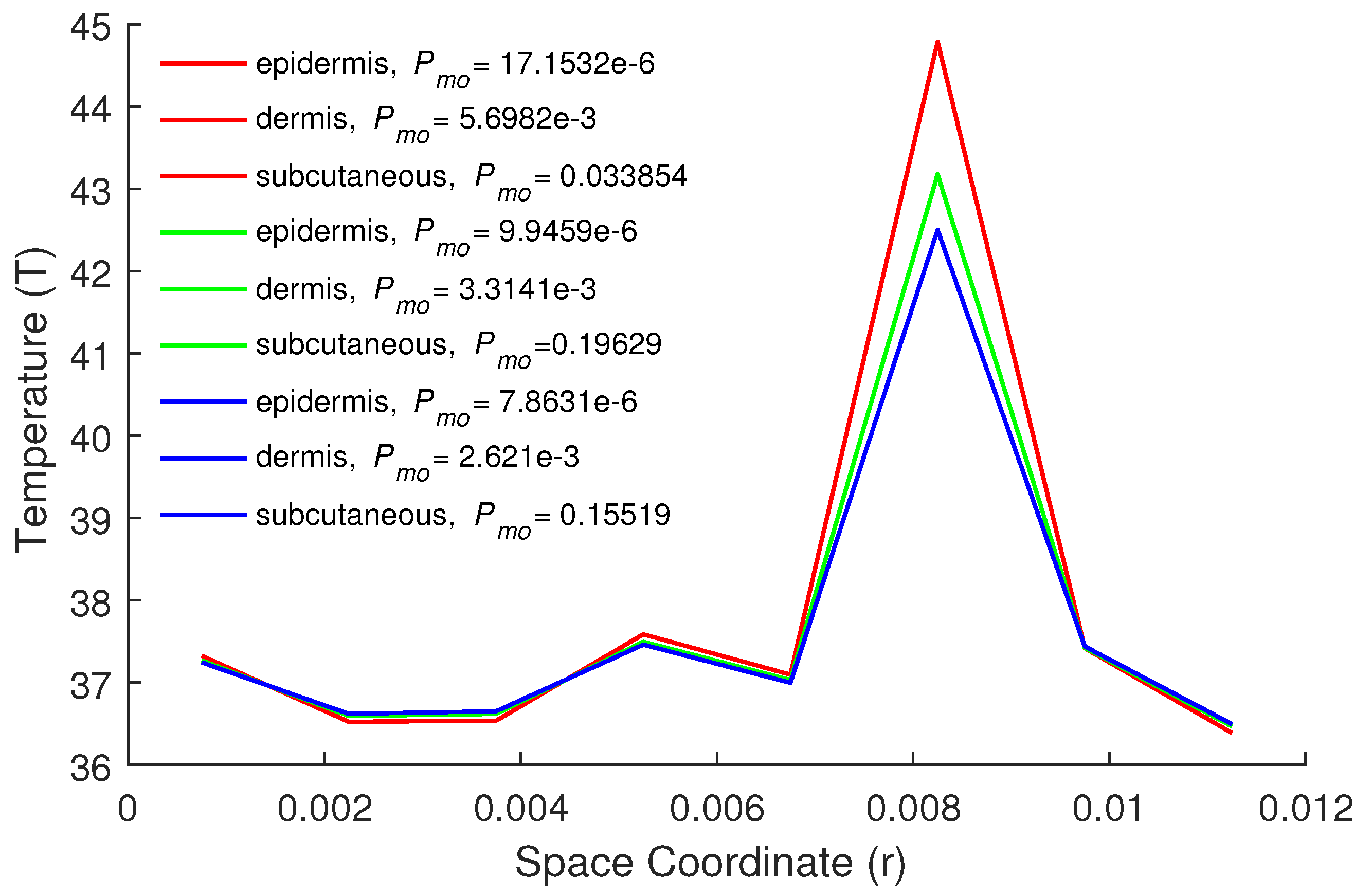


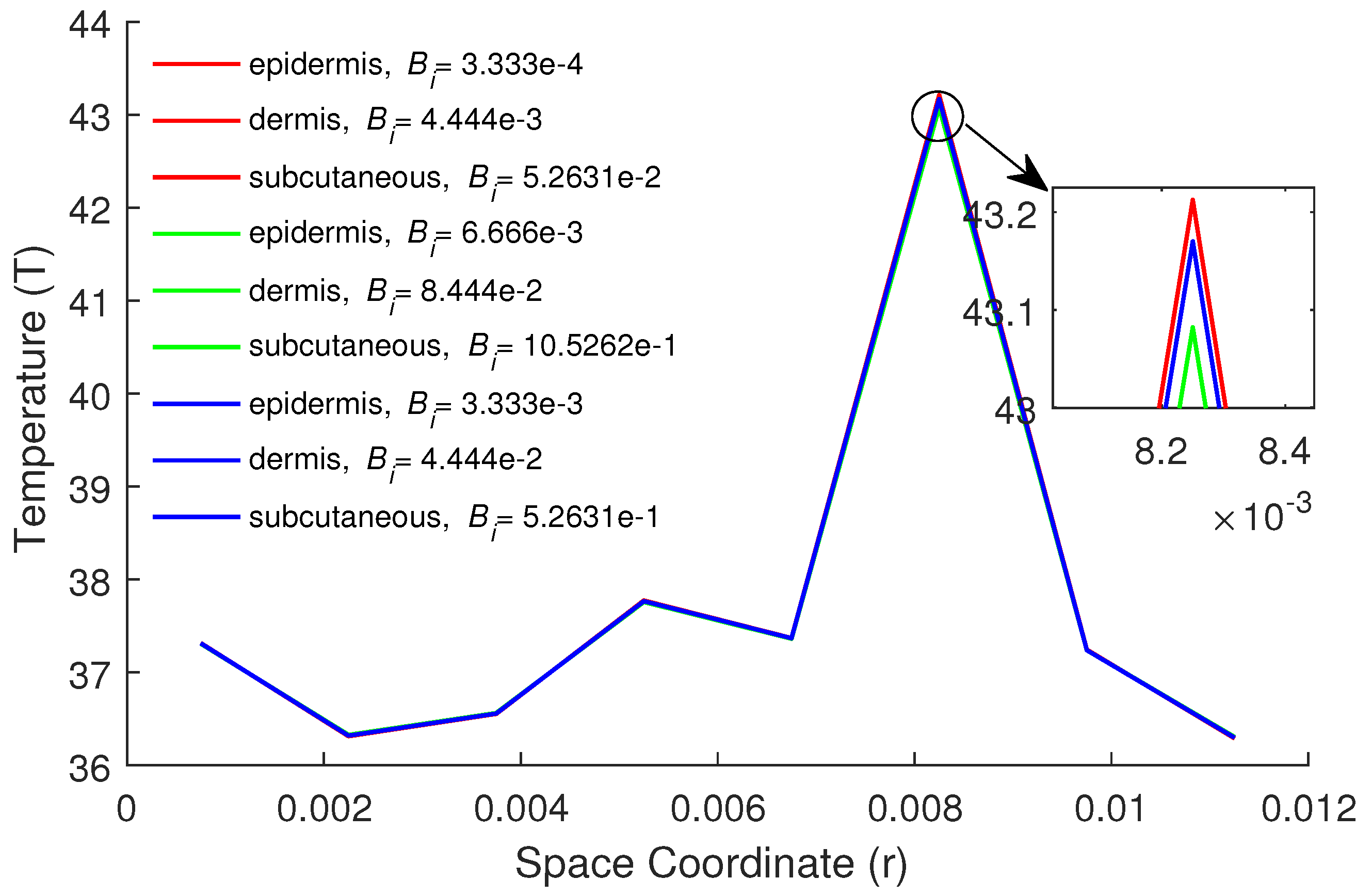
| Parameters | Epidermis | Dermis | Subcutaneous |
|---|---|---|---|
| Thickness (m) | 0.00008 | 0.002 | 0.01 |
| Blood perfusion rate (kg ms) | 0 | 0.00125 | 0.00125 |
| Thermal conductivity (W mC) | 0.24 | 0.45 | 0.19 |
| Specific heat (J kgC) | 3590 | 3330 | 2500 |
| Water diffusivity (ms) | 5 × 10 | 5 × 10 | 5 × 10 |
| Density (kg m) | 1200 | 1200 | 1200 |
| Water content (%) | 70 | 70 | 70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srivastava, H.M.; Irfan, M.; Shah, F.A. A Fibonacci Wavelet Method for Solving Dual-Phase-Lag Heat Transfer Model in Multi-Layer Skin Tissue during Hyperthermia Treatment. Energies 2021, 14, 2254. https://doi.org/10.3390/en14082254
Srivastava HM, Irfan M, Shah FA. A Fibonacci Wavelet Method for Solving Dual-Phase-Lag Heat Transfer Model in Multi-Layer Skin Tissue during Hyperthermia Treatment. Energies. 2021; 14(8):2254. https://doi.org/10.3390/en14082254
Chicago/Turabian StyleSrivastava, Hari Mohan, Mohd. Irfan, and Firdous A. Shah. 2021. "A Fibonacci Wavelet Method for Solving Dual-Phase-Lag Heat Transfer Model in Multi-Layer Skin Tissue during Hyperthermia Treatment" Energies 14, no. 8: 2254. https://doi.org/10.3390/en14082254
APA StyleSrivastava, H. M., Irfan, M., & Shah, F. A. (2021). A Fibonacci Wavelet Method for Solving Dual-Phase-Lag Heat Transfer Model in Multi-Layer Skin Tissue during Hyperthermia Treatment. Energies, 14(8), 2254. https://doi.org/10.3390/en14082254







