Harmonic Mitigation Using Passive Harmonic Filters: Case Study in a Steel Mill Power System
Abstract
1. Introduction
1.1. Brief Description of the Plate Mill System
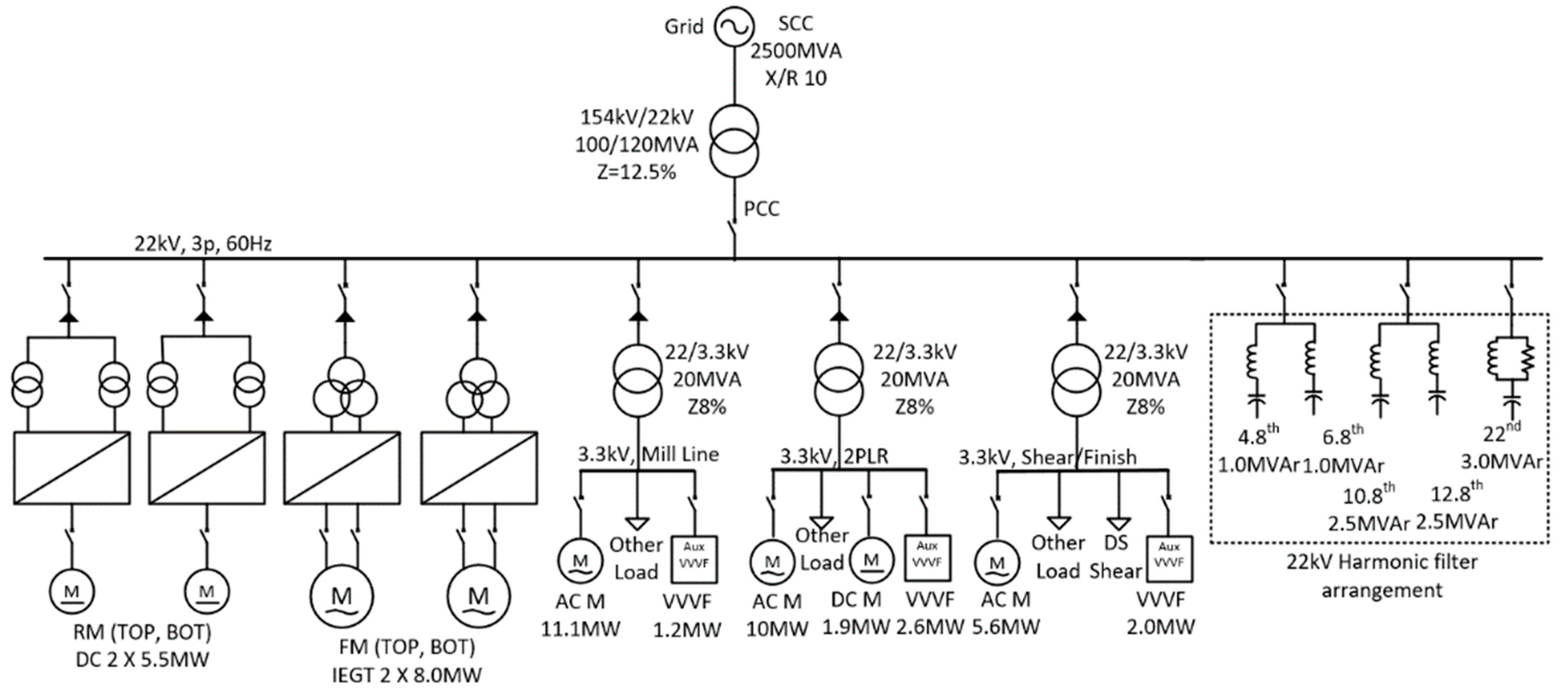
1.1.1. Simplified Single Line Drawing
1.1.2. Summation of Input Data
2. Harmonic Filter Design
2.1. Capacitor Banks
2.2. Series Reactors
2.2.1. DF Using K-Factor
2.2.2. DF Using
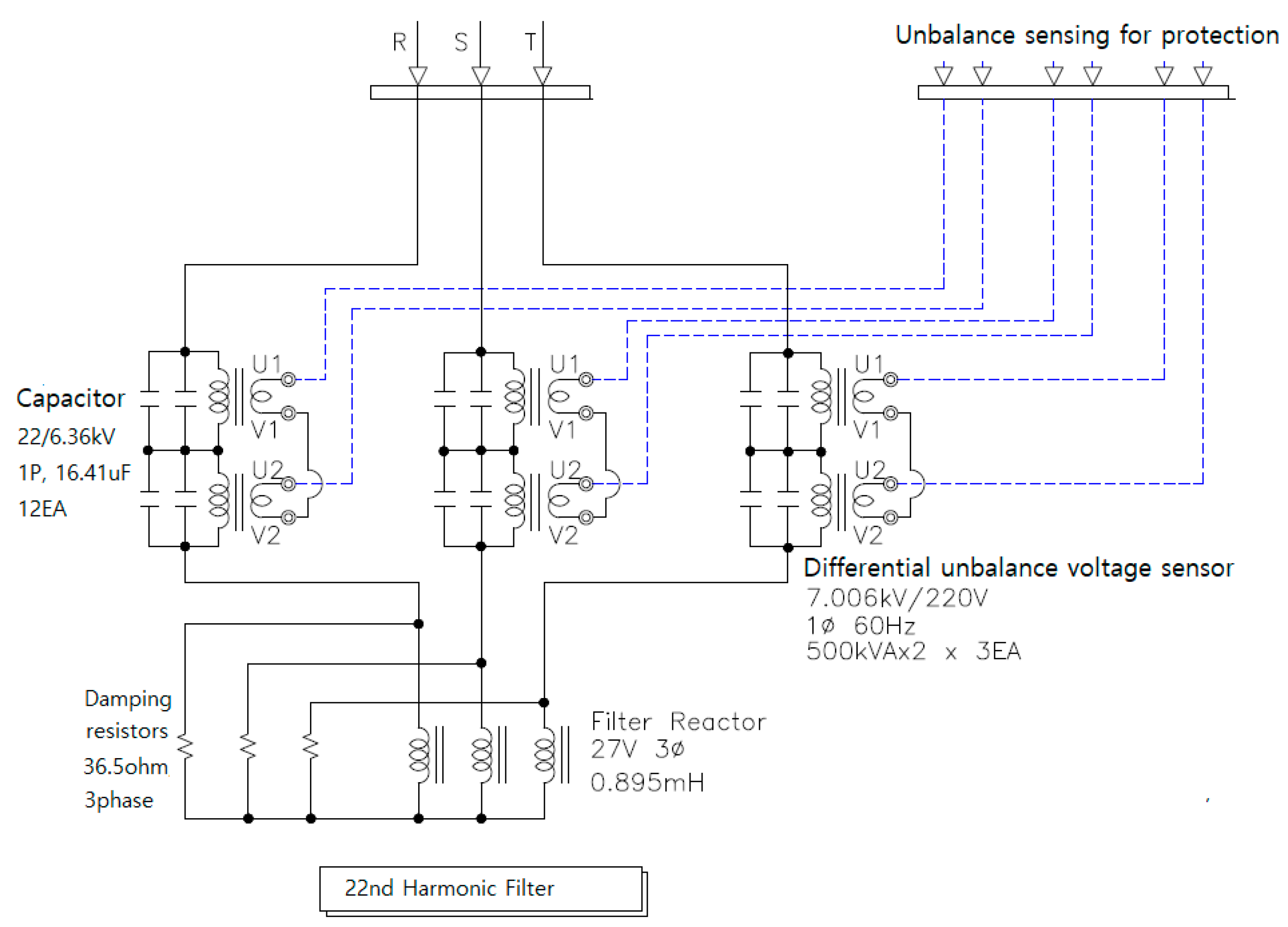
2.3. Harmonic Filter System
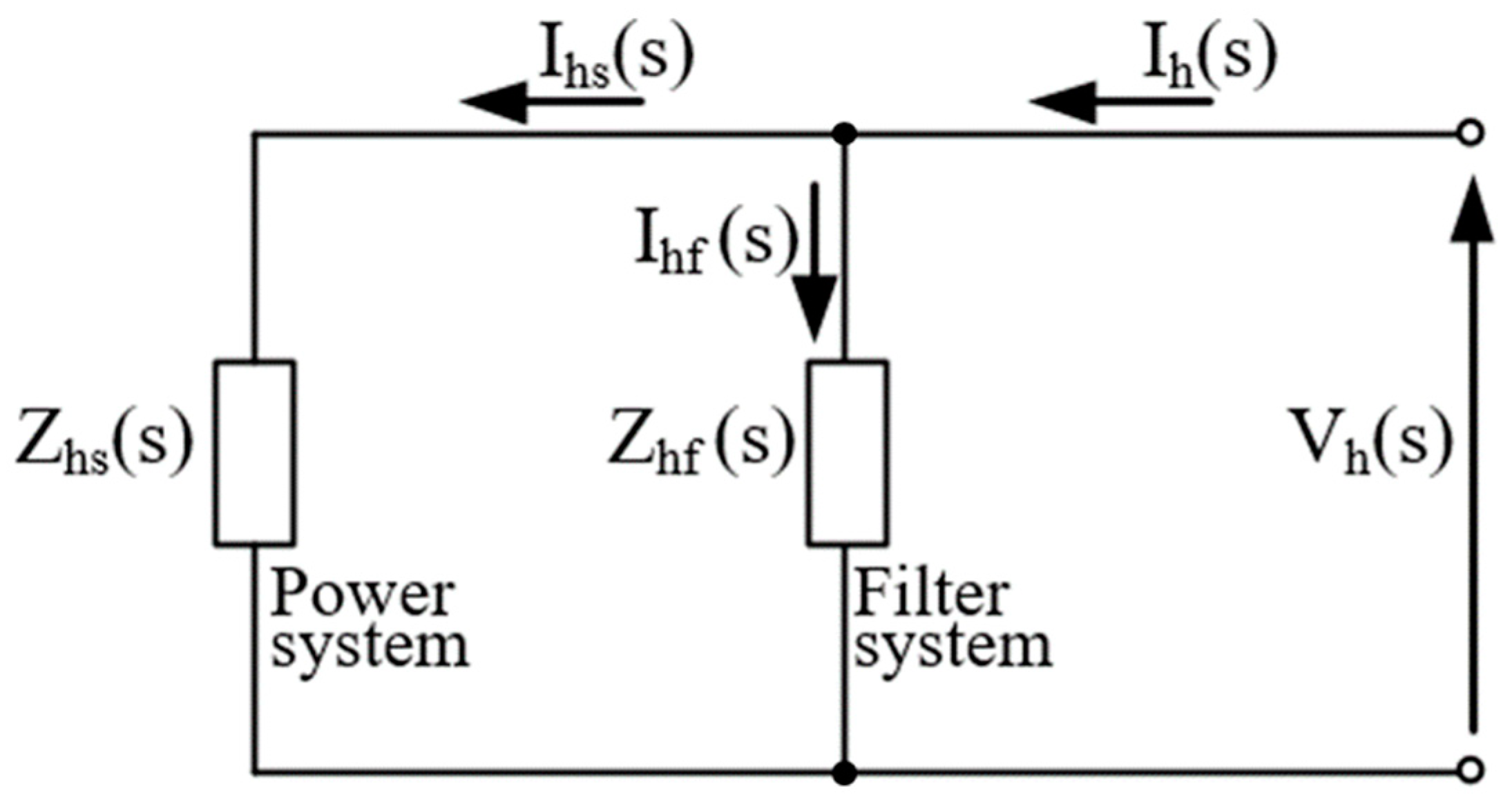
2.4. Distribution Network Topology and Current Divider
3. Easy Power System Software (ESA) Calculation Results
3.1. Without Filters
3.2. With Filters
4. Harmonic Filter Configuration and Measured Power Profile
4.1. Harmonic Filter Configuration
4.2. Validation of Results
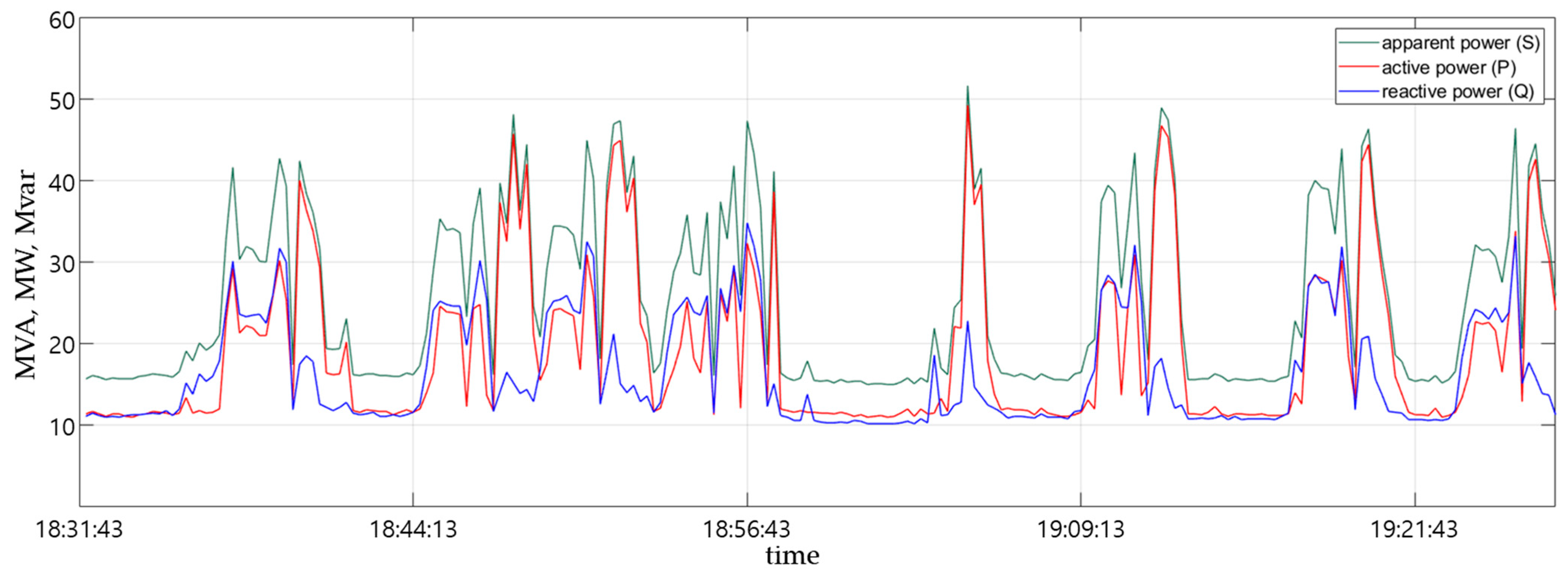
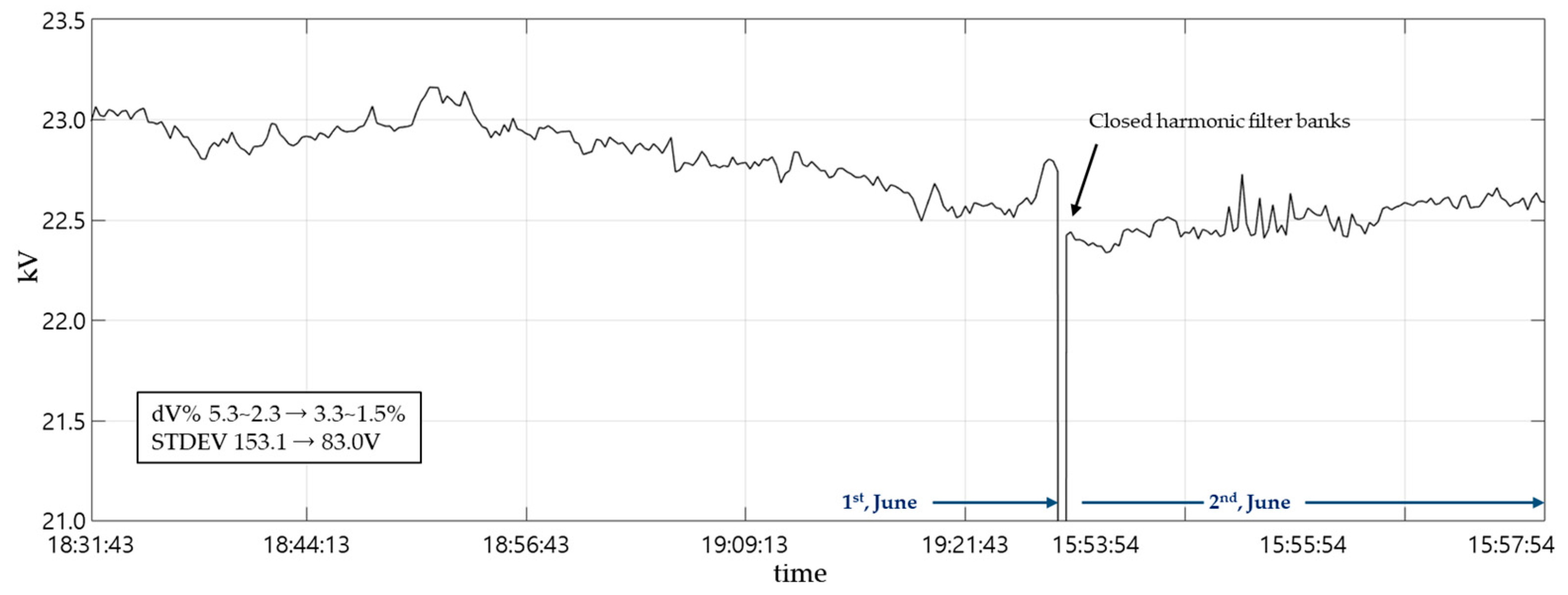
4.2.1. Variations in Power and Voltage
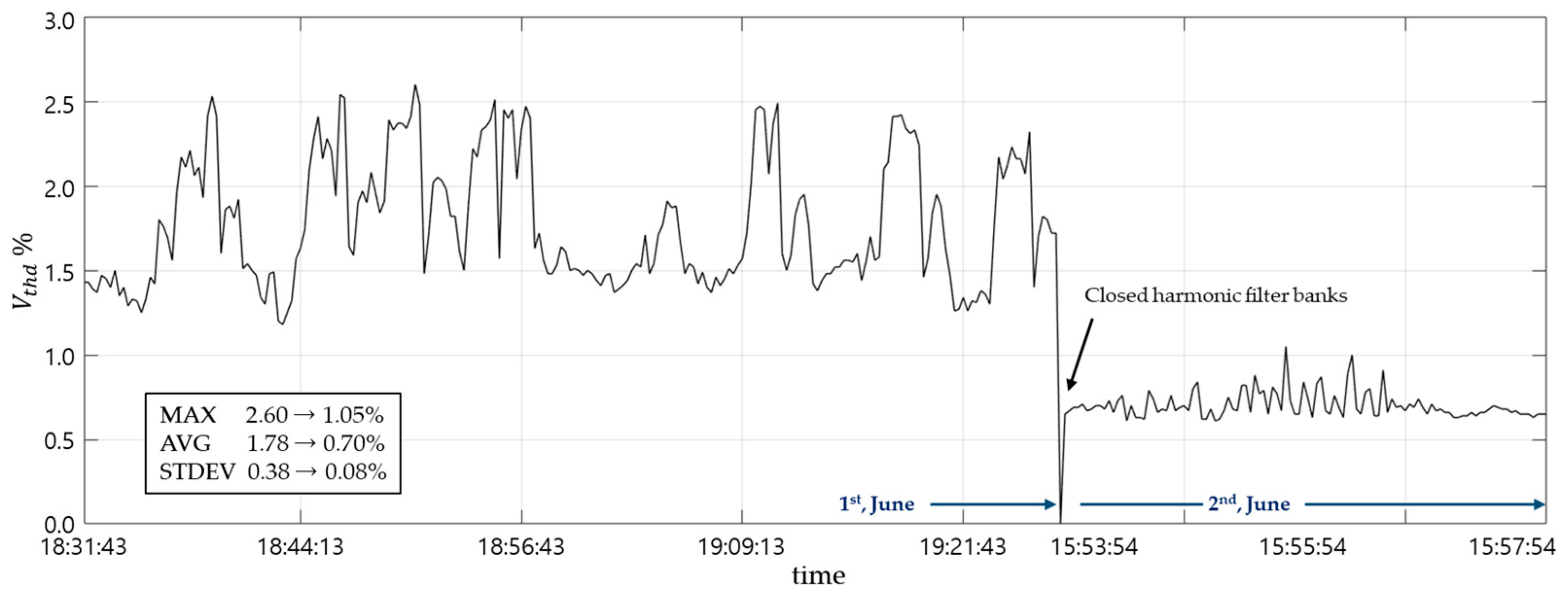
4.2.2. Voltage Distortion
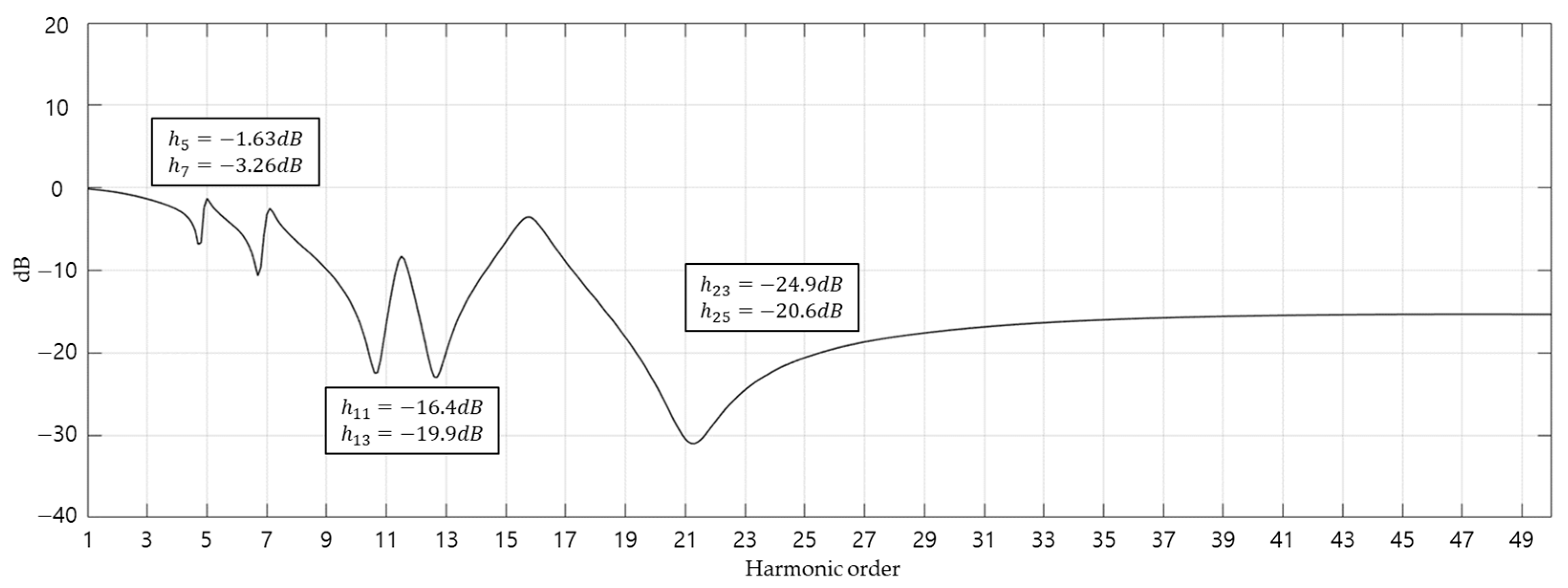
4.2.3. Voltage Harmonic Spectrum V5, V7, V11, and V13
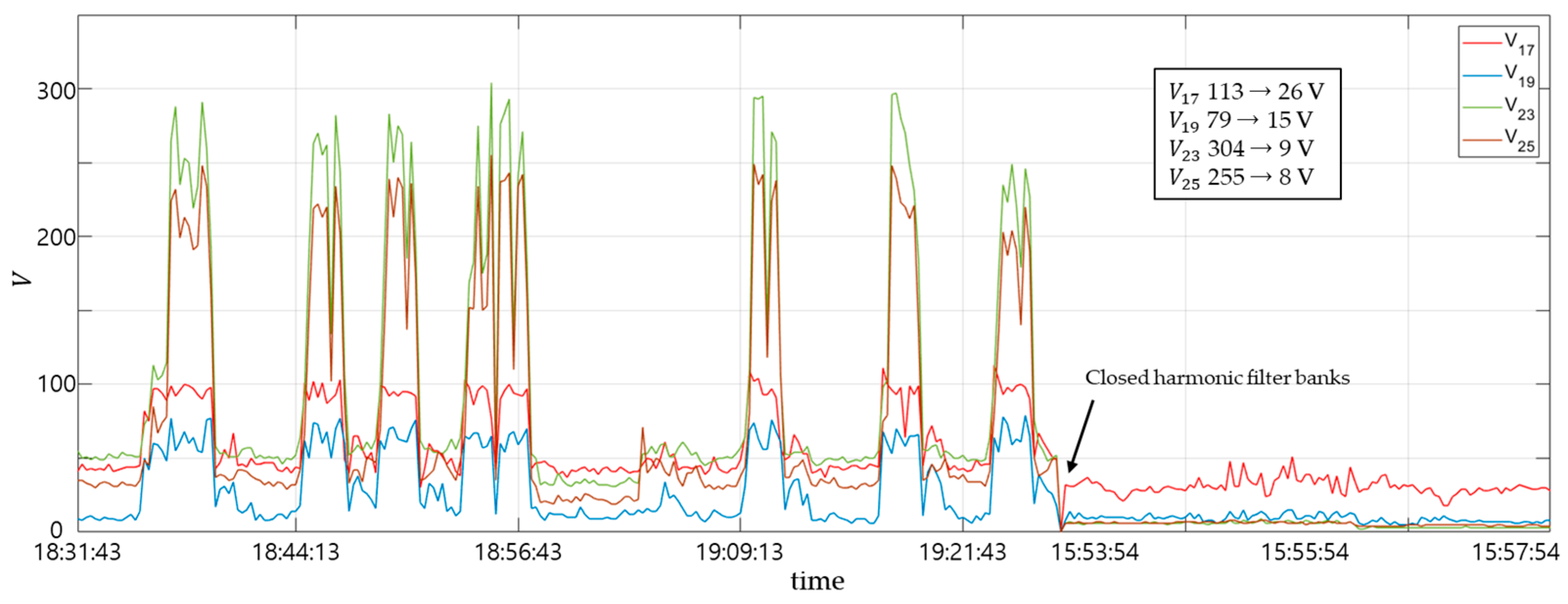
4.2.4. Voltage Harmonic Spectrum V17, V19, V23, and V25
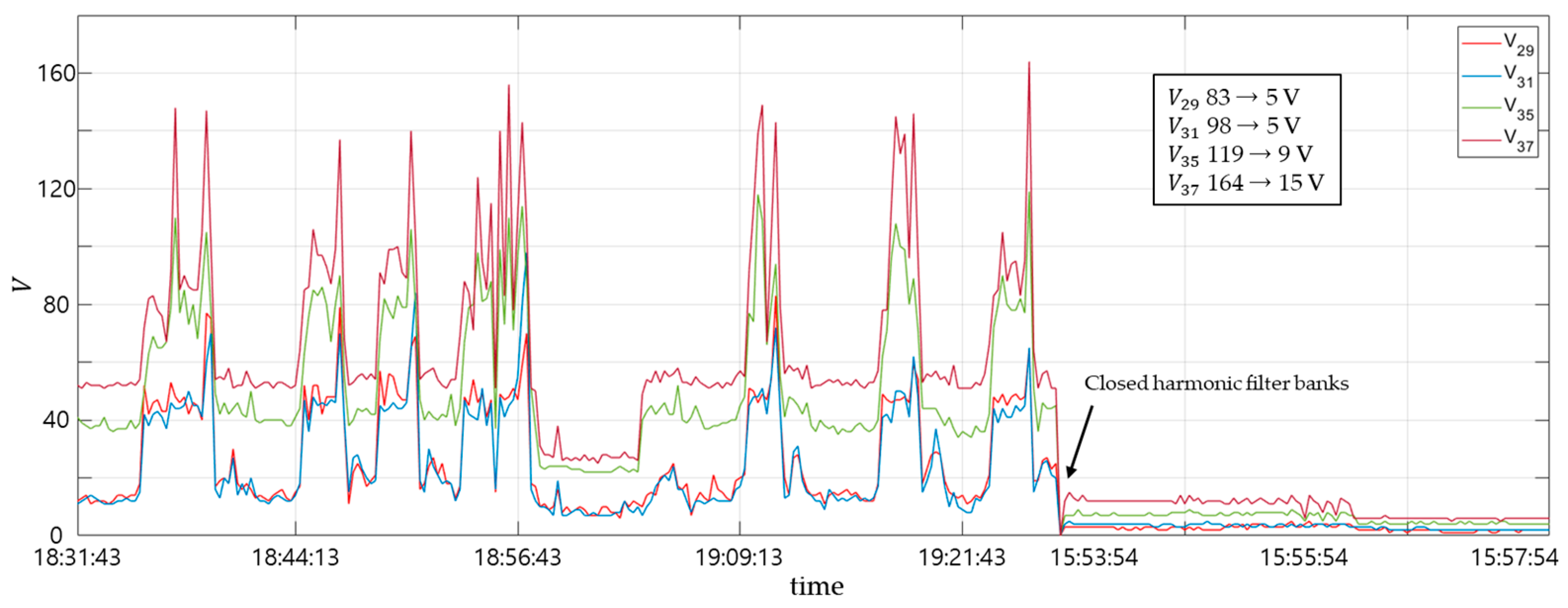
4.2.5. Voltage Harmonic Spectrum V29, V31, V35, and V37
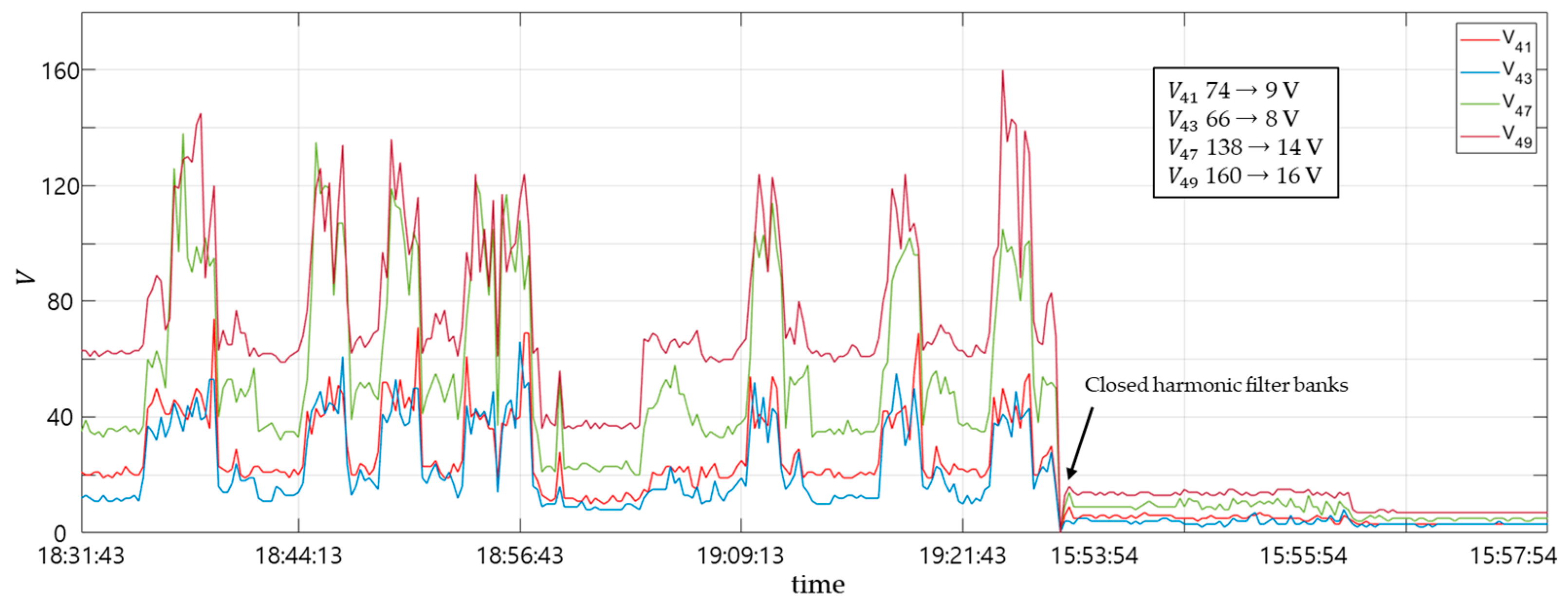
4.2.6. Voltage Harmonic Spectrum V41, V43, V47, and V49
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mjorning, L. ABB Drives and Control System for Hot Flat Rolling Mills Improves Yield and Quality; South East Asia iron and Steel Institute (SEAISI): Shah Alam, Malaysia, 2005. [Google Scholar]
- Hosoda, H.; Kodama, S.; Tessendorf, R. Large PWM Inverters for Rolling Mills. Iron Steel Technol. 2008, 5, 65–73. [Google Scholar]
- Emadi, A.; Nasiri, A.; Bekiarov, S.B. Uninterruptable Power Supplies and Active Filters; Illinois Institute of Technology: Chicago, IL, USA; CRC Press: Washington, DC, USA, 2005. [Google Scholar]
- Yazdani-Asrami, M.; Sadati, S.M.B.; Samadaei, E. Harmonic study for MDF industries: A case study. In Proceedings of the 2011 IEEE Applied Power Electronics Colloquium (IAPEC), Johor Bahru, Malaysia, 18–19 April 2011; pp. 149–154. [Google Scholar]
- Arrillaga, J.; Watson, N.R. Power System Harmonics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Yazdani-Asrami, M.; Song, W.; Zhang, M.; Yuan, W.; Pei, X. AC Transport Loss in Superconductors Carrying Harmonic Current with Different Phase Angles for Large-Scale Power Components. IEEE Trans. Appl. Supercond. 2021, 31, 1–5. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Mirzaie, M.; Akmal, A.A.S. No-load loss calculation of distribution transformers supplied by nonsinusoidal voltage using three-dimensional finite element analysis. Energy 2013, 50, 205–219. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Gholamian, S.A.; Mirimani, S.M.; Adabi, J. Influence of field-dependent critical current on harmonic AC loss analysis in HTS coils for superconducting transformers supplying non-linear loads. Cryogenics 2021, 113, 103234. [Google Scholar] [CrossRef]
- Napoles, J.; Leon, J.I.; Portillo, R.; Franquelo, L.G.; Aguirre, M.A. Selective harmonic mitigation technique for high-power converters. IEEE Trans. Ind. Electron. 2009, 57, 2315–2323. [Google Scholar] [CrossRef]
- Pogaku, N.; Green, T.C. Harmonic mitigation throughout a distribution system: A distributed-generator-based solution. IEE Proc. Gener. Transm. Distrib. 2006, 153, 350–358. [Google Scholar] [CrossRef]
- Sekar, T.C.; Rabi, B.J. A review and study of harmonic mitigation techniques. In Proceedings of the 2012 International Conference on Emerging Trends in Electrical Engineering and Energy Management (ICETEEEM), Tamil Nadu, India, 3–15 December 2012; pp. 93–97. [Google Scholar]
- Badrzadeh, B.; Gupta, M. Practical experiences and mitigation methods of harmonics in wind power plants. IEEE Trans. Ind. Appl. 2013, 49, 2279–2289. [Google Scholar] [CrossRef]
- Tischer, H.; Pfeifer, T. Hybrid filter for dynamic harmonics filtering and reduction of commutation notches-a case study. In Proceedings of the 2016 17th International Conference on Harmonics and Quality of Power (ICHQP), Belo Horizonte, Brazil, 16–19 October 2016; pp. 261–265. [Google Scholar]
- Kihwele, S. Modelling of Shunt Active Power Filter for Harmonics Case Study of Steel Industry. In Proceedings of the 2019 International Conference on Electronics, Information, and Communication (ICEIC), Auckland, New Zealand, 22–25 January 2019; pp. 1–2. [Google Scholar]
- de Miranda, G.C.; Primo, H.F.; Calenzani, H.T.; Camargos, I.A. Harmonic mitigation techniques applied to industrial power systems: Real case study with measurements. In Proceedings of the 2018 Simposio Brasileiro de Sistemas Eletricos (SBSE), Niteroi, Brazil, 12–16 May 2018; pp. 1–6. [Google Scholar]
- Gonzalez, D.A.; McCall, J.C. Design of filters to reduce harmonic distortion in industrial power systems. IEEE Trans. Ind. Appl. 1987, 3, 504–511. [Google Scholar] [CrossRef]
- Ludbrook, A. Harmonic filters for notch reduction. IEEE Trans. Ind. Appl. 1988, 24, 947–954. [Google Scholar] [CrossRef]
- Phipps, J.K. A transfer function approach to harmonic filter design. IEEE Ind. Appl. Mag. 1997, 3, 68–82. [Google Scholar] [CrossRef]
- Das, J.C. Passive filters-potentialities and limitations. IEEE Trans. Ind. Appl. 2004, 40, 232–241. [Google Scholar] [CrossRef]
- Jain, S.K.; Agrawal, P.; Gupta, H.O. Fuzzy logic controlled shunt active power filter for power quality improvement. IEE Proc. Electr. Power Appl. 2002, 149, 317–328. [Google Scholar] [CrossRef]
- IEEE Standards Association. IEEE Std 519-2014. Recommended Practice and Requirements for Harmonic Control in Electric Power Systems; IEEE Power and Energy Society: New York, NY, USA, 2014. [Google Scholar]
- Pérez-Donsión, M.; Pereira, S.J.; Oliveira, F.T. Harmonics and Flicker in an Iron and Steel Industry with AC arc furnaces. In Proceedings of the International Conference on Renewable Energies and Power Quality, Tenerife, Spain, 10–12 April 2019. [Google Scholar]
- Harmonic Working Group (IEEE PES T&D Committee). Guide for Applying Harmonic Limits on Power Systems, P519A/D6; IEEE: Piscataway, NJ, USA, 1999. [Google Scholar]
- Aye, T.M.; Naing, S. Analysis of Harmonic Reduction by Using Passive Harmonic Filters. IJSETR 2014, 3, 9142–9147. [Google Scholar]
- Kapoor, S.R.; Lalwani, M.K.; Tiwari, S. Harmonic Analysis and Reduction of Separately Excited DC Motor. In Proceedings of the 4th International Conference Advance Trend in Engineering, Technology and Research (ICATETR-2015), Kota, India, 19–20 June 2015; pp. 179–185. [Google Scholar]
- Almutairi, M.S.; Hadjiloucas, S. Harmonics Mitigation Based on the Minimization of Nonlinearity Current in a Power System. Designs 2019, 3, 29. [Google Scholar] [CrossRef]
- IEEE Std 1531-2003. IEEE Guide for Application and Specification of Harmonic Filters; IEEE: Piscataway, NJ, USA, 2003; pp. 1–66. [Google Scholar]
- IEEE Std C37.99-2000. IEEE Guide for the Protection of Shunt Capacitor Banks; IEEE: Piscataway, NJ, USA, 2000; pp. 1–108. [Google Scholar]
- IEEE Std C57.110™-2018. IEEE Recommended Practice for Establishing Liquid-Immersed and Dry-Type Power and Distribution Transformer Capability when Supplying Nonsinusoidal Load Currents; IEEE: Piscataway, NJ, USA, 2018; pp. 1–68. [Google Scholar]
- Tao, S.; Xiao, X.N. Comparing transformer derating computed using the harmonic loss factor FHL and K-factor. In Proceedings of the 2008 Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Nanjing, China, 6–9 April 2008; pp. 1631–1634. [Google Scholar]
- Meng, J.; Jiang, L.; Wang, Y. Study on the Influence of Harmonics on Load Loss of Transformer. In IOP Conference Series: Earth and Environmental Science, Proceedings of the 2020 International Conference on Green Energy, Environment and Sustainable Development, Wuhan, China, 24–25 April 2020; IOP Publishing: Bristol, UK, 2020; p. 012126. [Google Scholar]
- IEEE Std 3002.8-2018. IEEE Recommended Practice for Conducting Harmonic Studies and Analysis of Industrial and Commercial Power Systems; IEEE: Piscataway, NJ, USA, 2018; pp. 1–79. [Google Scholar]
- Orcajo, G.A.; Rodriguez, D.J.; Ardura, G.P.; Cano, J.M.; Norniella, J.G.; Llera, T.R.; Cifrian, R.D. Dynamic Estimation of Electrical Demand in Hot Rolling Mills. IEEE Trans. Ind. Appl. 2016, 52, 2714–2723. [Google Scholar] [CrossRef]




| Clarification | Description |
|---|---|
| Utility | 25,000 MVA, X/R 10 |
| Step down trans. | 154 kV/22 kV, 100 MVA, Z = 12.5% |
| RM TOP | 9.167 MW, −9.352 MVAR (167% of rating), DC motor |
| RM BOT | 9.167 MW, −9.352 MVAR (167% of rating), DC motor |
| FM TOP | 8.521 MW, 0.852 MVAR (107% of rating), synchronous motor |
| FM BOT | 8.521 MW, −0.852 MVAR (107% of rating), synchronous motor |
| Step down trans. | 22 kV/3.3 kV, 20 MVA, Z = 8%, 3 set |
| Mill line 3.3 kV | 16.4 MW, −11.1 MVAR (AC motor, FM field, VVVF, and others) |
| 2PLR 3.3 kV | 19.1 MW, −12.8 MVAR (AC motor, DC motor, VVVF, and others) |
| Shear/finishing 3.3 kV | 17.8 MW, −11.6 MVAR (AC motor, shear, VVVF, and others) |
| Harmonic Current , 22 kV Bus Base | ||||
|---|---|---|---|---|
| h Order | RM TOP | RM BOT | FM TOP | FM BOT |
| 5 | 0 | 0 | 1.81 | 1.81 |
| 7 | 0 | 0 | 0.31 | 0.31 |
| 11 | 16.66 | 16.66 | 4.6 | 4.6 |
| 13 | 14.1 | 14.1 | 3.53 | 3.53 |
| 17 | 0 | 0 | 0.4 | 0.4 |
| 19 | 0 | 0 | 1.25 | 1.25 |
| 23 | 6.97 | 6.97 | 1.25 | 1.25 |
| 25 | 6.42 | 6.42 | 0.65 | 0.65 |
| 29 | 0 | 0 | 0.21 | 0.21 |
| 31 | 0 | 0 | 0.14 | 0.14 |
| 35 | 3.93 | 3.93 | 0.49 | 0.49 |
| 37 | 3.72 | 3.72 | 0.65 | 0.65 |
| 41 | 0 | 0 | 0.07 | 0.07 |
| 43 | 0 | 0 | 0.13 | 0.13 |
| 47 | 1.95 | 1.95 | 0.44 | 0.44 |
| 49 | 1.87 | 1.87 | 0.64 | 0.64 |
| Harmonic Current , 22 kV Bus Base | |||
|---|---|---|---|
| h Order | Mill Line | 2PLR | Shear Finishing |
| 5 | 40.7 | 152.7 | 149.4 |
| 7 | 28.1 | 105.5 | 103.2 |
| 11 | 20 | 74.8 | 73.2 |
| 13 | 12.8 | 48 | 47 |
| 17 | 10.5 | 38.4 | 38.5 |
| 19 | 6.7 | 25.2 | 24.6 |
| 23 | 4.2 | 15.7 | 15.4 |
| 25 | 3.2 | 11.8 | 11.3 |
| Description | Unit | 4.8th HF Band Pass | 6.8th HF Band Pass | 10.8th HF Band Pass | 12.8th HF Band Pass | 22nd Hi-Pass |
|---|---|---|---|---|---|---|
| System VLL | kV | 22 | 22 | 22 | 22 | 22 |
| Bank capacity | kVAr | 1000 | 1000 | 2500 | 2500 | 3000 |
| Dimensional capacity | kVAr | 1046 | 1022 | 2522 | 2516 | 3006 |
| Bank capacitance | µF | 5.24 | 5.36 | 13.58 | 13.62 | 16.41 |
| Capacitor string voltage | kV | 23.01 | 22.49 | 22.19 | 22.14 | 22.05 |
| Bank current | A1 | 26.24 | 26.24 | 65.61 | 65.61 | 78.73 |
| SR% reactance | % | 4.38 | 2.18 | 0.87 | 0.62 | 0.21 |
| SR inductance | mH | 58.86 | 28.67 | 4.49 | 3.19 | 0.89 |
| SR reactance | Ω | 22.19 | 10.81 | 1.69 | 1.2 | 0.34 |
| SR ohmic resistance | Ω | 1.31 | 0.91 | 0.22 | 0.19 | 0.03 |
| SR X/R ratio | - | 16.9 | 11.9 | 7.5 | 6.3 | 10.1 |
| Quality factor Q | - | 80.9 | 80.8 | 80.9 | 80.6 | 5 |
| Damping R | Ω | - | - | - | - | 37 |
| Reactor voltage | V1 | 582.3 | 283.6 | 110.9 | 78.8 | 26.6 |
| Bus | Nominal Voltage (kV) | Voltage (pu) | Angle (deg) | pf | S (MVA) | |
|---|---|---|---|---|---|---|
| 154 kV | 154 | 1.0 | 0.0 | 2.24 * | 0.82 | 47.65 |
| 22 kV main | 22 | 0.97 | −2.8 | 9.27 * | 0.84 | 46.01 |
| RM TOP, BOT | 22 | 0.96 | −2.9 | 9.36 * | 0.70 | 15.72 |
| FM TOP, BOT | 22 | 0.96 | −2.9 | 9.36 * | 0.99 | 10.28 |
| ML 3.3 kV | 3.3 | 0.95 * | −4.2 | 10.23 * | 0.82 | 6.65 |
| 2PLR 3.3 kV | 3.3 | 0.95 * | −4.4 | 12.75 * | 0.82 | 7.74 |
| S/F 3.3 kV | 3.3 | 0.95 * | −4.3 | 12.68 * | 0.82 | 7.14 |
| Harmonic Current Distortion in Percent of Plant Loading | ||||||
|---|---|---|---|---|---|---|
| Harmonic Number | 3–10 | 11–16 | 17–22 | 23–34 | 35–50 | ITDD (%) |
| Odd Harmonics | 4.2 | 5.21 * | 1.08 | 1.72 * | 0.74 * | 8.75 |
| IEEE Limits | 10 | 4.5 | 4 | 1.5 | 0.7 | 12.00 |
| Even Harmonics | 0 | 0 | 0 | 0 | 0 | 0.00 |
| IEEE Limits | 2.5 | 1.13 | 1 | 0.38 | 0.17 | 3.00 |
| Plant Load kVA = 50,000 | ||||||
| PCC Isc/Iload = 55.0 | ||||||
| Harmonic Voltage Distortion in Percent of PCC Base Voltage | ||
|---|---|---|
| Max Individual | ||
| PCC Bus | 4.720 * | 9.267 * |
| IEEE Limits | 3 | 5.00 |
| PCC Base kV = 22.000 | ||
| Bus | Nominal Voltage (kV) | Voltage (pu) | Angle (deg) | pf | S (MVA) | |
|---|---|---|---|---|---|---|
| 154 kV | 154 | 1.0 | 0.0 | 0.68 | 0.91 | 42.60 |
| 22 kV main | 22 | 0.98 | −2.8 | 2.82 | 0.93 | 41.67 |
| RM TOP, BOT | 22 | 0.98 | −2.8 | 2.87 | 0.7 | 15.72 |
| FM TOP, BOT | 22 | 0.98 | −2.8 | 2.87 | 0.99 | 10.28 |
| ML 3.3 kV | 3.3 | 0.96 | −4.1 | 3.49 | 0.82 | 6.65 |
| 2PLR 3.3 kV | 3.3 | 0.96 | −4.3 | 5.91 | 0.82 | 7.74 |
| S/F 3.3 kV | 3.3 | 0.96 | −4.2 | 5.83 | 0.82 | 7.14 |
| Harmonic Current Distortion in Percent of Plant Loading | ||||||
|---|---|---|---|---|---|---|
| Harmonic Number | 3–10 | 11–16 | 17–22 | 23–34 | 35–50 | ITDD (%) |
| Odd Harmonics | 3.58 | 0.88 | 1.06 | 0.16 | 0.13 | 4.75 |
| IEEE Limits | 10 | 4.5 | 4 | 1.5 | 0.7 | 12.00 |
| Even Harmonics | 0 | 0 | 0 | 0 | 0 | 0.00 |
| IEEE Limits | 2.5 | 1.13 | 1 | 0.38 | 0.17 | 3.00 |
| Plant Load kVA = 50,000 | ||||||
| PCC Isc/Iload = 55.0 | ||||||
| Harmonic Voltage Distortion in Percent of PCC Base Voltage | ||
|---|---|---|
| Max Individual | ||
| PCC Bus | 1.484 | 2.819 |
| IEEE Limits | 3 | 5.00 |
| PCC Base kV = 22.000 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, B.; Lee, J.; Yoo, H.; Jang, G. Harmonic Mitigation Using Passive Harmonic Filters: Case Study in a Steel Mill Power System. Energies 2021, 14, 2278. https://doi.org/10.3390/en14082278
Park B, Lee J, Yoo H, Jang G. Harmonic Mitigation Using Passive Harmonic Filters: Case Study in a Steel Mill Power System. Energies. 2021; 14(8):2278. https://doi.org/10.3390/en14082278
Chicago/Turabian StylePark, Byungju, Jaehyeong Lee, Hangkyu Yoo, and Gilsoo Jang. 2021. "Harmonic Mitigation Using Passive Harmonic Filters: Case Study in a Steel Mill Power System" Energies 14, no. 8: 2278. https://doi.org/10.3390/en14082278
APA StylePark, B., Lee, J., Yoo, H., & Jang, G. (2021). Harmonic Mitigation Using Passive Harmonic Filters: Case Study in a Steel Mill Power System. Energies, 14(8), 2278. https://doi.org/10.3390/en14082278







