Pore-Scale Simulation of Particle Flooding for Enhancing Oil Recovery
Abstract
:1. Introduction
2. Mathematical Model
2.1. Oil–Water Flow Dynamics
2.2. Particle Dynamics
2.3. Fictitious Domain Method for Fluid–Particle Interaction Force
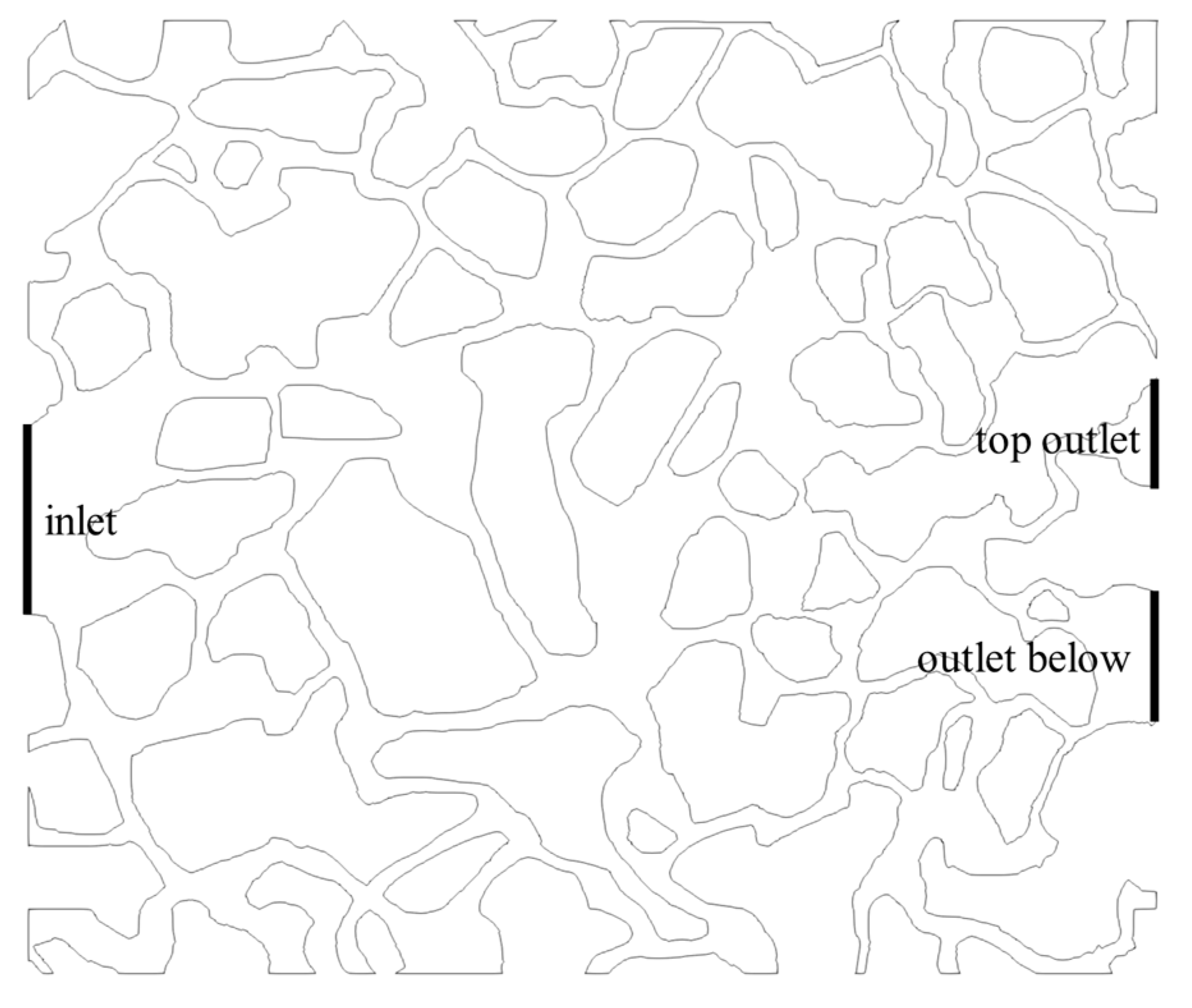
3. Physical and Numerical Conditions
3.1. Physical Model and Case Setup
3.2. Numerical Conditions
4. Result and Discussion
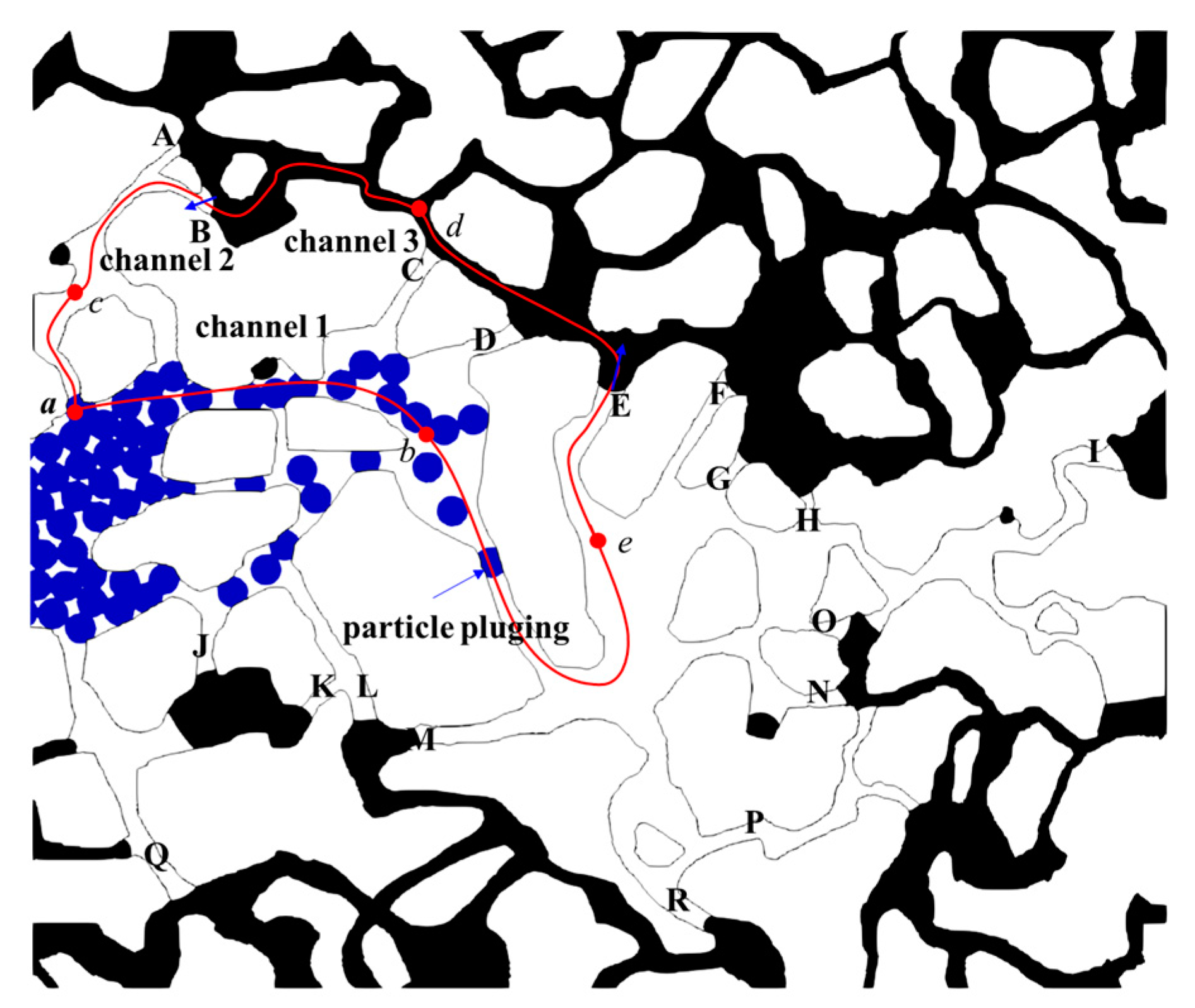
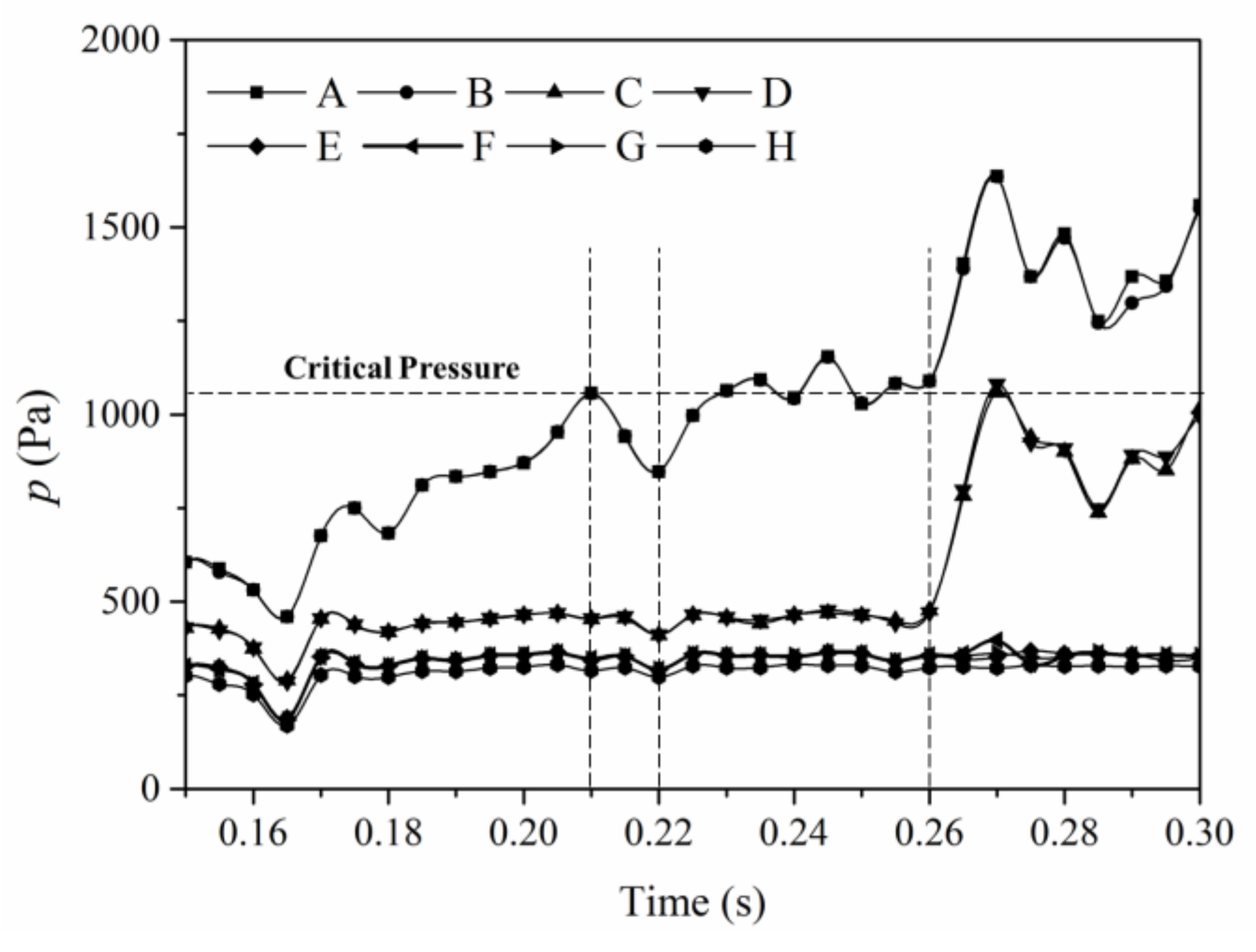
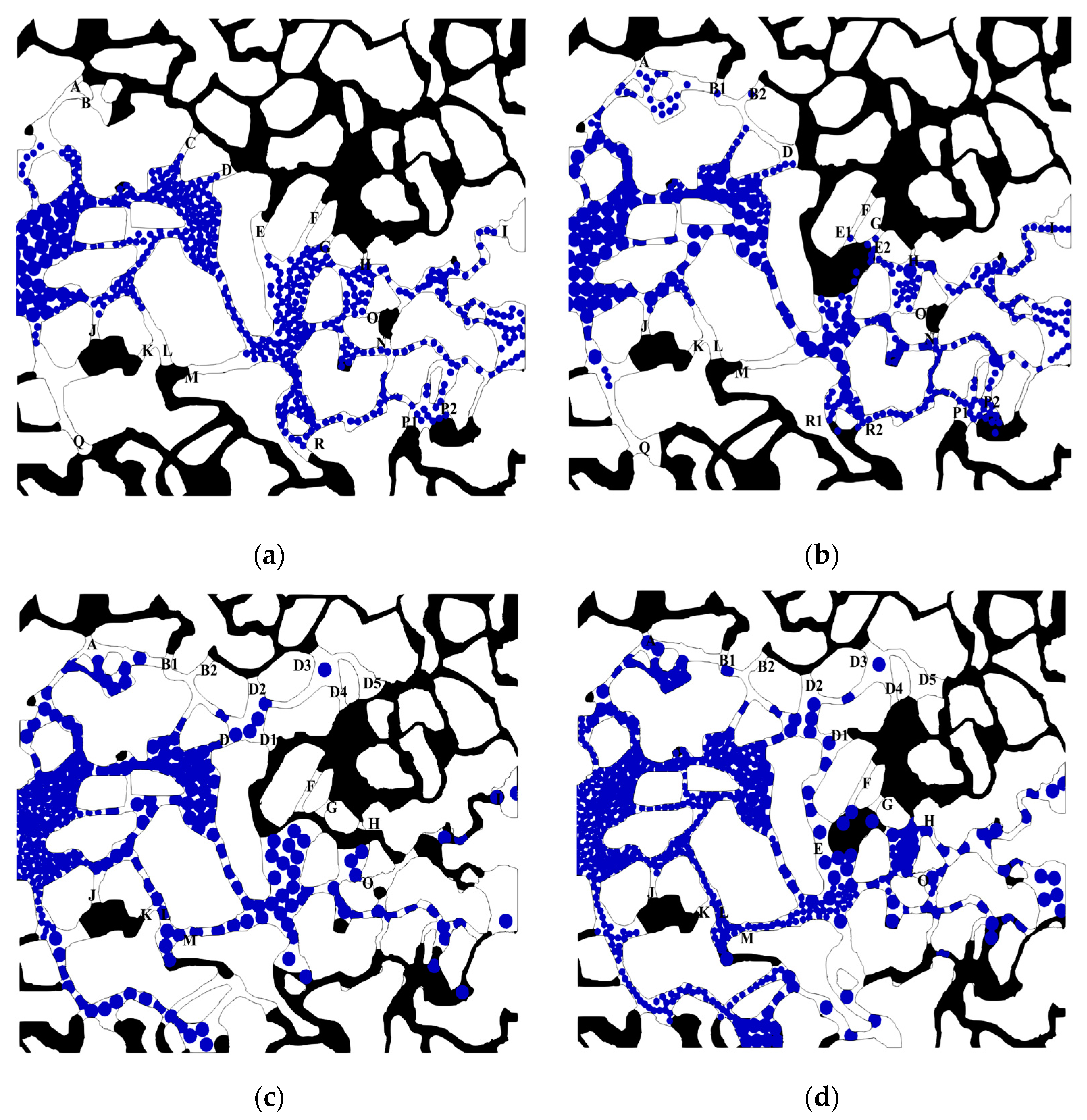
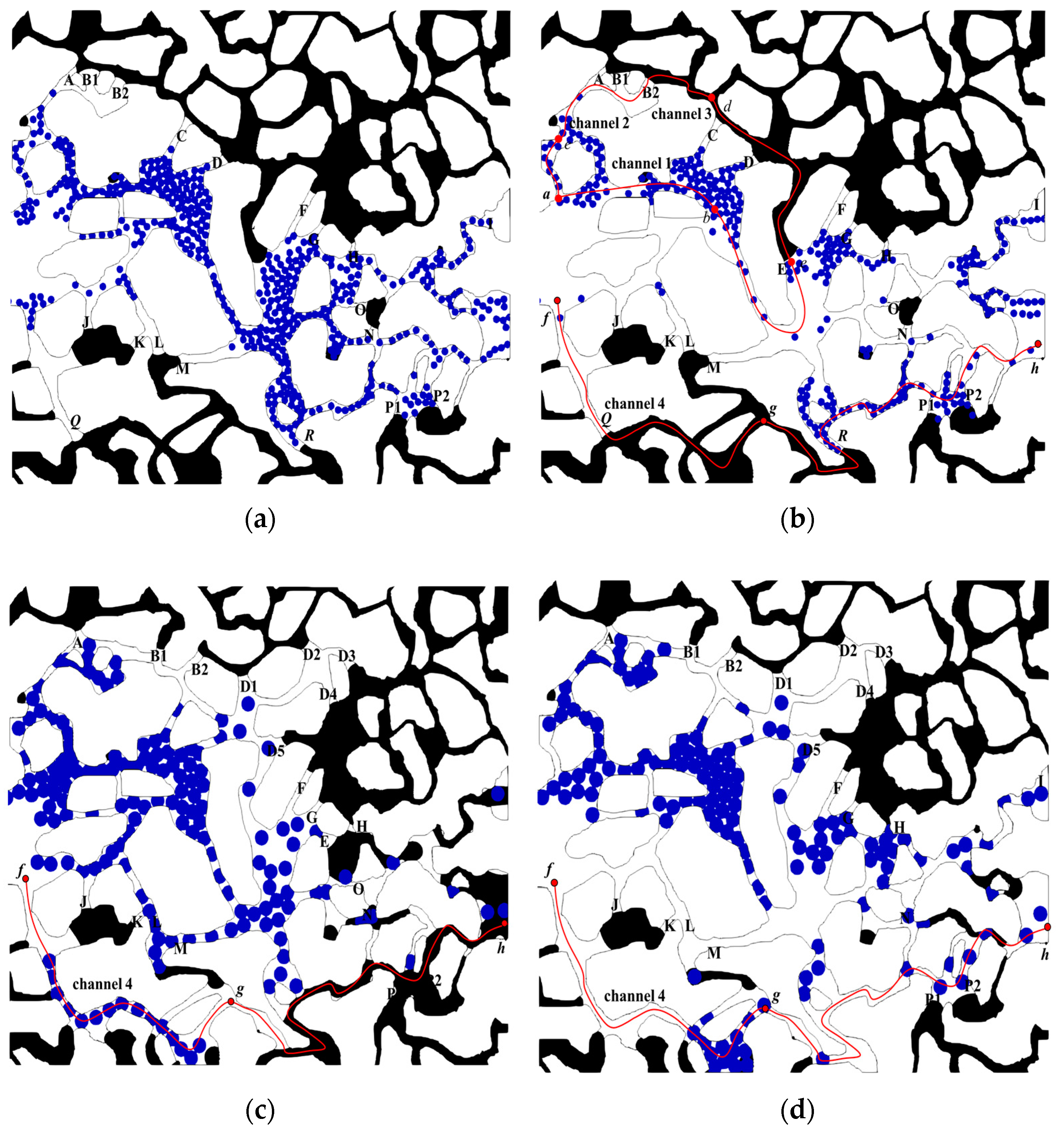
4.1. Trap Dynamics of the Residual Oil
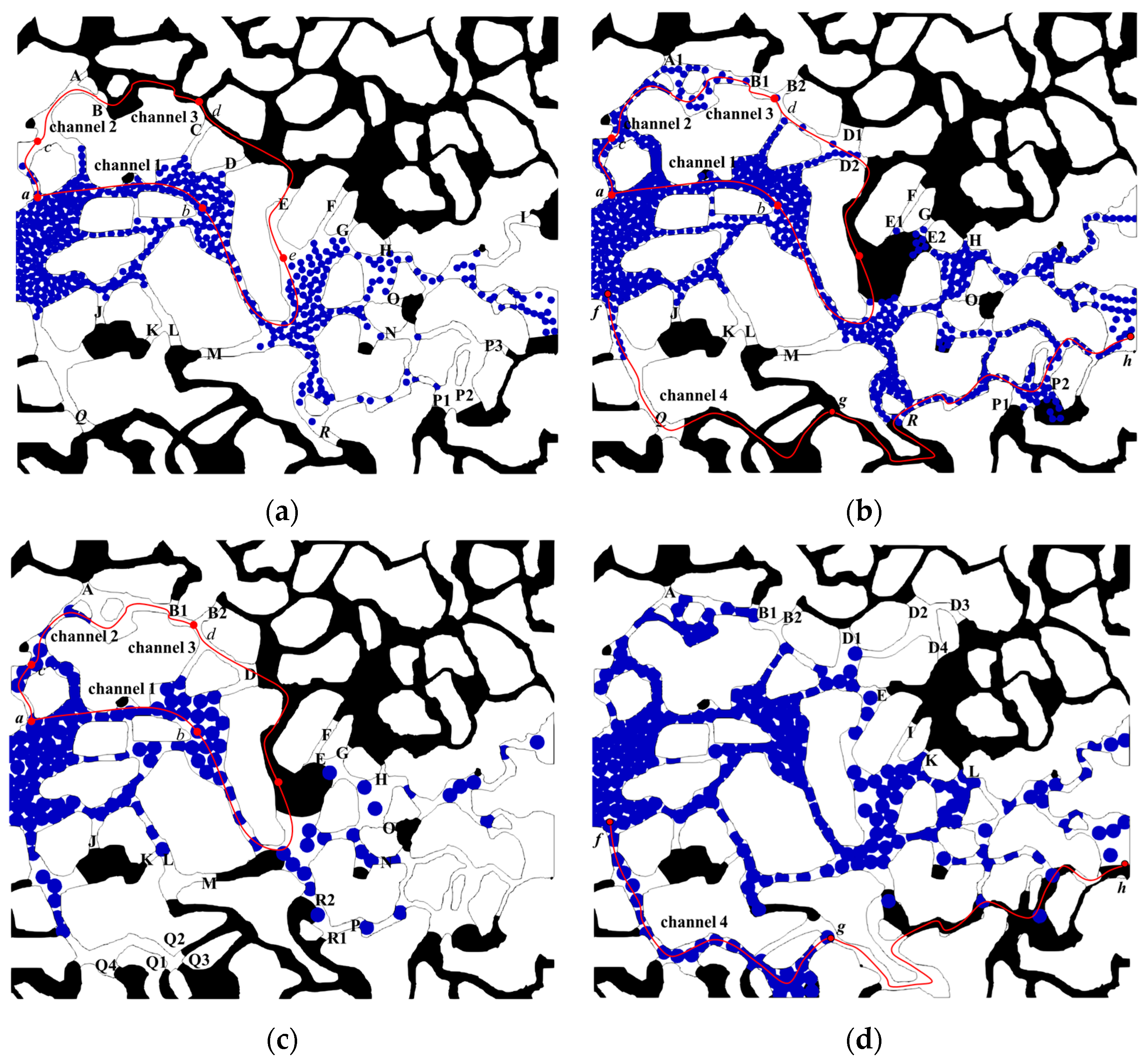
4.2. Start-Up of the Remaining Oil in Particle-Flooding Process
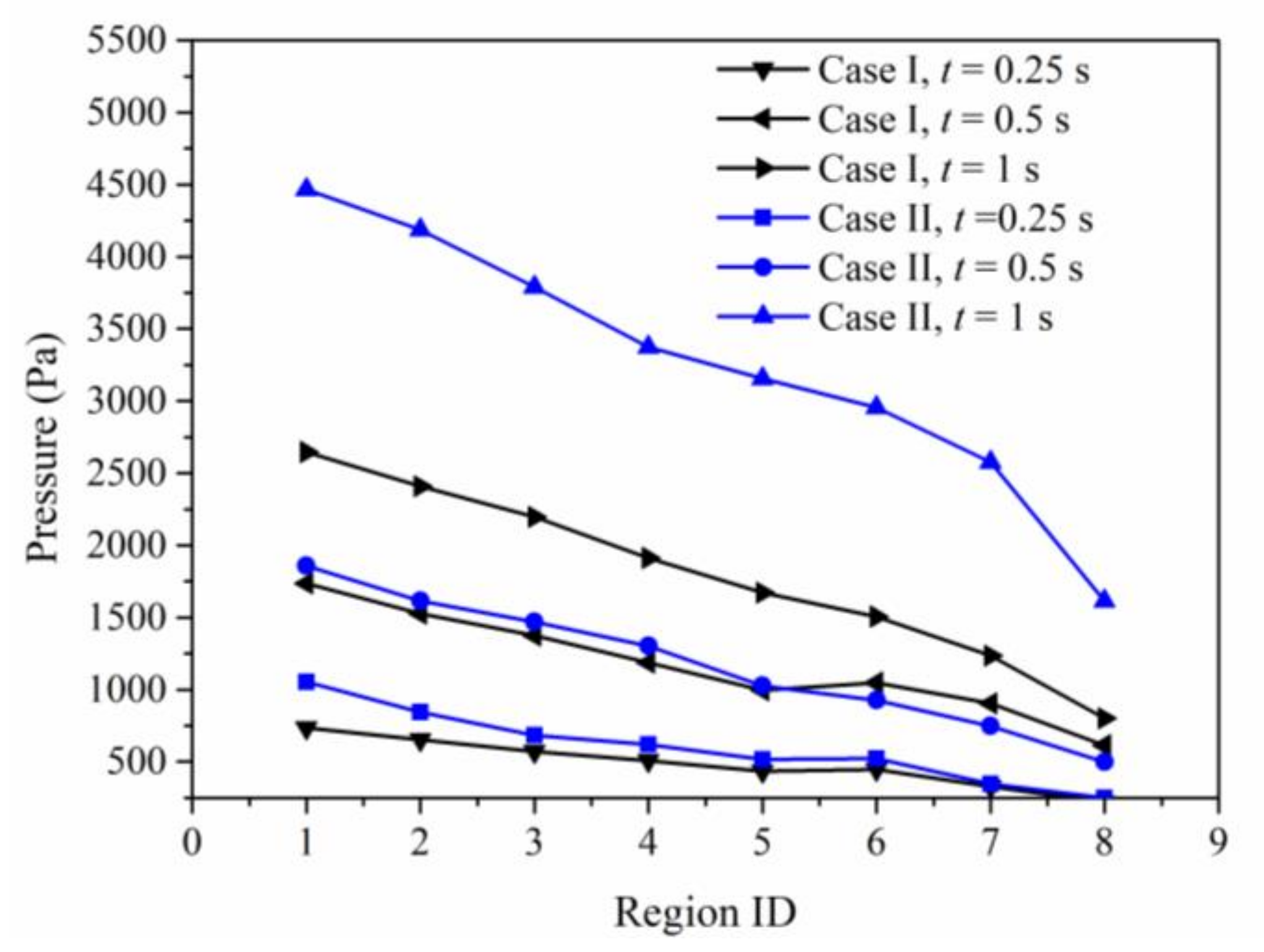
4.3. Effect of the Particle Size on Particle–Oil–Water Flow Behaviors
- The viscosity of water is smaller than that of oil, and the resistance of water channel is smaller than that of oil channel. Therefore, the particles tend to move along the channel with low resistance.
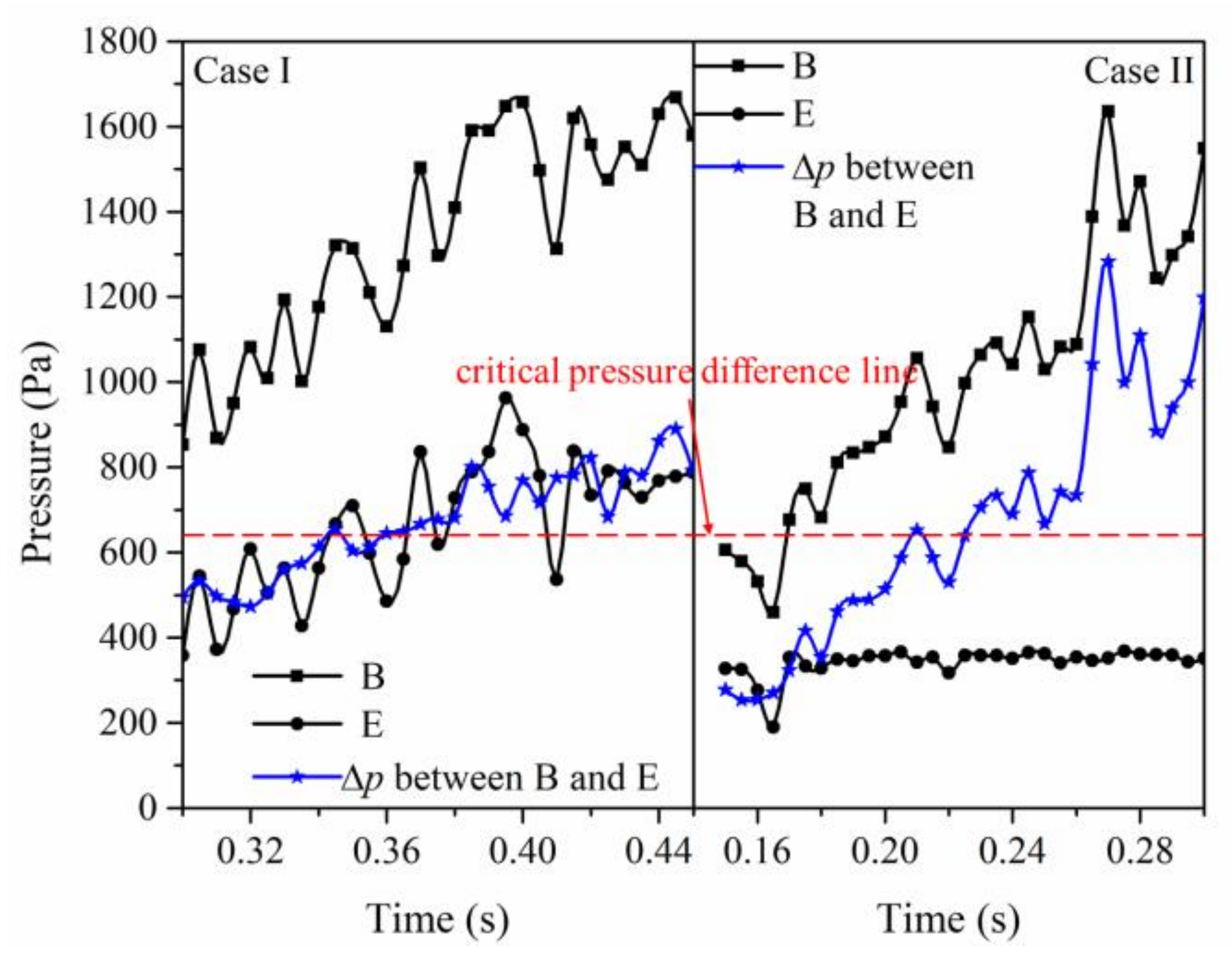
- There is a capillary barrier in the oil–water interface at the remaining oil boundary. When the displacement force is insufficient, the oil–water interface only deforms and does not move. At the beginning, there are few particles in the water channel, which cannot make enough pressure drop between different oil–water interfaces and the remaining oil remains stationary. These channels are blocked by static remaining oil, so that particles can only migrate in water channels.
- The addition of particles to the displacement fluid will increase the effective viscosity of the displacement fluid. The higher the particle concentration, the greater the effective viscosity of the system. The larger the effective viscosity is, the more obvious the increase of channel resistance is. The viscosity effect will make the inlet–outlet pressure difference increase with time. With only the viscosity effect there will be no large pressure difference fluctuation in the rising process.
- When the particle size is larger than the pore size, the particle will block the pore channel. When plugging, the upstream pressure will rise rapidly; when breaking through, the upstream pressure will drop rapidly. The plugging and breakthrough of particles will cause a large pressure fluctuation in the process of particle migration.
4.4. Particle–Oil–Water Behaviors in Different Particle Flooding Methods
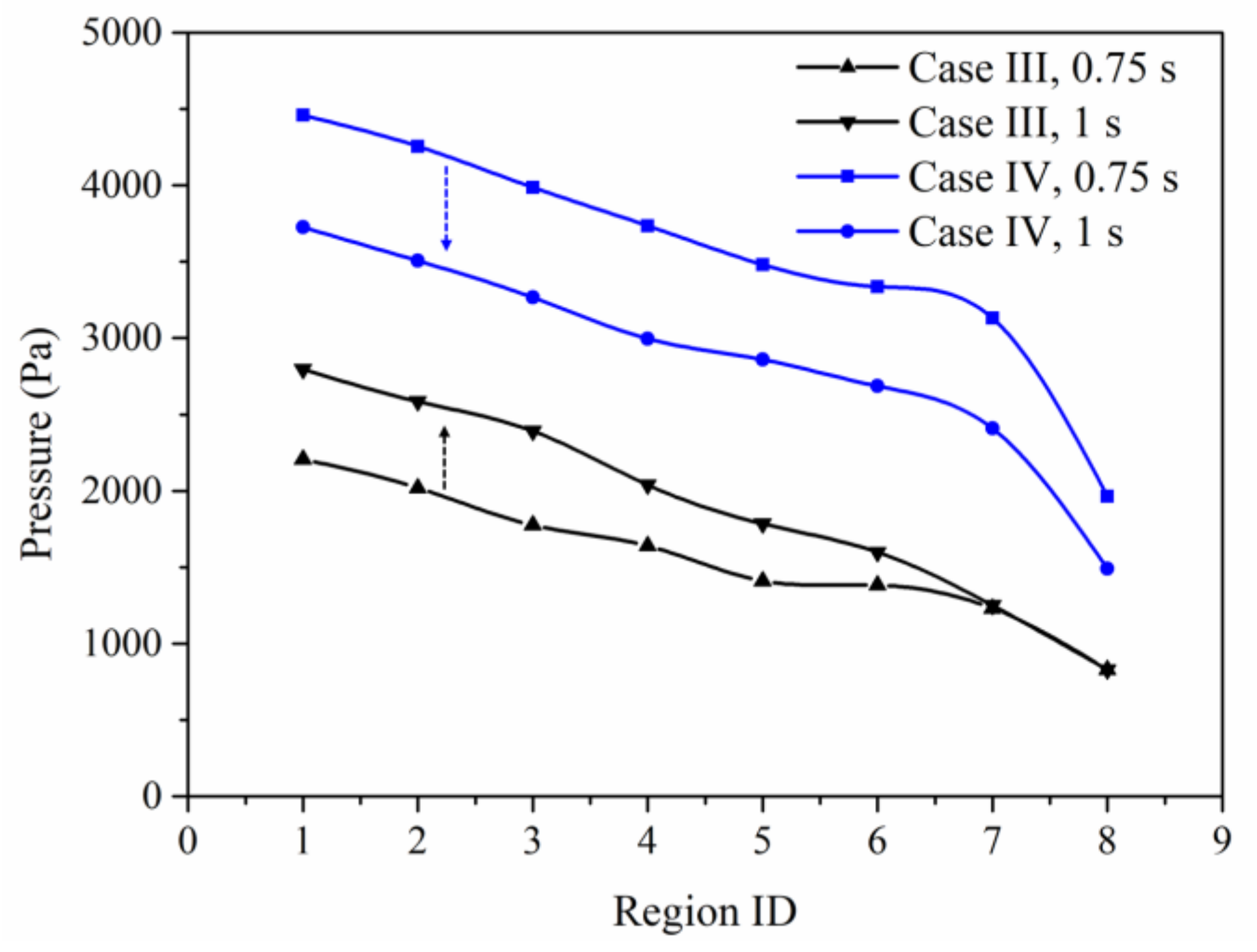
4.4.1. Alternate Injection of Big and Small Particles
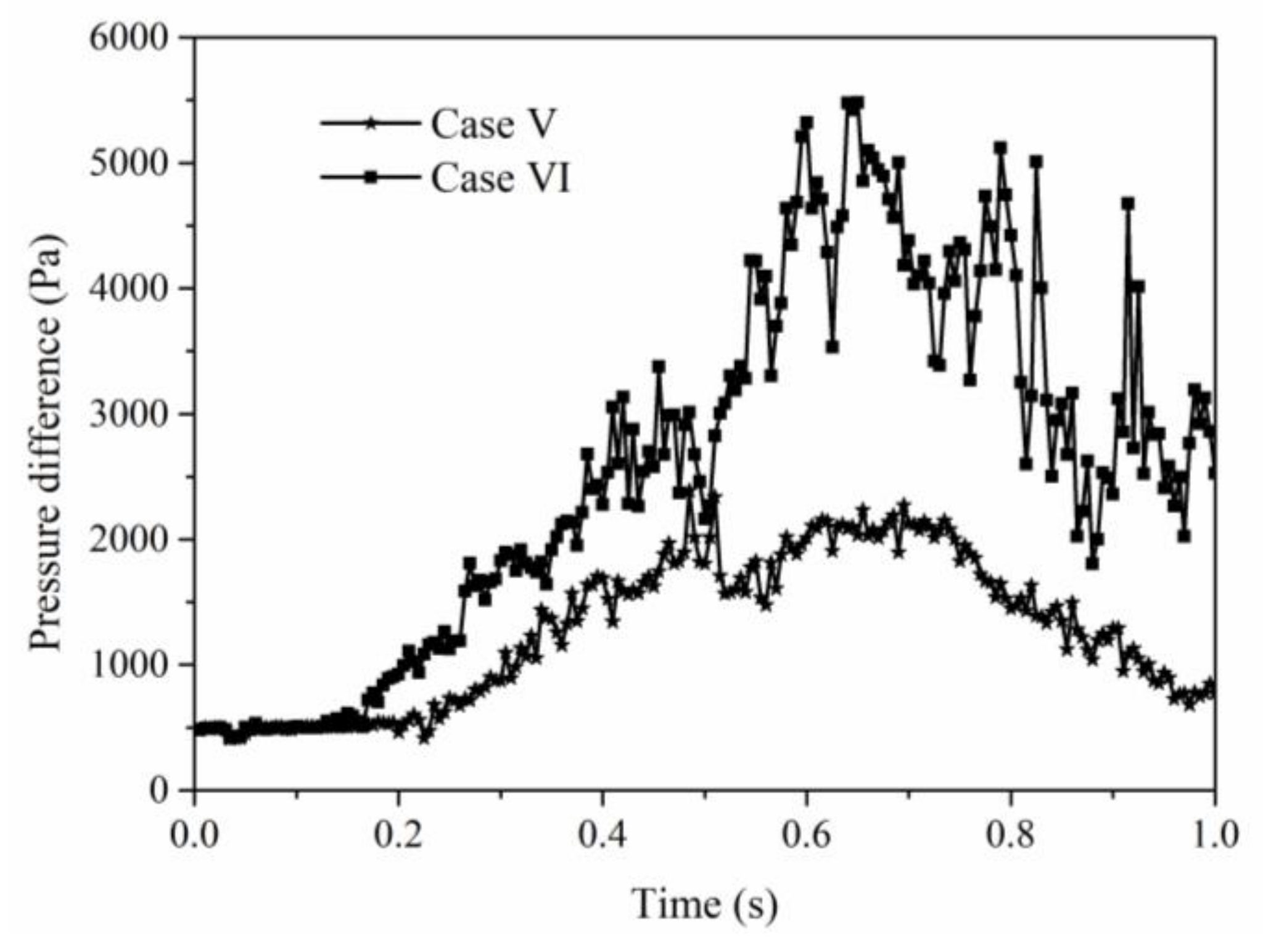
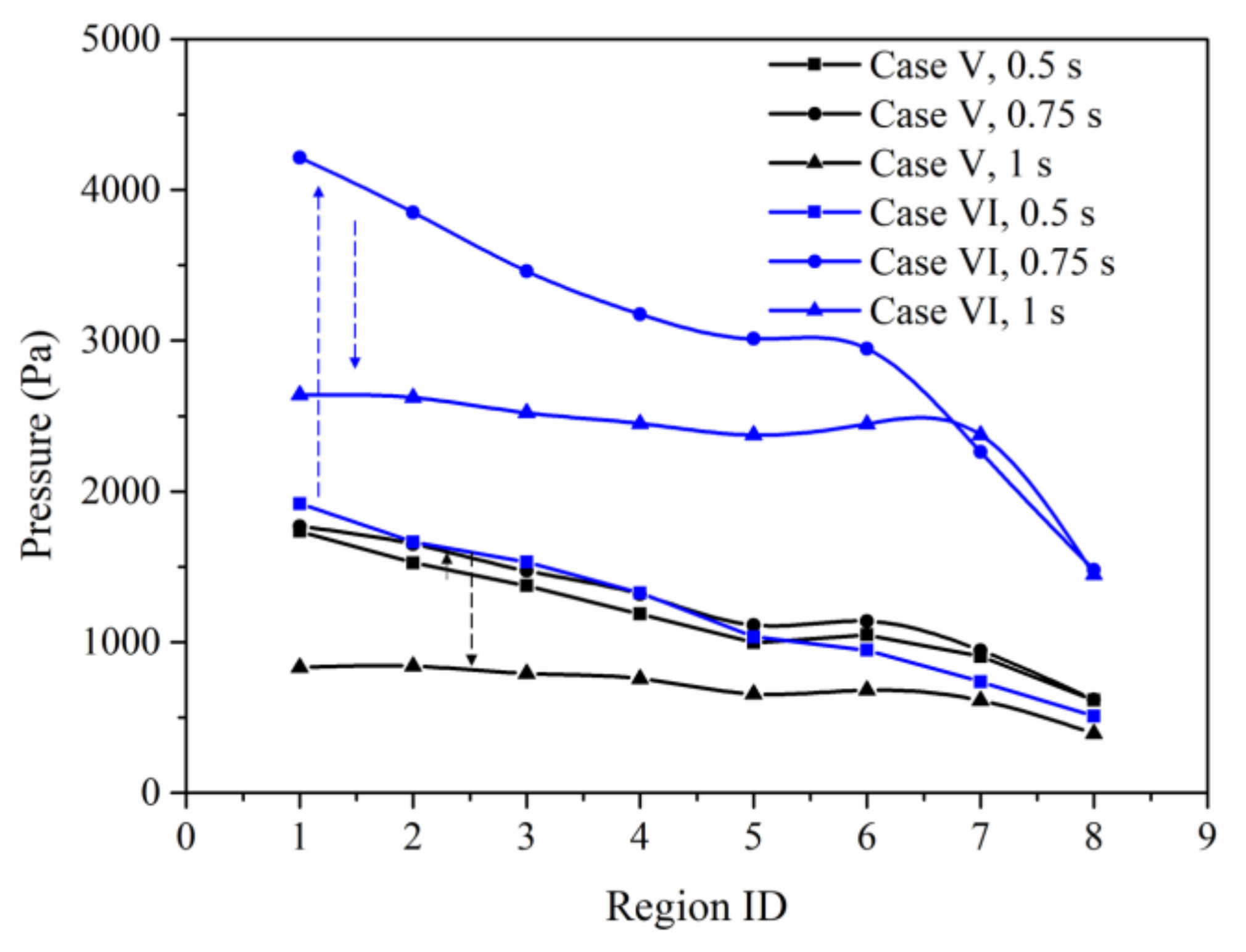
4.4.2. Slug Injection of Big or Small Particles
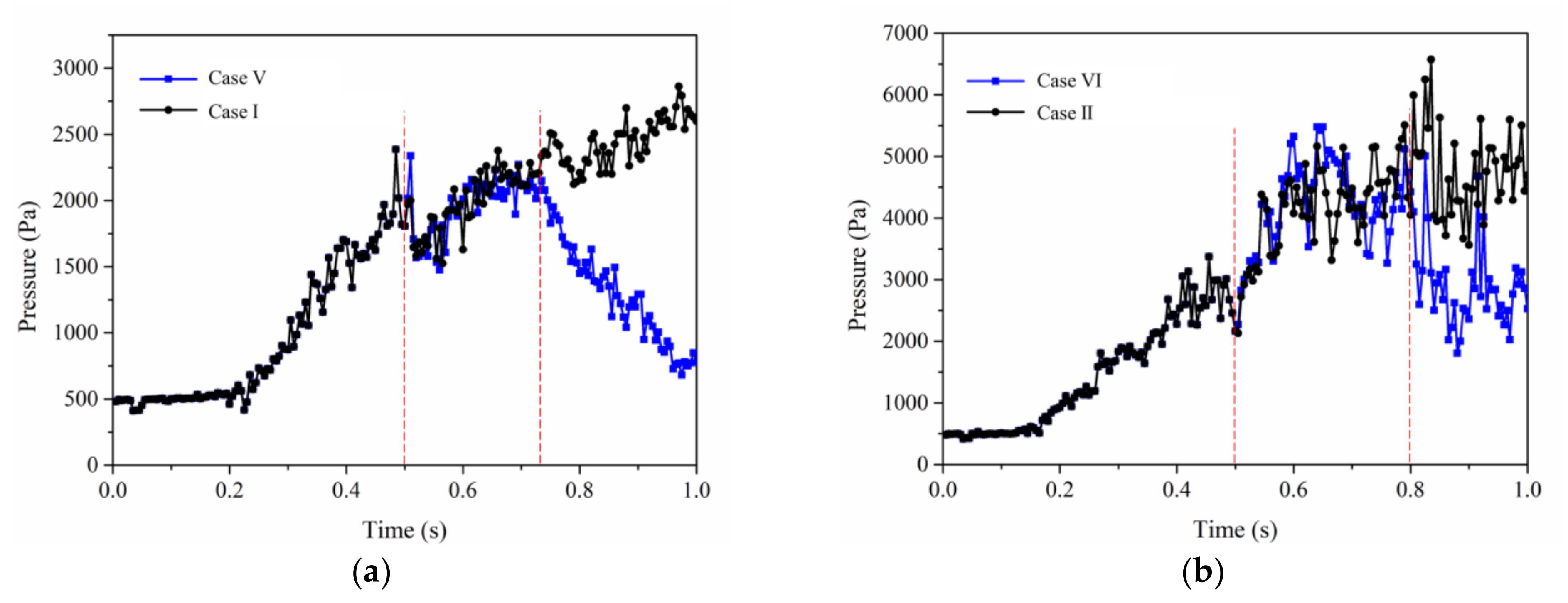
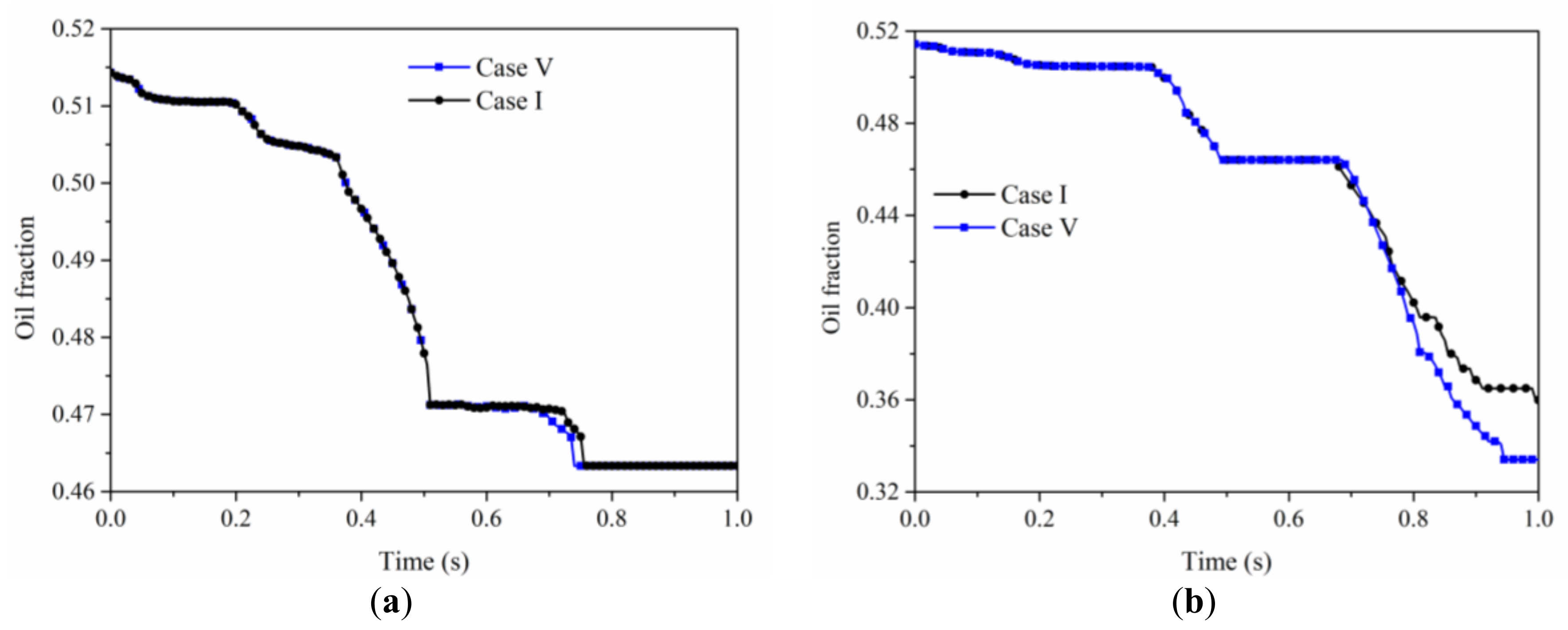
4.5. Comparison of Flow Behaviors among Different Flooding Methods
4.5.1. Flow Behaviors Comparison between Continuous Particle Injection and Slug Particle Injection
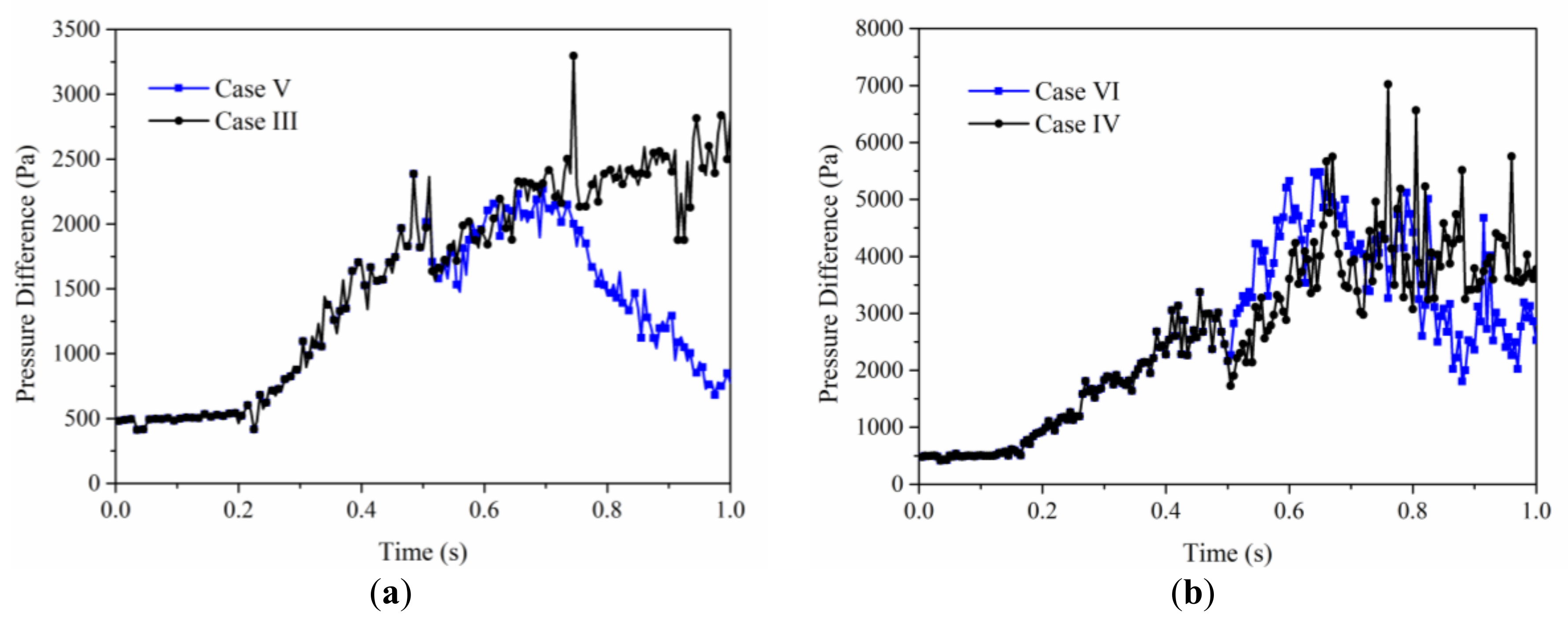
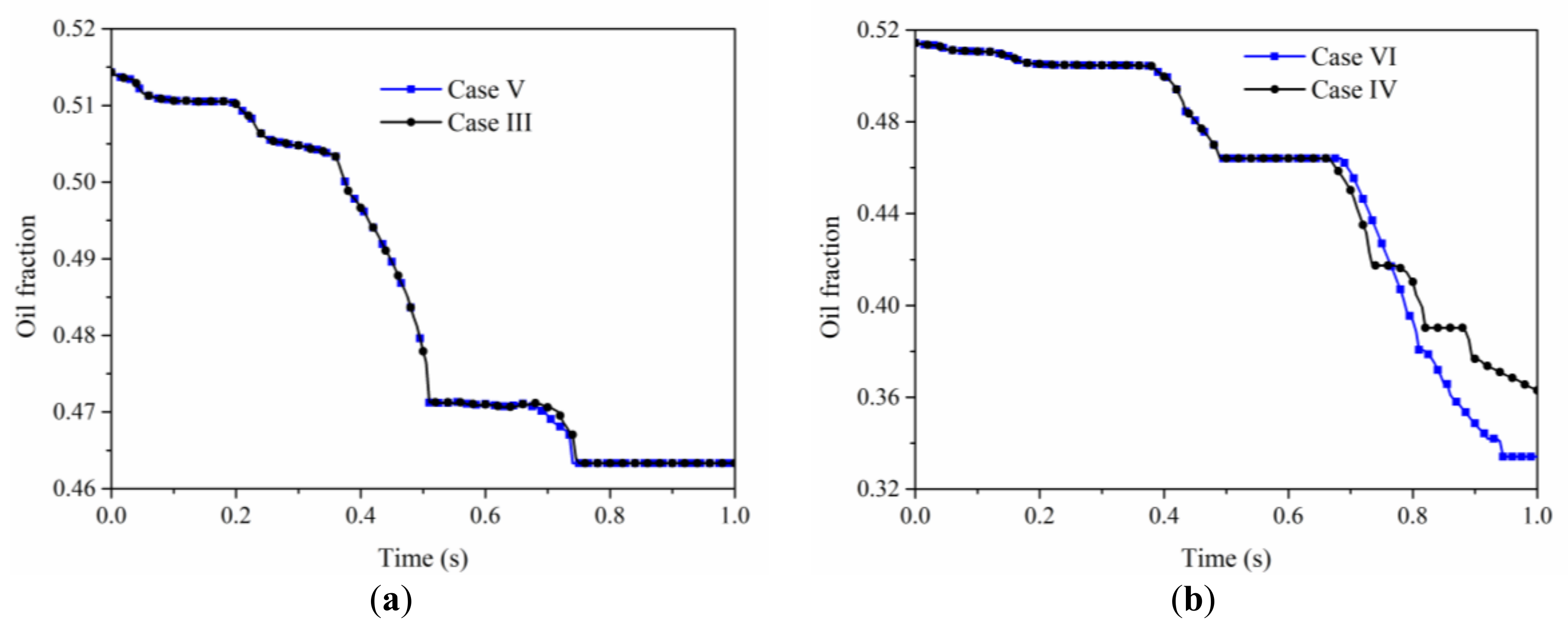
4.5.2. Multiphase Phase Behaviors Comparison between Continuous Particle Injection and Alternate Particle Injection
4.5.3. Multiphase Phase Behaviors Comparison between Slug Particle Injection and Alternate Particle Injection
5. Conclusions
- (1)
- When the pressure gradient gradually decreases so that the capillary resistance effect cannot be overcome, the movement of oil–water interface stops and the remaining oil is formed. There is a dynamic threshold in the process of producing remaining oil. Only when the dynamic threshold is exceeded can the remaining oil begin to move. In the process of particle flooding, the migration of particles in the water bearing channel increases the resistance of the water bearing channel, resulting in the formation of pressure difference at the water bearing side of different interfaces of the remaining oil. When the pressure difference exceeds the dynamic threshold, the remaining oil begins to move.
- (2)
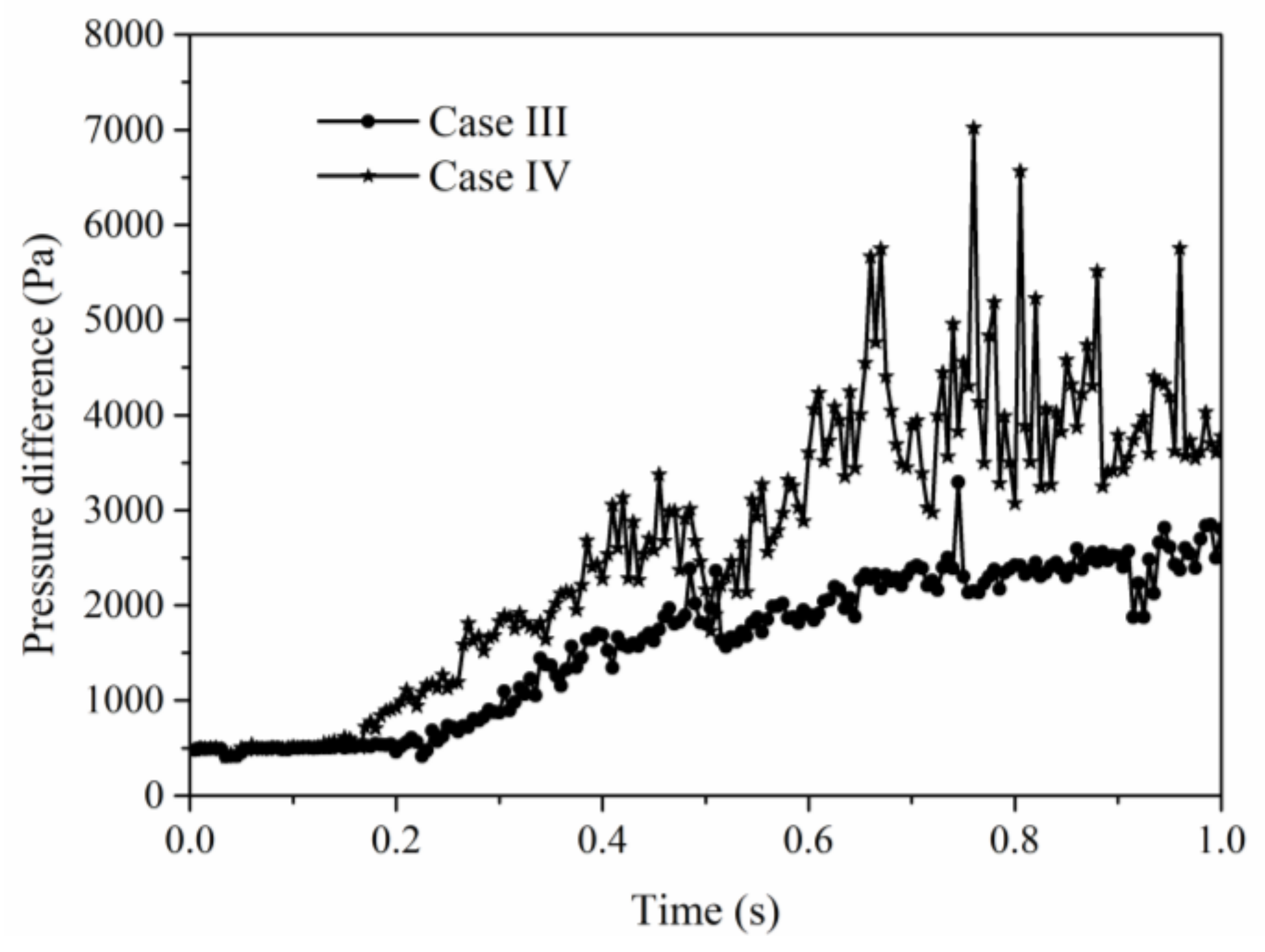
- In the process of particle flooding, large particles can cause higher pressure difference rise and pressure difference fluctuation, and the remaining oil production capacity is higher than that of small particles. Therefore, the oil production time with large particles is smaller than that with small particles. The final remaining oil production is also higher than that of small particles.
- (3)
- Through the analysis and pairwise comparison of multiphase fluid behavior and remaining oil production characteristics under three injection modes of continuous injection, slug injection and alternate injection, it is found that when the fluid medium with different resistance increasing ability is injected into the pores, different fluids can enter into different pore channels, promote the imbalance of remaining oil interface, and achieve the purpose of rapid production of remaining oil. There is the biggest difference between the resistance increasing ability of large particles and water to pores. While reducing the average injection pressure, different resistance can be formed in different channels. Therefore, the ultimate recovery rate of slug injection of large particles is the highest.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, S.; Pu, W. Migration and plugging of polymer microspheres (PMs) in porous media for enhanced oil recovery: Experi-mental studies and empirical correlations. Colloid Surf. B 2020, 297, 124774. [Google Scholar] [CrossRef]
- Lesin, V.I.; Koksharov, Y.A.; Khomutov, G.B. Magnetic nanoparticles in petroleum. Pet. Chem. 2010, 50, 102–105. [Google Scholar] [CrossRef]
- Negin, C.; Ali, S.; Xie, Q. Application of nanotechnology for enhancing oil recovery—A review. Petroleum 2016, 2, 324–333. [Google Scholar] [CrossRef]
- Foroozesh, J.; Kumar, S. Nanoparticles behaviors in porous media: Application to enhanced oil recovery. J. Mol. Liq. 2020, 316, 113876. [Google Scholar] [CrossRef]
- Liu, D.; Gu, Z.; Liang, R.; Su, J.; Ren, D.; Chen, B.; Huang, C.; Yang, C. Impacts of Pore-Throat System on Fractal Character-ization of Tight Sandstones. Geofluids 2020, 9, 1–17. [Google Scholar]
- Mack, J.C.; Smith, J.E. In-depth colloidal dispersion gels improve oil recovery efficiency. In Proceedings of the SPE/DOE Improved Oil Recovery Symposium, Tulsa, OH, USA, 17–20 April 1994. [Google Scholar]
- Yuan, J.; Sundén, B. On mechanisms and models of multi-component gas diffusion in porous structures of fuel cell electrodes. Int. J. Heat Mass Transf. 2014, 69, 358–374. [Google Scholar] [CrossRef]
- Akai, T.; Alhammadi, A.M.; Blunt, M.J.; Bijeljic, B. Modeling Oil Recovery in Mixed-Wet Rocks: Pore-Scale Comparison Be-tween Experiment and Simulation. Transp. Porous Med. 2019, 127, 393–414. [Google Scholar] [CrossRef] [Green Version]
- Raeini, A.Q.; Bijeljic, B.; Blunt, M.J. Numerical modelling of sub-pore scale events in two-phase flow through porous media. Transp. Porous Med. 2014, 101, 191–213. [Google Scholar] [CrossRef]
- Bijeljic, B.; Raeini, A.; Mostaghimi, P.; Blunt, M.J. Predictions of non-Fickian solute transport in different classes of porous media using direct simulation on pore-scale images. Phys. Rev. E 2013, 87, 013011. [Google Scholar] [CrossRef] [Green Version]
- Su, J.; Wang, L.; Gu, Z.; Zhang, Y.; Chen, C. Advances in Pore-Scale Simulation of Oil Reservoirs. Energies 2018, 11, 1132. [Google Scholar] [CrossRef] [Green Version]
- Su, J.; Chai, G.; Wang, L.; Cao, W.; Gu, Z.; Chen, C.; Xu, X.Y. Pore-scale direct numerical simulation of particle transport in porous media. Chem. Eng. Sci. 2019, 199, 613–627. [Google Scholar] [CrossRef]
- Raeini, A.Q.; Blunt, M.J.; Bijeljic, B. Direct simulations of two-phase flow on micro-CT images of porous media and upscaling of pore-scale forces. Adv. Water Resour. 2014, 74, 116–126. [Google Scholar] [CrossRef]
- Kokubun, M.E.; Muntean, A.; Radu, F.; Kumar, K.; Pop, I.; Keilegavlen, E.; Spildo, K.; Spildop, K. A pore-scale study of transport of inertial particles by water in porous media. Chem. Eng. Sci. 2019, 207, 397–409. [Google Scholar] [CrossRef] [Green Version]
- Kokubun, M.A.E.; Radu, F.A.; Keilegavlen, E.; Kumar, K.; Spildo, K. Transport of Polymer Particles in Oil–Water Flow in Porous Media: Enhancing Oil Recovery. Transp. Porous Media 2018, 126, 501–519. [Google Scholar] [CrossRef] [Green Version]
- Su, J.; Chai, G.; Wang, L.; Cao, W.; Yu, J.; Gu, Z.; Chen, C. Direct numerical simulation of pore scale particle-water-oil transport in porous media. J. Pet. Sci. Eng. 2019, 180, 159–175. [Google Scholar] [CrossRef]
- Su, J.; Chai, G.; Wang, L.; Yu, J.; Cao, W.; Gu, Z.; Chen, C.; Meng, W. Direct numerical simulation of particle pore-scale transport through three-dimensional porous media with arbitrarily polyhedral mesh. Powder Technol. 2020, 367, 576–596. [Google Scholar] [CrossRef]
- Ubbink, O. Numerical Prediction of Two Fluid Systems with Sharp Interfaces. Ph.D. Thesis, University of London, London, UK, 1997. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Su, J.; Gu, Z.; Xu, X.Y. Discrete element simulation of particle flow in arbitrarily complex geometries. Chem. Eng. Sci. 2011, 66, 6069–6088. [Google Scholar] [CrossRef]
- Tsuji, Y.; Tanaka, T.; Ishida, T. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe. Powder Technol. 1992, 71, 239–250. [Google Scholar] [CrossRef]
- Munjiza, A.; Andrews, K.R.F. NBS contact detection algorithm for bodies of similarsize. Int. J. Numer. Methods Eng. 2015, 43, 131–149. [Google Scholar] [CrossRef]
- Su, J.; Huang, C.; Gu, Z.; Chen, C.; Xu, X. An Efficient RIGID Algorithm and Its Application to the Simulation of Particle Transport in Porous Medium. Transp. Porous Media 2016, 114, 99–131. [Google Scholar] [CrossRef]
- Patankar, N.A.; Singh, N.A.; Joseph, D.; Glowinski, R.; Pan, T. A new formulation of the distributed Lagrange multipli-er/fictitious domain method for particulate flows. Int. J. Multiph. Flow 2000, 26, 1509. [Google Scholar] [CrossRef]
- Patankar, N.A. A Formulation for Fast Computations of Rigid Particulate Flows; Center for Turbulence Research Annual Research Briefs: Stanford, CA, USA, 2001; pp. 185–196. [Google Scholar]
- Jasak, H.; Weller, H.G.; Gosman, A.D. High resolution NVD differencing scheme for arbitrarily unstructured meshes. Int. J. Numer. Meth. Fluids 1999, 31, 431–449. [Google Scholar] [CrossRef]
- Wang, L.; Su, J.; Gu, Z.; Tang, L. Numerical study on flow field and pollutant dispersion in an ideal street canyon within a real tree model at different wind velocities. Comput. Math. Appl. 2021, 81, 679–692. [Google Scholar] [CrossRef]
- Crank, J.; Nicolson, P. A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type. Math. Proc. Camb. Philos. Soc. 1947, 43, 50–67. [Google Scholar] [CrossRef]
- Rougier, E.; Munjiza, A.; John, N.W.M. Numerical comparison of some explicit time integration schemes used in DEM, FEM/DEM and molecular dynamics. Int. J. Numer. Methods Eng. 2004, 61, 856–879. [Google Scholar] [CrossRef]





| Item | Description | Time Interval (s) |
|---|---|---|
| Case I | Continuous injection of small particles | (0, 1) small particles |
| Case II | Continuous injection of big particles | (0, 1) big particles |
| Case III | Alternate injection of small and big Particles | (0, 0.5) small particles (0.5, 1) big particles |
| Case IV | Alternate injection of big and small particles | (0, 0.5) big particles (0.5, 1) small particles |
| Case V | Slug injection of small particles | (0, 0.5) small particles (0.5, 1) water |
| Case VI | Slug injection of big particles | (0, 0.5) big particles (0.5, 1) water |
| Item | Value |
|---|---|
| Particle density/kg·m−3 | 1000 |
| Small particle size/m | 10−4 |
| Big particle size/m | 5 × 10−4 |
| Particle flow rate/kg·s−1 | 5 × 10−4 |
| Normal/tangential stiffness coefficient/N·m−1 | 800/200 |
| Normal/tangential damping coefficient/N·m−1 | 0.3/0.3 |
| Friction coefficient | 0.1 |
| Water density/kg·m−3 | 1000 |
| Water viscosity/kg·(m·s)−1 | 0.001 |
| Water flow rate/m·s−1 | 0.01 |
| Oil density/kg·m−3 | 800 |
| Oil viscosity/kg·(m·s)−1 | 0.0148 |
| Water oil interface tension/kg·s−2 | 0.07 |
| Physical Quantity | Boundaries | ||
|---|---|---|---|
| Inlet | Outlet | Wall | |
| Velocity | Fixed value | Zero gradient | Fixed value |
| Pressure | Zero gradient | Fixed value | Zero gradient |
| Water volume fraction | Fixed value | Zero gradient | Constant contact angle |
| Particle | Rebound | Exit | DEM |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Wang, L.; Wang, J.; Su, J. Pore-Scale Simulation of Particle Flooding for Enhancing Oil Recovery. Energies 2021, 14, 2305. https://doi.org/10.3390/en14082305
Liu X, Wang L, Wang J, Su J. Pore-Scale Simulation of Particle Flooding for Enhancing Oil Recovery. Energies. 2021; 14(8):2305. https://doi.org/10.3390/en14082305
Chicago/Turabian StyleLiu, Xiangbin, Le Wang, Jun Wang, and Junwei Su. 2021. "Pore-Scale Simulation of Particle Flooding for Enhancing Oil Recovery" Energies 14, no. 8: 2305. https://doi.org/10.3390/en14082305
APA StyleLiu, X., Wang, L., Wang, J., & Su, J. (2021). Pore-Scale Simulation of Particle Flooding for Enhancing Oil Recovery. Energies, 14(8), 2305. https://doi.org/10.3390/en14082305






