Effect of Effective Pressure on the Permeability of Rocks Based on Well Testing Results
Abstract
1. Introduction
2. Methods for Determining the Change in the Permeability
2.1. Porous Rocks
2.2. Fractured Rocks
2.3. Conclusions on the Methods for Determining the Change in Permeability
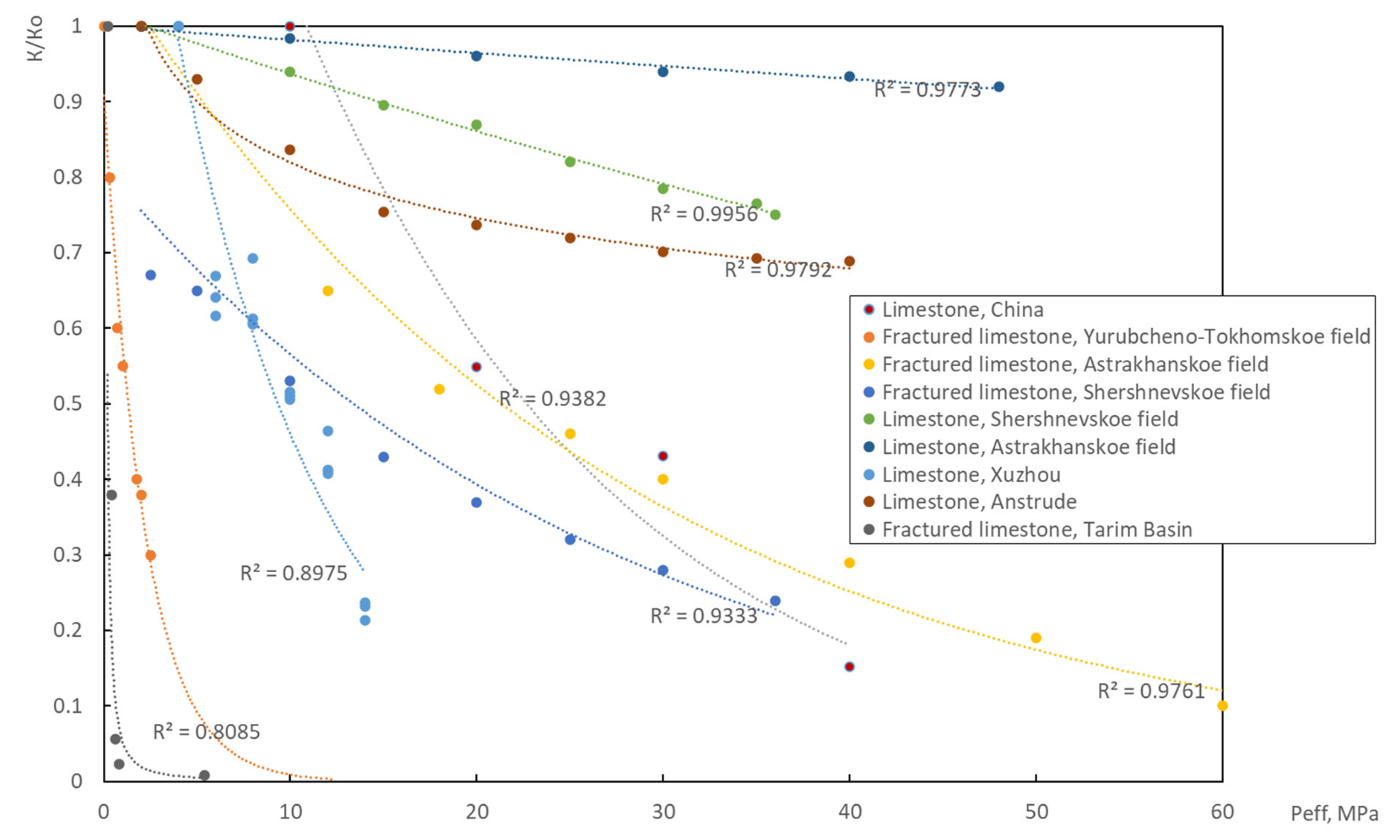
3. Changes in the Rocks Permeability Based on the Laboratory Studies
4. Changes in the Rocks Permeability Based on the Field Well Tests
- -
- carbonate layers C1t and D3fm are represented by fine-crystalline limestones, partially dolomitized. Due to the blurring of boundaries, the C1t and D3fm layers are combined into one production reservoir. The depth of the layers top is ranging from 2030 to 2400 m, the porosity is ranging from 7.1 to 12%, the permeability is ranging from 0.009 to 0.08 μm2, the initial reservoir pressure is ranging from 20.9 to 25 MPa.
- -
- terrigenous layers C1bb are represented by interbedded uneven-grained sandstones, siltstones and mudstones. The depth of the layers top is ranging from 2030 to 2350 m, the porosity is ranging from 14 to 18%, the permeability is ranging from 0.239 to 0.522 μm2, the initial reservoir pressure is ranging from 19.8 to 24.4 MPa.
- -
- carbonate layers C2b are represented by fine-grained limestones, dolomitized areas, with stylolite seams. The depth of the layers top is ranging from 1734 to 2104 m, the porosity is ranging from 9.7 to 16%, the permeability is ranging from 0.017 to 0.111 μm2, the initial reservoir pressure is ranging from 19.8 to 24.4 MPa.
- (1)
- Reservoir pressure near the well should not decrease below the oil gas saturation pressure during the period under consideration.
- (2)
- The well should produce the same fluid as in the initial period of the operation, the water cut should not exceed 5%.
- (3)
- No enhancing of oil recovery methods should be applied on the well during the period under consideration.
- (1)
- Determination of permeability using field well tests reflect the integral permeability of the formation, taking into account its zonal and layered heterogeneity. A decrease in reservoir pressure leads to the closure of fractures, disconnection of individual interlayers, as a result, the total permeability of the reservoir decreases sharply.
- (2)
- The selected core material, after being extracted from the well and natural stress relief, undergoes significant changes in the form of volumetric deformations and can no longer reflect the actual properties inherent in the original conditions of its bedding.
- (3)
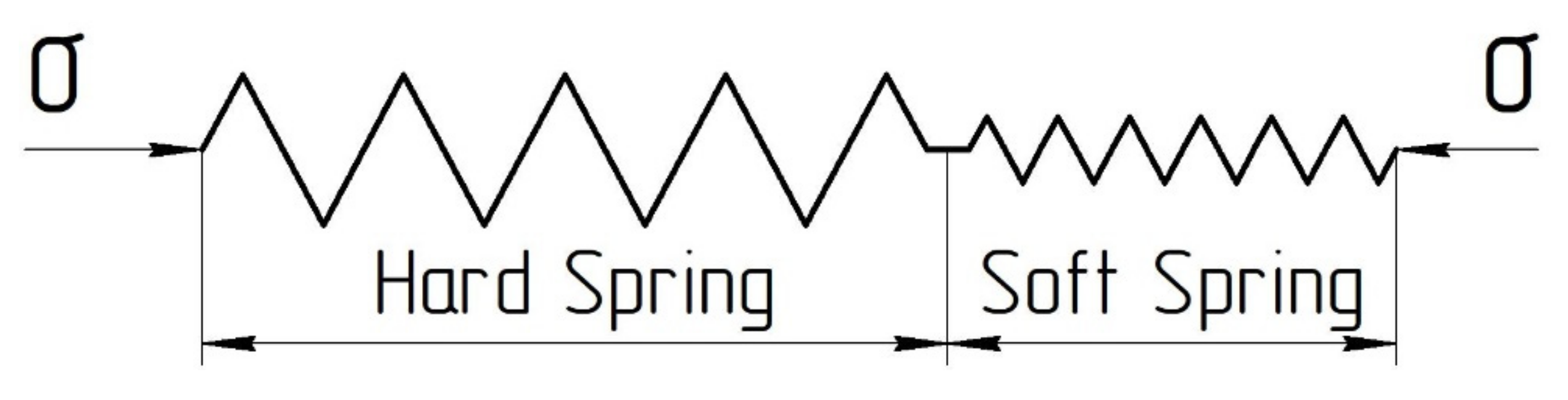
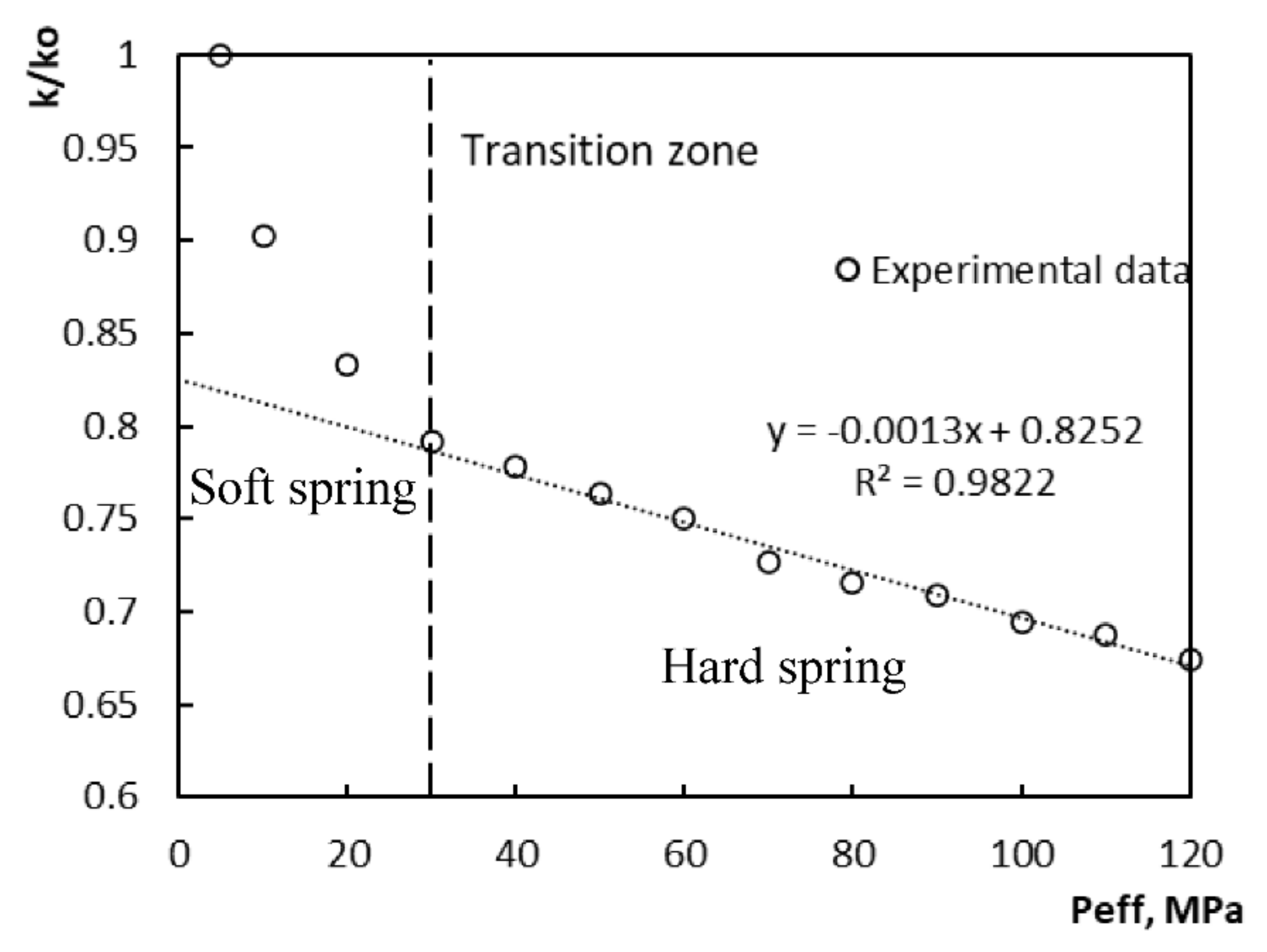
- The Two-Part Hooke’s Model can also be used to illustrate this change in permeability. On the basis of this model, it can be concluded that significant irreversible deformations are currently taking place in the formations of the oil fields indicated in Figure 6, as evidenced by a critical decrease in permeability with an increase in effective pressure. This fact suggests that significant oil reserves can be permanently lost in the reservoir. In this regard, predicting changes in permeability is an urgent task.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Peff | effective pressure |
| Peff0 | initial effective pressure |
| Pc | lithostatic (confining) pressure |
| Pf | pore fluid pressure |
| nk | effective stress ratio |
| k | permeability |
| ko | initial permeability |
| ρ | average density of the overlying rocks |
| h | depth of the top of the productive layer |
| A | coefficient of exponential equation |
| γ | exponent of exponential equation |
| B | coefficient in power law equations |
| n | exponent in power law equations |
References
- Xiao, B.; Zhang, Y.; Wang, Y.; Jiang, G.; Liang, M.; Chen, X.; Long, G. A fractal model for kozeny–carman constant and dimensionless permeability of fibrous porous media with roughened surfaces. Fractals 2019, 27. [Google Scholar] [CrossRef]
- Ehrenberg, S.N.; Nadeau, P.H. Sandstone vs. carbonate petroleum reservoirs: A global perspective on porosity-depth and porosity-permeability relationships. AAPG Bull. 2005, 89, 435–445. [Google Scholar] [CrossRef]
- Xiao, B.; Zhang, X.; Wang, W.; Long, G.; Chen, H.; Kang, H.; Ren, W. A fractal model for water flow through unsaturated porous rocks. Fractals 2018, 26. [Google Scholar] [CrossRef]
- Xiao, B.; Fan, J.; Ding, F. Prediction of Relative Permeability of Unsaturated Porous Media Based on Fractal Theory and Monte Carlo Simulation. Energy Fuels 2012, 26, 6971–6978. [Google Scholar] [CrossRef]
- Anselmetti, F.S.; Luthi, S.; Eberli, G.P. Quantitative characterization of carbonate pore systems by digital image analysis. AAPG Bull. 1998, 82, 1815–1836. [Google Scholar]
- Bjørlykke, K.; Høeg, K. Effects of burial diagenesis on stresses, compaction and fluid flow in sedimentary basins. Mar. Pet. Geol. 1997, 14, 267–276. [Google Scholar] [CrossRef]
- Bjørlykke, K. Fluid flow in sedimentary basins. Sediment. Geol. 1993, 86, 137–158. [Google Scholar] [CrossRef]
- Woody, R.E.; Gregg, J.M.; Koederitz, L.F. Effect of texture on petrophysical properties of dolomite: Evidence from the Cambrian-Ordovician of southeastern Missouri. AAPG Bull. 1996, 80, 119–132. [Google Scholar]
- Bloch, S.; Lander, R.H.; Bonnell, L. Anomalously high porosity and permeability in deeply buried sandstone reservoirs: Origin and predictability. AAPG Bull. 2002, 86, 301–328. [Google Scholar]
- Terzaghi, K. Principles of soil mechanics. Eng. News-Rec. 1925, 95, 987–990. [Google Scholar]
- Dobrynin, V.M. Effect of Overburden Pressure on Some Properties of Sandstones. Soc. Pet. Eng. J. 1962, 2, 360–366. [Google Scholar] [CrossRef]
- Fatt, I. The Biot-Willis Elastic Coefficients for a Sandstone. J. Appl. Mech. 1959, 26, 296–297. [Google Scholar]
- Nur, A.; Byerlee, J.D. An exact effective stress law for elastic deformation of rock with fluids. J. Geophys. Res. Space Phys. 1971, 76, 6414–6419. [Google Scholar] [CrossRef]
- Warpinski, N.R.; Teufel, L.W. Determination of the Effective-Stress Law for Permeability and Deformation in Low-Permeability Rocks. SPE Form. Eval. 1992, 7, 123–131. [Google Scholar] [CrossRef]
- Li, M.; Xiao, W.-L.; Guo, X.; Zhang, L.-H.; Zheng, L.-L. Laboratory Study of the Effective Pressure Law for Permeability of the Low-Permeability Sandstones from the Tabamiao Area, Inner Mongolia. Chin. J. Geophys. 2009, 52, 1402–1413. [Google Scholar] [CrossRef]
- Li, M.; Bernabé, Y.; Xiao, W.-I.; Chen, Z.-Y.; Liu, Z.-Q. Effective pressure law for permeability of E-bei sandstones. J. Geophys. Res. Space Phys. 2009, 114. [Google Scholar] [CrossRef]
- Ghabezloo, S.; Sulem, J.; Guédon, S.; Martineau, F. Effective stress law for the permeability of a limestone. Int. J. Rock Mech. Min. Sci. 2009, 46, 297–306. [Google Scholar] [CrossRef]
- Bernabé, Y. Comparison of the effective pressure law for permeability and resistivity formation factor in Chelmsford granite. Pure Appl. Geophys. PAGEOPH 1988, 127, 607–625. [Google Scholar] [CrossRef]
- Bernabé, Y. The effective pressure law for permeability during pore pressure and confining pressure cycling of several crystalline rocks. J. Geophys. Res. Space Phys. 1987, 92, 649. [Google Scholar] [CrossRef]
- Bernabe, Y. The effective pressure law for permeability in Chelmsford granite and Barre granite. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1986, 23, 267–275. [Google Scholar] [CrossRef]
- Robin, P.-Y.F. Note on effective pressure. J. Geophys. Res. Space Phys. 1973, 78, 2434–2437. [Google Scholar] [CrossRef]
- Gangi, A.F.; Carlson, R.L. An asperity-deformation model for effective pressure. Tectonophysics 1996, 256, 241–251. [Google Scholar] [CrossRef]
- Coyner, K. Effects of Stress, Pore Pressure, and Pore Fluids on Bulk Strain, Velocity, and Permeability in Rocks. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1984. [Google Scholar]
- Todd, T.; Simmons, G. Effect of pore pressure on the velocity of compressional waves in low-porosity rocks. J. Geophys. Res. Space Phys. 1972, 77, 3731–3743. [Google Scholar] [CrossRef]
- Li, Z.; Ripepi, N.; Chen, C. Comprehensive laboratory investigation of Klinkenberg Effect and its role on apparent permeability in various U.S. shale formations. In Proceedings of the 53rd US Rock Mechanics/Geomechanics Symposium, New York, NY, USA, 23–26 June 2019. [Google Scholar]
- Jones, F.O.; Owens, W.W. A Laboratory Study of Low-Permeability Gas Sands. J. Pet. Technol. 1980, 32, 1631–1640. [Google Scholar] [CrossRef]
- Ren, J.; Guo, P. A New Mathematical Model for Pressure Transient Analysis in Stress-Sensitive Reservoirs. Math. Probl. Eng. 2014, 2014, 485028. [Google Scholar] [CrossRef]
- Moradi, M.; Shamloo, A.; Asadbegi, M.; Dezfuli, A.D.; Asadbeigi, M. Three dimensional pressure transient behavior study in stress sensitive reservoirs. J. Pet. Sci. Eng. 2017, 152, 204–211. [Google Scholar] [CrossRef]
- Huang, Y.; Li, X.; Tan, X. Transient Pressure and Rate Decline Analysis for Horizontal Well in Stress-Sensitive Composite Reservoir. Math. Probl. Eng. 2018, 2018, 8672578. [Google Scholar] [CrossRef]
- Ren, J.; Guo, P. A general analytical method for transient flow rate with the stress-sensitive effect. J. Hydrol. 2018, 565, 262–275. [Google Scholar] [CrossRef]
- Bhullar, A.S.; Stewart, G.E.; Zimmerman, R.W. Perturbation Solution for One-Dimensional Flow to a Constant-Pressure Boundary in a Stress-Sensitive Reservoir. Transp. Porous Media 2021, 1–17. [Google Scholar] [CrossRef]
- Jiang, L.; Liu, J.; Liu, T.; Yang, D. Semi-analytical modeling of transient pressure behaviour for a fractured vertical well with hydraulic/natural fracture networks by considering stress-sensitive effect. J. Nat. Gas Sci. Eng. 2020, 82, 103477. [Google Scholar] [CrossRef]
- Kadeethum, T.; Salimzadeh, S.; Nick, H. Well productivity evaluation in deformable single-fracture media. Geothermics 2020, 87, 101839. [Google Scholar] [CrossRef]
- David, C.; Wong, T.-F.; Zhu, W.; Zhang, J. Laboratory measurement of compaction-induced permeability change in porous rocks: Implications for the generation and maintenance of pore pressure excess in the crust. Pure Appl. Geophys. PAGEOPH 1994, 143, 425–456. [Google Scholar] [CrossRef]
- Wong, T.-F.; Zhu, W. Brittle faulting and permeability evolution: Hydromechanical measurement, microstructural observation, and network modeling. In Washington DC American Geophysical Union Geophysical Monograph Series; AGU: Hoboken, NJ, USA, 1999; pp. 83–99. Available online: https://agupubs.onlinelibrary.wiley.com/doi/10.1029/GM113p0083 (accessed on 1 March 2021). [CrossRef]
- Zhang, Q.; Liu, J.; Xu, H.; Zeng, Y.; Wang, C.; Wang, L. Experimental Investigation on Permeability Evolution of Limestone Caprock under Coupled THM Processes. KSCE J. Civ. Eng. 2019, 23, 5090–5097. [Google Scholar] [CrossRef]
- Shi, L.; Zeng, Z.; Fang, Z.; Li, X. Investigation of the Effect of Confining Pressure on the Mechanics-Permeability Behavior of Mudstone under Triaxial Compression. Geofluids 2019, 2019, 1796380. [Google Scholar] [CrossRef]
- Bhandari, A.R.; Flemings, P.B.; Hofmann, R.; Polito, P.J. Stress-Dependent In Situ Gas Permeability in the Eagle Ford Shale. Transp. Porous Media 2018, 123, 1–20. [Google Scholar] [CrossRef]
- Ngwenya, B.T.; Elphick, S.C.; Kwon, O.; Main, I.G. Permeability evolution during progressive development of deformation bands in porous sandstones. J. Geophys. Res. Space Phys. 2003, 108. [Google Scholar] [CrossRef]
- Paterson, M.S. The equivalent channel model for permeability and resistivity in fluid-saturated rock-a re-appraisal. Mech. Mater. 1983, 2, 345–352. [Google Scholar] [CrossRef]
- Fischer, G.; Paterson, M. Chapter 9 Measurement of Permeability and Storage Capacity in Rocks during Deformation at High Temperature and Pressure. Int. Geophys. 1992, 51, 213–252. [Google Scholar]
- Simpson, G.; Guéguen, Y.; Schneider, F. Permeability enhancement due to microcrack dilatancy in the damage regime. J. Geophys. Res. Space Phys. 2001, 106, 3999–4016. [Google Scholar] [CrossRef]
- Vajdova, V.; Baud, P.; Wong, T.-F. Permeability evolution during localized deformation in Bentheim sandstone. J. Geophys. Res. Space Phys. 2004, 109. [Google Scholar] [CrossRef]
- Lion, M.; Skoczylas, F.; Ledésert, B. Determination of the main hydraulic and poro-elastic properties of a limestone from Bourgogne, France. Int. J. Rock Mech. Min. Sci. 2004, 41, 915–925. [Google Scholar] [CrossRef]
- Sulem, J.; Ouffroukh, H. Shear banding in drained and undrained triaxial tests on a saturated sandstone: Porosity and permeability evolution. Int. J. Rock Mech. Min. Sci. 2006, 43, 292–310. [Google Scholar] [CrossRef]
- Davy, C.A.; Skoczylas, F.; Barnichon, J.-D.; Lebon, P. Permeability of macro-cracked argillite under confinement: Gas and water testing. Phys. Chem. Earth Parts A/B/C 2007, 32, 667–680. [Google Scholar] [CrossRef]
- Watanabe, N.; Hirano, N.; Tsuchiya, N. Determination of aperture structure and fluid flow in a rock fracture by high-resolution numerical modeling on the basis of a flow-through experiment under confining pressure. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Connell, L.D.; Lu, M.; Pan, Z. An analytical coal permeability model for tri-axial strain and stress conditions. Int. J. Coal Geol. 2010, 84, 103–114. [Google Scholar] [CrossRef]
- Liu, W.; Li, Y.; Wang, B. Gas Permeability of Fractured Sandstone/Coal Samples under Variable Confining Pressure. Transp. Porous Media 2009, 83, 333–347. [Google Scholar] [CrossRef]
- Chen, H.-D.; Yuan-Ping, C.; Zhou, H.-X.; Li, W. Damage and Permeability Development in Coal during Unloading. Rock Mech. Rock Eng. 2013, 46, 1377–1390. [Google Scholar] [CrossRef]
- Alam, A.B.; Niioka, M.; Fujii, Y.; Fukuda, D.; Kodama, J.-I. Effects of confining pressure on the permeability of three rock types under compression. Int. J. Rock Mech. Min. Sci. 2014, 65, 49–61. [Google Scholar] [CrossRef]
- Heller, R.; Vermylen, J.; Zoback, M. Experimental investigation of matrix permeability of gas shales. AAPG Bull. 2014, 98, 975–995. [Google Scholar] [CrossRef]
- Bhandari, A.R.; Flemings, P.B.; Polito, P.J.; Cronin, M.B.; Bryant, S.L. Anisotropy and Stress Dependence of Permeability in the Barnett Shale. Transp. Porous Media 2015, 108, 393–411. [Google Scholar] [CrossRef]
- Ji, Y.; Hall, S.A.; Baud, P.; Wong, T.-F. Characterization of pore structure and strain localization in Majella limestone by X-ray computed tomography and digital image correlation. Geophys. J. Int. 2014, 200, 701–719. [Google Scholar] [CrossRef]
- Subramaniyan, S.; Quintal, B.; Madonna, C.; Saenger, E.H. Laboratory-based seismic attenuation in Fontainebleau sandstone: Evidence of squirt flow. J. Geophys. Res. Solid Earth 2015, 120, 7526–7535. [Google Scholar] [CrossRef]
- Yasuhara, H.; Kinoshita, N.; Ogata, S.; Cheon, D.-S.; Kishida, K. Coupled thermo-hydro-mechanical-chemical modeling by incorporating pressure solution for estimating the evolution of rock permeability. Int. J. Rock Mech. Min. Sci. 2016, 86, 104–114. [Google Scholar] [CrossRef]
- Huo, D.; Benson, S.M. Experimental Investigation of Stress-Dependency of Relative Permeability in Rock Fractures. Transp. Porous Media 2016, 113, 567–590. [Google Scholar] [CrossRef]
- Han, B.; Xie, S.Y.; Shao, J.F. Experimental Investigation on Mechanical Behavior and Permeability Evolution of a Porous Limestone under Compression. Rock Mech. Rock Eng. 2016, 49, 3425–3435. [Google Scholar] [CrossRef]
- Takeda, M.; Manaka, M. Effects of Confining Stress on the Semipermeability of Siliceous Mudstones: Implications for Identifying Geologic Membrane Behaviors of Argillaceous Formations. Geophys. Res. Lett. 2018, 45, 5427–5435. [Google Scholar] [CrossRef]
- Guzev, M.; Kozhevnikov, E.; Turbakov, M.; Riabokon, E.; Poplygin, V. Experimental Studies of the Influence of Dynamic Loading on the Elastic Properties of Sandstone. Energies 2020, 13, 6195. [Google Scholar] [CrossRef]
- Guzev, M.; Riabokon, E.; Turbakov, M.; Kozhevnikov, E.; Poplygin, V. Modelling of the Dynamic Young’s Modulus of a Sedimentary Rock Subjected to Nonstationary Loading. Energies 2020, 13, 6461. [Google Scholar] [CrossRef]
- Guzev, M.A.; Kozhevnikov, E.V.; Turbakov, M.S.; Riabokon, E.P.; Poplygin, V.V. Experimental Investigation of the Change of Elastic Moduli of Clastic Rocks under Nonlinear Loading. Int. J. Eng. 2021, 34, 750–755. [Google Scholar] [CrossRef]
- Poplygin, V.V.; Pavlovskaia, E.E. Investigation of the Influence of Pressures and Proppant Mass on the Well Parameters after Hydraulic Fracturing. Int. J. Eng. 2021, 34, 1066–1073. [Google Scholar]
- Riabokon, E.P.; Turbakov, M.S.; Kozhevnikov, E.V.; Poplygin, V.V.; Wiercigroch, M. Advanced Problems in Mechanics. In Proceedings of the XLVII International Summer School-Conference “Advanced Problems in Mechanics”, St. Petersburg, Russia, 24–29 June 2019; pp. 185–192. [Google Scholar] [CrossRef]
- Tiller, F.M. The Role of Porosity in Filtration, Part I: Numerical Methods for Constant Rate and Constant Pressure Filtration based on Kozeny’s Law. Chem. Eng. Prog. 1953, 49, 467–479. [Google Scholar]
- Gangi, A.F. Variation of whole and fractured porous rock permeability with confining pressure. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1978, 15, 249–257. [Google Scholar] [CrossRef]
- Jones, S.C. Two-Point Determinations of Permeability and PV vs. Net Confining Stress. SPE Form. Eval. 1988, 3, 235–241. [Google Scholar] [CrossRef]
- Rice, J.R. Chapter 20 Fault Stress States, Pore Pressure Distributions, and the Weakness of the San Andreas Fault. Int. Geophys. 1992, 51, 475–503. [Google Scholar] [CrossRef]
- Main, I.G.; Kwon, O.; Ngwenya, B.T.; Elphick, S.C. Fault sealing during deformation-band growth in porous sandstone. Geol. 2000, 28, 1131. [Google Scholar] [CrossRef]
- Kwon, O.; Kronenberg, A.K.; Gangi, A.F.; Johnson, B. Permeability of Wilcox shale and its effective pressure law. J. Geophys. Res. Space Phys. 2001, 106, 19339–19353. [Google Scholar] [CrossRef]
- Zhang, C.; Rothfuchs, T. Experimental study of the hydro-mechanical behaviour of the Callovo-Oxfordian argillite. Appl. Clay Sci. 2004, 26, 325–336. [Google Scholar] [CrossRef]
- Dong, J.-J.; Hsu, J.-Y.; Wu, W.-J.; Shimamoto, T.; Hung, J.-H.; Yeh, E.-C.; Wu, Y.-H.; Sone, H. Stress-dependence of the permeability and porosity of sandstone and shale from TCDP Hole-A. Int. J. Rock Mech. Min. Sci. 2010, 47, 1141–1157. [Google Scholar] [CrossRef]
- Yuan, S.; Harrison, J. Numerical modelling of progressive damage and associated fluid flow using a hydro-mechanical local degradation approach. Int. J. Rock Mech. Min. Sci. 2004, 41, 317–322. [Google Scholar] [CrossRef]
- Selvadurai, A.; Głowacki, A. Permeability Hysterisis of Limestone during Isotropic Compression. Ground Water 2007, 46, 113–119. [Google Scholar] [CrossRef]
- Witherspoon, P.A.; Gale, J.E. Mechanical and hydraulic properties of rocks related to induced seismicity. Eng. Geol. 1977, 11, 23–55. [Google Scholar] [CrossRef]
- Jones, F.O.J. A Laboratory Study of the Effects of Confining Pressure on Fracture Flow and Storage Capacity in Carbonate Rocks. J. Pet. Technol. 1975, 27, 21–27. [Google Scholar] [CrossRef]
- Nelson, R. Fracture Permeability in Porous Reservoirs: Experimental and Field Approach. Ph.D. Thesis, Texas A & M University, College Station, TX, USA, 1975. [Google Scholar]
- Sahimi, M. Flow and Transport in Porous Media and Fractured Rock; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2011. [Google Scholar] [CrossRef]
- Ma, D.; Miao, X.X.; Chen, Z.Q.; Mao, X.B. Experimental Investigation of Seepage Properties of Fractured Rocks under Different Confining Pressures. Rock Mech. Rock Eng. 2012, 46, 1135–1144. [Google Scholar] [CrossRef]
- Wong, L.N.Y.; Li, D.; Liu, G. Experimental Studies on Permeability of Intact and Singly Jointed Meta-Sedimentary Rocks under Confining Pressure. Rock Mech. Rock Eng. 2013, 46, 107–121. [Google Scholar] [CrossRef]
- Snow, D.T. Fracture deformation and changes of permeability and storage upon changes of fluid pressure. Q. Colo. Sch. Mines 1968, 63, 201–244. [Google Scholar]
- Walsh, J.B.; Brace, W.F. The effect of pressure on porosity and the transport properties of rock. J. Geophys. Res. Space Phys. 1984, 89, 9425–9431. [Google Scholar] [CrossRef]
- Walsh, J. Effect of pore pressure and confining pressure on fracture permeability. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1981, 18, 429–435. [Google Scholar] [CrossRef]
- Sigal, R.F. The pressure dependence of permeability. Petrophysics SPWLA J. Form. Eval. Reserv. Descr. 2002, 43, 92–102. [Google Scholar]
- Dvorkin, J.; Nur, A. Dynamic poroelasticity: A unified model with the squirt and the Biot mechanisms. Geophysics 1993, 58, 524–533. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Z.; Sun, Z.; An, S.; Zhang, W.; Liu, P.; Yao, J.; Ma, J. Research on Stress Sensitivity of Fractured Carbonate Reservoirs Based on CT Technology. Energies 2017, 10, 1833. [Google Scholar] [CrossRef]
- Kashnikov, Y.A.; Popov, S.N.; Gladyshev, S.V. Hydrodynamic modeling of development of turnejsko-famensky object of shershnevsky oil field with account for geomechanical effect of fracture deformation. In Geology, Geophysics and Development of Oil and Gas Fields; JSC “VNIIOENG”: Moscow, Russia, 2009; pp. 50–56. [Google Scholar]
- Kashnikov, Y.A.; Ashikhmin, S.G.; Obsharov, P.A. Experimental studies of the effect of long-acting high effective stresses on the filtration-capacitive characteristics of monolithic samples and samples with fractures. In Geology, Geophysics and Development of Oil and Gas Fields; JSC “VNIIOENG”: Moscow, Russia, 2008; pp. 51–54. [Google Scholar]
- Ashikhmin, S.G.; Kashnikov, Y.A.; Yakimov, S.Y. Experimental and theoretical research of change of collectors’ fracture permeability of Yurubcheno-Tokhomsky field. In Geology, Geophysics and Development of Oil and Gas Fields; JSC “VNIIOENG”: Moscow, Russia, 2013; pp. 36–41. [Google Scholar]
- Liu, H.-H.; Rutqvist, J.; Berryman, J.G. On the relationship between stress and elastic strain for porous and fractured rock. Int. J. Rock Mech. Min. Sci. 2009, 46, 289–296. [Google Scholar] [CrossRef]
- Zheng, J.; Zheng, L.; Liu, H.-H.; Ju, Y. Relationships between permeability, porosity and effective stress for low-permeability sedimentary rock. Int. J. Rock Mech. Min. Sci. 2015, 78, 304–318. [Google Scholar] [CrossRef]
- Morrow, C.A.; Shi, L.Q.; Byerlee, J.D. Permeability of fault gouge under confining pressure and shear stress. J. Geophys. Res. Solid Earth 1984, 89, 3193–3200. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, C.Y. Pore pressure generation in sedimentary basins: Overloading versus aquathermal. J. Geophys. Res. Solid Earth 1986, 91, 2153–2162. [Google Scholar] [CrossRef]
- Metwally, Y.M.; Sondergeld, C.H. Measuring low permeabilities of gas-sands and shales using a pressure transmission technique. Int. J. Rock Mech. Min. Sci. 2011, 48, 1135–1144. [Google Scholar] [CrossRef]
- Matthews, C.S.; Russell, D.G. Pressure Buildup and Flow Tests in Wells, Monograph Series, Society of Petroleum Engineers of AIME, Dallas (1967) 1. Available online: https://store.spe.org/Pressure-Buildup-and-Flow-Tests-in-Wells-P49.aspx (accessed on 1 March 2021).
- Mueller, T.D.; Witherspoon, P.A. Pressure Interference Effects within Reservoirs and Aquifers. J. Pet. Technol. 1965, 17, 471–474. [Google Scholar] [CrossRef]
- McKinley, R. Wellbore Transmissibility from Afterflow-Dominated Pressure Buildup Data. J. Pet. Technol. 1971, 23, 863–872. [Google Scholar] [CrossRef]
- Ramey, H.J., Jr.; Cobb, W.M. A General Buildup Theory for a Well in a Closed Drainage Area. J. Pet. Technol. 1971, 251, 1493–1505. [Google Scholar] [CrossRef]
- Dietz, D.N. Determination of Average Reservoir Pressure from Build-Up Surveys. J. Pet. Technol. 1965, 17, 955–959. [Google Scholar] [CrossRef]

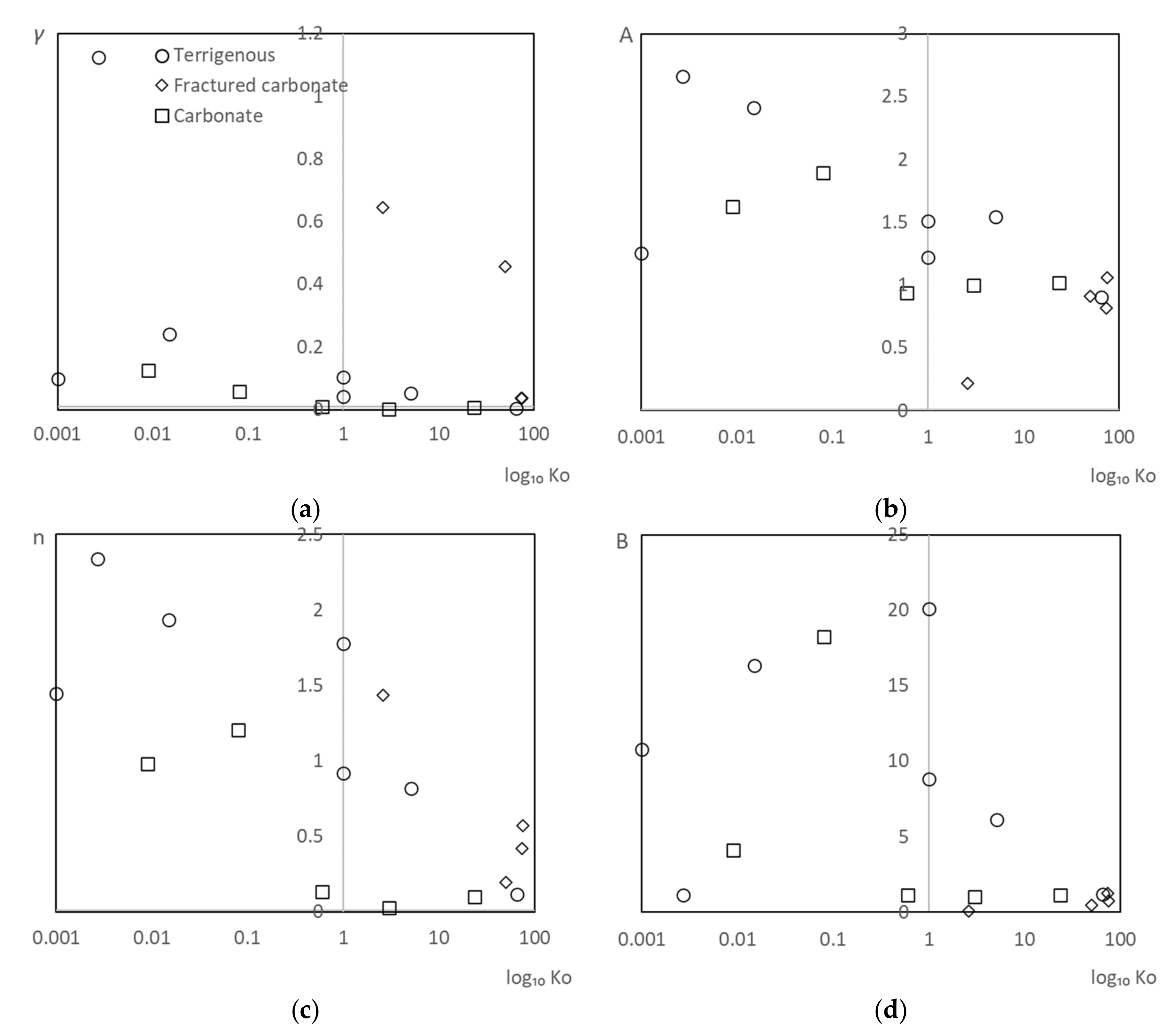

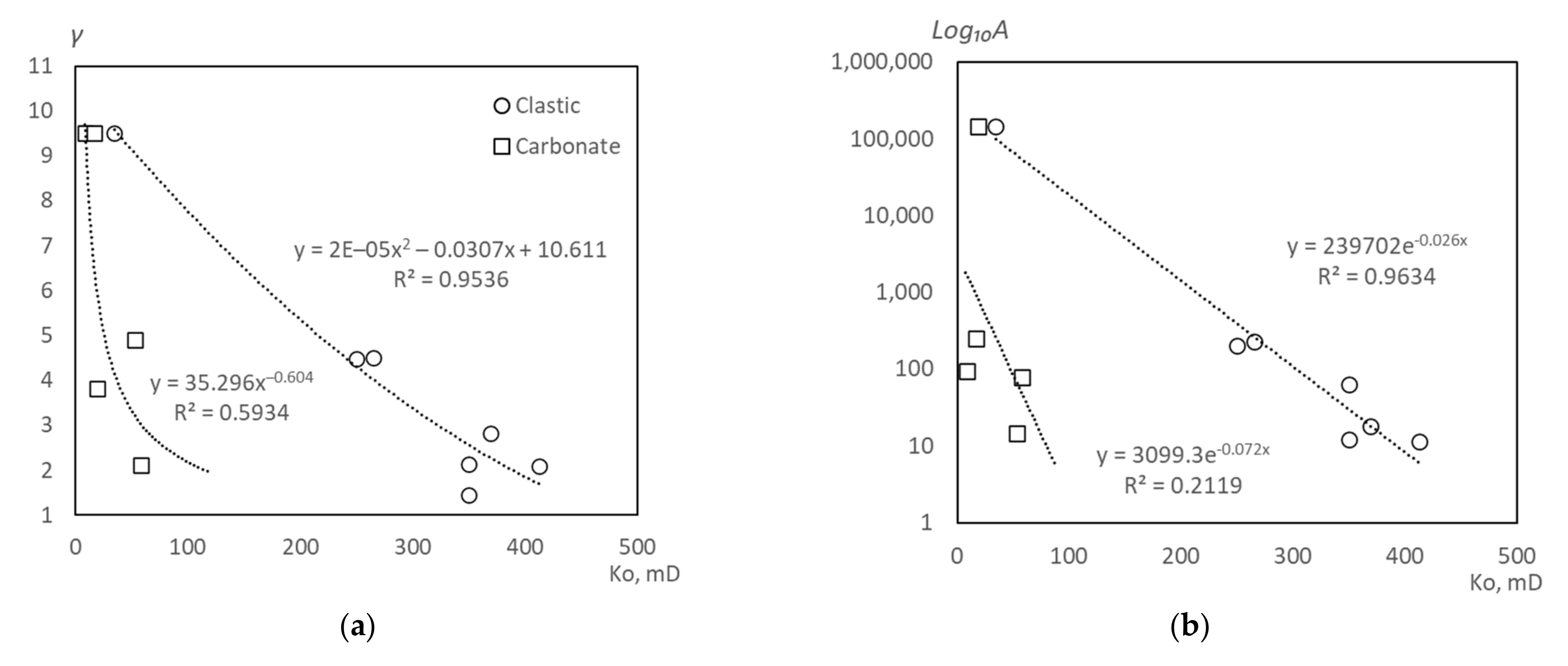
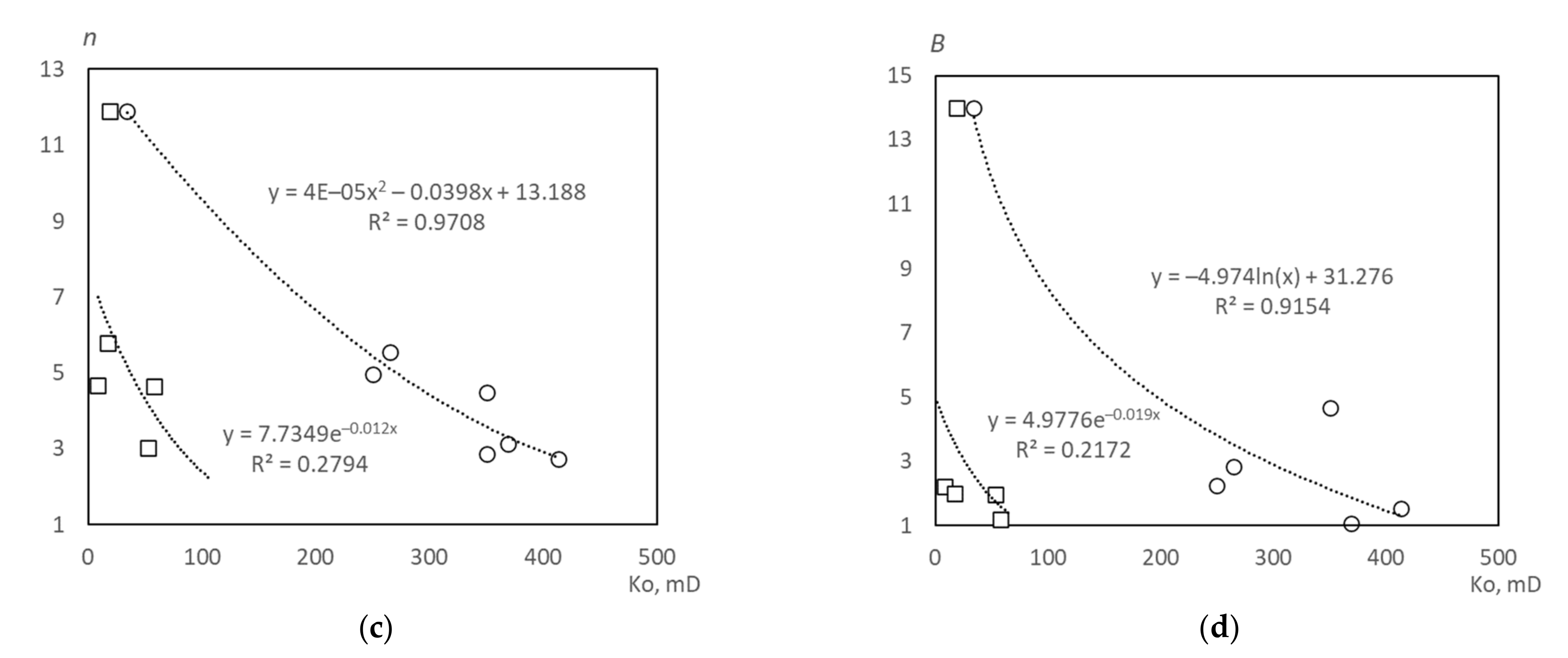
| Rock, Field, Source | Ko, mD | H, m | Exponential Law | Power Law | ||||
|---|---|---|---|---|---|---|---|---|
| γ | A | R2 | n | B | R2 | |||
| Limestone, Anstrude [58] | 0.6 | 40 | 0.009 | 0.940 | 0.84 | 0.136 | 1.119 | 0.98 |
| Fractured limestone, Tarim Basin [86] | 2.6 | 2000 | 0.645 | 0.218 | 0.52 | 1.434 | 0.053 | 0.81 |
| Limestone, Xuzhou [79] | 0.009 | 220 | 0.126 | 1.627 | 0.89 | 0.979 | 4.139 | 0.83 |
| Limestone, China [35] | 0.08 | 70 | 0.059 | 1.895 | 0.94 | 1.206 | 18.241 | 0.85 |
| Sandstone, Xuzhou [79] | 0.015 | 220 | 0.242 | 2.414 | 0.92 | 1.937 | 16.366 | 0.91 |
| Sandstone, E-bei [16] | 1 | 2760 | 0.104 | 1.218 | 0.98 | 1.778 | 20.078 | 0.92 |
| Sandstone, Gulf of Mexico II [84] | 5.1 | 2500 | 0.052 | 1.540 | 0.99 | 0.816 | 6.116 | 0.97 |
| Limestone, Astrakhanskoe [88] | 3 | 4000 | 0.002 | 0.997 | 0.98 | 0.026 | 1.028 | 0.89 |
| Limestone, Shershnevskoe [87] | 23.62 | 2100 | 0.008 | 1.019 | 0.99 | 0.098 | 1.118 | 0.83 |
| Mudstone, Yingcheng [37] | 1 | 220 | 0.041 | 1.507 | 0.94 | 0.917 | 8.829 | 0.88 |
| Fractured limestone, Yurubcheno-Tokhomskoe [89] | 50 | 2047 | 0.457 | 0.911 | 0.98 | 0.197 | 0.475 | 0.78 |
| Fractured limestone, Shershnevskoe [87] | 73.6 | 2100 | 0.036 | 0.813 | 0.93 | 0.419 | 1.227 | 0.94 |
| Fractured limestone, Astrakhanskoe [88] | 75.4 | 4000 | 0.036 | 1.059 | 0.97 | 0.573 | 0.737 | 0.73 |
| Sandstone, TCDP [72] | 65 | 900 | 0.003 | 0.906 | 0.85 | 0.117 | 1.195 | 0.99 |
| Shale, Wilcox, [70] | 0.0027 | 4000 | 1.125 | 2.663 | 0.90 | 2.337 | 1.132 | 0.91 |
| Shale, Devon [85] | 0.001 | 1600 | 0.099 | 1.251 | 0.95 | 1.448 | 10.813 | 0.99 |
| Type of Rock, Field (Layer) | Ko, mD | H, m | Exponential Law | Power Law | ||||
|---|---|---|---|---|---|---|---|---|
| γ | A | R2 | n | B | R2 | |||
| Terrigenous, Arkhangelskogo (C1bb) | 369 | 2280 | 17.97 | 2.83 | 0.70 | 1.07 | 3.14 | 0.69 |
| Terrigenous, Sibirskoe (C1bb) | 250 | 2250 | 199.49 | 4.48 | 0.75 | 2.26 | 4.97 | 0.74 |
| Terrigenous, Unvinskoe (C1bb) | 413 | 2230 | 11.25 | 2.08 | 0.54 | 1.52 | 2.74 | 0.54 |
| Terrigenous, Chashkinskoe (C1bb) | 265 | 2050 | 228.02 | 4.49 | 0.66 | 2.82 | 5.55 | 0.65 |
| Terrigenous, Yurchukskoe (C1bb) | 350 | 1900 | 62.62 | 2.14 | 0.69 | 2.1 | 4.49 | 0.68 |
| Terrigenous, well 742, Yurchukskoe (C1bb) | 350 | 2030 | 11.98 | 1.45 | 0.77 | 4.66 | 2.87 | 0.77 |
| Carbonate, Unvinskoe (C1t-D3fm) | 34.2 | 2200 | 145,588 | 9.51 | 0.72 | 14.01 | 11.88 | 0.73 |
| Carbonate, Arkhangelskogo (C1t-D3fm) | 8.5 | 2230 | 93.19 | 3.82 | 0.66 | 2.22 | 4.67 | 0.75 |
| Carbonate, Sibirskoe (C1t-D3fm) | 19 | 2400 | 145,588.45 | 9.51 | 0.73 | 14.01 | 11.88 | 0.73 |
| Carbonate, Sibirskoe (C1b) | 16.9 | 2100 | 254.26 | 4.89 | 0.58 | 2.01 | 5.78 | 0.58 |
| Carbonate, Chashkinskoe (C1t-D3fm) | 53 | 2120 | 14.71 | 2.11 | 0.63 | 1.98 | 3.02 | 0.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kozhevnikov, E.V.; Turbakov, M.S.; Riabokon, E.P.; Poplygin, V.V. Effect of Effective Pressure on the Permeability of Rocks Based on Well Testing Results. Energies 2021, 14, 2306. https://doi.org/10.3390/en14082306
Kozhevnikov EV, Turbakov MS, Riabokon EP, Poplygin VV. Effect of Effective Pressure on the Permeability of Rocks Based on Well Testing Results. Energies. 2021; 14(8):2306. https://doi.org/10.3390/en14082306
Chicago/Turabian StyleKozhevnikov, Evgenii Vasilevich, Mikhail Sergeevich Turbakov, Evgenii Pavlovich Riabokon, and Vladimir Valerevich Poplygin. 2021. "Effect of Effective Pressure on the Permeability of Rocks Based on Well Testing Results" Energies 14, no. 8: 2306. https://doi.org/10.3390/en14082306
APA StyleKozhevnikov, E. V., Turbakov, M. S., Riabokon, E. P., & Poplygin, V. V. (2021). Effect of Effective Pressure on the Permeability of Rocks Based on Well Testing Results. Energies, 14(8), 2306. https://doi.org/10.3390/en14082306






