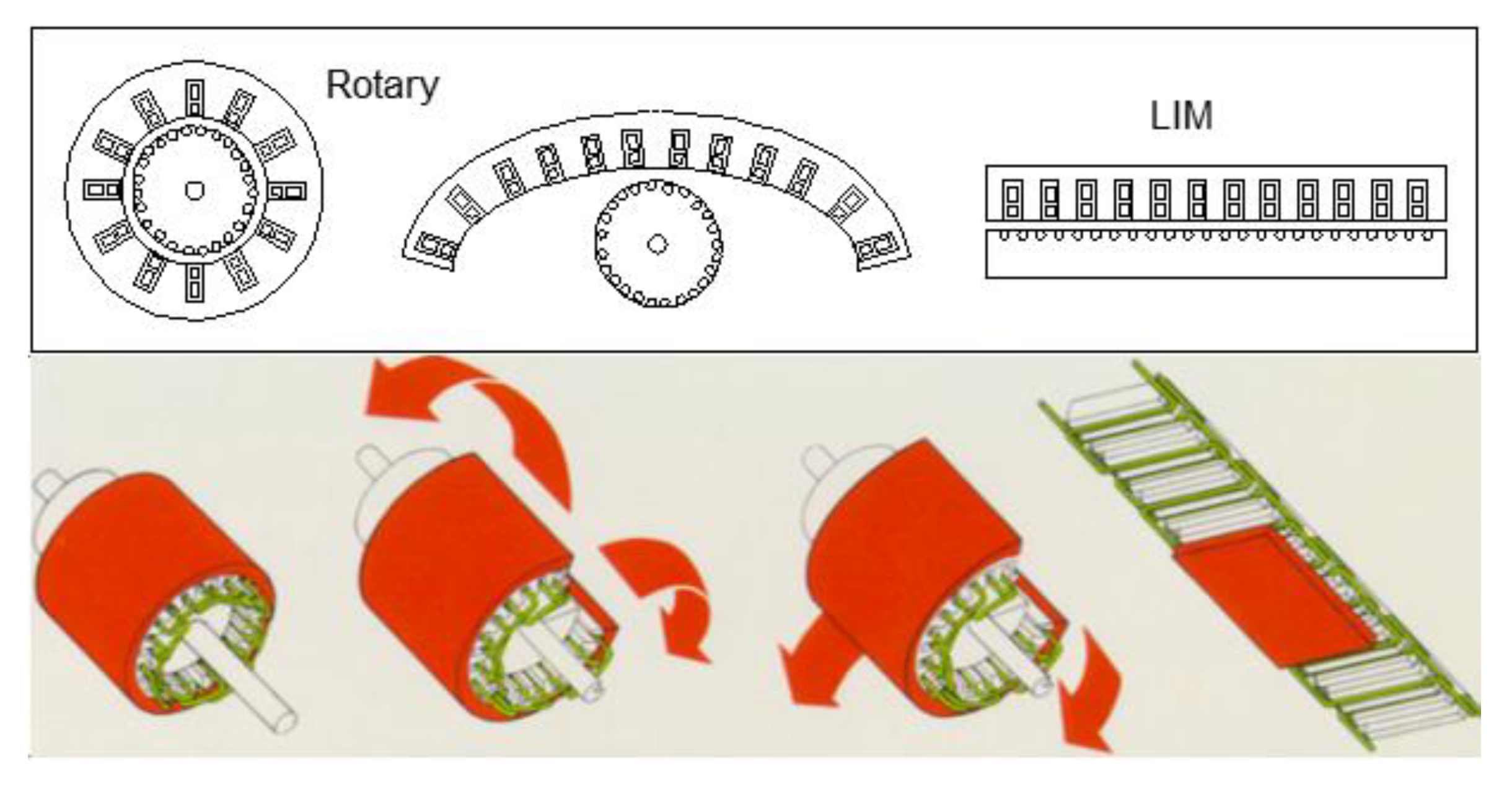
Linear Induction Motors in Transportation Systems
Abstract
1. Introduction
2. Overview of Linear Transportation Systems
2.1. Levitated LTS
2.2. Non-Levitated LTS
2.3. LTS with Synchronous Motors
2.4. LTS with Induction Motors
2.5. LTS with Superconducting Induction Motors
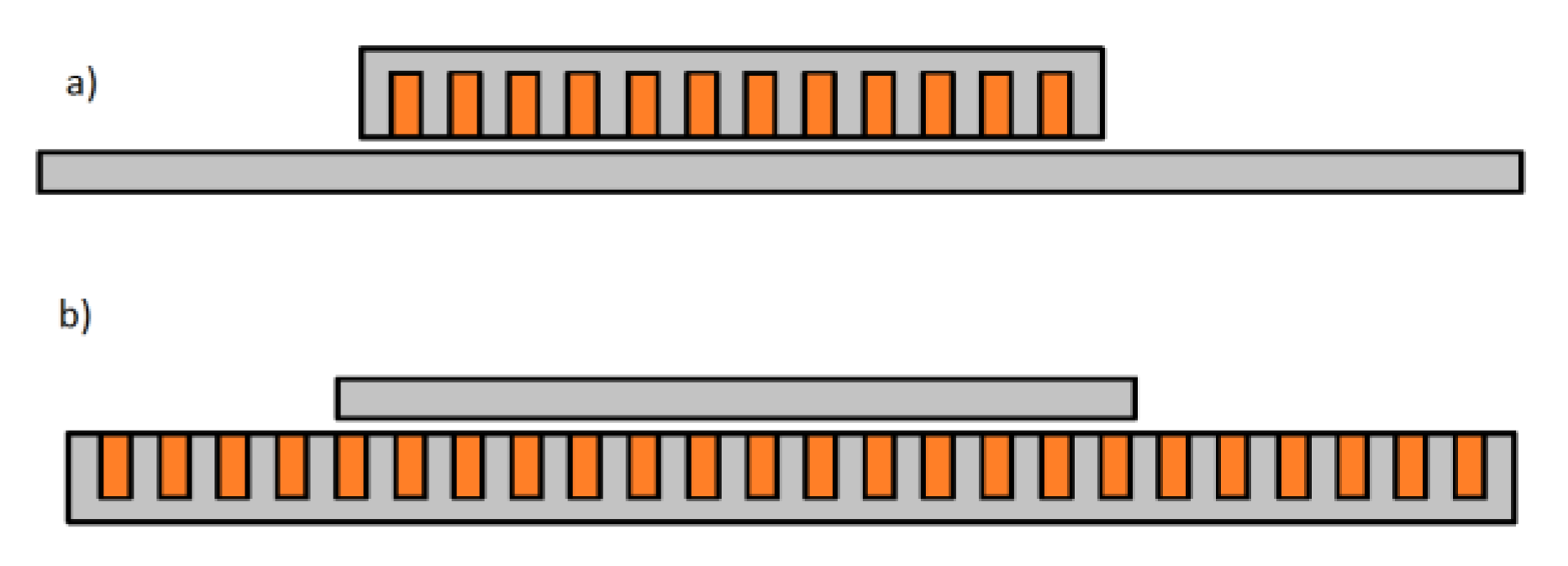
3. Linear Transportation Systems Using Induction Motors
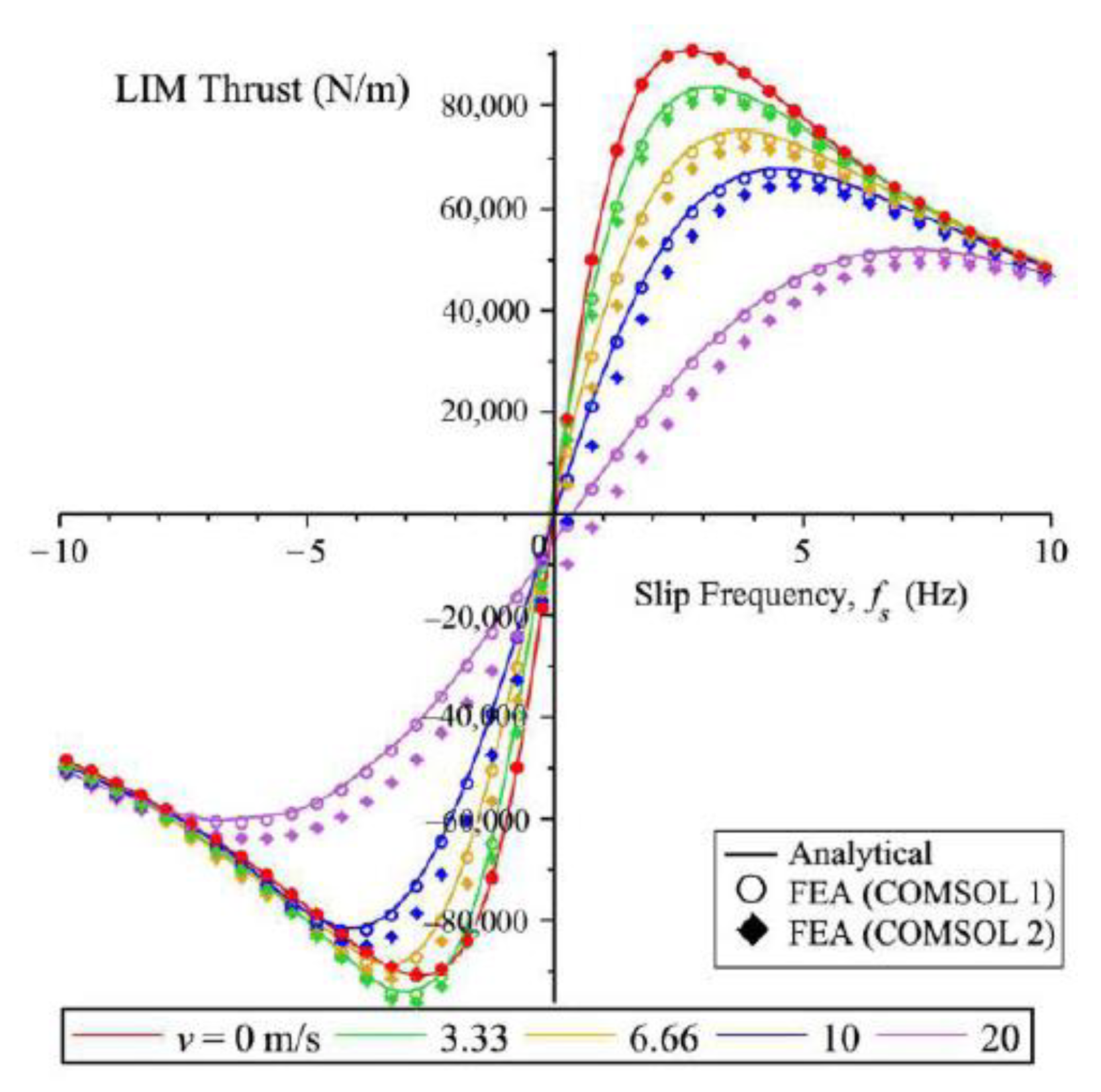
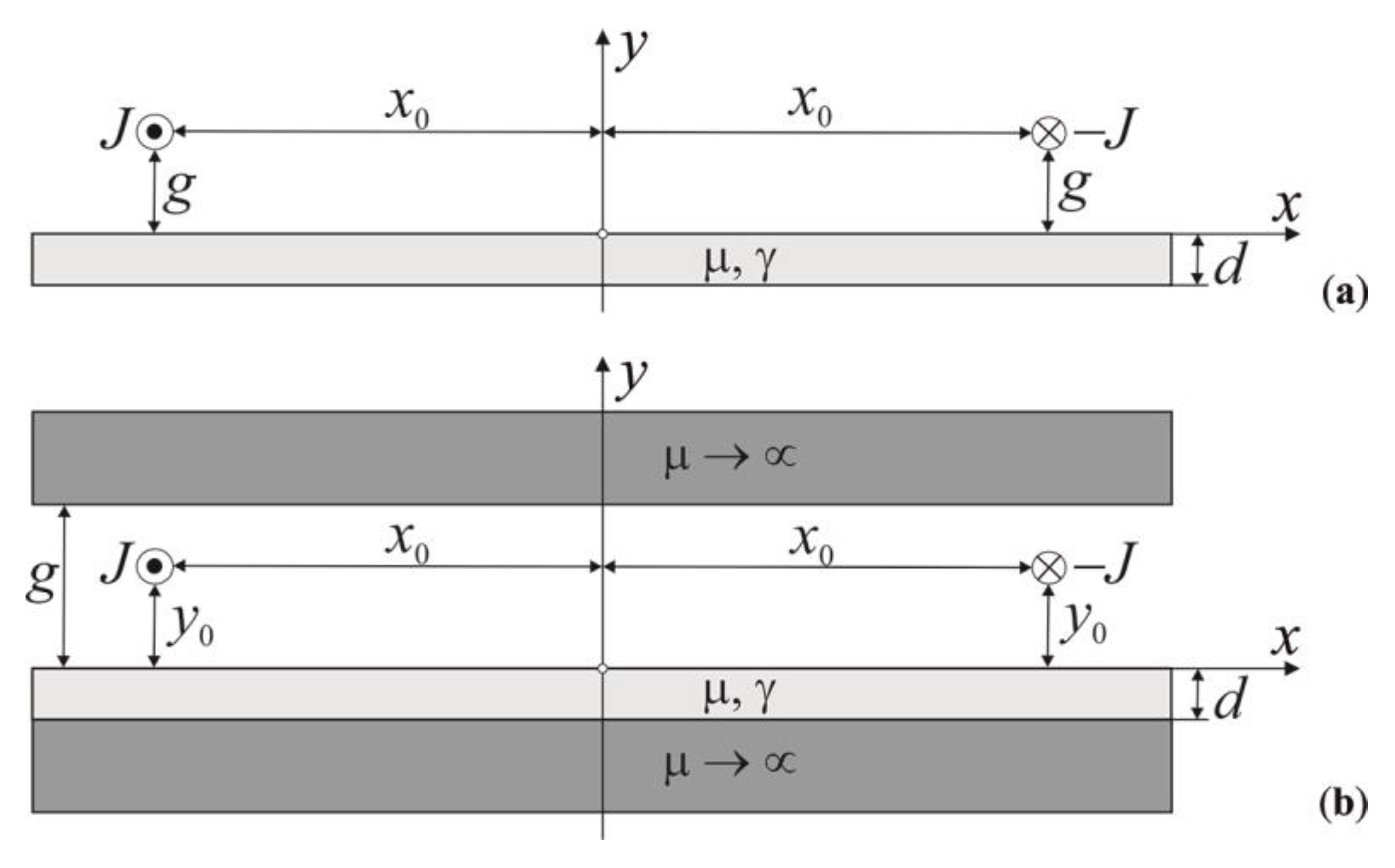
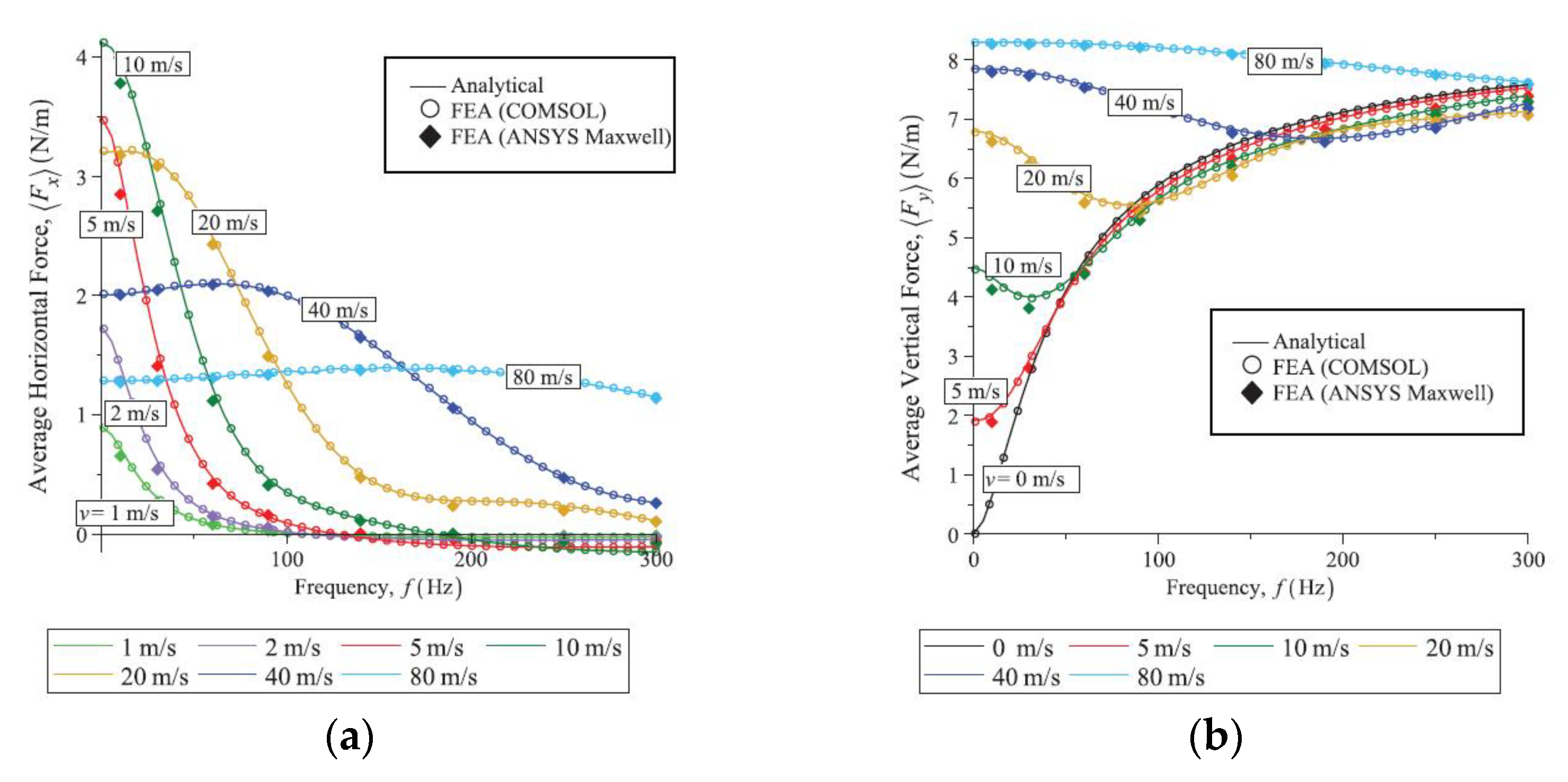
3.1. Analytical Solutions Applied for the LIM Evaluation
- A 2D analysis can be used;
- The iron magnetization curve is linear;
- The conductivity of the reaction rail is constant;
- Motion in the x-direction only is allowed.
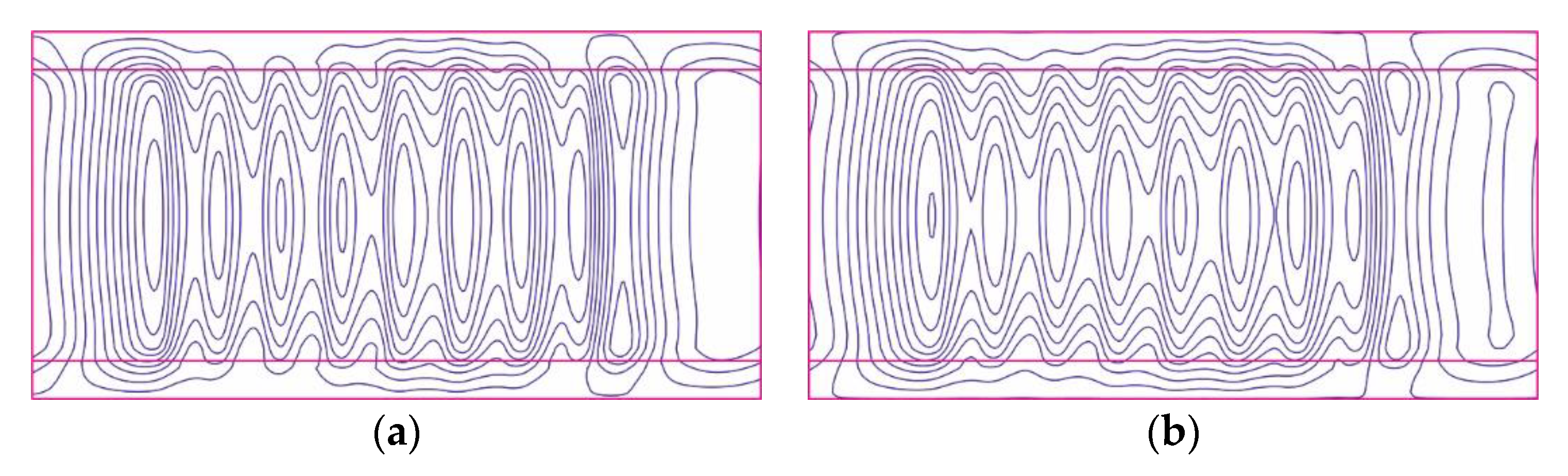
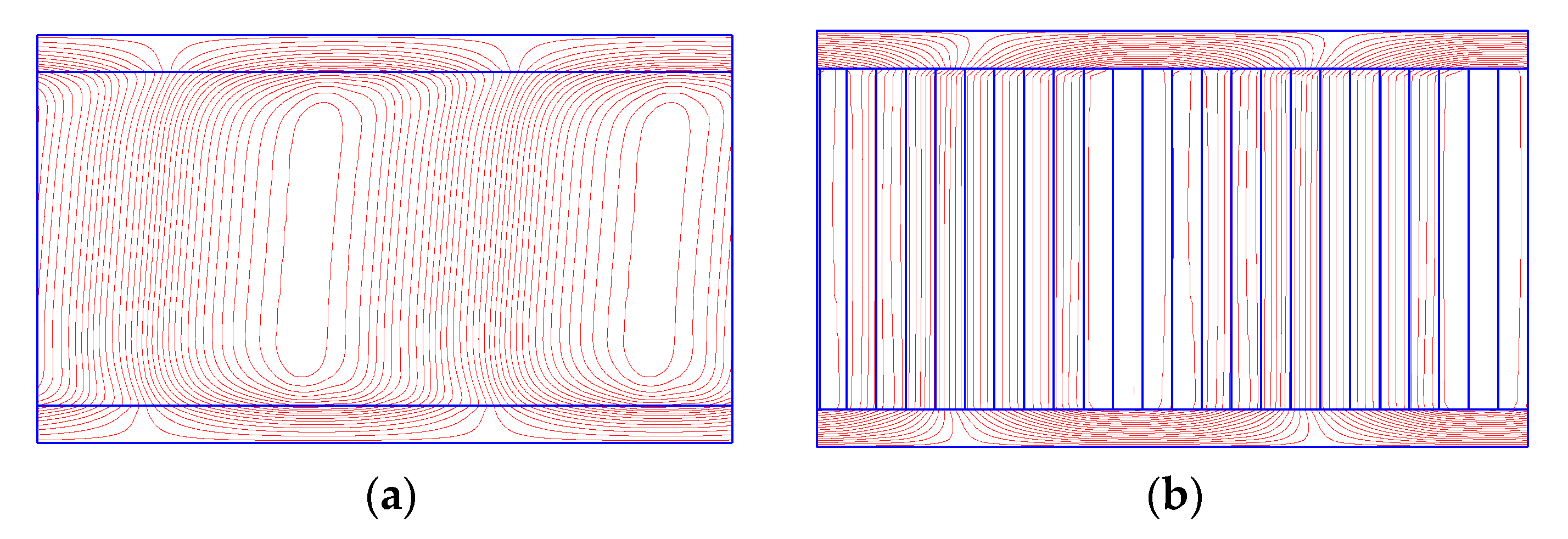
3.2. FE Methods Applied for Linear Induction Motors
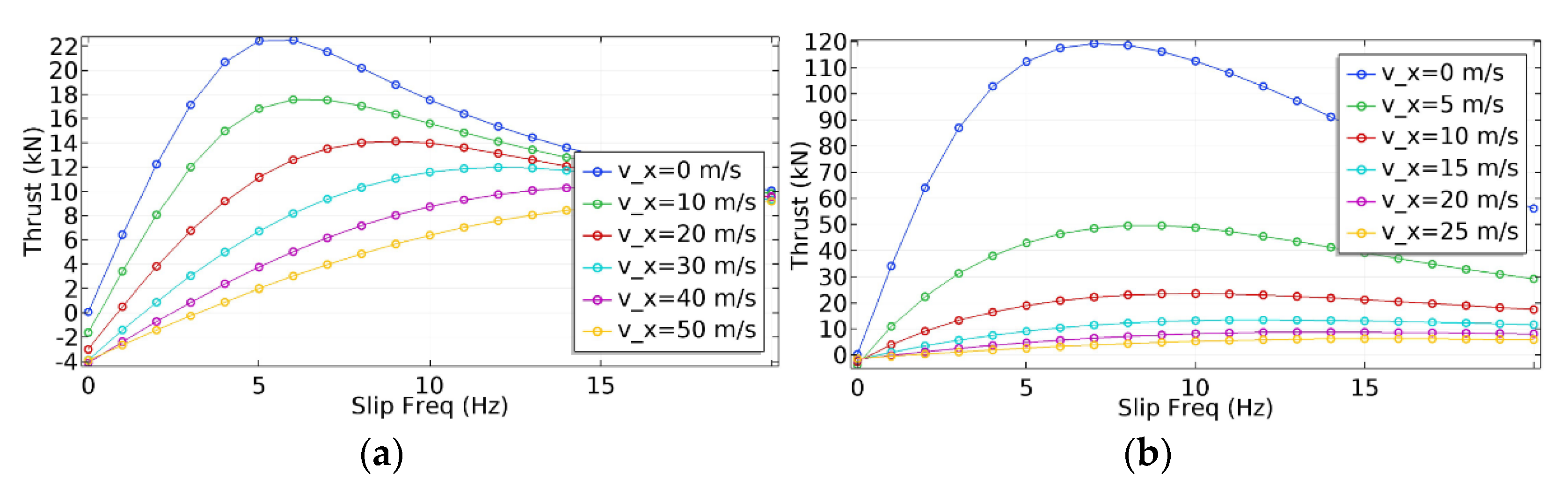
4. Selected Problems of LIM Applications
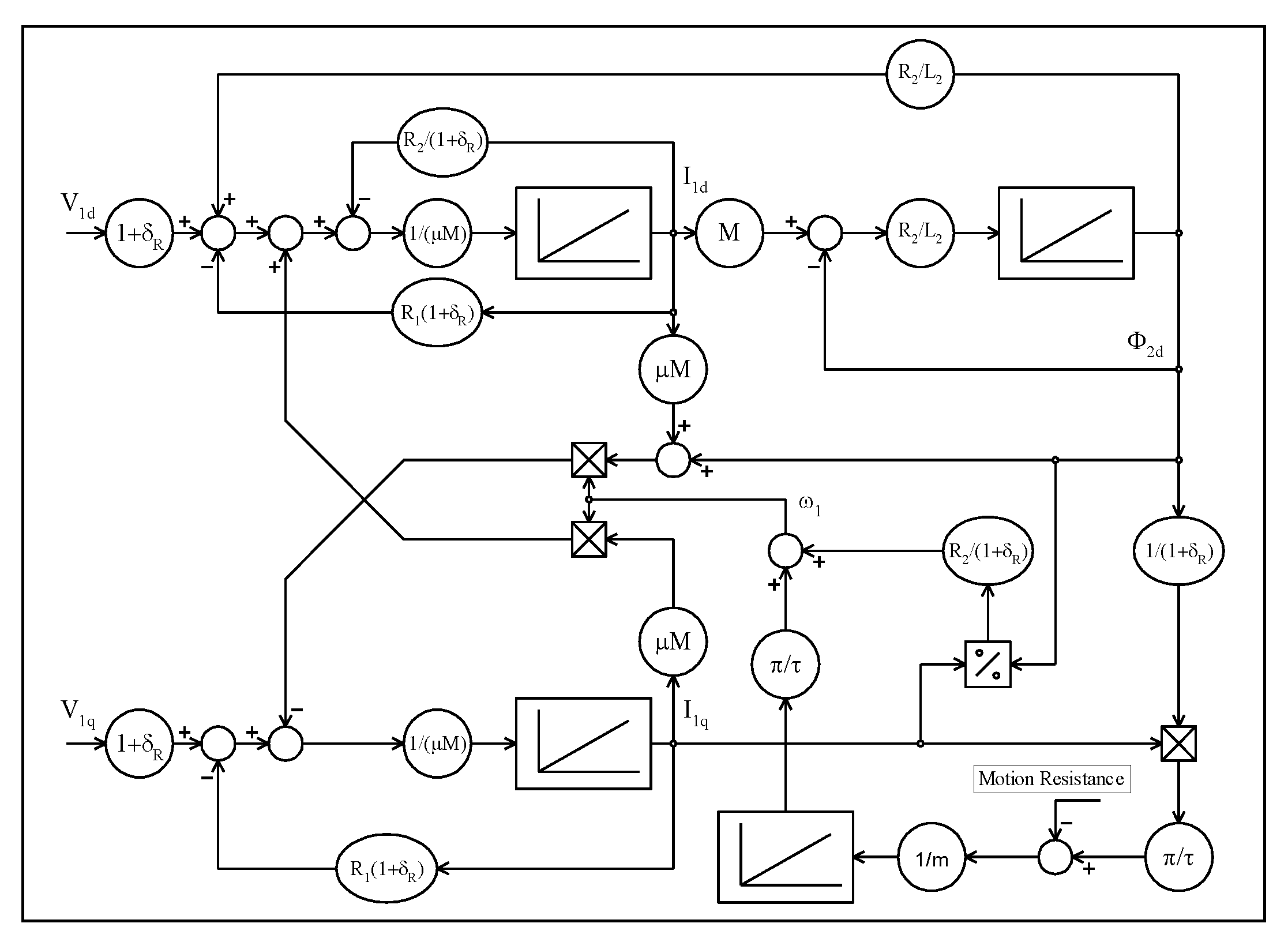
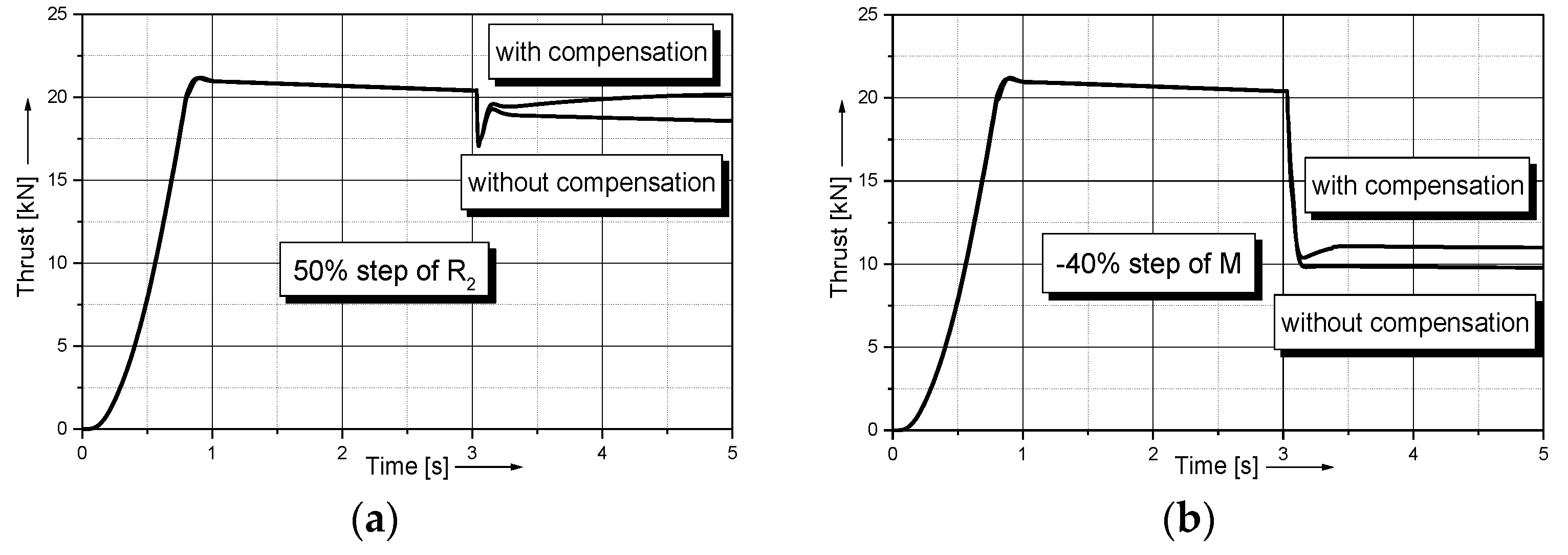
4.1. LIM Performance Control; Adaptive Control
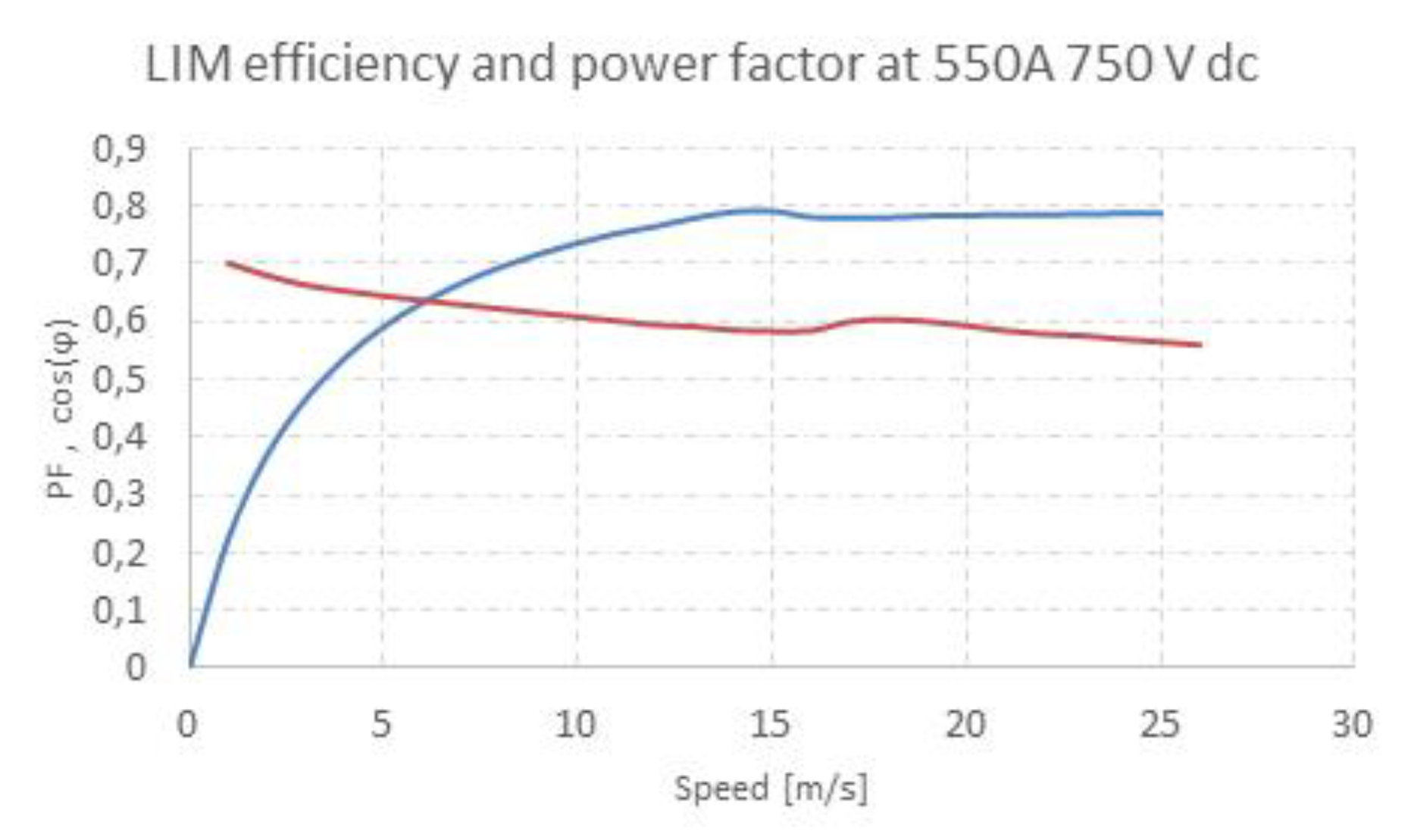
4.2. LIM Driven from the Voltage Inverter
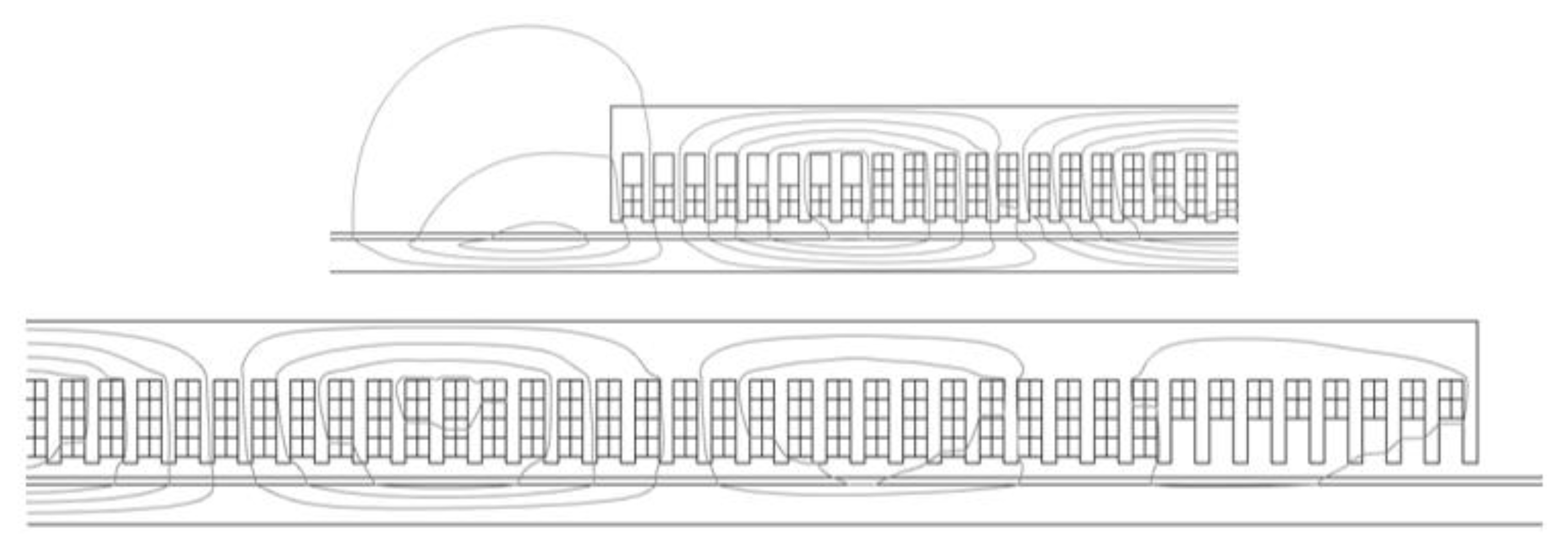
4.3. Losses in the Reaction Rail
4.4. Real-Time Temperature Rise Prediction of a Traction LIM
4.5. Superconductig LIM
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hellinger, R.; Mnich, P. Linear motor-powered transportation: History, present status, and future outlook. Proc. IEEE 2009, 97, 1892–1900. [Google Scholar] [CrossRef]
- Woronowicz, K.; Safaee, A. A novel linear induction motor equivalent-circuit with optimized end effect model. Can. J. Electr. Comput. Eng. 2014, 37, 34–41. [Google Scholar] [CrossRef]
- Woronowicz, K. Urban Mass Transit Systems: Current Status and Future Trends. In Proceedings of the ITEC 2014, Cologne, Germany, 13 August 2014. [Google Scholar]
- Byers, D.C. The Linear Induction Motor in Transit, a System View. In Proceedings of the 5th International Conference on Automated People Movers, Paris, France, 10–14 June 1996. [Google Scholar]
- Earnshaw, S. On the Nature of the Molecular Forces which regulate the Constitution of the Luminiferous Ether. Trans. Camb. Philos. Soc. 1842, 7, 97–112. [Google Scholar]
- Weh, H.; Steingröver, A.; Hupe, H. Design and Simulation of a Controlled Permanent Magnet. Int. J. Appl. Electromagn. Mater. 1992, 3, 199–203. [Google Scholar]
- Palka, R. Synthesis of magnetic fields by optimization of the shape of areas and source distributions. Electr. Eng. 1991, 75, 1–7. [Google Scholar] [CrossRef]
- Sikora, R.; Palka, R. Synthesis of Magnetic-Fields. IEEE Trans. Magn. 1982, 18, 385–390. [Google Scholar] [CrossRef]
- Braunbeck, W. Freely Suspended Bodies in Electric and Magnetic Fields. Z. Phys. 1938, 112, 753–763. [Google Scholar]
- May, H.; Palka, R.; Portabella, E.; Canders, W.-R. Evaluation of the magnetic field – high temperature superconductor interactions. Int. J. Comput. Math. Electr. Electron. Eng. 2004, 23, 286–304. [Google Scholar] [CrossRef]
- Patel, A.; Hopkins, S.; Giunchi, G.; Figini Albisetti, A.; Shi, Y.; Palka, R.; Cardwell, D.; Glowacki, B. The Use of an MgB2 Hollow Cylinder and Pulse Magnetized (RE)BCO Bulk for Magnetic Levitation Applications. IEEE Trans. Appl. Supercond. 2013, 23, 6800604. [Google Scholar] [CrossRef]
- Masada, E. Development of Maglev and Linear Drive Technology for Transportation in Japan. In Proceedings of the MAGLEV’95, Bremen, Germany, 26–29 November 1995; ISBN 3-8007-2155-4. [Google Scholar]
- Ji, W.; Jeong, G.; Park, C.; Jo, I.; Lee, H. A Study of Non-Symmetric Double-Sided Linear Induction Motor for Hyperloop All-In-One System (Propulsion, Levitation, and Guidance). IEEE Trans. Magn. 2018, 54, 1–4. [Google Scholar] [CrossRef]
- Ma, G.; Wang, Z.; Liu, K.; Qian, H.; Wang, C. Potentials of an Integrated Levitation, Guidance, and Propulsion System by a Superconducting Transverse Flux Linear Motor. IEEE Trans. Ind. Electron. 2018, 65, 7548–7557. [Google Scholar] [CrossRef]
- Lee, C.Y.; Jo, J.M.; Han, Y.J.; Bae, D.K.; Yoon, Y.S.; Choi, S.; Park, D.K.; Ko, T.K. Estimation of Current Decay Performance of HTS Electromagnet for Maglev. IEEE Trans. Appl. Supercond. 2010, 20, 907–910. [Google Scholar]
- Woronowicz, K. Linear motor drives and applications in rapid transit systems. In Proceedings of the Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 15–18 June 2014. [Google Scholar]
- Nasar, S.A.; Boldea, I. Linear Motion Electric Machines; John Wiley & Sons: New York, NY, USA, 1976. [Google Scholar]
- Cao, R.; Lu, M.; Jiang, N.; Cheng, M. Comparison between Linear Induction Motor and Linear Flux-Switching Permanent-Magnet Motor for Railway Transportation. IEEE Trans. Ind. Electron. 2019, 66, 9394–9405. [Google Scholar] [CrossRef]
- Weh, H. Linear Electromagnetic Drives in Traffic Systems and Industry. In Proceedings of the LDIA’95, Nagasaki, Japan, 31 May–2 June 1995. [Google Scholar]
- Cao, R.; Lu, M. Investigation of High Temperature Superconducting Linear Flux-Switching Motors With Different Secondary Structures. IEEE Trans. Appl. Supercond. 2020, 30, 1–5. [Google Scholar] [CrossRef]
- Ma, G.; Gong, T.; Zhang, H.; Wang, Z.; Li, X.; Yang, C.; Liu, K.; Zhang, W. Experiment and Simulation of REBCO Conductor Coils for an HTS Linear Synchronous Motor. IEEE Trans. Appl. Supercond. 2017, 27, 1–5. [Google Scholar] [CrossRef]
- Liu, B.; Badcock, R.; Shu, H.; Fang, J. A Superconducting Induction Motor with a High Temperature Superconducting Armature: Electromagnetic Theory, Design and Analysis. Energies 2018, 11, 792. [Google Scholar] [CrossRef]
- Liu, J.; Ma, H.; Cheng, J. Research on Superconducting Induction Maglev Linear Machine for Electromagnetic Launch Application. IEEE Trans. Plasma Sci. 2017, 45, 1644–1650. [Google Scholar] [CrossRef]
- Sotelo, G.G.; Sass, F.; Carrera, M.; Lopez-Lopez, J.; Granados, X. Proposal of a Novel Design for Linear Superconducting Motor Using 2G Tape Stacks. IEEE Trans. Ind. Electron. 2018, 65, 7477–7484. [Google Scholar] [CrossRef]
- Chen, X.; Zheng, S.; Li, J.; Ma, G.T.; Yen, F. A linear induction motor with a coated conductor superconducting secondary. Phys. C Supercond. Appl. 2018, 550, 82–84. [Google Scholar] [CrossRef]
- Palka, R.; Woronowicz, K.; Kotwas, J. Analysis of the Performance of Superconducting Linear Induction Motors. In Proceedings of the CEFC 2020, Pisa, Italy, 16–19 November 2020. [Google Scholar]
- Kircher, R.; Klühspies, J.; Palka, R.; Fritz, E.; Eiler, K.; Witt, M. Electromagnetic Fields Related to High Speed Transportation Systems. Transp. Syst. Technol. 2018, 4, 152–166. [Google Scholar] [CrossRef]
- Woronowicz, K.; Safaee, A. A novel linear induction motor equivalent-circuit with optimized end-effect model including partially-filled end slots. In Proceedings of the Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 15–18 June 2014. [Google Scholar]
- Woronowicz, K.; Palka, R. Optimised Thrust Control of Linear Induction Motors by a Compensation Approach. Int. J. Appl. Electromagn. Mech. 2004, 19, 533–536. [Google Scholar] [CrossRef]
- Woronowicz, K.; Palka, R. An advanced linear induction motor control approach using the compensation of its parameters. In Electromagnetic Fields in Electrical Engineering; IOS Press: Amsterdam, The Netherlands, 2002; pp. 335–338. [Google Scholar]
- Gieras, J.; Dawson, G.; Eastham, A. Performance calculation for single-sided linear induction motors with a double-layer reaction rail under constant current excitation. IEEE Trans. Magn. 1986, 22, 54–62. [Google Scholar] [CrossRef]
- Mendrela, E.A.; Gierczak, E. Two-dimensional analysis of linear induction motor using Fourier’s series method. Electr. Eng. 1982, 65, 97–106. [Google Scholar] [CrossRef]
- Nasar, S.A.; del Cid, L. Certain approaches to the analysis of single-sided linear induction motors. Proc. Inst. Electr. Eng. 1973, 120, 477–483. [Google Scholar] [CrossRef]
- Freeman, E.M.; Lowther, D.A. Normal force in single-sided linear induction motors. Proc. Inst. Electr. Eng. 1973, 120, 1499–1506. [Google Scholar] [CrossRef]
- Yamamura, S. Theory of Linear Induction Motors, 2nd ed.; Halster Press: New York, NY, USA, 1979. [Google Scholar]
- Borcherts, R.H.; Reitz, J.R. High-speed transportation via magnetically supported vehicles: A study of the magnetic forces. Transp. Res. 1971, 5, 197–209. [Google Scholar] [CrossRef]
- Fink, H.J. Instability of vehicles levitated by eddy current repulsion-case of an infinitely long current loop. J. Appl. Phys. 1971, 42, 3446. [Google Scholar] [CrossRef]
- Reitz, J.R. Force on a rectangular coil moving above a conducting slab. J. Appl. Phys. 1972, 43, 1547. [Google Scholar] [CrossRef]
- Langerholc, J. Torques and forces on a moving coil due to eddy currents. J. Appl. Phys. 1973, 44, 1587. [Google Scholar] [CrossRef]
- Lee, S.-W.; Menendez, R. Force on current coils moving over a conducting sheet with application to magnetic levitation. Proc. IEEE 1974, 62, 567–577. [Google Scholar]
- Tegopoulos, J.A.; Kriezis, E.E. Eddy Currents in Linear Conducting Media; Elsevier Science: New York, NY, USA, 1985. [Google Scholar]
- Adamiak, K. A method of optimization of winding in linear induction motor. Electr. Eng. 1986, 69, 83–91. [Google Scholar] [CrossRef]
- Kim, D.-K.; Kwon, B.-I. A novel equivalent circuit model of the linear induction motor based on finite element analysis and its coupling with external circuits. IEEE Trans. Magn. 2006, 42, 3407–3409. [Google Scholar] [CrossRef]
- Gieras, J.F.; Dawson, G.E.; Easthan, A.R. A new longitudinal end effect factor for linear induction motor. IEEE Trans. Energy Convers. 1987, 2, 152–159. [Google Scholar] [CrossRef]
- Satvati, M.R.; Vaez-Zadeh, S. End-effect compensation in linear induction motor drives. J. Power Electron. 2011, 11, 697–703. [Google Scholar] [CrossRef]
- Duncan, J. Linear induction motor—Equivalent-circuit model. IEEE Proc. B Electr. Power Appl. 1983, 130, 51–57. [Google Scholar] [CrossRef]
- Xu, W.; Zhu, J.G.; Zhang, Y.; Li, Y.; Wang, Y.; Guo, Y. An Improved Equivalent Circuit Model of a Single-Sided Linear Induction Motor. IEEE Trans. Veh. Technol. 2010, 59, 2277–2289. [Google Scholar] [CrossRef]
- Xu, W.; Zhu, J.G.; Zhang, Y.; Li, Z.; Li, Y.; Wang, Y.; Guo, Y.; Li, Y. Equivalent Circuits for Single-Sided Linear Induction Motors. IEEE Trans. Ind. Appl. 2010, 46, 2410–2423. [Google Scholar] [CrossRef]
- Lv, G.; Zeng, D.; Zhou, T. An Advanced Equivalent Circuit Model for Linear Induction Motors. IEEE Trans. Ind. Electron. 2018, 65, 7495–7503. [Google Scholar] [CrossRef]
- Zeng, D.; Lv, G.; Zhou, T. Equivalent circuits for single-sided linear induction motors with asymmetric cap secondary for linear transit. IEEE Trans. Energy Convers. 2018, 33, 1729–1738. [Google Scholar] [CrossRef]
- Dmitrievskii, V.; Goman, V.; Sarapulov, F.; Prakht, V.; Sarapulov, S. Choice of a numerical differentiation formula in detailed equivalent circuits models of linear induction motors. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Capri, Italy, 22–24 June 2016; pp. 458–463. [Google Scholar]
- Zare-Bazghaleh, A.; Naghashan, M.; Khodadoost, A. Derivation of Equivalent Circuit Parameters for Single-Sided Linear Induction Motors. IEEE Trans. Plasma Sci. 2015, 43, 3637–3644. [Google Scholar] [CrossRef]
- Sung, J.-H.; Nam, K. A new approach to vector control for a linear induction motor considering end effects. In Proceedings of the IEEE Industry Applications Society, Thirty-Fourth IAS Annual Meeting, Phoenix, AZ, USA, 3–7 October 1999; Volume 4, pp. 2284–2289. [Google Scholar]
- Huang, C.-I.; Hsu, K.-C.; Chiang, H.-H.; Kou, K.-Y.; Lee, T.-T. Adaptive fuzzy sliding mode control of linear induction motors with unknown end effect consideration. In Proceedings of the International Conference on Advanced Mechatronic Systems, Tokyo, Japan, 18–21 September 2012; pp. 626–631. [Google Scholar]
- Shiri, A.; Shoulaie, A. Design optimization and analysis of single-sided linear induction motor, considering all phenomena. IEEE Trans. Energy Convers. 2012, 27, 516–525. [Google Scholar] [CrossRef]
- Pucci, M. Direct field oriented control of linear induction motors. Electr. Power Syst. Res. 2012, 89, 11–22. [Google Scholar] [CrossRef]
- Shiri, A.; Shoulaie, A. End effect braking force reduction in high-speed single-sided linear induction machine. Energy Convers. Manag. 2012, 61, 43–50. [Google Scholar] [CrossRef]
- Kang, G.; Nam, K. Field-oriented control scheme for linear induction motor with the end effect. IET Electr. Power Appl. 2005, 152, 1565–1572. [Google Scholar] [CrossRef]
- Accetta, A.; Cirrincione, M.; Pucci, M.; Vitale, G. MRAS speed observer for high performance linear induction motor drives based on linear neural networks. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 1765–1772. [Google Scholar]
- Mirsalim, M.; Doroudi, A.; Moghani, J.S. Obtaining the operating characteristics of linear induction motors: A new approach. IEEE Trans. Magn. 2002, 38, 1365–1370. [Google Scholar] [CrossRef]
- Abdelqader, M.; Morelli, J.; Palka, R.; Woronowicz, K. 2-D quasi-static solution of a coil in relative motion to a conducting plate. Int. J. Comput. Math. Electr. Electron. Eng. 2017, 36, 980–990. [Google Scholar] [CrossRef]
- Woronowicz, K.; Abdelqader, M.; Palka, R.; Morelli, J. 2-D quasi-static Fourier series solution for a linear induction motor. Int. J. Comput. Math. Electr. Electron. Eng. 2018, 37, 1099–1109. [Google Scholar] [CrossRef]
- Freeman, E.M.; Papageorgiou, C.D. Spatial Fourier transforms: A new view of end effects in linear induction motors. Proc. Inst. Electr. Eng. 1978, 125, 747–7753. [Google Scholar] [CrossRef]
- Paudel, N.; Bird, J.Z. General 2-D steady-state force and power equations for a traveling time-varying magnetic source above a conductive plate. IEEE Trans. Magn. 2012, 48, 95–100. [Google Scholar] [CrossRef]
- Lee, S.; Lee, H.; Ham, S.; Jin, C.; Park, H.; Lee, J. Influence of the construction of secondary reaction plate on the transverse edge effect in linear induction motor. IEEE Trans. Magn. 2009, 45, 2815–2818. [Google Scholar]
- Singh, M.; Khajuria, S.; Marwaha, S. Thrust analysis and improvement of single sided linear induction motor using finite element technique. Int. J. Curr. Eng. Technol. 2013, 3, 563–566. [Google Scholar]
- Jeong, J.; Lim, J.; Park, D.; Choi, J.; Jang, S. Characteristic analysis of a linear induction motor for 200-km/h maglev. Int. J. Railw. 2015, 8, 15–20. [Google Scholar] [CrossRef]
- Abdollahi, S.E.; Mirzayee, M.; Mirsalim, M. Design and analysis of a double-sided linear induction motor for transportation. IEEE Trans. Magn. 2015, 51, 1–7. [Google Scholar] [CrossRef]
- Amiri, E.; Mendrela, E.A. A novel equivalent circuit model of linear induction motors considering static and dynamic end effects. IEEE Trans. Magn. 2014, 50, 120–128. [Google Scholar] [CrossRef]
- Palka, R.; Woronowicz, K.; Kotwas, J.; Xing, W.; Chen, H. Influence of different supply modes on the performance of linear induction motors. Arch. Electr. Eng. 2019, 68, 473–483. [Google Scholar]
- De Gersem, H.; Vande Sande, H.; Hameyer, K. Motional magnetic finite element method applied to high speed rotating devices. Int. J. Comput. Math. Electr. Electron. Eng. 2000, 19, 446–451. [Google Scholar]
- De Gersem, H.; Hameyer, K. Finite element simulation of a magnetic brake with a soft magnetic solid iron rotor. Int. J. Comput. Math. Electr. Electron. Eng. 2002, 21, 296–306. [Google Scholar] [CrossRef][Green Version]
- Introduction to COMSOL Multiphysics, Version 5.6, ©1998–2020 COMSOL. Available online: https://www.comsol.com/documentation (accessed on 25 February 2021).
- Sikora, R.; Lipinski, W.; Gawrylczyk, K.; Gramz, M.; Palka, R.; Ziolkowski, M. Analysis of the magnetic field in the end region of induction motor. IEEE Trans. Magn. 1982, 18, 674–678. [Google Scholar] [CrossRef]
- Sikora, R.; Gawrylczyk, K.; Gramz, M.; Gratkowski, S.; Ziolkowski, M. Magnetic field Computation in the End-Region of Electric Machines Using Various Boundary Conditions on Iron Surfaces. IEEE Trans. Magn. 1986, 22, 204–207. [Google Scholar] [CrossRef]
- Blaschke, F. The Principle of Field Orientation as Applied to the New Transvector Closed-Loop Control System for Rotating Machines. Siemens Rev. 1972, 34, 217–220. [Google Scholar]
- Trzynadlowski, A. The Field Orientation Principle in Control of Induction Motors; Kluwer Academic Publishers: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Boldea, I.; Nasar, S.A. Vector Control of AC Drives; CRC Press: London, UK, 1992. [Google Scholar]
- Leonhard, W. Control of Electric Drives; Springer: Berlin, Germany, 1985. [Google Scholar]
- Kaźmierkowski, M.P.; Tunia, H. Automatic Control of Converter-Fed Drives; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Kovács, P.K. Transient Phenomena in Electric Machines; Elsevier: Amsterdam, The Netherlands, 1984. [Google Scholar]
- Yamamura, S. AC Motors for High Performance Applications: Analysis and Control; Marcel Dekker: New York, NY, USA, 1986. [Google Scholar]
- Lipo, T.; Novotny, D. Principles of Vector Control and Field Estimation. In Introduction to Field Orientation and High Performance Drives; IEEE Tutorial Course: Minneapolis, MN, USA, 1985. [Google Scholar]
- Depenbrock, M. Direkte Selbstregelung (DSR) für hochdynamische Drehfeldantriebe mit Stromrichterspeisung. etz-Archiv 1985, 7, 211–218. [Google Scholar]
- Depenbrock, M. Direct Self-Control of the Flux and Rotary Moment of a Rotary-Field Machine. U.S. Patent 4,678,248, 7 July 1987. [Google Scholar]
- Takahashi, I.; Noguchi, T. A new quick response and high efficiency control strategy of an induction motor. IEEE Trans. Ind. Appl. 1986, IA-22, 820–827. [Google Scholar] [CrossRef]
- Tiitinen, P.; Pohjalainen, P.; Lalu, J. The next generation motor control method–Direct torque control (DTC). Eur. Power Electron. Drives 1995, 5, 14–18. [Google Scholar]
- Kazmierkowski, M.; Kasprowicz, A. Improved direct torque and flux vector control of PWM inverter-fed induction motor drives. IEEE Trans. Ind. Electron. 1995, 42, 344–350. [Google Scholar] [CrossRef]
- May, H.; Canders, W.-R.; Palka, R. Loss reduction in synchronous machines by appropriate feeding patterns. In Proceedings of the International Conference on Electrical Machines ICEM ’98, Istanbul, Turkey, 2–4 September 1998. [Google Scholar]
- May, H.; Palka, R.; Canders, W.-R. Optimized control of induction machines for dynamic torque requirements. In Electromagnetic Fields in Electrical Engineering; IOS Press: Amsterdam, The Netherlands, 2002; pp. 254–259. [Google Scholar]
- Woronowicz, K.; Safaee, A.; Maknouninejad, A. Enhanced Algorithm for Real Time Temperature Rise Prediction of a Traction LIM. In Proceedings of the Transportation Electrification Conference and Expo, ITEC 2018, Long Beach, CA, USA, 13–15 June 2018; pp. 616–620. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palka, R.; Woronowicz, K. Linear Induction Motors in Transportation Systems. Energies 2021, 14, 2549. https://doi.org/10.3390/en14092549
Palka R, Woronowicz K. Linear Induction Motors in Transportation Systems. Energies. 2021; 14(9):2549. https://doi.org/10.3390/en14092549
Chicago/Turabian StylePalka, Ryszard, and Konrad Woronowicz. 2021. "Linear Induction Motors in Transportation Systems" Energies 14, no. 9: 2549. https://doi.org/10.3390/en14092549
APA StylePalka, R., & Woronowicz, K. (2021). Linear Induction Motors in Transportation Systems. Energies, 14(9), 2549. https://doi.org/10.3390/en14092549