Experimental Characterization of an Adaptive Supersonic Micro Turbine for Waste Heat Recovery Applications
Abstract
:1. Introduction
2. Materials and Methods
2.1. Swallowing Capacity of a Supersonic Turbine
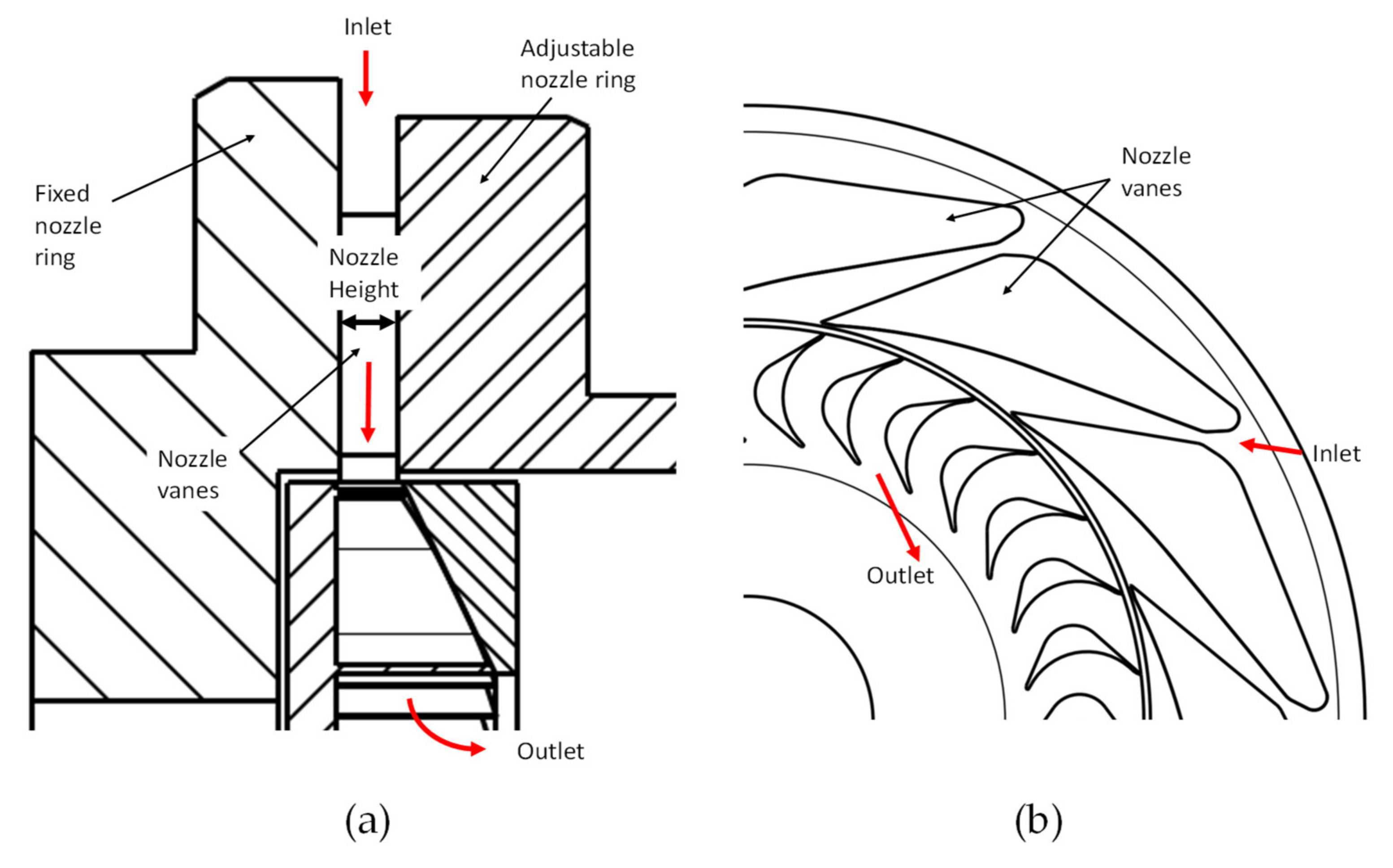
2.2. ANH Concept and Its Implementation
2.2.1. Fixed ANH Turbine (F-ANH)
2.2.2. Manually Adjusted Turbine Geometry (M-ANH)
2.2.3. Automatically Adjusted Turbine Geometry (A-ANH)
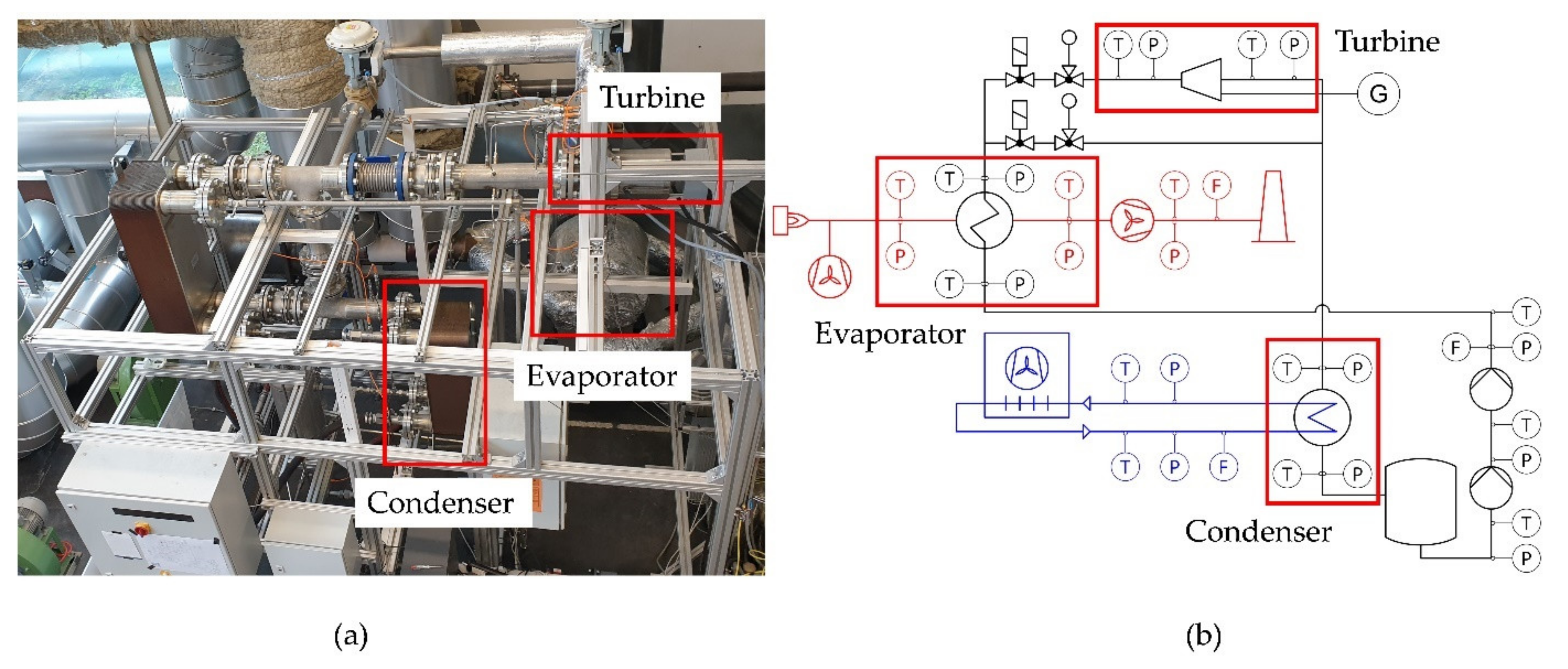
2.3. The ORC Test Rig
2.4. Energy Conversion Chain and Considered Conversion Steps
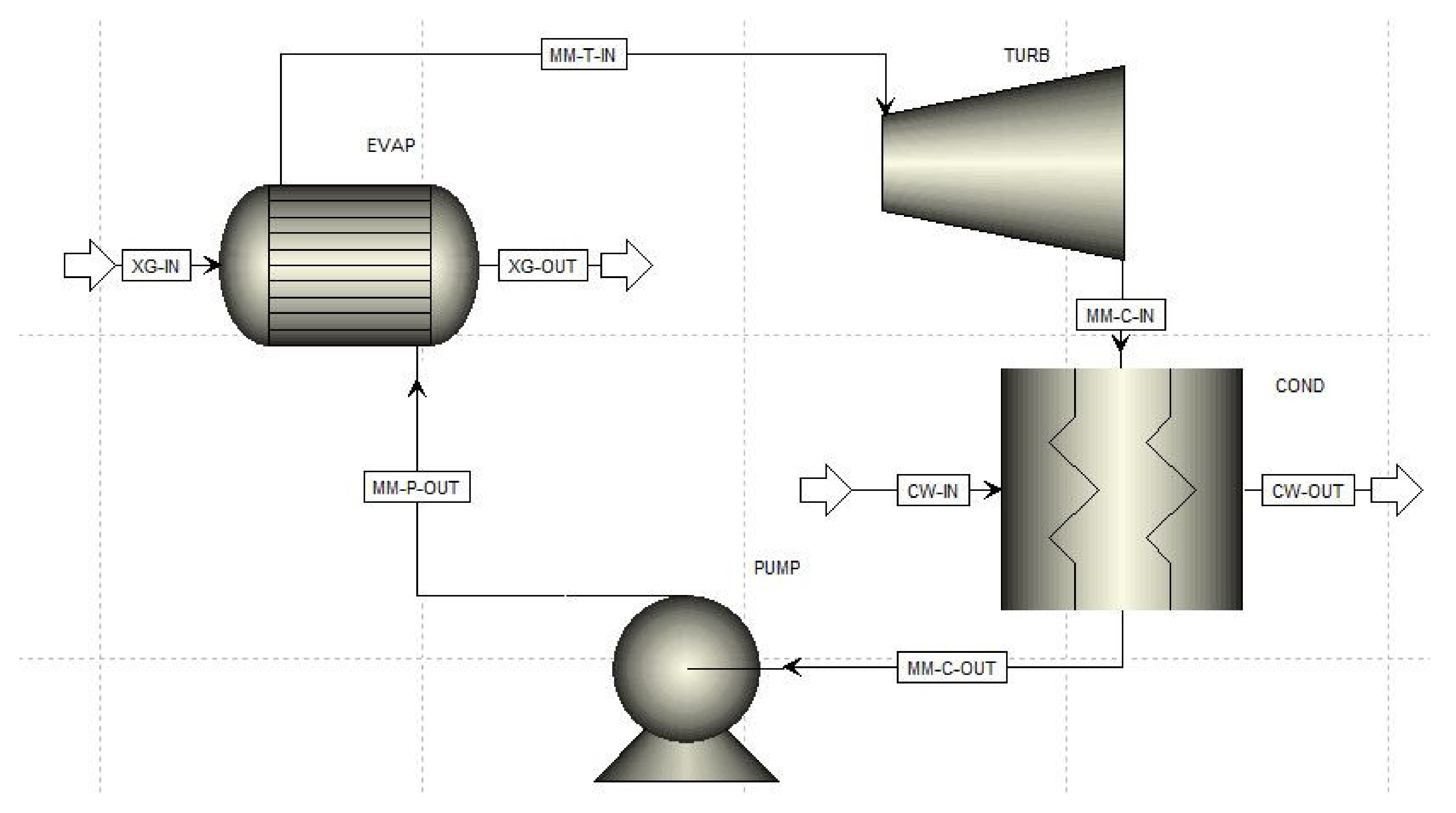
2.5. Semi-Empirical Model as Basis of Performance Evaluation
- Exhaust gas (XG-IN) composition (CO2, H2O, N2, O2)
- Exhaust gas mass flow rate
- Exhaust gas inlet temperature (XG-IN)
- Efficiency of the pumps (simulated as a single pump)
- Thermal capacity ( values, approximated by a power law approach for the evaporator (EVAP)
- Constant turbine inlet temperature of 190 °C (independent of mass flow rate)
- Efficiency of the turbine
- Condenser (COND) efficiency (by implementing a certain heat leakage)
- Degrees of subcooling of the working fluid (MM-C-OUT) in the condenser
- Cooling water inlet temperature (CW-IN)
3. Results and Discussion
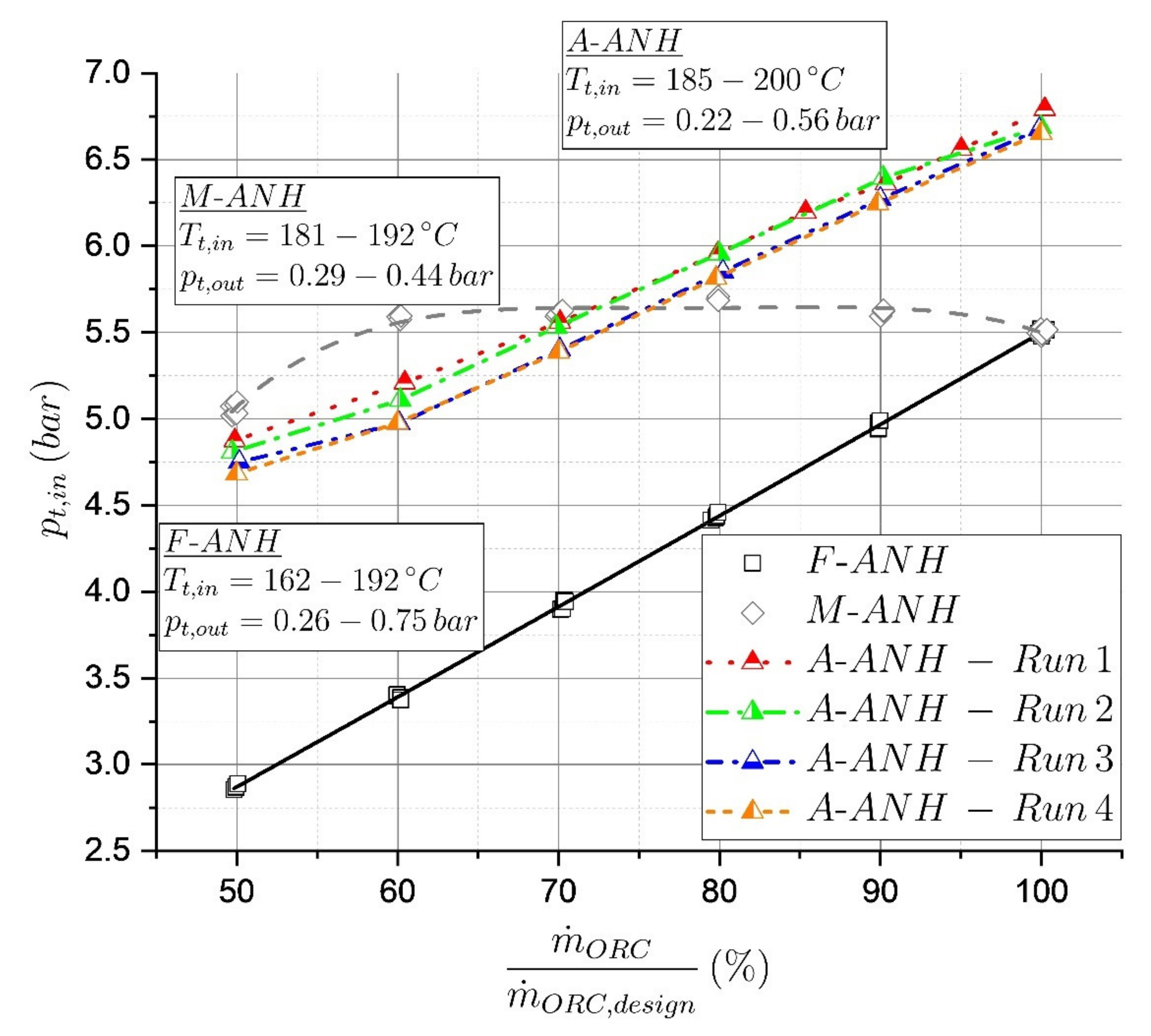
3.1. Swallowing Capacity and Turbine Inlet Pressure
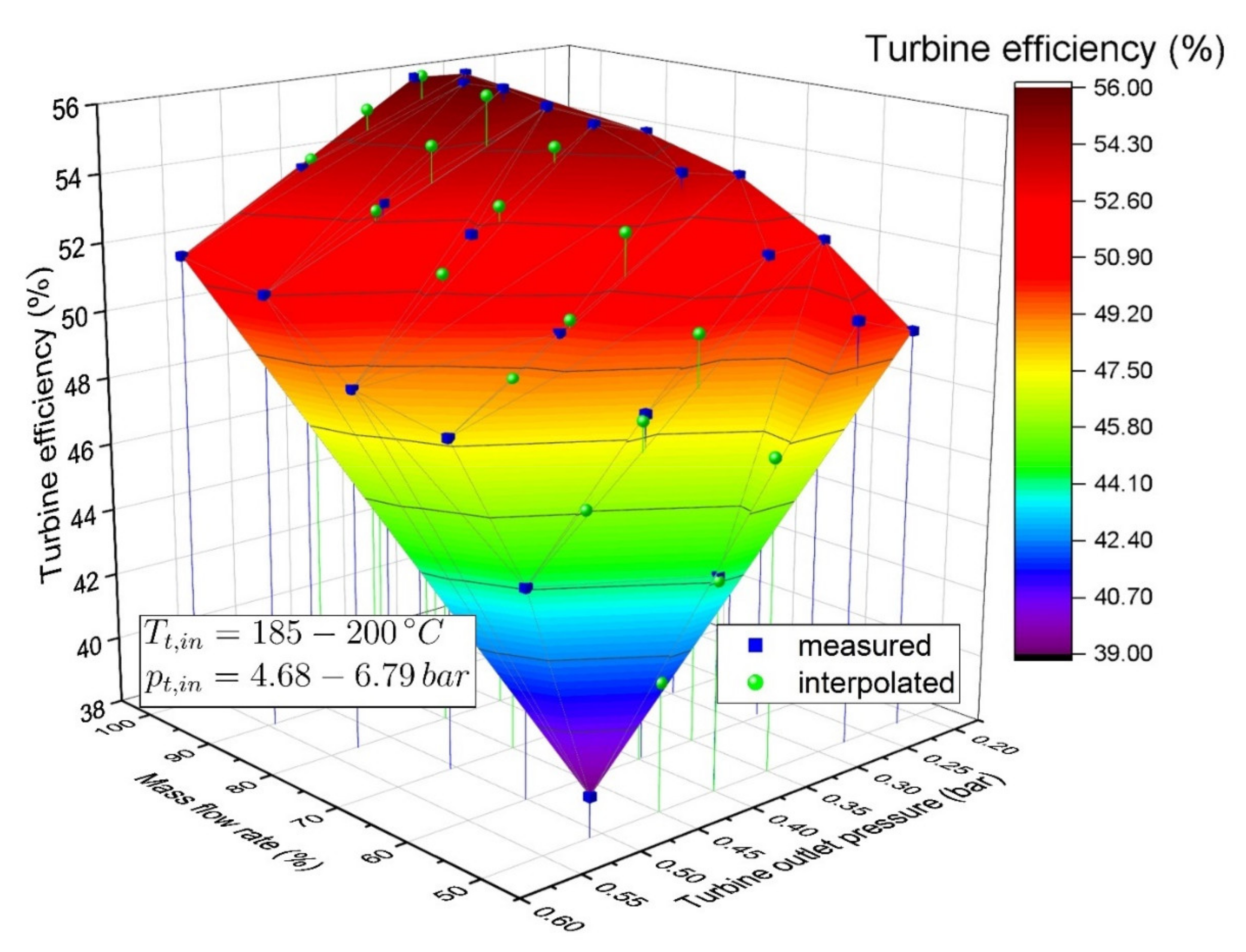
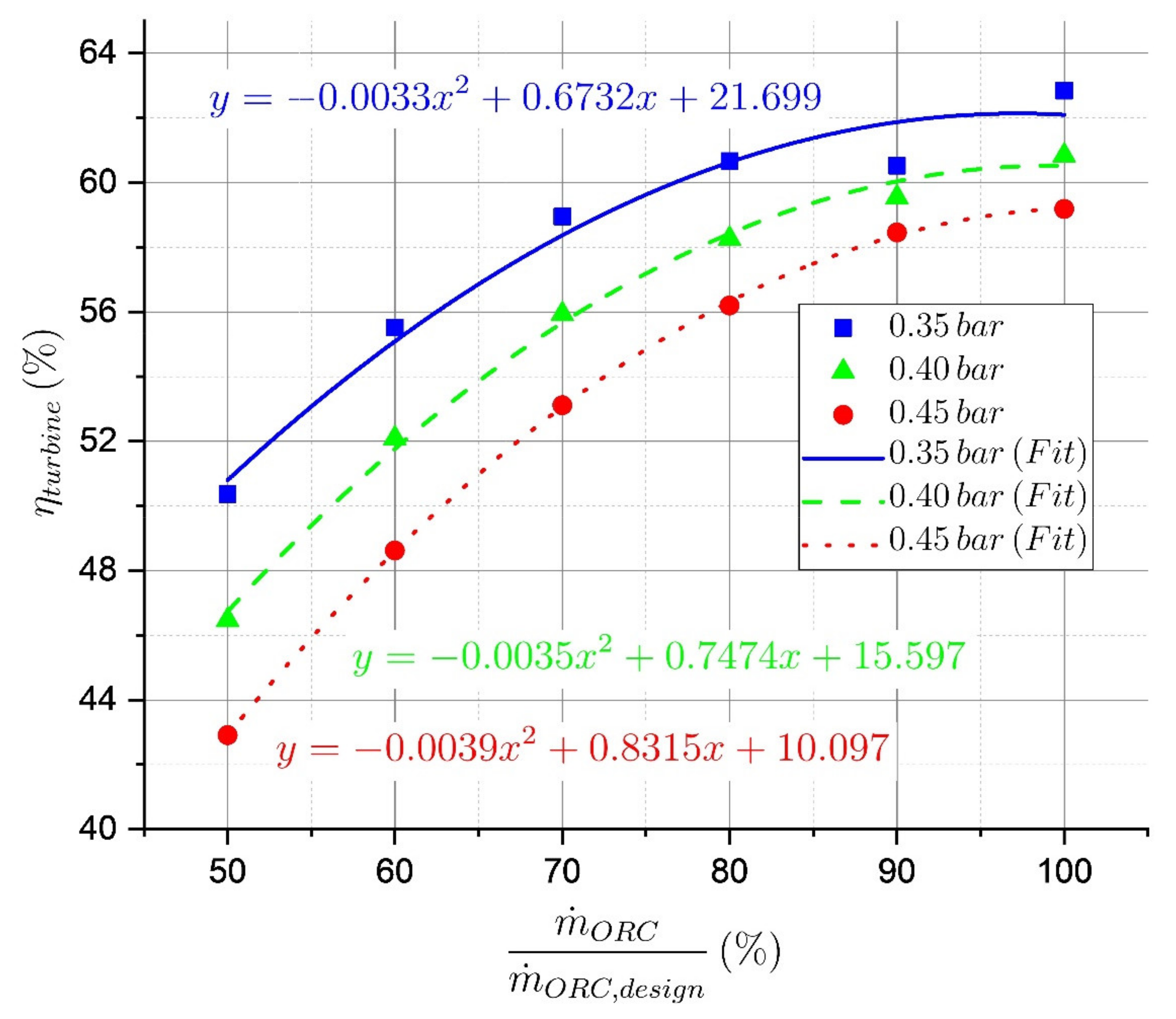
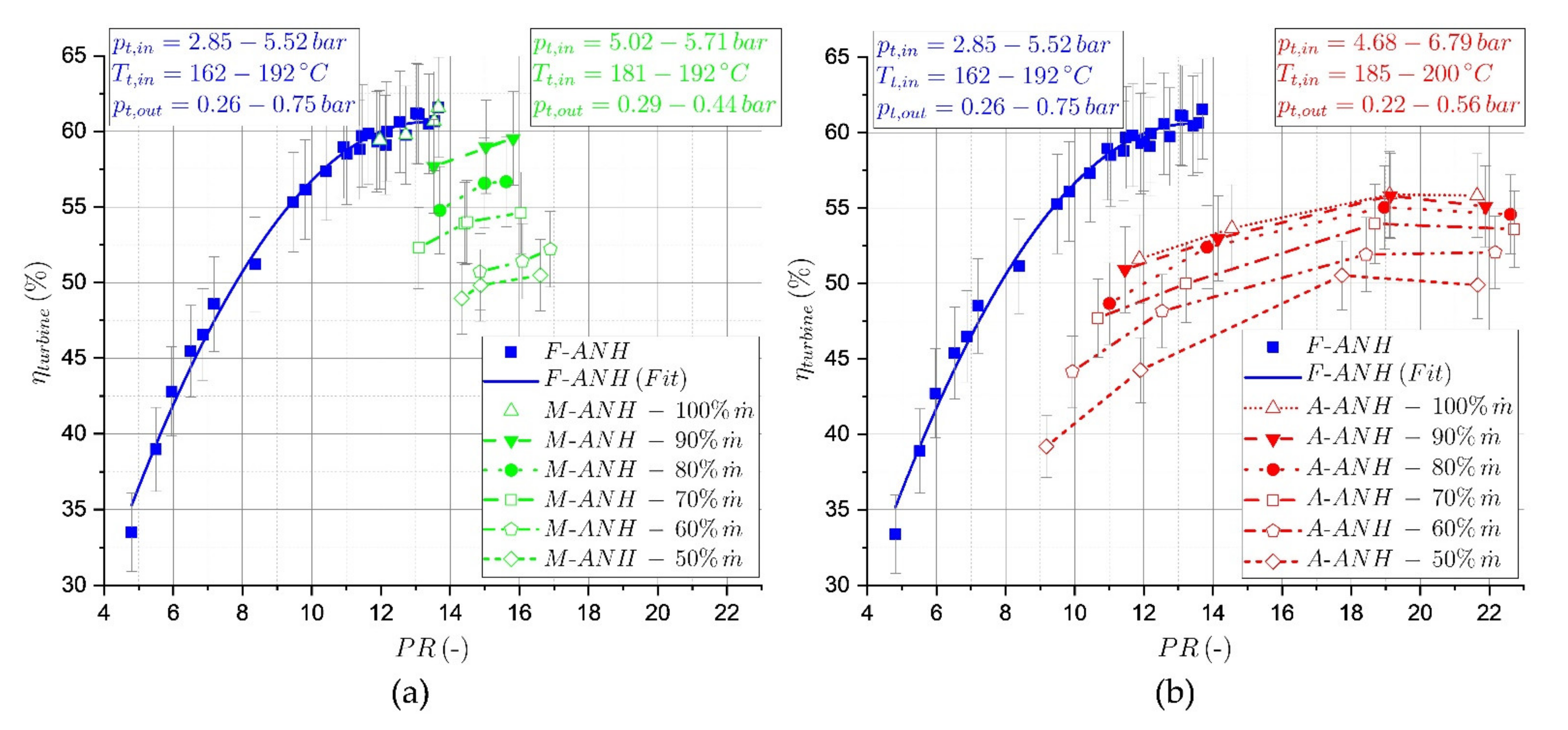
3.2. Turbine Efficiency for the Different Turbine Configurations
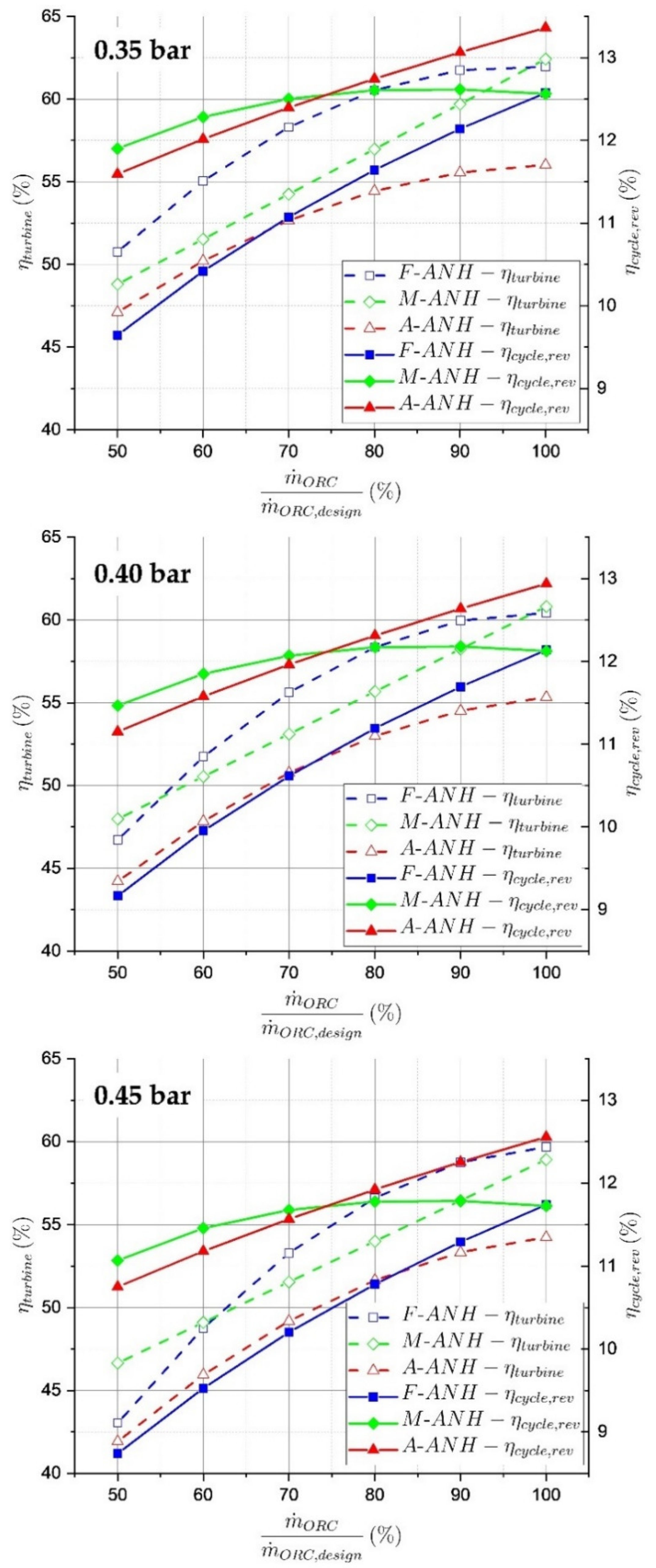
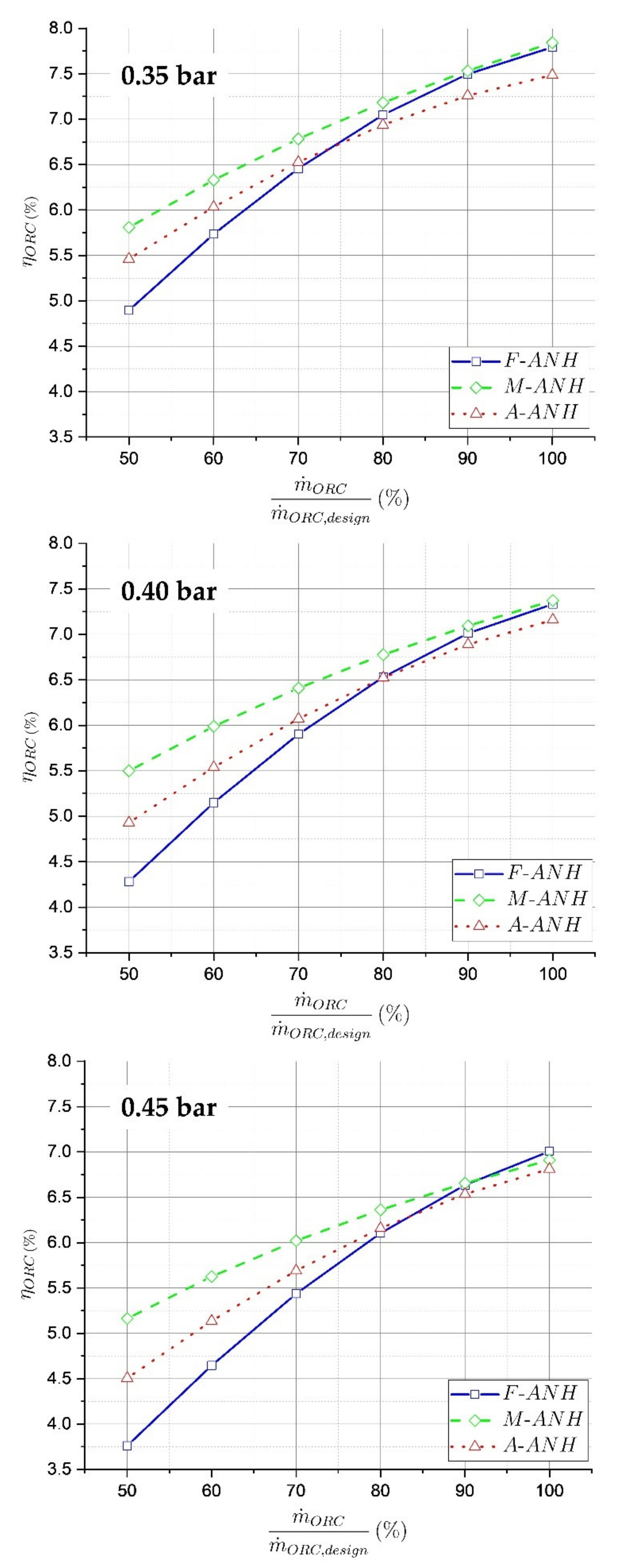
3.3. Turbine Efficiency, Reversible Cycle Efficiency and ORC Efficiency Calculated with the Digital Twin
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| area | (m2) | |
| enthalpy flux | (J/s) | |
| specific enthalpy | (J/s) | |
| isentropic exponent | (-) | |
| Mach number | (-) | |
| mass flow rate | (kg/s) | |
| efficiency | (%) | |
| power | (W) | |
| pressure | (Pa) | |
| pressure ratio | (%) | |
| heat flux | (W) | |
| specific gas constant | (J/kg/K) | |
| temperature | (K) | |
| thermal capacity | (W/K) | |
| exergy flux | (J/s) | |
| Subscripts | ||
| corr | corrected | |
| EC | electrical chain | |
| EG | exhaust gas | |
| EV | evaporator | |
| el | electric | |
| HU | heat utilization | |
| IE | isentropic expansion | |
| is | isentropic | |
| ORC | organic Rankine cycle | |
| rev | reversible | |
| st | static | |
| sup | supplied | |
| t | total | |
| ut | utilized | |
| WHR | waste heat recovery | |
| Abbreviations | ||
| ANH | adjustable nozzle height | |
| EAF | electric arc furnace | |
| EV | end value | |
| MV | measured value | |
| PCM | phase change material | |
| VTG | variable turbine geometry | |
| WHR | waste heat recovery |
References
- Pili, R.; Martínez, L.G.; Wieland, C.; Spliethoff, H. Techno-economic potential of waste heat recovery from German energy-intensive industry with Organic Rankine Cycle technology. Renew. Sustain. Energy Rev. 2020, 134, 110324. [Google Scholar] [CrossRef]
- Jiménez-Arreola, M.; Pili, R.; Wieland, C.; Romagnoli, A. Analysis and comparison of dynamic behavior of heat exchangers for direct evaporation in ORC waste heat recovery applications from fluctuating sources. Appl. Energy 2018, 216, 724–740. [Google Scholar] [CrossRef]
- Pili, R.; Romagnoli, A.; Spliethoff, H.; Wieland, C. Techno-Economic Analysis of Waste Heat Recovery with ORC from Fluctuating Industrial Sources. Energy Procedia 2017, 129, 503–510. [Google Scholar] [CrossRef]
- Nardin, G.; Meneghetti, A.; Magro, F.D.; Benedetti, N. PCM-based energy recovery from electric arc furnaces. Appl. Energy 2014, 136, 947–955. [Google Scholar] [CrossRef]
- Lecompte, S.; Oyewunmi, O.A.; Markides, C.N.; Lazova, M.; Kaya, A.; Broek, M.V.D.; De Paepe, M. Case Study of an Organic Rankine Cycle (ORC) for Waste Heat Recovery from an Electric Arc Furnace (EAF). Energies 2017, 10, 649. [Google Scholar] [CrossRef]
- Bause, T.; Campana, F.; Filippini, L.; Foresti, A.; Monti, N.; Pelz, T. Cogeneration with ORC at Elbe-Stahlwerke Feralpi EAF Shop. In Proceedings of the Iron & Steel Technology Conference and Exposition, Indianapolis, IN, USA, 5–8 May 2014. [Google Scholar]
- Ramirez, M.; Epelde, M.; de Arteche, M.G.; Panizza, A.; Hammerschmid, A.; Baresi, M.; Monti, N. Performance evaluation of an ORC unit integrated to a waste heat recovery system in a steel mill. Energy Procedia 2017, 129, 535–542. [Google Scholar] [CrossRef] [Green Version]
- Pantaleo, A.M.; Fordham, J.; Oyewunmi, O.; De Palma, P.; Markides, C.N. Integrating cogeneration and intermittent waste-heat recovery in food processing: Microturbines vs. ORC systems in the coffee roasting industry. Appl. Energy 2018, 225, 782–796. [Google Scholar] [CrossRef]
- Campana, F.; Bianchi, M.; Branchini, L.; De Pascale, A.; Peretto, A.; Baresi, M.; Fermi, A.; Rossetti, N.; Vescovo, R. ORC waste heat recovery in European energy intensive industries: Energy and GHG savings. Energy Convers. Manag. 2013, 76, 244–252. [Google Scholar] [CrossRef]
- Peris, B.; Navarro-Esbrí, J.; Moles, F.; Mota-Babiloni, A. Experimental study of an ORC (organic Rankine cycle) for low grade waste heat recovery in a ceramic industry. Energy 2015, 85, 534–542. [Google Scholar] [CrossRef]
- Arreola, M.J.; Pili, R.; Magro, F.D.; Wieland, C.; Rajoo, S.; Romagnoli, A. Thermal power fluctuations in waste heat to power systems: An overview on the challenges and current solutions. Appl. Therm. Eng. 2018, 134, 576–584. [Google Scholar] [CrossRef]
- König-Haagen, A.; Höhlein, S.; Brüggemann, D. Detailed exergetic analysis of a packed bed thermal energy storage unit in combination with an Organic Rankine Cycle. Appl. Therm. Eng. 2020, 165, 114583. [Google Scholar] [CrossRef]
- Schuster, S.; Markides, C.; White, A.J. Design and off-design optimisation of an organic Rankine cycle (ORC) system with an integrated radial turbine model. Appl. Therm. Eng. 2020, 174, 115192. [Google Scholar] [CrossRef]
- Hu, D.; Zheng, Y.; Wu, Y.; Li, S.; Dai, Y. Off-design performance comparison of an organic Rankine cycle under different control strategies. Appl. Energy 2015, 156, 268–279. [Google Scholar] [CrossRef]
- Manente, G.; Toffolo, A.; Lazzaretto, A.; Paci, M. An Organic Rankine Cycle off-design model for the search of the optimal control strategy. Energy 2013, 58, 97–106. [Google Scholar] [CrossRef]
- Feneley, A.J.; Pesiridis, A.; Andwari, A.M. Variable Geometry Turbocharger Technologies for Exhaust Energy Recovery and Boosting—A Review. Renew. Sustain. Energy Rev. 2017, 71, 959–975. [Google Scholar] [CrossRef]
- Kozak, D.; Mazuro, P.; Teodorczyk, A. Numerical Simulation of Two-Stage Variable Geometry Turbine. Energies 2021, 14, 5349. [Google Scholar] [CrossRef]
- Moustapha, H.; Zelesky, M.F.; Baines, N.C.; Japikse, D. Axial and Radial Turbines; Concepts ETI, Inc.: White River Junction, VT, USA, 2003; ISBN 9780933283121. [Google Scholar]
- Menny, K. Strömungsmaschinen: Hydraulische und Thermische Kraft- und Arbeitsmaschinen, 5th ed.; Teubner: Wiesbaden, Germany, 2011; ISBN 9783519463177. [Google Scholar]
- Dick, E. Fundamentals of Turbomachines; Springer: Dordrecht, The Netherlands, 2015; ISBN 978-94-017-9626-2. [Google Scholar]
- Stojkovski, F.; Lazarevikj, M.; Markov, Z.; Iliev, I.; Dahlhaug, O. Constraints of Parametrically Defined Guide Vanes for a High-Head Francis Turbine. Energies 2021, 14, 2667. [Google Scholar] [CrossRef]
- Polák, M. A Brief History of the Kaplan Turbine Invention. Energies 2021, 14, 6211. [Google Scholar] [CrossRef]
- Pfleiderer, C.; Petermann, H. Strömungsmaschinen, 7th ed.; Springer: Berlin, Germany, 2005; ISBN 9783540221739. [Google Scholar]
- Casartelli, D.; Binotti, M.; Silva, P.; Macchi, E.; Roccaro, E.; Passera, T. Power Block Off-design Control Strategies for Indirect Solar ORC Cycles. Energy Procedia 2015, 69, 1220–1230. [Google Scholar] [CrossRef] [Green Version]
- Rogo, C.; Hajek, T.; Chen, A.G. Variable Stator Radial Turbine; Nasa Lewis Research Center: Cleveland, OH, USA, 1984. [Google Scholar]
- Rogo, C. Variable Area Radial Turbine Fabrication and Test Program; Nasa Lewis Research Center: Cleveland, OH, USA, 1986. [Google Scholar]
- Streit, P.; Popp, T.; Winkler, J.; Scharf, R.; Weiβ, A.P. Numerical and experimental investigation of different technologies for adjusting the swallowing capacity of a cantilever ORC turbine. AIP Conf. Proc. 2020, 2323, 070001. [Google Scholar]
- Weiß, A.P.; Popp, T.; Müller, J.; Hauer, J.; Brüggemann, D.; Preißinger, M. Experimental characterization and comparison of an axial and a cantilever micro-turbine for small-scale Organic Rankine Cycle. Appl. Therm. Eng. 2018, 140, 235–244. [Google Scholar] [CrossRef]
- Weiß, A.P.; Novotný, V.; Popp, T.; Zinn, G.; Kolovratník, M. Customized Small-Scale ORC Turbogenerators—Combining a 1D-Design Tool, a Micro-Turbine-Generator-Construction-Kit and Potentials of 3D-Printing. In Proceedings of the 5th International Seminar on ORC Power Systems (ORC2019), Athens, Greece, 9 September 2019. [Google Scholar]
- Weiß, A.; Popp, T.; Zinn, G.; Preißinger, M.; Brüggemann, D. A micro-turbine-generator-construction-kit (MTG-c-kit) for small-scale waste heat recovery ORC-Plants. Energy 2019, 181, 51–55. [Google Scholar] [CrossRef]
- Weiß, A.P.; Novotný, V.; Popp, T.; Streit, P.; Špale, J.; Zinn, G.; Kolovratník, M. Customized ORC micro turbo-expanders—From 1D design to modular construction kit and prospects of additive manufacturing. Energy 2020, 209, 118407. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 9.1. Available online: https://tsapps.nist.gov/publication/get_pdf.cfm?pub_id=912382 (accessed on 12 October 2021).
- Popp, T.; Heberle, F.; Weiß, A.P.; Brüggemann, D. Thermodynamic Evaluation of an ORC Test Rig—From Comprehensive Experimental Results to a Simulation Model. In Proceedings of the 6th International Seminar on ORC Power Systems (ORC2021), Munich, Germany, 11–13 October 2021. [Google Scholar]
- Mišák, J. Fehlerrechnung für das Messsystem des ORC-Versuchskraftwerks am Zentrum für Energietechnik/Uni Bayreuth und Dessen Optimierung. Masterarbeit; Ostbayerische Technische Hochschule Amberg-Weiden: Amberg, Germany, 2021. (In German) [Google Scholar]
- Eyerer, S.; Dawo, F.; Kaindl, J.; Wieland, C.; Spliethoff, H. Experimental investigation of modern ORC working fluids R1224yd(Z) and R1233zd(E) as replacements for R245fa. Appl. Energy 2019, 240, 946–963. [Google Scholar] [CrossRef]


| (%) | (g/s) | (kWth) | (kWel) |
| 50 | 160 | 90–102 | 4.0 |
| 60 | 192 | 106–116 | 5.6 |
| 70 | 224 | 125–133 | 7.2 |
| 80 | 256 | 139–150 | 8.8 |
| 90 | 288 | 160–168 | 10.4 |
| 100 | 320 | 178–184 | 12.0 |
| Component | Type |
|---|---|
| Heat supply | Propane gas burner |
| Pumps | Centrifugal and piston diaphragm pump (both with variable frequency drive) |
| “Evaporator” | Plate and Shell type heat exchanger |
| Expander | Quasi-Impulse Cantilever turbine in F-ANH, M-ANH and A-ANH configuration |
| Condenser | Plate heat exchanger |
| Heat rejector | Air cooler |
| Measured Parameter | Type | Measuring Range | Accuracy of Measurement |
|---|---|---|---|
| Turbine inlet temperature | Omega PR-22-3-100-A-M3-150-M12 | −30–350 °C | 1 °C |
| Turbine inlet pressure | Omega PAA23SYC-10-M12 | 0–10 bar | 1.5% of EV |
| Turbine outlet pressure | Omega PAA23SY C-2-M12 | 0–2 bar | 1.5% of EV |
| Mass flow rate | ABB CoriolisMaster FCB330 | 0–416,667 g/s | 0.4% of MV |
| Power | Sieb & Meyer 0362111OF | 0–20 kW | N/A |
| Module | Measuring Range | Accuracy of Measurement |
|---|---|---|
| NI 9207 | 0–22 mA | 0.87% of MV + 0.05% of EV |
| NI 9208 | 0–22 mA | 0.76% of MV + 0.04% of EV |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popp, T.; Weiß, A.P.; Heberle, F.; Winkler, J.; Scharf, R.; Weith, T.; Brüggemann, D. Experimental Characterization of an Adaptive Supersonic Micro Turbine for Waste Heat Recovery Applications. Energies 2022, 15, 25. https://doi.org/10.3390/en15010025
Popp T, Weiß AP, Heberle F, Winkler J, Scharf R, Weith T, Brüggemann D. Experimental Characterization of an Adaptive Supersonic Micro Turbine for Waste Heat Recovery Applications. Energies. 2022; 15(1):25. https://doi.org/10.3390/en15010025
Chicago/Turabian StylePopp, Tobias, Andreas P. Weiß, Florian Heberle, Julia Winkler, Rüdiger Scharf, Theresa Weith, and Dieter Brüggemann. 2022. "Experimental Characterization of an Adaptive Supersonic Micro Turbine for Waste Heat Recovery Applications" Energies 15, no. 1: 25. https://doi.org/10.3390/en15010025
APA StylePopp, T., Weiß, A. P., Heberle, F., Winkler, J., Scharf, R., Weith, T., & Brüggemann, D. (2022). Experimental Characterization of an Adaptive Supersonic Micro Turbine for Waste Heat Recovery Applications. Energies, 15(1), 25. https://doi.org/10.3390/en15010025







