A Review of Modelling of the FCC Unit–Part I: The Riser
Abstract
1. Introduction
| Riser | ||
| Dimensions | ||
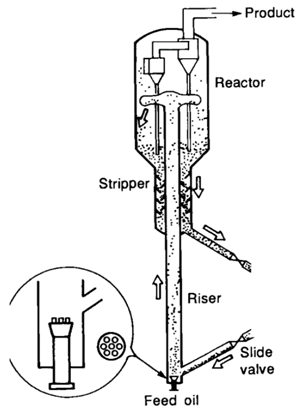 | Height | 30–40 m |
| Diameter | 1–2 m | |
| Operating Conditions | ||
| Gas oil inlet T | 150–300 °C | |
| Catalyst inlet T | 675–750 °C | |
| Solid circulation | >250 kg/m2s | |
| Catalyst to Oil (CTO) | 4–10 wt% | |
| Dispersion steam | 0–5 wt% | |
| Pressure | 150–300 kPa | |
| Solid Residence | 3–15 s | |
| Catalyst Properties | ||
| Average size | 70 µm | |
| Density | 1200–1700 kg/m2s | |
| Typical | m/s | |
| Geldart Group | ||
2. Fluid Catalytic Cracking (FCC) Riser
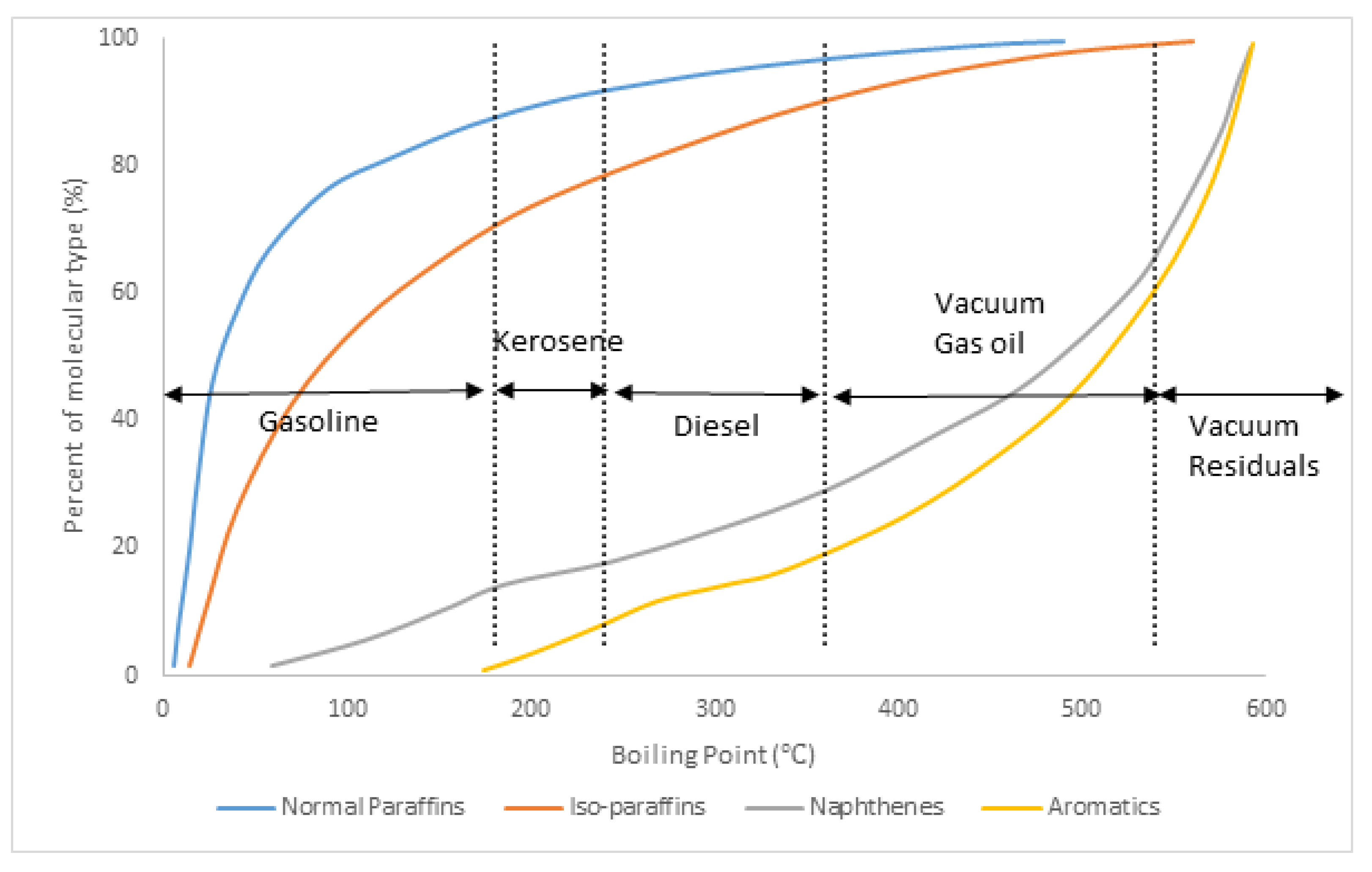
2.1. Feed and Product Characterisation
2.2. Reactions in the FCC Riser
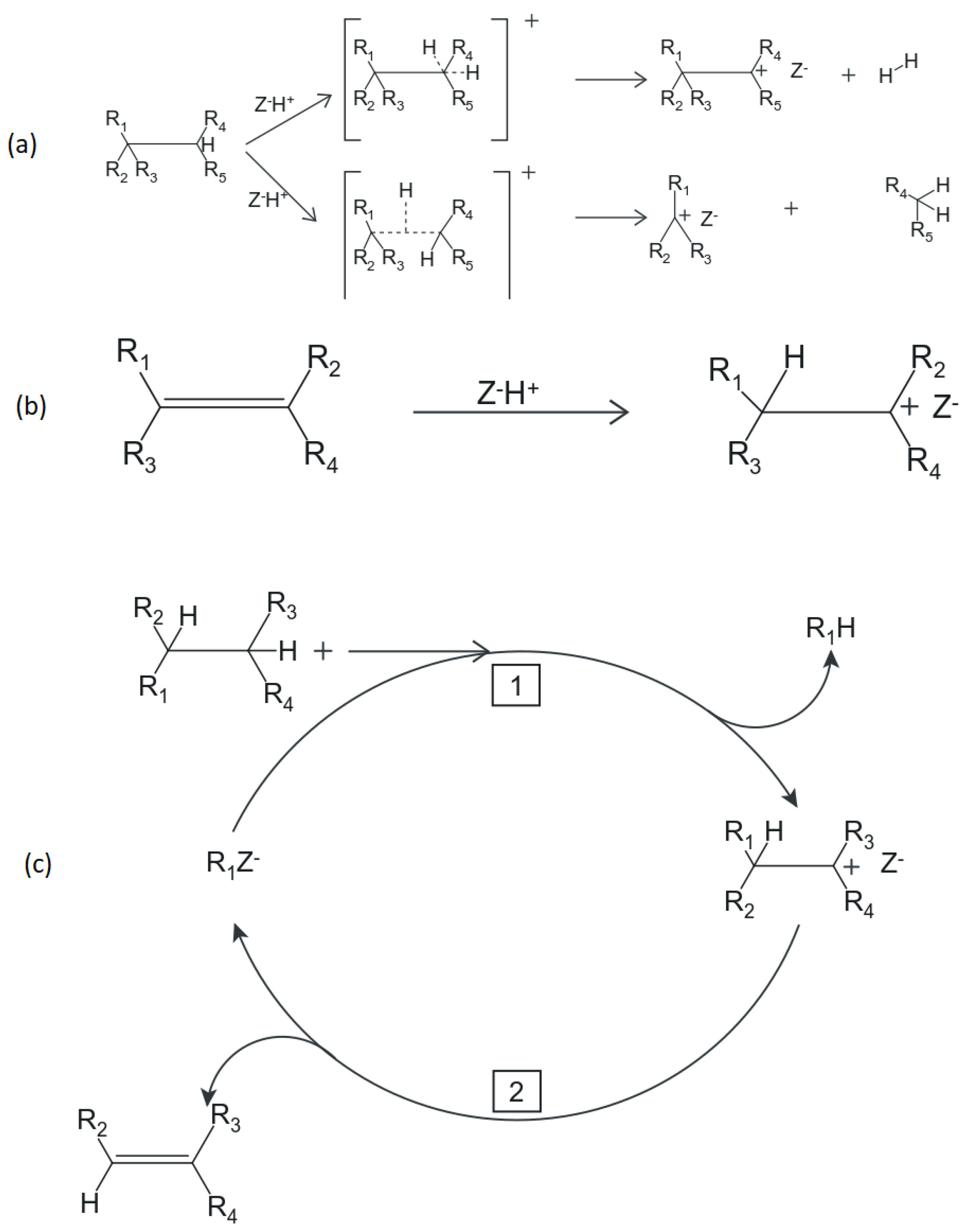
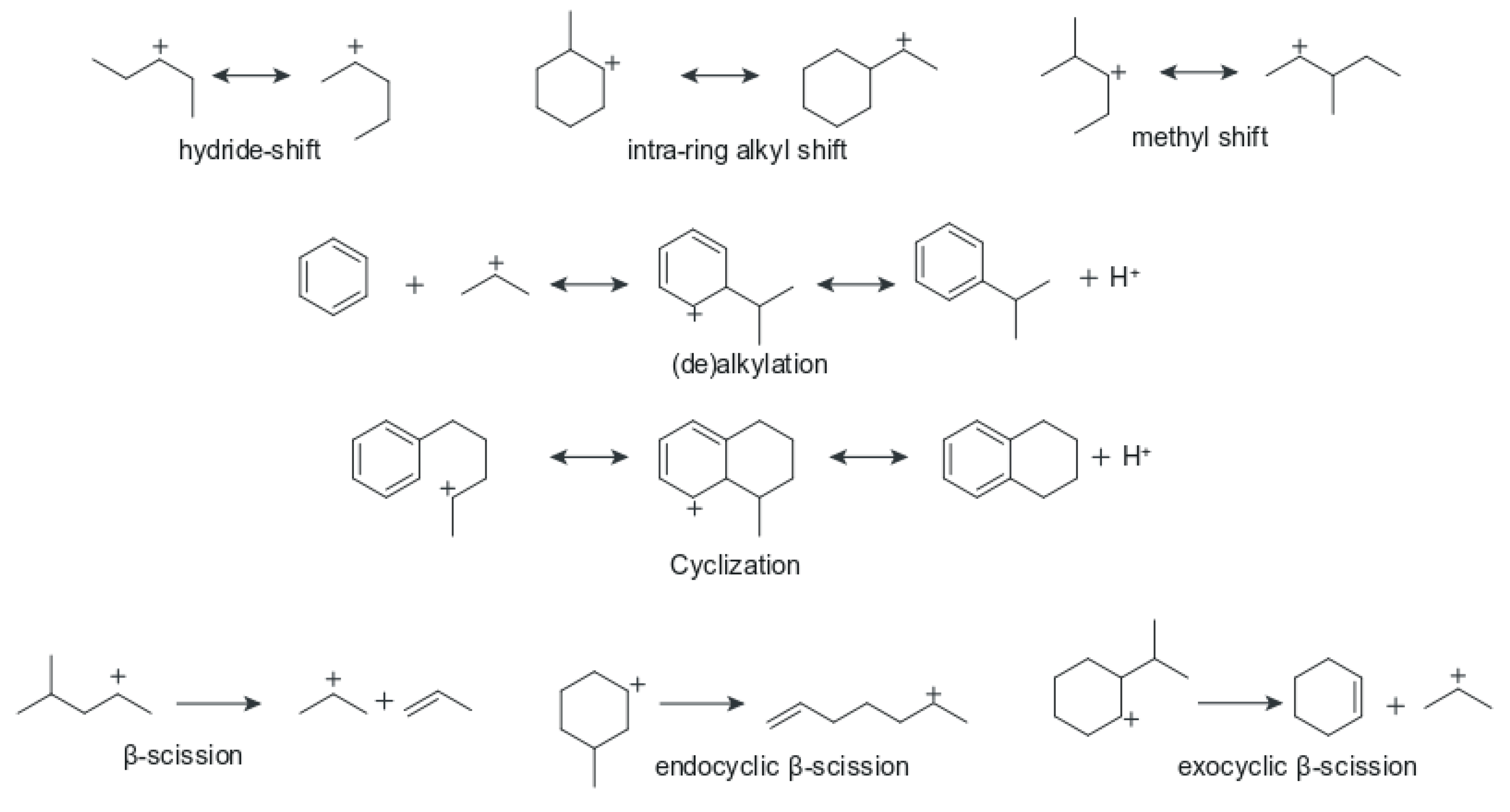
- Initiation: this is the first step that kicks off the cracking reactions. It is characterised by attack of an active sight on a reacting molecule to produce an activated complex (i.e., a carbocation). Initiation in the case of an olefin molecule is thought to proceed via the direct attack of a Brnsted acid site on the reactant double bond to form a carbenium ion [47]. This is the mechanism that would be expected for gaseous olefins, such as the case in the FCC riser [49]. On the other hand, there is some debate over the exact mechanism in which paraffins are activated, early work [50,51] suggested that activation of paraffins required the existence, even in small quantities, of olefins. In this mechanism, carbenium ion from the olefins (via the method described above for olefins) would abstract a hydride ion on a nearby paraffin to generate an activated paraffin carbenium ion. For a while, this mechanism was essentially correct [47], but its insufficiencies in accounting for observed complex product distributions warranted concern [52]. However, later Haag and Dessau [53,54] proposed a direct protonation method of the paraffin (the so-called Haag-Dessau mechanism), that drew inspiration from the 1994 Chemistry Nobel Prize winning work of George A. Olah (for contributions to the chemistry of hydrocarbons in super-acidic solutions) and did not require the presence of olefins in the activation of paraffins. Via this mechanism, a Brnsted acid site directly protonates the paraffin reactant molecule forming a carbonium ion complex which collapses by bond scission to give a carbenium ion. The protonation produces a carbenium ion together with either an alkane (in the event of a bond scission) or hydrogen (in the event of a bond scission) [53,54]. The Haag–Dessau mechanism gained some acceptance as it was supported by some researchers [55,56,57,58]. Furthermore, activation of paraffins by Lewis sites has also been proposed [46,59] involving the abstraction of a hydride from an alkane by a Lewis site resulting in a carbenium ion formation. However, evidence from [60,61] has questioned the contribution of Lewis sites. Nevertheless, more paraffin activation mechanisms have been suggested [62,63,64,65]. Generally, all these mechanisms agree that the initiation step will produce a carbenium ion, the subsequent steps after that become relatively routine and generally agreed upon by most researchers. Initiation of both olefins and paraffins is shown in Figure 2a,b.
- Propagation: this involves the transfer of a hydride ion from an adsorbed carbenium ion to a reactant molecule, and always results in the formation of another carbenium ion [47]. Simply put, a carbenium ion reacts with a paraffin or olefin so that another carbenium ion is formed in the process. In the case of a paraffin molecule interacting with a surface carbenium ion, it has been proposed that the chain propagation occurs when the carbocation abstracts a hydride ion on the reactant paraffin. The former carbocation then desorbs from the surface as a paraffin when the former paraffin is left adsorbed as a carbenium ion. The resulting carbenium ion can then either isomerise and/or crack further, which means the chain process continues. When the cracking occurs via protolytic attack or -scission, the resulting product is an olefin or a paraffin, respectively. Additionally, it is also thought that adsorbed carbenium ions may undergo 1,2 hydrogen shift so that the positive charge can migrate across the molecule giving a possibility of branching [47]. See Figure 2c for possible propagation mechanisms in the riser.
- Termination: this involves the desorption of the adsorbed carbenium ion to give an olefin, whilst restoring the active site to its initial state [47]. This step results in the termination of an active carbenium ion, thereby completing the chain.
- Both the feed and the product mixture of the system are very complicated mixtures of compounds, and their modelling is, to some extent, limited by the characterisation techniques available to the process engineer,
- The reaction network for the FCC system, using conventional gas oil feed, is too massive and too detailed to be modelled exactly. To some extent, modelling may be limited by computation power.
2.3. Kinetic Models of the Riser
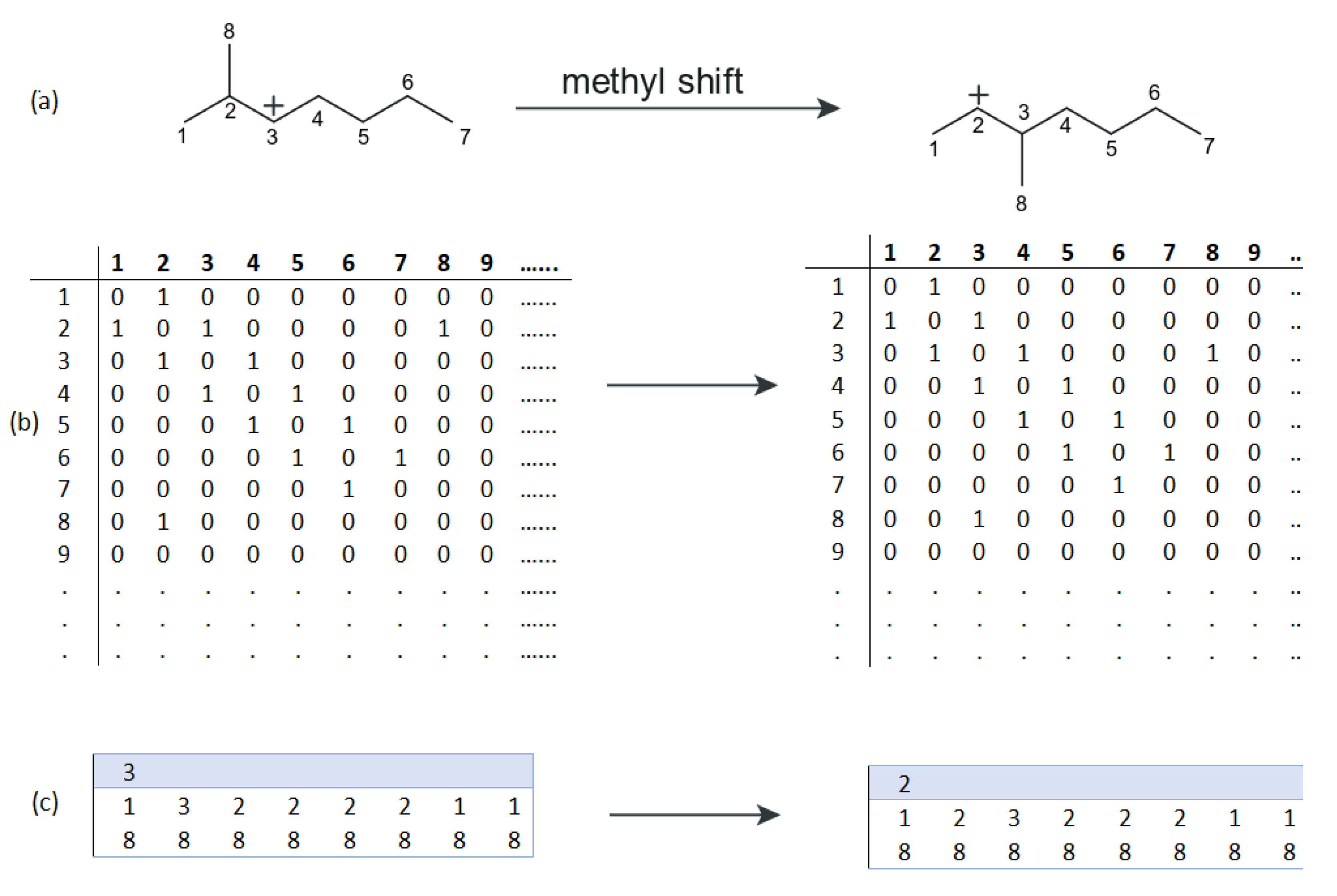
2.3.1. Discrete Lumping
2.3.2. Continuous Lumping
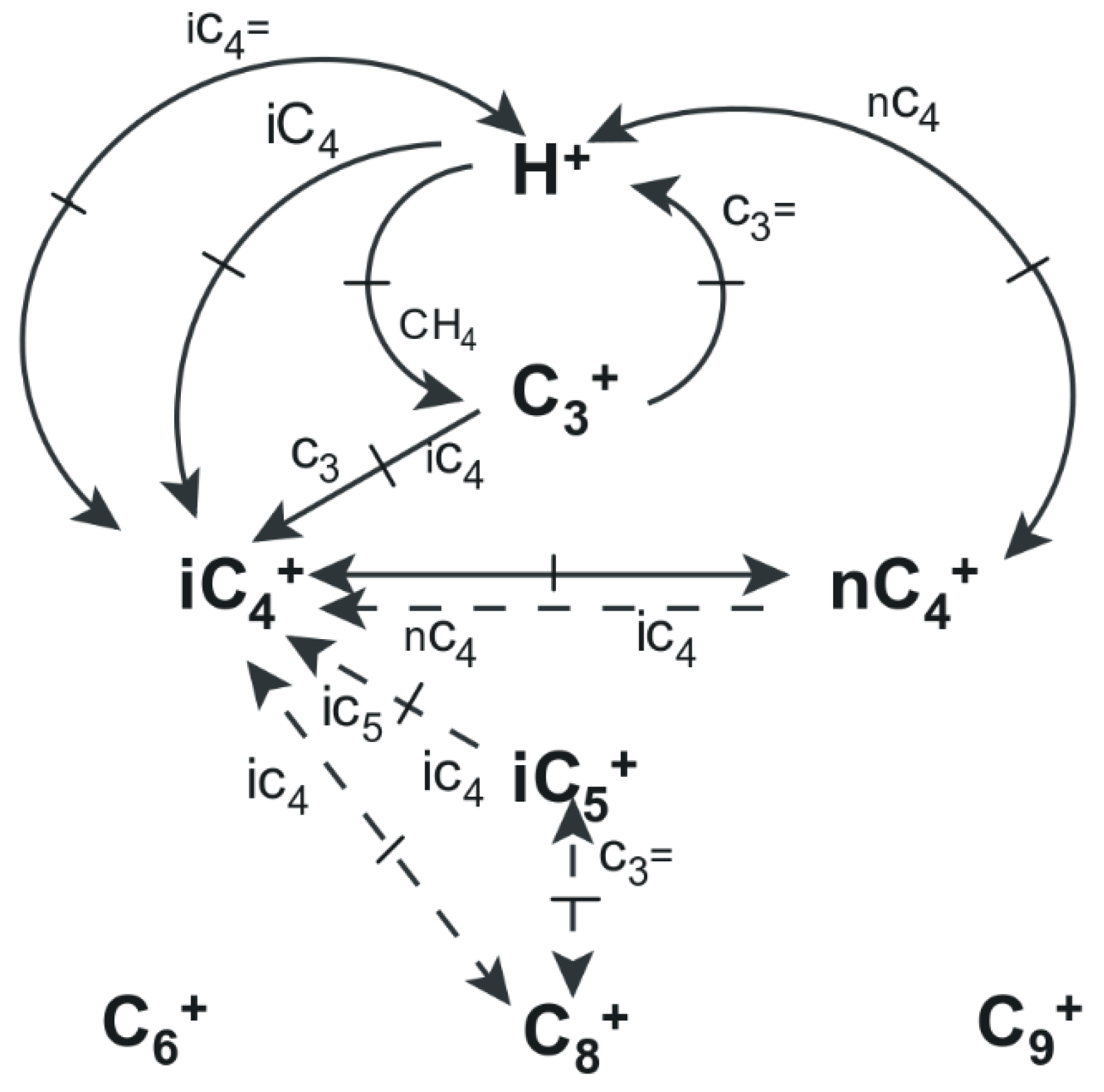
2.3.3. Single Event Kinetics and Structure-Oriented Lumping
2.3.4. Catalyst Deactivation Function
2.4. Riser Hydrodynamics
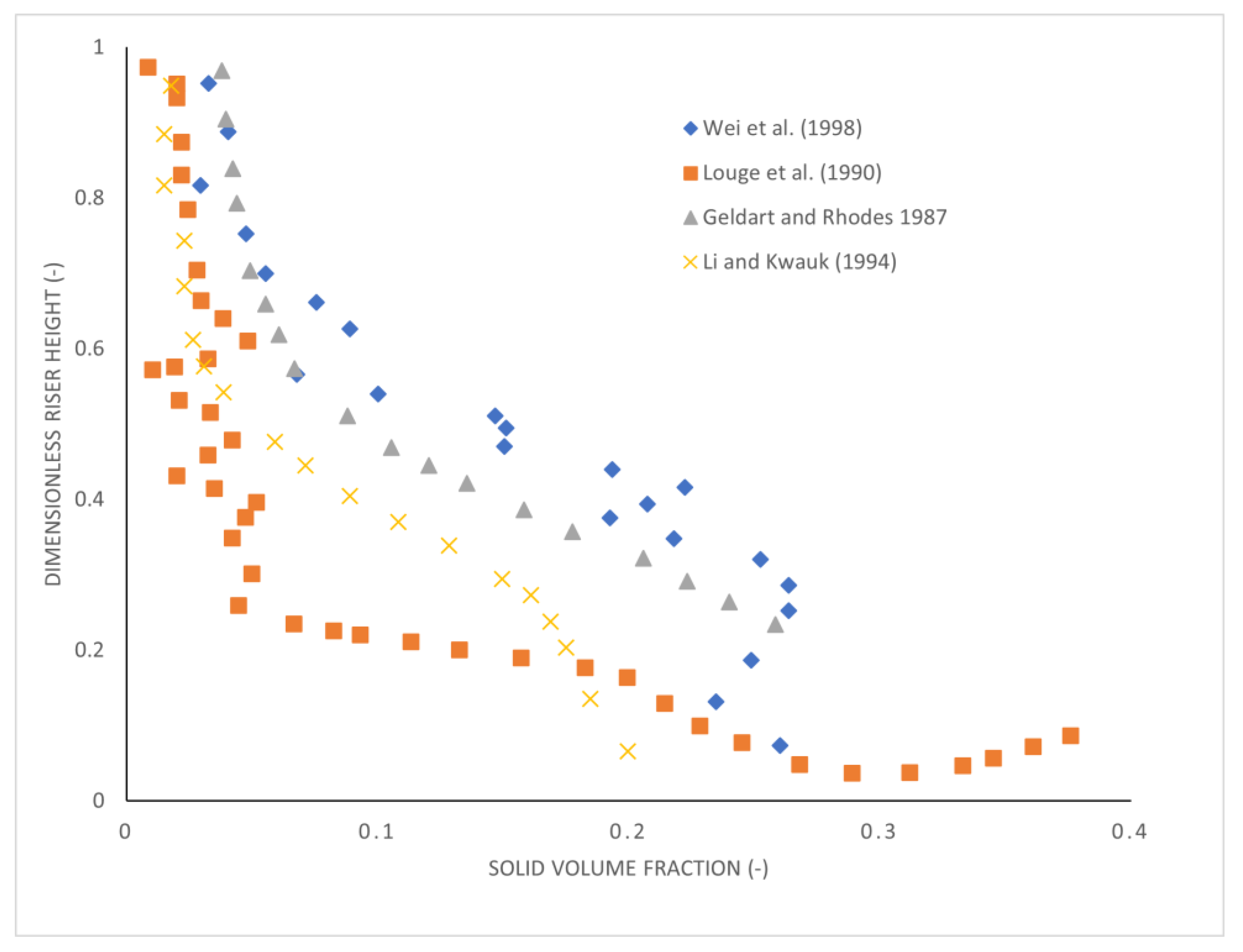
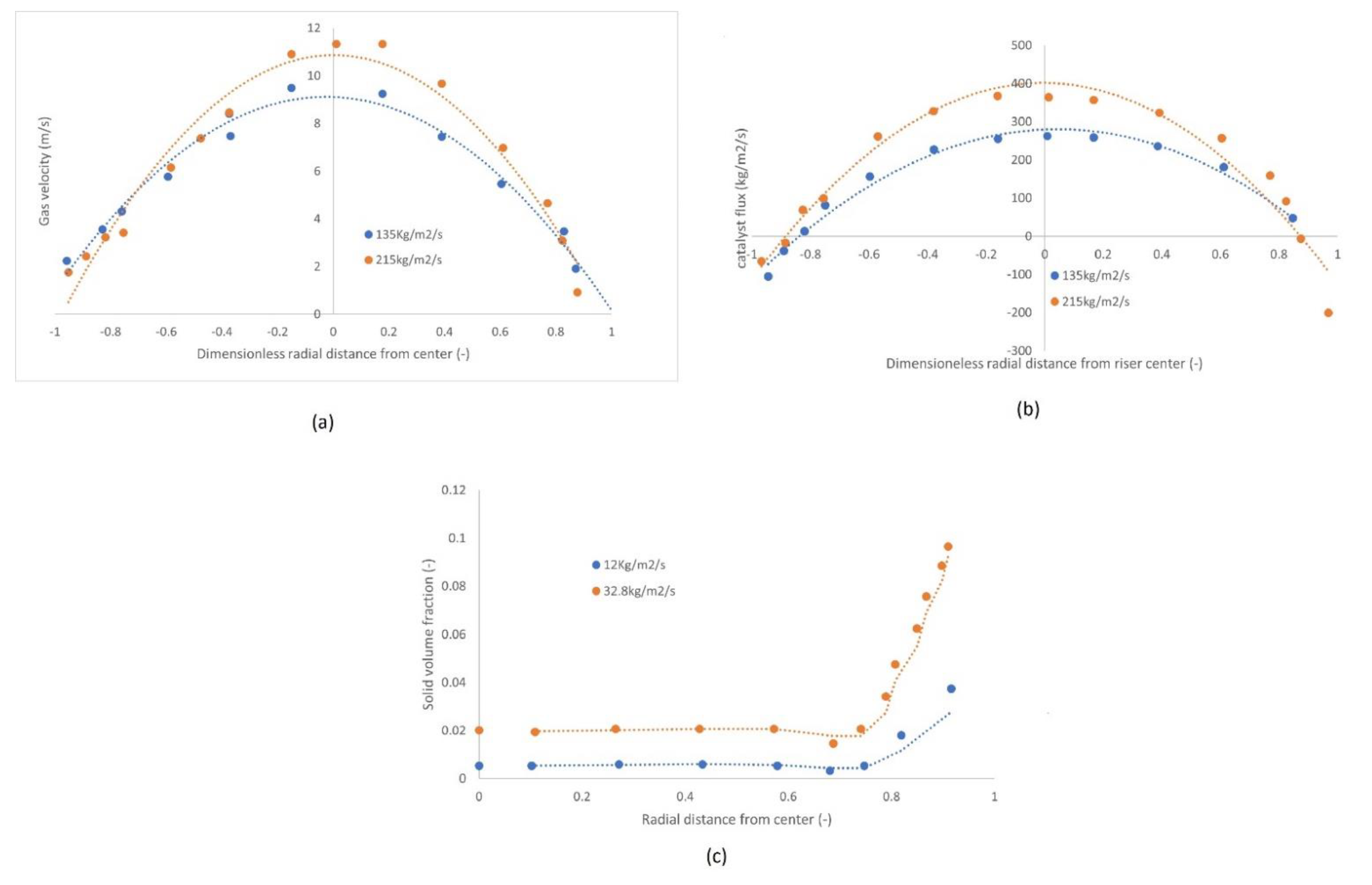
2.4.1. Axial and Radial Profiles
2.4.2. Gas and Solid Mixing
2.5. Hydrodynamic Models of Circulating Fluidised Bed (CFB) Risers
- Pseudo-homogeneous modelsThese assume that flow is turbulent, but non-isotropic so that variations present in the vertical directions may be different from those occurring horizontally [168], but no macroscopic flow heterogeneity in different regions of the bed is made, that is, at the macro scale flow is essentially similar through the bed. The mass balance equation will usually include dispersion coefficients for both axial and radial positions to account for mixing. Grace et al. [33] present the following general equation for simple homogeneous dispersion models:where are the source term and the rate equation for the gas component as defined by the kinetic model. Note that here only the gas equation is shown as this is usually the important mass balance for the process with gaseous products. In the case of one-dimensional models [161,171,184,186,187] the radial term may be dropped so that the dispersion equation becomes:Other possible simplifications include the assumption of steady state, which is quite common in FCC riser modelling due to the perceived insignificance of the riser dynamics compared to that of the regenerator [5]. If plug flow is assumed for the gas, , and if the gas is assumed to be well mixed, .
- Core–annulus modelsThese models are based on the core–annular profile that was observed in fully developed CFB risers by various researchers. The generalised core equations are shown below, contributions for core-annulus interchange from [32] and contributions for dispersion from [179]:Both axial and radial dispersion have been included, but for 1D models either one can be ignored. the transient term may also be ignored for steady-state simulation, which is a common assumption for modelling FCC risers. The gas in the core is usually assumed to be stagnant or be descending at relatively low velocity, hence convective flow terms may be ignored, the material balance equations for gas in this region are given by [32]:are the core radius and the riser radius respectively, and subscripts are the annulus and the core regions respectively. The convective flow terms may be included for the solid phase in order to capture the effect of the downward flow of solids in the annular region that is shown in Figure 8b.
2.6. Feed Vaporisation
| Authors | 1/2D | Kinetic Approach | Kinetic Model | Deactivation Function | Vaporisation | Material Balance | Momentum Balance Approach | Energy Balance |
|---|---|---|---|---|---|---|---|---|
| [2] | 1D | 10-lump model of [18] | Parameters from [18] Coking tendency by [18,142,206] | COC by [142] | Pseudo-homogenous phase, plug flow of gas and solids. | No slip | Thermal equilibrium | |
| [113] | 1D | Single event kinetics | 646 partially lumped components and reaction network with 44169 global reactions. | COC by [18], N2 deactivation considered. | Instant | Pseudo-homogenous phase, plug flow of gas. Empirical coke formation from Jacob [17] | N/A (gas-solid slip accounted for but not shown in equations) | Thermal equilibrium |
| [5,6] | 1D | 4-lump model | GS, GS, LG, CK lumps considered, parameters from [80] | COC | Instant | Two-phase gas-solid flow, plug flow of gas and solids. | E-E | Interphase resistance considered |
| [45] | 1D | Pseudo-component model | 50 pseudo-components considered, rates characterised by normal boiling temp and MR. | COC by [143] | Instant IG molar expansion | Compartments in series for gas and solids (pseudo-homogeneous). | E-E | Thermal equilibrium |
| [207] | 1D | 6-lump model of Takatsuka [208] | VGO, DO, LCO, GS, LPG, FG lumps considered | COC | Instant | Pseudo-homogenous phase, plug flow of gas. | E-L | Thermal equilibrium |
| [209,210] | 2D | 6-lump model of [211] | VGO, LCO, GS, LPG, FG, CK lumps considered, inverse parameter estimation used for parameters | COC | N/A | Pseudo-homogenous phase, plug flow of gas and solids with axial and radial axis. | E-E | Interphase resistance considered. |
| [188] | 1D | 4-lump model of [80] | GS, LG, GS, CK lumps considered, parameters from [80] | TOS by [14] | Instant | Plug flow for gas and solid (pseudo-homogeneous). | Empirical Slip factor correlation by Patience [212] | Thermal equilibrium |
| [213] | 1D | Semi-continuous model | Kinetic parameters expressed using the beta distribution [214] as a function of boiling point temp | COC by [137] | Instant | Plug flow for gas and solid (pseudo-homogeneous). | N/A | Thermal equilibrium |
| [88] | 1D | 4-lump model | GS, GS, LG, CK lumps considered, parameters form [188] | TOS by [14] | Instant | Pseudo-homogenous phase, plug flow of gas and solids. | N/A | Thermal equilibrium |
| [197] | 1D | 6-lump model of Takatsuka et al. [208] | VGO, LCO, GS, LPG, FG, CK lumps considered | COC | instant | Plug flow for gas and solid (pseudo-homogeneous). | E-E | Thermal equilibrium |
| [215] | 1D | Pseudo-component model | 42 pseudo components considered, rates characterised by normal boiling temp (ΔT = 30 °C) and densities. | COC from [45] | Instant | Pseudo-homogenous phase, plug flow of gas and solids. | E-E | Thermal equilibrium |
| [216] | 1D | 4-Lump model | VGO, GS, LG, CK lumps considered, kinetic parameters of [75,143] | COC by [143] | instant | Compartments or CSTR in series for gas and solids (pseudo-homogeneous). | E-L | Thermal equilibrium |
| [217] | 1D | 3-lump model of [74] | GO, GS, CK + LG lumps considered, parameters from [74] Coking rate by Lee [218] | COC | Instant | Pseudo-homogenous phase, plug flow of gas and solids | No slip | Thermal equilibrium |
| [219] | 1D | Pseudo-component model | Pseudo components considered; rates characterised by normal boiling temp (ΔT = 15–30 °C). | COC by [143] | Instant | Pseudo-homogenous phase, plug flow of gas and solids | E-E | Thermal equilibrium |
| [85] | 1D | 6-lump model | GO, DZ, GS, LPG, DG, CK lumps considered, parameter estimation for parameters. | COC as defined by [6] | Instant | Two-phase gas-solid flow, plug flow of gas and solids. | E-E | Interphase resistance considered |
| [220] | 1D | Hybrid structure-oriented model and bond-electron matrix | Feed molecular reconstruction Auto reaction generation similar to [221,222] Reaction network with 3827 molecules and 7572 reactions. Adsorption and diffusion considered. | COC from [86] Deactivation by N2 and heavy aromatics from [86] | Instant | Pseudo-homogenous phase, plug flow of gas and solids | N/A | Isothermal reactor |
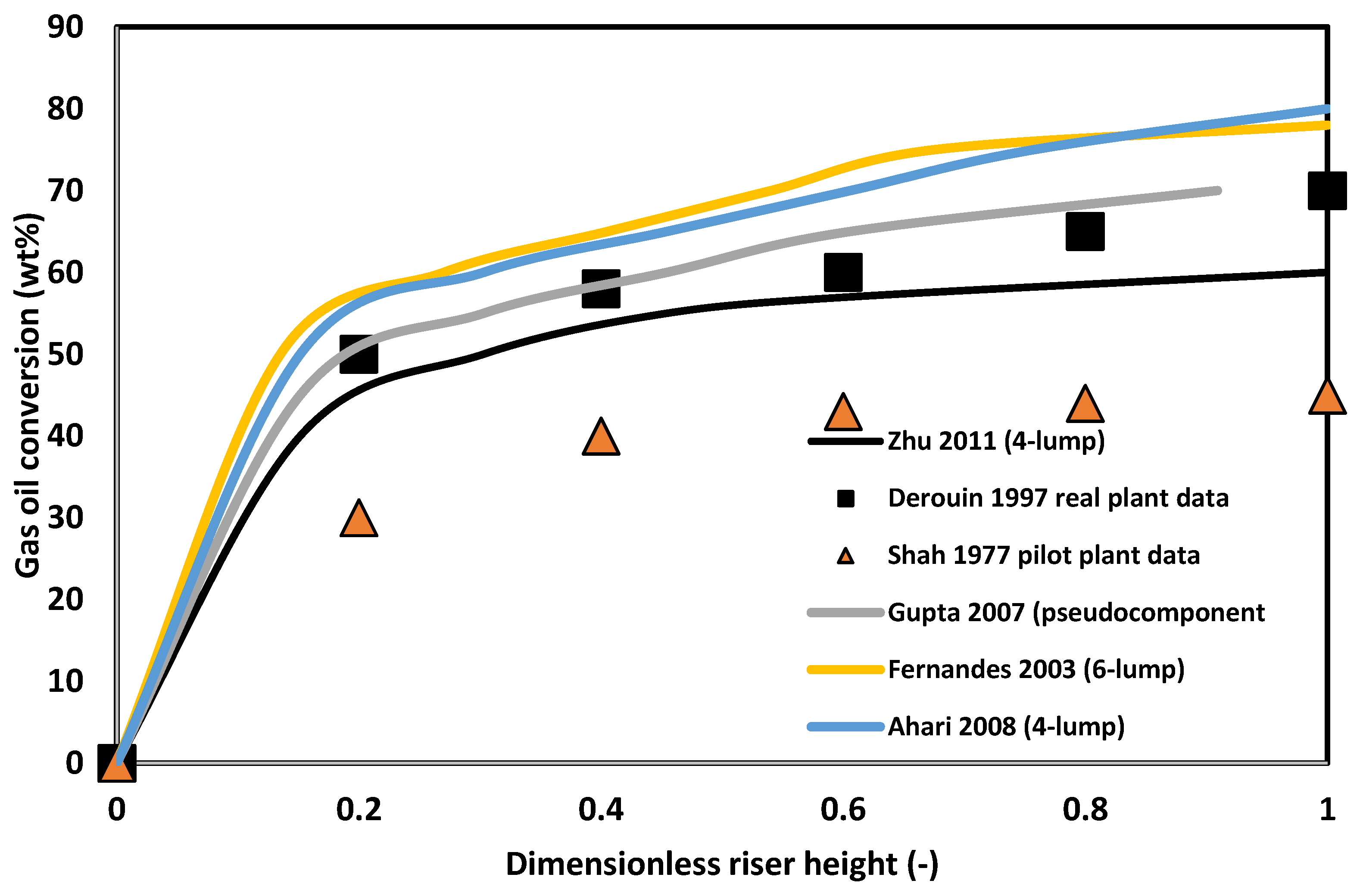
2.7. Riser Performance Prediction
2.8. Shortcomings and Future Recommendations
- (a)
- Vaporisation: the vaporisation has mostly been assumed to be instantaneous (Table 8) to avoid complicating the model. The recent review by Nguyen et al. [198] showed that models that describe vaporisation of atomised droplets in fluidised beds show wide variations in vaporisation times depending on flow conditions and, therefore, even if the assumption of rapid vaporisation may be valid in some cases, it may not be in others. Hence, this section needs to be considered more rigorously in the models to distinguish between the two cases, as ignoring it may lead to inaccurate predictions in certain cases.
- (b)
- Gas and solid dispersion: experimental data from tracer studies considered in this work showed that plug flow of gas may only be assumed in the case where the concentration of solids in the riser is low. However, Table 8 shows that researchers almost always assumed plug flow of gas, which may cause some inaccurate predictions in some cases where the plug flow assumption is inadequate. Hence, it is recommended that dispersion be considered, especially since the literature on dispersion coefficients of both solids and gases in CFB risers is vast.
- (c)
- Cluster formation and core–annular phase inhomogeneity: the literature about the flow structure of CFB risers is now generally in agreement about the core–annulus pattern in the fully developed region of the riser. However, all the models discussed in Table 8 have ignored this phenomenon and assumed that no flow separation is observed (i.e., pseudo-homogeneous) and, therefore, cannot predict the core–annulus profile or its effect on riser performance. 1D momentum balance equations for the riser have also been shown by Tsuo and Gidaspow [189] to be poor at describing the effect of particle clusters on flow, hence more 2D models are required to better predict the riser performance.
- (d)
- Kinetic modelling: Table 8 shows that most workers have overwhelmingly used discrete lumping methodology for describing the reactions in the FCC riser. Several workers have reported the values for the kinetic parameters for the conversion between different lumps which are then used by secondary workers in their models without any recalibration. However, as was discussed before, the lump parameters are very feedstock and catalyst dependent, and as shown by Shah et al. [7], these lumped kinetic parameters failed to predict well the experimental data of Nace et al. [16]. This is a clear indication that such parameters are highly influenced by reaction conditions, and therefore are more error prone when extrapolated to different operating conditions. The world has now come to a point where the computational power is great enough that molecular and structure-oriented lumping techniques such as single event kinetics which have been proved to produce parameters that are feedstock independent, are now worth pursuing. The literature on such parameters has also grown; therefore, such models can be incorporated in FCC models without the need for new parameter estimation exercises.
- (e)
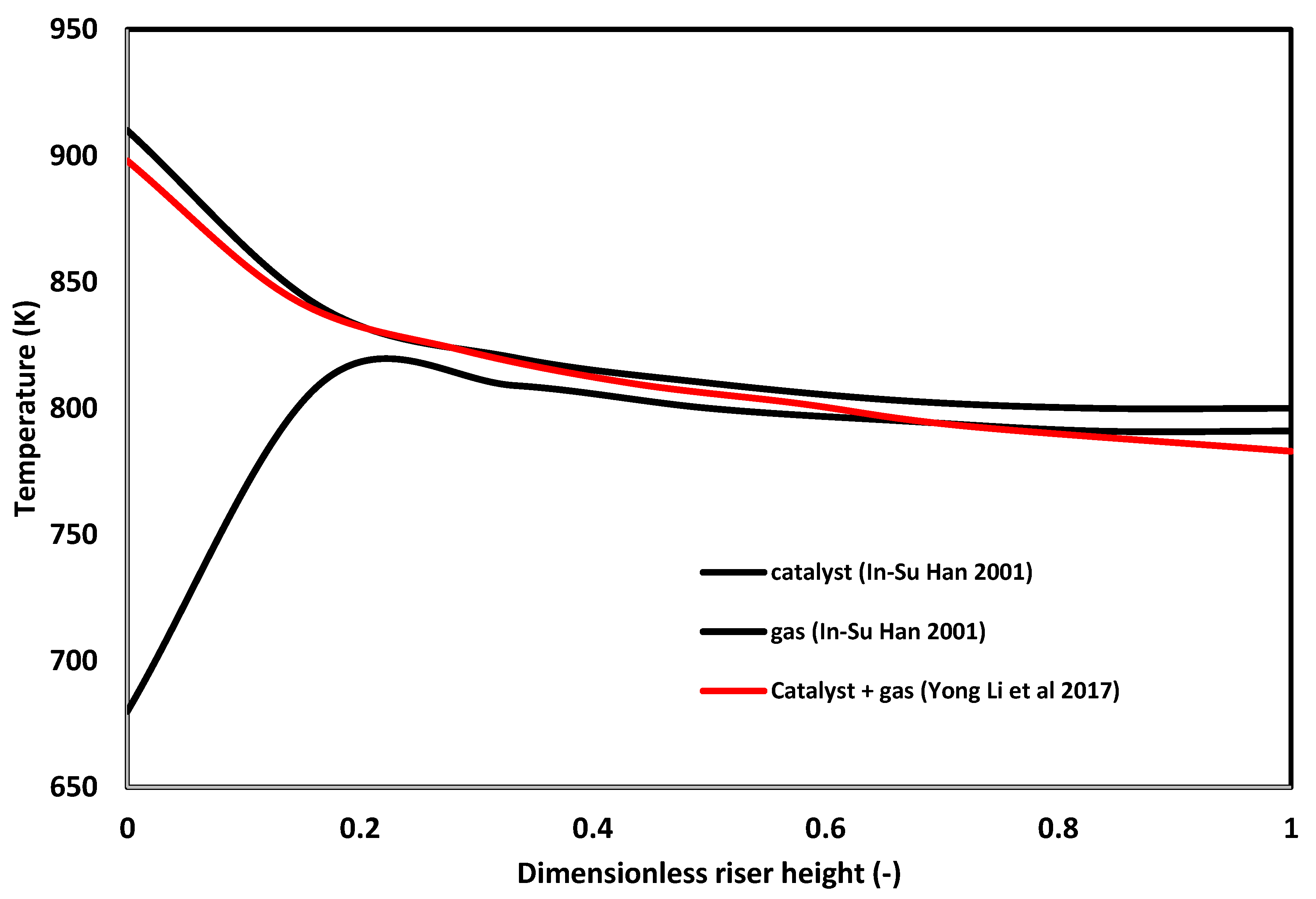
- Thermal balances: the majority of models in Table 8 assume that heat transfer resistance between the two phases may be ignored; however, as was shown by the model from [5], thermal equilibrium between the phases is not reached in the most significant region of the riser (first ) and, therefore, this would be expected to affect the model predictions. There is also a need to explore how the various heat transfer coefficients at the gas–catalyst interphase affect the model predictions as this is yet to be investigated.
- (f)
- Catalyst deactivation: various models for catalyst deactivation are available in the literature and have been used by resarchers for FCC riser simulations. However, the effect of these different deactivation models on the riser predictions is not yet fully understood, hence a comparative study of the effect off different deactivation models is required.
3. Modelling FCC Unit Constitutive Components
Disengager and Stripper
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Kunii, D.; Levenspiel, O. Fluidization Engineering; Butterworth-Heinemann: Oxford, UK, 1991. [Google Scholar]
- Arbel, A.; Huang, Z.; Rinard, I.H.; Shinnar, R.; Sapre, A.V. Dynamic and Control of Fluidized Catalytic Crackers. 1. Modeling of the Current Generation of FCC’s. Ind. Eng. Chem. Res. 1995, 34, 1228–1243. [Google Scholar] [CrossRef]
- Kunii, D.; Levenspiel, O. Entrainment of solids from fluidized beds I. Hold-up of solids in the freeboard II. Operation of fast fluidized beds. Powder Technol. 1990, 61, 193–206. [Google Scholar] [CrossRef]
- Kunii, D.; Levenspiel, O. Fluidized reactor models. 1. For bubbling beds of fine, intermediate, and large particles. 2. For the lean phase: Freeboard and fast fluidization. Ind. Eng. Chem. Res. 1990, 29, 1226–1234. [Google Scholar] [CrossRef]
- Han, I.-S.; Chung, C.-B. Dynamic modeling and simulation of a fluidized catalytic cracking process. Part I: Process modeling. Chem. Eng. Sci. 2001, 56, 1951–1971. [Google Scholar] [CrossRef]
- Han, I.-S.; Chung, C.-B. Dynamic modeling and simulation of a fluidized catalytic cracking process. Part II: Property estimation and simulation. Chem. Eng. Sci. 2001, 56, 1973–1990. [Google Scholar] [CrossRef]
- Shah, M.; Utikar, R.P.; Pareek, V.K.; Evans, G.M.; Joshi, J.B. Computational fluid dynamic modelling of FCC riser: A review. Chem. Eng. Res. Des. 2016, 111, 403–448. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, Y.; Zhu, J. Enhanced fluidization of group A particles modulated by group C powder. Powder Technol. 2020, 377, 684–692. [Google Scholar] [CrossRef]
- Shaul, S.; Rabinovich, E.; Kalman, H. Typical Fluidization Characteristics for Geldart’s Classification Groups. Part. Sci. Technol. 2014, 32, 197–205. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, J.; Zhu, J. Different bubble behaviors in gas-solid fluidized bed of Geldart group A and group C+ particles. Powder Technol. 2021, 384, 431–441. [Google Scholar] [CrossRef]
- Kong, W.; Tan, T.; Baeyens, J.; Flamant, G.; Zhang, H. Bubbling and Slugging of Geldart Group A Powders in Small Diameter Columns. Ind. Eng. Chem. Res. 2017, 56, 4136–4144. [Google Scholar] [CrossRef]
- Lee, J.-R.; Lee, K.-S.; Hasolli, N.; Park, Y.-O.; Lee, K.-Y.; Kim, Y.-H. Fluidization and mixing behaviors of Geldart groups A, B and C particles assisted by vertical vibration in fluidized bed. Chem. Eng. Process. Process. Intensif. 2020, 149, 107856. [Google Scholar] [CrossRef]
- Pinheiro, C.I.C.; Fernandes, J.L.; Domingues, L.; Chambel, A.J.S.; Graça, I.; Oliveira, N.M.C.; Cerqueira, H.S.; Ribeiro, F.R. Fluid Catalytic Cracking (FCC) Process Modeling, Simulation, and Control. Ind. Eng. Chem. Res. 2011, 51, 1–29. [Google Scholar] [CrossRef]
- Weekman, V. Lumps, Models, and Kinetics in Practice; A.I.Ch.E. Monograph Series: New York, NY, USA, 1979; Volume 75, pp. 1–29. [Google Scholar]
- Weekman, V.W., Jr. Kinetics and Dynamics of Catalytic Cracking Selectivity in Fixed-Bed Reactors. Ind. Eng. Chem. Process. Des. Dev. 1969, 8, 385–391. [Google Scholar] [CrossRef]
- Nace, D.M.; Voltz, S.E.; Weekman, V.W., Jr. Application of a Kinetic Model for Catalytic Cracking. Effects of Charge Stocks. Ind. Eng. Chem. Process. Des. Dev. 1971, 10, 530–538. [Google Scholar] [CrossRef]
- Jacob, S.M.; Gross, B.; Voltz, S.E.; Weekman, V.W. A lumping and reaction scheme for catalytic cracking. AIChE J. 1976, 22, 701–713. [Google Scholar] [CrossRef]
- Gross, B.; Jacob, S.M.; Nace, D.M.; Voltz, S.E. Simulation of Catalytic Cracking Process. U.S. Patent No. US3960707A, 1 June 1976. [Google Scholar]
- Arbel, A.; Rinard, I.H.; Shinnar, R.; Sapre, A.V. Dynamics and Control of Fluidized Catalytic Crackers. 2. Multiple Steady States and Instabilities. Ind. Eng. Chem. Res. 1995, 34, 3014–3026. [Google Scholar] [CrossRef]
- Elshishini, S.; Elnashaie, S. Digital simulation of industrial fluid catalytic cracking units: Bifurcation and its implications. Chem. Eng. Sci. 1990, 45, 553–559. [Google Scholar] [CrossRef]
- Quann, R.J.; Jaffe, S.B. Structure-oriented lumping: Describing the chemistry of complex hydrocarbon mixtures. Ind. Eng. Chem. Res. 1992, 31, 2483–2497. [Google Scholar] [CrossRef]
- Vynckier, E.; Froment, G.F. Modeling of the kinetics of complex processes based upon elementary steps. In Kinetic and Thermodynamic Lumping of Multicomponent Mixtures; Elsevier: Amsterdam, The Netherlands, 1991; pp. 131–161. [Google Scholar]
- Froment, G. Kinetic modeling of acid-catalyzed oil refining processes. Catal. Today 1999, 52, 153–163. [Google Scholar] [CrossRef]
- Dave, D.; Zhang, N. Multiobjective optimisation of fluid catalytic cracker unit using genetic algorithms. Comput. Aided Chem. Eng. 2003, 14, 623–628. [Google Scholar] [CrossRef]
- Mora, R.L.; Pascual, M.P.; Miranda, M. Maximixing Propylene Production in a FCC Unit. In Proceedings of the 19th World Petroleum Congress, Madrid, Spain, 29 June–3 July 2008. [Google Scholar]
- Akah, A.; Al-Ghrami, M. Maximizing propylene production via FCC technology. Appl. Petrochem. Res. 2015, 5, 377–392. [Google Scholar] [CrossRef]
- John, Y.M.; Patel, R.; Mujtaba, I.M. Maximization of propylene in an industrial FCC unit. Appl. Petrochem. Res. 2018, 8, 79–95. [Google Scholar] [CrossRef]
- Naik, D.V.; Karthik, V.; Kumar, V.; Prasad, B.; Garg, M.O. Kinetic modeling for catalytic cracking of pyrolysis oils with VGO in a FCC unit. Chem. Eng. Sci. 2017, 170, 790–798. [Google Scholar] [CrossRef]
- Naik, D.V.; Kumar, V.; Prasad, B.; Behera, B.; Atheya, N.; Singh, K.K.; Adhikari, D.K.; Garg, M.O. Catalytic cracking of pyrolysis oil oxygenates (aliphatic and aromatic) with vacuum gas oil and their characterization. Chem. Eng. Res. Des. 2014, 92, 1579–1590. [Google Scholar] [CrossRef]
- Zhang, R.; Li, L.; Liu, Z.; Meng, X. Nine-Lump Kinetic Study of Catalytic Pyrolysis of Gas Oils Derived from Canadian Synthetic Crude Oil. Int. J. Chem. Eng. 2016, 2016, 9148925. [Google Scholar] [CrossRef][Green Version]
- Grace, J.R. Fluidized Bed Reactor Modeling. In Chemical Reactors; ACS: Washington, DC, USA, 1981; Volume 22, pp. 3–18. [Google Scholar] [CrossRef]
- Berruti, F.; Pugsley, T.S.; Godfroy, L.; Chaouki, J.; Patience, G.S. Hydrodynamics of circulating fluidized bed risers: A review. Can. J. Chem. Eng. 1995, 73, 579–602. [Google Scholar] [CrossRef]
- Grace, J.R.; Avidan, A.A.; Knowlton, T.M. Circulating Fluidized Beds; Blackie Academic & Professional: Glasgow, UK, 1997. [Google Scholar]
- Harris, B.J. Modeling options for circulating fluidized beds: A core/annulus deposition model. In Circulating Fluidized Bed Technology IV; Elsevier: Amsterdam, The Netherlands, 1993; pp. 32–39. [Google Scholar]
- Godfroy, L.; Patience, G.S.; Chaouki, J. Radial Hydrodynamics in Risers. Ind. Eng. Chem. Res 1999, 38, 81–89. [Google Scholar] [CrossRef]
- Gupta, R.; Kumar, V.; Srivastava, V.K. Modeling and simulation of fluid catalytic cracking unit. Rev. Chem. Eng. 2005, 21, 95–131. [Google Scholar] [CrossRef]
- Vashisth, S.; Motlagh, A.H.A.; Tebianian, S.; Salcudean, M.; Grace, J.R. Comparison of numerical approaches to model FCC particles in gas–solid bubbling fluidized bed. Chem. Eng. Sci. 2015, 134, 269–286. [Google Scholar] [CrossRef]
- Rao, R.M.; Rengaswamy, R.; Suresh, A.; Balaraman, K. Industrial Experience with Object-Oriented Modelling: FCC case study. Chem. Eng. Res. Des. 2004, 82, 527–552. [Google Scholar] [CrossRef][Green Version]
- Sadeghbeigi, R. Fluid Catalytic Cracking Handbook; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar] [CrossRef]
- Behera, B.; Ray, S.S.; Singh, I. Structural characterization of FCC feeds from Indian refineries by NMR spectroscopy. Fuel 2008, 87, 2322–2333. [Google Scholar] [CrossRef]
- Tissot, B.P.; Welte, D.H. Kerogen: Composition and Classification. In Petroleum Formation and Occurrence; Springer: Berlin/Heidelberg, Germany, 1984; pp. 131–159. [Google Scholar] [CrossRef]
- Rodríguez, E.; Izaddoust, S.; Valecillos, J.; Bilbao, J.; Arandes, J.M.; Castaño, P.; Epelde, E.; Elordi, G. Lessening coke formation and boosting gasoline yield by incorporating scrap tire pyrolysis oil in the cracking conditions of an FCC unit. Energy Convers. Manag. 2020, 224, 113327. [Google Scholar] [CrossRef]
- Stratiev, D.S.; Marinov, I.; Nedelchev, A.; Velkov, I.; Stratiev, D.D.; Veli, A.; Mitkova, M.; Stanulov, K. Evaluation of approaches for conversion of ASTM into TBP distillation data of oil fractions. Oil Gas Eur. Mag. 2014, 4, 216–221. [Google Scholar]
- Behrenbruch, P.; Dedigama, T. Classification and characterisation of crude oils based on distillation properties. J. Pet. Sci. Eng. 2007, 57, 166–180. [Google Scholar] [CrossRef]
- Gupta, R.K.; Kumar, V.; Srivastava, V.K. A new generic approach for the modeling of fluid catalytic cracking (FCC) riser reactor. Chem. Eng. Sci. 2007, 62, 4510–4528. [Google Scholar] [CrossRef]
- Dwyer, J.; Rawlence, D.J. Fluid catalytic cracking: Chemistry. Catal. Today 1993, 18, 487–507. [Google Scholar] [CrossRef]
- Corma, A.; Orchillés, A. Current views on the mechanism of catalytic cracking. Microporous Mesoporous Mater. 2000, 35–36, 21–30. [Google Scholar] [CrossRef]
- Whitmore, F.C.; Schmerling, L.; Ipatieff, V.N. Advances in Catalysis; Academic Press: Cambridge, MA, USA, 1934; Volume 26. [Google Scholar]
- Hiraoka, K.; Kebarle, P. Stabilities and energetics of pentacoordinated carbonium ions. The isomeric protonated ethane ions and some higher analogs: Protonated propane and protonated butane. J. Am. Chem. Soc. 1976, 98, 6119–6125. [Google Scholar] [CrossRef]
- Pansing, W.F. The Catalytic Cracking of Hexadecane—Effects of Impurities, Olefins, and Steam. J. Phys. Chem. 1965, 69, 392–399. [Google Scholar] [CrossRef]
- Greensfelder, B.S.; Voge, H.H.; Good, G.M. Catalytic Cracking of Pure Hydrocarbons. Ind. Eng. Chem. 1945, 37, 1168–1176. [Google Scholar] [CrossRef]
- Kotrel, S.; Knözinger, H.; Gates, B. The Haag–Dessau mechanism of protolytic cracking of alkanes. Microporous Mesoporous Mater. 2000, 35-36, 11–20. [Google Scholar] [CrossRef]
- Haag, W.O.; Dessau, R.M. Duality of mechanism for acid-catalyzed paraffin cracking. In Proceedings of the 8th International Congress on Catalysis, Berlin, Germany, 2–6 July 1984; Volume 2, pp. 305–316. [Google Scholar]
- Haag, W.O.; Dessau, R.M.; Lago, R.M. Chemistry of Microporous Crystals. Stud. Surf. Sci. Catal. 1991, 60, 255–265. [Google Scholar]
- Narbeshuber, T.F.; Vinek, H.; Lercher, J.A. Monomolecular Conversion of Light Alkanes over H-ZSM- 5. J. Catal. 1995, 157, 388–395. [Google Scholar] [CrossRef]
- Lercher, J.A.; van Santen, R.R.; Vinek, H. Carbonium ion formation in zeolite catalysis. Catal. Lett. 1994, 27, 91–96. [Google Scholar] [CrossRef]
- Kwak, B.; Sachtler, W. Effect of Ga/Proton Balance in Ga/HZSM-5 Catalysts on C3 Conversion to Aromatics. J. Catal. 1994, 145, 456–463. [Google Scholar] [CrossRef]
- Krannila, H.; Haag, W.O.; Gates, B.C. Monomolecular and bimolecular mechanisms of paraffin cracking: N-butane cracking catalyzed by HZSM-5. J. Catal. 1992, 135, 115–124. [Google Scholar] [CrossRef]
- Tung, S.; Tung, S.E.; McIninch, E. Zeolitic aluminosilicate II. Surface oxide diffusion, dynamic (time variant) Lewis acids and catalytic activity with hexane on decationized Y. J. Catal. 1968, 10, 175–182. [Google Scholar] [CrossRef]
- Farneth, W.E.; Gorte, R.J. Methods for Characterizing Zeolite Acidity. Chem. Rev. 1995, 95, 615–635. [Google Scholar] [CrossRef]
- Abbot, J.; Guerzoni, F.N. Roles of Brønsted and Lewis sites during cracking of n-octane on H-mordenite. Appl. Catal. A Gen. 1992, 85, 173–188. [Google Scholar] [CrossRef]
- Kissin, Y.V. Primary Products in Hydrocarbon Cracking over Solid Acidic Catalysts under Very Mild Conditions: Relation to Cracking Mechanism. J. Catal. 1998, 180, 101–105. [Google Scholar] [CrossRef]
- Kissin, Y.V. Chemical Mechanism of Hydrocarbon Cracking over Solid Acidic Catalysts. J. Catal. 1996, 163, 50–62. [Google Scholar] [CrossRef]
- Kazansky, V.B.; Senchenya, I.N. Quantum chemical study of the electronic structure and geometry of surface alkoxy groups as probable active intermediates of heterogeneous acidic catalysts: What are the adsorbed carbenium ions? J. Catal. 1989, 119, 108–120. [Google Scholar] [CrossRef]
- Frash, M.V.; Solkan, V.N.; Kazansky, V.B. A quantum-chemical study of hydride transfer from alkanes to carbenium cations in the gas phase: A comparison with liquid- and solid-acid catalytic systems. J. Chem. Soc. Faraday Trans. 1997, 93, 515–520. [Google Scholar] [CrossRef]
- Caeiro, G.; Carvalho, R.; Wang, X.; Lemos, M.A.; Lemos, F.; Guisnet, M.; Ribeiro, F.R. Activation of C2–C4 alkanes over acid and bifunctional zeolite catalysts. J. Mol. Catal. A Chem. 2006, 255, 131–158. [Google Scholar] [CrossRef]
- Bartholomew, C.H.; Farrauto, R.J. Fundamentals of Industrial Catalytic Processes; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Yaluris, G.; Rekoske, J.E.; Aparicio, L.M.; Madon, R.J.; Dumesic, J.A. Isobutane Cracking over Y-Zeolites: I. Development of a Kinetic-Model. J. Catal. 1995, 153, 54–64. [Google Scholar] [CrossRef]
- Yaluris, G.; Rekoske, J.E.; Aparicio, L.M.; Madon, R.J.; Dumesic, J.A. Isobutane Cracking over Y-Zeolites: II. Catalytic Cycles and Reaction Selectivity. J. Catal. 1995, 153, 65–75. [Google Scholar] [CrossRef]
- Yaluris, G.; Madon, R.J.; Dumesic, J.A. 2-Methylhexane Cracking on Y Zeolites: Catalytic Cycles and Reaction Selectivity. J. Catal. 1997, 165, 205–220. [Google Scholar] [CrossRef]
- Cortright, R.D.; Dumesic, J.A.; Madon, R.J. Catalytic cycles for hydrocarbon cracking on zeolites. Top. Catal. 1997, 4, 15–26. [Google Scholar] [CrossRef]
- De Oliveira, L.P.; Hudebine, D.; Guillaume, D.; Verstraete, J.J. A Review of Kinetic Modeling Methodologies for Complex Processes. Oil Gas Sci. Technol. 2016, 71, 45. [Google Scholar] [CrossRef]
- Ho, T.C. Modeling of Reaction Kinetics for Petroleum Fractions. In Practical Advances in Petroleum Processing; Springer: New York, NY, USA, 2006; pp. 653–694. [Google Scholar] [CrossRef]
- Weekman, V.W.; Nace, D.M. Kinetics of catalytic cracking selectivity in fixed, moving, and fluid bed reactors. AIChE J. 1970, 16, 397–404. [Google Scholar] [CrossRef]
- Lee, L.-S.; Chen, Y.-W.; Huang, T.-N.; Pan, W.-Y. Four-lump kinetic model for fluid catalytic cracking process. Can. J. Chem. Eng. 1989, 67, 615–619. [Google Scholar] [CrossRef]
- Yen, L.C.; Wrench, R.E.; Ong, A.S. Reaction kinetic correlation equation predicts fluid catalytic cracking coke yields. Oil Gas J. 1988, 86, 2. [Google Scholar]
- Corella, J.; Francés, E. Analysis of the Riser Reactor of a Fluid Cracking Unit. ACS Symp. Ser. 1991, 452, 165–182. [Google Scholar] [CrossRef]
- Larocca, M.; Ng, S.; de Lasa, H. Fast catalytic cracking of heavy gas oils: Modeling coke deactivation. Ind. Eng. Chem. Res. 1990, 29, 171–180. [Google Scholar] [CrossRef]
- Ancheyta-Juárez, J.; López-Isunza, F.; Aguilar-Rodríguez, E. 5-Lump kinetic model for gas oil catalytic cracking. Appl. Catal. A Gen. 1999, 177, 227–235. [Google Scholar] [CrossRef]
- Ancheyta-Juárez, J.; López-Isunza, F.; Aguilar-Rodríguez, E.; Moreno-Mayorga, J.C. A Strategy for Kinetic Parameter Estimation in the Fluid Catalytic Cracking Process. Ind. Eng. Chem. Res. 1997, 36, 5170–5174. [Google Scholar] [CrossRef]
- Ancheyta-Juárez, J.; Murillo-Hernández, J.A. A Simple Method for Estimating Gasoline, Gas, and Coke Yields in FCC Processes. Energy Fuels 2000, 14, 373–379. [Google Scholar] [CrossRef]
- Dupain, X.; Gamas, E.D.; Madon, R.; Kelkar, C.P.; Makkee, M.; Moulijn, J.A. Aromatic gas oil cracking under realistic FCC conditions in a microriser reactor☆. Fuel 2003, 82, 1559–1569. [Google Scholar] [CrossRef]
- Bollas, G.M.; Lappas, A.A.; Iatridis, D.K.; Vasalos, I.A. Five-lump kinetic model with selective catalyst deactivation for the prediction of the product selectivity in the fluid catalytic cracking process. Catal. Today 2007, 127, 31–43. [Google Scholar] [CrossRef]
- Ancheyta-Juárez, J.; Sotelo-Boyás, R. Estimation of Kinetic Constants of a Five-Lump Model for Fluid Catalytic Cracking Process Using Simpler Sub-models. Energy Fuels 2000, 14, 1226–1231. [Google Scholar] [CrossRef]
- John, Y.M.; Mustafa, M.A.; Patel, R.; Mujtaba, I.M. Parameter estimation of a six-lump kinetic model of an industrial fluid catalytic cracking unit. Fuel 2019, 235, 1436–1454. [Google Scholar] [CrossRef]
- Xiong, K.; Lu, C.; Wang, Z.; Gao, X. Kinetic study of catalytic cracking of heavy oil over an in-situ crystallized FCC catalyst. Fuel 2015, 142, 65–72. [Google Scholar] [CrossRef]
- Souza, J.A.; Vargas, J.V.C.; von Meien, O.F.; Martignoni, W.P.; Ordonez, J.C. The inverse methodology of parameter estimation for model adjustment, design, simulation, control and optimization of fluid catalytic cracking (FCC) risers. J. Chem. Technol. Biotechnol. 2009, 84, 343–355. [Google Scholar] [CrossRef]
- Heydari, M.; Ebrahim, H.A.; Dabir, B. Modeling of an Industrial Riser in the Fluid Catalytic Cracking Unit. Am. J. Appl. Sci. 2010, 7, 221–226. [Google Scholar] [CrossRef]
- Wang, X.S.; Weng, H.X.; Mao, X.J.; Liu, F.Y.; Sha, Y.X.; Den, X.L. Investigation of the lumped kinetic model for catalytic cracking IV determination of kinetic parameters in heavy gas oil network. Acta Sin. 1988, 4, 11–17. [Google Scholar]
- Gao, H.; Wang, G.; Xu, C.; Gao, J. Eight-Lump Kinetic Modeling of Vacuum Residue Catalytic Cracking in an Independent Fluid Bed Reactor. Energy Fuels 2014, 28, 6554–6562. [Google Scholar] [CrossRef]
- Mao, X.; Weng, H.; Zhu, Z.; Wang, S.; Zhu, K. Investigation of the lumped kinetic model for catalytic cracking: III. Analyzing light oil feed and products and measurement of kinetic constants. Acta. Pet. Sin. 1985, 1, 11–18. [Google Scholar]
- Oliveira, L.L.; Biscaia, E. Catalytic cracking kinetic models. Parameter estimation and model evaluation. Ind. Eng. Chem. Res. 1989, 28, 264–271. [Google Scholar] [CrossRef]
- Sun, T.D.; Zhong, X.; Chen, Y.; Yu, B.T. Study and application of a lumping FCC kinetics model for vacuum residue. Petrol. Process. Petrochem. 2001, 32, 41–44. [Google Scholar]
- Watson, K.M.; Nelson, E.F. Improved Methods for Approximating Critical and Thermal Properties of Petroleum Fractions. Ind. Eng. Chem. 1933, 25, 880–887. [Google Scholar] [CrossRef]
- Edmister, W.C.; Lee, B.K. Applied Hydrocarbon Thermodynamics, 2nd ed.; Gulf Professional Publishing: Houston, TX, USA, 1984; Volume 1. [Google Scholar]
- Aris, R.; Gavalas, G.R. On the theory of reactions in continuous mixtures. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1966, 260, 351–393. [Google Scholar]
- Laxminarasimhan, C.S.; Verma, R.P.; Ramachandran, P.A. Continuous lumping model for simulation of hydrocracking. AIChE J. 1996, 42, 2645–2653. [Google Scholar] [CrossRef]
- Amhammed, M.M. Applications of Lumping Kinetics Methodology to Complex Reactive Mixtures. Ph.D. Thesis, Heriot-Watt University, Edinburgh, UK, 2013. [Google Scholar]
- Chou, M.Y.; Ho, T.C. Continuum theory for lumping nonlinear reactions. AIChE J. 1988, 34, 1519–1527. [Google Scholar] [CrossRef]
- Lababidi, H.M.S.; Alhumaidan, F.S. Modeling the Hydrocracking Kinetics of Atmospheric Residue in Hydrotreating Processes by the Continuous Lumping Approach. Energy Fuels 2011, 25, 1939–1949. [Google Scholar] [CrossRef]
- McCoy, B.J.; Wang, M. Continuous-mixture fragmentation kinetics: Particle size reduction and molecular cracking. Chem. Eng. Sci. 1994, 49, 3773–3785. [Google Scholar] [CrossRef]
- Cicarelli, P.; Astarita, G.; Gallifuoco, A. Continuous kinetic lumping of catalytic cracking processes. AIChE J. 1992, 38, 1038–1044. [Google Scholar] [CrossRef]
- Aris, R.; Astarita, G. Continuous lumping of nonlinear chemical kinetics. Chem. Eng. Process. Process. Intensif. 1989, 26, 63–69. [Google Scholar] [CrossRef]
- Astarita, G.; Ocone, R. Lumping nonlinear kinetics. AIChE J. 1988, 34, 1299–1309. [Google Scholar] [CrossRef]
- Peixoto, F.C.; de Medeiros, J.L. Reactions in multiindexed continuous mixtures: Catalytic cracking of petroleum fractions. AIChE J. 2001, 47, 935–947. [Google Scholar] [CrossRef]
- Peixoto, F.C.; Platt, G.M.; Pessoa, F.L.P. Vapor–liquid equilibria of multi-indexed continuous mixtures using an equation of state and group contribution methods. Chem. Eng. J. 2000, 77, 179–187. [Google Scholar] [CrossRef]
- Ho, T.C.; White, B.S. On the continuum approximation of large reaction mixtures. AIChE J. 2010, 56, 1894–1906. [Google Scholar] [CrossRef]
- Aris, R. Prolegomena to the rational analysis of systems of chemical reactions II. Some addenda. Arch. Ration. Mech. Anal. 1968, 27, 356–364. [Google Scholar] [CrossRef]
- Krambeck, F.J. Computers and modern analysis in reactor design. Inst. Chem. Eng. Symp. Ser. 1984, 87, 733. [Google Scholar]
- Chou, M.Y.; Ho, T.C. Lumping coupled nonlinear reactions in continuous mixtures. AIChE J. 1989, 35, 533–538. [Google Scholar] [CrossRef]
- McCoy, B.J. Continuous kinetics of cracking reactions: Thermolysis and pyrolysis. Chem. Eng. Sci. 1996, 51, 2903–2908. [Google Scholar] [CrossRef]
- Froment, G.F. Single Event Kinetic Modeling of Complex Catalytic Processes. Catal. Rev. 2005, 47, 83–124. [Google Scholar] [CrossRef]
- Dewachtere, N.V.; Santaella, F.; Froment, G.F. Application of a single-event kinetic model in the simulation of an industrial riser reactor for the catalytic cracking of vacuum gas oil. Chem. Eng. Sci. 1999, 54, 3653–3660. [Google Scholar] [CrossRef]
- Moustafa, T.M.; Froment, G.F. Kinetic Modeling of Coke Formation and Deactivation in the Catalytic Cracking of Vacuum Gas Oil. Ind. Eng. Chem. Res. 2003, 42, 14–25. [Google Scholar] [CrossRef]
- Feng, W.; Vynckier, E.; Froment, G.F. Single event kinetics of catalytic cracking. Ind. Eng. Chem. Res. 1993, 32, 2997–3005. [Google Scholar] [CrossRef]
- Surla, K.; Guillaume, D.; Verstraete, J.J.; Galtier, P. Kinetic Modeling using the Single-Event Methodology: Application to the Isomerization of Light Paraffins. Oil Gas Sci. Technol. 2011, 66, 343–365. [Google Scholar] [CrossRef][Green Version]
- D’Hooge, D.R.; Reyniers, M.-F.; Marin, G.B. Methodology for Kinetic Modeling of Atom Transfer Radical Polymerization. Macromol. React. Eng. 2009, 3, 185–209. [Google Scholar] [CrossRef]
- De Rybel, N.; van Steenberge, P.H.M.; Reyniers, M.-F.; Barner-Kowollik, C.; D’Hooge, D.R.; Marin, G.B. An Update on the Pivotal Role of Kinetic Modeling for the Mechanistic Understanding and Design of Bulk and Solution RAFT Polymerization. Macromol. Theory Simul. 2017, 26, 1600048. [Google Scholar] [CrossRef]
- Clymans, P.J.; Froment, G.F. Computer-generation of reaction paths and rate equations in the thermal cracking of normal and branched paraffins. Comput. Chem. Eng. 1984, 8, 137–142. [Google Scholar] [CrossRef]
- Prickett, S.E.; Mavrovouniotis, M.L. Construction of complex reaction systems—I. Reaction description language. Comput. Chem. Eng. 1997, 21, 1219–1235. [Google Scholar] [CrossRef]
- Joshi, P.V. Molecular and Mechanistic Modeling of Complex Process Chemistries: A Generic Approach to Automated Model Building. Ph.D. Thesis, University of Delaware, Newark, DE, USA, 1998. [Google Scholar]
- Christensen, G.; Apelian, M.R.; Hickey, K.J.; Jaffe, S.B. Future directions in modeling the FCC process: An emphasis on product quality. Chem. Eng. Sci. 1999, 54, 2753–2764. [Google Scholar] [CrossRef]
- Solorzano, R.Q.; Thybaut, J.W.; Marin, G.B. A single-event microkinetic analysis of the catalytic cracking of (cyclo)alkanes on an equilibrium catalyst in the absence of coke formation. Chem. Eng. Sci. 2007, 62, 5033–5038. [Google Scholar] [CrossRef]
- Solorzano, R.Q.; Thybaut, J.W.; Galtier, P.; Marin, G.B. Simulation of an industrial riser for catalytic cracking in the presence of coking using Single-Event MicroKinetics. Catal. Today 2010, 150, 319–331. [Google Scholar] [CrossRef]
- Xue, G.; Huixin, W.; Thybaut, J.; Marin, G. Catalytic cracking of cycloparaffins admixed with olefins: 2. Single-event microkinetic (semk) assessment. China Pet. Process. Petrochem. Technol. 2014, 16, 84–90. [Google Scholar]
- Standl, S.; Tonigold, M.; Hinrichsen, O. Single-Event Kinetic Modeling of Olefin Cracking on ZSM-5: Proof of Feed Independence. Ind. Eng. Chem. Res. 2017, 56, 13096–13108. [Google Scholar] [CrossRef]
- von Aretin, T.; Standl, S.; Tonigold, M.; Hinrichsen, O. Optimization of the product spectrum for 1-pentene cracking on ZSM-5 using single-event methodology. Part 2: Recycle reactor. Chem. Eng. J. 2017, 309, 873–885. [Google Scholar] [CrossRef]
- Standl, S.; Kirchberger, F.M.; Kühlewind, T.; Tonigold, M.; Sanchez-Sanchez, M.; Lercher, J.A.; Hinrichsen, O. Single-event kinetic model for methanol-to-olefins (MTO) over ZSM-5: Fundamental kinetics for the olefin co-feed reactivity. Chem. Eng. J. 2020, 402, 126023. [Google Scholar] [CrossRef]
- Beirnaert, H.C.; Alleman, J.R.; Marin, G.B. A fundamental kinetic model for the catalytic cracking of alkanes on a USY zeolite in the presence of coke formation. Ind. Eng. Chem. Res. 2001, 40, 1337–1347. [Google Scholar] [CrossRef]
- Quintana-Solórzano, R.; Thybaut, J.W.; Marin, G.B.; Lødeng, R.; Holmen, A. Single-Event MicroKinetics for coke formation in catalytic cracking. Catal. Today 2005, 107–108, 619–629. [Google Scholar] [CrossRef]
- Cerqueira, H.S.; Caeiro, G.; Costa, L.; Ribeiro, F.R. Deactivation of FCC catalysts. J. Mol. Catal. A Chem. 2008, 292, 1–13. [Google Scholar] [CrossRef]
- Guisnet, M.; Magnoux, P. Deactivation by coking of zeolite catalysts. Prevention of deactivation. Optimal conditions for regeneration. Catal. Today 1997, 36, 477–483. [Google Scholar] [CrossRef]
- Guisnet, M.; Magnoux, P. Organic chemistry of coke formation. Appl. Catal. A Gen. 2001, 212, 83–96. [Google Scholar] [CrossRef]
- Reyes, S.C.; Scriven, L.E. Analysis of zeolite catalyst deactivation during catalytic cracking reactions. Ind. Eng. Chem. Res. 1991, 30, 71–82. [Google Scholar] [CrossRef]
- Froment, G.F. A Quantitative Approach of Catalyst Deactivation by Coke Formation; Elsevier: Amsterdam, The Netherlands, 1980; pp. 1–19. [Google Scholar] [CrossRef]
- Forzatti, P.; Lietti, L. Catalyst deactivation. Catal. Today 1999, 52, 165–181. [Google Scholar] [CrossRef]
- Froment, G.F. The Modeling of Catalyst Deactivation by Coke Formation; Elsevier: Amsterdam, The Netherlands, 1991; pp. 53–83. [Google Scholar] [CrossRef]
- Rodríguez, E.; Elordi, G.; Valecillos, J.; Izaddoust, S.; Bilbao, J.; Arandes, J.M.; Castaño, P. Coke deposition and product distribution in the co-cracking of waste polyolefin derived streams and vacuum gas oil under FCC unit conditions. Fuel Process. Technol. 2019, 192, 130–139. [Google Scholar] [CrossRef]
- Froment, G. Modeling of catalyst deactivation. Appl. Catal. A Gen. 2001, 212, 117–128. [Google Scholar] [CrossRef]
- Corella, J. On the Modeling of the Kinetics of the Selective Deactivation of Catalysts. Application to the Fluidized Catalytic Cracking Process. Ind. Eng. Chem. Res. 2004, 43, 4080–4086. [Google Scholar] [CrossRef]
- Farag, H.; Ng, S.; de Lasa, H. Kinetic modeling of catalytic cracking of gas oils using in situ traps (FCCT) to prevent metal contaminant effects. Ind. Eng. Chem. Res. 1993, 32, 1071–1080. [Google Scholar] [CrossRef]
- Krambeck, F.J. Continuous mixtures in fluid catalytic cracking and extensions. In Mobil Workshop on Chemical Reaction in Complex Mixtures; van Nostrand Reinhold: New York, NY, USA, 1991; pp. 42–59. [Google Scholar]
- Pitault, I.; Forissier, M.; Bernard, J.R. Determination of Kinetic Constants of Catalytic Cracking in Microactivity Test Modeling. Can. J. Chem. Eng. 1995, 73, 498–504. [Google Scholar] [CrossRef]
- Fernandes, J.L.; Domingues, L.H.; Pinheiro, C.I.C.; Oliveira, N.M.C.; Ribeiro, F.R. Influence of different catalyst deactivation models in a validated simulator of an industrial UOP FCC unit with high-efficiency regenerator. Fuel 2012, 97, 97–108. [Google Scholar] [CrossRef]
- Davidson, J.F.; Clift, R.; Harrison, D. Fluidization, 2nd ed.; Academic Press: Cambridge, MA, USA, 1985. [Google Scholar]
- Bi, H.T.; Ellis, N.; Abba, I.A.; Grace, J.R. A state-of-the-art review of gas–solid turbulent fluidization. Chem. Eng. Sci. 2000, 55, 4789–4825. [Google Scholar] [CrossRef]
- Lim, K.S.; Zhu, J.X.; Grace, J.R. Hydrodynamics of gas-solid fluidization. Int. J. Multiph. Flow 1995, 21, 141–193. [Google Scholar] [CrossRef]
- Rhodes, M.J.; Geldart, D. The hydrodynamics of re-circulating fluidized beds. In Circulating Fluidized Bed Technology, Proceedings of the First International Conference on Circulating Fluidized Beds, Halifax, NS, Canada, 18–20 November 1985; Elsevier: Amsterdam, The Netherlands, 1985; pp. 193–200. [Google Scholar] [CrossRef]
- Louge, M.; Chang, H. Pressure and voidage gradients in vertical gas-solid risers. Powder Technol. 1990, 60, 197–201. [Google Scholar] [CrossRef]
- Li, I.; Kwauk, M. Two-Phase Flow: The Energy-Minimization Multi-Scale Method; Metallurgy Industry Press: Beijing, China, 1994. [Google Scholar]
- Wei, F.; Lin, H.; Cheng, Y.; Wang, Z.; Jin, Y. Profiles of particle velocity and solids fraction in a high-density riser. Powder Technol. 1998, 100, 183–189. [Google Scholar] [CrossRef]
- Pärssinen, J.H.; Zhu, J.-X. Particle velocity and flow development in a long and high-flux circulating fluidized bed riser. Chem. Eng. Sci. 2001, 56, 5295–5303. [Google Scholar] [CrossRef]
- Derouin, C.; Nevicato, D.; Forissier, M.; Wild, G.; Bernard, J.-R. Hydrodynamics of Riser Units and Their Impact on FCC Operation. Ind. Eng. Chem. Res. 1997, 36, 4504–4515. [Google Scholar] [CrossRef]
- Miller, A.; Gidaspow, D. Dense, vertical gas-solid flow in a pipe. AIChE J. 1992, 38, 1801–1815. [Google Scholar] [CrossRef]
- Martin, M.P.; Turlier, P.; Bernard, J.R.; Wild, G. Gas and solid behavior in cracking circulating fluidized beds. Powder Technol. 1992, 70, 249–258. [Google Scholar] [CrossRef]
- Martin, M.P.; Derouin, C.; Turlier, P.; Forissier, M.; Wild, G.; Bernard, J.R. Catalytic cracking in riser reactors: Core-annulus and elbow effects. Chem. Eng. Sci. 1992, 47, 2319–2324. [Google Scholar] [CrossRef]
- Senior, R.C.; Brereton, C. Modelling of circulating fluidised-bed solids flow and distribution. Chem. Eng. Sci. 1992, 47, 281–296. [Google Scholar] [CrossRef]
- Wong, R.; Pugsley, T.; Berrut, F. Modelling the axial voidage profile and flow structure in risers of circulating fluidized beds. Chem. Eng. Sci. 1992, 47, 2301–2306. [Google Scholar] [CrossRef]
- Noymer, P.D.; Glicksman, L.R. Descent velocities of particle clusters at the wall of a circulating fluidized bed. Chem. Eng. Sci. 2000, 55, 5283–5289. [Google Scholar] [CrossRef]
- Pandey, P.; Turton, R.; Yue, P.; Shadle, L. Nonintrusive Particle Motion Studies in the Near-Wall Region of a Pilot-Scale Circulating Fluidized Bed. Ind. Eng. Chem. Res. 2004, 43, 5582–5592. [Google Scholar] [CrossRef]
- Cankurt, N.T.; Yerushalmi, J. Gas Backmixing in High Velocity Fluidized Beds. In Fluidization; Cambridge University Press: Cambridge, MA, USA, 1978; p. 387. [Google Scholar]
- Cocco, R.; Shaffer, F.; Hays, R.; Karri, S.B.R.; Knowlton, T. Particle clusters in and above fluidized beds. Powder Technol. 2010, 203, 3–11. [Google Scholar] [CrossRef]
- McMillan, J.; Shaffer, F.; Gopalan, B.; Chew, J.W.; Hrenya, C.; Hays, R.; Karri, S.R.; Cocco, R. Particle cluster dynamics during fluidization. Chem. Eng. Sci. 2013, 100, 39–51. [Google Scholar] [CrossRef]
- Horio, M.; Kuroki, H. Three-dimensional flow visualization of dilutely dispersed solids in bubbling and circulating fluidized beds. Chem. Eng. Sci. 1994, 49, 2413–2421. [Google Scholar] [CrossRef]
- Horio, M.; Nonaka, A. A generalized bubble diameter correlation for gas-solid fluidized beds. AIChE J. 1987, 33, 1865–1872. [Google Scholar] [CrossRef]
- Grace, J. High-velocity fluidized bed reactors. Chem. Eng. Sci. 1990, 45, 1953–1966. [Google Scholar] [CrossRef]
- Bader, R.; Findlay, J.; Knowlton, T.M. Gas/solids flow patterns in a 30.5-cm-diameter circulating fluidized bed. In Circulating Fluidized Bed Technology, Proceedings of the Second International Conference on Circulating Fluidized Beds, Compiégne, France, 14–18 March 1988; Elsevier: Amsterdam, The Netherlands, 1988; pp. 123–137. [Google Scholar] [CrossRef]
- Van Deemter, J.J. Mixing. Fluidization; Academic Press: New York, NY, USA, 1985; pp. 331–355. [Google Scholar]
- Stubington, J.F.; Chan, S.W. On the phase location and rate of volatiles combustion in bubbling fluidized bed combustors. Chem. Eng. Res. Des. 1990, 68, 195–201. [Google Scholar]
- Li, J.; Weinstein, H. An experimental comparison of gas backmixing in fluidized beds across the regime spectrum. Chem. Eng. Sci. 1989, 44, 1697–1705. [Google Scholar] [CrossRef]
- Li, Y.; Wu, P. A study on axial gas mixing in a fast fluidized bed. In Circulating Fluidized Bed Technology III; Basu, P., Ed.; Pergamon Press: Toronto, ON, Canada, 1991; pp. 581–586. [Google Scholar]
- Zhu, J.X.; Bi, H.T. Development of CFB and High Density Circulating Fluidized Beds. In Circulating Fluidized Bed Technology IV; Avidan, A.A., Ed.; AIChE: New York, NY, USA, 1993. [Google Scholar]
- Schugerl, K. Experimental Comparison of Mixing Processes in Two and Three Phase Fluidized Beds. In Proceedings of the International Symposium on Fluidization, Eindhoven, The Netherlands, 6–9 June 1967; pp. 782–794. [Google Scholar]
- Dry, R.J.; White, C.C. Gas residence-time characteristics in a high-velocity circulating fluidised bed of FCC catalyst. Powder Technol. 1989, 58, 17–23. [Google Scholar] [CrossRef]
- Van Zoonen, D. Measurements of diffusional phenomena and velocity profiles in a vertical riser. In Proc. Symp. on The Interaction between Fluids and Particles, 1962; Instn, Chem. Engrs: Rugby, UK, 1962; pp. 64–71. [Google Scholar]
- Brereton, C.M.H.; Grace, J.R.; Yu, J. Axial gas mixing in a circulating fluidized bed. In Circulating Fluidized Bed Technology, Proceedings of the Second International Conference on Circulating Fluidized Beds, Compiégne, France, 14–18 March 1988; Elsevier: Amsterdam, The Netherlands, 1988; pp. 307–314. [Google Scholar] [CrossRef]
- Bai, D.R. Residence time distributions of gas and solids in a circulating fluidized bed. In Fluidization VII; Engineering Foundation: New York, NY, USA, 1992; pp. 195–202. [Google Scholar]
- Helmrich, H.; Schugerl, K.; Janssen, K. Decomposition of NaHCO3 in laboratory and bench scale circulating fluidized bed reactors. In Circulating Fluidized Bed Technology, Proceedings of the First International Conference on Circulating Fluidized Beds, Halifax, NS, Canada, 18–20 November 1985; Elsevier: Amsterdam, The Netherlands, 1986; pp. 161–166. [Google Scholar] [CrossRef]
- Werther, J.; Hartge, E.U.; Kruse, M.; Potter, O.E.; Nicklin, D.J. Gas mixing and interphase mass transfer in the circulating fluidized bed. In Fluidization VII; Engineering Foundation: New York, NY, USA, 1992; pp. 257–264. [Google Scholar]
- Couturier, M.; Doucette, B.; Stevens, D.; Poolpol, S.; Razbin, V. Temperature, gas concentration and solid mass flux profiles within a large circulating fluidized bed combustor. In Proceedings of the Eleventh International Conference on Fluidized Bed Combustion, Montreal, QC, Canada, 21–24 April 1991; pp. 21–24. [Google Scholar]
- Zheng, Q.; Xing, W.; Lou, F. Experimental study on radial gas dispersion and its enhancement in circulating fluidized beds. In Fluidization VII; Engineering Foundation: New York, NY, USA, 1992; pp. 285–293. [Google Scholar]
- Svensson, A. Fluid Dynamics of the Bottom Bed of Circulating Fluidized Bed Boilers. Ph.D. Thesis, Chalmers University of Technology, Gothenburg, Sweden, 1995. [Google Scholar]
- Svensson, A.; Johnsson, F.; Leckner, B. Bottom bed regimes in a circulating fluidized bed boiler. Int. J. Multiph. Flow 1996, 22, 1187–1204. [Google Scholar] [CrossRef]
- Wei, F.; Lin, S.; Yang, G. Gas and solids mixing in a commercial FCC regenerator. Chem. Eng. Technol. 1993, 16, 109–113. [Google Scholar] [CrossRef]
- Lee, G.S.; Kim, S.D. Axial mixing of solids in turbulent fluidized beds. Chem. Eng. J. 1990, 44, 1–9. [Google Scholar] [CrossRef]
- Edwards, M.; Avidan, A. Conversion model aids scale-up of mobil’s fluid-bed MTG process. Chem. Eng. Sci. 1986, 41, 829–835. [Google Scholar] [CrossRef]
- Foka, M.; Chaouki, J.; Guy, C.; Klvana, D. Natural gas combustion in a catalytic turbulent fluidized bed. Chem. Eng. Sci. 1994, 49, 4269–4276. [Google Scholar] [CrossRef]
- Ahari, J.S.; Farshi, A.; Forsat, K. A mathematical modeling of the riser reactor in industrial FCC unit. Pet. Coal 2008, 50, 15–24. [Google Scholar]
- Tsuo, Y.P.; Gidaspow, D. Computation of flow patterns in circulating fluidized beds. AIChE J. 1990, 36, 885–896. [Google Scholar] [CrossRef]
- Gidaspow, D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Drew, D.A. Mathematical Modeling of Two-Phase Flow. Annu. Rev. Fluid Mech. 1983, 15, 261–291. [Google Scholar] [CrossRef]
- Lu, H.; Gidaspow, D.; Wang, S. Computational Fluid Dynamics and the Theory of Fluidization; Springer: Singapore, 2021. [Google Scholar]
- Pugsley, T.S.; Berruti, F. A predictive hydrodynamic model for circulating fluidized bed risers. Powder Technol. 1996, 89, 57–69. [Google Scholar] [CrossRef]
- Sabbaghan, H.; Sotudeh-Gharebagh, R.; Mostoufi, N. Modeling the acceleration zone in the riser of circulating fluidized beds. Powder Technol. 2004, 142, 129–135. [Google Scholar] [CrossRef]
- Fernandes, J.L.; Pinheiro, C.I.C.; Oliveira, N.M.C.; Inverno, J.; Ribeiro, F.R. Model Development and Validation of an Industrial UOP Fluid Catalytic Cracking Unit with a High-Efficiency Regenerator. Ind. Eng. Chem. Res. 2008, 47, 850–866. [Google Scholar] [CrossRef]
- Xu, G.; Kato, K. Hydrodynamic equivalent diameter for clusters in heterogeneous gas–solid flow. Chem. Eng. Sci. 1999, 54, 1837–1847. [Google Scholar] [CrossRef]
- Fernandes, J.L.; Pinheiro, C.I.C.; Oliveira, N.; Ribeiro, F.R. Modeling and simulation of an operating industrial fluidized catalytic cracking (FCC) riser. In Proceedings of the 2nd Mercosur Congress on Chemical Engineering and 4th Mercosur Congress on Process Systems Engineering, Rio de Janeiro, Brazil, 14–18 August 2005; pp. 1–4. [Google Scholar]
- Nguyen, T.T.B.; Mitra, S.; Pareek, V.; Joshi, J.B.; Evans, G. Comparison of vaporization models for feed droplet in fluid catalytic cracking risers. Chem. Eng. Res. Des. 2015, 101, 82–97. [Google Scholar] [CrossRef]
- Ali, H.; Rohani, S.; Corriou, J.-P. Modelling and Control of a Riser Type Fluid Catalytic Cracking (FCC) Unit. Chem. Eng. Res. Des. 1997, 75, 401–412. [Google Scholar] [CrossRef]
- Du, B.; Warsito, W.; Fan, L.-S. Flow dynamics of gas-solid fluidized beds with evaporative liquid injection. China Particuology 2006, 4, 1–8. [Google Scholar] [CrossRef]
- Gehrke, S.; Wirth, K.E. Evaporating liquid in a high-density riser. In Proceedings of the International Congress on Particle Technology, Nuremberg, Germany, 27–29 March 2007. [Google Scholar]
- Newton, D.; Fiorentino, M.; Smith, G.B. The application of X-ray imaging to the developments of fluidized bed processes. Powder Technol. 2001, 120, 70–75. [Google Scholar] [CrossRef]
- Bruhns, S.; Werther, J. An investigation of the mechanism of liquid injection into fluidized beds. AIChE J. 2005, 51, 766–775. [Google Scholar] [CrossRef]
- Ahmadi Motlagh, A.H.; Pougatch, K.; Maturi, A.; Salcudean, M.; Grace, J.R.; Grecov, D.; McMillan, J. CFD Study of Wet Agglomerate Growth and Breakage in a Fluidized Bed Containing Hot Silica Sand Particles with Evaporative Liquid Injection. Ind. Eng. Chem. Res. 2019, 58, 4396–4411. [Google Scholar] [CrossRef]
- Ahmadi Motlagh, A.H.; Grace, J.R.; Briens, C.; Berruti, F.; Farkhondehkavaki, M.; Hamidi, M. Experimental analysis of volatile liquid injection into a fluidized bed. Particuology 2017, 34, 39–47. [Google Scholar] [CrossRef]
- Voorhies, A. Carbon Formation in Catalytic Cracking. Ind. Eng. Chem. 1945, 37, 318–322. [Google Scholar] [CrossRef]
- Fernandes, J.L.; Verstraete, J.J.; Pinheiro, C.I.C.; Oliveira, N.M.C.; Ribeiro, F.R. Dynamic modelling of an industrial R2R FCC unit. Chem. Eng. Sci. 2007, 62, 1184–1198. [Google Scholar] [CrossRef]
- Takatsuka, T.; Sato, S.; Morimoto, Y.; Hashimoto, H. A reaction model for fluidized-bed catalytic cracking of residual oil. Int. Chem. Eng. 1987, 27, 107–116. [Google Scholar]
- Souza, J.A.; Vargas, J.V.C.; Von Meien, O.F.; Martignoni, W.; Amico, S.C. A two-dimensional model for simulation, control, and optimization of FCC risers. AIChE J. 2006, 52, 1895–1905. [Google Scholar] [CrossRef]
- Souza, J.A.; Vargas, J.V.C.; Von Meien, O.F.; Martignoni, W.P. Modeling and simulation of industrial fcc risers. Therm. Eng. 2007, 6, 19–25. [Google Scholar] [CrossRef]
- Petrobras Six. Riser Improvement Project; Internal Report; Springer: São Mateus do Sul, Brazil, 2001. (In Portuguese) [Google Scholar]
- Patience, G.S.; Chaouki, J.; Berruti, F.; Wong, R. Scaling considerations for circulating fluidized bed risers. Powder Technol. 1992, 72, 31–37. [Google Scholar] [CrossRef]
- Hernández-Barajas, J.R.; Vázquez-Román, R.; Félix-Flores, M.G. A comprehensive estimation of kinetic parameters in lumped catalytic cracking reaction models. Fuel 2009, 88, 169–178. [Google Scholar] [CrossRef]
- Gupta, P.L.; Gupta, R.C. The monotonicity of the reliability measures of the beta distribution. Appl. Math. Lett. 2000, 13, 5–9. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Jiang, H.; Chu, J.; Zhou, J.; Shao, S. Modeling fluid catalytic cracking risers with special pseudo-components. Chem. Eng. Sci. 2013, 102, 87–98. [Google Scholar] [CrossRef]
- Arya, D.; Gupta, R.K. Simulation Studies on Variable Cluster Size in FCC Riser Reactor. Part. Sci. Technol. 2014, 32, 144–150. [Google Scholar] [CrossRef]
- Boum, A.; Corriou, J.P.; Latifi, A. Comparison of model predictive control strategies for a fluidized catalytic cracker. Int. J. Eng. Technol. 2017, 6, 181–190. [Google Scholar] [CrossRef][Green Version]
- Lee, E.; Groves, F.R., Jr. Mathematical model of the fluidized bed catalytic cracking plant. Trans. Soc. Comput. Simul. Int. 1985, 2, 219–236. [Google Scholar]
- Li, Y.; Chu, J.; Zhang, J. A new generic reaction for modeling fluid catalytic cracking risers. Chin. J. Chem. Eng. 2017, 25, 1449–1460. [Google Scholar] [CrossRef]
- Chen, Z.; Feng, S.; Zhang, L.; Wang, G.; Shi, Q.; Xu, Z.; Zhao, S.; Xu, C. Molecular-level kinetic modeling of heavy oil fluid catalytic cracking process based on hybrid structural unit and bond-electron matrix. AIChE J. 2020, 67, e17027. [Google Scholar] [CrossRef]
- He, S.; Lucio-Vega, J.; Zhang, L.; Shi, Q.; Horton, S.R.; Al-Khattaf, S.; Al-Jundi, I.; Elmutasim, O.; Zhao, S.; Klein, M.T. Integrating Visualization Methods with Chemical Kinetics Model Solution and Editing Tools. Energy Fuels 2017, 31, 9881–9889. [Google Scholar] [CrossRef]
- Chen, Z.; Feng, S.; Zhang, L.; Shi, Q.; Xu, Z.; Zhao, S.; Xu, C. Molecular-level kinetic modelling of fluid catalytic cracking slurry oil hydrotreating. Chem. Eng. Sci. 2019, 195, 619–630. [Google Scholar] [CrossRef]
- Zhu, C.; Jun, Y.; Patel, R.; Wang, D.; Ho, T.C. Interactions of flow and reaction in fluid catalytic cracking risers. AIChE J. 2010, 57, 3122–3131. [Google Scholar] [CrossRef]
- Shah, Y.T.; Huling, G.P.; Paraskos, J.A.; McKinney, J.D. A Kinematic Model for an Adiabatic Transfer Line Catalytic Cracking Reactor. Ind. Eng. Chem. Process. Des. Dev. 1977, 16, 89–94. [Google Scholar] [CrossRef]
- Shi, J.; Wang, Y.; Yang, W.; Tang, Y.; Xie, Z. Recent advances of pore system construction in zeolite-catalyzed chemical industry processes. Chem. Soc. Rev. 2015, 44, 8877–8903. [Google Scholar] [CrossRef] [PubMed]
- García-Dopico, M.; García, A.; Santos Garcíac, A. Modelling fluidized catalytic cracking unit stripper efficiency. Chem. Ind. Chem. Eng. Q. 2015, 21, 95–105. [Google Scholar] [CrossRef]
- García-Dopico, M.; García, A.; Garcíac, A.S. Modelling coke formation and deactivation in a FCCU. Appl. Catal. A Gen. 2006, 303, 245–250. [Google Scholar] [CrossRef]
| Review | Aspect of FCC Modelling Covered/Reviewed |
|---|---|
| Grace [31] |
|
| Berruti et al. [32] |
|
| Godfroy et al. [35] |
|
| Gupta et al. [36] |
|
| Pinheiro et al. [13] |
|
| Shah et al. [7] |
|
| Madhusudana Rao et al. [38] |
|
| Feed | Products | ||
|---|---|---|---|
| Elemental analysis | Distillation boiling point cuts | ||
| C (wt%) | 86.60 | Dry gas ( (wt%) | 4 |
| H (wt%) | 12 | LPG ( (wt%) | 4 |
| N (wt%) | 0.23 | Gasoline ( (wt%) | 27 |
| S (wt%) | 1.17 | Light cycle oil () (wt%) | 28 |
| PONA Composition | Heavy cycle oil () (wt%) | 18 | |
| Paraffins (wt%) | 62.3 | Coke (wt%) | 9 |
| Naphthenes (wt%) | 29.3 | ||
| Aromatics (wt%) | 8.5 | ||
| Sulphur containing (wt%) | 5.5 | ||
| Distillation boiling point cuts | |||
| Gasoline (wt%) | 1.5 | ||
| Diesel () | 3 | ||
| Diesel (wt%) | 95.5 | ||
| Physical Properties | |||
| Density () | 0.93 | ||
| American Petroleum Institute (API) gravity (°API) | 21.1 | ||
| Viscosity (cst at 100 °C) | 8.6 | ||
| Mw (g/mol) | 405.3 | ||
| HHV (Mj/kg) | 42 | ||
| 4—Lump Parameters of Ancheyta-Juarez [80] | |||
| Transformation | |||
| Units | Value | ||
| Deactivation () | |||
| 6—Lump Parameters of Yakubu [85] | |||
| Parameter | ||
|---|---|---|
| Model | Feed and Product Characterisation | Reaction Chemistry | Main Features |
|---|---|---|---|
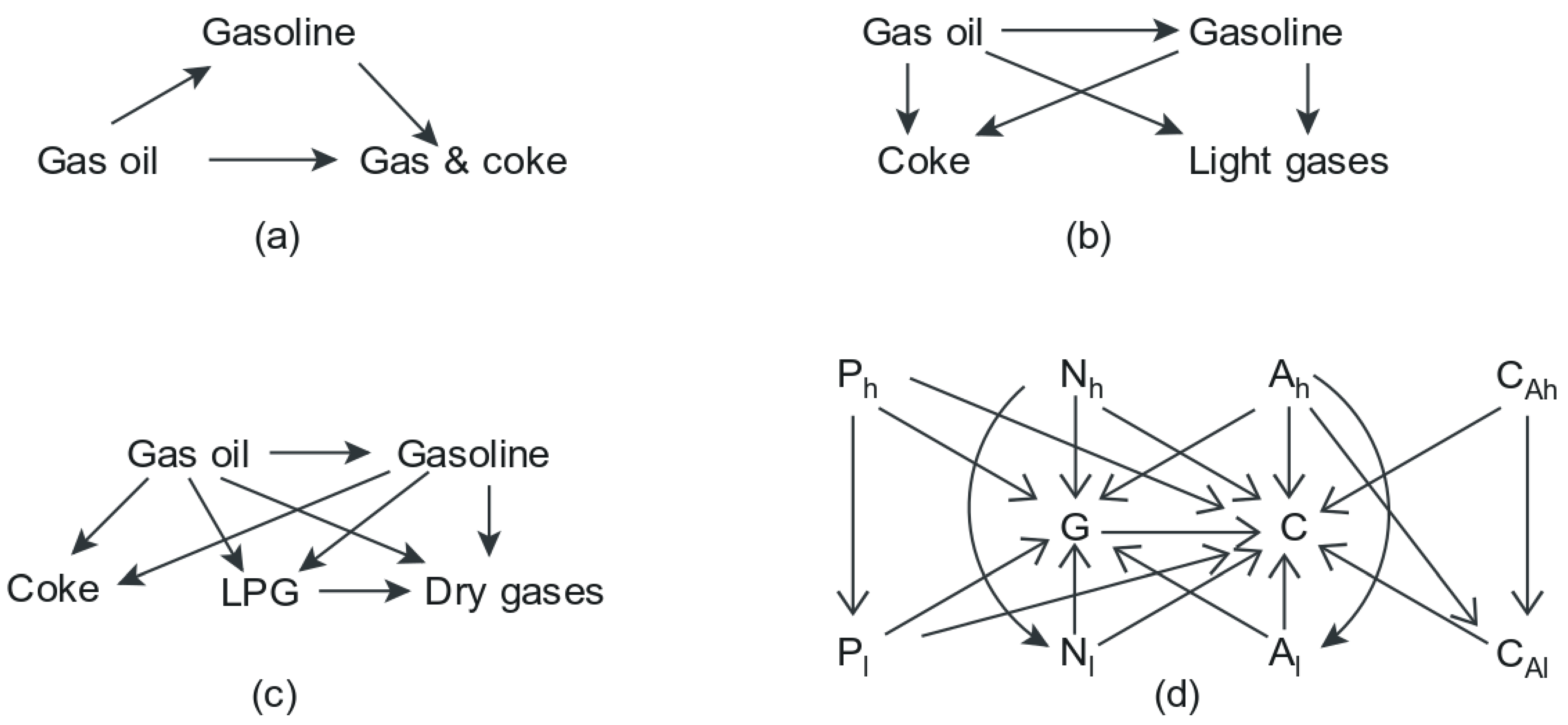
| Discrete lumping | Components of the reaction mixture grouped into lumps based on boiling point range or carbon number and molecular structure. | Reactions considered as one-to-one transformations between lumps, usually higher boiling point lumps to lower boiling point lumps, although the connections between the lumps have usually varied between different researchers. This approach is empirical and not representative of the carbenium ion chemistry that is known to govern cracking reactions. | Model parameters are the frequency factors and activation energies of the lump-to-lump transformations. These models are simple and less computationally demanding because the large complex reaction mixture has been reduced to a small number of lumps. |
| Continuous Lumping | Reaction mixture thought of as a continuous mixture of an infinite number of molecules, which are characterised by normalised TBP. | Properties of individual components in the mixture such as reactivity can be indexed via normalised boiling point. The individual components in the mixture are assumed to all be involved in the same type of reaction, i.e., all assumed to be undergoing fragmentation or cracking; however, it is known that other types of reactions are also taking place in the riser due to carbenium ion chemistry (e.g., isomerisation, alkylation etc.) | The model parameters are the parameters associated with the relationship between reactivity and normalised TBP (e.g., & ) and parameters associated with the yield function. |
| Single event kinetics | Molecular reconstruction methods | A computer algorithm creates a reaction network of elementary steps between the molecules in the reaction mixture based on carbenium ion theory. The algorithm uses the numerical representation of the reacting species together with the reaction rules to create a large network consisting of all intermediate carbenium ions. | The parameters are the frequency factors and activation energies of the specific elementary steps. Very detailed feed characterisation is required to determine the values of the kinetic parameters which makes this model very time consuming. However, because of the fundamental nature of the reaction chemistry, the parameters determined are intrinsic and will extrapolate well for changing feeds. |
| TOS | Weekman [15] model parameters | Jacob et al. [17] are model parameters | |
| COC | Farag et al. [141] is a model parameter | Krambeck [142] is a model parameter | Pitault et al. [143] are model parameters |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selalame, T.W.; Patel, R.; Mujtaba, I.M.; John, Y.M. A Review of Modelling of the FCC Unit–Part I: The Riser. Energies 2022, 15, 308. https://doi.org/10.3390/en15010308
Selalame TW, Patel R, Mujtaba IM, John YM. A Review of Modelling of the FCC Unit–Part I: The Riser. Energies. 2022; 15(1):308. https://doi.org/10.3390/en15010308
Chicago/Turabian StyleSelalame, Thabang W., Raj Patel, Iqbal M. Mujtaba, and Yakubu M. John. 2022. "A Review of Modelling of the FCC Unit–Part I: The Riser" Energies 15, no. 1: 308. https://doi.org/10.3390/en15010308
APA StyleSelalame, T. W., Patel, R., Mujtaba, I. M., & John, Y. M. (2022). A Review of Modelling of the FCC Unit–Part I: The Riser. Energies, 15(1), 308. https://doi.org/10.3390/en15010308








