Gas Hold-Up and Mass Transfer in a Vessel with an Unsteady Rotating Concave Blade Impeller
Abstract
:1. Introduction
2. Experimental Set-Up
2.1. Methods
2.2. States of Gas Dispersion
3. Results
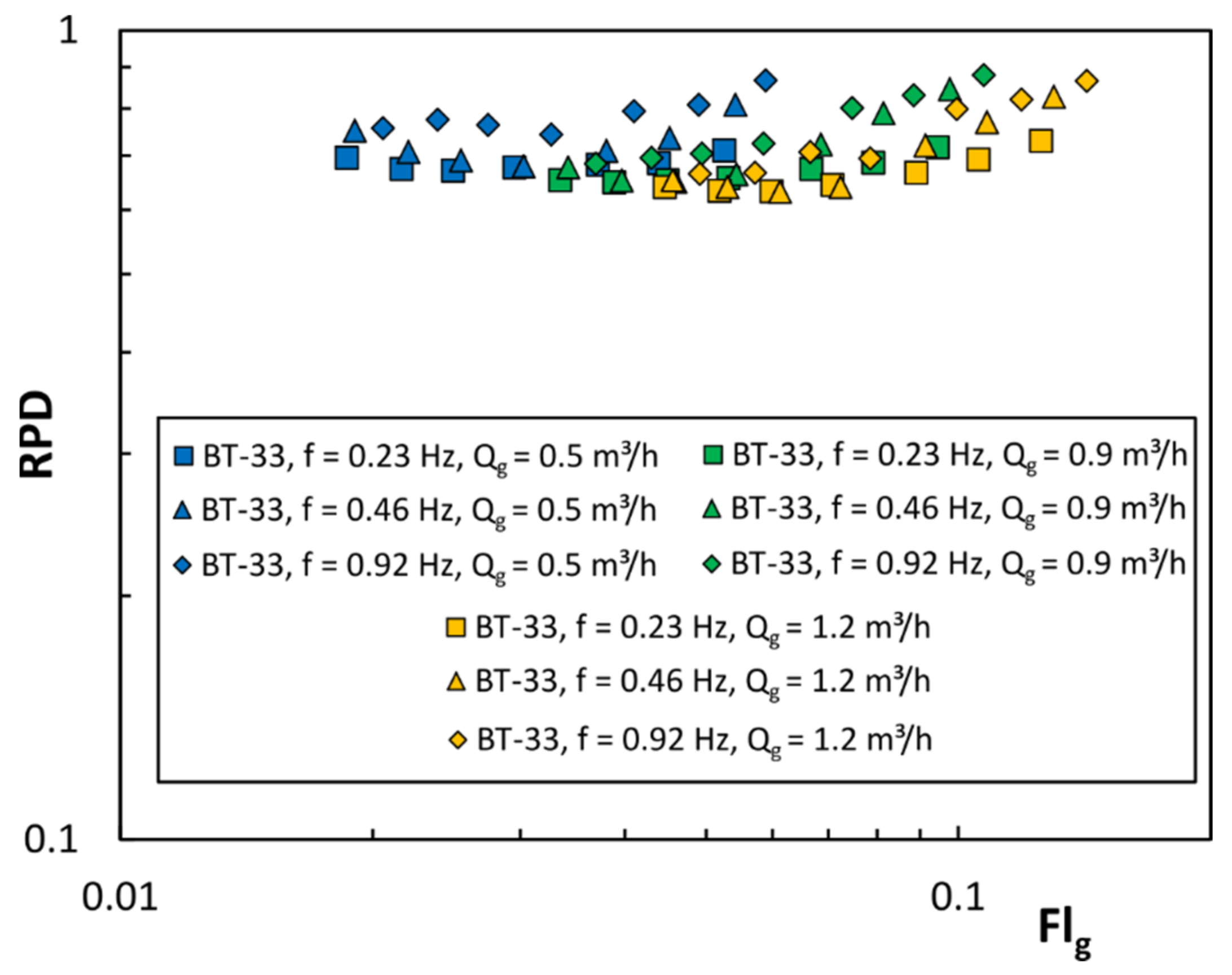
3.1. Power Requirements
3.1.1. Liquid Mixing
3.1.2. Gas-Liquid Mixing
3.2. Gas Hold-Up
3.3. Volumetric Mass Transfer Coefficient KLa
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| a | interfacial area per volume unit, (m2/m3) |
| C | impeller bottom clearance, (m) |
| c | oxygen concentration, (mg/L) |
| CD | drag coefficient |
| CI | inertia coefficient |
| D | impeller diameter, (m) |
| DL | diffusion coefficient in the liquid phase |
| Ds | ring sparger diameter, (m) |
| DV | vessel diameter, (m) |
| Flg | gas flow number, Flg = Qg/(ND3ρ) |
| f | oscillation frequency, (Hz) |
| HL | liquid height, (m) |
| KC | Keaulegan-Carpenter number |
| kLa | volumetric mass transfer coefficient, (s−1) |
| N | impeller speed, (s−1) |
| P | mixing power, (W) |
| Po | power number, Po = P/(N3D5ρ) |
| Q | flow rate, (m3s−1) |
| Re | Reynolds number, Re = ND2ρ/η |
| RPD | relative power demand, RPD = Pg/Pu |
| T | temperature, (°C) |
| TS | torque, (Nm) |
| t | time, (s) |
| V | volume, (m3) |
| v | velocity, (m/s) |
| Greek letters | |
| εg | gas hold-up |
| ρ | density, (kg m−3) |
| σ | interfacial tension, (Nm−1) |
| ω | angular frequency, (rad s−1) |
| Subscripts | |
| max | maximum |
| min | minimum |
| t | instantaneous |
| * | equilibrium |
| 0 | initial |
| g | gassed conditions |
| u | ungassed conditions |
| c | continuous phase |
References
- Ni, X.; Mackley, M.R.; Harvey, A.P.; Stonestreet, P.; Baird, M.H.I.; Rama Rao, N.V. Mixing through oscillations and pulsations—a guide to achieving process enhancements in the chemical and process industries. Chem. Eng. Res. Des. 2003, 81, 373–383. [Google Scholar] [CrossRef]
- Ni, X.; Gao, S. Scale-up correlation for mass transfer coefficients in pulsed baffled reactors. Chem. Eng. J. Biochem. Eng. J. 1996, 63, 157–166. [Google Scholar] [CrossRef]
- Ni, X.; Gao, S.; Cumming, R.H.; Pritchard, D.W. A comparative study of mass transfer in yeast for a batch pulsed baffled bioreactor and a stirred tank fermenter. Chem. Eng. Sci. 1995, 50, 2127–2136. [Google Scholar] [CrossRef]
- Yoshida, M.; Taguchi, Y.; Yamagiwa, K.; Ohkawa, A.; Abe, M.; Tezura, S.; Shimazaki, M. Design and operation of unbaffled aerated agitated vessels with unsteadily forward-reverse rotating impellers handling viscous Newtonian liquids. J. Chem. Technol. Biotechnol. 2003, 78, 474–483. [Google Scholar] [CrossRef]
- Yoshida, M.; Kimura, A.; Yoneyama, A.; Tezura, S. Design and operation of unbaffled vessels agitated with an unsteadily forward–reverse rotating impeller handling solid–liquid dispersions. Asia-Pac. J. Chem. Eng. 2012, 7, 572–580. [Google Scholar] [CrossRef]
- Yoshida, M.; Watanabe, M.; Yamagiwa, K.; Ohkawa, A.; Abe, M.; Tezura, S.; Shimazaki, M. Behaviour of gas-liquid mixtures in an unbaffled reactor with unsteadily forward-reverse rotating impellers. J. Chem. Technol. Biotechnol. 2002, 77, 678–684. [Google Scholar] [CrossRef]
- Yoshida, M.; Akiho, M.; Nonaka, H.; Yamagiwa, K.; Ohkawa, A.; Tezura, S. Mixing and mass transfer characteristics of an unbaffled aerated agitation vessel with unsteadily forward-reverse rotating multiple impellers. Lat. Am. Appl. Res. 2005, 35, 37–42. [Google Scholar]
- Woziwodzki, S. Unsteady mixing characteristics in a vessel with forward-reverse rotating impeller. Chem. Eng. Technol. 2011, 34, 767–774. [Google Scholar] [CrossRef]
- Takahashi, K.; Takahata, Y.; Kurisaka, K.; Sekine, H. Mixing performance experiments in an agitated vessel equipped with a pitched paddle subjected to unsteady agitation. J. Chem. Eng. Jpn. 2011, 44, 852–858. [Google Scholar] [CrossRef]
- Kato, Y.; Tada, Y.; Ban, M.; Nagatsu, Y.; Iwata, S.; Yanagimoto, K. Improvement of mixing efficiencies of conventional impeller with unsteady speed in an impeller revolution. J. Chem. Eng. Jpn. 2005, 38, 688–691. [Google Scholar] [CrossRef] [Green Version]
- Yoshida, M.; Shigeyama, M.; Hiura, T.; Yamagiwa, K.; Ohkawa, A.; Tezura, S. Liquid-Phase Mixing in an Unbaffled Agitated Vessel with an Unsteady Forward-Reverse Rotating Impeller. Asia-Pac. J. Chem. Eng. 2007, 2, 659–664. [Google Scholar] [CrossRef]
- Yoshida, M.; Wakura, Y.; Yamagiwa, K.; Ohkawa, A.; Tezura, S. Liquid Flow Circulating within an Unbaffled Vessel Agitated with an Unsteady Forward-Reverse Rotating Impeller. J. Chem. Technol. Biotechnol. 2010, 85, 1017–1022. [Google Scholar] [CrossRef]
- Yoshida, M.; Taguchi, Y.; Yamagiwa, K.; Ohkawa, A.; Abe, M.; Tezura, S.; Shimazaki, M. Mixing Characteristics of Liquid Phase in an Unbaffled Vessel Agitated by Unsteadily Forward-Reverse Rotating Multiple Impellers. Lat. Am. Appl. Res. 2004, 34, 35–40. [Google Scholar]
- Yoshida, M.; Nagai, Y.; Yamagiwa, K.; Ohkawa, A.; Tezura, S. Turbulent and Laminar Mixings in an Unbaffled Agitated Vessel with an Unsteadily Angularly Oscillating Impeller. Ind. Eng. Chem. Res. 2009, 48, 1665–1672. [Google Scholar] [CrossRef]
- Woziwodzki, S. Mixing of Viscous Newtonian Fluids in a Vessel Equipped with Steady and Unsteady Rotating Dual-Turbine Impellers. Chem. Eng. Res. Des. 2014, 92, 435–446. [Google Scholar] [CrossRef]
- Woziwodzki, S.; Broniarz-Press, L. Mixing of Shear-Thinning Fluid with Yield Stress in a Vessel with Unsteadily Rotating Impeller. In Proceedings of the 14th European Conference on Mixing, Warsaw, Poland, 10 September 2012; pp. 515–521. [Google Scholar]
- Middleton, J.C.; Smith, J.M. Gas-liquid mixing in turbulent systems. In Handbook of Industrial Mixing. Science and Practice; Paul, E.L., Atiemo-Obeng, V., Kresta, S.M., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2004; pp. 585–635. [Google Scholar]
- Yoshida, M.; Kitamura, A.; Yamagiwa, K.; Ohkawa, A. Gas hold-up and volumetric oxygen transfer coefficient in an aerated agitated vessel without baffles having forward-reverse rotating impellers. Can. J. Chem. Eng. 1996, 74, 31–39. [Google Scholar] [CrossRef]
- Yoshida, M.; Yamagiwa, K.; Ohkawa, A.; Takahashi, K.; Shimazaki, M.; Abe, M. Torque of drive shaft with unsteadily rotating impellers in an unbaffled aerated agitation vessel. Mater. Technol. 1999, 17, 19–31. [Google Scholar]
- Yoshida, M.; Ito, A.; Yamagiwa, K.; Ohkawa, A.; Abe, M.; Tezura, S.; Shimazaki, M. Power characteristics of unsteadily forward-reverse rotating impellers in an unbaffled aerated agitated vessel. J. Chem. Technol. Biotechnol. 2001, 76, 383–392. [Google Scholar] [CrossRef]
- Yoshida, M.; Yamagiwa, K.; Ito, A.; Ohkawa, A.; Abe, M.; Tezura, S.; Shimazaki, M. Flow and mass transfer in aerated viscous Newtonian liquids in an unbaffled agitated vessel having alternating forward-reverse rotating impellers. J. Chem. Technol. Biotechnol. 2001, 76, 1185–1193. [Google Scholar] [CrossRef]
- Woziwodzki, S.; Broniarz-Press, L. Power characteristics of unsteadily rotating rushton turbine in aerated vessel. Tech. Trans. 2014, 2-Ch, 155–164. [Google Scholar]
- Frankiewicz, S.; Woziwodzki, S. Effect of Blade Shape on Unsteady Mixing of Gas-Liquid Systems. In Practical Aspects of Chemical Engineering; Lecture Notes on Multidisciplinary Industrial Engineering; Springer: Cham, Switzerland, 2018; pp. 127–136. ISBN 978-3-319-73977-9. [Google Scholar]
- Frankiewicz, S.S.; Woziwodzki, S. Gas-Liquid Mixing in an Unbaffled Vessel with a Forward-Reverse Rotating Scaba Impeller. In Practical Aspects of Chemical Engineering; Ochowiak, M., Woziwodzki, S., Mitkowski, P.T., Doligalski, M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 79–88. ISBN 978-3-030-39867-5. [Google Scholar]
- Woziwodzki, S. Application of Morison Equation in Unsteady Mixing Characteristics. In Practical Aspects of Chemical Engineering; Ochowiak, M., Woziwodzki, S., Mitkowski, P.T., Doligalski, M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 491–499. ISBN 978-3-030-39867-5. [Google Scholar]
- Bouaifi, M.; Roustan, M. Bubble size and mass transfer coefficients in dual-impeller agitated reactors. Can. J. Chem. Eng. 1998, 76, 390–397. [Google Scholar] [CrossRef]
- Kiełbus-Rąpała, A.; Karcz, J. Mass transfer in multiphase mechanically agitated systems. In Mass Transfer in Multiphase Systems and Its Applications; El-Amin, M., Ed.; InTech: London, UK, 2011; ISBN 978-953-307-215-9. [Google Scholar]
- Van’t Riet, K. Review of measuring methods and results in nonviscous gas-liquid mass transfer in stirred vessels. Ind. Eng. Chem. Process. Des. Dev. 1979, 18, 357–364. [Google Scholar] [CrossRef]
- Bakker, A. Hydrodynamics of Stirred Gas-Liquid Dispersions; Technische Univesiteit Delft: Delft, The Netherlands, 1992. [Google Scholar]
- Chapman, C.M.; Nienow, A.W.; Cooke, M.; Middleton, J.C. Particle-gas-liquid mixing in stirred vessels. Part II: Gas-liquid mixing. Chem. Eng. Res. Des. 1983, 61, 82–95. [Google Scholar]
- Zheng, Z.; Sun, D.; Li, J.; Zhan, X.; Gao, M. Improving oxygen transfer efficiency by developing a novel energy-saving impeller. Chem. Eng. Res. Des. 2018, 130, 199–207. [Google Scholar] [CrossRef]
- Sarpkaya, T. Wave Forces on Offshore Structures; Cambridge University Press: Cambridge, NY, USA, 2010. [Google Scholar]
- Jesus, S.S.; Santana, A.; Filho, R.M. Hydrodynamic and mass transfer study in a mechanically stirred hybrid airlift bioreactor based on impeller type. Int. J. Chem. Eng. Appl. 2014, 5, 41–45. [Google Scholar] [CrossRef] [Green Version]
- Vasconcelos, J.M.T.; Orvalho, S.C.P.; Rodriguez, A.M.A.F.; Alvez, S.S. Effect of blade shape on the performance of six-bladed disk turbine impellers. Ind. Eng. Chem. Res. 2000, 39, 203–213. [Google Scholar] [CrossRef]
- Woziwodzki, S.; Broniarz-Press, L.; Radecki, R. Mieszanie układów ciecz-gaz w mieszalniku z mieszadłem A310 wykonującym ruch nieustalony. Inż. Apar. Chem. 2015, 54, 364–365. [Google Scholar]
- Higbie, R. The Rate of Absorption of a Pure Gas into a Still Liquid during Short Periods of Exposure. Trans. AIChE 1935, 31, 365–389. [Google Scholar]
- Calderbank, P.H. Physical rate processes in industrial fermentation. Part I: The interfacial area in gas-liquid contacting with mechanical agitation. Chem. Eng. Res. Des. 1958, 36, 443–463. [Google Scholar]
- Kolmogorov, A.N. On the Disintegration of Drops in a Turbulent Flow. Dokl. Akad. Nauk SSSR 1949, 66, 825–828. [Google Scholar]
- Martín, M.; Montes, F.J.; Galán, M.A. Physical explanation of the empirical coefficients of gas-liquid mass transfer equations. Chem. Eng. Sci. 2009, 64, 410–425. [Google Scholar] [CrossRef]







| Author | System | Impeller | Course | Scope |
|---|---|---|---|---|
| Yoshida et al. [18] | air-water | delta AJITER | sinusoidal | gas hold-up mass transfer |
| Yoshida et al. [19] | air-water | delta AJITER | sinusoidal | power requirements gas hold-up mass transfer mixing time |
| Yoshida et al. [20,21] | air-millet jelly | delta AJITER | sinusoidal | power requirements gas hold-up mass transfer |
| Yoshida et al. [6,7] | air-water | Rushton turbine delta | sinusoidal | power requirements mixing time |
| Yoshida et al. [4] | air-ethanol air-glycerol air-millet jelly | delta AJITER | sinusoidal | power requirements gas hold-up mass transfer |
| Woziwodzki and Broniarz-Press [22] | air-water | Ruhton turbine PBT | triangle with/without change of direction of rotation | power requirements |
| Frankiewicz and Woziwodzki [23,24] | air-water | BT-6, BT-4, BT-4E Scaba 6SRGT | triangle | power requirements |
| Impeller | C1 | C2 | C3 | C4 | R2 |
|---|---|---|---|---|---|
| BT-33 | 0.432 | 0.167 | 0.621 | −0.108 | 0.729 |
| BT-4 | 0.156 | 0.136 | 0.412 | −0.029 | 0.931 |
| BT-6 | 0.204 | 0.111 | 0.439 | −0.035 | 0.918 |
| Impeller | C5 | C6 | C7 | R2 |
|---|---|---|---|---|
| BT-33, BT-4, BT-6, RT | 0.02 | 0.408 | 0.431 | 0.941 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frankiewicz, S.; Woziwodzki, S. Gas Hold-Up and Mass Transfer in a Vessel with an Unsteady Rotating Concave Blade Impeller. Energies 2022, 15, 346. https://doi.org/10.3390/en15010346
Frankiewicz S, Woziwodzki S. Gas Hold-Up and Mass Transfer in a Vessel with an Unsteady Rotating Concave Blade Impeller. Energies. 2022; 15(1):346. https://doi.org/10.3390/en15010346
Chicago/Turabian StyleFrankiewicz, Sebastian, and Szymon Woziwodzki. 2022. "Gas Hold-Up and Mass Transfer in a Vessel with an Unsteady Rotating Concave Blade Impeller" Energies 15, no. 1: 346. https://doi.org/10.3390/en15010346





